Estimating the Probability of Clonal Relatedness of Pairs of Tumors in Cancer Patients

Abstract

Next generation sequencing panels are being used increasingly in cancer research to study tumor evolution. A specific statistical challenge is to compare the mutational profiles in different tumors from a patient to determine the strength of evidence that the tumors are clonally related, i.e. derived from a single, founder clonal cell. The presence of identical mutations in each tumor provides evidence of clonal relatedness, although the strength of evidence from a match is related to how commonly the mutation is seen in the tumor type under investigation. This evidence must be weighed against the evidence in favor of independent tumors from non-matching mutations. In this article we frame this challenge in the context of diagnosis using a novel random effects model. In this way, by analyzing a set of tumor pairs, we can estimate the proportion of cases that are clonally related in the sample as well as the individual diagnostic probabilities for each case. The method is illustrated using data from a study to determine the clonal relationship of lobular carcinoma in situ with subsequent invasive breast cancers where each tumor in the pair was subjected to whole exome sequencing. The statistical properties of the method are evaluated using simulations, demonstrating that the key model parameters are estimated with only modest bias in small samples in most configurations.

1. Introduction

In recent years there have been increasing numbers of studies evaluating the clonal relatedness of distinct tumors in the same patient to determine whether the tumors arise from a common ancestral cell or if they developed entirely independently. Examples include studies that compared patterns of losses of heterozygosity (e.g. Imyanitov et al. 2002) and studies involving comparisons of genome-wide copy number arrays (e.g. Bollet et al. 2008). Clonality testing of this nature seeks to determine if the tumors share somatic mutations or copy number changes, providing evidence that the tumors arose from the same precursor, clonal cell. The technology for conducting these investigations has changed as genetic technology has evolved, from studies of a few markers of loss of heterozygosity to genome-wide studies of copy number profiling to, more recently, comparisons of mutational profiles from next generation sequencing. Based on such data, the determination of clonal relatedness is fundamentally statistical since many of the somatic changes in the tumors may have occurred after the tumors have evolved separately, so that the somatic fingerprints of the tumors may be quite different even if the tumors are truly clonal. Our group has developed statistical tests for clonal relatedness for use in various settings, including studies comparing patterns of losses of heterozygosity and genome-wide copy number changes (Begg et al. 2007; Ostrovnaya et al. 2010a,b).

Ostrovnaya et al. (2015) recently proposed a statistical test for clonal relatedness based on a comparison of the patterns of mutations observed in the two tumors from a sequencing panel. A likelihood ratio test was constructed, conditioned on the observed mutations in the two tumors being compared, taking into account the distinct, and widely varying marginal probabilities of the specific mutations. These marginal probabilities are important since a shared mutation that is very rare, i.e. where the marginal probability of the mutation is very small, provides much stronger evidence that the tumors are related than a shared mutation at a common locus, where independent occurrences of the same mutation in the tumors are more likely. The test was constructed as a classical significance test, where the null hypothesis is that the tumors are independent. An important practical characteristic of the test is that it can be applied to stand-alone cases, without the need for a larger sample of cases, as long as we have information on the marginal probability of occurrence of each specific observed mutation. However, an important drawback of using significance testing in this way is that, while the test can provide strong evidence against the null, i.e. in favor of clonal relatedness, it does not capture the strength of evidence in favor of the null hypothesis, i.e. the hypothesis that the tumors are independent. In particular, if no shared mutations are observed, there is no evidence for clonality. This is an important issue, since absence of detected matches does not define independent tumors. Clonal tumors must possess some matching somatic events, but the sequencing panel may simply not cover the genes in which the matches have occurred. Logic suggests that the more non-matching events observed the stronger the evidence that the tumors are independent, yet the p-value of the test is always 1 when no matches are observed, regardless of how many non-shared mutations are observed. The goal of this article is to propose a model quantifying the evidence of clonal relatedness for every case, with or without observed shared mutations. We use the entire sample of cases to estimate population parameters that permit us to assess the strength of evidence for and against clonal relatedness for each individual case. The proposed approach involves using a random effects model to capture the variation in the mutational profiles in pairs of clonally related tumors, and using this information to estimate the probabilities of clonality for each individual case. The statistical properties of the method are examined using simulations.

The method is illustrated using a recently published study that examined the clonal relatedness of pre-malignant lobular carcinoma in situ (LCIS) with subsequent invasive breast cancers (Begg et al. 2016). The tumors in the study were profiled using exome sequencing. We emphasize that although exome sequencing searches for somatic mutations in the coding regions of all genes, matching mutations could exist in the non-coding regions of the genome, or could be gains or losses of segments of an allele, i.e. copy number changes. Consequently, absence of shared mutations in the exome does not guarantee that the tumors are independent. Our analysis is focused on the estimation of the overall proportion of cases that are truly clonal, and the diagnostic probabilities of each individual case.

2. Methods

2.1 Basic Formulation and Notation

We consider a sample consisting of n cases (j = 1,…,n) with each case having two anatomically distinct tumors. There are G potential genetic loci at which somatic mutations can occur. We note that typically G will be a very large number. It is difficult to define it precisely since more than one type of substitution can occur at each nucleotide and since there is an innumerable number of potential insertions and deletions. However, essentially all of the information regarding the classification of the case as clonal versus independent is contained in the somatic mutations that are actually observed to occur (Ostrovnaya et al. 2015). Consequently we can adopt an analysis that is conditioned on observed mutations and as a result precise definition of G is unnecessary. We therefore define {G_j} as the set of mutations observed in either or both of the two tumors of the j^th case. The marginal probabilities of these individual mutations are influential, as the probability of the same mutation being observed in two independent tumors decreases as the marginal probability decreases. We define {p_i} to be the known marginal probabilities of the mutations in the dataset, where i indexes the specific mutation.

For each case the observed mutations can be classified as either shared or private. A shared mutation is one that is present in both tumors while a private mutation is one that has been observed in only one of the tumors. Let A_j denote the set of observed mutations in the j^th case that are shared and let B_j be the set of private mutations. Thus G_j = A_j∪B_j.

The proposed method relies on a case-specific parameter, the clonality signal ξ_j This represents, in the context of the evolution of the tumors, the relative duration of the period in which the original clonal cell accumulated mutations, prior to the period where the two tumors evolved separately and accrued additional independent mutations (see Figure 1). Thus ξ_j represents the probability that an observed mutation occurred during the clonal phase as opposed to the independent phase of tumor development. For independent tumors, ξ_j= 0 It follows that for a case with a given clonality signal the probabilities of observing shared and private mutations at each locus are given by:-

Figure 1.

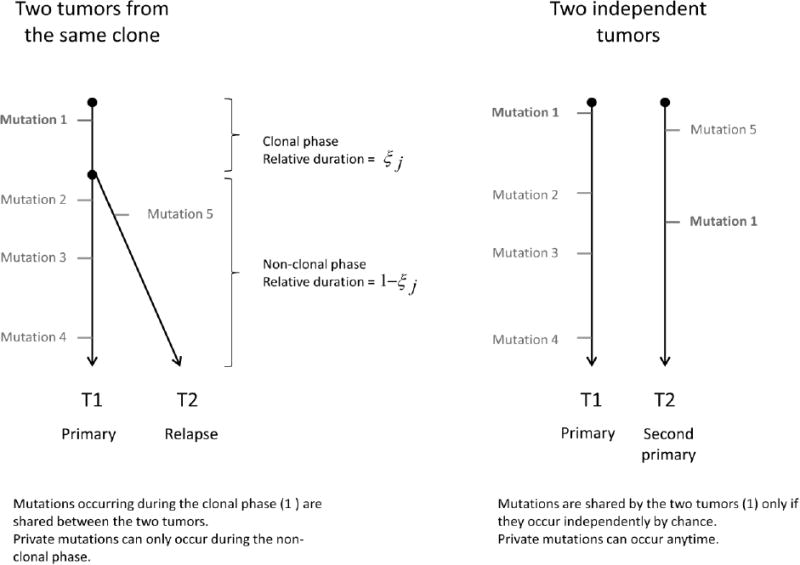
Schema of two tumors from the same clone versus two independent tumors.

$$\{\begin{array}{c}P(i\in A_j|{\xi }_j)={\xi }_j{p}_i+(1-{\xi }_j)p_i^2\\ P(i\in B_j|{\xi }_j)=2(1-{\xi }_j\left)p_i\right(1-p_i)\\ P(i\in G_j|{\xi }_j)={\xi }_j{p}_i+(1-{\xi }_j\left)p_i\right(2-p_i)\end{array}$$ (1)

We further define π to be the proportion of clonal cases in the population, i.e. the proportion of cases for which ξ_j>0. Finally, we denote by C_j the event {case j is clonal} and by C̄_j the event {case j is not clonal}. The primary goals of our analysis are to estimate π, and to determine the individual probabilities that the tumor pairs in each case are clonally related tumors. In our example involving breast cancer cases having both a pre-malignant LCIS lesion and an invasive tumor, π is the proportion of cases for which the LCIS is the precursor of the invasive tumor.

2.2 Parameter Estimation

Let Y_j= (A_j, B_j) denote the data from the j^th case. We use a likelihood conditional on the observed mutations. Let L_j(π,ξ_j) be the contribution to the conditional likelihood of an individual case, defined by:

$$L_j(\pi ,{\xi }_j)=\pi P\left(Y_j\right|{\xi }_j,C_j)+(1-\pi \left)P\right(Y_j{|\overline{C}}_j)$$

Where

$$P(Y_j|{\xi }_j,C_j)={{\prod }_{i\in G_j}\left\{\frac{{\xi }_j+(1-{\xi }_j)p_i}{{\xi }_j+(1-{\xi }_j)(2-p_i)}\right\}}^{I\left[i\in A_j\right]}{\left\{\frac{2(1-{\xi }_j)\left(1-p_i\right)}{{\xi }_j+(1-{\xi }_j)\left(2-p_i\right)}\right\}}^{I\left[i\in B_j\right]}$$

and

$$P\left(Y_j|{\overline{C}}_j\right)={\prod _{i\in G_j}\left(\frac{p_i}{2-p_i}\right)}^{I\left[i\in A_j\right]}{\left\{\frac{2\left(1-p_i\right)}{2-p_i}\right\}}^{I\left[i\in B_j\right]}$$

We consider the clonality signal ξ_j as a random effect with probability density g(ξ_j) We assume that ξ_j=0 with probability 1–π and that, with probability π, φ_j=– log (1 –ξ_j) follows a logN (μ, σ²) distribution. The corresponding density of the clonality signal is thus zero-inflated but has a flexible structure for modeling the positive random effects in the range 0<ξ_j≤1 It depends on μ and σ², corresponding to the mean and variance of φ_j on the log scale. Thus the parameter μ indicates the mean magnitude of the clonality signal and σ² characterizes the extent to which this varies from case to case, among cases that are truly clonal. We also explored the use of the Beta distribution, as discussed later in Section 4.

The marginal likelihood for the entire sample is obtained by integrating the individual contributions over the distribution of the random effects as follows:

$$L(\pi ,\mu ,\sigma )={\prod }_{j=1}^n{\int }_0^1{L}_j(\pi ,{\xi }_j)g({\xi }_j)d{\xi }_j$$ (2)

The model parameters π,μ and σ are estimated by maximizing the likelihood L(π, μ, σ). The integral in (2) is approximated using adaptive quadrature. The function is maximized using a Newton-like method (Byrd et al. 1995). The variance of the parameters is estimated from the Hessian matrix.

Finally, using the parameter estimates and the data from each individual case, we can obtain the diagnostic probability that the tumors of a given case are clonally related, i.e. P (C_j|Y_j). This probability can be estimated using Bayes formula:

$$P\left(C_j|Y_j\right)=\frac{\widehat{\pi }{\int }_0^{1}P\left(Y_j|{\xi }_j,C_j\right)g\left({\xi }_j\right)d{\xi }_j}{\widehat{\pi }{\int }_0^{1}P\left(Y_j|{\xi }_j,C_j\right)g\left({\xi }_j\right)d{\xi }_j+\left(1-\widehat{\pi }\right)P\left(Y_j{|\overline{C}}_j\right)}$$ (3)

3. Application: evaluation of LCIS as a precursor of invasive breast cancer

We illustrate the method using data from a recently published study that was designed to investigate the hypothesis that LCIS is a frequent precursor of invasive breast cancer, as opposed to merely a marker of increased risk, the prevailing hypothesis for the past 40 years (Begg et al. 2016). The study included cases with LCIS lesions, some of which also had ipsilateral invasive breast cancers. We focus on the 22 examples of invasive breast cancers for which exome sequencing data were available for both the invasive lesion and an index LCIS lesion. The mean number of mutations per tumor was 34 (range, 15 to 56).

The results are summarized in Table 1. Columns 2-4 display the numbers of mutations observed in each tumor and the numbers of these that were shared. Details of the individual mutations observed and their marginal probabilities of occurrence are supplied in Supplementary Table 1 of Begg et al. (2016). The marginal probabilities were estimated based on their observed relative frequencies in breast cancers in the Cancer Genome Atlas (Cancer Genome Atlas Network 2012) combined with our current study. Among the 22 studied pairs, 14 pairs (64%) had a probability of being clonal exceeding 50%, which we interpret as evidence favoring clonality from the whole-exome sequencing (identified by an asterisk in Table 1). These cases had at least one shared mutation. Using the methods from Section 2 the proportion of clonal cases in the population was estimated at 75% (95% confidence interval, 34-100%). The parameters of the normal distribution were estimated to be μ̂ = −2.26 and σ̂ = 1.47, representing a density function that is positively skewed, i.e. for the preponderance of clonal cases the clonality signal is considerably less than 0.5. In cases with at least one observed shared mutation, the estimated probabilities of clonal relatedness ranged from 0.87 to >0.99. The probabilities of clonal relatedness in cases with no observed shared mutations range from 0.31 to 0.38.

Table 1. Data and Diagnostic Probabilities.

Pair	Number of mutations observed			Probability Pair is Clonal	P-Value from the Hypothesis Test
	LCIS	Invasive	Shared
24a*	36	34	25	>0.99	<10-4
24b*	29	34	2	>0.99	4. 10-4
26	29	32	0	0.35	1
46a	46	15	0	0.35	1
46b	37	15	0	0.38	1
47a*	29	25	7	>0.99	<10-4
47b*	22	25	7	>0.99	<10-4
47c*	29	30	1	0.94	0.02
47d*	22	30	1	0.87	0.03
48a*	33	40	20	>0.99	<10-4
48b*	22	40	1	0.94	0.03
53a*	21	23	2	>0.99	2. 10-4
53b*	17	23	1	0.97	0.02
55*	31	36	6	>0.99	<10-4
68	44	33	0	0.31	1
69*	56	31	18	>0.99	<10-4
73	26	42	0	0.33	1
74a	34	34	0	0.33	1
74b	37	34	0	0.32	1
74c*	43	34	3	>0.99	<10-4
75a*	46	39	15	>0.99	<10-4
75b	22	29	0	0.38	1

Model parameter estimates: μ̂ = −2.26, σ̂ = 1.47, π̂ = 0.75.

^*Asterisks identify patients with evidence favoring clonality.

In this example, all pairs with a single shared mutation have a high probability of being clonal (>85%). The reason is that the shared mutation is a rare mutation, i.e. a mutation with an estimated marginal probability of occurrence of 0.001 (pairs 47c, 48b, 53b) and 0.003 (pair 47d). To illustrate the influence of this marginal probability we have recalculated the probability of clonal relatedness for case 47c by replacing the marginal probability of the shared mutation with the values 0.01 and 0.1, representing the frequencies of more commonly occurring mutations. In these circumstances the probability of clonality would be reduced from 94% to 68% and 42%, respectively.

Similarly, we can assess the sensitivity of the probability to the total number of mutations when no shared mutations are observed. Let's consider case 26, with 32 and 29 observed mutations in the two tumors (61 total), but none shared. In this case the probability of clonality is 35%. This probability would be 26% if 100 mutations were observed. By contrast, the probability would be 61% if only 10 mutations were observed, and it becomes closer to the estimated π̂ as the number decreases.

We also analyzed the data using the previously proposed clonality test (Ostrovnaya et al. 2015). These p-values are in the final column of Table 1. We see that all cases with at least one match are significant at the 5% level. In this sense the two methods are consistent, classifying these patients as clonal and the remaining cases as independent. However, our modeled approach adds important insight beyond the use of individual statistical tests. While the individual tests have the advantage that they can be applied to individual patients without recourse to the analysis of a dataset of many patients, and only need specification of the marginal mutation probabilities of each the mutations observed, the test always leads to a p-value of 1 for cases with no matches observed. By contrast, the random effects model provides individual diagnostic probabilities for every case, and provides probabilistic recognition of the possibility that the case might be clonal even if no matches are observed on the genes in the panel employed. As can be seen from Table 1, in this study these probabilities are relatively high, ranging from 0.32 to 0.38, due to both the high overall probability that a case is clonal (π̂=0.75), and the fact that several cases are diagnosed as clonal with a low frequency of matches, leading to a high estimate of the random effects variance σ̂ =1.47.

Finally, we acknowledge that each of the 22 cases analyzed involves a unique invasive lesion but in fact some tumor pairs actually come from the same case (indicated by the case numbers). For example in case #24 there were two distinct LCIS lesions, and we tested these separately for clonal relatedness with the same invasive lesion. The model is based on the implicit assumption that these pairs are independent.

4. Statistical Properties

Our data analysis in Section 3 was based on a relatively small sample size with a modest proportion of cases determined to be clonal. Further, since the model parameters, especially those defining the random effects distribution of clonality signals, are derived primarily from the subset of cases that are clonal, evaluation of the statistical properties of the method is essential, especially for datasets with small sample sizes.

Analyses of this type will inevitably involve large numbers of genetic loci, most of which will have a very small probability of experiencing a mutation in any given tumor, and a much smaller number of hot spot mutations with relatively large mutation probabilities. We simulated data using the framework of the breast cancer data in Section 3 to construct the distribution of marginal mutation probabilities. These probabilities of mutation p_i,i = 1, … G, were sampled with replacement from the set of observed mutations in the breast cancer study. We set G= 19000 mutational loci, representing in theory the set of distinct mutations that could occur. In reality there are billions of loci in the exome that could experience a mutation. The use of G = 19000 was chosen to produce a mean of 34 mutations per case, similar to the mean observed in our LCIS study. We varied the true values of the parameters, π, μ and σ and the sample size n. Each of 200 simulation runs was then generated as follows. For each case, we determined randomly with probability π whether or not the case was clonal. For each clonal case, we simulated its clonality signal ξ_j=1-exp(-φ_j), where φ_j is sampled from a log-normal distribution with parameters (μ, σ). Figure 2 displays the selected distributional scenarios used in our simulations. These scenarios were chosen to reflect settings where the typical signals produce few matches (scenarios 1 and 2), where the typical signals lead to mutations being predominantly matches (scenarios 4 and 5), and one scenario (3) where there is typically a more even distribution of matches and non-matches. For each distinct potential mutation i, we determined if a clonal or a private or no mutation was observed by sampling from trinomial probabilities (p_A,p_B,1 − p_A − p_B), where p_A = P(i ∈ A_j|ξ_j) and p_B = P(i ∈ B_j|ξ_j) as defined in (1). If the case involved independent tumors then the trinomial sampling probabilities were replaced with p_A = P(i ∈ A_j|ξ_j = 0) and p_B = P(I ∈ B_j|ξ_j = 0). The resulting dataset was then analyzed using the method from Section 2 and the results summarized as described below.

Figure 2.

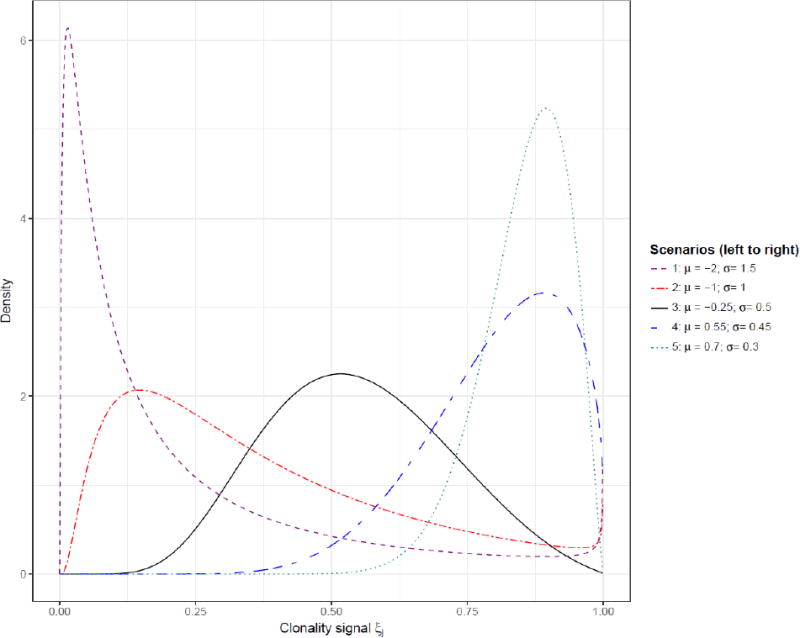
Different scenarios for the simulations.

In Table 2 we display results for three sample size settings: n=25, representing the approximate size of our breast cancer example, n=100 and n=1000. For each configuration, biases of the parameter estimates were calculated by subtracting the true parameter value from the mean of the parameter estimates from the 1000 simulations. We see that the clonal prevalence parameter π is estimated with essentially no bias in large sample sizes and very modest bias in small sample sizes, except for the extreme scenario 1 where somewhat larger biases are observed. The high number of small values for the signal ξ_j in this scenario makes it difficult for the model to distinguish between clonal cases with low signals and non-clonal cases with a null signal. The parameters of the random effects distribution of the clonality signals, μ and σ, are estimated with nearly no bias for large sample sizes, and with modest biases for medium and small sample sizes. These parameters are, however, not of intrinsic importance. What is important is their effect on the estimates of the predicted probabilities of clonal relatedness for each individual case.

Table 2. Simulation results - lognormal distribution.

Scenario		π			μ		σ		Prediction Error
		Estimate	(sd)	Bias	Estimate	Bias	Estimate	Bias
N=25 cases
π	(μ; σ)
0.10	Sc 1: (-2.0; 1.5)	0.139	(0.218)	0.039	-1.62	0.38	1.06	-0.44	0.103
	Sc 2: (-1; 1)	0.122	(0.139)	0.022	-1.08	-0.08	0.74	-0.26	0.046
	Sc 3: (-0.25; 0.50)	0.108	(0.069)	0.008	-0.38	-0.13	0.45	-0.05	0.013
	Sc 4: (0.55; 0.45)	0.104	(0.062)	0.004	0.40	-0.15	0.43	-0.02	0.009
	Sc 5: (0.7; 0.3)	0.104	(0.061)	0.004	0.56	-0.14	0.36	0.06	0.009
0.25	Sc 1: (-2.0; 1.5)	0.273	(0.189)	0.023	-1.91	0.09	1.08	-0.42	0.105
	Sc 2: (-1; 1)	0.262	(0.115)	0.012	-1.10	-0.10	0.82	-0.18	0.035
	Sc 3: (-0.25; 0.50)	0.250	(0.090)	0.000	-0.28	-0.03	0.41	-0.09	0.003
	Sc 4: (0.55; 0.45)	0.249	(0.088)	-0.001	0.53	-0.02	0.38	-0.07	0.001
	Sc 5: (0.7; 0.3)	0.249	(0.087)	-0.001	0.69	-0.01	0.26	-0.04	0.000
0.50	Sc 1: (-2.0; 1.5)	0.528	(0.211)	0.028	-2.04	-0.04	1.32	-0.18	0.137
	Sc 2: (-1; 1)	0.506	(0.116)	0.006	-1.06	-0.06	0.95	-0.05	0.034
	Sc 3: (-0.25; 0.50)	0.499	(0.100)	-0.001	-0.27	-0.02	0.47	-0.03	0.002
	Sc 4: (0.55; 0.45)	0.498	(0.100)	-0.002	0.54	-0.01	0.42	-0.03	0.000
	Sc 5: (0.7; 0.3)	0.498	(0.100)	-0.002	0.69	-0.01	0.27	-0.03	0.000
0.75	Sc 1: (-2.0; 1.5)	0.747	(0.168)	-0.003	-1.97	0.03	1.35	-0.15	0.122
	Sc 2: (-1; 1)	0.759	(0.103)	0.009	-1.04	-0.04	0.96	-0.04	0.037
	Sc 3: (-0.25; 0.50)	0.754	(0.087)	0.004	-0.26	-0.01	0.47	-0.03	0.002
	Sc 4: (0.55; 0.45)	0.754	(0.087)	0.004	0.54	-0.01	0.43	-0.02	0.000
	Sc 5: (0.7; 0.3)	0.754	(0.087)	0.004	0.69	-0.01	0.28	-0.02	0.000
N = 100 cases
π	(μ ; σ)
0.10	Sc 1: (-2.0; 1.5)	0.121	(0.122)	0.021	-1.98	0.02	1.17	-0.33	0.051
	Sc 2: (-1; 1)	0.105	(0.040)	0.005	-1.10	-0.10	0.90	-0.10	0.013
	Sc 3: (-0.25; 0.50)	0.100	(0.031)	0.000	-0.27	-0.02	0.44	-0.06	0.001
	Sc 4: (0.55; 0.45)	0.100	(0.031)	0.000	0.54	-0.01	0.40	-0.05	0.000
	Sc 5: (0.7; 0.3)	0.100	(0.031)	0.000	0.69	-0.01	0.26	-0.04	0.000
0.25	Sc 1: (-2.0; 1.5)	0.266	(0.101)	0.016	-2.09	-0.09	1.42	-0.08	0.058
	Sc 2: (-1; 1)	0.251	(0.050)	0.001	-1.04	-0.04	0.96	-0.04	0.013
	Sc 3: (-0.25; 0.50)	0.250	(0.043)	0.000	-0.27	-0.02	0.48	-0.02	0.001
	Sc 4: (0.55; 0.45)	0.250	(0.043)	0.000	0.54	-0.01	0.43	-0.02	0.000
	Sc 5: (0.7; 0.3)	0.250	(0.043)	0.000	0.69	-0.01	0.29	-0.01	0.000
0.50	Sc 1: (-2.0; 1.5)	0.508	(0.113)	0.008	-2.05	-0.05	1.47	-0.03	0.069
	Sc 2: (-1; 1)	0.497	(0.054)	-0.003	-1.01	-0.01	0.98	-0.02	0.013
	Sc 3: (-0.25; 0.50)	0.498	(0.049)	-0.002	-0.26	-0.01	0.49	-0.01	0.001
	Sc 4: (0.55; 0.45)	0.498	(0.049)	-0.002	0.54	-0.01	0.45	0.00	0.000
	Sc 5: (0.7; 0.3)	0.499	(0.049)	-0.001	0.69	-0.01	0.30	0.00	0.000
0.75	Sc 1: (-2.0; 1.5)	0.764	(0.115)	0.014	-2.07	-0.07	1.48	-0.02	0.081
	Sc 2: (-1; 1)	0.750	(0.051)	0.000	-1.03	-0.03	0.99	-0.01	0.014
	Sc 3: (-0.25; 0.50)	0.750	(0.044)	0.000	-0.27	-0.02	0.50	0.00	0.001
	Sc 4: (0.55; 0.45)	0.751	(0.044)	0.001	0.54	-0.01	0.45	0.00	0.000
	Sc 5: (0.7; 0.3)	0.751	(0.044)	0.001	0.69	-0.01	0.30	0.00	0.000
N = 1000 cases
π	(μ; σ)
0.10	Sc 1: (-2.0; 1.5)	0.104	(0.022)	0.004	-2.07	-0.07	1.50	0.00	0.014
	Sc 2: (-1; 1)	0.100	(0.011)	0.000	-1.01	-0.01	0.99	-0.01	0.003
	Sc 3: (-0.25; 0.50)	0.101	(0.010)	0.001	-0.26	-0.01	0.50	0.00	0.000
	Sc 4: (0.55; 0.45)	0.101	(0.010)	0.001	0.54	-0.01	0.45	0.00	0.000
	Sc 5: (0.7; 0.3)	0.101	(0.010)	0.001	0.69	-0.01	0.30	0.00	0.000
0.25	Sc 1: (-2.0; 1.5)	0.249	(0.028)	-0.001	-2.01	-0.01	1.48	-0.02	0.016
	Sc 2: (-1; 1)	0.248	(0.015)	-0.002	-1.01	-0.01	0.99	-0.01	0.004
	Sc 3: (-0.25; 0.50)	0.249	(0.014)	-0.001	-0.26	-0.01	0.50	0.00	0.000
	Sc 4: (0.55; 0.45)	0.250	(0.014)	0.000	0.54	-0.01	0.45	0.00	0.000
	Sc 5: (0.7; 0.3)	0.250	(0.014)	0.000	0.69	-0.01	0.30	0.00	0.000
0.50	Sc 1: (-2.0; 1.5)	0.496	(0.031)	-0.004	-2.00	0.00	1.48	-0.02	0.019
	Sc 2: (-1; 1)	0.498	(0.019)	-0.002	-1.01	-0.01	0.99	-0.01	0.004
	Sc 3: (-0.25; 0.50)	0.500	(0.017)	0.000	-0.26	-0.01	0.50	0.00	0.000
	Sc 4: (0.55; 0.45)	0.500	(0.017)	0.000	0.54	-0.01	0.45	0.00	0.000
	Sc 5: (0.7; 0.3)	0.500	(0.017)	0.000	0.69	-0.01	0.30	0.00	0.000
0.75	Sc 1: (-2.0; 1.5)	0.744	(0.033)	-0.006	-2.00	0.00	1.48	-0.02	0.023
	Sc 2: (-1; 1)	0.748	(0.016)	-0.002	-1.01	-0.01	1.00	0.00	0.005
	Sc 3: (-0.25; 0.50)	0.750	(0.014)	0.000	-0.26	-0.01	0.50	0.00	0.000
	Sc 4: (0.55; 0.45)	0.750	(0.014)	0.000	0.54	-0.01	0.45	0.00	0.000
	Sc 5: (0.7; 0.3)	0.750	(0.014)	0.000	0.69	-0.01	0.30	0.00	0.000

Data are generated with an average number of mutations per cases ≈34, to correspond to the LCIS study.

Number of loci = 19,000; 1000 simulations per scenario.

The predicted probabilities are estimated using (3) while true probabilities were calculated using (3) with π and the true parameters for the distribution of ξ_j replacing the corresponding estimates. The prediction error is defined as the mean absolute difference between the two measures. Prediction errors computed during the simulations, using 100 new cases that were not involved in the model estimation, are relatively small for small sample size and almost null for large sample sizes, except for scenario 1 where it can reach 14% when n=25.

More extensive simulations were conducted to explore the extent to which the statistical properties are influenced by a lower number of mutations per case. We present analogous results when there are 10 mutations on average per tumor (Supplemental Table 1) and 5 mutations per tumor (Supplemental Table 2). These configurations are more typical of sequencing panels in which only important genes are selectively genotyped, as opposed to all genes as in our breast cancer example. They are also representative of other cancer types, such as liquid or pediatric cancers, for which the average number of mutations is lower (Vogelstein et al. 2013). As expected, the results show larger biases, especially when estimating π in the settings where the random effect density concentrates near zero as in scenario 1 and, to a lesser extent, scenario 2. Even in large samples, the model has difficulty distinguishing clonal from independent cases when the clonality signal is frequently low among clonal cases, since the probability distributions of matches will often be similar between clonal and independent cases in this setting.

We also studied alternative models for the random effects distribution, notably the beta model. However, although π was estimated typically with modest bias the estimates for the distribution parameters α and β were heavily biased (data not shown). To assess the robustness of the lognormal model to model misspecification we simulated data according to a Beta distribution and estimated the model assuming the lognormal distribution. Results are displayed in Table 3. The biases are substantially higher than when the models are aligned as in Table 1. However the biases are generally modest for π except when π is very large, and the prediction errors are modest, demonstrating that model mis-specification has limited adverse consequences on the key parameter estimates.

Table 3.

Simulation results - data simulated according to a Beta distibution, estimation assuming a log-normal distribution.

Scenario		π			μ	σ	Prediction Error
		Estimate	(sd)	Bias	Estimate	Estimate
N = 25 cases
π	(α ; β)
0.10	Sc 1: (0.8; 0.8)	0.114	(0.114)	0.014	-0.56	0.85	0.041
	Sc 2: (1; 1)	0.116	(0.109)	0.016	-0.57	0.79	0.037
	Sc 3: (2; 2)	0.112	(0.108)	0.012	-0.58	0.63	0.028
	Sc 4: (0.9; 3.0)	0.111	(0.142)	0.011	-1.42	0.87	0.063
0.25	Sc 1: (0.8; 0.8)	0.244	(0.101)	-0.006	-0.50	0.96	0.034
	Sc 2: (1; 1)	0.246	(0.097)	-0.004	-0.50	0.87	0.027
	Sc 3: (2; 2)	0.254	(0.086)	0.004	-0.47	0.62	0.011
	Sc 4: (0.9; 3.0)	0.259	(0.171)	0.009	-1.64	0.74	0.082
0.50	Sc 1: (0.8; 0.8)	0.474	(0.110)	-0.026	-0.44	1.07	0.040
	Sc 2: (1; 1)	0.483	(0.111)	-0.017	-0.43	0.97	0.030
	Sc 3: (2; 2)	0.497	(0.103)	-0.003	-0.44	0.68	0.012
	Sc 4: (0.9; 3.0)	0.466	(0.147)	-0.034	-1.56	0.84	0.082
0.75	Sc 1: (0.8; 0.8)	0.714	(0.101)	-0.036	-0.42	1.08	0.046
	Sc 2: (1; 1)	0.727	(0.099)	-0.023	-0.43	0.98	0.036
	Sc 3: (2; 2)	0.742	(0.088)	-0.008	-0.42	0.70	0.013
	Sc 4: (0.9; 3.0)	0.693	(0.130)	-0.057	-1.53	0.88	0.091
N=100 cases
π	(α; β)
0.10	Sc 1: (0.8; 0.8)	0.096	(0.034)	-0.004	-0.40	0.99	0.012
	Sc 2: (1; 1)	0.098	(0.033)	-0.002	-0.44	0.91	0.009
	Sc 3: (2; 2)	0.099	(0.032)	-0.001	-0.44	0.66	0.004
	Sc 4: (0.9; 3.0)	0.105	(0.094)	0.005	-1.61	0.80	0.033
0.25	Sc 1: (0.8; 0.8)	0.234	(0.046)	-0.016	-0.38	1.06	0.019
	Sc 2: (1; 1)	0.240	(0.045)	-0.010	-0.41	0.97	0.014
	Sc 3: (2; 2)	0.247	(0.044)	-0.003	-0.42	0.70	0.005
	Sc 4: (0.9; 3.0)	0.227	(0.057)	-0.023	-1.52	0.88	0.034
0.50	Sc 1: (0.8; 0.8)	0.470	(0.054)	-0.030	-0.39	1.10	0.031
	Sc 2: (1; 1)	0.477	(0.053)	-0.023	-0.42	0.99	0.022
	Sc 3: (2; 2)	0.493	(0.052)	-0.007	-0.42	0.71	0.008
	Sc 4: (0.9; 3.0)	0.450	(0.060)	-0.050	-1.51	0.91	0.050
0.75	Sc 1: (0.8; 0.8)	0.707	(0.050)	-0.043	-0.39	1.11	0.041
	Sc 2: (1; 1)	0.721	(0.048)	-0.029	-0.42	1.01	0.029
	Sc 3: (2; 2)	0.739	(0.044)	-0.011	-0.42	0.72	0.009
	Sc 4: (0.9; 3.0)	0.680	(0.062)	-0.070	-1.51	0.91	0.069

5. Discussion

In this work we aimed at assessing clonal relatedness based on comparisons of somatic mutational profiles of two tumors. We have framed the problem as one of differential diagnosis, rather than significance testing. The proposed method estimates three quantities of importance: the proportion of clonal cases in the population of interest, the distribution of the clonality signal, and individual probabilities of clonality for each case. This addresses the problem that the significance testing approach does not provide quantitative evidence in favor of the (null) hypothesis that the tumors are independent, regardless of the numbers of non-matching mutations observed (Ostrovnaya et al. 2015). We resolved this problem by modeling the data from the entire sample of cases using a random effects model with a marginal likelihood, estimating the proportion of cases that are clonal, and reframing the problem as one of diagnosis. In our illustrative example based on a relatively small sample of cases with LCIS paired with an invasive breast cancer in which exome sequencing was performed on all of the tumors we were able to successfully obtain estimates of all of the relevant probabilities. Our simulations demonstrate that the method has good properties even for relatively small sample sizes as in the example.

Our study of LCIS and invasive cancers addressed a theoretical question of interest to breast cancer specialists: is LCIS a precursor of invasive cancer or merely a marker of elevated risk? Clonality studies are clearly useful for addressing specific scientific questions of this nature. Moreover these methods are likely to have much broader clinical applicability as sequencing of tumors becomes more common practice in the clinic. Although formal testing for clonal relatedness is not yet commonly used in clinical practice, its potential value is clear. For example, in breast cancer it has been found that the patient's survival probability is lower for patients with a locoregional recurrence compared to patients with a second primary cancer, emphasizing the importance of distinguishing local recurrences from ipsilateral second primaries (Witteveen et al. 2015). In this and numerous other clinical settings, determining whether two tumors are clonally related can have important clinical implications, since the presence of distinct, clonally related tumors represents metastasis and the consequent need for systemic therapy, while two independent tumors might both be effectively treated by local therapy, such as surgery, depending on the clinical context (Klevebring et al. 2015). Recent publications have demonstrated that pathologists' judgment can frequently be wrong, notably when diagnosing multiple lung tumors (Girard et al. 2009; Wang et al. 2009). Increasingly, cancer hospitals are introducing genetic tests to sequence tumors as a routine clinical tool (Wagle et al. 2012). The primary goal is to identify “actionable” mutations that could serve as targets for drugs specially designed to act against the identified mutations. The routine availability of information on mutations in such gene panels will inevitably provide data that can potentially be used for clonality testing when a new tumor is identified in the patient and there is doubt as to whether this represents an independent primary cancer or a recurrence of the initial tumor. However, gene panels for clinical use typically contain far fewer genes than the whole exome panel used in our study. As a result the numbers of observed mutations will necessarily be much smaller, and it is intuitive that there is a greater chance that shared mutations will not be observed in tumor pairs that are truly clonal.

The illustration of our method in the breast LCIS study is limited by a small sample size, resulting in imprecision in the parameter estimates. If these methods were to be employed ultimately in clinical practice, the parameter estimates would ideally be derived from a suitably large dataset and the diagnostic algorithm could use (3) with the estimates supplied.

Our proposed method makes a number of assumptions. First, we assume that the marginal mutation probabilities are known, when in fact they are estimated. This is a significant limitation, since it is common to observe mutations that have never previously been observed. We used a common sense estimator of n^-1 in these situations, where n is the total number of genotyped cases observed to date in both our study and the TCGA resource. However, this probability can be quite influential, especially for cases with a single match. Finding the most appropriate strategy for assigning these probabilities is a topic for future research. Second, we assume that the order in which mutations occur is random, when in fact it is plausible that common mutations are more likely to occur earlier in tumor evolution. Third, uncertainty exists with respect to the accuracy of mutation calling. Further research is needed to explore the impact of these assumptions on the properties of the method. Our approach is conceptually similar to other mixture models that have been developed to account for an excess of zeros in count data, notably using Poisson regression (see for example Lam et al. 2006, Ma et al. 2009, and Wong and Lam 2013 for application in medical studies), although the model structure and estimation strategies we have used are novel in this context.

In summary, we have developed a practical statistical modeling approach to a complex problem involving the use of genomic data to diagnose tumor pairs as related (clonal) or independent. Our method involves a novel application of well known statistical strategies, including random effects modeling and zero inflated distributions, applied to sparse data. Our simulations demonstrate that the method has good statistical properties in relatively large samples. In the small sample setting, although the parameters of the random effects distribution are estimated with bias, the method succeeds in estimating the key diagnostic parameters with only modest bias.