Functional Multiple Indicators, Multiple Causes Measurement Error Models

Summary

Objective measures of oxygen consumption and carbon dioxide production by mammals are used to predict their energy expenditure. Since energy expenditure is not directly observable, it can be viewed as a latent construct with multiple physical indirect measures such as respiratory quotient, volumetric oxygen consumption, and volumetric carbon dioxide production. Metabolic rate is defined as the rate at which metabolism occurs in the body. Metabolic rate is also not directly observable. However, heat is produced as a result of metabolic processes within the body. Therefore, metabolic rate can be approximated by heat production plus some errors. While energy expenditure and metabolic rates are correlated, they are not equivalent. Energy expenditure results from physical function, while metabolism can occur within the body without the occurrence of physical activities. In this manuscript, we present a novel approach for studying the relationship between metabolic rate and indicators of energy expenditure. We do so by extending our previous work on MIMIC ME models to allow responses that are sparsely observed functional data, defining the sparse functional multiple indicators, multiple cause measurement error (FMIMIC ME) models. The mean curves in our proposed methodology are modeled using basis splines. A novel approach for estimating the variance of the classical measurement error based on functional principal components is presented. The model parameters are estimated using the EM algorithm and a discussion of the model’s identifiability is provided. We show that the defined model is not a trivial extension of longitudinal or functional data methods, due to the presence of the latent construct. Results from its application to data collected on Zucker diabetic fatty rats are provided. Simulation results investigating the properties of our approach are also presented.

1. Background

Obesity results from a chronic imbalance between energy intake and energy expenditure. Objective measures of oxygen consumption and carbon dioxide production by mammals are used to predict their energy expenditure, which results from the basal metabolism, thermic effect of food, and physical activity (Hills et al., 2014). Energy expenditure can be viewed as a latent construct with multiple indicators including respiratory quotient (RQ), volumetric oxygen consumption (VO₂), and volumetric carbon dioxide production (VCO₂). A subject’s VO₂ represents the amount of oxygen input needed by the body to perform its metabolic function. It measures the oxygen required to oxidize energy substrates such as glucose, carbohydrates, free fatty acids, and amino acids. While VCO₂ is the output of metabolic processes, it measures the carbon dioxide production (CO₂) from oxidation processes. RQ represents a quotient of CO₂/VCO₂. Even though the motivating example for the current manuscript is based on an energy expenditure study in animal models, interest also lies in assessing daily energy expenditure in humans as well, see (Passmore and Durnin, 1955; Ainslie et al., 2003; Leonard, 2010).

Energy is required to maintain life processes. Additionally, energy is neither created nor destroyed according to the first law of thermodynamics. Thus, in animals, energy is only converted from one form to another. Metabolism describes the process of converting food energy into biological energy used by the body to perform its functions. Metabolic rate is defined as the rate at which metabolism occurs. Additionally, the rate of metabolism in the body depends on activity level. For example, metabolic rate is higher among individuals who are more active when compared to sedentary subjects. Although metabolic rate is not directly observable, it is well known that heat is produced as an output of metabolism. Thus, it can easily be assumed that metabolic rate is approximated by heat production plus some unknown measurement error, introducing classical measurement error. Our current work focuses on assessing the relationship between metabolic rate and indicators of energy expenditure. While it is well known that energy expenditure and metabolic rates are correlated, the two constructs are not identical. Energy expenditure results primarily from the hydrolysis of adenosine triphosphate (ATP) and metabolic rate describes the rate at which metabolism occurs in the body. Some chemical processes within the body require energy in the form of ATP, guanosine triphosphate (GTP), or uridine triphosphate (UTP), while others do not. Our work is not the first to consider the relationship between metabolic rate and energy expenditure, see (Carpenter et al., 1995; Papamandjaris et al., 1998; Ricquier, 2005; Ouellet et al., 2012). For example, Carpenter et al. (1995) conducted a meta-analysis evaluating the influence of body composition, resting metabolic rate on variation in total energy expenditure (Carpenter et al., 1995). Most of the literature mentioned in the meta-analyses focused on regression and correlation techniques. The resting metabolic rates included in the studies were predicted from the height, weight, and age based on equations provided by the World Health Organization (1973). In this manuscript, we provide methods based on structural equation models and measurement error for an improved understanding of the relationship between metabolic rate and energy expenditure. In doing so, we recognize that metabolic rate is unobservable; however, heat production can reliably be used as its proxy measure. A better understanding of energy metabolism is expected to aid in the development of means to prevent metabolic and obesity-related diseases.

As a chronic syndrome, obesity is a risk factor for metabolic diseases (including type II diabetes) and cardiovascular diseases. Ovine interferon tau (IFNT) was discovered for its regulatory role in the reproductive cycle of sheep (Bazer and Johnson, 1991). We recently showed that oral administration of IFNT stimulates oxidation of energy substrates and reduces adiposity in Zucker diabetic fatty (ZDF) rats, animals genetically prone to obesity due to a deficiency in their leptin receptors. We also suggested that our finding may have broad implications for preventing and treating obesity-related diseases in mammals (Tekwe et al., 2013). In understanding how treatment with IFNT affects indicators of energy expenditure after adjusting for metabolic rate and energy intake, a variation of the multiple indicators, multiple causes measurement error (MIMIC ME) models can be applied. This article develops a methodology that allows simultaneous assessments of the impact of ovine IFNT (Bazer and Johnson, 1991) treatment, energy intake, and metabolic rate on multiple indicators of a latent construct, energy expenditure. Heat production, VO₂, VCO₂, and RQ are measured as curves and are best represented as sparsely observed functions of time. We extend our previous work on MIMIC ME models (Tekwe et al., 2014) to allow sparse functional outcomes in the presence of classical measurement error, defining the functional multiple indicators, multiple causes measurement error (FMIMIC ME) model.

The rest of the article is organized as follows: in Section 2, we define the functional MIMIC measurement error (FMIMIC ME) model and Section 3 briefly describes a likelihood-based estimation method to fit the model using the EM algorithm. We then apply the model to our motivating example in Section 4. The results of a simulation study investigating the merits of the proposed approach are given in Section 5. We conclude with some remarks in Section 6.

2. Functional MIMIC Measurement Error Models

2.1. The General Model

The Multiple Indicators, Multiple Causes Models (MIMIC) is a structural equation model with a single latent construct (Jöreskog and Goldberger, 1975; Posey et al., 2015) used to study underlying effects of an unobservable latent variable, L, on a set of outcomes or indicators. Additionally, the model can also be used to assess the validity of potential indicators used to define a latent construct. The model has been applied in various settings including the assessment of early tobacco experiences on current smoking status (Ríos-Bedoya et al., 2009), to study behavioural and psychological symptoms of dementia (Proitsi et al., 2011), to study physical and cognitive function in aging research (Mast and Lichtenberg, 2000), in studies of customer equity management (Bruhn et al., 2008), to study home environmental factors on respiratory symptoms and asthma in Chinese children (Dong et al., 2014), to assess the impact of radiation exposure and dyslipidemia on physical indicators of dyslipidemia among atomic bomb survivors (Tekwe et al., 2014), and to study the effects of ionizing radiation exposure on indicators of genetic damage among atomic bomb survivors (Tekwe et al., 2016). The MIMIC model extends confirmatory factor analysis and path models to allow covariates.

The classical MIMIC model assumes that the multiple causes, X_i, are measured without error, while all the outcome models are assumed to be of a linear form. However, there are times when the relationship between some of the outcome models and the underlying latent construct are best explained by curves rather than lines. Additionally, it is also not always feasible or possible to measure some of the causal variables directly, introducing potential measurement error on the surrogate measures (Fuller, 1987; Carroll et al., 2006). In our current setting, the functional data appear as sparsely observed curves over a given period, and we consider these curves are the units in the data analysis (Müller, 2005; Silverman and Ramsay, 2005).

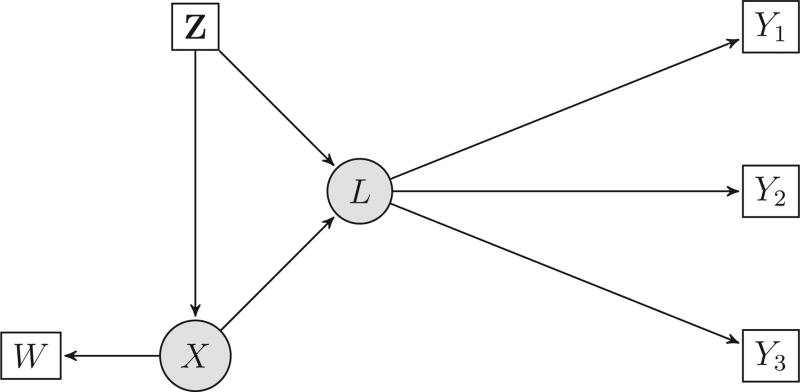
Suppose that there are j = 1, …, J functional indicators, and i = 1, …, n subjects. Let W_i denote the measured version of a scalar X_i, and let Z_i be additional covariates measured without error. Let L_i be an unobserved latent construct that is a function of an unobserved variable X_i and some observed covariates Z_i, see Figure 1. Finally, let Q(·) and R(·) be basis functions.

Figure 1.

The model when J = 3. Given Z = vector of error free covariates, X = the covariate measured with error, and L = the underlying latent construct, the outcomes Y_j(t) are independent.

The functional MIMIC measurement error model (FMIMIC ME) for the ith individual at time t is

$$Y_{\mathit{\text{ij}}}(t)=X_i{\beta }_{1j}+{\beta }_{2j}{L}_i+{\mathbf{Z}}_i^{\mathrm{T}}{\mathit{\gamma }}_j+{\mathbf{Q}}_j^{\mathrm{T}}(t){\mathbf{c}}_j+{\mathbf{R}}_j^{\mathrm{T}}(t){\mathbf{b}}_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ij}}}(t);$$ (1)

$$L_i=X_i{\alpha }_1+{\mathbf{Z}}_i^{\mathrm{T}}{\mathit{\alpha }}_2+{\eta }_i;$$ (2)

$$W_i=X_i+U_i,$$ (3)

$$X_i={\alpha }_0+{\mathbf{Z}}_i^{\mathrm{T}}{\mathit{\alpha }}_3+{\nu }_i,j=1,\cdots ,J.$$ (4)

In the functional MIMIC ME model, the outcome variables Y_ij(t) are sparsely observed functional data. The Y_ij(t)’s are multiple indicators of L_i obtained at time t and are best represented by curves. The ε_ij(t) describe an error process and are assumed white noise with mean 0 and variance ${\sigma }_j^2$. Equation (1) represents the outcome equation, while equation (2) is the causal equation model, making up the MIMIC component of the model. The equation (3) is considered the measurement error component of the model. We make the following assumptions:

1. The ε_ij(t) are independent of one another and (X_i, L_i, Z_i, b_ij, U_i), with mean zero and variance ${\sigma }_j^2$.

2. The random effects b_ij = Normal(0, Λ_j) are mutually independent and are also independent of (η_i, U_i, X_i, ν_i, Z_i). This means that the correlations among the functional responses Y_ij(·) for different j come from X_i and η_i, but this assumption is easily relaxed.

3. The random variable η_i has mean zero and for identifiability var(η_i) = 1. In addition, η_i is also independent of (U_i, Z_i, X_i).

4. The measurement errors $U_i=\text{Normal}(0,{\sigma }_u^2)$ and are also independent of (Z_i, X_i, ν_i). As in all measurement error models, additional data are necessary in order to estimate ${\sigma }_u^2$, as in our example in Section 4.

5. The random variables ${\nu }_i=\text{Normal}(0,{\sigma }_{\nu }^2)$ are also independent of Z_i.

The identifiability of the model is discussed in Web Appendix D.

2.2. Reduced Form Equations

The reduced form equations are obtained by substituting L_i in equation (2) into (1). The reduced form equation for the FMIMIC ME model is

$${\mathbf{Y}}_{\mathit{\text{ij}}}(t)=X_i{\kappa }_{1j}+{\eta }_i{\beta }_{2j}+{\mathbf{Z}}_i^{\mathrm{T}}{\kappa }_{2j}+{\mathbf{Q}}_j^{\mathrm{T}}(t){\mathbf{c}}_j+{\mathbf{R}}_j^{\mathrm{T}}(t){\mathbf{b}}_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ij}}}(t);$$ (5)

where κ_1j = β_1j + β_2jα₁ denotes total effect of X_i while κ_2j = γ_j + β_2jα₂ are the total effects of the error free covariates Z_i. The likelihood used to obtain the estimated model parameters for the functional MIMIC ME model are based on the likelihood for the reduced form models. The effects of the underlying latent construct, L_i are assessed through β_2j. Finally, the direct effects of X_i on the responses are assessed through κ_1j.

Remark 1

In terms of directed graphs, an interesting submodel of model (1) is

$$Y_{\mathit{\text{ij}}}(t)={\beta }_{2j}{L}_i+{\mathbf{Q}}_j^{\mathrm{T}}(t){\mathbf{c}}_j+{\mathbf{R}}_j^{\mathrm{T}}(t){\mathbf{b}}_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ij}}}(t),$$ (6)

which says that the effect of (X, Z) on the responses is explained completely by their effect on L. We can investigate whether model (6) holds in the following manner. If (6) holds, then β_1j = γ_j = 0. Thus, if α₁ ≠ 0, this implies that κ_2j/κ_1j = α₂/α₁ is independent of j. Since (κ_1j, κ_2j) are estimable from the reduced form equation (5), we can either use model selection methods or test the null hypothesis is H₀ : κ_2j/κ_1j = κ_2j′/κ_1j′ for all (j, j′). The only way that model (6) can fail to hold and the null hypothesis remains true is if there is a constant c₁ and a vector c₂ independent of (j) such that β_1j = c₁β_2j and γ_2j = c₂β_2j for all (j), a coincidence that would be remarkable.

2.3. Connection to Mixed Effects Models

The FMIMIC ME model can be seen as a form of multivariate linear mixed effects models with a complicated error structure due to η_i. In addition to the random effects, the outcome models in equation (1) also include the latent construct, η_i. Thus, the presence of the latent construct makes this model different from trivial extensions of methods developed for longitudinal or functional data. To see this, suppose ${\eta }_{\mathit{\text{ij}}}={\eta }_i{\beta }_{2j}=\text{Normal}(0,{\sigma }_{{\eta }_j}^2)$, where η_ij is not independent across all j. The covariance matrix of η_ij has a special form indicated as

$$\left(\begin{array}{c}\hfill {\eta }_{i1}\hfill \\ \hfill {\eta }_{i2}\hfill \\ \hfill {\eta }_{i3}\hfill \\ \hfill ⋮\hfill \\ \hfill {\eta }_{\mathit{\text{iJ}}}\hfill \end{array}\right)~\text{Normal}\left\{\right(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill ⋮\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{c}\hfill {\beta }_{21}\hfill \\ \hfill {\beta }_{22}\hfill \\ \hfill {\beta }_{23}\hfill \\ \hfill ⋮\hfill \\ \hfill {\beta }_{2J}\hfill \end{array}\left){\left(\begin{array}{c}\hfill {\beta }_{21}\hfill \\ \hfill {\beta }_{22}\hfill \\ \hfill {\beta }_{23}\hfill \\ \hfill ⋮\hfill \\ \hfill {\beta }_{2J}\hfill \end{array}\right)}^{\mathrm{T}}\right\}$$ (7)

The η_ij’s are correlated across j with a highly structured covariance structure that does not allow standard mixed effects program to be used in its estimation. Additionally, the crucial part of the model is the estimation of β_2j, the coefficient on the latent construct. Standard mixed effects programs are not currently able to estimate the effects of the latent construct on its multiple outcomes.

3. Estimation of the FMIMIC ME Model

3.1. Joint Distributions

To implement the EM-algorithm, we first compute the joint distribution of the observed data and the unobserved random effects given Z_i. Define 𝒥_ij to be a matrix of ones of the appropriate dimension. The conditional means and covariance of the observed data given Z_i are

$$E({\mathbf{Y}}_{\mathit{\text{ij}}}|{\mathbf{Z}}_i)=\{{\alpha }_0{\kappa }_{1j}+{\mathbf{Z}}_i^{\mathrm{T}}({\mathit{\alpha }}_3{\kappa }_{1j}+{\kappa }_{2j})\}{\mathbf{1}}_{\mathit{\text{ij}}}+{\mathbf{Q}}_{\mathit{\text{ij}}}{\mathbf{c}}_j;$$

$$E(W_i|{\mathbf{Z}}_i)=E(X_i|{\mathbf{Z}}_i)={\alpha }_0+{\mathbf{Z}}_i^{\mathrm{T}}{\mathit{\alpha }}_3;$$

$$\text{cov}({\mathbf{Y}}_{\mathit{\text{ij}}}|{\mathbf{Z}}_i)=({\kappa }_{1j}^2{\sigma }_{\nu }^2+{\beta }_{2j}^2){𝒥}_{\mathit{\text{ij}}}+{\mathbf{R}}_{\mathit{\text{ij}}}{\mathbf{\Lambda }}_j{\mathbf{R}}_{\mathit{\text{ij}}}^{\mathrm{T}}+{\sigma }_j^2{\mathbf{I}}_{\mathit{\text{ij}}};$$

$$\text{var}(W_i|{\mathbf{Z}}_i)={\sigma }_{\nu }^2+{\sigma }_u^2;$$

$$\text{cov}({\mathbf{Y}}_{\mathit{\text{ij}}},{\mathbf{Y}}_{\mathit{\text{ij}}}^{\mathrm{T}}|{\mathbf{Z}}_i)=({\kappa }_{1j}{\kappa }_{1j^{\mathrm{T}}}{\sigma }_{\nu }^2+{\beta }_{2j}{\beta }_{2j^{\mathrm{T}}}){𝒥}_{\mathit{\text{ij}}};$$

$$\text{cov}({\mathbf{Y}}_{\mathit{\text{ij}}},W_i|{\mathbf{Z}}_i)={\kappa }_{1j}{\sigma }_{\nu }^2{\mathbf{1}}_{\mathit{\text{ij}}}$$

The remaining conditional covariates given Z_i involving the latent variables are given as $\text{cov}({\mathbf{Y}}_{\mathit{\text{ij}}},X_i|{\mathbf{Z}}_i)={\kappa }_{1j}{\sigma }_{\nu }^2{\mathbf{1}}_{\mathit{\text{ij}}}$, cov(Y_ij, η_i|Z_i) = β_2j1_ij, cov(Y_ij, b_ij|Z_i) − R_ijΛ_j, cov(Y_ij, b_ik|Z_i) = 0, $\text{var}(X_i|Z_i)={\sigma }_{\nu }^2,\text{ cov}(X_i,W_i|Z_i)={\sigma }_{\nu }^2$, cov(X_i, η_i|Z_i) = 0, cov(X_i, b_ij|Z_i) = 0, cov(W_i, η_i|Z_i) = 0, cov(W_i, b_ij|Z_i) = 0, var(η_i|Z_i) = 1, cov(η_i, b_ij|Z_i) = 0, cov(b_ij|Z_i) = Λ_j.

Order the missing data for the jth functional response for person i as ${𝒢}_i={(X_i,{\eta }_i,{\mathbf{b}}_{i1}^{\mathrm{T}},‥,{\mathbf{b}}_{\mathit{\text{iJ}}}^{\mathrm{T}})}^{\mathrm{T}}$ and write the observed data as ${𝒟}_{\mathit{\text{iobs}}}={({\mathbf{Y}}_{i1}^{\mathrm{T}},\dots ,{\mathbf{Y}}_{\mathit{\text{iJ}}}^{\mathrm{T}},W_i)}^{\mathrm{T}}$. Then, given Z_i, the joint covariance matrix of (𝒢_i, 𝒟_iobs) is Σ apportioned to have block diagonals Σ₁₁ and Σ₂₂ and off diagonals blocks Σ₁₂ and ${\mathbf{\sum }}_{12}^{\mathrm{T}}$. Thus, given Z_i, (𝒢_i, 𝒟_iobs) = Normal(μ_i, Σ), where ${\mathit{\mu }}_i={({\mathit{\mu }}_{i1}^{\mathrm{T}},{\mathit{\mu }}_{i2}^{\mathrm{T}})}^{\mathrm{T}}={({\alpha }_0+{\mathbf{Z}}_i^{\mathrm{T}}{\mathit{\alpha }}_3,{0,}^{\mathrm{T}},{\mathit{\mu }}_{i2}^{\mathrm{T}})}^{\mathrm{T}}$. Assuming normality of the random effects, this means that $E({𝒢}_i|{𝒟}_{\mathit{\text{iobs}}},{\mathbf{Z}}_i)={\mathit{\mu }}_{i1}+{\mathbf{\sum }}_{12}{\mathbf{\sum }}_{22}^{-1}({𝒟}_{\mathit{\text{iobs}}}-{\mathit{\mu }}_{i2})$ and $\text{cov}({𝒢}_i|{𝒟}_{\mathit{\text{iobs}}},{\mathbf{Z}}_i)={\mathbf{\sum }}_{11}-{\mathbf{\sum }}_{12}{\mathbf{\sum }}_{22}^{-1}{\mathbf{\sum }}_{12}^{\mathrm{T}}$. Thus, for any matrix C₁, and any matrix C₂,

$$E({\mathbf{C}}_1{𝒢}_i|{𝒟}_{\mathit{\text{iobs}}},{\mathbf{Z}}_i)={\mathbf{C}}_1\{{\mathit{\mu }}_{i1}+{\mathit{\sum }}_{12}{\mathit{\sum }}_{22}^{-1}({𝒟}_{\mathit{\text{iobs}}}-{\mathit{\mu }}_{i2})\};$$ (8)

$$\text{cov}({\mathbf{C}}_1{𝒢}_i|{𝒟}_{\mathit{\text{iobs}}},{\mathbf{Z}}_i)={\mathbf{C}}_1({\mathit{\sum }}_{11}-{\mathit{\sum }}_{12}{\mathit{\sum }}_{22}^{-1}{\mathit{\sum }}_{12}^{\mathrm{T}}){\mathbf{C}}_1^{\mathrm{T}}.$$ (9)

Also,

$$E({\mathbf{C}}_1{𝒢}_i{𝒢}_i^{\mathrm{T}}{\mathbf{C}}_2^{\mathrm{T}}|{𝒟}_{\mathit{\text{iobs}}},{\mathbf{Z}}_i)={\mathbf{C}}_1\{{\mathit{\mu }}_{i1}+{\mathbf{\sum }}_{12}{\mathbf{\sum }}_{22}^{-1}({𝒟}_{\mathit{\text{iobs}}}-{\mathit{\mu }}_{i2})\}\times {\{{\mathit{\mu }}_{i1}+{\mathbf{\sum }}_{12}{\mathbf{\sum }}_{22}^{-1}({𝒟}_{\mathit{\text{iobs}}}-{\mathit{\mu }}_{i2})\}}^{\mathrm{T}}{\mathbf{C}}_2^{\mathrm{T}}+{\mathbf{C}}_1({\mathbf{\sum }}_{11}-{\mathbf{\sum }}_{12}{\mathbf{\sum }}_{22}^{-1}{\mathbf{\sum }}_{12}^{\mathrm{T}}){\mathbf{C}}_2^{\mathrm{T}},$$ (10)

3.2. Complete Data Loglikelihood

From (3)–(4), the covariance matrix of (W_i, X_i) given Z_i is Σ_wx, which has variances $({\sigma }_{\nu }^2+{\sigma }_u^2,{\sigma }_{\nu }^2)$ and covariance ${\sigma }_{\nu }^2$. Let the collection of all parameters be denoted by Ω. Recall that there are i = 1, …, n subjects. Let M_ij be the number of observed responses for subject i, outcome j, and let the times at which Y_ij(·) is observed be t_ijk for k = 1, …, M_ij. Define AB(•) = ABA^T.

Define 1_ij to be the M_ij × 1 vector of ones and define ${𝒥}_{\mathit{\text{ij}}}={\mathbf{1}}_{\mathit{\text{ij}}}{\mathbf{1}}_{\mathit{\text{ij}}}^{\mathrm{T}}$. Define I_ij to be the identity matrix of size M_ij. Write Y_ij = (Y_ij1, …, Y_ijMij)^T and similarly, write Q_ij, R_ij, and ε_ij to be the stacked versions of ${\mathbf{Q}}_j^{\mathrm{T}}(t_{\mathit{\text{ijk}}})$, R_j(t_ijk), and ε(t_ijk). As a preliminary to the EM-calculations, we will compute the joint distribution of (Y_ij, X_i, W_i, η_i, b_ij) given Z_ij. Then

$${\mathbf{Y}}_{\mathit{\text{ij}}}={\mathbf{Z}}_i^{\mathrm{T}}{\mathit{\kappa }}_{2j}{\mathbf{1}}_{\mathit{\text{ij}}}+{\mathbf{Q}}_{\mathit{\text{ij}}}{\mathbf{c}}_j+X_i{\kappa }_{1j}{\mathbf{1}}_{\mathit{\text{ij}}}+{\eta }_i{\beta }_{2j}{\mathbf{1}}_{\mathit{\text{ij}}}+{\mathbf{R}}_{\mathit{\text{ij}}}{\mathbf{b}}_{\mathit{\text{ij}}}+{\mathit{\epsilon }}_{\mathit{\text{ij}}}.$$

The complete data loglikelihood is

$$\mathrm{Ł}(\mathbf{\Omega })=-(1/2)\sum _{j=1}^J\sum _{i=1}^n{M}_{\mathit{\text{ij}}}\text{ log}({\sigma }_j^2)-\sum _{j=1}^J\sum _{i=1}^n{\{{\mathbf{Y}}_{\mathit{\text{ij}}}-{\mathbf{Z}}_i^{\mathrm{T}}{\mathit{\kappa }}_{2j}{\mathbf{1}}_{\mathit{\text{ij}}}-{\mathbf{Q}}_{\mathit{\text{ij}}}{\mathbf{c}}_j-X_i{\kappa }_{1j}{\mathbf{1}}_{\mathit{\text{ij}}}-{\eta }_j{\beta }_{2j}{\mathbf{1}}_{\mathit{\text{ij}}}-{\mathbf{R}}_{\mathit{\text{ij}}}{\mathbf{b}}_{\mathit{\text{ij}}}\}}^{\mathrm{T}}\{•\}/(2{\sigma }_j^2)-\sum _{i=1}^n{\eta }_i^2/2-(1/2)\sum _{i=1}^n(W_i-{\alpha }_0-{\mathbf{Z}}_i^{\mathrm{T}}{\mathit{\alpha }}_3,X_i-{\alpha }_0-{\mathbf{Z}}_i^{\mathrm{T}}{\mathit{\alpha }}_3){\mathbf{\sum }}_{\mathit{\text{wx}}}^{-1}{(•)}^{\mathrm{T}}-(1/2)n\text{ log}(|{\mathbf{\sum }}_{\mathit{\text{wx}}}|)-(1/2)n\sum _{j=1}^J\text{log}(|{\mathbf{\Lambda }}_j|)-(1/2)\sum _{i=1}^n\sum _{j=1}^J{\mathbf{b}}_{\mathit{\text{ij}}}^{\mathrm{T}}{\mathbf{\Lambda }}_j^{-1}{\mathbf{b}}_{\mathit{\text{ij}}}.$$

Once the elements of Ω have been estimated, re-sampling approaches such as nonparametric bootstrap can be used to obtain the uncertainties around the estimated parameters, as well as their confidence intervals.

4. Application

4.1. The Data

Male ZDF rats were obtained from Charles River Laboratories at the age of 23 days and fed a Purina 5008 diet throughout the study. The Purina 5008 diet consists of 23.5% crude protein, 6.0% fat, 34.9% starch, 2.6% sucrose, 0.5% glucose plus fructose, 6.8% minerals, 3.8% fiber and 17,364 kJ gross energy/kg (Fu et al., 2005). The animals were housed in a temperature- and humidity-controlled facility on a 12-hour light: 12-hour dark cycle. The study was approved by the Texas A&M University Animal Use and Care Committee (Fu et al., 2005; Tekwe et al., 2013).

The details of the experiment have been described elsewhere (Tekwe et al., 2013). But briefly, at 28 days of age, six rats were assigned randomly to receive either drinking water (distilled and deionized water) that delivered 0, 4, or 8 µg IFNT/kg body weight per day. Concentrations of IFNT in the drinking water were adjusted daily based on the volume of water consumed to provide the desired treatment dosages. The drinking water was changed every other day and the rats were studied over an eight-week period. At 12 weeks of age, each animal was placed in an Oxymas instrument (Columbus Instruments, Columbus, OH) for 24 hours to obtain measures of heat production used to approximate daily metabolic rate. The Oxymas instrument was also used to obtain measures of the indicators of energy expenditure data approximately every 5 to 10 minutes over 24 hours. Thus, all data collected on the indicators of energy expenditure and heat production were obtained once over a 24 hour period. The rats had free access to food and drinking water during the observational period and the following indicators of energy expenditure were obtained: volumetric O₂ consumption (L/h/kg BW) (VO₂), volumetric CO₂ production (L/h/kg BW) (VCO₂), respiratory quotient (moles of CO₂ production/moles of O₂ consumption) (Tekwe et al., 2013).

4.2. Model Application to Data

In our example, we have one underlying construct L_i = energy expenditure, with several causal variables including body weight and food intake, which are all assumed to be measured without error. There are three treatment groups (control, low dose IFNT, high dose IFNT) that are also error-free covariates. Metabolic rate, X_i is a true covariate that is not directly observable and is assumed to be approximated by heat production, W_i, but with an error. Some of the indicators for metabolic rate include RQ, VCO₂, and VO₂. In this study, we assess the impact of IFNT treatment, body weight, energy expenditure on the outcome measures of metabolic rate. A question of interest is to determine how metabolic rate predicts indicators of energy expenditure.

In the model application, the function-valued data were obtained every 5–10 minutes and were averaged to obtain hourly measured values. There are six animals per treatment group, resulting in 18 animals total. See Figure 1 in the Supplementary materials for the graphical illustration of our example. We consider energy expenditure as a latent construct with multiple indicators, while the metabolic rate is not directly observable but is approximated by heat production plus an unknown measurement error. The FMIMIC ME model can be used to assess impacts of metabolic rate, and therapeutic measures designed to combat obesity such as IFNT on indicators of energy expenditure. Questions such as, does metabolic rate predict indicators of energy expenditure or can IFNT be considered a treatment option for increasing daily energy expenditure among animal models genetically prone to obesity can be answered with the current application.

4.3. Estimation of ${\sigma }_u^2$

Additional data or information on X_i are needed to identify the model. In this section, we show that the measurement error in the FMIMIC ME model can be estimated using functional data analysis methods. We illustrate that the curves can be re-parameterized as smooth functions and methods from functional data analysis can be used to obtain the distribution of X_i. Therefore, we can identify the measurement error component of the model without having direct observations on X_i for subjects in the study.

In our example, there are systematic time trends in the measurement error model. Observations are obtained at equally spaced times t₁, …, t_K. For k = 1, …, K, the measurement error model in equation (3) is reformulated as

$$W_i(t_k)=\mu (t_k)+f_i(t_k)+{\psi }_i(t_k),$$ (11)

$$E\{f_i(t_k)\}=0.$$ (12)

The error terms ψ_i(t_k) are independent and identically distributed with mean zero and variance ${\sigma }_{\psi }^2$ and are also independent of f_i(·). There are a variety of principal component approaches to fitting model (11)–(12), example, the usual Karhunen–Loeve approach (Silverman and Ramsay, 2005) approach or the much simpler method of (Zhou et al., 2008).

We define X_i as the “truth” or the average of the functions, f_i(·), for the ith individual, that is, $X_i=K^{-1}{\sum }_{k=1}^K\{\mu (t_k)+f_i(t_k)\}$. Our observed surrogate is

$$W_i=K^{-1}{\sum }_{k=1}^K{W}_i(t_k)=X_i+K^{-1}{\sum }_{k=1}^K{\psi }_i(t_k)=X_i+U_i,$$

where U_i is independent of X_i, E(U_i) = 0, $\text{var}(U_i)=K^{-1}{\sigma }_{\psi }^2={\sigma }_u^2$, and $\text{var}(X_i)=\text{var}(W_i)-{\sigma }_u^2={\sigma }_x^2$. In this case, σ_xu = 0.

A two-stage algorithm was used for the estimations. In the first stage, the fpca.mle function of the FPCA package in R was used to obtain an estimate of the variance of the measurement error term, ${\sigma }_u^2$ (Peng et al., 2011). Then, we used quadratic splines with four basis functions to fit the nonlinear component of the mean function. In the application data, we used BIC to select the number of basis functions, with the number of basis ranging from 3 to 9. The BIC values were compared, and they ranged from 204.18 for four basis functions to 880.94 for nine basis functions. Therefore, the model with four basis functions was selected. By choosing the number of knots/basis functions through criteria such as the BIC, spline regression models can be used without penalties (Carroll and Ruppert, 2006; Xue and Yang, 2006). In the current manuscript, we use unpenalized spline regression while the number of basis functions were chosen using BIC.

The second stage involves using the EM algorithm to obtain maximum likelihood estimates of Ω following estimation ${\sigma }_u^2$ as ${\hat{\sigma }}_u^2$ from stage 1. Parametric bootstrap based on the EM parameters estimates was used to estimate uncertainties associated with each estimated parameter.

Recall that since $\text{var}(W_i|{\mathbf{Z}}_i)={\sigma }_{\nu }^2+{\sigma }_u^2$, the estimated value for ${\sigma }_{\nu }^2$ is obtained by subtracting ${\hat{\sigma }}_u^2$ from the sample variance of the W_i.

4.4. Results

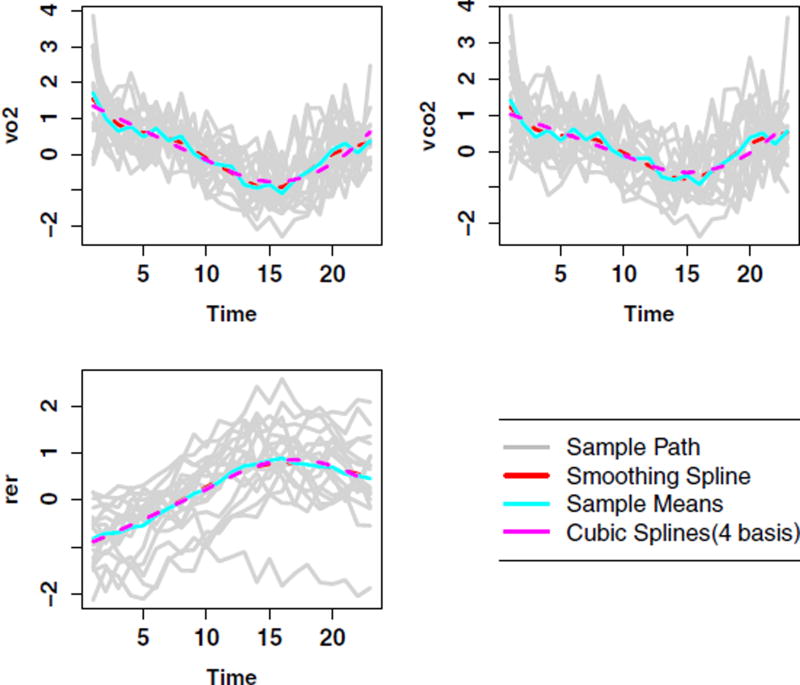
The plots of each outcome against the times of observation in Figure 2 illustrate the nonlinearity of the data. Additionally, we see that the use of quadratic splines with four basis functions adequately captures the curvilinear pattern observed for the outcomes over time. To verify if models that allow the modeling of time trends are needed, we first fit least squares based fixed effects approaches that solely adjust for error free covariates. The least squares based residuals were subsequently plotted against time for each outcome. The diagnostic plots also indicated that the use of least squares based methods does not account for time trends for all the outcome models (see Web Figure S1 of Web Appendix A). Thus, confirming that using fixed effects models do not provide adequate model fit to the data.

Figure 2.

Plots of the outcome models against time illustrating the nonlinear nature of the data as well as the trends across time.

Table 1 provides a summary of the results from the model application. Based on our analyses, no statistical differences were found between the low dose IFNT treatment group when compared to the control group for VO₂ based on a 95% confidence interval (−0.22, 0.52). However, a marginal significance was observed between the high dose IFNT group when compared to the control (−0.60, 0.03). The body weight of the animals had a statistically significant impact on VO₂, while their energy intakes per kg body weight did not. Energy expenditure was not found to be statistically significant on the volume of oxygen consumption after adjusting for the error free covariates and metabolic rate. This finding can be potentially due to the limited number of animals included in the study, see Table 1 for details.

Table 1.

Results from the application of the FMIMIC ME model to study the impact of IFNT and metabolic rate on indicators of energy expenditure among the ZDF rats. Here, VCO₂ = volumetric oxygen consumption, VO₂ = volumetric carbon dioxide production, and RQ = respiratory quotient, β̂_cme = classical measurement error adjusted estimates, β̂_un = unadjusted parameter estimates, %change = (β̂_un − β̂_cme)/(β̂_cme) × 100% = percentage change in the unadjusted estimates from the classical measurement error adjusted estimates, EI = energy intake, MR = metabolic rate, EE = energy expenditure, SE = bootstrap standard error, and CI = 95% bootstrap confidence intervals.

VO2	β̂cme	SE	CI	β̂un	%change
L vs. C	0.14	0.19	(−0.22,0.52)	0.20	25
H vs. C	−0.27	0.16	(−0.60, 0.03)	−0.32	10.34
Weight	−0.25	0.08	(−0.41,−0.10)	−0.27	3.70
EI	−0.01	0.11	(−0.27, 0.17)	−0.06	200
MR (X)	0.24	0.06	(0.07, 0.31)	0.19	−13.64
EE (η)	−0.09	0.06	(−0.16,0.06)	0.13	18.18
VCO2	β̂cme	SE	CI	β̂un	%change
L vs. C	−0.20	0.25	(−0.64,0.36)	−0.10	44.44
H vs. C	−0.09	0.22	(−0.56,0.30)	−0.14	40.00
Weight	−0.22	0.11	(−0.44,−0.02)	−0.21	0.0
EI	0.14	0.15	(−0.23,0.38)	0.04	−63.64
MR (X)	0.45	0.08	(0.24, 0.55)	0.36	−16.28
EE (η)	−0.08	0.07	(−0.20,0.11)	0.18	63.64
RQ	β̂cme	SE	CI	β̂un	%change
L vs. C	−0.70	0.28	(−1.23,−0.10)	−0.66	−12
H vs. C	0.07	0.21	(−0.36,0.48)	0.004	−94.29
Weight	0.04	0.11	(−0.18,0.25)	0.04	−20
EI	0.14	0.17	(−0.24,0.43)	0.04	−69.25
MR (X)	0.44	0.09	(0.18,0.53)	0.38	−15.56
EE (η)	0.07	0.06	(−0.10,0.17)	0.08	162.5

Body weight was also found to have a significant impact on the production of carbon dioxide, VCO₂ (−0.44, −0.02), while no other statistically significance was observed for the error free covariates. Metabolic rate was also found to have a statistically significant impact on VCO₂ (0.24, 0.55).

Similarly, for RQ, most of the error free covariates were not statistically significant. However, a significant difference was observed between the low dose IFNT treatment group when compared to the control treatment (p = 0.004). RQ was also not found to be an indicator of energy expenditure based on this data (−0.10, −0.17). However, metabolic rate was found to have a statistically significant impact on RQ after adjusting for the error free covariates (0.18, 0.53).

Plots of the sample variance functions and model-based variance functions of the residuals from the FMIMIC ME application are provided in Web Figure S2. These plots show the heteroscedasticity of the variance functions over time. There appears to be more variability at the beginning as well as towards the ends of the periods of observations for VCO₂ and VO₂, while a mild increasing variability is observed for RQ based on the sample variance. Observed patterns of the model-based variance functions for both VCO₂ and VO₂ are also similar, while the variability associated with RQ is over a smaller range. Heat maps for the correlation matrices were also obtained for the residuals. The matrices of the residuals from the FMIMIC ME application indicate that the residuals are not independent over time and observations closest in time are more correlated (plot not shown).

Plots of residuals from least squares fit to the data illustrate that the least squares fits do not account for the time trends in the data. On the other hand, plots of the residuals from the application show the adequacy of the FMIMIC ME model in accounting for the time trends (see Web Figures S3 and S4). The plots confirm the dramatically improved fit of the FMIMIC ME application when compared to least squares based methods.

4.5. Impact of Measurement Error in Model Application

In our application, $\widehat{{\sigma }_u^2}=0.252,{\widehat{{\sigma }_{\nu }}}^2=0.747$, and $\widehat{\mathit{\text{var}}(W)}=1$. The reliability ratio in this example was λ = 0.75, indicating that the presence of measurement error, attenuates the impact of the imprecisely measured causal variable, metabolic rate by 25%. Thus, failure to account for measurement error in this setting underestimates the impact of the imprecisely measured covariate. This under-estimation is also indicated in Table 1. In the table, β̂_un represents the unadjusted parameter estimates. We find that the unadjusted coefficients on metabolic rate were all under-estimated for the three outcomes considered.

5. Simulation Study

In this section, we assess the performance of the FMIMIC ME model and its sensitivity to misspecification of ${\sigma }_u^2$. We generated 100 independent data sets with n = 30 subjects each with three treatment groups. We allowed the time for all subjects to be equidistant and also allowed all subjects to have the same number of measurements, that is, 23. The generated data were based on the model fit parameters described in Section 4. The error-free covariates Z_i were also generated from their sampling distributions based on the motivating example.

The impact of adjusting for ${\sigma }_u^2$ on the error free covariates depends on the error-free covariate and the outcome model. Since metabolic rate (X) is the imprecisely measured true covariate, our interest lies in assessing the failure of accounting for measurement error on its relationship with the three outcomes. In general, we found that failing to account for the measurement error associated with metabolic rate tended to under-estimate its coefficients in all the three outcome models (see estimated $\widehat{{\beta }_{0.0}}$ on X in Web Table S1). Therefore, the impact of measurement error on the coefficients on metabolic rate is to attenuate the estimated coefficients towards the null. On the other hand, we found that the coefficients on energy expenditure (η) were generally over-estimated when we failed to account for measurement error.

The simulated data were based on ${\sigma }_u^2=0.25$. Sensitivity studies were performed based on the simulated data with choices of ${\sigma }_u^2=(0.0,0.05,0.16,0.25,0.75)$. Based on the sensitivity analyses (see Web Table S1 of Web Appendix C), we found that in general, the impact of misspecifying the variance of the classical measurement error on error-free covariates depended on the outcome model as well as the error-free covariate. However, assuming values of ${\sigma }_u^2$ lesser than its true value tended to under-estimate the coefficients on the imprecisely measured covariates; while it led to over-estimating the coefficient on η. On the other hand, assuming higher values for ${\sigma }_u^2$ tended to over-estimate the coefficient on X (metabolic rate), while under-estimating the coefficient on η = energy expenditure.

5.1. Performance Assessment: Estimating ${\sigma }_u^2$

In addition to the sensitivity analysis, we also conducted a simulation study to assess the ability of our proposed method to accurately estimate the variance of the measurement error. Rather than performing the estimation in two stages, where $\widehat{{\sigma }_u^2}$ is first estimated and assumed to be fixed in the second stage, we estimated the variance as part of the EM estimation steps. To achieve this, we generated 200 data sets using the estimated parameters from the reduced form model (see Table 1) as the true parameters with ${\sigma }_u^2=0.25$. The simulation results indicated that the methods performed adequately well in estimating the measurement error variance closer to the truth and the coefficients on both β₂ and κ₁ in all the outcome models. Specifically, the estimated measurement error variance was 0.27 with a 95% confidence interval of (0.24, 0.30). The estimated values and 95% confidence intervals for β₂, the coefficient on η, in the outcome models were −0.16(−0.25, −0.04), −0.11(−0.23, −0.002), 0.07(−0.04, 0.17), respectively. Finally, values for $\widehat{{\mathit{\kappa }}_1}$ and their corresponding 95% confidence intervals were 0.33(0.19, 0.46), 0.53(0.36, 0.69), 0.43(0.29, 0.57), respectively. All the confidence intervals contained the true values. Simulation results for the error-free coefficients also indicated that the proposed methods performed adequately well in their estimations.

6. Conclusion

We extended the linear MIMIC ME model to allow for sparse functional outcomes, defining the FMIMIC ME model. A novel approach for using heat production as a proxy measure for true metabolic rate through the use of B-splines was also provided. EM algorithm was used for estimation. The FMIMIC ME model can be used to assess impacts of both error free and imprecisely measured true function-valued covariates on sparse function-valued physical indicators of a latent construct. The model is motivated by an obesity study assessing the impact of IFNT on three indicators of energy expenditure, namely VO₂, VCO₂, and RQ. We found statistically significant relationships between metabolic rate and the multiple indicators for activity energy expenditure. Overall, there was not enough evidence to indicate that the use of IFNT modifies the predictors of energy expenditure. In this manuscript, we successfully applied the proposed model to determine if metabolic rate is a predictor of the indicators of energy expenditure. However, we did not have enough evidence to conclude that INFT treatment influenced the indicators of energy expenditure among the animals due to the small sample size of the motivating data. Additionally, we found that failure to account for measurement error associated with the imprecisely measured true covariate attenuated its effects towards the null while inflating the effects of the latent construct on its multiple outcomes.

The novelty of our current model is the extension of the classical MIMIC model to allow sparsely observed functional outcomes. Additionally, the use of methods from functional data analysis to estimate the variance of the classical measurement error in the structural equation setting is also novel.