Abstract
Zeolites are widely applied as solid acid catalysts in various technological processes. In this work we have computationally investigated how catalytic reactivity scales with acidity for a range of zeolites with different topologies and chemical compositions. We found that straightforward correlations are limited to zeolites with the same topology. The adsorption energies of bases such as carbon monoxide (CO), acetonitrile (CH3CN), ammonia (NH3), trimethylamine (N(CH3)3), and pyridine (C5H5N) give the same trend of acid strength for FAU zeolites with varying composition. Crystal orbital Hamilton populations (COHP) analysis provides a detailed molecular orbital picture of adsorbed base molecules on the Brønsted acid sites (BAS). Bonding is dominated by strong σ donation from guest molecules to the BAS for the adsorbed CO and CH3CN complexes. An electronic descriptor of acid strength is constructed based on the bond order calculations, which is an intrinsic parameter rather than adsorption energy that contains additional contributions due to secondary effects such as van der Waals interactions with the zeolite walls. The bond order parameter derived for the CH3CN adsorption complex represents a useful descriptor for the intrinsic acid strength of FAU zeolites. For FAU zeolites the activation energy for the conversion of π-adsorbed isobutene into alkoxy species correlates well with the acid strength determined by the NH3 adsorption energies. Other zeolites such as MFI and CHA do not follow the scaling relations obtained for FAU; we ascribe this to the different van der Waals interactions and steric effects induced by zeolite framework topology.
1. Introduction
Zeolites are well-defined microporous crystalline solids widely applied in various technological processes.1 The crystalline architecture of these materials is built of SiO4 and AlO4 tetrahedra linked by corner-sharing O atoms resulting in three-dimensional frameworks containing channels and cavities of molecular dimensions. The presence of tetrahedral Al3+ sites in the lattice gives rise to localized framework negative charge that is balanced by extraframework cations. The compensation for the negative charge by protons gives rise to strong Brønsted acidity.2 The most important processes, in which zeolites play a major role, are fluid catalytic cracking (FCC), hydrocracking, gasoline isomerization, the Mobil–Badger process for the synthesis of ethylbenzene, isomerization of xylenes, and toluene disproportionation.3,4 The unique catalytic properties of zeotype materials have also led to emerging applications related to sustainable chemistry technologies such as the catalytic conversions of renewables and environmental protection.5
Understanding the relationship between structure and reactivity is still among the key research topics of heterogeneous catalysis research.6 Conventionally, the acidic properties of zeolites are experimentally assessed by adsorption of basic probe molecules such as carbon monoxide, amines, or pyridine.7,8 Upon adsorption these bases react with the zeolite Brønsted acid sites (BAS) and the acid strength is correlated either directly to the heat of adsorption measured by calorimetry or temperature-programmed desorption or indirectly to the degree of perturbation of the adsorbed molecules, which can be monitored by spectroscopy (e.g., Fourier transform infrared (FTIR), NMR).
Despite a general consensus that acidity is key to the catalytic properties of zeolites, it has been difficult to ascertain quantitative structure–reactivity relations.9 Unlike homogeneous Brønsted acids, whose properties can be directly related to intrinsic acidity via pKa values, the acid activity of solids also depends on secondary effects related to the specific structural and topological properties. Furthermore, the substantial heterogeneity of acid sites due to the presence of defects and other structural inhomogeneities of practical zeolite catalysts additionally complicates establishing structure–performance relations solely from experimental data.10 Over the past decade, the development of scaling relations represents an important advance in the field of theoretical heterogeneous catalysis.11−14 These scaling relations rely on correlations between adsorption properties of chemical intermediates across different catalyst surfaces. Together with the Brønsted–Evans–Polanyi relationships,15,16 which link activation barriers to thermochemical reaction energies, it allows description of the catalytic activity in terms of descriptors such as adsorption energies of reaction intermediates. Despite the widespread use of the descriptor-based method in metal (oxide) surface catalysis, its application in zeolite catalysis has been limited so far.17−19
The intrinsic strength of the BAS in zeolites can be determined by the deprotonation energy (DPE), which is the energy required to dissociate the Brønsted proton to an infinite distance.20−25 Iglesia et al.23−29 demonstrated a good correlation between the DPE values and the turnover rates and rate constants of catalytic reactions such as alcohol dehydration and skeletal isomerization of alkenes on zeolites and Keggin polyoxometalate (POM) clusters. Niwa and co-workers30 also found that the apparent activation barrier of alkane cracking strongly correlates with the DPE for a series of HY and cation-exchanged HY zeolites. However, more recent studies suggest that the DPE is an incomplete descriptor to capture the catalytic activity of solid acids, because other factors such as the interaction of the cationic transition state with the conjugate anionic zeolite framework also affects catalyst reactivity.18,31,32 An alternative acidity descriptor for zeolites is the adsorption heat of bases. The theoretical work by Borges et al.33 showed that a linear relationship exists between the adsorption enthalpy of ammonia and the activation energy for the protolytic cracking of n-hexane in H–ZSM zeolites. This is consistent with the experimentally observed correlation between the turnover frequency and the activation energy of catalytic alkane cracking with the zeolite acidity measured by the heat of ammonia adsorption.34 Studt et al.17,18 also employed the heat of ammonia adsorption as a reactivity descriptor for the activity of chabazite zeolite and zeotype (silicoaluminophosphate) acid catalysts toward methanol–alkene reactions. They showed that the heat of ammonia adsorption can be used as a good descriptor for the energy of intermediates and transition states as well as the rate of alkene methylation predicted from microkinetic modeling. On the other hand, no general scaling relations were observed among different zeolite topologies (CHA, AEI, and AFI).19
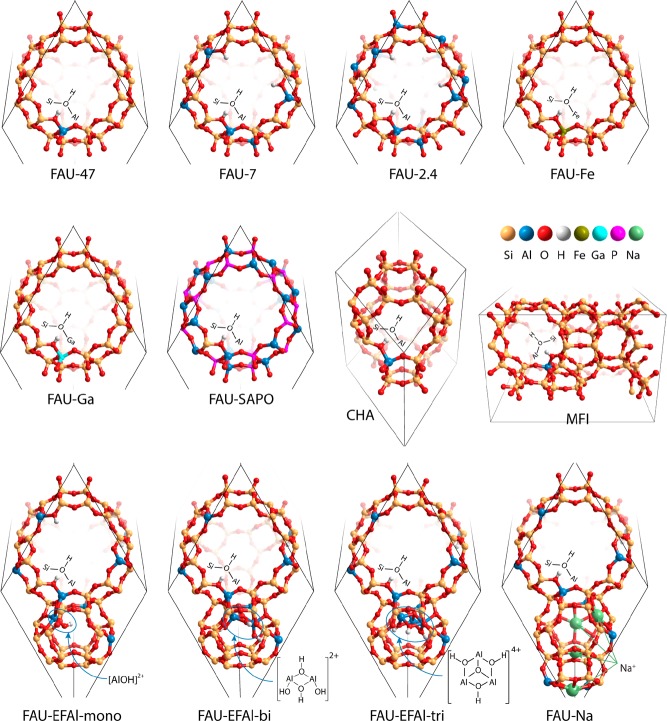
In this work we employed periodic density functional theory (DFT) calculations to investigate in detail the interaction of acidic sites in zeolite with common basic molecular probes and with alkenes to explore scaling relations between zeolite acidity and catalytic reactivity. To this end, we analyzed the effect of the variation of the zeolite chemical composition and topological properties (Figure 1) on the computed acid properties. FAU models were constructed with varying density of Al substitution (Si/Al ratio), different substituted heteroatom (Fe and Ga zeolites), silicoaluminophosphate (SAPO) form, and the presence of extraframework cations. High silica CHA and MFI models were also investigated to account for the effect of pore size and zeolite topology. In the search for a fundamental acidity descriptor, crystal orbital Hamilton populations (COHP) analysis was employed to quantify the chemical interactions and bonding characteristics between the zeolite BAS and the adsorption probes. Alkene (isobutene and ethene) protonation was used as a model hydrocarbon activation process used to probe the catalytic reactivity of the zeolite models.
Figure 1.
Computational models of zeolites: faujasite (FAU) zeolites with different Si/AlF ratios [FAU-47 (Si/Al = 47), FAU-7 (Si/Al = 7), and FAU-2.4 (Si/Al = 2.4)], heteroatom models [FAU-Fe (Si/Fe = 47) and FAU-Ga (Si/Ga = 47)], silicoaluminophosphate SAPO-37 [FAU-SAPO (Si:P:Al = 1:23:24)], extraframework-cation-containing models [FAU-EFAl-mono (Si/AlF = 7 and Si/Altotal = 6), FAU-EFAl-bi (Si/AlF = 7 and Si/Altotal = 5.3), FAU-EFAl-tri (Si/AlF = 7 and Si/Altotal = 4.7), and FAU-Na (Si/Al = 7)], and high-silica CHA (Si/Al = 35) and MFI (Si/Al = 95).
2. Methods
2.1. DFT Calculations
Periodic DFT calculations were performed with VASP 5.3.5 using the Perdew–Burke–Ernzerhof (PBE) functional.35−38 The electron–ion interactions were described with the projected augmented waves (PAW) method.39,40 The Brillouin zone sampling was restricted to the Γ point.41 The energy cutoff was set to 500 eV. van der Waals interactions were described by the dispersion-corrected DFT-D2 method.42 Convergence was assumed to be reached when the force on each atom was below 0.03 eV Å–1. A modest Gaussian smearing of 0.05 eV was applied to band occupations around the Fermi level, and the total energies were extrapolated to σ → 0. The minimum-energy reaction paths and the corresponding transition states were determined by the climbing image nudged elastic band (CI-NEB) method.43 The maximum energy geometries along the reaction path obtained with the CI-NEB method were further optimized using a quasi-Newton algorithm.
2.2. Zeolite Models
Models with FAU topology were simulated by a rhombohedral unit cell (Si48O96).44 To construct Al-substituted FAU models with varied acidity, both lattice Al density and the presence of extraframework species were considered. Defect-free Al-FAU sites with different Si/AlF ratios of 47, 7, and 2.4 were constructed by introducing, respectively, 1, 6, and 14 AlF lattice substitutions per unit cell. Faujasite contains only one crystallographically distinct T site. Similar to our previous studies,45,46 the locations of framework Al were selected on the basis of the stability analysis. The Brønsted protons as charge-compensating cations were introduced at the O1 positions, which have been earlier identified as the preferred proton-acceptor sites.47 The cell parameters were optimized for the defect-free zeolite models. The optimized lattice parameters were as follows: FAU-47, a = b = c = 17.29 Å, α = β = γ = 60°; FAU-7, a = b = c = 17.44 Å, α = β = γ = 60°; FAU-2.4, a = b = c = 17.65 Å, α = β = γ = 60°. The increase of the unit cell dimensions with decreasing Si/AlF ratio is consistent with the experimental observations.48,49
All FAU models containing extraframework cations were made from a unit cell with Si/AlF = 7. Three FAU models modified by EFAl species (Figure 1, FAU-EFAl-mono, FAU-EFAl-bi, and FAU-EFAl-tri) were considered, which contain mononuclear [AlOH]2+, binuclear [Al2O4H4]2+, and trinuclear [Al3O4H3]4+, respectively, as identified with high intrinsic stabilities in our previous studies.45,46 These cationic EFAl species were located in the faujasite sodalite cages with vicinal supercage BAS, and the induced positive charge by EFAl species was compensated by removing the protons to keep the system neutral. The Na-containing model (Figure 1, FAU-Na) was built by replacement of the trinuclear EFAl cluster with four Na cations located in the six-membered rings of the sodalite cage, facing the hexagonal prisms. Full geometry optimization with extraframework cations and guest molecules was performed with fixed cell parameters.
The iron- and gallium-substituted zeolite models (Figure 1, FAU-Fe and FAU-Ga) were obtained by isomorphous substitution of framework Al in FAU-47 model with trivalent Fe and Ga, and the lattice parameters were kept same as the optimized values of the FAU-47 model. In the case of the FAU-Fe model, spin-polarized calculations were carried out with high spin state (S = 5/2) identified as the most stable configuration. SAPO-37 (Figure 1, FAU-SAPO), which is the silicoaluminophosphate form of FAU, contains AlPO4 units with isomorphous substitution of siliceous FAU framework, and one proton was introduced by substitution of P by Si in the unit cell. The optimized lattice parameters of FAU-SAPO are a = b = c = 17.48 Å, and α = β = γ = 60°.
The high silica CHA (Si/Al = 35) and MFI (Si/Al = 95) zeolite models (Figure 1, CHA and MFI) were represented by periodic 36T and 96T unit cells, respectively. Similar to the FAU-47 model, one lattice Si was replaced by an Al atom to introduce a BAS. Chabazite contains a single T site, and the Brønsted proton was placed on the O2 oxygen site, which represents one out of two highly populated acid sites.50 In the MFI model, an Al atom was introduced at the T12 crystallographic position51 at the channel intersection, and the charge-compensating proton was located on the O20 position following the thermodynamic considerations by Svelle et al.52 The optimized lattice parameters of CHA and MFI models were as follows: for CHA, a = b = 13.74 Å, c = 14.84 Å, α = β = 90°, γ = 120°; for MFI, a = 20.03 Å, b = 19.91 Å, c = 13.39 Å, α = β = γ = 90°.
2.3. Chemical-Bonding Analysis
Electronic structure analysis was performed with the LOBSTER 2.1.0 program.53−56 The partial density of states (PDOS) and crystal orbital Hamilton populations (COHP) were used to analyze chemical bonding of the systems. The PDOS plots provide information on the partial electron density distribution of a particular atomic orbital. The COHP densities give the electron density distribution of bonding and antibonding orbital fragments. Here the negative contributions of COHP (−COHP) were plotted, and the positive/negative peaks in the plots indicate the bonding/antibonding interaction regimes. All the figures were plotted with the Fermi level set as the reference point at 0 eV. The bond orders were computed by the density derived electrostatic and chemical (DDEC) method.57,58
3. Results and Discussion
3.1. Adsorption of Bases
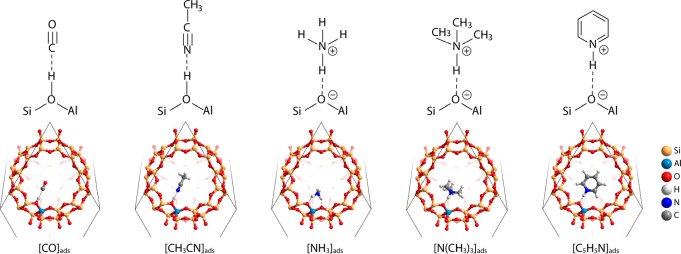
The acid strength of zeolite models was probed by studying their adsorption complexes with base molecules of varying strength and size, namely, carbon monoxide (CO), acetonitrile (CH3CN), ammonia (NH3), trimethylamine (N(CH3)3), and pyridine (C5H5N). These molecular probes are commonly employed in experimental studies to assess acidities of solid catalysts.8 The strength of the bases can be accessed by their proton affinity, which is the negative of the enthalpy change in the reaction between the bases and proton to form the conjugate acids in the gas phase.59 According to the proton affinity, the strength of the base probes follows the trend CO (594 kJ/mol) < CH3CN (779 kJ/mol) < NH3 (854 kJ/mol) < N(CH3)3 (949 kJ/mol) < C5H5N (930 kJ/mol).60 Besides the base strength of the probes, the adsorption heats of these bases in microporous zeolites are also affected by the strength of the acid sites as well as the confinement effect due to different molecular sizes of the probes.
We have optimized the adsorption complexes in zeolites with one probe molecule per unit cell. Independent of the zeolite model, the adsorption complexes of a particular probe are structurally similar. Representative optimized structures of the adsorption complexes formed in the high-silica Al-substituted faujasite model (FAU-47) are shown in Figure 2. The interaction of CO and CH3CN with BAS gives rise to molecular adsorption complexes, where the bonding is dominated by donor–acceptor-type interaction between the lone pairs of the adsorbed molecule and the acidic proton. On the contrary, the adsorption of much stronger NH3, N(CH3)3, and C5H5N bases results in the complete deprotonation of BAS to form contact ion-pair complexes confined in the zeolite cages.
Figure 2.
Adsorption of different base molecules at a Brønsted acid site (BAS) in FAU-47.
DFT-computed adsorption energies (ΔEads) are summarized in Table 1. ΔEads is the relative energy of the adsorption complex with respect to the free model and the probe in the gas phase (ΔEads = Eads – Emodel – Eprobe). For the faujasite (FAU) models, the adsorption heats (−ΔEads) increase in the sequence CO < CH3CN < NH3 < N(CH3)3 < C5H5N. The experimentally reported adsorption heat of CO on a faujasite-type H–Y zeolite (Si/Al = 5.6) is 26 kJ/mol,61 which is close to our calculated value of 30 kJ/mol for FAU-7 model with a similar Si/Al ratio. Expectedly, due to its very low basicity, ΔEads(CO) does not vary significantly for the different FAU models, predicting that the CO molecular probe is not sufficiently sensitive to discriminate acidity variations. The differences in acidity of the models can be appreciated by more basic adsorption probes. Experimental studies reported adsorption heats of 110 kJ/mol for ammonia on a low-silica HY,62 while the adsorption heats of 150 and 180 kJ/mol were reported for ammonia and pyridine, respectively, on a high-silica H-form of faujasite.63 The computed adsorption energies for the current FAU models (Table 1) are in good agreement with these experimental values. The trend shows that the intrinsic acid strength gradually increases with decreasing Al density in the framework (increasing Si/AlF ratio). The acid strength of bridging OH groups is a function of the electronegativity of the T atoms both in the first coordination sphere and in the second coordination sphere of BAS. For Al-FAU, the decrease of Al concentration at next-nearest-neighbor (NNN) positions leads to increased acid strength. This effect manifests itself only at low-to-intermediate Si/Al ratios (typically Si/Al < 5).64 For high dilution of framework Al (high Si/Al ratio), the NNN-Al effect vanishes and the acid strength levels off.45 A more direct way to affect zeolite acidity is to vary the heteroatom substituting for Si in the framework. For the current models, the measured acid strength of the high-silica FAU models increases with decreasing electronegativity of the T atom: FAU-47 (χAl = 1.61) > FAU-Ga (χGa = 1.81) > FAU-Fe (χGa = 1.83), in agreement with previous experimental and theoretical studies.10,65
Table 1. Adsorption Energies and Corresponding Dispersion Contributions (ΔEads and ΔEads(D), in kJ/mol) of Base Molecules in Zeolite Modelsa.
| [CO]ads |
[CH3CN]ads |
[NH3]ads |
[N(CH3)3]ads |
[C5H5N]ads |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| zeolite model | ΔEads | ΔEads(D) | ΔEads | ΔEads(D) | ΔEads | ΔEads(D) | ΔEads | ΔEads(D) | ΔEads | ΔEads(D) |
| FAU-47 | –35 | –8 | –90 | –15 | –142 | –16 | –185 | –45 | –192 | –44 |
| FAU-7 | –30 | –9 | –68 | –16 | –125 | –16 | –162 | –47 | –157 | –46 |
| FAU-2.4 | –30 | –8 | –60 | –15 | –104 | –16 | –145 | –47 | –144 | –46 |
| FAU-Fe | –31 | –7 | –82 | –15 | –129 | –14 | –176 | –43 | –181 | –43 |
| FAU-Ga | –32 | –7 | –85 | –16 | –138 | –15 | –186 | –45 | –191 | –43 |
| FAU-SAPO | –32 | –8 | –83 | –15 | –120 | –15 | –174 | –44 | –178 | –43 |
| FAU-Na | –35 | –8 | –93 | –15 | –142 | –16 | –199 | –44 | –212 | –45 |
| FAU-EFAl-mono | –42 | –8 | –106 | –17 | –188 | –15 | –241 | –44 | –252 | –45 |
| FAU-EFAl-bi | –45 | –10 | –119 | –17 | –189 | –17 | –248 | –47 | –270 | –44 |
| FAU-EFAl-tri | –45 | –10 | –120 | –17 | –183 | –15 | –252 | –43 | –268 | –42 |
| MFI | –42 | –16 | –115 | –52 | –166 | –24 | –223 | –92 | –200 | –85 |
| CHA | –41 | –15 | –108 | –35 | –159 | –26 | –217 | –69 | –205 | –63 |
Dispersion contribution is computed based on the equation ΔEads = ΔEads(DFT) + ΔEads(D). ΔEads(DFT) and ΔEads(D) are the contributions from DFT-calculated energy and the dispersion component, respectively, of the total adsorption energy ΔEads.
Aluminophosphates (AlPO4) can be obtained in similar porous structures as aluminosilicate zeolites, in which a pair of Si4+ ions is substituted by Al3+ and P5+. Acidic silicoaluminophosphate (SAPO) zeotypes are obtained by substituting a fraction of P5+ by Si4+. Experimental studies66−70 report that SAPO-type zeolites usually display weaker acidity than their aluminosilicate counterparts (for example, SAPO-34 vs SSZ-13 materials with the CHA topology). Consistent with these experimental observations, the comparison of the ΔEads values of base probes (Table 1, FAU-SAPO vs FAU-47, ΔEads[CH3CN] = −83 vs −90 kJ/mol, ΔEads[NH3] = −120 vs −142 kJ/mol, ΔEads[N(CH3)3] = −174 vs −185 kJ/mol, and ΔEads[C5H5N] = −178 vs −192 kJ/mol) indicates weaker acid strength of BAS in FAU-SAPO than in FAU-47. The weaker acidity in SAPO was proposed to be due to the higher flexibility of the Al–O–P unit than the Si–O–Si unit.66,69 Due to the larger atomic size of Al atom than Si, the substitution of Al into SiO2 framework causes a stronger compression of the Si–OH–Al bridge resulting in higher acidity. The more facile relaxation of the Al–O–P units counteracts this compression in SAPO giving rise to a lower acidity of BAS.
Besides the decreased framework Al content, there has also been significant debate on the role of extraframework Al (EFAl) species on the enhanced acidity of BAS.48,71,72 Previous theoretical studies have also demonstrated a pronounced acidity enhancement due to the presence of hard Lewis acid cations in close vicinity to BAS, e.g., in partially alkali and alkaline earth metal exchanged zeolites.73,74 For such alkali metal modified and EFAl-modified zeolites, the ΔEads values of bases (Table 1, FAU-47 vs FAU-Na vs FAU-EFAl, ΔEads[N(CH3)3] = −185 vs −199 vs −241 ∼ −252 kJ/mol, and ΔEads[C5H5N] = −192 vs −212 vs −252 ∼ −268 kJ/mol) show the following acid strength trend: FAU-47 < FAU-Na < FAU-EFAl. Both the Na cations and EFAl cationic species enhance the strength of the nearby BAS, and this promoting effect is much more significant for EFAl-containing zeolites. Such an effect has been earlier suggested to originate from the polarization of BAS by cationic species.75−77
The results presented so far indicate that, even for faujasite-type materials in which all T sites are equivalent, the acid strength of BAS is affected by local variations in the framework composition as well as by the presence of extraframework species. This indicates that in practical zeolites the exact Al distribution, the Al content, and the presence of extraframework cations will add to the heterogeneity in the strength of the BAS.78,79
Figure 3 presents the computed adsorption energies of different bases in FAU models as a function of the adsorption energies of pyridine. Pyridine adsorbs the strongest among the bases considered in this study. For all the other four bases, the adsorption enengies correlate linearly with the ΔEads(C5H5N). Thus, it is expected that the calorimetric characterization of acid strength with these bases would give the same trend for faujasite zeolites. The slopes of the trendlines indicate that the sensitivity of these bases for probing acid strength follows the trend C5H5N > N(CH3)3 > NH3 > CH3CN > CO. A higher proton affinity of a base benefits proton transfer in the adsorption complex. CO and CH3CN with proton affinities of 594 and 779 kJ/mol, respectively, are only adsorbed by hydrogen-bonding interaction, while for NH3 (854 kJ/mol), N(CH3)3 (949 kJ/mol), and C5H5N (930 kJ/mol) with increased proton affinity, proton tranfer occurs upon adsorption.
Figure 3.
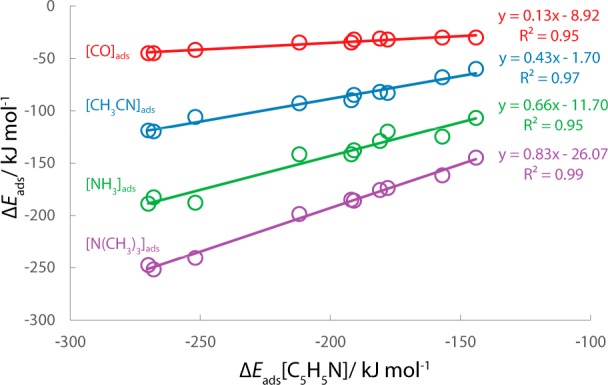
Scaling relations between the adsorption energies (ΔEads) of different base molecules in FAU zeolites.
The dispersion interactions between guest molecules and zeolite walls are particularly important for adsorption in zeolites. For each guest molecule (Table 1), the dispersion contribution ΔEads(D) does not depend on the FAU model. The average values are −8, −16, −16, −45, and −44 kJ/mol for CO, CH3CN, NH3, N(CH3)3, and C5H5N, respectively. The dispersion interaction is strongly affected by the size of the base. For example, when the H atoms in NH3 are substituted by methyl groups as in N(CH3)3 (Figure 4), the dispersion contribution increases from −16 to −45 kJ/mol. For the same base, the dispersion interaction with the zeolite wall is independent of the acid strength, which may be due to the similarity of the local structure of BAS in FAU zeolites.
Figure 4.
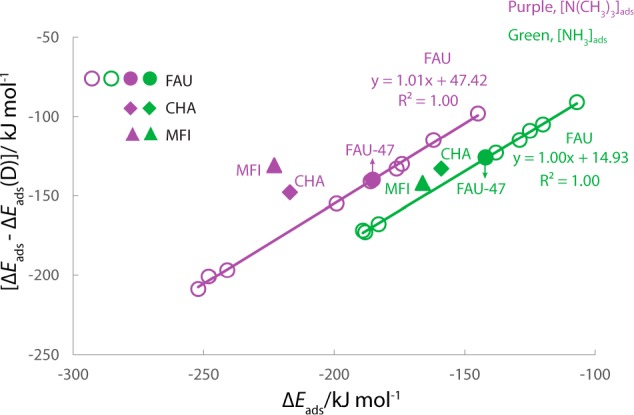
Dispersion effect on adsorption energies of NH3 and N(CH3)3 in different zeolites.
The effect of zeolite topology was studied by comparing the results obtained for CHA and MFI zeolite models with those for FAU-47. The BAS in MFI is located at the channel intersection (Figure 1, MFI), and the adsorption of bases can occur in both straight and sinusoidal channels (Figure S1). It is found that the adsorption energies of these bases in both locations are similar (Table S1), and here we only present the results of base adsorption in the sinusoidal channels (Table 1). Experimental studies reported that the adsorption heats for CO, CH3CN, NH3, N(CH3)3, and C5H5N on MFI zeolites are 29,80 110,81 145–155,63,82 205,82 and 200 kJ/mol,63 respectively. The experimental adsorption heats of ammonia on CHA-type zeolites with different Si/Al ratios are in the range 131–144 kJ/mol.69 The calculated ΔEads’s of bases in Table 1 cohere well with these experimental data, although in some cases the ΔEads’s are slightly overestimated due to the inability of the PBE+D method employed in this study to reach chemical accuracy in adsorption energy calculations.83 The ΔEads’s of CH3CN, NH3 and N(CH3)3 (Table 1) indicate that the acid strength (defined as the ability to protonation of a base) increases as FAU-47 < CHA < MFI, consistent with early theoretical work employing CH3CN to probe the acid strength in high-silica zeolites.84 The dispersion contributions vary significantly for different framework structures, and this is particularly notable for the bulky base (Table 1). As shown in Figure 4, the dispersion-uncorrected adsorption energies (ΔEads – ΔEads(D)) of NH3 still produce the same acidity trend as ΔEads, because the influence of ΔEads(D) is only minor. However, for the bulky N(CH3)3 probe, the absence of the dispersion corrections changes the acid trend predicted by the ΔEads of N(CH3)3 (Figure 4). The results suggest that the effect of dispersion forces should be carefully considered when determining the acidity trends by adsorption heat of bases.85
3.2. Chemical Bonding in Zeolites
Next, we compared the PDOS and COHP for the free zeolite BAS and the acid site interacting with CO and CH3CN. Figure 5 shows results obtained for the hydroxyl group of BAS in FAU-47. Two PDOS domains can be distinguished below the Fermi level, namely the PDOS domain dominated by the occupied O(2s) atomic orbital (around −21 eV) and the PDOS domain dominated by the occupied O(2p) atomic orbitals (from −10 to the Fermi level). Above the Fermi level, the unoccupied PDOS are dominated by the H(1s) atomic orbital. Figure 5b shows the bonding area below the Fermi level and it includes two regimes, namely, the interaction between H(1s) and O(2s) and the interaction between H(1s) and O(2pz). There is no interaction between H(1s) and O(2px,2py), because the orbital symmetries do not match. The antibonding feature is located on the H(1s) atomic orbital mainly above the Fermi level, which strongly overlaps with the SiO and AlO unoccupied antibonding electron conduction band regimes (Figure S2). The strong contribution of the O(2s) and O(2pz) interaction in the antibonding OH bond regime is indicative of the significant hybridization.
Figure 5.
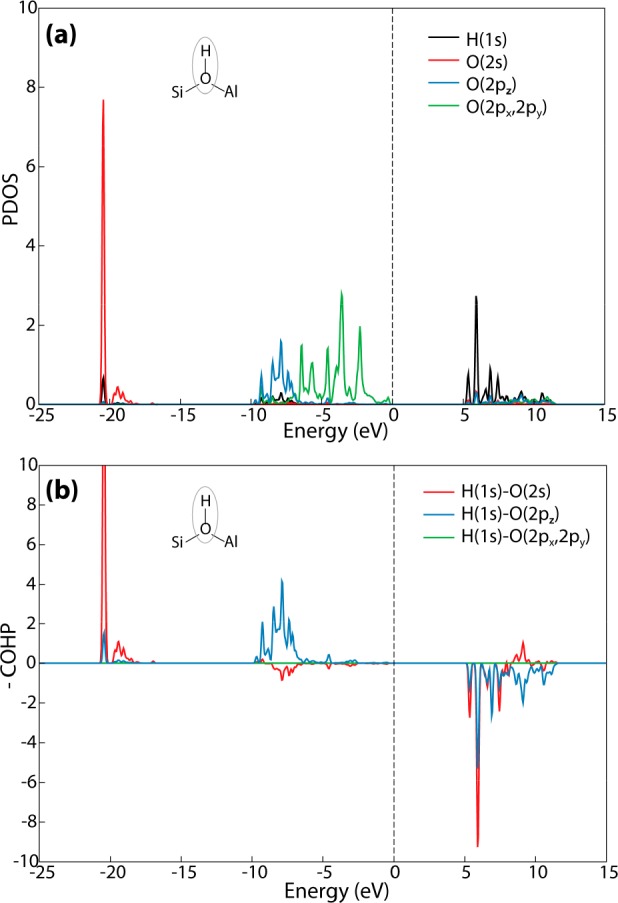
(a) PDOS for H and O atoms of BAS in FAU-47 zeolite. (b) COHP for the respective O–H bond. The z-axis is considered to be ordinated along the OH bond.
We carried out a similar chemical bonding analysis for the adsorption complexes of CO and CH3CN (Figure S3). Because of the requirement of orbital symmetry matching, only σ orbitals contribute to the bonding and antibonding interaction for these probes. The chemical bonding interaction in CO adsorption complex can be described as a weak electron donation from the CO σ electron density (Figure S3b, 3σ (−23 eV), 4σ (−8 eV), and 5σ (−3 eV) in the Supporting Information) into the antibonding unoccupied OH bond. This leads to the perturbation of the OH and CO bonds, respectively, resulting in a red shift of the OH stretch and a blue shift of the CO stretch consistent with infrared spectroscopy experiment.8 In the CH3CN adsorption complexes, the strongest bonding and antibonding interactions below the Fermi level are located between −10 and −5 eV (Figure S3d), corresponding to the interaction of the lone pair orbital in CH3CN with the BAS. The highest occupied molecular orbital (HOMO) of CH3CN (around −2 eV) has no interaction with the BAS because of the orbital symmetry mismatch. The stronger adsorption of CH3CN compared with CO is reflected by a stronger bonding interaction between H and N than that between H and C. This also results in a stronger perturbation of OH in the BAS, giving rise to a much larger red shift of OH vibrational frequency in CH3CN adsorption complex observed in the experiment.86
Base adsorption methods are widely used to titrate the number of protons in zeolites, and the desorption temperature is an indicator for the acid strength.10 There are conflicting opinions in the literature whether adsorption energies or desorption temperatures are adequate measures of proton acidity. Alternatively, spectrometric methods are used to probe the strength of proton sites. It has been recommended to use the shifts of OH frequencies as the acidity measures when perturbed by CO and especially acetonitrile as such probes.87−89 Here we study the relation between the adsorption energies of probe molecules and changes in bond strengths as determined by the bond order (BO) calculations. As the basicity of CO is low, the variations in zeolite acidity do not affect the BOs of OH and HC bonds in the corresponding adsorption complexes (Table S2). With increasing acid strength of zeolite models, the interaction between the terminal N atom in CH3CN and the proton becomes stronger with a simultaneous weakening of the OH bond in BAS. For FAU zeolites the values of BO(HN) and BO(OH) display the same trend of acid strength as determined by the ΔEads[CH3CN] (Figure 6, Table S2). However, MFI and CHA zeolites do not follow the trend of FAU. For example, the values of BO(HN) and BO(OH) in CHA are similar to those in FAU-47, indicating their similar intrinsic acid strength, but the adsorption energy of CH3CN is much larger in CHA than in FAU-47. The local structure of acid sites varies in topologically different zeolites, which results in very different van der Waals interactions (−35 kJ/mol in CHA vs −15 kJ/mol in FAU-47 for CH3CN adsorption). Thus, for different zeolite structures the chemical bonding changes are better probes for intrinsic acid strength, because they do not contain additional physical adsorption effects that are sometimes significantly contributing to the adsorption energies of probe molecules.
Figure 6.
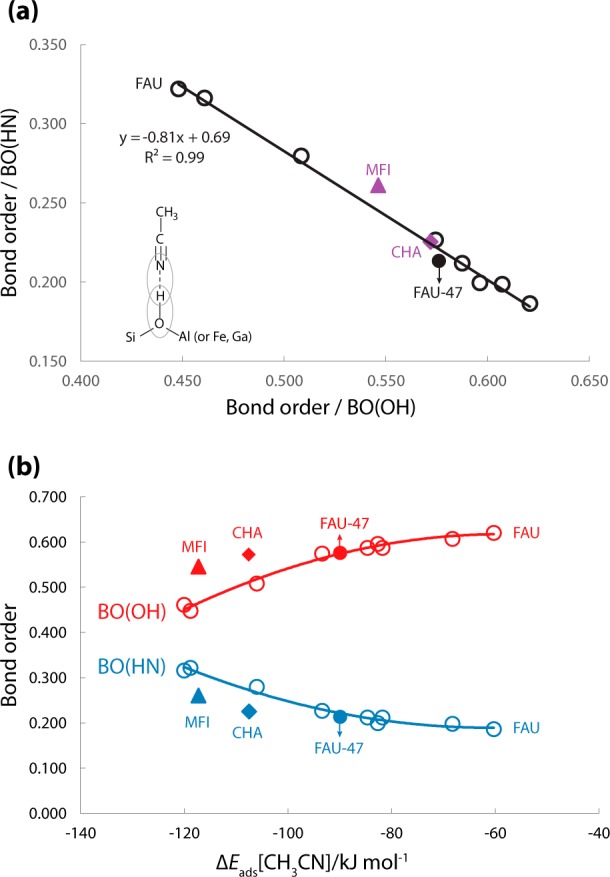
(a) Correlation between bond order (BO) of OH and HN bonds in adsorption complexes of CH3CN and (b) their variation as a function of the acetonitrile adsorption energy ΔEads[CH3CN].
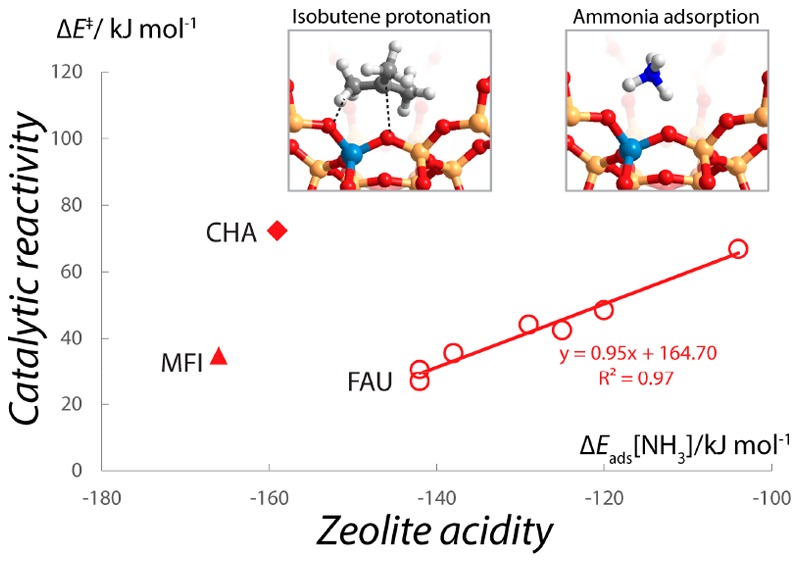
3.3. Catalytic Reactivity
We further analyzed the dependency between acidity and reactivity of zeolites using protonation of isobutene as a model reaction. The acid strength was determined by the adsorption energy of NH3, which has been successfully applied as a reactivity descriptor for catalytic conversion such as the methanol–olefin reactions and protolytic alkane cracking.17,18,45 The reaction of isobutene with BAS may yield isobutoxy or tert-butoxy intermediates depending on which position of the double bond is protonated.90,91 Here we only consider the formation of tert-butoxy, which is the kinetically preferred pathway (Figure 7a). The formation energies (ΔE) of the respective π adsorption complex (Ads-C4), transition state (TS-C4), and tert-butoxy species (Alkoxy-C4) with reference to the free zeolite model and gas-phase isobutene are listed in Table 2. For all the FAU models, the dispersion contributions (ΔE(D) to the ΔE of Ads-C4, TS-C4, and Alkoxy-C4 increase sequentially. For each reaction intermediate or TS, the variation of ΔE(D) among different FAU models is only minor. In MFI and CHA zeolites the dispersion interactions have a much stronger stabilization effect for all the intermediates and transition states along the reaction path of isobutene transformation (Table 2).
Figure 7.
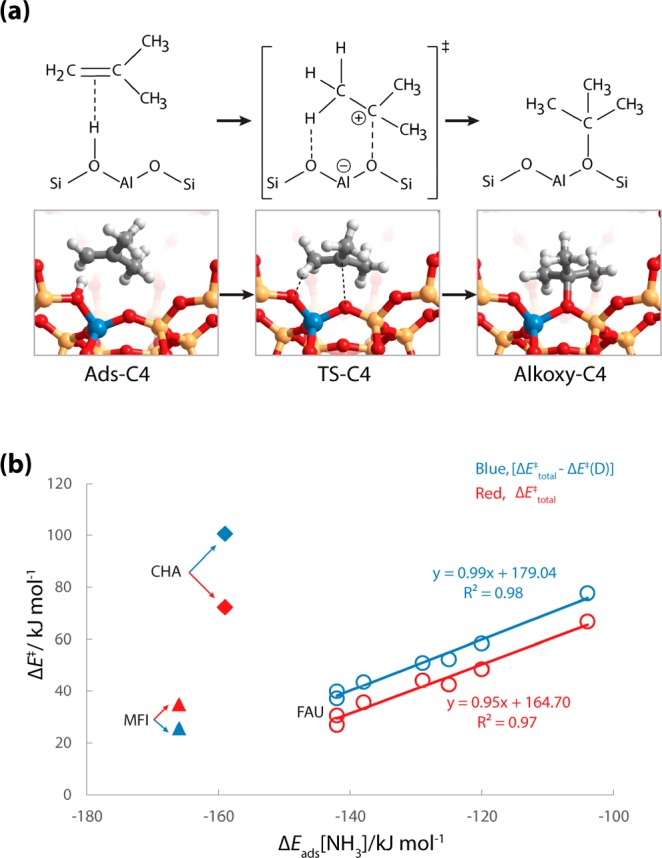
(a) Transformation of isobutene into tert-butoxy species in zeolites. (b) Scaling relations between ΔEads[NH3] and activation barriers (ΔE⧧) of isobutene transformation. The activation barriers with (ΔE⧧total) and without [ΔE⧧total – ΔE⧧(D)] dispersion corrections are indicated in red and blue, respectively.
Table 2. Formation Energies (ΔE) of π Complex (Ads-C4), Carbenium-Ion-like Transition State (TS-C4), and Surface tert-Butoxy Species (Alkoxy-C4) with Respect to Free Model and Gas-Phase Isobutene (all energies are in kJ/mol)a.
| Ads-C4 |
TS-C4 |
Alkxoy-C4 |
activation
barriers |
|||||
|---|---|---|---|---|---|---|---|---|
| zeolite modelb | ΔE | ΔE(D) | ΔE | ΔE(D) | ΔE | ΔE(D) | ΔE⧧total | ΔE⧧total – ΔE⧧(D) |
| FAU-47 | –73 | –40 | –42 | –50 | –73 | –60 | 30 | 40 |
| FAU-7 | –70 | –43 | –27 | –52 | –76 | –63 | 43 | 52 |
| FAU-2.4 | –69 | –44 | –2 | –55 | –34 | –64 | 67 | 78 |
| FAU-Fe | –68 | –40 | –24 | –47 | –87 | –59 | 44 | 51 |
| FAU-Ga | –71 | –41 | –35 | –49 | –81 | –62 | 36 | 44 |
| FAU-SAPO | –68 | –42 | –20 | –52 | –71 | –61 | 49 | 59 |
| FAU-Na | –75 | –42 | –49 | –52 | –66 | –66 | 27 | 37 |
| MFI | –97 | –79 | –62 | –70 | –86 | –77 | 35 | 26 |
| CHA | –97 | –70 | –24 | –98 | –27 | –101 | 72 | 101 |
The corresponding dispersion components of ΔE are indicated as ΔE(D). Activation barriers (ΔE≠total) and respective dispersion-uncorrected values (ΔE≠total – ΔE≠(D)) are listed separately.
As the estimated energy barriers in EFAl-containing models are even lower than 5 kJ/mol (Table S3), we ignore these models here to minimize the methodological error from DFT calculations.
Our results suggest that, despite the substantial effect of the dispersive stabilization of the zeolite framework on the computed barriers for isobutene protonation, dispersion itself does not depend on the acidity of zeolites with the same topology and is therefore likely determined by the pore structure of the zeolite. In FAU zeolites the activation barriers with (ΔE⧧total) and without [ΔE⧧total – ΔE⧧(D)] dispersion corrections give very similar slopes of the fitting trend (Figure 7b), indicating the independency of the dispersion effect on the acid strength. The decreased intercept of the trendline of dispersion-corrected activation barriers implies that the dispersion interaction decreases the reaction barriers by around 10 kJ/mol for all FAU zeolites. In CHA the effect of dispersion interaction is even stronger; it decreases the barrier by 29 kJ/mol. However, for MFI the inclusion of dispersion effects raises the barrier by 9 kJ/mol. The isobutene protonation occurs at the intersection of sinusoidal and straight channels in MFI (Figure S4), and the optimized structures show that the tert-butyl fragment in the TS is bent to the straight channel to a larger extent than the isobutene fragment in the π complex. This may lead to a decreased dispersion stabilization effect on the TS compared with the π complex, because for guest molecules the sinusoidal channel provides a better confinement and, accordingly, dispersion stabilization than the straight channel with a larger cavity (Table S1). The results suggest that the effect of the dispersion interactions on the catalytic reaction barriers varies significantly among different zeolite topologies. This is consistent with the experimental and theoretical studies by Iglesia et al.92,93 showing that the reactivity difference of topologically different zeolites is dominantly affected by the confinement effect mediated by van der Waal interactions.
The activation barriers (ΔE⧧) of isobutene transformation in FAU zeolites correlates well with the acid strength determined by ΔEads[NH3] (Figure 7b). Nevertheless, the ΔE⧧’s in MFI and CHA are higher than that of FAU with the same acid strength as scaled from the ΔEads[NH3]. This may be originated from the stronger steric interaction between the bulky isobutene and zeolite walls in MFI/CHA than in FAU. This is particularly notable for the small-pore CHA model. In the TS, the distance between the positive carbon center of tert-butyl cation and to-be-bounded zeolite framework oxygen is much shorter in CHA than in MFI and FAU (Figure S5). Although this provides stronger dispersion stabilization of TS in CHA, the steric effect also becomes significant, which destabilizes the TS and additionally increases the activation barrier. This proposition is further validated by the comparison of the computed energetics for the protonation reactions of ethene (Figure S6 and Table S4). For FAU-47, MFI, and CHA models, the estimated activation barriers for ethene (isobutene) conversion are 70 (30), 79 (35), and 70 (72) kJ/mol, respectively. The ethene protonation is expected to have a higher barrier than that of isobutene because it proceeds via a primary carbenium-like TS with much less stability than the tertiary carbenium TS involved in the isobutene transformation. However, for CHA zeolite both reactions proceed with very similar activation barriers. The smaller molecular size of ethene makes its transformation bear much weaker steric interaction with the zeolite walls. The expected decreased activation barrier due to the nature of carbenium-like TS is compensated by the larger steric interaction of isobutene with the zeolite wall. Therefore, the steric effect also represents one important factor determining the catalytic reactivity of zeolites.
The formation energies of tert-butoxy do not give any correlation with the acidity (Table 2). Here the Brønsted–Evans–Polanyi relationship is not applicable, because more acidic zeolites with weaker OH bonds will lead to the formation of less stabilized alkoxy species with lower activation barriers.94 In all FAU zeolites the local structure of BAS is similar, and the variation of dispersion and steric effect is similar among different models. As the generated alkoxy species are attached to neighboring oxygen sites, the intrinsic basicity of these site may also influence the stability of alkoxy species.95 The formation energy of tert-butoxy (Table 2) suggests its lower stability in CHA than in other topologies, which may be due to the larger destabilization effect of framework distortion induced by steric repulsion.96 This gives an indication that the small-pore zeolites may bias the free carbocation more than the alkoxy species generated from the corresponding alkene.
4. Conclusion
In summary, the scaling relations for zeolite acidity and catalytic reactivity were explored using a variety of zeolite models. The acid strength of faujasite (FAU) zeolites was tuned by varying framework composition or introducing extraframework cations. The properties of CHA and MFI were further compared with FAU to account for the effect of zeolite topology. For FAU zeolites the adsorption energies of bases such as CO, CH3CN, NH3, N(CH3)3, and C5H5N give the same trend of acid strength, and the sensitivity of these bases for probing acidity follows the trend C5H5N > N(CH3)3 > NH3 > CH3CN > CO. In the adsorption complexes the dispersion interaction with zeolite wall is stronger for bases with larger molecular size, and the dispersion contributions are independent of acid strength in topologically similar zeolites.
COHP analysis provides a detailed molecular orbital picture of adsorbed bases on the BAS. The orbital interaction only occurs when symmetry matches. For CO and CH3CN adsorption, strong σ donation from guest molecules to the BAS was observed. The bond order parameters derived for the CH3CN adsorption complex are a useful descriptor for the intrinsic acid strength of FAU zeolites, which gives a consistent acidity trend as probed by the adsorption energies.
For MFI and CHA with different framework topologies, the dispersion contributions for the stabilization of guest molecules vary significantly from FAU zeolites, particular for bulky bases. MFI and CHA zeolites do not follow the scaling trend of FAU zeolites, and the scaling relations derived from the adsorption energies of bases and related bond order parameters seem only applicable in zeolites with the same topology and similar local structures of acid sites. The catalytic reactivity of isobutene conversion into alkoxy species were evaluated for different zeolite models. The acid strength determined by adsorption energies of NH3 gives good correlation with the activation barriers of isobutene protonation in FAU zeolites. The effect of dispersion interaction on activation barriers varies for different zeolite framework types but shows similarity for the same FAU topology, and the steric effect between reactant and zeolite wall also represents one important factor determining the catalytic reactivity.
Acknowledgments
C.L. thanks the China Scholarship Council (CSC) for financial support. The Netherlands Organization for Scientific Research (NWO) is acknowledged for providing access to the supercomputer facilities. The authors acknowledge support from The Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC). E.A.P. thanks the Government of the Russian Federation (Grant 074-U01) and the Ministry of Education and Science of the Russian Federation (Project 11.1706.2017/4.6) for support.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.7b08176.
Extended computational results, additional supporting data (PDF)
Author Present Address
∥ C.L. and E.A.P.: Inorganic Systems Engineering Group, Department of Chemical Engineering, Delft University of Technology, Van der Maasweg 9, 2629 HZ Delft, The Netherlands.
The authors declare no competing financial interest.
Supplementary Material
References
- Corma A. State of the Art and Future Challenges of Zeolites as Catalysts. J. Catal. 2003, 216, 298–312. 10.1016/S0021-9517(02)00132-X. [DOI] [Google Scholar]
- Primo A.; Garcia H. Zeolites as Catalysts in Oil Refining. Chem. Soc. Rev. 2014, 43, 7548–7561. 10.1039/C3CS60394F. [DOI] [PubMed] [Google Scholar]
- Corma A. Inorganic Solid Acids and Their Use in Acid-Catalyzed Hydrocarbon Reactions. Chem. Rev. 1995, 95, 559–614. 10.1021/cr00035a006. [DOI] [Google Scholar]
- Weitkamp J. Zeolites and Catalysis. Solid State Ionics 2000, 131, 175–188. 10.1016/S0167-2738(00)00632-9. [DOI] [Google Scholar]
- Zeolites in Sustainable Chemistry: Synthesis, Characterization and Catalytic Applications; Xiao F.-S., Meng X., Eds.; Springer: Berlin, 2016. [Google Scholar]
- Bordiga S.; Groppo E.; Agostini G.; van Bokhoven J. A.; Lamberti C. Reactivity of Surface Species in Heterogeneous Catalysts Probed by in Situ X-Ray Absorption Techniques. Chem. Rev. 2013, 113, 1736–1850. 10.1021/cr2000898. [DOI] [PubMed] [Google Scholar]
- Farneth W. E.; Gorte R. J. Methods for Characterizing Zeolite Acidity. Chem. Rev. 1995, 95, 615–635. 10.1021/cr00035a007. [DOI] [Google Scholar]
- Sandoval-Díaz L.-E.; González-Amaya J.-A.; Trujillo C.-A. General Aspects of Zeolite Acidity Characterization. Microporous Mesoporous Mater. 2015, 215, 229–243. 10.1016/j.micromeso.2015.04.038. [DOI] [Google Scholar]
- Boronat M.; Corma A. Factors Controlling the Acidity of Zeolites. Catal. Lett. 2015, 145, 162–172. 10.1007/s10562-014-1438-7. [DOI] [Google Scholar]
- Derouane E. G.; Védrine J. C.; Pinto R. R.; Borges P. M.; Costa L.; Lemos M. A. N. D. A.; Lemos F.; Ribeiro F. R. The Acidity of Zeolites: Concepts, Measurements and Relation to Catalysis: A Review on Experimental and Theoretical Methods for the Study of Zeolite Acidity. Catal. Rev.: Sci. Eng. 2013, 55, 454–515. 10.1080/01614940.2013.822266. [DOI] [Google Scholar]
- Norskov J. K.; Bligaard T.; Rossmeisl J.; Christensen C. H. Towards the Computational Design of Solid Catalysts. Nat. Chem. 2009, 1, 37–46. 10.1038/nchem.121. [DOI] [PubMed] [Google Scholar]
- Medford A. J.; Vojvodic A.; Hummelshøj J. S.; Voss J.; Abild-Pedersen F.; Studt F.; Bligaard T.; Nilsson A.; Nørskov J. K. From the Sabatier Principle to a Predictive Theory of Transition-Metal Heterogeneous Catalysis. J. Catal. 2015, 328, 36–42. 10.1016/j.jcat.2014.12.033. [DOI] [Google Scholar]
- Greeley J. Theoretical Heterogeneous Catalysis: Scaling Relationships and Computational Catalyst Design. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 605–635. 10.1146/annurev-chembioeng-080615-034413. [DOI] [PubMed] [Google Scholar]
- Reuter K.; Plaisance C. P.; Oberhofer H.; Andersen M. Perspective: On the Active Site Model in Computational Catalyst Screening. J. Chem. Phys. 2017, 146, 040901. 10.1063/1.4974931. [DOI] [PubMed] [Google Scholar]
- Bligaard T.; Nørskov J. K.; Dahl S.; Matthiesen J.; Christensen C. H.; Sehested J. The Brønsted–Evans–Polanyi Relation and the Volcano Curve in Heterogeneous Catalysis. J. Catal. 2004, 224, 206–217. 10.1016/j.jcat.2004.02.034. [DOI] [Google Scholar]
- Santen R. A. v.; Neurock M.; Shetty S. G. Reactivity Theory of Transition-Metal Surfaces: A Brønsted–Evans–Polanyi Linear Activation Energy–Free-Energy Analysis. Chem. Rev. 2010, 110, 2005–2048. 10.1021/cr9001808. [DOI] [PubMed] [Google Scholar]
- Brogaard R. Y.; Wang C.-M.; Studt F. Methanol–Alkene Reactions in Zeotype Acid Catalysts: Insights from a Descriptor-Based Approach and Microkinetic Modeling. ACS Catal. 2014, 4, 4504–4509. 10.1021/cs5014267. [DOI] [Google Scholar]
- Wang C.-M.; Brogaard R. Y.; Weckhuysen B. M.; Nørskov J. K.; Studt F. Reactivity Descriptor in Solid Acid Catalysis: Predicting Turnover Frequencies for Propene Methylation in Zeotypes. J. Phys. Chem. Lett. 2014, 5, 1516–1521. 10.1021/jz500482z. [DOI] [PubMed] [Google Scholar]
- Wang C.-M.; Brogaard R. Y.; Xie Z.-K.; Studt F. Transition-State Scaling Relations in Zeolite Catalysis: Influence of Framework Topology and Acid-Site Reactivity. Catal. Sci. Technol. 2015, 5, 2814–2820. 10.1039/C4CY01692K. [DOI] [Google Scholar]
- Sauer J. Acidic Sites in Heterogeneous Catalysis: Structure, Properties and Activity. J. Mol. Catal. 1989, 54, 312–323. 10.1016/0304-5102(89)80149-X. [DOI] [Google Scholar]
- Gorte R. J. What Do We Know About the Acidity of Solid Acids?. Catal. Lett. 1999, 62, 1–13. 10.1023/A:1019010013989. [DOI] [Google Scholar]
- Lee C.; Parrillo D. J.; Gorte R. J.; Farneth W. E. Relationship between Differential Heats of Adsorption and Brønsted Acid Strengths of Acidic Zeolites: H-ZSM-5 and H-Mordenite. J. Am. Chem. Soc. 1996, 118, 3262–3268. 10.1021/ja953452y. [DOI] [Google Scholar]
- Macht J.; Janik M. J.; Neurock M.; Iglesia E. Catalytic Consequences of Composition in Polyoxometalate Clusters with Keggin Structure. Angew. Chem., Int. Ed. 2007, 46, 7864–7868. 10.1002/anie.200701292. [DOI] [PubMed] [Google Scholar]
- Janik M. J.; Macht J.; Iglesia E.; Neurock M. Correlating Acid Properties and Catalytic Function: A First-Principles Analysis of Alcohol Dehydration Pathways on Polyoxometalates. J. Phys. Chem. C 2009, 113, 1872–1885. 10.1021/jp8078748. [DOI] [Google Scholar]
- Macht J.; Janik M. J.; Neurock M.; Iglesia E. Mechanistic Consequences of Composition in Acid Catalysis by Polyoxometalate Keggin Clusters. J. Am. Chem. Soc. 2008, 130, 10369–10379. 10.1021/ja803114r. [DOI] [PubMed] [Google Scholar]
- Jones A. J.; Carr R. T.; Zones S. I.; Iglesia E. Acid Strength and Solvation in Catalysis by MFI Zeolites and Effects of the Identity, Concentration and Location of Framework Heteroatoms. J. Catal. 2014, 312, 58–68. 10.1016/j.jcat.2014.01.007. [DOI] [Google Scholar]
- Knaeble W.; Carr R. T.; Iglesia E. Mechanistic Interpretation of the Effects of Acid Strength on Alkane Isomerization Turnover Rates and Selectivity. J. Catal. 2014, 319, 283–296. 10.1016/j.jcat.2014.09.005. [DOI] [Google Scholar]
- Macht J.; Carr R. T.; Iglesia E. Functional Assessment of the Strength of Solid Acid Catalysts. J. Catal. 2009, 264, 54–66. 10.1016/j.jcat.2009.03.005. [DOI] [Google Scholar]
- Macht J.; Carr R. T.; Iglesia E. Consequences of Acid Strength for Isomerization and Elimination Catalysis on Solid Acids. J. Am. Chem. Soc. 2009, 131, 6554–6565. 10.1021/ja900829x. [DOI] [PubMed] [Google Scholar]
- Niwa M.; Suzuki K.; Morishita N.; Sastre G.; Okumura K.; Katada N. Dependence of Cracking Activity on the Brønsted Acidity of Y Zeolite: DFT Study and Experimental Confirmation. Catal. Sci. Technol. 2013, 3, 1919–1927. 10.1039/c3cy00195d. [DOI] [Google Scholar]
- Deshlahra P.; Carr R. T.; Iglesia E. Ionic and Covalent Stabilization of Intermediates and Transition States in Catalysis by Solid Acids. J. Am. Chem. Soc. 2014, 136, 15229–15247. 10.1021/ja506149c. [DOI] [PubMed] [Google Scholar]
- Deshlahra P.; Iglesia E. Toward More Complete Descriptors of Reactivity in Catalysis by Solid Acids. ACS Catal. 2016, 6, 5386–5392. 10.1021/acscatal.6b01402. [DOI] [Google Scholar]
- Borges P.; Ramos Pinto R.; Lemos M. A. N. D. A.; Lemos F.; Védrine J. C.; Derouane E. G.; Ramôa Ribeiro F. Activity–Acidity Relationship for Alkane Cracking over Zeolites: n-Hexane Cracking over HZSM-5. J. Mol. Catal. A: Chem. 2005, 229, 127–135. 10.1016/j.molcata.2004.11.012. [DOI] [Google Scholar]
- Katada N.; Sota S.; Morishita N.; Okumura K.; Niwa M. Relationship between Activation Energy and Pre-Exponential Factor Normalized by the Number of Brønsted Acid Sites in Cracking of Short Chain Alkanes on Zeolites. Catal. Sci. Technol. 2015, 5, 1864–1869. 10.1039/C4CY01483A. [DOI] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 14251–14269. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab Initio Molecular Dynamics for Open-Shell Transition Metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 48, 13115–13118. 10.1103/PhysRevB.48.13115. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- Grimme S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- Henkelman G.; Jónsson H. Improved Tangent Estimate in the Nudged Elastic Band Method for Finding Minimum Energy Paths and Saddle Points. J. Chem. Phys. 2000, 113, 9978–9985. 10.1063/1.1323224. [DOI] [Google Scholar]
- Hriljac J. A.; Eddy M. M.; Cheetham A. K.; Donohue J. A.; Ray G. J. Powder Neutron Diffraction and 29Si MAS NMR Studies of Siliceous Zeolite-Y. J. Solid State Chem. 1993, 106, 66–72. 10.1006/jssc.1993.1265. [DOI] [Google Scholar]
- Liu C.; Li G.; Hensen E. J. M.; Pidko E. A. Relationship between Acidity and Catalytic Reactivity of Faujasite Zeolite: A Periodic DFT Study. J. Catal. 2016, 344, 570–577. 10.1016/j.jcat.2016.10.027. [DOI] [Google Scholar]
- Liu C.; Li G.; Hensen E. J. M.; Pidko E. A. Nature and Catalytic Role of Extraframework Aluminum in Faujasite Zeolite: A Theoretical Perspective. ACS Catal. 2015, 5, 7024–7033. 10.1021/acscatal.5b02268. [DOI] [Google Scholar]
- Czjzek M.; Jobic H.; Fitch A. N.; Vogt T. Direct Determination of Proton Positions in D-Y and H-Y Zeolite Samples by Neutron Powder Diffraction. J. Phys. Chem. 1992, 96, 1535–1540. 10.1021/j100183a009. [DOI] [Google Scholar]
- Sohn J. R.; DeCanio S. J.; Fritz P. O.; Lunsford J. H. Acid Catalysis by Dealuminated Zeolite Y. 2. The Roles of Aluminum. J. Phys. Chem. 1986, 90, 4847–4851. 10.1021/j100411a026. [DOI] [Google Scholar]
- Almutairi S. M. T.; Mezari B.; Filonenko G. A.; Magusin P. C. M. M.; Rigutto M. S.; Pidko E. A.; Hensen E. J. M. Influence of Extraframework Aluminum on the Brønsted Acidity and Catalytic Reactivity of Faujasite Zeolite. ChemCatChem 2013, 5, 452–466. 10.1002/cctc.201200612. [DOI] [Google Scholar]
- Smith L. J.; Davidson A.; Cheetham A. K. A Neutron Diffraction and Infrared Spectroscopy Study of the Acid Form of the Aluminosilicate Zeolite, Chabazite (H-SSZ-13). Catal. Lett. 1997, 49, 143–146. 10.1023/A:1019097019846. [DOI] [Google Scholar]
- Olson D. H.; Kokotailo G. T.; Lawton S. L.; Meier W. M. Crystal Structure and Structure-Related Properties of ZSM-5. J. Phys. Chem. 1981, 85, 2238–2243. 10.1021/j150615a020. [DOI] [Google Scholar]
- Svelle S.; Tuma C.; Rozanska X.; Kerber T.; Sauer J. Quantum Chemical Modeling of Zeolite-Catalyzed Methylation Reactions: Toward Chemical Accuracy for Barriers. J. Am. Chem. Soc. 2009, 131, 816–825. 10.1021/ja807695p. [DOI] [PubMed] [Google Scholar]
- Dronskowski R.; Bloechl P. E. Crystal Orbital Hamilton Populations (COHP): Energy-Resolved Visualization of Chemical Bonding in Solids Based on Density-Functional Calculations. J. Phys. Chem. 1993, 97, 8617–8624. 10.1021/j100135a014. [DOI] [Google Scholar]
- Deringer V. L.; Tchougréeff A. L.; Dronskowski R. Crystal Orbital Hamilton Population (COHP) Analysis as Projected from Plane-Wave Basis Sets. J. Phys. Chem. A 2011, 115, 5461–5466. 10.1021/jp202489s. [DOI] [PubMed] [Google Scholar]
- Maintz S.; Deringer V. L.; Tchougréeff A. L.; Dronskowski R. Analytic Projection from Plane-Wave and PAW Wavefunctions and Application to Chemical-Bonding Analysis in Solids. J. Comput. Chem. 2013, 34, 2557–2567. 10.1002/jcc.23424. [DOI] [PubMed] [Google Scholar]
- Maintz S.; Deringer V. L.; Tchougréeff A. L.; Dronskowski R. Lobster: A Tool to Extract Chemical Bonding from Plane-Wave Based DFT. J. Comput. Chem. 2016, 37, 1030–1035. 10.1002/jcc.24300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manz T. A.; Limas N. G. Introducing DDEC6 Atomic Population Analysis: Part 1. Charge Partitioning Theory and Methodology. RSC Adv. 2016, 6, 47771–47801. 10.1039/C6RA04656H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Limas N. G.; Manz T. A. Introducing DDEC6 Atomic Population Analysis: Part 2. Computed Results for a Wide Range of Periodic and Nonperiodic Materials. RSC Adv. 2016, 6, 45727–45747. 10.1039/C6RA05507A. [DOI] [Google Scholar]
- Muller P. Glossary of Terms Used in Physical Organic Chemistry (IUPAC Recommendations 1994). Pure Appl. Chem. 1994, 66, 1077–1184. 10.1351/pac199466051077. [DOI] [Google Scholar]
- Hunter E. P.; Lias S. G.. Proton Affinity Evaluation. In NIST Chemistry WebBook; Linstrom P. J., Mallard W. G., Eds; NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD. http://webbook.nist.gov (accessed Oct 1, 2017). [Google Scholar]
- Otero Areán C.; Manoilova O. V.; Tsyganenko A. A.; Turnes Palomino G.; Peñarroya Mentruit M.; Geobaldo F.; Garrone E. Thermodynamics of Hydrogen Bonding between Co and the Supercage Brønsted Acid Sites of the H-Y Zeolite – Studies from Variable Temperature IR Spectrometry. Eur. J. Inorg. Chem. 2001, 2001, 1739–1743. . [DOI] [Google Scholar]
- Katada N.; Kageyama Y.; Takahara K.; Kanai T.; Ara Begum H.; Niwa M. Acidic Property of Modified Ultra Stable Y Zeolite: Increase in Catalytic Activity for Alkane Cracking by Treatment with Ethylenediaminetetraacetic Acid Salt. J. Mol. Catal. A: Chem. 2004, 211, 119–130. 10.1016/j.molcata.2003.10.001. [DOI] [Google Scholar]
- Parrillo D. J.; Gorte R. J. Characterization of Acidity in H-ZSM-5, H-ZSM-12, H-Mordenite, and H-Y Using Microcalorimetry. J. Phys. Chem. 1993, 97, 8786–8792. 10.1021/j100136a023. [DOI] [Google Scholar]
- Xu B.; Bordiga S.; Prins R.; van Bokhoven J. A. Effect of Framework Si/Al Ratio and Extra-Framework Aluminum on the Catalytic Activity of Y Zeolite. Appl. Catal., A 2007, 333, 245–253. 10.1016/j.apcata.2007.09.018. [DOI] [Google Scholar]
- Wang Y.; Zhou D.; Yang G.; Miao S.; Liu X.; Bao X. A DFT Study on Isomorphously Substituted MCM-22 Zeolite. J. Phys. Chem. A 2004, 108, 6730–6734. 10.1021/jp0376875. [DOI] [Google Scholar]
- Sastre G.; Lewis D. W. Modelling of Brønsted Acidity in AFI and CHA Zeotypes. J. Chem. Soc., Faraday Trans. 1998, 94, 3049–3058. 10.1039/a803843k. [DOI] [Google Scholar]
- Bordiga S.; Regli L.; Cocina D.; Lamberti C.; Bjørgen M.; Lillerud K. P. Assessing the Acidity of High Silica Chabazite H-SSZ-13 by FTIR Using Co as Molecular Probe: Comparison with H-SAPO-34. J. Phys. Chem. B 2005, 109, 2779–2784. 10.1021/jp045498w. [DOI] [PubMed] [Google Scholar]
- Bleken F.; Bjørgen M.; Palumbo L.; Bordiga S.; Svelle S.; Lillerud K.-P.; Olsbye U. The Effect of Acid Strength on the Conversion of Methanol to Olefins over Acidic Microporous Catalysts with the CHA Topology. Top. Catal. 2009, 52, 218–228. 10.1007/s11244-008-9158-0. [DOI] [Google Scholar]
- Katada N.; Nouno K.; Lee J. K.; Shin J.; Hong S. B.; Niwa M. Acidic Properties of Cage-Based, Small-Pore Zeolites with Different Framework Topologies and Their Silicoaluminophosphate Analogues. J. Phys. Chem. C 2011, 115, 22505–22513. 10.1021/jp207894n. [DOI] [Google Scholar]
- Wu L.; Hensen E. J. M. Comparison of Mesoporous SSZ-13 and SAPO-34 Zeolite Catalysts for the Methanol-to-Olefins Reaction. Catal. Today 2014, 235, 160–168. 10.1016/j.cattod.2014.02.057. [DOI] [Google Scholar]
- DeCanio S. J.; Sohn J. R.; Fritz P. O.; Lunsford J. H. Acid Catalysis by Dealuminated Zeolite-Y: I. Methanol Dehydration and Cumene Dealkylation. J. Catal. 1986, 101, 132–141. 10.1016/0021-9517(86)90236-8. [DOI] [Google Scholar]
- Beyerlein R. A.; McVicker G. B.; Yacullo L. N.; Ziemiak J. J. The Influence of Framework and Nonframework Aluminum on the Acidity of High-Silica, Proton-Exchanged Fau-Framework Zeolites. J. Phys. Chem. 1988, 92, 1967–1970. 10.1021/j100318a051. [DOI] [Google Scholar]
- Gonzales N. O.; Chakraborty A. K.; Bell A. T. A Density Functional Theory Study of the Effects of Metal Cations on the Brøsted Acidity of H-ZSM-5. Catal. Lett. 1998, 50, 135–139. 10.1023/A:1019095808885. [DOI] [Google Scholar]
- Vayssilov G. N.; Rösch N. Influence of Alkali and Alkaline Earth Cations on the Brønsted Acidity of Zeolites. J. Phys. Chem. B 2001, 105, 4277–4284. 10.1021/jp0041048. [DOI] [Google Scholar]
- Jiao J.; Kanellopoulos J.; Wang W.; Ray S. S.; Foerster H.; Freude D.; Hunger M. Characterization of Framework and Extra-Framework Aluminum Species in Non-Hydrated Zeolites Y by 27Al Spin-Echo, High-Speed MAS, and MQMAS NMR Spectroscopy at B0 = 9.4 to 17.6 T. Phys. Chem. Chem. Phys. 2005, 7, 3221–3226. 10.1039/b508358c. [DOI] [PubMed] [Google Scholar]
- Jiao J.; Ray S. S.; Wang W.; Weitkamp J.; Hunger M. Effect of Dehydration on the Local Structure of Framework Silicon Atoms in Zeolites Y Investigated by Solid-State NMR Spectroscopy. Z. Anorg. Allg. Chem. 2005, 631, 484–490. 10.1002/zaac.200400329. [DOI] [Google Scholar]
- Huang J.; Jiang Y.; Marthala V. R. R.; Thomas B.; Romanova E.; Hunger M. Characterization and Acidic Properties of Aluminum-Exchanged Zeolites X and Y. J. Phys. Chem. C 2008, 112, 3811–3818. 10.1021/jp7103616. [DOI] [Google Scholar]
- Kennes K.; Demaret C.; Van Loon J.; Kubarev A. A. V.; Fleury G.; Sliwa M.; Delpoux O.; Maury S.; Harbuzaru B.; Roeffaers M. B. J. Assessing Inter and Intra-Particle Heterogeneity in Alumina-Poor H-ZSM-5 Zeolites. ChemCatChem 2017, 9, 3440–3445. 10.1002/cctc.201700696. [DOI] [Google Scholar]
- Sierka M.; Eichler U.; Datka J.; Sauer J. Heterogeneity of Brønsted Acidic Sites in Faujasite Type Zeolites Due to Aluminum Content and Framework Structure. J. Phys. Chem. B 1998, 102, 6397–6404. 10.1021/jp981670i. [DOI] [Google Scholar]
- Otero Areán C. Dinitrogen and Carbon Monoxide Hydrogen Bonding in Protonic Zeolites: Studies from Variable-Temperature Infrared Spectroscopy. J. Mol. Struct. 2008, 880, 31–37. 10.1016/j.molstruc.2007.11.004. [DOI] [Google Scholar]
- Lee C. C.; Gorte R. J.; Farneth W. E. Calorimetric Study of Alcohol and Nitrile Adsorption Complexes in H-ZSM-5. J. Phys. Chem. B 1997, 101, 3811–3817. 10.1021/jp970711s. [DOI] [Google Scholar]
- Parrillo D. J.; Gorte R. J.; Farneth W. E. A Calorimetric Study of Simple Bases in H-ZSM-5: A Comparison with Gas-Phase and Solution-Phase Acidities. J. Am. Chem. Soc. 1993, 115, 12441–12445. 10.1021/ja00079a027. [DOI] [Google Scholar]
- Chiu C.-c.; Vayssilov G. N.; Genest A.; Borgna A.; Rösch N. Predicting Adsorption Enthalpies on Silicalite and HZSM-5: A Benchmark Study on DFT Strategies Addressing Dispersion Interactions. J. Comput. Chem. 2014, 35, 809–819. 10.1002/jcc.23558. [DOI] [PubMed] [Google Scholar]
- Simperler A.; Bell R. G.; Foster M. D.; Gray A. E.; Lewis D. W.; Anderson M. W. Probing the Acid Strength of Brønsted Acidic Zeolites with Acetonitrile: An Atomistic and Quantum Chemical Study. J. Phys. Chem. B 2004, 108, 7152–7161. 10.1021/jp035673t. [DOI] [Google Scholar]
- Derouane E. G.; Chang C. D. Confinement Effects in the Adsorption of Simple Bases by Zeolites. Microporous Mesoporous Mater. 2000, 35–36, 425–433. 10.1016/S1387-1811(99)00239-5. [DOI] [Google Scholar]
- Zecchina A.; Geobaldo F.; Spoto G.; Bordiga S.; Ricchiardi G.; Buzzoni R.; Petrini G. FTIR Investigation of the Formation of Neutral and Ionic Hydrogen-Bonded Complexes by Interaction of H-ZSM-5 and H-Mordenite with CH3CN and H2O: Comparison with the H-NAFION Superacidic System. J. Phys. Chem. 1996, 100, 16584–16599. 10.1021/jp960433h. [DOI] [Google Scholar]
- van Santen R. A.; Kramer G. J. Reactivity Theory of Zeolitic Broensted Acidic Sites. Chem. Rev. 1995, 95, 637–660. 10.1021/cr00035a008. [DOI] [Google Scholar]
- Zecchina A.; Buzzoni R.; Bordiga S.; Geobaldo F.; Scarano D.; Ricchiardi G.; Spoto G. Host- Guest Interactions in Zeolite Cavities. Stud. Surf. Sci. Catal. 1995, 97, 213–222. 10.1016/S0167-2991(06)81892-6. [DOI] [Google Scholar]
- Gorte R. J.; White D. Measuring Sorption Effects at Zeolite Acid Sites: Pursuing Ideas from W.O. Haag. Microporous Mesoporous Mater. 2000, 35–36, 447–455. 10.1016/S1387-1811(99)00241-3. [DOI] [Google Scholar]
- Tuma C.; Kerber T.; Sauer J. The tert-Butyl Cation in H-Zeolites: Deprotonation to Isobutene and Conversion into Surface Alkoxides. Angew. Chem., Int. Ed. 2010, 49, 4678–4680. 10.1002/anie.200907015. [DOI] [PubMed] [Google Scholar]
- Dai W.; Wang C.; Yi X.; Zheng A.; Li L.; Wu G.; Guan N.; Xie Z.; Dyballa M.; Hunger M. Identification of tert-Butyl Cations in Zeolite H-ZSM-5: Evidence from NMR Spectroscopy and DFT Calculations. Angew. Chem., Int. Ed. 2015, 54, 8783–8786. 10.1002/anie.201502748. [DOI] [PubMed] [Google Scholar]
- Jones A. J.; Zones S. I.; Iglesia E. Implications of Transition State Confinement within Small Voids for Acid Catalysis. J. Phys. Chem. C 2014, 118, 17787–17800. 10.1021/jp5050095. [DOI] [Google Scholar]
- Herrmann S.; Iglesia E. Elementary Steps in Acetone Condensation Reactions Catalyzed by Aluminosilicates with Diverse Void Structures. J. Catal. 2017, 346, 134–153. 10.1016/j.jcat.2016.12.011. [DOI] [Google Scholar]
- Rozanska X.; van Santen R. A.; Demuth T.; Hutschka F.; Hafner J. A Periodic DFT Study of Isobutene Chemisorption in Proton-Exchanged Zeolites: Dependence of Reactivity on the Zeolite Framework Structure. J. Phys. Chem. B 2003, 107, 1309–1315. 10.1021/jp021646b. [DOI] [Google Scholar]
- Schoonheydt R. A.; Geerlings P.; Pidko E. A.; van Santen R. A. The Framework Basicity of Zeolites. J. Mater. Chem. 2012, 22, 18705–18717. 10.1039/c2jm31366a. [DOI] [Google Scholar]
- Sarazen M. L.; Iglesia E. Stability of Bound Species During Alkene Reactions on Solid Acids. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, E3900–E3908. 10.1073/pnas.1619557114. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.