Abstract
Reverse electrodialysis (RED) is a membrane-based renewable energy technology that can harvest energy from salinity gradients. The anticipated feed streams are natural river and seawater, both of which contain not only monovalent ions but also divalent ions. However, RED using feed streams containing divalent ions experiences lower power densities because of both uphill transport and increased membrane resistance. In this study, we investigate the effects of divalent cations (Mg2+ and Ca2+) on RED and demonstrate the mitigation of those effects using both novel and existing commercial cation exchange membranes (CEMs). Monovalent-selective Neosepta CMS is known to block divalent cations transport and can therefore mitigate reductions in stack voltage. The new multivalent-permeable Fuji T1 is able to transport divalent cations without a major increase in resistance. Both strategies significantly improve power densities compared to standard-grade CEMs when performing RED using streams containing divalent cations.
1. Introduction
There is an increasing need for sustainable and clean energy sources because the use of fossil fuels has significant environmental drawbacks, such as greenhouse gas emissions. One of the emerging clean energy approaches is to harness salinity gradient energy, in which a difference in salinity between two solutions is used to harvest energy.1,2 At locations where rivers flow into the sea, there are two distinct water reservoirs with a difference in salinity that can be used to generate salinity gradient energy. These bodies of water mix anyway and therefore the environmental impact of such a process is expected to be nil. The salinity gradient can be harvested through a reverse electrodialysis (RED) process.2
RED uses ion exchange membranes to harvest energy from a salinity difference between two aqueous streams. Cation exchange membranes (CEMs) and anion exchange membranes (AEMs) are stacked in an alternating way with spacers in between to allow the flow of river and seawater. At both ends of the stack, electrodes and an electrolyte solution are used to transfer the ionic current from the salinity gradient into an electrical current. Under lab-scale conditions, gross power densities in the range of 2.2–2.9 W/m2 of membrane area have been achieved using artificial river and seawater streams containing only NaCl.3−5 However, the natural and abundant sources for RED power harvesting are natural river and seawater streams. As well as NaCl, these also contain divalent ions (such as Ca2+, Mg2+, and SO42–).6−8 Previous work has shown that the presence of these divalent ions leads to a decrease in RED power densities.7,8
Such decrease in power densities in RED in the presence of divalent cations can be due to (1) the transport of divalent cations against the overall concentration gradient (uphill transport) or (2) an increase in membrane electrical resistance.7,8 Uphill transport is well-known from both diffusion dialysis9,10 and RED,7,8 and results in divalent cations being transported from the low concentration side to the high concentration side when a large excess of monovalent cations is present on the concentrated side of the membrane. This is a purely entropic process (i.e., mixing) in which the entropy gained by moving two monovalent ions from the concentrated to the diluted side outweighs the entropy lost by the single divalent ion moving from the dilute to the concentrated side.
The second negative effect of the presence of divalent ions in RED stems from an increase in the membrane resistance due to interactions between the divalent ions and the fixed charged groups in the membrane. The electrical resistance is a measure of the required driving force (voltage) to transport charge (ionic current) through a membrane. If the driving force needed to transport ions increases, then the resistance of the membrane for these ions will also increases. The membrane resistance increases if, in addition to monovalent salts, there are divalent cations present,11 and Badessa et al.12 hypothesize that a chelating effect of divalent cations is the cause of this resistance increase. In other words, the increase in membrane resistance is due to a single divalent cation binding to two fixed charged groups in the membrane. Moreover, those authors indicate that there is a correlation between activation energies to transport ions through membranes and the corresponding membrane resistances, such that monovalent ions, such as Na+, that have low transport activation energies result in a low membrane resistance. However, anion exchange membranes do not exhibit the significant increase in resistance for divalent anions, which are common in natural waters, as shown by Krivcik et al.13 Also in porous membrane applications, cations show a high variability in properties as compared to anions. Anions do not differ as much as cations in terms of hydrated radius and hydration free energy, which are measures of the interaction of the ion with the surrounding water.14 For these reasons, cations are assumed to affect the performance most.
Both effects resulting of divalent cations, namely, uphill transport and membrane resistance increase, are shown schematically in Figure 1A and B. Mitigation strategies, as presented graphically in Figure 1C and D, will be discussed in the next subsection.
Figure 1.
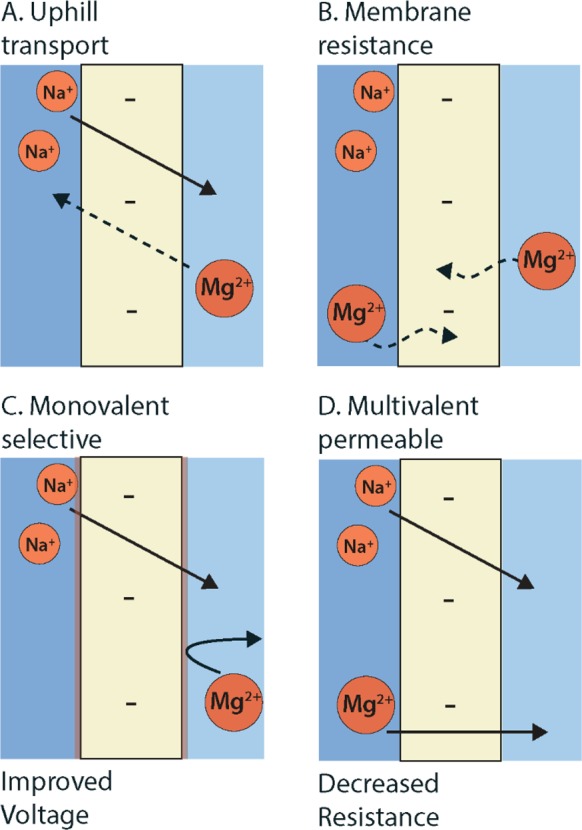
Effect of divalent cations on cation exchange membranes in RED: (A) Principle of uphill transport from divalent cations from the river water (right) to the seawater (left). (B) Membrane resistance increases because of divalent cation binding inside the membrane. Mitigation strategies are (C) monovalent-selective membranes to prevent uphill transport and (D) multivalent-permeable membranes to prevent resistance increase.
In this study, we investigate the negative effects of the presence of divalent cations in RED. Moreover, we present strategies to mitigate these effects using various types of cation exchange membranes (CEMs), as shown in Figure 1. Two strategies are considered. In the first approach, the use of monovalent-selective membranes (Figure 1C) is expected to reduce the transport of divalent cations, such as Mg2+ against the concentration gradient (Figure 1A). In the second approach, multivalent-permeable membranes (Figure 1D), recently developed specifically for RED in natural water streams, are expected not to suffer from significant resistance increase in the presence of divalent cations (Figure 1B). In these multivalent-permeable membrane type the negative charges are structured, providing pathways for ion transport. This construct is assumed to decrease the strong multiple binding of divalent cations, hence lowering the membrane resistance for these specific ions. We perform a detailed RED stack analysis on obtainable voltage, stack resistances and power densities for divalent cations at concentrations found in natural waters using these two types of cation exchange membranes. These special membranes are compared with existing standard-grade membranes, and the stack results are related to the specific membrane properties.
2. Theory
2.1. Open Circuit Voltage
The open circuit voltage (OCV) equals the voltage of a RED cell that is not subject to a load. A high OCV results in a high power density. The OCV (V) can be calculated according to the modified Nernst eq 1.15 The voltage is given for one cell pair which consists of one AEM and one CEM with river water flowing on one side and seawater flowing on the other side
| 1 |
where EOCV is the open circuit voltage (V), R is the gas constant (J/K·mol), T is the temperature (K), z is the valence of the ion (−), and F is the Faraday constant (s·A/mol). α is the permselectivity of the membrane (with α = 1 representing a perfect charge-selective membrane) and Cc and Cd are the Na+ or Cl– concentrations (M) in the concentrated stream (seawater) and diluted stream (river water) respectively. γ (−) is the activity coefficient of the respective ion in solution at a known concentration as determined from the CRC handbook.16
In the case of ideal membranes (α = 1) and solutions containing only NaCl (z = 1) with typical river and seawater concentrations (0.017 and 0.5 M)7 at room temperature (T = 293 K), the OCV is 0.143 V/cell, implying a stack voltage of 1.43 V for 10 cell pairs.
2.1.1. Uphill Transport
The OCV and uphill transport have the same fundamental origin, namely, the electromotive force (EMF) generated by a concentration gradient across charge-selective membranes. Uphill transport—or the exchange of ions against a concentration gradient—can be explained by looking at the Donnan potential as expressed in eq 2.
| 2 |
For a CEM with typical cations found in RED, the separate Donnan potentials for Na+ and Mg2+ can be determined by inserting the appropriate concentrations, charge (valence) and activity coefficients for each ion i in eq 2. Salt concentrations of 0.5 and 0.017 M for sea and river water, respectively, are typical in RED feed waters.7 In natural waters, about 10 mol % of Na+ in both streams is replaced by Mg2+.
Calculating the Donnan potentials of Na+ and Mg2+ across a CEM allows the prediction of the transport direction.7 The Donnan potential over a perfect CEM (α = 1) with 10% Mg2+ in the feed streams is 0.079 V for Na+ and 0.039 V for Mg2+. These cations influence each other, so Na+ and Mg2+ will start moving until the overall Donnan potential is balanced, achieving equilibrium (EDon,Na+ = EDon,Mg2+) and maintaining charge neutrality (two Na+ exchange for one Mg2+). From the initial starting condition, the Na+ driving force is higher than that of the Mg2+ and, through ion exchange, the Donnan potential for Na+ will decrease while that for Mg2+ will increase. In practice, this creates a reduced concentration gradient for Na+ and an increased one for Mg2+. The calculated Donnan potentials and equilibrium concentrations are provided in the Supporting Information (SI) 1.
2.2. Resistance
In RED, the total stack resistance is an important parameter because the higher the resistance, the lower the power density. The total stack resistance consists of the Ohmic resistances of the membranes, the electrodes and the feedwater compartments, and the non-Ohmic resistances, which are among others the resistances of the diffusion boundary layers.
The Ohmic resistances act in series, so they can be summed up as shown in eq 3. Typically, CEMs have higher resistances than AEMs in RED, and the river water compartment has a very high resistance compared to the other resistances because of its low salt concentration and is often the dominant resistance.3
| 3 |
In eq 3, the resistances are area resistances (R) expressed in Ω·m2, and RW and SW are river water and seawater, respectively. Non-Ohmic resistances are challenging to study in RED because of their transient nature, as they consist of diffusion boundary layers and double layers in channels.3
2.3. Gross and Net Power Density
The power density expresses the power that can be generated per meter squared of membrane area. The gross power density (Pgross) depends directly on the OCV (EOCV,stack) and stack resistance (Rstack), and it is calculated as17
| 4 |
where EOCV,stack is in V, j is current density in A/m2, and Rstack is in Ω·m2. Nm is the total number of both anion and cation membranes (rather than cell pairs).
The net power density (Pnet in W/m2 membrane) can be calculated by subtracting the pumping losses from the gross power density. The (normalized) pumping losses can be calculated as
| 5 |
where Δp is the average pressure drop over the river and seawater compartment (Pa), Φ is the average flow rate of river and seawater in m3/s, and A is the total membrane area in meters squared.
3. Materials and Methods
3.1. Membranes and Chemicals
The following ion exchange membranes were used in this study: heterogeneous Ralex CMH-PES (MEGA, Czech Republic), homogeneous monovalent-selective Neosepta CMS (Astom Corp. Ltd., Japan), homogeneous multivalent-permeable Fuji T1, homogeneous Type I CEM, homogeneous T0 CEM, and homogeneous Type I AEM (FUJIFILM, The Netherlands).
MgCl2·6H2O, CaCl2·2H2O, K3Fe(CN)6, and K4Fe(CN)6·3H2O were purchased from Sigma-Aldrich. NaCl (Emprove Ph. Eur. Grade) was obtained from Merck.
3.2. Membrane Characterization
Before the measurements, membranes were soaked in 0.5 M NaCl for 48 h to exchange them to Na+-form for the CEMs and Cl–-form for the AEMs. The CEMs were soaked for 48 h in 0.5 M MgCl2, a mixture of 0.45 M NaCl and 0.05 M MgCl2, and 0.5 M NaCl, respectively, for the resistance measurements in pure Mg2+, a mixture of 90% Na+ and 10% Mg2+, and pure Na+. In the same solutions, the membrane resistances are measured, to compare with RED data and determine the selectivity of Na/Mg.
The membrane thickness was measured by a digital screw micrometer (Mitutoyo 293–240, Mitutoyo Co., Japan). Membrane area and specific resistance measurements were performed in a six-compartment cell, as described in previous work.18,19 When measuring the membrane in MgCl2, AEMs rather than CEMs are used as auxiliary membranes to prevent mixing with the NaCl shielding solution. Both AC and DC resistances were measured, as AC allows for Ohmic resistance analysis. DC resistance measurements included non-Ohmic resistances and allowed measuring the repulsion of divalent cations by monovalent-selective membranes. For all these measurements, a potentiostat (PGSTAT302N) equipped with a frequency response analyzer (FRA) was controlled by NOVA software (Metrohm Autolab, The Netherlands).
Membranes were evaluated according to their resistances in NaCl and MgCl2, and the ratio of these resistances defines their transport selectivity, as shown in eq 6.13 Here, selectivity is based on electrical resistance measurements for different ions and not as a ratio of ions transported.20 As in the case of RED operation, resistance is a more accurate predictor than specific ion fluxes. Rmg and Rna are membrane resistances (Ω·cm2) in Mg2+ and Na+ form respectively and SNaMg (−) is selectivity.
| 6 |
3.3. Stack Performance Evaluation
A cross-flow stack (REDstack B.V., The Netherlands) of active area 6.5 × 6.5 cm (42.25 cm2) and 10 cell pairs was equipped with Ti/Ru–Ir Electrodes (MAGNETO Special Anodes B.V., The Netherlands). Masterflex peristaltic pumps (Cole-Parmer) were used to pump the feed and the electrolyte solutions. Solution concentrations and conductivities of the feed waters are given in the Supporting Information (SI 2). The feed streams were switched in the following order: from pure NaCl, to 10% Mg2+ in only seawater, to both streams with 10% Mg2+, to 10% Mg2+ in only river water, and back to pure NaCl. In-house built pulsation dampeners were used for both feed streams. The stack was assembled with membranes presoaked in 0.5 M NaCl. Polyamide woven spacers were obtained from Deukum (Deukum GmbH, Germany) and had a thickness of 200 μm with a void fraction of 0.726 and a free surface fraction of 0.476. A torque of 2 N m was applied on the stack in a cross-wise fashion. The outer membranes were FUJFILM T0 CEMs as these are able to retain the electrode rinse solution. The resistances of the extra outer CEM, the electrode rinse solution and the electrodes were subtracted from the measured stack resistances.
Since in this study, CEMs are compared rather than stack hydrodynamics, the stack was in all cases equipped with the same spacers and operated at the same flow rate of 53 mL/min (linear flow velocity of 0.92 cm/s), and the resulting average pressure drop was found to be 0.13 bar at an electrolyte pressure of 0.22 bar. This results in a small overpressure on the electrolyte of 0.09 bar to ensure packing of the membranes. The flow speed is chosen such that it is close to the value needed to obtain the optimal net power density.3
Before electrochemical analysis of a stack, current is applied (20 A/m2) for 20 min to ensure equilibration of the ion exchange membranes with the ionic feed solutions. Subsequently, the OCV and the AC and DC resistances were measured. For AC resistance measurements, three measurements are performed, at 10, 5, and 1 kHz and an amplitude of 0.01 A (2.4 A/m2) with 0.125 s integration time for the frequency response analyzer in the potentiostat. For the DC resistance, ten current steps from 0 to 50 A/m2 and ten steps back to 0 A/m2 are applied to calculate the resistance and to assess the stability (hysteresis) of the system (see SI 3). The effective OCV is determined from the IV curve used for DC resistance at zero current density, as this gives a realistic value of the OCV for the obtainable power density. In theory, a linear IV curve should be obtained. However, in practice the curve is not completely linear because of changing water compartment resistance among other reasons (see SI 3 for the experimental IV curves). To improve the accuracy of the power density data, measurements at multiple current densities were performed to find the optimum current density for power production. Each current density was applied for 10 s (1.4 times the stack residence time) before the voltage over the electrodes was measured. If the two measurements did not overlap, which is an indication that the cations are not yet in equilibrium within the membranes, the same procedure was repeated until overlap was achieved. Finally, reported power densities are maximum gross power densities, which are calculated using the OCV and Rstack—based on the DC resistance—at the optimal experimental current density.
4. Results and Discussion
4.1. Membrane Characterization
The properties of ion exchange membranes determine the stack performance, especially in the presence of divalent cations. To understand stack effects, we first studied individual cation exchange membranes for their ability to conduct the various cations.
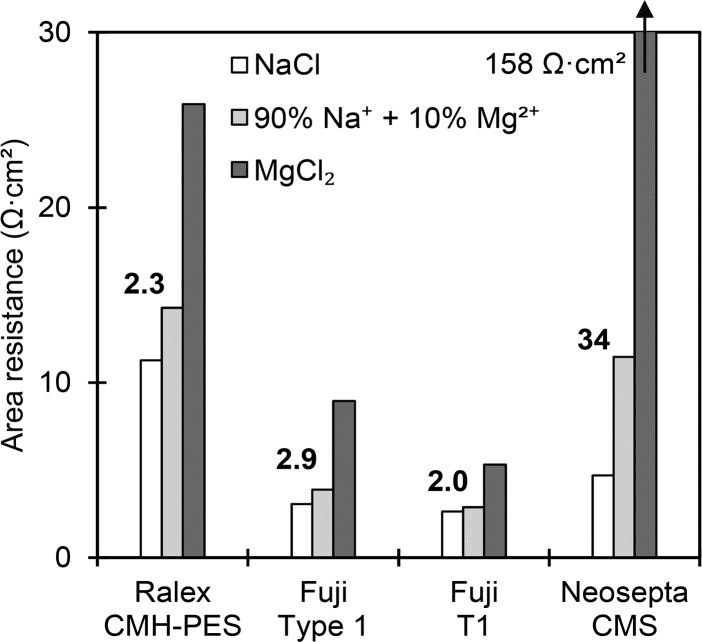
The area resistance is a membrane property and can be a predictor of the performance, whereas the specific resistance is the Ohmic area resistance normalized over the thickness of the membrane (the specific resistances are shown in SI 4). In Figure 2, the area resistances of the membranes in solutions with NaCl, a mixture of 90% NaCl and 10% MgCl2, and MgCl2 are all shown. The numbers next to the bars are the SNaMg values calculated using eq 6. In this study, all membranes had area resistances between 2.6 and 11.3 Ω·cm2. Both Fuji and Neosepta membranes are thin (125–150 μm), so they have low area resistances in the case of NaCl, in contrast to the Ralex membrane, which is thick (680 μm) and therefore has a high area resistance.
Figure 2.
Measured area resistance (determined by direct current) of CEMs in 0.5 M NaCl, a mixture of 90% NaCl and 10% MgCl2, and MgCl2 respectively. Values next to bars are transport selectivities calculated by eq 6. The MgCl2 resistance for CMS was very high due to the tailored transport properties for monovalent cations.21
In addition to thickness effects, effects for monovalent over divalent cations are investigated. In MgCl2, the area resistance of the monovalent-selective CMS membrane (158 Ω·cm2) showed a remarkable difference of over 10 times greater compared to the other CEMs. In mixtures of 90% NaCl and 10% MgCl2, similar trends were found, although differences between membranes were smaller due to the lower Mg2+ concentration. These resistances are of interest for the RED stack experiments on this mixture with 10% MgCl2. These results give a clear picture of the (different) cation transport behavior of these CEMs, since T1 allowed Mg2+ transport (low resistance Mg2+), while CMS blocked it (high resistance Mg2+). Further detailed membrane characterization is given in SI 4 (IEC and water content), as well as in SI 5 (ion exchange isotherms).
4.2. RED Stack Performance
4.2.1. OCV
Once we had a clear view of the membrane transport properties, we investigated the performance in a RED stack and compared the results to calculations based on the previously described theory. RED stack performance measurements were performed using simulated river and seawaters (aqueous NaCl solutions). Natural compositions fluctuate over time and location; hence, we chose the divalent cation composition comparable to that used in previous research: replacing 10% of NaCl by MgCl2 in river and seawater.
In Table 1, in general a decrease of OCV was observed after introducing divalent cations. As the Nernst potential is reduced by a factor of 2 for pure solutions of only divalent ions (see eq 1), partially replacing sodium for divalent cations lowers the potential. However, this is a very small effect on the OCV.
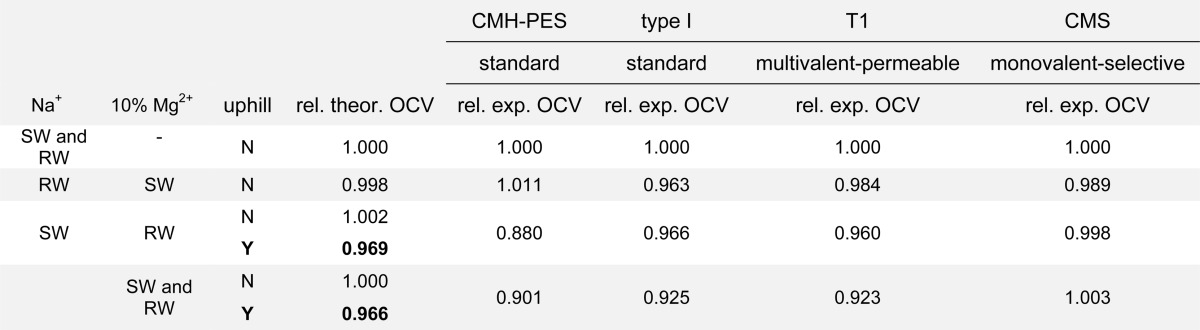
Table 1. Solutions Used in Studies and the Relative OCV (Experimental Value Divided by Theoretical, Calculated Value) OCV per Cell [V]a.
Errors in the relative OCV values are ±0.010.
In Table 1, the experimental OCV values were calculated relative to the values obtained in NaCl. By doing this, only effects of divalent cations on membranes are taken into account and stack effects such as co-ion leakage are excluded. The calculated (theoretical) values were based on only the EMF of the monovalent-species present (Na+ and Cl–), with or without uphill transport. If uphill transport is taken into account, the exchange of Mg2+ in the river water to the seawater by Na+ is considered and the OCV is calculated using the concentrations obtained at equilibrium. For this equilibrium, in all cases the exchange of Mg2+ with Na+ was nearly complete (see SI 1 Figure S1.2, at equilibrium there was only 0.11 mM of Mg2+ left in the river water).
All membranes showed a drop in OCV when Mg2+ is present in either feed stream. In this subsection the various contributions to this OCV drop are discussed. The CMH-PES showed a drop in relative OCV (to 0.88); however, the calculated change for uphill transport (to 0.97) does not seem to justify this drop. Possibly this disagreement is due to CMH-PES’s heterogeneous nature.8 The monovalent-selective CMS showed a near constant relative OCV for all the feed streams, even with divalent cations. Clearly, the effect of Mg2+ on the OCV through uphill transport was mitigated as even with only Mg2+ in the river water (implying a high driving force for uphill transport), there is no significant decrease in relative OCV. As for the multivalent-permeable T1 and standard-grade type I, the drop in relative OCV was very similar in all cases. For both these membranes, the presence of Mg2+ in the river water decreased the experimental relative OCV by 3.4–4.0%. These values, when error margins are considered, agreed with the relative theoretical OCV (3.1%). It seems that by correcting for the equilibrium concentrations obtained by equalizing EMFs, one can predict the relative OCV decrease when divalent cations are present. In addition to uphill transport, another effect was decreasing the OCV: when there is Mg2+ in the seawater, relative decreases of 3.7%, 1.7%, and 1.1% for type 1, T1, and CMS, respectively, were observed. This OCV decrease was different for each membrane and cation, and can be caused by cation and charged-group interactions. This decrease has been observed in single-membrane permselectivity measurements for different cations,22,23 which can explain the OCV decrease we observed in this study. Although these single-membrane experiments22,23 were performed in pure solutions, these findings are expected to be applicable to the mixed systems studied here.
Finally, if we consider Mg2+ in both river and seawater, both effects (of uphill transport and permselectivity decrease) played a role in OCV loss. For standard-grade type I and multivalent-permeable T1, there was a relative drop of 7.3–7.5%, which seems to suggest that both uphill transport (3.4% loss) and permselectivity decreases (1.7–3.7% loss) were causing this OCV reduction. In summary, we showed and decoupled the effects on OCV when divalent cations are present: uphill transport, permselectivity decrease, or a combination thereof.
4.2.2. Resistance
Stack resistances for the various CEMs in a RED system both with and without divalent cations are evaluated. The total (ohmic and non-ohmic) resistance was generally 110–125% of the ohmic resistance (see SI 6 and SI 7 for Mg2+ and Ca2+ data, respectively). The non-Ohmic resistance was the highest with divalent cations present but no clear trends between different membranes were observed. In this section, the ohmic stack resistance was calculated and compared with experimental results (shown in Figure 3).
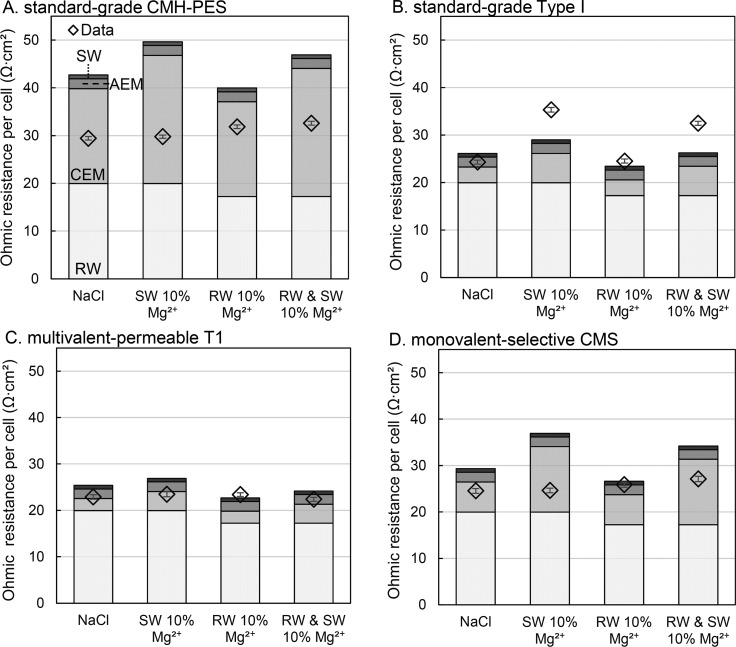
Figure 3.
Ohmic area resistance for NaCl and 10% Mg2+ in river and seawater feed streams for Ralex CMH-PES, Fuji type I, Fuji T1, and Neosepta CMS. Diamonds show the measured total stack Ohmic area resistances and bars show the calculated Ohmic area resistances for the individual stack components.
Ohmic resistances of all components were calculated, as described in section 2, and compared with the experimental total ohmic resistance of a cell. Resistances for the AEM and the seawater compartment have a low relative contribution due to a low anion membrane area resistance (1.0 Ω·cm2) and a high concentration of salt, respectively. However, the river water—due to its low conductivity resulting from the low concentration of salt—and the CEM—resulting from a high membrane area resistance—account for most of the cell resistance. In this study, the feed compositions were next changed from NaCl to 10% Mg2+ (and 90% Na+). When Mg2+ was introduced in the river water, the resistance of the river water will be lower due to a 10% higher concentration of Cl–. When Mg2+ was introduced in seawater, its resistance will also decrease slightly. These solution conductivity changes are shown in SI 7. In addition, introducing Mg2+ in seawater will increase the CEM resistance, as seen in Figure 2. The CEM resistance was assumed to be the membrane resistance measured in 10% Mg2+. However, this assumption is not fully valid, as in a RED stack one side of the membrane faces a high concentration solution and the other side a low concentration.18 This assumption gave a reasonable approximation when using the current experimental setup.
For CMH-PES, a standard-grade heterogeneous membrane, the measured cell resistance did not change dramatically after introducing Mg2+ in either feed stream. This was expected as a low selectivity of 2.3 (shown in SI 2) implies a low relative change in resistance. However, the resistance of this membrane was high and this led to the highest cell resistances of all membranes. The overestimation of the calculated resistances can be caused by co-ion diffusion as a result of low permselectivity, which was also shown by the low OCV.
For type I, a standard-grade homogeneous membrane, a large change in resistance was observed after introducing Mg2+ in the seawater stream. A large change in resistance was expected from the selectivity of 2.9. However, in the experiments an even larger change was observed though the trend is as predicted.
For the multivalent-permeable T1, there was no significant change in experimental cell resistance, as can be expected from the low selectivity of 2.0. The resistance of this membrane was hardly affected by Mg2+, which clearly demonstrates its ability to permeate divalent cations, and this resulted in the lowest absolute cell resistance of all stacks, especially with divalent cations.
Finally, for the monovalent-selective CMS, a large change in resistance was calculated due to the high selectivity; however, hardly any change in resistance was observed in experiments. The monovalent-selective properties are the cause for Mg2+ being hindered in exchanging with this membrane. Our hypothesis is, therefore, that over time the resistance of CMS will increase. Future studies involving long-term experiments could verify this hypothesis.
4.2.3. Power Density
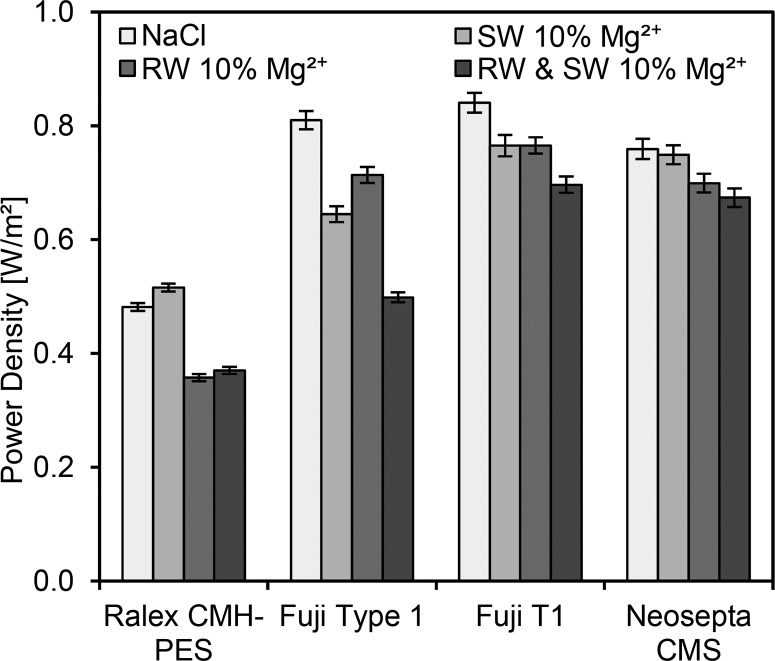
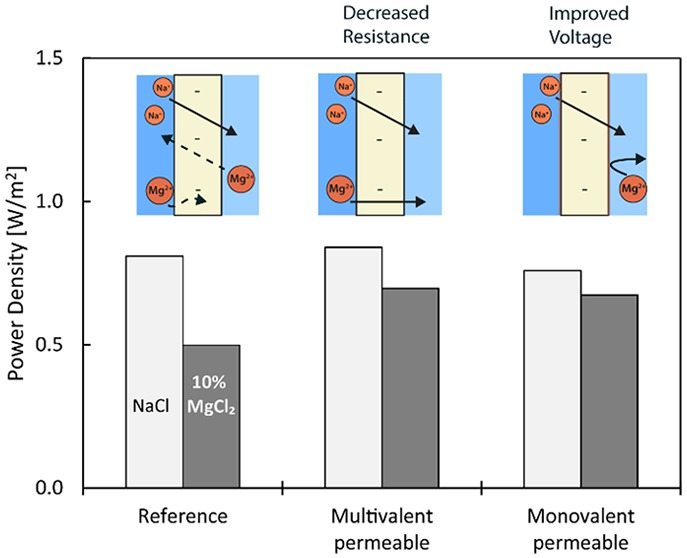
Gross power densities were calculated from the OCV and resistance data given in previous sections (see eq 5). In this study, hydrodynamics (flow velocity, spacers, and temperature) and pressure drops were kept constant, so as to focus on the ions and membranes. For comparison with other work, net power densities can be calculated by subtracting pumping losses (of 0.27 W/m2 for all stacks described in this study) using eq 3 and 4. Gross power density is affected by both OCV and resistance changes, and it is considered to represent the output performance in RED, which makes it a suitable measure for comparison. The power densities for all membranes with all feed compositions are shown in Figure 4. In general, all membranes showed a decrease in power density once divalent cations are introduced. Power densities of CMH-PES were lower than those of other membranes because of lower permselectivity and higher resistance but were not affected by divalent cations as much as other membranes. For the type I membrane, a clear decrease in power density (of 38%) was observed when divalent cations are present, and this is a result of both uphill transport and resistance increase. Results for type I (formerly known as V1) and CMH-PES for NaCl were similar to those reported by Vermaas et al.8 Following the introduction of 10% MgSO4, similar gross power densities as shown in this work (0.50 W/m2 for type I and 0.37 W/m2 for CMH-PES) were obtained in their work (0.5 W/m2 for FUJI type I and 0.3 W/m2 for Ralex CMH-PES), which is surprising as MgCl2 contains no divalent anions.8 This could suggest the dominant effect of cations, but needs to be studied in depth to be confirmed. In this study, it can be concluded that multivalent-permeable T1 had the highest power density in NaCl, but it decreased with divalent cations, mostly because of OCV losses as discussed earlier. However, the obtained gross power density of 0.70 W/m2 was the highest achieved for the studied membranes with 10% divalent cations in this study. Monovalent-selective CMS had a lower power density in NaCl compared to type I and T1; because of its high membrane resistance, it does, however, have the highest OCVs (see SI 8). If divalent cations were introduced, only a minor decrease in power density (to 0.67 W/m2) is observed due to its ability to block divalent cation transport and thus uphill transport.
Figure 4.
Gross power densities (W/m2) with Mg2+ in feed streams for heterogeneous Ralex CMH-PES, standard-grade Fuji type I, multivalent-permeable Fuji T1 and monovalent-selective Neosepta CMS. To obtain net power densities, 0.27 W/m2 pumping losses need to be subtracted.
To study the effect of the other naturally abundant divalent cation Ca2+, RED experiments with type I and T1 with 10% Ca2+ as feedwater were performed. Similar gross power density effects were observed (data shown in SI 7), suggesting a universal effect of naturally abundant divalent cations.
These results stress the need for additional stack evaluation with realistic ionic compositions of natural feed streams to predict the realistic RED power densities. This study showed that RED power densities can be improved by selecting a cation exchange membrane suitable for the cation composition of the feed streams. Multivalent-permeable membranes did not suffer from significant resistance increase and are therefore recommended for streams with high divalent cation contents. Monovalent-selective membranes are able to mitigate uphill transport and are therefore suggested for river water with high divalent cation content. Both these special-grade membranes significantly improve power densities by at least 30% (or 0.15 W/m2) compared to standard CEMs.
To improve RED in the presence of divalent cations even further, future studies could focus on strategies to mitigate both uphill transport and resistance increase. Moreover, the effect of divalent anions should be studied separately as well to describe their influence.
Acknowledgments
This work was performed in cooperation with Wetsus, the European Centre of Excellence for Sustainable Water Technology (www.wetsus.eu). Wetsus is cofunded by the Dutch Ministry of Economic Affairs, the Ministry of Infrastructure and Environment, the Province of Fryslân, and the Northern Netherlands Provinces. The authors would like to sincerely thank the participants of the “Blue Energy” research theme for many fruitful discussions and their financial support.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.est.7b03858.
Additional information about uphill transport, detailed ion exchange membrane characterization, feedwater composition, and stack experimental data, such as resistance and OCVs (including mixtures with Ca2+) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Pattle R. E. Production of Electric Power by mixing Fresh and Salt Water in the Hydroelectric Pile. Nature 1954, 174 (4431), 660–660. 10.1038/174660a0. [DOI] [Google Scholar]
- Post J. W.; Veerman J.; Hamelers H. V. M; Euverink G. J. W.; Metz S. J.; Nymeijer K.; Buisman C. J. N. Salinity-gradient power: Evaluation of pressure-retarded osmosis and reverse electrodialysis. J. Membr. Sci. 2007, 288 (1–2), 218–230. 10.1016/j.memsci.2006.11.018. [DOI] [Google Scholar]
- Vermaas D. A.; Saakes M.; Nijmeijer K. Doubled Power Density from Salinity Gradients at Reduced Intermembrane Distance. Environ. Sci. Technol. 2011, 45 (16), 7089–7095. 10.1021/es2012758. [DOI] [PubMed] [Google Scholar]
- Kim H.-K.; Lee M.-S.; Lee S.-Y.; Choi Y.-W.; Jeong N.-J.; Kim C.-S. High power density of reverse electrodialysis with pore-filling ion exchange membranes and a high-open-area spacer. J. Mater. Chem. A 2015, 3 (31), 16302–16306. 10.1039/C5TA03571F. [DOI] [Google Scholar]
- Moreno J.; Slouwerhof E.; Vermaas D. A.; Saakes M.; Nijmeijer K. The Breathing Cell: Cyclic Intermembrane Distance Variation in Reverse Electrodialysis. Environ. Sci. Technol. 2016, 50 (20), 11386–11393. 10.1021/acs.est.6b02668. [DOI] [PubMed] [Google Scholar]
- Galama A. H.; Daubaras G.; Burheim O. S.; Rijnaarts H. H. M.; Post J. W. Seawater electrodialysis with preferential removal of divalent ions. J. Membr. Sci. 2014, 452, 219–228. 10.1016/j.memsci.2013.10.050. [DOI] [Google Scholar]
- Post J. W.; Hamelers H. V. M; Buisman C. J. N. Influence of multivalent ions on power production from mixing salt and fresh water with a reverse electrodialysis system. J. Membr. Sci. 2009, 330 (1–2), 65–72. 10.1016/j.memsci.2008.12.042. [DOI] [Google Scholar]
- Vermaas D. A.; Veerman J.; Saakes M.; Nijmeijer K. Influence of multivalent ions on renewable energy generation in reverse electrodialysis. Energy Environ. Sci. 2014, 7 (4), 1434–1445. 10.1039/C3EE43501F. [DOI] [Google Scholar]
- Miyoshi H. Diffusion coefficients of ions through ion excange membrane in Donnan dialysis using ions of different valence. J. Membr. Sci. 1998, 141 (1), 101–110. 10.1016/S0376-7388(97)00297-4. [DOI] [Google Scholar]
- Higa M.; Tanioka A.; Miyasaka K. Simulation of the transport of ions against their concentration gradient across charged membranes. J. Membr. Sci. 1988, 37 (3), 251–266. 10.1016/S0376-7388(00)82432-1. [DOI] [Google Scholar]
- Sata T.; Sata T.; Yang W. Studies on cation-exchange membranes having permselectivity between cations in electrodialysis. J. Membr. Sci. 2002, 206 (1–2), 31–60. 10.1016/S0376-7388(01)00491-4. [DOI] [Google Scholar]
- Badessa T.; Shaposhnik V. The electrodialysis of electrolyte solutions of multi-charged cations. J. Membr. Sci. 2016, 498, 86–93. 10.1016/j.memsci.2015.09.017. [DOI] [Google Scholar]
- Křivčík J.; Neděla D.; Hadrava J.; Brožová L. Increasing selectivity of a heterogeneous ion-exchange membrane. Desalin. Water Treat. 2015, 56 (12), 3160–3166. 10.1080/19443994.2014.980970. [DOI] [Google Scholar]
- Tansel B. Significance of thermodynamic and physical characteristics on permeation of ions during membrane separation: Hydrated radius, hydration free energy and viscous effects. Sep. Purif. Technol. 2012, 86, 119–126. 10.1016/j.seppur.2011.10.033. [DOI] [Google Scholar]
- Weinstein J. N.; Leitz F. B. Electric Power from Differences in Salinity: The Dialytic Battery. Science 1976, 191 (4227), 557–559. 10.1126/science.191.4227.557. [DOI] [PubMed] [Google Scholar]
- CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press/Taylor & Francis: Boca Raton, FL, 2017. [Google Scholar]
- Vermaas D. A.; Veerman J.; Yip N. Y.; Elimelech M.; Saakes M.; Nijmeijer K. High Efficiency in Energy Generation from Salinity Gradients with Reverse Electrodialysis. ACS Sustainable Chem. Eng. 2013, 1 (10), 1295–1302. 10.1021/sc400150w. [DOI] [Google Scholar]
- Galama A. H.; Vermaas D. A.; Veerman J.; Saakes M.; Rijnaarts H. H. M.; Post J. W.; Nijmeijer K. Membrane resistance: The effect of salinity gradients over a cation exchange membrane. J. Membr. Sci. 2014, 467, 279–291. 10.1016/j.memsci.2014.05.046. [DOI] [Google Scholar]
- Długołęcki P.; Ogonowski P.; Metz S. J.; Saakes M.; Nijmeijer K.; Wessling M. On the resistances of membrane, diffusion boundary layer and double layer in ion exchange membrane transport. J. Membr. Sci. 2010, 349 (1–2), 369–379. 10.1016/j.memsci.2009.11.069. [DOI] [Google Scholar]
- Güler E.; van Baak W.; Saakes M.; Nijmeijer K. Monovalent-ion-selective membranes for reverse electrodialysis. J. Membr. Sci. 2014, 455, 254–270. 10.1016/j.memsci.2013.12.054. [DOI] [Google Scholar]
- Tuan L. X.; Mertens D.; Buess-Herman C. The two-phase model of structure microheterogeneity revisited by the study of the CMS cation exchange membrane. Desalination 2009, 240 (1–3), 351–357. 10.1016/j.desal.2007.10.098. [DOI] [Google Scholar]
- Cassady H. J.; Cimino E. C.; Kumar M.; Hickner M. A. Specific ion effects on the permselectivity of sulfonated poly(ether sulfone) cation exchange membranes. J. Membr. Sci. 2016, 508, 146–152. 10.1016/j.memsci.2016.02.048. [DOI] [Google Scholar]
- D’Alessandro S. Equilibrium and transport properties of ion-exchange membranes. J. Membr. Sci. 1984, 17 (1), 63–69. 10.1016/S0376-7388(00)81387-3. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.