Abstract
In prediction of genomic values, the single-step method has been demonstrated to outperform multi-step methods. In statistical analyses of longitudinal traits, the random regression test-day model (RR-TDM) has clear advantages over other models. Our goal in this study was to evaluate the performance of a model that integrates both single-step and RR-TDM prediction methods, called the single-step random regression test-day model (SS RR-TDM), in comparison with the pedigree-based RR-TDM and genomic best linear unbiased prediction (GBLUP) model. We performed extensive simulations to exploit the potential advantages of SS RR-TDM over the other two models under various scenarios with different levels of heritability, number of quantitative trait loci, as well as selection scheme. SS RR-TDM was found to achieve the highest accuracy and unbiasedness under all scenarios, exhibiting robust prediction ability in longitudinal trait analyses. Moreover, SS RR-TDM showed better persistency of accuracy over generations than the GBLUP model. In addition, we also found that the SS RR-TDM had advantages over RR-TDM and GBLUP in terms of its being a real data set of humans contributed by the Genetic Analysis Workshop 18. The findings of our study demonstrated the feasibility and advantages of SS RR-TDM, thus enhancing the strategies for genomic prediction of longitudinal traits in the future.
Introduction
Complex traits with multiple phenotypic values changing over time are called time-dependent or longitudinal traits. Knowledge of the genetic effects influencing longitudinal patterns is important to predict phenotypic progression in longitudinal analyses. Thus far, genetic effect prediction for longitudinal data had been mainly based on the traditional random regression test-day model (RR-TDM; Schaeffer and Dekkers, 1994), which is a very sophisticated model based on pedigree and is commonly used in genetic evaluation. RR-TDM was originally developed for the statistical analyses of longitudinal data, when observations were recorded at multiple time points.
Since the seminal work of Meuwissen et al. (2001), genomic data coupled with corresponding statistical modeling approaches were successfully implemented into genomic prediction. Currently, huge progress has been achieved in genomic prediction in animal breeding (for example, VanRaden et al., 2009; Koivula et al., 2015), plant breeding (for example, Zhong et al., 2009) and human genetics (for example, de los Campos et al., 2013). Although we can enhance the genomic prediction ability for traditional single-record traits by using the strategy of genomic selection, genomic prediction for longitudinal traits had not received extensive attention in practice so far.
In terms of different strategies of utilizing training data in the analyses, methods for genomic prediction can be generally classified into two categories: multi-step and single-step. The multi-step method involves two steps for genomic evaluation: (1) constructing a response variable obtained from regular genetic evaluation, and (2) genomic prediction associating the response variable with marker information. Although this could be applied easily with no major change to the regular genetic evaluation system, the multi-step procedure resulted in lower accuracies, bias and loss of information (Legarra et al., 2009). Moreover, with multi-step approaches, genotyped individuals could not contribute to the evaluation of their non-genotyped relatives in pedigree. To overcome these shortcomings, Legarra et al. (2009) and Christensen and Lund (2010) proposed the single-step method in parallel, which utilized pedigree, genomic and phenotypic data simultaneously in genomic evaluation. The single-step approach has the advantages of predicting all genotyped and non-genotyped individuals simultaneously and less prediction bias (Vitezica et al., 2011; Christensen et al., 2012). Application of the single-step method in genomic evaluation of domestic animals has been explored in many studies so far (for example, Christensen et al., 2012; Koivula et al., 2015).
In addition to the better prediction performance in comparison with the multi-step approach, the single-step method has the property of straightforward extension to RR-TDM for genomic prediction of longitudinal traits. Prior to the availability of a large amount of genotypic data, RR-TDM has been widely used in the improvements of longitudinal traits in livestock (for example, Schaeffer et al., 2000). Considering the advantages of the single-step method and RR-TDM in genetic prediction, it is expected that their combination should result in better performance of genomic prediction. This has preliminarily been investigated by a recent study of Koivula et al. (2015). In their study, the single-step (SS) RR-TDM model was implemented for the genomic evaluation of Nordic Red Dairy cows for milking performance, which showed higher accuracies and less bias in the prediction compared to the traditional RR-TDM model. Although SS RR-TDM has theoretical advantages over other methods in genomic evaluation, it has not been clear whether it will outperform the commonly used multi-step genomic prediction for longitudinal traits under various scenarios.
Accordingly, the goal of this study was to investigate the performance of SS RR-TDM in genomic evaluation under various scenarios through extensive simulations and real data validation. We also explored its persistency of prediction accuracies over generations. By incorporating the single-step strategy into a random regression model, we offer for the first time a systematic evaluation of the feasibility and effectiveness of SS RR-TDM methodology in longitudinal trait genomic prediction, further broadening the scope of single-step strategy application in the practice of genomic prediction.
Materials and methods
Statistical model
We constructed a SS RR-TDM with a longitudinal phenotypic variable decomposed as follows:
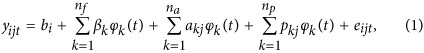 |
where yijt is the phenotypic record of individual j at time point t within the ith level of fixed effect b; βk is the kth fixed regression coefficient; akj and pkj are the kth random regression coefficient for additive genetic and permanent environmental effects, respectively, for individual j; φk(t) is the kth covariate for the observation of individual j made at time point t; nf, na and np are the numbers of fixed, random additive and random permanent environmental covariates; and eijt is the time-independent random residual error for each observation. Specifically, permanent environmental effects are the permanent and non-transmissible effects, such as dominance effects, epistatic effects and permanent stunting when young (Lush, 1943). They were different between individuals, and therefore were assumed to be random effects. In model (1), fixed and random regressions can be defined as covariance functions with different expressions, for example, Wilmink function (Wilmink, 1987) and Legendre polynomials (Kirkpatrick et al., 1990).
The matrix representation of the model is accordingly denoted as
where y is the vector of phenotypes; b1 is the vector of fixed effects; b2 is the vector of fixed regression coefficients; a and p are vectors of random regressions for additive genetic effect and permanent environmental effect; X1, X2, Q and Z are design matrices of b1, b2, a and p, respectively; e is the vector of residuals. X1 contains indicator variables for time-independent fixed effects (ones and zeroes), and X2, Q and Z contain time-dependent covariates.
It was assumed that
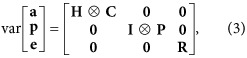 |
where I is an identity matrix with dimensions equal to the number of effect levels, ⊗ is the Kronecker product, C and P are (co)variance matrices of additive genetic and permanent environmental regression coefficients, 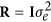 with
with 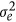 standing for residual variance, and H is the combined relationship matrix. According to Legarra et al. (2009), H was defined as
standing for residual variance, and H is the combined relationship matrix. According to Legarra et al. (2009), H was defined as
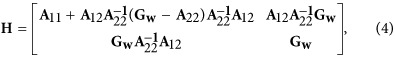 |
where A11, A12 and A22 are partitions of A, the numerator relationship matrix based on pedigree, and subscripts 1 and 2 refer to ungenotyped and genotyped individuals, respectively. Gw is derived from an adjusted kinship matrix G*, and is constructed using both pedigree and genotype information. It is expressed as
with
where w reflects the fraction of genetic variance not being captured by single-nucleotide polymorphism (SNP) markers (Christensen et al., 2012) and can also be used to avoid singular problems of the G matrix (VanRaden, 2008), and G is genomic relationship matrix constructed by the first method of VanRaden (2008):
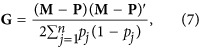 |
where M is a matrix of SNP genotypes for each individual, P is a matrix of 2 times the observed allele frequency of the second allele p at locus j (pj). Ideally, allele frequencies in the base population should be used in the construction of G; however, they were not available in most practical situations. In consideration of simplicity in implementation, we used observed allele frequencies of genotyped individuals in our study, which was also a good reference and was commonly used in other studies (for example, Wolc et al., 2011; Christensen et al., 2012). In principle, the additive genetic variance using G is identical to that using A (Habier et al., 2007).
In Equation (6), G* was considered as the adjusted G matrix for avoiding potential incompatibility in scale between G* and A22 involved in the H matrix (Chen et al., 2011; Vitezica et al., 2011). G* was computed based on the approach of Christensen et al. (2012).
The corresponding mixed model equations (MME) for equation (2) are
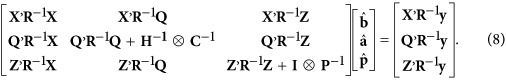 |
In the solutions of this MME, each individual has na regression coefficients as predictions for additive genetic effects. Predicted genetic value (PGV) of individual j for any particular time point t of interest, for example, systolic and diastolic blood pressure at a particular age, could be simply achieved as follows:
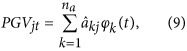 |
where φk(t) and na are as described in equation (1), and 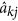 is the solution for the kth regression coefficient of individual j. If the accumulated PGV for a period of time is of interest, for example, 305 days’ milk yield in dairy cattle or egg production during the first 22 weeks of production in layer chicken, it could be calculated by adding up the PGVs at different time points over a specific period.
is the solution for the kth regression coefficient of individual j. If the accumulated PGV for a period of time is of interest, for example, 305 days’ milk yield in dairy cattle or egg production during the first 22 weeks of production in layer chicken, it could be calculated by adding up the PGVs at different time points over a specific period.
To exploit the potential advantages of SS RR-TDM over its conventional counterparts, we also performed genetic/genomic prediction with the two widely used models, that is, the regular pedigree-based RR-TDM evaluation approach and the multiple-step method of genomic best linear unbiased prediction (GBLUP).
The GBLUP model (VanRaden, 2008) is defined as follows:
where y is a n × 1 vector of the response variable; μ is the overall mean; 1n is a vector of n ones; g is the n × 1 vector of additive genomic effects with the distribution 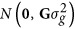 ; Z is the corresponding incidence matrix; and e is the vector of random residuals with the distribution
; Z is the corresponding incidence matrix; and e is the vector of random residuals with the distribution 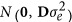 . G is the previously mentioned genomic relationship matrix with 0.02 added to its diagonal elements to avoid singular problems, and D is the diagonal matrix.
. G is the previously mentioned genomic relationship matrix with 0.02 added to its diagonal elements to avoid singular problems, and D is the diagonal matrix.
It is notable that, in the GBLUP model, both PGV and its de-regressed proof (DRP) were used as response variables in the simulation analyses. Reliabilities of PGV were obtained following the procedure proposed by Jamrozik et al. (2000). DRP derivation and the corresponding reliability were calculated according to Garrick et al. (2009). D was treated as the identity matrix when PGV was considered the response variable, while D with elements dii=1/wi was used as the diagonal matrix when DRP was considered the response variable, where the weighting factor was defined as 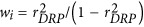 , with
, with 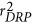 being the reliability of DRP.
being the reliability of DRP.
In the regular RR-TDM approach, decomposition of phenotypic value was the same as that in SS RR-TDM except that the additive genetic relationship between individual pairs was described by the A matrix. Solutions of random regression coefficients of additive genetic effects from both the regular RR-TDM approach and the SS RR-TDM approach were converted to the total or average PGV over the particular time period, which was consistent with those estimated in the GBLUP model.
The (co)variance components involved in the regular RR-TDM and GBLUP model were estimated using average information restricted maximum likelihood (AI-REML; Gilmour et al., 1995). The (co)variance components used in the SS RR-TDM approach were those estimated with the regular RR-TDM model. We employed DMU package (Madsen and Jensen, 2010) to estimate the (co)variance components and solve the MME. The H and H−1 matrices were also computed by DMU.
Simulation study
To evaluate the performance of different prediction models that were investigated in this study, longitudinal traits were simulated under various scenarios. Population and genomic data simulation was done using the QMSim software (Sargolzaei and Schenkel, 2009), and the longitudinal phenotypes were simulated by our own program. Simulated phenotypes were further used by QMSim for selection in the recent generations.
Genomic data simulation
Both historical and recent population structures were simulated by QMSim. The simulation was initiated with a base population of 50 males and 50 females, denoted as generation −1000, followed by 999 discrete historical generations (generation −999 to −1) with the same population size and an equal sex ratio. After 1000 historical generations, the recent population was generated from generation −1 to generation 0 with population size expanded from 100 to 4000 (2000 males and 2000 females), where each female had 80 offspring. Then, this recent population size was kept for 10 generations with a random mating of 50 randomly selected males and all females from the same generation.
The simulated genome consisted of 10 chromosomes with the same length of 1 Morgan. On each chromosome, 30 000 evenly distributed SNP markers were simulated in generation −1000. Initially, all loci were set to be bi-allelic with allele frequencies of 0.5. Recurrent mutations were simulated at a rate of 2.5 × 10−3 per locus per meiosis for markers in the subsequent generations of the historical population. The number of recombinations per chromosome was sampled from a Poisson distribution, P(λ=1). In the last generation of the historical population (generation −1) the whole genome was equally partitioned into 20 010 bins. In each bin, the marker with the maximum minor allele frequency (MAF) among all markers was used for further statistical analyses. Thus, the total number of markers was 20 010.
Longitudinal phenotypic data simulation
We simulated phenotypic observations involving time-dependent effects, that is, the mean of the population, the effects of quantitative trait loci (QTL) and permanent environmental effect, and the time-independent random residual error. The three time-dependent effects for an individual were simulated according to the Wilmink function:
where w0, w1 and w2 are regression parameters regarding the time point t. Using the estimates of regression parameters from the study of Cobuci et al. (2005), the mean curve of the population was modeled as y(t)=45−0.05t−28 exp (−0.05t). Estimates of (co)variance components in their study were used in our following simulations of additive and permanent environmental effects.
Here we described the simulation of the longitudinal phenotypic data in detail under scenario 1, and it was similar for other scenarios. We randomly selected 100 SNP markers with MAF>0.1 in generation 0 as the true QTL. Each QTL had effects on all three regression parameters and allele substitute effects were drawn from a multivariate normal distribution 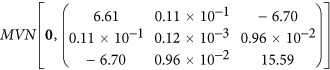 (Cobuci et al., 2005). Additive genetic (co)variances for wi and wj were determined as
(Cobuci et al., 2005). Additive genetic (co)variances for wi and wj were determined as
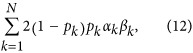 |
where pk is the MAF of the kth QTL in generation 0, αk and βk are effects of the kth QTL on wi and wj, and N is the total number of QTL. Random regression parameters αk were then scaled to ensure the additive genetic variances were equal to the diagonal elements in the covariance matrix of the multivariate normal distribution mentioned above. The additive genetic value of each regression coefficient for individual i was calculated as 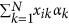 , where xik is the genotype of individual i at the kth QTL, and αk is the aforementioned allele substitute effect of QTL on the specific regression coefficient. Genotype was coded as 0 and 2 for two homozygotes, and as 1 for heterozygote. Thus, based on the genetic values of the three regression coefficients, the true additive genetic values of an individual over time can be generated using the aforementioned Wilmink function.
, where xik is the genotype of individual i at the kth QTL, and αk is the aforementioned allele substitute effect of QTL on the specific regression coefficient. Genotype was coded as 0 and 2 for two homozygotes, and as 1 for heterozygote. Thus, based on the genetic values of the three regression coefficients, the true additive genetic values of an individual over time can be generated using the aforementioned Wilmink function.
The permanent environmental effect for each individual can be modeled using the Wilmink function, which is the linear function of the three regression coefficients (w0, w1 and w2) drawn from the multivariate normal distribution 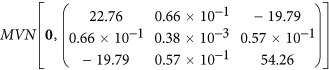 (Cobuci et al., 2005). The sampled permanent environmental effects were further scaled to achieve the heritability of 0.3 for the cumulated longitudinal observations, which was defined as the cumulated value of observations from consecutive time points of 5 to 305. The heritability was calculated as
(Cobuci et al., 2005). The sampled permanent environmental effects were further scaled to achieve the heritability of 0.3 for the cumulated longitudinal observations, which was defined as the cumulated value of observations from consecutive time points of 5 to 305. The heritability was calculated as
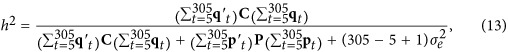 |
where qt and pt are vectors of covariates at time point t for the additive genetic and permanent environmental effects, C and P are (co)variance matrices of the additive genetic and permanent environmental regression coefficients, and 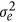 is the residual variance.
is the residual variance.
Thus, 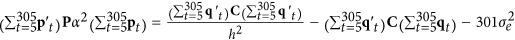 , where α is a scalar >0. Herein, C was calculated according to (13); P and
, where α is a scalar >0. Herein, C was calculated according to (13); P and 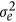 were the true values used in the simulation. To obtain the heritability of 0.3, the true permanent environmental effects chosen were products of the sampled permanent environmental effects and the solution of α. Thus, permanent environmental effects on an individual at a specific time could be obtained based on the Wilmink function.
were the true values used in the simulation. To obtain the heritability of 0.3, the true permanent environmental effects chosen were products of the sampled permanent environmental effects and the solution of α. Thus, permanent environmental effects on an individual at a specific time could be obtained based on the Wilmink function.
Finally, the simulated observation at a specific time point was the summation of the time-dependent effects, including the mean of the population, additive genetic value, permanent environmental effect, and time-independent residual effect. The residual effect for each observation was sampled from the normal distribution N(0, 16).
The simulated trait was measured at several time points (t). The first time point of measurement was sampled from the discrete uniform distribution DU (7, 37), and subsequent time points were generated by adding intervals sampled from DU (15, 36). The last time point was set to be not greater than 305. Longitudinal phenotypes were simulated for both males and females.
We further perturbed each single simulation parameter in the default scenario at a time to allow different data scenarios (Table 1) for model comparison. The perturbed parameters were heritability (0.1, 0.3 and 0.5), number of QTL (10, 100 and 500) and selection design in the recent generations (random selection vs selection based on PGV estimated from regular RR-TDM). All the scenarios were repeated 20 times to reduce sampling error.
Table 1. Summary of heritability (h 2), number of QTL (nQTL), selection design, traininga and testing populations for each scenario.
| Scenarios | h2 | nQTL | Selection designsb | Testing populationsc |
|---|---|---|---|---|
| 1 | 0.3 | 100 | Random | g=4, 5, 6, 7, 8, 9, 10 |
| 2 | 0.3 | 100 | PGV | g=4, 5, 6, 7, 8, 9, 10 |
| 3 | 0.1 | 100 | Random | g=4 |
| 4 | 0.5 | 100 | Random | g=4 |
| 5 | 0.3 | 10 | Random | g=4 |
| 6 | 0.3 | 500 | Random | g=4 |
Individuals in the training population (n=1000) were all sires (n=100) and other randomly selected individuals (n=900) from generations 1 and 2 for all scenarios.
In all scenarios, sires were either selected based on predicted genetic value (PGV) from the pedigree-based random regression model or selected randomly (Random) from each of generations 1–10.
Individuals in the testing population were randomly selected from each particular generation (g). The size of the testing population was 1000.
Simulation data analyses
For genomic prediction of each replicate of each scenario, we used a training population (n=1000) with all 100 sires and other randomly selected 900 individuals from generations 1 and 2, which had both genotypic and phenotypic data. The testing population consisted of 1000 individuals from each testing generation 4–10, which had only genotypic data (Table 1). Meanwhile, phenotypes of all individuals in generation 3 were used in the analyses. The pedigree of all related individuals was used for construction of the A and H matrices for the regular RR-TDM and SS RR-TDM models.
In the analyses with regular RR-TDM and SS RR-TDM, fixed regression coefficients represented the mean curve of the population, and covariates in X, Q and Z were the parameters in the Wilmink function (10) fitted on time point t. In the construction of the H matrix in SS RR-TDM, we set w as 0.05. For the GBLUP model, both cumulated PGV and corresponding DRP were used as response variables. The cumulated PGV was computed as 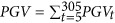 , where PGVt is the predicted genetic value at time point t with the regular RR-TDM. As PGV was a regressed variable, predictions from GBLUP with PGV as the response variable were divided by the average reliability of PGV in the training set (Guo et al., 2010).
, where PGVt is the predicted genetic value at time point t with the regular RR-TDM. As PGV was a regressed variable, predictions from GBLUP with PGV as the response variable were divided by the average reliability of PGV in the training set (Guo et al., 2010).
In comparison of the performance of different models, the assessment was based on prediction accuracy, bias and mean squared error (MSE). Accuracy was computed as the correlation between true genetic values and PGV; bias was measured as the deviation of regression coefficient (true genetic values on PGV) from 1; and MSE was computed as the average square of the difference between true genetic values and PGV centered on 0.
Real data analyses on GAW18 data set
To further validate the prediction performance of the SS RR-TDM, we performed our analyses with a real data set of systolic blood pressure (SBP), which can be characterized as a longitudinal trait changing with age. The data were provided by Genetic Analysis Workshop 18 (GAW18) (http://www.gaworkshop.org), and included SBP measurements of 932 participants from 20 large pedigrees and genotypic data of 959 individuals. The genotypes of 464 individuals were generated via sequencing and those of the remaining individuals were genotyped via imputation. Only genotypes on odd-numbered autosomes were available for both sequenced and imputed individuals. The illustration on the real data was detailed elsewhere (Almasy et al., 2014).
Following the criteria of Yao et al. (2014), the markers were pruned using PLINK 1.07 (Purcell et al., 2007) to maintain the linkage disequilibrium (r2) between each other less than 0.9, and a total of 690 551 common SNPs (MAF⩾0.05) were finally determined for the follow-up analyses.
Similar to simulation studies, we compared three different prediction models, including SS RR-TDM, regular RR-TDM and GBLUP, in the analyses of the GAW18 data set. Before implementing predictions with different models, we performed pedigree-based RR-TDM using the whole data set to obtain PGVs and their reliabilities. These PGVs were assumed as true genetic values for model comparisons. In both SS RR-TDM and regular RR-TDM analyses, gender, year of examination, medication usage and current tobacco smoking were considered as fixed effects, while permanent environmental and additive genetic effects were treated as random effects in the time-dependent model. We adopted Legendre polynomials of order 3 for fixed factor (gender) regressions and Legendre polynomials of order 2 for additive genetic regression in the model. To investigate the effect of w on prediction quality, the value of w was set to 0 and 0.8 in generating the weighted genomic relationship matrix Gw in SS RR-TDM. In the analyses with the GBLUP model, the response variable was PGV of average SBP from the age of 10 to 100 years, which was obtained from predictions of pedigree-based RR-TDM.
For prediction quality evaluation, we conducted 5-fold cross-validation for each of the three prediction models. Specifically, 20 families were randomly partitioned into five subsets, each with four families and at least a total of 180 genotyped individuals. Each of four subsets was in turn used as the training set, and the remaining set served as the testing set. Phenotypes of individuals in the testing set were assumed to be unknown. In order to maintain relationships between the training and testing sets, especially for RR-TDM, which only used pedigree, we moved one individual from each family in the testing set to the training set. In selection of these individuals, we tried to choose from later generations and avoid genotyped individuals. If there were no individuals meeting the conditions, we selected one individual from the last generation and assumed their genotypic data as unknown in cross-validation. Then, PGVs were predicted for individuals in the testing set. For each replicate, we calculated the accuracy, bias and MSE as mentioned above in the analyses of simulated data, using genotyped individuals in the testing set. Individuals in the testing set were selected to have reliabilities of PGV > 0.3 from the pedigree-based RR-TDM analysis using all individuals (averaging 130 individuals in the testing set). The whole procedure of 5-fold cross-validation was repeated 20 times to determine the average accuracy, bias and MSE.
Results
Simulation study
Prediction quality of different models
Table 2 lists the accuracies, biases and MSE of the three models in prediction of individuals in the validation set of generation 4 under the default scenario. The results clearly demonstrate that marker-based genomic prediction models (GBLUP and SS RR-TDM) achieve higher accuracies than the pedigree-based method (regular RR-TDM). For the two marker-based methods, SS RR-TDM clearly further outperformed the GBLUP model in prediction accuracy.
Table 2. The prediction accuracies, biases (|1-b|) and mean squared errors (MSE) of different models under the default scenario across 20 replicatesa.
| Modelsb | Accuracies±s.e. | |1-b|±s.e. | MSE±s.e. (× 10 000) |
|---|---|---|---|
| Regular RR-TDM | 0.50±0.01A | 0.08±0.01A | 37.77±1.32A |
| GBLUP (DRP) | 0.65±0.01B | 0.25±0.03B | 30.12±1.25B |
| GBLUP (PGV) | 0.65±0.01B | 0.24±0.01B | 31.47±1.25C |
| SS RR-TDM | 0.71±0.01C | 0.06±0.01A | 25.02±1.00D |
Abbreviations: DRP, de-regressed proof; GBLUP, genomic best linear unbiased prediction; PGV, predicted genetic value; SS RR-TDM, single-step random regression test-day model.
Common capital letters within columns donate no significant difference at the 0.01 level by paired t-test.
Bias was measured as the deviation of regression coefficients (true additive genetic value on predicted genetic value) from 1. The results were from the default scenario with a heritability of 0.3, 100 QTL and random selection of sires in each generation.
Models applied were pedigree-based random regression test-day model (Regular RR-TDM), genomic best linear unbiased prediction (GBLUP) with response variables of predicted genetic value (GBLUP (PGV)) and de-regressed proof (GBLUP(DRP)), and single-step RR-TDM.
There was no significant difference in prediction bias between the SS RR-TDM and the regular RR-TDM, and these two models had lesser bias than the GBLUP model. MSE is another commonly used measure of prediction quality, which assesses the overall quality of the model. Significant differences existed in MSE among different models, and SS RR-TDM fitted the data best. For the GBLUP model, the performance of analyses with PGV and DRP as response variables was very similar in terms of accuracy, bias and MSE (Table 2). Similar rankings of different models in prediction quality were also observed in other scenarios.
Prediction quality under different heritabilities and numbers of QTL
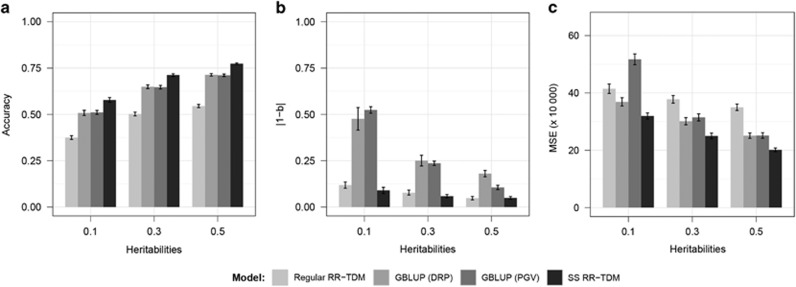
As shown in Figure 1, SS RR-TDM outperformed other models in all the three measures of prediction quality. For all the three models, significantly higher accuracy and less bias were achieved with higher heritability (based on paired t-test). In particular, the prediction biases of SS RR-TDM and regular RR-TDM were lower than those of the GBLUP models for the low-heritability (h2=0.1) trait (Figure 1b). This indicated that the single-step approach had more appealing advantages over the multi-step approaches with low-heritability traits.
Figure 1.
Quality of prediction (average over 20 replicates) for different statistical models with alternative heritabilities (number of QTL=100, random selection). The training set consisted of all the sires (n=100) and other randomly selected individuals (n=900) from generations 1 and 2. Phenotypic information was available for all individuals in generations 1–3. The testing set consisted of 1000 individuals from generation 4. (a) Accuracies; (b) prediction biases: deviation of the regression coefficient (true genetic values on predicted genetic values) from 1; (c) mean squared errors (MSE).
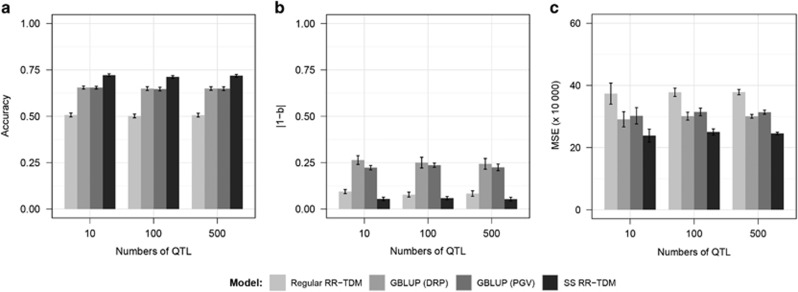
Prediction quality for various numbers of QTL is presented in Figure 2, which also shows that SS RR-TDM achieved a significant advantage over the other models. For any of the methods, prediction accuracy and bias did not fluctuate significantly with the change in number of QTL.
Figure 2.
Quality of prediction (average over 20 replicates) for different statistical models with alternative numbers of QTL (heritability=0.3, random selection). The training set consisted of all the sires (n=100) and other randomly selected individuals (n=900) from generations 1 and 2. Phenotypic information was available for all individuals in generations 1–3. The testing set consisted of 1000 individuals from generation 4. (a) Accuracies; (b) prediction biases: deviation of the regression coefficient (true genetic values on predicted genetic values) from 1; (c) mean squared errors (MSE).
Persistency of accuracy and bias over generations
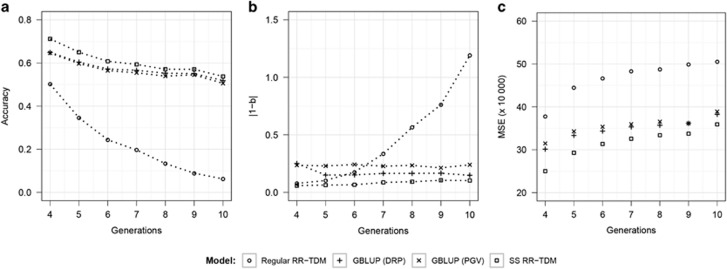
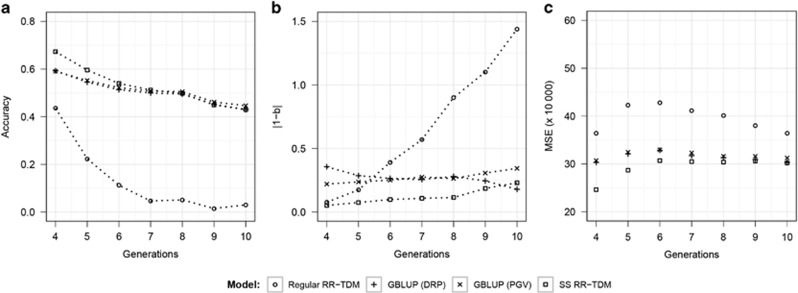
The persistency of accuracy and bias for different models over six generations are presented in Figure 3 (scenario 1 of random selection) and Figure 4 (scenario 2 of non-random selection). The results clearly indicate the advantages of the SS RR-TDM over the other two prediction models. Overall, accuracies for all models decreased over generations in both scenarios. Regular RR-TDM resulted in the greatest decline in accuracies over generations under both scenarios. The accuracies of marker-based models showed more obvious decreases over generations in scenario 2 than in scenario 1. SS RR-TDM maintained the highest accuracies over generations under scenario 1. For scenario 2, SS RR-TDM had the best accuracies over generations 4–6, and it achieved similar accuracies with the GBLUP model in generations 7–10 (Figure 4a). Meanwhile, SS RR-TDM always had the lowest prediction biases and MSE for both two scenarios, except that its prediction bias was larger than that of the GBLUP model with DRP as response variable in generation 10 of scenario 2 (Figure 4b). These results indicate the potential advantages of SS RR-TDM, especially when the population is under random selection.
Figure 3.
Quality of prediction (average over 20 replicates) for different statistical models in prediction of individuals from generation g (g=4–10) under the default scenario (heritability=0.3, number of QTL=100, random selection). The training set consisted of all the sires (n=100) and other randomly selected individuals (n=900) from generations 1 and 2. Phenotypic information was available for all individuals in generations 1–3. The testing set consisted of 1000 individuals from generation g. (a) Accuracies; (b) prediction biases: deviation of the regression coefficient (true genetic values on predicted genetic values) from 1; (c) mean squared errors (MSE).
Figure 4.
Quality of prediction (average over 20 replicates) for different statistical models in prediction of individuals from generation g (g=4–10) under the non-random selection design (selection based on predicted genetic value). The training set consisted of all the sires (n=100) and other randomly selected individuals (n=900) from generations 1–2. Phenotypic information was available for all individuals in generations 1–3. The testing set consisted of 1000 individuals from generation g. (a) Accuracies; (b) prediction biases: deviation of the regression coefficient (true genetic values on predicted genetic values) from 1; (c) mean squared errors (MSE).
Comparing the performance of all models under two scenarios (1 and 2) in prediction of a specific generation, that is, generation 4, we found that the accuracy of each model under the non-random selection (scenario 2) was significantly lower than that under the random selection (scenario 1). Accuracies of the non-random selection for all three models also decreased faster over generations than those under random selection.
Study of real data from GAW18
Table 3 presents the accuracies, biases and MSE with different models for the real data set of human blood pressure. SS RR-TDM with w=0 performed best in terms of all the three prediction quality measures, followed by GBLUP and SS RR-TDM with w=0.8. Pedigree-based RR-TDM was the worst model in the cross-validation. The results also indicate that the value of w had a significant effect on the prediction quality of SS RR-TDM in analyses of this data set.
Table 3. The prediction accuracies, biases (|1-b|) and mean squared errors (MSE) for the average systolic blood pressure (SBP) at ages of 10-100 for the GAW18 workshop data seta.
| Models | Accuracies±s.e. | |1-b|±s.e. | MSE±s.e. |
|---|---|---|---|
| Regular RR-TDM | 0.05±0.02a | 2.52±0.24a | 90.62±2.15a |
| GBLUPb | 0.14±0.01b | 0.65±0.05b | 89.79±2.12ab |
| SS RR-TDM (w=0)c | 0.16±0.01c | 0.50±0.04c | 89.52±2.15b |
| SS RR-TDM (w=0.8) | 0.11±0.01b | 1.73±0.18d | 89.93±2.15b |
Abbreviations: GAW18, Genetic Analysis Workshop 18; GBLUP, genomic best linear unbiased prediction; SS RR-TDM, single-step random regression test-day model.
Significant test: Common lowercase letters within columns indicate no significant difference at the 0.05 level by paired t-test.
Results are means of 20 replicates of fivefold cross-validation.
Average of the predicted genetic values of SBP at ages of 10–100 estimated from the regular RR-TDM was used as the response variable in the GBLUP model.
w is a parameter used in the construction of the combined relationship matrix in the single-step method.
Discussion
With the simulated longitudinal data and real data from GAW18, we extensively investigated the performance of SS RR-TDM in genomic prediction, in comparison with the regular RR-TDM and GBLUP models. The results showed that SS RR-TDM outperformed other models in most cases in terms of all the measures of prediction quality, that is, accuracy, bias and MSE, and in all scenarios of different heritabilities, numbers of QTL and selection designs.
Advantages of SS RR-TDM in prediction quality
From our simulation results, we found that marker-based models, the GBLUP and SS RR-TDM models, outperformed the pedigree-based model (RR-TDM). For the pedigree-based method, accuracy is only contributed by the genetic relationship between individuals, which can be explained by the pedigree-based numerator relationship matrix. However, marker-based methods further exploited linkage disequilibrium (LD) and cosegregation to capture the linkages of SNP markers and QTL (Habier et al., 2013). Therefore, maker-based models could achieve higher accuracies.
Among marker-based models, SS RR-TDM achieved higher accuracies than the GBLUP model, especially in the case of random selection (Figure 3a). This is because, using the H matrix in the single-step method was equivalent to imputing missing genotypes of individuals with phenotypic but no genotypic data (Christensen and Lund, 2010), and thus enlarged the training sets. The advantage in terms of accuracy of the single-step method over the pedigree-based and multi-step methods was also observed in other studies (for example, Christensen et al., 2012; Koivula et al., 2015). We further enlarged the training population to include 4000 individuals from the first 2 generations to compare performance of different models under the default scenario. The results showed that SS RR-TDM still outperformed the GBLUP model (Supplementary Table S1). As we expected, with a larger training set, prediction accuracy increased and bias decreased for models using genomic information.
One of the concerns regarding GBLUP is double counting. In our study, DRP was calculated using the method proposed by Garrick et al. (2009), which removed the parent average (PA) effect in PGV. However, in the simulation study, similar accuracies were observed for GBLUP with DRP and PGV as response variables, for example, in Table 2. When only pedigree was used, prediction of PGV of an individual used information from parents, own phenotypes and progeny. In our simulation study, all individuals in the training set had their own phenotypes and only about half of them had known parents in pedigree. Compared with the situation where the predicted individual had no phenotype, PGV herein contained less information from parents. Therefore, the difference between PGV and DRP was small and the degree of double counting in GBLUP was low in our study. This may be the reason why GBLUP with PGV and DRP achieved similar results.
However, removing the PA effect in PGV also means that less information could be used in evaluation, even though including PA may lead to double counting in GBLUP. Moreover, compared with the PA computed using all the phenotypic data and pedigree, the DGV of individuals in the testing set will contain less amount of phenotypic information if none of the genotyped individual’s relatives have been genotyped. The simple way to resolve this problem is calculating an index by combining DGV with PA (VanRaden et al., 2009). Under the default scenario in our simulation study, the index of DGV with PA, which was calculated as in Guo et al. (2010), increased the accuracies from 0.65 to 0.67 and from 0.63 to 0.66 for GBLUP with PGV and DRP as response variables, respectively. However, prediction accuracy of the index was still lower than that of SS RR-TDM (0.71). This is consistent with the findings in Lourenco et al. (2014), where the single-step method performed better than the index. In practice, if the DGV and PA have already been calculated, the index is a better choice than each of them. But SS RR-TDM is the most simple, accurate and suitable method for evaluation of longitudinal traits.
In our study, SS RR-TDM had less bias compared to the GBLUP model. Other studies also reported that the single-step approach achieved lesser biases than the GBLUP model (Vitezica et al., 2011; Christensen et al., 2012). This may be because the single-step method combined all individuals of different generations in the joint analysis, and the multi-step approach mostly separated the training and validation sets in different generations. In addition to higher accuracy and less bias, SS RR-TDM has the advantages of being able to generate the PGV curve over time and easily compute the PGV of a particular time point or period.
Influence of heritability and number of QTL on prediction
For all the models used in our study, accuracy increased and bias decreased with heritability (Figures 1a and b). Similar results were also found for the multi-step method, including GBLUP, BayesB and a mixture model approach in real data studies (for example, Luan et al., 2009). The simulation study of Guo et al. (2010) used both Bayesian non-linear models and the GBLUP model, and also observed that high heritability resulted in higher accuracy and lower bias compared to low heritability. These results confirmed the theoretical expectation that much more phenotypes were necessary to achieve certain accuracies for low-heritability traits.
In our study, we observed that accuracy and bias for all the models did not change obviously with the number of QTL (Figures 2a and b). Daetwyler et al. (2010) investigated the effect of genetic architecture on the prediction accuracy of marker-based genomic prediction models. They also found that the GBLUP model presented a relatively constant accuracy across different numbers of QTL. In another simulation study, higher accuracy was achieved for smaller numbers of QTL with the BayesB model, and also the GBLUP model resulted in similar accuracies for different numbers of QTL (Clark et al., 2011). Based on these results, we inferred that the marker-based models used in this study, that is, SS RR-TDM and GBLUP, which simply assumed that all markers had equivalent marker variances, were insensitive to the number of QTL. The Bayesian type model with unequal marker variances assumption for the single-step approach applied to longitudinal data still needs more investigation.
Persistency of accuracy and bias over generations
According to our results, accuracies decreased over generations with all models under scenario 1 (random selection) and scenario 2 (non-random selection based on PGV). The decrease over generations was most obvious for the regular RR-TDM, which was only based on the pedigree. The marker-based models (GBLUP and SS RR-TDM) showed more robust accuracies over generations (Figures 3a and 4a). Similar results were observed for the GBLUP and Bayesian methods in the real data analyses of Wolc et al. (2011), which can be attributed to the facts that the regular RR-TDM only used pedigree information, and the genetic relationship between the training and testing sets became more and more distant when the testing generation increased. However, in our analyses, the accuracy of marker-based models was mainly attributed to the additive genetic relationship between individuals and the population-wide linkage disequilibrium (LD) of the marker and QTL (Habier et al., 2013). When the generation between the testing and training sets was apart, marker-based models still utilized LD, which was more persistent over generations than the genetic relationship.
When the testing generation was not very distant from that of the training set, that is, generations 4 and 5, SS RR-TDM achieved better accuracies than the GBLUP model (Figure 3a and Figure 4a). The possible reason was that SS RR-TDM used genotypes of the training set (generations 1 and 2) and also the imputed genotypes of generation 3, but the GBLUP model could only use genotypes of the training set (generations 1 and 2). Therefore, SS RR-TDM had a larger size of training set (generations 1, 2 and 3) than that of the GBLUP model. However, the advantage of SS RR-TDM over the GBLUP model disappeared at testing generations 7–10 under the scenario of non-random selection (Figure 4a). This could be because the relationship between the testing and training sets became more apart for generations 6–10 under non-random selection. Thus, the imputed genotypes of generation 3, which used genotypes of both the training and testing sets, were less accurate compared with those for the testing generations 4 and 5.
For marker-based models, accuracies declined more rapidly under scenario 2 of selection based on PGV (non-random selection). One possible reason was that the relationship of the testing and training sets became more distant at a certain generation in scenario 2 than in scenario 1. This was contributed by the higher selection pressure of the non-random selection. Meanwhile, higher selection pressure of non-random selection could also accelerate the change in MAF of markers and the reduction of genetic variance. This would increase the breakdown of LD of markers and QTL. Akanno et al. (2014) also reported higher accuracies of genomic prediction over generations under random selection. Muir (2007) observed similar results in his simulation study.
In our study, the MME of SS RR-TDM was solved by the best linear unbiased prediction method (Henderson, 1975). In this method, the MME has to be solved at every generation to obtain the prediction of testing individuals, even without adding additional genotypic or phenotypic information to the training set. Wang et al. (2012) showed that SNP effects could be back-solved from PGVs using the main single-step evaluation. Liu et al. (2014) proposed an extended model of the single-step method, namely, the single-step SNP model, which could directly estimate marker effects to avoid re-estimation in a short period of time. These would be helpful in practical applications. Fernando et al. (2014) presented Bayesian methods for the single-step approach. These methods allow the indirect prediction based on SNP effects, which do not require the MME to be solved at each round prediction of the testing set. However, it was suggested to re-train the models at a specific interval of generations in genomic predictions (Muir, 2007), which was also necessary for the single-step approach according to our results (Figures 3 and 4). Wolc et al. (2011) also suggested continuous phenotyping and genotyping for the single-step approach if economic conditions permit. This is more warranted when the population is under non-random selection.
Study of real data from GAW18
Apart from the simulation study, we also explored the performance of different models in analyses of a real data set of human systolic blood pressure provided by GAW18. In this real data set, genotypic information was only available for odd-numbered chromosomes, and this would have a negative effect on the performance of marker-based methods. Even so, cross-validation results clearly demonstrated that SS RR-TDM with a w of 0 was the best model in analyses of longitudinal data (Table 3).
Furthermore, SS RR-TDM with w=0 performed significantly better than with w=0.8. Besides avoiding the singularity of the G matrix, w also reflects the fraction of genetic variance not described by markers (Christensen et al., 2012). The smaller the value of w, the more the genetic variance that is attributed to markers. Under the cross-validation design we adopted, genomic information was more valuable for prediction than pedigree. Therefore, it is reasonable that SS RR-TDM with a smaller w achieved better performance.
As mentioned, the strategy we used in cross-validation would reduce the contribution of PA in prediction. We adopted this strategy because our study situation was closer to reality, where usually only a limited number of family members could have longitudinal data.
With regard to the regular RR-TDM and SS RR-TDM models, as 246 of the 932 individuals had only one measurement, these data may not fit the random regression test-day model efficiently. Moreover, as there were only genotypes of half the chromosomes available, the advantage of the SS RR-TDM could not be fully explored by this GAW18 data set. We expect that more benefits of the SS RR-TDM model could be realized with a real data set with markers that spanned all chromosomes.
Some issues about implementation of SS RR-TDM
In the single-step method, the construction of H matrix involves several parameters and some of them were shown to have effects on the accuracy and unbiasedness of prediction (Vitezica et al., 2011; Christensen et al., 2012; Koivula et al., 2015). However, in the analyses of simulated data, w was only set to 0.05 in each analysis. As the results explicitly showed that SS RR-TDM with w=0.05 outperformed other methods in all the three measures of prediction quality, we did not test other values of w. In analyses of real data, we performed SS RR-TDM with two values of w (0 and 0.8), with other parameters being set as constant the results (Table 3). This analysis indicated that the choice of w significantly affected the performance of the single-step method. Previous studies in animal breeding have shown that w only has a minor effect on prediction quality (VanRaden, 2008; Koivula et al., 2015). The difference in our study’s conclusion may be attributed to the cross-validation design we employed. As mentioned above, the cross-validation design proved that pedigrees was included, corresponding to the smaller value of w would be much less useful than marker information. Thus, SS RR-TDM would perform better when more genotypic information was included, corresponding to the smaller value of w. Therefore, it could be concluded that the effect of parameters depends on data structure and the trait analyzed. In implementation of single-step genomic evaluation, it is better to test different combinations of these parameters to find out the optimal parameters for prediction.
Our simulation study used relatively small data sets, but clearly demonstrated the benefits of SS RR-TDM under various scenarios. However, one main obstacle to applying this model in practice was the computing time required for large data sets. More researches in the computing efficiency of the single-step approach are necessary.
In general, the SS RR-TDM model described herein is a simple extension of the single-step method to the genomic evaluation using the random regression test-day model. Liu et al. (2014) proposed the single-step SNP model, where marker effects can be modeled with different distributions than in Bayesian models. Meanwhile, Fernando et al. (2014) presented a class of Bayesian methods for the single-step approach. As proved in multi-step approaches, Bayesian methods showed advantages when marker density increased (Meuwissen and Goddard, 2010) and they captured more LD information than the GBLUP method (Zhong et al., 2009). We believe that it is meaningful to develop single-step genomic evaluation using the random regression model based on Bayesian methods when marker density increases explosively in the era of genome sequencing.
Data archiving
All simulated data analyzed in the present study are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.8df69.
Acknowledgments
We thank the editor and the two anonymous reviewers for their constructive comments and suggestions that greatly improved our manuscript. The GAW18 whole genome sequence data were provided by the T2D-GENES Consortium, which is supported by NIH grants U01 DK085524, U01 DK085584, U01 DK085501, U01 DK085526, and U01 DK085545. The other genetic and phenotypic data for GAW18 were provided by the San Antonio Family Heart Study and San Antonio Family Diabetes/Gallbladder study, which are supported by NIH grants P01 HL045222, R01 DK047482, and R01 DK053889. Andrew R Wood is supported by European Research Council grant SZ-245 50371-GLUCOSEGENES-FP7-IDEAS-ERC. We appreciate the financial support from the National Natural Science Foundations of China (31272419), the National Major Development Program of Transgenic Breeding (2014ZX0800953B), the Program for Changjiang Scholar and Innovation Research Team in University (IRT_15R62) and China Agriculture Research System (CARS-36).
Footnotes
Supplementary Information accompanies this paper on Heredity website(http://www.nature.com/hdy)
The authors declare no conflict of interest.
Supplementary Material
References
- Akanno EC, Schenkel FS, Sargolzaei M, Friendship RM, Robinson JA. (2014). Persistency of accuracy of genomic breeding values for different simulated pig breeding programs in developing countries. J Anim Breed Genet 131: 367–378. [DOI] [PubMed] [Google Scholar]
- Almasy L, Dyer TD, Peralta JM, Jun G, Wood AR, Fuchsberger C et al. (2014). Data for Genetic Analysis Workshop 18: human whole genome sequence, blood pressure, and simulated phenotypes in extended pedigrees. BMC Proc 8 (Suppl 1): S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CY, Misztal I, Aguilar I, Legarra A, Muir WM. (2011). Effect of different genomic relationship matrices on accuracy and scale. J Anim Sci 89: 2673–2679. [DOI] [PubMed] [Google Scholar]
- Christensen OF, Lund MS. (2010). Genomic prediction when some animals are not genotyped. Genet Sel Evol 42: 2–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen OF, Madsen P, Nielsen B, Ostersen T, Su G. (2012). Single-step methods for genomic evaluation in pigs. Animal 6: 1565–1571. [DOI] [PubMed] [Google Scholar]
- Clark SA, Hickey JM, van der Werf JHJ. (2011). Different models of genetic variation and their effect on genomic evaluation. Genet Sel Evol 43: 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cobuci JA, Euclydes RF, Lopes PS, Costa CN, Torres RD, Pereira CS. (2005). Estimation of genetic parameters for test-day milk yield in Holstein cows using a random regression model. Genet Mol Biol 28: 75–83. [Google Scholar]
- Daetwyler HD, Pong-Wong R, Villanueva B, Woolliams JA. (2010). The impact of genetic architecture on genome-wide evaluation methods. Genetics 185: 1021–1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G, Vazquez AI, Fernando R, Klimentidis YC, Sorensen D. (2013). Prediction of complex human traits using the genomic best linear unbiased predictor. PLoS Genet 9: e1003608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernando RL, Dekkers JCM, Garrick DJ. (2014). A class of Bayesian methods to combine large numbers of genotyped and non-genotyped animals for whole-genome analyses. Genet Sel Evol 46: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrick DJ, Taylor JF, Fernando RL. (2009). Deregressing estimated breeding values and weighting information for genomic regression analyses. Genet Sel Evol 41: 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmour AR, Thompson R, Cullis BR. (1995). Average information REML: An efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 51: 1440–1450. [Google Scholar]
- Guo G, Lund MS, Zhang Y, Su G. (2010). Comparison between genomic predictions using daughter yield deviation and conventional estimated breeding value as response variables. J Anim Breed Genet 127: 423–432. [DOI] [PubMed] [Google Scholar]
- Habier D, Fernando RL, Dekkers JCM. (2007). The impact of genetic relationship information on genome-assisted breeding values. Genetics 177: 2389–2397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D, Fernando RL, Garrick DJ. (2013). Genomic BLUP Decoded: A Look into the Black Box of Genomic Prediction. Genetics 194: 597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson CR. (1975). Best Linear Unbiased Estimation and Prediction under a Selection Model. Biometrics 31: 423–447. [PubMed] [Google Scholar]
- Jamrozik J, Schaeffer LR, Jansen GB. (2000). Approximate accuracies of prediction from random regression models. Livest Prod Sci 66: 85–92. [Google Scholar]
- Kirkpatrick M, Lofsvold D, Bulmer M. (1990). Analysis of the Inheritance, Selection and Evolution of Growth Trajectories. Genetics 124: 979–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koivula M, Stranden I, Poso J, Aamand GP, Mantysaari EA. (2015). Single-step genomic evaluation using multitrait random regression model and test-day data. J Dairy Sci 98: 2775–2784. [DOI] [PubMed] [Google Scholar]
- Legarra A, Aguilar I, Misztal I. (2009). A relationship matrix including full pedigree and genomic information. J Dairy Sci 92: 4656–4663. [DOI] [PubMed] [Google Scholar]
- Liu Z, Goddard ME, Reinhardt F, Reents R. (2014). A single-step genomic model with direct estimation of marker effects. J Dairy Sci 97: 5833–5850. [DOI] [PubMed] [Google Scholar]
- Lourenco DAL, Misztal I, Tsuruta S, Aguilar I, Ezra E, Ron M et al. (2014). Methods for genomic evaluation of a relatively small genotyped dairy population and effect of genotyped cow information in multiparity analyses. J Dairy Sci 97: 1742–1752. [DOI] [PubMed] [Google Scholar]
- Luan T, Woolliams JA, Lien S, Kent M, Svendsen M, Meuwissen THE. (2009). The Accuracy of Genomic Selection in Norwegian Red Cattle Assessed by Cross-Validation. Genetics 183: 1119–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lush JL. (1943) Animal Breeding Plans. Iowa State University Press: Ames, Iowa. [Google Scholar]
- Madsen P, Jensen J. (2010) University of Aarhus, Faculty Agricultural Sciences (DJF), Dept of Genetics and Biotechnology. Research Centre Foulum: Tjele, Denmark. [Google Scholar]
- Meuwissen T, Goddard M. (2010). Accurate prediction of genetic values for complex traits by whole-genome resequencing. Genetics 185: U623–U338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen THE, Hayes BJ, Goddard ME. (2001). Prediction of total genetic value using genome-wide dense marker maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muir WM. (2007). Comparison of genomic and traditional BLUP-estimated breeding value accuracy and selection response under alternative trait and genomic parameters. J Anim Breed Genet 124: 342–355. [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D et al. (2007). PLINK: A tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 81: 559–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargolzaei M, Schenkel FS. (2009). QMSim: a large-scale genome simulator for livestock. Bioinformatics 25: 680–681. [DOI] [PubMed] [Google Scholar]
- Schaeffer LR, Dekkers JCM. (1994) Proceedings of the 5th World Congress on Applied Livestock Production, Vol. XVIII. pp 443–446.
- Schaeffer LR, Jamrozik J, Kistemaker GJ, Van Doormaal BJ. (2000). Experience with a test-day model. J Dairy Sci 83: 1135–1144. [DOI] [PubMed] [Google Scholar]
- VanRaden PM. (2008). Efficient methods to compute genomic predictions. J Dairy Sci 91: 4414–4423. [DOI] [PubMed] [Google Scholar]
- VanRaden PM, Van Tassell CP, Wiggans GR, Sonstegard TS, Schnabel RD, Taylor JF et al. (2009). Invited review: reliability of genomic predictions for North American Holstein bulls. J Dairy Sci 92: 16–24. [DOI] [PubMed] [Google Scholar]
- Vitezica ZG, Aguilar I, Misztal I, Legarra A. (2011). Bias in genomic predictions for populations under selection. Genet Res 93: 357–366. [DOI] [PubMed] [Google Scholar]
- Wang H, Misztal I, Aguilar I, Legarra A, Muir WM. (2012). Genome-wide association mapping including phenotypes from relatives without genotypes. Genet Res 94: 73–83. [DOI] [PubMed] [Google Scholar]
- Wilmink JBM. (1987). Adjustment of Test-Day Milk, Fat and Protein Yield for Age, Season and Stage of Lactation. Livest Prod Sci 16: 335–348. [Google Scholar]
- Wolc A, Arango J, Settar P, Fulton JE, O'Sullivan NP, Preisinger R et al. (2011). Persistence of accuracy of genomic estimated breeding values over generations in layer chickens. Genet Sel Evol 43: 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao C, Leng N, Weigel K, Lee K, Engelman C, Meyers K. (2014). Prediction of genetic contributions to complex traits using whole genome sequencing data. BMC Proc 8 (Suppl 1): S68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong SQ, Dekkers JCM, Fernando RL, Jannink JL. (2009). Factors affecting accuracy from genomic selection in populations derived from multiple inbred lines: a barley case study. Genetics 182: 355–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.