Genetic signatures of variation in population size in a native fungal pathogen after the recent massive plantation of its host tree

Abstract

Historical fluctuations in forests’ distribution driven by past climate changes and anthropogenic activities can have large impacts on the demographic history of pathogens that have a long co-evolution history with these host trees. Using a population genetic approach, we investigated that hypothesis by reconstructing the demographic history of Armillaria ostoyae, one of the major pathogens of the maritime pine (Pinus pinaster), in the largest monospecific pine planted forest in Europe (south-western France). Genetic structure analyses and approximate Bayesian computation approaches revealed that a single pathogen population underwent a severe reduction in effective size (12 times lower) 1080–2080 generations ago, followed by an expansion (4 times higher) during the last 4 generations. These results are consistent with the history of the maritime pine forest in the region characterized by a strong recession during the last glaciation (~19 000 years ago) and massive plantations during the second half of the nineteenth century. Results suggest that recent and intensive plantations of a host tree population have offered the opportunity for a rapid spread and adaptation of their pathogens.

Introduction

For several years, a large number of studies have documented disease outbreaks on plants associated with fungal or fungus-like (that is, oomycetes) pathogens (Anderson et al., 2004). Pathogen outbreaks can cause dramatic losses in crops, as illustrated by the nineteenth century Irish potato famine due to the introduction of Phytophthora infestans in Ireland (Gómez-Alpizar et al., 2007). Genetic studies on the origin(s) and the evolutionary history of these fungal diseases have shown that they are often associated with host-tracking, that is, the fungal pathogen follow the geographical spread of its original host during agricultural development (for example, Gladieux et al., 2008; Munkacsi et al., 2008; Robert et al., 2012; Fontaine et al., 2013). By contrast, in natural ecosystems, such as forests, disease outbreaks are largely due to introductions of exotic fungal pathogen species on native, and generally naive, hosts (Gonthier et al., 2007; Gross et al., 2014; Desprez-Loustau et al., 2016). Many fungal pathogens are assumed to have co-evolved with their host trees and so cause little damage in wild forest ecosystems (for example, Gilbert, 2002; Ennos, 2015). In these natural ecosystems, with complex networks of biological interactions (for example, Arnold et al., 2003), disease outbreaks are usually associated with rare and dramatic environmental changes (Gilbert, 2002). Over the past few decades, several studies have reported increasing impacts of native fungal species on their original hosts that could be due to recent climatic changes or intensification of human activities (Coakley et al., 1999; Ennos, 2001; Rosenzweig et al., 2001; Harvell et al., 2002; Woods et al., 2005; Lieberei, 2007). Increase of monospecific planted forests during the last 50 years may offer favourable conditions for the spread and build-up of local pathogen populations on their host tree as suggested in various studies (for example, Perkins and Matlack, 2002; Pautasso et al., 2005; Lieberei, 2007; Labbé et al., 2015). However, only a few studies investigated the geographical origin and genetic diversity of these emerging fungal pathogens in intensively managed forest ecosystems (but see Sakalidis et al., 2016), precluding any conclusions on their epidemiological and evolutionary dynamics.

Basidiomycete A. ostoyae (Romagn., Herink) is the causal agent of root- and butt-rot on a large number of coniferous species in the northern hemisphere (Wargo and Shaw III, 1985; Guillaumin et al., 1993). Among the European Armillaria species, A. ostoyae is the most damaging pathogen of conifers, infecting roots and killing host tissues to obtain resources (Guillaumin et al., 1993). Depending on the host species and forest management strategy, A. ostoyae may act as a secondary pathogen (that is, infecting only weakened trees) or a primary parasite (that is, infecting healthy and unstressed trees; Guillaumin and Legrand, 2005). This species is especially damaging to planted coniferous forests with high densities of sensitive host trees (Wargo and Shaw III, 1985; Lung-Escarmant and Guyon, 2004). A. ostoyae is a typical soil-borne pathogen species alternating between parasitic and saprophytic stages with inoculum that persist within forest stands between silvicultural rotations (Rishbeth, 1988). A. ostoyae can persist in the soil in roots and stumps and act as sources for new infections (Rishbeth, 1988; Lung-Escarmant and Guyon, 2004). Infection by A. ostoyae occurs via two distinct processes. First, tree-to-tree transmission occurs through root contacts (Zeller, 1926; Childs and Zeller, 1929) or through rhizomorphs. These mycelial cords are formed in infected roots and can extend through the soil to reach new hosts (Rishbeth, 1988). Second, basidiospores, the wind-dispersed sexual spores, may germinate on fresh wood substrate (for example, stumps and partly buried stem segments; Rishbeth, 1988), generating a haploid mycelium. The haploid mycelium must fuse with another sexually compatible spore to form a new diploid mycelium able to infect a new host. This dispersal mechanism mainly occurs at few hundred meters with possible rare long dispersal events (Dutech et al., 2017).

The Landes de Gascogne forest (southwestern France; Figure 1) harbor the largest contiguous monospecific maritime pine (P. pinaster) forest in Europe (that is, one million hectares). In this area, reports of pine mortality due to A. ostoyae has been increasing over the last 30 years (Lung-Escarmant and Taris, 1984). The first cases of maritime pine mortality caused by A. ostoyae were detected near the Atlantic coast in 1920 (Guyot, 1928). These reports occurred shortly after the start of the intensive plantation of maritime pine during the second half of the nineteenth century, which increased the forest area from ~250 000 to ~750 000 ha in only 50 years (Temple, 2011). Lévy and Lung-Escarmant (1998) suggested that A. ostoyae recently emerged from the pre-existing large plantations (that is, anterior to 1857; Vallauri et al., 2012). For example, the pathogen on the drained part of the region could have been the source of inoculum for the colonization of the contiguous newly planted forests. This hypothesis is in agreement with the current geographical distribution of the pathogen mainly localized in the coastal area in the vicinity of these pre-existing forest areas (Labbé et al., 2015). This is also consistent with the decreasing eastward gradient in genetic diversity observed in the pathogen population of the Landes de Gascogne forest (Prospero et al., 2008). In our case, a gradient may be caused by successive founder events from a source population along the coast to the newly colonized inland tree hosts (Excoffier et al., 2009). However, testing this hypothesis requires performing a temporal monitoring of a root disease on trees, which is notoriously difficult (for example, Morrison et al., 2000). Therefore, there is little support for the hypothesis that the increasing mortalities due to A. ostoyae over the last 30 years are actually related to a recent expansion of the pathogen population(s). An alternative hypothesis is that the trees exhibited a higher expression of symptoms due to environmental changes, such as climatic changes (Kubiak et al., 2017), alternatively, an increased reporting rates for 30 years due to intensive field surveys.

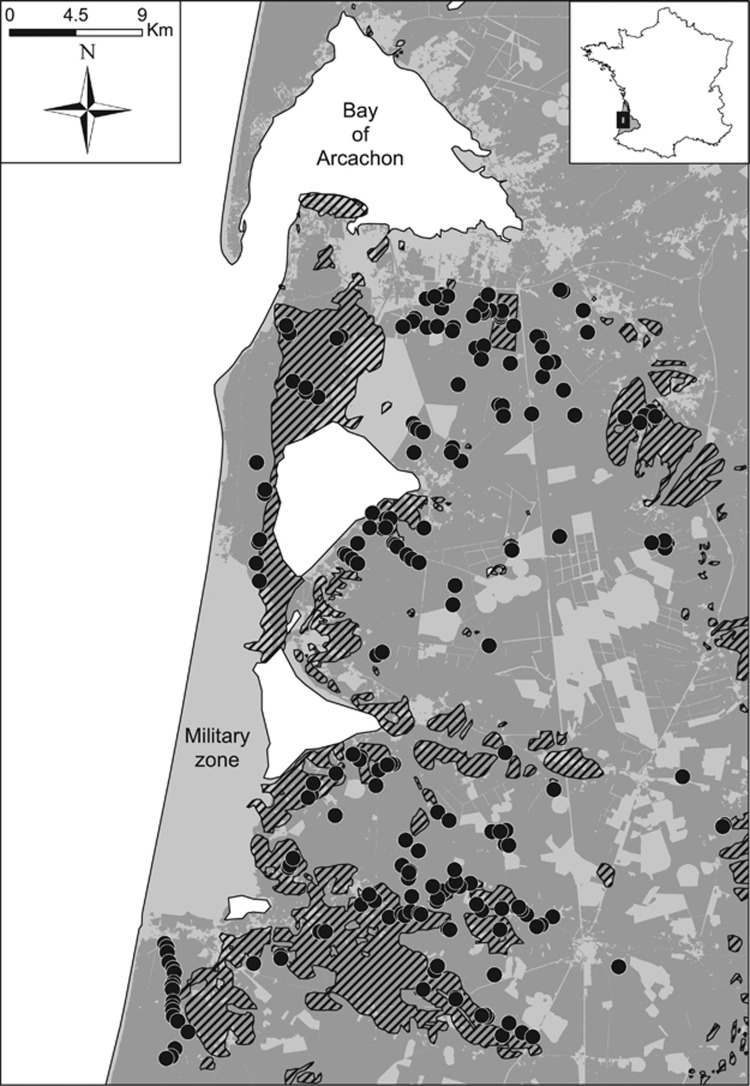
Figure 1.

Geographical locations of the A. ostoyae samples. The black dots indicated sampling localities of A. ostoyae collected on dead and dying maritime pines. The ancient forest areas (Cassini; Vallauri et al., 2012) are indicated by black hatched areas, the recent forest areas (IGN BD Forest, v.2) are indicated in dark grey, and the unforested areas are indicated in light grey, with the exception of the restricted military zone in the west part of the sampling area.

A first investigation of the genetic diversity by Prospero et al. (2008) showed no significant evidence of genetic differentiation among the sampled A. ostoyae disease centers at the scale of the entire Landes de Gascogne forest. This result raised questions about the number of genetically distinct sources at the origin of this potential expansion. However, this previous study focused mainly on samples collected from few disease foci (31), mostly smaller than one hectare, and mainly composed of only one clonal genotype (identified based on five microsatellite markers). Additional analysis relying on a larger set of molecular markers and an enlarged sampling of disease centers would be required to infer the colonization process of the new afforested areas by this fungal pathogen. New population genetic approaches based on approximate Bayesian computation (ABC) also offer a simulation-based framework to test this hypothesis of pathogen population expansion (Barrès et al., 2012; Dutech et al., 2012; Fontaine et al., 2013; Sakalidis et al., 2016).

In this study, we re-assessed the genetic diversity of A. ostoyae sampling a larger number of disease centers than in Prospero et al. (2008) and avoid clonal genotypes by sampling only one single isolate per disease center. We focused on the coastal area, which is supposed to be the main source of the recent expansion in the Landes de Gascogne, and where the disease is also the most frequently reported (Labbé et al., 2015). We first analysed the genetic structure of A. ostoyae to confirm the hypothesis that the fungal expansion in the investigated area come from a single gene pool. Then, we reconstructed the demographic history of the local pathogen population testing various plausible scenarios using an ABC approach (Beaumont et al., 2002; Csilléry et al., 2010). This approach includes the identification of the best fitting model to the observed genetic diversity and then estimating the timing and intensity of each demographic event. The last glacial maximum (that is, ~19 000 years ago) has led to major range shifts in the distribution of the European temperate and boreal forest, with the flora of south-western France being primarily dominated by periglacial tundra and few sparse boreal forests (that is, mixed and coniferous forests; Frenzel et al., 1992). As A. ostoyae is associated with the presence of coniferous species (Guillaumin et al., 1993), we can thus expect that the major recession of coniferous forest during the height of the glaciations also led to a major contraction of the pathogen populations. Inversely, the large maritime pine plantations during the nineteenth and twentieth centuries should have favoured its expansion. Thus, the signature of demographic contraction-expansion should have left a genetic footprint detectable with ABC approaches.

Materials and methods

Study area and sampling

The study area covered about a quarter of the current forest in the Landes de Gascogne (~240 000 ha) and encompassed both pre-existing forest areas and afforested areas since the nineteenth century (Figure 1). Two hundred twenty-one samples of subcortical mycelium (190) or fruiting bodies (31) of A. ostoyae were collected between 2012 and 2014 from dead and dying maritime pines (Figure 1). These samples were spaced at a minimum distance of 100 m to reduce the possibility of sampling clonal genotypes from the same disease focus commonly observed at this spatial scale (Prospero et al., 2008). About 2 mg of mycelium were collected for each field sample by carefully avoiding wood material, lyophilized in a microtube during 12 h at −45 °C and 0.3 mbar, and stored at −80 °C until the DNA extraction.

DNA extraction, microsatellites and SNPs genotyping

Total genomic DNA was extracted from lyophilized mycelium with cetyltrimethylammonium bromide extraction buffer, following the protocol of Prospero et al. (2008). The extraction products were purified using the innuPREP PCR pure kit (Analytik Jena, Biometra, Germany) and stored at −20 °C. DNA concentration was determined using a NanoDrop spectrometer (NanoDrop Technology, San Diego, CA, USA) and adjusted to 10 ng μl⁻¹ using a STARTlet 8-channel robot (Hamilton Co., Bonaduz, GR, Switzerland).

Each mycelium sample was genotyped using 14 polymorphic microsatellite markers: AoSSR21a, AoSSR74a, AoSSR75a (Langrell et al., 2001), CAG25a, CAG77a (Worrall et al., 2004), Arm05, Arm09, Arm15, Arm16 (Prospero et al., 2010), AoB8A4Z, AoB8PN1, AoB9MK4, AoCE9NK and AoCFZOL (Malausa et al., 2011). We designed two multiplexed sets which co-amplified seven microsatellite markers each (Supplementary Table S1). The multiplex PCR was conducted using the Qiagen Multiplex PCR kit (Qiagen, Hilden, Germany). The two multiplexed PCR mixes were composed of 3 μL of sterile water, 4 μl of Qiagen Multiplex Buffer (2 ×), 2 μl of primer premix (primer pairs concentrations indicated in the Supplementary Table S1) and 3 μl of DNA (10 ng μl⁻¹). PCR cycling was carried out using a Labcycler 48 thermocycler (SensoQuest Biomedical Electronics, Göttingen, Germany) using the same thermal cycling programs for the two multiplexes: an initial denaturation step at 95 °C during 15 min; followed by 34 cycles of denaturation at 94 °C for 30 s, primer annealing at 55 °C for 1 min and extension at 72 °C for 45 s, and a final extension at 60 °C for 30 min. After testing the successful amplifications of the PCR products on 1% agarose gels stained with GelRed (Biotium, Hayward, CA, USA), genotyping was performed on a capillary sequencer (ABI 3730; Applied Biosystems, Foster city, CA, USA). Individuals with unclear genotypes were genotyped twice.

The samples were also genotyped at 27 single-nucleotide polymorphism (SNP) markers identified in 24 genes present as single copy orthologues in most fungal genomes (Dutech et al., 2016, 2017). These SNPs were multiplexed, and genotyped using the MassARRAY Analyser 4 system (Agena Bioscience, San Diego, CA, USA) according to the iPLEX protocol from Sequenom (Gabriel et al., 2009). Results were inspected and analysed using the MassARRAY Typer Analyzer v.4.0 software (Agena Bioscience).

Genetic diversity and structure

Clonal genotypes were identified using GENCLONE software v.2.0 (Arnaud-Haond and Belkhir, 2007). Genetic analyses were performed with only one representative individual for each genotype to remove the effect of clonal structure on the analysis. Genotypes with more than five missing markers (30%) were discarded. Linkage disequilibrium among markers was tested using a permutation test (1000 permutations) implemented in GENEPOP v.4.2 (Rousset, 2008). For each marker, fixation index (F_IS), genetic diversity (H_e) and allelic richness (A_r) were estimated using GENEPOP. Departure of allele frequencies from Hardy–Weinberg equilibrium was also tested with GENEPOP using an exact test (499 permutations). The nominal P-value of 0.05 was adjusted for multiple comparisons using a false discovery rate correction and performed in R v.2.15.1 statistical software (Benjamini and Hochberg, 1995; Core Team R, 2015). We used micro-checker v.2.2.3 software (Van Oosterhout et al., 2004) to check for the occurrence of null alleles and possible genotyping errors in the data.

We investigated the population genetic structure of A. ostoyae using two individual-based methods: the Bayesian model-based clustering method implemented in STRUCTURE v2.3.4 (Pritchard et al., 2000) and a principal component analysis (Jombart et al., 2009). The Bayesian model-based clustering method of STRUCTURE was conducted using an admixture model, assuming correlated allele frequencies among clusters and using both uniform priors (standard model) and sampling location priors (Locprior model) for the population of origin of each individual (that is, the nearest city). For each analysis, we performed a series of independent runs with different values for the number of clusters (K), testing all values from 1 to 10. Each run used 500 000 Markov chain Monte Carlo iterations after a burn-in period of 50 000 iterations. We conducted 10 independent replicates for each value of K, to ensure the stability of Markov chain Monte Carlo results. We identified the number of K that best explains the data by computing the posterior probability of the data Ln(D) for each K following STRUCTURE user guide. To identify potentially distinct clustering solutions at each K, we used CLUMPAK v.1.1 (Kopelman et al., 2015) to compute a symmetric similarity coefficient between pairs of runs using the Greedy algorithm, 100 random input sequences and the G’ statistic. To identify genetic clustering of individuals we also conducted a principal component analysis (Patterson et al., 2006) on the allele frequencies to provide a complementary view to the Bayesian clustering analyses independently of any model assumptions (Jombart et al., 2009). We used ADEGENET v.2.0.1 R statistical package to conduct the principal component analysis (Jombart, 2008).

Demographic history

Rational of the methodology

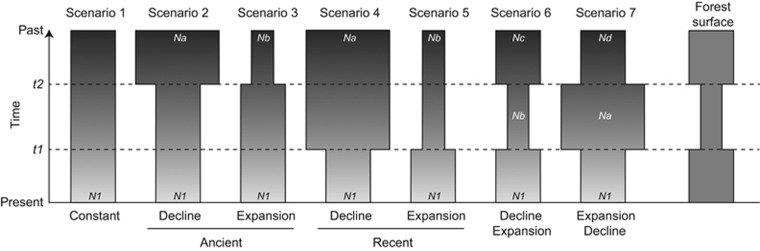
We investigated which demographic history best describes the genetic diversity of A. ostoyae in our studied area using the standard ABC method (linear discriminant analysis, ABC-LDA; Beaumont et al., 2002; Estoup et al., 2012) as well as a new ABC approach, the ABC random forest (ABC-RF; see section ‘Model choice’ for explanations on its specificities; Pudlo et al., 2016). These coalescent-based methods simulate thousands of pseudo-observed data sets (PODs) comparable to our observed data under various demographic models and compares them to identify which model best explain the observed data. We tested seven plausible scenarios of demographic changes (Figure 2). The first scenario consisted of a null hypothesis of constant effective population size (N₁) through time, irrespective of any changes in the forest surface. The six other scenarios consist of different combinations of pathogen population size changes that can be related to the host population size: the contraction of the forest during the last glaciation (t₂ between 100 and 5000 generations) or the recent increase of the forest area during the massive plantation of the second half of the nineteenth century (t₁ within the last 100 generations). Each parameter defining a scenario was considered as random variable drawn into prior distributions defined in Supplementary Table S2. We conducted our ABC analysis considering only the microsatellite data, as SNPs data cannot be analysed jointly with microsatellite in DIYABC (Cornuet et al., 2010), and the low number of SNPs did not provided enough resolution. Our ABC approach included three steps: (1) identification of the demographic scenario that best describes the observed data; (2) estimation of the marginal posterior distributions for each parameter of the best demographic scenario; and (3) evaluation of the goodness-of-fit between the posterior parameter distribution–model combination and the observed data.

Figure 2.

Graphical representations of the seven scenarios of A. ostoyae population size evolution in the Landes forest of Gascogne considered in the ABC analyses. The time scale is indicated by the arrow on the left. The time was measured backward in generations before the present. A schematic representation of the forest surface evolution is indicated on the extreme right of the figure. Further details on each scenario and parameters are provided in the text and in Supplementary Table S2.

Model choice

We identified the scenario(s) best- fitting the data in the ABC framework using a RF process (ABC-RF; Breiman, 2001; Pudlo et al., 2016). RF is one of the main machine learning algorithm for classification and regression. This algorithm uses the prediction of a collection of bootstrapped decision trees (that is, the forest) to perform classification of the scenarios using a set of variables (that is, summary statistics). Compared with standard model-choice procedures (Cornuet et al., 2010), ABC-RF (i) offers a larger discriminative power; (ii) is more robust against the choice and number of summary statistics; (iii) allows for a drastic reduction in the computing effort; and (iv) provides a more reliable approximation of the posterior probability of the selected scenario (Pudlo et al., 2016). The ABC-RF analysis was conducted by simulating 10⁴ PODs per scenario using the coalescent simulator implemented in DIYABC v.2.1.0 (Cornuet et al., 2010; Pudlo et al., 2016). We summarized each POD using all single population summary statistics (S) available in DIYABC for microsatellite marker including the mean number of alleles per locus (A), the mean expected heterozygosity (H_e), the mean allele size variance over all markers (V), the Garza and Williamson index across markers (M_GW), together with the linear discriminant functions (LDA) as additional synthetic variables (Pudlo et al., 2016). The ABC-RF analysis provides a classification vote representing the number of times a scenario is selected as the best one among n trees in the constructed RF. The scenario with the highest number of classification vote was selected as the best scenario among a total of 500 trees (Breiman, 2001; Pudlo et al., 2016). Posterior probabilities and prior error rates (that is, the probability of choosing a wrong model when drawing model index and parameter values into priors; Pudlo et al., 2016) of the best scenario were computed over 10 replicate analyses (Fraimout et al., 2017). We used abcrf v.1.5.0 R statistical package to conduct the ABC-RF analyses (Pudlo et al., 2016).

We duplicated the analysis using one of the widely used standard ABC method based on LDA (ABC-LDA; Beaumont et al., 2002; Cornuet et al., 2008). For each scenario, we simulated 10⁶ PODs, which were summarized using the following set of summary statistics (S): A, H_e and V. The posterior probability of each competing scenario was estimated using a polychotomous logistic regression (Cornuet et al., 2010) on the 1% PODs closest to the real data set. We evaluated the power of our ABC analysis to discriminate between competing scenarios by analysing simulated data sets with the same number of loci and individuals as our real data set. As described by Cornuet et al. (2010), we estimated the type I error probability as the proportion of instances in which the selected scenario did not show the highest posterior probability among the competing scenarios, for 1000 simulated data sets generated under the best-supported scenario. Similarly, we estimated the type II error probability, by simulating 1000 data sets for each of the six other alternative scenarios and calculating the mean proportion of instances in which the best-supported model was incorrectly selected as the most probable scenario.

Estimation of the parameters

For both ABC-RF and ABC-LDA analyses, we estimated the posterior distributions of the demographic parameters under the best demographic scenario(s) using the standard ABC method implemented in DIYABC (Beaumont et al., 2002; Cornuet et al., 2008). We then used local linear regressions on the 1% closest of PODs, after the application of a logit transformation to parameter values (Beaumont et al., 2002; Cornuet et al., 2008). For ABC-RF, we applied the method to the same number of PODs as simulated for ABC-LDA (that is, 10⁶ PODs per scenario) and the same subset of summary statistics as used for ABC-LDA (that is, A, H_e and V), to avoid any correlation among explanatory variables during the regression step (Blum et al., 2013).

Model checking

For both ABC-RF and ABC-LDA analyses, we conducted the model checking procedure implemented in DIYABC to evaluate the goodness-of-fit between the posterior parameter distribution and the observed data following Gelman et al. (1995). The model checking procedure was conducted by simulating 1000 PODs under the best model-posterior combination, with sets of parameter values drawn with replacement from the posterior parameter distribution. This generated a posterior cumulative distribution function for each summary statistic considered (A, H_e, V and M_GW), providing an estimation of how well the fitted model can reproduce the observed summary statistics.

Results

Genetic diversity and structure

Only two out of the 221 genotyped individuals (separated by 143 m) had the same multilocus genotype and were classified as clones. After keeping only one representative sample of this clone, removing the genotypes with more than five missing alleles (that is, 6% of the genotypes), the remaining data set included 206 individuals with less than 3.5% missing data. We identified a total of 141 different alleles over the microsatellite and SNP markers, ranging from 2 alleles (AoB8PN1 and all SNP markers) to 11 alleles (AoB8A4Z and AoSSR74a). The mean expected heterozygosity (H_e) was 0.53 (s.e.±0.06) and ranged from 0.02 to 0.82 for the microsatellite markers and was 0.35 (s.e.±0.03) and ranged from 0.09 to 0.50 for the SNP markers (Table 1). The mean allelic richness of the microsatellite markers was 5.86 (s.e.±0.77) and ranged from 2 to 10.62.

Table 1. Genetic diversity and fixation indices at the microsatellite and SNP markers for A. ostoyae from the south-western France.

Marker	NA (%)	Ar	He	Ho	FIS
Microsatellite
AoB8A4Z	16.0	10.24	0.804	0.734	0.087
AoB8PN1a	3.9	2.00	0.243	0.000	1.000***
AoB9MK4	7.8	3.47	0.457	0.432	0.055
AoCE9NKa	23.3	4.93	0.375	0.082	0.781***
AoCFZOLa	6.3	2.45	0.016	0.005	0.666***
AoSSR21aa	43.2	7.00	0.706	0.368	0.480***
AoSSR74aa	19.9	10.62	0.821	0.358	0.565***
AoSSR75aa	7.8	8.60	0.640	0.368	0.425***
Arm05	3.4	3.97	0.599	0.618	−0.033
Arm09a	3.9	8.42	0.627	0.409	0.348***
Arm15	2.9	5.00	0.559	0.490	0.123
Arm16	8.3	7.83	0.720	0.714	0.008
CAG25a	11.2	4.64	0.564	0.525	0.069
CAG77a	6.8	2.85	0.304	0.318	−0.045
SNP
FG487_1	0.0	2.00	0.361	0.413	−0.144
FG524_3	1.0	2.00	0.358	0.368	−0.027
FG529_1	7.8	2.00	0.342	0.311	0.093
FG543_5	0.0	2.00	0.403	0.403	0.001
FG652_1	1.9	2.00	0.497	0.505	−0.016
FG686_1	1.0	2.00	0.304	0.304	−0.000
FG691_1	22.3	2.00	0.498	0.488	0.021
FG692_2	3.4	2.00	0.408	0.407	0.001
FG698_3	1.0	2.00	0.491	0.515	−0.048
FG716_1	1.0	2.00	0.265	0.294	−0.109
FG716_8a	1.0	2.00	0.262	0.230	0.120
FG730_3	1.5	2.00	0.351	0.335	0.047
FG735_1	1.0	2.00	0.484	0.451	0.068
FG747_4	0.5	2.00	0.207	0.234	−0.130
FG756_1	0.0	2.00	0.500	0.485	0.029
FG762_5	1.0	2.00	0.295	0.299	−0.015
FG771_1a	1.0	2.00	0.310	0.294	0.051
FG771_3	1.0	2.00	0.464	0.412	0.112
FG788_1a	1.0	2.00	0.128	0.088	0.312***
FG848_1	0.0	2.00	0.323	0.316	0.022
FG848_6a	1.0	2.00	0.216	0.206	0.045
FG893_1	1.5	2.00	0.354	0.340	0.040
MS334_3	0.0	2.00	0.401	0.398	0.008
MS441_2	0.5	2.00	0.229	0.215	0.064
MS452_3	0.0	2.00	0.350	0.325	0.072
MS467_8a	17.0	2.00	0.444	0.181	0.592***
MS481_1	0.5	2.00	0.089	0.093	−0.046
All
Multilocus	5.7	3.32	0.409	0.349	0.146***

Abbreviations: A_r, allelic richness; F_IS, fixation index (*P⩽0.05; **⩽0.01; ***⩽0.001); H_e, unbiased expected heterozygosity (Nei, 1973); Na (%), mean percentage of missing allele.

^aMarkers excluded from analyses.

Out of the total 41 markers analysed, nine markers (seven microsatellites and 2 SNPs) displayed a strong and significant deficit of heterozygotes compared with what would be expected under Hardy–Weinberg equilibrium. This result is likely due to null alleles, as suggested by the micro-checker program (data not shown). These markers were excluded from all subsequent analyses to avoid any bias (Table 1). Significant linkage disequilibrium was also detected between three SNP marker pairs (FG716_1 and FG716_8; FG771_1 and FG771_3; and FG848_1 and FG848_6). Only one SNP for each pair was retained for subsequent analyses (FG716_1, FG771_3 and FG848_1). After this cleaning and LD pruning step, the final data set used for the analysis included 29 markers (7 microsatellites and 22 SNP markers), displaying a mean F_IS value of 0.02 (s.e.±0.01), not significantly departing from Hardy–Weinberg equilibrium expectation (P-value=0.09).

Consistently with the lack of departure from Hardy–Weinberg equilibrium, the Bayesian clustering analyses suggested that only one genetic pool occurred in our sampling of A. ostoyae in the Landes forest de Gascogne with a posterior probability that the data include only one cluster (K=1) equal to one for both the standard and Locprior model of STRUCTURE (Supplementary Figure S1). Consistently with this result, the principal component analysis did not show any evidence of genotype clustering (Supplementary Figure S2). These results suggest no genetic structure among geographic areas, which mean that all A. ostoyae genotypes can be considered as coming from a single panmictic population.

Demographic history

Among the seven demographic scenarios tested, the model choice procedure based on the ABC-RF showed that scenario 6 had the highest posterior probability of 22.2% (s.d.±4.7%) with a prior error rate of 73.8% (s.d.±0.0% Table 2; Figure 2). Similarly, the ABC-LDA analysis showed that the scenario 6, but also the scenario 2, provided a significant better fit to the data than the other scenarios (Figure 2), with a posterior probability of 27% and 28%, respectively (Table 2). A second ABC-LDA analysis comparing only these scenarios 6 and 2 showed that these scenarios shared similar posterior probability of 49% and 51%, respectively.

Table 2. Model choice procedure of the ABC approaches used for comparing demographic scenarios of A. ostoyae in the Landes de Gascogne.

	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5	Scenario 6	Scenario 7
ABC–RF
Votes (s.d.)	54.5 (± 5.6)	102.8 (± 7.7)	66.6 (± 8.0)	40.4 (± 6.4)	27.8 (± 3.9)	198.5 (± 8.9)	9.4 (± 2.8)
Post. Prob. (s.d.)	–	–	–	–	–	0.22 (± 0.05)	–
Prior error rate (s.d.)	–	–	–	–	–	73.8% (± 0.0%)	–
ABC-LDA
Post. Prob. (95% CI)	0.15 (0.15–0.16)	0.28 (0.27–0.28)	0.07 (0.07–0.08)	0.1 (0.09–0.10)	0.11 (0.10–0.11)	0.27 (0.26–0.27)	0.03 (0.03–0.03)
Performance
D1	15.2%	12.4%*	8.9%	6.9%	12.2%	10.3%§	5.6%
D2	12.1%†	23.0%	4.9%†	10.5%†	6.5%†	18.3%†§	2.1%†
D3	11.1%	5.7%*	13.1%	5.2%	12.2%	6.9%§	11.1%
D4	15.2%	24.7%*	11.4%	49.4%	6.3%	15.2%§	12.2%
D5	15.3%	9.70%*	16.1%	2.3%	31.2%	21.2%§	9.7%
D6	8.8%‡	11.5%*‡	4.7%‡	4.2%‡	8.3%‡	16.4%	2.0%‡
D7	22.3%	13.00%*	40.9%	21.5%	23.3%	11.7%§	57.3%

Abbreviations: ABC, approximate Bayesian computation; ABC-RF, ABC random forest; D, proportion of case in which the model choice procedure was able to select a scenario as the most probable with non-overlapping confidence intervals of the posterior probabilities of each scenario; Post. Prob., relative posterior probability for each scenario; s.d., s.d. over 10 replicate analyses.

The number of random forest votes of each scenario was averaged over 10 replicate analyses. For the ABC-RF analysis, the posterior probability and prior error rates of the best scenario were averaged over 10 replicate analyses. Type I or α error rates (risk to exclude the focal scenario when it is the true one) for scenario 2 and scenario 6 are indicated with ‘†’ and ‘‡’, respectively. Type II or β error rates (risk under scenario 2 (here: 9.1%) is marked with ‘*’ and under scenario 6 ‘§’. Demographic scenarios are shown in Figure 2.

Scenario 6 and 2 assume both an ancient contraction of A. ostoyae population followed by a period of low effective population size (Figure 2), with effective population sizes change from 9480 (95% confidence interval (CI): 2490–9830, N_c) to 796 (95% CI: 343–3530, N_b;) and from 6740 (95% CI: 1640–9790, N_a) to 876 (95% CI: 453–4290, N₁), respectively (Supplementary Figure S3 and Supplementary Table S3). According to the scenario 6 and 2, this contraction occurred between 1080 (95% CI: 274–4,830, t₂) and 2080 (95% CI: 308–4860, t₂) generations ago, respectively (Supplementary Figure S3 and Supplementary Table S3). The scenario 6 also suggests that this population contraction was followed by a recent expansion, 4.10 (95% CI: 3.06–96.8, t₁) generation ago, to reach the current effective size of 3150 (95% CI: 883–4890, N₁) individuals (Supplementary Figure S3 and Supplementary Table S3).

The simulation-based assessment of the robustness in our scenario choice with the ABC-LDA analysis revealed on the one hand a relatively high type-I error rate, with only 16.4% and 23.0% of the simulations generated under scenarios 6 and 2 properly recovered by the model choice procedure (Supplementary Table S3). This indicates a low sensitivity of our ABC-LDA analysis considering our data set. On the other hand, estimates of type-II error rates were very low for scenario 6 and scenario 2. Less than 6.6% of the simulations generated under each scenario other than scenario 6 were wrongly identified as being produced by this scenario (Supplementary Table S3). This indicates a very strong power (94.4%) to discriminate this scenario 6 from the others considering the data and models tested. Similarly, scenario 2 received a type-II error rate of 9.1% in average, and thus a power of 90.9% to discriminate this scenario from the others. This ABC-LDA analysis has thus overall very good power. In addition, simulated data sets under the two best scenarios (that is, scenario 6 and 2) using their posterior parameter distributions were able to produce values for each summary statistic that were consistent with those observed from the real data, indicating a good goodness-of-fit of the fitted model to the data (Supplementary Table S4).

Discussion

A single homogeneous gene pool is at the origin of the A. ostoyae colonisation

The expansion of A. ostoyae in the Landes de Gascogne forest was assumed to originate from the coastal forests which existed before the large pine plantations of the nineteenth century (Labbé et al., 2015). Our results show that a single homogeneous gene pool occurs along the coast (that is, about a quarter of the whole forest). This result is consistent with the absence of genetic differentiation estimated among the 31 disease centers sampled in Prospero et al. (2008) at the scale of the whole maritime pine forest of the Landes de Gascogne. This genetic homogeneity may thus indicate that either only one single pre-existing forest was at the origin of the current expansion, or that the A. ostoyae populations established in the different pre-existing forests were not genetically differentiated enough. The absence of any genetic subdivision at the scale of our study area also suggests that dispersal ability of this species is large enough to homogenize the gene pool. This result contrasts with the clustered distribution of the disease (Labbé et al., 2015) and the limited dispersal of the basidiospores, both occurring at the scale of few kilometres (Dutech et al., 2017). The observed genetic homogeneity thus suggests that a single source population of A. ostoyae colonized the planted forest, and that spatially limited spore dispersal and rare long dispersal events are enough to maintain population genetic homogeneity at the geographic scale of the study.

Genetic signatures of a population bottleneck

Among the seven plausible demographic scenarios tested, the best ones identified by the ABC-RF and ABC-LDA analyses (that is, scenarios 6 and 2) suggest that the A. ostoyae population underwent a severe contraction between ~1080 and ~2080 generations ago resulting in a population size 12 times lower than the estimated ancestral population size. This contraction episode would have then been followed by a population expansion, leading to a population size four times larger during the last four generations. The relatively high prior error rate of the demographic scenario supporting a contraction followed by an expansion (that is, scenario 6) may demonstrate the limited information from the seven microsatellite markers. However, simulation-based studies showed that ABC method can provided good results with as few as five markers (Guillemaud et al., 2010). Furthermore, given the very fast mutation rate of microsatellite loci (Bruford and Wayne, 1993), these markers are well-suited to detect recent demographic changes. A limited sample size may be another possible explanation for the low-power of our analysis to detect demographic events. However, the 206 isolates used in this study are far larger than the minimum sample size per population of 30 individuals required to characterize the allele frequencies in a population with accuracy (Guillemaud et al., 2010). A more likely explanation is the difficulty in detecting recent expansions using population genetic data. This is consistent with the second highest number of votes garnered by the scenario that assumes only an ancient decline of the A. ostoyae population (that is, scenario 2) in the ABC-RF analysis, and with the high probability of this scenario in the ABC-LDA analysis. The signal in the data depends on the magnitude of the population size change, and also on the accumulation of new mutations along the coalescent trees, which is a function of mutation rate of the genetic markers analysed (Girod et al., 2011). Even by using markers with high mutation rates such as microsatellite markers, some time is required before an equilibrium state between mutation and genetic drift is reached, and thus before the genetic diversity is representative of the effective population size. Moreover, the combination of an ancient contraction and a recent expansion is probably difficult to detect, because the genetic signal is attracted by the most important events in the coalescent tree.

The severe contraction of the A. ostoyae population between ~1080 and ~2080 generations ago likely correspond to the maximal contraction of the forest occurring during the last glacial maximum, which led to major southward shifts in a large number of temperate species in Europe (Guillaumin et al., 1993; Taberlet et al., 1998). At that time the presence of coniferous species (Guillaumin et al., 1993) was restricted to a few sparse individuals in the region (Frenzel et al., 1992). Although A. ostoyae may remain in dead wood for decades (Rishbeth, 1972), it is unlikely that it would persist for one thousand years. An alternative explanation to the population recession of A. ostoyae would be a long-distance migration event of an A. ostoyae inoculum from another conifer forest in Europe between ~1080 and ~2080 generations ago. Such a migration event may be associated with a genetic bottleneck if a limited number of genotypes had colonized the area, producing a signal similar to population contraction (for example, Dutech et al., 2012). In this study, the two hypotheses cannot be differentiated. A genetic analysis of several A. ostoyae populations covering various forests across Europe would be required to differentiate alternative hypotheses and retrace the possible routes and timings of colonisation. Regardless, the events that influenced the genetic diversity (for example, contraction) must have occurred many generations before the present time. By contrast, the genetic pattern consistent with population expansion likely took place more recently, possibly only around four generations ago. Population expansion is likely associated with the intensive plantation of maritime pine on the ancient marshes during the nineteenth century (Temple, 2011). The significant increase of the maritime pine area since this period may have allowed A. ostoyae pathogen to infect a larger number of new host resources leading to a rapid and significant population growth.

Inferring population demographic parameters in A. ostoyae

Generation times for root rot pathogens such as Armillaria are difficult to estimate due to overlapping generations and variation in age at first reproduction. However, time between the establishment of one mycelial colony and the colonization of a new disease center via sexual spores is likely long. First, fruiting bodies are not produced each year and depend upon the climatic conditions (Wargo and Shaw III, 1985; Ferguson et al., 2003). Second, fruiting bodies are generally produced on dead or dying trees in the Landes de Gascogne (F. Labbé personal observation). The death of adult conifer trees may happened long after initial infection, as the adult trees have shown partial resistance and thus live trees may contain infection in the roots in latent necrosis (Robinson, 1997; Labbé et al., 2015). This mechanism delays the age of the first fructification in the older pine populations. Finally, the germination of an haploid basidiospore and its fusion with another compatible haplotype is assumed to be a rare event occurring only under limited environmental conditions (Rishbeth, 1988). However, most of the mycelial development is underground, and new progenies are difficult to detect in nature (Rishbeth, 1988), thus complicating the estimation of reproductive age.

An estimation of the age at first reproduction in A. ostoyae can be attempted using the two generation times obtained from the ABC analysis. If we assume that the decline of the A. ostoyae population (~2080 or ~1080 generations ago) coincided with the last glacial maximum (that is, ~19 000 years ago), then an estimated generation time for A. ostoyae would be roughly between 9 and 18 years (with a CI of 4 to 69 years). Similarly, if we assumed that the population expansion (four generations ago) occurred at the beginning of the first plantations (~150 years ago), or more recently during the development of intensive silviculture for wood production (~50 years ago), an estimated generation time would be between ~38 and ~15 years (with a CI of 2 to 51 and of 1 to 20, respectively). Therefore, through the use of the two calibration points coinciding with major demographic events known from this maritime pine forest, we estimated a similar generation time ranging approximately 10 to 20 years. This may represent a very rough average estimate of the first reproduction age of A. ostoyae, but is still quite consistent with the life-cycle of the fungus described above.

The current effective population size of A. ostoyae estimated using the ABC analysis, was between ~876 and ~3150 individuals (CI: 453–4890). This estimate may appear small compared with the large area occupied by the maritime pine in the surveyed area (~20 000 ha); therefore effective density would be less than one breeding individual per 10 ha. Our estimate was quite similar to that obtained for the same species from a coastal population in this region using a genetic method based on linkage disequilibrium and yielding an estimate of less than one breeding individual per ha (Dutech et al., 2017). Population size is an important parameter for pathogenic fungi but only a few studies have attempted to estimate it. For example, a much larger effective population size of ~4.4 × 10⁹ individuals was estimated for Erysiphe graminis, a foliar pathogen of barley with asexual and sexual reproduction (Damgaard and Giese, 1996). In contrast, our results are more similar with the effective population size of ~1,700 individuals estimated for another fungal pathogen Puccinia striiformis in Gansu province in China (agent of the wheat yellow/stripe rust; Ali, 2013). These large differences likely reflect the differences in sampling design, methods, or life-cycles. However, our estimate of a small effective population size might reflect the low yearly fructification rate per genotype and the low estimated success of spore germination as described above.

Conclusion

The slow and mainly underground life cycle of a soil-borne pathogen makes it generally difficult to monitor and thus to confirm population outbreak (Labbé et al., 2015). In agreement with an ongoing spread of this pathogen in the forest, the present study showed that the population genetics approach is an efficient alternative to complement the labour-intensive monitorings to investigate the dynamics of these fungal pathogens. The increase in the host area offers an opportunity for the pathogen to adapt to these new environments characterized by homogeneous and denser host populations. For instance, a significant variability in aggressiveness has recently been reported for this pathogen population (Labbé et al., 2017). We can thus expect an increase in its biological traits against the local variety of maritime pine under some conditions (Alizon and Michalakis, 2015). Furthermore, our ABC approach was successful at providing the first demographic estimate of generation time for this species, which may be relevant to parametrize individual-based epidemiological models for fungal pathogens (for example, Xhaard et al., 2012). These models, which simulate different dispersal process from different source populations, could then be compared with population genetic inferences such as those conducted in this study. The combination between population genetics and epidemiological modelling may prove successful at predicting future disease outbreaks of root rot pathogens in recent developments of tree plantations (Wingfield et al., 2015).

Data archiving

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.fp112.