Abstract
The molybdenum trisamidoamine (TAA) complex [Mo] (=(3,5-(2,4,6-i-Pr3C6H2)2C6H3NCH2CH2N)Mo) carries out catalytic reduction of N2 to ammonia by protons and electrons at room temperature. A key intermediate in the proposed [Mo] nitrogen reduction cycle is nitrido-Mo(VI), [Mo(VI)]N: the addition of [e−/H+] to [Mo(VI)]N to generate [Mo(V)]NH might in principle follow one of three possible pathways: direct proton-coupled electron transfer; H+ first, then e−; e− then H+. In this study, the paramagnetic Mo(V) intermediate {[Mo]N}− and [Mo]NH transfer product were generated by irradiating the diamagnetic [Mo]N, {[Mo]NH}+ Mo(VI) complexes respectively, with γ-rays at 77 K, and their electronic and geometric structures were characterized by electron paramagnetic resonance (EPR), electron nuclear double resonance (ENDOR) spectroscopies combined with quantum chemical computations. In combination with previous X-ray studies this creates the rare situation where each one of the four possible states of an [e−/H+] delivery has been characterized. Because of the degeneracy of the electronic ground states of both, {[Mo(V)]N}− and [Mo(V)]NH, only multi-reference based methods such as the complete active space self-consistent field (CASSCF) and related methods provide a qualitatively correct description of the electronic ground state and vibronic coupling. The molecular g-values of {[Mo]N}− and [Mo]NH exhibit large deviations from the free electron value ge. Their actual values reflect the relative strengths of vibronic and spin-orbit coupling. In the course of the computational treatment, the utility and limitations of a formal two-state model that describes this competition between couplings are illustrated, and implications of our results for the chemical reactivity of these states are discussed.
TOC image
Introduction
The molybdenum trisamidoamine (TAA) complex [Mo] (=(3,5-(2,4,6-i-Pr3C6H2)2C6H3NCH2CH2N)Mo) shown in chart 1 is the active species in the catalytic reduction of N2 to ammonia by protons and electrons at room temperature.1–3 Despite its low turnover rate this complex represented a major advance in the field of catalytic nitrogen fixation and activation, as the first well-defined molecular catalyst of nitrogen reduction. Some of the key intermediates of the reaction cycle have been crystallized and studied spectroscopically,1–4 the magnetic properties of the key intermediates, [Mo]N2 and [Mo]NH3, as well as of the CO inhibited form, have been studied in detail,5,6 and the entire reaction pathway has been investigated with quantum chemical methods.7–11
Chart 1.
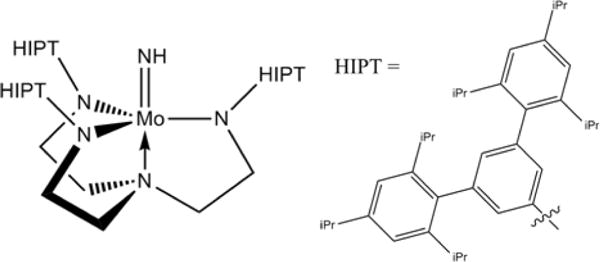
The [Mo]NH complex
The [Mo]N2, [Mo]NH3, and [Mo]CO complexes are low spin (S = ½) d3, which is rare in metal coordination compounds. It has been demonstrated that their unique geometric and electronic structure have a remarkable effect on the molecular g-tensor of the three complexes. The TAA ligand enforces a trigonal symmetry on the molybdenum center leading to partial occupation of a set of doubly occupied orbitals. This partial occupation in turn leads to strong ‘in-state’ spin-orbit coupling (SOC) and Jahn-Teller (JT) vibronic coupling that compete with each other, resulting in the so-called ‘Pseudo-Jahn-Teller’ (PJT) effect.12 The combined results of ligand field theory analysis and quantum chemical methods revealed that the molecular g-tensor is governed by the ‘in-state’ SOC, which is effectively diminished with increasing JT distortion. Hence the g-values can be regarded as sensitive probe of the ratio between SOC and JT coupling. More recently, the TAA ligand has received attention owing to its use in iron-based single molecule magnets (SMM),13,14 and parallel efforts in the synthesis and characterization of trigonal Fe complexes,15–20 likewise reveal such properties, and indeed have yielded nitrogen reduction catalysts.21,22
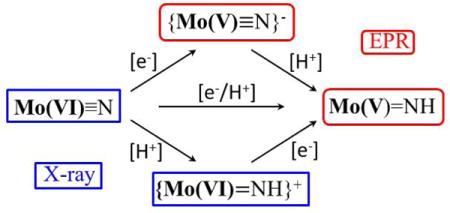
In the proposed [Mo] nitrogen reduction cycle there are four Mo(V) paramagnetic (S = ½) intermediates, namely [Mo]N2H2, {[Mo]N2H3}+, [Mo]NH, and {[Mo]NH2}+, in addition to the two Mo(III) complexes.1–3 Though the diamagnetic Mo(VI) intermediates {[Mo]N2H2}+, [Mo]N, and {[Mo]NH}+ that fall just one step before the Mo(V) species in the catalytic cycle are well characterized, the Mo(V) intermediates could not be observed ([Mo]N2H2) and/or isolated ([Mo]NH) during synthesis.4 As illustrated in Figure 1, the addition of [e−/H+] to [Mo(VI)]N to generate [Mo(V)]NH might in principle follow one of three possible pathways: direct proton-couple ET; H+ first, then e−; e− then H+. In the present study, the paramagnetic Mo(V) species {[Mo]N}−, and [Mo]NH were instead generated by irradiating the diamagnetic [Mo]N, {[Mo]NH}+ complexes respectively, with γ-rays at 77 K. Although cyclic voltammetry shows that {[Mo]N}− is formed reversibly at low potential (E1/2 = −2.68 V vs. Fc+/Fc (Pt)),23 it has never been isolated. Thus, the combination of the previous X-ray diffraction studies and the present spectroscopic/theoretical investigation of {[Mo(V)]N}− and {[Mo]NH} enable the rare situation where each one of the four possible states of [e−/H+] delivery can be characterized.
Figure 1.
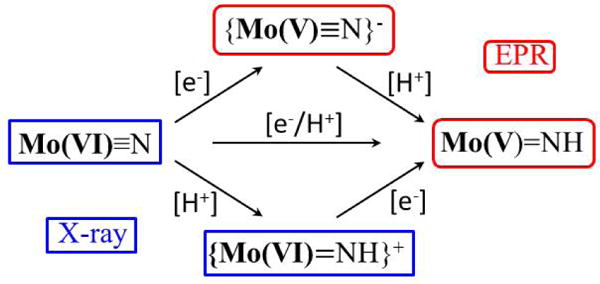
The three possible pathways for addition of [e−/H+] to [Mo]N As shown, and discussed in text, two states have been structurally characterized; two are characterized here by paramagnetic resonance and computational methods.
We here use the electron paramagnetic resonance (EPR), electron nuclear double resonance (ENDOR) spectroscopic techniques combined with the computational studies to characterize the electronic and geometric structure of these two Mo(V) intermediates,{[Mo]N}−, [Mo]NH. The first part of this report describes the investigation of the electronic structures of cryoreduced {[Mo]N}− and the protonated form [Mo]NH with quantum chemical methods. The degeneracy of the electronic ground states of both compounds (vide infra) prohibits the usage of density functional theory (DFT) for the calculation of the electronic structure and magnetic properties. Only multi-reference based methods such as the complete active space self-consistent field (CASSCF) and related methods provide the necessary flexibility for a qualitatively correct description of the electronic ground state and vibronic coupling. Moreover the strong ‘in-state’ SOC cannot be treated by regular linear response approaches but requires an explicit evaluation via quasi-degenerate perturbation theory. In the second part the EPR spectra of the two complexes are reported and first interpreted in terms of a two-orbital model for a doubly degenerate 2E ground state, then analyzed in the light of the quantum-chemical results of the first part. The molecular g-values of {[Mo]N}− and [Mo]NH exhibit large deviations from the free electron value ge. Their actual values serve as a probe of the relative strengths of vibronic and spin-orbit coupling. The third and final part discusses bonding to the ligands surrounding Mo as revealed by their nuclear hyperfine interactions. 14,15N ENDOR spectroscopy identifies the axial nitride ligand of {[Mo]N}−, and shows it to have a small isotropic nuclear hyperfine coupling (∼ 3 MHz), a result nicely captured by the calculations. In contrast, the calculations predicts a large isotropic hyperfine coupling (∼ 10 MHz) for the axial imido nitrogen of MoNH, and rationalize an inability to measure these couplings directly. 1,2H ENDOR experiments agree with the calculation of a bent structure for Mo-N-H with a substantial isotropic coupling for the imido proton. In the course of this treatment, the utility and limitations of the two-state model are illustrated, and implications for the chemical reactivity of these states are discussed.
Materials and Methods
Synthesis
Solutions of [Mo]N, and {[Mo]NH}+ were synthesized as described in the literature.4 The solutions were frozen in liquid nitrogen for cryoreduction and for subsequent EPR/ENDOR measurements. Solutions of diamagnetic [Mo]N, and {Mo(VI)NH}+ were cryoreduced at 77 K, using γ-rays to form paramagnetic {[Mo]N}−, and [Mo]NH respectively24.
EPR and ENDOR Measurements
The 35 GHz pulsed EPR and ENDOR measurements at ∼2 K, were carried out using a locally constructed spectrometer described in detail previously25. Field swept electron spin echo (ESE) EPR were collected with the two pulse echo sequence: π/2-τ-π-τ-echo. Pulsed ENDOR experiments employed either the Davies (π-T-π/2-τ-π-τ-echo), or the MIMS sequence (π/2-τ-π/2-T-π/2-τ-echo), where T is the time interval for which the RF pulse is applied26. Data acquisition for the pulse measurements utilized the SpecMan software package27 (http://specman.4epr.com) in conjunction with a Spin-Core PulseBlaster ESR_PRO 400 MHz word generator and an Agilent technologies Acquiris DP235 500 MS/sec digitizer.
For a single molecular orientation and for nuclei with a nuclear spin of I = ½ (1H, 15N), the ENDOR transitions for the ms = ± ½ electron manifolds are observed at frequencies given by the equation
| (1) |
where νn is the nuclear Larmor frequency and A is the orientation-dependent hyperfine coupling. For I ≥ 1 (14N, 2H), the two ENDOR lines are further split by the orientation-dependent nuclear quadrupole interaction (3P). The peaks are then observed at frequencies dictated by a modified version of the equation above
| (2) |
It is well documented that by analyzing the 2D field-frequency ENDOR spectra collected at various fields across the EPR envelope, the complete nuclear hyperfine and quadrupole principal values could be determined.28–31
Computational Details
All calculations on Mo(V) complexes performed in this work were conducted with the ORCA quantum chemistry program package.32 Density functional theory as well ab initio wave function calculations used the zero’th order regular approximation (ZORA) utilizing a model potential introduced by van Wüllen.33,34 Accordingly, the segmented all-electron relativistically contraction (SARC) versions of the TZVP and SV(P) basis sets, SARC-TZVP and SARC-SV(P), were used throughout the work.35 The Resolution of Identity (RI) approximation was applied for all integral transformations.
Analogous to a previous investigation of the [Mo] complex,5 a slightly reduced model structure of the full complex geometry has been used for many calculations. The applied model is in accordance with model 1″ of reference 8. It features the molybdenum center, the nitrido/imido ligand and the TAA ligand but the large HIPT groups have been replaced by ethyl groups in order to safe substantial computational costs without completely losing the electron donating effect of the HIPT groups (Figure 2). Geometry optimization of the model structure comprised of two steps. First, the full complex geometry has been fully optimized using the BP8636,37 functional together with the SARC-TZVP (Mo, N) and the SARC-SV(P) (C, H) basis set.35 Then the HIPT groups have been replaced by ethyl groups, which then were optimized separately at the same level of theory. Furthermore a second set of structures was generated by optimizing the model structure with respect to the average of the first two electronic states (the two members of 2E-term) utilizing the state-averaged CAS-SCF(7,8) method (vide infra). In the following these structures will be referred to as ‘symmetric’ structures since their first coordination shell exhibits almost perfect C3V symmetry. The most important structural parameters of the first coordination shell of the fully relaxed and the symmetric structures can be found in the Supporting Information. In the case of the optimization to the symmetric limit of [Mo]NH the Mo-Nimido-H bond angle is close to 180° which is an artifact of the energy minimization with respect to the average of the lowest two states. Of course, this chemically unreasonable geometry leads to a significant change of the metal ligand bond pattern. Therefore we have manually adjusted this angle to a value of 154° (the value obtained from the fully relaxed optimization) for the multiplet calculations in the symmetric limit (vide infra).
Figure 2.
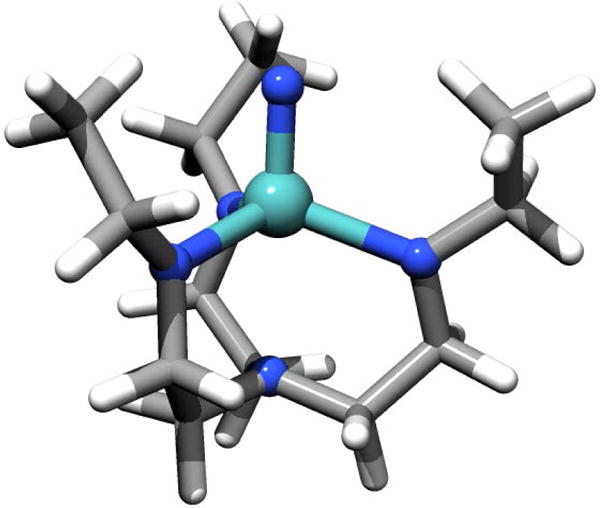
Model structure of [Mo]N−. The HIPT groups have been replaced by smaller ethyl groups, which retain an electron donating effect but are computationally less demanding.
In the course of this work three sets of multireference ab initio calculations were conducted that employ the CASSCF method with different active spaces and varying levels of treatment of dynamic electron correlation effects. The first set of calculations consists of the aforementioned geometry optimizations to the symmetric limit and a set of scans of the Jahn-Teller potential energy surface. In both cases an active space with 7 electrons in 8 orbitals has been chosen, with the shape of the active orbitals being the result of an optimization according to the variational principle. For {[Mo]N}− the active orbitals correspond to the five metal d orbitals as well as the three p-orbitals of the nitrido axial ligand (Figure 3). By contrast, the active orbitals of [Mo]NH comprise one amido p orbital, three metal d orbitals (dxz, dyz and a combination of the dxy and orbitals) as well as four p-orbitals (2px/y and 3px/y) of the axial nitrido ligand. These choices are expected to provide a balanced description of the Mo-N bond in both complexes, and hence, is a good basis for their qualitative discussion.
Figure 3.
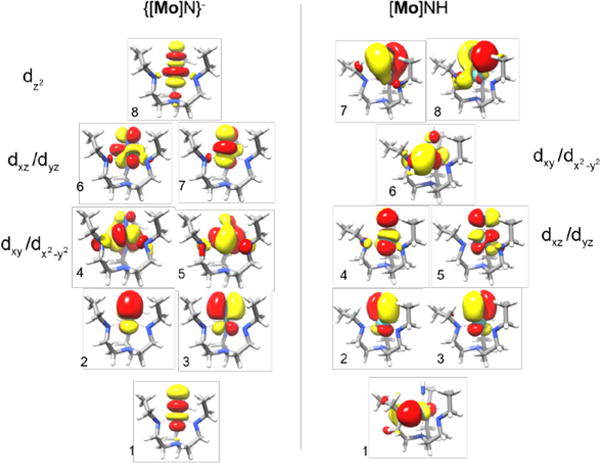
Active orbitals of {[Mo]N}− (left) and [Mo]NH (right) in CASSCF(7,8) and NEVPT2(7,8) calculations. Both sets of orbitals are obtained as natural orbitals of converged CASSCF(7,8) calculations. Note, in the case of [Mo]NH the and its bonding counterpart as well as the dxy orbital are not contained in the active space. The enumeration of the orbitals refers to the decomposition into contributions from atomic orbitals given in Table 1 and Table 2.
Of course, the shape and composition of the active orbitals alters as the corresponding geometry changes but their main character remained unchanged throughout. Dynamical electron correlation was taken into account in the framework of the second-order N-electron valence perturbation theory (NEVPT2) scheme for the potential energy surface scans while they were neglected during the geometry optimizations.
The second set of calculations comprises only single-point energy and g-tensor evaluations. They feature an active space of 13 electrons in 11 orbitals and use NEVPT2 to incorporate dynamical electron correlation. In the case of [Mo]N− the 11 active orbitals that resulted from optimizations with respect to the variational principle include the five metal d-based orbitals, the three p-orbitals and the one s-orbital of the nitrido axial ligand and two σ-bonding orbitals associated with the equatorial amido ligands (cf Figure SI 8). For [Mo]NH the active orbitals correspond to four metal d orbitals (dxz, dyz, dxy and ), four p-orbitals of the axial ligand and three σ-bonding orbitals associated with the equatorial amido ligands (cf. Figure SI 9), again the result of optimizations with respect to the variational principle. This second set of calculations is the most elaborate and also most accurate calculation performed. The inclusion of the equatorial ligand bonding orbitals in the active space will ensure that the ligand field induced by the N/NH as well as the supporting ligand is balanced.
A third set of calculations was performed that only features the minimal active space of 1 electron in the 5 metal d-based orbitals (cf. Figure SI 10 and Figure SI 11). For this set of calculations, dynamical electron correlation effects are described by means of the difference dedicated configuration interaction with a maximum number of two degrees of freedom (DDCI2). In the course of the DDCI2 procedure thresholds of Tpre = 10−4 for the selection of configurations in the reference space and Tsel = 10−6 for the selection of configurations in the CI part were applied. The higher order correlation terms included in DDCI2 make up for some of the deficiencies of the small active spaces and are a convenient basis for discussing some qualitative features of the investigated systems.
Note, that in all three sets of calculations multiple electronic states were evaluated and that the CASSCF orbitals were optimized in a state-averaged fashion. The actual number of calculated states will be indicated in the description of each individual calculation.
Molecular g-tensors have been calculated using either linear response DFT or, for the multireference calculations, the formalism introduced by Gerloch and McMeeking.38,39 In order to obtain g-tensors from linear response DFT, a set of coupled perturbed Kohn-Sham equations had to be solved for a set of self-consistent Kohn-Sham orbitals and a magnetic field perturbation. A more detailed description of this procedure can be found in reference38. The formalism proposed by Gerloch and McMeeking was used for g-tensor calculations with multireference wave functions: Complete Active Space Self-Consistent Field (m,n) calculations (CASSCF(m,n)) where m is the number of active electrons in n active orbitals were conducted at the optimized geometries. Dynamic correlation effects were then taken into account by either the NEVPT2 or the DDCI2 scheme.40–44 In the following we will denote a set of CASSCF(m,n) and subsequent NEVPT2 or DCCI2 calculations as NEVPT2(m,n) or DCCI2(m,n). However, it should be noted that in the case of NEVPT2 only the energy correction to the state energies from perturbation theory is used whereas the form of the wave function is left unchanged. The resulting set of eigenstates {|I⟩} forms a basis in which the Born-Oppenheimer Hamiltonian is presumed to be diagonal. On top of these non-relativistic calculations, SOC is introduced in the framework of quasi-degenerate perturbation theory (QDPT). This means that the SOC operator is diagonalized in the basis of eigenstates {|I⟩}. For the evaluation of SOC integrals the spin-orbit mean-field Hamiltonian ĤSOMF is used, which appears as an effective one-electron operator45,46:
| (3) |
The presented approach accounts for SOC to infinite order but suffers from truncation of the incomplete basis of {|I⟩} functions. The diagonalization yields eigenfunctions which appear as pairwise degenerate functions ϕ and , the so-called Kramer’s pairs. An external magnetic field splits the degeneracy of these pairs via the Zeeman term ĤZee that is then added to the Hamiltonian:
| (4) |
with
| (5) |
Here, μB is the Bohr magneton, ge is the Landé factor, B is the magnetic flux density and and Ŝ are the total orbital and spin angular momentum operators, respectively. It has been shown that diagonalization of the Zeeman term in the basis of the Kramer’s doublet is equivalent to finding the eigenvalues of the Zeeman term in the basis of fictitious spin functions |+⟩ and |−⟩ in the spin-Hamiltonian. Hence, the square of the g-tensors can be calculated according to39,47 (μ, ν=x, y, z):
| (6) |
Results
Electronic structure and PJT
The tripodal ligand enforces an idealized C3V symmetric coordination environment to the central Mo(V) ion. As outlined previously, it is this special environment that accounts for the unusual magnetic properties of the derivatives of the [Mo] complex.5 In a C3V-symmetric ligand field the five metal d-orbitals are split into two degenerate pairs (e) and one non-degenerate orbital (a1), where the orbitals can be expressed either as conventional, real d-orbitals or as eigenfunctions of the z-component of the orbital angular momentum, ml = ±2, ±1, 0 (l=2):
| (7) |
Hence, the d1 configuration of the {[Mo]N}− and [Mo]NH complexes gives rise to three different doublet states: Two orbitally doubly degenerate 2E states and one orbitally non-degenerate 2A1 state. NEVPT2(13,11) calculations including the 15 lowest states on the ‘symmetric’ structures of both complexes allowed for a qualitative and quantitative analysis of their d-d multiplet structure. The corresponding molecular orbitals involved in these calculations of course are linear combinations of these metal d-orbitals and ligand orbitals. Table 3 summarizes the calculated energetic levels of the d-multiplets and their respective dominant configurations as obtained from the CASSCF calculation.
Table 3.
Excitation energies and dominant configurations of the d-d multipltes for [Mo]N− and [Mo]NH from NEVPT2(13,11) calculations as described in the text. An excitation energy of 0 cm−1 signifies the electronic ground state.
| Electronic State | Dominant Configuration | [Mo]NH | [Mo]N− |
|---|---|---|---|
| 2Ea | (3e)1 | 0 cm−1 | 20300 cm−1 |
| 2Eb | (4e)1 | 17500 cm−1 | 0 cm−1 |
| 2A1 | (4a1)1 | 24500 cm−1a) | 27500 cm−1a) |
a)These excitation energies have been determined by NEVPT2(1,5) calculations because of interfering CT states in the NEVPT(13,11) calculations.
The energies presented in Table 3 show that addition of a proton to {[Mo]N}− leads to a change in the electronic ground state configuration. In the case of {[Mo]N}− the 4e(x2-y2,xy) orbital manifold is singly occupied whereas the electronic ground state of [Mo]NH corresponds to a singly-occupied 3e(xz,yz) manifold. For both complexes the complementary 2E state is the first excited state while the respective 2A1 state is highest in energy. Due to the size of the active space and the limited number of calculated states, the actual energy of the 2A1 state could not be determined since a series of charge transfer states occur lower in energy than the highest d-d state. In the case of [Mo]NH the orbital optimization even rotated the metal dz orbital out of the active space which impedes a calculation of the 2A1 state. Consequently, in Table 3 the excitation energy for the 2A1 states obtained from the corresponding NEVPT2(1,5) are given for this state. They can be regarded as reasonable approximations to the results that would have been obtained from NEVPT2(13,11) calculations. For the present case of d1 configurations the qualitative frontier orbital schemes highlighted in Figure 4 directly correspond to the ordering of the calculated d-d excited states. They differ in the energetic order of the 3e and 4e orbitals. A qualitative explanation for these results can be given in the framework of ligand field theory. The ligand field created by the TAA ligand has a dominating component perpendicular to the molecular axis and arises from the Mo-Namido σ-interactions. It destabilizes the 4e(x2-y2,xy) orbitals relative to the 3e(xz,yz) orbitals. On the other hand, the axial ligand generates a ligand field along the molecular axis that destabilizes the metal d-orbitals in the order dz2 > dxz, yz > dxy, x2−y2. Accordingly the 2A1 state is by far the highest in energy among the d-d excited states for both complexes.
Figure 4.
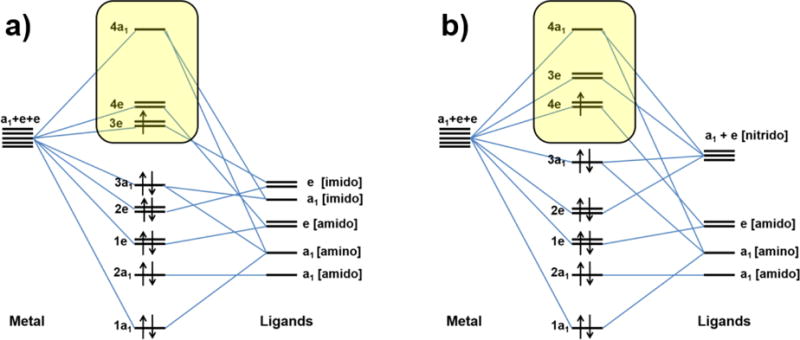
Schematic MO diagram of [Mo]NH (a) and [Mo]N− (b). In both cases the 4a1(z2) orbital is strongly destabilized by the axial ligand. The energetic order of the 3e(xz,yz) and 4e(x2-y2,xy) orbitals changes with the loss of the proton due to the different ligand field strengths of the imido and the nitrido ligands (see text).
The energetic order of the 3e and 4e orbitals depends on the relative strengths of ligand fields created by the TAA ligand and the axial ligand. Since the TAA ligand is a common feature of both complexes, the energetic order depends only on the ligand field strength of the axial ligand. In previous works it has been found that for [Mo]L (L = NH3, N2, CO) the 3e orbitals are lower in energy than the 4e orbitals. The same situation is met for [Mo]NH. In case of {[Mo]N}− due to the extraordinarily strong π-interaction created by the nitrido ligand, the energetic order of 3e and 4e orbitals is inversed. Accordingly the numbering used here no longer refers to the energetic order of the orbitals. All interactions between the ligand and metal orbitals are summarized in the qualitative molecular orbital scheme presented in Figure 4.
Despite their different electronic ground state configurations {[Mo]N}−, and [Mo]NH share some critical properties. They both have a doubly degenerate 2E ground state that is subject to JT distortion which can be described by the well-known E ⊗ e coupling scheme.12 Furthermore the 2E ground state exhibits unquenched orbital angular momentum leading to strong ‘in-state’ spin-orbit coupling (SOC). The SOC splits the orbital and spin-degeneracy and thus competes with the JT distortion resulting in the so-called ‘Pseudo-Jahn-Teller-effect’. As described in detail elsewhere,5 the PJT effect forces the system to distort along a ‘composite’ mode of vibration leading to two separate molecular adiabatic potential energy surfaces (APES) with energies defined in terms of the force constant, K, of the “composite” mode along which the distortion ρ occurs, λ the SOC constant and F, the linear Jahn-Teller coupling constant.
| (8a) |
The equilibrium displacement on the lower surface occurs at a distortion, ρ0, at which point the
| (8b) |
By comparison of the optimized geometries of the symmetric and the fully optimized structures it was possible to determine the nature of the mode of distortion. As in the previous ([Mo]L, L = N2, NH3 and CO) cases they are dominated by transversal movement of the axial ligands and bending motion of the equatorial ligands as illustrated in Figure 5.
Figure 5.
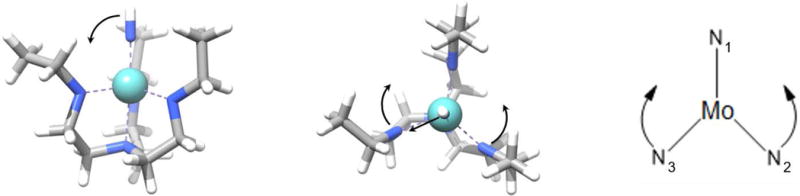
Modes of distortion for [Mo]NH. In the equatorial plane, N2 and N3 bend towards N1 resulting in reduced angles of ∠ (N1MoN3) = 109° and ∠ (N1MoN2) = 112°. Consequently, the angle ∠ (N2MoN3) = 123° is significantly larger. Note, the sum of all three angles does not equal 360° as the angles were determined from the three-dimensional structure rather than a two-dimensional projection. As indicated in the left and middle panel the axial nitrogen moves towards N3. Interestingly, the adjacent hydrogen slightly bends towards the gap between N1 and N3. For {[Mo]N}− an analogous combination of equatorial bending and transversal motion is observed.
Magnetic Measurements
EPR g-values and the formal PJT theory
Figure 6 shows the 35 GHz, EPR spectra of the frozen solution of [Mo]NH, and {[Mo]N}− recorded at 2K. The EPR spectrum of {[Mo]N}− shows axial symmetry, gǁ = 1.69 < g⊥ = 1.91. The g tensor for [Mo]NH is near-axial, g = [(gǁ = g3) = 1.86 < {g1 = 1.98, g2 = 1.96}], with a smaller g-spread than {[Mo]N}−. The similarity of the EPR spectra for the two complexes despite the fact that they have different 2E ground states can be understood in terms of the ‘pseudo Jahn-Teller’ (PJT) effect wherein spin-orbit coupling competes with interactions that split the orbital degeneracy, lowers the molecular symmetry, and lowers the total energy of the molecule.5 Foremost among the degeneracy-lifting terms is the JT vibronic coupling to a symmetry-lowering distortion along a composite ‘interaction’ ea coordinate, but deviations from trigonal symmetry such as occurs in [Mo]NH, other electronic interactions, and indeed non-covalent solvent effects in solution or crystal packing effects in a crystal, can contribute.
Figure 6.
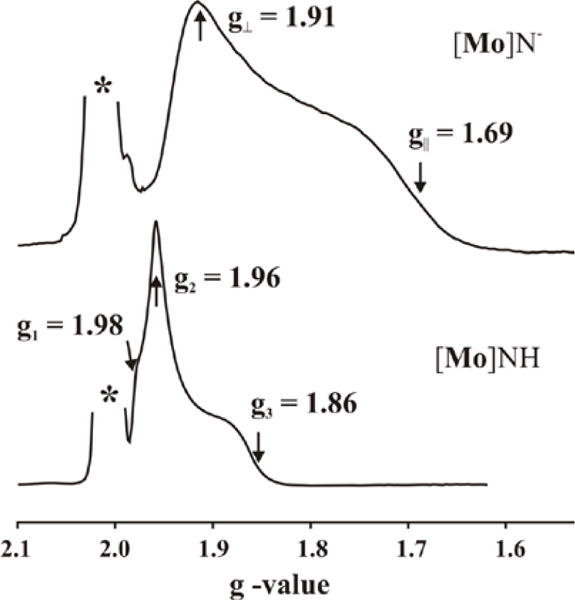
Field swept ESE-EPR for {[Mo]N}− and [Mo]NH. The (*) represents the epr signal at g ~ 2 of matrix free radicals generated during cryoreduction. For clarity, the epr signal of the radical is cut off. The unique g values (gǁ, g⊥) are shown with arrows. Conditions, two pulse echo detected EPR: microwave frequency, 34.881–34.965 GHz; π = 80 ns; τ = 700 ns; repetition time, 100 ms.
Within the previously introduced two-orbital model for a doubly degenerate 2E ground state, the mixing and splitting of the orbital doublet can be described formally5 in terms of a dimensionless parameter, r, and fictitious angle θ
| (9) |
The numerator is a sum of two types of terms, V = Vvib + Vl. The first term is the vibronic coupling energy at the equilibrium distorted position on the ground APES, Vvib = Fρ0, The second term in the numerator, Vl, is the sum of the additional contributions enumerated in the previous paragraph. The denominator, λ is the spin-orbit coupling (SOC) parameter, which traditionally is taken to be the ionic SOC constant, λSOC, multiplied by a ‘covalency parameter’, k, defined such that (1-k) represents the fraction of d-electron density delocalized onto the ligands. Within this model the g values can be written as5
| (10a) |
| (10b) |
and the The PJT splitting between the ground APES minimum and the excited APES at the equilibrium value of the distortion,
| (11) |
According to the quantum calculations presented above, ml = 2 for {[Mo]N}−,but ml = 1 for [Mo]NH, as is the case for the d3 Mo(III) complexes previously studied by paramagnetic resonance methods.5,6
The physical picture behind the deviation of the g (gǁ, g⊥) values from the free electron value can be understood as follows. In the limit of non-distorted trigonal symmetry (no JT effect, 2θ = 0), the strong ‘in-state’ SOC leads to antiferromagnetic coupling of orbital and spin angular momentum along the z axis resulting in a gǁ value of −2 and 0 for {[Mo]N}− (4e)1 and [Mo]NH (3e)1, respectively, in the ionic limit of k = 1. As the signs of the g-values are not resolved in ordinary EPR measurements, one would measure a value of |gǁ| = +2 for {[Mo]N}− in a three-fold symmetric conformation. As shown in Figure 7, the absolute value of g|| for {[Mo]N}− rapidly decreases from 2 to 0 and then slowly increases towards the free electron value ge with increasing Jahn Teller splitting. For [Mo]NH g|| starts at 0 in the limit of no distortion and increases as the PJT becomes larger.
Figure 7.
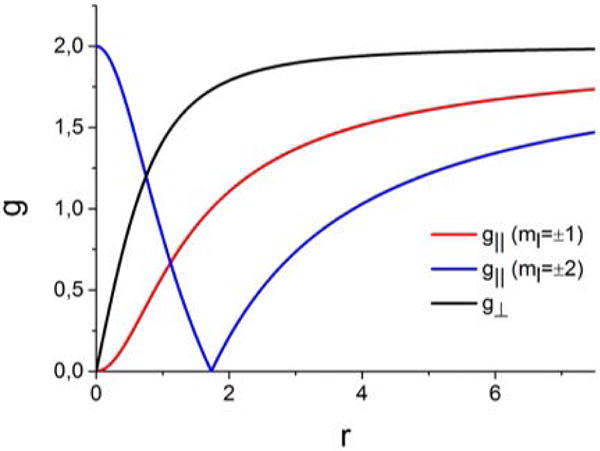
Evolution of the molecular g-values for a singly occupied orbital with ml = ±1, as appropriate for [Mo]NH and ml = ±2, as for {[Mo]N}−, with increasing PJT splitting within the two-orbital model and the ionic limit of k = 1. For convenience, an ionic SOC constant of λSOC = 800 cm−1 was used for both. Within the two-orbital model, the g-tensor is predicted to be axial at all points.
As a secondary effect, the SOC along the z-axis quenches the magnetic moment perpendicular to it. Thus g⊥ vanishes in the limit of a three-fold symmetry, r = 0. The Jahn-Teller splitting progressively diminishes the orbital angular momentum which in turn reduces the ‘in-state’ SOC. This is reflected in a progressive increase of g⊥ towards the free-spin value, ge = 2 as presented in Figure 7.
Treating the measured g-values with Eqs 9, 10 gives a small value, r = 3.2 (EJT = 3352 cm−1) for {[Mo]N}− and a larger value for [Mo]NH, r = 7 (EJT = 7071 cm−1). The larger r for Mo-N-H can be attributed to the non-linear geometry, which, along with the larger SOC parameter for Mo(V) (1000cm−1) compared to Mo(III) (800 cm−1) acts to enhance the splitting of the orbital degeneracy. The rhombicity of the g-tensor of [Mo]NH reflects SOC to other d orbital, that is not included in the two-orbital model.
For {[Mo]N}−, this treatment gives unrealistically low values for the ‘covalency parameter’, k, which commonly are interpreted as representing the metal-d character of the 3/4e orbital, k = 0.25. In part, a low value can be understood by noting that in the idealized C3v symmetry of {[Mo]N}− Telser and McGarvey showed how this symmetry-lowering mixes the eb 3E and 4E orbitals,48 which diminishes the covalency parameter, k,18 for {[Mo]N}−. However, it would seem that this low value also reflects limitations to the two-orbital model. In the case of [Mo]NH a more realistic value of k = 0.5 is obtained. A discussion of covalency and the mixing of states with different parentage from the point of view of quantum chemical calculations for both complexes will be given below.
Quantum Chemical Computations of g-values
[Mo]NH
The formal PJT analysis predicts a large splitting between the equilibrium ground state APES and the first excited APES for [Mo]NH. A NEVPT2(13,11) calculation of the lowest ten electronic states on the model structure of the complex (Figure 2) supports this assessment. It yielded an excitation energy of 6000 cm−1 for the first excited state, which is on the same order as the value obtained from the two-orbital model. This large intra- 2E splitting is a result of the presence of the imido proton that is effective in breaking the symmetry. Evaluation of the g-tensor at the same level of theory yields values of g1 = 1.99, g2 = 1.96 and g3 = 1.87 which is in excellent agreement with the experimental values and consistent with the results obtained from DDCI2(1,5) (g1 = 1.98, g2 = 1.95 and g3 = 1.80). Considering the large PJT splitting, EJT, the electronic ground state of the desymmetrized structure may be regarded as genuinely non-degenerate. Thus, the application of the standard linear response DFT methodology to the calculation of the molecular g-tensor is reasonable. A great advantage of standard DFT calculations is their low computational cost, which allows the inclusion of the full HIPT groups in the g-tensor calculation. At this point it has to be noted that linear response DFT incorporates SOC only to second order in perturbation theory while the NEV-PT2 approach treats SOC to infinite order. However, the g-values obtained from linear response DFT (g1 = 1.99, g2 = 1.96, g3 = 1.88) are almost equally close to the experimental data as the above presented NEVPT2 values. In order to elucidate the effect of truncation of the HIPT groups on the g-tensor a linear response DFT calculation was also performed for the model structure of [Mo]NH. It gives almost identical results (g1 = 1.99, g2 = 1.97, g3 = 1.88) as the calculation on the full complex. This indicates that truncation of the model does not significantly influence the results of NEVPT2 g-tensor calculations.
The average metal-d character of the 3e orbitals in the Kohn-Sham determinant is 47%, which is close to the value obtained from the two-orbital model. This corresponds to strongly covalent bonds between the metal and the ligands, especially the axial imido ligand, although one has to keep in mind that DFT tends to overestimate covalency in transition metal complexes.49 In the large active-space CASSCF(13,11) calculations, which should provide a rather balanced description of the [Mo]NH bonds, the metal character in the open-shell orbitals is 59% and 69% respectively. For comparison, the averaged metal-d character of the natural DDCI2 orbitals that correspond to the 3e manifold in [Mo]NH is 55% which is close to the value obtained for [Mo]NH in the two-orbital model. These numbers appear to be sensible and the description of the bond is further supported by the good agreement between calculated and experimental g-values that react sensitively to both the intra- 2E excitation energy as well as the covalent dilution of the d-orbitals.
An analysis of the spin distribution evaluated at the DDCI2(1,5) level provides insight into the electronic structure at the distorted geometry of [Mo]NH. Figure 8 shows the spin density at an isosurface value of 0.003 unpaired electrons. In agreement with the CASSCF results, it reveals that the electron spin is mainly located in an antibonding combination of Mo dxz/dyz orbital and imido px/py orbital. This finding supports the assessments made above about the electronic structure of [Mo]NH (Figure 4). Furthermore it is seen that the spin distribution is significantly tilted with respect to the molecular z-axis resulting from the geometrical distortion and leading to a non-negligible admixture of Mo and equatorial ligand p orbitals. In a configuration interaction (CI) picture this spin distribution corresponds to a distortion-induced mixing of 2Eb states to the electronic ground 2Ea state.
Figure 8.
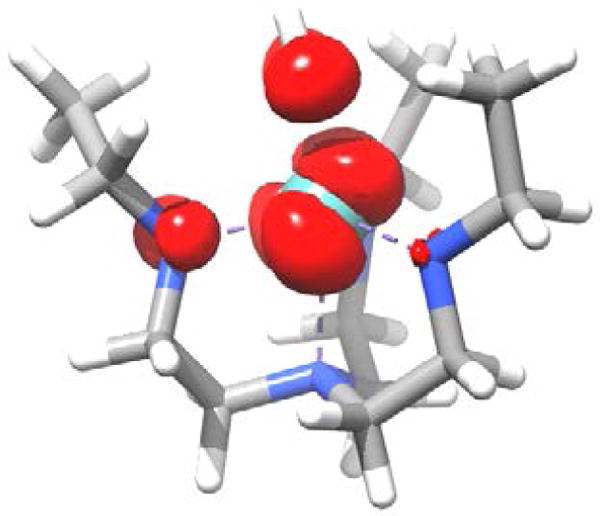
Electron Spin density of the electronic ground state of [Mo]NH obtained from a DDCI(1,5) calculation at an isovalue of 0.003 electron spins.
{[Mo]N}−
The two-orbital model predicts a significantly smaller PJT for {[Mo]N}− compared to [Mo]NH (vide supra). The NEVPT2(13,11) calculation for the lowest five states of the model structure of {[Mo]N}− supports this result. It yielded an energy difference of 4200 cm−1 between the electronic ground and the first excited state, which is again in the same order as the two-orbital value. In order to draw a further comparison between the two-orbital model and the NEVPT2 calculations a scan along the mode of distortion for {[Mo]N}− was performed. A detailed description of how to perform such a scan is given elsewhere.5 Relative energies of the four lowest electronic states as well as molecular g-tensors were calculated with the NEVPT2(7,8) method at each point of the scan (Figure 9). Note that this slightly reduced active space was chosen for the scan because it still provides a balanced description of the metal-ligand bonding but does not cause as many problems with convergence as the full 13 electron in 11 orbitals active space. As expected, the degeneracy of the four 2E states is lifted even for the approximately C3V-symmetric structure due to SOC and the imperfect trigonal symmetry of the complex geometry. The first excited Kramer’s pair lies ~1000 cm−1 above the lowest pair. Thus, one is close to true orbital degeneracy and hence linear response or perturbation theory would be invalid for the calculation of the g-tensor, as indicated by the very large deviations of the g-values from the free-electron value (in fact, linear response DFT yields g-values for the complete structure of {[Mo]N}− yields values of g1 = 1.99, g2 = 1.98, g3 = 1.78 that are in strong disagreement with experiment).
Figure 9.
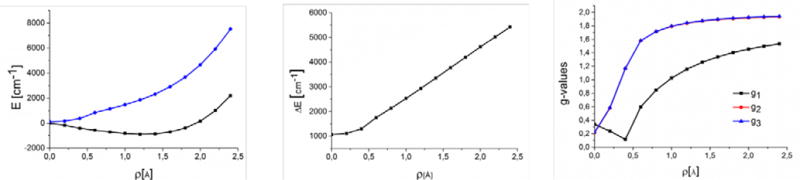
Evolution of the nonrelativistic NEVPT2(7,8) energy (left panel) of the lowest two Kramer’s pairs, the difference of the first energy of the lowest Kramer’s pair (calculated on the NEVPT2(7,8) level) after inclusion of spin-orbit coupling (middle panel) and the molecular g-values (right panel) for {[Mo]N}− with increasing distortion of the molecular geometry from C3V symmetry. More precisely, the quantity ρ on the x-axis of all three panels is the displacement along the Jahn-Teller active interaction coordinate (see above). Note that the lines for g2 and g3 are virtually indistinguishable at all points of the scan, which corresponds to an axial g-tensor as predicted within the 2-orbital model (Fig 5)
The calculated g-values follow closely the trend predicted by the two-orbital model (Figure 7). The g-tensor remains axial at all points of the scan. Furthermore the three g-values evolve similarly to the ml = ±2 case in Figure 7. Thus the physical picture drawn for the g-tensor above within the two-orbital model agrees with the quantum chemical calculations.
However, for the limiting cases of an undistorted and a fully distorted geometry, the NEVPT2(7,8) calculations numerically differ considerably from the two-orbital values. The g‖-value at the C3V symmetric structure is calculated to be 0.35, which is significantly lower than the value of 2 predicted by two-orbital model. Furthermore the g⊥ value is predicted to be 0.22, whereas it is predicted to be equal to zero by the two-orbital model. These findings have two causes: a) strong covalency present in the {[Mo]N}− complex and b) coupling of SOC to higher excited d-d states that are not included in the two-orbital model. The NEVPT2(7,8) calculations on {[Mo]N}− at the distorted geometry predict g-values of g1 = 1.91 g2 = 1.90 and g3 = 1.39. While the first two g-values match the experimentally observed values almost perfectly, the third value is predicted significantly lower. Enlargement of the active space to 13 electrons in 11 orbitals leads to improved values of g1 = 1.91, g2 = 1.91 and g3 = 1.48. However, the deviation of g3 from the experimental value is still not negligible. However, the results are considered to be satisfactory given the very steep dependence of the g-values of the precise energetic position of the first excited state (compare Figure 9). In the calculations this will depend on many details including basis set, higher order contributions of dynamic electron correlation, geometry, treatment of the environment, possible contributions from vibronic coupling, the precise treatment of relativistic effects among many others. All of these factors can change the calculated excitation energy by a few hundred wavenumbers. This is inconsequential for the g-tensor if the excitation energy is as large as several thousand wavenumbers but does show up prominently in the results if it is less than a thousand wavenumbers. From this perspective, the CASSCF(13,11)/NEVPT2 results are excellent.
It is known that CASSCF consistently underestimates covalency which in the present case acts to increase the g3 value. In the framework of the previously applied DDCI2 method dynamic correlation effects are taken into account for the computation of all three terms in equation (4).5,43,44 As a result, a DDCI2(1,5) calculation of the model structure of {[Mo]N}− yields an increased g3 value of 1.55, while the other two values remain almost unaffected (g1 = 1.92, g2 = 1.91). Thus these results are internally consistent and are considered to be in good agreement with experiment. We thus believe that the electronic ground state description provided by the applied multireference methods and the physical picture behind the molecular g-values presented above is largely correct. Nevertheless it is interesting to note that the DDCI2(1,5) calculations yield values closer to the experiment than even the NEVPT2(13,11) calculations. We tentatively attribute this observation to the fact that the former uses the entire correlated wavefunctions and densities during the evaluation of SOC matrix elements, whereas the latter only employs spin-densities on the CASSCF(13,11) level together with NEVPT2(13,11) state energies.
The spin density distribution of the electronic ground state of {[Mo]N}− obtained from the DDCI2(1,5) wavefunction reveals that the spin is mainly located in the 4e manifold (Figure 10). However, its considerable tilt out of the equatorial plane reflects, as above, the distortion induced mixing of states with 2Eb and 2Ea parentage. The averaged metal d-character of the natural DDCI2 orbitals that correspond to the 4e orbital manifold is 81% which is in good agreement with 78% metal character obtained from the CASSCF(13,11) calculations.
Figure 10.
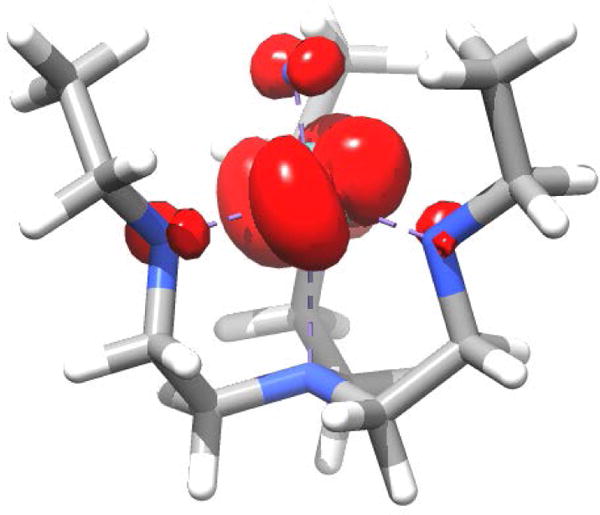
Electron Spin density of the electronic ground state of {[Mo]N}− obtained from a DDCI2(1,5) calculation at an isovalue of 0.003 electron spins. The tilt out of the equatorial plane reflects the mixing of states with 2Eb and 2Ea parentage.
These values strongly differ from the covalency parameter k = 0.25 obtained from the two-orbital model. This highlights that the two-orbital model oversimplifies the electronic structure by absorbing multiple complex effects such as covalency and the aforementioned excited state-mixing into the single parameter k. As a result this parameter is artificially reduced to an unphysical value of k = 0.25. The more realistic value of around 80% indicates that the bonding of the metal orbitals to the equatorial amido ligands is less covalent than the bonding between the dxz/dyz orbitals and the axial imido ligand in [Mo]NH.
Quantum Chemical Computations of Hyperfine Interaction Parameters
Although it has to be stressed that orbital covalency is not a physical observable but a chemical concept to describe the nature of a chemical bond, hyperfine coupling constants and quadrupole interaction parameters provide a direct probe of the spin and charge density distributions. Thus, these values as calculated for the nitride and imido ligands of {[Mo]N}− and [Mo]NH within the linear response DFT framework are presented in Table 4, and discussed below in the context of the corresponding quantities as estimated by ENDOR spectroscopy. We have resorted here to DFT calculations since the CASSCF wavefunction, even the largest ones, are missing spin-polarization and hence provide unrealistic values for the important Fermi contact contribution to the hyperfine coupling. While, in principle, this can be remedied by higher-order dynamic correlation treatments such as NEVPT2, the NEVPT2 response density is not available and hence one would also only obtain CASSCF quality results. Except for the slight overestimation of covalency, the DFT spin-densities for the ground state are expected realistic since they provide a qualitatively similar description of the metal-ligand bonds as the more elaborate multireference calculations.
Table 4.
Calculated nuclear hyperfine parameters that were obtained using the B3LYP functional together with the TZVP basis set and the ZORA Hamiltonian on the full [Mo]X (X=N3− and NH2−) model. The given Euler angles refer to the principle axis system of the molecular g-tensor.
| Hyperfine tensor (MHz) |
Euler angles (degrees) |
e 2qQ/h (MHz) |
||||||
|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | α | β | γ | |||
| {[Mo]14N}− | N nitrido | −8 | −2 | 1 | −11 | 38 | −78 | −3.47 |
| [Mo]NH | N imido | 30 | 0 | 0 | −30 | 70 | −20 | −1.77 |
| H imido | 11 | 2 | 23 | 30 | 75 | 0 | ||
14,15N ENDOR for [Mo]NH and {[Mo]N}−
The molybdenum ions of {[Mo]N}−/[Mo]NH have five nitrogen ligands in the first coordination sphere: the three amido nitrogen’s in a plane perpendicular to the molecular axis plus the axial amino nitrogen, all associated with TAA, along with the axial nitride/imido ligand. However, with the aid of isotopic labeling the nitride and imide nitrogens can be identified.
{[Mo]N}−
Figure 11a shows the nitrogen Davies ENDOR spectra for {[Mo]14N}−, and 50% labeled {[Mo]15N}− collected at g⊥ = 1.91. As with the MoN2 complex,5 the dynamics of the JT effect lead to poorly-resolved 14/15N ENDOR spectra. Nevertheless, two distinct peaks are seen in the {[Mo]14N}− spectrum at 5.3 and 8.5 MHz, riding on a broad background feature, and lose intensity in the spectrum from 50% labelled {[Mo]15N}−. Assignment of these as the ν+,± doublet (eq 2) from 14N nitride split by the quadrupole interaction, |3P⊥| = 3.2 MHz, leads to a 14N nitride hyperfine coupling, |A(14N)⊥| = 5.8 MHz. This assignment correctly predicts the appearance of a single feature for the labeled {[Mo]15N}− at ν+ = 9.6 MHz, based on the relation, |gn (15N)/gn(14N)| = 1.4 = |A(15N)/A(14N)|. The absolute sign of the spin density on N, ρ(N) ∝ A⊥(15N)/gn(15N) < 0, was determined by the Variable Mixing Time (VMT) PESTRE technique (Figure SI 3). A negative spin-population is consistent with the DFT calculations that predict −0.07 unpaired electrons on the nitrido ligand (Löwdin analysis). Although it is not possible to resolve features from the other coordinating nitrogens, we can estimate the 14N hyperfine couplings from the TAA ligands to be less than 6 MHz. This finding is consistent with the DFT calculations that predict hyperfine couplings for the amido nitrogens of 3–7 MHz and the amino nitrogen of <1 MHz.
Figure 11.
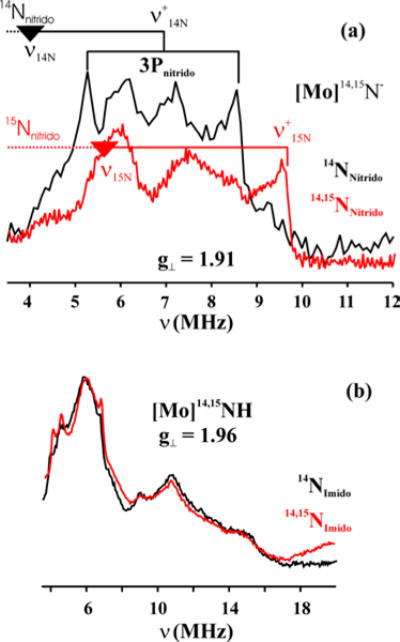
(a) Davies 14,15N ENDOR of {[Mo]14N}−, and 50%15N labeled {[Mo]14,15N}− at g⊥ = 1.91. The quadruple splitting for the nitride nitrogen is shown as 3P; nuclear Larmor frequencies, ν14N/15N = 3.9/5.5 MHz, (b) Davies 14,15N ENDOR of [Mo]14NH, and 50%15N labeled [Mo]14,15NH at g2 = 1.96. Conditions: microwave frequency, 34.881–34.965 GHz; π = 200 ns; τ = 700 ns; trf = 30 μs; repetition time, 50 ms;
The ν+ peak from15N nitride of {[Mo]14,15N}− in ENDOR spectra collected away from g⊥, quickly broadens and moves towards low frequency and becomes lost (Figure SI 1) near gǁ, with the 14N peaks showing a similar trend, behavior demonstrating that |A||(N)| ≪ |A⊥(N)|. The quantum chemical calculations predict a tensor (Anitride(14N)= [−8 −2 1]) MHz with small isotropic negative coupling (Aiso ∼ −3 MHz), in agreement with the ENDOR and VMT-PESTRE measurements. As shown in Figure SI 2, simulation of the 2D pattern of spectra collected at multiple fields with simulations that employ the calculated tensor are indeed in satisfactory agreement with the experimental data.
It is also possible to estimate the quadrupole interaction parameter for the 14N nitride, |e 2qQ/h| from the spectrum of Figure 11a. In the near-trigonal symmetry of the complex, the quadrupole interaction is expected to be effectively axial, with the unique value, P||, along g||. The quadrupole tensor is traceless, P|| + 2P⊥ = 0, and thus, the measurement of |P⊥| yields the interaction parameter, |e 2qQ/h| = 4|P⊥| = 4.2 MHz. This parameter reflects the difference between the charge density in the nitride 2pσ orbital along the Mo-N bond (N3) and the average of the densities in the two orthogonal 2pπ orbitals, and the experimental and calculated value, e 2qQ/h = −3.47 MHz, are in excellent agreement (Table 4). In SI we present a simplified, heuristic discussion of these bonding interactions through use of the Townes-Dailey model, in which the quadrupole parameter for Mo-bound nitride is simply proportional to the difference between the charge density in the nitride 2pσ orbital along the Mo-N bond (N3) and the average of the densities in the two orthogonal 2pπ orbitals.
[Mo]NH
Although the ENDOR spectra of [Mo]14NH and 50% labelled [Mo]15NH measured at g2 = 1.96 are rich in peaks, there is no observable difference between them that can be assigned to the imido nitrogen, Figure 11b. The ENDOR spectra of [Mo]14NH, collected away from g2 quickly become featureless (Figure SI 4), which compounds the difficulty in assigning an imido nitrogen signal. The quantum chemical calculations predict a highly anisotropic hyperfine tensor (A = [30, 0, 0] with Aiso = 10 MHz) for the imido nitrogen. Simulations of the ENDOR spectra predicted with this tensor are spread over the frequency scale (see Figure SI 6) without sharp features. This, along with the poor resolution of the spectra, may help to rationalize the failure to observe the nitride signals.
Although the background 14N ENDOR signals from other coordinating nitrogens are unresolved, we can estimate that 14N hyperfine couplings from the TAA ligand are less than 6 MHz. This is in agreement with the calculations, which predict amido nitrogen HFCs along the principle g-tensor axes of 3–7 MHz, with an even smaller coupling to the amino nitrogen of around 2 MHz. Interestingly, the 14N ENDOR spectra of MoNH show additional peaks at frequencies above 10 MHz in the range of 10–16 MHz which are not observed in MoN−. For example, the peak at around 11 MHz is a double quantum peak of nitrogen with hyperfine coupling of A∼3 MHz (Figure SI 5). This could well be from one of the in-plane amido nitrogens.
1,2H and 95,97Mo ENDOR for [Mo]NH and {[Mo]N}−
1,2H ENDOR
Figure 12 shows 1H DAVIES ENDOR spectra for the two complexes recorded at the respective maxima (g⊥) of their EPR spectra. The proton ENDOR features for {[Mo]N}− are centered at the 1H Larmor frequency, and as expected, exhibit signals from protons of the HIPT ligands, with hyperfine couplings of less than 5 MHz.50 In addition, a weak, broad peak centered at −12 MHz relative to the proton Larmor frequency is observed, which can be assigned as the ν+ ~ 44 MHz branch of the mI = ± ½ doublet for the I = 5/2 95,97Mo ion, as discussed below.
Figure 12.
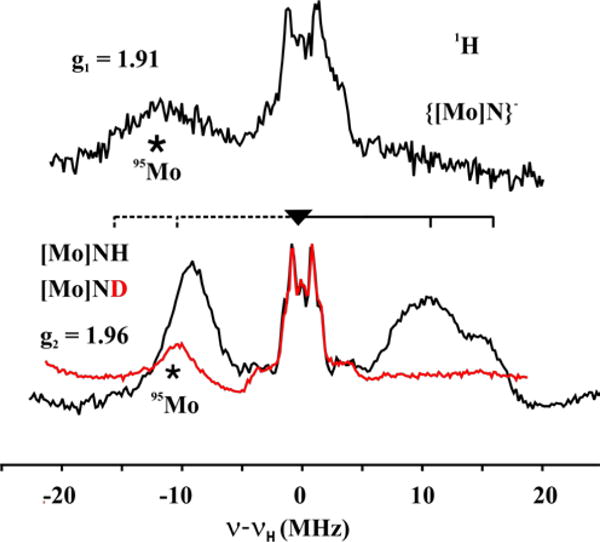
Davies 1H ENDOR of {[Mo]N}−, [Mo]NH (each black), and [Mo]ND (red) at g⊥ = 1.91, 1.96 respectively. For [Mo]NH, the brace shows the broad distribution of the proton coupling. The broad feature (*) observed at −12 MHz is contribution from 95,97Mo as explained in the text. Conditions: microwave frequency, 34.881–34.965 GHz; π = 120 ns; τ = 700 ns; trf = 60 μs; repetition time, 50 ms; RF frequency randomly hopped.
The weakly-coupled 1H features from the HIPT ligand are also observed for [Mo]NH, as expected. The spectrum for [Mo]NH also shows intense 1H signals with significantly stronger coupling; the broad ν+ ~ 7–17 MHz feature of a strongly-coupled 1H, plus its ν− partner, which is distorted in part because of overlap with a signal from 95,97Mo. The assignment of this broad 1H feature to the imido proton is confirmed by the 1H spectrum of the 2H labeled sample, MoN 2H: H/D exchange abolishes the broad 1H ν+/ν− doublet but leaves both the 1H features from HIPT and the weak, broad 95,97Mo peak centered at −10 MHz relative to the proton Larmor frequency (fig 12).
The 2D pattern of 1H ENDOR spectra collected across the full EPR envelope for [Mo]NH (Figure SI 7) show two resolved broad features at fields between g1(1.98) and g2(1.96), suggesting two major but poorly defined NH conformers have been trapped, with couplings at g1 of ~ 22 and 30 MHz. These features merge and the coupling decreases as the field is increased towards g3 = 1.86, where A3 ~ 18(6) MHz. Precise hyperfine tensors cannot be obtained from the broad and poorly-resolved features of the overlapping 1H responses from the two N1H conformers, but we can estimate that each has an isotropic coupling of roughly, |Aiso| ~ 20 MHz.
95,97Mo ENDOR
The 95,97Mo ENDOR response (*) seen at g┴ for {[Mo]N}− (Figure 12) corresponds to a hyperfine coupling of |A(95,97Mo)⊥| ≈ 80 MHz. Although the possibility that the relatively narrow width of this feature is indicative of a relatively small quadrupole interaction, it is by far more likely that the interaction is large and this signal corresponds to the mI = +1/2 ⟷ −1/2 transition, and that additional branches associated with the quadrupole-split mI = ± 3/2, 5/2 features are not observable. In spectra collected across the EPR envelope (Fig SI 12), the 95,97Mo signal for {[Mo]N}− is quickly lost away from g┴, likely because of strong anisotropy in the couplings. The calculations in fact show a strong anisotropy. The calculated hyperfine tensor is essentially axial, with A(95,97Mo)⊥ ≈ 77 MHz, in excellent agreement with experiment, and A(95,97Mo)|| = 167 MHz.
The 95,97Mo feature for {[Mo]NH} in the g┴ region also corresponds to a hyperfine coupling A(95,97Mo)⊥ ≈ 80 MHz (Figure 12), essentially the same as that for {[Mo]N}−. For {[Mo]NH} the95,97Mo signal is visible, and shifts little over most of the EPR envelope, between g1 = 1.98 and g ~1.90 → g3, (Figure SI 7), suggesting that the 95,97Mo coupling is largely isotropic, A(95,97Mo)iso ≈ 80 MHz. The calculations yield an isotropic coupling that matches this quite well, A(95,97Mo)iso = 77 MHz, but shows an appreciable anisotropy.
Discussion
In this work we have presented a combined spectroscopic and theoretical study of the catalytically active [Mo]NH complex and its derivative [Mo]N−. On the basis of our findings we were able to establish a coherent picture of the complex electronic structure and magnetic properties of both these Mo(V) compounds, thus completing an in-depth characterization of the four states of Figure 1. The tripodal trisamidoamine ligand together with the axial amido- and imido- moieties creates an idealized C3V–symmetric ligand field around the Mo(V) centers. In the case of [Mo]NH, our correlated multireference quantum chemical calculations predict that the imposed ligand field results in an 2E electronic ground state that features a half-filled e(xz,yz) shell. This prediction is in agreement with previous findings made for analogous Mo(III) and similar Fe complexes.13,14
As observed previously for [Mo]NH3 and [Mo]N2, the half-occupation of the orbitally degenerate e(xz,yz) shell and the presence of unquenched spin-orbit coupling effects leads to a Pseudo-Jahn-Teller behavior.5 The competing effects of spin-orbit and Jahn-Teller coupling result in a delicate equilibrium that is effectively probed by our measurements of the molecular g-values. In-state spin-orbit coupling forces the g-values, in particular the component along the molecular z-axis, away from free electron value, whereas the Jahn-Teller distortion has the opposite effect by lifting this (near) degeneracy. Hence, the experimentally observed molecular g-values give insight into the relative strength of both effects. Our analysis of the experimental data in the framework of a 2-orbital model even allows for an assignment of a numerical value to the relative strength. For [Mo]NH we find a strong Jahn-Teller splitting states resulting in two well separated states with 2E parentage. Moreover, the analysis indicates a strong mixing of metal and ligand orbitals for the e(xz,yz) manifold.
Our CASSSCF/NEVPT2 calculations of the molecular g-tensor for [Mo]NH is in excellent agreement with the observed experimental values thus confirming the overall picture of the electronic structure, while give deep insights into details of that structure. Interestingly, almost the same numerical agreement between experiment and theory is achieved with simple DFT calculations. We believe that this observation is due to the clear separation of the electronic ground state from the first excited state. Generally, only correlated multireference calculations provide the required flexibility and accuracy to reliably predict the electronic structure of such complicated cases. Another consequence of the strong Jahn-Teller coupling is the distortion-induced mixing of states with 2E(xy, x2-y2) parentage to the electronic ground state. This mixing, which by construction is not described in our 2-orbital model, is mostly responsible for the rhombicity of the molecular g-tensor. Furthermore, as the mixing shifts the HOMO out of the sterically overloaded x-y plane, it may facilitate the attack of the imido nitrogen by an electrophile such as a proton. A similar argument has been made previously for tripodal Fe compounds.18
Our calculations predict that the {[Mo]N−} precursor to [Mo]NH in the catalytic cycle has a qualitatively different electronic ground state. For {[Mo]N−}, the electronic ground state is still a 2E-state but with a half-filled e(xy,x2-y2) shell. This change is induced by the extraordinarily strong ligand field along the molecular z-axis created by the amido ligand. Despite the qualitative differences to [Mo]NH, we again find a Pseudo-Jahn-Teller behavior with an equilibrium of spin-orbit and Jahn-Teller coupling for {[Mo]N−}, although with slightly altered physical parameters. Analysis of the experimentally observed molecular g-values within the 2-orbital model indicates that the equilibrium is tilted towards the spin-orbit coupling compared to [Mo]NH. This finding is intelligible considering the fact that the e(xy,x2-y2) shell corresponds to the M = ±2 manifold of the Mo d-orbitals whereas the e(xz,yz) shell corresponds to the M = ±1 manifold. Our CASSCF/NEVPT2 calculations of the molecular g-values again achieve good agreement with the experimentally observed values thus validating our in-depth electronic structure description.
It is important to note that the change of character of the electronic ground state is likely to be accompanied by a change of reactivity. For example, the shift of the HOMO out of the x-y plane into the z-direction may lead to a lowering of the barrier for an electrophilic attack at the nitride ligand.
The formal two-orbital model indicates that the parameter r, the ratio of JT coupling to SOC (eq 9), is ~ two-fold larger for [Mo]NH than for {[Mo]N−}. However, within this model, according to eq 9, the JT coupling is in fact ~ four-fold greater for [Mo]NH, because in the denominator the factor k for the SOC of [Mo]NH is twice that for {[Mo]N−}. The large JT coupling reflects the non-linearity of the Mo-N-H moiety, as discussed above. Comparing the parameters, r, for the three-fold d 1{[Mo(V)]N−} with those of the three-fold d3 Mo(III)-L, L= N2, CO, and NH3,5 once one takes in into account the differences in k, one finds that the JT coupling is essentially the same for the two configurations, despite the difference in ground state, 4E for the former versus 3E for the latter (Figure 4). The latter is significant in terms of the SOC interactions inside the given E-term. For the 4e-set of orbitals, which is based on the Mo dxy and dx2-y2 orbitals, the angular momentum matrix element along the z-axis is +/−2, whereas for the 3e set, which is comprised of the Mo based dxz and dyz orbitals, the corresponding matrix element is +/−1. Hence, effectively, the SOC interaction in the 4E term is twice as large as in the 3E term. This general trend is modulated by metal-ligand covalency. Thus, for {[Mo(V)]N−} vibronic coupling is induced by partial occupation of orbitals with mostly character that are involved in the σ-type bonding of the Mo center to the equatorial amide ligands in {[Mo(V)]N−}. In contrast, the origin of vibronic coupling in the three d3 complexes and [Mo]NH is the partial occupation of orbitals with mostly dxz/dyz character that facilitate π-bonding of the Mo center to the axial ligands. Moreover, one has to keep in mind that for {[Mo(V)]N−} SOC acts to lower the gǁ value whereas it leads to an increase of gǁ for Mo(III)-L, L= N2, CO, and NH3.5
In addition to the molecular g-tensor we have measured the 14,15N and 95,97Mo ENDOR of [Mo]N and 1,2H, 14,15N and 95,97Mo ENDOR of [Mo]NH. The 14,15N hyperfine coupling measured by ENDOR for [Mo]N is small, in keeping with the orthogonality of both the σ and π orbitals on N to the 4e spin-bearing orbitals on Mo. The experimental and calculated 14N hyperfine couplings are in excellent agreement. The negative sign of aiso for 14N, as both calculated and determined by experiment, corresponds to delocalization through spin polarization of the Mo-N bonding orbitals. The measured quadrupole coupling is in excellent agreement with the calculated value, and indicates σ donation from N to Mo is much more significant that π back-donation to N. It may be noted that the bonding in an analogous trigonal d3 Fe(V)≡N complex appears to be quite different. Whereas the Mo-bound nitride has a distinct difference in the occupancies of nitrogen 2pσ versus 2pπ orbitral, analyses of the 14N quadrupole and hyperfine couplings of the Fe-nitride ligand support a surprising picture in which the Fe(V) ion binds an essentially spherically symmetric nitride trianion.18 The 14,15N hyperfine coupling for [Mo]14,15NH could not be resolved, and calculations suggest that this results from a highly anisotropic interaction tensor. However, the 1,2H signals were readily detected and interpretable with an anisotropic coupling tensor with substantial isotropic coupling, aiso(1H) ~ 20 MHz, with satisfactory agreement between computation and experiment.
Finally, we can use the present results to comment on the alternative pathways for [e−/H+] addition during the reduction of [Mo(VI)]N to [Mo(V)]NH during catalysis, Figure 1. The ability to trap and crystallographically characterize {[Mo(VI)]NH}+ clearly demonstrates that the ‘proton-first’ pathway is accessible during catalytic reduction of N2. However, the present characterization by experiment and theory of {[Mo(V)]N}−, in the context of earlier calculations on the reaction mechanism, nonetheless suggest that the ‘electron-first’ pathway is feasible.11
Summary
Our analysis shows that Jahn-Teller and spin orbit coupling effects have a significant impact on the electronic structures of [Mo]NH and [Mo]N− and are absolutely key for understanding the physics and chemistry of these compounds. In particular the magnetic properties of these compounds are governed by the delicate balance of the two effects. Furthermore, together with our previous work on [Mo] complexes we have established the combination of EPR spectroscopy and correlated multirefence quantum chemical calculations as a valuable tool to probe and analyze the electronic structure of compounds with near-degenerate ground states.5 14,15N and 1,2H hyperfine couplings from the axial −N and −NH ligands provide stringent tests of the validity of quantum calculations, and in fact calculation and experiment are in excellent agreement. The 95,97Mo hyperfine couplings should provide a useful benchmark in considerations of the state of Mo in synthetic and biological multimetallic clusters. This becomes particularly relevant for the case of the FeMo-cofactor catalytic cluster of nitrogenase, where the oxidation state Mo(III) has recently been suggested for the Mo center on the basis of spectroscopic experiments and quantum chemical calculations.51
Supplementary Material
Table 1.
Important atomic orbital contributions to the active orbitals in CASSCF(7,8) and NEVPT2(7,8) calculations on the ethyl model of {[Mo]N}−. All contribution are given in %.
| Orbital |
|
dxz | dyz |
|
dxy | Nitrido N p |
Amino N p |
Amido N p |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 53.6 | 0.0 | 0.0 | 0.0 | 0.0 | 35.6 | 1.4 | 1.4 | ||
| 7 | 0.0 | 4.7 | 42.5 | 0.0 | 5.0 | 42.0 | 0.0 | 2.2 | ||
| 6 | 0.0 | 42.4 | 4.9 | 4.9 | 0.0 | 42.1 | 0.0 | 2.0 | ||
| 5 | 0.0 | 0.6 | 4.8 | 0.0 | 75.7 | 3.2 | 0.0 | 8.0 | ||
| 4 | 0.0 | 5.0 | 0.4 | 75.7 | 0.0 | 3.2 | 0.0 | 8.2 | ||
| 3 | 0.0 | 20.7 | 18.1 | 0.1 | 0.0 | 55.9 | 0.0 | 0.2 | ||
| 2 | 0.0 | 18.2 | 20.7 | 0.0 | 0.0 | 55.9 | 0.0 | 0.1 | ||
| 1 | 33.9 | 0.0 | 0.0 | 0.0 | 0.0 | 60.0 | 0.3 | 0.0 |
Table 2.
Important atomic orbital contributions in to the active orbitals in CASSCF(7,8) and NEVPT2(7,8) calculations on the ethyl model of [Mo]NH. All contribution are given in %.
| Orbital |
|
dxz | dyz |
|
dxy | Imido N p |
Amino N p |
Amido N p |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 0.9 | 5.0 | 0.1 | 0.1 | 4.0 | 63.0 | 0.0 | 8.3 | ||
| 7 | 0.0 | 0.0 | 4.5 | 0.7 | 5.6 | 70.3 | 0.1 | 2.8 | ||
| 6 | 4.7 | 1.6 | 0.3 | 30.1 | 1.7 | 35.1 | 0.1 | 7.1 | ||
| 5 | 0.0 | 21.1 | 35.4 | 3.8 | 0.9 | 32.0 | 0.0 | 2.5 | ||
| 4 | 0.0 | 33.8 | 21.8 | 2.1 | 3.4 | 31.4 | 0.0 | 2.9 | ||
| 3 | 0.0 | 35.5 | 0.0 | 0.4 | 0.1 | 58.0 | 0.0 | 0.3 | ||
| 2 | 0.0 | 0.0 | 35.3 | 0.1 | 0.2 | 58.5 | 0.0 | 0.3 | ||
| 1 | 2.6 | 0.1 | 1.0 | 12.3 | 1.0 | 62.5 | 0.1 | 0.4 |
Table 5.
Experimentally observed and calculated bond angles for [Mo]N and [Mo]NH.
| MoN | MoN− | MoNH+ | MoNH | |
|---|---|---|---|---|
| Crystal structure | calculations | Crystal structure | calculations | |
| N5-Mo-N1 | 103 | 97 | 103 | 93 |
| N5-Mo-N2 | 102 | 107 | 103 | 106 |
| N5-Mo-N3 | 102 | 110 | 102 | 110 |
| N5-Mo-N4 | 172 | 169 | ||
| Mo-N5-H | 13(full)/26(ethyl) |
Synopsis.
The molybdenum trisamidoamine (TAA) complex [Mo] (=(3,5-(2,4,6-i-Pr3C6H2)2C6H3NCH2CH2N)Mo) carries out catalytic reduction of N2 to ammonia by protons and electrons at room temperature. A key intermediate in the proposed [Mo] nitrogen reduction cycle is nitrido-Mo(VI), [Mo(VI)]N: the addition of [e−/H+] to [Mo(VI)]N generates [Mo(V)]NH In combination with previous X-ray studies, EPR/ENDOR and multli-reference based computational studies of {[Mo(V)]N}− and [Mo(V)]NH create the rare situation where each one of the four possible states of an [e−/H+] delivery has been characterized. Jahn-Teller and spin orbit coupling effects have a significant impact on the electronic structures of [Mo]NH and [Mo]N− and are absolutely key for understanding the physics and chemistry of these compounds
Acknowledgments
Financial support of this work is gratefully acknowledged: The Max Planck Society, FN and MR; the NSF (MCB 1515981) and NIH (GM 111097, BMH, and GM 31978, RRS); MR gratefully acknowledges funding by the Otto-Hahn award program of the Max-Planck Society, and MRR is grateful to the Austrian Science Foundation for an Erwin-Schrödinger fellowship (J2822–N19). MR would also like to thank C. Roemelt for assistance with figures.
Footnotes
Supporting Information Available: Orientation selective14,15N, 1H ENDOR spectra of Mo14,15N−, Mo14,15N1H; ENDOR simulations; calculated active orbitals of MoN−, MoNH; Townes-Dailey Quadrupole Analysis; 12 figures in all.
References
- 1.Yandulov DV, Schrock RR. Catalytic Reduction of Dinitrogen to Ammonia at a Single Molybdenum Center. Science. 2003;301:76–78. doi: 10.1126/science.1085326. [DOI] [PubMed] [Google Scholar]
- 2.Yandulov DV, Schrock RR. Reduction of Dinitrogen to Ammonia at a Well-Protected Reaction Site in a Molybdenum Triamidoamine Complex. J Am Chem Soc. 2002;124:6252–6253. doi: 10.1021/ja020186x. [DOI] [PubMed] [Google Scholar]
- 3.Yandulov DV, Schrock RR, Rheingold AL, Ceccarelli C, Davis WM. Synthesis and Reactions of Molybdenum Triamidoamine Complexes Containing Hexaisopropylterphenyl Substituents. Inorg Chem. 2003;42:796–813. doi: 10.1021/ic020505l. [DOI] [PubMed] [Google Scholar]
- 4.Yandulov DV, Schrock RR. Studies Relevant to Catalytic Reduction of Dinitrogen to Ammonia by Molybdenum Triamidoamine Complexes. Inorg Chem. 2005;44:5542. doi: 10.1021/ic040095w. [DOI] [PubMed] [Google Scholar]
- 5.McNaughton RL, Roemelt M, Chin JM, Schrock RR, Neese F, Hoffman BM. Experimental and Theoretical Epr Study of Jahn-Teller Active [Hiptn3n]Mol Complexes (L = N2, Co, Nh3) J Am Chem Soc. 2010;132:8645–8656. doi: 10.1021/ja1004619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McNaughton RL, Chin JM, Weare WW, Schrock RR, Hoffman BM. Epr Study of the Low-Spin [D3; S =1/2], Jahn-Teller-Active, Dinitrogen Complex of a Molybdenum Trisamidoamine. J Am Chem Soc. 2007;129:3480–3481. doi: 10.1021/ja068546u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Le Guennic B, Kirchner B, Reiher M. Nitrogen Fixation under Mild Ambient Conditions: Part I-the Initial Dissociation/Association Step at Molybdenum Triamidoamine Complexes. Chemistry–A European Journal. 2005;11:7448–7460. doi: 10.1002/chem.200500935. [DOI] [PubMed] [Google Scholar]
- 8.Schenk S, LeGuennic B, Kirchner B, Reiher M. First Principles Investigation of the Schrock Mechanism of Dinitrogen Reduction Employing the Full Hiptn3n Ligand. Inorg Chem. 2008;47:3634–3650. doi: 10.1021/ic702083p. [DOI] [PubMed] [Google Scholar]
- 9.Studt F, Tuczek F. Energetic and Mechanism of a Room-Temperature Catalytic Process for Ammonia Synthesis (Schrock Cycle): Comparison with Biological Nitrogen Fixation. Angewandte Chemie, International Edition. 2005;44:5639–5642. doi: 10.1002/anie.200501485. [DOI] [PubMed] [Google Scholar]
- 10.Neese F. The Yandulov/Schrock Cycle and the Nitrogenase Reaction: Pathways of Nitrogen Fixation Studied by Density Functional Theory. Angewandte Chemie, International Edition. 2006;45:196–199. doi: 10.1002/anie.200502667. [DOI] [PubMed] [Google Scholar]
- 11.Thimm W, Gradert C, Broda H, Wennmohs F, Neese F, Tuczek F. Free Reaction Enthalpy Profile of the Schrock Cycle Derived from Density Functional Theory Calculations on the Full [Mo(Hipt)N3n] Catalyst. Inorg Chem. 2015;54:9248–9255. doi: 10.1021/acs.inorgchem.5b00787. [DOI] [PubMed] [Google Scholar]
- 12.Bersuker IB. The Jahn-Teller Effect. Cambridge University Press; Cambridge: 2006. [Google Scholar]
- 13.Neese F, Pantazis DA. What Is Not Required to Make a Single Molecule Magnet. Faraday Discuss. 2011;148:229–238. doi: 10.1039/c005256f. discussion 299–314. [DOI] [PubMed] [Google Scholar]
- 14.Atanasov M, Ganyushin D, Pantazis DA, Sivalingam K, Neese F. Detailed Ab Initio First-Principles Study of the Magnetic Anisotropy in a Family of Trigonal Pyramidal Iron(Ii) Pyrrolide Complexes. Inorg Chem. 2011;50:7460–7477. doi: 10.1021/ic200196k. [DOI] [PubMed] [Google Scholar]
- 15.Del Castillo TJ, Thompson NB, Peters JC. A Synthetic Single-Site Fe Nitrogenase: High Turnover, Freeze-Quench (57)Fe Mossbauer Data, and a Hydride Resting State. J Am Chem Soc. 2016;138:5341–5350. doi: 10.1021/jacs.6b01706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Suess DLM, Tsay C, Peters JC. Dihydrogen Binding to Isostructural S = 1/2 and S = 0 Cobalt Complexes. J Am Chem Soc. 2012;134:14158–14164. doi: 10.1021/ja305248f. [DOI] [PubMed] [Google Scholar]
- 17.Saouma CT, Peters JC. M≡E and M=E Complexes of Iron and Cobalt That Emphasize Three-Fold Symmetry (E = O, N, Nr) Coord Chem Rev. 2011;255:920–937. doi: 10.1016/j.ccr.2011.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cutsail GE, III, Stein BW, Subedi D, Smith JM, Kirk ML, Hoffman BM. Epr, Endor, and Electronic Structure Studies of the Jahn-Teller Distortion in an Fe(V) Nitride. J Am Chem Soc. 2014;136:12323–12336. doi: 10.1021/ja505403j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Smith JM, Subedi D. The Structure and Reactivity of Iron Nitride Complexes. Dalton Transactions. 2012;41:1423–1429. doi: 10.1039/c1dt11674f. [DOI] [PubMed] [Google Scholar]
- 20.McSkimming A, Harman WH. A Terminal N2 Complex of High-Spin Iron(I) in a Weak, Trigonal Ligand Field. J Am Chem Soc. 2015;137:8940–8943. doi: 10.1021/jacs.5b06337. [DOI] [PubMed] [Google Scholar]
- 21.Rittle J, Peters JCAn. Fe-N2 Complex That Generates Hydrazine and Ammonia Via Fe Horizontal Linennh2: Demonstrating a Hybrid Distal-to-Alternating Pathway for N2 Reduction. J Am Chem Soc. 2016 doi: 10.1021/jacs.6b01230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Anderson JS, Rittle J, Peters JC. Catalytic Conversion of Nitrogen to Ammonia by an Iron Model Complex. Nature. 2013;501:84–87. doi: 10.1038/nature12435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Munisamy T, Schrock RR. An Electrochemical Investigation of Intermediates and Processes Involved in the Catalytic Reduction of Dinitrogen by [Hiptn3n]Mo (Hiptn3n = (3,5-(2,4,6-I-Pr3c6h2)2c6h3nch2ch2)3n) Dalton Trans. 2012;41:130–137. doi: 10.1039/c1dt11287b. [DOI] [PubMed] [Google Scholar]
- 24.Davydov R, Hoffman BM. Active Intermediates in Heme Monooxygenase Reactions as Revealed by Cryoreduction/Annealing, Epr/Endor Studies. Archives of Biochemistry and Biophysics. 2011;507:36–43. doi: 10.1016/j.abb.2010.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Davoust CE, Doan PE, Hoffman BM. Q-Band Pulsed Electron Spin-Echo Spectrometer and Its Application to Endor and Eseem. J Magn Reson. 1996;119:38–44. [Google Scholar]
- 26.Schweiger A, Jeschke G. Principles of Pulse Electron Paramagnetic Resonance. Oxford University Press; Oxford, UK: p. 2001. [Google Scholar]
- 27.Epel B, Gromov I, Stoll S, Schweiger A, Goldfarb D. Spectrometer Manager: A Versatile Control Software for Pulse Epr Spectrometers. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering. 2005;26B:36–45. [Google Scholar]
- 28.Hoffman BM. Electron Nuclear Double Resonance (Endor) of Metalloenzymes. Acc Chem Res. 1991;24:164–170. [Google Scholar]
- 29.Doan PE. The Past, Present, and Future of Orientation-Selected Endor Analysis: Solving the Challenges of Dipolar-Coupled Nuclei. In: Telser J, editor. Paramagnetic Resonance of Metallobiomolecules. American Chemical Society; 2003. pp. 55–81. [Google Scholar]
- 30.Hoffman BM, Gurbiel RJ, Werst MM, Sivaraja M. In: Advanced Epr Applications in Biology and Biochem. Hoff AJ, editor. Elsevier; Amsterdam: 1989. pp. 541–591. [Google Scholar]
- 31.DeRose VJ, Hoffman BM. Protein Structure and Mechanism Studied by Electron Nuclear Double Resonance Spectroscopy. In: Sauer K, editor. Methods Enzymol. Vol. 246. Academic Press; New York: 1995. pp. 554–589. [DOI] [PubMed] [Google Scholar]
- 32.Neese F. The Orca Program System. Wiley Interdisciplinary Reviews-Computational Molecular Science. 2012;2:73–78. [Google Scholar]
- 33.van Lenthe E, Baerends EJ, Snijders JG. Relativistic Regular Two-Component Hamiltonians. J Chem Phys. 1993;99:4597–4610. [Google Scholar]
- 34.van Wüllen C. Molecular Density Functional Calculations in the Regular Relativistic Approximation: Method, Application to Coinage Metal Diatomics, Hydrides, Fluorides and Chlorides, and Comparison with First-Order Relativistic Calculations. J Chem Phys. 1998;109:392. [Google Scholar]
- 35.Pantazis DA, Chen X-Y, Landis CR, Neese F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. Journal of Chemical Theory and Computation. 2008;4:908–919. doi: 10.1021/ct800047t. [DOI] [PubMed] [Google Scholar]
- 36.Becke AD. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Physical Review A: Atomic, Molecular, and Optical Physics. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 37.Perdew JP. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Physical Review B. 1986;33:8822–8824. doi: 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
- 38.Neese F. Prediction of Electron Paramagnetic Resonance G Values Using Coupled Perturbed Hartree-Fock and Kohn-Sham Theory. J Chem Phys. 2001;115:11080–11096. [Google Scholar]
- 39.Gerloch M, McMeeking RF. Paramagnetic Properties of Unsymmetrical Transition Metal Complexes. Journal of the Chemical Society, Dalton Transactions: Inorganic Chemistry. 1975:2443–2451. [Google Scholar]
- 40.Angeli C, Cimiraglia R, Evangelisti S, Leininger T, Malrieu JP. Introduction of N-Electron Valence States for Multireference Perturbation Theory. J Chem Phys. 2001;114:10252. [Google Scholar]
- 41.Angeli C, Cimiraglia R, Malrieu JP. N-Electron Valence State Perturbation Theory: A Fast Implementation of the Strongly Contracted Variant. Chem Phys Lett. 2001;350:297–305. [Google Scholar]
- 42.Angeli C, Cimiraglia R, Malrieu JP. N-Electron Valence State Perturbation Theory: A Spinless Formulation and an Efficient Implementation of the Strongly Contracted and of the Partially Contracted Variants. J Chem Phys. 2002;117:9138. [Google Scholar]
- 43.Miralles J, Daudey J-P, Caballol R. Variational Calculation of Small Energy Differences. The Singlet-Triplet Gap in Hexaclorodicuprate (2−) Chem Phys Lett. 1992;198:555–562. [Google Scholar]
- 44.Miralles J, Castell O, Caballol R, Malrieu J-P. Specific Ci Calculation of Energy Differences: Transition Energies and Bond Energies. Chemical Physics. 1993;172:33–43. [Google Scholar]
- 45.Hess BA, Marian CM, Wahlgren U, Gropen O. A Mean-Field Spin-Orbit Method Applicable to Correlated Wavefunctions. Chem Phys Lett. 1996;251:365–371. [Google Scholar]
- 46.Neese F. Efficient and Accurate Approximations to the Molecular Spin-Orbit Coupling Operator and Their Use in Molecular G-Tensor Calculations. J Chem Phys. 2005;122:034107. doi: 10.1063/1.1829047. [DOI] [PubMed] [Google Scholar]
- 47.Bolvin H. An Alternative Approach to the G-Matrix: Theory and Applications. ChemPhysChem. 2006;7:1575–1589. doi: 10.1002/cphc.200600051. [DOI] [PubMed] [Google Scholar]
- 48.McGarvey BR, Telser J. Simple Ligand-Field Theory of D4 and D6 Transition Metal Complexes with a C3 Symmetry Axis. Inorg Chem. 2012;51:6000–6010. doi: 10.1021/ic201189a. [DOI] [PubMed] [Google Scholar]
- 49.Neese F, Solomon EI. Magnetism: Molecules to Materials. Wiley-VCH Verlag GmbH & Co. KGaA; 2003. Interpretation and Calculation of Spin-Hamiltonian Parameters in Transition Metal Complexes; pp. 345–466. [Google Scholar]
- 50.Kinney RA, Hetterscheid DGH, Hanna BS, Schrock RR, Hoffman BM. Formation of {[Hiptn3n]Mo(Iii)H}− by Heterolytic Cleavage of H2 as Established by Epr and Endor Spectroscopy. Inorg Chem. 2010;49:704–713. doi: 10.1021/ic902006v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Bjornsson R, Lima FA, Spatzal T, Weyhermuller T, Glatzel P, Bill E, Einsle O, Neese F, DeBeer S. Identification of a Spin-Coupled Mo(Iii) in the Nitrogenase Iron-Molybdenum Cofactor. Chemical Science. 2014;5:3096–3103. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


