The adder phenomenon emerges from independent control of pre- and post-Start phases of the budding yeast cell cycle

Summary

Although it has long been clear that cells actively regulate their size, the molecular mechanisms underlying this regulation have remained poorly understood. In budding yeast, cell size primarily modulates the duration of the cell division cycle by controlling the G1/S transition known as Start. We have recently shown that the rate of progression through Start increases with cell size because cell growth dilutes the cell cycle inhibitor Whi5 in G1. Recent phenomenological studies in yeast and bacteria have shown that these cells add an approximately constant volume during each complete cell cycle, independent of their size at birth. These results seem to be in conflict, as the phenomenological studies suggest that cells measure the amount they grow, rather than their size, and that size control acts over the whole cell cycle, rather than specifically in G1. Here, we propose an integrated model that unifies the adder phenomenology with the molecular mechanism of G1/S cell size control. We use single cell microscopy to parameterize a full cell cycle model based on independent control of pre- and post-Start cell cycle periods. We find that our model predicts the size-independent amount of cell growth during the full cell cycle. This suggests that the adder phenomenon is an emergent property of the independent regulation of pre- and post-Start cell cycle periods rather than the consequence of an underlying molecular mechanism measuring a fixed amount of growth.

Introduction

Cell size affects cell physiology in key ways because it determines the scale of organelles and biosynthetic processes [1,2]. To control cell size in a proliferating population, cell growth is coupled to division in a wide range of species from bacteria to metazoans [3–5].

The coupling between growth and division can take a variety of phenomenological forms and a veritable zoology of nomenclature has emerged to describe them including adders, timers, sizers, and their stochastic counterparts [6–10]. For example, fission yeast exhibits behavior close to a sizer, where the amount of growth in the cell cycle compensates for differences in cell size at birth so that all cells divide at approximately the same size [11–14]. In contrast, several bacterial species exhibit adders, where the amount of growth in a full cell cycle is constant, independent of cell size at birth [7,15–21]. Thus, bacteria of initially different sizes revert to the mean size over several cell cycles. Importantly, sizers, timers and adders are idealized discrete scenarios representing only a small subset of possible phenomena. For example, E. coli exhibits adder behavior in fast growth conditions, but deviates from this pattern in slower growth conditions [19]. Even within a given growth condition, an organism can exhibit different size control behaviors depending on its size at birth [22]: fission yeast born at wild type sizes exhibit sizers, but fission yeast born at larger sizes exhibit adders [11].

Although observations and categorization of cell size control are abundant, it is unclear how the observed phenomena arise from regulatory networks controlling cell division. For example, budding yeast exhibits an adder across the entire cell cycle from birth to division [16]. However, it is unclear how this would arise from the known cell cycle network given that it is modular [23], i.e., the G1/S transition is driven by different kinase and transcription factor complexes than the G2/M transition [24]. Thus, there is no obvious candidate for a mechanism that might implement an adder over the entire cell cycle.

The long-standing consensus for budding yeast is that size control mainly takes place in the first cell cycle of newborn ‘daughter’ cells [6,23]. Specifically, the Start transition in G1, just before initiation of DNA replication, marks the end of the size-dependent period of the daughter cell cycle. The duration of the remainder of the cell cycle, including the S/G2/M phases, is only weakly dependent on cell size and growth conditions [23,25–27]. Recently, progress has been made in understanding the size control mechanism linking growth to Start. Independent of their size, cells are born with similar amounts of the cell cycle inhibitor Whi5 [28]. Since Whi5 is a stable protein and not synthesized during G1, cell growth dilutes Whi5 to drive progression through Start. In contrast to Whi5, the concentrations of other important cell cycle activators, such as the G1 cyclin Cln3, are maintained at constant concentration throughout G1. This mechanism ensures that smaller born cells have an initially higher cell cycle inhibitor to activator ratio, which is decreased by subsequent cell growth.

Despite this advance in understanding how budding yeast cells link growth to division in G1, it remains unclear how the Whi5 dilution mechanism participates in ensuring an adder over the entire cell cycle because the key G1 regulators Whi5 and its antagonist Cln3 have no reported functions outside of G1. This raises the question of whether or not the phenomenological adder reflects an underlying mechanistic adder, i.e., a yet unidentified molecular mechanism that directly measures growth over the full cell cycle. Or, is there another way to reconcile existing models of budding yeast G1/S size control with the adder phenomenon?

To determine if existing models of budding yeast G1/S size control are compatible with the adder phenomenon, we used single cell imaging combined with analytical models and simulations. We show that a model based on a cell-size-dependent rate for passing Start is sufficient to explain the key properties of budding yeast G1/S size control. Once cell size is accounted for, the amount of time spent in G1 provides no substantial improvement in predicting passage through Start. To construct a full cell cycle model, we also identified the key parameters determining progression through post-Start phases of the cell cycle. This full cell cycle model has no direct coupling between pre- and post-Start cell cycle periods and reproduces the observed steady-state cell size distribution and birth-size-independent growth over a complete cell cycle. Thus, we demonstrate that the phenomenological adder is an emergent property of two distinct cell cycle modules rather than a consequence of an underlying molecular adder mechanism. Consistent with this picture, we examined mutations influencing G1 progression and found that they eliminate the phenomenological adder.

Results

The phenomenological adder is unlikely to arise from a mechanistic adder

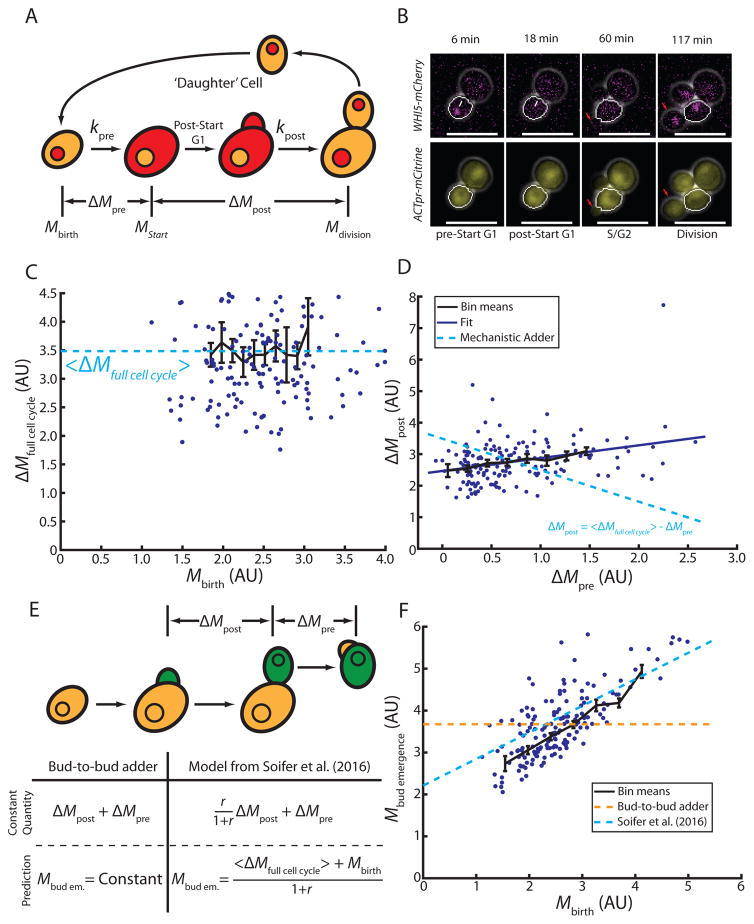
To investigate the origin of the adder phenomenon in budding yeast, we examined growth and division in single cells (Figure 1A). We used live cell microscopy to measure cell size as the geometric volume (V) or the amount of a fluorescent protein driven by the ACT1 promoter (ACT1pr-mCitrine; Figure 1B), which is expected to correlate with cellular protein content, and therefore cell mass (M) [23]. Consistent with previous reports [16], we found that budding yeast exhibits an adder behavior. The amount of growth of a newborn cell over the complete first cell cycle does not depend on birth size, whether we measure size as estimated volume or total mCitrine fluorescence intensity (Figure 1C, S1A). We find a linear fit to these data does not reveal statistically significant deviation from a size-independent constant (p=0.07, volume; p=0.97, fluorescence intensity). Consistent with the notion that size control in budding yeast mainly takes place in the first cell cycle, newborn ‘daughter’ cells exhibit an adder behavior during their first cell cycle, but in subsequent cell cycles (‘mother’ cells), growth is positively correlated with size at the beginning of G1 (Figure S1B, slope=0.34, p=6.1e–4, R=0.48). We decided to focus on haploid cells grown in media containing 2% glycerol and 1% ethanol as its carbon source because of the pronounced G1/S size control effect in these conditions [23]. However, we note that the adder phenomenon is also present in haploid cells grown on glucose (Figure S1C) and in diploid cells grown in the presence of various carbon sources [16]. Although a previous report [29], based on data from [23], suggested that total cell cycle growth was negatively correlated with birth size, we reanalyze these data using linear regression and find they are consistent with our results (S1D,E). We find no statistically significant negative correlation between birth size and total growth in any of the data sets.

Figure 1. Single cell measurements demonstrate the absence of a mechanistic adder in budding yeast.

(A) Schematic illustrating the first cell cycle of ‘daughter’ cells. (B) Representative fluorescence and phase contrast images highlighting key events during the cell cycle. Daughter cell segmentation is shown in white. White arrows indicate Whi5-mCherry nuclear exit marking Start. Red arrows show the growing bud/newborn daughter. (C) Cell growth in daughter cells during the entire cell cycle as a function of birth mass (in arbitrary units, AU, n=165). Dashed line shows fit assuming constant added mass, ΔM. (D) Post-Start growth is weakly correlated with pre-Start growth (solid line shows linear fit, R = 0.32, n=165). Linear anticorrelation with slope -1 would be expected from an ideal mechanistic adder (dashed line). (E) Schematic illustrating proposed adder models implemented between subsequent budding events. Green indicates the mass included in each model. The table shows predictions from the bud-to-bud adder model and the model from Soifer et al. for the mass at bud emergence. M_{bud em} abbreviates mass at bud emergence, M_{bud emergence}. (F) Mass at bud emergence as a function of birth mass (n=73). Predictions are shown for a bud-to-bud adder model (orange) and the model proposed in [16] (blue). All bars represent binned means and standard errors. See also Figure S1.

While budding yeast behaves as a phenomenological adder, it is not clear whether this originates from a molecular mechanism directly measuring cell growth through the full cell cycle. A key prediction for such a mechanistic adder is that growth post-Start, ΔM_post, should directly compensate variation in growth pre-Start, ΔM_pre, to ensure a constant total growth, ΔM_{full cell cycle} = ΔM_pre+ ΔM_post (Figure 1A). This implies an inverse correlation between growth before and after Start: ΔM_post = ΔM_{full cell cycle} − ΔM_pre. Note that in the absence of a mechanistic adder, this inverse correlation at the single cell level is not required for the adder phenomenon to be observed in averages of single cell data. To illustrate that an adder can result from independent cell cycle phases, consider the following hypothetical example. Assume that growth in pre- and post-Start periods, ΔM_pre and ΔM_post respectively, were independent adders with Gaussian distributed noise, σ_pre and σ_post. Total growth for each cell is then given by ΔM_{full cell cycle} = ΔM_pre + σ_pre + ΔM_post + σ_post. Averaging results in an adder for 〈ΔM_{full cell cycle}〉 = ΔM_pre + ΔM_post = constant because this Gaussian noise has a mean of 0. At the same time, plotting ΔM_post + σ_post as a function of ΔM_pre + σ_pre would show no correlation because the two processes are independent, i.e., σ_pre and σ_post are uncorrelated.

Therefore, to directly test the existence of a mechanistic adder, we examined the correlation between cellular growth pre- and post-Start in single cells. To identify the time point of Start, we monitored the localization of fluorescently tagged endogenous Whi5, which is rapidly exported from the nucleus at Start [30]. Post-Start growth is not negatively correlated with pre-Start growth (Figure 1D, slope=0.41, p=3.2e–5, R=0.32). We therefore conclude that it is unlikely that there exists an underlying molecular mechanism measuring total growth from birth to division.

The adder phenomenon is not the consequence of a mechanistic adder between two budding events

While our results suggest that there is no mechanistic adder measuring growth from birth to division, it remains possible that cells measure a constant amount of growth between any point in two subsequent cell cycles. Specifically, because size control mainly takes place at the G1/S transition, the adder could be implemented between two budding events (Figure 1E). Most of the growth during S/G2/M phases of the budding yeast cell cycle is directed into the bud, and the mother itself grows little. Therefore, the amount of growth between two budding events roughly corresponds to the size of the daughter cell at its first bud emergence. Thus, a mechanism where cells ensure a constant amount of growth between two budding events is equivalent to cells perfectly controlling their size at bud emergence. Therefore, size at bud emergence should also be independent of size at birth. However, it is well established that budding yeast size control at the G1/S transition is imperfect, meaning that while smaller born cells do grow more during G1, this compensation is not sufficient to result in birth-size-independent sizes at bud emergence [6,23] (Figure 1F).

While the dependence of size at bud emergence on birth size rules out the simplest version of a mechanistic adder operating between two budding events, an alternative mechanism linking the birth-to-division adder to the G1/S transition has recently been proposed by Soifer et al. [16]. In this model, the constant parameter between budding events is the amount of growth during S/G2/M multiplied with the ratio of bud-to-total cell size and then added to the amount of growth of the daughter cell during G1. Soifer et al. also propose one possible molecular interpretation offering a link to the Whi5 dilution model. In contrast to experimental evidence [28], the model proposed by Soifer et al. is deterministic, assuming that cells pass Start at a threshold Whi5 concentration. Thus, the model can only make predictions about average cell behavior and cannot predict the distribution of cell sizes at bud emergence. However, it does predict average size at bud emergence, M_budding, as a function of cell birth size, M_birth, the average bud-to-mother size ratio at cytokinesis, r, and the average growth between birth and division, 〈ΔM_{full cell cycle}〉. M_budding is then given by $M_{\mathit{budding}}=\frac{\langle \mathrm{\Delta }{M}_{\mathit{full}\mathit{cell}\mathit{cycle}}\rangle +M_{\mathit{birth}}}{1+r}$ (see supplement to [16]). To test this model, we calculate 〈ΔM_{full cell cycle}〉 and r from direct measurements. As shown in Figure 1F, the model is not consistent with the data.

Taken together, our analysis suggests that the adder phenomenon is not the consequence of a specific mechanism measuring total growth throughout the full cell cycle. Instead, we propose that the adder emerges from independent regulation of growth in pre- and post-Start periods.

Passage through Start is primarily determined by current cell size, not cell age

To test the hypothesis that the adder results from independently regulated pre- and post-Start periods, we separately modeled each of these periods. We then combined these independent models to obtain a full cell cycle model to test if the adder can arise from distinct control mechanisms pre- and post-Start.

It has recently been shown that dilution of the cell cycle inhibitor Whi5 allows cells to sense size during G1 [28]. Since Whi5 concentration is roughly inversely proportional to cell volume, this suggests that a key predictor for Start should be cell volume (or the related quantity cellular protein content). However, in addition to the Whi5 dilution model, other mechanisms have been proposed to contribute to G1/S size control. Specifically, it has been proposed that cells integrate activity of the G1 cyclin Cln3 in complex with the cyclin-dependent kinase Cdk1 [31]. This model predicts that the rate at which cells progress through Start should also depend on cell age. Other possible predictive parameters could be birth size, cell growth rate, and the total amount of growth since cell birth [6,32].

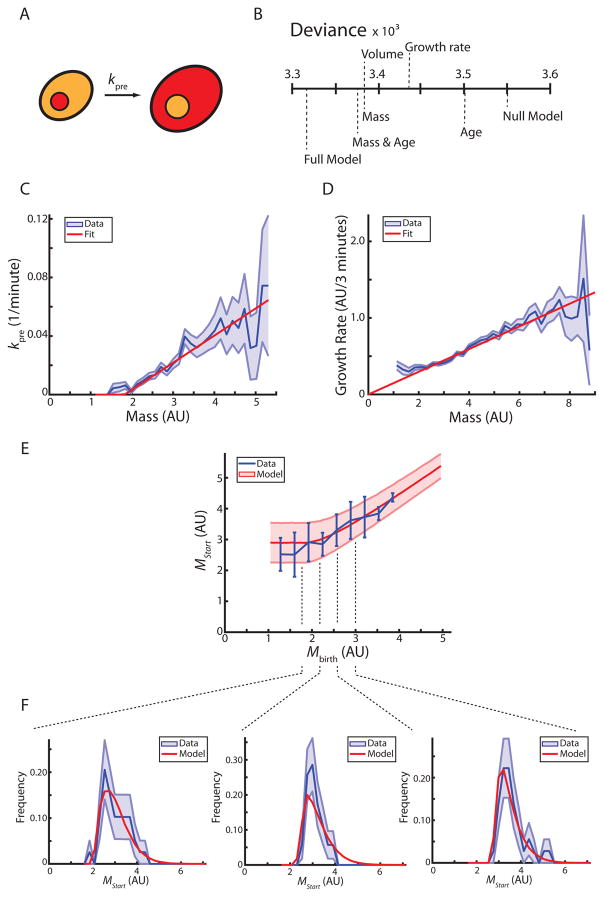
To test these models of Start (Figure 2A), we measured a series of parameters for each cell to identify the parameters most predictive of passage through Start. At each time point of a movie, each pre-Start daughter cell is characterized by its volume, total mCitrine fluorescence intensity, age, total growth since birth, volume or mCitrine intensity at birth, and average growth rate during pre-Start G1. We also determined for each cell whether it passed Start within the next frame of the movie. Data for all cells from several independent experiments were aggregated and each timepoint for each cell was treated as an independent observation. We performed a series of logistic regressions to predict passage through Start as a function of each of the individual parameters. We then used the deviance, a metric for the quality of the prediction, to compare different models. The metrics for cell size (geometric volume and total mCitrine reporter intensity) are the best single predictors (Figure 2B, Table S1). To test whether the ability to predict passage through Start can be improved by using a second parameter in addition to cell size measured by mCitrine fluorescence intensity (which we call ‘cell mass’ from here on), we performed two-parameter logistic regressions of cell mass in combination with one of the other parameters. Strikingly, including any single additional parameter, such as cell age or average growth rate during pre-Start G1, did not substantially improve the predictive power of the model (Figure 2B, Table S1).

Figure 2. Pre-Start size control is recapitulated by a model based on a mass-dependent rate of passing Start.

(A) Schematic illustrating pre-Start G1 in daughter cells. Whi5-mCherry (red) nuclear exit defines passage through Start. (B) Logistic regressions identify cell size (volume or mass) as the major predictive parameter for passage through Start. Deviance measures how much of the data is not explained by the model (see methods). (C) The rate at which cells pass Start is shown as a function of cell mass (blue, +/− standard error). A linear fit (red) is used in the model. (D) The growth rate of daughter cells (amount of growth between two frames, 3 minutes) is shown as a function of cell mass (blue, +/− standard error). A linear fit, as expected from exponential growth, is shown in red. (E) Cell mass at Start is shown as a function of birth mass (blue, +/− standard deviation). Model prediction is shown in red (+/− standard deviation, n=165). (F) Marginal distributions of mass at Start conditioned on birth mass from (E) showing data (blue) and model (red). Standard deviation is estimated from 10000 bootstraps of the data. See also Figure S2, Table S1.

The results from these regressions support the Whi5-dilution model and oppose the Cln3 integration model. In the Whi5-dilution model, volume sets Whi5 concentration, which in turn determines the rate of passing Start. At each time point, there is a chance of passage through Start, which only depends on the current Whi5 concentration. In other words, two pre-Start cells that are the same size have the same chance of passing Start regardless of how large they were at birth or how long they have been in G1. In contrast, the finding that cell age is a poor predictor of passage through Start contradicts models that would imply a strong age dependence. In particular, it is not consistent with cells integrating constant Cln3-dependent activity over the course of G1 [31]. We also did not find a strong dependence on average growth during G1, but this may be due to our limited ability to measure variation in instantaneous growth rates. It therefore remains possible that undetected variation in growth rate on the timescale of minutes is important for passage through Start.

A model based on a size-dependent rate of passing Start reproduces experimental observations

Our regression models suggest that cell size is the key predictor of passage through Start. We therefore sought to explore how well a model based on a cell-mass-dependent instantaneous rate of passing Start can account for experimental observations. Using the data set described above, we calculated the instantaneous rate at which cells pass Start, k_pre, as a function of cell mass, M (Figure 2C). Consistent with the observation that the budding yeast G1/S transition is a highly stochastic process that results in an ‘imperfect sizer’ [23,33], we found no strict threshold, but rather a mass-dependent increase in the rate at which cells pass Start. The monotonic increase of k_pre with cell mass is consistent with the Whi5-dilution model, which predicts that decreases in Whi5 concentration due to cell growth result in an increase in the probability of passage through Start.

To complete our minimal model, we estimated a cell-mass-dependent mass accumulation rate by calculating frame-to-frame changes in total mCitrine reporter intensity. As shown in Figure 2D, the average mass accumulation rate increases in proportion to cell mass. In other words, the relative mass accumulation rate, $\frac{1}{M}\frac{dM}{dt}$, is independent of cell mass. For our model, we decided to neglect potential cell-to-cell variability in the relative mass accumulation rate and assume exponential mass accumulation (Figure 2D). While we consistently use the mCitrine-reporter based estimations of cell mass to parametrize our model, we note that, in contrast to the fluorescent reporter measurements (Figure 2D), growth measured by geometric estimation of cell volume strongly deviates from exponential growth at larger cell volumes. Above 70 fl, the absolute growth rate, $\frac{dV}{dt}$, seems to reach a plateau, consistent with linear growth (Figure S2).

By combining our model for cell growth with a linear fit to the measured mass-dependent rate of progression through Start, k_pre, we can predict the average cell mass at Start as a function of birth mass (Figure 2E). Because the cell-size-dependent rate of passage through Start is non-zero over a range of sizes, smaller born cells have non-zero probability of passing through Start at small sizes. This results in mean cell sizes at Start that increase with birth sizes. In addition to calculating means, which are consistent with experimental observations, our model can be used to calculate the complete distributions of masses at Start for any given birth mass. Indeed, our model distributions are in good agreement with single cell measurements (Figure 2F), demonstrating that the statistical features of passage through Start can largely be explained by a simple model accounting for a mass-dependent rate of passage through Start.

A model for the post-Start cell cycle recapitulates experimental observations

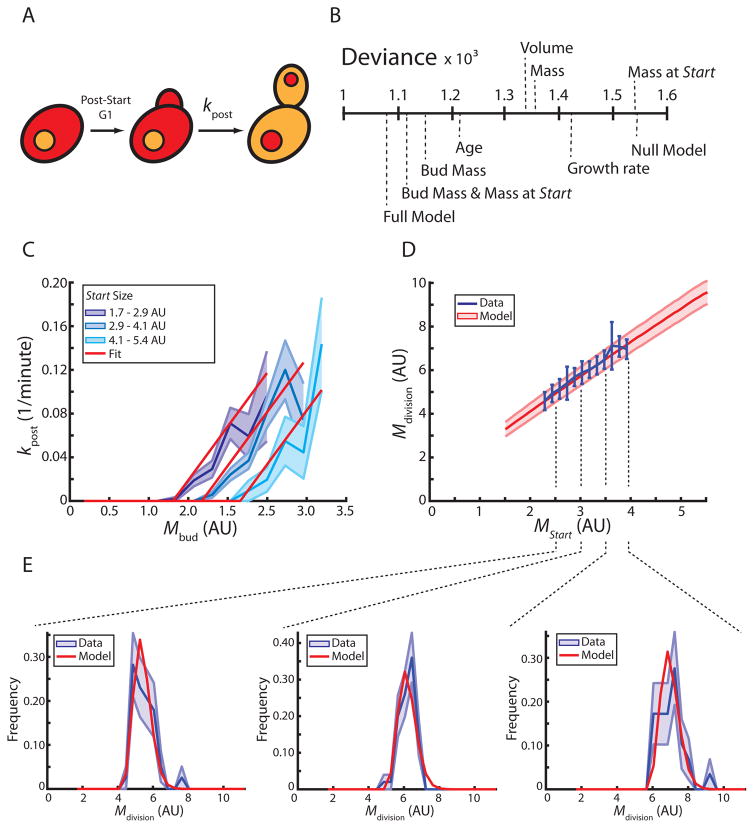
Regression analysis showed that passage through Start is determined by cell size. Next, we asked whether a similar analysis could identify the primary determinants of progression through the post-Start phases of the cell cycle (Figure 3A). Again, we performed logistic regressions to determine how well single parameters predict whether a given post-Start cell finishes division within the next 3 minutes (Figure 3B, Table S1). Of the tested parameters, bud mass (total fluorescence intensity of the mCitrine reporter in the bud) is the best predictor.

Figure 3. A model for post-Start cell cycle progression.

(A) Schematic illustrating post-Start cell cycle phases in daughter cells. Whi5-mCherry (red) re-enters the nucleus prior to cell division. (B) Logistic regressions identify bud mass and cell mass at Start as the major predictive parameters for cell division (cell separation). Deviance measures how much of the data is not explained by the model (see methods). (C) The rate at which post-Start daughter cells divide as a function of bud mass (blue, +/− standard error, n=165). Cells are binned according to mass at Start. A two-dimensional linear fit is used for the model (n=165). Average cell mass at Start of cells in each bin was used to show the corresponding fit (red). (D) Cell mass at division as a function of mass at Start (blue, n=165). Model prediction is shown in red (+/− standard deviation). (E) Marginal distributions of mass at division conditioned on mass at Start from (D) showing data (blue) and model (red). Standard deviation is estimated from 10000 bootstraps of the data. See also Figure S3, Table S1.

To test if bud mass alone is sufficient to explain the phenomenology of post-Start growth, we built a model to predict post-Start growth as a function of cell mass at Start. In analogy to the model for pre-Start growth shown in Figure 2, we treat division as a probabilistic process whose rate, k_post, depends exclusively on the mass of the bud, M_bud. We find that this model does not recapitulate the mass at division as a function of mass at Start.

Since bud mass alone was insufficient to model the post-Start cell cycle, we sought to identify which additional parameter could be added to the model. To do this, we performed a series of two-parameter logistic regressions and found that the addition of cell mass at Start, M_Start, most improves the regression model (Figure 3B, Table S1). Next, we asked whether building a model based on bud mass and cell mass at Start is sufficient to describe post-Start growth. We assume that the rate at which cells divide, k_post (M_bud, M_Start), depends linearly both on M_bud and M_Start (Figure 3C). Cell growth was modelled as described above (Fig 2D; supplementary information). This model accurately describes growth in the post-Start cell cycle (Figure 3D, 3E).

A full cell cycle model based on independent pre- and post-Start modules recapitulates the adder phenomenon

So far, we have constructed independent models for the pre- and post-Start periods of the cell cycle. While the independent models capture the growth behavior of cells during these periods, it remains to be shown that they can be combined into a full cell cycle model consistent with other experimental observations.

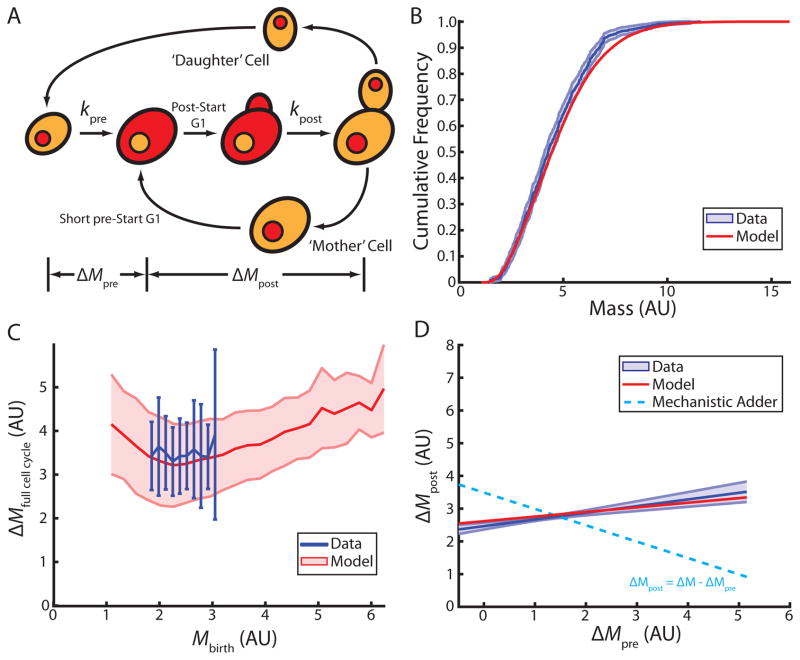
A complete cell cycle model must also account for the asymmetric division of budding yeast (Figure 4A). In addition to the first cell cycle of newborn daughter cells, it must include consecutive cell cycles, i.e., the cell cycles of mother cells. Mother cell growth as a function of cell mass is similar to that found in daughter cells, with the noticeable exception of the short period of G1 in mother cells, where growth is slower (Figure S4A,B). We therefore estimated growth rate separately for G1 mother cells. It was previously shown that mother cells have a very short pre-Start G1 due to the asymmetric localization of specific transcription factors [34,35]. We therefore decided to neglect the specific regulation of pre-Start G1 in mother cells and model the mother cell cycle in analogy to the post-Start period in daughter cell cycles (Figure S4C,D). Combining these measurements for mothers with the models for pre- and post-Start daughter cells enabled us to simulate steady state growth and division of a population of cells. This model accurately reproduces the empirically determined steady state population mass distribution (Figure 4B).

Figure 4. Full cell cycle model based on independent regulation of pre- and post-Start periods recapitulates single cell data.

(A) Schematic illustrating full cell cycle model. Pre- and post-Start periods are defined by Whi5-mCherry nuclear export (red), bud emergence, and cell separation. (B) Cumulative distribution of cell masses in a steady state population (blue, 95% confidence bounds) (n=643). Model prediction shown in red. (C) Full cell cycle growth as a function of birth mass (blue, +/− standard deviation) (n=165). Model prediction shown in red (+/− standard deviation). (D) Full cell cycle model recapitulates the weak correlation between growth during the pre- and post-Start periods (red, R=0.25, slope=0.28, p<1e–10). Linear fit to the data shown in blue (+/− standard deviation of the fit from 10000 bootstraps of the data, R=0.32, slope=0.41, p=3.2e–5). Dashed line shows the prediction of an ideal mechanistic adder. See also Figure S4.

Having established a minimal model for independent progression through pre- and post-Start periods, we asked whether this model explains the adder phenomenon (Figure 1C). Indeed, we find this model accurately predicts the observation that, within a physiological range of cell masses, daughter cells grow a constant amount over a complete cell cycle, independent of their mass at birth (Figure 4C). Moreover, while this model recapitulates the phenomenological adder, the amounts of growth in pre- and post-Start periods are not negatively correlated. Consistent with our experimental observations, the amount of growth post-Start is positively correlated with growth pre-Start (Figure 4D,1D). This slight positive correlation can be explained by indirect coupling through cell size. Cells that grow more during the pre-Start period tend to be larger at Start resulting in more growth post-Start (Figure 3D). Furthermore, this model predicts size at bud emergence as a function of size at birth (Figure S4E). This result demonstrates that the observed adder phenomenon from birth to division can be explained without the existence of a molecular mechanism measuring total growth from cell birth to division. Instead, the adder phenomenon in budding yeast is an emergent property of independent mechanisms controlling passage through key events of the cell cycle.

Changes in the rate of passing Start are sufficient to eliminate the adder phenomenon

Our analysis revealed that the adder phenomenon is an emergent property of independent pre- and post-Start periods. This implies that the adder phenomenon is sensitive to changes in the control of either of those two periods. For example, we predict that the specific size-dependence of the rate of passing Start, k_pre, is critical for the adder phenomenon.

To test our hypothesis that the specific size-dependence of Start is required for the adder phenomenon, we asked what would happen if the relationship between cell mass and the rate of progression through Start was altered. First, we examined how growth during pre-Start G1 depends on the mass-dependence of k_pre. We therefore consider an arbitrary time-dependent rate k_pre (t) of passage through Start. The probability density function of a cell born at time t₀ = 0 to pass Start at time t is then equal to the current time-dependent rate for the cell to pass Start, k_pre(t), multiplied by the probability that the cell has not yet passed Start, e^−K_pre(t), where $K_{\mathit{pre}}(t)={\int }_0^t{k}_{\mathit{pre}}(T)dT$. Assuming exponential growth, so that $M(t)=M_0{e}^{\frac{t}{\tau }}$, and that kpre(t) is dependent only on the mass of the cell at time t, we find the probability distribution for a cell born with mass M_birth to pass Start at cell mass M to be

$$p(M)=\frac{p(t)}{\frac{\partial M}{\partial t}}=\frac{\tau }{M}{k}_{\mathit{pre}}(\tau ln\frac{M}{M_{\mathit{birth}}})e^{-K_{\mathit{pre}}(\tau ln\frac{M}{M_{\mathit{birth}}})}.$$

The expectation value of the cell mass at Start given birth mass is then

$$\langle M_{\mathit{Start}}\rangle ={\int }_{M_{\mathit{birth}}}^{\infty }\tau k_{\mathit{pre}}(\mathrm{M})e^{-K_{\mathit{pre}}(\tau ln\frac{M}{M_{\mathit{birth}}})}dM.$$

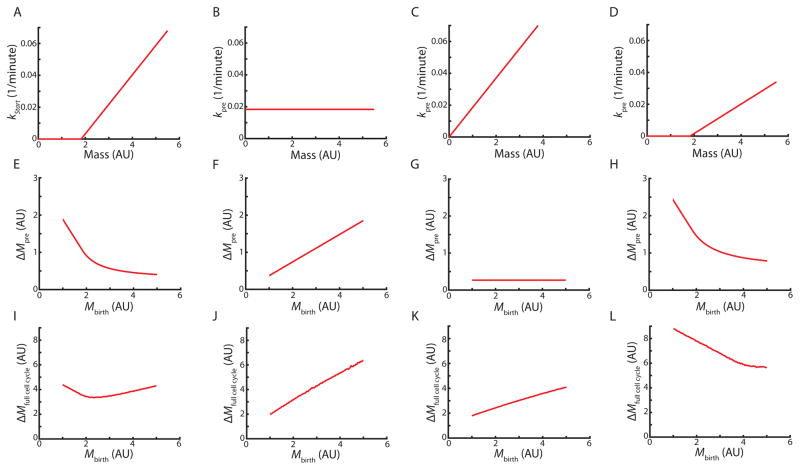
This framework allows us to calculate the average mass at Start as a function of birth mass for different mass-dependencies of the rate of passing Start, k_pre. First, we examined the case described above (Figure 2C) where k_pre was determined from a fit to the experimental data so that k_pre = max (0,a(M − M₀)) (Figure 5A). The relationship between birth mass and mass at Start for this rate model is consistent with the experimental data (Figure 5E,S5).

Figure 5. Analytical model shows that the adder phenomenology depends on pre-Start G1 control.

Relationships between cell mass and the rate of progression through Start (A–D) determine the growth during the pre-Start period (E–H) and the full cell cycle (I–L). For each scenario, the same experimentally determined growth and division rates (Figure 3) are used to model the post-Start period of the cell cycle. See also Figure S5.

We combined the models used to independently simulate growth in pre- and post-Start periods (Figure 2 and 3) to calculate the average mass added during the full cell cycle as a function of birth mass. As expected from the simulations shown in Figure 4C, this recapitulates the adder phenomenon (Figure 5I).

We next asked if changing the mass-dependent rate at which cells pass Start without changing the post-Start model disrupts the adder phenomenon. We first examined what would happen if the rate of progression through Start was constant, i.e., was independent of cell mass and time in G1 so that k_pre = a (Figure 5B,F,J). In this case, the average growth in pre-Start G1 is proportional to birth mass. As a consequence, growth during the full cell cycle increases with birth mass and is therefore not consistent with an adder. To test if the adder behavior can be disrupted in different ways, we examined the effect of shifting the linear dependence of k_pre on cell mass to the origin while maintaining the slope, i.e., k_pre = aM. This results in an adder for pre-Start growth, but not for the entire cell cycle (Figure 5C,G,K). We next decreased the slope of the mass-dependence while maintaining the threshold mass, M₀, so that $k_{\mathit{pre}}=\mathit{max}(0,\frac{a}{2}(M-M_0))$ (Figure 5D,H,L). This results in total cell cycle growth decreasing as a function of birth mass. Again, this modification breaks the adder. Thus, we conclude that if progression through the post-Start period is not changed, the adder requires a specific mass-dependence of k_pre, such that a wide variety of modifications to this mass-dependence disrupt the adder.

G1 size control mutants break the adder phenomenon

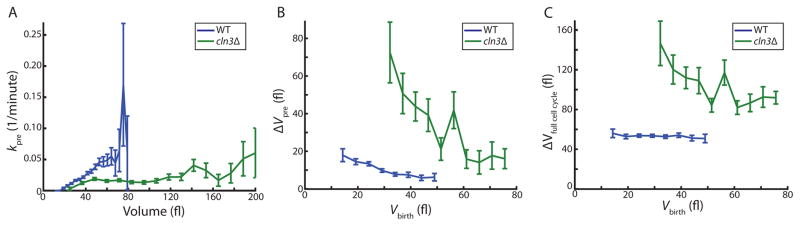
Our analysis predicts that genetically manipulating Start should disrupt the adder. To test this, we measured cell growth in cells lacking the G1 cyclin CLN3 (cln3Δ), whose deletion results in a prolonged G1 duration and an increase in cell size [36,37]. Consistent with the previously observed large cell size phenotype, we find that the rate of progression through Start as a function of cell volume, k_pre(V), is significantly changed in cln3Δ cells compared to wildtype cells, but still shows cell-size-dependence (Figure 6A). This results in a clear change in the dependence of pre-Start growth on birth volume (Figure 6B). This shift in the amount of pre-Start growth is not compensated post-Start, as would be expected if there was a molecular adder mechanism controlling growth over the entire cell cycle (Figure S6A,B). As a consequence, the adder phenomenon is not observed in cln3Δ cells. Rather, growth over the full cell cycle declines with increasing birth volume. To test if the disruption of the adder in cln3Δ cells is a special case, we also performed a similar analysis on cells containing an additional copy of the G1 cell cycle inhibitor WHI5 (2xWHI5). 2xWHI5 cells also do not exhibit an adder (Figure S6D–F). Thus, mutations affecting G1 control at Start are likely to break the adder.

Figure 6. Deletion of the G1 cyclin CLN3 breaks the adder.

(A) The rate at which cells progress through Start as a function of cell volume for wild type (blue, n=394) and cln3Δ (green, n=197) cells. (B) Growth during the pre-Start period as a function of birth volume. (C) Growth during the full cell cycle as a function of birth volume. All bars represent binned means and standard errors. See also Figure S6.

Discussion

Budding yeast size control has long been thought to take place at the G1/S transition in daughter cells because this period has the strongest inverse correlation between the amount of time spent growing and initial cell size [25]. The correlation between S/G2/M duration and cell size is much weaker [38]. Thus, mechanistic work on size control has been focused on the G1 phase of daughter cells. However, it has recently been shown that daughter cells grow a constant amount over the course of their cell cycle, independent of birth size, i.e., exhibited the adder phenomenon [16]. This raised the question as to whether there exists an unidentified underlying molecular mechanism ensuring the adder.

Here, we have shown that the observed adder phenomenon emerges from independently regulated pre- and post-Start cell cycle periods and does not originate from an underlying molecular mechanism that directly measures accumulated growth through the entire cell cycle or between budding events. A cell that happens to pass Start early, growing less during the pre-Start period, does not compensate by increasing its growth during the remainder of the cell cycle as would be expected from a mechanistic adder. Furthermore, a full cell cycle model based on independent models for the pre- and post-Start periods of the cell cycle recapitulates the adder and other experimental observations. Finally, mutations specific to the G1 size control mechanism break the adder phenomenon.

The modular nature of cell cycle regulation implies that it is useful to study size-dependence of cell cycle progression in each period separately. So far, the budding yeast cell size field has focused on the more strongly size-dependent G1/S transition and a basic understanding of the molecular mechanism is emerging. Here, our work is consistent with the idea that cell size alone determines the rate of passage through Start. Regression analysis revealed that the stochastic passage through Start is best predicted by cell size, and multivariate models including time spent in G1 have little additional predictive value. This rules out all timer-based models for passage through Start. Our regression model for the post-Start period revealed that bud size best predicts the timing of cell separation. While the size-dependence of post-Start growth has been previously reported, and some molecular progress has been made, the underlying regulatory mechanisms remain to be identified [26,27,39–42].

The finding that in budding yeast the adder does not rely on a molecular mechanism that measures growth through the entire cell cycle puts the fact that the adder phenomenon is observed across diverse phyla in a new perspective. Simply observing an adder does not imply that a molecular mechanism is dedicated to measuring the amount of growth throughout the cell cycle. Instead, independent mechanisms controlling size-dependent growth in distinct cell cycle periods can result in a phenomenological adder. For example, while mechanistic adder models have been proposed to explain the adder observed in E. coli [7,15–21], it remains possible that the adder results from distinct mechanisms controlling the relationship between cell growth, the onset of DNA replication, and cell division [21]. If future studies reveal that the adder generally emerges from independently regulated cell cycle periods rather than from some easy-to-implement class of molecular mechanisms, we will be faced with the question of why evolution converged upon this size control strategy in such distantly related species.

STAR Methods

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Jan Skotheim (skotheim@stanford.edu).

Experimental Model and Subject Details

Budding yeast strains used in this study were congenic to w303. Full genotypes of all strains used in this study are listed in Key Resources Table. Strains were constructed from laboratory stocks using standard methods. For microscopy experiments, cells were cultured at low density overnight to insure exponential growth in synthetic complete (SC) media containing 2% glycerol and 1% ethanol or 2% glucose as the carbon source before transfer to the microscope chamber.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Bacterial and Virus Strains
Biological Samples
Chemicals, Peptides, and Recombinant Proteins
Critical Commercial Assays
Deposited Data
Experimental Models: Cell Lines
Experimental Models: Organisms/Strains
Budding yeast: DCB77: MATα ura3::ACT1pr-mCitr-Cyc1term-URA3 whi5::WHI5-mCherry-KanMX ADE2	This Study	N/A
Budding yeast: JE103: MATa ADE2	Skotheim Lab	N/A
Budding yeast: KSY108-1: MATα ADE2 whi5::WHI5-mCitrine-HIS3	Skotheim Lab [28]	N/A
Budding yeast: KSY110-1: MATα ADE2 whi5::WHI5-mCitrine-HIS3 ura3::WHI5-mCitrine-URA3	Skotheim Lab [28]	N/A
Budding yeast: KSY146-1: MATα ADE2 whi5::WHI5-mCitrine-HIS3 cln3::CglaTRP1	This Study	N/A
Oligonucleotides
Recombinant DNA
Software and Algorithms
Full Cell Cycle Model	This Study	https://github.com/devoncb/full_cell_cycle_model
Custom Segmentation Scripts	[43]	N/A
Other

Method Details

Microscopy

Imaging and pedigree tracking was largely performed as in [28]. Specifically, cells were grown in Y04C plates controlled by a Cellasic microfluidic device in SC media containing 2% glycerol and 1% ethanol or 2% glucose flowing under 2 psi pressure. Images were taken every 3 minutes using an Observer Z1 microscope equipped with an automated stage and a plan-apo 63x/1.4NA oil immersion objective. Whi5-mCitrine and mCitrine driven by the ACT1 promoter were imaged using a 400ms exposure under illumination from a Colibri 505 LED module at 25% power. Whi5-mCherry was imaged by exposure for 500ms using a Colibri 540–580 LED module at 50% power. Cells grown in the microscope were checked for growth rate and experiments where the average cell growth rate deviated from the expected growth rate for those conditions were excluded. For all strains, at least two replicate experiments were performed.

Cell and nuclear segmentation were performed as described in [43]. Briefly, cells were segmented based on the phase image. We began by manually selecting cells in the final image and working backwards. A cell at each timepoint was tracked by identifying boundaries by generating a probability of cell location based on a series of watershed filters. Cell positions were further refined by penalizing non-cell space from the previous timepoint. Geometric volume was estimated by performing a rotation of the segmented area around the longest axis. Total fluorescence was calculated as the sum of pixel intensities within each cell region at each timepoint. We further improved background subtraction by accounting for variation in background fluorescence in each frame of the movie. In each frame, cell and non-cell area was defined. We then applied a 4-pixel average filter and the background was taken to be the median filtered pixel value of the non-cell area. As previously, differences in background fluorescence due to cell volume were accounted for [28]. Visual inspection of phase contrast images was used to determine the timing of cell separation, i.e., the time of cell birth, division, and bud emergence. Nuclei were segmented by fitting a 2-dimensional Gaussian function to the Whi5 fluorescence channel. Whi5 nuclear export was identified using the single cell traces of nuclear Whi5 fluorescence.

Cell cycle model

The model simulates cell growth and progression through Start, bud emergence and cell division. Each computational step models one minute of cell growth and cell-cycle transition decisions. We use measured growth and transition rates as described in Figures 2, 3, and S4 to perform these computations. We separately modeled 1^st generation cells (‘daughters’) and subsequent generation cells (‘mothers’), which have different growth rates and cell cycle transition rates.

Daughter Cell Model

Daughter cells proceed through 3 different periods of the cell cycle: pre-Start G1, post-Start G1, and S/G2/M. In each of these periods, a simulated cell grows according to a single, cell cycle-independent growth rate, as obtained from the linear fit to the data shown in Figure 2D. We then modeled growth according to the equation Mt=i+1 = M_t=ie^αΔt, where Δt = 1 minute is the time step in the simulation. During pre-Start G1, daughter cells have a probability of passing Start during the subsequent minute, p_pre = 1 − e^−k_pret, which was calculated from the linear fit of the instantaneous rate of passing Start k_pre = max(0, a(M − M₀)) (shown in Figure 2C). Using the Matlab function randsample() we then simulated the stochastic cell decisions at each time point.

The post-Start period of the daughter cell cycle is modeled in two periods corresponding to the period before and the period after bud emergence, termed ‘post-Start G1’ and ‘S/G2/M’ respectively. We model post-Start G1 as a cell mass-dependent deterministic timer. Post-Start duration was determined through a linear fit of the measured duration from Whi5-mCherry nuclear exit to bud emergence as a function of cell mass at Start (Figure S3A). This fit is used to compute the time a simulated cell waits before budding and entering S/G2/M phases (rounded to the nearest minute).

During S/G2/M, most of the cell growth takes place in the bud. However, a small fraction of growth takes place in the cell body. Specifically, cell bodies grow an amount which is approximately independent of their initial mass and the duration of S/G2/M (Figure S3B,C). The rate of cell body growth for each cell was calculated by dividing the average cell body growth by the average S/G2/M duration conditioned on its size at Start. During each S/G2/M time step of the simulation, we add the corresponding amount of cell body growth to the cell body and the remainder of growth as modeled using the overall cellular growth rate to the bud. Exit from S/G2/M is modeled as a stochastic transition whose probability is a function of the mass at Start and current bud mass (Figure 3C). We used a linear fit to estimate the dependence of the rate of cell division on both Start mass and bud mass according to the equation k_post = max(0, aM_bud + bM_Start + c)) and compute the probability of dividing according to p_post = 1 − e^−k_postt. Sampling is performed as described above using the Matlab function randsample().

Mother Cell Model

To model a population of cycling cells, we additionally had to generate a model for mother cells. Mothers have a very short pre-Start period of their cell cycle [23], which we neglected in the simulation. Instead, we model mother cell cycles much as we modeled the daughter cell post-Start period. Mother cells have a single G1 period with a duration dependent on mass at the beginning of G1, followed by S/G2/M. As for daughter cells, mother division rates are dependent on the mass of the bud and the mother mass at beginning of G1. These parameters were obtained from fits to data for mother cells (Figure S4A–D).

Another key deviation from the daughter model is that, although mother S/G2/M growth rate is similar to that of daughters, mother G1 growth rate is substantially different from the G1 growth rate of daughters (Figure S4B). For the full cell cycle simulation, we therefore pool data for daughter cells and S/G2/M mother cells to obtain a global exponential growth rate. For mother growth during G1 we assumed a linear dependence of growth rate on cell size, $\frac{dM}{dt}=aM+b$. This means that mass as a function of time is given by $M(t)=\frac{(a{M}_{\mathit{initial}}+b)e^{at}-b}{a}$. We fit the values of a and b to measured mother growth data (Figure S4B) and applied the above equation to simulate growth in the model.

Simulating Growth and Division

To generate the model predictions in Figures 2 and 3, we used the model for daughter cells described above. We simulated 10⁶ cells, uniformly spanning the range of empirically measured initial masses for pre- and post-Start, to calculate the distribution of masses at the end of these periods.

To generate the model predictions shown in Figure 4, we combined the models for daughter and mother cell growth described above. At the end of each simulated cell cycle, a new mother and a new daughter cell are generated, resulting in an exponential increase of the population size. To deal with computational limitations, we set a maximum population size. If the population exceeds this threshold at the end of any time iteration, cells are randomly removed from the population.

We ensured that steady state is reached in the full cell cycle simulation. To generate a population of cells used to seed the simulation, we begin with a small population of 100 cells each of the mean mass obtained from microscopy measurements. We run the seeding simulation for 5000 one-minute time steps (approximately 25 consecutive daughter cell divisions in one pedigree) with a population maximum of 200, until the mean cell mass and mean cell cycle distribution do not noticeably change over time. 100 of these cells from the seeding population are then randomly selected and used to seed the larger subsequent simulations. 5 independent simulations with large population size (10000 cells) were run for 2000 simulated minutes. Before finishing the simulation, we checked that the mean cell mass and cell cycle distributions were at steady state. The resulting data from the 5 simulations was then pooled for plotting and analysis.

Simulated cells were analyzed in a similar way as the cells measured in microscopy experiments. For each simulated cell, we identify the time of birth, Start, bud emergence, and division as well as the corresponding cell and bud mass at those times. These values are used to calculate the duration of each period of the cell cycle and corresponding amount of cell growth.

Quantification and Statistical Analysis

Measurement of cell size

Cell mass was measured using a fluorescent reporter expressed from the ACT1 promoter (1kb) [23]. We used the fluorescent protein mCitrine because budding yeast autofluorescence is low in that range of the spectrum. As reported previously, the total fluorescence intensity largely correlates with geometric cell volume [23]. However, we noticed distinct deviation at large cell sizes, where growth rate as measured from geometric volume ceases to be exponential (Figure S2). For the analysis in Figure 6, we used geometric estimates of cell size. Otherwise, the fluorescent reporter was used throughout.

Growth rate calculation for pre-Start logistic regressions

While the instantaneous growth rate is not accessible from our data due to experimental limitations, we can calculate the average relative growth rate during pre-Start G1, $\frac{1}{M}\frac{dM}{dt}$, assuming exponential growth. Multiplication with the mass at a given time point allows us to estimate the absolute growth rate, $\frac{dM}{dt}$.

Estimating key cell cycle progression predictors by logistic regression

We used the Matlab function glmfit() to perform multivariate logistic regressions and calculate deviance, which is a generalized sum of squared residuals. The differences in deviance can be used to find p-values comparing two models where the parameters of one are a subset of the parameters of the other.

Calculation of the rate of passage through Start and cell division

Treating each time point and each cell as an independent event allows us to calculate the probability of cells passing Start and the probability of dividing within 3 minutes, which is the frame rate of the movie. The probability, p, of a stochastic event occurring at time t, is related to the instantaneous rate of that event, k, by the equation p = 1 − e^−kt. This allows us to calculate the rate at which cells pass Start (Figure 2C) and the rate of cell division (Figure 3C).

Statistical Evaluation

The definition of error bars is provided in the figure legends. Sample size (n) indicates the number of cells measured. P values for fits and correlation coefficients were computed using the built-in Matlab fitlm() and corrcoef() functions respectively.

Data and Software Availability

The microscopy data and segmentation software described above may be acquired by contacting Jan Skotheim (skotheim@stanford.edu). The full cell cycle model is available at https://github.com/devoncb/full_cell_cycle_model.