A Likelihood-Free Approach for Characterizing Heterogeneous Diseases in Large-Scale Studies

Abstract

We propose a non-parametric approach for characterizing heterogeneous diseases in large-scale studies. We target diseases where multiple types of pathology present simultaneously in each subject and a more severe disease manifests as a higher level of tissue destruction. For each subject, we model the collection of local image descriptors as samples generated by an unknown subject-specific probability density. Instead of approximating the probability density via a parametric family, we propose to side step the parametric inference by directly estimating the divergence between subject densities. Our method maps the collection of local image descriptors to a signature vector that is used to predict a clinical measurement. We are able to interpret the prediction of the clinical variable in the population and individual levels by carefully studying the divergences. We illustrate an application this method on simulated data as well as on a large-scale lung CT study of Chronic Obstructive Pulmonary Disease (COPD). Our approach outperforms classical methods on both simulated and COPD data and demonstrates the state-of-the-art prediction on an important physiologic measure of airflow (the forced respiratory volume in one second, FEV1).

1 Introduction

We propose a method that exploits large-scale sample sizes to study heterogeneous diseases. More specifically, we target diseases where each patient can be thought as a superposition of different processes, or subtypes, and where the pathology is not always located in the same place. Our goal is to provide a scalable algorithm that quickly evaluates the statistical power of various feature extraction methods for prediction of a clinical measurement. Scalability and interpretability are at the core of our algorithm. Our motivation comes from a study of Chronic Obstructive Pulmonary Disease (COPD), but the resulting model is applicable to a wide range of heterogeneous disorders.

Emphysema, or destruction of air sacs, is an important phenotype in COPD. Emphysema itself has multiple subtypes with distinct pathological and radiological appearances [17]. Understanding the differences between the subtypes is important since each subtype is associated with different risk factors [19]. Various local image descriptors (e.g., intensity and texture features) have been proposed to describe disease subtypes using lung CT images [12,21]. To model the local image descriptors, one can view a patient in a dataset as a mixture of multiple processes and can then statistically estimate the image representation of the patient’s subtypes from image data [2,3]. However, each image descriptor has its own statistical properties, and to model a descriptor statistically requires careful selection of a likelihood function and the noise distribution. For example, while histogram-based methods often result in non-negative features (e.g., [18]), features extracted using a wavelet approach (e.g., [5]) usually have no sign restriction. While the multivariate Gaussian distribution might be appropriate for the latter, it may not be a good choice for the former.

The goal of our method is to quickly screen different feature extraction methods without an explicit likelihood assumption. We use the predictive power of a clinical variable as a quantitative evaluation measure. The premise of a large sample size is that, as the dataset grows, the chance of observing more phenotypically similar patients increases. We leverage this idea and non-parametrically estimate divergences between the densities (which correspond to individual patients) from image data instead of directly parametrizing the probability densities. Our estimator is based on a nearest neighbor graph that can be constructed efficiently [13]. The graph enables us to map the predictions of the clinical measurements back to the anatomical domain. The mapping delineates a few anatomical regions which can be used for clinical interpretation. The proposed approach is highly parallelizable which makes it appropriate for large-scale studies.

We evaluate the performance of our method on a simulated dataset as well as a large-scale COPD lung CT dataset. In both experiments, our method outperforms the classical parametric bag-of-words model (BOW). We also study two different divergences. Our experiments demonstrate the importance of the choice of the divergence on the performance the method.

2 Method

We assume that the image domain of each subject in a dataset is divided into relatively homogeneous spatially contiguous regions. The number of regions may vary amongst subjects. To simplify the explanation of our method, we assume the spatially contiguous regions are patches of image regions; the method is applicable for superpixels with no modification.

Each subject is represented by a collection of features extracted from the regions. We let ψ(υ) ∈ ℝ^d denote the d–dimensional image signature of the patch υ. We assume that the image descriptors are randomly generated from K prototypical tissue types shared across subjects in the population. Let p^I (·; θ_k) denote the distribution for the image signature of the tissue type k which is parametrized by θ_k. While θ₁, ⋯, θ_K are shared across the population, the mixture proportion may vary amongst subjects. Hence, the distribution of image signatures for subject i (i.e., p_i) is:

$$\psi (\upsilon )~p_i,p_i(·)=\sum _{k=1}^K{\pi }_k^i{p}^I(·;{\theta }_k),\sum _{k=1}^K{\pi }_k^i=1$$ (1)

where ${\pi }^i=[{\pi }_1^i,\cdots ,{\pi }_K^i]$ is the mixture proportion for subject i. In the literature, this type of model is referred to as an admixture [1] or a topic model [4]. It generalizes the mixture model by allowing subject data to have subject-specific membership to population-level image signatures of the disease subtypes. The πⁱ characterizes each subject in the spectrum of the disease. It is common to assume a specific form of p^I (·). Such assumptions are mostly made to ensure inference of the parameters is computationally convenient. For example [2,3] assumed p^I to be a multivariate Gaussian density with a conjugate prior. However, a computationally convenient assumption is not necessarily the best choice for the likelihood. By contrast, in this paper we propose to side step inference of θ_k, πⁱ by avoiding an explicit assumption on p^I. Instead, we estimate the divergences between p_i’s and embed them in a lower dimensional manifold, which results in an implicit characterization of the subjects. We trade the interpretability of a parametric model with a flexibility of a non-parametric model. We will show in Sect. 2.3 that how some of the interpretability can be retrieved via a careful inspection of the divergence computation. Finally, it is worth mentioning that our method does not replace explicit probabilistic modeling (e.g., topic modeling) but it provides an objective approach to screen different local image descriptors for probabilistic methods such as [2,3].

In the following sections, we first introduce the notion of a k-nearest neighbor graph (Sect. 2.1), which is used in the estimator (Sect. 2.2) and enables us to interpret the predictions (Sect. 2.3).

2.1 k–Nearest Neighbor Graph

First, we formally define the directed k-nearest neighbor (k–NN) graph which will be used in the following sections. Let 𝒢_k = (𝒱, ψ, 𝒟) denote the directed k–NN graph. Let S_i represent the collection of patches from subject i. We define the collection of nodes in the graph as 𝒱 = ∪_iS_i. For a patch υ in the dataset (i.e., υ ∈ 𝒱), ψ(υ) denotes the corresponding d-dimensional local image descriptor (i.e., ψ : 𝒱 → ℝ^d) and 𝒟(·, ·) represents a Euclidean distance in the d-dimensional space. For a given collection S_i, we define a function ι_k,Si : 𝒱 → S_i that returns the index of the k’th nearest neighbor node of υ in the collection S_i based on the distance 𝒟 in the feature space defined by ψ. We call ι_k,Si an index function. Hence, for υ₁ ∈ S_i and υ₂ ∈ S_j, there is a edge υ₂ → υ₁ if ι_k,Si (υ₂) = υ₁. We assume that the graph 𝒢 does not have self-loops, i.e., if υ ∈ S_i, ι_k,Si (υ) returns the k-nearest neighbor not counting υ itself.

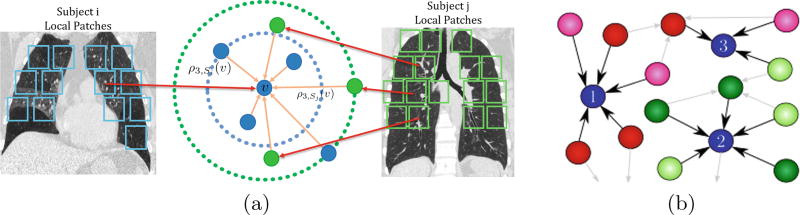
For brevity of the notation, we introduce a few short-hand notations: ρ_k,Si (υ) denotes 𝒟(ψ(ι_k,Si (υ)), ψ(υ)) which is the k–NN distance of υ from the closest local descriptor in S_i (see Fig. 1a). For each node in the graph, we define the notion of the popularity of a node with respect to another subject (see Fig. 1b). The popularity of node υ ∈ S_i with respect to subject j is defined as the degree of incoming edges from the collection S_j normalized by the total number of patches in the subject j, namely

$$\forall \upsilon \in S_i,{[{\phi }_{S_i}(S_j)]}_{\upsilon }=\frac{1}{|S_j|}\sum _{t\in S_j|t\to \upsilon }1$$ (2)

We view φ_Si (S_j) ∈ ℝ^|S_i| as a popularity vector where the entry υ is defined by Eq. 2. It is straightforward to see that entries of φ_Si sums to one. In the following sections, we use the k–NN graph to define similarity between subjects and to interpret the results.

Fig. 1.

A schematic showing a few nodes of the k–NN graph. (a) The filled blue and green circles represent image features from subjects i and j respectively. The blue and green dashed lines indicate ρ_3,Si (υ) and ρ_3,Sj (υ). (b) Part of the k–NN graph for subject blue is highlighted. The colors indicate different subjects. While the node 2 is more popular amongst the green subjects, node 1 is more popular amongst the red subjects. (Color figure online)

2.2 Non-parametric Estimation of the Similarity

Subject Dissimilarity

We model subject i as a bag of local image descriptors generated by an unknown density, i.e., ∀υ ∈ 𝒱, ψ(υ) ~ p_i.We use two well-known divergences to compute the dissimilarity between densities: the Kullback-Leibler (KL) divergence and the Hellinger (HE) distance:

$$\text{KL}:\text{ KL}(p_i\Vert p_j)={\int }_{{\mathrm{ℝ}}^d}\text{log}\frac{p_i(x)}{p_j(x)}{p}_i(x)\mathit{\text{dx}},$$

$$\text{HE}:\text{ HE}(p_i\Vert p_j)=1-{\int }_{{ℝ}^d}{p}_i^{\frac{1}{2}}(x)p_j^{\frac{1}{2}}(x)\mathit{\text{dx}}.$$ (3)

While HE is a real distance, KL is not symmetric and does not satisfy the triangle inequality. We will address this issue later in this section. We would like to estimate the divergences without assuming a parametric form for the probability densities.

With mild assumptions on the probability density, p_i can be represented as p_i(x) = f_i(x)/Z_fi, where f_i(x) is an unknown positive function and and Z_fi is the corresponding normalizer (i.e., Z_fi = ∫ f_i(x)dx; if f_i(x) is a probability density, Z_fi = 1). To estimate f(x), we consider a polynomial expansion of log f(x) around x, namely log f(u)|_x ≈ a₀ + (u − x)^T a₁ + (u − x)^T a₂(u − x) where a₀, a₁, a₂ are scalar, vector and matrix parameters, respectively, and vary depending on x. We use the state-of-the-art local log-likelihood method [11] to estimate the local parameters. The local log-likelihood of the function f_i at point x is:

$${ℒ}_x(f_i)=\sum _{\upsilon \in S_i}w\left(\frac{x-\psi (\upsilon )}{h}\right)\text{ log }{f}_i(\psi (\upsilon ))-|S_i|\int w\left(\frac{y-x}{h}\right)f_i(y)\mathit{\text{dy}},$$ (4)

where |S_i| is the cardinality of collection S_i and w(x) is a window function with bandwidth h. Since the approximation of log f_i(x) is locally valid, it is reasonable to keep h small; if h goes to infinity, Eq. 4 amounts to the ordinary likelihood estimation and the last term converges to |S_i|Z_f.

For certain choices of the window function, f_i has a closed-form solution [11]. For computational reasons, we use the step function: w(x) = 𝕀(‖x‖ ≤ 1) (see the Appendix A for other choices and the corresponding computational costs). Choosing a data-independent bandwidth is one of the impediments of the non-parametric density estimation. However, we are not interested in density estimation, but rather in estimating a functional of a pair of densities, namely the divergences. In this case, we consider a choice of bandwidth that is local and adaptive, i.e., h is a function of x [7]. We set the h to the k–NN distance from x; h ≡ ρ_k,Si (x) similar to [7,15]. Optimizing Eq. 4, we get the following form for f [11],

$${\hat{f}}_i(x)=\frac{1}{|S_i|h\int w(x)\mathit{\text{dx}}}\sum _{\upsilon \in S_i}w(\psi (\upsilon ))=\frac{k}{|S_i|C_{d{\rho }_{k,S_i}^d}(x)},$$ (5)

where $C_d\equiv \frac{{\pi }^{d/2}}{\mathrm{\Gamma }(d/2+1)},C_d{\rho }_{k,S_i}^d(x)$ are the volumes of d-dimensional balls with radius of one and ρ_k,Si (x) respectively, and Γ(·) is the Gamma function. An illustration of this concept can be seen in Fig. 1a. Using the re-substitution, we estimate the HE and KL divergences as (See the Appendix A for detail):

$$\text{KL}:\widehat{\text{KL}(p_i\Vert p_j)}=\frac{d}{|S_i|}\sum _{\upsilon \in S_i}\text{log}\frac{{\rho }_{k,S_i}(\upsilon )}{{\rho }_{k,S_j}(\upsilon )}+\text{log}\frac{|S_j|}{|S_i|-1},$$

$$\text{HE}:\widehat{\text{HE}(p_i,p_j)}=1-\frac{{(|S_i|-1)}^{\frac{1}{2}}\mathrm{\Gamma }{(k)}^2}{|S_i|{|S_j|}^{\frac{1}{2}}\mathrm{\Gamma }(k+\frac{1}{2})\mathrm{\Gamma }(k-\frac{1}{2})}\sum _{\upsilon \in S_i}{\left(\frac{{\rho }_{k,S_i}(\upsilon )}{{\rho }_{k,S_j}(\upsilon )}\right)}^d.$$ (6)

The estimators are unbiased and consistent. In other words, as the number of patches (S_i, S_j) increases, the estimations converge to the true value (See the Appendix A for details).

Subject Similarity

Our aim is to derive a Positive Semi-Definite (PSD) similarity kernel between subjects. In other words, if the entries of a matrix K represent the pairwise similarities between subjects, K should be a PSD matrix. One way of defining a kernel is by exponentiating the negative of the distance between two elements. However, the KL divergence is neither symmetric nor does it satisfy the triangle inequality. Hence, defining a kernel based on KL may not result in a PSD kernel. To ensure positive definiteness, we exponentiate the symmetric KL and project the resulting matrix onto a PSD cone. Namely, we define L̃_ij = exp (−KL_sym(p_i, p_j)/σ²), where the σ is a parameter of the kernel and ${\text{KL}}_{\text{sym}}(p_i,p_j)=\widehat{\text{KL}}(p_i\Vert p_j)+\widehat{\text{KL}}(p_j\Vert p_i)$. We define the similarity between subjects i and j (k(S_i, S_j)) as the ij-th element of the similarity matrix,

$$k(S_i,S_j)={[K_{\sigma }]}_{\mathit{\text{ij}}},K_{\sigma }={\text{Proj}}_{\text{PSD}}({\stackrel{\sim }{L}}_{\sigma }),K_{\sigma }={\mathit{\text{BB}}}^T,$$ (7)

where B is the Cholesky decomposition of the similarity matrix. The columns of B can be viewed as new representation for the subjects in the N-dimensional space (N is the number of subjects). Proj_PSD (·) denotes the projection onto the PSD cone. For the projection, we set all negative eigenvalues to zero. We adopt the so-called median trick [20] in the kernel machine and set σ to the median of the divergence.

We explained how to compute the similarity kernel given collections of local image descriptors. In the next section, we explain how to interpret the similarities between subjects on the population and individual levels.

2.3 Can We Trust the Prediction?

To trust the prediction, we would like to be able to interpret the predicted values. We perform interpretation on the population and individual levels.

Population-Level

To interpret the similarities on the population level, we observe that parametric mixtures of densities reside on a low-dimensional statistical manifold [9]. Therefore, we use the new representation of the subject-specific distribution (i.e., Eq. 7) and apply the Locally Linear Embedding (LLE) algorithm [24] to empirically chart individuals on a lower dimensional space. We use the coordinates of subjects in the embedding space to predict the clinical measurement.

Individual-Level

To interpret the results on the individual level, we map the predicted value to the image domain to present it to a clinician. Similar ideas have been explored in the machine learning context [23]. The prediction model estimates the clinical measurement from the image data through a complicated chain: computation of the divergences and the kernel, projection onto the PSD, and finally regression or classification. In clinical settings, it is important to identify regions of anatomy that are the most relevant to a model’s predictions. We use the notation g_cplx(S_i) to denote the chain of operations resulting in the prediction. For the individual-level interpretation, our aim is to identify a few patches in the lung image of each subject that are the most relevant to the prediction (i.e., g_cplx(S_i)). We construct N sparse linear regressions that are good local approximations of g_cplx around each subject. Let us consider subject i; we use the popularity vector of subject i with respect to other subjects (i.e., φ_Si (·) defined in Eq. 2) as the input features to the local sparse linear regression. To account for the notion of locality, we use the similarity kernel (Eq. 7) to weight the error term in the regression. Finally, we add a ℓ₁-norm regularization term to the cost function to encourage a parsimonious number of patches. More specifically, for subject i, we solve the following optimization problem:

$${\text{min}}_{\omega }\ell (S_i;\omega )≔{\text{min}}_{\omega }{\sum }_{n=1}^{N}k(S_i,S_n){(g_{\text{cplx}}(S_n)-\underset{g_{\text{loc}}(S_i,S_n;\omega )}{\underbrace{\langle \omega ,{\phi }_{S_i}(S_n)\rangle }})}^2+\lambda {\Vert \omega \Vert }_1$$ (8)

where 〈·, ·〉 denotes the inner product, g_loc and g_cplx are the local and the complex predictors, respectively, and φ_Si (S_n) ∈ ℝ^|S_i| is the popularity vector of patches in subject i with respect to subject n (defined in Eq. 2). Using the popularity, we investigate the patches whose popularities (i.e., resemblance to each other in terms of local image features) amongst other subjects is locally predictive of g_cplx. Note that we use the prediction of the clinical measurement and not the measurement itself because we are interested in locally interpreting g_cplx. We use a cross-validated LARS algorithm [6] to find the optimal λ on the regularization path.

2.4 Computational Cost

Computing the divergences for each subject (i.e., rows of L̃_σ matrix) can be done independently, hence it is parallelizable (one task per row). Estimating the divergences requires the construction of a k–NN graph. We use an approximate nearest neighbor approach [13] to construct the graph. For subject i, the cost is approximately linear with both |S_i| and d. Computing all pairs of divergences from the graph is quadratic in the number of subjects (N). It is also parallelizable per subject. A naïve computational cost of the embedding is O(N³), but there are approximate approaches that are not explored in this paper. Finally, the interpretation step can be done independently for each subject, so it, too, is easily parallelizable. The computational cost of the LARS algorithm for subject i is O(|S_i|³ + |S_i|²N), which is a few minutes for each subject in our dataset.

3 Experiments

In this section, we evaluate our algorithm on simulated and clinical datasets. We compare our method with the popular parametric bag-of-words model (k-means algorithm). We also investigate the importance of choosing the correct divergence.

3.1 Simulation

To evaluate our method on simulated data, we start by generating 2000 subjects, where each subject has a different level of disease severity and a set of 400 image patches. We sample the level of severity (y) from a Gaussian distribution clipped to the range of 0 to 400 with a mean of 200 and a standard deviation of 175. Each subject has (400 – floor(y)) “normal” patches drawn randomly from the MNIST dataset and y “abnormal” patches. The abnormal patches are novel digits synthesized by overlaying random pairs of 0 and 1 images from the MNIST dataset. Two samples of simulated subjects with different degrees of severity are shown in the left half of Fig. 2a. To reduce the dimensionality of the patches from 28 × 28, we train a three layer feed-forward neural network on a held out dataset (not used for data generation) to classify 0–9 (the novel digits not included). We pass all normal and abnormal patches through the network and use a 20-dimensional output of the layer before the last layer as features.

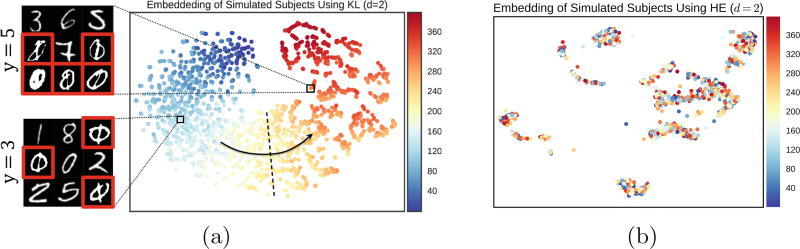
Fig. 2.

Embedding of simulated data in 2D using KL and HE. (a) Embedding for KL. Dots denote simulated subjects and colors correspond to the severity, y. The embedding using KL captures the disease severity with the arrow indicating increasing severity. Sample slices from two different subjects are shown. (b) Embedding for HE. Unlike KL, it fails to capture the structure of the population. (Color figure online)

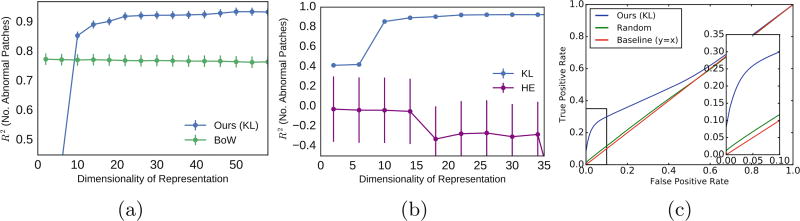
We compute the new representation of the features using KL and HE (Eq. 7) and apply LLE to assign a set of low-dimensional coordinates for each subject. Then, we use the low-dimensional representation as the features for a linear ridge regression to predict y. Figure 2 visualizes the 2D embedding for the simulated subjects using KL (Fig. 2a) and HE (Fig. 2b). Each dot represents one subject and the color of the dot indicates the simulated disease severity y. While there is a clear trend in disease severity from left to right using KL divergence, the 2D embedding using HE does not show any trend. Figure 3 demonstrates that this effect is not caused by the dimensionality of the embedding. Figure 3a compares the performance of embedding using KL and BOW in predicting y while Fig. 3b compares the performance of the two divergences. The y-axis is R² and the x-axis is the dimensionality of the representation. The performance is measured as the R² value for 50-fold cross validation against the dimensionality of the representation. While KL significantly outperforms BOW, HE has negative a R² suggesting LLE cannot accurately approximate the manifold structure induced by the HE divergence. The Eq. 8 is designed to detection just a few patches that are sufficiently informative in prediction of y in similar subjects. Since it does not detect all abnormal patches, it is not optimal for detection purpose. Nevertheless, we can compute the false positive rate of the selected patches to evaluate the individual-level interpretation on the simulated data. Figure 3c shows the ROC curve comparing our method with random selection. The interpretation method requires the popularity vector, hence BOW is not included in this evaluation. For real data, a gold standard evaluation of the individual-level interpretation requires human observation and rating.

Fig. 3.

Performance of our method. (a) compares KL to BOW while (b) illustrates the importance of the divergence choice. While KL outperforms BOW, the HE divergence has a negative R², indicating that LLE is not able to accurately approximate the structure of the latent space. (c) The ROC curve indicates the ability of our subject level interpretation method to detect abnormal patches in comparison with random selection. The box in the right shows the zoomed in area of the curve for FPR < 10%.

3.2 COPD Study

We apply our method to lung CT images of 6,253 subjects from the COPDGene study [16]. First, we evaluate various image signatures in term of predicting the severity of disease as measured by a lung function: the Forced Expiratory Volume in one second (FEV₁). Second, we show how our method can characterize a patient in the spectrum of COPD present in the population. Third, we compare the performance of the non-parametric approach with a threshold-based image measurement commonly used by clinicians, as well as the classical BOW method, which uses k–means clustering. The threshold-based method measures the percentage of voxels with intensity values less than −950 Hounsfield Unit (HU) computed from the inspiratory and expiratory images. Those measurements reflect what is clinically used to quantify emphysema and the degree of gas trapping. Note that our method has access to the inspiratory images only.

We first segment the lung area. Then, instead of patches, we apply an over-segmentation method [8] to divide the lung area into spatially homogeneous superpixels. The superpixels follow the boundaries of anatomy better than the patches; the method explained in Sect. 2 is readily applicable for superpixels without any modification. We extract both histogram and texture features from each superpixel as they have been shown to be important in characterizing emphysema [18,21]. For the histogram features, we divide the intensity histogram of each superpixel into 32 bins following Sorensen et al. [21]. We follow the pipeline introduced in [22] and extract the Harilick features from the Gray-Level Cooccurance Matrix (GLCM); the Harilick features already incorporate the intensity information. We use a rotationally invariant image feature proposed by Liu et al. [10] as the texture feature. The method views the histogram of the gradient as a continuous angular signal and uses spherical harmonics to extract features from it (referred to as sHOG).

Figure 4a reports the performance of various image signatures for a 100 dimensional embedding for KL density. The y-axis is the average R² using 50-fold cross validation for predicting FEV₁, while the horizontal line denotes the prediction using the threshold-based baseline. The error bar shows the 95% confidence interval computed using the bootstrapping method. The combination of sHOG and histogram features yields the best performance. In the rest of the experiments, we report the results using the sHOG and the histogram features.

Fig. 4.

Performance evaluation: (a) Comparing different image features. The blue bar is our method (KL divergence) and the green is BOW. The y-axis is R² of predicting FEV₁. The horizontal red line is the image threshold-based baseline. KL outperforms both methods. The combination of sHOG and histogram features results in the best performance. (b) Comparing R² versus dimensionality of the representation for KL. (c) Comparing KL and HE (purple line). The graph shows the choice of divergence is crucial. (Color figure online)

Figure 4b, c reports the performance of the embedding approach using KL, HE, and BOW against the dimensionality of the representation (i.e., the cluster size of k–means and the embedding dimensionality). While our KL-based method outperforms k-means, HE is significantly worse than both approaches. This plot emphasizes the importance of the choice of the right divergence and is consistent with the results from the simulation. Although R² = 0.55 for KL may seem low, it is significantly higher than the traditional measurements of emphysema based on a single threshold. Furthermore, our local image descriptors are more sensitive to emphysema while FEV₁ is spirometry measurement affected by emphysema, airway disease and many other factors.

In Fig. 5a, we use 2D embedding to visualize only one-third of the population (to avoid visual clutter). Each dot in the scatter plot represents a patient, and its color denotes FEV₁. As the temperature of the color increases, so does the COPD severity. Even 2D embedding captures the structure of the disease; subjects on the bottom right are healthier than subjects on the top left of the embedding space. The results in Fig. 4b confirms this observation in higher dimensional embedding. Figure 5b, c show parts of the anatomy selected by the interpretation algorithm to be the most relevant to the prediction. The figures show one slice of a subject’s lung CT. The colored patches are the regions selected by the interpretation algorithm (Sect. 2.3). For example, regions on the bottom right are obviously abnormal.

Fig. 5.

Interpretation on the population and the individual levels. (a) Embedding COPD subjects in 2D space. A dot denotes a subject and the color represent the disease severity (FEV₁). The hotter the color, the more severe the disease. (b), (c) Individual level interpretation, showing a slice of lung CT image before (b) and after overlaying (c) the regions selected by our algorithm; the color indicates the sign of ω. (Color figure online)

4 Conclusion

We proposed a non-parametric approach for characterizing heterogeneous diseases such as COPD. Our method summarizes the image data of each subject from a collection of local image descriptors to one signature vector per subject. The vector represents the coordinates of the subject in a latent low-dimensional space, which can be used for prediction of a clinical variable or visualization of the entire population. The scalable and non-parametric nature of the method enabled us to evaluate various image features quickly. Our method is readily applicable to more sophisticated feature extraction schemes such as deep learning for each patch. We showed that our approach outperforms the parametric bag-of-words (k-means) method. We experimented with two well-known divergences (KL and HE), and the results demonstrated the importance of the choice of divergence.

A Appendix

Non-parametric Inference

In this section, we first show that the unnormalized density f(x) has a closed-form using locally constant approximation. Then, we show why the second-order approximation is computationally expensive for our problem. Finally, we provide more detail on the approximation of the KL and HE divergences.

Assuming a locally constant function for f(x) = exp(a₀), we can compute a closed-form solution for a₀ by differentiating Eq. 4 with respect to a₀:

$$\frac{d{ℒ}_x(f_i)}{{\mathit{\text{da}}}_0}=\sum _{\upsilon \in S_i}w\left(\frac{x-\psi (\upsilon )}{h}\right)-|S_i|\int w(\frac{y-x}{h})e^{a_0}\mathit{\text{ dy}}=0$$

If we set h ≡ ρ_k,Si (x) and use the step window function (w(x) = 𝕀(‖x‖ ≤ 1)), the first term in the right hand-side becomes exactly k and the second term is the volume of a d-dimensional hyper-sphere with radius h which is C_dh^d, and we arrive at Eq. 5. For the Gaussian window function, the first term becomes a weighted sum k points in the vicinity of x and the second term has the same closed-form as the normalizer of the Gaussian distribution.

If we set h to a constant and use the Gaussian window function and the second-order polynomial, i.e., log f(u)|_x ≈ a₀ + (u − x)^T a₁ + (u − x)^T a₂(u − x), the local parameters have closed-forms [7,11]:

$$a_0=\text{log}(A_0)-\frac{{\Vert A_1\Vert }^2}{A_0^2}-(d\text{ log }\sqrt{2\pi }+(d+1)\text{ log }n),a_1=\frac{1}{{\mathit{\text{hA}}}_0}{A}_1,$$

$$a_2=\frac{1}{2h^2}{I}_{d\times d}-\frac{A_0}{2h^2}{(A_2-A_1{A}_1^T)}^{-1}$$

where A₀ ≡ Σ_υ∈Si α_υ(x) and ${\alpha }_{\upsilon }(x)\equiv \text{exp }(-\frac{{\Vert \psi (\upsilon )-x\Vert }^2}{2h^2})$, for $D(x,\upsilon )\equiv \frac{1}{h}(\psi (\upsilon )-x)$, A₁ ≡ Σ_υ∈Si α_υ(x)D(x, υ), and A₂ ≡ Σ_υ∈Si α_υ(x)D(x, υ)D(x, υ)^T. It is straightforward to see computing a₂ demands inversion of a d × d matrix (O(d³)) which needs to be done for every patch hence it is computationally prohibitive.

The KL divergence is a straightforward substitution of Eq. 5. Our estimator for HE is proposed by Poczos et al. [14]. The HE estimator is also based on substitution. The minor adjustment (the term behind the summation in Eq. 6) makes sure that the estimator is unbiased.