Laminar organization of encoding and memory reactivation in the parietal cortex

Summary

Egocentric neural coding has been observed in parietal cortex (PC), but its topographical and laminar organization is not well characterized. We used multi-site recording to look for evidence of local clustering and laminar consistency of linear and angular velocity encoding in multi-neuronal spiking activity (MUA) and in the high-frequency (300–900 Hz) component of the local field potential (HF-LFP), believed to reflect local spiking activity. Rats were trained to run many trials on a large circular platform, either to LED-cued goal locations or as a spatial sequence from memory. Tuning to specific self-motion states was observed, and exhibited distinct cortical depth-invariant coding properties. These patterns of collective local and laminar activation during behavior were reactivated in compressed form during post-experience sleep, and temporally coupled to cortical delta waves and hippocampal sharp wave ripples. Thus, PC neuron motion encoding is consistent across cortical laminae, and this consistency is maintained during memory reactivation.

A fundamental framework for neural coding in the parietal cortex is egocentric (Andersen et al., 1985; McNaughton et al., 1994; Nitz, 2006; Save et al., 2005; Save and Poucet, 2000; Schindler and Bartels, 2013; Whitlock et al., 2012; Wilber et al., 2014; Wolbers et al., 2008). Some studies have also found evidence for allocentric (world-centered) encoding in parietal cortex, including head direction cells (Chen et al., 1994; Chen and Nakamura, 1998; Wilber et al., 2014). Subjective assessment of head direction tuning in parietal cortex suggested common tuning across depth on a given tetrode potentially because of modular organization (Chen et al., 1994; Wilber et al., 2014). The existence of larger organizational structure of these single cells has been postulated by the theoretical or computational approaches (Byrne et al., 2007; McNaughton et al., 1995; Xing and Andersen, 2000), but larger organizational structure has not been empirically confirmed.

Behaviorally relevant neural activity patterns from single cells are reactivated during memory consolidation (Dupret et al., 2010; Lansink and Pennartz, 2014). Thus, we hypothesized that the modular structure may also be reflected in reactivation during post-experience-sleep – a postulated mechanism of memory consolidation originally demonstrated at the single cell level in hippocampus (Wilson and McNaughton, 1994) and subsequently shown for hippocampal-parietal interactions (Qin et al., 1997). However, to our knowledge, no study has looked for evidence of modular level reactivation.

Linking spiking activity with local field potential (LFP) features has been a growing area of research, most often finding the correlation between the spiking levels and LFP envelope in the high-gamma range (Crone et al., 2011; Liu and Newsome, 2006; Ray and Maunsell, 2011); however, the high-gamma range includes synaptic current oscillations (Colgin et al., 2009; Fries, 2005) and not just spike-related currents. Therefore, we aimed to test whether the modular organization reflected in multi-unit activity (MUA) is also detectable in high frequency (HF) LFP (300–900 Hz), which to our knowledge has not been attributed to any functional or physiological correlates other than spiking. The HF-LFP signal provides better temporal stability, relative to single cell recordings that are prone to minor electrode drift, and therefore produces a more reliable readout for long-term studies and for brain machine interfaces (Gilja et al., 2012). Similarly, a recent apparent connection between single unit recording studies in rodents (grid cells in rats; Hafting et al., 2005) and fMRI data in humans (Constantinescu et al., 2016; Doeller et al., 2010), suggests that collective recordings may reveal a larger organizational structure of encoding that had largely been described at the single cell level in rodents. Thus, study of modularity of neural coding in animals using collective measures of local neural activity can help to bridge the gap between human and animal studies of neural coding and dynamics.

Previous studies had suggested depth invariant encoding of head direction tuning; however, head direction cells are relatively rare in parietal cortex (Wilber et al., 2014). Therefore, we set out to look for evidence of population level modular organization and modular memory reactivation of a more prominent reference frames in parietal cortex: self-motion tuning (McNaughton et al., 1994; Whitlock et al., 2012; Wilber et al., 2014).

Results

Modular Tuning to Motion State

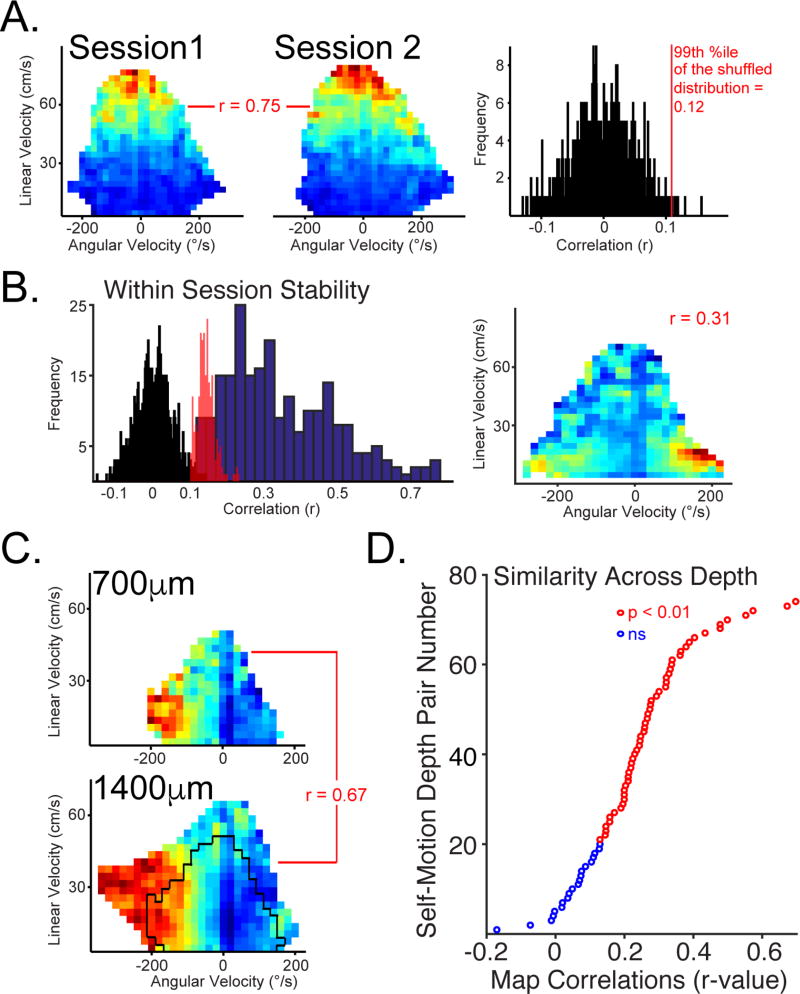
We looked for evidence of population level encoding in egocentric coordinates in the rat parietal cortex. To do this, we assessed MUA recorded on single tetrodes as a function of linear, and angular velocity in rats that had been trained to either run 1) a cued random spatial sequence (rats 1 & 2) or 2) a complex repeating element spatial sequence from memory (rat 3). We determined if parietal cortex MUA had a preferred self-motion state (e.g., right turn) by plotting firing rate as a function of the combination of the rat’s current linear and angular velocity. MUA was classified as having a preferred self-motion state if the self-motion rate maps for two behavioral sessions were significantly positively correlated (i.e., self-motion rate maps; Whitlock et al., 2012). We found that the MUA recorded on a single tetrode was frequently significantly tuned to a specific self-motion state (i.e., specific combination of linear and angular velocity; Fig. 1A & B). In fact, nearly every tetrode that was positioned in parietal cortex for at least one session met the criteria for self-motion tuning (41 of 44 tetrodes; 93%). This tuning was also apparent when trial segments where overlaid with spike locations, which revealed heightened activity during the motion state to which the MUA was tuned (e.g., high speed forward motion, Fig. S1A & B).

Figure 1. Self-Motion tuning in parietal cortex is invariant across cortical laminae. See also Figs. S1-5, and Tables S1-2.

A. Left Two Plots. Multi-unit activity (MUA) recorded for a single day’s recording session and from a single tetrode were classified as having a preferred-self motion state if the self-motion maps for two behavioral sessions (from the whole day recording session) were significantly positively correlated. Self-motion maps from two behavioral sessions and corresponding correlation value are shown for one MUA example. Right. The shuffled distribution and critical r-value corresponding to the 99^th percentile. B. Left. The random shuffle distribution for the within-session correlation values from A (black bars) but with a different bin-size to better match the frequency counts across histograms shown here. The full distribution of random shuffle critical values (red bars with 70% opacity) and the full distribution of significant within-session correlation values from all data analyzed for the present paper (blue bars). Right. Example of a self-motion map with lower (r=0.31) within-session stability. Example of a self-motion map with higher within-session stability is shown in A. C. Same as in A; however, data came from two separate recording sessions obtained when the tetrode was at two depths (700µm above and 1400µm below). Black outline on lower motion rate map illustrates that for cross-depth comparisons behavior can vary considerably, and this analysis is limited to common data points. D. The sorted correlation value for MUA for each pair of depths where the tetrode was moved at least 100µm and the session data for each depth met the significance criteria described in A. Pairs of depths with significantly correlated motion maps were colored red (calculated as described in A, but across depth as in C). Thus, self-motion tuning is consistent across cortical depths for a particular tetrode. Data comes from all tetrodes that met this criteria from all rats.

Next, we compared the MUA tuning we observed in the present paper to single units tuned to specific motion states from our previous paper (Wilber et al., 2014). We found that for single and multi-unit data from the same tetrode and data set, most single units had motion tuning that fell within the tuning of the MUA (77%). However, single unit data was often more specific and thus corresponded to a subset of the MUA tuning range (Fig. S1C). Finally, we utilized an approach designed to produce large numbers of trials (up to 1400) and coverage of a large range of behavioral states; however, some behavioral states had greater representation (low velocity). Therefore, we assessed the relationship between occupancy of behavioral state and motion state tuning to look for potential confounds. We found no evidence that behavioral occupancy contributed to the specific motion state tuning that we observed (Fig. S2A & B). Further, we observed coverage of the full range of motion states across animals; though, right turn encoding was less frequent in the rat 2 which executed fast left but not right turns, possibly because right turn modules were not detected due to the lack of right turn behavior (Fig. S2C). Additional examples of self-motion tuned MUA are shown in Figure S3.

Interestingly, MUA motion tuning appeared to be invariant across depth. To quantify this observation, we collected all pairs of recording sessions where the tetrode was at least 100µm from the comparison location and the self-motion maps for both sessions were significant (p’s<0.01). For each of these pairs we tested the two maps for significant similarity versus a random shuffle distribution using the same method as for within-day sessions. Interestingly, self-motion tuning appeared to be consistent across cortical laminae because tuning was consistent on a single tetrode when recordings were compared even for very large spacing between recording depths (Fig. 1C and S4A-C). In fact, a large majority of comparisons were significant (Fig. 1D; 73%), indicating significant correlation in self-motion tuning across a range of cortical depths for a particular tetrode. The consistency of MUA tuning across cortical depth was highly similar in all three rats, including rat 3, which performed a different task (Fig. S4A-C). As an additional control, we performed depth correlations across tetrodes, instead of within tetrodes, but in an otherwise identical manner (i.e., we took each pair of sessions that was separated by at least 100µm but across, not within tetrodes). We found significantly fewer cross-tetrode map correlations that were significant across depth samples (χ²₍₁₎=5.68, p<0.05; within: 73.0%; across: 57.8%) and significantly more across-tetrode correlations with an r-value<0 (χ²₍₁₎=5.09, p<0.05; within: 6.8%; across: 17.3%).

Another possible confound is that significant depth correlations may come predominantly from more closely spaced (but >100µm) depth samples. Therefore, as an additional control, we compared the distance between significant and non-significant depth correlations. The distribution of spacing between depth samples for significant versus non-significant depth correlations was highly overlapping with spacing between significant samples that was actually slightly greater than the spacing between non-significant samples (significant 280µm±25 and non-significant 241µm±31; Mean±SEM). Consistent with the high degree of overlap, there was not a significant difference in depth spacing for significant versus non-significant depth correlations (t₍₇₂₎=0.85, p=0.40), suggesting that closer spacing was not responsible for the significant depth correlations. Finally, marking lesions confirmed that tetrodes were at the expected depth at the conclusion of the experiment (and consistent with turning records had often been advanced through all of cortex); however, this did not rule out the possibility that tetrodes were periodically catching then advancing. So, we also compared a profile of the tetrode amplitude spacing across depths (McNaughton et al., 1983). Comparison of these profiles for each depth measurement confirmed that tetrodes had been moving smoothly between samples and not periodically catching then advancing in larger than intended jumps (Fig. S5A & B).

Finally, if we substituted the amplitude of the HF-LFP envelope (300–900Hz) for MUA firing rate, similar tuning maps were observed and were often significantly correlated with the corresponding MUA map (Fig. S5C), consistent with the theory that the HF-LFP signal reflects neuronal spiking. Further, we took each data set with significant within-session MUA motion map stability and compared the correlation values for single recording session (behavioral session 1 vs behavioral session 2 maps) obtained using HF-LFP signal to the correlation values obtained when generating the same maps with MUA. We found that these correlation values are significantly correlated (r=0.29, p<0.01). It should be noted that although correspondence can be quite good for these two measures and often subjectively appears very impressive, during behavior at least, the HF signal produces poorer tuning on average. We quantified this reduction in HF tuning by taking all of the self-motion maps that were “significant” at one of two different thresholds (p<0.05 or p<0.01). Then we compared the number of instances where a self-motion map is significant at p<0.05 (but not p<0.01) versus significant at the higher p<0.01 level for HF vs MUA. We found that significantly more MUA data sets were significant at the higher (p<0.01) level (χ²₍₁₎=5.03, p<0.05).

Finally, in order to determine if the modular motion tuning we observed was truly predictive of behavior, we decoded the self-motion state from MUA or HF-LFP simultaneously recorded from up to 17 tetrodes in rat parietal cortex (Fig. S6 and Table S1). We encoded the neural data using a generalized linear model, which assumes that the MUA or HF-LFP envelope amplitudes on a single tetrode follow a Poisson distribution whose mean depends on a normalized combination of linear and head angular velocity. Two-fold cross-validation was performed on four datasets from two rats and had high decoding accuracy, with averaged correlation coefficient being 0.60±0.05 (Mean±SD) for MUA and 0.67±0.03 for the HF-LFP-based model. The present results demonstrate that even with HF-LFP, where tuning during behavior can be weaker, there is still high predictive validity of the population activity in parietal cortex for decoding self-motion state.

Patchy, modular topographical organization of motion correlates

In contrast to the high degree of laminar consistency of behavioral correlates, the topographic organization was patchy and modular: sometimes, a tuning pattern was consistent across several near-by sites, but there were also abrupt transitions between some neighboring sites. Illustrations of this organization are provided (Fig. 2). Finally, we illustrated the recording locations for all motion-tuned modules, which are distributed along the anterior-posterior axis of the rat parietal cortex (Fig. 3).

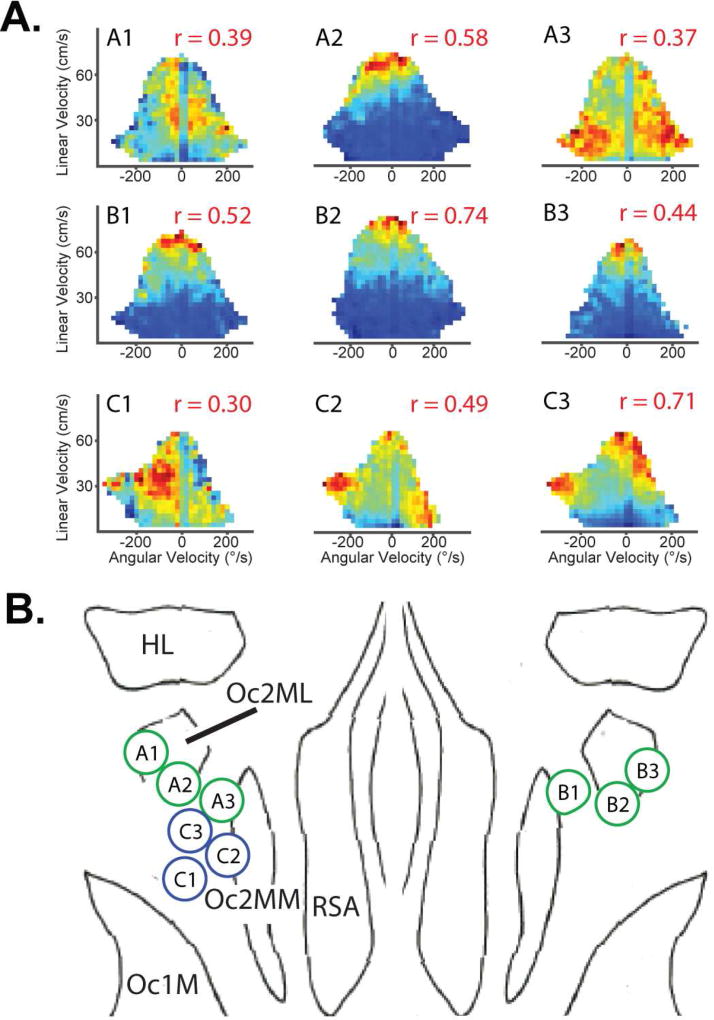
Figure 2. Illustration of patchy modularity of multi-unit activity (MUA) behavioral correlates in parietal cortex. See also Fig. S9.

A. Rows A and B represent behavioral self-motion activity rate maps for three nearby electrodes in left and right hemispheres respectively from rat 1. Row C is from the left hemisphere of rat 2. The relative positions of the electrodes are shown in B, where the minimum distance between recording locations is ~300µm. In Row A, the self-motion map change abruptly from position to position, whereas in the Row B, the self-motion rate maps are quite similar across position. Row C illustrates a combination of these effects. The rate maps were highly consistent in the laminar dimension for each location (Fig. 1). For illustration, the session with the most significant behavior map was selected for each electrode. Thus, sessions were different for the examples in Rows A and B (and thus map shape varied), but was the same for the examples in Row C. Note, some MUA data sets show tuning to multiple motion states (e.g., C2 and C3), possibly as a result of recording from a region that bridges multiple regions each with a distinct tuning states. The depth correlations for Row A ranged from 0.20–0.30 (left), 0.14–0.21 (middle), and was 0.24 (right). For Row B, no depth correlations (left), 0.23–0.50 (middle), and 0.25–0.36 (right). For Row C, 0.16 (left), 0.48 (middle), and 0.48 (right). Numbers in red the top right of each plot indicate the r-value for the within session map correlation. B. Placement of the tetrodes used to record the data in A is shown on a surface view in the horizontal plane (outlines indicate the 95% confidence interval for each region; adapted from: Zilles, 1985). The topography of the various tuning states suggests that functional cell types are not segregated into different anatomical regions. Occipital cortex, area 2, mediomedial part (Oc2MM). Occipital cortex, area 2, mediolateral part (Oc2ML). Occipital cortex, area 1, monocular part (Oc1M). Agranular retrosplenial cortex (RSA).

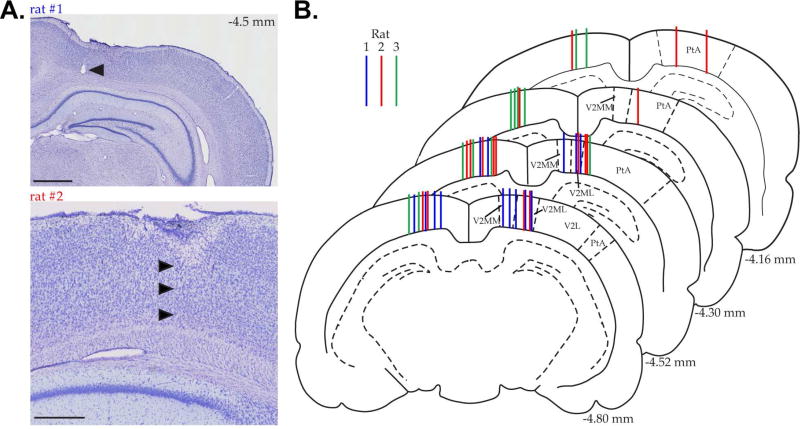
Figure 3. Recording locations in parietal cortex.

A. Nissl-stained coronal section (top) showing the marking lesion from a tetrode in rat 1 (black arrowhead). This tetrode tract is an example of the most medial tetrode placement and demonstrates that recordings did not encroach on the retrosplenial cortex. Scale bar=1mm. Nissl-stained sagittal section (bottom) showing an example of a tetrode tract in rat 2 (black arrowheads). Scale bar=500µm. B. Coronal sections throughout the anterior (top) to posterior (bottom) extent of the rat parietal cortex (Paxinos and Watson, 1998) color coded by rat (15 blue tracts-rat 1, 16 red tracts-rat 2, and 10 green tracts-rat 3). Each tract indicates the profile for a tetrode that recorded at least one session with significant within-session stability. Note, this represents nearly every tetrode that was in parietal cortex during the experiment: 41/44 tetrodes. Distance posterior to bregma is listed for each slice (lower right). Secondary visual cortex, lateral area (V2L), medolateral area (V2ML) and mediomedial area (V2MM). Parietal association cortex (PtA).

Template Matching

Parietal modular activation patterns during slow wave sleep resemble patterns observed during the task

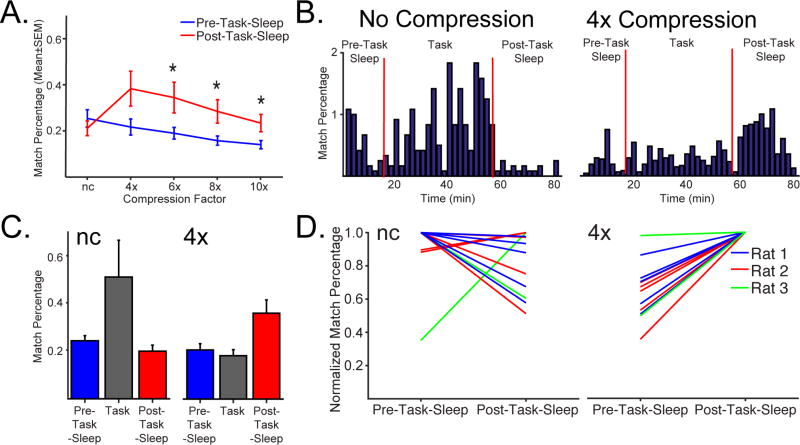
In order to test the hypothesis that modular template matching during sleep is a part of memory consolidation process and does not simply reflect the reverberation of certain activity patterns during sleep, we compared the match percentages between the pre-task-sleep and post-task-sleep across ‘no compression’ and range of equally spaced compression factors (4–10x). For MUA templates, post-task-sleep had significantly higher template matching percentage (percentage of time bins with a match that exceeded Z-score value of 3) than pre-task sleep (Fig. 4A; main effect of sleep session, F_{(1, 11)}=11.34, p<0.01) and this effect varied significantly across compression factors (sleep session x compression factor interaction; F_{(4, 44)} =11.18, p<0.0001). In addition, there was a main effect of compression factor (F_{(4, 44)}=6.97, p<0.001). Planned comparisons were conducted for pre- versus post- task-sleep for each compression factor. Post-task-sleep had significantly more template matches for 6x, 8x, and 10x (Fs_{(1, 22)} >4.73, p<0.05) but not 4x (F_{(1, 22)}=3.98, p=0.058) compression factors, while pre- and post- task-sleep match percentage did not differ for ‘no-compression’ (F_{(1, 22)} =0.75, p=0.40).

Figure 4. Compressed modular sequence reactivation. See also Fig. S7 and Table S3-4.

A. Mean (±SEM) match percentage [(n matches/n time bins)*100] across the compression factors for multi-unit activity (MUA) templates during slow-wave sleep. Template matching increases between pre- (blue) and post-task-sleep (red) for compressed data, but not for ‘no-compression’ (nc). Match percentage varied significantly across compression factors (F_(4,44)=11.18, p<0.0001) and reactivation peaked at 4x compression. B. Example of MUA showing the match percentage (2min bins) for ‘no-compression’ (left) and 4x compression (right), over the pre-task-sleep, task and post-task-sleep. For ‘no-compression’, there is a high match percentage during the task, but not post-task-sleep. For the 4x compression (right), match percentage is higher in post-task-sleep, relative to both pre-task-sleep and task. C. Mean of the pre-task-sleep, task and post-task-sleep as was calculated for each session and averaged across time bins that are shown in B. Then a mean for all sessions was calculated for each rat. Finally, the mean (±SEM) of the rat mean data shows that across rats reactivation is stronger in post-task rest when a 4x compression factor is applied, but not for nc. To avoid the possible contribution of awake reactivation to template matching during task, only the contiguous movement periods (>5cm/s) longer than 2s were used for template matching. D. Normalized match percentage (match percentage/peak match percentage for that session) across ‘no-compression’ (left) and 4x (right) compression factors for MUA templates for each session for each of 3 rats. Reactivation consistently increases between pre- and post-task-sleep for compressed data, but not for ‘no compression’. Datapoints are normalized to pre-task-sleep values. A-D. Only the slow-wave sleep (SWS) periods are used from sleep and n is the number of data sets (n=12). * p<0.05.

Similar to MUA-based reactivation measures, HF amplitude post-task sleep had significantly higher template matching than pre-task-sleep (Fig. S7A; main effect of sleep session, F_{(1, 11)}=21.51,p< 0.001) and this effect varied across compression factors (sleep session x compression factor interaction; F_{(4, 44)}=9.20,p< 0.001). In addition, there was a main effect of compression factor (F_{(4, 44)}=21.51, p<0.0001). Planned comparisons for pre- versus post- task-sleep for each compression factor showed that for ‘no-compression’ pre-task-sleep did not significantly differ from post-task-sleep (F_{(1, 22)} =1.47, p=0.24), while post-task-sleep had significantly more matches than pre-task-sleep for 4x–10x compression factors (Fs_{(1, 22)} >5.87, p<0.05).

As illustrated for the MUA template example in Figure 4B, for ‘no-compression’, there is a high match density during the task, and low match density in post-task-sleep. A dramatically different pattern is shown for 4x compression, where the match percentage was much higher in post-task-sleep, relative to both pre-task-sleep and task. Next we used animals as n and found that the animal mean match percentages for pre- vs post- task-sleep varied dramatically across compression factor (‘no compression’ & 4x; Fig. 4C) as a function of task phase. First, post-task-sleep was greater than pre-task-sleep but only for 4x compressed data. Second, the matches were much higher during the task phase for ‘no compression’ than for 4x compression, reflecting that the templates do match well to the behavior session that was used to generate them. Stronger template matching during post-task rest was not just observed for the session means (Fig. 4A), individual time bins for individual data sets (Fig. 4B) and the rat means (Fig. 4C), but also when the pre- versus post- task-sleep (normalized to post-task-sleep) was plotted for no- versus 4x compression data for each session for each rat (Fig. 4D). Nearly identical results were obtained for HF amplitude (Fig. S7A-B). Overall, template based reactivation measures increased in post-task-sleep.

In addition to the Z-score threshold method described above, we also compared the distributions of the original and shuffled template Z-scored correlation coefficients. We found a significant difference between original versus shuffled templates in a large majority of datasets for both the MUA and HF-LFP templates (92% of datasets for nc, and 98% of datasets for 4–10x compression factors; two-sample Kolmogorov-Smirnov test with Bonferroni correction, all p<0.0001). When testing for the differences in mean Z-score coefficients between the original and shuffled MUA and HF-LFP templates, there was a significant main effect of template (original template>shuffled template; Fs_(1,11)>6.65, p<0.05) and compression factor (Fs_(4,44)>12.05, p<0.0001), as well as a significant interaction (Fs_(4,44)>12.05, p<0.0001). Planned comparisons revealed that the mean Z-scores of the original templates are significantly higher than the shuffled distribution for the 4–10x compression factors (Fs_(1,22)>8.72, p<0.01), but not for ‘no-compression’ (Fs_(1,22)<1.69, p>0.20).

Reactivation of ensembles of single cells in parietal cortex

We also performed template matching for datasets with many well-isolated single cells (Mean±SEM: 21+/−4 single cells; range 10–31; n=5 data sets; 1–2 datasets/rat). In all 5 datasets, match percentage for 4x compression, but not ‘no compression’, was consistently higher in the post-task-sleep, relative to pre-task-sleep (Fig. S7C). In addition, the distributions of template matching correlation coefficients for 4x compression were significantly different between the original and shuffled templates for all the analyzed single-unit datasets (two sample Kolmogorov-Smirnov test, followed by Bonferroni correction; p<0.0001).

Parietal cortex multi-neuronal reactivation is coupled with cortical delta waves and hippocampal sharp wave ripples (SWRs)

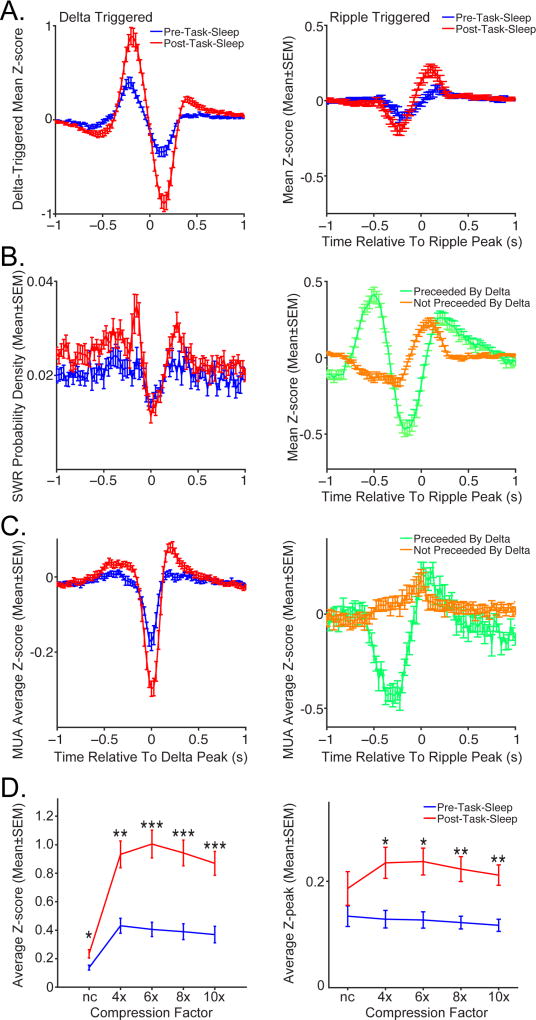
Finally, we explored the role of cortical dynamics and hippocampal-cortical interactions during sleep in modular memory reactivation by characterizing the coupling of parietal cortex template matches centered on cortical delta wave troughs (DWTs) and hippocampal sharp wave ripples (SWRs). For the DWT-triggered MUA template matching profile (Fig. 5A left) there is a pronounced decrease 100–200ms following the DWT, as well as two distinct peaks, a larger one ~200ms prior to the delta trough and a smaller one ~300–400 ms after DWT (but only for post-task-sleep). Notably, timing and amplitude of these peaks coincide with the peaks in SWR probability density, around the DWT (Fig. 5B left). The trough in template matching is likely due to decreased spiking during down states, which coincide with delta wave troughs (Battaglia et al., 2004). During these low spiking periods (Fig. 5C left), degree of matching to behavioral neuronal activity patterns is very low. It is unlikely that the amplitude of template matching peaks surrounding the DWT are driven simply by simultaneous peaks in spiking activity (Fig. 5C left), as the DWT-triggered MUA spiking profile shows the opposite pattern, with larger peak following the DWT. The profile for SWR-triggered Z-scored template matching is quite different from the DWT profile. SWR-triggered Z-scores have a pronounced trough ~300ms prior to SWRs and a peak ~100ms following SWRs (Fig. 5A right). This pattern is likely the result of superposition of two distinct SWR-triggered Z-scored profiles (Fig. 5B right), dependent on the presence of DWTs during 400ms window preceding SWRs (DWTs precede SWRs 20–30% of the time).

Figure 5. Modular sequence reactivation of multiunit spiking activity (MUA) templates in parietal cortex are enhanced around cortical delta wave troughs (DWTs) and hippocampal sharp-wave ripples (SWRs). See also Fig. S7 and Table S3.

A. Event-triggered average template matching Z-score (Mean ± SEM) for delta wave trough (DWT left) and sharp wave ripple (SWR right) for post-task-sleep (red), relative to pre-task-sleep (blue). A prominent dip in Z-score occurs 100–300ms after DWT, preceded by a larger peak (200–400ms) and followed by a smaller peak (300–500ms). SWR-triggered Z-score has a different profile, characterized by a dip 300–400ms before SWR and peak 50–150ms after SWR. B. Left. SWR probability density (Mean±SEM) centered on DWT. Larger peak in SWR probability density before DWT coincides with larger peak in DWT-triggered Z-score. Right. SWR-triggered average Z-score for SWRs preceded or not preceded by delta wave. The presence of delta wave prior to SWR is strongly predictive of SWR-triggered Z-score profile. Specifically, there is a large dip before SWRs that are preceded by delta wave (green), but small deflection when the SWRs are not preceded by delta wave (orange), both followed by comparable peak. C. Z-scored sum of event-triggered multi-unit spiking (Mean±SEM) on all tetrodes for DWTs (left) and SWRs preceded or not preceded by delta wave (right). DWTs are associated with down states, periods of widespread cortical neuronal silence and consequently low Z-scores. SWRs are generally coupled with increase in cortical spiking. Presence of large dip in spiking prior to SWR depends on the presence (green) or absence (orange) of a delta wave. D. Maximum event-triggered Z-score (Mean±SEM) across compression factors for DWTs (left) and SWRs (right). Peak amplitudes varied significantly across compression factors (Fs_(4,44) >3.01, p<0.05). A-D. n is the number of data sets (n=12). For both DWTs and SWRs, maximum event-triggered Z-score amplitudes were significantly higher in post-task-sleep (red), relative to pre-task-sleep (blue) baseline. Only slow-wave sleep periods were included in the analysis. * p<0.05. ** p<0.001. *** p<0.0001.

We found that the strength of both DWT-triggered and SWR-triggered template match increases as a function of experience, as it was larger during post-task sleep for MUA based templates (Fig. 5A&D), and also for HF amplitude based templates (Fig. S7D-E). Between-epoch comparisons of the peak amplitude of peri-DWT Z-scores (Fig. 5D left) revealed significant main effects of sleep session (Fs_(1,11) >35.55, p<0.0001) and compression factor (Fs_(4,44)>82.13, p<0.0001), as well as significant sleep session x compression factor interaction (Fs_(4,44)>17.70, p<0.0001). Planned comparisons showed that for both MUA and HF-LFP templates peri-DWT peak amplitude significantly increased during post-task-sleep for all the compression factors (4–10x) and ‘no-compression’ (Fs_(1,22)>8.03, p<0.01). Similarly, SWR-triggered Z-score peak was significantly greater during post-task-sleep for both MUA and HF-LFP templates (Fig. 5D right; main effect of sleep session; Fs_{(1, 11)}>16.69, p<0.01), and the effect of sleep session varied significantly across compression factors (Fs_{(4, 44)} >3.01, p<0.05). The only difference between HF and MUA measures was that there was a significant main effect of compression factor for HF amplitude templates (Fig. S7E; F_{(4, 44)}=18.87, p<0.001), but not MUA templates (F_(4,44)=3.01, p=0.25). To follow-up on the significant interaction for MUA and HF amplitude data, planned comparisons for pre- versus post- task sleep were conducted for each compression factor. The SWR-triggered Z-score amplitude was significantly larger for all compressed data (4x-10x; Fs_{(1, 22)} >4.77, p<0.05), but not for ‘no-compression’ (Fs_{(1, 22)}<1.97, p>0.17). Thus, for both MUA and HF signal templates, the amplitude of SWR-triggered Z-score was significantly larger for post-task-sleep particularly for all compression factors.

In order to compare the event-triggered template matching peaks with respect to baseline, we used the baseline periods away from the negative dips around DWTs and SWRs. Specifically, the baseline periods were at least 400ms from the nearest detected DWT or SWR (outside-of-event). Using this approach, we found that reactivation was also significantly higher during periods preceding DWTs (−400–0ms), as well as following SWRs (0–400ms), in both sleep epochs.

First, for DWT data, there was a significant main effect of window position (out-of-event versus event-centered) for both MUA and HF-LFP templates (outside-DWT or pre-DWT; Fs_(1,11)>57.66, p<0.0001) and compression factor (Fs_(4,44)>31.92, p<0.0001), as well as significant interaction between the window position and compression factor (Fs_(4,44)>22.99, p<0.0001). The pre-DWT mean Z-scores for MUA and HF-LFP templates were significantly higher, relative to out-of-DWT baseline in both sleep epochs, for the compression factors 4–10x (Fs_(1,22)>44.73, p<0.0001). MUA and HF-LFP templates differed slightly for ‘no-compression’, for MUA the differences were not significant (Fs_(1,22)<3.38, p>0.05), while for HF-LFP pre-DWT mean Z-score was significantly higher during post-task-sleep (F_(1,22)=43.78, p<0.0001).

Second, for SWR data MUA and HF-LFP template mean Z-scores there is a significant main effect of window position (outside-SWR or post-SWR; Fs_(1,11) >9.67, p<0.005) and compression factor (Fs_(4,44)>3.94, p<0.01), as well as significant interaction between the window position and compression factor (Fs_(4,44)>2.63, p<0.05), except that there was a non-significant main effect of window position for MUA template during pre-task-sleep (F_(1,11)<2.54, p>0.10) and non-significant interaction between window position and compression factor for HF-LFP template during post-task-sleep (F_(4,44)<2.53, p>0.05). Planned comparisons showed that the post-SWR mean Z-score was significantly higher than the outside-SWR baseline, for both MUA and HF-LFP templates for the compression factors 4–10x (Fs_(1,22)>4.44, p<0.05). There was not a significant difference for ‘no-compression’ during pre-task-sleep (Fs_(1,22)<0.41, p>0.5), while during post-task-sleep Z-scores for ‘no-compression’ were significantly higher post-SWR than outside-SWR (Fs_(1,22)>7.32, p<0.05).

Parietal cortex modules are sequentially active and Granger causality suggests potential directional influences between the modules

The proportion of spike train pairs with significantly different center of mass average positions were 20.9+/−4.7 % across the datasets, suggesting a presence of sequential structure. We also found triplet structure in 7 out of 12 datasets (Fig. S9). Finally, we tested for interactions between modules, by applying Granger causality to pairs of tetrodes. Overall, the proportion of pairs with significant Granger causality in at least one frequency band was 52.3+/−1.3%. The low gamma band had the largest proportion of signal pairs with significant interactions in the (27.5+/−1.0 %), followed by the beta (23.5+/−1.1 %) and theta bands (23.5+/−1.7 %). Significant interactions were mostly unidirectional (74.1% for low gamma, 80.9% for beta and 83.5% for theta band). There was no significant correlation between the presence of significant Granger causality within electrode pair and the similarity of self-motion tuning for any of the frequency bands tested (Spearman test; p>0.05), suggesting that none of the frequency bands tested represents an exclusive channel of communication between the similarly tuned modules.

Sleep parameters

To assess the possible differences in sleep architecture between pre-task-sleep and post-task-sleep we compared the durations of different sleep states (SWS, REM), as well as their ratios across these sleep epochs. There was not a significant effect of sleep epoch on the duration of REM sleep or REM/SWS ratio (ts₍₁₁₎<0.98, p>0.35; Table S4). SWS duration was significantly greater in post-task-sleep (ts₍₁₁₎>2.23, p<0.05); however, match percentage reflects the number of matches/time unit so more slow-wave sleep will not impact this measure.

Estimated number of units per multi-unit activity (MUA) data set

Last, to ensure that small numbers of single cells were not driving the effects we observed, we used the number of spikes/single unit to extrapolate an estimated number of single units per MUA data set. We found on average 33 single units/MUA data set (Table S2). Similarly, when we performed the same calculation on the subset of data used for reactivation analyses, we found on average 51 single units/MUA data set (Table S3).

Discussion

We have shown modular coding of movement in parietal cortex. The coding is consistent across a range of cortical depths, strengthening the idea that this meso-scale coding is organized in a modular fashion. In addition, we found that there are interactions between modules during post-task-sleep as measured by matching templates, reflecting the task segments leading up to the reward zone, to modular activity patterns during sleep. These modular memory reactivation events suggest that inter-modular interactions are involved in normal learning and memory. Finally, we demonstrated that the high frequency LFP amplitude from a given tetrode produces a result that is highly similar to the multi-unit activity for both modular motion tuning and memory reactivation.

Single unit recording studies and behavioral studies have pointed towards an egocentric reference frame in parietal cortex. However, this is the first demonstration of mesoscale functional encoding from a local population of single cells organized around a specific motion preference. A potential implication is that coordinate transformation networks may exist embedded within a functional module for executing the appropriate action sequence (Byrne et al., 2007; McNaughton et al., 1995; Wilber et al., 2014; Xing and Andersen, 2000). In fact, the motion modules could serve as a common output reference frame to a brain network for decision related computations involving parietal cortex (Goard et al., 2016; Hanks et al., 2015; Harvey et al., 2012; Licata et al., 2016). In other words, modular movement based encoding may be a fundamental coding framework in parietal cortex. This common tuning, likely reflecting high intrinsic connectivity among the single units (i.e., a module; Buxhoeveden and Casanova, 2002), is suggestive of a cell assembly. Such a functional module may be precisely the effector unit theorized to be critical for sufficient size to trigger responses in target areas (Breitenberg and Schulz., 1991; Bush and Sejnowski, 1994; Gabbott et al., 1987), either at the column (Mountcastle, 1997; Szentagothai, 1975), or possibly even macrocolumn level (Mountcastle, 2003).

We also assessed MUA recorded on single tetrodes as a function of head direction, and egocentric cue light location (not shown). In contrast to our previous single unit analysis, we did not find convincing evidence for MUA tuning to head direction, or egocentric cue light location (Chen et al., 1994; Wilber et al., 2014). There were a few MUA data sets with putative tuning to head direction or egocentric cue-direction; however, because these rare data sets sharply contrasted the pervasive tuning to motion state, we did not pursue analyses of these behavioral variables further. It is possible the lack of head direction tuning for MUA, but presence of common head direction tuning clustering with single cells, means that the head direction tuned cortical columns are present but are very narrow and thus not detected with MUA.

In addition to head direction encoding, other types of world-centered (allocentric) encoding have been reported in parietal cortex that could exist at the modular level, but were not assessed here (Nakamura, 1999). It should be noted that we did not examine all known encoding modes in parietal cortex. One encoding framework that seems likely to exist at the modular level is route-centered encoding, described in detail at the single unit level (Nitz, 2006, 2012). Unfortunately, the task we employed here is not optimal for detecting route-centered modulation. Similarly, outside parietal cortex, there are numerous examples of local cell populations that share functional similarities, including primary visual areas, and the barrel cortex (Petersen, 2007; Sincich and Horton, 2005). Local populations with functional similarity also exist in higher cortical areas, for example, grid cells in the medial entorhinal cortex (Moser et al., 2014; Roudi et al., 2015) or object feature columns in inferior temporal cortex (Tsunoda et al., 2001). Presumably, the current approach can be applied to further understanding of many of these brain systems.

We demonstrated modular reactivation in parietal cortex at the ensemble level, using template matching. This method was previously applied in memory reactivation studies of ensembles of isolated single cells (Euston et al., 2007; Louie and Wilson, 2001; Pavlides and Winson, 1989; Skaggs and McNaughton, 1996; Tatsuno et al., 2006; Wilson and McNaughton, 1994). Although the resemblance between the behavioral and sleep activity patterns could be due to simple re-occurrence of the similar patterns across the sleep-wake cycle, multiple lines of evidence support the notion of modular memory reactivation in the present study. First, the behavioral template matching was more prevalent during post-task, relative to pre-task sleep, an effect present after normalizing for the SWS duration in each sleep epoch (Fig. 4). This suggests that the difference in probability of certain brain activity patterns between pre- and post- task-sleep is affected by intervening experience, one of the critical requirements for the detection of memory-related processes. Second, consistent with numerous reports of memory reactivation occurring at the temporally compressed timescale (Euston et al., 2007; Nadasdy et al., 1999; Peyrache et al., 2009; Wilson and McNaughton, 1994), we observed increased matching during post-task-sleep for the range of compression factors (4–10x) while no significant change was observed for non-compressed patterns. Temporal compression during memory consolidation is a hallmark of memory reactivation that is postulated to create the optimal conditions for spike-timing dependent plasticity (Lansink and Pennartz, 2014; Markram et al., 1997). Finally, temporal coupling of modular reactivation in parietal cortex with SWRs suggests that, similar to reactivation in medial pre-frontal cortex (Euston et al., 2007; Peyrache et al., 2009), this process is part of hippocampo-cortical communication during sleep; also a hallmark of memory consolidation (Maingret et al., 2016).

We found some matching with pre-task-sleep activity, consistent with previous reports (Dragoi and Tonegawa, 2011; Peyrache et al., 2009). This is consistent with the idea that the information incoming during experience modifies pre-existing patterns (Luczak et al., 2009). The reactivated patterns resemble the templates constructed based on the average activity during approach to reward locations, and therefore likely encode the behavioral sequence reinforced by subsequent reward. Reactivation of behavioral pattern averaged over many different spatial trajectories, containing a range of head direction, cue direction, motion state and other tuning properties of parietal cortex, supporting the abstraction role of memory consolidation (Lewis and Durrant, 2011), where the regular aspects of episodic memory are extracted into the semantic domain.

In addition to modular reactivation, we demonstrated reactivation of single cell ensembles in parietal cortex. This finding is complementary to Qin et al. (1997), who found reactivation of behavioral patterns in parietal cortex during post-task-sleep based on the experience-induced change in patterns of pairwise cross-correlations at the level of whole sleep epoch. The current finding extends the notion of single cell reactivation in parietal cortex from generalized activity patterns from the entire behavioral session (Qin et al., 1997) to specific activity patterns from a repetitive component of a task.

We also assessed the degree of modular sequential activity during behavior using a previously described latency measure (Luczak et al., 2009) and found evidence of significant temporal offsets within about 20% of module pairs. In a majority of analyzed datasets we also identified triplets of sequentially active modules. Finally, Granger causality suggests potential causal interactions within about 50% of module pairs in at least one of the frequency bands with established functional importance for communication within cortex (beta and low gamma, Benchenane et al., 2010; Brovelli et al., 2004) or between the cortex and hippocampus (theta, Benchenane et al., 2010). These findings suggest potential functional interactions between the parietal cortex modules.

Finally, we showed that the HF-LFP signal has nearly identical reactivation dynamics compared to dynamics observed with MUA activity. Although the exact contribution of LFP generation mechanisms to different frequency ranges are a matter of debate (Buzsáki et al., 2012), correlation between the HF amplitude and MUA activity suggests that the instances of low correlation between MUA and HF amplitude we observed are due to spike subsampling on the individual electrode. However, both MUA and HF amplitude were effectively used to decode behavior.

Consistent with numerous reports describing cortical-hippocampal interactions, we found enhanced reactivation of behavioral templates simultaneously with cortical delta waves and SWRs in the hippocampal CA1 (Jung et al., 1998; Peyrache et al., 2009; Siapas and Wilson, 1998; Singer and Frank, 2009). This relation is complex, as the delta waves and SWRs tend to co-occur at higher than chance level (Battaglia et al., 2004; Siapas and Wilson, 1998) and the observed reactivation events could be largely driven by the cortical neuronal excitability state shaped both by delta oscillations and enhanced hippocampal output during SWRs.

In summary, we have shown modular self-motion tuning in rat parietal cortex. These motion modules also participate in memory re-activation as measured by templates constructed from the pre-reward task phase. Our findings suggest a potential fundamental level of organization in the rat in parietal cortex and open up an avenue for bridging the gap between macro-level measures of brain activation in humans and unit recording studies in non-human animals.

STAR Methods

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Ivan Skelin (ivan.skelin.m@gmail.com).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Three healthy male Fisher-Brown Norway hybrid rats, 5–10 months of age (rat 1 5months 345g; rat 2 5months 390-g, and rat 3 10months 417g at first surgery) were housed in hanging wire cages with a PVC tube for enrichment (2–3 rats per cage) prior to surgery. Rats were obtained from the University of Lethbridge breeding colony and had no history of previous procedures. Rats were bred from female F344 and male Brown Norway rats (Charles River). Light/dark cycle information is described in Table 1. All experiments were carried out in accordance with protocols approved by the University of Lethbridge Animal Welfare Committee and conformed to NIH Guidelines on the Care and Use of Laboratory Animals.

Table 1. Training and testing conditions and data sets for depth correlations.

Recording sessions refers to daily sessions that were typically split into two 50min behavioral sessions separated by a 50min rest session. Number of sessions and number of multi-unit activity (MUA) data sets that were included in the depth correlations analyses for each rat.

Rat #	Task Type	Light/Dark Cycle Phase During Testing	# Recording Session	# Sessions for Depth Correlations	# MUA Sets For Depth Correlations
1	Random Lights	Light	25	14	46
2	Random Lights	Light	23	18	55
3	Spatial Sequence Task	Dark	16	15	75
Total			64	47	176

METHODS DETAILS

Rats underwent surgery for implantation of bilateral stimulating electrodes aimed at the medial forebrain bundle (MFB; 2.8mm posterior from bregma, 1.7mm from midline, 7.8mm ventral from dura). After recovery from surgery, rats were trained to nose poke for MFB stimulation. Then, brain stimulation parameters (200µs half cycle, 150 Hz biphasic 70–110µA current applied for 300–450ms) were adjusted to find the minimal intensity and duration that was sufficient for maintaining maximal responding. Next, rats with optimal MFB stimulation underwent surgery to implant a custom 18-tetrode bilateral “hyperdrive” (n=2; similar to: Kloosterman et al., 2009) or 18-tetrode unilateral hyperdrive aimed at the left parietal cortex (n=1; almost identical to: Kloosterman et al., 2009).

Controls for medial forebrain bundle (MFB) stimulation effects

MFB stimulation was necessary to obtain sufficient trials for some analyses. To ameliorate concerns about MFB effects on parietal cortex neural activity, data were removed for the brain stimulation duration plus an additional post-stimulation 20ms blackout period (Bower et al., 2005; Euston and McNaughton, 2006; Euston et al., 2007; Johnson et al., 2010; Wilber et al., 2014). In addition, MFB stimulation was delivered in one hemisphere and recordings were obtained from both hemispheres for 2 of 3 rats. For these rats, we compared the proportion of tetrodes that met the criteria for self-motion tuning in the same versus opposite hemisphere to brain stimulation. Similar to our previous reports on single cells (Wilber et al., 2014), there were no differences in proportion of significantly self-motion tuned sessions (significant within-day session 1 vs session 2 stability, p<0.01) between hemispheres when self-motion tuning was measured with MUA (χ²₍₁₎=2.29, p=0.13) and HF-LFP signals (χ²₍₁₎=0.28, p=0.60). Further, in previous experiments where it was possible to obtain sufficient coverage for analyses using food reward, identical results were obtained using both MFB stimulation and food reward, suggesting that the results obtained from MFB experiments are generalizable (Euston and McNaughton, 2006). This suggests MFB stimulation did not directly influence the activity patterns we observed.

Surgical Procedure

Recording arrays consisted of 18 tetrodes and 3–4 reference electrodes. Each tetrode consisted of four polyimide-coated nichrome wires (12.5µm diameter) twisted together (Kanthal Palm Coast). The recording arrays were positioned over the parietal cortex (centered 4.5mm posterior from bregma and +/−2.95mm from midline) arranged in 1 or 2 closely packed guide-tube bundles with center-to-center tetrode spacing of ~300µm. The arrays were positioned to target the average parietal cortex region for which we thoroughly characterized the connection densities (Mesina et al., 2016; Wilber et al., 2015). These recording coordinates in rats are likely to correspond in the mouse to the anteriormedial, posteriormedial, and mediomedial areas (Wang and Burkhalter, 2007; Wang et al., 2012; Wilber et al., 2014).

Behavior

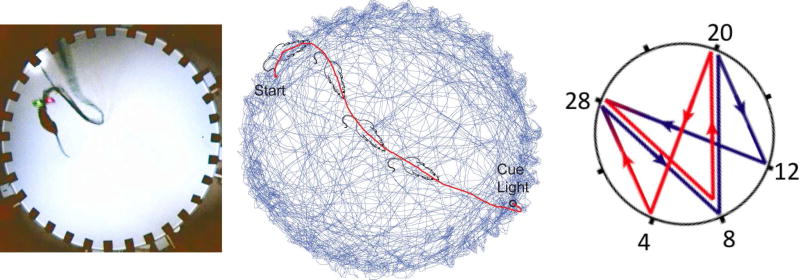
Training and testing took place on a large (1.5m diameter) circular platform with 32 light cues evenly distributed around the perimeter. A custom computer program (interfaced with the maze via a field-programmable gate array, FPGA card, National Instruments) controlled maze events and the delivery of MFB stimulation rewards via a Stimulus Isolator (World Precision Instruments A365) when the rat entered a 10cm diameter zone in front of the active cue light, and generated a coded timestamp in the Neuralynx system for each maze event. First, alternation training was achieved using barriers to restrict the movement of the rat to alternating between a pair of cue lights on opposite sides of the maze. To ensure cues were visually salient, lights were flashed at ~3 Hz (with equal on/off time) when activated. The first light was activated until the rat reached that reward zone and received MFB stimulation and then the cue light in the opposite reward zone was activated. Alternation training continued until rats reached asymptote performance (rat 1=27 days and rat 2=9 days; rat 3=20 days). The data reported here for rats 1 and 2 comes from the next, random lights task, in which sequences of up to 900 elements were drawn randomly with replacement from the 32 light/reward zones, with each LED light remaining active until the rat reached it. A different random sequence was used for each behavioral session. The data reported here for rat 3 comes from the last, spatial sequence task that followed training on the random lights task (except for data for determining the range of motion map tuning, to more accurately characterize motion tuning for this rat we included random lights data when available). For the spatial sequence task, rats were trained to navigate through an 8-item repeating element sequence of reward zones (Fig. 6). This task consisted of 3 traversals through the sequence with cue lights illuminated immediately (cued) and 3 traversals with a 5s delay (delay-cued), thus demonstrating sequence memory (Bower et al., 2005). For delay-cued trials, trained rats completed the trial before the appearance of light cues ≥90% of the time on average. See Table 1 for additional details.

Figure 6. Apparatus, reference frames, and learned motion sequence.

Left. Apparatus. Rats 1 and 2 were trained to run a random spatial sequence to 32 light locations. This task requires the rat to learn to execute a stereotyped motion sequence. Middle. Single segment from the random lights task (red) overlaid on 99% transparent random subset (1/5^th) of the trials from that session (blue). The route to the goal becomes a series of stereotyped motion sequences. Right. Schematic of the spatial sequence task. The rat starts at zone 12 and continued to zone 28 8 20 4 28 8 20 & 12. Rat 3 learned to execute this spatial sequence from memory (without cueing).

Rats 1–2 were housed in a vivarium with lights on between 07:30 and 19:30 and were tested during the light cycle. Rat 3 was housed in a reverse light/dark cycle vivarium and tested during the dark cycle. For rat 3, prominent distal cues were arranged around the perimeter of a large room (~4.5m × 6m). For the remaining rats, prominent cues (strips of white curtain) were displayed on 1–2 walls of a square curtain that hung ~1m beyond the edge of the apparatus (Table 1). For all rats and sessions, dim ambient light illuminated the maze from above.

Recording Procedures

A custom electrode interface board attached to the recording array with independently drivable tetrodes connected 3 unity-gain headstages (HS-27 Neuralynx) to the recording system (Neuralynx). Tetrodes were referenced to an electrode in the corpus callosum and advanced as needed, up to 60µm/day, while monitoring the audio and visual signal of the unit activity, but adjustments were carried out generally after a given day’s recording to allow stabilization (see below for more detail). Once a large number of units in the parietal cortex were obtained, alternation training commenced. Thresholded (adjusted prior to each session) spike waveforms were filtered 0.6 to 6 kHz and digitized at 32 kHz. A continuous trace was simultaneously collected from one of the tetrode wires (filtered 0.1 to 9kHz, and digitized at 2034.75 Hz and referenced to an electrode in corpus callosum) for processing as a LFP and associated timestamps were collected for up to 18 tetrodes. Rat position and head direction were tracked using colored domes of reflective tape (Fig. 6), and on-line position information was used to trigger MFB stimulation rewards. Position and head direction data were collected at 60 Hz as interleaved video (rats 1 & 3) or 30 Hz (rat 2) and co-registered with spikes, LFPs, and stimuli.

Spike data were automatically overclustered using KlustaKwik then manually adjusted using a modified version of MClust (A.D. Redish). All spike waveforms with a shape, and across tetrode cluster signature suggesting that they were likely MUA and not noise, were manually selected and merged into a single MUA cluster. Thus, MUA clusters included both well-isolated single units and poorly isolated single units. MUA clusters were considered unique if a) the tetrode was moved >100µm from the previous session and b) the distributions of spike clusters were clearly unrelated between the two sessions (Fig. S5; http://klustakwik.sourceforge.net; Harris et al., 2000). For single-unit analyses only (not MUA analyses) three additional criteria were applied: 1) Only spike clusters with <0.4% of the spikes in the first 2ms on the autocorrelation were included. 2) Only spike clusters with <15% threshold cut (as assessed by peaks plots) over the course of the entire ~5h recording session were included. 3) Only spike clusters with well-defined cluster boundaries were included for analyses.

LFP analyses were performed using custom-written Matlab code (Mathworks, Nattick, MA) or Freely Moving Animal (FMA) Toolbox (http://fmatoolbox.sourceforge.net/). The LFP signal was collected at 2034.75 Hz and subsequently resampled to 2000 Hz for further analysis, using the Matlab resample function. The amplitude of the HF-LFP signal was obtained by digitally filtering the raw signal in the 300–900 Hz range using a 4-th order zero-phase Chebyshev filter and calculating the absolute value of the Hilbert transformed filtered signal.

Parietal Cortex Data

Data recorded from a subset of the sessions (47 sessions) included MUA clusters with significant within-session tuning that were further assessed because the tetrode met the unique depth criteria from the previous session as described above (Table 1). Each recording session consisted of three 50min rest sessions intermixed with two 50min behavioral sessions on the apparatus (except for 12 sessions of the 47 total sessions presented here). The remaining 12 sessions consisted of one behavioral session between two rest sessions, followed by a 4h break during which the animal was returned to the vivarium before returning for a second round of a 50min behavioral session between two more 50min rest sessions. For these 12 sessions only 1 of the rest-task-rest sessions was analyzed as a recording session.

Histology

After the final recording session, rats were deeply anesthetized with Euthasol and transcardially perfused with 0.1M phosphate buffered saline followed by 4% paraformaldehyde. The whole head was postfixed in 4% paraformaldehyde with electrodes in place for 24h, then brains were extracted and cryoprotected in 30% sucrose. Frozen sections were cut (40µm) using a sliding microtome or custom block-face imaging system (Leica vibratome), mounted on chrome alum-subbed slides, stained with cresyl-echt violet, and imaged using a NanoZoomer Imaging system (Hamamatsu).

QUANTIFICATION AND STATISTICAL ANALYSIS

Self-Motion Analyses

Position and head direction data were utilized to map the self-motion reference frame for each MUA cluster. For these analyses, position data were interpolated and smoothed by convolution with a Hamming window that was 1s long. In addition, head direction data gaps <1s were transformed using directional cosines for interpolation using the interp1 function in Matlab, then transformed back to polar coordinates (Gumiaux et al., 2003). Next, head angular velocity, linear velocity and MUA activity rate were calculated for each video frame using a 100ms sliding window. Finally, the occupancy and number of MUA spikes for each 3cm/s by 20°/s bin were calcula ted and converted to firing rate for each bin with >0.5 s of occupancy. For illustrative purposes (not analyses), the self-motion activity rate maps were smoothed by convolving with a Gaussian function (σ=1; Whitlock et al., 2012; Wilber et al., 2014). The self-motion colormaps represented a range of MUA (or HF) activity rates from 0 to the maximum. No adjustments were made to the standard, evenly spaced colormap. MUA clusters were classified as having a preferred-self motion state if the common points with sufficient occupancy (>0.5 s) from the self-motion maps for the first and second daily session (or split ½ for a small subset of the data) were significantly positively correlated (p<0.01). This was generally the most conservative criterion for self-motion cells of the three criteria reported by Whitlock et al. (2012). Specifically, for each MUA cluster, to determine if cells had “significant” self-motion properties, the map from the first daily behavioral session was shuffled by randomly permuting the bins of the rate map, a correlation coefficient was computed between the first session (shuffled map) and the second session (unshuffled map), and this process was repeated 500 times. Then, the second behavioral session map was shuffled, the correlation coefficient was computed between the second session (shuffled map) and the first behavioral session (unshuffled map), and this process was repeated 500 times (total 1000 shuffles/MUA data set). The entire shuffled data set for each MUA data set was used to calculate a critical r-value for the 99^th percentile. For the day recording sessions with two behavioral sessions, stability was assessed by comparing across the two sessions (35 data sets) and for the 12 recording sessions where a single behavioral epoch was available, split ½ measures of stability were used (i.e., a single session was split in ½ based on time and the first ½ was compared to the second ½).

Neural Decoding

We developed a Bayesian state-space framework to decode the self-motion state from pooled MUA or HF-LFP simultaneously recorded from up to 18 tetrodes in rat parietal cortex in four datasets (rat 1 and rat 2 – 2 recording sessions/rat). Data sets were selected based on an ideal combination of large numbers of tetrodes in parietal cortex, and best performance. The firing rate was calculated in non-overlapping 50ms bins. The HF-LFP and kinematic recordings (linear and head angular velocity) were also down-sampled in the same time bins. We encoded the neuronal firing rates using a generalized linear model (Truccolo et al., 2005), which assumes that MUA or HF-LFP on a single tetrode follows a Poisson distribution whose mean depends on the overall kinematic motion. Here, the overall motion was a normalized combination of linear and head angular velocity. That is,

$$\mathit{\text{motion}}=\sqrt{{(\frac{\mathit{\text{linear velocity}}}{\mathit{\text{std}}(\mathit{\text{linear velocity}})})}^2+{(\frac{\mathit{\text{head angular velocity}}}{\mathit{\text{std}}(\mathit{\text{head angular velocity}})})}^2}$$

where std(·) denotes the standard deviation calculation. Note, that as a normalized measurement, the overall motion is unitless. Each recording session has two behavioral sessions. Each behavioral session had more than 200 trials where each trial was defined from the starting time a LED light is on to the time it is reached by the rat. We use one behavioral session as training data to identify the parameters in the model, and the other as testing data to predict kinematic motion using MUA or HF-LFP. The generalized linear model was learned from training data along with a linear Gaussian model that characterizes kinematic motion over time. Inference of kinematics is performed using a point process filter which gives an efficient recursive method in real-time (Eden et al., 2004). Twofold cross-validation was performed on the four datasets. The decoding accuracy was measured using Pearson correlation coefficient (which can range −1 to 1).

Estimated number of units per multi-unit activity (MUA) data set

We made use of single unit data that was spike sorted blind to present analyses for our previous paper (rats 1 and 2; Wilber et al., 2014) or for unpublished analyses several years prior (rat 3). Data from each tetrode with significant MUA tuning stability that also had well-isolated single units (51 MUA data sets from 3 rats and 21 recording session data sets) were used to estimate the number of single units in each MUA data set.

Memory Replay Analyses

First, still periods were extracted from the rest sessions as described previously (Euston et al., 2007). The raw position data from each video frame was smoothed by convolution of both x and y position data with a normalized Gaussian function with standard deviation of 120 video frames. After smoothing, the instantaneous velocity was found by taking the difference in position between successive video frames. An epoch during which the velocity dropped below 0.78 pixels/s (~0.3cm/s) for more than 2min was considered a motionlessness period. All analyses of rest sessions were limited to these motionless periods. To avoid the possible contribution of awake reactivation during the task to template matching, only the contiguous movement periods (>5cm/s) longer than 2s were used in quantifying the template matching during task. Slow wave sleep (SWS) and rapid eye movement (REM) sleep were distinguished using automatic K-means clustering of the theta/delta power ratio extracted from the CA1 pyramidal layer LFP recorded during the ‘stillness’ periods (Girardeau et al., 2009). Only slow wave sleep periods were included in the analysis. Delta wave troughs (DWT), which correspond to down states (Battaglia et al., 2004), were detected by digitally filtering the LFP trace from representative cortical electrode in the 0.5–4 Hz range and detecting the peaks in the inverted signal that exceeded a mean+1.5 SD threshold. SWRs were detected from the CA1 LFP digitally filtered in the 75–300 Hz. Events with peaks >5 SD above the mean and duration less than 100ms were considered SWRs. The SWR duration included the contiguous periods surrounding the peak and exceeding 2 SD above the mean. The SWR detection accuracy was visually validated on the subset of each analyzed dataset.

Template Matching

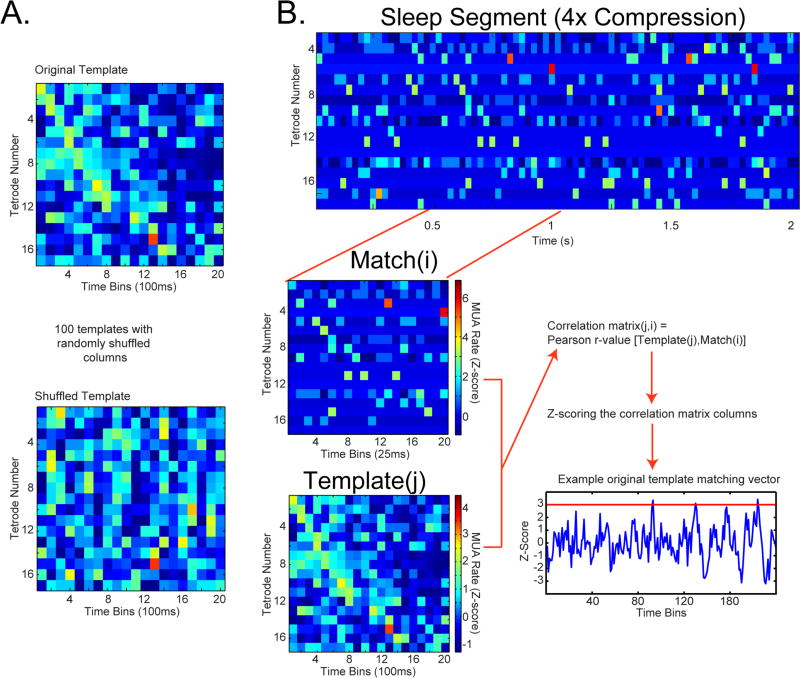
We performed template matching analysis, previously used to show the simultaneous reactivation of isolated single cell ensembles in the medial prefrontal cortex (Euston et al., 2007; Louie and Wilson, 2001). The criteria for the inclusion of a dataset in the template matching analysis was at least 12min of SWS and 600 SWRs during both pre- and post-task-sleep, and at least 50 trials during the task. Template matrices (number of tetrodes x number of time bins; Fig. 7A) were generated from the trial-averaged multiunit activity (MUA template) or Hilbert-transformed high frequency amplitude (HF template), extracted from a 2s/trial windows that preceded the arrival at the reward site, and binned to 100ms bins. Only trials longer than the template duration (2s) were included. The time window was chosen based on evidence that reactivation of the hippocampal activity patterns is more prominent for the task phase immediately preceding the reward (Diba and Buzsaki, 2007; Foster and Wilson, 2006; McNamara et al., 2014; Singer and Frank, 2009). The time bin choice was based on previous reports of template matching using isolated single unit activity (Euston et al., 2007; Johnson et al., 2010), where a 100ms bin was deemed optimal for capturing task-related neuronal dynamics. In order to eliminate tetrodes with sparse and/or poorly approach-motion-modulated activity, only the tetrodes with average reward approach period MUA >1 Hz and reward approach period binned spike train coefficient of variation >0.25 were included in the template. Coefficient of variation was calculated over twenty 100ms time bins. For single cell reactivation template matching analysis, the procedure was the same, except that the firing rate threshold for inclusion in template was 0.15 Hz and coefficient of variation threshold was 0.3. Only the templates containing ≥6 tetrodes or single cells in parietal cortex were retained. To allow comparison between the MUA and HF template matching, HF templates were constructed from the same set of tetrodes that passed the MUA-based screening. To eliminate the influence of signal (MUA, HF, or single cell) amplitude variability between tetrodes, the binned signal was Z-scored for each tetrode separately. Consistent with previous reports, we found that memory reactivation was consistently stronger for the post-task-sleep session in data sets with two task and three sleep epochs (Euston et al., 2007). Therefore, we restricted our subsequent analyses to these data sets (12 sets of pre-task-sleep, task, and post-task-sleep from 3 rats).

Figure 7. Template matching method. See also Fig. S8.

A. Shuffling procedure. Above. Example original template. Multiunit activity (MUA) or high-frequency (HF) amplitude on each tetrode (row) is averaged over all trials, binned at 100ms, and Z-scored. Below. Template shuffling procedure. Position of each column (instantaneous MUA or HF amplitude over all the tetrodes) was randomly permuted in order to produce 100 shuffled templates while preserving the overall MUA or HF amplitude levels, as well as the instantaneous correlation between tetrodes. B. Template matching procedure. Above. MUA data segment from post-task-sleep. Activity during sleep is sparse, so samples are more variable. Activity on each tetrode (row) was binned (bin size=100ms/compression factor) and Z-scored. Below Left. Example match window from the sleep epoch (above) and template (below). Pearson correlation coefficient was calculated between the template and equally sized slow-wave sleep (SWS) segments of the sleep session, which were produced by sliding the template window over the sleep epoch with a 1-bin step size. This creates a correlation matrix (n templates x n SWS time bins). Each column of the correlation matrix is Z-scored; this value reflects the degree of similarity of a given template to sleep activity at given sleep time window, relative to the distribution across the original and all shuffled templates. Bottom right: Example original template matching trace. Z-scores >3 are considered matches.

Due to the time-compressed nature of re-activation reported previously for single-cell memory reactivation studies (Euston et al., 2007; Peyrache et al., 2009; Wilson and McNaughton, 1994), we performed template matching for several evenly spaced compression factors: ‘no-compression’, 4x, 6x, 8x, and 10x. All of the template matching analyses were limited to SWS periods. Signal from the sleep periods was processed in the same way as for behavioral templates, except that the bin size was adjusted according to the compression factor (bin size=100ms/compression factor; e.g. for the 4x compression, the sleep bin size=25ms), to capture the compressed nature of neural reactivation during sleep.

To test the matching of a given template and the pattern of activity during sleep (matching significance), each template was shuffled repeatedly to generate 100 shuffled templates. The shuffling procedure consisted of randomly permuting the position of each column in the template (population vector), preserving the overall activity levels and instantaneous correlations between the signals on different tetrodes, but scrambling the sequential patterns. A Pearson correlation coefficient was calculated between each template and the series of candidate matches, generated by sliding the template-size window over the sleep epoch (Fig. 7B). This resulted in a matrix of Pearson correlation coefficients r, where the element r^i,j corresponded to the correlation coefficient between the i-th template and j-th candidate match. The correlation matrices were Z-scored across individual time bins (columns), and the resulting Z-score values reflected the template similarity to the corresponding sleep segment at given time step, relative to the distribution that included the original and 100 shuffled templates. Z-score values above 3 were considered matches (Fig. S8B-D). The threshold for matching significance was that the number of matches from the original template had to exceed the number of matches from all of the 100 shuffled templates for a given sleep epoch (p<0.001).

For comparison of template matching between the pre- and post-task-sleep, match percentage was obtained by dividing the number of matches by the number of SWS time bins for each sleep epoch. For the comparisons between the original and shuffled templates, means and distributions of Z-score values obtained from the original and shuffled templates were compared within epoch (Fig. S8A). For the DWT-triggered and SWR-triggered average analysis, the original template Z-score traces +/−1s around each DWT or SWR peak time were averaged, obtaining the event-triggered averaged Z-score for a given sleep epoch. The peri-event reactivation strength was defined as the maximum averaged event-triggered Z-score value within +/−1s window surrounding detected event. To compare the peri-event Z-score values with baseline, mean Z-score values from the peri-event windows showing event-triggered peaks in Z-score (−400–0ms pre-DWT or 0–400ms post-SWR) were compared with mean Z-score values from the periods at least 400ms from nearest detected DWT or SWR (outside-DWT or outside-SWR).

Modular sequences in the parietal cortex

In order to begin testing of the hypothesis that parietal cortex modules are sequentially active during behavior, individual electrode spike trains from the last 2s of each trial were binned (25ms bin size) and center of mass was calculated. The spike trains were rank-ordered based on latency, defined as the spike train center of mass distance from the window onset (Luczak et al., 2009). The lower latency rank order values indicated the likelihood of spikes on a given tetrode to occur earlier, relative to spikes from tetrodes with higher latency rank order values.

Modular interactions in parietal cortex

To test for putative directional influences between the parietal cortex modules, we computed Granger causality for LFP signals from all the tetrode pairs. The Granger causality method is based on the notion that if the state of signal A at time t is better predicted by the state of signal B at time t-1 than by the state of A at t-1, than signal B is exhibiting Granger causality on signal A (Bastos et al., 2015; Granger, 1969; reviewed by Seth et al., 2015). The LFP signal from the last 2s of each trial was downsampled to 250 Hz and detrended to improve stationarity. The Multivariate Granger Causality Toolbox (Barnett and Seth, 2014) was used to calculate model order m for each dataset, based on the Akaike information criterion, which determines the optimal model order for the given spectral resolution while avoiding overfitting (Barnett and Seth, 2014). The obtained m values were in the range of 5–7, equivalent to 20–28ms. Granger causality indices were calculated using the ft_connectivity function from the FieldTrip toolbox, for the frequency range 5–50 Hz, with 1 Hz frequency resolution. Significance of Granger causality indices was tested by creating a null distribution, consisting of 100 trial sets. For each trial set, LFP signals from the randomly selected 50% of trials were reversed in the time domain. Granger causality was assessed for several functionally relevant bands (theta 5–10 Hz, beta 15–30 Hz and low gamma 31–50 Hz).

Statistical Analyses

Two-way repeated measures ANOVA (both variables were repeated measures) was used to assess the main effect of sleep session (pre-versus post- task sleep), the main effect of compression factor (‘no compression’, 4x, 6x, 8x, and 10x), and interactions (sleep session x compression factor) on template matching measures. Significant interactions were followed up by planned comparisons (F-tests) comparing pre-task versus post-task-sleep for each compression factor. Except where noted otherwise, p<0.05 was considered statistically significant. For example, one exception was for self-motion map correlations, for these analyses we used the historical critical value of 0.01 (Whitlock et al., 2012; Wilber et al., 2014). In addition, center of mass latencies for different electrode spike trains were compared with two-tail t-test. Distributions of Z-scores for the original and shuffled templates were compared with Kolmogorov-Smirnov test. In the case where all pairwise comparisons were made, tests were followed by Bonferroni correction for multiple comparisons. All p-values<0.0001 were listed as p<0.0001 no matter how small (i.e., p<0.0000001 was listed as p<0.0001). Granger causality from channel A to B was considered significant for a given frequency band (theta, beta or gamma) if the Granger indices for at least 1/3 of frequency bins within band were above the 99% confidence interval of the shuffled distribution. Two-way repeated measures ANOVAs were performed using Prism (GraphPad Software) and all other statistical analyses were performed in MATLAB. Sample sizes were not predetermined with statistical methods, but were based on the standard for the field. Statistical details of the experiment can be found in this section of the methods, and in some cases in the results and figure legends. N can represent the number of tetrodes, data sets, trials or rats and is specified where the data is presented. Nearly all descriptive statistics are presented as Mean+/−Standard Error of Mean (SEM), except in the rare case, that we felt standard deviation (SD) was the more appropriate way to present the data. In all cases use of SEM or SD is specified.

DATA AND SOFTWARE AVAILABILITY

The datasets and custom MATLAB code will be made available upon reasonable request.