Analyzing optical imaging of Ca²⁺ signals via TIRF microscopy: the limits on resolution due to chemical rates and depth of the channels

Abstract

High resolution total internal reflection (TIRF) microscopy (TIRFM) together with detailed computational modeling provides a powerful approach towards the understanding of a wide range of Ca²⁺ signals mediated by the ubiquitous inositol 1,4,5-trisphosphate (IP₃) receptor (IP₃R) channel. Exploiting this fruitful collaboration further requires close agreement between the models and observations. However, elementary Ca²⁺ release events, puffs, imaged through TIRFM do not show the rapid single-channel openings and closings during and between puffs as are present in simulated puffs using data-driven single channel models. TIRFM also shows a rapid equilibration of 10ms after a channel opens or closes which is not achievable in simulation using standard Ca²⁺ diffusion coefficients and reaction rates between indicator dye and Ca²⁺. Furthermore, TIRFM imaging cannot decipher the depth of the channel with respect to the microscope, which will affect the change in fluorescence that the microscope detects, thereby affecting its sensitivity to fast single-channel activity. Using the widely used Ca²⁺ diffusion coefficients and reaction rates, our simulations show equilibration rates that are eight times slower than TIRFM imaging. We show that to get equilibrium rates consistent with observed values, the diffusion coefficients and reaction rates have to be significantly higher than the values reported in the literature, and predict the channel depth to be 200–250nm. Finally, we show that with the addition of noise, short events due to 1–2ms opening and closing of channels that are observed in computational models can be missed in TIRFM.

Introduction

Calcium (Ca²⁺) is a universal signaling ion that controls diverse cellular functions. [3, 4, 13]. Elucidating Ca²⁺ signaling mechanism is therefore crucial for not only normal cell function but also understanding a wide range of pathological conditions such as neurological diseases [2, 5, 10, 11, 30], heart diseases [32], and mitochondrial dysfunction [15, 20, 30, 33, 34].

High resolution fluorescence microscopy and patch-clamp are the two main experimental techniques used for investigating wide range of Ca²⁺ signals from single channel events called blips to puffs due to concerted opening of multiple channels in a cluster of a few channels to whole cell waves. Recent advances in imaging techniques enable us to resolve Ca²⁺ signals at the single channel level within the intact environment [9, 10, 25, 29]. Nevertheless, they are unable to disect the coupling between individual channels as a function of their spatial organization, and connecting the single channel function to global Ca²⁺ signals. Patch-clamp techniques on the other hand, provide exquisite resolution of channel gating, but provide no spatial information [24]. Patch-clamp techniques are also bounded by the intracellular location of IP₃R which causes them to be inaccessible to patch-clamp recording within intact cells. Other studies involving excised nuclei or lipid bilayer reconstitution provide no spatial information and disrupt Ca²⁺-induced Ca²⁺ release (CICR) processes that determines interactions between channels in a cluster [13, 29]. None of these techniques is capable of addressing the full spectrum of Ca²⁺ signals. Modeling approaches can bridge these scales, but on the other, require step-by-step validation by experiments to make meaningful predictions.

Over the last twenty five years several models for the kinetics of single IP₃R have been developed [7, 8, 14, 22, 27, 28, 31, 36, 37]. Two models in particular replicate all observations about single IP₃R including the gating of the channel in 3 distinct gating modes over a broad range of ligand dependencies, dwell-times, and latency distributions [7, 22, 28, 36]. Both these models were built on extensive single-channel patch-clamp data on IP₃R [17, 18, 23, 39].

Cluster models built on Ullah’s and Siekmann’s models reproduce many observations about puffs [6, 7, 36, 38]. However, one major discrepancy between these models and experimental studies exists. Simulated puffs exhibit high amount of single-channel activity as compared to experimental TIRFM signals. Unlike experimental data, both models exhibit, fast (1–2ms duration) opening and closings of single channels between and during puffs. While investigating this discrepancy was a motivating factor for this study, we found that besides the possible missed single-channel events in TIRFM experiments, the widely accepted values of the free Ca²⁺ diffusion coefficient (D_Ca), and the binding/unbinding rates of Ca²⁺ to dye (α_f, β_f) are too slow to account for experimentally observed single-channel TIRFM signals. Experimental values of D_Ca in cytoplasm have ranged from 530µm²/s [12] to the most widely accepted and cited value of 223µm²/s [1]. Here, we show that the accepted values of D_Ca, α_f, and β_f used in computational studies are incompatible with experimentally observed TIRFM events, and examine the implications on TIRFM of these new parameters through simulated puffs. We find that to replicate single channel and puff TIRFM signals, larger values of D_Ca and on/off rates must be used. We also show that such short 1–2ms opening and closings of channels can be missed in TIRFM when the optimal experimental signal-to-noise ratio (SNR) of greater than or equal to 8 is considered.

Computational Methods

The Model

We follow the protocol outlined in [26] and simulate the diffusion of Ca²⁺ throughout the cuboid cytosolic space as shown in Fig. 1a in [26]. The bottom of the cubic box represents the ER membrane where a single Ca²⁺ channel is placed at the center. No-flux boundary conditions are applied to the plasma membrane while the other five sides of the box are held at a constant resting concentration for all signaling species.

Figure 1.

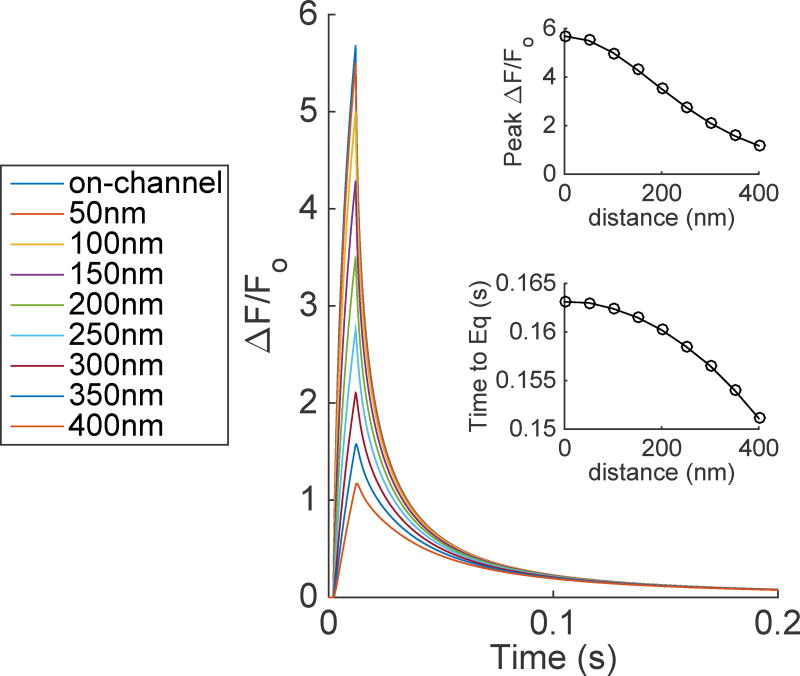
Time evolution of TIRFM signals from a 10ms single Ca²⁺-channel opening. The distance in the positive x-direction was varied to show how ΔF/F_o is dependent upon distance from the channel. The top and bottom insets show the peak ΔF/F_o and time to equilibrate (Time to Eq.) after the channel has closed as a function of distance from the channel. Using standard conditions: D_Ca=223µm²/s, D_CaF=15µm²/s, α_f=150 µM⁻¹s⁻¹, and β_f=450 s⁻¹.

The model includes the following species [26]: cytosolic free calcium ions (Ca²⁺), free stationary buffer (S), Ca²⁺-bound S (CaS), free cytosolic Ca²⁺ indicator dye (Cal), and Ca²⁺-bound cal (CalCa). In Figs 6 and 7, we evaluate the effect of mobile buffer (M), EGTA, on the simulation results. CalCa can represent any fluorescent Ca²⁺ indicator dye, but our parameter values listed in Table 1 correspond to Cal-520. Indicator dye Cal-520 has recently been shown to be the optimal indicator for faithfully detecting Ca²⁺ puffs [21].

Figure 6.

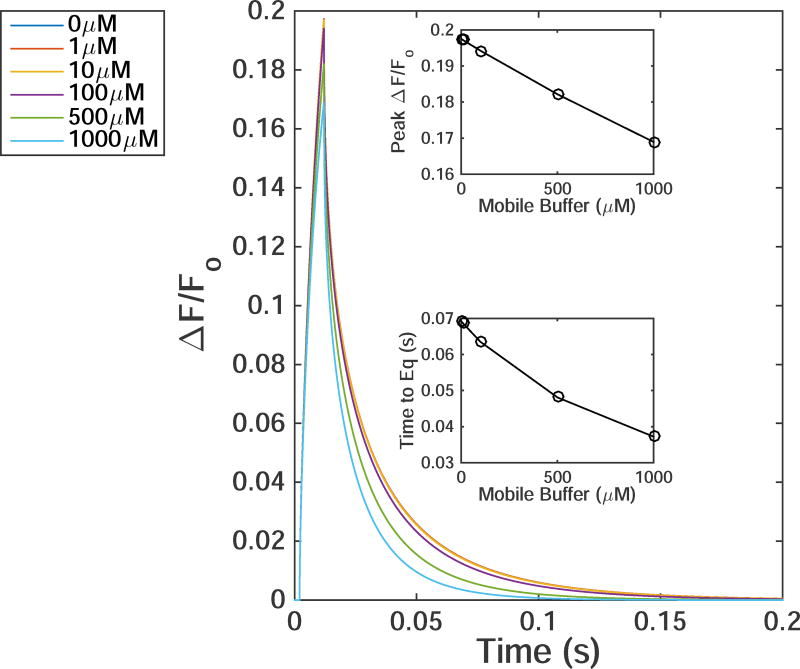
Time evolution of TIRFM signals from a 10ms single Ca²⁺-channel opening with increasing value of [EGTA]. For all simulations D_Ca=223µm²/s, D_CaF=74µm²/s, α_f=100/(µMs), and β_f=33/s was used. The top and bottom-inset shows the peak ΔF/F_o and time to equilibrate after the channel closes as a function of mobile buffer, respectively.

Figure 7.

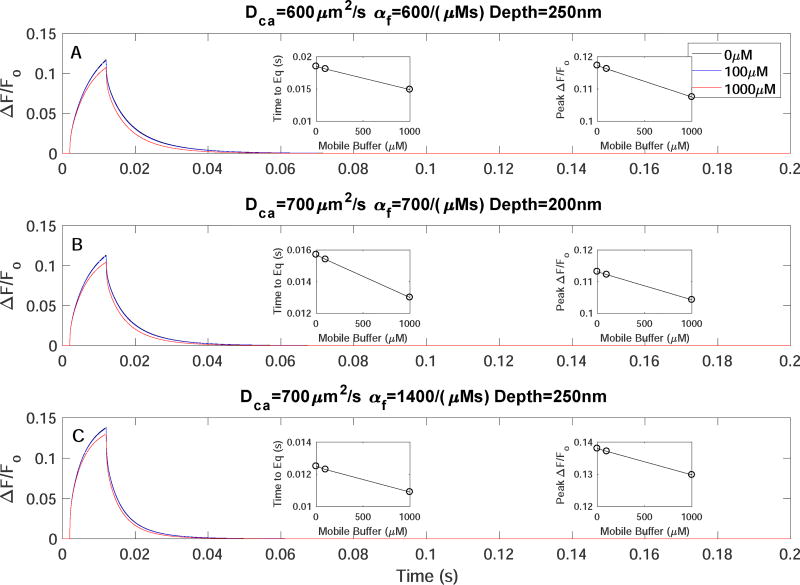
Mobile buffer EGTA does not affect the kinetics of TIRFM signals. Time evolution of TIRFM signals from a 10ms single Ca²⁺-channel opening with increasing [EGTA]=0 (black),100 (blue), 1000µM (red) for A) D_Ca=600µm²/s, α_f=600/(µMs), depth=250nm, B) D_Ca=700µm²/s, α_f=700/(µMs), depth=200nm, and C) D_Ca=700µm²/s, α_f=1400/(µMs), depth=250nm.

Table 1.

Parameter values used for simulations

Parameters	Values
Height of cytosol box	2.05µM
Length of cytosol box	4.05 µM
Width of cytosol box	4.05 µM
Free Ca2+ diffusion coefficient (Dca)	200–700 µm2s−1
Resting Ca2+ concentration ([Ca2+]rest)	0.05 µM
Bound indicator dye and Ca2+ diffusion coefficient (DCaF)	Dca/3
Total indicator dye concentration ([Cal]T)	40µM
Dissociation constant (κF)	0.3 µM
Smoluchowski capture radius (rc)	0.00005–0.0008µm
On-rate (αf)	see eq. 3 µM−1s−1
Off-rate (βf)	κF*αf
Mobile Buffer (EGTA) diffusion Coefficient (DCaM)	200 µm2s−1
Total mobile buffer concentration ([EGTA])	0µM – 1000µM
Dissociation constant (κM)	0.15 µM
On-rate (αm)	5 µM−1s−1
Off-rate (βm)	0.75 s−1
Total stationary buffer concentration ([S]T)	300 µM
Dissociation constant (κT)	2 µM
On-rate (αs)	400 µM−1s−1
Off-rate (βs)	800 µM−1s−1
Maximum Ca2+ current (IMax)	0.1 pA
Endoplasmic Reticulum concentration ([Ca2+]Er)	600 µM

We consider reactions of S, M, and Cal with free Ca²⁺ as

$$[{\text{Ca}}^{2+}]+[X]\underset{{\beta }_X}{\overset{{\alpha }_X}{\rightleftharpoons }}[\text{CaX}]$$ (1)

where X represents S, M, or Cal, α and β are the forward and backward binding rate, and [] represents the concentration of different species, respectively.

The reaction-diffusion equations for free Ca²⁺ with diffusion coefficient D_Ca is:

$$\frac{\partial [{\text{Ca}}^{2+}]}{\partial t}={\mathrm{D}}_{\text{Ca}}{\nabla }^2[{\text{Ca}}^{2+}]+{\delta }_0{\mathrm{J}}_{\text{Ch}}+{\beta }_{\mathrm{s}}[\text{CaS}]-{\alpha }_s[{\text{Ca}}^{2+}]{([\mathrm{S}]}_{\mathrm{T}}-[\text{CaS}])+{\beta }_{\mathrm{f}}[\text{CalCa}]-{\alpha }_f[{\text{Ca}}^{2+}]({[\text{Cal}]}_{\mathrm{T}}-[\text{CalCa}])+{\beta }_{\mathrm{m}}[\text{CaM}]-{\alpha }_m[{\text{Ca}}^{2+}]({[\mathrm{M}]}_{\mathrm{T}}-[\text{CaM}])$$ (2)

in which the channel distribution function δ₀ is 1 at the grid element containing the channel and 0 otherwise. The binding rate, α_f is given by the equation:

$${\alpha }_f=4\pi {\mathrm{r}}_{\mathrm{c}}({\mathrm{D}}_{\text{Ca}}+{\mathrm{D}}_{\text{CaF}})$$ (3)

where r_c is the Smoluchowski capture radius of dye for free Ca²⁺. D_Ca and D_CaF are the diffusion coefficients for free Ca²⁺ and Ca²⁺-bound dye, respectively [35]. Note that typical units for rate constants are 1/(µMs), while typical units for r_c are length (10⁻³µm) and diffusion coefficients are typically given in µm²/s. To convert α_f from units of µm³/s to 1/(µMs) we multiply the right hand side of eq. 3 by 602/(µm³µM). The rate equation for [CalCa] is given as

$$\frac{\partial [\text{CalCa}]}{\partial t}=D_{\text{CaF}}{\nabla }^2[\text{CalCa}]+{\alpha }_{\mathrm{F}}({[\text{CalCa}]}_{\mathrm{T}}-[\text{CalCa}])-{\beta }_{\mathrm{F}}[\text{CalCa}].$$ (4)

For Ca²⁺-bound M, CaM with diffusion coefficient D_CaM, we have

$$\frac{\partial [\text{CaM}]}{\partial t}=D_{\text{CaM}}{\nabla }^2[\text{CaM}]+{\alpha }_{\mathrm{M}}({[\text{CaM}]}_{\mathrm{T}}-[\text{CaM}])-{\beta }_{\mathrm{M}}[\text{CaM}].$$ (5)

CaS is given by the rate equation,

$$\frac{\partial [\text{CaS}]}{\partial t}={\alpha }_S({[\mathrm{S}]}_{\mathrm{T}}-[\text{CaS}])-{\beta }_{\mathrm{s}}[\text{CaS}]$$ (6)

The total concentrations for Ca²⁺ indicator ([Cal]_T), EGTA ([M]_T), and stationary buffer ([S]_T) are given in Table 1. The channel flux is expressed as

$${\mathrm{J}}_{\text{Ch}}=\frac{{\mathrm{I}}_{\text{Ch}}}{2\mathrm{F}\delta \mathrm{V}},$$ (7)

where F=9.65×10⁻¹¹ CFmol⁻¹, δV is the small cytosolic volume around the channel pore (dx³ where dx = 50nm) and the single channel current is given by I_Ch=υ_Ch([Ca²⁺]_Er−[Ca²⁺]) where [Ca²⁺]_Er is Ca²⁺ concentration in the ER and υ_Ch is the maximum Ca²⁺ flux through the channel. The maximum value of the channel current (I_Max) that would flow immediately upon opening of the channel is I_Max=υ_Ch[Ca²⁺]_Er because the resting free cytosolic [Ca²⁺] is negligible (50nM).

The resting values of [CalCa], [CaM], and [CaS] are given as:

$${[\text{CalCa}]}_{\text{Rest}}=\frac{{[\text{CalCa}]}_{\mathrm{T}}}{1+\frac{{\kappa }_{\mathrm{F}}}{{{\text{Ca}}^{2+}}_{\text{Rest}}}}$$ (8)

$${[\text{CaM}]}_{\text{Rest}}=\frac{{[\text{CaM}]}_{\mathrm{T}}}{1+\frac{{\kappa }_{\mathrm{M}}}{{{\text{Ca}}^{2+}}_{\text{Rest}}}}$$ (9)

and

$${[\text{CaS}]}_{\text{Rest}}=\frac{{[\text{CaS}]}_{\mathrm{T}}}{1+\frac{{\kappa }_{\mathrm{S}}}{{{\text{Ca}}^{2+}}_{\text{Rest}}}}$$ (10)

The finite difference method was used to solve the partial differential equations given in this section. We used a time increment, Δt=0.5µs and spatial grid Δx=50nm. Thus, the cytosolic space was represented by a lattice of 81×81×41 grid elements as in [26].

Calculating fluorescence signals

Our aim is to simulate TIRFM signals from a single IP₃R channel and compare them to signals recorded in [21, 29]. The model takes into account changes in [CalCa] that occur in 4 dimensions (x,y,z,time). We assume that fluorescence is linearly proportional to [CalCa] in which free [Cal] is non-fluorescent and a calculated weighted average of [CalCa] throughout the cytosolic volume corresponding to the microscope point-spread-function (p.s.f.) is used to predict changes in fluorescence that would be imaged experimentally. Representative p.s.f.’s of TIRF microscopes can be found in Fig. 5B in [26] in which the p.s.f. follows a Gaussian function in the lateral plane, but decays exponentially in the axial (z) dimension. In the simulations presented here, we focus the microscope on the plane of the ER membrane (bottom of the box in [26]). The TIRFM signal at any given point (x,y,z) is given by:

$$\text{TIRF}(\mathrm{x},\mathrm{y},\mathrm{z})=\frac{1}{{\mathrm{V}}_{\text{TIRF}}}\int \int \int \text{dxdydz}[\text{CalCa}](\mathrm{x},\mathrm{y},\mathrm{z})\mathrm{x}\text{ exp }(-\frac{{(\mathrm{x}-{\mathrm{x}}_o)}^2}{{\sigma }_{\mathrm{x}}}-\frac{{(\mathrm{y}-{\mathrm{y}}_0)}^2}{{\sigma }_{\mathrm{y}}})\text{ exp }(-\frac{\mathrm{z}}{{\gamma }_{\mathrm{z}}})$$ (11)

where σ_x=σ_y=0.0225µm² and γ_z=0.15µm² which replicates the experimentally observed lateral full width at half maximum (FWHM) of 250 nm and an e-fold decline over 150nm in the axial direction. V_TIRF is defined as the weighted volume at the channel point:

$${\mathrm{V}}_{\text{TIRF}}=\int \int \int \text{dxdydz exp}(-\frac{{\mathrm{x}}^2}{{\sigma }_{\mathrm{x}}}-\frac{{\mathrm{y}}^2}{{\sigma }_{\mathrm{y}}})\text{ exp }(-\frac{\mathrm{z}}{{\gamma }_{\mathrm{z}}})$$ (12)

Figure 5.

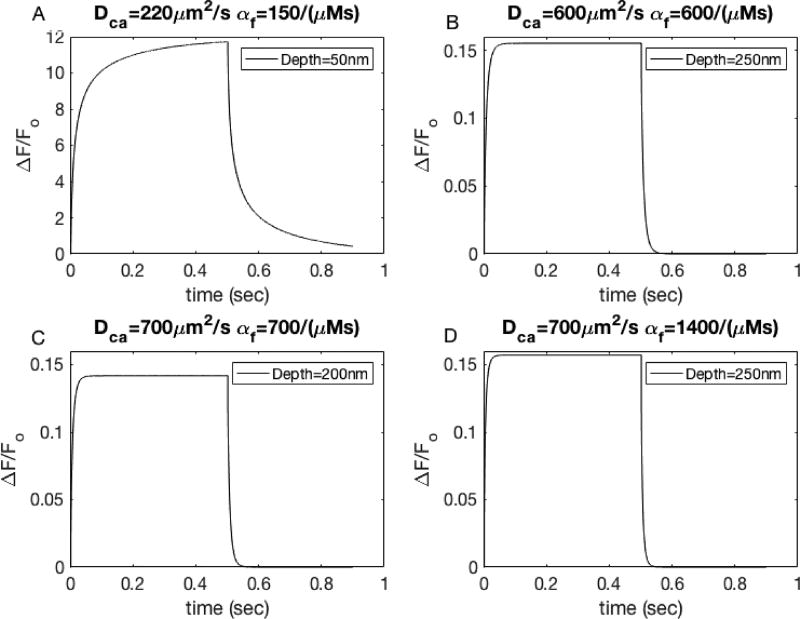
Higher diffusion coefficients and on- and off-rates for Ca²⁺ binding to dye lead to single channel events that resemble those observed experimentally. Simulation of 500ms channel opening under (A) standard conditions of D_Ca=223µm²/s, α_f=150/(µMs), depth=50nm, (B) D_Ca=600µm²/s, α_f=150/(µMs), depth=250nm, (C) D_Ca=700µm²/s, α_f=700/(µMs), depth=200nm, and (D) D_Ca=700µm²/s, α_f=1400/(µMs), depth=250nm.

Results

Fig. 1 shows the time evolution of TIRFM signals originating from a single Ca²⁺-channel located on the plasma membrane (bottom of the box). We let the channel open for 10ms - typical mean open time for single IP₃R [26, 29]. The diffusion coefficients used in Fig. 1 for free Ca²⁺ and Ca²⁺ bound fluorescent dye are the values that have been widely accepted and cited. We will call these standard conditions (see Table 2) [1]. In this figure, we vary the microscope distance with respect to the positive x-direction in order to illustrate how the peak change in fluorescence (ΔF/F_o) and time to equilibration is inversely proportional to the lateral distance of the microscope from the channel.

Table 2.

Standard Condtions for Ca²⁺ signaling

Parameters	Values
Free Ca2+ diffusion coefficient	223 µm2s−1
Bound indicator dye and Ca2+ diffusion coefficient	15 µm2s−1
Dissociation constant (κF)	3.0 µM
On-rate (αf)	150 µM−1s−1
Off-rate (βf)	κF*αf

It has been shown experimentally that fluorescence signals due to single channel events from IP₃R termed ’unitary blip’ show a maximum ΔF/F_o of 0.11 ± 0.01 [21, 29] for both widely used Ca²⁺ fluorescent dyes Fluo-4 and Cal-520. Multiple channel events, puffs, have higher ΔF/F_o of approximately 2–3. It is clear from the top-inset of Fig. 1 that the peak ΔF/F_o is much higher when we focus directly on the single Ca²⁺-channel. Furthermore, it was reported that a blip displays a ”rectangular” signal, demonstrating equilibration between the Ca²⁺ through the channel and the fluorescent dye in the cytoplasm of 10–15ms (see Fig. 2 of [29]). It is clear from Fig. 1 that unlike experimental observations, ΔF/F_o does not reach equilibrium in 10ms. Once the channel has closed, we see a rapid drop in ΔF/F_o. The bottom-inset of Fig. 1 shows the time till equilibration is reached, which is taken to be ΔF/F_o=0.01, as this is below the baseline noise observed experimentally. As expected, the time to equilibration is inversely proportional to the distance from the channel. Just 400nm from the channel, the time far exceeds the experimentally observed values of 10–15ms [21, 29].

Figure 2.

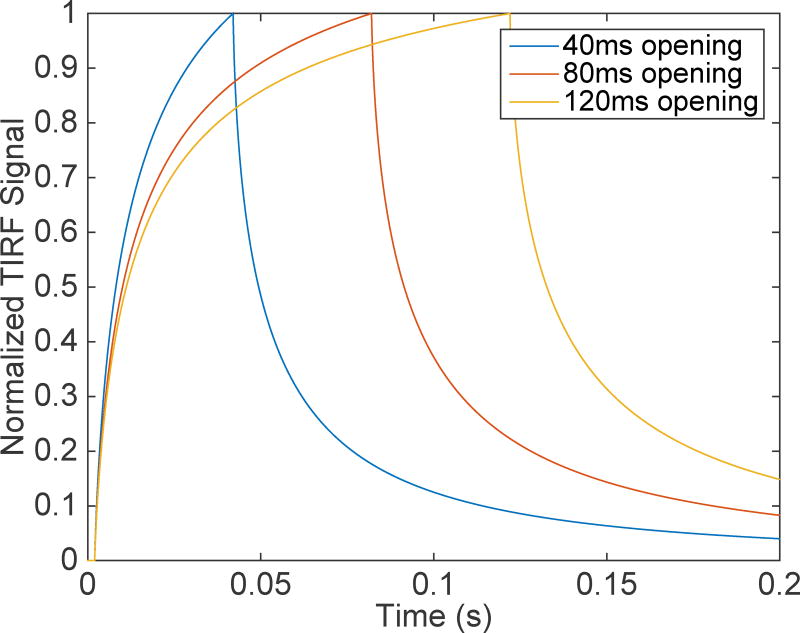
Time evolution of normalized TIRF signals for 40ms (Blue), 80ms (Red), and 120ms (yellow) single Ca²⁺-channel openings.

To further illustrate the point that standard conditions and on-/off- rates widely used in simulation are too slow, Fig. 2 shows normalized single Ca²⁺-channel events for various open times of the channel. We allow the channel to remain open for 40ms (blue), 80ms (red), and 120ms (yellow). It is clear that even with the longer duration, the TIRF signal does not equlibrate with channel openings 12 times longer than the mean open time reported in experiments.

Channel depth analysis

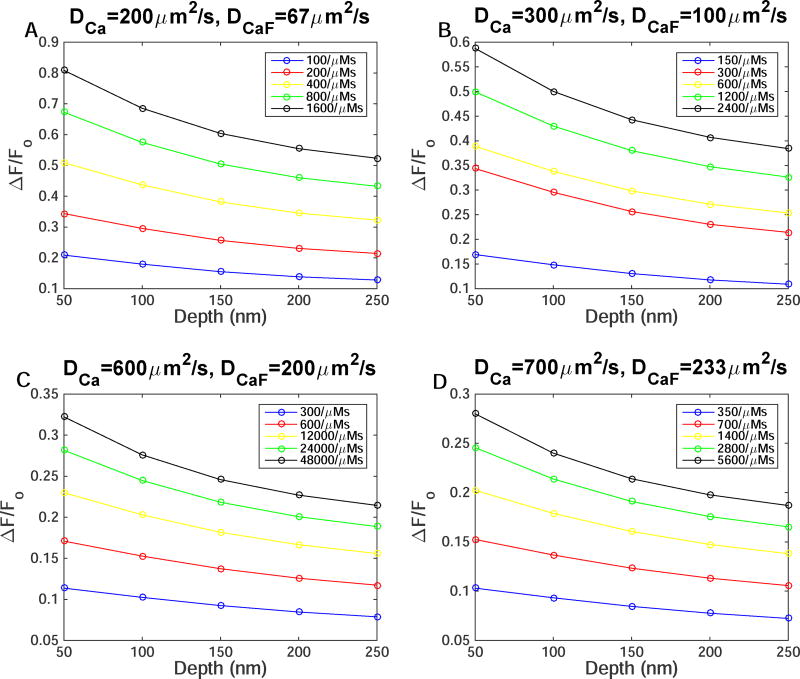
In TIRFM experiments, the user has control of the microscope stage in the (x,y) direction, but the depth of the channel or cluster that is being focused on is somewhat unknown. In the following, we vary the depth of the channel with respect to the microscope to evaluate the effect of the channel depth on TIRFM signal. We also vary the reaction rate for Ca²⁺ binding to the dye and the diffusion coefficients of free Ca²⁺ (eq 3) to look for the conditions where the dye kinetics from simulation would match experimental observations. For the remaining of this paper, we keep the diffusion coefficients of Ca²⁺-bound dye to be one-third of D_Ca. Fig. 3 shows peak ΔF/F_o after a 10ms single Ca²⁺-channel opening for D_Ca=200 (Fig. 3a), 300 (Fig. 3b), 600 (Fig. 3c), and 700 µm²/s (Fig. 3d). Lines with different colors represent different on- and off -rates for Ca²⁺ binding to the dye. For example, the blue line represents r_c=0.00005µm, and we double r_c each time so that the red line represents r_c=0.0001µm and so on up to r_c=0.0008µm (black line). The legend for each box shows the on-rate (α_f) for each set of simulations. We then vary the depth of the channel but keep the microscope focused on the (x,y) grid of the channel (unlike Fig. 1). We vary r_c within a reasonable range to vary α_f. Note that β_f changes accordingly in order to keep the dissociation constant fixed at experimentally observed values. As expected, the maximum ΔF/F_o decreases as the depth increases. Fig. 3 also shows an inverse relation between D_Ca and ΔF/F_o. That is, as we increase D_Ca, peak ΔF/F_o decreases. Increasing α_f increases ΔF/F_o. We can pick out several combinations for D_Ca, α_f, and depth of the channel that would result in experimentally observed ΔF/F_o for single Ca²⁺-channel events (~ 0.11 ΔF/F_o) but the time to equilibration must also be accounted for in order to make a comparison between theoretical and experimental values.

Figure 3.

The effect of diffusion coefficients, depth of the channel, on- and off-rates of Ca²⁺ binding to the dye on peak fluorescence. Maximum ΔF/F_o as a function of depth as α_f increases due to increasing r_c with (A) D_Ca=200µm²/s, (B) D_Ca=300µm²/s, (C) D_Ca=600µm²/s, and (D) D_Ca=700µm²/s.

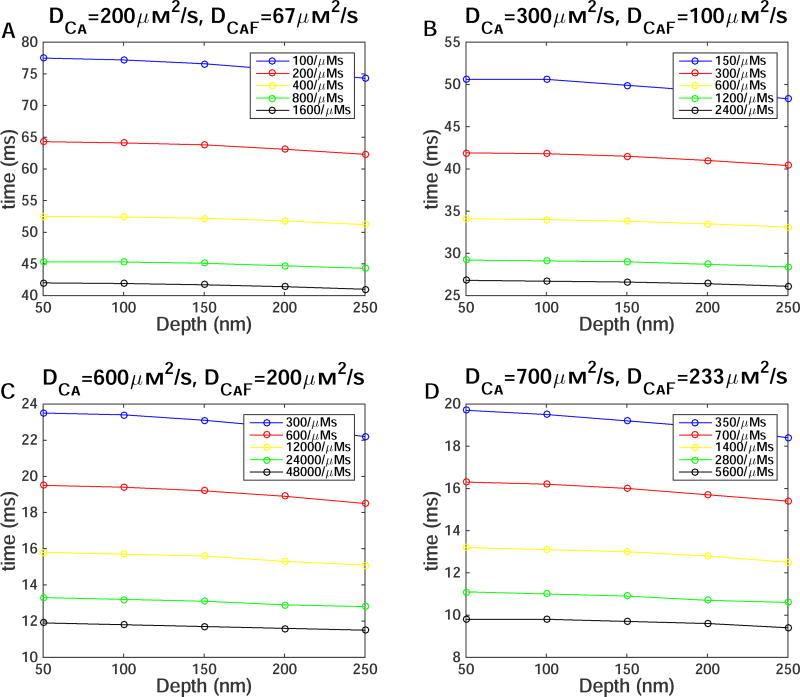
Fig. 4 shows the duration that the TIRFM signal takes to equilibrate after the channel closes in simulations from Fig. 3. The equilibration time decreases as we increase D_Ca and α_f. We can use Fig. 3 and Fig. 4, to map the parameters D_Ca, α_f, and depth of the channel that would replicate experimentally observed fluorescence signals. As discussed above, experimental TIRFM during blips reach peak ΔF/F_o ~ 0.11 and equilibrate in 10–15ms after the channel closes. These simulations show that D_Ca and α_f must be much higher than the widely used values. Furthermore, the depth of the channel clearly makes a difference in the peak ΔF/F_o value that is recorded in experiments. The parameter values that most closely reproduce the kinetics of indicator dye used in TIRFM are 1) D_Ca=600µm²/s, α_f=600/(µMs), depth=250nm, 2) D_Ca=700µm²/s, α_f=700/(µMs), depth=200nm, and 3) D_Ca=700µm²/s, α_f=1400/(µMs), depth=250nm.

Figure 4.

The effect of diffusion coefficient, depth of the channel, on- and off-rates of Ca²⁺ binding to dye on equilibration time. Time to equilibration after the channel closes as a function of depth as the α_f increases due to increasing r_c with (A) D_Ca=200µm²/s, (B) D_Ca=300µm²/s, (C) D_Ca=600µm²/s, and (D) D_Ca=700µm²/s.

To illustrate how these parameters result in fluorescence signals that closely resemble the experimentally observed TIRF signals, we simulate a 900ms experiment in which a channel is open for 500ms. Fig. 5A shows standard conditions. Like Fig. 2, the signal continues to rise even if we let the channel stay open longer than 500ms. Furthermore, the ΔF/F_o is 2 orders of magnitude higher than the unitary signal. Fig. 5B–D shows the 500ms channel-opening simulation for the 3 sets of parameters mentioned above. It is clear, that the larger values of D_Ca, α_f, and depth of the channel produce a signal that more closely resembles the unitary signal seen in the experiments. The signal equilibrates and plateaus in around 10ms and once the channel closes, the decay is within the same time period. Also, the peak value of ΔF/F_o is much closer to the 0.11 value. Later, these parameter sets will be used for simulating puffs to determine possible missed events in TIRFM signals.

The effect of mobile buffer EGTA on peak fluorescence and equilibration time

The above simulations did not consider any mobile Ca²⁺ buffer other than the Cal-520 indicator dye. In the following, we include mobile buffer EGTA to see if it changes the conclusions above. Fig. 6 shows the time trace of simulated single-channel TIRFM signals in the presence of various concentrations of EGTA. For each simulation D_Ca=223µm²/s, D_CaF=74µm²/s, α_f=100/(µMs) are used. The top and bottom insets show the peak ΔF/F_o and time to equilibrate, respectively for each simulation as a function of [EGTA]. For [EGTA] of 1–10µM the difference in peak ΔF/F_o and time to equilibrate is essentially negligible. At 100µM the peak ΔF/F_o and time to equilibrate is 10% and 28% smaller respectively, as compared to control conditions (no EGTA). Increasing [EGTA] to 1000µM increases these differences to 15% and 33%, respectively. Thus, even adding a 1000µM [EGTA] wouldn’t result in dye kinetics consistent with experimental observations at standard parameter values. To further illustrate the point that the mobile buffer does not change our final conclusions, we show the effect of 100µM and 1000µM [EGTA] on TIRFM signals using the 3 optimal parameter sets deduced above (Fig. 7). The insets in each panel show the time to equilibrate once the channel is closed (left) and the peak ΔF/F_o (right) for the corresponding parmaters with varying [EGTA]. The same modest change in kinetics of TIRFM signal is observed.

Possible Experimentally Missed Events

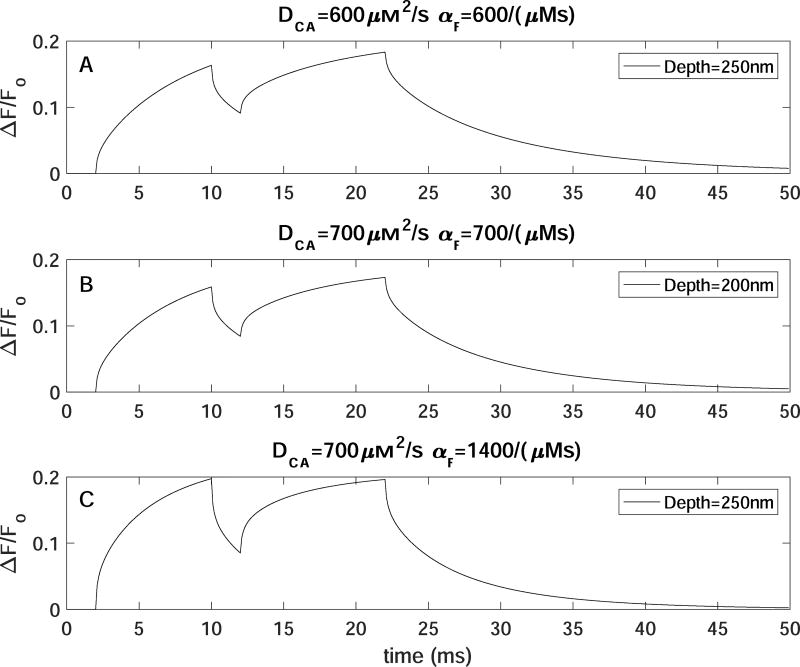
Fig. 8A–C shows a simulated time trace from two channels in a cluster in which the microscope is focused on the first channel at the center of the box and the second channel is located 100nm in the negative x-direction. We use the three optimal sets of parameters in the conditions with no EGTA. We simulate a situation in which the second channel opens 2ms after the first channel closes. In Fig. 8A–B, ΔF/F_o reaches ~0.15 during the 8ms opening of 1st channel. Once the first channel closes at t=10ms, ΔF/F_o drops to 0.9 before the second channel opens at 12ms where ΔF/F_o starts increasing again. Within 5ms of a channel closing and another channel opening 2ms later, the TIRFM signal reaches its peak value from the first opening. Fig. 8C shows the same sequence of events, except the peak ΔF/F_o from the first channel opening is ~0.2. These simulations have an infinite SNR which is unrealistic for TIRFM experiments. We thus expand this experiment to include 5 channels on a cluster and add a SNR of 8 in the same manner as the molecular shot noise in section 4.3 of [26]. We choose a SNR of 8 because that is the optimal SNR achieved in experiments for Cal-520 when comparing different fluorescent dyes [21]. The channels are laid out so that the first channel is in the center of the box, the other 4 channels are placed at (x,y) coordinates of (−100,0), (100,0), (0,−100), and (0,100) in nm with respect to the center channel. With this set-up, we simulate a puff such that at the peak of the puff, a single channel closes, and another opens 2ms later, just as in Fig. 8.

Figure 8.

Simulating two channels with optimal conditions. Time trace simulation of 2 channels in which the second channel located 100nm away from the center channel opens 2ms after the first channel closes with (A) D_Ca=600µm²/s, α_f=150/(µMs), depth=250nm, (B) D_Ca=700µm²/s, α_f=700/(µMs), depth=200nm, and (C) D_Ca=700µm²/s, α_f=1400/(µMs), depth=250nm

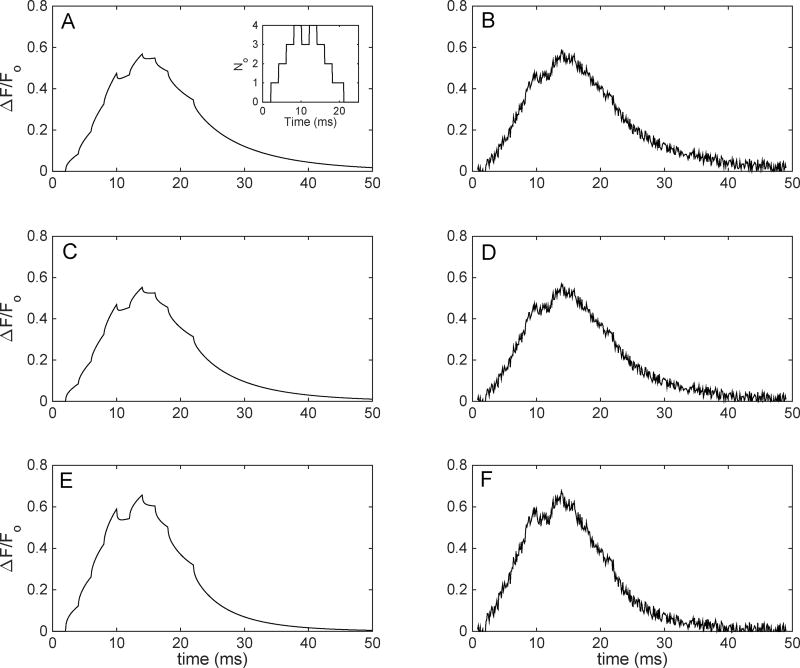
Fig. 9 shows time traces of the number of channels open and the TIRFM signal for the simulated puffs as described above. As the inset in Fig. 9 shows, the first channel opens at t=2ms, with the next 3 opening at 2ms intervals afterwards. At t=8ms we have 4 channels open, then the first channel closes at 10ms, leaving 3 channels open. At 12ms, the last channel opens, which creates the same situation at the peak of the puff as in Fig. 8. The remaining channels close at 14ms, 16ms, 18ms, and 22ms. Time traces for these events for the 3 optimal conditions without and with noise are shown in the left and right column, respectively. With noise, the 2ms closing and opening that happens between 12 and 14ms creates a plateau in the TIRFM signal as is regularly seen in experimental TIRFM signals [29]. These plateaus have been attributed to a single channel that stays open until the next channel opens or closes which would change the TIRFM signal and would be detected by the experiment. Thus, at 10ms the TIRFM experiment would determine that 4 channels are open, whereas only 3 are open until 12ms when the 4th channel opens without noise, where in experiment this would be mistaken for a 5th channel opening. Without noise, (Fig. 9A,C,E) the closure of the channel at 10ms is clearly visible but is washed out by the addition of noise (Fig. 9B,D,F) as is present in TIRFM experiment. Thus, we believe that a closure of one channel and reopening of another within 2ms would result in a missed event. As mentioned before, the depth of the cluster is unknown to the user and any cluster at a depth greater than 250nm could lead to many single-channel events that occur within 2ms to be washed out by the noise in the system. Furthermore, with the addition of high concentrations of [EGTA] (not shown), ΔF/F_o would decrease further, and thus would make it relatively more difficult to experimentally estimate the number of open channels and short openings and closings.

Figure 9.

Time traces of a 5 channel puff simulation under various conditions with-out and with noise with a SNR equal to 8. Puff simulation at D_Ca=600µm²/s, α_f=150/µMs, depth=250nm (A, B), D_Ca=700µm²/s, α_f=700/µMs, depth=200nm (C, D), and D_Ca=700µm²/s, α_f=1400/µMs, depth=250nm (E, F). Panels in left column are without noise, while those in the right columns are with noise.

Discussion

A close agreement between computational and experimental tools is crucial in developing a clear picture of the mechanisms of Ca²⁺-release through IP₃R and bridging several spatiotemporal scales of Ca²⁺ signaling ranging from single channel events to waves at whole cell and tissue levels. Recent advances in patch clamp and imaging techniques have enabled us to develop realistic models of Ca²⁺ signaling. Predictions from these models are quantitative in nature and allow direct comparison with experiments. Optical approaches such as TIRFM in particular have made it possible to provide information about channels that are inaccessible to patch clamp techniques. These high resolution imaging techniques also provide spatial information about channel locations, and allow simultaneous recordings through multiple channels. Studying Ca²⁺-release through IP₃R channels with TIRFM is especially helpful because of their location on the ER membrane. However, some discrepancies between the detailed biophysical models and TIRFM exist that need to be addressed. In particular, we report that the widely accepted values of diffusion coefficient of Ca²⁺ and the binding and unbinding rates of Ca²⁺ to the imaging dye lead to inconsistencies between experimental and theoretical results. All these parameters are key to Ca²⁺ signaling and interpreting experimental results.

Previously, Ca²⁺ range of action was determined by measurement of its diffusion coefficient in cytosolic extract from Xenopus laevis oocytes [1]. In Allbritton et al., 1992, the authors take precautions to avoid sequestration of Ca²⁺ by internal stores, that was not previously done in [16] when measuring movements of Ca²⁺. In [1], the Ca²⁺ was layered on top of cytosolic extract in a thin tube and allowed to diffuse for various periods of time. Once the tube was frozen, concentrations of the labeled radioactive Ca²⁺ was measured and the value of D_Ca was determined. The value of D_Ca was dependent upon the amount of free Ca²⁺ added to the cytosolic extract. The value of D_Ca=223µm²/s reported in [1] is the standard value that is widely accepted and used in theoretical studies. While many precautions were taken to measure D_Ca without sequestration, Fig. 3 of [1] shows the dependance of D_Ca on free Ca²⁺ added to the system and does not show signs of saturation at the reported value of 223µm²/s. Furthermore, the Allbritton et al., 1992 study did not cite a previous study [12] where similar sequestration precautions were taken and a value of D_Ca ~ 530µm²/s was reported.

As shown in Fig. 1 and Fig. 2, this widely accepted value for D_Ca used in many studies simulating blips and puffs, does not produce the results seen in single channel TIRFM. A theoretical study by Shuai and Parker in 2005 using the same modeling methods as used here, shows a similar result in which 10ms channel openings do not equilibrate and ΔF/F_o is much larger than experimental TIRFM single-channel openings. Although, this is not addressed in the study, they claim that under standard conditions, TIRFM should resolve single Ca²⁺-channel events as brief as 1 ms with a SNR ≥10 [26]. With these standard conditions that produce a larger TIRFM signal in simulations, the resolution of 1ms appears to be achievable; although they note that previously published experimental records do not achieve this resolution [26]. Making the D_Ca significantly larger (600–700µm²/s), as well as speeding up the on-/off- rates of Ca²⁺ binding to fluorescent dye, and considering the depth of the channel close to 200nm as in Fig. 3 and 4, allows us to determine parameters that closely resemble the experimental TIRFM signal for single-channel Ca²⁺-release through IP₃R. To our knowledge, the ’standard values’ for D_Ca is being widely used in most computational studies, although a value off D_Ca=600µm²/s was recently used to explore the link between bioenergetics and motor neuron degeneration [19]. A TIRFM study by [9], imaged Ca²⁺-permeable channels on the plasma membrane of Xenopus oocytes where they were able to simultaneously resolve gating kinetics, voltage dependance, and localization of channels. In the experimental set-up, the authors estimated a ~200nm distance between the cover glass of the microscope and the membrane. This estimate supports the channel distance estimated in our simulations. Fig. 5 shows the TIRFM time traces using the optimal parameters (D_Ca=600–700µm²/s, α_f =600–1400/(µMs), channel depth=200–250nm) that more closely resemble the experimental results for a single-channel opening as seen in [29] where single-channel TIRFM signal plateaus within 10–15ms of opening. The equilibration of the signal within 10–15ms upon the channel opening and closing and the max ΔF/F_o in Fig. 5B–D provide an optimal parameter set to model TIRFM signals from puffs.

One overlooked discrepancy between experimental TIRFM signals from puffs and simulations is the high amount of single channel activity that occurs in simulation (see Fig. 2 of [6]). Instead of having no channel activity to a sudden cooperative opening of IP₃R channels as seen in experiments, simulations show ’flickering’ of single-channels before the puff occurs. There is also significantly more single channel activity in simulated puffs as compared to observed puffs. Additionally, during a puff, TIRFM signals plateau quickly which appears to equilibrate before another channel opens [29]. With this in mind, we wanted to determine whether the TIRFM experiments can in fact detect single channel openings within a 2 ms time interval. That is, can TIRFM experiments using the best dye available, Cal-520 detect every channel closing and opening within 2ms resolution? We find that with the optimal values of D_Ca and on-/off- rates for Ca²⁺ binding to the dye that produce a TIRFM signal closer to experimental results, these 2ms events will be most likely missed for a SNR≥8. This could lead to reporting more channels open than interpreted by experiment.

Conclusion

Through computational modeling and comparison with experimental observations, we determine that D_Ca in the range of 600–700µm²/s yields a much better comparison with the TIFRM data. Similarly, the binding rate of Ca²⁺ with fluorescent dye yields a better comparison when the on rate is in the 600–1400/(µMs) range. While these parameters are much larger than previously reported, we find that these values lead to results that closely resemble TIRFM signals. Moreover, we are aware of no compelling physical arguments against the higher α_f and D_Ca rates. We also found that single channel events with duration less than 2ms will likely be missed.

Elementary Ca²⁺ release events imaged through total internal reflection fluorescence (TIRF) microscopy differs from those simulated through data-driven single channel models. We simulate TIRF signals due to single and cluster channels and determine diffusion coefficients and binding/unbinding rates for fluorescence dyes that display TIRF signals that more closely resemble experiment.