Abstract
Morphology is an important particle (both biological and synthetic) property and potentially a useful marker for label-free particle separation. We present in this work a continuous-flow morphology-based fractionation of a heterogeneous mixture of drug-treated yeast cells in dilute ferrofluids. Such a diamagnetic cell separation technique utilizes the negative magnetophoretic motion to direct pre-focused yeast cells to morphology-dependent streamlines in a laminar flow. The separation performance is evaluated by comparing the exiting positions of the four classified groups of yeast cells: Singles, Doubles, Triples, and Others. We also develop a three-dimensional numerical model to simulate the separation process by the use of the experimentally determined correction factor for each group of non-spherical cells. The determining factors in this separation are studied both experimentally and numerically, the results of which show a reasonable agreement.
I. INTRODUCTION
Morphology, here specifically denoting shape and size, is a fundamental characteristic of both biological and synthetic particles.1,2 It can be used to identify, for example, bacteria of different types including rod-shaped bacilli and round-shaped cocci.3 Moreover, the morphological change of bioparticles is often associated with their biological functions. For example, budding yeast cells change from single spheres to bispherical twins or larger aggregates during the mitotic cell cycle, which has been widely used in the research of mitosis to understand the cellular reproduction.4 In addition, morphology is an important indicator of cell states. For example, the morphological change of red blood cells has been long known to be accompanied by a disease such as sickle-cell anemia5 and malaria.6 Therefore, morphology is a useful passive marker that can potentially be used to fractionate and sort bioparticles for applications in both biological research and clinical diagnostics.
A variety of microfluidic approaches have been developed to separate and sort (bio)particles by their intrinsic properties; however, a majority of them are based on the difference in the particle size.7–10 Only until recently has the shape (or, more accurately, morphology, in some cases, that includes the change in both the shape and the size of bioparticles) been used to separate particles in a continuous flow with either an externally applied force field (categorized as active methods) or an internal flow-induced force field (categorized as passive methods). Among active shape-based particle separations, Valero et al.11 employed multi-frequency dielectrophoresis to obtain synchronized yeast cells in the anaphase of the cell cycle. Kose et al.12 utilized the electric-current generated frequency-dependent magnetic force and torque to separate sickle and healthy red blood cells in a custom-made biocompatible ferrofluid. Zhou and Xuan13 exploited the shape-dependent magnetic force (and in turn magnetophoretic motion) to fractionate a sheath-focused mixture of equal-volumed spherical and peanut-shaped diamagnetic particles in a ferrofluid. Later, Zhou et al.14 separated magnetic particles (or diamagnetic particles in a ferrofluid) of dissimilar shapes under a uniform magnetic field by the use of the shape-dependent magnetic torque (and in turn magnetic rotation).15
Passive shape-based particle separation has been demonstrated by Sugaya et al.16 via hydrodynamic filtration and Beech et al.17 via deterministic lateral displacement. Both microfluidic techniques make use of steric effects to place particles into morphology-dependent streamlines at the asymmetric bifurcation of a laminar flow through a network of microchannels16 or around an array of obstacles.17 DuBose et al.18 used curvature-induced dielectrophoresis in DC electrokinetic flow to separate particles of different shapes in an asymmetric double-spiral microchannel at a low throughput. In contrast, Masaeli et al.19 demonstrated a high-throughput sorting of spheres and rods (with varying aspect ratios) as well as yeast cells at various cell cycle stages via shape-dependent inertial focusing in a straight large aspect-ratio (height/width) rectangular microchannel. A similar method has also been used very recently to separate microalga Euglena gracilis by the same group.20 Lu and Xuan21 implemented an efficient sheath-flow separation of spherical and peanut particles (named elasto-inertial pinched flow fractionation or eiPFF in short) using the shape-dependence of elastic lift in a viscoelastic polymer solution. Later, the same force was utilized by Lu et al.22 to demonstrate a sheathless separation of particles by shape in a straight small aspect-ratio (height/width) rectangular microchannel. The flow throughput in the latter experiment appears to bridge the gap between the demonstrated dielectrophoretic18 and inertial separations.19,20
However, a majority of active and passive shape-based particle separations have thus far been reported only for binary mixtures of particles with a specific shape difference. We demonstrate herein a continuous-flow magnetic fractionation of drug-treated yeast cells with four primary groups of morphologies in dilute ferrofluids. Compared to the mixture of equal-volumed spherical and peanut-shaped polystyrene particles in our recently demonstrated separation,13 yeast cells vary in both shape and size after the drug treatment, leading to a complicated heterogeneous mixture. We also develop a 3D numerical model to understand and predict the effects of the flow rate, flow rate ratio (between the sheath fluid and cell suspension), and ferrofluid concentration on this morphology-based cell separation.
II. EXPERIMENTAL SECTION
A. Fabrication of microfluidic chips
Figure 1(a) shows a picture of the microfluidic chip used in our experiments, which was fabricated with polydimethylsiloxane (PDMS) using a custom-modified soft lithography method.23 The T-shaped channel consists of a 12 mm long main branch and two 8 mm long side-branches with a width of 100 μm and a depth of 25 μm everywhere. There is a 2 mm long, 900 μm wide expansion connecting each branch with its reservoir, where an array of posts is designed for filtration of debris (at the two inlet reservoirs) or enhanced cell separation (at the outlet reservoir). A Neodymium-Iron-Boron permanent magnet (B421, 1/4 in. × 1/8 in. × 1/16 in., K&J Magnets, Inc.) was embedded into the PDMS slab. It was positioned 500 μm (edge to edge distance) away from the main branch and 3 mm upstream from the expansion of the main branch. The magnetization direction of the magnet is along the 1/16″ thickness, which was set to point toward the main branch of the microchannel.
FIG. 1.
(a) Top-view picture of a T-shaped microchannel (filled with green food dye for clarity) for morphology-based yeast cell fractionation in dilute ferrofluids. The block arrows indicate the flow direction in each branch of the microchannel. The separation of yeast cells is viewed at the expansion of the main branch. (b) Zoom-in image of drug-treated yeast cells that are classified into four groups with different shapes and sizes: Singles, Doubles (i.e., with single buds), Triples (i.e., with two buds), and Others.
B. Preparation of yeast cells
To obtain yeast cells with aberrant morphology, the culture of Cryptococcus neoformans was treated with N-(2-chloro-4-pyridyl)-N-phenylurea (CAS Number: 68157-60-8; Sigma Aldrich), a synthetic plant cytokinin known as forchlorfenuron (FCF), which interrupts cytokinesis in Saccharomyces cerevisiae.24 FCF (AC456290010; ACROS Organics) was dissolved in 100% ethanol to a 250 mM stock. C. neoformans strain H99 cells25 were grown in the yeast extract peptone dextrose (YPD) medium overnight at 24 °C and refreshed next day to the cell density of 107 cells/ml before treatment. They were then incubated in the YPD medium with either 0.25 or 0.5 mM FCF overnight at 37 °C. After the overnight FCF treatment, cells were fixed for 1 h with 3.7% formaldehyde, spun down, and re-suspended in phosphate buffered saline (PBS) solution. Figure 1(b) shows a zoom-in image of the FCF-treated yeast cells that exhibit various shapes and sizes. To facilitate the analysis, we classify these cells into four groups: Singles with no buds, Doubles with a single bud, Triples with two buds, and Others with three or more cells or buds. Their equivalent spherical diameters were each determined using the following steps: first, measure the average dimensions of 3–5 representative cells of each cell group; then, develop a three-dimensional model in COMSOL® 5.1 with the same cell dimensions and structure (assuming spherical for each cell or bud) as measured; finally, calculate the overall cell volume using the geometry package in COMSOL. The obtained equivalent spherical diameters are 4.5 μm for Singles, 5.5 μm for Doubles, 6.2 μm for Triples, and 8.0 μm for Others.
C. Manipulation of yeast cells in ferrofluids
The drug-treated yeast cells were re-suspended in diluted EMG 408 ferrofluids (Ferrotec Corp.) to a final concentration of 105–106 cells/ml prior to experiments. The original ferrofluid is a suspension of superparamagnetic particles of 10 nm in diameter at a volume concentration of 1.2%. It was diluted by deionized water (Fisher Scientific) to 0.05×, 0.1×, and 0.2× the original concentration. To prevent further cell aggregations and adhesions to channel walls, a small amount of Tween 20 (0.1% v/v, Fisher Scientific) was added to the yeast cell suspension in each type of ferrofluid. The cell suspension was stirred using a vortex mixer (Fisher Scientific) for homogenization immediately before the test. It was injected along with the sheath ferrofluid (clean solution free of cells) into the T-shaped microchannel by an independent infusion syringe pump (KD Scientific). The motion of yeast cells was visualized at the T-junction and the main branch expansion of the microchannel, which was recorded using an inverted microscope (Nikon Eclipse TE2000U, Nikon Instruments) equipped with a CCD camera (Nikon DS-Qi1Mc). The obtained digital images were processed using the Nikon imaging software (NIS-Elements Advanced Research ver. 2.30). They were further analyzed in ImageJ software (National Institute of Health) using the function “Analyze Particles” to get the probability distribution function (PDF) of each group of cells. The potential impact of dilute ferrofluids on yeast cell viability has been demonstrated to be negligible in our previous studies26 and hence was not investigated in this work.
III. THEORETICAL SECTION
A. Mechanism of diamagnetic cell fractionation
Yeast cells in the ferrofluid suspension are pre-focused by the sheath ferrofluid (a clean solution free of cells) to a tight stream along the sidewall of the main branch on the side of the magnet [see Fig. 1(a)]. They each experience a negative magnetic force, , due to their much smaller magnetization than the suspending ferrofluid13,27,28
| (1) |
where is the vacuum permeability, is the cell volume, is the ferrofluid magnetization, is the magnetic field at the cell center, and is used to account for the shape-dependence of the magnetic force that decreases with the cell sphericity and becomes 1 for a spherical cell.13,29 The ferrofluid magnetization, , is collinear with the magnetic field, , with the magnitude being determined from the Langevin equation27
| (2) |
| (3) |
where is the volume fraction of the magnetic nanoparticles in the ferrofluid, A/m is the saturation moment of these nanoparticles (determined from , where both the saturation magnetization, A/m, and the volume fraction, , of the original EMG 408 ferrofluid are obtained from the manufacturer's website), is the nominal diameter of magnetic nanoparticles, is the Boltzmann constant, and is the ferrofluid temperature.
The magnetic force, , on a cell is balanced by the viscous drag force, , exerted by the flow, which in small Reynolds number flows (to be explained later) can be expressed as30
| (4) |
where is the ferrofluid viscosity, is the equivalent spherical diameter of the cell, is the ferrofluid velocity, is the cell velocity, is the drag coefficient accounting for the wall retardation effects on cell motion, and is the shape factor that is equal to 1 for a spherical cell and increases with the cell non-sphericity.30 The resulting cell velocity (assumed to reach the terminal value instantly in smaller Reynolds number flows, to be explained later in Sec. IV A) is thus given by13
| (5) |
where is the shape-dependent correction factor for magnetophoretic cell velocity. It is important to note that this combined factor reduces to 1 for spherical cells and is not a function of cell size. The dependences of , or more precisely the cross-stream magnetophoretic motion [the second term on the right hand side of Eq. (5)], on the cell size (in terms of ) and shape (in terms of ) lead to cell fractionation by morphology in the width direction of the main branch. This continuous-flow diamagnetic cell separation is further enhanced at the expansion of the main branch due to local hydrodynamic spreading.31
B. Simulation of cell trajectories
We developed a 3D numerical model in COMSOL 5.1 to simulate the transport and fractionation of yeast cells in dilute ferrofluids, which was solved using the Palmetto Cluster at Clemson University. This model considers only the action of the flow field on the motion of cells via Eq. (5) while neglecting the re-action of the moving cells on the flow field. We first calculated the steady-state flow field, , in the T-shaped microchannel from the conventional continuity and Navier-Stokes equations using The Laminar Flow module in COMSOL
| (6) |
| (7) |
where and are the ferrofluid density and pressure, respectively. Then, the Streamline function was used to plot the trajectory of single cells via the cell velocity, , in Eq. (5), where the value of the shape-dependent correction factor, , for each group of non-spherical cells was determined by fitting the predicted cell trajectories with the experimentally obtained streak images. The magnetic field components were obtained directly from Furlani's analytical formulae for rectangular magnets32 and introduced into the model as variables. The exact experimental conditions (e.g., channel dimensions, equivalent spherical cell diameters, and fluid properties) were used in the simulation. We considered one hundred cells (specifically 20 and 5 in the channel width and depth directions, respectively) for each of the four cell groups (i.e., Singles, Doubles, Triples, and Others) and assumed that their initial positions are evenly distributed at the channel inlet. The important material properties involved in the simulation are summarized in Table I. Other details of the model are referred to our recent paper23,33 and skipped here for brevity.
TABLE I.
Material properties used in the simulation.23,33
| Symbol | Description | Value |
|---|---|---|
| Residual magnetization of the magnet | 1.05 × 1 A/m | |
| Original ferrofluid concentration (1× EMG 408) | 1.2% | |
| d | Diameter of magnetic nanoparticles in ferrofluids | 10 nm |
| Saturation moment of magnetic nanoparticles in ferrofluids | 4.38 × 1 A/m | |
| Dynamic viscosity of ferrofluids | 1.05 × 1 kg/ms | |
| Mass density of ferrofluids | 1070 kg/ |
IV. RESULTS AND DISCUSSION
A. Demonstration of yeast cell fractionation by morphology
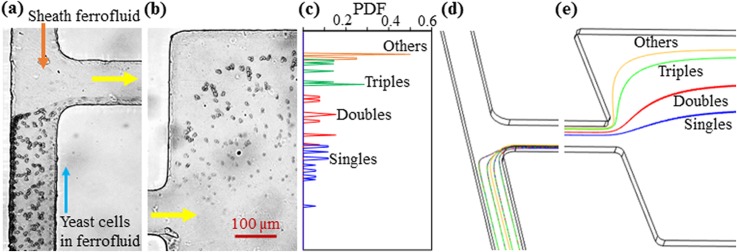
Figure 2 demonstrates the magnetic fractionation of drug-treated yeast cells in 0.1× EMG 408 ferrofluid based on morphology. The flow rates of the sheath ferrofluid and yeast cell suspension are 180 μl/h and 9 μl/h, respectively. The corresponding Reynolds number, , was estimated to be around 0.8 in the main branch of the microchannel, where kg/m3 is the ferrofluid density, m/s is the average ferrofluid velocity, μm is the hydraulic channel diameter, and kg/m s is the ferrofluid viscosity. As the calculated cell Reynolds number, , is smaller than 0.1 even for the largest yeast cell group (i.e., Others with an average equivalent spherical diameter of 8.0 μm), the inertial lift34 is not expected to play a significant role in the demonstrated yeast cell fractionation in Fig. 2. The mixed four groups of yeast cells in the ferrofluid are pre-focused at the T-junction by the sheath ferrofluid to a thin layer along the sidewall of the main branch that is closer to the magnet [Fig. 2(a)]. They experience negative magnetophoresis in the flow of ferrofluid through the main branch and get pushed away from the sidewall at a morphology-dependent rate, leading to a continuous-flow fractionation at the expansion of the main branch [Fig. 2(b)]. The PDF plots of the four cell groups in Fig. 2(c) further illustrate this morphology-based cell separation. However, there is still visible overlapping between the PDF plots due to the complex variations in both the cell size and shape as well as cell dispersion (due to insufficient sheath focusing as well as the parabolic fluid velocity profile, particularly that in the channel depth direction).
FIG. 2.
Demonstration of magnetic fractionation of yeast cells in the flow of 0.1× EMG 408 ferrofluid through a T-shaped microchannel: (a) experimental image at the T-junction; (b) experimental image at the expansion of the main branch; (c) PDF plots of the four groups of yeast cells at the expansion of the main branch [obtained from the cell distribution in (b)]; (d) predicted cell trajectories (only four cells are illustrated for each group in the horizontal plane for clarity) at the T-junction, and (e) predicted cell trajectories at the expansion of the main branch. The flow rates of the sheath ferrofluid and yeast cell suspension are 180 μl/h and 9 μl/h, respectively, in both the experiment and the simulation. The block arrows in (a) and (b) indicate the flow directions.
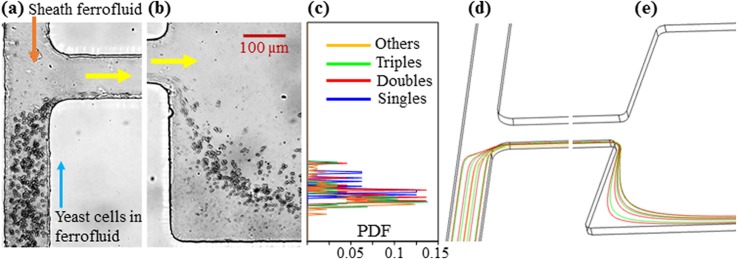
Figure 2 also shows the numerically predicted trajectories of the four groups of yeast cells (isometric view, only four cells of each group in the same horizontal plane are used for the illustration) at the T-junction (d) and the expansion of the main branch (e). To match the average exiting cell positions in the experimental image, we set the shape-dependent correction factor, in Eq. (5), to 1.08, 1.22, and 1.88 for the three non-spherical cell groups, i.e., Doubles, Triples, and Others [see Fig. 1(b)], respectively. Note that the value of for single spherical cells (i.e., Singles) is set to 1 by nature. The same values are used in the parametric study of the effects of the flow rate (Sec. IV B), flow rate ratio (Sec. IV C), and ferrofluid concentration (Sec. IV D) in the following sections. As such, the “effective” cell surface area, i.e., in Eq. (5), for negative magnetophoresis was calculated to be 20.25 for Singles, 28.01 for Doubles, 31.51 for Triples, and 34.04 for Others. It is therefore the combined cell size and shape effects, or simply the cell morphology difference, that lead to the observed diamagnetic yeast cell fractionation in Fig. 2(b). To study the potential impact of the so-called pinched flow fractionation35 as well as the inertial effects,36 we performed a control experiment under exactly the same conditions as those in Fig. 2 except that the permanent magnet was removed. The experimental observations in this control experiment are presented in Figs. 3(a)–3(c), where the four groups of yeast cells are found to still remain mixed at the expansion of the main branch without noticeable separations. This result is visually consistent with the numerical simulation in Figs. 3(d) and 3(e).
FIG. 3.
Control experiment and simulation for yeast cell fractionation in the flow of 0.1× EMG 408 ferrofluid through a T-shaped microchannel when the permanent magnet is removed [also see Fig. 1(a)]: experimental images at the T-junction (a) and the expansion of the main branch (b); PDF plots of the four groups of yeast cells at the expansion of the main branch (c); predicted cell trajectories at the T-junction (d) and the expansion of the main branch (e) in an isometric view of the microchannel. All other experimental conditions remain identical to those in Fig. 2. The block arrows in (a) and (b) indicate the flow directions.
B. Effect of the flow rate
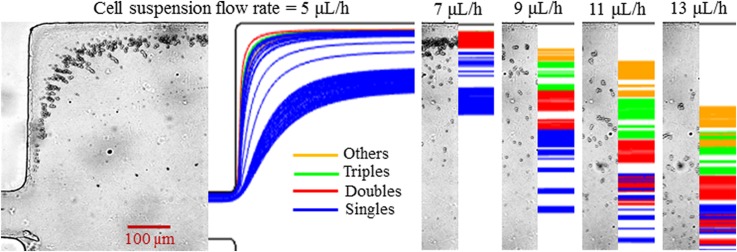
Figure 4 shows the experimental (left plot in each panel) and numerical (right plot in each panel) results of the flow rate effect on morphology-based yeast cell fractionation in 0.1× EMG 408 ferrofluid. The flow rate of the yeast cell suspension varies from 5 to 13 μl/h, while the flow rate ratio between the sheath ferrofluid and cell suspension remains at 20. As seen from the cell images at the expansion of the main branch in Fig. 4 (left plot for each flow rate), the cross-stream diamagnetic deflection from the lower sidewall decreases with the increasing flow rate for each group of yeast cells due to the reduced exposure time to magnetic field gradients. However, the separation distance between cell groups does not decrease monotonically. At a 5 μl/h cell flow rate, all four groups of yeast cells achieve a (nearly) full channel-width deflection in the main branch and hence still mix with each other at the expansion of the main branch. When the cell flow rate increases to 7 μl/h, Singles cells and part of the Doubles cells can no longer reach the upper sidewall of the channel expansion, leading to their separation from Triples and Others cells. When the cell flow rate is further increased to 9 μl/h (also see Fig. 2), only Others cells can still be deflected across almost the entire channel width. Therefore, the best separation of the four groups of yeast cells should take place at a cell flow rate slightly smaller than 9 μl/h. Further increasing the cell flow rate reduces both the displacement of each cell group and the gap among them. The predicted cell trajectories in Fig. 4 (right plot for each flow rate, 100 cells were tracked for each group) exhibit a visually reasonable agreement with the experimental observation at each flow rate. Note that in our simulation, the value of the shape-dependent correction factor, in Eq. (5), was kept equal to that used in Figs. 2 and 3 for each group of cells.
FIG. 4.
Flow rate effect on diamagnetic yeast cell fractionation by morphology in 0.1× EMG 408 ferrofluid. The flow rate ratio between the sheath ferrofluid and the yeast cell suspension is fixed at 20 when the latter is varied from 5 μl/h to 13 μl/h. The left and right plots at each flow rate show the experimental cell image and the numerically predicted cell trajectories, respectively.
C. Effect of the flow rate ratio
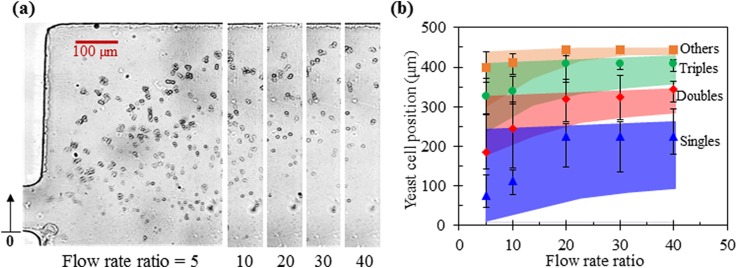
Figure 5 shows the effect of the flow rate ratio between the sheath ferrofluid and cell suspension on yeast cell fractionation in 0.1× EMG 408 ferrofluid. The sheath flow rate is fixed at 180 μl/h, while the cell flow rate is varied from 4.5 μl/h (i.e., with a ratio of 40) to 36 μl/h (i.e., with a ratio of 5). With the increase in the flow rate ratio, the total flow rate in the main branch decreases, yielding a greater cross-stream deflection for all four groups of yeast cells. However, as viewed from the cell images in Fig. 5(a), the Others cells already reach the upper sidewall at the flow rate ratio of 30. Hence, a further increase in the flow rate ratio does not apparently improve the cell separation even though the dispersion of each cell group can still become smaller in principle. A quantitative view of the magnetic deflection and separation of the four groups of yeast cells (symbols with error bars) is shown in Fig. 5(b), where the numerically simulated cell positions (colored bands) are superimposed for a direct comparison. Overall, our numerical model predicts the experimentally observed stream location of each cell group at the expansion of the main branch with a good agreement. However, the predicted enhancing effect of the increasing flow rate ratio on yeast cell fractionation is not obvious in the experiment, which should be due to the continuous size variation and complex shape variation of real cells.
FIG. 5.
Effect of the flow rate ratio between the sheath ferrofluid (fixed at 180 μl/h) and cell suspension (varied from 36 μl/h to 4.5 μl/h) on yeast cell fractionation by morphology in 0.1× EMG 408 ferrofluid: (a) Superimposed images of four groups of yeast cells at the expansion of the main branch; (b) Comparison of the experimentally measured (symbols with error bars to cover the span of the cell stream) and numerically predicted (colored band) positions of each cell group at the expansion of the main branch. The upright arrow in the right-most image of (a) indicates the reference point to which the position of each group of cells in (b) was measured.
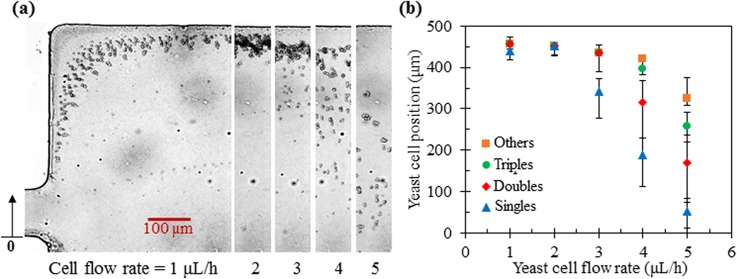
D. Effect of the ferrofluid concentration
The effect of the ferrofluid concentration on yeast cell fractionation is straightforward because it affects only the cross-stream cell magnetophoresis [see Eqs. (1) and (2)] while leaving the ferrofluid flow velocity intact. As such, decreasing (increasing) the ferrofluid concentration would reduce (increase) the flow rate at which the cell separation takes place if the flow rate ratio between the ferrofluid sheath and cell suspension remains constant. Figure 6 shows the yeast cell behaviors at the expansion of the main branch when the flow rate of cell suspension in 0.05× EMG 408 ferrofluid is varied from 1 μl/h to 5 μl/h. The flow rate ratio between the 0.05× EMG 408 ferrofluid sheath and the cell suspension is fixed at 20. Both the cell images in Fig. 6(a) and the measured exiting positions of each cell group in Fig. 6(b) indicate that the best separation is achieved at the cell flow rate of 4 to 5 μl/h, which is lower than the best cell flow rate of nearly 9 μl/h in 0.1× EMG 408 ferrofluid (see Fig. 4). In contrast, the cell flow rate for the best yeast cell fractionation in 0.2× EMG 408 ferrofluid (data now shown due to the similarity to Fig. 6 except for the values of the flow rate) becomes around 12 μl/h. This flow throughput is still low as compared to the passive elastic- [on the order of 100 μl/h (Ref. 22)] and inertial- [over 1 ml/h (Refs. 19 and 20)] lift based cell separations. Further increasing the ferrofluid concentration while maintaining its biocompatibility37,38 can enhance the throughput. Another simple approach is to use a stronger magnet39 or even multiple stacked magnets.40 In addition, a much deeper channel (could be of mm depth) can potentially be used to increase the throughput because the magnet field gradient extends over the entire depth of mm-thick permanent magnets.
FIG. 6.
Yeast cell fractionation in 0.05× EMG 408 ferrofluid at various flow rates of the cell suspension: (a) Superimposed images of four groups of yeast cells at the expansion of the main branch; (b) Experimentally measured (symbols with error bars to cover the span of the cell stream) positions of each cell group at the expansion of the main branch. The flow rate ratio between the sheath fluid and yeast cell suspension is fixed at 20. The upright arrow In the right-most image of (a) indicates the reference point to which the position of each group of cells in (b) was measured.
V. CONCLUSIONS
We have extended our recent work13 to demonstrate a continuous-flow fractionation of drug-treated yeast cells with varying sizes and shapes in the flow of dilute ferrofluids through a T-shaped microchannel. The heterogeneous mixture of cells is first aligned via sheath-flow focusing and then diamagnetically deflected to morphology-dependent flow paths under a non-uniform magnetic field. The resulting cell separation at the expansion of the main branch has been evaluated by measuring and comparing the exiting positions of the classified four groups of yeast cells, i.e., Singles, Doubles, Triples, and Others. Also, the effects of the flow rate, flow rate ratio between the sheath fluid and cell suspension, and ferrofluid concentration have each been experimentally investigated. Moreover, we have developed a 3D numerical model to simulate the cell trajectories in the flow of ferrofluids through the microchannel under the experimental conditions. With an experimentally determined correction factor for each group of non-spherical yeast cells (i.e., Doubles, Triples, and Others), our model has been found to predict the experimentally measured exiting cell positions in the parametric studies with a reasonable agreement. In addition, we have discussed the possible routes to enhance the flow throughput of the demonstrated diamagnetic cell fractionation technique.
ACKNOWLEDGMENTS
This work was supported in part by the China Scholarship Council (CSC)-Chinese Government Graduate Student Overseas Study Program (Q.C.), NIH under Grant No. 1R15 AI119801-01 (L.K.), and NSF under Grant No. CBET-1150670 (X.X.).
References
- 1. Jadhao V., Thomas C. K., and de la Cruz M. O., Proc. Natl. Acad. Sci. U.S.A. 111, 12673–12678 (2014). 10.1073/pnas.1413986111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Champion J. A. and Mitragotri S., Proc. Natl. Acad. Sci. U.S.A. 103, 4930–4934 (2006). 10.1073/pnas.0600997103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Janca J., Halabalova V., and Rzicka J., J. Chromatogr., Sect. A 1217, 8062–8071 (2010). 10.1016/j.chroma.2010.10.082 [DOI] [PubMed] [Google Scholar]
- 4. Martin S. G., Cell Cycle 8, 3643–3647 (2009). 10.4161/cc.8.22.9891 [DOI] [PubMed] [Google Scholar]
- 5. Ebert E. C., Nagar M., and Hagspiel K. D., Clin. Gastroenterol. Hepatol. 8, 483–489 (2010). 10.1016/j.cgh.2010.02.016 [DOI] [PubMed] [Google Scholar]
- 6. Anstey N. M., Russell B., Yeo T. W., and Price R. N., Trends Parasitol. 25, 220–227 (2009). 10.1016/j.pt.2009.02.003 [DOI] [PubMed] [Google Scholar]
- 7. Pamme N., Lab Chip 7, 1644–1659 (2007). 10.1039/b712784g [DOI] [PubMed] [Google Scholar]
- 8. Gossett D. R., Weaver W. M., Mach A. J., Hur S. C., Tse H. T., Lee W., Amini H., and Di Carlo D., Anal. Bioanal. Chem. 397, 3249–3267 (2010). 10.1007/s00216-010-3721-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Karimi A., Yazai S., and Ardekani A. M., Biomicrofluidics 7, 021501 (2013). 10.1063/1.4799787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Sajeesh P. and Sen A. K., Microfluid. Nanofluid. 17, 1–52 (2014). 10.1007/s10404-013-1291-9 [DOI] [Google Scholar]
- 11. Valero A., Braschler T., Rauch A., Demierre N., Barral Y., and Renaud P., Lab Chip 11, 1754–1760 (2011). 10.1039/c1lc00007a [DOI] [PubMed] [Google Scholar]
- 12. Kose A. R., Fischer B., Mao L., and Koser H., Proc. Natl. Acad. Sci. U.S.A. 106, 21478–21483 (2009). 10.1073/pnas.0912138106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Zhou Y. and Xuan X., Appl. Phys. Lett. 109, 102405 (2016). 10.1063/1.4962638 [DOI] [Google Scholar]
- 14. Zhou R., Bai F., and Wang C., Lab Chip 17, 401–406 (2017). 10.1039/C6LC01382A [DOI] [PubMed] [Google Scholar]
- 15. Zhou R., Sobecki C. A., Zhang J., Zhang Y., and Wang C., Phys. Rev. Appl. 8, 024019 (2017). 10.1103/PhysRevApplied.8.024019 [DOI] [Google Scholar]
- 16. Sugaya S., Yamada M., and Seki M., Biomicrofluidics 5, 24103 (2011). 10.1063/1.3580757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Beech J. P., Holm S. H., Adolfsson K., and Tegenfeldt J. O., Lab Chip 12, 1048–1051 (2012). 10.1039/c2lc21083e [DOI] [PubMed] [Google Scholar]
- 18. DuBose J., Lu X., Patel X. S., Qian S., Joo S. W., and Xuan X., Biomicrofluidics 8, 014101 (2014). 10.1063/1.4862355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Masaeli M., Sollier E., Amini H., Mao W., Camacho K., Doshi N., Mitragotri S., Alexeev A., and Di Carlo D., Phys. Rev. X 2, 031017 (2012). 10.1103/PhysRevX.2.031017 [DOI] [Google Scholar]
- 20. Li M., Munoz H. E., Goda K., and Di Carlo D., Sci. Rep. 7, 10802 (2017). 10.1038/s41598-017-10452-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Lu X. and Xuan X., Anal. Chem. 87, 11523–11530 (2015). 10.1021/acs.analchem.5b03321 [DOI] [PubMed] [Google Scholar]
- 22. Lu X., Zhu L., Hua R., and Xuan X., Appl. Phys. Lett. 107, 264102 (2015). 10.1063/1.4939267 [DOI] [Google Scholar]
- 23. Zhou Y., Kumar D. T., Lu X., Kale A., DuBose J., Song Y., Wang J., Li D., and Xuan X., Biomicrofluidics 9, 044102 (2015). 10.1063/1.4926615 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Iwase M., Okada S., Oguchi T., and Toh-e A., Genes Genet. Syst. 79, 199–206 (2004). 10.1266/ggs.79.199 [DOI] [PubMed] [Google Scholar]
- 25. Perfect J. R., Ketabchi N., Cox G. M., Ingram C. W., and Beiser C. L., “ Karyotyping of Cryptococcus neoformans as an epidemiological tool,” J. Clin. Microbiol. 31, 3305–3309 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Zeng J., Chen C., Vedantam P., Tzeng T., and Xuan X., Microfluid. Nanofluid. 15, 49–55 (2013). 10.1007/s10404-012-1126-0 [DOI] [Google Scholar]
- 27. Rosensweig R. E., Annu. Rev. Fluid Mech. 19, 437–461 (1987). 10.1146/annurev.fl.19.010187.002253 [DOI] [Google Scholar]
- 28. Liang L. and Xuan X., Biomicrofluidics 6, 044106 (2012). 10.1063/1.4765335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Gao Y., Jian Y. C., Zhang L. F., and Huang J. P., J. Phys. Chem. C 111, 10785–10791 (2007). 10.1021/jp0705673 [DOI] [Google Scholar]
- 30. Happel J. and Brenner H., Low Reynolds Number Hydrodynamics ( Springer Press, 1973). [Google Scholar]
- 31. Li D., Lu X., Song Y., Wang J., Li D., and Xuan X., Biomicrofluidics 10, 054104 (2016). 10.1063/1.4962875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Furlani E. P., Permanent Magnet and Electromechanical Devices: Materials, Analysis, and Applications ( Academic Press, 2001). [Google Scholar]
- 33. Zhou Y., Song L., Yu L., and Xuan X., J. Magn. Magn. Mater. 412, 114–122 (2016). 10.1016/j.jmmm.2016.04.001 [DOI] [Google Scholar]
- 34. Zhang J., Yan S., Yuan D., Alici G., Nguyen N. T., Warkiani M. E., and Li W., Lab Chip 16, 10–34 (2016). 10.1039/C5LC01159K [DOI] [PubMed] [Google Scholar]
- 35. Yamada M., Nakashima M., and Seki M., Anal. Chem. 76, 5465–5471 (2004). 10.1021/ac049863r [DOI] [PubMed] [Google Scholar]
- 36. Lu X. and Xuan X., Anal. Chem. 87, 4560–4565 (2015). 10.1021/acs.analchem.5b00752 [DOI] [PubMed] [Google Scholar]
- 37. Zhao W., Cheng R., Lim S. H., Miller J. R., Zhang W., Tang W., Xie J., and Mao L., Lab Chip 17, 2243–2255 (2017). 10.1039/C7LC00327G [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Zhao W., Cheng R., Jenkins B. D., Zhu T., Okonkwo N. E., Jones C. E., Davis M. B., Kavuri S. K., Hao Z., Schroeder C., and Mao L., Lab Chip 17, 3097–3111 (2017). 10.1039/C7LC00680B [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Vojtisek M., Tarn M. D., Hirota N., and Pamme N., Microfluid. Nanofluid. 13, 625–635 (2012). 10.1007/s10404-012-0979-6 [DOI] [Google Scholar]
- 40. Zhu T., Cheng R., Lee S. A., Rajaraman E., Eiteman M. A., Querec T. D., Unger E. R., and Mao L., Microfluid. Nanofluid. 13, 645–654 (2012). 10.1007/s10404-012-1004-9 [DOI] [PMC free article] [PubMed] [Google Scholar]