Surface-enhanced Raman scattering analysis of urine from deceased donors as a prognostic tool for kidney transplant outcome

Abstract

We report the utility of surface-enhanced Raman scattering (SERS) analysis of urine from deceased donors for prognosis of kidney transplant outcomes. Iodide-modified silver nanoparticles were used as the enabler for sensitive measurements of urine proteins. Principal component analysis (PCA) and linear discriminant analysis (LDA) were employed for the statistical analysis of the SERS data. Thirty urine samples in three classes were analysed. The ATN class consists of donors whose kidneys had acute tubular necrosis (ATN), the most common type of acute kidney injury (AKI) with high risk of poor graft performance in recipients, yet yielded acceptable transplant outcome. The DGF class is comprised of donors whose kidney had delayed graft function (DGF) in recipients. The control class includes donors whose kidneys did not have donor ATN or recipient DGF. We show a sensitivity of more than 90% in differentiating the ATN class from the DGF and control classes. Our methodology can thus help clinicians choose kidneys in the high-risk ATN category for transplant which would otherwise be discarded. Our research is impactful in that it could serve as a valuable guidance to expand the deceased donor pool to include those perceived as high-risk AKI type based on common urinary biomarkers.

Graphical Abstract

Scheme of SERS analysis of urine samples from deceased donors for kidney transplant outcome indication.

1. Introduction

The total number of candidates on the waiting list for kidney transplant has increased steadily from approximately 58,000 in 2004 to 99,306 at the end of October 2016 [1,2]. There are two types of donors for kidney transplants, living donors and deceased donors. Since 2004, the number of kidney transplants from living donors has slightly decreased. Over the same time period, the number of kidney transplants from deceased donors has increased from 6,325 to 8,304. Unfortunately, demand for kidney transplants still outstrips the supply, and over 5,000 people die every year while awaiting kidney transplant.

Despite the urgent demand for more kidney donors, a large percentage of kidneys from deceased donors are not used for transplant, especially when donors have a terminal creatinine concentration above 1.5 mg/dL [3]. The elevated terminal creatinine is a sign of acute kidney injury (AKI), which can be associated with poor transplant outcomes [4,5]. Transplant centers have been reluctant to use kidneys with AKI, and many kidneys are discarded because of this reason. However, some studies involving deceased donor kidney transplants have reported that kidneys with AKI had similar transplant outcomes compared with kidneys without AKI [4,6–11].

We have previously reported the association of AKI with kidney transplant outcomes [8]. We evaluated 1,632 deceased donors and classified them as having AKI stage 1–3 or no AKI. The 6-month estimated glomerular filtration rate (eGFR) was similar across the AKI categories and suggested that transplant clinicians should consider expanding the kidney pool by accepting selected donors with AKI, given the acceptable 6-month allograft function of kidneys from AKI donors.

Several scoring systems and algorithms have been established to study the transplant outcomes using donor AKI kidneys from deceased donors. Terminal serum creatinine, which can be used to calculate an eGFR, is often used to evaluate deceased donor kidneys. The creatinine and eGFR, however, are not reliable indicators of kidney status during the episode AKI [12]. Other novel biomarkers have shown promising association with the clinical outcomes, such as neutrophil gelatinase-associated lipocalin (NGAL), kidney injury molecule-1 (KIM-1), interleukin-18 (IL-18) in both urine and serum [13–19].

A majority of the studies on these novel biomarkers were based on the urine or blood collected from recipients. However, the analysis of recipient biomarkers does not help in the decision to accept or not accept a deceased donor kidney for transplant. There are challenges in establishing the association of donor biomarkers with transplant outcomes. For instance, Buemi et al. measured the plasma and urine NGAL in both donors and recipients to examine their predictive ability of renal function after transplant. No correlation was observed between donors’ plasma and urine NGAL and the occurrence of post-transplant DGF [18].

SERS is a powerful, label-free analytical technique with excellent sensitivity and molecular specificity. Traditional Raman spectroscopy is already widely used for chemical analysis with high molecular specificity. However, the exceedingly low Raman scattering cross section (~10⁻³⁰ cm²/molecule) makes the conventional Raman technique suitable only for measurement of high analyte concentrations. SERS is a type of Raman scattering spectroscopy that is conducted with the aid of noble metal (typically Ag and Au) nanostructures. Collective excitation of free electrons in the conduction band of the metal nanostructure, commonly known as localized surface plasmon resonance (LSPR) under light irradiation, results in an electromagnetic (EM) field that is significantly higher than that of the incident irradiation. The field amplification by LSPR is responsible for the enormous gain (up to 10¹⁴) in the Raman scattering cross section, dramatically increasing detection sensitivities ranging from parts per million to single molecules [20]. SERS has been extensively exploited for bioanalysis [21–24], biosensing [23,25–28], and diagnostics [29–31]. We have also demonstrated the use of SERS of patient urine for early prognosis of acute kidney transplant rejection with very encouraging results [20].

Evaluation of donor urine samples by SERS offers several important advantages. First, SERS does not require any special sample preparation and can be performed very quickly often in seconds. Second, SERS can potentially be carried out using inexpensive, hand-held, fiber-optic Raman probes, which offers the possibility that SERS can eventually be field-deployed for timely evaluation and efficient procurement of deceased donor organs. Third, as a vibrational spectroscopy technique, SERS measurements can reveal the presence of multiple molecules and functional groups, rather than target just a single biomarker in urine.

In this paper, we present a SERS investigation of urine from deceased kidney donors and demonstrate its potential in predicting kidney transplant outcome.

2. Methods

2.1. Kidney donors and urine samples

Urine samples from 30 deceased kidney donors were analyzed in this study. Detailed clinical information of each donor is shown in supplemental information (Table S1). This study used data from the Organ Procurement and Transplantation Network (OPTN). The OPTN data system includes data on all donor, wait-listed candidates, and transplant recipients in the US, submitted by the members of the Organ Procurement and Transplantation Network (OPTN), and has been described elsewhere. The Health Resources and Services Administration (HRSA), U.S. Department of Health and Human Services provides oversight to the activities of the OPTN contractor. Each donor had donated both kidneys. Donors were defined as three classes: donor acute tubular necrosis (ATN) on biopsy, recipient delayed graft function (DGF), and control. with a population of 10 for each class. The controls had neither donor ATN nor recipient DGF. ATN is a histologic manifestation of kidney damage, but ATN is not always associated with clinically apparent AKI. DGF is clinically apparent AKI after transplant and is defined as the need for dialysis in the recipient within the first week after the transplant. Detailed descriptions and definitions of each group are summarized in Table 1. Kidneys of ATN class had high donor AKI risk which made clinician hesitant to use them in transplant. However, the transplant outcomes of kidneys in ATN class were acceptable. For 7 out of 10 donors in ATN class, both kidneys did not have DGF after transplant. For the remaining three pairs of kidneys, only one of each pair had recipient DGF.

Table 1.

Definition and description of 3 classes

Class name	Population	Definition
ATN*	10	Donors with biopsy proven ATN in both kidneys
DGF**	10	Both kidneys from the donor had DGF in recipients after transplant
Control	10	No donor AKI***, no donor ATN and no recipient DGF

^*ATN: acute tubular necrosis.

^**DGF: delayed graft function.

^***AKI: acute kidney injury.

2.2. Iodide-modified silver nanoparticles

Iodide-modified silver nanoparticles (Ag-I NPs) were employed to enable SERS measurements of the urine samples. The iodide modification process of silver nanoparticles (AgNPs) used in this study was established by Xu et al. [32] by mixing potassium iodide (KI) with concentrated AgNPs colloidal solution. The synthesis of AgNPs colloidal solution was described in our earlier publications [33,34]. Briefly, silver nitrate was reduced into metal AgNPs by sodium citrate under UV light exposure and continuous stirring in water bath. The AgNPs had an average size of 40±5 nm in diameter and a ζ potential of approximately −40 mV.

The synthesized AgNPs colloidal solution was aliquoted into 1.5 mL centrifuge tubes and centrifuged at 10,000 RPM for 10 min. The clear supernatant was carefully pipetted away and each 1 mL AgNPs colloidal solution was approximately concentrated into 10 μL. The concentrated AgNPs colloidal solution was then mixed with the same volume of KI solution (1mM) and sonicated for 1 min. The mixture was allowed 1-hour incubation at room temperature for a complete modification and was then immediately used for SERS measurements. For each SERS measurement, 1.5 μL urine was mixed with the same volume of concentrated Ag-I NPs colloidal solution. The mixture was dropped on a small piece of silicon wafer followed by SERS analysis immediately.

UV-vis absorption spectroscopy was used to characterize AgNPs and Ag-I NPs colloidal solutions (Figure S1). There is a slight blue shift in the resonance wavelength after iodide modification. The resonance wavelengths for AgNPs and Ag-I NPs are 416 nm and 400 nm respectively. The blue shift is a result of the changing of surface chemistry and the local dielectric environment of the nanoparticles. The ζ potential of Ag-I NPs is −20 mV, slightly higher than that of AgNPs due to variance in surface adsorbed ligands, in agreement with the work of Xu et al. [32].

The SERS spectra of a randomly selected urine sample from the DGF class using both AgNPs and Ag-I NPs are demonstrated in Figure S2. AgNPs exhibited significant spectral features at 1000 and 1300–1500 cm⁻¹, which can be a challenge in SERS analysis. On the other hand, Ag-I NPs offered a much clear spectral background, enabling the measurements of spectral features at around 1000 cm⁻¹.

2.3. SERS measurement and data pre-processing

The optical setup of our Raman system was reported in our earlier paper [33]. Briefly, a 632.8 nm laser was used as the excitation source and the laser power was approximately 0.5 mW to avoid overheating. Data acquisition time is 20 sec. Five SERS spectra were collected for each urine and Ag-I NPs mixture. The measurements were repeated in the same fashion in another round of experiments with excellent reproducibility. A total of 300 spectra were acquired, 10 for each urine sample. The SERS measurements were carried out in blind without clinical information being made available to avoid any real or perceived bias in data acquisition and treatment.

The raw spectra were truncated from 500 to 1800 cm⁻¹ using Specwin32, and the truncated spectra were smoothed and baseline corrected using Labspec. The treated spectra were then normalized by the area under the curve in OriginLab. A fifth order polynomial was used for baseline correction [35].

2.4. Statistical analysis

The SERS measurements yielded a huge collection of Raman spectra, which by themselves were rich in spectral details. Principal component analysis (PCA), a commonly used classification method in Raman analysis [36–40], was firstly employed as a variable reduction procedure. In PCA analysis, the data are unlabelled and the analysis is only based on the data’s feature. The process of PCA starts from decomposition of averaged data matrix into a set of orthogonal vectors, which are ranked from descending order of the contribution of overall variance of all data. The vectors are called principal component (PC) and the weight of the contribution of each vector to each original data set is called scores. Specifically for Raman spectrum, PCs are a set of spectra and scores are the weight of each PC’s contribution to the original Raman spectrum. Mathematically, one original spectrum S is decomposed into Σ PC_i × S_i + e, where PC_i are orthogonal spectra, S_i are the corresponding scores to each PC, and e is the averaged spectrum of all original data. In most cases of Raman analysis, the first several PCs constitute more than 95% of overall variance. Thus, we will not compromise noticeably accuracy by investigating the scores of first several PCs compared with analysing hundreds of intensities recorded for each spectrum.

Linear discriminant analysis (LDA) was then applied to the new data set of the dimensionally reduced variables for classification analysis. The principle of LDA is to generate a hyperplane, on which the projection of each observation can be separated into several segments according to their classes. Mathematically, the goal of LDA is to generate a linear function, y = a₀ + a₁x₁ + a₂x₂ + .…. + a_nx_n, where x_i are the variables and a_i are the parameters to be determined by LDA in such a way that the classes will be discriminated the best.

The association of scores of each PC with clinical characteristics was evaluated using logistic regression and Chi-square test. The validation of PCA-LDA classifier was tested using 10-fold cross validation. In 10-fold cross validation, the 300 SERS spectra were randomly partitioned into 10 groups of equal size (30 spectra in each group). Then, 9 groups were used as training data for PCA-LDA classification, and the remaining group was employed as the test group to evaluate the performance of such classifier. All 10 groups were tested in the same fashion, and the average performance was reported. PCA and LDA were performed in Matlab using statistics toolbox. Logistic regression and Chi-square test were calculated using SAS.

3. Results

3.1. Protein detection enhancement

AgNPs colloidal solution was firstly used for SERS measurements. However, PCA results did not show a promising clustering of any class. The PCA scatter plot of SERS spectra based on AgNPs colloidal solution is shown in supporting information (Figure S3). Urine is a very complex matrix consisting of various compounds, of which the concentration may be significantly different from person to person, especially for major components including urea, uric acid, etc. However, such variances of the concentration of most urinary components are not necessarily related to the functionality of kidney. The fluctuation in the concentration of these irrelevant urinary components has a significantly impact on the SERS spectra. To minimize the unrelated components and maximize the influence of potential biomarkers, especially proteins and peptides, Ag-I NPs colloidal solution was utilized to increase the sensitivity of protein and minimize the inherent background of the colloidal solution itself. The iodide modification of AgNPs not only provided an iodide monolayer, which replaced the surface adsorbates (mainly citrate group used in reduction reaction) from the nanoparticles, but also prevented the protein from denaturation because of its strong chemical interaction with silver [32]. Comparison of SERS enhancement of hemoglobin using AgNPs and Ag-I NPs was shown in Figure S4. As indicated, Ag-I NPs had a clear advantage over regular AgNPs in SERS measurements of proteins, consistent with published work [31].

3.2. Raman spectral features of urine

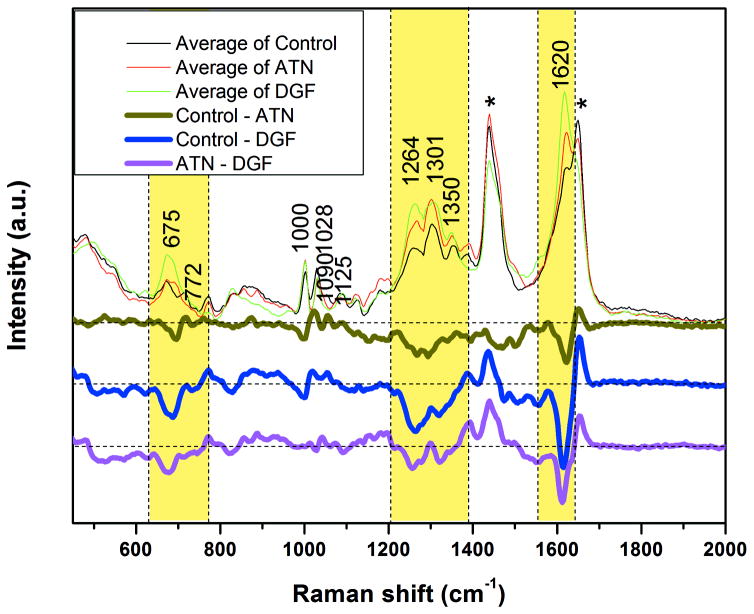
Average Raman spectra and spectral differences between each two classes are shown in Figure 1. Common urinary amino acids were observed, such as phenylalanine at 1001 cm⁻¹ and collagen at 1264 cm⁻¹. Dominant Raman peak is at 1620 cm⁻¹, which corresponds to the ring stretching mode of porphyrin. Tentative Raman band assignments are shown in Table 2 [41–45]. Because the urine samples were stored at −80°C and thawed before SERS measurements, the impact of freeze and thaw cycle on SERS spectra was investigated. We did not find appreciable effect on the SERS spectral features over six freeze-thaw cycles (Figure S5)

Figure 1.

Average spectra of the three classes and their spectral difference. Spectral difference curves are the subtraction of average spectrum of one class from another class. For example, control – DGF curve (blue bold line) is the result of average of control (light blue line) minus average of DGF (light green line). Three spectral difference curves (bold curves at the bottom) are vertically shifted for a clearer viewing. The horizontal dash lines on each spectral difference curve are the zero intensity position. Highlighted regions over 630–772, 1204–1390, 1552–1641 cm⁻¹ are selected for PCA analysis. * Inherent peaks from Ag-I NPs colloidal solution.

Table 2.

Tentative Raman band assignments

Raman bands (cm−1)	Tentative assignments
675	Glycerol; glutathione
772	Alanine
1000	Phenyl ring breath (Amino acid, phenylalanine); symmetrical C-N stretch of (urea)
1028	Coenzyme A
1125	Adenine
1264	Collagen; Amide III (protein)
1301	CH2 bending mode, collagen wagging mode
1350	Guanine
1620	Ring stretching (porphyrin)

3.3. Association of prominent SERS spectral features with donor clinical characteristics

3.3.1. Significant spectral distinction between DGF and control classes

SERS spectra with full informative Raman shift range (600–1700 cm⁻¹) were used for PCA initially. A trend of bias in the distribution of control and DGF classes along PC1 vector was observed (Figure S6). To maximize the overall SERS spectral variance between control and DGF classes and minimize the irrelevant variance (such as inherent peaks from Ag-I NPs colloidal solution), three spectral ranges were selected for PCA analysis, namely 630–772, 1204–1390 and 1552–1641 cm⁻¹ (highlighted area in Figure 1). 1552–1641 cm⁻¹ was chosen because the absolute intensity was high in the spectral difference between control and DGF. 630–772 and 1204–1390 cm⁻¹ were selected because the ratio of variance to their original peak intensity was high. To estimate the contribution to the spectral variance from the selected Raman shift range, the integral of the absolute intensity of PC1 and PC2 spectra, which were based on 300 SERS spectra using full Raman shift range, was calculated. The integral ratio of the selected Raman shift ranges to the full range Raman shift are 64.46% and 54.50% respectively for PC1 and PC2 (Figure S7). All PCA and LDA analyses in this study were based on these three selected ranges unless stated otherwise.

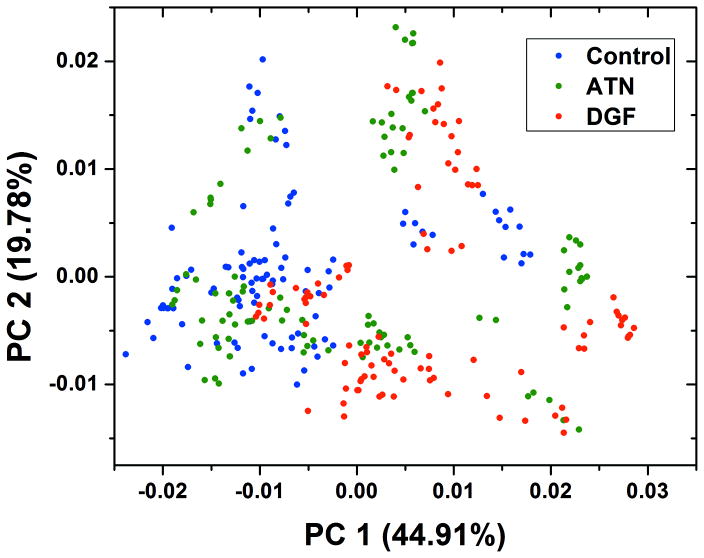
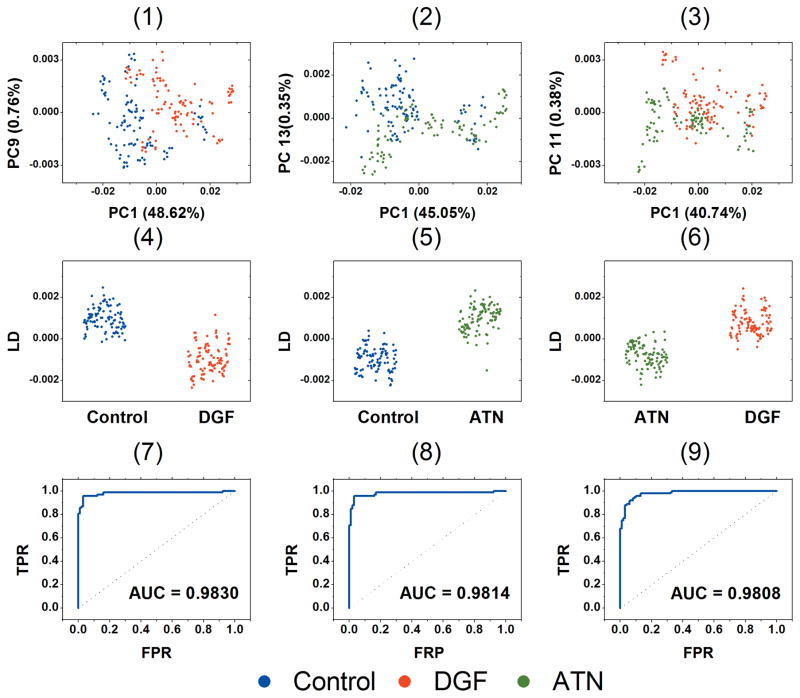
Figure 2 shows the scatter plot of PC1 and PC2 based on the selected wavenumber ranges for the three classes. All 300 spectra were used in PCA, and each data point represents a single spectrum. PC1 and PC2 have the highest variance of all data with a total cumulative variance of 64.69%. The scatter plot shows the overall relative similarity and variance of all 300 spectra. The control class and DGF class have a trend of separation along the PC1 vector, where most control data have negative PC1 scores, and most DGF data have positive values. For the ATN class, there is no clear separation or clustering.

Figure 2.

Score plot of PC1 and PC2 of PCA analysis using all 300 SERS spectra. The contribution of variance of PC1 and PC2 are 44.91% and19.78% respectively.

3.3.2. Risk prediction for the ATN class to develop DGF

The clinical characteristics of donors in ATN class overlap with donors in the DGF class, as shown by the PCA score plot in Figure 2. For donors in DGF class, both kidneys from each donor had DGF after transplant. Based on the clinical diagnosis, there were three DGF cases in ATN class, but only one kidney from each donor had DGF in recipients after transplant. Because there were such similarities in the presence of DGF in transplant outcomes between ATN and DGF classes, we hypothesized that the six ATN cases who have positive average PC1 score values (0.0012, 0.0048, 0.0052, 0.0054, 0.0162, 0.0223), had a higher probability of developing DGF after transplant.

Among the three DGF cases in the ATN group, two cases (average PC1 score 0.0223 and 0.0054) had a positive average PC1 score. The other one, however, had a negative average PC1 score (−0.0158). Besides DGF, there are four cases of slow graft function (SGF) in the ATN class. Among these four cases, two showed positive average PC1 scores (0.0162 and 0.0052). To summarize, among the six ATN donors who were in the DGF region based on the PCA analysis of SERS spectra (with positive PC1 score), two were clinically diagnosed as DGF, and two were diagnosed as SGF.

Based on Figure 2, there is an appreciable spectral variance between the control and the DGF classes along the PC1 vector. To study the ability of PCA in distinguishing the DGF class from the control class, PCA was then conducted only on spectra of the DGF and the control classes using selected ranges of the Raman shifts.

3.3.3. Effect of kidney fibrosis and kidney atherosclerosis on classification

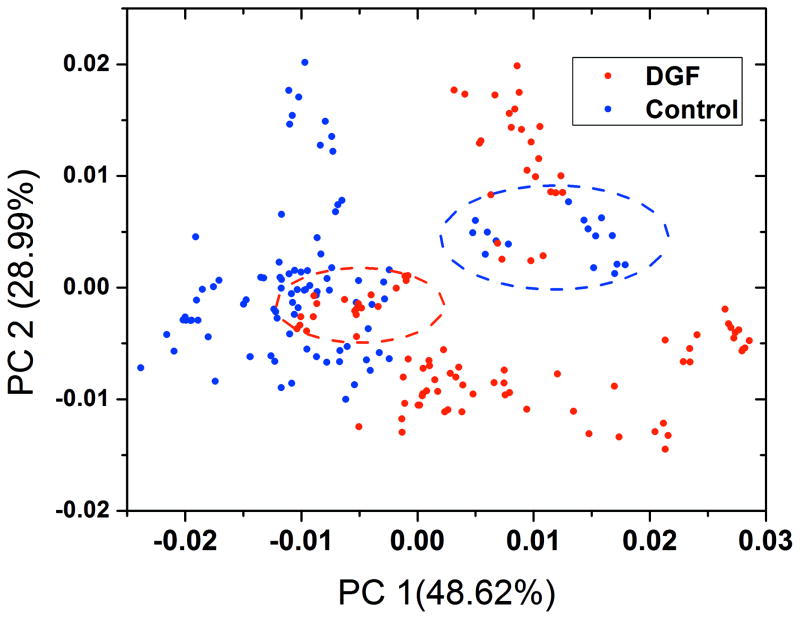
Figure 3 shows the scatter plot of PC1 and PC2 based on control and DGF classes. By taking away the ATN data, the dispersion of data point of these 2 classes is almost identical as they are in Figure 2, which indicated that it is the control and DGF classes that contribute to the dominant variances among all data matrix. There are two clusters of outliers in each class that sit in the other class’s region. Because 10 spectra of each urine sample were used in PCA analysis, spectra from the same urine are of high similarity. Thus, each cluster of outlier represents spectra from a single urine sample. So Figure 3 shows that both control and DGF classes have 2 outliers that have similar spectral features with the other class.

Figure 3.

PCA scatter plot of PC1 and PC2 of control and DGF classes. The contribution of variance of PC1 and PC2 are 48.62% and 28.99% respectively. The red circle and blue circle demonstrate the outliers of the DGF class and the control class, respectively.

We believe that kidney fibrosis (KF) and kidney atherosclerosis (KA) might contribute to the outlying of the 2 control cases. The two outliers of the control class are among the 3 cases that had mild form of donor KF and KA respectively based on the clinical diagnosis. The 7 remaining donors in the control class did not have KF or KA. In the ATN class, the presence of donor KA and KF also seems to have a contribution to the unique SERS spectral features of DGF class. There are 4 out of 6 donors in ATN class who had donor KF and/or KA are in the DGF region in the PCA scatter plot (Figure 2). In the DGF class, there are two outliers located in the control region. Both of them lacked KF and KA diagnosis. We note that the SERS measurements and the PCA-LDA analyses were all carried out blind with detailed clinical information being withheld from the investigators till completion of classifications to avoid any real or perceived bias regarding the hypothesized effect of KF and KA. Based on the spectral similarity of KF and KA cases with the DGF class, donors with KF and KA may exhibit urinary SERS features in a similar way as DGF, given the correlation between biopsy and PCA. Further studies involving more urine samples are needed to support this hypothesis.

3.4. Classification improvement

The classification between each pair of classes was firstly investigated, and LDA was applied on both raw spectra and scores of PCs. PCA is an unsupervised dimension reduction method, which does not take the class identities of data into account when generating a new space of data. The significant overlapping among the three classes in the PCA scatter plot implies that the most prominent variances of all SERS spectra do not have strong associations with their class information. Thus, LDA was used to achieve a better classification performance.

3.4.1. Data size-dependent performance of LDA

Unlike PCA, LDA is a supervised classification tool that aims at finding a hyperplane that can separate data the most based on their classes. LDA does not necessarily depend on data of reduced complexity, so all intensities within the selected range of Raman shifts was firstly used in LDA test. The 10-fold cross validation was then adapted to validate the accuracy and repeatability of this classifier. The performance of LDA on raw spectral data, however, was not very promising. The sensitivity and specificity of DGF are 64.0% and 74.0% respectively, with an overall accuracy of 69.5%.

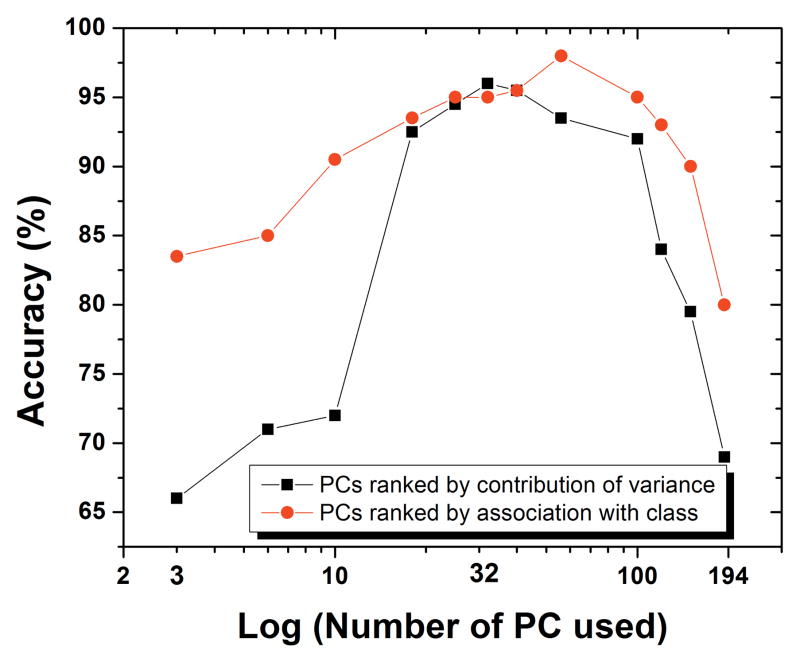
The poor performance of LDA when using raw spectra data is because all information, regardless of its association to the class identity, was enclosed in the analysis. We found that excessive amounts of subtle spectral information would hinder the performance of LDA. To prove this point, we adapted conventional PCA-LDA by using the first several PCs in LDA. The change of performance of LDA with the number of first PCs used is shown in Figure 4. The black curve shows the results when PCs were ranked by their contribution to the data’s overall variance, which is the regular way that PCs are ranked in PCA. When only first 3 PCs were used, the accuracy was only 66%. As more PCs were used, the accuracy increased and a maximum of 96% was reached when 36 PCs were used. When more than 36 PCs were used, the accuracy decreased even though more information were included in LDA. Because PCs are ranked in a descending order of the overall variance of all data, PCs of lower order contains more subtle spectral information than PCs of higher orders. Thus, excessive subtle information would reduce the performance of LDA since the accuracy dropped to 67% when all 194 PCs were used.

Figure 4.

Enhanced PCA-LDA classification performance when use PCs with high associations with class identity in LDA. The curves shows the accuracy of control DGF binary classification when different number PCs were used in LDA based on 10-fold cross validation. Black curve corresponds to the result based on PCs ranked by the contribution of the overall all variance (regular rank of PC in PCA). Red curve present the results when PCs were ranked by their association with class identities.

3.4.2. Classifications using optimized PCA-LDA analysis

The purpose of using PCA is to reduce the complexity of data. Using 36 PCs does not serve this purpose very much. To reduce the PC used in LDA but not sacrificing too much efficiency of PCA-LDA, PCs with higher associations with their class identities are preferentially used in LDA to achieve a better classification performance. To evaluate the association of scores of each PC with the class identities, logistic regression was applied. The PCs then were ranked by an ascending order of the P-value, which is defined as the possibility of null hypothesis used in statistics. When P-value is less than 0.05, it is suggested that null hypothesis is rejected, which alternatively means the variable has a significant association with the response. In the analysis of binary classification below, PCs with P-values less than 0.05 were used in LDA. By using PCs with high associations with classes, the data complexity used on LDA was further reduced and the performance was not affected much.

In Figure 4, the red curve shows the enhanced performance of PCA-LDA classifier for control DGF binary classification when PCs were ranked by their association with the class identities. The accuracy of the classifier was about 83% when the 3 PCs which the highest association with the class identities were used (namely PC1, PC9 and PC20). This is a tremendous improvement comparing with the accuracy of only 64% when the first 3 PCs were used in LDA (namely PC1, PC2 and PC3). Moreover, the accuracy approached 90% faster when use PCs with stronger association with class identities. So the evaluation of the PCs with class reduces the amount of PCs used in LDA.

Logistic regression is commonly used as an independent classification tool for categorical results analysis. To the best of our knowledge, this is the first time that logistic regression is used to enhance the performance of the conventional PCA-LDA analysis. The impact of the adaption of logistic regression before the LDA step is the significant data size reduction. The reduced data complexity can contribute to a faster data processing and less power consuming on the potential prognostic tool that uses this approach.

Figure 5 shows the scatter plots of PCA and LDA of binary classification study of the three class pairs. In PCA scatter plot, the two PCs that had the lowest P values were used to present the best separation. Based on the statistical analysis of scores of each PC and the class, the PCs that had a P value less than 0.05, which suggested that null hypothesis was rejected, were used in LDA. In control and DGF pair, nine PCs (PC1, PC9, PC20, PC6, PC7, PC21, PC3, PC15 and PC2 ranked in ascending order of P-value, with a total variance of 85.52%) were used in LDA. In control and ATN pair, eight PCs (PC1, PC13, PC11, PC5, PC12, PC4, PC21 and PC10, with a total variance of 54.11%) were used in LDA. In ATN and DGF pair, the PC5, which ranked the 10^th in the association with class, still had a low P value of 0.0247, and the ten PCs already provided enough information for an excellent performance of LDA. So in this pair, ten PCs (PC1, PC11, PC16, PC10, PC4, PC2, PC19, PC15, PC6 and PC5, with a total variance of 76.22%) were used in LDA. The P values of each PC for all three binary classifications are shown in Table S2.

Figure 5.

The first row are the scatter plots of PCA. The PCs of the first two highest association with classes are used to present best separation. The second row are 1-D scatter plots of LDA based on the ten PCs with the first ten highest association with the class. The third row are the ROC curves of 10-fold cross validation based on the LDA. The AUC for the three binary classifications are 0.9830, 0.9814 and 0.9808 respectively. The first column is control and DGF classes; the second column is control and ATN classes; the third column is ATN and DGF classes.

The lowest order of PC used in the PCA-LDA analysis above is PC21. Figure S8 shows the loading spectra of PC1, PC21, and PC130 of the PCA results of the control and the DGF classes. There are 194 PCs generated by the PCA for each pair of classes. PC130 is a randomly selected low order PC to demonstrate the noise signal. For PC130, the spectrum randomly oscillated at every 2 cm⁻¹, which is the wavenumber resolution of the spectrum. In PC 21, however, the spectrum still shows significant spectral information, which can contribute to the classification in the following LDA process.

The validation of LDA on each pair of cases was evaluated by 10-fold cross validation and the receiver operating characteristics (ROC) curves are plotted. All LDA models are highly efficient and reproducible based on the results of 10-fold cross validation. The areas under the curve (AUC) are 0.9830, 0.9814 and 0.9808 for each pair of classes. Table 3 shows the confusion matrix of 10-fold cross validation of the PCA-LDA classifier based the binary classification of each pair of classes. By using the PCs with high associations with the classes, the performance of LDA has a significant improvement over LDA using raw spectra data. Confusion matrix summarizes the true positive prediction (PP), true negative prediction (NP), false positive prediction (FP) and false negative prediction (FN), based on which the sensitivity, specificity and accuracy were derived. The sensitivity equals to PP/(PP+FP), the specificity equals to TN/(TN+FN), and the accuracy is the average of sensitivity and specificity. Although based on the scatter plot of PC1 and PC2, the control and DGF cases have the higher trend of variance than the other two classes pairs, the sensitivity of DGF over control is 86%, which is the lowest among three pairs. This implies that spectra of the two outliers of DGF are of high similarities as control spectra and the PCA-LDA classifier cannot differentiate them very accurately.

Table 3.

Confusion matrix of 10-fold cross validation of PCA-LDA classifier on binary classification of each pair of classes.

Control and DGF, DGF as positive
		Predicted class
		DGF	Control
True class	DGF	86	14
	Control	7	93
Sensitivity		86.00%
Specificity		93.00%
9 PCs used for LDA.
Cumulative variance = 85.52%
Accuracy = 89.50%

Control and ATN, ATN as positive
		Predicted class
		ATN	Control
True class	ATN	96	4
	Control	3	97
Sensitivity		96.00%
Specificity		97.00%
8 PCs used for LDA
Cumulative variance = 54.11%
Accuracy = 96.50%

ATN and DGF, DGF as positive
		Predicted class
		DGF	ATN
True class	ATN	91	9
	DGF	4	96
Sensitivity		96.00%
Specificity		91.00%
10 PCs used for LDA.
Cumulative variance = 76.22%
Accuracy = 93.50%

For other two class pairs, the sensitivities are both 96%, which indicates a very efficient and reliable classification. The specificities of all classifications are >90%, and the highest is ATN class at 97% in the ATN and control binary classification. This suggests that the SERS spectral features are highly specific to their clinical diagnosis.

3.5. Multi-class classifications

Similar to the binary classification, PCA-LDA was then conducted on all three classes based on PCs with significant associations with class. In multi-class classification, data of all three classes were used and classified at the same time. Scores of nine PCs were used in LDA, namely PC1, PC13, PC14, PC6, PC12, PC2, PC19, and PC10, with a total weight of 74.72%. Table 4 shows the confusion matrix and performance of PCA-LDA of all three classes based on 10-fold cross validation. The average performance of this classifier is 74.44% in accuracy. DGF has the highest sensitivity over all three classes at 79%. This is consistent with the fact that there are two outliers of DGF urine samples whose spectral features are highly similar to urines in the control class. The sensitivity and precision for three classes classification are between 70% and 80%

Table 4.

Confusion matrix of 10-fold cross validation of PCA-LDA classifier on three classes using 9 PCs and 30 PCs.

LDA using 9 PCs		Predicted class
		Control	ATN	DGF
True class	Control	70	6	24
	ATN	18	75	7
	DGF	9	12	79
		Positive classes
		Control	ATN	DGF
Sensitivity		70.00%	75.00%	79.00%
Precision		72.16%	80.64%	71.81%
9 PCs used, total weight = 74.72%
Accuracy = 74.77%

LDA using 30 PCs		Predicted class
		Control	ATN	DGF
True class	Control	81	9	10
	ATN	4	91	5
	DGF	2	11	87
		Positive classes
		Control	ATN	DGF
Sensitivity		81.00%	91.00%	87.00%
Precision		93.10%	82.00%	85.29%
30 PCs used, total weight = 99.53%
Accuracy = 86.57%

Such a degraded performance compared with binary classification is due to the insufficient information included in LDA calculation. To enhance the performance of LDA, more PCs were used and the best performance was achieved when the first thirty PCs were included in LDA (Table 4). The total weight of first thirty PCs were 99.53%, and the accuracy increased to 86.57%. The sensitivity of ATN is 91%, which is the highest among all three classes. There are in a total amount of 194 PCs generated by PCA, and the accumulative weight of PCs not used on LDA (from PC30 to PC194) is only 0.57%. This subtle amount of information, however, will hinder the performance of LDA in a similar way as the binary classification shown in Figure 4 and the accuracy will drop to 69.00%.

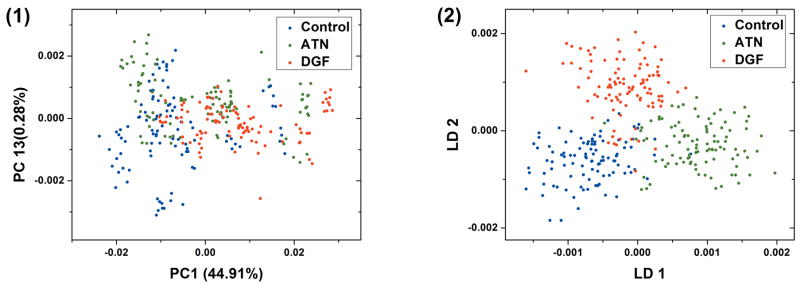
Figure 6 shows the scatter plot of PCA and LDA of all three classes. The PCA scatter plot uses PC1 and PC13, of which the scores have the highest association with class. The use of PC1 and PC13 is only for illustration purpose and to show the best visual separation of all three classes that PCA can deliver. The LDA scatter plot was based on the first thirty PCs with a total weight of 99.57% and shows a much better separation of the three classes compared with PCA. The control and ATN classes can be separated by LD1. The DGF can be differentiated from control and ATN by LD2.

Figure 6.

Scatter plot of PCA and LDA of 3 classes. (1) Scatter plot of PCA. The 2 PCs with the highest association with classes are chosen to show best separation of classes. (2) Scatter plot of LDA. The first 30 PCs are used in LDA.

4. Discussion

The sensitivity of ATN class is the best among all three classes in both binary classification and multi-class classification in the PCA-LDA analysis. In PCA, however, the ATN class has a significant overlapping with control and DGF classes. This is because in the process of PCA, class identities are not considered in the reorganization of the data matrix. The goal of PCA is to find a set of PCs that can demonstrate the majority of variance of all data and reduce the data complexity by dropping PCs of low weight in contribution. The unique spectral features that have high associations with the class identities are not necessarily the dominant variances of spectra. It is worth noting that in both binary classification and multi-class classification, the PCs that have the second highest association with class are of very minus contribution to the overall variance. Thus PCA might not reveal all the specific features of class identities.

LDA, in contrast, is aiming at projecting each data into a linear hyperplane that has minimum inter-class distance and maximum intra-class distance. By evaluating the association of each PC to the class identity, PCs with higher association with class can be used in LDA to achieve an excellent performance. This is a more computationally efficient way compared with regular PCA-LDA analysis, which simply adapts as many PCs the best classification results and accuracy.

However, the performance of LDA is not always optimum by only using PCs with high associations with class. In multi-class classification, more information is required to have acceptable performance. In multi-class classification, the LDA performance degraded significantly when only the PCs with a P value smaller than 0.05 was used. To reach the best performance, more information needs to be used. On the other hand, the performance of LDA will not always get better when more information is used. The maximum classification accuracy will be achieved when a certain amount of PCs are used and further subtle information will reduce the accuracy of LDA. So the amount of PC used in LDA can be chosen in different ways to balanced computational cost and overall performance.

The LDA results show a very promising classification ability of three classes, especially for the ATN class, of which the sensitivity is ≥90% in both binary classification and multi-class classifications. The ability to differentiate the ATN class from the DGF class is especially valuable, since the kidneys of ATN class are the ones that can be saved and utilized, while the kidneys in DGF class are the ones that have poor performance and should have been discarded. This methodology is thus of significant value to transplant physicians when they seek to determine which deceased donor kidneys to accept. Our results show potential in determining the kidneys which have donor ATN but with an acceptable transplant outcome.

Besides the high sensitivity, another important aspect of this study is that the analysis is based on urine of donors, which enables the clinicians to have the results while making decisions about which donor kidneys to accept for use in transplantation. The SERS analysis of urine is a non-invasive, label-free sensing technology, and the whole sensing set up can be packed onto a portable, hand-held tool since various portable Raman spectrometers are commercially available now.

Moreover, the SERS experiment requires minimum sample preparation and instrument training. With all these advantages, this approach has the potential to be transformed into a highly sensitive and specific point of care prognostic tool for quality selection of kidneys from deceased donors, which can help clinicians to expand the kidney pool from deceased donors by utilizing kidneys with high AKI risk.

5. Conclusion

In this work, we have demonstrated the utility of SERS measurements of urine from deceased donors and associated PCA-LDA analysis as a potential tool to predict kidney transplant outcomes. SERS provides a non-invasive and label-free detection of subtle changes in urine that have a high level of correlation with DGF. By utilizing PCA-LDA and logistic regression, more than 90% of sensitivity can be achieved in differentiating high donor AKI risk kidney with acceptable transplant outcomes (ATN class) from the ones with recipient DGF (DGF class). Both ATN and DGF classes show unique spectral features and can be classified efficiently from the control class. The occurrence of recipient DGF results in the main spectral differences in most intense spectral features from the control class, while the occurrence of donor ATN affects more subtle features of SERS spectra. To summarize, SERS has the potential to provide an early indication of deceased donor kidney transplant outcome before transplantation and can be a great asset to clinicians for expanding the deceased donor kidney pool by utilizing kidneys with high donor AKI risk as perceived by other biomarkers.