Abstract
Purpose
Glomerular basement membrane segmentation is an ultimate step in several image processing applications for kidney diseases and abnormalities in microscopic images. However, extracting the glomerular basement membrane (GBM) regions accurately is considered challenging because of the large variants in the microscopic images. The contribution of this work is to propose a computer-aided detection system to provide accurate GBM segmentation.
Methods
A novel GBM segmentation algorithm is developed based on neutrsophic set and shearlet transform. Firstly, the shearlet features are extracted from the microscopic image samples using shearlet transform. Afterward, the neutrosophic image is defined using shearlet features, and the indeterminacy on the neutrosophic image is reduced using an α-mean operation. Lastly, the k-means clustering algorithm is applied to segment the neutrsophic image and the GBM is identified using its intensity feature.
Results
Three metrics, namely the average distance (AvgDist), the Hausdorff distance (Hdist), and percentage overlap area (POA); were employed to assess the proposed method performance. The results established that the proposed method achieved smaller distance errors and larger POAs. For the tested image, the average of AvgDist, HDist and POA are 1.99204, 4.59535 and 0.67857, respectively. The results established that the cases were segmented accurately using the proposed NS based shearlet transform.
Conclusions
The new method utilizing the shearlet features and neutrosophic set improved the accuracy of GBM segmentation. Further study is underway to improve an automated CAD system using the refined segmentation results.
Keywords: Neutrosophic set, Shearlet transform, Segmentation, k-Means clustering, Renal diseases, Renal glomerular
Introduction
Kidney has an energetic role in the urinary system for maintaining the electrolytes and water balance in the blood as well as eliminating the waste form the body. Nephron, the functional kidney unit, consists of the renal tubule and renal corpuscle. In turn, the renal corpuscle comprises glomerulus and Bowman’s capsule that filters the blood components [1]. Typically, the filtration process through the glomerulus is accomplished mainly by the glomerular basement membrane (GBM). Abnormal variations and pathological changes in the GBM may occur due to several diseases, where diabetes mellitus causes GBM thickening, Alport syndrome causes thickness variation of the GBM, and familial hematuria causes GBM thinning [2]. Several diseases can manifest renal corpuscle structure changes, including the variation in the corpuscles morphometric components. Furthermore, the kidney suffers from several metabolic/structural changes with obesity, such as GBM thickening, hyper filtration of the glomerular, and Bowman’s capsule expansion. Hence, studying renal corpuscle’s pathological changes can provide imperative information in screening such diseases.
Microscopic analysis of kidney tissue in the animal models samples is a significant tool to the pathologists for diagnosing above diseases. These microscopic samples’ images enclose both the glomerulus as well as other irrelevant tissues. The irrelevant tissues along with other several factors, namely the irregular shape of the glomerulus, and the difference in staining intensity of microscopic images, affect the extraction of the glomerulus/GBM from microscopic sample’s image. Limited number of consistent procedures has been established for GBM quantitative analysis. Osawa et al. [3] studied manually the thickness of GBM. Saxela et al. [4] developed a method for analyzing the thin basement membranes in abnormal glomeruli. These manual approaches are prone to errors, time consuming, and subjective.
For renal corpuscle detection, researchers are interested to develop automatic object detection algorithms that can handle the glomerulus non-rigid shapes in the microscopic images, to measure the changes in the glomerulus intensity of the microscopic images under analysis, and to identify the boundaries accurately by fitting an ellipse to each glomerulus. In order to track the GBM’s center line, the uniformity, intensity continuity, intensity difference, and smoothness of the GBM have been measured [5]. Papageorgiou et al. [6] carried out a sliding window approach to detect the glomerulus in the kidney images. Contemporary glomerulus segmentation studies have been developed. Rangayyan et al. [7] developed a semi-automated segmentation procedure to analyze the GBM based on active contour models (ACM). However, while the standard parametric ACM fit the object tracking tasks, it miscarries to track multiple close objects, such as in the case of GBM. Thus, manual GBM walls’ construction is required to resolve the active contour leakage. Kato et al. [8] proposed a new descriptor called segmental histogram of oriented gradients (HOG) for detecting the glomerulus from the whole kidney sections. Zhang and Hu [9] extracted the glomerulus extraction by fitting curve optimization.
Optimization algorithms also have a significant role in the glomerulus segmentation. Xie and Ma [10] represented glomerulus shape accurately using the genetic algorithm that explored the optimal B-spline curve. Zhang et al. [11] employed the genetic algorithm to extract edges in the glomerulus area. Zhang and Fan [12] developed a genetic algorithm based watershed transform for glomerulus extraction. However, this optimization based glomerulus segmentation techniques suffer from the time consuming problem due to large searching space.
In order to detect GBM, it is necessary to segment microscopic image firstly, which is a difficult process due to the diversity/complexity of the microscopic images and the influence of the capturing process factors including the contrast, illumination, and noise. Fuzzy theory performs efficient segmentation as it preserves more information compared to the classic segmentation procedures. Additionally, clustering algorithm, named fuzzy c-means (FCM), identify the data segment to two or more clusters using membership. Nevertheless, classical set method cannot evaluate the indeterminacy of every element in the set. Hence, fuzzy set has been performed to handle the uncertainty.
Lately, neutrosophy offers a prevailing method for handling indeterminacy. In image segmentation, the Neutrosophic set (NS) approaches have been used efficiently [13, 14]. In addition, the NS is used for image thresholding [15]. It is an overall prevailing frame for generalizing the model of classic set, interval valued fuzzy set, fuzzy set, and interval-valued intuitionistic fuzzy set. The FCM’s inability has been solved by Guo and Sengur [16] through an uncertain data clustering procedure named neutrosophic c-means (NCM) clustering, to cluster a typical data points. The NCM united the fuzzy c-means and NS frameworks to calculate degrees of determinant/indeterminate clusters for each data. The results established that this technique is efficient for data clustering and image processing. Guo and Cheng [13] carried out a segmentation techniques based on the γ-means clustering. The image is transformed into the NS domain that is defined by three membership sets, namely T, I and F, where the entropy in NS is calculated for the indeterminacy evaluation. Two operators, namely α-mean and β-enhancement, have been used to reduce the indeterminacy. Guo et al. [17] carried out the NS for segmentation of lung images. Zhang et al. [18] developed neutrosophy to design a completely automated segmentation algorithm. In order to achieve superior results, Cheng and Guo [19] proposed the NS with the k-means for image segmentation, where for varying entropy, the k-means clustering was poor. Zhang et al. [14] proposed a neutrosophic domain, and then the watershed algorithm has been carried out to segment the image in this domain.
Typically, the segmentation techniques uses texture or color features based on the similarity/discontinuity of the pixels associated to their local neighborhood [25]. Edge detection procedures based on discontinuity divide the image using the detected isolated points, lines and edges. Multi-resolution analysis has been used in segmentation techniques, where large objects are segmented in coarse images, while small details are identified in higher resolution images. Particularly, segmentation based on wavelets and multi-scale approaches are efficient in microscopic image processing for image segmentation, de-blurring, and de-noising [20–22].
Sengur and Guo [23] proposed an effective automated method for segmentation of color texture image based on NS and multi-resolution wavelet transformation. The color-/texture-information is mapped on NS and wavelet domain, and then the segmentation has been performed using a c–k-means clustering. However, in multi-dimensional applications, wavelets suffer from critical limitations owing to the poor directional sensitivity of the analyzing functions supplementary to the wavelet transform; thus, they are relatively ineffective for representing anisotropic features and edges in the microscopic images. In order to resolve this limitation, a novel class of enhanced multi-scale approaches has been emerged, comprising the curvelets and shearlets [24]. These approaches contain the advantages of multi-scale analysis with the capability to powerfully encode directional information. Optimally, shearlets offer sparse illustration for two-dimensional data enclosing edge discontinuities [25]. Generally, shearlet-based algorithms have been applied for microscopic images de-noising. The results proved the superiority of shearlet-based algorithms competing wavelet-based methods [26].
From above studies, only few related works have been carried out on microscopic images segmentation based on NS, particularly for segmenting the GBM. Consequently, the current work combines the advantages of neutrosophic set and shearlet transform to segment the renal corpuscle indicating the GBM in the microscopy kidney-tissue sample images. A fully automated microscopic image segmentation technique is developed based on NS and shearlet transform. The neutrosophic image is newly defined in shearlet domain and then segmented via k-means clustering algorithm. The proposed method is tested using dataset of rats’ renal corpuscle images that attained by light microscope.
The structure of the remaining sections is as follows. “Proposed method” introduces the different methodologies along with the proposed system in the present study. “Experimental results and discussions” analyses the obtained results to validate the proposed technique. Lastly, “Conclusion” concludes the present study.
Proposed method
This work proposes a GBM segmentation algorithm using NS and shearlet transform in albino rats microscopic images. At first, the shearlet transform is employed on the image and the shearlet features are extracted. Then, the image is mapped into NS domain where the map functions are defined using the shearlet features, and a typical operation in neutrosophic set, namely α-mean operation is taken on the image to remove its indeterminacy. Lastly, the segmentation is performed via the k-means clustering on the truth membership matrix of the image in the NS.
Shearlet transform
Intensity discontinuity is the most important features in the microscopic images to identify the locations of region of interest (ROI) as well as to capture the orientations. However, the traditional wavelet transform (WT) is inefficient to provide significant geometrical information of the objects or distribution due to wavelets are isotropic and are incapable of accommodating edges in images (anisotropic features) [27]. On the contrary, an extension of wavelets, namely shearlets can accommodate anisotropic features [28]. Shearlet transform is designed to combine the geometric features and the multi-scale analysis by creating a non-isotropic form of WT. It addresses anisotropic and directional information at various scales of an image. Shearlets provide a highly competent depiction of images with edges. The shearlet representation consists of an assembly of well-localized waveforms at different orientations, scales, and locations. In addition, these forms have highly anisotropic shapes. Thus, shearlet transform is mainly well adapted to signify edges and other anisotropic objects that considered the most dominant features in typical microscopic images. It provides approximately optimally sparse depictions for a large class of functions that are convenient to model images [28].
The shearlets are constructed by applying scaling, parabolic shearing, and translation operators on the basis functions. Typically, the scaling operator is essential to produce waveforms having anisotropic support. The dilation operators’ family is used, which depends on a parabolic scaling matrix. In addition, to change the waveforms’ orientations, an orthogonal transformation is applied at which the shearing operator is selected based on the shearing matrix S. This shearing matrix uses a variable which is related to the slopes instead of the angles to parameterize the orientations. Lastly, a translation operator is applied based on a standard operator. These three operators, namely scaling, shearing and translation are combined to define the shearlet transform. Shearlets are non-adaptive technique where a shearing matrix is used to control the shearing functions. The shearlet transform can be explained based on the composite wavelets that are given by [29]:
| 1 |
where j, l ∊ Z, k ∊ Z 2, ξ ∊ L 2(R 2)and A and S are invertible matrices having |det S| = 1. Shearlet is considered a special example of L 2(R 2), when and , where A = A 0 represents the anisotropic dilation matrix, and S = S 0 represents the shearing matrix. This shearing matrix is used to control the shearlet transform directionality. Typically, the shearlet transform is expressed as [30]:
| 2 |
| 3 |
| 4 |
For , and , where for l = 0, 1 and i = 1, …, L, and if represents a frame for L 2(R 2), then the function is in the shearlets’ system. Afterwards, the extracted features using the shearlet transform are mapped on the NS domain to remove the indeterminacy.
Neutrosophic image and α-mean operation
Recently, the neutrosophic theory extended from classical fuzzy theory denotes that neutrosophy has been successfully used in many applications for reducing the uncertainty and indeterminacy. In the neutrosophy theory, every event has certain degree of truth (T), falsity (F) and indeterminacy (I) for independent deliberation from each other. The previously reported studies demonstrated that the NS has a vital role in image processing.
In the image domain, the pixel P(i, j) is transformed into the neutrosophic domain, P NS(i, j) = {T(i, j), I(i, j), F(i, j)}, where T(i, j), I(i, j) and F(i, j) are the membership values belonging to white set, indeterminate set and non-white set; respectively as T, I and F are the neutrosophic components. An element g in set N is defined as g(T, I, F), where T identifies true in the set, I identifies the indeterminate in the set, and F identifies false in the set.
In the proposed method, the image is transformed into NS domain using shearlet feature values as follows:
| 5 |
| 6 |
where T and I are the true and indeterminate membership values in the NS. ST L(x, y) is the low frequency component of the shearlet feature at the current pixel P(x,y). In addition, ST Lmax and ST Lmin are the maximum and minimum of the low frequency component of the shearlet feature in the whole image, respectively. ST H(x, y) is the high frequency component of the shearlet feature at the current pixel P(x,y). Moreover, ST Hmax and ST Hmin are maximum and minimum of the high frequency component of the shearlet feature in the whole image; respectively. In the proposed method, we only use T and I for segmentation.
In order to decrease the indeterminacy of the NS, an α-mean operation is taken on subset T that is expressed as:
| 7 |
where is the value after the α-mean operation, and w is the size of local window.
After the α-mean operation, the entropy of the indeterminacy subset T is decreased. In addition, the elements distribution in I becomes more uniform. Iteratively, the operation is performed until the entropy value of the subset T, is kept unchanged. The entropies of set Tare used for evaluating the elements distribution in the neutrosophic domain:
| 8 |
where En T is the entropies of the sets T and p T(i) is the probabilities of elements in T whose values equal to i. Finally, the regions in the mapped image are clustered using the k-means clustering for accurate segmentation of the GBM.
Clustering algorithm
k-means clustering is an effective approach to partition m objects into K clusters at which each object fits to the certain cluster according to the closest center [31]. It yields exactly K different clusters that have the greatest possible distinction. The objective of k-means clustering is to minimize squared error function, or the total intra-cluster variance.
In the present work, the k-means clustering technique is defined for the NS and it handles the neutrosophic image after the α-mean operation. The k-means’ objective function is given by:
| 9 |
where b is the number of clusters, n j is the number of cases, is the distance function, and the centroid of the cluster Z Tj is given by:
| 10 |
where n j is the number of the elements of cluster C j. The preceding methodology is applied to segment the GBM as explained below.
Proposed neutrosophic segmentation algorithm
In the proposed method, the shearlet transform is combined with the NS and the clustering algorithm for albino rats’ microscopic image GBM segmentation. In the first step, the green channel is extracted from colored image. The shearlet transform is then used for features extraction, which afterwards are transformed into the NS domain to reduce the indeterminacy. Subsequently, the NS indeterminacy is decreased using the α-mean operation on subset T until the entropy of the indeterminate subset T becomes unchanged. Finally, the mapped image’s pixels in the NS domain are categorized using the proposed K-mean clustering. The number of clusters is determined according to the prior knowledge in the Microscopic Images, where there are three categories according to their intensity values, namely the glomerular basement, tissue and background. At this number of clusters, each object fits to the certain cluster according to the closest center for efficiently identify (segment) the GBM regions. The steps of the proposed approach can be summarized as follows.
Experimental results and discussions
Materials
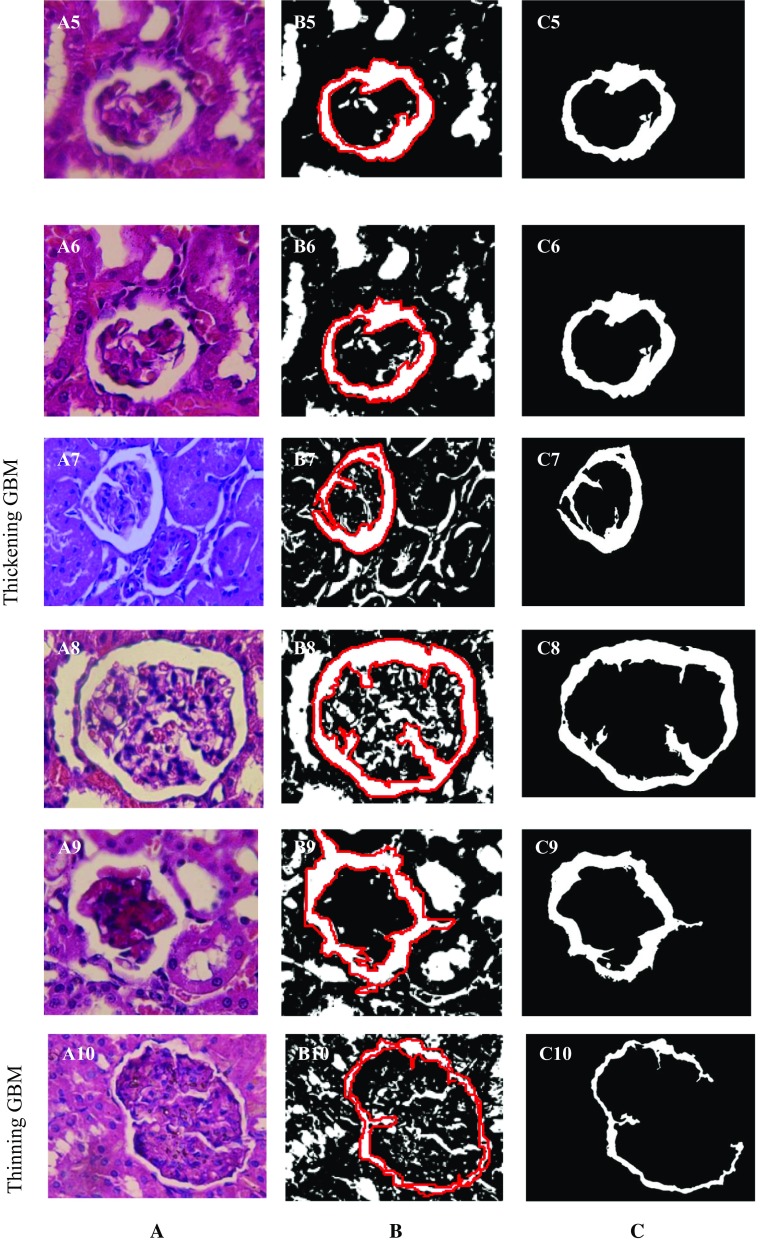
A dataset of rats’ kidney images acquired in the Laboratory of Anatomy Department, Faculty of Medicine, Tanta University, Egypt is used to evaluate the proposed work. The samples images have been captured through a light microscope at X1000 magnification. The tested albino rats’ samples are categorized according to the GBM size into three cases, namely i) control including normal samples, ii) samples of thickening GBM, and iii) thinning GBM. Figure 1a illustrates the original colored samples images of these three cases, where Fig. 1A1–A4 demonstrates the control cases as which the GBM has its normal dimensions; Fig. 1A5–A9 illustrates the thickening GBM case at which the bowman’s space width increases, and Fig. 1A10 illustrates an example of the third case, namely thinning GBM, where the bowman’s space width decreases.
Fig. 1.
Light microscopic histological images of different kidney rat’s capsule, a colored original samples images, b golden standard (marked by expert), and c automated segmented samples using the proposed approach based on NS
Segmentation results
In order to assess the proposed approach performance on segmentation, many microscopic images are used to test the proposed approach and the results are compared with the ground truth results which are obtained by an experienced doctor. Ten images in three different cases are selected randomly to demonstrate the performance of the proposed technique as illustrated in Fig. 1.
Figure 1 established the effectiveness of the proposed segmentation procedure compared to the golden standard marked in red GBM, even in the case of the thinning GBM.
Evaluation
Manually, the cell wall boundaries in the microscopic images under concern are outlined by a skilled expert. Afterward, these marked images were used as the reference standard for performance assessment of the proposed GBM segmentation method. In order to assess the detection results quantitatively, three metrics, namely POA, Hdist, and AvgDist, were calculated to compare the segmentation results with the expert’s manual segmentation ones. These metrics are defined as follows:
| 11 |
| 12 |
| 13 |
where A C and A M are the automated segmented area and the manually outlined area surrounded by the boundaries C and M. ∪ and ∩ are the union and intersection of two sets, respectively. The distance between a segmented boundary point c i and a reference standard point r j is Dist(c i , r j), or equivalently, Dist(r j ,c i).
In comparison with expert’s manual outlines, three performance metrics are considered on the corresponding images and the average values are computed to evaluate the proposed method performance. For the all tested images, the average of POA, HDist and AvgDist are 0.67857, 4.59535 and 1.99204, respectively. Table 1 reports the detailed evaluation results for each image.
Table 1.
Detailed values of the evaluation metrics for the image in Fig. 1
| Image name | POA | HDist | AvgDist |
|---|---|---|---|
| A1 | 0.6577 | 4.4721 | 1.4938 |
| A2 | 0.5810 | 3.7417 | 1.3695 |
| A3 | 0.5883 | 4.8990 | 1.4830 |
| A4 | 0.6972 | 5.5678 | 3.0519 |
| A5 | 0.7646 | 4.5826 | 1.5133 |
| A6 | 0.7848 | 4.0000 | 1.3039 |
| A7 | 0.7627 | 3.7417 | 1.6097 |
| A8 | 0.7055 | 5.5678 | 2.8581 |
| A9 | 0.6860 | 4.6904 | 2.2451 |
| A10 | 0.5579 | 4.6904 | 2.9921 |
| Average value | 0.67857 | 4.59535 | 1.99204 |
Table 1 along with Fig. 1 establishes that all cases are segmented accurately using the proposed method.
Discussion
Different diseases affect the kidney leading to significant metabolic and structural changes that affect the renal corpuscle, its glomerulus, Bowman’s capsule and the GBM. Consequently, the glomerular size and the GBM can be considered indexes that indicate the kidney condition. In order to achieve accurate measurements for further diagnosis, efficient segmentation step is required to identify the GBM. Shearlet transform has inherent turning sensitivity compared to Gabor filter. Thus, it is suitable to characterize small contours in the microscopic images. Shearlet transform captures the detected edges’ visual information at multiple scales and different orientations by applying a multi-scale decomposition. In addition, in order to reduce the indeterminacy degree, an indeterminacy filter is constructed including the indeterminacy value on feature image using NS.
In the current work, a novel NS based on shearlet transform is carried out that followed by k-means clustering as a proposed segmentation process. The proposed approach reduced the independency in the images through the NS operation on the shearlet transform and further segmented the image using the k-means clustering algorithm. Evaluation metrics were measured using dataset of rats’ renal corpuscle images that captured in the Anatomy Department, Faculty of Medicine, Tanta University, Egypt. In addition, the related reported studies in the introduction established that few previous works has been conducted on microscopic images for GBM segmentation. Consequently, a comparative study with other segmentation on the same dataset is difficult. Rangayyan et al. [7] were concerned with detecting and measuring the GBM width based on the active contour modeling on 34 TEM images without evaluating the segmentation process. Kato et al. [8] applied the segmental HOG for glomeruli detection using a segmentation algorithm to locate the glomeruli’s boundary. The results established 90.1% F-measures. However, in the current work, the golden standard marked GBM by expert (Fig. 1) was used for comparison with the proposed approach using the POA, HDist and AvgDist as evaluation metrics of the proposed measurement of the NS based shearlet transform for segmenting the GBM with the k-means clustering algorithm. In addition, the measured performance metrics are in line with the same results as larger POAs and smaller distance errors, which proved the effectiveness of the proposed method. However, it is recommended to increase the size of the dataset to achieve better results. In addition, the proposed method can be applied to test different types of images.
Conclusion
Manual identification of renal corpuscle and GBM is time consuming, tedious, and inaccurate. Thus, automated segmentation for identification and GBM detection become demanding. The new proposed method utilizing the shearlet features and neutrosophic set improved the accuracy of glomerular basement membrane segmentation. Accurate and automated GBM segmentation is an essential step for the diagnosis of several kidney diseases based on image analysis of microscopic images. This study established that the new proposed technique using the shearlet features and fusion with NS domain enhanced the GBM segmentation. Further study is underway to improve automated CAD system using the refined segmentation.
Acknowledgement
We have been greatly indebted Dr. Ahmed Ashour, Anatomy Department, Faculty of Medicine, Tanta University, Egypt, for providing the dataset in the current work.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Schwartz MM, Jennette JH, Olson JL, Silva FG. Pathology of the kidney. New York: Lippincott Williams & Wilkins; 2007. [Google Scholar]
- 2.Kefalides NA, Borel JP. Basement membranes: cell and molecular biology. Houston: Gulf Professional Publishing; 2005. [Google Scholar]
- 3.Osawa G, Kimmelstiel P, Sailing V. Thickness of glomerular basement membranes. Clin Pathol. 1966;45:7–20. doi: 10.1093/ajcp/45.1.7. [DOI] [PubMed] [Google Scholar]
- 4.Saxela S, Davies DJ, Kirsner RLG. Thin basement membranes in minimally abnormal glomeruli. Clin Pathol. 1990;43:32–38. doi: 10.1136/jcp.43.1.32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ong SH, Giam ST, Jayasooriah, Sinniah R. Adaptive window-based tracking for the detection of membrane structures in kidney electron micrographs. Mach Vis Appl. 1993;6:215–223. doi: 10.1007/BF01212300. [DOI] [Google Scholar]
- 6.Papageorgiou C, Poggio T. A trainable system for object detection. Int J Comput Vision. 2000;38(1):15–33. doi: 10.1023/A:1008162616689. [DOI] [Google Scholar]
- 7.Rangayyan RM, Kamenetsky I, Benediktsson H. Segmentation and analysis of the glomerular basement membrane in renal biopsy images using active contours: a pilot study. J Digit Imaging. 2010;23(3):323–331. doi: 10.1007/s10278-009-9188-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kato T, Relator R, Ngouv H, Hirohashi Y, Takaki O, Kakimoto T, Okada K. Segmental HOG: new descriptor for glomerulus detection in kidney microscopy image. BMC Bioinform. 2015;16(1):316. doi: 10.1186/s12859-015-0739-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhang J, Hu J. Glomerulus extraction by optimizing the fitting curve. In: Proceedings of the ISCID’08 international symposium, vol. 2; 2008. pp. 169–172.
- 10.Xie M, Ma Z. Research of edge detection for B-spline wavelet. Acta Electron Sin. 1999;27:106–108. [Google Scholar]
- 11.Zhang J, Zhu H, Qian X, Huang T: Genetic algorithm for edge extraction of glomerulus area. In: Proceedings of the international conference on information acquisition, vol. 335–338; 2004.
- 12.Zhang J, Fan J. Glomerulus extraction based on genetic algorithm and watershed transform. In: Proceedings of the international conference intelligent robots and systems, vol. 4863–4866; 2006.
- 13.Guo Y, Cheng HD. New Neutrosophic approach to image segmentation. Pattern Recogn. 2009;42(5):587–595. doi: 10.1016/j.patcog.2008.10.002. [DOI] [Google Scholar]
- 14.Zhang M, Zhang L, Cheng HD. A neutrosophic approach to image segmentation based on watershed method. Signal Processing. 2010;90(5):1510–1517. doi: 10.1016/j.sigpro.2009.10.021. [DOI] [Google Scholar]
- 15.Ye J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J Intell Fuzzy Syst. 2014;26(5):2459–2466. [Google Scholar]
- 16.Guo Y, Sengur A. NCM: neutrosophic c-means clustering algorithm. Pattern Recogn. 2015;48(8):2710–2724. doi: 10.1016/j.patcog.2015.02.018. [DOI] [Google Scholar]
- 17.Guo Y, Zhou C, Chan HP, Chughtai A, Wei J, Hadjiiski LM, Kazerooni EA. Automated iterative neutrosophic lung segmentation for image analysis in thoracic computed tomography. Med Phys. 2013 doi: 10.1118/1.4812679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang M, Zhang L, Cheng H. Segmentation of ultrasound breast images based on a neutrosophic method. Opt Eng. 2010;49(11):117001. doi: 10.1117/1.3505854. [DOI] [Google Scholar]
- 19.Cheng H-D, Guo Y. A new neutrosophic approach to image thresholding. New Math Nat Comput. 2008;4(3):291–308. doi: 10.1142/S1793005708001082. [DOI] [Google Scholar]
- 20.Dima A, Scholz M, Obermayer K. Automatic segmentation and skeletonization of neurons from confocal microscopy images based on the 3-D wavelet transform. IEEE Trans Image Process. 2002;11:790–801. doi: 10.1109/TIP.2002.800888. [DOI] [PubMed] [Google Scholar]
- 21.Vonesch C, Unser M. A fast multilevel algorithm for wavelet-regularized image restoration. IEEE Trans Image Process. 2009;18(3):509–523. doi: 10.1109/TIP.2008.2008073. [DOI] [PubMed] [Google Scholar]
- 22.Chang CW, Mycek MA. Total variation versus wavelet-based methods for image denoising in fluorescence lifetime imaging microscopy. J Biophotonics. 2012;5:449–457. doi: 10.1002/jbio.201100137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sengur A, Guo Y. Color texture image segmentation based on neutrosophic set and wavelet transformation. Comput Vis Image Underst. 2011;115(8):1134–1144. doi: 10.1016/j.cviu.2011.04.001. [DOI] [Google Scholar]
- 24.Candes EJ, Donoho DL. New tight frames of curvelets and optimal representations of objects with piecewise C 2 singularities. Commun Pure Appl Math. 2004;56:216–266. [Google Scholar]
- 25.Guo K, Labate D. Optimally sparse multidimensional representation using shearlets. SIAM J Math Anal. 2007;39:298–318. doi: 10.1137/060649781. [DOI] [Google Scholar]
- 26.Guo K, Labate D. Characterization and analysis of edges using the continuous shearlet transform. SIAM J Imaging Sci. 2009;2:959–986. doi: 10.1137/080741537. [DOI] [Google Scholar]
- 27.Labate D, Laezza F, Negi P, Ozcan B, Papadakis M. Efficient processing of fluorescence images using directional multiscale representations. Math Model Nat Phenom. 2014;9(5):177–193. doi: 10.1051/mmnp/20149512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Easley GR, Labate D. Image processing using shearlets. Shearlets. 2012;7:283–325. doi: 10.1007/978-0-8176-8316-0_8. [DOI] [Google Scholar]
- 29.Labate D, Lim WQ, Kutyniok G, Weiss G. Sparse multidimensional representation using shearlets. Proc. SPIE. 2005;5914:59140U. doi: 10.1117/12.613494. [DOI] [Google Scholar]
- 30.Lim WQ. Discrete shearlet transform: new multiscale directional image representation. In: SAMPTA’09; 2009.
- 31.Khan SS, Ahmad A. Cluster center initialization algorithm for k-means clustering. Pattern Recogn Lett. 2004;25(11):1293–1302. doi: 10.1016/j.patrec.2004.04.007. [DOI] [Google Scholar]