Abstract
Three dimensional (3D) manual segmentation of the prostate on magnetic resonance imaging (MRI) is a laborious and time-consuming task that is subject to inter-observer variability. In this study, we developed a fully automatic segmentation algorithm for T2-weighted endorectal prostate MRI and evaluated its accuracy within different regions of interest using a set of complementary error metrics. Our dataset contained 42 T2-weighted endorectal MRI from prostate cancer patients. The prostate was manually segmented by one observer on all of the images and by two other observers on a subset of 10 images. The algorithm first coarsely localizes the prostate in the image using a template matching technique. Then, it defines the prostate surface using learned shape and appearance information from a set of training images. To evaluate the algorithm, we assessed the error metric values in the context of measured inter-observer variability and compared performance to that of our previously published semi-automatic approach. The automatic algorithm needed an average execution time of ∼60 s to segment the prostate in 3D. When compared to a single-observer reference standard, the automatic algorithm has an average mean absolute distance of 2.8 mm, Dice similarity coefficient of 82%, recall of 82%, precision of 84%, and volume difference of 0.5 cm3 in the mid-gland. Concordant with other studies, accuracy was highest in the mid-gland and lower in the apex and base. Loss of accuracy with respect to the semi-automatic algorithm was less than the measured inter-observer variability in manual segmentation for the same task.
Keywords: Image segmentation, Magnetic resonance imaging, 3D segmentation, Endorectal receive coil, Automatic segmentation, Validation
Introduction
Prostate cancer (PCa) is the most commonly diagnosed cancer in men in North America, excluding skin carcinoma. More than 30,000 deaths from PCa are estimated in the USA and Canada in 2015 [1, 2]. Magnetic resonance (MR) imaging (MRI), due to its potential for diagnosis and staging of PCa [3, 4], is one of the imaging modalities utilized in multiple diagnosis and therapeutic procedures. Contouring of the prostate on MRI could assist with PCa diagnosis and therapy planning. More specifically, T2-weighted (T2w) MRI is superior to other MRI sequences for anatomic depiction of the prostate gland and the surrounding tissues [5]. The use of an endorectal (ER) receive coil helps MRI acquisition performance in terms of image quality and spatial resolution [6] and used for research studies that require highly optimized prostate MRI for new investigation (e.g., lesion boundary localization) [7, 8]. However, it deforms and displaces the prostate gland [9], produces some ER coil-based imaging artifacts [10], and detects more details that challenge the adaptation of computer-assisted prostate contouring algorithms designed for non-ER MRI to this context.
Prostate boundary delineation may play an important role for radiation therapy planning, MR-guided biopsy, or focal therapy. Manual segmentation of prostate MRI, however, is a laborious and time-consuming task that is subject to inter-observer variability [11]. This motivates the need for fast and reproducible segmentation algorithms for T2w ER prostate MRI. There have been several algorithms published for segmentation of the prostate on T2w ER MRI. Martin et al. [12] presented a semi-automatic algorithm for segmentation of the prostate on MRI based on registration of an atlas to the test image. They evaluated their method on 17 MR images using manual segmentations performed by a single operator as the reference standard. To measure the segmentation error of their method, they used a surface-based metric for different regions of interest (ROIs) including the whole prostate gland, base, mid-gland, and apex regions. They also used region-based metrics but for the whole gland only. They reported higher atlas registration error, yielding higher segmentation error, for their approach on smaller prostates (less than 25 cm3). Vikal et al. [13] developed a two-dimensional (2D) slice-by-slice segmentation algorithm based on shape modeling for three-dimensional (3D) segmentation of the prostate on T2w MRI. Their semi-automatic method was initialized by user selection of prostate center point on one of the central slices of the prostate. In their method, segmentation starts from the selected central slice. The segmentation on each 2D slice is used as an initialization for segmenting its adjacent slice. They evaluated their method on three images using the mean absolute distance (MAD) and Dice similarity coefficient [14] (DSC), compared to a single reference standard developed by consensus of two expert observers. Toth and Madabhushi [15] developed a semi-automatic segmentation algorithm based on a landmark-free active appearance model and level set shape representation method. To evaluate their method, they applied the algorithm to 108 T2w ER MRI and compared the results to manual segmentations performed by one observer using the MAD for the whole gland only and the DSC for whole-gland, apex, mid-gland, and base. Although results were reported for a second observer on a subset of 17 images, inter-observer variability of their method was not reported. Liao et al. [16] presented a coarse-to-fine hierarchical automatic segmentation algorithm for prostate segmentation on T2w MRI. They used the MAD, DSC, and Hausdorff distance error metrics for evaluation of their method on the whole gland using a manual reference segmentation performed by one observer on 66 T2w MR images. Cheng et al. [17] developed an automatic approach consisting of two main steps: first, a coarse segmentation based on an adaptive appearance model and then a segmentation refinement using a support vector machine. They used region-based metrics computed only within the whole gland to evaluate their method, using manual reference segmentations verified by one radiologist. Cheng et al. [18] also presented a slice-by-slice segmentation of the prostate on T2w ER MRI using a combination of an atlas-based active appearance model with a deep learning model. They trained their active appearance model on 100 images and measured the segmentation error of their algorithm within the whole prostate gland against a single-operator reference segmentation on 20 test images using region-based (i.e., DSC, TP, FN, and FP) and volume-based (i.e., ΔV) error metrics. Guo et al. [19] presented an automatic segmentation method for T2w prostate MRI acquired with or without an ER coil. They used a stacked sparse auto-encoder framework to extract the deep learning features and then used a sparse patch matching combined with shape modeling to segment the prostate. They evaluated their method on 66 images with a single reference segmentation using DSC, precision, MAD, and Hausdorff distance. The computation time for their method on a MATLAB platform was more than 45 min per image. There are also several segmentation algorithms presented in the literature that were tested only on non-ER MRI datasets or a combination of ER and non-ER MRI datasets [20–23]. The nature of the non-ER MRI datasets in terms of image appearance, prostate shape, and image artifacts and noise is substantially different form ER MRI datasets, and this challenges the performance comparison. In 2012, 11 teams were involved in a challenge for prostate MRI segmentation, called PROMISE12, held as part of the Medical Image Computing and Computer-Assisted Intervention (MICCAI) conference. The challenge tested the performance of the segmentation algorithm presented by each team in two steps: an online and a live challenge. The image dataset used by the challenge contained both ER and non-ER MR images, and the results were evaluated against one set of manual segmentations provided by one expert and reviewed and edited, if necessary, by another expert using surface-, region-, and volume-based metrics for the whole gland, apex, and base regions [23]. In most previously published work, segmentation performance has been evaluated by comparison against a single manual reference segmentation. However, there is high inter-observer variability in contouring the prostate in MRI [11] and changing the manual reference segmentation used for segmentation evaluation likely has a substantial impact on the reported segmentation performance. Therefore, it is necessary to consider this variation when validating segmentation algorithms. Furthermore, in most published studies, the algorithm results have been evaluated using only one or two error metrics. Since each metric is sensitive to certain types of errors (e.g., the MAD is sensitive to large, spatially localized errors, whereas the DSC is sensitive to smaller, global errors), there is not a single globally accepted metric for comprehensive evaluation of segmentation algorithms. Thus, using a set of metrics that is sensitive to different types of error, such as surface disagreement, regional misalignment, and volume differences, yields a more comprehensive algorithm evaluation. Moreover, the accuracy and repeatability of the prostate segmentation varies for different parts of the gland in manual [11] and computer-based [12, 13, 15, 24] segmentations. Some groups reported segmentation error only for the whole prostate gland without reporting the error for the gland subregions such as the apex, mid-gland, and base. Segmentation error metrics computed for the whole gland are challenging to interpret, since large errors in the apex and base regions can be offset by smaller errors in the mid-gland. When the segmentations are used to guide radiation or ablative interventions, this is especially important since the apex and base are near to sensitive structures such as the bladder, urethra, and penile bulb. Finally, substantial differences in image appearance, prostate shape, image noise, and image artifacts, challenge the comparison between methods that are evaluated on non-ER MR images and those that are tested on ER MRI images.
We previously described a semi-automatic segmentation approach for ER prostate MRI based on local appearance and shape characteristics and evaluated its performance in comparison with manual segmentation in terms of accuracy and inter-operator variability [24]. We applied our evaluation using different types of error metrics (i.e., surface-, region-, and volume-based metrics) and assessed the performance of the algorithm over the whole prostate gland as well as within the apex, mid-gland, and base subregions. Our semi-automatic segmentation method required that the user select four initial points to run the contouring algorithm. Thus, the algorithm’s segmentation results depended on the user’s judgment of the correct loci for these points. This included a requirement that the user indicate the apex-most and base-most slices of the prostate, which is a challenging task with substantial inter-observer variability.
Although many segmentation algorithms have been proposed, an operator-independent algorithm that has been comprehensively validated using multiple complementary error metrics against a multi-observer reference standard remains elusive. In this paper, we build on our previous semi-automated segmentation algorithm to develop a fully automated T2w ER prostate MRI segmentation approach that has no dependence on user input. We compare the fully automatic segmentation performance to the semi-automatic and manual approaches. We address the following four research questions in this paper. (1) What is the segmentation error of the automated algorithm when compared to a single-observer manual reference standard? (2) What is the difference in the time required to use our automated segmentation algorithm and our semi-automated segmentation algorithm? (3) What is the difference in segmentation error between our automated algorithm and our semi-automated algorithm? (4) Is the measured misalignment between the computer-assisted segmentations and the manual segmentations within the range of inter-expert variability in manual segmentation?
Materials and Methods
Materials
The dataset contained 42 axial T2w fast spin echo ER MR images acquired from patients with biopsy-confirmed PCa. Twenty-three of the images were acquired with TR = 4000–13,000 ms, TE 156–164 ms, and NEX = 2, and for the other 19 images, TR = 3500–7320 ms, TE = 102–116 ms, and NEX = 1–2. Nine and 33 images were obtained with 1.5 and 3.0-T field strengths, respectively. The voxel sizes varied from 0.27 × 0.27 × 2.2 to 0.44 × 0.44 × 6 mm, covering the range typically seen in clinical prostate MRI. Four different MRI scanners were used for image acquisition: MAGNETOM Avanto, MAGNETOM Verio (Siemens Medical Solutions, Malvern, PA), Discovery MR 750, and Signa Excite (General Electric Healthcare, Waukesha, WI). The study was approved by the research ethics board of our institution, and written informed consent was obtained from all patients prior to enrolment. All 42 MR images were initially segmented manually by one observer (either a radiologist or a graduate student under advisement of a radiologist) followed by review and adjustment of the contours by an expert senior radiology resident with experience reading >100 prostate MRI scans. Two additional manual segmentations were performed on a subset of 10 images performed by two expert observers (one radiologist and one radiation oncologist). The prostate volumes in the dataset calculated based on the available manual segmentations ranged from 15 to 89 cm3 with mean ± standard deviation of 35 ± 14 cm3.
We also selected 12 ER MR images from a training dataset of MICCAI PROMISE12 challenge for algorithm evaluations. We selected those images that are similar to our dataset in terms of imaging protocol (i.e., endorectal images with balloon surrounding endorectal coil filled with fluid yielding a dark appearance on MRI). This dataset contained 3.0-T ER T2w MR images. The voxel size of the images varied from 0.25 × 0.25 × 2.2 to 0.25 × 0.25 × 3.0 mm [23]. The challenge organizers provided a single manual reference segmentation for each image.
Automated Segmentation
Our automatic segmentation approach consists of two main parts: training and segmentation, described in “Training” and “Segmentation” sections, respectively. In this paper, we focus on automation of the manual steps of our previously published semi-automated method. Thus, we describe elements common to our automatic and semi-automatic approaches at a high level; full details on these elements are available in our published article [24].
Training
We use the approach to training described in our published article [24] reporting on our semi-automated segmentation method. The training method is described at a high-level here. During training, the algorithm learns the local appearance of the prostate border by extracting 36 locally defined circular mean intensity image patches and generates a 2D statistical shape model for the prostate on each axial cross section of the prostate. To extract the mean intensity image patches, we first spatially normalized all the prostates in the training set to define a spatial correspondence between axial slices of all the training images. For each slice in a set of corresponding axial slices, a set of anatomically corresponding points was defined on the prostate border (a total of 36 points on each slice) and for each point, a circular patch centered at that point was selected. By computing the average of the intensities of the corresponding pixels across all the patches obtained from the corresponding points, a set of 36 mean intensity patches was generated, each corresponding to one anatomical point on the prostate border. The 36 defined border points were also used for building a statistical point distribution model (PDM) of prostate shape on each selected axial cross section.
Segmentation
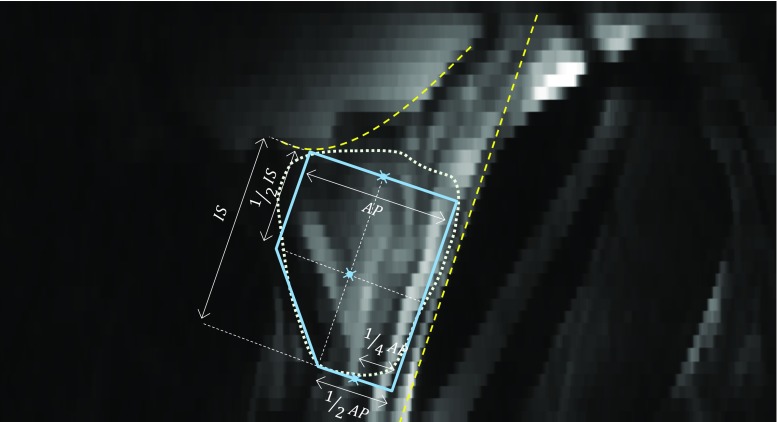
To segment the prostate in a new MR image, the algorithm first coarsely localizes the region containing the prostate on the mid-sagittal slice of the image based on the anatomy. There are several computer-assisted anatomy-based object detections for medical images presented in the literature (e.g., reference [25]). Usually, these methods have been designed for accurate object recognition and localization and they are computationally expensive. Moreover, these methods are not customized for a specific application. In our case, due to our algorithm’s demonstrated low sensitivity to initialization [24], a coarse localization of the prostate is sufficient for initialization. Therefore, we designed a fast and simple algorithm to localize the prostate. We performed the localization by automatically positioning a template shaped similarly to a prototypical prostate on the mid-sagittal plane (blue polygon in Fig. 1). The algorithm then searches within a region defined according to this template to define the 3D prostate boundary. This high-level process resolves to a four-step procedure: (1) anterior rectal wall boundary determination, (2) inferior bladder boundary determination, (3) coarse prostate localization by template fitting, and (4) 3D prostate boundary localization. Each of these four steps is described in detail in the following paragraphs.
Fig. 1.
Automatic coarse localization of the prostate. The dashed line shows the estimated tangent line to the rectal wall. The dashed curve shows the estimated bladder border. The solid line polygon is the template used to select the center points for apex, mid-gland, and base. The prostate boundary based on manual segmentation has been overlaid with a d otted line for reference. AP and IS are, respectively, anterioposterior and inferior-superior dimensions of the prostate measured during routine clinical ultrasound imaging. The three indicated points on the template define the three estimated center points for the prostate
The first step was to fit a line to the anterior rectal wall boundary on the mid-sagittal slice of the MRI. Candidate points lying on the anterior rectal wall boundary were selected by finding loci of minimum first derivative along line intensity profiles oriented parallel to the axial planes and running from anterior to posterior on the mid-sagittal plane. This approach was chosen due to the observation that the intensity generally transitions sharply from bright to dark at the rectal wall boundary. To reduce the search space, we restricted our search to a domain covering 50% of the width of the mid-sagittal plane in the anteroposterior direction, offset 20% from the posterior-most extent of the mid-sagittal plane. Within this domain, 10 equally spaced lines (every second line) nearest to the mid-axial plane were searched. For robustness to outlier candidate points, we computed a least-trimmed squares fit [26] line to the candidate points, with the optimizer tuned to treat 40% of the candidate points as outliers. We took the resulting best-fit line to represent the anterior rectal boundary (posterior-most yellow dashed line in Fig. 1).
The second step was to fit a curve to the inferior bladder boundary on the mid-sagittal slice of the MRI. Candidate points lying on the inferior bladder boundary were selected by finding loci of minimum first derivative along line intensity profiles oriented parallel to the anterior rectal boundary determined in the previous step and running from superior to inferior on the mid-sagittal plane. This approach was chosen due to the observation that the intensity generally transitions sharply from bright to dark at the inferior bladder boundary. To reduce the search space, we restricted our search to line segments lying within the superior half of the image, starting 5 mm anterior to the rectal wall with 2-mm spacing between them. We eliminated implausible candidate points in two stages. In the first stage, points forming a locally concave shape near the posterior side, inconsistent with anatomy of the inferior aspect of the bladder, were eliminated. In the second stage, we computed a least-trimmed squares fit [26] polynomial curve (second-order curve in the case of a convex configuration of the remaining points; first-order curve otherwise) to the remaining candidate points, with the optimizer tuned to treat 20% of the candidate points as outliers. We took the resulting curve to represent the inferior bladder boundary (superior-most yellow dashed curve in Fig. 1).
The third step was to fit the prostate template (described by the dimensions shown in Fig. 1) to the image using the anatomic boundaries found in the first and second steps. This was done by defining the dimensions of the template to match the anteroposterior (AP) and inferior-superior (IS) dimensions of the prostate on the test image; this information is readily available in every clinical case from the prostate ultrasound examination conducted prior to MRI. The template was then positioned parallel to and 3 mm anterior to the rectal wall line (along a line perpendicular to the rectal wall line), inferior to the bladder boundary curve with a single point of contact between the bladder boundary and the template (Fig. 1).
The fourth and final step was to define the 3D surface of the prostate detected and localized by the template. After fitting the template to the image, we extract a set of three points (three blue crosses in Fig. 1) from the template: the prostate center points on (1) the apex-most slice, (2) the base-most slice, and (3) the mid-gland slice equidistant to the apex- and base-most slices. We then interpolate these three center points using piecewise cubic interpolation to estimate the center points for all of the axial slices between the apex and the base. We then use the approach to prostate boundary localization described in reference [24] reporting on our semi-automated segmentation method. The approach is described at a high level here. For each slice, we oriented a set of 36 equally spaced rays emanating from the center point, one corresponding to each of the learned mean intensity patches. For each ray, we translated the corresponding mean intensity patch to find the point whose circular image patch has the highest normalized cross-correlation with the corresponding mean intensity path. Shape regularization was performed within each slice using the corresponding PDM, followed by 3D shape regularization. Full details are available in our published article [24].
Validation
To evaluate the accuracy of the segmentation algorithm, we used complementary boundary-based, regional overlap-based, and volume-based metrics. This allows the user of the method to understand its applicability to a specific intended workflow. For instance, the use of this algorithm for planning whole-prostate radiation would increase the importance of low error in a boundary-based metric, whereas the use of the algorithm in a retrospective study correlating prostate size with clinical outcome would focus on accuracy of a volume-based metric. We used the MAD as the boundary-based error metric; the DSC, recall rate, and precision rate as regional overlap-based error metrics; and the volume difference (ΔV) metric to evaluate the automatic segmentation against manual segmentation. The DSC value can be computed from the recall and precision rates and therefore can be seen as redundant. However, in this paper, we reported recall and precision because they explain the segmentation error type together better than DSC by itself. We also reported DSC values for comparison purposes, since DSC is a widely used error metric in the literature. We measured all five metrics in 3D for the whole prostate gland and also for the inferior-most third of the gland (corresponding to the apex region), the middle third of the gland (corresponding to the mid-gland region), and the superior-most third of the gland (corresponding to the base region).
The MAD measures the misalignment of two surfaces in 3D in terms of absolute Euclidean distance. To calculate the MAD in a unilateral fashion, the surface of each shape is defined as a set of points, with one of the two shapes designated as the reference. The MAD is the average of the absolute Euclidean distances between each point on the non-reference set to the closest point on the reference set. Specifically,
| 1 |
where X and Y are the point sets (Y is the reference set), N is the number of points in X, p is a point in X, q is a point in Y, and D(p, q) is the Euclidean distance between p and q. The MAD is an oriented metric and is therefore not invariant to the choice of reference shape. This can be addressed by calculating the bilateral MAD, which is the average of the two unilateral MAD values calculated taking each shape as the reference.
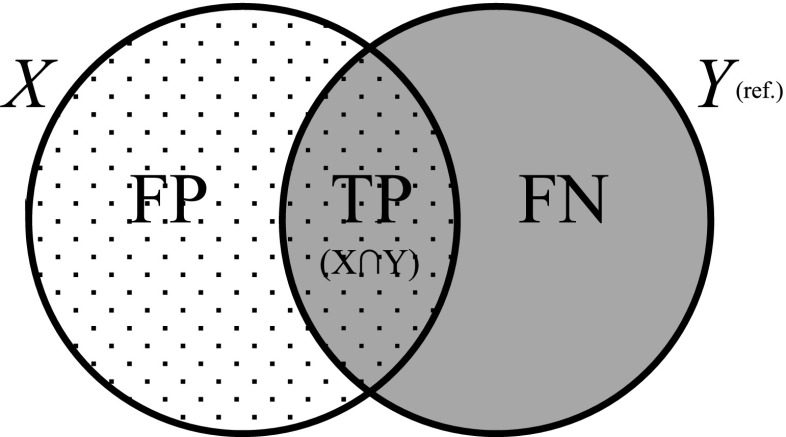
To calculate the DSC [14], recall rate, and precision rate [24], we measured the volume overlap between the two 3D shapes. Figure 2 and Eqs. (2), (3), and (4) define DSC, recall, and precision, respectively.
| 2 |
| 3 |
| 4 |
Fig. 2.
Elements used to calculate the DSC, recall, and precision validation metrics. X and Y are the two shapes, with Y taken as the reference shape. FP false positive, TP true positive, FN false negative
We subtract the volume of the reference shape from the volume of the test shape to calculate the signed volume difference (ΔV) metric
| 5 |
where V algorithm and V reference are the prostate volumes given by the segmentation algorithm and manual reference segmentation, respectively. We also calculate the percentage ratio of ΔV to the reference volume (V reference). Negative and positive values of ΔV indicate undersegmentation and oversegmentation, respectively.
Experiments
For all of the experiments in this paper, all algorithm parameters were tuned identically to those used in reference [24] to allow for direct comparison of the results.
Comparison of Automatic and Semi-Automatic Segmentation: Accuracy and Time
Testing on Our Dataset
We ran the automatic segmentation algorithm on our dataset of 42 3D images and compared the results to a single manual reference segmentation using leave-one-patient-out cross-validation. We compared each segmentation result against the reference using our five error metrics on the four ROIs: the whole gland, apex, mid-gland, and base regions. We applied one-tailed heteroscedastic t tests [27] to compare the performance of the automatic segmentation to the semi-automatic segmentation. We measured the average execution time for the automatic segmentation approach across the 42 images and compared it to the average of semi-automatic execution time across the same dataset and identical running conditions, using a one-tailed t test. We also parallelized the automatic algorithm execution on four CPU cores using the MATLAB distributed computing toolbox.
Testing on PROMISE12 Images
We also ran the automatic and semi-automatic algorithm on a subset of 12 MICCAI PROMISE12 challenge images using our dataset of 42 images to train the algorithm. We compared each segmentation result against the reference using the similar evaluation scheme as used in “Testing on Our Dataset” (five error metrics and four ROIs). We applied one-tailed heteroscedastic t tests to compare the performance of the automatic segmentation to the semi-automatic segmentation.
Comparison of Automatic and Semi-Automatic Segmentation Versus Inter-Operator Variability in Manual Segmentation
We ran the automatic algorithm on the subset of 10 images for which we had three manual reference segmentations. For comparison, we also applied our semi-automatic algorithm [24] to the same dataset using nine different operators (four radiation oncologists, one radiologist, one senior radiology resident, one imaging scientist, and two graduate students, all with clinical and/or research experience with prostate imaging). We used the remaining 32 images for training both algorithms. We compared each segmentation result against the manual reference segmentations using our five error metrics on the four ROIs: the whole gland, apex, mid-gland, and base regions.
For the automatic segmentation method, we calculated the mean and standard deviation of each metric for each ROI across all 10 images and three references, defined aS
| 6 |
and
| 7 |
where Metric is a function computing any one of the five metrics (e.g., MAD); is the mean value of the metric for automatic segmentation across all the images and all the references; is the standard deviation of the metric; M = 10 and K = 3 are the number of images and references, respectively; is the manual segmentation by the kth operator on the ith image; and is the automatic segmentation on the ith image. For the semi-automatic segmentation, we calculated the mean and standard deviation of each metric for each ROI across all 10 images, three references and nine operators, defined as
| 8 |
and
| 9 |
where is the mean value of the metric across all the semi-automatic labels, all the images, and all the references; is the standard deviation of the metric; N = 9 is the number of operators; and is the semi-automatic segmentation by the jth operator on the ith image.
We used simultaneous truth and performance level estimation (STAPLE) [28] to generate one reference segmentation from each triplet of manual segmentations performed on each image. We then computed and using the STAPLE reference exactly as in Eqs. (6)–(9), with K = 1 (reflecting the use of a single STAPLE reference rather than three manual references).
We compared the semi-automatic and automatic approaches separately for both explained scenarios (three manual references and single STAPLE reference) using one-tailed heteroscedastic t tests. We defined the range of mean values of each metric () when we compared three manual segmentations pairwise as
| 10 |
and
| 11 |
where
| 12 |
and
and are the manual segmentations for ith image by observers m and n, respectively. We compared the mean metric values for semi-automatic and automatic segmentation ( and ) to this range in order to interpret the in the context of inter-observer variability for manual segmentation.
Results
Comparison of Automatic and Semi-Automatic Segmentation: Accuracy and Time
The results in this section address research questions (1), (2), and (3) as described in the “Introduction.”
Testing on Our Dataset
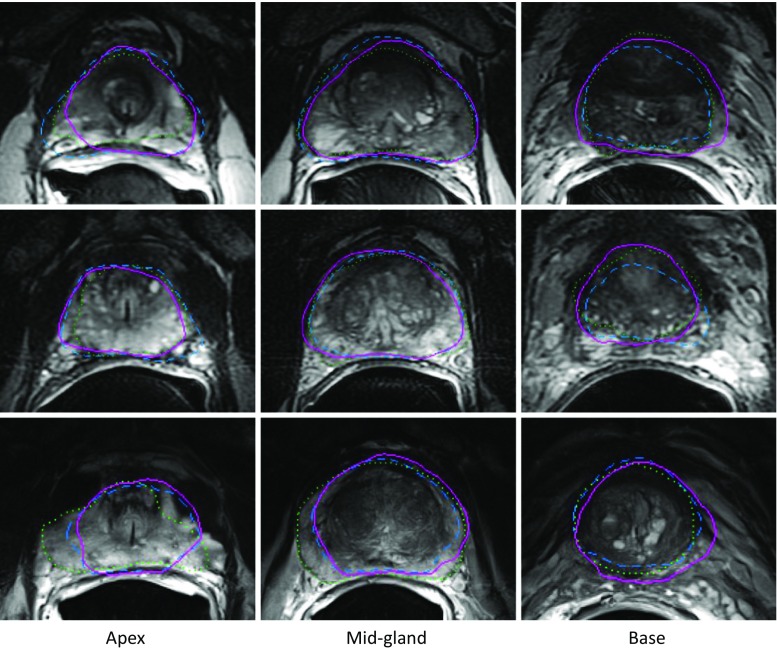
In answer to research question (1) (“What is the segmentation error of the automated algorithm when compared to a single-observer manual reference standard?”), Table 1 shows our automatic segmentation error on 42 T2w MR images as compared against one manual reference segmentation. The results of the t tests (α = 0.05) showed that using the automatic algorithm significantly increased the error in terms of MAD and DSC in all the ROIs, relative to the semi-automatic algorithm, in answer to research question (3) (“What is the difference in segmentation error between our automated algorithm and our semi-automated algorithm?”). Recall rates significantly decreased for the whole gland, apex, and mid-gland and significantly increased for the base when we used the automatic segmentation algorithm. The precision rate also showed more error within the whole gland, mid-gland, and base. No significant changes were detected within the apex in terms of the precision rate. We did not detect a significant increase in error for the whole gland and mid-gland in terms of ΔV. The absolute value of ΔV was significantly increased within the apex and significantly decreased within the base. Figure 3 shows qualitative results of automatic and semi-automated segmentation at an apex, a mid-gland, and a base slice for three sample prostates.
Table 1.
Accuracy of automatic segmentation: mean ± standard deviation of MAD, DSC, recall, precision, and ΔV
| Region of interest | MAD (mm) | DSC (%) | Recall (%) | Precision (%) | ΔV (cm3) | ΔV (%) |
|---|---|---|---|---|---|---|
| Whole gland | 3.2 ± 1.2b | 71 ± 11b | 69 ± 15b | 76 ± 12b | −3.6 ± 10.4 | −8 ± 20 |
| Apex | 2.8 ± 1.3b | 66 ± 15b | 62 ± 23b | 81 ± 17 | −3.3 ± 5.1b | −9 ± 16b |
| Mid-gland | 2.8 ± 1.1b | 82 ± 9b | 82 ± 15b | 84 ± 10b | −0.5 ± 3.6 | −1 ± 9 |
| Base | 3.8 ± 1.7b | 64 ± 15b | 71 ± 21a | 69 ± 22b | 0.2 ± 7.5a | 2 ± 20a |
Fig. 3.
Qualitative results of automatic, semi-automatic, and manual segmentations for three sample prostates. Each row shows the results at three 2D cross sections of one prostate: the left one at apex subregion, the middle one at mid-gland subregion, and the right one at base subregion. The automatic algorithm’s segmentations are shown with solid magenta contours, the semi-automatic algorithm’s segmentations are showed with dashed blue contours, and the manual segmentations are shown with dotted green contours (color figure online)
In answer to research question (2) (“What is the difference in the time required to use our automated segmentation algorithm and our semi-automated segmentation algorithm?”), we measured the mean ± standard deviation execution time using an unoptimized MATLAB implementation on a single CPU core for coarse prostate localization that was 3.2 ± 2.1 s, and for 3D segmentation, that was 54 ± 13 s. We also parallelized the automatic segmentation algorithm and ran it on four CPU cores using the MATLAB distributed computing toolbox, and the average execution time across the 42 images decreased to 17 ± 4 s (i.e., about 3.2 times faster). The average operator interaction time for semi-automatic segmentation initialization was 28 s [24].
Testing on PROMISE12 Images
The key result of this section was the accuracy of the automatic and semi-automatic algorithms on a new dataset with a different reference observer (i.e., 12 ER MRIs of PROMISE12 challenge dataset) when the algorithms were trained on a different dataset (i.e., our dataset of 42 ER MRIs). Table 2 shows the results for automatic segmentation, and Table 3 shows the results for semi-automatic segmentation. The tables also compare the results to our results based on our image dataset. The statistically significant differences between error values are indicated on the tables based on a heteroscedastic one-tailed t test (α = 0.05).
Table 2.
Accuracy of automatic segmentation tested on 12 ER MR images of PROMISE12 dataset: mean ± standard deviation of MAD, DSC, recall, precision, and ΔV
| Region of interest | MAD (mm) | DSC (%) | Recall (%) | Precision (%) | ΔV (cm3) | ΔV (%) |
|---|---|---|---|---|---|---|
| Whole gland | 3.7 ± 2.0 | 72 ± 13 | 70 ± 15 | 76 ± 14 | −7.2 ± 19.9 | −6 ± 21 |
| Apex | 4.5 ± 2.9a | 61 ± 18 | 73 ± 19 | 59 ± 25a | 4.1 ± 9.2a | 9 ± 22a |
| Mid-gland | 2.6 ± 1.3 | 83 ± 9 | 78 ± 15 | 92 ± 6a | −4.4 ± 7.5 | −5 ± 8 |
| Base | 3.3 ± 1.4 | 70 ± 13 | 65 ± 19 | 83 ± 16a | −6.8 ± 13.4 | −9 ± 18a |
aShows statistically significant differences between the error values of the table and the error values of Table 1 (p < 0.05)
Table 3.
Accuracy of semi-automatic segmentation tested on our dataset (42 images) and 12 ER MR images of PROMISE12 dataset: mean ± standard deviation of MAD, DSC, recall, precision, and ΔV
| Region of interest | Dataset (N) | MAD (mm) | DSC (%) | Recall (%) | Precision (%) | ΔV (cm3) | ΔV (%) |
|---|---|---|---|---|---|---|---|
| Whole gland | Our dataset (42) | 2.0 ± 0.5 | 82 ± 4 | 77 ± 9 | 88 ± 6 | −4.6 ± 7.2 | −12 ± 14 |
| PROMISE12 (12) | 2.4 ± 0.8 | 80 ± 6 | 73 ± 10 | 90 ± 6 | −12.5 ± 17.6 | −19 ± 15 | |
| Apex | Our dataset (42) | 2.0 ± 0.7 | 79 ± 6a | 82 ± 14a | 80 ± 13 | 0.1 ± 3.3a | 1 ± 8a |
| PROMISE12 (12) | 2.3 ± 0.6 | 76 ± 4a | 72 ± 11a | 84 ± 11 | −2.4 ± 4.4a | −3 ± 6a | |
| Mid-gland | Our dataset (42) | 1.6 ± 0.5 | 90 ± 3 | 90 ± 7 | 91 ± 6 | −0.1 ± 2.0 | 0 ± 5 |
| PROMISE12 (12) | 2.2 ± 1.4 | 87 ± 8 | 85 ± 15 | 92 ± 7 | −2.8 ± 7.7 | −2 ± 9 | |
| Base | Our dataset (42) | 2.6 ± 0.8 | 73 ± 10 | 61 ± 14 | 93 ± 6 | −4.5 ± 3.7 | −13 ± 8 |
| PROMISE12 (12) | 2.8 ± 0.9 | 73 ± 9 | 60 ± 13 | 96 ± 6 | −7.3 ± 6.2 | −14 ± 6 |
aShows statistically significant differences (p < 0.05)
Comparison of Automatic and Semi-Automatic Segmentation Versus Inter-Operator Variability in Manual Segmentation
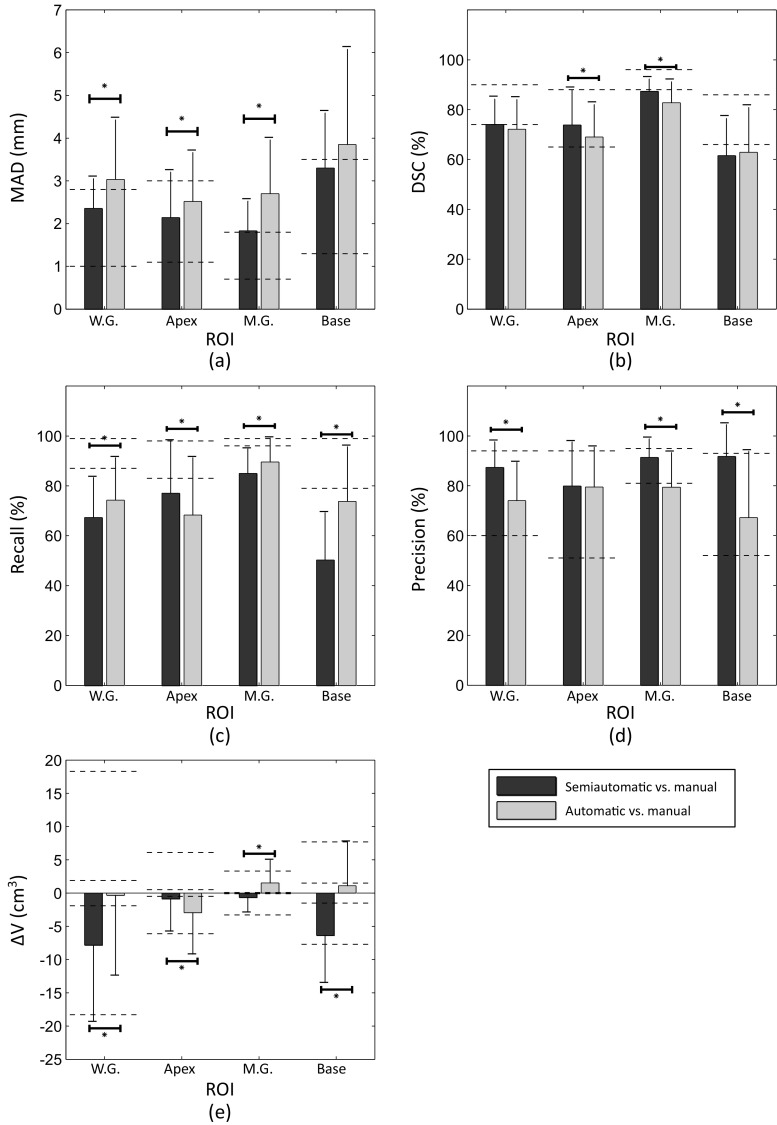
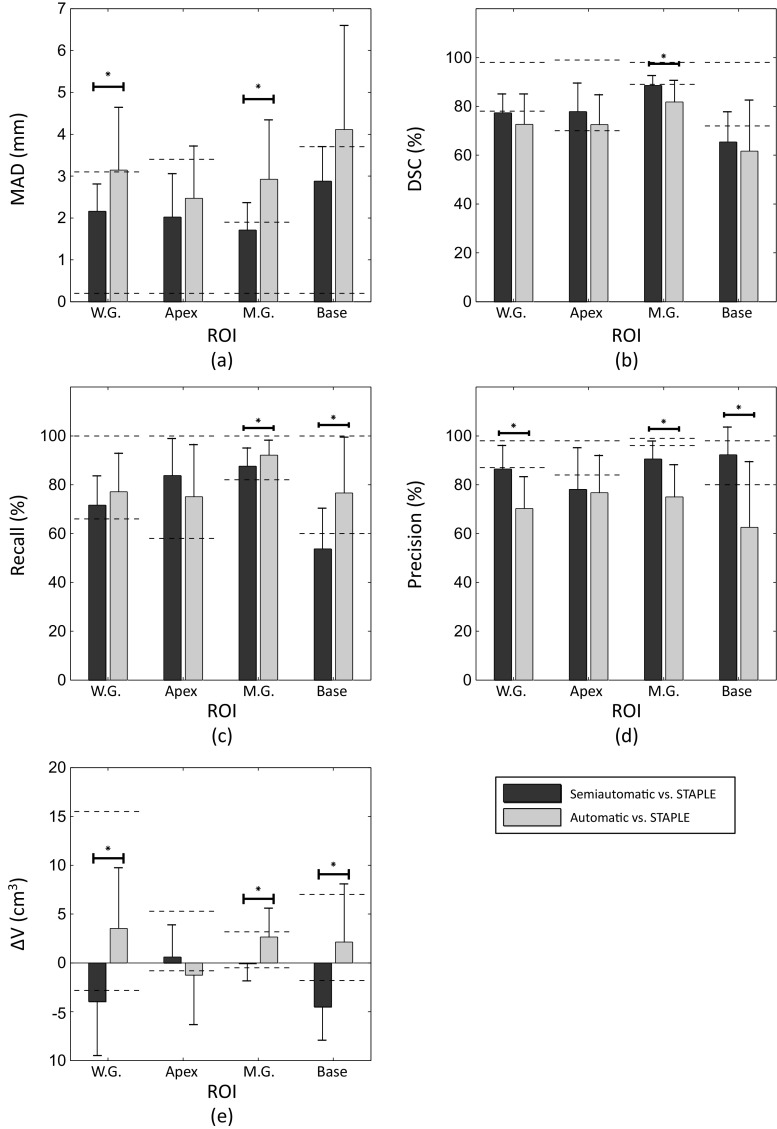
The results in this section address research question (4) as described in the “Introduction.” In this experiment, the key result was that the accuracy of semi-automatic and automatic segmentation algorithms approached the observed inter-operator variability range in manual segmentation. Figure 4 shows the mean ± standard deviation of the five metric values for each ROI for semi-automatic and automatic segmentation algorithms, compared with the range of the mean of each metric within each ROI in pairwise comparison of the three manual reference segmentations. Note that the dashed lines in Fig. 4e report absolute volume differences on both sides of zero; this does not indicate that the differences are necessarily bounded by zero but rather reflects a lack of natural reference standard when multiple manual segmentations are compared. Figure 5 shows the mean ± standard deviation values for the five metrics for each region of interest for semi-automatic and automatic segmentation algorithms in comparison with STAPLE reference segmentations. We overlaid using dashed lines the results of each metric’s lower and upper bounds at each ROI given by comparison of the three manual reference segmentations to the STAPLE reference. Note that in both Figs. 4 and 5, if the metric value for each algorithm is located within the range or at the lower error side, it means that the algorithm accuracy performed within the observed inter-expert observer variability in manual segmentation. The differences in performance revealed by the different error metrics reinforce that these metrics are complementary and provide different information about the nature of the errors arising from the algorithm.
Fig. 4.
Accuracy of the computer-based segmentations versus inter-operator variability of manual segmentation. The average accuracy of one set of 10 automatic and nine sets of 10 semi-automatic segmentations in comparison with three manual reference segmentations in terms of (a) MAD, (b) DSC, (c) recall, (d) precision, and (e) ΔV. The dashed line segments show the observed range of each metric at each ROI in pairwise comparison between three manual segmentations. For ΔV, the ranges are based on the absolute value of ΔV due to lack of reference in comparison of two manual segmentations. The error bars show one standard deviation. The significant differences detected between semi-automatic and automatic segmentation at different ROIs have been indicated on the graphs with an asterisk (p value < 0.05)
Fig. 5.
Accuracy of the computer-based segmentations versus inter-operator variability of manual segmentation. The average accuracy of one set of 10 automatic and nine sets of 10 semi-automatic segmentations in comparison with STAPLE reference segmentation in terms of (a) MAD, (b) DSC, (c) recall, (d) precision, and (e) ΔV. The dashed line segments show the observed range of each metric at each ROI in comparison between three manual segmentations and STAPLE reference. The error bars show one standard deviation. The significant differences detected between semi-automatic and automatic segmentation at different ROIs have been indicated on the graphs (p value < 0.05)
Discussion
In this work, we measured the segmentation error increased or decreased when using a fully automatic version of a previously published semi-automatic segmentation algorithm. Such comparisons are routinely performed in the literature, often using a small number of validation metrics and a single-observer reference standard.
In this work, we extended our analysis beyond this traditional approach to include a comparison of the algorithm performance differences to inter-observer variability in segmentation error metrics resulting from different expert manual segmentations. Measuring performance differences between algorithms—those presented in this paper or in other literature—in the context of expert manual segmentation variability is important to understanding the practical importance of algorithm performance differences.
Comparison of Automatic and Semi-Automatic Segmentation: Accuracy and Time
For comparison to our previous results and other published work, we conducted an experiment using a single manual reference segmentation to measure the accuracy of our automatic algorithm. In terms of most of the metrics, there was a statistically significant difference between automatic and semi-automatic segmentation errors. On average, by switching from semi-automatic segmentation to automatic segmentation, MAD increased by 1.2 mm, DSC decreased by 11%, recall decreased by 8%, precision decreased by 12%, and the error in prostate volume decreased by 1 cm3 (4%) for the whole gland. According to the results based on our multi-reference and/or multi-operator experiments (Fig. 4), the absolute value of the average ΔV based on automatic segmentation on whole gland significantly decreased from approximately 7 to less than 1 cm3. This illustrates the complementary nature of the validation metrics and the varying utility of different segmentations for different purposes. Whereas the automatic segmentations may be less preferable to the semi-automatic segmentations for therapy planning, the automatic segmentations may be preferable for correlative studies involving prostate volume and clinical outcomes.
The nature of the dataset used in PROMISE12 challenge is different from our dataset in terms of the consistent use of the an ER coil for MRI acquisition; our dataset contained only images acquired using the ER coil, whereas the PROMISE12 dataset contained a some with and some without the ER coil. However, if we compare our results in Table 1 to the published results in [23] where applicable, our results are within the range of the metric values reported for the PROMISE12 challenge.
In the semi-automatic approach, the operator provided coarse prostate localization, whereas in the automatic approach, this was done entirely by the algorithm. To compare the time required for this step in both contexts, the mean measured operator interaction time for semi-automatic segmentation was approximately 30 s [24], whereas the mean measured time required for automatic coarse prostate localization was measured in this study to be approximately 3 s using unoptimized MATLAB code on a single CPU core.
Comparison of Automatic and Semi-Automatic Segmentation Versus Inter-Operator Variability in Manual Segmentation
The measured segmentation error differences between the automatic and the semi-automatic approaches are nearly always smaller than the measured differences between manual observer contours (differences between gray and black bars versus differences between dashed lines on Fig. 4) and also smaller than the measured differences between manual observer contours and a STAPLE consensus contour (Fig. 5). This suggests that the performance differences measured between these two algorithms may be less than the differences we would expect when comparing the different observers’ manual contours.
We observe that the top of the dark gray bar corresponding to the MAD metric for semi-automatic segmentation in Fig. 4 for the whole gland lies within the range of variability between the expert observers’ manual contours. This indicates that on average, the semi-automatic segmentation algorithm’s whole-gland segmentation error, as measured by MAD, is within the range of human expert variability in manual contouring. This means that further investment of engineering efforts to improve this metric for this algorithm may not lead to major benefits to the ultimate clinical workflow, since the algorithm’s error is already smaller than the difference that might be observed between the expert observers’ manual contours. The fact that the top of the light gray bar in the same part of the figure lies higher than the range given by the dashed lines indicates that this is not the case for the fully automatic algorithm; further error reduction in terms of MAD on the whole gland may be warranted, with the caveat that such improvement must be measured using a multi-observer reference standard. Inter-observer variability in manual segmentation would likely mask small improvements in the MAD; this is evidenced by the size of the gap between the dashed lines (1.8 mm), compared to the 0.6-mm improvement in the MAD that would be necessary to yield equal performance to the semi-automatic algorithm. We observe in Fig. 4 that for the MAD, DSC, precision, and ΔV metrics, algorithm performance is near or within the range of human expert variability; this is the case more often for the semi-automatic algorithm. The performance of the algorithms in terms of the recall metric suggests that overall, both algorithms tend to undersegment the prostate to an extent where there is practically important room for improvement. This is especially true for the base region of the prostate. Interestingly, in terms of the recall metric, the automatic algorithm had statistically significantly better performance than the semi-automatic algorithm for every anatomic region except for the apex, with substantially better performance in the base region. This is concordant with our observations [24] of large inter-observer variability in determining the slice location of the base during initialization of the semi-automated algorithm; determining where the prostate base ends and the bladder neck begins is a challenging task even for expert physicians. The observations made in Fig. 5, where the range of observer variability relative to a STAPLE reference is shown, are generally concordant with observations made on Fig. 4.
Taken as a whole, these observations highlight the value of measuring inter-observer variability in manual segmentation, using complementary segmentation error metrics, and measuring segmentation error in different anatomic regions known to pose varying levels of challenge to expert operators and automated algorithms. Analysis of these quantities as performed previously allows us to determine the best ways to focus further engineering efforts to improve automated segmentation algorithms. A clinical end user can identify the segmentation error metrics of greatest relevance to the user’s intended application of the algorithm and use the plots in Fig. 4 to determine whether a particular algorithm’s segmentation error in terms of those metrics is within the range of human expert variability in manual segmentation. If so, the algorithm is ready to be moved forward for full retrospective validation and then prospective testing within the intended clinical workflow. If the analysis shows that there is room for improvement to bring the algorithm within the range of human performance for one or more anatomic regions, further engineering efforts can be specifically focused accordingly. We anticipate that this form of segmentation performance analysis will enrich future studies of automated segmentation algorithms intended for use on the prostate and other anatomic structures, enabling a means for determining the point at which an algorithm is ready to move forward from bench testing toward clinical translation.
Limitations
The results of our work should be considered in the context of its strengths and limitations. First, although the automatic segmentation algorithm does not require any user interaction with the images, it does depend on estimates of the IS and AP dimensions of the prostate. These dimensions would normally be determined on the routine clinical ultrasound imaging that is performed as part of ultrasound-guided biopsy before an MRI study would be conducted. However, for emerging MRI-guided procedures in some centers, ultrasound imaging may not always be performed prior to MRI. In these instances, the gland dimensions could be estimated based on the digital rectal examination (DRE), which would always be performed prior to MRI. However, the impact of DRE-derived prostate dimensions on the performance of this algorithm is unknown. This would be an important avenue of future study. In this study, the IS and AP dimensions taken from manual MRI prostate segmentation were used as surrogates for the measurements that would be taken during clinical ultrasound, and the performance sensitivity of the automatic segmentation method to these measurements was not determined. Second, our 3D segmentation algorithm requires the AP symmetry axis of the prostate for orientation information. Since during MRI acquisition, the MR technologist aligns the mid-sagittal plane of the scan to the mid-sagittal plane of the prostate using localizer scans, we assumed that the AP symmetry axis of the prostate gland is oriented parallel to AP axis of the image and assumed that all three prostate center points (at the apex, mid-gland, and base) are located on the mid-sagittal plane of the image. These assumptions are supported by our observations that segmentation algorithm is robust to perturbations of the AP symmetry axis and center point selection [24], but nevertheless, we felt it important to acknowledge these assumptions. Third, the small size of our dataset (42 single-reference images and 10 multi-reference images) limits the strength of the conclusions of our work. Fourth, the performance of this algorithm is unknown for prostate MR images acquired without the use of an ER coil. There, another avenue for important future work would be to test the performance of this algorithm for non-ER coil MRI acquired using modern 3T scanners and acquisition protocols that will likely achieve widespread clinical use. Finally, we used MR image intensity as the only image feature for prostate border detection. Although using other image-derived features might add complexity to the method and may make the algorithm slower, it could improve the accuracy of the segmentation. Moreover, for a more comprehensive assessment of the segmentation algorithm, we need to study the effects of post-segmentation manual editing on prostate segmentation time, accuracy, and reproducibility; this is the subject of our ongoing work.
Conclusions
This study presented a fully automatic, highly parallelizable prostate segmentation algorithm for T2w ER MRI that produces a 3D segmentation in approximately 1 min using an unoptimized sequential implementation. Segmentation error increase with respect to a previously published semi-automatic algorithm was less than the measured inter-observer variability in manual segmentation for the same task. The segmentation error metric values were greatest in the prostatic base, and this suggests that for our algorithms, engineering efforts should be focused on further improvement of the segmentation of the base, which is challenging even for human experts. The analysis approach taken in this paper provides a means for determining the readiness of a segmentation algorithm for clinical use and for focusing further engineering efforts on the most practically relevant performance issues.
Acknowledgements
The authors gratefully acknowledge the late Dr. Cesare Romagnoli for his support and scientific contribution to this work.
This work was supported by the Ontario Institute for Cancer Research and the Ontario Research Fund. This work was also supported by Prostate Cancer Canada and is proudly funded by the Movember Foundation—Grant # RS2015-04. A. Fenster holds a Canada Research Chair in Biomedical Engineering and acknowledges the support of the Canada Research Chair Program. A. D. Ward holds a Cancer Care Ontario Research Chair in Cancer Imaging.
Compliance with Ethical Standards
The study was approved by the research ethics board of our institution, and written informed consent was obtained from all patients prior to enrolment.
References
- 1.Siegel RL, Miller KD, Jemal A. Cancer statistics, 2015. CA Cancer J Clin. 2015;65(1):5–29. doi: 10.3322/caac.21254. [DOI] [PubMed] [Google Scholar]
- 2.Canadian Cancer Society’s Advisory Committee on Cancer Statistics, Canadian Cancer Statistics 2015, in Canadian Cancer Society. 2015
- 3.Kurhanewicz J, Vigneron D, Carroll P, Coakley F. Multiparametric magnetic resonance imaging in prostate cancer: present and future. Curr Opin Urol. 2008;18(1):71–7. doi: 10.1097/MOU.0b013e3282f19d01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shukla-Dave A, Hricak H. Role of MRI in prostate cancer detection. NMR Biomed. 2014;27(1):16–24. doi: 10.1002/nbm.2934. [DOI] [PubMed] [Google Scholar]
- 5.Akin O, Sala E, Moskowitz CS, Kuroiwa K, Ishill NM, Pucar D, Scardino PT, Hricak H. Transition zone prostate cancers: features, detection, localization, and staging at endorectal MR imaging. Radiology. 2006;239(3):784–92. doi: 10.1148/radiol.2392050949. [DOI] [PubMed] [Google Scholar]
- 6.Gilderdale DJ, de Souza NM, Coutts GA, Chui MK, Larkman DJ, Williams AD, Young IR. Design and use of internal receiver coils for magnetic resonance imaging. Br J Radiol. 1999;72(864):1141–51. doi: 10.1259/bjr.72.864.10703469. [DOI] [PubMed] [Google Scholar]
- 7.Anwar M, Westphalen AC, Jung AJ, Noworolski SM, Simko JP, Kurhanewicz J, Roach M, 3rd, Carroll PR, Coakley FV. Role of endorectal MR imaging and MR spectroscopic imaging in defining treatable intraprostatic tumor foci in prostate cancer: quantitative analysis of imaging contour compared to whole-mount histopathology. Radiother Oncol. 2014;110(2):303–8. doi: 10.1016/j.radonc.2013.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gibson E, Bauman GS, Romagnoli C, Cool DW, Bastian-Jordan M, Kassam Z, Gaed M, Moussa M, Gomez JA, Pautler SE, Chin JL, Crukley C, Haider MA, Fenster A, Ward AD. Toward prostate cancer contouring guidelines on magnetic resonance imaging: dominant lesion gross and clinical target volume coverage via accurate histology fusion. Int J Radiat Oncol Biol Phys. 2016;96(1):188–96. doi: 10.1016/j.ijrobp.2016.04.018. [DOI] [PubMed] [Google Scholar]
- 9.Kim Y, Hsu IC, Pouliot J, Noworolski SM, Vigneron DB, Kurhanewicz J. Expandable and rigid endorectal coils for prostate MRI: impact on prostate distortion and rigid image registration. Med Phys. 2005;32(12):3569–78. doi: 10.1118/1.2122467. [DOI] [PubMed] [Google Scholar]
- 10.Husband JE, Padhani AR, MacVicar AD, Revell P. Magnetic resonance imaging of prostate cancer: comparison of image quality using endorectal and pelvic phased array coils. Clin Radiol. 1998;53(9):673–81. doi: 10.1016/S0009-9260(98)80294-8. [DOI] [PubMed] [Google Scholar]
- 11.Smith WL, Lewis C, Bauman G, Rodrigues G, D'Souza D, Ash R, Ho D, Venkatesan V, Downey D, Fenster A. Prostate volume contouring: a 3D analysis of segmentation using 3DTRUS, CT, and MR. Int J Radiat Oncol Biol Phys. 2007;67(4):1238–47. doi: 10.1016/j.ijrobp.2006.11.027. [DOI] [PubMed] [Google Scholar]
- 12.Martin S, Daanen V, Troccaz J. Atlas-based prostate segmentation using an hybrid registration. Int J CARS. 2008;3(6):8. doi: 10.1007/s11548-008-0247-0. [DOI] [Google Scholar]
- 13.Vikal S, Haker S, Tempany C, Fichtinger G. Prostate contouring in MRI guided biopsy. Proc SPIE. 2009;7259:72594A. doi: 10.1117/12.812433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26(3):297–302. doi: 10.2307/1932409. [DOI] [Google Scholar]
- 15.Toth R, Madabhushi A. Multifeature landmark-free active appearance models: application to prostate MRI segmentation. IEEE Trans Med Imaging. 2012;31(8):1638–50. doi: 10.1109/TMI.2012.2201498. [DOI] [PubMed] [Google Scholar]
- 16.Liao, S., Y. Gao, Y. Shi, A. Yousuf, I. Karademir, A. Oto, and D. Shen, Automatic prostate MR image segmentation with sparse label propagation and domain-specific manifold regularization. 2013, Springer. p. 511–523. [DOI] [PMC free article] [PubMed]
- 17.Cheng R, Turkbey B, Gandler W, Agarwal HK, Shah VP, Bokinsky A, McCreedy E, Wang S, Sankineni S, Bernardo M, Pohida T, Choyke P, McAuliffe MJ. Atlas based AAM and SVM model for fully automatic MRI prostate segmentation. Conf Proc IEEE Eng Med Biol Soc. 2014;2014:2881–5. doi: 10.1109/EMBC.2014.6944225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cheng, R., H.R. Roth, L. Lu, S. Wang, B. Turkbey, W. Gandler, E.S. McCreedy, H.K. Agarwal, P. Choyke, and R.M. Summers, Active appearance model and deep learning for more accurate prostate segmentation on MRI, in SPIE Medical Imaging. 2016, International Society for Optics and Photonics. p. 97842I-97842I-9.
- 19.Guo Y, Gao Y, Shen D. Deformable MR prostate segmentation via deep feature learning and sparse patch matching. IEEE Trans Med Imaging. 2016;35(4):1077–89. doi: 10.1109/TMI.2015.2508280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Qiu W, Yuan J, Ukwatta E, Sun Y, Rajchl M, Fenster A. Prostate segmentation: an efficient convex optimization approach with axial symmetry using 3-D TRUS and MR images. IEEE Trans Med Imaging. 2014;33(4):947–60. doi: 10.1109/TMI.2014.2300694. [DOI] [PubMed] [Google Scholar]
- 21.Mahapatra D, Buhmann JM. Prostate MRI segmentation using learned semantic knowledge and graph cuts. IEEE Trans Biomed Eng. 2014;61(3):756–64. doi: 10.1109/TBME.2013.2289306. [DOI] [PubMed] [Google Scholar]
- 22.Makni N, Puech P, Lopes R, Dewalle AS, Colot O, Betrouni N. Combining a deformable model and a probabilistic framework for an automatic 3D segmentation of prostate on MRI. Int J Comput Assist Radiol Surg. 2009;4(2):181–8. doi: 10.1007/s11548-008-0281-y. [DOI] [PubMed] [Google Scholar]
- 23.Litjens G, Toth R, van de Ven W, Hoeks C, Kerkstra S, van Ginneken B, Vincent G, Guillard G, Birbeck N, Zhang J, Strand R, Malmberg F, Ou Y, Davatzikos C, Kirschner M, Jung F, Yuan J, Qiu W, Gao Q, Edwards PE, Maan B, van der Heijden F, Ghose S, Mitra J, Dowling J, Barratt D, Huisman H, Madabhushi A. Evaluation of prostate segmentation algorithms for MRI: the PROMISE12 challenge. Med Image Anal. 2014;18(2):359–73. doi: 10.1016/j.media.2013.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shahedi M, Cool DW, Romagnoli C, Bauman GS, Bastian-Jordan M, Gibson E, Rodrigues G, Ahmad B, Lock M, Fenster A, Ward AD. Spatially varying accuracy and reproducibility of prostate segmentation in magnetic resonance images using manual and semiautomated methods. Med Phys. 2014;41(11):113503. doi: 10.1118/1.4899182. [DOI] [PubMed] [Google Scholar]
- 25.Chen X, Bagci U. 3D automatic anatomy segmentation based on iterative graph-cut-ASM. Med Phys. 2011;38(8):4610–22. doi: 10.1118/1.3602070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Atkinson AC, Cheng T-C. Computing least trimmed squares regression with the forward search. Statistics and Computing. 1999;9(4):251–263. doi: 10.1023/A:1008942604045. [DOI] [Google Scholar]
- 27.Woolson, R.F. and W.R. Clarke, Statistical methods for the analysis of biomedical data. Vol. 371. 2011 Wiley
- 28.Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans Med Imaging. 2004;23(7):903–21. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]