Abstract
Background
Following a stroke, intrinsic muscle properties such as stiffness may be altered, which is accompanied by increased spasticity and contractures. Previously, quantification of muscle stiffness has been based off of indirect measurements. Using shear wave ultrasound elastography, direct measurements of muscle material properties can be made.
Methods
Our aim was to evaluate material properties, specifically passive stiffness, using shear wave ultrasound elastography across a range of muscle lengths, in the medial gastrocnemius and the tibialis anterior in chronic stroke survivors.
Findings
Our main results show significant increases of 27.7% and 26.9 % in shear wave velocity of stroke-impaired medial gastrocnemius compared to the unimpaired contralateral side at 90° ankle angle (P=0.033) and 15° plantarflexion (P=0.001), respectively. However, no significant difference was found in the tibialis anterior between the two sides. Relatively weak correlations were found between SW velocity in the medial gastrocnemius and joint stiffness for both the non-paretic (ρ=0.384, P=0.001), and paretic side (ρ=0.363, P=0.002). Additionally, muscle stiffness estimates of stroke-impaired tibialis anterior from joint torque and angle measurements were significantly greater by 23.1% (P=0.033) than the unimpaired contralateral side. However, no significant difference was found in the medial gastrocnemius.
Interpretation
These results indicate that there are non-uniform changes in passive stiffness of stroke-impaired muscle. Therefore, muscles need to be evaluated individually to access alterations. Additionally, interpretation of joint-based calculations of muscle stiffness should be made cautiously. Having the ability to non-invasively assess muscle stiffness adaptations in vivo would aid in prognosis, evaluation, and treatment following a stroke.
Keywords: Ultrasound, stroke, muscle, stiffness, shear wave elastography
1. Introduction
In neurologically impaired individuals, changes in muscle material properties can accompany spasticity and contracture1–4. These changes may affect the intrinsic mechanical properties of a joint. Specifically, stroke survivors often have increased passive joint stiffness3–5. However, these stiffness estimates lack differentiation between the articular structures, ligaments, tendons, and individual muscles that cross the joint3,6–8. Often, muscle stiffness of a functional group of muscles, such as the plantarflexors, is estimated through indirect measurements of joint torque4,9,5, calculating limb dynamics3, or kinematic protocols10. Direct methods to measure the elastic modulus of whole muscle have only been used in animal experiments, and for humans, direct methods have only been applied to single fibers11 or fiber bundles12. Spastic muscle cells have been shown to be significantly stiffer than non-spastic muscle cells11; however, non-spastic fiber bundles were significantly stiffer than spastic fiber bundles12. So while there is consensus that changes occur in the material properties of spastic muscle, there is a lack of in vivo measurements of stiffness of individual muscles.
Recently, shear wave (SW) ultrasound elastography has been used to quantify muscles stiffness in a variety of lower extremity13,14 and upper extremity muscles in healthy individuals15–18. SuperSonic Imaging (SSI) uses acoustic forces to induce SWs through the tissue and tracks the propagation of the SWs using ultra-fast ultrasonic imaging to calculate SW velocity19. SW velocity is related to the shear modulus of the tissue such that SWs travel faster in a stiffer material20. The length dependence of SW velocity in passive muscle of healthy subjects has been documented in the medial gastrocnemius (MG)13,21,22 tibialis anterior (TA)23, and biceps brachii24. SW velocity is also dependent upon activation level13,16,18. Furthermore, an increase in SW velocity has been found in passive stroke impaired bicep brachii muscle compared to the contralateral non-impaired muscle25. Similar results have been observed in the more affected limb in children with hemiplegic cerebral palsy (CP)26,27, suggesting that passive stiffness may be higher in spastic muscle. However, there are no quantitative measures of muscle stiffness of individual muscles of the lower extremity in stroke survivors. Identifying muscular changes, specifically stiffness and architecture, could provide clinicians with a quantitative tool in for evaluating muscle in stroke survivors and could impact rehabilitation.
Therefore, the goal of this study was to investigate the differences in the material properties, specifically passive stiffness, by measuring the SW velocity in the MG and TA in chronic stroke survivors across the range of motion (RoM) of the ankle. We hypothesized that SW velocity is higher in muscles of the paretic side compared to the non-paretic side. We also aimed to compare SW velocity values to current common methods of measuring stiffness at the joint, as well as joint-based estimates of muscle stiffness.
2. Methods
2.1 General set up
Fourteen individuals with chronic hemiparesis (Table 1) participated in the study. All subjects were ambulatory, and were not currently receiving physical therapy. They had no history of botulinum toxin treatments at least six months prior to testing. Informed consent was obtained from the participants prior to testing and Northwestern University’s Institutional Review Board approved all procedures.
Table 1.
Subject demographics
| Variable | Averages | SD | Range |
|---|---|---|---|
| Age (years) | 60.1 | 5.9 | 46–68 |
| Height (m) | 1.7 | 0.1 | 1.5–1.8 |
| Body mass (kg) | 77.6 | 12.5 | 58.0–96.4 |
| Time post stroke (years) | 10.6 | 7.3 | 4.3–29.3 |
| Fugl-Meyer | 19.1 | 6.1 | 8–28 |
| Sex (male/female) | 6/8 |
Participants were seated upright with their foot secured to the dynamometer (Biodex Medical System, Inc. Shirley, NY, USA) and their knee in maximum extension. The ankle center of rotation, as defined as the mid-line between the malleoli, was aligned with the rotation axis of the dynamometer. During each trial, torque and position data were collected from the Biodex dynamometer at a sampling rate of 2000 Hz. Subjects were instructed to remain relaxed during this study, and muscle activity was monitored visually for increased amplitude from baseline during image capture by measuring electromyography (EMG) signals (Bagnoli, Delsys, Inc. Boston, MA, USA). Subjects were given adequate time to become comfortable and familiar the experimental set up. EMG was monitored for burst of muscle activity.
2.2 Ultrasound
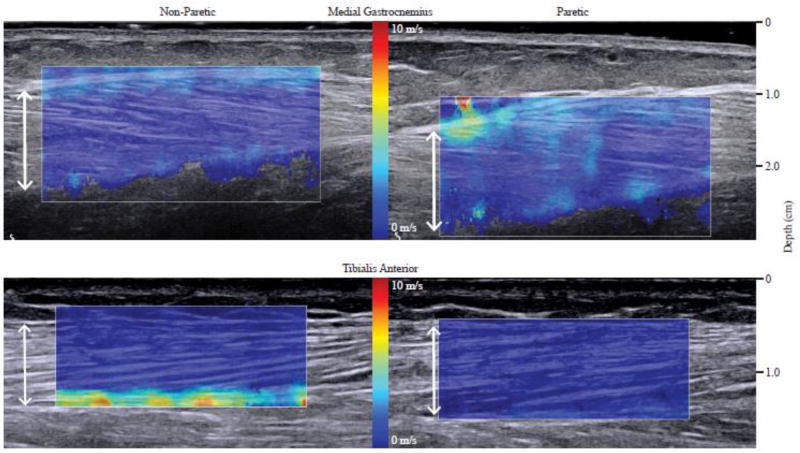
Ultrasound images were captured using a SW elastography ultrasound system (Aixplorer SuperSonic Imagine, Aix en Provence, France), with a linear transducer array (4–15 MHz, SuperLinear, 15-4, Vermon, France)19. Images from the MG and TA were captured from both the non-paretic and paretic leg (three images per randomized ankle position, both B-mode and SW elastography). Technical details of this SSI technology have been described previously19. The transducer was positioned at the mid-belly region of the muscle and oriented parallel to the fascicle plane as verified in the B-mode image (Fig. 1). A custom neoprene sleeve held the transducer in place to minimize undesired translation and to normalize transducer pressure on the subject. The SW velocity region of interest (RoI) was manually placed over the muscle belly (Fig.1). The width of the RoI was set to 30mm and the depth was set to the thickness of the muscle. Images were exported to a computer for off-line processing.
Fig. 1.
Shear wave ultrasound images of the non-paretic (left) and the paretic (right) of the medial gastrocnemius (top) and tibialis anterior (bottom) muscles in the 90° ankle angle. White arrows indicate measurement of muscle thickness.
2.3 Procedure
Subjects were instructed to remain relaxed during this study. The paretic side was tested first so that the torque values of the non-paretic side could be matched to the paretic side. The ankle was passively moved by the experimenter to one of the six ankle positions: neutral defined as the ankle at 90°, 15° plantarflexion (PF), maximum dorsiflexion (DF), maximum PF, and two intermediate angles. The two intermediate angles were chosen at angles where the torque on the paretic side was between the torque at maximum DF and neutral or maximum PF and neutral, respectively.
2.4 Data Analysis
All processing was performed using custom-written software in MATLAB (Mathworks, Natick, USA). The details on image processing are described elsewhere25. Briefly, SW velocity values from the RoI were extracted via the custom written software. In order to only include SW velocity values from the muscle belly, areas between the superficial and deep aponeurosis in the MG, and the superficial and middle aponeurosis in the TA were manually cropped (Fig. 1). The mean SW velocity was then calculated from all the SW velocity values within the cropped RoI.
Muscle thickness, fascicle length, and pennation angle were measured from the B-mode ultrasound images for all trials. Thickness was measured by digitizing and taking the average of the distance between the superficial and deep aponeurosis in the MG and between the superficial and middle aponeurosis in the TA28. To measure fascicle length, three points along a fascicle were manually selected, digitized, and fit with a linear line. Fascicle length was calculated by extrapolating the intersection with both aponeurosis and calculating the distance between respective intersection points. Average fascicle length was taken as the mean of three digitized fascicles per trial. Pennation angle was calculated as the angle between the digitized fascicle and the superficial aponeurosis and was averaged across the three digitized fascicles for each trial. Any trial where the fascicles or the aponeurosis were not clearly visible was discarded. Repeatability from two separate sessions has been reported previously28.
Position and torque data were filtered using a 20-Hz low-pass filter. To obtain the average toque and position for each trial, the filtered signals where averaged over a 500ms window around the time of image capture. In order to compare the SW velocity at similar ankle angles in both the MG and TA for each subject, the SW velocity – ankle angle data were fit with a quadratic equation for each muscle of each side. We examined the fit quality of linear, quadratic, and third order polynomial equations. While both quadratic and third order polynomial equations had significantly higher coefficients of determination than a linear fit, there was no significant difference between the two. Therefore, we used the lowest order equation to evaluate the fits. From the quadratic equation, SW velocity for both sides was extrapolated at maximum PF and maximum DF from the paretic side. SW velocity was also compared to passive joint stiffness, which was calculated as the change in joint torque as a function of ankle angle across the RoM.
Estimates of MG and TA muscle stiffness from torque and ankle angle measurements were also calculated. The MG and TA moment arms throughout the RoM of each subject was obtained from OpenSim29 using a lower extremity model by Arnold et al.30. The shared passive force between the lateral and medial gastrocnemius muscles was assumed to be proportional to the cross-sectional area; the passive force of the MG muscle was determined to be 61% of the total gastrocnemius force5. Muscle stiffness was calculated as the slope of the estimated muscle force – angle relationship for both the MG and TA.
2.5 Clinical Tests
Clinical tests were conducted by a licensed physical therapist; other physical measurements were made by the experimenter. The Fugl-Meyer assessment of motor recovery after a stroke was used as a test for motor impairment31. Physical examination measurements included passive and active RoM of the hip, knee, and ankle joints. The passive RoM measurements involved the experimenter moving the limb to maximum flexion and extension while all muscles were at rest. In contrast, for the active RoM measurements, subjects were instructed to actively move the limb to maximum flexion and extension, for each joint. Hip angles were defined as the angle between the lateral midline of the pelvis and the lateral midline of the femur (180° is neutral, flexion < 180° to extension > 180°) and knee angles were defined as the angle between the lateral midline of the femur and the lateral midline of the fibula (flexion 0° to extension 180°). Ankle angles were defined as the angle between the lateral midline of the fibula and parallel to the 5th metatarsal (neutral is 90°; plantar flexion < 90° to dorsiflexion > 90°).
2.6 Statistical Analysis
The SW velocity data were not normally distributed as tested using the Anderson-Darling test. Thus, the non-parametric Friedman test was conducted to compare the SW velocity, ankle angle, torque, muscle architecture, joint stiffness, and muscle stiffness estimates between the non-paretic and paretic sides in both muscles. A Spearman Rho correlation was performed to evaluate the relationship between SW velocity and torque, ankle angles, and fascicle strain. A Spearman Rho correlation was also used to evaluate the relationship between SW velocity and clinical measurements, muscle architecture, joint stiffness, and muscle stiffness estimates on each leg and muscle independently. Significance was set at P<0.05.
3. Results
3.1 Shear wave velocity
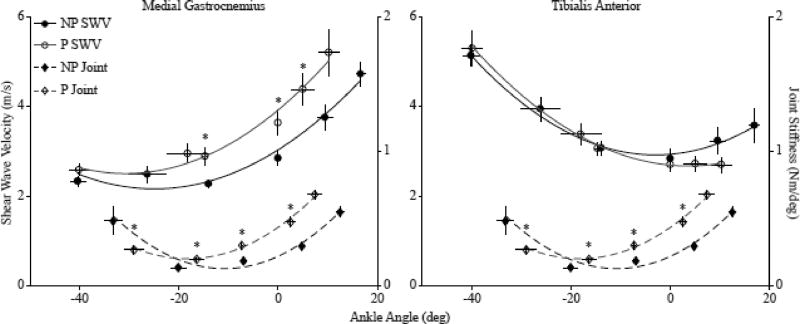
The average MG SW velocity across all subjects increased as ankle angle increased from plantarflexion to dorsiflexion with an average quadratic fit of r2 =0.95 (0.04) for the non-paretic side and r2 =0.87 (0.19) for the paretic side (Fig. 2). The average SW velocity in the TA increased from dorsiflexion to plantarflexion, with an average quadratic fit of r2 =0.86 (0.14) for the non-paretic side, and r2 =0.96 (0.08) for the paretic side (Fig. 2).
Fig. 2.
The relationships between shear wave velocity and ankle angle across all subjects (paretic, P-white circles; non-paretic, NP-black circles) for the medial gastrocnemius (left) and tibialis anterior (right). The relationship between joint stiffness and average ankle angle across all subjects (paretic, P- white triangles, non-paretic, NP- black triangles). The shear wave velocity, joint stiffness and ankle angle were averaged across all subjects at each position. The error bars are standard mean error. * P<0.05.
We found significant differences in the SW velocity in the MG between the non-paretic and paretic side at different ankle positions. The SW velocity in the paretic MG muscle was on average 27.7% greater than the non-paretic muscle at 90° (P=0.033) and on average 26.9% greater that the non-paretic at 15° PF (P=0.001) (Fig. 2). In order to compare SW velocity at the maximum DF angles, which were significantly different between the two sides, the maximum DF SW velocity was extrapolated from the quadratic fit equation for each subject at the maximum DF angle of the paretic side. While it was not significant, the extrapolated SW velocity of the MG on the paretic side was 26.9% greater than the non-paretic side (P=0.285). There was no significant difference in SW velocity between the paretic and non-paretic TA at any ankle angle (Fig. 2). The SW velocity of the paretic side in the MG and TA at the torque-matched position between maximum PF and neutral was 18.7% (P=0.109) greater and 14.7% (P=0.109) less than the non-paretic side, respectively. The SW velocity of the paretic side in the MG and TA at the torque-matched position between neutral and maximum DF was 16.8% (P=0.033) greater and 16.3% (P=0.109) less than the non-paretic side respectively.
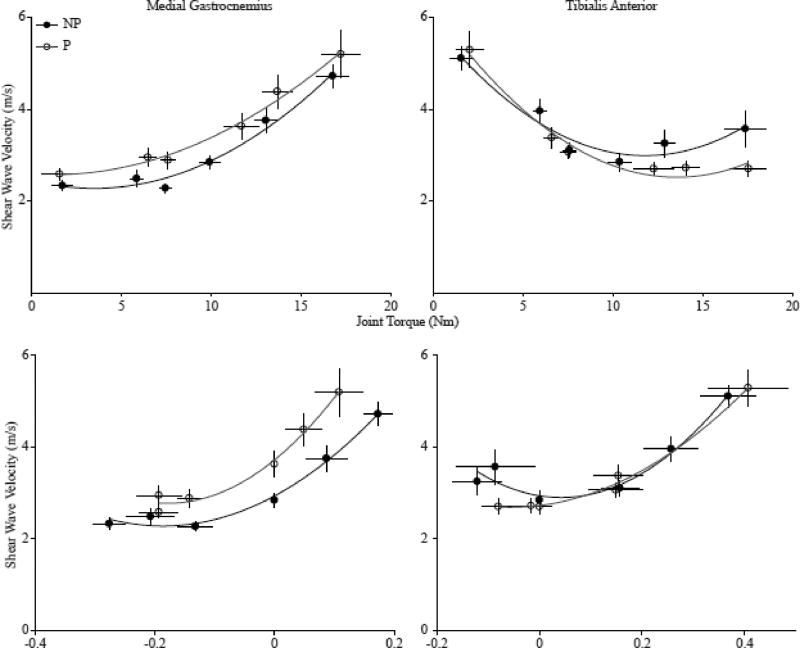
We found that ankle angle, joint torque, and fascicle strain all had a significant correlation with SW velocity in both the MG and TA (Table 2). In the MG, SW velocity increased nonlinearly as ankle torque increased with an average quadratic fit of r2 =0.92 (0.05) for the non-paretic side, and r2 =0.87 (0.18) for the paretic side across all subjects (Fig. 3). Conversely, in the TA, SW velocity decreased non-linearly as ankle torque increased with an average quadratic fit of r2=0.78 (0.17) for the non-paretic side, and r2 =0.87 (0.15) for the paretic side across all subjects. For both the MG and TA, SW velocity increased non-linearly as fascicle strain increased (MG: non-paretic: r2=0.71 (0.21); paretic: r2=0.55 (0.28); TA: non-paretic: r2=0.37 (0.27); paretic: r2=0.48 (0.21)).
Table 2.
Spearman Rho Correlation Results
| Relationship | ρ | P-value | ||
|---|---|---|---|---|
| MG | TA | MG | TA | |
| SW Velocity vs Ankle Angle | 0.705 | −0.574 | <0.001 | |
| SW Velocity vs Joint Torque | 0.626 | −0.475 | <0.001 | |
| SW Velocity vs Fascicle Strain | 0.665 | 0.397 | <0.001 | |
Fig. 3.
The relationships between the 1) shear wave velocity and average joint torque (top) and 2) shear velocity and the average fascicle strain (bottom) across all subjects for the medial gastrocnemius (left) and tibialis anterior (right) for both the paretic side (P, white circles) and non-paretic side (NP, black circles). The shear wave velocity, joint torque, and fascicle strain were averaged across all subjects at each position. The error bars are standard mean error.
3.2 Joint Torque and Stiffness
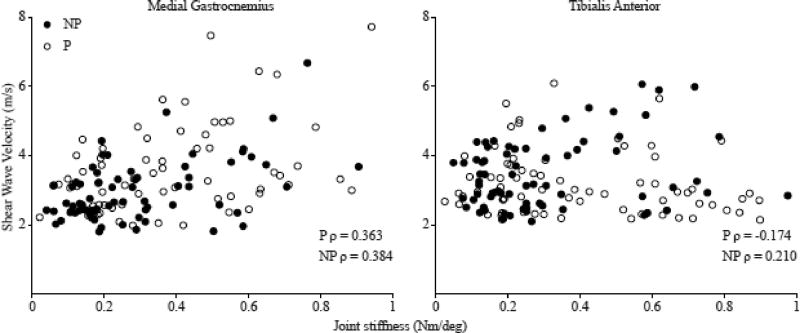
Joint torque during trials in the MG on the paretic side was 18.0% (P=0.001) greater than the non-paretic side with a 90° ankle angle. Joint torque during trials on the TA on the paretic side was 9.1% (P=0.008) greater than the non-paretic side at the intermediate angle between neutral and maximum DF. No other significant differences in joint torque were found at any ankle position for either the MG or TA. As there was no significant difference in the calculated joint stiffness during the MG and TA trials for either the non-paretic or paretic side (non-paretic P=0.71; paretic P=0.57), for analysis between the paretic and non-paretic sides, we report the average joint stiffness calculated from all trials from each side. However, for the correlations between joint stiffness and SW velocity, joint stiffness was separated by MG and TA trials. A significant difference in joint stiffness between the paretic and non-paretic sides was found; joint stiffness between 15° PF and 90° was 62.7% greater on the paretic side compared to the non-paretic side (P=0.001) (Fig 2). Relatively weak correlations were found between SW velocity and the calculated joint stiffness in the MG for both the non-paretic (ρ=0.384, P=0.001), and paretic side (ρ=0.363, P=0.002). However, no correlation was found between SW velocity and passive joint stiffness in the TA on either the non-paretic (ρ=0.210, P=0.081), or paretic side (ρ=−0.174, P=0.151) (Fig. 4).
Fig. 4.
The relationship between joint stiffness calculated as the change in torque over the change in angle and shear wave velocity for the medial gastrocnemius (left) and tibialis anterior (right), for the paretic side (white circles) and non-paretic side (black circles). MG: NP: P=0.001, P: P=0.002, TA NP; P=0.081, P: P=0.151. Each data point represents the joint stiffness between the six positions, generating 5 data points per subject.
3.3 Joint based estimates of muscle stiffness
Muscle stiffness in the MG and TA, estimated as the slope of muscle force – ankle angle relationship, was 20.0% (P=0.102) and 23.1% (P=0.033) higher on the paretic side compared to the non-paretic side, respectively. In the non-paretic TA, when the ankle was in maximum PF, as SW velocity increased, the muscle stiffness estimate also increased (ρ=0.763, P=0.002). A strong correlation was found between the muscle stiffness estimates in both the MG and TA with the joint stiffness calculations between 15° PF and neutral on both the non-paretic and paretic side (NP: MG: ρ=0.717, P=0.004; TA: ρ=−0.772, P=0.001; P: MG: ρ=0.869, P<0.001; TA: ρ= −0.911, P<0.001).
3.4 Muscle Architecture
From the B-mode ultrasound images, no significant differences in the muscle thickness, fascicle length, or pennation angle between the non-paretic and paretic side were found in either the MG or TA in any ankle position. In the MG at 90° on both the non-paretic and paretic side, as muscle thickness increased, the SW velocity decreased (non-paretic: ρ=−0.565, P=0.035; paretic: ρ=−0.648, P=0.012). However, the same relationship was not found in the TA at any ankle angle. The fascicle strain at 15° PF in the MG on the paretic side was 7.6% (P=0.021) greater compared to the non-paretic side. No other significant differences in fascicle strain were found at any ankle angle for either the MG or TA.
3.5 Clinical Assessments
The non-paretic leg had significantly 1) greater active RoM at the ankle, knee, and hip, and 2) greater passive RoM at ankle and knee (Table 3). We found that the maximum passive DF angle of the non-paretic side was 38.6% greater than paretic side (P=0.008) and the maximum DF angle on the paretic side also correlated with the time since the stroke (ρ=0.578, P=0.030). The Fugl-Meyer score was correlated with the SW velocity of the paretic side in the TA at 15° PF (ρ=−0.586, P=0.035); however, no correlations were found in the MG at any ankle angle.
Table 3.
Range of Motion Results
| Joint | Active | Passive | ||||
|---|---|---|---|---|---|---|
| Non-Paretic | Paretic | P-Value | Non-Paretic | Paretic | P-Value | |
| Ankle | 49.6 (6.7)° | 27.9 (8.4)° | <0.001 | 55.3 (4.7)° | 47.2 (8.2)° | 0.008 |
| Knee | 81.5 (18.3)° | 33.2 (27.1)° | 0.001 | 99.7 (37.8)° | 88.9 (29.8)° | 0.013 |
| Hip | 84.8 (20.6)° | 71.8 (18.0)° | 0.013 | 123.2 (22.3)° | 117.3 (23.5)° | 1.000 |
4. Discussion
Our main findings include a substantial increase in SW velocity of stroke-impaired MG compared to the unimpaired contralateral side, indicating greater passive stiffness, but not in the TA. This indicates that changes in material properties such as stiffness may be muscle specific post-stroke. Although there was an increase in joint stiffness of the paretic side compared to the non-paretic side, there was only a relatively weak correlation between SW velocity and joint stiffness in the MG. This suggests that increased joint stiffness cannot be fully explained by increased muscle stiffness. Additionally, muscle stiffness estimates from joint torque and angle measurements were only higher in stroke-impaired TA indicating that joint-based stiffness measurements may not be sensitive to changes in muscle stiffness.
Previous work has demonstrated that stroke survivors have increased joint stiffness on the paretic side compared to the non-paretic side and controls at the elbow32 and ankle3,5,9 for which passive stiffness of soft tissue has been characterized as a primary contributor. Other methods have been used to estimate muscle stiffness indirectly3,6,9,10. Increased ankle joint stiffness has been attributed to the passive material properties of the Achilles tendon and triceps surae post stroke3–5. Gao et al. (2009) found significant differences in ankle joint torque between stroke survivors and controls and extended their calculations to include estimates of MG stiffness through computer simulations5. For comparison, we performed the same calculations based on our experimental data and although our values are similar, we found no significant differences in the joint-based estimates of muscle stiffness between the paretic and non-paretic side in the MG, but did find significant differences in the TA. As our SW velocity values were significantly different between the two sides in the MG but not the TA, this emphasizes that joint-based stiffness measurements may not be sensitive to changes in muscle stiffness. While we found that the SW velocity in the MG on the non-paretic and paretic side correlated with joint stiffness, the weak correlation indicates that other muscles and other non-contractile tissues, such as the Achilles tendon, likely contribute substantially to joint stiffness. Poor correlations have previously been found in healthy young adults between SW velocity in both the MG and Achilles tendon and joint stiffness21. Furthermore, while both joint stiffness and SW velocity have a non-linear relationship with ankle angle, there are distinct differences between the curves as seen in Figure 2. Johns and Wright33 reported that muscles only contribute 41% to the passive resistance to movement with tendons likely providing the highest resistance to movement near the end ranges of joint motion. Joint stiffness increases due to lengthening of the musculature around the ankle; for the MG this occurs during dorsiflexion, and for the TA, this occurs during plantarflexion. Other non-muscular elements may contribute significantly to passive joint stiffness and the agonist-antagonist relationship between the MG and TA may account for the discrepancies between the joint stiffness and SW velocity.
Previously, using SW ultrasound elastography, we observed increased SW velocity in stroke-impaired biceps brachii compared to the non-impaired. The results of this study demonstrate that other muscles, such as the gastrocnemius muscle, may also be affected by stroke. We observed a 27.7% increase and a 26.9% increase in the paretic MG compared to the non-paretic MG at 90° and 15° PF, respectively. The SW velocity values from five older adults (age-matched to stroke subjects, unpublished), in both the MG and TA are similar to those in the non-paretic limb across the entire RoM. Sources of passive stiffness include connective tissue within the extracellular matrix (ECM)34, myofilaments, including actin and myosin, and intramuscular proteins, mainly titin. There is little information on sources of increased stiffness in stroke-impaired muscle. Much of what is known about spastic muscle is from work in individuals with CP. Through biopsies in individuals with CP, collagen, the primary protein in the ECM2,35, has been found to be increased in spastic muscle12,36–38. Different isoforms of titin may also relate to differences in passive stiffness39. Following ischemia-induced cardiomyopathy, the titin isoform changes to a different stiffer isoform40. Similar changes in the ECM may occur in spastic stroke-impaired muscle.
Interestingly, there were no differences in SW velocity in the TA between the paretic and non-paretic side. This suggests that adaptations in muscle material properties following a stroke may be muscle specific. There are multiple factors that may contribute to increased SW velocity in the MG on the paretic side, but not in the TA. The MG is a bi-articular muscle such that its length and activation are modulated differently than the TA. Previously, in a rat model, following immobilization of the hind limb, significant architectural changes, including changes in fiber length, muscle weight, and fiber cross sectional area, were found in the MG and soleus, but not in the TA. These differences were hypothesized to be primarily due to the difference in anatomical attachment and the difference in the relative stimulus to the muscle resulting from the immobilization41. Similarly, Ramsay et al42 observed that muscles of the paretic side were significantly smaller than those of the non-paretic side, except in the TA, semimembranosus, and gracilis, indicating that atrophy occurs non-uniformly following a stroke. Additionally, the fiber type distribution is different between the MG and TA. The MG has roughly an equal distribution of Type 1 and Type 2 fibers whereas the TA has primarily Type 1 fibers43,44. There is a lack of agreement in the literature whether fiber type redistribution occurs in spastic muscle2; however, there are differences in the titin isoform between fast and slow twitch fibers that could, in part, modulate stiffness45. Therefore, increases in passive stiffness could be the result of changes in the titin isoform and the redistribution of fibers.
We found no significant difference in any architectural parameters between the non-paretic and paretic side in either the MG or TA. Our results are similar to previous findings in the TA of no significant difference in post-stroke architecture46. However, in the MG, significant differences in fascicle length have been found when compared to controls9. While we did not find a significant difference between the non-paretic and paretic side, the fascicle lengths presented here are comparable to those previously reported9. This may indicate that adaptations also occur on the non-paretic side after a stroke. It should be noted that muscle contraction dynamics and the passive force – length relationship is a function of sarcomere length, for which fascicle length is not a surrogate measure47. In subjects with CP, while no difference in fascicle length was found when compared to typically developing children, the sarcomere length was found to be significantly higher47. Therefore, no definitive conclusions can be drawn regarding the influence of length on the increase in passive stiffness without investigating at the sarcomere level. However, the lack of differences in muscle architecture suggests that increased muscle stiffness is not primarily due to changes in muscle architecture post-stroke.
A limitation to SW ultrasound elastography includes the lack of information one can extract about the source of muscle stiffness. Coupling these measurements with biopsies and sarcomere length measurements would enhance our understanding of what is modulating passive stiffness in stroke-impaired muscle. The sensitivity of SW ultrasound elastography to muscle activation, although an asset in other work, must be considered when applied to spastic muscle. While EMG activity was monitored during the trials, it is possible that there was muscle activity below the noise threshold of our EMG equipment. SW velocity is sensitive to activation level13,16,18 such that an increase of 4.7 m/s was observed between passive and maximum contraction13; therefore, low levels of activation below the amplitude of noise measured by our EMG system could influence our SW velocity measurements. However, since it was undetectable, we believe that is appropriate to label the trials as passive.
5. Conclusion
Using SW ultrasound elastography, we were able to quantify the material properties of stroke-impaired and the contralateral MG and TA of chronic stroke survivors. SW velocity in the MG of the paretic side was greater than on the non-paretic side, but similar increases were not observed in the TA, which suggest that the MG and TA do not adapt uniformly following a stroke. We also demonstrate that SW velocity in MG and TA of both the paretic and non-paretic side is length dependent. Although there was an increase in joint stiffness of the paretic side compared to the non-paretic side, the relatively weak correlation between SW velocity and joint stiffness in the MG indicates that increased joint stiffness cannot be fully explained by increased muscle stiffness. Therefore, it is important to have the ability differentiate between articular structures and muscles. Knowing the magnitude of increased passive stiffness and which muscle is the primary contributor to increased joint stiffness would affect the treatment prescribed. Information regarding which muscles are affected and to what degree could aid in diagnosing the cause of functional deficits and improve patient specific treatment protocols.
Highlights.
Increased shear wave velocity in the medial gastrocnemius on the paretic side
No difference between the paretic and non-paretic shear wave velocity in the tibialis anterior
Changes in muscle material properties following a stroke are muscle specific
Acknowledgments
We thank all the participants for taking part in this study. Funding for this study was provided by the National Institutes of Health. S.S.M. Lee, A. Terman, and R. Santana are supported by the NIH National Institute of Child Health and Human Development Grant K12HD073945.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Foran JR, Steinman S, Barash IA, Chambers H, Lieber RL. Structural and mechanical alterations in spastic skeletal muscle. Dev Med Child Neurol. 2005;47(10):713–717. doi: 10.1017/S0012162205001465. [DOI] [PubMed] [Google Scholar]
- 2.Lieber RL, Steinman S, Barash IA, Chambers H. Structural and functional changes in spastic skeletal muscle. Muscle & nerve. 2004;29(5):615–627. doi: 10.1002/mus.20059. [DOI] [PubMed] [Google Scholar]
- 3.Sinkjær T, Magnussen I. Passive, intrinsic and reflex-mediated stiffness in the ankle extensors of hemiparetic patients. Brain. 1994;117(2):355–363. doi: 10.1093/brain/117.2.355. [DOI] [PubMed] [Google Scholar]
- 4.Thilmann AF, Fellows SJ, Ross HF. Biomechanical changes at the ankle joint after stroke. J Neurol Neurosurg Psychiatry. 1991;54(2):134–139. doi: 10.1136/jnnp.54.2.134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gao F, Grant TH, Roth EJ, Zhang LQ. Changes in passive mechanical properties of the gastrocnemius muscle at the muscle fascicle and joint levels in stroke survivors. Archives of physical medicine and rehabilitation. 2009;90(5):819–826. doi: 10.1016/j.apmr.2008.11.004. [DOI] [PubMed] [Google Scholar]
- 6.Chardon MK, Suresh NL, Rymer WZ. An evaluation of passive properties of spastic muscles in hemiparetic stroke survivors. IEEE; 2010. pp. 2993–2996. [DOI] [PubMed] [Google Scholar]
- 7.De Vlugt E, de Groot JH, Schenkeveld KE, Arendzen J, van der Helm FC, Meskers CG. The relation between neuromechanical parameters and Ashworth score in stroke patients. J Neuroengineering Rehabilitation. 2010;7(1):35. doi: 10.1186/1743-0003-7-35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Roy A, Krebs HI, Bever CT, Forrester LW, Macko RF, Hogan N. Measurement of passive ankle stiffness in subjects with chronic hemiparesis using a novel ankle robot. Journal of neurophysiology. 2011;105(5):2132–2149. doi: 10.1152/jn.01014.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gao F, Zhang LQ. Altered contractile properties of the gastrocnemius muscle poststroke. J Appl Physiol. 2008;105(6):1802–1808. doi: 10.1152/japplphysiol.90930.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lamontagne A, Malouin F, Richards C. Contribution of passive stiffness to ankle plantarflexor moment during gait after stroke. Archives of physical medicine and rehabilitation. 2000;81(3):351–358. doi: 10.1016/s0003-9993(00)90083-2. [DOI] [PubMed] [Google Scholar]
- 11.Fridén J, Lieber R. Spastic muscle cells are shorter and stiffer than normal cells. Muscle & nerve. 2003;27(2):157–164. doi: 10.1002/mus.10247. [DOI] [PubMed] [Google Scholar]
- 12.Lieber RL, Runesson E, Einarsson F, Fridén J. Inferior mechanical properties of spastic muscle bundles due to hypertrophic but compromised extracellular matrix material. Muscle & nerve. 2003;28(4):464–471. doi: 10.1002/mus.10446. [DOI] [PubMed] [Google Scholar]
- 13.Chernak LA, DeWall RJ, Lee KS, Thelen DG. Length and activation dependent variations in muscle shear wave speed. Physiological measurement. 2013;34(6):713–721. doi: 10.1088/0967-3334/34/6/713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sasaki K, Toyama S, Ishii N. Length-force characteristics of in vivo human muscle reflected by supersonic shear imaging. J Appl Physiol. 2014;117(2):153–162. doi: 10.1152/japplphysiol.01058.2013. [DOI] [PubMed] [Google Scholar]
- 15.Bouillard K, Nordez A, Hodges PW, Cornu C, Hug F. Evidence of changes in load sharing during isometric elbow flexion with ramped torque. J Biomech. 2012;45(8):1424–1429. doi: 10.1016/j.jbiomech.2012.02.020. [DOI] [PubMed] [Google Scholar]
- 16.Lapole T, Tindel J, Glay R. Contracting biceps brachii elastic properties can be reliably characterized using supersonic shear imaging. Eur J Appl Physiol. 2015;115(3):497–505. doi: 10.1007/s00421-014-3037-0. [DOI] [PubMed] [Google Scholar]
- 17.Nordez A, Hug F. Muscle shear elastic modulus measured using supersonic shear imaging is highly related to muscle activity level. J Appl Physiol. 2010;108(5):1389–1394. doi: 10.1152/japplphysiol.01323.2009. [DOI] [PubMed] [Google Scholar]
- 18.Yoshitake Y, Takai Y, Kanehisa H, Shinohara M. Muscle shear modulus measured with ultrasound shear-wave elastography across a wide range of contraction intensity. Muscle & nerve. 2014;50(1):103–113. doi: 10.1002/mus.24104. [DOI] [PubMed] [Google Scholar]
- 19.Bercoff J, Tanter M, Fink M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. IEEE Trans Ultrasonics, Ferroelectrics, and Freq Control. 2004;51(4):396–409. doi: 10.1109/tuffc.2004.1295425. [DOI] [PubMed] [Google Scholar]
- 20.Brandenburg JE, Eby SF, Song P, Zhao H, Brault JS, Chen S, An KN. Ultrasound Elastography: The New Frontier in Direct Measurement of Muscle Stiffness. Archives of physical medicine and rehabilitation. 2014;95(11):2207–2219. doi: 10.1016/j.apmr.2014.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chino K, Takahashi H. The association of muscle and tendon elasticity with passive joint stiffness: In vivo measurements using ultrasound shear wave elastography. Clinical Biomechanics. 2015;30(10):1230–1235. doi: 10.1016/j.clinbiomech.2015.07.014. [DOI] [PubMed] [Google Scholar]
- 22.Maïsetti O, Hug F, Bouillard K, Nordez A. Characterization of passive elastic properties of the human medial gastrocnemius muscle belly using supersonic shear imaging. J Biomech. 2012;45(6):978–984. doi: 10.1016/j.jbiomech.2012.01.009. [DOI] [PubMed] [Google Scholar]
- 23.Koo TK, Guo JY, Cohen JH, Parker KJ. Quantifying the passive stretching response of human tibialis anterior muscle using shear wave elastography. Clinical Biomechanics. 2014;29(1):33–39. doi: 10.1016/j.clinbiomech.2013.11.009. [DOI] [PubMed] [Google Scholar]
- 24.Gennisson JL, Deffieux T, Mace E, Montaldo G. Viscoelastic and anisotropic mechanical properties of in vivo muscle tissue assessed by supersonic shear imaging. Ultrasound Med Biol. 2010;36(5):789–801. doi: 10.1016/j.ultrasmedbio.2010.02.013. [DOI] [PubMed] [Google Scholar]
- 25.Lee SSM, Spear S, Rymer WZ. Quantifying Changes In Material Properties Of Stroke-Impaired Muscle. Clinical Biomechanics. 2015;30(3):269–275. doi: 10.1016/j.clinbiomech.2015.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Brandenburg J, Eby S, Song P, Kingsley-Berg S, Bamlet W, Sieck G, An K. Quantifying passive muscle stiffness in children with and without cerebral palsy using ultrasound shear wave elastography. Dev Med Child Neurol. 2016 doi: 10.1111/dmcn.13179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lee SSM, Gaebler-Spira D, Zhang LQ, Rymer WZ, Steele KM. Use of shear wave ultrasound elastography to quantify muscle properties in cerebral palsy. Clinical Biomechanics. 2016;31:20–28. doi: 10.1016/j.clinbiomech.2015.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lee SSM, Piazza SJ. Built for speed: musculoskeletal structure and sprinting ability. J Exp Biol. 2009;212(22):3700–3707. doi: 10.1242/jeb.031096. [DOI] [PubMed] [Google Scholar]
- 29.Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE transactions on biomedical engineering. 2007;54(11):1941–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- 30.Arnold EM, Ward SR, Lieber RL, Delp SL. A model of the lower limb for analysis of human movement. Annals Biomedical Engineering. 2010;38(2):269–279. doi: 10.1007/s10439-009-9852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gladstone DJ, Danells CJ, Black SE. The Fugl-Meyer assessment of motor recovery after stroke: a critical review of its measurement properties. Neurorehabilitation and Neural Repair. 2002;16(3):232–240. doi: 10.1177/154596802401105171. [DOI] [PubMed] [Google Scholar]
- 32.Mirbagheri MM, Settle K, Harvey R, Rymer WZ. Neuromuscular abnormalities associated with spasticity of upper extremity muscles in hemiparetic stroke. Journal of neurophysiology. 2007;98(2):629–637. doi: 10.1152/jn.00049.2007. [DOI] [PubMed] [Google Scholar]
- 33.Johns R, Wright V. Relative importance of various tissues in joint stiffness. J Appl Physiol. 1962;17(5):824–828. [Google Scholar]
- 34.Gajdosik RL. Passive extensibility of skeletal muscle: review of the literature with clinical implications. Clinical Biomechanics. 2001;16(2):87–101. doi: 10.1016/s0268-0033(00)00061-9. [DOI] [PubMed] [Google Scholar]
- 35.Lieber RL, Ward SR. Cellular Mechanisms of Tissue Fibrosis. 4. Structural and functional consequences of skeletal muscle fibrosis. Am J Physiol-Cell Physiology. 2013;305(3):C241–C252. doi: 10.1152/ajpcell.00173.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Booth CM, Cortina-Borja MJF, Theologis TN. Collagen accumulation in muscles of children with cerebral palsy and correlation with severity of spasticity. Dev Med Child Neurol. 2001;43(5):314–320. doi: 10.1017/s0012162201000597. [DOI] [PubMed] [Google Scholar]
- 37.Castle ME, Reyman TA, Schneider M. Pathology of spastic muscle in cerebral palsy. Clin Orthop. 1979;142:223–233. [PubMed] [Google Scholar]
- 38.Smith LR, Lee KS, Ward SR, Chambers HG, Lieber RL. Hamstring contractures in children with spastic cerebral palsy result from a stiffer extracellular matrix and increased in vivo sarcomere length. J Physiol. 2011;589(10):2625–2639. doi: 10.1113/jphysiol.2010.203364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Labeit S, Kolmerer B. Titins: giant proteins in charge of muscle ultrastructure and elasticity. Science. 1995;270:293–296. doi: 10.1126/science.270.5234.293. [DOI] [PubMed] [Google Scholar]
- 40.Neagoe C, Kulke M, del Monte F, Gwathmey J, de Tombe P, Hajjar R, Linke W. Titin isoform switch in ischemic human heart disease. Circulation. 2002;106(11):1333–1341. doi: 10.1161/01.cir.0000029803.93022.93. [DOI] [PubMed] [Google Scholar]
- 41.Spector S, Simard C, Fournier M, Sternlicht E, Edgerton V. Architectural alterations of rat hind-limb skeletal muscles immobilized at different lengths. Exp Neurol. 1982;76(1):94–110. doi: 10.1016/0014-4886(82)90104-2. [DOI] [PubMed] [Google Scholar]
- 42.Ramsay JW, Barrance PJ, Buchanan TS, Higginson JS. Paretic muscle atrophy and non-contractile tissue content in individual muscles of the post-stroke lower extremity. J Biomech. 2011;44(16):2741–2746. doi: 10.1016/j.jbiomech.2011.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dahmane R, Djordjevi9010D; S, Šimunič B, Valenčič V. Spatial fiber type distribution in normal human muscle: histochemical and tensiomyographical evaluation. J Biomech. 2005;38(12):2451–2459. doi: 10.1016/j.jbiomech.2004.10.020. [DOI] [PubMed] [Google Scholar]
- 44.Johnson M, Polgar J, Weightman D, Appleton D. Data on the distribution of fibre types in thirty-six human muscles: an autopsy study. J Neurol Sci. 1973;18(1):111–129. doi: 10.1016/0022-510x(73)90023-3. [DOI] [PubMed] [Google Scholar]
- 45.Horowits R. Passive force generation and titin isoforms in mammalian skeletal muscle. Biophys J. 1992;61(2):392–398. doi: 10.1016/S0006-3495(92)81845-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ramsay J, Wessel M, Buchanan T, Higginson J. Poststroke muscle architectural parameters of the tibialis anterior and the potential implications for rehabilitation of foot drop. Stroke Research and Treatment. 2014;2014 doi: 10.1155/2014/948475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mathewson M, Ward S, Chambers H, Lieber R. High resolution muscle measurements provide insights into equinus contractures in patients with cerebral palsy. J Orthop Res. 2015;33(1):33–39. doi: 10.1002/jor.22728. [DOI] [PMC free article] [PubMed] [Google Scholar]