CONSTITUTIVE MODELING OF HUMAN FEMOROPOPLITEAL ARTERY BIAXIAL STIFFENING DUE TO AGING AND DIABETES

Abstract

Atherosclerotic obstructive disease of the femoropopliteal artery (Peripheral Arterial Disease, PAD) is notorious for high treatment failure rates. Older age and diabetes mellitus (DM) are among the major risk factors for PAD, and both are associated with increased arterial stiffness. Our goal was to develop a constitutive model describing multiaxial arterial stiffening, and use it to portray aging of normal and diabetic human femoropopliteal arteries (FPA). Fresh human FPAs (n=744) were obtained from 13–82-year-old donors. Arteries were tested using planar biaxial extension, and their behavior was modeled with a constitutive relation that included stiffening functions of age. FPA diameter, wall thickness, circumferential, and longitudinal opening angles increased with age, while longitudinal pre-stretch decreased. Diameter and circumferential opening angle did not change with age in subjects with DM. Younger FPAs were more compliant longitudinally but became more isotropic with age. Arteries with DM stiffened significantly faster in the circumferential direction than arteries without DM. Constitutive model accurately portrayed orthotropic stiffening with age of both normal and diabetic arteries. Constitutive description of FPA aging contributes to understanding of arterial pathophysiology and can help improve fidelity of computational models investigating device-artery interaction in PAD repair by providing more personalized arterial properties.

Graphical Abstract

We have analyzed n=744 human femoropopliteal artery (FPA) specimens from 13–82 year old tissue donors using biaxial tensile testing to derive constitutive description of FPA aging in diabetic and non-diabetic subjects. The proposed constitutive model provides a tool to describe human FPA aging in a continuous fashion.model allows determination of FPA mechanical properties for subjects of any given age in the range of 13–82 years. These results contribute to understanding of FPA pathophysiology and can help improve fidelity of computational models investigating device-artery interaction in peripheral arterial disease repair by providing more personalized arterial properties. In addition, they can guide the development of new materials tunable to diabetic and non-diabetic arteries of different ages.

1 INTRODUCTION

Peripheral arterial disease (PAD) often manifests as occlusive atherosclerotic lesions in the femoropopliteal artery (FPA) obstructing blood flow to the lower limb. It is associated with high morbidity, mortality, and impairment in the quality of life. Older age and Diabetes Mellitus (DM) are among major risk factors for PAD[1], and patients with DM are 2–4 fold more likely to develop the disease[2], and are 15-fold more likely to have an amputation compared to non-diabetic PAD patients[3–5].

Significant evidence suggests that arterial stiffness is a key component in aging and in the pathogenesis of DM[6–8]. Aging is characterized by altered turnover and crosslinking of collagen, degradation of elastin, its replacement by collagen and proteoglycans, and increased production of advanced glycation end-products (AGEs) and cross-links resulting in overall stiffening of the artery[8]. Glycation and AGEs formation in the carbonyl-enriched environment of DM is believed to have profound effects on enhancing age-related arterial stiffening[8], but exact contribution of DM to arterial stiffness in human FPAs is poorly understood.

Arterial stiffness is a multi-directional measure because arterial properties are anisotropic. Human FPAs contain mainly circumferentially-oriented smooth muscle cells (SMCs) in the media, longitudinal elastic fibers in the external elastic lamina (EEL) and adventitia, and helically-oriented collagen fibers in the adventitia[9–11]. Recent work[12] reported constitutive parameters for human FPAs in seven age groups, demonstrating that FPA undergoes multiaxial stiffening with faster changes occurring longitudinally due to degradation and fragmentation of elastin in the EEL[9,12]. This analysis was based on a large sample size (n=579) that included a wide range of ages, but data were presented for seven discrete age groups with no means of interpolating arterial properties between the presented ages. 1

Current work further explores these data supplemented with an additional 165 human FPAs, and proposes a way of incorporating aging explicitly into the constitutive relation between Cauchy stresses and stretches to allow for continuous description of mechanical properties with respect to age. Using this approach, orthotropic FPA mechanical properties can be determined for subjects of any given age, not just the seven age groups described previously. In addition, the framework will be applied to describe age-related multi-axial stiffening of human FPAs in subjects with and without DM. In combination with morphometric data on arterial diameters, wall thickness, opening angles, and longitudinal pre-stretch in subjects with and without DM that will also be summarized here, these data will aid computational models by reducing the required number of inputs to simulate material response to just two parameters: patient’s age and DM status. Furthermore, for cases when DM status is unknown, a set of constitutive parameters describing aging of FPAs irrespective of DM status will also be provided.

2. METHODS

2.1 Arterial specimens, mechanical testing, and data reduction

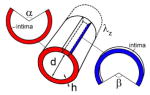
Fresh FPAs (n=744) from organ and tissue donors (n=466) were obtained from the Nebraska Organ Recovery System (NORS) within 24h of subject’s death after obtaining consent from the next of kin. Donors were predominantly Caucasian (94%) males (81%) and on average 55±15 years old (range 13–82 years old). Self-reported DM was present in 26% of subjects, 47% had hypertension, 10% Coronary Artery Disease, 25% dyslipidemia, 54% were either past or current tobacco users, 21% abused alcohol, and 50% had Body Mass Index of ≥30. Longitudinal pre-stretch λ_z was measured prior to excision of the artery from the body using an umbilical tape[11]. Arterial rings and longitudinal sections were used to determine FPA diameter (d), wall thickness (h), and circumferential (α) and longitudinal (β) opening angles using photographs and image analysis[12]. Circumferential and longitudinal opening angles were measured according to schematic presented in Table 1.

Table 1.

Morphometric parameters and residual stretches for all subjects considered together, and divided into non-DM and DM groups. Note that the total number of subjects in each group not necessarily equals to the sum of DM and non-DM subjects because DM status for several subjects was unknown. Here n is the number of specimens in the age group, d is the inner diameter, h is wall thickness (both in the load-free configuration), α is circumferential opening angle, β is longitudinal opening angle, λ_z is in situ longitudinal pre-stretch. Note that longitudinal strip curves intima upward, likely due to presence of pre-stretched longitudinally-oriented elastic fibers in the EEL[9]. Measurements of the opening angles are presented schematically in the right panel.

Age group, years	n	Mean age, years	d, mm	h, mm	α, °	β, °	λz
All subjects together
11–20	34	16.5	2.81±0.60	1.37±0.32	125±47	90±86	1.55±0.13
21–30	31	24.8	3.28±0.76	1.42±0.36	149±69	107±67	1.41±0.13
31–40	56	35.7	3.64±0.86	1.45±0.39	151±55	151±60	1.38±0.08
41–50	73	46.8	3.76±1.22	1.58±0.50	165±63	183±63	1.26±0.08
51–60	174	56.1	3.74±1.33	1.65±0.57	165±65	242±45	1.19±0.11
61–70	162	65.0	4.15±1.28	1.91±0.51	193±78	268±46	1.16±0.07
71–80	43	75.7	4.65±1.28	1.88±0.47	155±64	304±30	1.12±0.06
Subjects with DM
11–20	1
21–30	0
31–40	3	40.0	4.14±0.38	1.49±0.14	181±24	195±74	1.30±0.08
41–50	13	46.1	4.03±1.01	1.66±0.70	124±61	171±86	1.26±0.10
51–60	51	56.7	3.96±1.32	1.66±0.56	156±68	246±50	1.15±0.12
61–70	53	64.7	3.96±1.35	1.96±0.58	167±84	270±60	1.15±0.07
71–80	18	76.7	4.81±1.30	1.84±0.42	148±74	305±30	1.08±0.03
Subjects without DM
11–20	32	16.4	2.80±0.61	1.39±0.32	125±45	90±88	1.55±0.14
21–30	30	24.7	3.30±0.75	1.40±0.34	145±65	108±68	1.41±0.13
31–40	52	35.3	3.57±0.84	1.45±0.40	149±56	147±59	1.38±0.08
41–50	58	46.9	3.67±1.28	1.55±0.45	173±57	184±57	1.26±0.08
51–60	117	55.7	3.62±1.35	1.62±0.58	167±60	239±42	1.21±0.10
61–70	90	65.1	4.16±1.14	1.88±0.50	200±71	262±36	1.18±0.07
71–80	21	75.3	4.43±1.15	1.84±0.51	152±47	301±32	1.12±0.06

Planar biaxial tests were performed on 13×13mm (when permitted by diameter) arterial samples, and data were collected after the arteries were preconditioned for 10–20 equibiaxial cycles to achieve a repeatable response. The first 30% of samples were tested in load-controlled mode with 7 different force-ratios (1:1, 1:2, 1:4, and 1:10 on each axis) using a custom-build device[13]. Specimens were attached using stainless-steel hooks and loops of surgical suture which allowed the samples to shear freely. Since no sizable shear was observed[9], the other 70% of arteries were tested using the rake attachment system of CellScale. These samples were tested in stretch-controlled mode at 0.01s⁻¹ strain rate[12] using CellScale Biotester equipped with “250g” (max load 2.5N) Honeywell Sensotec load cells and 19 different stretch-ratios ranging from 1:1 to 1:0.1 on each axis. Equibiaxial stability checks were performed before and after the testing sequence to ensure that the specimens had not accumulated damage as they went through the battery of tests.

Experimental data obtained from both devices were then used to determine unique sets of constitutive parameters for the 4-fiber FPA constitutive model[11] using nonparametric bootstrapping. Bootstrapping allowed to assess parameter uniqueness irrespective of the type of test performed, i.e. load- or stretch-controlled. Specimens that produced a good fit (R_θ,z² > 0.9) were used to generate 19 stress-controlled loading protocols for each sample, which were then used to determine constitutive parameters representative of seven age groups as described in Kamenskiy et al[12]. These data were then used to determine stiffening functions described below.

2.2 Incorporation of stiffening into the constitutive model

Human FPA wall was assumed to contain an extracellular matrix composed of randomly organized amorphous ground substance, longitudinal elastic fibers, circumferential SMCs, and two families of collagen fibers oriented at an angle γ to the longitudinal axis[9–12]. For planar biaxial extension with no shear, isochoric Cauchy stresses for such material can be taken in the form:

$$\begin{gathered} \overline{t_{zz}}(t)=D_{gr}(t)C_{gr}\left({\lambda }_z^2-\frac{1}{{\lambda }_{\theta }^2{\lambda }_z^2}\right)+C_1^{el}\langle {(I_4^{el})}^{D_{el}(t)}-1\rangle exp\left(C_2^{el}{({(I_4^{el})}^{D_{el}(t)}-1)}^2\right){\lambda }_z^2 \\ +2C_1^{\mathit{col}}\langle {(I_4^{\mathit{col}})}^{D_{\mathit{col}}(t)}-1\rangle exp(C_2^{\mathit{col}}{({(I_4^{\mathit{col}})}^{D_{\mathit{col}}(t)}-1)}^2){\lambda }_z^2{cos}^2\gamma \\ \overline{t_{\theta \theta }}(t)=D_{gr}(t)C_{gr}\left({\lambda }_{\theta }^2-\frac{1}{{\lambda }_{\theta }^2{\lambda }_z^2}\right)+C_1^{\mathit{smc}}\langle {(I_4^{\mathit{smc}})}^{D_{\mathit{smc}}(t)}-1\rangle exp\left(C_2^{\mathit{smc}}{({(I_4^{\mathit{smc}})}^{D_{\mathit{smc}}(t)}-1)}^2\right){\lambda }_{\theta }^2 \\ +2C_1^{\mathit{col}}\langle {(I_4^{\mathit{col}})}^{D_{\mathit{col}}(t)}-1\rangle exp(C_2^{\mathit{col}}{({(I_4^{\mathit{col}})}^{D_{\mathit{col}}(t)}-1)}^2){\lambda }_{\theta }^2{sin}^2\gamma . \end{gathered}$$ (1)

Here Macaulay brackets $\langle (·)\rangle =\frac{1}{2}[(·)+\mid (·)\mid ]$ filter positive values such that fibers only contribute to stresses during tension, but not during compression, and (C_gr, $C_1^{el},C_2^{el},C_1^{\mathit{col}},C_2^{\mathit{col}},C_1^{\mathit{smc}},C_2^{\mathit{smc}}$, γ) are constitutive parameters for the youngest age group.

Further, invariants of the right Cauchy-Green tensor C for each direction are defined as:

$$\begin{gathered} I_4^{el}={\lambda }_z^2, \\ {I}_4^{\mathit{smc}}={\lambda }_{\theta }^2, \\ {I}_4^{\mathit{col}}={\lambda }_z^2{cos}^2\gamma +{\lambda }_{\theta }^2{sin}^2\gamma \end{gathered}$$ (2)

and D_{{gr,el,smc,col}}(t) are stiffening functions of age t that modify these invariants. Note that stiffening functions for elastin, SMC, and collagen are incorporated into the power of I₄, while ground substance is assumed to stiffen linearly. I₄ has physical meaning of the square of stretch in the direction of fiber, therefore D amplifies stretch for each constituent as a function of age. Obviously, D > 1 simulates material stiffening, D = 1 recovers the initial elastic response, while D < 1 simulates softening. Note too, that formulating strain energy density function directly in terms of modified invariants will not produce Cauchy stresses in (1) unless the derivative is taken with respect to the modified invariants $I_4^D$ to obtain stress.

The first step to determining stiffening functions D(t) was to obtain initial elastic constitutive parameters. This was achieved by setting D = 1 and performing minimization with lsqnonlin function of MATLAB (MathWorks, Natick, Massachusetts, USA) and using specimens from the youngest age group. This produced a set of eight initial constitutive parameters that were kept constant during further minimization to find the stiffening functions. Since stiffening functions D(t) can be different for the ground substance, elastin, SMCs, and collagen, and also change as a function of age t, for n age groups 4n variables need to be determined by minimizing the error between (1) and the experimental data. In order to reduce the number of variables, stiffening of the intramural constituents was represented by an exponential function of the form Ae^B·t + C, which reduced the number of stiffening parameters to be determined by minimization to 12 irrespective of the number of age groups, and provided a continuous description with respect to age t.

2.3 Statistical analysis

Ranges of mechanical properties for each age group were determined by calculating 25^th and 75^th percentiles for Cauchy stress-stretch responses using prctile function of MATLAB. Coefficient of determination R² was used to assess how well the model described arterial stress-stretch responses. All loading protocols that were used to characterize arterial behavior across all age groups were combined into two long vectors representing longitudinal and circumferential Cauchy stresses. Cumulative coefficients $R_z^2$ and $R_{\theta }^2$ were then calculated to assess the overall fit quality in longitudinal and circumferential directions for all ages and all loading protocols. Two-sample two-tailed pair-wise t-tests were performed with ttest2 function of MATLAB with statistical significance set at p<0.05 to assess differences between subjects with and without DM, as well as to assess differences between age groups. Analysis was performed by aggregating all samples into long arrays, and comparing these arrays rather than the reduced mean values obtained for each age group. Pearson linear correlation coefficient r was calculated using the corr function of MATLAB to assess strength of linear correlation between variables. The hypothesis of no correlation was tested against the alternative that there is a nonzero correlation assuming statistical significance at p<0.05.

3. RESULTS

3.1 Morphometric parameters and residual stretches

Morphometric parameters for subjects with and without DM are presented in Table 1. Mean values and standard deviations for the internal diameter (d), wall thickness (h), circumferential (α) and longitudinal (β) opening angles, and longitudinal pre-stretch (λ_z) are provided for each age group along with mean age and the number of specimens in the group that was used to derive morphometric values. Note that our database had only one subject with DM younger than 31 years, and only 4 subjects younger than 41 years of age. Note too that DM status was not clear for several subjects, therefore the sum of DM and non-DM specimens not always equaled to the number of total specimens analyzed. For reference, males accounted for 59% of the youngest age group, 90–94% of the 21–30-year-old and 61–70-year-old groups, and 73–75% of 31–60-year-old subjects.

When all specimens were considered together irrespective of DM status, FPA diameter (r=0.30), wall thickness (r=0.33), and both α (r=0.21) and β (r=0.75) opening angles increased with age (p<0.01), while longitudinal pre-stretch λ_z (r=−0.76) reduced (p<0.01). The same results were observed for subjects without DM; however FPAs affected by DM demonstrated somewhat different trends. Wall thickness (r=0.23) and longitudinal opening angle β (r=0.54) still increased with age (p=0.01 and p<0.01 respectively), and pre-stretch λ_z (r=−0.42) reduced (p<0.01), although correlation was weaker. However, diameter (r=0.10) and circumferential opening angle α (r=0.08) demonstrated no correlation with age (p=0.23, p=0.35 respectively) for diabetic FPAs.

Two-sample t-test performed for 41–80-year-old subjects with and without DM analyzed by age groups showed no difference in terms of diameter (p=0.13–0.35), wall thickness (p=0.52–0.70), or longitudinal opening angle β (p=0.36–0.72). Differences between DM and non-DM subjects were observed in terms of circumferential opening angle α in 41–50-year-old (p<0.01) and 61–70-year-old groups (p=0.02). Longitudinal pre-stretch was different in 51–60-year-old subjects with and without DM (p=0.02).

3.2 Arterial stiffening due to aging

A total of n=573 samples had an R_θ,z² > 0.9 after non-parametric bootstrap, and were used to generate stress-controlled loading protocols for all subjects together irrespective of their DM status. These protocols were then used to generate material responses representing the “average” sample in each age group by 4 averaging stretches for each given level of Cauchy stress[12]. Numbers of specimens per age group that were used to generate stress-stretch curves along with mean age of the group, and constitutive parameters are presented in Table 2.

Table 2.

Constitutive parameters for all FPAs. N is sample size per age group that was used to derive these parameters.

Age group, years	n	Mean age, years	Cgr (kPa)	$C_1^{el}$ (kPa)	$C_2^{el}$	$C_2^{\mathit{smc}}$ (kPa)	$C_2^{\mathit{smc}}$	$C_1^{\mathit{col}}$ (kPa)	$C_2^{\mathit{col}}$	γ (°)
11–20	34	16.5	10.59	21.05	0.21	2.94	2.20	3.83	2.08	60.95
21–30	31	24.8	14.02	15.86	0.49	4.52	4.17	2.52	4.06	55.49
31–40	56	35.7	11.57	17.07	0.91	4.86	3.72	1.96	4.90	57.38
41–50	73	46.8	13.20	17.69	1.98	7.93	7.82	2.32	10.11	49.22
51–60	174	56.1	13.48	20.35	4.09	12.21	11.56	3.55	15.39	47.81
61–70	162	65.0	7.31	23.90	5.76	14.21	12.94	5.23	21.35	46.64
71–80	43	75.7	6.88	33.28	11.59	32.71	15.24	8.87	34.32	44.96

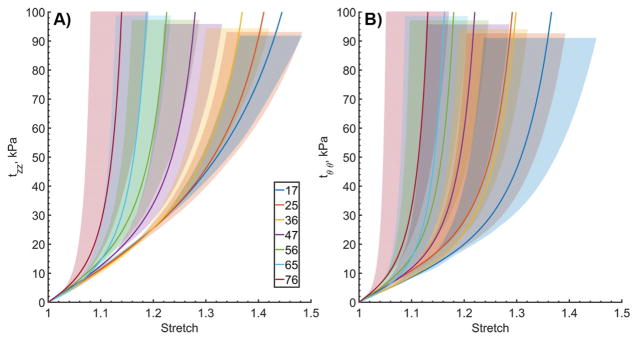
Ranges of mechanical responses for each age group are plotted in Figure 1. For clarity only equibiaxial loading protocols are included in this figure. Panel A demonstrates longitudinal Cauchy stress – stretch responses, while panel B represents them for the circumferential direction. Solid lines plot mean responses for each age group, while shaded areas bound 25^th and 75^th percentiles. In both directions, significant overlap between age groups can be appreciated. Longitudinally, overlaps are present between the three youngest age groups, but arteries of subjects older than 41 years of age do not overlap with those of teenagers or subjects 21–30 years old. Similarly, 71–80-year-old arteries do not overlap with those of the 41–50-year-old or younger subjects. Circumferentially, ranges of mechanical responses are wider, and overlaps are observed between the four youngest age groups. Arteries of subjects older than 51 years do not overlap with those of the teenagers, and the oldest age group does not overlap with the arteries younger than 40 years old.

Figure 1.

Ranges of (A) longitudinal and (B) circumferential equibiaxial Cauchy stresses plotted against longitudinal and circumferential stretch in all seven age groups. Age groups are represented by different colors. Solid lines demonstrate average stress-stretch response per group, and legend summarizes average ages (years). Shaded semi-transparent regions show 25^th and 75^th percentile ranges, they have different heights for better visual representation.

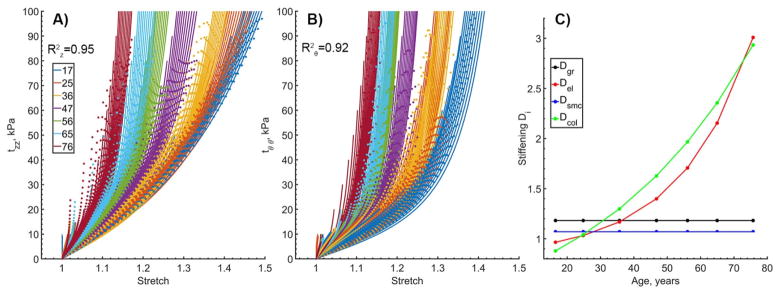
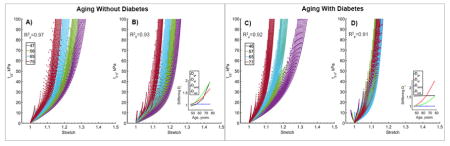
Portrayal of arterial stiffening with age using D functions is demonstrated in Figure 2. Experimental curves in both longitudinal (A) and circumferential (B) directions are provided for all 19 stress-controlled loading protocols to demonstrate the quality of fit under a wide range of loading conditions. Data for all seven age groups are plotted with solid lines, while model fit is represented by dots. The model demonstrates good fit for all age groups and all protocols with an overall $R_z^2=0.95$ and $R_{\theta }^2=0.92$ calculated cumulatively for all loading protocols. Change in stiffening functions D with age is demonstrated in Panel C. Stiffening of the ground substance and SMC attained constant values, and stiffening of the collagen was portrayed by a two-parameter exponential function. Constitutive parameters that were used to describe aging of the FPA presented in Figure 2 are summarized in the first column of Table 3.

Figure 2.

Constitutive model fits to all 19 stress-controlled loading protocols for each of the age groups. Colors represent age groups, while curves of the same color represent different loading protocols. Longitudinal (A) and circumferential (B) Cauchy stresses are plotted versus longitudinal and circumferential stretches. Data are presented with solid lines, while model fits are plotted with dotted lines. Change in the stiffening functions D with age is demonstrated in Panel C. R² values calculated for both longitudinal and circumferential directions across all ages and all protocols are provided to demonstrate the quality of fit. Average age in each group is provided in the legend. Constitutive and stiffening parameters used to generate these graphs are summarized in Table 3 first column.

Table 3.

Constitutive parameters describing aging of the femoropopliteal arteries with and without diabetes (DM)

	Aging of All specimens	Aging Without DM	Aging With DM
t, years	11–80	41–80	41–80
Elastic constitutive parameters
Cgr, kPa	10.59	13.27	12.95
$C_1^{el}$, kPa	21.05	17.36	17.46
$C_2^{el}$	0.21	2.18	1.81
$C_1^{\mathit{smc}}$, kPa	2.94	6.64	24.33
$C_2^{\mathit{smc}}$	2.20	7.17	14.79
$C_1^{\mathit{col}}$, kPa	3.83	2.02	5.15
$C_2^{\mathit{col}}$	2.08	9.48	15.94
γ, °	60.95	48.34	52.81
Stiffening functions
Dgr	1.18	0.0004e0.1042t + 0.9073	1.56
Del	0.0669e0.0460t + 0.8225	0.0191e0.050t + 0.8213	0.0541e0.0458t + 0.5222
Dsmc	1.07	1	1
Dcol	0.6283e0.0203t	0.1412e0.0322t + 0.3221	0.0056e0.0615t + 0.8855
Fit quality
$R_z^2$	0.95	0.97	0.92
$R_{\theta }^2$	0.92	0.93	0.91

Across all age groups most FPAs were more compliant longitudinally than circumferentially (p<0.01) as determined by comparing longitudinal and circumferential stretches at 100kPa equibiaxial stress. Aging produced orthotropic stiffening with faster changes occurring longitudinally than circumferentially, resulting in more isotropic behavior of older FPAs (p<0.01).

3.3 Aging of diabetic and non-diabetic arteries

In order to describe aging of diabetic and non-diabetic arteries separately, specimens from each age group were divided into those with and without DM. A total of 139 (24%) samples that had an R_θ,z² > 0.9 after non-parametric bootstrap were obtained from subjects with DM. Constitutive parameters describing FPAs with and without DM in different age groups are presented in Table 4. Note that our database had only three subjects with DM younger than 40 years of age, therefore the analysis was performed for subjects in the last four age groups, i.e. 41–80 years old.

Table 4.

Constitutive parameters for subjects with and without DM. N is sample size per group that was used to derive these parameters.

Age group, years	n	Mean age, years	Cgr, (kPa)	$C_1^{el}$ (kPa)	$C_2^{el}$	$C_1^{\mathit{smc}}$ (kPa)	$C_2^{\mathit{smc}}$	$C_1^{\mathit{col}}$ (kPa)	$C_2^{\mathit{col}}$	γ (°)
Subjects with DM
11–20	1
21–30	0
31–40	3	40.0	14.10	6.77	3.38	7.90	7.04	1.96	8.51	49.23
41–50	13	46.1	12.95	17.46	1.81	24.33	14.79	5.15	15.94	52.81
51–60	51	56.7	16.39	26.23	5.42	38.55	20.78	4.18	29.86	45.30
61–70	53	64.7	8.85	26.53	5.51	20.95	16.72	6.45	24.23	46.58
71–80	18	76.7	7.21	50.75	13.45	40.00	15.07	10.95	39.36	43.85
Subjects without DM
11–20	32	16.4	10.55	20.79	0.21	2.99	2.13	3.86	2.04	60.95
21–30	30	24.7	14.45	16.11	0.50	5.08	4.26	2.44	4.06	54.64
31–40	52	35.3	11.37	17.40	0.87	4.81	3.55	2.02	4.68	57.87
41–50	58	46.9	13.27	17.36	2.18	6.64	7.17	2.02	9.48	48.34
51–60	117	55.7	12.47	18.20	3.54	6.88	9.62	3.27	11.61	49.07
61–70	90	65.1	7.11	21.92	6.21	12.82	11.48	4.64	20.07	46.11
71–80	21	75.3	6.22	29.02	10.44	32.95	14.94	8.07	33.11	44.36

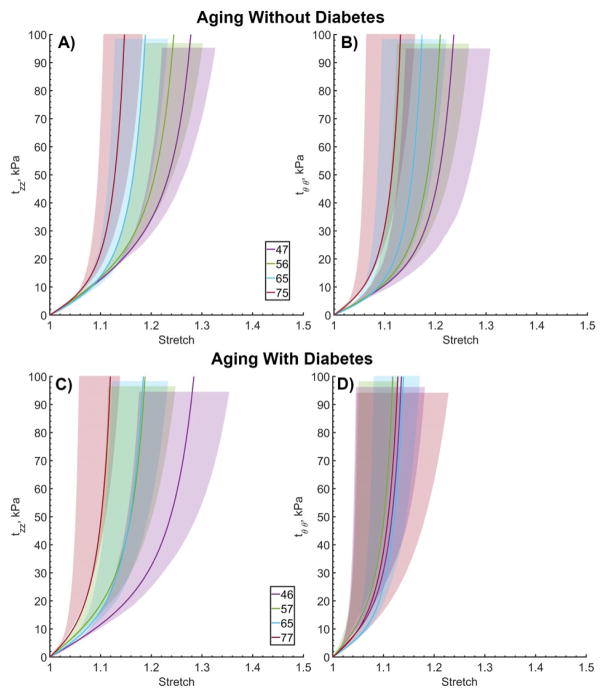
Ranges of mechanical responses for 41–80-year-old subjects without and with DM are presented in Figure 3. FPAs without DM are plotted in panels A and B, while arteries with DM are plotted in panels C and D. Solid lines represent equibiaxial mean Cauchy stress-stretch curves, while shaded areas represent 25^th and 75^th percentiles calculated for each age group. Longitudinally, arteries with and without DM were similar, with no overlap between mechanical responses of 71–80 and 41–50-year-old subjects. However, circumferentially diabetic FPAs were significantly stiffer than non-DM arteries (p<0.05). There were no statistically significant difference in circumferential stretch at 100 kPa stress between 41–50 and 71–80-year-old DM groups (p=0.91) or between 41–50-year-old diabetic FPAs and 71–80-year-old non-diabetic FPAs (p=0.90). These results indicate that in the circumferential direction, a middle-aged diabetic FPA has already acquired stiffness of an old artery.

Figure 3.

Ranges of (A, C) longitudinal and (B, D) circumferential equibiaxial Cauchy stresses plotted against longitudinal and circumferential stretch for subjects without (top) and with (bottom) diabetes. Age groups are represented by different colors. Solid lines demonstrate average stress-stretch response per group. Shaded semi-transparent regions show 25^th and 75^th percentile ranges. Legend summarizes average ages (years) in each group. Shaded regions have different heights for better visual representation.

Similarly to the results obtained for the combined sample, FPAs without DM were more compliant longitudinally than circumferentially but became more isotropic with age (p<0.01). The same occurred in FPAs with DM, but circumferential compliance did not change significantly with age and maximum circumferential stretch at 100 kPa equibiaxial stress was fluctuating around 1.13±0.01 for all age groups (Figure 4). Two-sample t-test confirmed this observation demonstrating that circumferentially diabetic FPAs were significantly stiffer than non-diabetic arteries in subjects 41–70 years old (p<0.01), but not in 71–80 year-old subjects (p=0.43). Figure 3 and Figure 5 demonstrate that circumferential stress-stretch curves of younger diabetics “cluster” around the 71–80 year old response, but that stress-stretch behavior in the oldest age group is somewhat similar to that of the FPA without DM. In the longitudinal direction, FPAs with and without DM were different in subjects 51–60 and 71–80 years old (p<0.01), but not in 41–70 or 61–70-year-old subjects (p=0.41, p=0.54), with “clustering” observed only for the 51–70-year-old FPAs.

Figure 4.

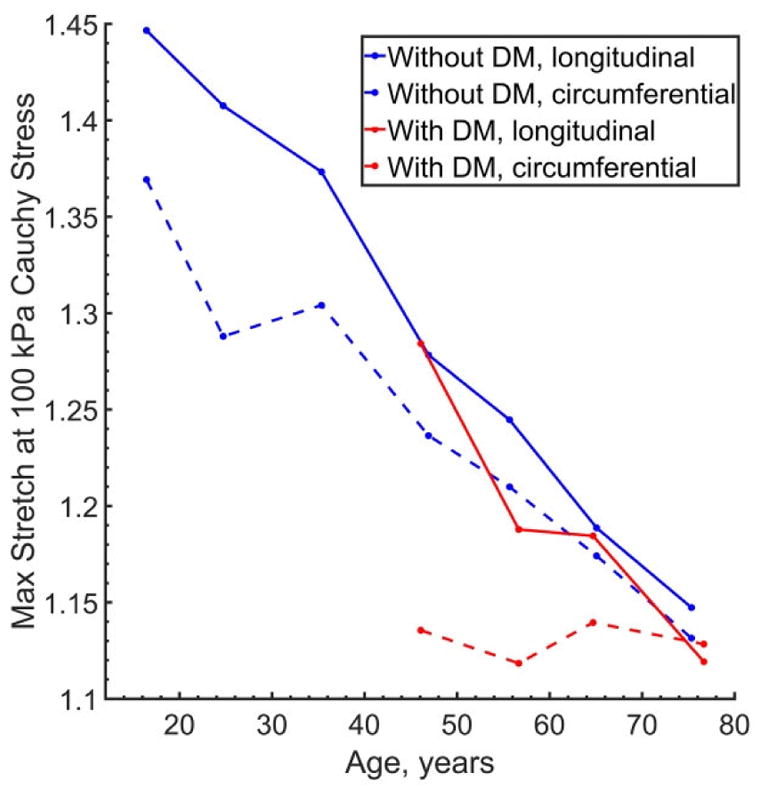
Change in maximum stretches corresponding to 100 kPa equibiaxial Cauchy stress with age for subjects with (red) and without (blue) diabetes (DM). Solid lines represent longitudinal direction, while dashed lines represent circumferential direction. Note that while FPAs stiffen in both longitudinal and circumferential directions, longitudinal stiffening occurs faster resulting in the overall more isotropic behavior of older FPAs. Note too that while longitudinal stiffening of FPAs with DM generally follows that of non-diabetic FPAs, diabetic arteries are significantly stiffer than non-diabetic arteries circumferentially even at younger ages.

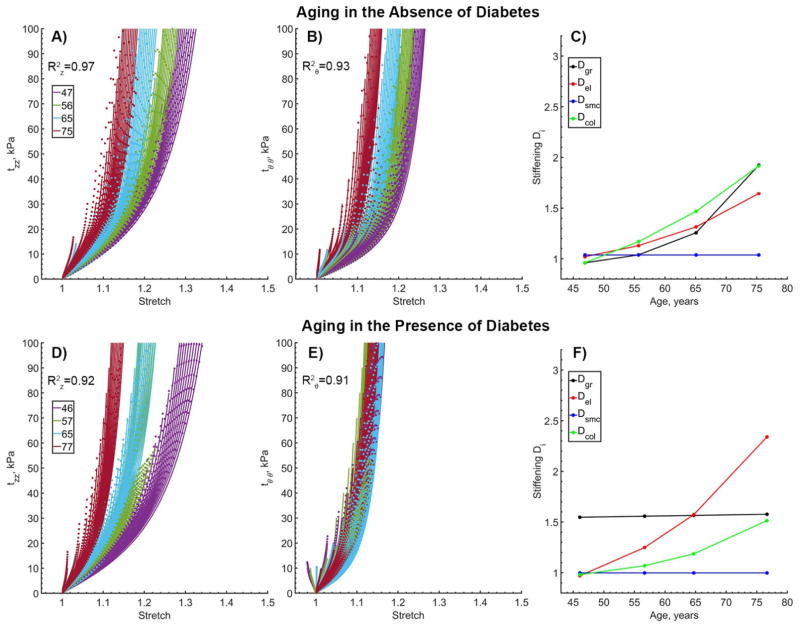
Figure 5.

Changes in longitudinal (z) and circumferential (θ) Cauchy stress – stretch relations (A,B,D,E) with age and stiffening functions (C,F) for subjects without (panels A–C) and with (panels D–F) diabetes. Model fits are presented with dotted lines while data are plotted using solid lines. Multiple curves of the same color represent different loading protocols with different loading-ratios. R² values are provided to demonstrate the quality of fit for all protocols and all age groups. Note the overall stiffer behavior of diabetic arteries in the circumferential direction and clustering of the curves around the oldest age group. Constitutive and stiffening parameters that were used to generate these graphs are summarized in Table 3, second and third columns.

Constitutive description of FPA aging without and with DM is presented in Figure 5 panels (A–C) and (D–F) respectively. In both cases the model adequately described orthotropic stiffening with $R_{z,\theta }^2>0.9$. Change in stiffening functions D with age is demonstrated in panels C and F. The graphs show no stiffening of the SMCs, but exponential stiffening of elastin and collagen with age. Stiffening of ground substance for non-diabetic FPAs also demonstrated an exponential increase, while for subjects with DM it attained a constant value of 1.56. Constitutive and stiffening parameters used to generate graphs in Figure 5 are summarized in Table 3 (2^nd and 3^rd columns).

4. DISCUSSION

Arterial stiffness is an independent predictor of mortality both in the diabetic population and in the population as a whole[6]. However, stiffening is difficult to characterize and model in a constitutive fashion, because it is a function of age and risk factors, and may affect longitudinal and circumferential directions of the artery differently. Current work introduced a straightforward approach of incorporating multiaxial stiffening into the constitutive relation describing experimentally observed changes due to aging of normal and diabetic FPAs.

The proposed method is based on incorporating exponential functions into the invariants of the right Cauchy-Green tensor to amplify the principal stretches. The advantage of using this simplified approach as opposed to say the mixture theory[14] to describe planar biaxial mechanical properties of an aging artery, is that it does not entail the change of the reference configuration or residual stresses. While these characteristics are essential when describing arterial growth and remodeling, during planar biaxial experiments performed here all residual stresses are assumed to be released by virtue of cutting the tube into a flat sheet, and reference configuration is the same for all samples. Therefore, incorporation of stiffening functions directly into the invariants to ensure zero stresses at λ_θ,z = 1 for all D is preferred.

Using stiffening functions we were able to accurately describe experimentally observed multiaxial effects of aging in both diabetic and non-diabetic populations. The constitutive model captured significantly higher longitudinal (as compared to circumferential) compliance of young FPAs that is thought to be attributed to longitudinally oriented elastic fibers in the EEL[9,10,12]. Elastin is a mechanically and chemically stable protein that is formed during the perinatal period[15]. Cyclic mechanical loads imposed by heart function and walking, coupled with deleterious biochemical influence of risk factors, accelerate degradation and fragmentation of elastin with age and result in longitudinal stiffening of the artery described here.

Interestingly, longitudinal stiffness of diabetic FPAs was changing with age similarly to that of the non-diabetic arteries, suggesting that elastin was affected to a lesser degree than other arterial constituents. Our previous study of in situ longitudinal pre-stretch[11] indirectly supports this finding by demonstrating that DM did not affect FPA pre-stretch when the analysis was done controlling for age. Crosslinks mediated by advanced glycation end-products are known to confer a high resistance to enzymatic proteolysis and a decrease in degradation rate[6], but DM is also known to enhance production of matrix metalloproteinases that stimulate breakdown of collagen and elastin[16]. Based on our results, DM does not appear to be protective of longitudinal stiffening as it is protective from abdominal aortic aneurisms[17,18], but it does not appear to accelerate longitudinal stiffening either. These results require further research to understand the characteristics of elastic fibers in diabetic FPAs.

While DM did not appear to have a significant influence on longitudinal compliance, its effects on circumferential stiffness and ability to remodel in this direction were substantial. Diabetic subjects in their forties had circumferential stiffness of a seventy-year-old artery, and their FPAs did not change their diameter or circumferential opening angle with age. This is in contrast to non-diabetic FPAs that increased their diameter, wall thickness, circumferential, and longitudinal opening angles as they aged, either to keep stresses at the homeostatic target[9,15] or to reduce them to avoid mechanical injury[12].

Mechanical properties of the FPA in the circumferential direction are likely determined by collagen and SMCs. Glycation and formation of advanced glycation end-products are known to profoundly affect arterial stiffening in a carbonyl-enriched environment[8] by causing detrimental cross-linking of collagen molecules[6]. Sugar moieties such as glucose, fructose, and glycolytic adductions, interact with the free amino acid residues of proteins, which leads to the formation of Schiff base and Amadori products[19]. In subjects with hyperglycemia, the reversible Amadori products slowly undergo rearrangements which ultimately leads to the irreversible formation of advanced glycation end-products[6] that cross-link the proteins and contribute to arterial stiffening[20].

In addition to cross-linking proteins, the abnormal metabolic state that accompanies DM causes arterial dysfunction and alters functions of endothelial and smooth muscle cells[2]. Diabetic endothelial cells are known to elaborate cytokines that decrease synthesis of new collagen by SMCs[21]. DM also impairs NO synthase activation, increases production of superoxide[6], induces SMC hypertrophy via increased production of endothelin-1[2], and stimulates their atherogenic activity, i.e. enhanced migration[22] and apoptosis[23]. All these changes render the FPA wall more susceptible to atherosclerosis that is associated with higher stiffness[2].

Finally, elevated glucose levels play an important role in transforming SMCs into osteoblast-like cells that produce medial calcification[24] quite commonly found in FPAs of PAD patients[11]. In fact, PAD patients with DM are significantly more likely to present with arterial calcification than PAD patients without DM[25]. While the molecular cues underpinning the calcification process remain elusive[26,27], the stiffening effects of calcification are quite clear. In fact, ankle-brachial index that is typically used to assess PAD severity in patients with DM can be unusually high (>1.40) because of the calcification that renders the arteries non-compressible circumferentially by a cuff[28]. Since SMCs that transfer into osteoblast-like cells are oriented primarily circumferentially in the FPA, glucose-induced calcification is likely to affect the artery in the circumferential direction as well – both in terms of stiffness and in terms of remodeling ability, i.e. the ability to change diameter and opening angle with age. This speculation is supported by the results of mechanical testing presented here.

In summary, our study was designed to develop a constitutive description of experimentally observed human FPA stiffening due to age and DM that can serve to improve our understanding of PAD pathophysiology and facilitate computational models that rely on arterial properties. As with any other study, these results should be viewed in the context of study limitations. First, the constitutive description of aging is phenomenological as is the 4-fiber-family constitutive model used to describe mechanical properties. Though the model is motivated by FPA histological structure, the sole purpose of its parameters is to provide a good fit to the experimental data, not to interpret the underlying physical phenomena. Furthermore, our goal was to allow determination of FPA mechanical properties for any given age, not to simulate arterial aging. Continuous simulation of aging requires evolution of the reference configuration and inclusion of the accumulating residual deformations which are not accounted for by a simple formulation considered here. The second limitation is related to the influence of cofounding risk factors that were not considered. While controlling for unmodifiable risk factors in patients with DM is challenging as virtually none of the senior diabetic patients are healthy, the effects of modifiable risk factors, such as smoking or large body mass index on arterial stiffness, will be considered in our future studies. Self-reported DM status and lack of distinction between diabetes types I and type II is another limitation. The two types of diabetes may have different effects on stiffness, as is the duration of the disease and its control with medications. With regards to the latter however, it is unclear whether improvement in DM control is associated with reduction in arterial stiffness, and whether pharmacologic interventions targeting glucose dysregulation are associated with improved clinical outcomes[6]. Lastly, our study did not differentiate between male and female arteries because our database included primarily male subjects (81%). Gender-specific differences in diameter and distensibility of the popliteal artery however have previously been reported[29], and need to be further investigated. While these limitations are being addressed, the provided description of FPA stiffening due to aging and DM can help improve fidelity of computational models by providing more personalized arterial properties, and can guide the development of new materials tunable to diabetic and non-diabetic arteries of different ages.