Designing 3D Selective Adiabatic Radiofrequency Pulses with Single and Parallel Transmission

Abstract

Purpose

To introduce a method of designing single and parallel transmit (pTx) three-dimensional adiabatic π pulses for inverting and refocusing spins that are insensitive to transmit B₁ (B₁⁺) inhomogeneity.

Theory and Methods

A 3D adiabatic pulse is created by replacing each piece-wise constant element (or sub-pulse) of an adiabatic full passage (AFP) by a 2D selective pulse. In this study, the parent AFP is an HS1 and each sub-pulse is a 2D pulse derived from a jinc function designed using a spiral k-trajectory. Spatial-selectivity in the third direction is achieved by blipping the slab-selective gradient between sub-pulses, yielding a rectangular slab profile identical to that of the parent AFP. The slew-rate limited sub-pulse can be undersampled utilizing pTx, thus shortening the overall pulse width. Simulations and experiments demonstrate the quality of spatial selectivity and adiabaticity achievable.

Results

The 3D adiabatic pulse inverts and refocus spins in a sharply demarcated cylindrical volume. When stepping RF amplitude, an adiabatic threshold is observed above which the flip angle remains π. Experimental results demonstrate that pTx is an effective means to significantly improve pulse performance.

Conclusion

A method of designing three-dimensional adiabatic pulses insensitive to B₁ inhomogeneity has been developed. pTx can shorten these pulses while retaining their adiabatic character.

INTRODUCTION

Frequency-modulated (FM) pulses have unique characteristics and certain advantages as compared to conventional constant-frequency amplitude-modulated (AM) pulses. By modulating both the frequency and amplitude functions independently, the duration of the radiofrequency (RF) pulse can be decoupled from its bandwidth, which, for most pulses, is dictated by the pulse time-bandwidth product or R-value. This decoupling facilitates even distribution of RF energy with respect to time by sequentially exciting, inverting, or refocusing the different spin isochromats. When using the chirp or hyperbolic secant (HS1) (1) pulse, this sequential excitation produces a transverse phase that varies quadratically along the frequency-swept direction (2,3).

FM pulses are widely used in in vivo MRS. Often, these experiments are carried out with surface coils to maximize receive sensitivity given the low concentration of metabolites. The spatial variation in flip angle due to the highly inhomogeneous transmit B₁ (B₁⁺) produced by surface coils can be overcome by sweeping the frequency in a manner that satisfies the so-called “adiabatic condition” (4,5). Specifically, the adiabatic condition requires the rate at which a magnetization vector M rotates around the effective field vector B_eff to be much greater than the rate at which B_eff changes its orientation during the pulse. Accordingly, when M is initially aligned with B_eff, M will follow B_eff during the pulse, provided the adiabatic condition is satisfied at all times. Hence, adiabatic pulses enable uniform rotations of magnetization, even with a B₁ that spatially varies by an order of magnitude or more, as long as it is above a certain threshold, making the pulse highly tolerant to extreme B₁⁺ variation.

Spatially selective adiabatic pulses are advantageous for certain niche applications. For example, they can improve the selectivity of a pencil beam excitation T₂-prep sequence (6) when replacing the non-selective adiabatic π pulses. Additionally, three-dimensional (3D) adiabatic pulses can be used to enable reduced field of view (FOV) image acquisition with improved time-efficiency, spatial resolution or both. They can also be used to enhance navigator signals by selectively targeting a specific organ, thus generating high fidelity navigator signals that specifically originate from the moving organ. Furthermore, their high tolerance to inhomogeneous transmit B₁⁺ makes them attractive for application at high fields, where B₁⁺ inhomogeneity is more pronounced.

Two-dimensional (2D) selective adiabatic pulses have been introduced by Conolly and colleagues, where selective inversion of an infinitely long cuboid is accomplished by sampling k-space with amplitude modulation in one orthogonal direction and frequency modulation in another (7). Although suited to be used for certain organs such as the diaphragm, these 2D pulses are not suitable for organs such as the heart, which require 3D selectivity.

Parallel transmission (pTx) (8–10) integrates the transmit B₁⁺ profiles of multiple transmitters into the RF pulse design process, providing the pulse designer extra degrees of freedom. This results in distinct RF waveforms that are independently dispatched through multiple coils. By exploiting the unique spatial B₁⁺ profile provided by each coil, undersampling of excitation k-space is permitted, analogous to parallel imaging. This provides a means to decrease the pulse duration of conventional multidimensional RF pulses, which are inherently long due to the limited gradient capability and expanded k-space range that must be traversed compared to one-dimensional (1D) RF pulses. Moreover, this accelerated selective excitation is also beneficial in reducing the sensitivity to static field (B₀) inhomogeneity.

In this work, we 1) introduce a new method of designing 3D adiabatic pulses based on a sub-pulse approach, 2) demonstrate the feasibility of such 3D adiabatic pulses at 4T in both phantom and human studies, and 3) demonstrate the compatibility of the proposed method with pTx at 7T through phantom studies. Our pTx results show that when combined with 2D pTx pulse design, the proposed method can maintain 3D selectivity while either shortening the total pulse duration or eliminating unwanted sidebands in the imaging FOV. To the best of our knowledge, this is the first demonstration of 3D adiabatic pulses using both single transmit (1Tx) and pTx.

THEORY

Parent Pulse Design

The basic approach in designing 3D adiabatic pulses is to selectively excite in two-dimensions using a sequence of 2D sub-pulses and to modulate the amplitude and phases of these consecutive 2D sub-pulses in accordance with some choice of “parent” adiabatic pulse. In this work, to ensure that the adiabatic condition is equally satisfied for all Larmor frequencies in the sweep range, the parent pulse is chosen from the class of adiabatic pulses possessing offset-independent adiabaticity (OIA) (4,5). Accordingly, by evenly distributing RF energy with respect to time, adiabatic full passage (AFP) occurs and the longitudinal magnetization is inverted from M_z to −M_z. Perhaps the most well-known pulse that can drive the adiabaticity based on the OIA principle is the hyperbolic secant pulse (1). The pulse function of the HS1 in complex form is given by

$${\omega }_1^{\text{HS}1}(t)={\omega }_1^{max}\text{sech}(\beta \tau )e^{i\mu (ln(\text{sech}\beta \tau ))}$$ [1]

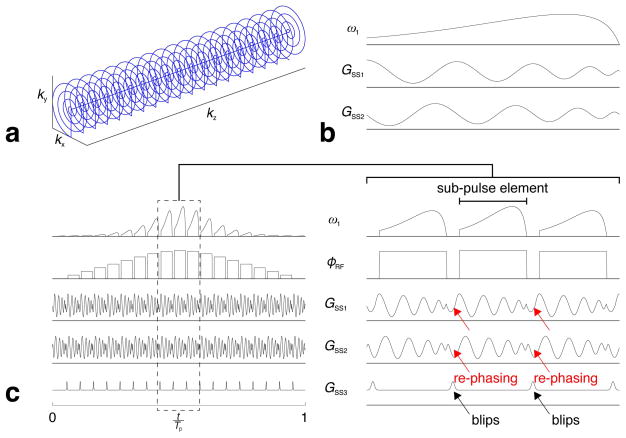
where ${\omega }_1^{max}$ is maximum RF amplitude (rad/s), τ = 2t/T_p − 1 is a normalized time parameter with respect to pulse length T_p spanning the range [−1, 1], and β and μ are real constants. The modulation functions of the continuous version of HS1, when applied in the presence of a constant gradient, are shown in Fig. 1a.

Figure 1.

RF amplitude (ω₁), phase (ϕ_RF), and gradient (G_ss) functions of the (a) continuous and (b) blipped HS1 adiabatic pulse. The peak RF amplitude is higher for the 3D HS1 than for the blipped HS1 to keep the same area (and adiabaticity) for both. An infinite number of aliasing sidebands are produced with the blipped HS1, whereas the continuous HS1 pulse produces only a baseband in frequency space.

In practice, to rotate magnetization adiabatically, the parent pulse is discretized by applying an RF pulse train composed of samples of the continuous form during a continuous gradient. The gradient can also be discretized by replacing the continuous gradient with gradient blips inserted between each piece-wise constant segment (11). An example of such discretization for an HS1 is shown Fig. 1b. The latter pulse is referred to as the “blipped HS1”. Unlike the continuous case, the blipped version produces an infinite number of aliasing sidebands due to the time domain parent pulse being multiplied by a Dirac comb function in the discretization process, which is equivalent to convolution in the reciprocal domain. For a Dirac comb with spacing Δt = T_p/N_seg, where N_seg is the total number of sampled segments, the Nyquist criterion is given by

$$N_{\text{seg}}\ge N_{\text{Nyq}}=bw·T_{\mathrm{p}}=R$$ [2]

where N_Nyq is the minimum number of samples required to avoid aliasing and bw is the bandwidth of the pulse.

Designing Three-dimensional Adiabatic Pulses

The key idea in designing 3D adiabatic pulses is to replace the non-selective hard pulse elements of the blipped HS1 with 2D selective ones, thereby increasing the selectivity from one dimension to three dimensions. For the purpose of the present demonstration, we create a 3D adiabatic pulse by combining an HS1 parent pulse (Fig. 1b) with a number of sub-pulses derived from a jinc function based on a fully sampled 2D spiral k-trajectory (12) (Fig. 2b). First, the parent adiabatic pulse is discretized and sufficiently oversampled, followed by each piece-wise constant pulse segment being binned for the sub-pulse elements. Within each bin, a sufficiently sampled sub-pulse is placed and complex multiplied by the corresponding parent pulse segment. This is equivalent to modulating the amplitudes of consecutive sub-pulse elements by the parent amplitude function and adding the parent and sub-pulse phases (Fig. 2c). To re-center k-space for the subsequent sub-pulse element, re-phasing gradients are inserted between the sub-pulses to nullify the area accrued under the gradients during the previous sub-pulse element (Fig. 2c). The result is a 2D adiabatic pulse that is able to selectively invert or refocus spins within an infinitely long cylinder. Slab selectivity is provided by the gradient blips along the slice/slab direction between sub-pulse elements as in the blipped HS1. As a result, the final 3D pulse can be used to invert or refocus magnetization within a cylinder of finite height.

Figure 2.

(a) The k-space trajectory of the 3D adiabatic pulse. (b) RF amplitude (ω₁) and gradient (G_SS1 and G_SS2) functions of the sub-pulses from which the 3D adiabatic pulse is constructed. Each sub-pulse is a 2D jinc that traverses k-space on a 3.5-turn spiral. (c) The full 3D adiabatic pulse (left) and an expanded view of 3 of the 19 sub-pulse elements (right). The envelop of the 3D adiabatic pulse is based on HS1 using R = 9.5, whereby the amplitudes of consecutive sub-pulses are modulated by the parent amplitude function, and the parent and sub-pulse phases are added. Re-phasing gradients are inserted between sub-pulses to nullify the gradient area accrued and re-center k-space. Gradient blips applied in the remaining orthogonal direction (G_SS3) shifts each spiral k-space trajectory in that direction to achieve full 3D volume localization. A total pulse duration of T_p = 23 ms was used in simulations and experiments.

From a k-space perspective, this 3D pulse traverses a 3D k-trajectory composed of N_seg identical 2D spiral trajectories cascaded in the third dimension with equal spacing. In choosing a trajectory for the sub-pulse, other trajectories such as a raster trajectory can also be used. The 2D trajectory chosen defines basic properties such as resolution and FOV, while RF weighting determines excitation profile. A 3D adiabatic pulse designed based on this trajectory (Fig. 2a) and used throughout this study is shown in Fig. 2c. Note that this 3D adiabatic pulse reduces to a 2D adiabatic pulse of Conolly et al (7) when the 2D sub-pulses are replaced by 1D slice selective sub-pulses.

The proposed 3D adiabatic pulse design is fully compatible with pTx as long as the sub-pulse is designed according to the linear low-tip-approximation (13). Design of pTx 3D adiabatic pulses is straightforward and is done by simply replacing the 1Tx 2D sub-pulses with pTx 2D sub-pulses. With pTx, shorter 2D sub-pulses can be designed without compromising 2D selectivity. Using these shorter pTx sub-pulses to generate the 3D adiabatic pulse can increase RF performance in terms of bandwidth and sideband separation; for a given number of sub-pulse segments N_seg, using shorter pTx sub-pulses reduces the total pulse length, thereby increasing the bandwidth; for a given total pulse length, shorter pTx sub-pulses allow increased sampling of the parent pulse, thereby pushing the sidebands further away in space.

Imaging Sequences for Evaluating the 3D Adiabatic π Pulse

One way to measure the slice profile(s) produced by a π pulse entails subtracting signals measured in two separate experiments, whereby in just one of the two experiments, the inversion pulse is applied prior to the excitation pulse (Supporting Fig. S1a). An alternative rapid method is through a spin-echo sequence, where the π pulse is used for spatially-selective refocusing following a non-selective excitation pulse. Of note, when using an odd number of adiabatic π pulses (Supporting Fig. S1b), the different isochromats in the direction of the blipped frequency sweep experience different echo times (TE) due to the spatiotemporal dependence of the π rotation produced by the pulse. When applying an even number of π pulses (Supporting Fig. S1c), the spatially quadratic phase along the frequency sweep direction is eliminated and all spins experience the same net amount of evolution before and after the π pulses. This enables all isochromats within the spatially selective volume to experience an identical TE, with the added advantage of balancing any gradient imperfections. To ensure that the acquired signals originated exclusively as a spin-echo coherence, half sine crusher gradients are placed before and after the 3D refocusing pulses, while for double echoes, the crusher amplitudes of the first and second refocusing pulses are applied with different strength to avoid any undesired stimulated echoes.

METHODS

3D Adiabatic Pulse Design with 1Tx

The proposed 3D adiabatic pulse design was first evaluated in the context of single transmit by validating the principles through both simulations and experiments. Simulations were carried out using an in-house Bloch simulator programmed in C language and interfaced with MATLAB (MathWorks, Inc., Natick, Massachusetts, USA). The 3D adiabatic pulse was constructed from 19 sub-pulses, each of which was a jinc weighted 2D pulse (256 time steps) obtained by sampling k-space on a 3.5-turn spiral trajectory. Sampling radius, k_r,max, was 0.14 cycles/cm, resulting in a spatial resolution of 3.5 cm in the radial direction. The parent HS1 pulse used to define the amplitudes and phases of the jinc sub-pulses had a time-bandwidth product of R = 9.5 (Figure 2). The total pulse duration was T_p = 23 ms. The resulting M_z profiles were obtained from a 48×48×48 single isochromat matrix. Peak RF power was linearly swept to confirm spatially selective inversion and adiabaticity.

Pulse bandwidth evaluation was carried out by stepping an offset frequency, such as one that occurs due to chemical shift, δ. Relative specific absorption rates (SAR) were estimated by taking the time integral of B₁(t)-squared, with peak B₁ scaled to produce 95% inversion (M_z = −0.9M₀). To verify its use as a 3D refocusing pulse, four separate simulations of the single spin-echo sequence were generated and summed using EXORCYCLE phase cycling (14). It was confirmed that the resulting transverse magnetization after selective refocusing was identical to the profile attained after selective inversion of the initial magnetization.

To demonstrate the feasibility of the proposed 3D adiabatic pulses, we conducted phantom and human experiments on a Varian DirectDrive^™ console (Agilent Technologies, Santa Clara, CA) interfaced to a 90 cm 4T magnet (Oxford Magnet Technlology, Oxfordshire, UK) and a clinical gradient system (model SC72, Siemens, Erlangen, Germany). All experiments used a 16-element transverse electromagnetic (TEM) head coil (15) for RF transmission and reception. For phantom experiments, the same pulse verified through simulations was used as a refocusing π pulse in a double spin echo sequence on a cylindrical water phantom doped with 1.5% agar and 0.1 mM Gd (T₁ ~ 1 s and T₂ ~ 160 ms). The gradients, which were well within the gradient slew-rate constraint, were measured (16) and fine-tuned for all three directions. Although the spiral gradients showed minimum distortion, the gradient blips along the slab/slice direction exhibited a prolonged undershoot that leaked into the subsequent sub-pulse. To compensate for this, a gradient corrected parent HS1 pulse was regenerated, which was then used to construct a gradient corrected 3D pulse.

Images of the human brain from healthy volunteers were obtained under a protocol approved by our institution’s IRB. Double spin-echo images using 3D adiabatic π pulses and standard spin-echo images with identical sequence parameters were obtained for comparison.

3D Adiabatic Pulse Design with pTx

pTx 3D adiabatic pulses were designed and experimentally verified. To demonstrate the improvements afforded by such pTx 3D adiabatic pulses, phantom experiments were carried out on a Siemens MAGNETOM system (90 cm 7T actively shielded magnet with clinical whole body gradients) capable of receiving 32 channels and transmitting through two modes: 1) 1Tx mode using a single transmit channel driven by a combined 8 kW RF power amplifier, and 2) pTx mode using 16 transmit channels, each powered by a 1 kW RF amplifier. In conducting the experiments, pTx mode data were acquired using an 8 channel transmit, 32 channel receive (Nova 8Tx32Rx) head coil (Nova Medical, Wilmington, MA), while 1Tx mode data were acquired using a single channel transmit, 32 channel receive (Nova 1Tx32Rx) head coil for comparison. All data were acquired on a spherical phantom.

A pTx 2D sub-pulse which targeted a circular in-plane pattern was designed (17) based on the B₁⁺ profile of 8 transmit channels. Specifically, it was designed using a spiral k-trajectory with half the number of turns used in the fully sampled trajectory (Supporting Fig. S2), thus undersampling by half along the radial direction. The 8 B₁⁺ maps of the Nova 8Tx32Rx coil were obtained (Supporting Fig. S2) within a transverse slice using a hybrid B₁⁺ mapping method (17). The target pattern was manually drawn and positioned at the center of the transverse slice. The pulse design problem was formulated in the image domain (10) as a least squares minimization and was solved using conjugate gradient iterations. The 8 distinct pTx sub-pulses generated were used to design 8 distinct 3D pulses driven adiabatically by their respective parent HS1 pulse, which were then applied to each coil element in parallel to produce pTx adiabatic π rotation. Two pTx 3D adiabatic pulses, one using the same number of sub-pulse segments (i.e. N_seg = 19), thereby reducing the total pulse length by nearly half (T_p = 14 vs 24 ms), and another using the same total pulse duration but twice the segments (i.e. N_seg = 38), were designed.

To demonstrate the benefit of designing pulses with pTx, different 1Tx mode 3D pulses were generated for comparison. These were: 1) A baseline pulse nearly identical to the one used in the 4T studies. Due to the different gradient specifications of the 7T system, the originally used k-trajectory required some sampling adjustments, resulting in a slightly longer pulse (T_p = 24 vs 23 ms). 2) A pulse designed using the same number of sub-pulse segments as the baseline pulse (i.e. N_seg = 19), but with jinc-derived sub-pulses created from the undersampled spiral trajectory used in pTx (T_p = 14 ms). 3) A pulse designed with twice the number of sub-pulse segments of the baseline pulse (i.e. N_seg = 38) while maintaining pulse length (T_p = 24 ms) by using the same undersampled jinc-derived sub-pulses as above.

The inversion patterns of the five 3D adiabatic pulses (two pTx pulses and three 1Tx pulses) were evaluated by acquiring inversion-recovery (IR) GRE images with matched imaging parameters. In all experiments, second order B₀ shimming was performed prior to image acquisition to minimize off-resonance effects within a 6 cm thick slab encompassing the 4 cm thick slab inversion.

RESULTS

3D Adiabatic Pulse Design with 1Tx

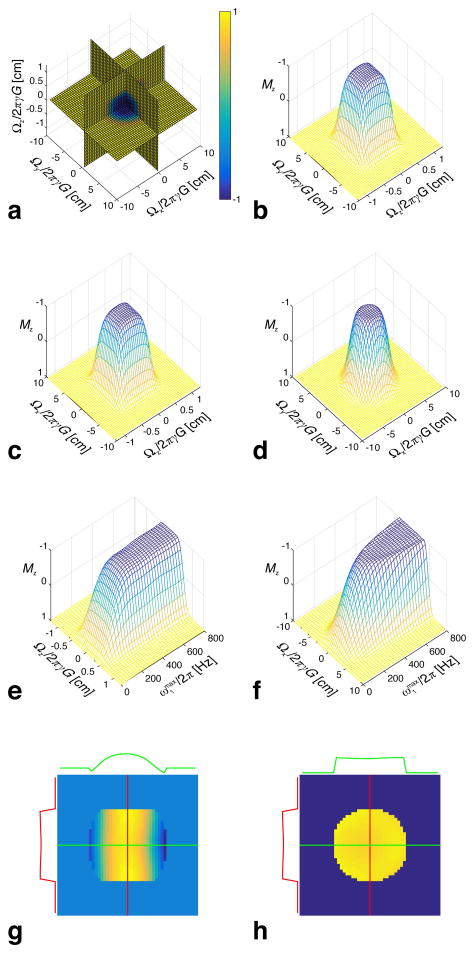
The volumetric slice image and inversion profiles along the axial (Ω_x-Ω_y), coronal (Ω_x-Ω_z), and sagittal (Ω_y-Ω_z) planes are shown in Figs. 3a–d. In the axial view, a circular shape is selectively inverted, whereas orthogonal to it in the z direction, a rectangular shape is inverted as can be seen in the coronal and sagittal views. Thus, the 3D pulse selectively inverts a cylinder of finite height.

Figure 3.

(a) Volumetric slice plot and inversion profiles along the (b) Ω_y-Ω_z plane, (c) Ω_x-Ω_z plane, and (d) Ω_x-Ω_y plane obtained from Bloch simulations using the pulse in Fig. 2 exhibits inversion of a cylinder with finite height. Sweeping the RF amplitude ( ${\omega }_1^{max}$)

and plotting the trace of M_z through the center for various offset frequencies along both the (e) Ω_z-direction and (f) Ω_x-direction exhibit both a linear and adiabatic regime. Phase profile in the sagittal (g) and axial (h) planes show a flat profile within the circular inversion region, while a quadratic profile produced by the parent HS1 is exhibited along the frequency sweep direction.

When sweeping the RF amplitude ( ${\omega }_1^{max}$) and plotting the trace of M_z through the center for various offset frequencies along both the radial (Ω_x) and height (Ω_z) directions, several properties are revealed. Namely, in the Ω_z direction (Fig. 3e), a linear regime ( ${\omega }_1^{max}/2\pi =0~250\text{Hz}$) as well as an adiabatic regime ( ${\omega }_1^{max}/2\pi \ge 325\text{Hz}$) are observed, similar to the profile produced by the blipped HS1. In the Ω_x direction (Fig. 3f), similar linear and adiabatic regimes are observed; however, the profile along the radial direction increases and flattens out as ${\omega }_1^{max}$ increases. The latter is a consequence of the cone-shaped excitation profile generated by the low resolution sub-pulse. Since the center of the cone achieves adiabaticity first and the outer radius achieves adiabaticity later, the radial profile eventually flattens out as ${\omega }_1^{max}$ is increased.

Bandwidth was assessed independently along both the height (Ω_z) and radial (Ω_r) directions. Within each direction, both the spatial and spectral bandwidths were evaluated by obtaining the inversion profiles for varying offset frequency. The spatial bandwidths were determined based on the blipped gradients in the height direction and the maximum spiral gradient amplitude in the radial direction. The results are displayed in Fig. 4. For comparison, the bandwidth along the height direction was analyzed for the continuous HS1 (Fig. 1a), blipped HS1 (Fig. 1b), and 3D adiabatic pulse (Fig. 2c) along the height dimension. As expected, spatial displacement due to the off-resonance sensitivity (Δx = δ/bw · thk ) for the continuous HS1 (Fig. 4a) is linear with respect to offset frequency, where Δx is the spatial displacement of inversion thickness thk produced by a pulse of bandwidth bw for an offset δ. Spatial displacement equivalent to the inversion thickness occurs at an off-resonance equal to the pulse bw (= 488 Hz). For the blipped HS1 pulse (Fig. 4b), aliasing sidebands are present and shift together with the baseband in the same linear manner with respect to the offset frequency. However, the inversion profile falls off according to a sinc modulation as the offset is increased, which stems from the hard sub-pulse elements. The offset frequency at which inversion falls to half maximum occurs at δ = ±625 Hz. Similarly, along the height dimension of the 3D adiabatic pulse (Fig. 4c), the inversion profile shows linear displacement with chemical shift and an additional modulation along the chemical shift dimension with a Gaussian-like profile dropping off to half maximum at δ = ±725 Hz.

Figure 4.

Simulation results depicting inversion profile dependency on frequency offset in the spatial (Ω) and chemical shift (δ) dimensions, for (a) continuous HS1, (b) blipped HS1, and 3D adiabatic pulse along the height (c) and radial (d) directions. Spatial displacement is a linear function of frequency offset, and aliasing sidebands modulated by a (b) sinc function are present in the chemical-shift dimension of the blipped HS1. Along the height direction (c), Gaussian-like modulation is present in the chemical-shift dimension of the 3D adiabatic pulse. Frequency offset in the radial direction (Ω_r) (d) show no spatial aliasing sidebands within the frequency range considered, whereas aliasing sidebands do occur in the chemical-shift dimension.

The spatial bandwidths along both the Ω_x and Ω_y (radial) directions are dictated by the bandwidth of the 2D jinc pulse assuming a gradient corresponding to the maximum amplitude of the spiral gradients, and are the same due to radial symmetry. The spatial bandwidth along the Ω_z (height) direction is dictated by the frequency sweep range of the parent HS1. Spatial bandwidth and spectral bandwidth were evaluated by assessing the inversion profiles for varying offset frequency in each direction. Within the frequency range considered, there are no spatial aliasing sidebands in the radial direction (radial sidebands appear at 45 kHz, equivalent to 20 cm from the center in spatial coordinates). However, aliasing occurs in the off-resonance direction with the baseband profile falling to half maximum at δ = ±233 Hz (Fig. 4d). For all pulses, the bandwidths in the spatial directions were extracted based on full width half maximum (FWHM) criteria at δ = 0, while the spectral bandwidth was extracted using FWHM at Ω_z,Ω_r = 0. In the Ω_z direction, both the spatial and spectral bandwidths were approximately equal to the bandwidth of the pulse. However, in the spectral dimension, both the blipped HS1 (Fig. 4b) and 3D adiabatic HS1 pulse (Fig. 4c) showed ~5% lower bandwidth compared to the continuous HS1 (Fig. 4a). This is explained by the extra sinc and Gaussian-like modulation, respectively, as offset frequency increases. In the Ω_r direction, the spectral bandwidth agreed with the pulse bandwidth. However, the spatial bandwidth created by the spiral gradients was much greater. These results are listed in Table 1.

Table 1.

	${\omega }_1^{max}/2\pi$ 1	SAR2	spatial-bw (Hz/γG)	δ-bw (Hz)
continuous HS1	185	1.12	1	488
blipped HS1	175	1	0.98	466
3D adiabatic (Ωz)3	270	1.14	0.98	460
3D adiabatic (Ωr)4	270	1.14	6.85	466

¹Peak RF power needed for 95% inversion (M_z = −0.9M₀)

²Calculations taken from the time integral of B₁(t)-squared is reported relative to blipped HS1

³along the height direction

⁴along the radial direction

A bandwidth comparison was carried out for the fully sampled pulse and pTx. Along the height direction, like the fully sampled pulse, the pTx pulse exhibits the same linear dependence on offset frequency and has a Gaussian-like profile as a function of offset frequency. Also, like the fully sampled pulse, along the radial direction, the spatial bandwidth of the pTx pulse is much greater than the spectral bandwidth. However, the bandwidths in both spatial and spectral dimensions are approximately twofold greater than those of the fully sampled pulse, which is due to the twofold decrease in pulse length for the same R-value (= 9.5). Likewise, along the radial direction, no spatial aliasing sidebands were observed within the frequency range considered, while aliasing sidebands occurred in the spectral offset direction. The bandwidths in both the spatial and spectral dimensions are also approximately twofold greater due to the same reason.

As compared to the blipped HS1 pulse (Fig. 1b), the peak B₁ needed for 95% inversion (M_z = −0.9M₀) was greater for the continuous HS1 (Fig. 1a), which can be explained by the sharper inversion profile it produces. The greater peak B₁ of the 3D adiabatic pulse relative to the blipped HS1 pulse, which is due to the smaller area of the jinc modulation function, is directly proportional to the area ratio between the constant hard pulse element and the jinc modulation element ( ${[{\omega }_1^{max}]}_{\text{jinc}}={[{\omega }_1^{max}·\text{area}]}_{\text{hard}}/{[\text{area}]}_{\text{jinc}}$). Based on this, the relative SAR with respect to the blipped HS1 pulse calculated by taking the time integral of B₁(t)-squared was 112% for the continuous HS1 pulse and 114% for the 3D adiabatic pulse. The relative SAR for pTx mode was 1.5 times greater with respect to the circularly polarized (CP) mode, with a peak ${\omega }_1^{max}/2\pi$ of 35 Hz for each coil operating in CP mode and an average of 119 Hz for each coil operating in pTx mode. This reflects the twofold increase in bandwidth of the pTx pulses.

Results of the phantom experiment are shown in Figure 5. The axial, sagittal, and coronal views (Figs. 5a–c) of the phantom were obtained from a double spin-echo sequence using an adiabatic half passage (AHP) for excitation and adiabatic full passage for slice refocusing. The corresponding views obtained with the double spin-echo sequence using 3D selective refocusing (Figs. 5d–f) reveal a cylindrical volume, agreeing well with simulation results (Figs. 5g–i). Overlaying the trace plots of Figs. 5a,b (green) and Figs. 5d,e (red) shows the excellent spatial selectivity of this π pulse. The experimental 3D profiles appear slightly sharper as compared to the simulation results due to the image being obtained from a double spin-echo scheme, whereas the simulation shown is the inversion profile following application of a single pulse. Spatial selectivity profiles along the radial and height directions were also obtained for various RF amplitudes (Fig. 5j,k). In agreement with simulation results, the radial profile increases and flattens out as ${\omega }_1^{max}$ increases and the profile along the height direction resembles that of an HS1.

Figure 5.

(a) Axial, (b) sagittal, and (c) coronal views of the phantom used. Compared with corresponding views (d–f) acquired using the double-spin echo sequence clearly shows selective refocusing of a cylinder with finite height, in good agreement with simulation results (g–i). Experimental results exhibit slightly better selectivity than simulation results due to being obtained with a double-echo sequence. Refocusing profile along the radial (j) and height (k) direction for various ${\omega }_1^{max}$ demonstrates adiabatic property.

In vivo images of the human brain are shown in Figure 6. Fig. 6a and Fig. 6c are the axial and coronal views acquired from double spin-echo (FOV = 256 × 256 × 256 mm, matrix size = 128 × 64 × 64) using 3D selective adiabatic refocusing. Minimum TE (limited by SAR constraints) was used. Comparing with standard spin-echo images (Figs. 6b,d) acquired using identical sequence parameters (TE = 70 ms, TR = 1 s) clearly shows selective refocusing of a finite height cylindrical volume encapsulating the ventricles. The curved profile along the frequency direction of the coronal view is due to B₀ inhomogeneity. This was verified by switching the direction of the frequency sweep, which flipped the downward curvature of the original profile upwards. This can be mitigated by increasing the bandwidth of the parent pulse. Linear traces taken along the horizontal (green) and vertical (red) axes show no π-refocusing beyond the radius of inversion in the axial view, while sidebands, marked by gold dashed lines in Fig. 6c, emerged along the frequency sweep direction in the coronal view. In both coronal views (Figs. 6c,d), flow artifacts are present due to absence of flow compensation during acquisition.

Figure 6.

(a) Axial and (c) coronal views acquired from double spin-echo (FOV = 256 × 256 × 256 mm, matrix size = 128 × 64 × 64) using 3D selective adiabatic refocusing. Comparing with standard axial (b) and coronal (d) spin-echo images acquired from identical sequence parameters (TE = 70 ms, TR = 1 s) shows selective refocusing of a finite height cylindrical volume encapsulating the ventricles. The curved profile along the frequency direction of the coronal view is due to B₀ inhomogeneity. Linear traces taken along the horizontal (green) and vertical (red) axes are shown for comparison. Sidebands appear along the frequency sweep direction marked by the gold dashed line (c). Flow artifacts are present due to absence of flow compensation during acquisition.

3D Adiabatic Pulse Design with pTx

Figure 7 demonstrates the advantages of using pTx 3D adiabatic pulses over its single transmit counterpart. While retaining its circular in-plane inversion fidelity (Fig. 7a vs c), the pTx 3D pulse designed with the same pulse length but twice the segments, was able to eliminate the undesired sidebands observed in the single transmit baseline pulse within the imaging FOV (Fig. 7f vs h). Likewise, the pTx 3D pulse designed with the same number of segments (and thus reduced pulse length), also preserved its circular in-plane inversion fidelity (Fig. 7a vs e). In contrast, both 1Tx 3D pulse counterparts produced an in-plane inversion pattern contaminated by undesired radial aliasing (Fig. 7a vs b and d). Further, this experimentally observed in-plane aliasing agreed well with the corresponding Bloch simulation results provided in the online supplemental materials.

Figure 7.

Parallel transmission experimental results. The spiral trajectory of the 2D sub-pulse was undersampled by a factor of 2 to introduce radial aliasing. pTx was applied utilizing 8 transmit profiles, which successfully eliminated radial aliasing. Axial views of the inversion profile produced by (a) original pulse (T_p = 24 ms), (b) pulse generated using 2x increased parent HS1 sampling and radially undersampled sub-pulse (T_p = 24 ms), (c) pulse generated using 2x increased parent HS1 sampling and pTx sub-pulses (T_p = 24 ms), (d) pulse generated with original parent HS1 sampling and radially undersampled sub-pulse (T_p = 14 ms), and (e) pulse generated with original parent HS1 sampling and pTx sub-pulses (T_p = 14 ms). Corresponding coronal views (f–j) of the inversion profile produced by each pulse. pTx is able to improve the relevant performance of the 3D pulse by either removing the aliasing sidebands (c, h) or shortening the overall pulse width (e, j).

DISCUSSION AND CONCLUSION

We have described a new method for designing 3D spatially selective adiabatic full passage pulses that are fully compatible with parallel transmission. The feasibility of this method using a single transmit setup was validated and demonstrated at 4T through simulations and experiments on both phantom and humans. To minimize the overall duration of the pulse, the 2D spiral sub-pulses were minimized in length within the gradient hardware specifications, resulting in a sub-pulse length of 1 ms, while an R-value of 9.5 for the parent pulse was used to limit the number of sub-pulse elements (N_seg ) to 19 based on oversampling by twice the Nyquist rate (18). The final pulse length was 23 ms. Furthermore, the compatibility of the proposed method with pTx was demonstrated at 7T by designing pTx 3D adiabatic pulses. The advantages of these pTx 3D pulses over their single transmit counterpart were demonstrated with simulations and phantom experiments. Our results suggest that the use of pTx can effectively reduce the total pulse length significantly or push the unwanted sidebands outside the FOV or both, without compromising the in-plane inversion fidelity.

When designing the 2D sub-pulse, sampling k-space by spiraling in and spiraling out in an alternating manner eliminates the need for the k-refocusing re-phasing gradients and can thus shorten the pulse to 21 ms. Nevertheless, the gradient hardware performance is the main limiting factor that determines the minimum pulse length achievable. For the gradient trajectory design used in this study, a slew rate corresponding to the 4T Varian system of 100 T/m/s was used. Although the slew rate available was not maximized when designing the gradient shapes, the overall pulse length can be decreased by $\frac{1}{\sqrt{2}}$, resulting in a 16 ms pulse when using gradient hardware standard on clinical systems such as the Siemens 7T system used for the pTx experiments (slew rate = 200 T/m/s). However, this comes at the expense of a $\sqrt{2}$ times higher peak RF amplitude.

In the current study, all 3D adiabatic pulses were designed based on an HS1 parent pulse. As a result, relatively high peak RF power was required to achieve B₁⁺-insensitive inversion or refocusing, especially when designing shorter pulses using pTx. To reduce the peak power requirement, one may consider adiabatic pulses of lower peak B₁ requirements. For example, if an HS8 pulse is used, the peak power can be reduced by a factor of 4 (5). However, this comes at the cost of a less sharp profile.

Although their ability to refocus spins was demonstrated in this study by using a double spin-echo sequence, our 3D adiabatic pulses can also be used for refocusing in a single spin-echo sequence. The major advantage of using a single refocusing pulse is the reduction in RF power deposition or SAR, which is especially desirable for ultra-high-field applications. An alternative approach to achieving 3D selectivity with a single spin echo sequence would be to excite with a 2D RF pulse and refocus with a 1D conventional (i.e. sinc) or adiabatic refocusing pulse. It will be interesting to investigate how this approach would compare to that using our 3D pulses.

Our human data acquired at 4T (Fig. 6) using a single transmit 3D adiabatic pulse exhibited a curved slab profile in areas of relatively large B₀ inhomogeneity due to its relatively low bandwidth along the slab select direction. The slab bandwidth can be increased by decreasing the duration of the parent pulse while maintaining its R-value. Accordingly, the slab bandwidth can be increased simply by decreasing the length of the 2D sub-pulse while maintaining the same number of parent pulse samples, which reduces the total pulse duration. An example of such a pulse was demonstrated in our pTx experiment (i.e., 14 ms pTx 3D pulse). However, reduction in pulse length will lead to an increase in RF power demand. An alternative way to increase bandwidth without the power penalty is to design a new parent pulse with increased R-value while keeping the total pulse length constant and increasing the number of parent samples accordingly. The 24 ms pTx 3D pulse used in our pTx experiment would have been such a pulse had we chosen a higher R-value when designing the parent pulse.

One limitation of the pTx 3D adiabatic pulse design presented in the current study is that the constituent pTx sub-pulses were only optimized to a single transverse slice (3 mm thickness) located in the middle of the target cylinder (4 cm thickness). Although the 3D pulse composed of such pTx sub-pulses presented satisfactory in-plane selectivity across the entire cylinder (Fig. 7), this may not be the case if large through-plane B₁⁺ variations are present (i.e., when targeting a longer cylinder or imaging the human brain). In such cases, one may need to design the pTx 3D pulse by optimizing the pTx 2D sub-pulse simultaneously to multiple slices within the target cylinder.

Because of its insensitivity to B₁⁺ inhomogeneity, our pTx 3D adiabatic pulse is expected to have utility for ultra-high-field applications. However at ultra-high-field, the local SAR becomes a limiting RF safety factor that needs to be addressed. In this proof-of-principle study, the constituent pTx 2D subpulses were designed only by controlling the integrated RF power (which is proportional to the global SAR). Alternatively, for a given parent pulse shape and adiabatic overdriving level, one can design the constituent pTx 2D subpulses by incorporating explicit constraints on both global and local SAR (19,20) to ensure compliance with safety guidelines.

In summary, we have introduced a new method for designing 3D spatially selective adiabatic pulses that are fully compatible with parallel transmission. The feasibility of this method for pulse design with single transmission was demonstrated and validated at 4T through simulations as well as phantom and human experiments. The advantage of integrating pTx into the design procedure was also demonstrated at 7T by designing pTx 3D pulses to either reduce pulse length or push the sidebands farther away in space. Because of its ability to produce 3D selectivity with high fidelity and large insensitivity to B₁⁺ inhomogeneity, the proposed method may offer utility for a number of applications such as inner volume imaging and navigator acquisition, even at ultra-high-field, where severe B₁⁺ inhomogeneity is present.

Supplementary Material

Supp online

Supporting Figure S1. Imaging Sequences. 3D adiabatic pulse used in an inversion recovery scheme (a), where it can be subtracted from an identical measurement without inversion applied to extract the profile. 3D adiabatic pulse can also be used as a spatially-selective π-refocusing pulse following a non-selective π/2 excitation in either (b) single spin-echo or (c) double spin-echo configuration. Double spin-echo compensates for the spatially quadratic phase along the frequency sweep direction, enabling isochromats within the spatially selective volume to experience identical echo times with the added advantage of balancing any residual gradient imperfections.

Supporting Figure S2. Parallel transmission. The spiral trajectory of the 2D sub-pulse was undersampled by 2 (a), introducing radial aliasing as shown by simulation (b). pTx was applied utilizing 8 transmit profiles (d), which successfully eliminated radial aliasing as shown by simulation (c). The yellow line indicates the ROI used to generate pTx sub-pulses via spatial domain approach (10).