Abstract
Reliable prediction and diagnosis of concussion is important for its effective clinical management. Previous model- based studies largely employ peak responses from a single element in a pre-selected anatomical region of interest (ROI) and utilize a single training dataset for injury prediction. A more systematic and rigorous approach is necessary to scrutinize the entire white matter (WM) ROIs as well as ROI-constrained neural tracts. To this end, we evaluated injury prediction performances of the 50 deep WM regions using predictor variables based on strains obtained from simulating the 58 reconstructed American National Football League (NFL) head impacts. To objectively evaluate performance, repeated random subsampling was employed to split the impacts into independent training and testing datasets (39 and 19 cases, respectively, with 100 trials). Univariate logistic regressions were conducted based on training datasets to compute the area under the receiver operating characteristic curve (AUC), while accuracy, sensitivity, and specificity were reported based on testing datasets. Two tract-wise injury susceptibilities were identified as the best overall via pair-wise permutation test. They had comparable AUC, accuracy, and sensitivity, with the highest values occurring in SLF (superior longitudinal fasciculus; 0.867–0.879, 84.4–85.2%, and 84.1–84.6%, respectively). Using metrics based on WM fiber strain, the most vulnerable ROIs included genu of corpus callosum, cerebral peduncle, and uncinate fasciculus, while genu and main body of corpus callosum, and SLF were among the most vulnerable tracts. Even for one un-concussed athlete, injury susceptibility of the cingulum (hippocampus) right was elevated. These findings highlight the unique injury discriminatory potentials of computational models, and may provide important insight into how best to incorporate WM structural anisotropy for investigation of brain injury.
Keywords: Concussion, deep white matter, fiber strain, injury susceptibility, tractography
1. Introduction
Traumatic brain injury (TBI) is a leading cause of morbidity and mortality in the United States (CDC 2015). Of the estimated 1.7–3.8 million individuals suffering from TBI each year in the United States alone, 75% are classified as mild traumatic brain injury (mTBI) or concussion (CDC 2015). The public awareness of concussion and its adverse cognitive and neurodegenerative consequences is growing ((NRC) 2014). A reliable prediction and diagnosis of TBI, including concussion, is important for effective management of this prevailing neurological disorder.
Despite decades of active research, the biomechanical mechanisms behind TBI remain elusive. Historically, efforts have been focused on characterizing head impact kinematics, using linear and/or rotational acceleration peak magnitudes and their variants. However, as head rotation is considered the main mechanism for mTBI and that angular velocity, as opposed to acceleration, is more predictive of strains (Zhao and Ji 2016), recent metrics have explicitly incorporated peak angular velocity (e.g., Rotational Injury Criterion (RIC) and Power Rotational Head Injury Criterion (PRHIC) (Kimpara and Iwamoto 2012), and Brain Injury Criterion (BrIC) (Takhounts et al. 2013).
Unfortunately, these empirically derived kinematic metrics do not directly inform brain mechanical responses that are thought to initiate injury (King et al. 2003). In part, this may explain why no consensus has been reached on the most appropriate metric for injury prediction. To estimate impact-induced responses, finite element (FE) models of the human head are important tools (Yang et al. 2011). Model-estimated brain responses have been shown to be more effective in predicting injury than kinematic metrics alone (Zhang et al. 2004; Marjoux et al. 2008; Takhounts et al. 2008; Giordano and Kleiven 2014a; Hernandez et al. 2014). In addition, FE models also enable correlating tissue deformation with specific concussion symptomatic measures (Viano et al. 2005), which is not feasible for kinematic metrics.
Improving the models’ injury predictive power is an ongoing, constant process. Sophisticated head models continue to emerge with more anatomical details (Mao et al. 2013), representing subject-specific anatomies (Ji et al. 2015), and characterizing anisotropic material properties of the white matter (WM) (Sahoo et al. 2014; Giordano and Kleiven 2014b). Lately, there are also efforts to integrate information from neuroimages (Fahlstedt et al. 2015; Miller et al. 2016), e.g., WM structural anisotropy (Wright and Ramesh 2012; Garimella and Kraft 2016), into biomechanical modeling for injury analysis. This aligns well with in vitro studies that suggest strain component along axonal longitudinal direction responsible for axonal injury (Cullen and LaPlaca 2006). Initial evidence indicates that WM fiber orientation-dependent strain (termed “fiber strain”, “axonal strain”, or “tract-oriented strain”) improves injury prediction performance relative to its isotropic counterpart, maximum principal strain (Chatelin et al. 2011; Wright et al. 2013; Giordano and Kleiven 2014a; Sullivan et al. 2014; Ji et al. 2015).
Regardless of the injury predictor variables employed, previous model-based studies typically utilize responses from a single pre-selected anatomical region of interest (ROI) to assess injury risk. The commonly used CSDM (cumulative strain damage measure) relies on maximum principal strain of the entire brain (Bandak and Eppinger 1994), while a variant is defined on generic ROIs (Weaver et al. 2012). Other generic or more targeted ROIs, including the corpus callosum, midbrain, and brainstem, are also common choices. For example, the maximum shear stress in the brainstem was found to correlate the strongest with the occurrence of mTBI when analyzing 24 NFL head impacts (9 concussions vs. 15 non-injury cases; (Zhang et al. 2004). Using an expanded dataset (58 impacts; 25 concussions vs. 33 non-injury cases), Kleiven studied 8 tissue injury predictors in 6 brain regions. He found that strain in the gray matter and CSDM0.1 (using a strain threshold of 0.1) in the WM had the highest accuracy in concussion classification (Kleiven 2007). After incorporating WM material property anisotropy, however, their model indicated that instead, peak axonal strain within the brainstem had the highest predictive power (Giordano and Kleiven 2014a).
These conflicting reports on the “best” predictor variable and brain ROI to achieve the most accurate injury prediction highlight current challenges in studying the biomechanical mechanisms of TBI. Conceptually, model-based brain injury prediction is analogous to an ill-posed optimization problem—using model-estimated responses to “fit” the given binary injury data. First, errors in the “input variables”, head impact kinematics, seem unavoidable. Laboratory-reconstructed NFL head impacts had a reported error of up to 11% for impact velocity and a maximum error of 25% for resultant angular acceleration (Newman et al. 2005). However, error magnitude in angular velocity was not available, even though it is considered as the primary injury mechanism (Takhounts et al. 2013) and more predictive of strains (Kleiven 2006); Zhao and Ji 2015; Zhao and Ji 2016). For on-field head impacts, temporally validated rotational acceleration/velocity profiles appear yet to be developed (Beckwith et al. 2012; Allison et al. 2014).
Second, the “optimizer”, FE models of the human head, could vary substantially due to uncertainties in model assumptions (material properties of the brain in particular (Chatelin et al. 2010). The lack of high-quality experimental data especially in live humans under injury-causing impacts (Hardy et al. 2001; Hardy et al. 2007; Sabet et al. 2008) also precludes sufficient, reliable model validations (Yang et al. 2011). Consequently, even “validated” head models could produce substantially discordant brain responses under identical head impacts (Ji et al. 2014a).
Third, and equally importantly, the “objective function” is also under-defined. Well-documented and accepted brain injury cases including both impact kinematics and clinical injury diagnoses are lacking and are subject to errors. Thus, a single “training dataset” has been used in previous studies to evaluate injury prediction performance. A separate “testing dataset” is not widely available to enable an independent performance verification, even though this is considered necessary and important (Anderson et al. 2007; Sullivan et al. 2014). Taken together, these uncertainties and lack of high quality, well-accepted injury data could yield multiple “local minima” in the optimization, which may explain previous conflicting observations based on the same injury dataset. However, they may not necessarily correspond to the true “global minimum”.
Given these challenges, potentially there could be data “over-fitting” concerns when attempting to pinpoint a specific injury predictor and ROI for the best performance, especially when using responses from a single element (e.g., peak maximum strain regardless of the location in a given ROI; (Zhang et al. 2004; Giordano and Kleiven 2014a)). Therefore, there is a need for more systematic and objective evaluation and comparison of the injury predictors’ performances. Here, we employed a repeated random subsampling technique to train and optimize injury predictors while reporting their performances using independent testing datasets. This is a popular cross-validation technique (Arlot and Celisse 2010), but does not appear to have been applied in model-based TBI studies to date. Further, we analyzed injury prediction performances and vulnerabilities of the entire deep WM ROIs as well as ROI-constrained neural tracts from whole-brain tractography (Zhao et al. 2016). Instead of relying on peak responses from a single element from a predefined ROI, we used data sampling across all of the deep WM ROIs/neural tracts. Similarly, regional vulnerabilities were also evaluated via data sampling of predictor responses across all of the simulated head impacts.
These injury analyses significantly extended previous model-based TBI studies to formulate a more systematic and rigorous approach for evaluation of injury prediction performance. A generic head model was also established with the directly associated neuroimages and whole-brain tractography, which was a critical stepping stone towards better integration of neuroimaging and TBI biomechanics studies in the future. Therefore, findings from this work may provide important insight into how best to predict injury for improved mitigation and clinical management.
2. Methods
2.1 Image registration and geometrical transformation
Essential to this study was to integrate structural neuroimaging into biomechanical modeling. This required transforming all image volumes, their corresponding geometrical entities, and the head FE model into a common coordinate system. For convenience, we have chosen the coordinate system of the Worcester Head Injury Model (WHIM; formerly known as the Dartmouth Head Injury Model or DHIM; (Ji et al. 2015; Zhao et al. 2016) as a common reference. The WHIM was created based on high-resolution T1-weighted MRI (at an isotropic resolution of 1 mm3) of an individual. It had a resolution of 3.3±0.79 mm for the brain. Diffusion tensor imaging (DTI) of the same individual provided WM fiber orientations at discrete voxels (at an isotropic resolution of 2 mm3) and real-valued fiber sampling points of the whole-brain tractography (at a resolution of 1 mm). In comparison, the standard ICBM-DTI-81 WM atlas (Mori et al. 2008) averaged from a group of 81 healthy adults served as the WM ROI anatomical constraints. This atlas is provided within another standard anatomical template (ICBM-152). Fig. 1 schematically illustrates how these image volumes were registered to transform their corresponding geometrical entities into the WHIM common coordinate system. A rigid registration was performed between the T1-weighted MRI and DTI anatomical image (b=0) of the same individual. In contrast, a non-linear registration using the FNIRT tool in FSL was applied to transform the ICBM-DTI-81 atlas into the WHIM space (Andersson et al. 2007).
Fig. 1.
Schematic illustration of image volume registrations to transform all geometrical entities into the common reference coordinate system of the Worcester Head Injury Model (WHIM).
2.2 The Worcester Head Injury Model
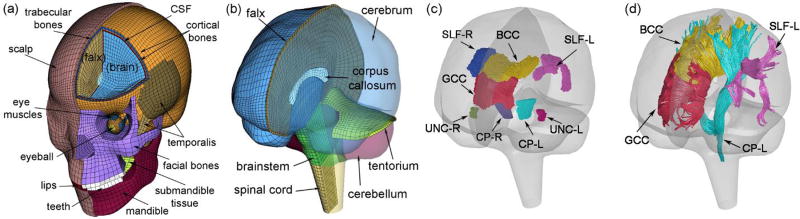
Details of the Worcester Head Injury Model (WHIM; Fig. 2), including model creation, mesh quality, assignment of material properties and boundary conditions, and validation performances have been reported extensively in recent publications (Ji et al. 2015; Ji and Zhao 2015; Zhao et al. 2016; Zhao and Ji 2016). Therefore, they are not repeated here. Importantly, the WHIM has achieved an overall “good” to “excellent” validation (as assessed by correlation score based on Normalized Integral Square Error (Donnelly et al. 1983; Kimpara et al. 2006)) at the low (~250–300 rad/s2 for a live human volunteer), mid (~1.9–2.3 krad/s2 for cadaveric impact tests C755-T2 and C383-T1), and high (~11.9 krad/s2 for cadaveric test C393-T4) levels of head angular acceleration magnitudes provided important confidence of the fidelity in WHIM-estimated brain responses.
Fig. 2.
The exterior features (a) and intracranial components (b) of the WHIM (formerly known as the Dartmouth Head Injury Model or DHIM), along with eight representative WM ROIs (c) and four corresponding neural tracts from the whole-brain tractography (showing a 10% random subset; d).
2.3 Simulation of the NFL reconstructed head impacts
We used the 58 reconstructed NFL head impacts as model inputs (Newman et al. 2000), which included 25 concussions and 33 non-injury cases. Details of video recording analysis (Pellman et al. 2003) and the procedures of head impact reconstruction (Newman et al. 2000; Newman et al. 2005) were previously reported. Briefly, all head impact accelerations were collected at 10 kHz following the SAE J211 protocol. The acceleration profiles were pre-processed according to the CFC 1000 requirements (Newman et al. 2000). Identical to previous studies (Newman et al. 2000; Kleiven 2007), all acceleration profiles were filtered using the CFC 180 low-pass filter. The resulting time histories of the linear and angular accelerations were prescribed to the WHIM head center of gravity (CG) to induce brain mechanical responses.
2.4 Voxel- and tract-wise WM fiber strains
Whole-brain tractography was generated using the DTI of the same individual selected to develop the baseline WHIM, as previously reported (Zhao et al. 2016). This led to ~35 k fibers and ~3.3 million sampling points in total. Using the transformed ICBM-DTI-81 atlas (Fig. 1) as anatomical constraints, the 50 deep WM ROIs (see Appendix A) and their corresponding neural tracts were identified within the WHIM (illustrated in Fig. 2c and d; (Zhao et al. 2016)).
For each impact simulated, element-wise maximum principal strain and strain tensor were extracted at every time step during the entire impact simulation (temporal resolution of 1 ms). Fiber strain at each WM voxel or fiber sampling point was calculated, at every time step, using the corresponding fiber orientation and strain tensor of the nearest element (Ji et al. 2015). For all strains, their peak values across the entire impact simulation, regardless of the time of occurrence, were used. They were denoted as εp and εn for maximum principal strain and fiber strain, respectively. Due to the large number of fibers for each WM neural tract, a 10% random subset was utilized for improved computational efficiency. This led to an average of 183±42 (range of 88–307) fibers for a given WM neural tract. The down-sampling did not significantly alter strain or injury susceptibility measures (Zhao et al. 2016).
2.5 Injury susceptibility measures in the deep WM neural tracts
A tract-wise injury susceptibility index (φtract) was established for a given neural tract as the fraction of “injured” WM fibers (i.e., εn greater than a threshold, determined in Section 2.8, regardless of the occurrence location along the given fiber):
| (1) |
However, a potential weakness of this, perhaps over-simplified, definition was that it did not differentiate the relative likelihood of injury to a given fiber according to the number of sampling points exposed to high strains (e.g., a fiber with either one or 100% of the sampling points “injured” would be treated equally). To characterize this “confidence” in injury likelihood, a weighting factor, w, was devised:
| (2) |
Applying w to the binary injury status (0 and 1 for “uninjured” and “injured”, respectively) of each fiber led to the following enhanced tract-wise injury susceptibility index:
| (3) |
Further, a sampling point-based susceptibility index was also established to describe the fraction of “injured” fiber sampling points:
| (4) |
Essentially, and extended the concept of CSDM, which was originally developed for the entire brain, to individual WM neutral tracts (Zhao et al. 2016). The former further accounted for the distribution of “injured” sampling points among fibers.
2.6 Injury predictor variables
While tissue strain is considered as a primary variable to assess injury risk and severity, no consensus exists how best to describe the tissue strain status. Common choices include the maximum strain magnitude from a single element in a particular region, regardless of the time of occurrence or location (i.e., peak strain (Zhang et al. 2004; Giordano and Kleiven 2014a)), or a dichotomous variant describing the percentage of tissue volume experiencing large strains (e.g., CSDM (Takhounts et al. 2008) or Pop90 (Sullivan et al. 2014)). In this study, we evaluated the performances of peak strain, regional average strain, and the dichotomous variants based on either εp or εn. Specifically, a total of nine strain-based injury predictor variables were evaluated, as summarized in Table 1. All strains were evaluated on MR voxel locations by interpolating from neighboring FE elements, except for tract-wise injury susceptibilities for which εn was evaluated at higher resolution fiber sampling points. For clarity, here we referred to an injury predictor as the predictor variable obtained from a given ROI or neural tract.
Table 1.
Summary of injury predictor variables used in this study.
| Predictor Variable | Definition | Example References | ||
|---|---|---|---|---|
| Largest strain | Peak εp | Largest value of εp from a single FE element or voxel | (Zhang et al. 2004; Giordano and Kleiven 2014a) | |
| Peak εn | Largest value of εn from a single FE element or voxel | (Giordano and Kleiven 2014a) | ||
| Average strain | Average εp | Regional average of εp | (Ji et al. 2014b; Zhao and Ji 2015) | |
| Average εn | Regional average of εn | In this study | ||
| Injury susceptibility index |
|
Volume fraction of “injured” voxels based on εp in a ROI | (Giordano and Kleiven 2014a) | |
|
|
Volume fraction of “injured” voxels based on εn in a ROI | In this study | ||
| φtract | Tract-wise injury susceptibility index, Eqn. 1 | (Zhao et al. 2016) | ||
|
|
Enhanced tract-wise injury susceptibility index, Eqn. 3 | In this study | ||
|
|
Fraction of “injured” fiber sampling points based on εn in a neural tract, Eqn. 4 | (Zhao et al. 2016) |
2.7 Repeated random subsampling and Logistic regression
The 58 NFL head impact cases were randomly split into training (39 cases, or approximately two-thirds) and testing (the remaining 19 cases) datasets. This process was repeated 100 times (considered sufficiently large) (Arlot and Celisse 2010). For each training dataset in a random subsampling trial, a standard univariate logistic regression was performed against the binary injury statuses (0 and 1 for “uninjured” and “injured”, respectively) for each injury predictor. A receiver operating characteristic (ROC) curve was generated to export the area under the curve (AUC). The logistic regression model was then applied to the corresponding non-overlapping testing dataset for injury prediction. The resulting numbers of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) were used to calculate performance measures such as the accuracy, sensitivity, and specificity according to the following equations:
| (5) |
| (6) |
| (7) |
For each random trial, this produced four 9-by-50 matrices encoding the AUC, accuracy, sensitivity, and specificity, respectively (9 predictor variables and 50 WM ROIs/neural tracts). Combining all of the 100 random trials led to four corresponding 9-by-50-by-100 matrices, which were used for subsequent evaluation.
2.8 Optimal εthresh for injury susceptibility indices
The dichotomous injury susceptibility indices (Table 1) depended on a strain threshold. A definitive εthresh for the human brain has not been established. An in vivo study suggests a wide range (0.09–0.47 to induce impairment (Bain and Meaney 2000)). Thresholds from other model-based studies also varied depending on the region (e.g., 0.21 in the corpus callosum (Kleiven 2007); 0.26 (Kleiven 2007) or 0.19 (Zhang et al. 2004) in the gray matter) or type of strain (e.g., 0.21 in maximum principal strain (Kleiven 2007) or 0.07 in axonal strain in the corpus callosum (Giordano and Kleiven 2014a)). As even “validated” head injury models can produce substantially discordant strains under identical head impact conditions (Ji et al. 2014a), these thresholds were not directly applicable here.
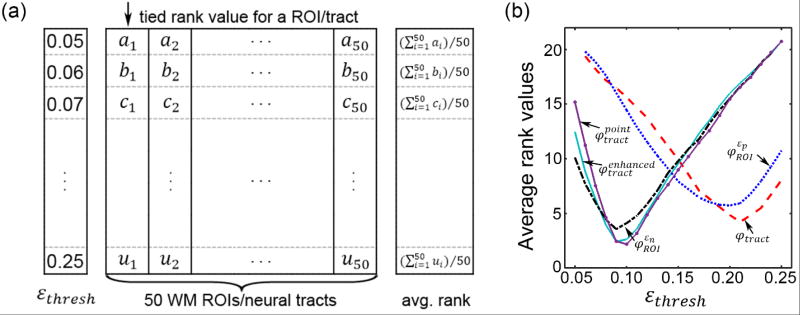
Instead, the following method was adopted within the repeated random subsampling framework, which was an extension to that applied to determine the threshold for CSDM (Giordano and Kleiven 2014a). Specifically, for each training dataset and a given injury susceptibility index, a range of candidate thresholds (εthresh; 21 unique values within a range of 0.05–0.25 at a step size of 0.01, based on the previous studies) were enumerated to define the susceptibility index for a given WM ROI/neural tract. A logistic regression analysis was then conducted, from which a Wald χ2 test was performed. A significant relationship was said to exist between the injury risk and the predictor when the p-value was less than 0.05, with a lower value indicating a more significant relationship. Next, for each WM ROI/neural tract, tied rank values were assigned to score εthresh in the order of their corresponding χ2 test p-values (Wilcoxon 1946), where a lower value led to a smaller rank value. At each εthresh value, the average rank value across all WM ROIs/neural tracts was used to represent its overall performance. The optimal εthresh corresponding to the smallest rank value was then identified (Table 2). Essentially, this was to minimize the overall p-value, or to maximize the significance of risk-response relationship, for the group of ROIs/tracts. This process is illustrated in Fig. 3 for a typical training dataset. Finally, an average optimal εthresh among the trials was obtained for each injury susceptibility index, which was subsequently used in a separate round of repeated random subsampling to evaluate injury prediction performances. The three εn-based metrics, , and , had an optimal εthresh of 0.09–0.10, which was consistent with the lower bound of a conservative injury threshold of 0.09 established from an in vivo optical nerve stretching experiment (Bain and Meaney 2000).
Table 2.
Summary of the average strain threshold (εthresh; from 100 random trials) and standard deviation for each injury susceptibility index.
| Susceptibility index variable |
|
|
φtract |
|
|
||||
|---|---|---|---|---|---|---|---|---|---|
| Optimal εthresh | 0.20±0.01 | 0.09±0.01 | 0.21±0.01 | 0.10±0.01 | 0.10±0.01 |
Fig. 3.
(a) Illustration of the ranking approach to identify the optimal εthresh based on the training dataset in a typical round of random subsampling trial. For each WM ROI/neural tract, a tied rank was assigned for each εthresh according to the Wald χ2 test p-values. For each εthresh, an average rank value was obtained, as shown. (b) Average rank values as a function of εthresh. For each injury susceptibility measure, the one that yielded the smallest (i.e., the best) average rank value was chosen as the optimal εthresh (Table 2).
2.9 Relative injury prediction performance among predictor variables
For each predictor variable, its performance measures in each WM ROI/neural tract were averaged across the 100 subsampling trials. This led to a 9-by-50 matrix of average values for each performance measure. To assess the relative performances among these predictor variables, we performed a pair-wise one-sided permutation test (see Appendix B) based on the average AUC, accuracy, sensitivity, and specificity (9×8=72 pairs for each performance metric) sampled across all of the 50 deep WM ROIs/neural tracts. The predictor variables were then ranked by the number of times that a given candidate was found to have a significantly larger average value than others (as determined by the permutation test p-values).
2.10 Relative vulnerability among deep WM ROIs and neural tracts
Identifying the most vulnerable WM ROIs or neural tracts may be of clinical significance to potentially relate impacts to specific brain functional alteration as well as for potential targeted therapeutic treatment in the future. Here, we defined the relative vulnerabilities among the 50 ROIs/neural tracts as the frequency that each region experienced responses larger than others. Similarly, for each injury predictor variable (Table 1), we employed one-sided permutation test based on paired-sample t-statistics, using the response values of the ROIs/neural tracts sampled across the 58 simulated head impacts. A total of 50×49 = 2450 pairs of permutation test were conducted for a given injury predictor variable. Finally, their relative vulnerabilities were ranked.
3. Data analysis
All head impacts were simulated using Abaqus/Explicit (Version 6.12; Dassault Systèmes, France). For each impact, element-wise peak strains during the entire simulated event were obtained. For injury predictor variables that required a pre-determined threshold, an optimal threshold value was determined. Repeated random subsampling was utilized to assess injury performances. For each performance measure, average values across all of the WM ROIs/neural tracts were used to conduct one-sided permutation tests based on paired-sample t-statistics. For each injury predictor variable, the relative vulnerabilities of the WM ROIs/neural tracts were ranked to identify the top five most vulnerable ones. Injury thresholds at 50% injury probability were computed. Finally, representative distributions of strain and injury susceptibility responses for a pair of striking and struck athletes (non-concussed and concussed, respectively) were also illustrated.
For each head impact (100 ms in duration), the computational cost was ~120 min for impact simulation with 8 CPUs and ~60 min for response extraction (parallel processing on 12 CPUs). All data analyses were performed with in- house MATLAB programs (R2016a; MathWorks, Natick, MA) on a 12-core Linux machine (Intel Xeon X5560, 2.80 GHz, 126 GB memory).
4. Results
4.1 Injury prediction performances
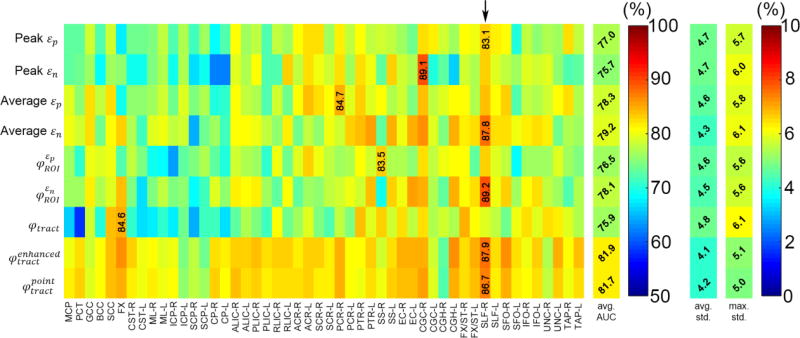
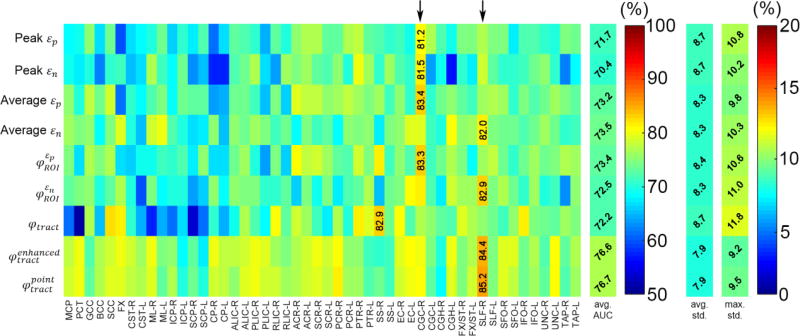
Figs. 4–7 summarize the average AUC, accuracy, sensitivity, and specificity for the 9 injury predictor variables across the 50 ROIs/neural tracts. For each predictor variable, the performance consistency among the 100 subsampling trials was assessed in terms of standard deviation (either further averaged across the 50 regions or using the maximum value to represent the “extreme” case). In general, AUC based on training datasets had the highest consistency, which was not surprising as this variable was a more stable measure. Other performance measures based on independent testing datasets were also largely consistent among the subsampling trials, perhaps, with an exception of the original φtract in terms of sensitivity and specificity (maximum standard deviation reached 37.3% and 33.6%, respectively; Figs. 6 and 7).
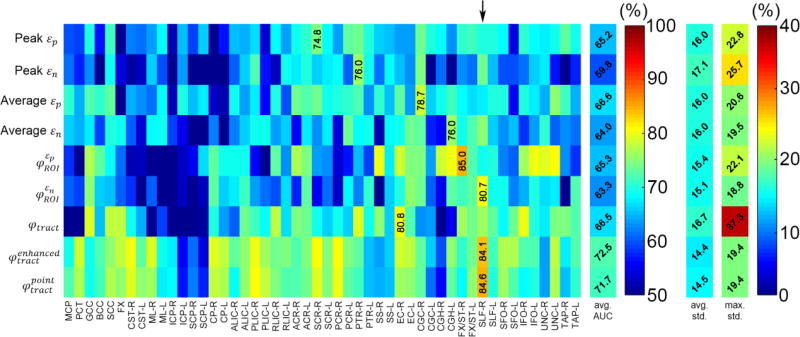
Fig. 4.
Summary of AUCs averaged from 100 random subsampling trials based on the training datasets, shown as a 9×50 intensity-encoded image. Each row corresponds to an injury predictor variable while each column represents a WM ROI/neural tract. The average AUC value for each injury predictor variable, regardless of the region, is also shown, along with the average and maximum standard deviations of the AUC samples across the 100 trials. Five of the nine injury predictor variables achieved the largest AUCs (averaged across trials) in the SLF-R (arrow).
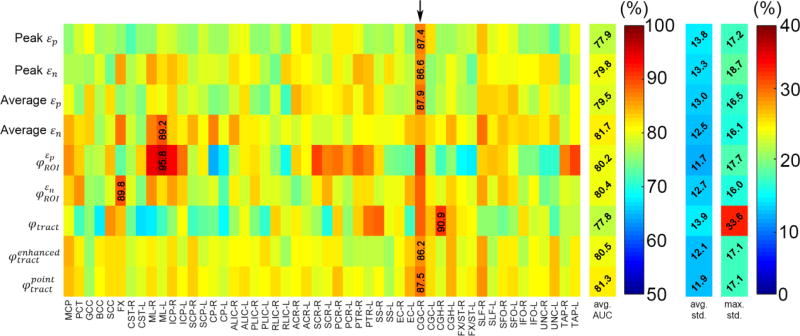
Fig. 7.
Summary of average specificity based on the testing datasets. Five of the nine injury predictor variables achieved the best specificity score in the CGC-R (arrow).
Fig. 6.
Summary of average sensitivity measures based on the testing datasets. Three of the nine injury predictor variables achieved the best sensitivity score in the SLF-R (arrow).
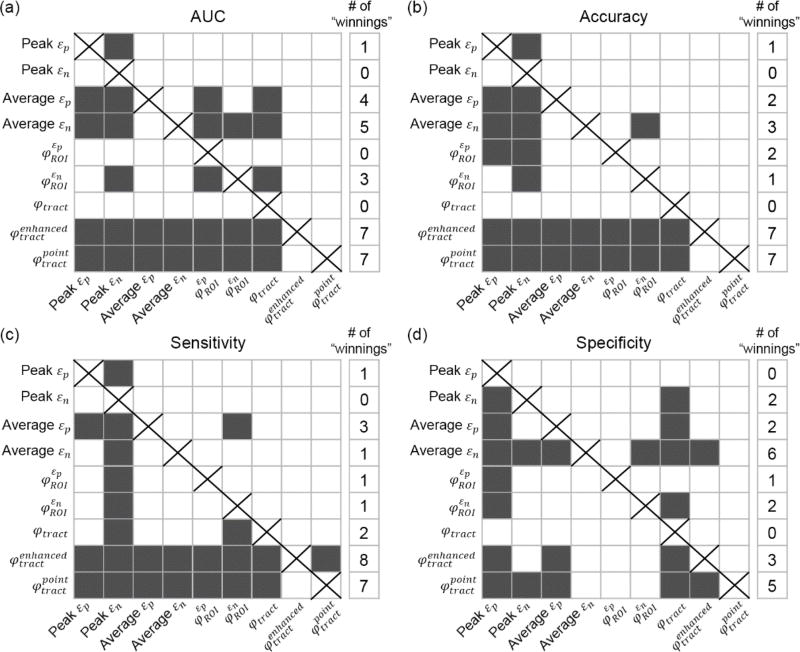
The two tract-wise injury susceptibility indices, and , consistently achieved the highest AUC, accuracy, and sensitivity (averaged from the 50 regions; Figs. 4–7). However, without weighting the “confidence” of injury for each fiber within a neural tract, the original φtract had the worst average AUC (tied with peak εn; Fig. 4). It was intriguing to observe that 5 of the 9 injury predictor variables achieved the best AUC in SLF-R (superior longitudinal fasciculus right) among the 50 deep WM regions. Similarly, 4 (3) of the 9 metrics had the best accuracy sensitivity) in the same region. Overall, the same three metrics, and , performed the best in AUC, accuracy and sensitivity in SLF-R (Figs. 4–6). In terms of specificity, however, 5 of the 9 metrics, including and , performed the best in CGC-R (cingulate gyrus right; Fig. 7). Pair-wise permutation tests based on performances sampled across the 50 regions confirmed that the two tract-wise injury susceptibility indices, and , were the best overall, despite the statistically significant but subtle difference in sensitivity between themselves; 72.5% vs. 71.7%) and specificity (slightly lower than that for average εn; Fig. 8). For each best performer (i.e., region of the highest values in each row in Figs. 4–7), its metric value was significantly higher than most of the other remaining regions (at least 90% or 44 out of the other 49), according to permutation tests.
Fig. 8.
Pair-wise performance comparisons between the injury predictor variables in terms of AUC (a), accuracy (b), sensitivity (c), and specificity (d). Each square in a row represents whether the performance measure was significantly larger (dark gray; otherwise, white) than that in a column (self-comparisons along the diagonal excluded).
4.2 Injury vulnerability and threshold
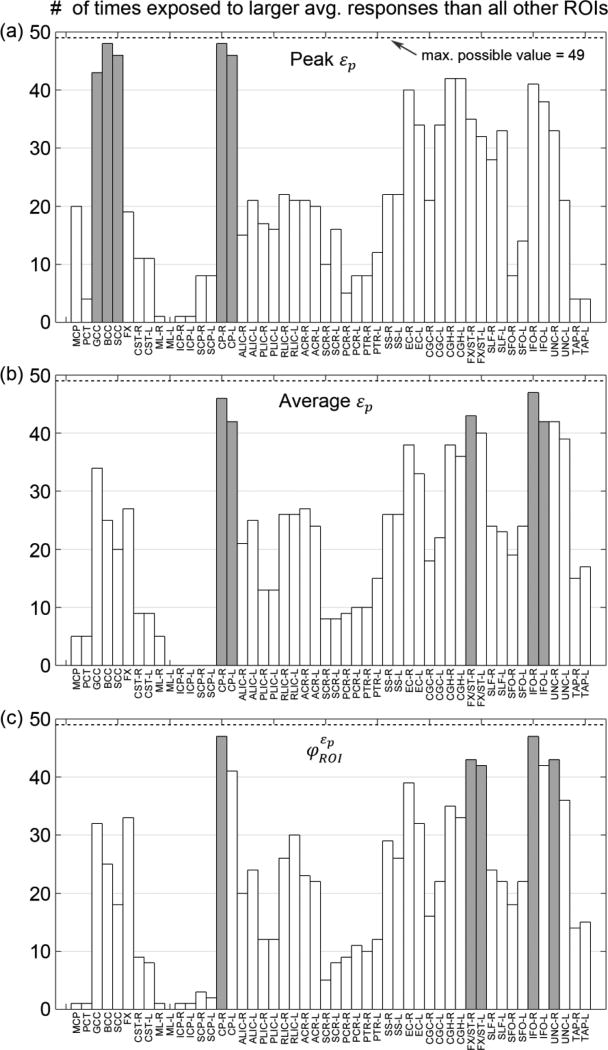
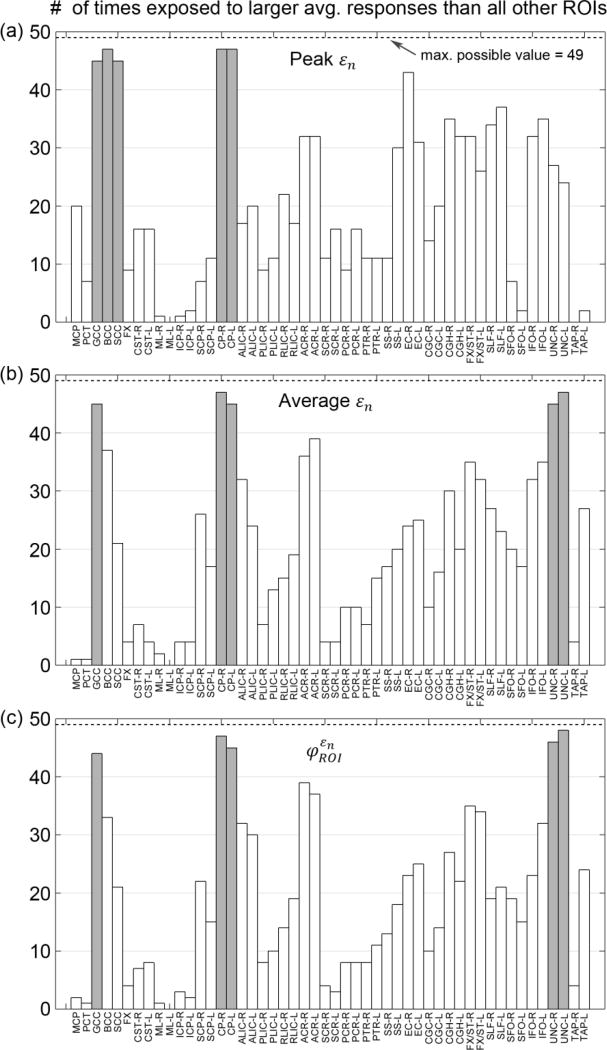
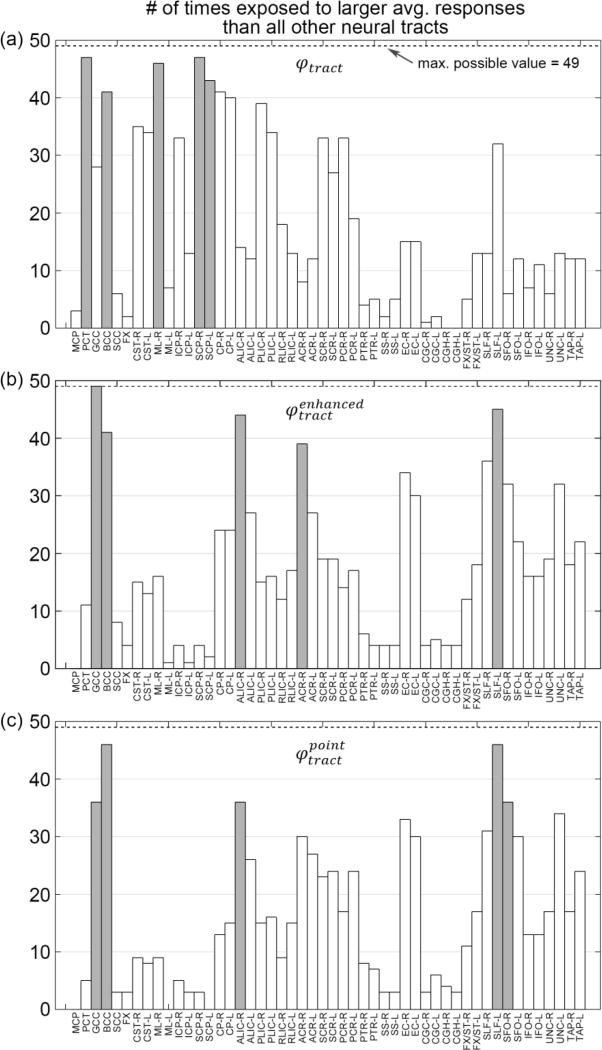
The relative vulnerabilities for ROI-based injury predictor variables using εp and εn are reported in Fig. 9 and Fig. 10, respectively. Results for tract-based predictor variables are given in Fig. 11. For ROI-based variables, CP-R (cerebral peduncle right) consistently ranked within the top five most vulnerable regions (highlighted; Fig 9 and 10). When using εn for injury prediction, GCC (genu of corpus callosum), besides CP, was also identified within the top five (Fig. 10). When using the tract-wise injury predictors (Fig. 11), however, BCC (body of corpus callosum) was consistently found to experience high vulnerability. Perhaps most interestingly, for the top five most vulnerable neural tracts identified by the two best performing injury predictors, and , four of them overlapped. They were GCC, BCC, SLF-L (superior longitudinal fasciculus left) and ALIC-R (anterior limb of internal capsule right; Fig 11b and c). Finally, thresholds at the 50% injury probability are summarized for the predictor variables (Table 3).
Fig. 9.
The number of times that a given WM ROI had an average response value (from the 58 simulated head impacts) significantly larger than others using injury predictors based on εp: peak εp (a), average εp (b), and (c). Their respective top five most vulnerable ROIs are highlighted (gray).
Fig. 10.
The number of times that a given WM ROI had an average response value significantly larger than others using injury predictors based on εn: peak εn (a), average εn (b), and (c). Their respective top five most vulnerable ROIs are highlighted.
Fig. 11.
The number of times that a given WM neural tract had an average response value significantly larger than others using injury predictors established from tract-wise εn: φtract (a), (b), and (c). Their respective top five most vulnerable neural tracts are highlighted.
Table 3.
Summary of injury predictor thresholds at the 50% injury probability (averaged from the 50 deep WM ROIs/tracts).
| Peak εp | Peak εn | Average εp |
Average εn |
|
|
φtract |
|
|
|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg. ± Std. | 0.252 ±0.044 | 0.201 ±0.046 | 0.205 ±0.043 | 0.097 ±0.020 | 0.495 ±0.218 | 0.410 ±0.136 | 0.605 ±0.142 | 0.475 ±0.069 | 0.411 ±0.057 | ||||
| Range | [0.161, 0.363] | [0.127, 0.335] | [0.133, 0.293] | [0.057, 0.141] | [0.045, 0.843] | [0.122, 0.697] | [0.268, 0.912] | [0.228, 0.616] | [0.246, 0.553] |
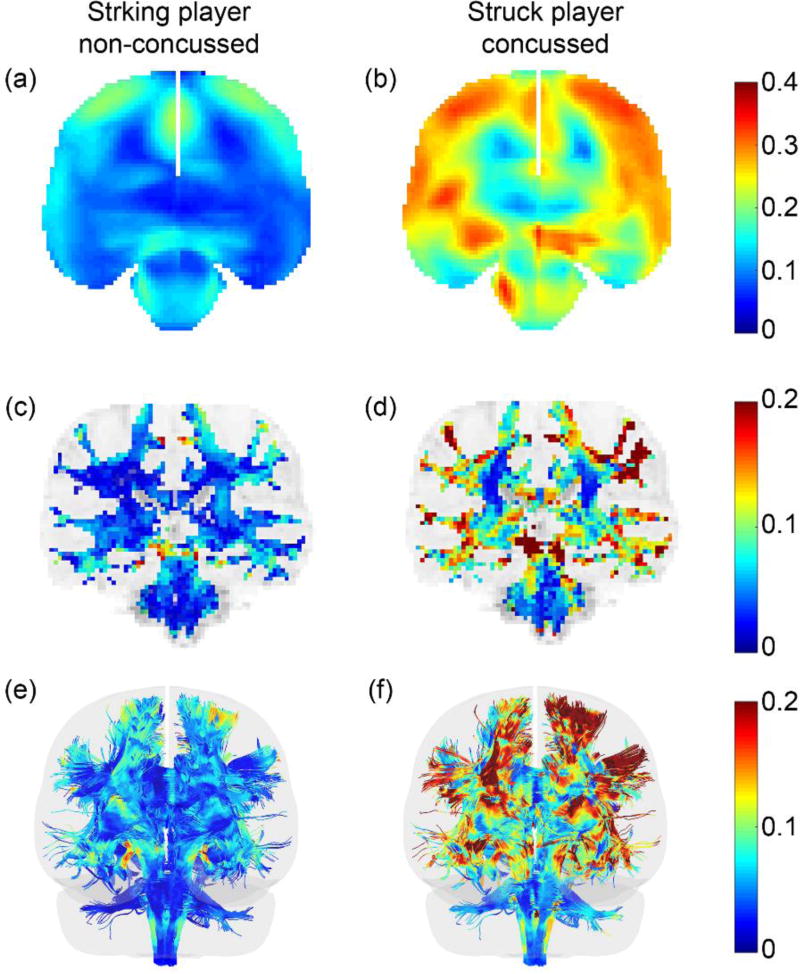
4.3 Illustration from selected cases
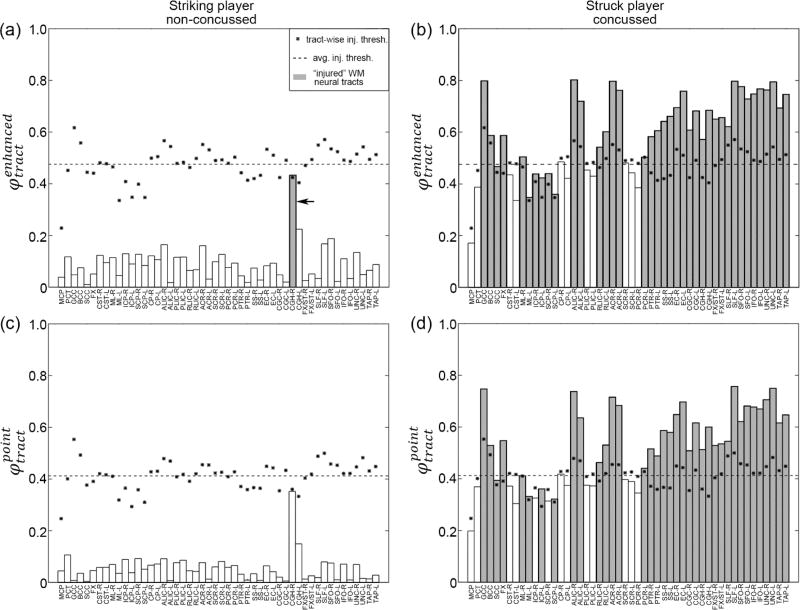
Distributions of εp, voxel- and tract-wise εn are shown for a pair of striking and struck athletes (non-concussed and concussed, respectively) involved in the same head collision (Case157). For the striking player, large εn responses occurred in the midbrain region (Fig. 12c). For the concussed player, higher εp and εn mostly occurred in the peripheral subcortical areas and the midbrain (Fig. 12b and d). The injury susceptibilities using the two best predictors are also illustrated (Fig. 13). Perhaps as expected, most of the tracts in the struck/concussed athlete experienced injury susceptibilities greater than the respective tract-wise thresholds. While the opposite was true for the striking/un-concussed athlete, CGH-R (cingulum (hippocampus) right) also experienced elevated that exceeded its injury threshold.
Fig. 12.
Brain strain distributions for a pair of striking/struck athletes involved in the same head collision. (a and b): peak εp resampled on a coronal plane; (c and d): peak εn in a coronal MR image; and (e and f): peak εn along a 10% subset of the whole-brain tractography. For the resampled strain map, only regions corresponding to the brain parenchyma are shown – other regions such as falx and tentorium appear as empty space. All responses are peak values during the entire impact, regardless of the time of occurrence (vs. a time-frozen snapshot (Kleiven 2007)). The peak magnitudes of resultant angular acceleration and velocity were 3807 rad/s2 and 25 rad/s for the striking athlete, and were 7083 rad/s2 and 38 rad/s for the struck player, respectively.
Fig. 13.
Illustration of injury susceptibilities using (top) and (bottom) for the same pair of athletes. Stars/dashed lines represent tract-wise/average injury thresholds at a 50% probability for concussion. Potentially “injured” tracts (i.e., susceptibilities exceeding the corresponding tract-wise thresholds) are highlighted in gray. Even for the un-concussed athlete, in CGH-R still exceeded its tract-wise threshold (arrow).
5. Discussion
Numerous biomechanical (Yang et al. 2011) and neuroimaging (Bigler and Maxwell 2012; Shenton et al. 2012) studies exist that attempt to elucidate the mechanisms behind traumatic brain injury (TBI). However, their integration remains rather limited. Our study using whole-brain tractography and a well-established WM atlas to analyze brain injury in contact sports is an important extension to previous efforts (Kraft et al. 2012; Wright et al. 2013; Giordano and Kleiven 2014b; Sullivan et al. 2014; Ji et al. 2015; Zhao et al. 2016). Instead of similarly pinpointing a specific injury predictor variable in a given brain ROI for injury prediction, here we systematically analyzed injury prediction performances and vulnerabilities of the entire deep WM ROIs and neural tracts. Further, a repeated random subsampling technique was employed to objectively evaluate prediction performances in order to avoid or minimize “over-fitting” concerns in previous efforts where a single training dataset was used.
5.1 Injury prediction performance
The two tractography-based injury susceptibility indices, and , consistently had the best overall predictive power, while peak εn performed the worst in general (Fig. 8). Without weighting the “confidence” of injury in each WM fiber, however, the performance of φtract degraded significantly. The two best performers virtually had identical AUC and accuracy. Their responses as sampled across the 58 impacts were highly correlated (Pearson correlation coefficients close to 1.0 for all of the neural tracts; range of 0.989–0.998, p<0.0001). This suggests certain inherent concordance between the two. This was not surprising, given that the two predictor variables would become identical if a neural tract were to be composed of a single fiber. However, unlike depends on the total number of “injured” sampling points only, and is invariant to their distribution among the fibers. Therefore, some subtle, but statistically significant, differences were found in their sensitivity and specificity (Fig. 8cd). Further investigation is necessary to discern their similarities/differences as well as implications in assessing injury risk.
The regional average εp and εn within a given ROI consistently outperformed their peak counterparts found in a single element, regardless of its location, for all of the performance measures (Fig. 8). The regional averages were also slightly (but significantly) better in AUC than their dichotomized counterparts, and ; however, their comparisons in other performance measures were inconclusive. In addition, and did not differ in performance between themselves, except that the latter had a larger average AUC than the former based on training datasets (Fig. 8a). Regardless, these tract- and ROI-wise findings indicated that on a group-basis, fiber orientation-dependent strain along WM neural tracts may be more effective in injury prediction than the ROI-based counterparts.
The most injury discriminative WM ROIs/neural tracts were also observed. Note that because of head symmetry relative to the mid-sagittal plane (WHIM, WM atlas, and largely for whole-brain tractography as well), the ROI/tract results should be interpreted bilaterally. For example, findings regarding SLF-R would be equally applicable to its contralateral counterpart, SLF-L (e.g., considering mirrored head impacts (Zhao and Ji 2015)).
SLF appeared to be one of the most injury discriminative neural tracts across a number of εn-based predictor variables that consistently achieved the best AUC, accuracy, and sensitivity. For example, the two best performers, and in this region, had an accuracy and sensitivity of 84.4–85.2% and 84.1–84.6%, respectively, and the corresponding specificity score was only slightly less than CGC (85.4–86.3% vs. 86.2–87.5%). Interestingly, the same neural tract, SLF, was also among the most vulnerable ones, both biomechanically (Fig. 11) and in neuroimaging ((Bigler and Maxwell 2012; Gardner et al. 2012); further see below).
5.2 Injury vulnerability
The relative vulnerabilities depended on the injury predictor variables used. For ROI-based predictor variables, CP (cerebral peduncle, near the brainstem and midbrain) was consistently found to be among the most vulnerable ROIs, regardless of whether εp or εn was used (Fig. 9 and 10). This agreed well with typical reports of vulnerability in this region (Zhang et al. 2004; Viano et al. 2005). Large εp and εn occurred near this area even for the striking/uninjured athlete (Fig. 9ac; similarly for the other). Regardless, the regional average responses and susceptibility measures yielded more consistent findings than when using peak values. For example, three of the top five most vulnerable ROIs were identical (CP-R, FX/ST-R (fornix and stria terminalis), and IFO-R (inferior fronto-occipital fasciculus)) when using average εp and as predictor variables. In comparison, average εn and identified the same top five most vulnerable ROIs (GCC, CP-L/R and UNC-L/R (uncinated fasciculus)). These ROI-wise observations agreed well with a previous study utilizing a subset of the NFL impact cases, where fornix, midbrain, and corpus callosum were found to experience the largest strains (Viano et al. 2005).
For the two best injury predictors based on neural tracts, the top four most vulnerable ones were identical (GCC, BCC, ALIC-R and SLF-L; Fig. 11). In general, this agreed well with neuroimaging studies in the context of sports-related concussion. Certain neural tracts, including GCC (genu of the corpus callosum), SLF, UNC, the inferior longitudinal fasciculus, internal capsule, among others, are known to be more susceptible to mTBI (Kraus et al. 2007; Niogi et al. 2008; Bigler and Maxwell 2012). For example, using tract-based spatial statistics (TBSS), significant increase in mean diffusivity (MD) was observed in the SLF for concussed collegiate athletes playing football ((Cubon et al. 2011); significant changes in DTI parameters are considered indications of damages to the underlying WM). An increased fractional anisotropy (FA) was also found in the GCC and BCC in injured student athletes (Zhang et al. 2010a), while a decreased FA and increased apparent diffusion coefficient (ADC) were found in internal capsule based on a cohort of 81 professional male boxers and 12 male controls (Chappell et al. 2006). In general, these results also agreed with other neuroimaging findings using data from traffic accidents (Messé et al. 2011; Xiong et al. 2014), falls, and assaults (Messé et al. 2011).
Even for un-concussed players, in CGH-R (cingulum (hippocampus) right) was found to have exceeded the corresponding injury threshold (Fig. 12). This appeared to agree with the notion that athletes even without a clinically diagnosed concussion could still experience significant changes in neuroimaging (Talavage et al. 2014; Bazarian et al. 2014) or cognitive alteration (McAllister et al. 2012; McAllister et al. 2014), presumably a result from local tissue deformation.
Taken together, our biomechanical investigation, especially for results based on εn (Fig. 10 and Fig. 11), appeared to reinforce reports from various neuroimaging studies that have identified the corpus callosum, SLF, UNC, and internal capsule as more frequently injured in mTBI patients (Bigler and Maxwell 2012). Undoubtedly, further studies and more independent models (further see below) are necessary to verify the concordance between biomechanical and neuroimaging findings on a same sizable population in the future. Nevertheless, collectively, these findings do seem to provide a multi-faceted insight into the mechanisms of mTBI.
5.3 Comparison with previous findings
The corpus callosum ranked among the most vulnerable regions for εn-based predictors. However, it did not have the best injury predictive power. For example, AUC of 0.812 and 0.809 for and in the main body, respectively, lower than that for SLF-R: 0.879 and 0.867, respectively; Fig. 4). Further, peak εn in the main body of corpus callous achieved relatively poor AUC, accuracy, sensitivity, specificity scores (0.685, 62.3%, 43.9%, and 79.0%). In contrast, peak εn in this region was one of the “best” injury predictors for the latest KTH model that reported an AUC of 0.9488 (Giordano and Kleiven 2014a). This was notably higher than those achieved in our study. Unfortunately, injury prediction performances based on independent testing datasets were not available in that study to enable a direct, more objective comparison.
Nevertheless, these findings, once again, highlight differences among models. A more systematic and objective comparison of brain responses across models may be valuable to gain further confidence in model-based injury studies. This is particularly true given the challenges for reliable, high-quality model validations at present (Yang et al. 2011) and the fact that significant differences exist even among “validated” models (Ji et al. 2014a). The approach presented here (random subsampling and evaluation of the entire deep WM ROIs and neural tracts via a standard WM atlas) may provide a common framework for future model comparisons (vs. simply peak responses in generic regions (Ji et al. 2014a)). With more independent models analyzing an identical injury dataset using the same approach, the observed concordance between biomechanical and neuroimaging findings may be further reinforced.
5.4 Limitations
Limitations of WHIM on the use of isotropic, homogeneous (vs. anisotropic, heterogeneous) material properties of the brain, and resolution mismatch between FE elements and DTI voxels have been discussed (Ji et al. 2015; Zhao et al. 2016). They are not repeated here. Extensive discussions also exist on errors in the impact kinematics (Newman et al. 2005), the resulting uncertainties in model results, and implications in injury prediction such as under-sampled non-injury cases that could have biased injury thresholds (Zhang et al. 2004; Kleiven 2007; Giordano and Kleiven 2014a). These random kinematic errors likely could significantly influence results on an individual basis. This will be the subject of a future “sensitivity” evaluation. However, they are unlikely to significantly alter the group-wise results presented here such as the relative discriminative power among the injury predictor variables (as indicated by the consistency among random trials; Figs. 4–7) or vulnerabilities among the ROIs/tracts. Importantly, a model-based TBI study is analogous to an ill-posed optimization problem – uncertainties and potential errors will likely persist in virtually all aspects involved. A systems or integrated approach is important to ultimately elucidate the mechanisms behind TBI (Zhao et al. 2016). When additional injury datasets are available, further independent evaluations would reveal whether the findings in this study based on the limited NFL dataset could be generalized to other at-risk populations.
There are several other limitations. First, we have used neuroimaging and whole-brain tractography from one individual to study the NFL athletes on a group-wise basis. Individual variability could not be assessed because their neuroimages were unavailable. Despite this limitation, it must be recognized that our generic head model was a critical stepping stone towards more individualized integration of neuroimaging with TBI biomechanics studies in the future. The model-image mismatch was similar to a recent study that used 2D head models (vs. 3D here) developed from images of a normal individual to study injury of a reconstructed accident in ice-hockey of a different subject (Wright et al. 2013). Another study correlated simulated strain patterns from a generic model with injury findings from individual neuroimages for three reconstructed bicycle accidents, where model and images differed in size and shape (Fahlstedt et al. 2015). An image-atlas-based model represented “averaged” neuroimages but not specific individuals (Miller et al. 2016). Further work is necessary to understand the implications of using generic vs. individualized model and/or neuroimages in injury characterization; however, this is beyond the scope of this study. Nevertheless, importantly, our generic model with the associated neuroimages and whole-brain tractography may provide a valuable tool to enable better integration of neuroimaging and TBI biomechanics studies in the future, especially given that most 50th percentile head models do not yet have detailed neuroimages directly associated with (Zhang et al. 2004; Kleiven 2007; Kimpara and Iwamoto 2012; Takhounts et al. 2013; Giordano and Kleiven 2014a; Sahoo et al. 2016).
Second, a more complete WM atlas also exists (containing as many as 130 ROIs (Zhang et al. 2010b), which was employed before (Wright et al. 2013). Here, we chose to focus on the deep WM ROIs/neural tracts because certain regions deep in the brain appear more susceptible to mTBI based on neuroimaging findings (Kraus et al. 2007; Bigler and Maxwell 2012). In addition, there is inconsistency in representing the brain-skull boundary conditions in FE head models (e.g., frictional sliding interface (Kleiven 2007) vs. direct nodal sharing via a layer of soft CSF in between the brain and skull (Takhounts et al. 2003; Ji et al. 2015). Thus, there could be greater response uncertainty in cortical and sub-cortical regions. Although using ROIs/tracts only in the deep WM did not necessarily eliminate the concern, it was a reasonable compromise, at least at present, to enable our study along this line of research.
Finally, we have used a univariate logistic regression in each WM region (ROI/neural tract) independently to assess injury risk. As concussion is diffuse in nature, a binary brain injury may well have involved damages to multiple (vs. a single) WM ROIs and/or neural tracts (Fig. 13bd). It is reasonable to assume that combining responses from all of these regions could improve injury prediction performance. In this case, responses from each WM region (ROI or tract) could serve as unique “features” to enable more sophisticated analysis techniques – multi-variate logistic regression or machine learning (e.g., support vector machine (Hernandez et al. 2014) – for more effective injury classification. In addition, strain rate (Cullen and LaPlaca 2006), the combination of strain and strain rate (King et al. 2003), inter-regional differences in injury tolerance (Elkin and Morrison 2007), as well as “sustained maximum principal strain” (Fijalkowski et al. 2009) that considers the duration of above-threshold strains (vs. peak strains alone in this study) could also be incorporated. These will be the subjects of future investigations.
6. Conclusion
Using WHIM to simulate brain strain responses in NFL head collisions, we found that two injury susceptibility indices based on fiber strain along WM neural tracts had the best overall performance. SLF (superior longitudinal fasciculus) appeared to be among the most injury discriminative neural tracts (e.g., AUC and accuracy up to 0.879 and 85.2%, using training and testing datasets, respectively, based on tract-wise injury susceptibilities at an optimal strain threshold of 0.10). It was also among the top most vulnerable ones, along with corpus callosum. These findings highlight the unique injury discriminatory potentials of computational models, and may provide important insight into how best to incorporate WM structural anisotropy for investigation of brain injury. Future studies include 1) applying multi-variate analysis techniques to classify injury, while accounting for inter-regional differences in tolerance; 2) investigating the significance of neuroimaging inter-subject variability and accuracy of neural tracts on brain injury risk; and 3) assessing the generalizability of the findings to other at-risk populations using additional, independent injury datasets.
Fig. 5.
Summary of average accuracy measures based on the testing datasets. Four of the nine injury predictor variables achieved the best accuracy score in the CGC-R and SLF-R (four for each; arrows).
Acknowledgments
Funding is provided by the NIH grants R01 NS092853 and R21 NS088781. The authors are grateful to the National Football League (NFL) Committee on Mild Traumatic Brain Injury (MTBI) and Biokinetics and Associates Ltd. for providing the reconstructed head impact kinematics. The authors thank Dr. Thomas W. McAllister at Indiana University for providing neuroimaging data, Dr. James C. Ford and Dr. Laura A. Flashman at Dartmouth College, and Dr. Richard M. Greenwald and Mr. Jonathan Beckwith at Simbex, LLC, for their help. In addition, they thank Dr. Qiang Liu at Dartmouth College, and Ms. Chiara Giordano at Royal Institute of Technology (KTH) for helpful discussions.
APPENDIX A: DESCRIPTION OF DEEP BRAIN WHITE MATTER ATLAS
Table A1.
ICBM-81 deep brain white matter atlas labels and regions of interest (ROI)
| ID | Label | ROI name |
|---|---|---|
| 1 | MCP | Middle cerebellar peduncle |
| 2 | PCT | Pontine crossing tract (a part of MCP) |
| 3 | GCC | Genu of corpus callosum |
| 4 | BCC | Body of corpus callosum |
| 5 | SCC | Splenium of corpus callosum |
| 6 | FX | Fornix (column and body of fornix) |
| 7 | CST-R | Corticospinal tract right |
| 8 | CST-L | Corticospinal tract left |
| 9 | ML-R | Medial lemniscus right |
| 10 | ML-L | Medial lemniscus left |
| 11 | ICP-R | Inferior cerebellar peduncle right |
| 12 | ICP-L | Inferior cerebellar peduncle left |
| 13 | SCP-R | Superior cerebellar peduncle right |
| 14 | SCP-L | Superior cerebellar peduncle left |
| 15 | CP-R | Cerebral peduncle right |
| 16 | CP-L | Cerebral peduncle left |
| 17 | ALIC-R | Anterior limb of internal capsule right |
| 18 | ALIC-L | Anterior limb of internal capsule left |
| 19 | PLIC-R | Posterior limb of internal capsule right |
| 20 | PLIC-L | Posterior limb of internal capsule left |
| 21 | RLIC-R | Retrolenticular part of internal capsule right |
| 22 | RLIC-L | Retrolenticular part of internal capsule left |
| 23 | ACR-R | Anterior corona radiata right |
| 24 | ACR-L | Anterior corona radiata left |
| 25 | SCR-R | Superior corona radiata right |
| 26 | SCR-L | Superior corona radiata left |
| 27 | PCR-R | Posterior corona radiata right |
| 28 | PCR-L | Posterior corona radiata left |
| 29 | PTR-R | Posterior thalamic radiation (include optic radiation) right |
| 30 | PTR-L | Posterior thalamic radiation (include optic radiation) left |
| 31 | SS-R | Sagittal stratum (include inferior longitidinal fasciculus and inferior fronto-occipital fasciculus) right |
| 32 | SS-L | Sagittal stratum (include inferior longitidinal fasciculus and inferior fronto-occipital fasciculus) left |
| 33 | EC-R | External capsule right |
| 34 | EC-L | External capsule left |
| 35 | CGC-R | Cingulum (cingulate gyrus) right |
| 36 | CGC-L | Cingulum (cingulate gyrus) left |
| 37 | CGH-R | Cingulum (hippocampus) right |
| 38 | CGH-L | Cingulum (hippocampus) left |
| 39 | FX/ST-R | Fornix (cres) / Stria terminalis (cannot be resolved with current resolution) right |
| 40 | FX/ST-L | Fornix (cres) / Stria terminalis (cannot be resolved with current resolution) left |
| 41 | SLF-R | Superior longitudinal fasciculus right |
| 42 | SLF-L | Superior longitudinal fasciculus left |
| 43 | SFO-R | Superior fronto-occipital fasciculus (could be a part of anterior internal capsule) right |
| 44 | SFO-L | Superior fronto-occipital fasciculus (could be a part of anterior internal capsule) left |
| 45 | IFO-R | Inferior fronto-occipital fasciculus right |
| 46 | IFO-L | Inferior fronto-occipital fasciculus left |
| 47 | UNC-R | Uncinate fasciculus right |
| 48 | UNC-L | Uncinate fasciculus left |
| 49 | TAP-R | Tapatum right |
| 50 | TAP-L | Tapatum left |
APPENDIX B: ONE-SIDED PERMUTATION TEST
We adopted a non-parametric, one-sided permutation test (Rice 2006) to compare injury prediction performances and vulnerabilities of the deep WM ROIs/neural tracts. A paired-sample t-statistic is first calculated according to:
| (A1) |
| (A2) |
where d̄ is the mean of the difference between two samples, x and y; s is the standard deviation of d; and n is the sample size. The pseudo-algorithm for the permutation test is described below:
Step 1. For a given pair of data samples, calculate the baseline paired-sample t-statistic, T0, using Eqns. A1 and A2.
Step 2. Randomly flip the pairs of values from the two samples to generate two new samples.
Step 3. Compute a new paired-sample t-statistic, Tperm, using the newly generated samples from Step 2.
Step 4. Repeat Steps 2–3 by Nperm times (e.g., 100).
- Step 5. Calculate a probability p-value:
(A3)
where “#(Tperm > T0)” is the number of permutations where Tperm is found to be greater than T0. A p-value smaller than a given threshold (e.g., 0.05) is considered a strong indication that the given pair has a statistically significant difference.
Footnotes
Conflict of interest
We have no competing interests.
References
- (NRC) I of M (IOM) and NRC. Sports-related concussions in youth: improving the science, changing the culture. Washington, DC: 2014. [PubMed] [Google Scholar]
- Allison Ma, Kang YS, Bolte JH, et al. Validation of a helmet-based system to measure head impact biomechanics in ice hockey. Med Sci Sports Exerc. 2014;46:115–23. doi: 10.1249/MSS.0b013e3182a32d0d. [DOI] [PubMed] [Google Scholar]
- Anderson AE, Ellis BJ, Weiss Ja. Verification, validation and sensitivity studies in computational biomechanics. Comput Methods Biomech Biomed Engin. 2007;10:171–84. doi: 10.1080/10255840601160484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson JLR, Jenkinson M, Smith S. Non-linear registration aka Spatial normalisation FMRIB Technial Report TR07JA2. In Pract. 2007;22 [Google Scholar]
- Arlot S, Celisse A. A survey of cross-validation procedures for model selection *. Stat Surv. 2010;4:40–79. [Google Scholar]
- Bain AC, Meaney DF. Tissue-level thresholds for axonal damage in an experimental model of central nervous system white matter injury. J Biomech Eng. 2000;122:615–622. doi: 10.1115/1.1324667. [DOI] [PubMed] [Google Scholar]
- Bandak FA, Eppinger RH. A Three-Dimensional Finite Element Analysis of the Human Brain Under Combined Rotational and Translational Accelerations; Proceedings, 38th Stapp Car Crash Conf., SAE Paper No. 942215; 1994. pp. 145–163. [Google Scholar]
- Bazarian JJ, Zhu T, Zhong J, et al. Persistent, Long-term Cerebral White Matter Changes after Sports-Related Repetitive Head Impacts. PLoS One. 2014;9:e94734. doi: 10.1371/journal.pone.0094734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckwith JG, Greenwald RM, Chu JJ. Measuring head kinematics in football: correlation between the head impact telemetry system and Hybrid III headform. Ann Biomed Eng. 2012;40:237–48. doi: 10.1007/s10439-011-0422-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bigler ED, Maxwell WL. Neuropathology of mild traumatic brain injury: Relationship to neuroimaging findings. Brain Imaging Behav. 2012;6:108–136. doi: 10.1007/s11682-011-9145-0. [DOI] [PubMed] [Google Scholar]
- CDC. Report to Congress on Traumatic Brain Injury in the United States: Epidemiology and Rehabilitation. 2015. [DOI] [PubMed] [Google Scholar]
- Chappell MH, Uluğ AM, Zhang L, et al. Distribution of microstructural damage in the brains of professional boxers: A diffusion MRI study. J Magn Reson Imaging. 2006;24:537–542. doi: 10.1002/jmri.20656. [DOI] [PubMed] [Google Scholar]
- Chatelin S, Constantinesco A, Willinger R. Fifty years of brain tissue mechanical testing: From in vitro to in vivo investigations. Biorheology. 2010;47:255–276. doi: 10.3233/BIR-2010-0576. [DOI] [PubMed] [Google Scholar]
- Chatelin S, Deck C, Renard F, et al. Computation of axonal elongation in head trauma finite element simulation. J Mech Behav Biomed Mater. 2011;4:1905–19. doi: 10.1016/j.jmbbm.2011.06.007. [DOI] [PubMed] [Google Scholar]
- Cubon Va, Putukian M, Boyer C, Dettwiler A. A diffusion tensor imaging study on the white matter skeleton in individuals with sports-related concussion. J Neurotrauma. 2011;28:189–201. doi: 10.1089/neu.2010.1430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cullen DK, LaPlaca MC. Neuronal response to high rate shear deformation depends on heterogeneity of the local strain field. J Neurotrauma. 2006;23:1304–19. doi: 10.1089/neu.2006.23.1304. [DOI] [PubMed] [Google Scholar]
- Donnelly BR, Morgan RM, Eppinger RH. Durability, repeatability and reproducibility of the NHTSA side impact dummy. Stapp Car Crash J. 1983;27:299–310. [Google Scholar]
- Elkin BS, Morrison B. Region-specific tolerance criteria for the living brain. Stapp Car Crash J. 2007;51:127–38. doi: 10.4271/2007-22-0005. [DOI] [PubMed] [Google Scholar]
- Fahlstedt M, Depreitere B, Halldin P, et al. Correlation between injury pattern and finite element analysis in biomechanical reconstructions of traumatic brain injuries. J Biomech. 2015;48:1331–1335. doi: 10.1016/j.jbiomech.2015.02.057. [DOI] [PubMed] [Google Scholar]
- Fijalkowski RJ, Yoganandan N, Zhang J, Pintar FA. A Finite Element Model of Region-Specific Response for Mild Diffuse Brain Injury. 2009 doi: 10.4271/2009-22-0007. [DOI] [PubMed] [Google Scholar]
- Gardner A, Kay-Lambkin F, Stanwell P, et al. A systematic review of diffusion tensor imaging findings in sports-related concussion. J Neurotrauma. 2012;29:2521–38. doi: 10.1089/neu.2012.2628. [DOI] [PubMed] [Google Scholar]
- Garimella HT, Kraft RH. Modeling the mechanics of axonal fiber tracts using the embedded finite element method. Int j numer method biomed eng. 2016;02823:26–35. doi: 10.1002/cnm.2823. [DOI] [PubMed] [Google Scholar]
- Giordano C, Kleiven S. Evaluation of Axonal Strain as a Predictor for Mild Traumatic Brain Injuries Using Finite Element Modeling. 2014a doi: 10.4271/2014-22-0002. [DOI] [PubMed] [Google Scholar]
- Giordano C, Kleiven S. Connecting fractional anisotropy from medical images with mechanical anisotropy of a hyperviscoelastic fibre-reinforced constitutive model for brain tissue. J R Soc Interface. 2014b;11:1–14. doi: 10.1098/rsif.2013.0914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardy WN, Foster CD, Mason MJ, et al. Investigation of Head Injury Mechanisms Using Neutral Density Technology and High-Speed Biplanar X-ray. Stapp Car Crash J. 2001;45:337–68. doi: 10.4271/2001-22-0016. [DOI] [PubMed] [Google Scholar]
- Hardy WN, Mason MJ, Foster CD, et al. A Study of the Response of the Human Cadaver Head to Impact. Stapp Car Crash J. 2007;51:17–80. doi: 10.4271/2007-22-0002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez F, Wu LC, Yip MC, et al. Six Degree of Freedom Measurements of Human Mild Traumatic Brain Injury. Ann Biomed Eng. 2014;43:1918–1934. doi: 10.1007/s10439-014-1212-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji S, Ghadyani H, Bolander RP, et al. Parametric Comparisons of Intracranial Mechanical Responses from Three Validated Finite Element Models of the Human Head. Ann Biomed Eng. 2014a;42:11–24. doi: 10.1007/s10439-013-0907-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji S, Zhao W. A pre-computed brain response atlas for instantaneous strain estimation in contact sports. Ann Biomed Eng. 2015;43:1877–1895. doi: 10.1007/s10439-014-1193-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji S, Zhao W, Ford JC, et al. Group-wise evaluation and comparison of white matter fiber strain and maximum principal strain in sports-related concussion. J Neurotrauma. 2015;32:441–454. doi: 10.1089/neu.2013.3268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji S, Zhao W, Li Z, McAllister TW. Head impact accelerations for brain strain-related responses in contact sports: a model-based investigation. Biomech Model Mechanobiol. 2014b;13:1121–36. doi: 10.1007/s10237-014-0562-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimpara H, Iwamoto M. Mild traumatic brain injury predictors based on angular accelerations during impacts. Ann Biomed Eng. 2012;40:114–26. doi: 10.1007/s10439-011-0414-2. [DOI] [PubMed] [Google Scholar]
- Kimpara H, Nakahira Y, Iwamoto M, et al. Investigation of anteroposterior head-neck responses during severe frontal impacts using a brain-spinal cord complex FE model. Stapp Car Crash J. 2006;50:509–44. doi: 10.4271/2006-22-0019. [DOI] [PubMed] [Google Scholar]
- King AI, Yang KH, Zhang L, et al. Is head injury caused by linear or angular acceleration?. IRCOBI Conference; Lisbon, Portugal. 2003. pp. 1–12. [Google Scholar]
- Kleiven S. Evaluation of head injury criteria using a finite element model validated against experiments on localized brain motion, intracerebral acceleration, and intracranial pressure. Int J Crashworthiness. 2006;11:65–79. [Google Scholar]
- Kleiven S. Predictors for Traumatic Brain Injuries Evaluated through Accident Reconstructions. Stapp Car Crash J. 2007;51:81–114. doi: 10.4271/2007-22-0003. [DOI] [PubMed] [Google Scholar]
- Kraft RH, McKee PJ, Dagro AM, Grafton ST. Combining the finite element method with structural connectome-based analysis for modeling neurotrauma: connectome neurotrauma mechanics. PLoS Comput Biol. 2012;8:e1002619. doi: 10.1371/journal.pcbi.1002619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraus MF, Susmaras T, Caughlin BP, et al. White matter integrity and cognition in chronic traumatic brain injury: a diffusion tensor imaging study. 2007:2508–2519. doi: 10.1093/brain/awm216. [DOI] [PubMed] [Google Scholar]
- Mao H, Zhang L, Jiang B, et al. Development of a finite element human head model partially validated with thirty five experimental cases. J Biomech Eng. 2013;135:111002–15. doi: 10.1115/1.4025101. [DOI] [PubMed] [Google Scholar]
- Marjoux D, Baumgartner D, Deck C, Willinger R. Head injury prediction capability of the HIC, HIP, SIMon and ULP criteria. Accid Anal Prev. 2008;40:1135–1148. doi: 10.1016/j.aap.2007.12.006. [DOI] [PubMed] [Google Scholar]
- McAllister TW, Flashman La, Maerlender a, et al. Cognitive effects of one season of head impacts in a cohort of collegiate contact sport athletes. Neurology. 2012;78:1777–84. doi: 10.1212/WNL.0b013e3182582fe7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAllister TW, Ford JC, Flashman L a, et al. Effect of head impacts on diffusivity measures in a cohort of collegiate contact sport athletes. Neurology. 2014;82:63–9. doi: 10.1212/01.wnl.0000438220.16190.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messé A, Caplain S, Paradot G, et al. Diffusion tensor imaging and white matter lesions at the subacute stage in mild traumatic brain injury with persistent neurobehavioral impairment. Hum Brain Mapp. 2011;32:999–1011. doi: 10.1002/hbm.21092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller LE, Urban JE, Stitzel JD. Development and validation of an atlas-based finite element brain model model. Biomech Model. 2016 doi: 10.1007/s10237-015-0754-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S, Oishi K, Jiang H, et al. Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. Neuroimage. 2008;40:570–582. doi: 10.1016/j.neuroimage.2007.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman J, Shewchenko N, Welbourne E. A proposed new biomechanical head injury assessment function-the maximum power index. Stapp Car Crash J. 2000;44:215–247. doi: 10.4271/2000-01-SC16. [DOI] [PubMed] [Google Scholar]
- Newman JA, Beusenberg MC, Shewchenko N, et al. Verification of biomechanical methods employed in a comprehensive study of mild traumatic brain injury and the effectiveness of American football helmets. J Biomech. 2005;38:1469–81. doi: 10.1016/j.jbiomech.2004.06.025. [DOI] [PubMed] [Google Scholar]
- Niogi SN, Mukherjee P, Ghajar J, et al. Extent of microstructural white matter injury in postconcussive syndrome correlates with impaired cognitive reaction time: a 3T diffusion tensor imaging study of mild traumatic brain injury. AJNR Am J Neuroradiol. 2008;29:967–73. doi: 10.3174/ajnr.A0970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pellman EJ, Viano DC, Tucker A, Casson IR. Concussion in professional football: location and direction of helmet impacts — part 2. Neurosurgery. 2003;53:1328–1341. doi: 10.1227/01.neu.0000093499.20604.21. [DOI] [PubMed] [Google Scholar]
- Rice JA. Mathematical statistics and data analysis. 3. Duxbury Advanced; Belmont, MA: 2006. [Google Scholar]
- Sabet AA, Christoforou E, Zatlin B, et al. Deformation of the human brain induced by mild angular head acceleration. J Biomech. 2008;41:307–315. doi: 10.1016/j.jbiomech.2007.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahoo D, Deck C, Willinger R. Development and validation of an advanced anisotropic visco-hyperelastic human brain FE model. J Mech Behav Biomed Mater. 2014;33:24–42. doi: 10.1016/j.jmbbm.2013.08.022. [DOI] [PubMed] [Google Scholar]
- Sahoo D, Deck C, Willinger R. Brain injury tolerance limit based on computation of axonal strain. Accid Anal Prev. 2016;92:53–70. doi: 10.1016/j.aap.2016.03.013. [DOI] [PubMed] [Google Scholar]
- Shenton ME, Hamoda HM, Schneiderman JS, et al. A review of magnetic resonance imaging and diffusion tensor imaging findings in mild traumatic brain injury. Brain Imaging Behav. 2012;6:137–92. doi: 10.1007/s11682-012-9156-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan S, Eucker S a, Gabrieli D, et al. White matter tract-oriented deformation predicts traumatic axonal brain injury and reveals rotational direction-specific vulnerabilities. Biomech Model Mechanobiol. 2014 doi: 10.1007/s10237-014-0643-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takhounts EG, Craig MJ, Moorhouse K, et al. Development of Brain Injury Criteria (BrIC) Stapp Car Crash J. 2013;57:243–66. doi: 10.4271/2013-22-0010. [DOI] [PubMed] [Google Scholar]
- Takhounts EG, Ridella SA, Tannous RE, et al. Investigation of Traumatic Brain Injuries Using the Next Generation of Simulated Injury Monitor (SIMon) Finite Element Head Model. Stapp Car Crash J. 2008;52:1–31. doi: 10.4271/2008-22-0001. [DOI] [PubMed] [Google Scholar]
- Takhounts EGE, Eppinger RRH, Campbell JQ, et al. On the Development of the SIMon Finite Element Head Model. Stapp Car Crash J. 2003;47:107–133. doi: 10.4271/2003-22-0007. [DOI] [PubMed] [Google Scholar]
- Talavage TM, Nauman E, Breedlove EL, et al. Functionally-Detected Cognitive Impairment in High School Football Players Without Clinically-Diagnosed Concussion. J Neurotrauma. 2014;31:327–338. doi: 10.1089/neu.2010.1512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viano DC, Casson IR, Pellman EJ, et al. Concussion in professional football: Brain responses by finite element analysis - Part 9. 2005 doi: 10.1227/01.neu.0000186950.54075.3b. [DOI] [PubMed] [Google Scholar]
- Weaver AA, Danelson KA, Stitzel JD. Modeling brain injury response for rotational velocities of varying directions and magnitudes. Ann Biomed Eng. 2012;40:2005–18. doi: 10.1007/s10439-012-0553-0. [DOI] [PubMed] [Google Scholar]
- Wilcoxon F. Individual comparisons of grouped data by ranking methods. J Econ Entomol. 1946;39:269. doi: 10.1093/jee/39.2.269. [DOI] [PubMed] [Google Scholar]
- Wright RM, Post A, Hoshizaki B, Ramesh KT. A multiscale computational approach to estimating axonal damage under inertial loading of the head. J Neurotrauma. 2013;30:102–18. doi: 10.1089/neu.2012.2418. [DOI] [PubMed] [Google Scholar]
- Wright RM, Ramesh KT. An axonal strain injury criterion for traumatic brain injury. Biomech Model Mechanobiol. 2012;11:245–60. doi: 10.1007/s10237-011-0307-1. [DOI] [PubMed] [Google Scholar]
- Xiong K, Zhu Y, Zhang Y, et al. White matter integrity and cognition in mild traumatic brain injury following motor vehicle accident. Brain Res. 2014;1591:86–92. doi: 10.1016/j.brainres.2014.10.030. [DOI] [PubMed] [Google Scholar]
- Yang K, Mao H, Wagner C, et al. Modeling of the Brain for Injury Prevention. In: Bilston LE, editor. Studies in Mechanobiology, Tissue Engineering and Biomaterials. Springer-Verlag Berlin Heidelberg; 2011. pp. 69–120. [Google Scholar]
- Zhang K, Johnson B, Pennell D, et al. Are functional deficits in concussed individuals consistent with white matter structural alterations: Combined FMRI & DTI study. Exp Brain Res. 2010a;204:57–70. doi: 10.1007/s00221-010-2294-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Yang KH, King AI. A Proposed Injury Threshold for Mild Traumatic Brain Injury. J Biomech Eng. 2004 doi: 10.1115/1.1691446. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Zhang J, Oishi K, et al. Atlas-guided tract reconstruction for automated and comprehensive examination of the white matter anatomy. Neuroimage. 2010b;52:1289–1301. doi: 10.1016/j.neuroimage.2010.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W, Ford JC, Flashman LA, et al. White Matter Injury Susceptibility via Fiber Strain Evaluation using Whole-Brain Tractography. J Neurotrauma. 2016;33:1834–1847. doi: 10.1089/neu.2015.4239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W, Ji S. Brain strain uncertainty due to shape variation in and simplification of head angular velocity profiles. Biomech Model Mechanobiol. 2016 doi: 10.1007/s10237-016-0829-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W, Ji S. Parametric investigation of regional brain strain responses via a pre-computed atlas. IRCOBI Conference; Lyon, France. 2015. pp. 208–220. [Google Scholar]