TumourMetrics: a comprehensive clinical solution for the standardization of DCE-MRI analysis in research and routine use

Abstract

Background

A reliable analysis methodology is needed to provide valuable imaging biomarkers for clinical trials, with particular regards to dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) application using pharmacokinetic (PK) model analysis. In order to address this scientific challenge, we provided a comprehensive analysis solution that could overcome the impediments to clinical research and routine use.

Methods

TumourMetrics has been designed to meet the Quantitative Imaging Biomarkers Alliance (QIBA) v.1.0 profile. The quality performance was assessed using the QIBA test data and our customizable numeric phantom. The analysis workflow is made customizable to facilitate standardization of optimized protocol across centers.

Results

Our quantification workflow estimated the PK model parameters accurately. The method is robust, almost fully automatic and allows a direct integration of the results into the diagnostic workflow.

Conclusions

The analysis is easy-to-use and accessible for routine implementation of DCE-MRI into clinical practice.

Introduction

Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is a noninvasive widely used method of investigating the tumour vasculature environment.

For a brief description, the measurement technique consists of repeated (dynamic) T1-weighted acquisitions following a bolus injection of low-molecular weight gadolinium-chelate contrast agent (Gd). As the measured signal enhancement is related to the uptake of Gd in the investigated tissues vasculature, the method is sensitive to the quality of tumour vascularization and related characteristics of tumour angiogenesis, like vascular permeability, extracellular extravascular space, vascular volume, and blood flow. However, these measurements suffer from considerable variation in acquisition methods, analysis approaches and operator procedure, making very difficult direct comparison of the results in multi-centric trials. As a result of this, several studies demonstrated higher diagnostic performance using pharmacokinetic (PK) modelling. The aim for this quantitative approach has been to overcome the unwanted dependences like the subject inter- and intra-variability, the inter observer variability, so that the derived parameters only reflect the local tissue properties. The added value of this quantitative method for tissue characterization has been shown in the prostate, liver, head and neck (1-3).

In recent years, the development of novel anti-angiogenic and anti-vascular cancer therapies has led to important considerations regarding the potentiality for DCE-MRI measurement to be used as an imaging biomarker of drug efficacy in clinical trials of angiogenesis inhibitors, because conventional end points based on reduction in tumour size may be inadequate for evaluating the clinical response. However, the results published by many investigators, particularly in clinical studies (4) are not directly comparable because of significant discrepancies in equipment, data acquisition protocol, PK model used, parameter estimation methods and quantitative imaging endpoints.

In 2004, the NCI CIP MR Workshop on translational research in cancer published guidance on how and under which conditions to apply these techniques for use in phase 1/2a trials of anti-cancer therapeutics affecting tumour vascular function (5). An European update of this guideline was published by Leach et al. (6), and more recently, guidance to practical aspects for successfully implementing the methodology was presented by the Quantitative Imaging Biomarkers Alliance (QIBA) group (7).

In the present context where there is no global consensus on standardized software, data analysis is proposed to be performed centrally. What usually happens is that the solution comes either from the trial investigator research group using custom-designed validated software, or from partnering with a specialized software company. As imaging practicians of participating sites, we experienced that this situation does not clearly support the use of DCE-MRI for further developments, because of the lack of facilities to access or to implement the methodology into clinical practice. The implementation may require long term investment in resources that could not be reached at most centers. Combined with the apparent complexity to integrate the post-processing task into the routine reviewing and reporting process, outside of academic institutions, there are likely to be few radiologists in clinical practice who will be familiar or enthusiast with the use of these software.

Therefore, the purpose of the present project is threefold: (I) to present standardized analysis methods for the quantification of DCE-MRI data to achieve the required compliance level of multi-centric trials; (II) to validate the quality performance of the methods; (III) to provide an easy-to-use and accessible solution for routine implementation into clinical practice.

Existing analysis software

Among existing medical software, several custom-designed post-processing tools have been made available for free for educational and research purposes [Toppcat (8), DcemriS4 (9), DATforDCEMRI (10), DCEMRI.jl (11) …]. These in-house solutions are commonly a collection of functions built under a programming environment such as Matlab, LabView or IDL. They are mostly designed for a specific study and with limited functionalities, such as reading and reporting in DICOM format, incorporating AIF data, or integrating the T₁ map calculation, thus involving expertise and programing competence for clinical implementation in order to meet the global consensus requirements on standardized software.

Beside this, scanner and software vendors have started to provide a complete PACS integrated clinical solution. In this concept, the DCE-MRI post-processing is easily performed and ready for interpretation, and results may be integrated into the formatted reporting of studies. Dedicated applications like Tissue 4D (Siemens), DCE Tool (OsiriX), iCAD (Nashua), DynaCAD (Invivo), GenIQ (GE), T1 permeability (Philips) and Olea Sphere (Olea Medical Solutions Inc.) are capable to perform DCE-MRI analysis based on PK modelling methods. Although all of these solutions can incorporate a common basic Tofts model, only GenIQ, Intetellispace and Olea Sphere can process individual AIF measurement as expected in anti-cancer therapy trials, while Aegis and DynaCad did not implement a T₁ mapping process. Beyond these prerequisite components, multiple differences in the analysis approaches, such as the determination of contrast arrival time, the fit optimization method and the definition of noise may also have significant influence on the calculation of the PK parameters (12-14). Consequently, the standardization of the methods and analysis algorithms used remains a major challenge, and will require significant collaboration between manufacturers to adopt the same methodology to achieve an “industry standards”, or to allow flexible parametrization of the analysis protocol, with enough open access to implement specific and novel analysis approaches, while preserving some proprietary components. In the present situation where it is likely a difficult commercial issue for industry to adopt such a policy, we think that TumourMetrics could be a standardized clinical solution.

Key features of TumourMetrics

For a brief overview, the TumourMetrics module for DCE-MRI is a comprehensive software application for the quantitative evaluation of DCE-MRI studies in clinical practice. The base configuration runs as plugins in the PACS viewer, but it can also be made standalone in any external local PC workspace. The intensive computational tasks needed for parameter maps calculations are programmed in C⁺⁺, whereas tasks like viewing, segmentation, statistics or appropriate analysis, and reporting, that require operator interactivity on the resulted maps runs as plugins in ImageJ, a public domain open source Java-based image processing program authored and maintained by Wayne Rasband at the National Institute of Mental Health (rsb.info.nih.gov/ij/).

Beyond the main task common to PK analysis software, several features in the workflow make TumourMetrics suitable to be used as a platform for comprehensive analysis and diagnostic decision support:

• ❖ Fully compliant with the QIBA v.1.0 profile (5).

• ❖ Quality performance of the proposed methodology validated using the QIBA test data.

• ❖ Can be standalone or integrated to PACS for automatic reading and reporting.

• ❖ Full automated workflow, excepted in the determination of the measured AIF, where the segmentation of the feeding artery is performed semi-automatically. Because an inadequate AIF severely impacts on the reliability of DCE-MRI parameters, this step needs to be validated by the operator. The key feature of the automated process relies on the recognition of the study type contained in the Dicom study description (e.g., prostate, breast). TumourMetrics package provides study configuration files for breast, prostate, head and neck and research studies. All analysis parameters are set in these files to perform automatically the QA and the calculation workflow. Other parameters like the r₁ relaxivity of Gd contrast agent are read in allocated data files during the processing.

• ❖ Flexible design to meet the specificity of new study trials and the continual evolution of analysis approaches.

• ❖ Innovative parametric classification of suspicious voxels, semi-automated ROI selection tools, improving the inter-observer reproducibility.

• ❖ Total volume parametric segmentation with histogram analysis.

• ❖ Including a versatile numeric phantom generator of dynamic and T1 mapping series based on Buckley (15) data to enable comparison with other analysis methods or with new model.

• ❖ No format incompatibility issues to import studies from main scanner manufacturers.

• ❖ Not requiring dedicated workstation, special training and prerequisite data manipulation (i.e., format conversion) imposed by many of commercial or research software.

Methods

Description of the workflow

Input

Transfer of the DCE-MRI and T1 mapping series in the working space:

• ❖ Directly from PACS viewer, with variable levels of integration.

• ❖ Or manually from all other supports.

Running of PK analysis

• ❖ Identification of the study type to apply the pre-defined analysis protocols. Each protocol is a customizable text file that contains needed information to perform the analysis automatically.

• ❖ Identification of series used for variable flip angle (FA) method.

• ❖ Quality assurance checking

• ❖ Motion correction (optional): make use of Elastix (16).

• ❖ T₁₀ mapping and conversion to Gd concentration.

• ❖ Application of the AIF method defined in the protocol.

• ❖ Fitting routine.

• ❖ Generate parametric images with color interpretation.

• ❖ Send the results to PACS.

Interpretation and reporting

• ❖ Direct launch to ImageJ graphical user interface (GUI).

• ❖ User login.

• ❖ Reporting of findings to PACS.

Output: DICOM formatted color-coded parameter maps

• ❖ K^trans (min⁻¹): volume transfer constant. This parameter is the most often used DCE-MRI end-point for early phase trials of anti-cancer therapy.

• ❖ Kep (min⁻¹): symmetric exchange rate of contrast agent across the capillary wall. The ratio of K^trans by Kep is Ѵe, the volume fraction of extra-vascular extra-cellular space (EES) in the voxel.

• ❖ Ѵp: is the volume fraction of blood plasma within a voxel, related directly to angiogenesis.

• ❖ Z₀ (s): is the central reduced value of the arrival time t0, a better means to detect an early enhancement, which is common in tumours.

• ❖ WO (%): washout expressed as (S_wash-in − S_late)/S_late, where S_wash-in is the maximal enhancement and S_late the enhancement at last measurement.

• ❖ IAUGCbn: is the blood normalized initial (over 60 min by default) area under the Gd curve in the voxel.

T₁₀ determination

The implemented algorithm makes use of the 3D spoiled gradient-echo (SPGRE) with variable FA known as DESPOT1 (17). The method can include 2 to 10 measurements using different FAs θ from which T₁₀ maps with the same coverage as DCE-MRI is achieved. In the analysis protocol, T₁₀ value can also be fixed for specific need.

Conversion to Gd concentration

For a typical SPGRE acquisition, the conversion of relative enhancement S(t)/S₀ to concentration of Gd in tissue C_t(t) is determined by:

$$C{}_{\text{t}}\left(\text{t}\right)\text{=}\frac{\text{-1}}{{\text{r}}_{1}TR}\left[\frac{TR}{T_{10}}+\ln \left(\frac{\left(\frac{S\left(t\right)}{S_0}\frac{1-E}{1-\cos \left(\theta \right)E}-1\right)}{\left(\frac{S\left(t\right)}{S_0}\cos \left(\theta \right)\frac{1-E}{1-\cos \left(\theta \right)E}-1\right)}\right)\right]$$ [1]

where E=e^−TR/T10, r₁ is the relaxivity of Gd chelate and θ is the acquisition FA.

AIF methods

The extended Tofts model (described below) requires that C_p, the concentration-time course of contrast agent in the vascular compartment is modelled by an arterial input function (AIF) which reflects the blood supply to the examined tissue. The analysis protocol can be set to use a subject-specific AIF by direct measurement, or a generic mathematic function.

Subject-specific AIF

For a better reproducibility, we implemented a semi-automated search algorithm to generate a locally optimal AIF. The method consists first of a user-defined box that delimits the search region to the input vessels. By using the ImageJ GUI, the task is assisted by an automatic display of the subtraction series presenting the maximal arterial enhancement, this helps the operator to locate easily the vascular structure before defining the box. Then the search algorithm identifies all voxels above a signal intensity threshold (by default 90% of the whole maximum), and using a region growing method, extends the selection in the whole imaging volume entering in the threshold. Next, the Gd concentrations under the selection were corrected to plasma concentrations using:

$$AI{F}_{plama}=AI{F}_{blood}/\left(1-Htc\right)$$

where by default, the hematocrit Hct is 0.45, but is adjustable in GUI. Then, C_p is calculated using Eq. [1], by assuming an arterial blood T₁₀ of 1,440 ms.

A mathematical modelling of this measured AIF is then calculated using bi-exponential (by default), Orton (18) or mixed model (19):

$$C_p(t)=D[a_1{(t-t_0)}^{c}exp(-m_1(t-t_0))+a_{2}exp(-m_2(t-t_0))]$$ [2]

with D (mmol/kg) the dose of contrast agent, t₀ the arrival time in tissue, a₁, a₂ describing the exponential components amplitude with decay m₁, m₂, and c simulating the bolus dispersion effect, which equals 0 for bi-exponential, 1 for Orton and any other values for mixed models.

The purpose of this modelling is to produce an AIF free of pulsatile and body motion artifact. All options are let open, including the possibility to choose a standard AIF (below), or the model-free measurement, depending on the study design. This should be set by special consensus in the study protocol.

Standard and population-averaged AIF

If AIF cannot be sampled adequately, a more robust parameter estimate can be achieved by using a population-averaged AIF. From the literature, we optionally included for different range of temporal resolution (TS) 3 commonly used bi-exponential AIF {c=0 in Eq. [2]} obtained from healthy general population:

• ❖ Weinmann (20): (TS >20 s) a₁ =3.99 kg/L, a₂ =4.78 kg/L, m₁ =0.144 min⁻¹, m₂ =0.0111 min⁻¹.

• ❖ Fritz-Hansen (21): (6< TS <20 s) a₁ =24 kg/L, a₂ =6.2 kg/L, m₁ =3.0 min⁻¹, m₂ =0.016 min⁻¹.

• ❖ Parker (22): (TS <6 s) a₁ =65 kg/L, a₂ =13 kg/L, m₁ =4.9 min⁻¹, m₂ =0.08 min⁻¹.

A custom designed AIF can also be set in the analysis protocol.

Fitting algorithm and strategy

The general consensus for clinical trials is to apply the general bi-compartmental PK model described by Tofts et al. (23). In theory, the model considers the exchange between plasmatic and EES compartments within the capillary endothelium acting as a symmetric semi-permeable membrane. Therefore, under the assumption that the contrast agent is well-mixed in the blood plasma, the equilibrium is described by:

$$\frac{d{C}_t\left(t\right)}{dt}=v_p\frac{d{C}_p\left(t\right)}{dt}+K^{trans}\left[C_p\left(t\right)-\frac{\left(C_t\left(t\right)-v_p{C}_p\left(t\right)\right)}{v_e}\right]$$ [3]

For a bi-exponential AIF model (2), the analytic solution of this differential equation is:

$$C_t\left(t>t_0\right)=D{K}^{trans}{\displaystyle \sum _{i=1}^2\frac{a_i\left(\exp \left(-K_{ep}\left(t-t_0\right)\right)-\exp \left(-m_i\left(t-t_0\right)\right)\right)}{\left(m_i-K_{ep}\right)}}+D{v}_p{\displaystyle \sum _{i=1}^2{a}_i\exp \left(-m_i\left(t-t_0\right)\right)}$$ [4]

where kep =K^trans/Ѵ_e is symmetric exchange rate of contrast agent across the capillary wall.

This time equation directly relates the measured concentration data to model parameters K^trans, Kep and Ѵp, as well as t₀, which have to be extracted using a non-linear fitting algorithm (bellow).

For any forms of AIF model, the general solution of (3) is written:

$$C_{\text{t}}\left(t\right)=v_p{C}_p\left(t\right)=K^{trans}{\displaystyle {\int }_0^t{C}_p}\left(t\text{'}\right)\exp \left(-\frac{K^{trans}}{v_e}\left(t-t\text{'}\right)\right)dt\text{'}$$ [5]

and usually, it is calculated using deconvolution techniques via the transfer function:

$$H\left(i\omega \right)=\frac{C_t\left(i\omega \right)}{C_p\left(i\omega \right)}=\frac{v_p{v}_{e}i\omega +K^{trans}\left(v_p+v_e\right)}{v_{e}i\omega +K^{trans}}$$ [6]

where iω is the variable in frequency domain.

In time or in frequency domain, two fitting routines that can be set freely in the analysis protocol have been implemented in C⁺⁺ for rapid pixel-wise estimation of the model parameters. We included the commonly used Levenberg-Marquardt (LM) algorithm (24) and adapted the BOBYQA algorithm (25) which was initially written in FORTRAN. What makes the difference is the way in which the iterative steps minimize the χ² to approach the global best-fit: the LM is a “line search” method which determines directionally the value of fitting parameters, whereas BOBYQA uses the trust region algorithm to minimize χ² within small regions surrounding the current estimate of the solution and is less likely to find local minima, but is more computationally demanding.

Report of error estimate

Estimates of uncertainty are reported using RMS (root mean square) error map for each fitting parameter. Additionally, all relevant steps in the fitting process (number of iterations, χ², uncertainty on parameter estimate, fit failures…) can be inspected in a text file for QA or debugging purpose.

Parametric color maps

The pre-contrast images are used for fusion with overlay colors. The analysis protocol contains flexible color cut-offs for each output parameters described above. These cut-offs should be pre-defined as the standard deviation SD in normal like tissue involved in the tumour type, i.e., by measuring them in breast normal glandular tissue, or arbitrarily in the peripheral normal zone of the prostate, so that sub-normal voxels can be detected and classified into 4 color-coded subsets: blue-green-red for parameter values exceeding 1SD-2SD-3SD, and below 1SD no color is attributed. As a result of this definition, subset0 is the whole histogram volume, subsets1 include all the color-coded voxels, subset2 cumulate the green and red, subset3 is red. These cut-offs act as “scaling” or “clustering” purpose, and do nothing to change the quantification results, but have consequent impact on the computer-assisting method described next.

Viewing and reporting

The GUI (Figure 1) is composed of multiple images stacks which allows easy 4-dimensional inspection of parametric mapping in synchronization with the subtraction images, and auxiliary windows for tools, in-line curve display of enhancement curve over 3×3 voxels cursor, and segmentation results. Segmentations can be performed semi-automatically on the tumour total volume and on hot spot ROI, and can be inspected and readjusted manually in consistence with an edit base validation protocol.

Figure 1.

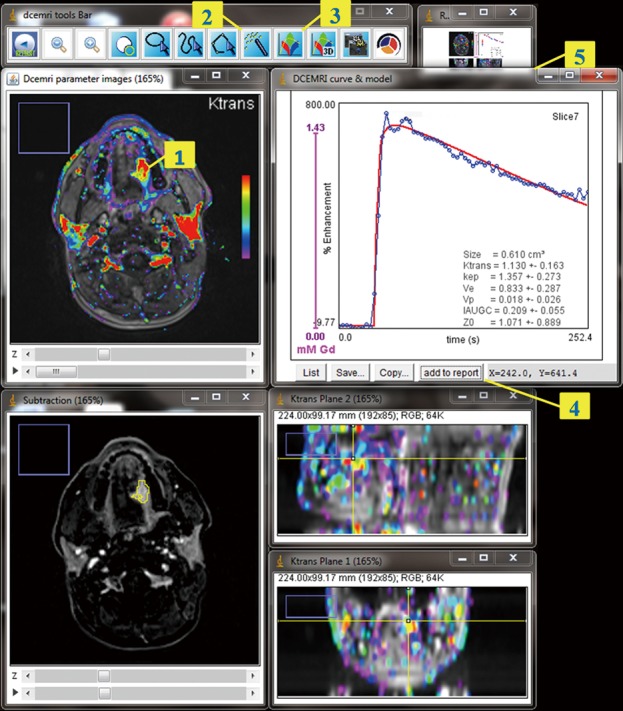
GUI for visualization and analysis. Screen capture in the course of hot-spot ROI approach: in this example, the user reviewed the DCE-MRI parametric images in synchronization with subtraction images, and focused on the lesion image that showed the largest area colored with the most significant K^trans value [1]. Clicking inside this area with the threshold tool [2] automatically created the ROI that contains all contiguous voxels with K^trans equal or above the pointed cutoff value. The user confirmed the ROI and clicked the plot tool [3] to have a display of the measured kinetic curve, the model best fit and its parameters. The finding was then added to report [4] with the reference and orthogonal projection images [5]. GUI, graphical user interface; DCE-MRI, dynamic contrast-enhanced magnetic resonance imaging.

The “hot-spot” method differs from the classical assessment in that the parameter calculations are not averaged over a user-dependent ROI, but rather the user locates a color-coded seed-point from which a region growing algorithm segments a contiguous region that most highly characterizes the tumour. With this method, the hot-spot result is the average of parameter values in the segmented voxels, and is likely to be more reproducible.

In the total volume method, the whole tumour is enclosed inside a user-defined bounding box using assistance of orthogonal views. Parameter values in the resulted selection are then plotted using single- or bi-parameters (K^trans vs. Kep) histograms, showing the classification of voxels in subsets. Functional volume response can also be assessed on the blended histograms, and is proposed as an approach to describe quantitatively the functional changes in tumour along follow-up.

Quality performance validation

The initiative to provide synthetic DCE-MRI data is already being undertaken by Buckley (15) and the QIBA group. For our validation, both phantoms were used, the difference is that the Buckley data simulates a realistic breast tumour, but requires to be converted to DICOM images, whereas the QIBA data is a ready-for-use DICOM data set, except that parameter space in low values of K^trans may be less typical of tumour characteristics. The rationale behind this extreme condition could be to provide a test that allows the estimate of uncertainty and quantitation limit, and to handle the occurrence of fitting failure, as K^trans =0 min⁻¹ or extremely low is ill-conditioned, so precluding any precision for Ѵe or Kep in the PK model.

The QIBA data consists of 2 sets of DICOM part 10 synthetic noise-free images corresponding to the basic Tofts and the extended Tofts model. To test basic Tofts, we used the QIBA v06 RevC phantom provided by RSNA (26). The simulation parameters are: 0.5 s resolution time, 1,321 sampling, 30° FA, 5 ms TR, 1,000 ms T₁₀ in tissue, 1,440 ms T₁₀ in blood, 45% hematocrit. Injection of contrast agent occurred at 60 seconds, assuming a T₁ relaxivity of the gadolinium contrast agent of 4.5 mmol⁻¹ sec^-1. The test image is organized as a top and a bottom 50×10 pixels trips between which patches of 10×10 pixels are allocated for combinations of K^trans and Ѵe in the following scheme: K^trans varies along Y-axis over (0.01, 0.02, 0.05, 0.1, 0.2, 0.35) min⁻¹ and Ѵe takes values (0.01, 0.05, 0.1, 0.2, 0.5) along X-axis. The top-left 10×10 pixels strip also contains the peak of the vascular region and the time label and the top-right 25×10 pixels correspond to ill-conditioning (K^trans =0, Ѵe =0.5). Finally, the vascular region is the bottom 50×10 pixels strip of the image.

For the extended Tofts phantom, we used the dcemri_testdata_v2 provided by RSNA (27). Related to the first phantom, differences in the parameterization are: 0.5 s resolution time, 661 sampling and 25° FA. The data contains 10×10 pixels to patch each combination of K^trans, Ѵe and Ѵp in the following scheme: K^trans varies along X-axis over (0, 0.01, 0.02, 0.05, 0.1, 0.2) min⁻¹, Ѵe takes values (0.1, 0.2, 0.5) recurrently along Y-axis, while Ѵp takes (0.001, 0.005, 0.01, 0.02, 0.05, 0.1) for each recurrence of Ѵe. The vascular region is the bottom 60×20 pixels strip of the image.

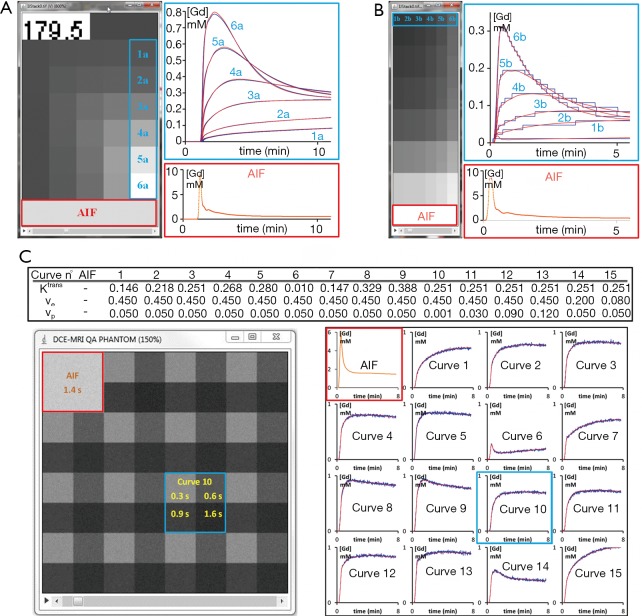
Buckley’s data has two sets, one simulating the breast tumour and the other the brain meningioma response, both consisting in an AIF and 13 concentration curves using different combinations of K^trans, Ѵe and Ѵp, with a resolution time of 1 s and 301 samplings. In this work, we present the results for breast data with an extension of the original parameter space by 2 additional curves with different Ѵe, giving 1 AIF and 15 combinations for the extended Tofts model (Figure 2). To obtain the DCE-MRI images compatible with current clinical use, we generated a dynamic set of phantom images as well as a set of variable FA images for T1 mapping. The concentration data were first converted to MR signal intensities as described by the Bloch equation of spoiled gradient-echo sequence. Each time-intensity curve was patched into 64×64 pixels, giving a 256² phantom image and, repeating this allocation for each time points, we obtained the dynamic series images. Subsequently, variable experimental conditions that could affect the performance of the PK quantification software can be incorporated. The final phantom can include customizable perturbation extends towards the image noise, the tissue native T1, the overall onset time, the time delay between arterial input and tissue vasculature, and the measurement protocol (time resolution, repetition time, echo time, FA). In the first experiment, we incorporated 4 tissue T₁₀ (300, 600, 900 and 1,200 ms) arranged 2×2 per patch, and assumed an equilibrium magnetization of 5,000, 30° FA, 4.63 ms TR, 1,440 ms T₁₀ in blood and 45% hematocrit. In the second experiment, a noise of σ =0.2 was added.

Figure 2.

Simulated phantoms used for software validation. The 3 phantoms consisted of a time series images stack which allowed the extraction of time-concentration curves (right aside) simulated with known combinations of the related model parameter values (blue curves). The validation involved estimating the true values using a curve fitting method in the way that the resulted curves (red) are best closed to the original. (A) QIBA basic Toft phantom at sampling time of 179.5 s (top strip label). The AIF was extracted from the bottom strip (red contour). As an example, tissue regions (blue contour) simulated with Ѵe =0.5 and the set of K^trans values ranging from 0.01 min⁻¹ (1a) to 0.35 min⁻¹ (6a) gave a graphical insight of the resulting best-fit. (B) QIBA extended Tofts phantom at contrast enhancement. The tissue regions marked with blue contour was simulated with Ѵe =0.1, Ѵp =0.001 and the set of K^trans values ranging from 0 min⁻¹ (1b) to 0.2 min⁻¹ (6b). (C) Parameter values of Buckley simulated data in breast (Table), extended by 2 custom simulations [14, 15], and bellow the resulted in-house numeric phantom after addition of Gaussian noise (σ =0.2) and inclusion of 4 tissues with variable T1 native value. The image patch generated from curve 10 (blue outline) was contrasted by the T1 values as labelled, while based on the same model parameters. The various curves shapes and the fitting were obtained by sampling a random ROI of one pixel over the image patches with T1 =900 s. AIF, arterial input function; QIBA, Quantitative Imaging Biomarkers Alliance.

In our routine workflow, TumourMetrics has now been evaluated as a diagnostic aid tool for multi-parametric assessment of tumours in prostate, breast and head and neck. We also made the software available to the European MR section of EORTC Imaging Group, and at the time of writing, a multi-centric trial (EORTC 90111) is under our central analysis. The last demonstration is a case which shows the concept for clinical application.

For all experiments, we used the subject-specific AIF with deconvolution method (as suggested in the QIBA profile) and the Bobyqa fitting algorithm which showed the best results in the tested parameter space of phantoms. In the fitting process, the values of the parameters were constrained within upper and lower bounds of (0.001, 1.8) for K^trans, (0.01, 1.0) for Ѵe, and if applicable (0.001, 1) for Ѵp. RMS errors and intraclass correlation coefficients (ICCs) were calculated to determine the bias and the absolute agreement between estimates and true parameters value. A 3.4 GHz Intel Core i7-2600 running on Windows 7 was used.

Results

QIBA basic Tofts data

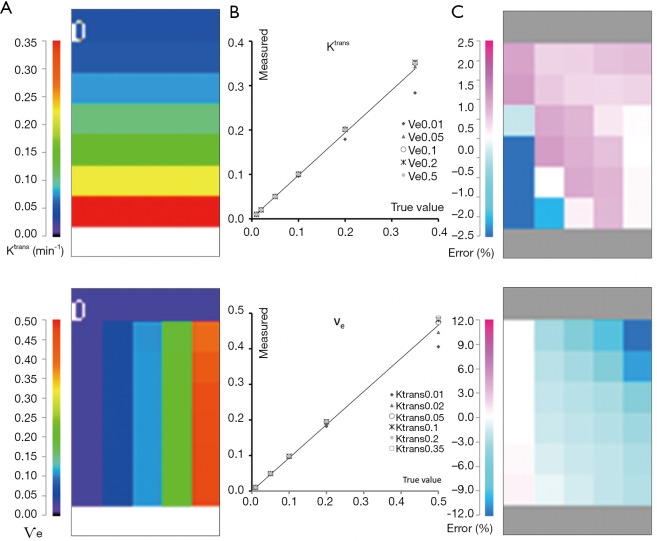
The computation time to fit all the voxels was about 8 s. Figure 3 presents a scaled color map of the estimates and the associated errors expressed in % difference to known truth values. The % errors on K^trans varied within (−15.2, 5.7), with a RMS error of 1.9%. Largest errors occurred for 2 points in the region of low Ѵe values. % errors for Ѵe were within (−15.3, 5.4) with RMS error of 2.2%, and were largest for 3 points in the region of high K^trans. In this tested parameter space, both parameters were correlated to true values with ICCs >0.995.

Figure 3.

Validation of the QIBA basic Tofts data. (A) Parametric map of K^trans (top) and Ѵe (bottom) contrasted with the color lookup table on left. (B) Correlation between measured and true parameter values showing the influence of the counterpart parameter (marker style) in the simulated range. This influence is also shown with the error map in (C), obtained by expressing the % differences to the true values (error %) and applying the look-up table as scaled on the left. QIBA, Quantitative Imaging Biomarkers Alliance.

QIBA extended Tofts data

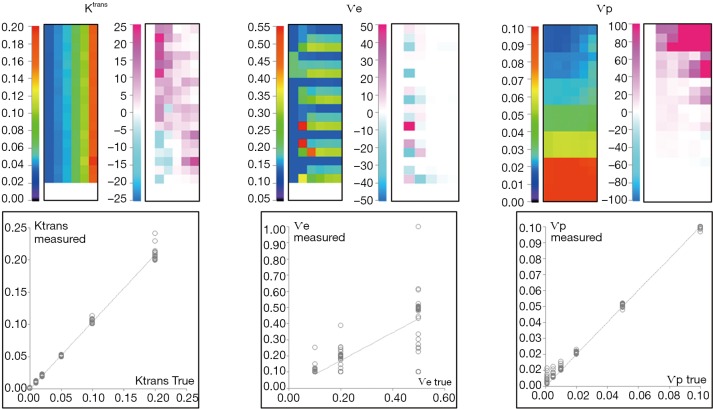
The computation time was 52 s. As shown in Figure 4, the % error to known truth was from (−8, 23) for K^trans, (−27, 50) for Ѵe and (−4.6, >100) for Ѵp. In the same order, the RMS error was 0.9%, 23% and 0.7% with ICCs of 0.997, 0.76 and 0.998. Largest fit errors could be explained by ill-fitting condition at low K^trans values, except that this strong dependence between K^trans and Ѵe had little influence on Ѵp, for which the error was rather overemphasized when expressed relatively to very low reference values. Also, the equilibrium magnetization used to simulate these data was relatively low, thus resulting in bad discretization of low signal, and increased the uncertainty of Ѵe estimate as pointed by the poor R coefficient. K^trans and Ѵp didn’t suffer from this effect because their estimation relies predominantly on the initial high intensities part of enhancement curves.

Figure 4.

Validation of the QIBA extended Tofts data. The upper side shows the parametric map of K^trans, Ѵe and Ѵp estimates and their corresponding error map. The correlation between estimates and true values are presented below. QIBA, Quantitative Imaging Biomarkers Alliance.

Buckley breast data

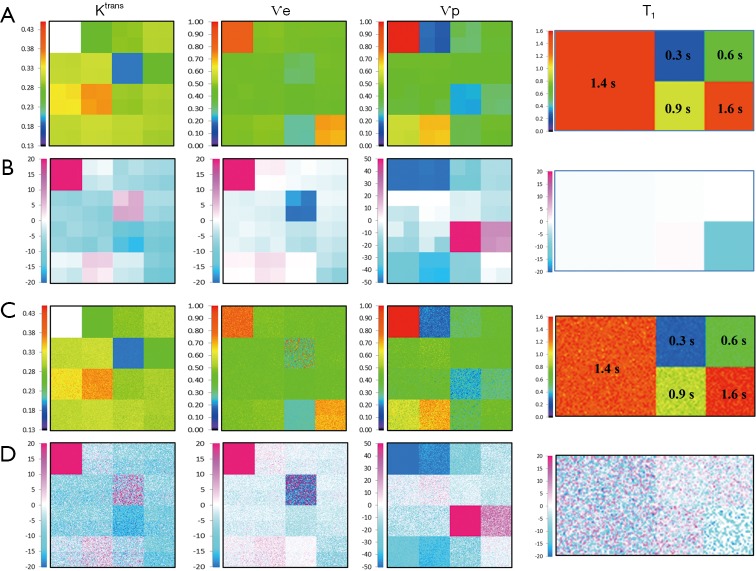
A complete data set including 2 optimized FAs images was generated. The value of these FAs was determined according to DESPOT1 by assuming a T₁ of 900 ms in tissue and an acquisition TR of 5.5 ms. The computation time to fit the 256² voxels was about 164 s. Color map images representing the measured parameter values and the associated % error in noise-free and noise-added cases are shown in Figure 5, while the quantification results can be compared in Figure 6.

Figure 5.

Validation using the Buckley breast data, noise-free (A,B) and with σ =0.2 noise (C,D). (A,C) Parametric map of K^trans, Ѵe, Ѵp and T1. (B,D) Accuracy of the quantifications expressed as % differences to the true values and presented in scaled color map.

Figure 6.

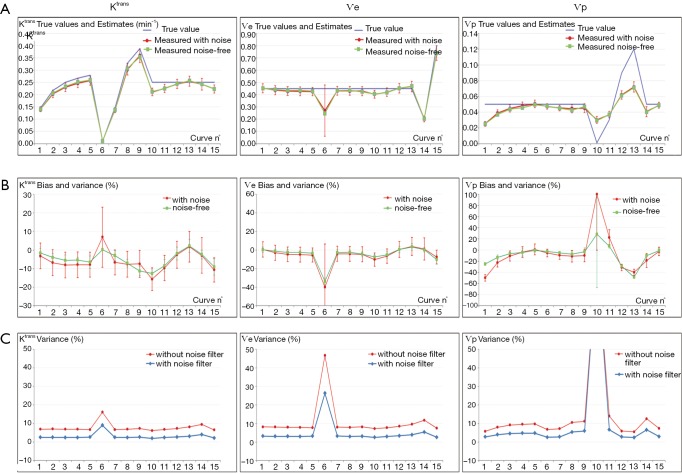
Validation of Buckley breast data using the extended Tofts model. For the noise-free and noise-added set: (A) true values and the measured values in the 15 simulated curves, the error bar (red) representing the standard deviation induced by noise. (B) Bias expressed as the % difference between measured and true parameter values. The variance represented by the error bars refers to the standard deviation scaled in % to the true value. For the noise-added data (red), the variance is induced by noise, while for the noise-free data (green) the variance represents the effect of variable native T1. (C) Compares the variances induced by noise when using a 3×3 kernel average filter.

In the noise-free case measured on tissue T₁ of 900 ms, the % error to known truth was from (−15, 7.9) for K^trans, (−45, 4.6) for Ѵe and (−49, 29,200) for Ѵp. In the same order, the RMS error was 2.1%, 3.2% and 8.2% with ICCs of 0.94, 0.89 and 0.87. In the K^trans parameter space, excepted for slight overestimation in 2 extreme conditions (K^trans very low and Ѵp highest), all estimates were systematically underestimated with a maximum error in the region of low Ѵp values. In the Ѵe parameter space, the estimates matched well their true value except when K^trans is very low, situation already met previously. Next for Ѵp, again the largest overestimated error was related to its very low simulated value, so there is no substantive concern, but the underestimation related to low K^trans values should be much more significant, when related to the results for K^trans, because this shows that even with a resolution time of 1 s, the extended Tofts model wasn’t accurate enough in resolving the ambiguous perfusion and permeability meaning of K^trans. So, we think that when using the extended Tofts model, the interpretation of K^trans should be carefully related to Ѵp in terms of dependence.

Next for the determination of T₁, the values matched the true data very accurately within a range of 0.3 to 1.44 s, scoring a maximum error of −2.8%, RMS of 0.87 and ICC of 0.999. At 1.6 s, the linearity began to be impaired with an error of −12%. The effect of the tissue native T₁ on the accuracy of PK parameters is presented by the error bars in Figure 6A, which shows that the influence exists, but caused minor errors compared to PK model fitting errors.

Finally, a noise of σ =0.2 was added to the phantom to test the precision of our quantification. The parametric maps were analyzed using the ROI selection tools supplied by our GUI. The parameter values in the ROI were averaged in the corresponding patch and reported with the associated standard deviation (SD) in Figure 6B. The results showed no significant difference between the noise-free values and the noise-added means, and the variances expressed as SD ×100/true value indicated that a noise SD of 5 (1/σ) propagated a typical error of the order of 10% on the PK parameter estimates. Also, the influence of noise on T₁ determination was to a lesser extend similar, scoring a variance of 6% (Figure 5C).

Example with clinical data

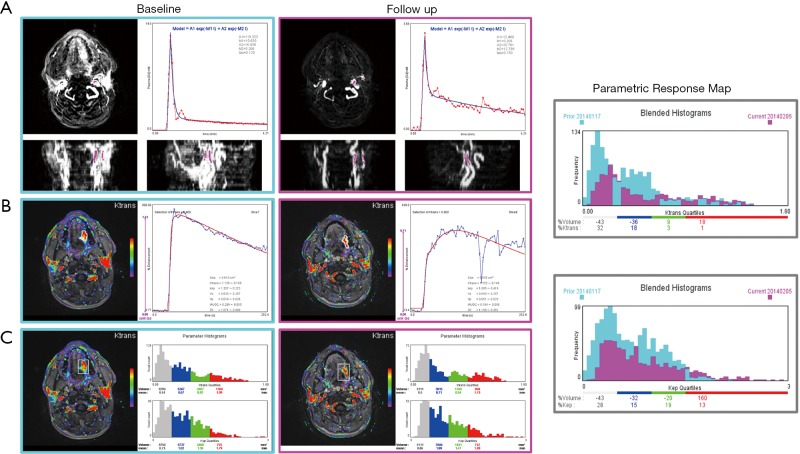
We report here a case from EORTC 90111-24111 multicenter trial relating metabolic response after 2 weeks of treatment with neo-adjuvant afatinib in squamous cell carcinoma of the head and neck. Morphologic conventional MRI, diffusion weighted imaging (DWI) and DCE-MRI were acquired at baseline and after treatment 1 day before surgery with respect to a standardized imaging guideline. The analysis protocol was setup to include individual AIF measurement, T₁ mapping, noise filter, the extended Tofts model and the BOBYQA fitting algorithm. The DCE-MRI data was acquired with a resolution time of 3.9 s, sampling 64 series with an imaging matrix of 192² pixels ×20 slices. The computation time to process all the 737,280 voxels was about 260 s. The resulted parametric response maps were assessed using the parameter values measured in hot-spot ROI and total volume histogram clustered by a cutoff value of 0.3 for K^trans and 0.5 for Kep as described above. Figure 7 shows the analysis reports at baseline and after treatment from the same operator. Despite the semi-automated segmentation method intended to reduce the observer variability in the selection of the input vessels, the AIF differed significantly between the two visits. Such individual variations in AIF measurement has been reported (28,29), and should be independent of operator, especially since the 2 segmentations appeared very similar. In this example, the analysis with hot- spot showed minor increase of K^trans (2%), whereas Ѵe decreased by 18%. When accessed by the parametric volume change, the tumour size decreased globally, except in the high K^trans and higher Kep values. At the same time, the conventional morphologic evaluation showed a discreet reduction of the tumour size (1.7 cm × 2 cm vs. 1.5 cm × 1.6 cm). These findings suggest heterogeneous changes in the tumour vascularity, but in the context of this trial, we are not able to conclude what represents the therapeutic meaning of these changes. This is our first experience using the TumourMetrics software in multicenter clinical trial, with the purpose first to validate the reliability and the usability of this analysis tool in clinical practice and multicentric clinical research and, if the condition is satisfied, to validate the potential use of DCE-MRI as a biomarker of treatment response.

Figure 7.

Example of treatment response assessment: analysis reports of a squamous cell carcinoma before and after 2 weeks of neo-adjuvant treatment with (A) semi-automated AIF measurement, (B) hot-spot ROI analysis, (C) total volume histogram, and at right the proposed parametric response map of K^trans and Kep to assess the total tumour volume change. AIF, arterial input function.

Discussion

Globally, our quantification method estimated the parameters accurately, unless there are extreme circumstances where K^trans meets a small Ѵe <0.05, and vice-versa when Ѵe gathers with very small K^trans <0.01. The situation between K^trans and Ѵp is that they are competing against each other when the balance is becoming unequal, while keeping their respective proportionality towards true values. So, we recommend special caution when using the extended Tofts in the clinical achievable time resolution (3 s for a best), because the conflict between K^trans and Ѵp is increasing with the time resolution (30,31), and both parameters should be reported. For this reason, the QIBA profile recommends the use of basic Tofts. We cannot say in the scope of this study if using the basic model to quantify high resolution time data if Ѵp exists is more accurate or clinically relevant, given that the tumours vascularization is an essential micro-environmental indication for anti-vascular and radiotherapy treatments. Large clinical trials are needed to validate the approach, and this is what the present project would be aimed. In the meantime, simulation studies with our numeric phantom are under investigation to help understanding this issue.

Most clinical CAD software applies a smoothing filter on DCE-MRI data to reduce the noise effect, thus our software also incorporated this option in the setting of analysis protocol. As shown in Figure 6C, the filter globally reduced the % variance to values lesser than the errors on parameters.

Regarding the advantages of TumourMetrics, we acknowledge that in clinical practice, other analysis tools such as those provided by MR scanner vendors may be fully or partly compliant with QIBA and could be equally efficient as for quality performance. At our knowledge, there was not QIBA test data validation using these clinical solutions that has been published to make the comparison. In a recent study, Beuzit et al. compared the accuracy and reproducibility among five of mostly used clinical software using in-house simulated data and clinical data (32). Their results showed significant errors in calculated parameters and poor inter-software reproducibility. This variability may be mainly explained by the different methods used to process all steps of parameters quantification, given that some of these were not fully compliant with the QIBA recommendations.

In our work, we used publicly available simulated data. Assuming that the method used by Beuzit et al. for the generation of in-house simulated data was the same, a rough comparison of ICCs could be made: for our Buckley data ICCs was 0.94 for K^trans and 0.89 for Ѵe, while the overall ICCs yielded by Beuzit et al. were respectively 0.5 and 0.67.

Conclusions

We still emphasize that our objective was not to demonstrate that our software is doing better than other commercial or non-commercial software, but to provide a reliable freely accessible DCE-MRI post-processing software that firstly ensures the compliance with the standardization of analysis methods, and secondly achieves an easy integration of DCE-MRI in routine clinical practice, but also as a clinical research tool. In our knowledge, there is no open source and freely accessible software application that can achieve these objectives by dealing with the needs of community radiologists.

The package includes both the PK quantification of DCE-MRI data and a straightforward interpretation GUI which limits the inter-operator variability. The software has been first designed for easy integration into the clinical workflow. At our radiology department, TumourMetrics runs as a plugin in the diagnostic workstation and provides means for complete interpretation of breast and prostate studies without the need of dedicated workstation. By selecting the patient study from the PACS viewer, a single click starts the application with the computation of parametric maps. The process time generally falls under one minute, so that reading physician will stay focused on the same investigation, and without transition, the results obtained are interpreted using our home-developed GUI for visualization, ROI and VOI analysis and reporting. For the quality assessment, the DICOM structure info of parametric maps records all parameters of methods used for PK quantification like AIF, FAs for T1 mapping or fitting algorithm. For a full clinical integration, all results and analysis reports are signed using user login, and automatically transferred to the PACS.

To address the issue of standardization in both DCE-MRI quantification and analysis in ROI and VOI, our software can be set to be fully compliant with the widely accepted QIBA DCE-MRI Profile, since set up to facilitate the standardization, development, and validation of quantitative imaging biomarkers.

Finally, the reliability of our results has been demonstrated using publicly available simulated data, providing an important basis for multicenter reproducibility of the method. Moreover, a quantification protocol can be made fit for purpose to ensure prospectively a strict consistency between each center participating in a clinical trial: this has a major interest in oncology and also in series focusing on rare diseases.

We think that this open source solution gives the possibility to develop easily additional approaches to tumour measurements, i.e., improving the ROI or volume segmentation tools or new quantification methods to evaluate the heterogeneity of tumours, as well as heterogeneous response to treatment.

Ethical Statement: All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. This article does not contain any studies with animals performed by any of the authors. For this type of study formal consent was not required.