Eye patches: protein assembly of index-gradient squid lenses

Abstract

A parabolic relationship between lens radius and refractive index allows spherical lenses to avoid spherical aberration. We show that in squid, patchy colloidal physics resulted from an evolutionary radiation of globular S-crystallin proteins. Small angle x-ray scattering experiments on lens tissue show colloidal gels of S-crystallins at all radial positions. Sparse lens materials form via low-valence linkages between disordered loops protruding from the surface. The arms are polydisperse and bind via a set of hydrogen bonds between disordered side chains. Peripheral lens regions with low particle valence form stable, volume-spanning gels at low density, while central regions with higher average valence gel at higher densities. The proteins demonstrate an evolved set of linkers for self-assembly of nanoparticles into volumetric materials.

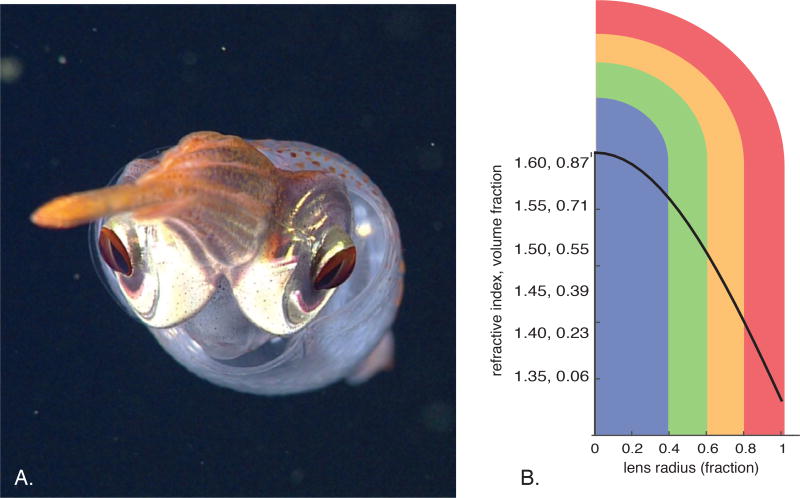
Maxwell showed that a “perfect medium” in a spherical lens would require a parabolic relationship between radial position and refractive index. This optical design has evolved in parallel in both fishes and decapod squid (1, 2), since in the light-limited ocean, this strategy optimizes sensitivity and acuity (Fig. 1A) (3). Here we describe the physical and material mechanisms underlying the evolution of this medium in squid.

Figure 1.

Relationships between lens radius, refractive index, protein structure and network structure. A) In situ photograph of a decapod squid showing spherical, gradient index lenses. B) Lens radius vs. refractive index, with an overlay showing the relationship between lens radius and the color-coding used in this work to identify discretized tissue samples (blue for r<40%, green for 40%<r<60%, orange for radii 60%<r<80% and red for r>80%.

In amorphous biological materials such as lenses, the concentration of material in aqueous cellular fluid determines the refractive index. The squid lens is cellular, so to a first approximation it might be possible to build a graded-index lens from protein solutions in an array of cells in which each cell has a higher concentration than the cell next to it. However, dissolved proteins would not likely result in a transparent lens. Most proteins interact attractively, such that aging of these solutions would lead to aggregation and light scattering. At some concentrations thermal motion can also cause light scattering (4, 5). Any aging is especially problematic since squid lens proteins do not undergo renewal: ribosomes and nuclei are strongly light scattering and are expelled from the developing cells (6).

“S-crystallins” are the set of proteins that constitute the refractive material in squid lens; they are all close variants of the glutathione s-transferase (GST) enzyme (7). This group of proteins has experienced episodes of strong positive (i.e., directional) evolutionary selection relative to GST, suggesting that the many similar genetic copies in fact serve different functional roles (8). One of the most obvious but unexplained features of S-crystallins is a pair of unstructured peptide loops protruding from the folded, globular surface of the protein that bear little sequence similarity to other proteins (7, 8). These disordered sequences are encoded at the center of the linear amino acid sequence and the protein folds on either side of this central disordered region. Since S-crystallins are dimeric, the rotational symmetry of the dimer results in a neighboring pair of loops protruding from one end. The lengths of these loops and the surface charges of the proteins in the group vary (8).

The thermodynamic behavior of protein mixtures is typically rationalized using thermodynamic theories for isotropic particles (9, 10). These theories, however, cannot account for the absence of local density fluctuation throughout the lens that occurs with S-crystallins. We find that “patchy colloid” theory (11) can account for this apparent paradox of a gradient of protein volume fractions from 0–1 that escapes aging and local density fluctuation at all points in the gradient. This theory considers the interactions of colloids, or particles that are much larger than atoms, but small enough to undergo thermal collisions. The particles are considered “patchy” because they interact through hard-sphere repulsion plus attractive potentials that are localized to a few angularly small patches on the surface (11, 12). A surprising prediction of patchy colloid theory is that as particles’ average valence (the average number of patches per particle) approaches two, stable liquid-like materials form at arbitrarily low densities (11, 13). Conversely, as the average valence of the particles increases, the minimum density at which the system will gel can also be controlled (12, 13).

Results

Lens gradient

The relationship Maxwell described between radial position and refractive index is shown here for a spherical lens that focuses an aberration-free image for a single wavelength onto the retina (Fig. 1B, (1, 14)):

$$n(r)=\frac{n_c}{1+(\frac{n_c}{n_e}-1)r^2}$$ Eq. 1

Here, n(r) is the index at the dimensionless, fractional radial position r, n_c is the index at the center of the lens, n_e is the index at the peripheral edge of the lens (16). In fish and squid lenses, n_c approaches the theoretical maximum for dry protein (~1.6), and n_e is close to that of the seawater in which the lens is immersed (~1.34) (14, 15).

We independently characterized the density gradient in squid lens and verified three premises: 1) that it is an increase in S-crystallin concentration alone, not a change in average amino acid refractive increment, that causes the observed relationship between radius and index; 2) that the shape of this relationship is consistent with the description in eq. 1; and 3) that the lower and upper bounds of the index range are 1.33 and 1.62, giving protein packing fraction (Φ) of 0.04 to ~1.0 (8,16–17). To partition the continuous density gradient of the lens into an experimentally tractable number of samples, we dissected tissue from individual lenses into four concentric sections, with the outer edge of each subsample extending inward from fractions of roughly 100%, 80%, 60%, and 40% of the total lens radius (Fig. 1B). We refer to these concentric tissue samples as the 100%, 80%, 60% and 40% layers, and results from these samples are color-coded with red, orange, green, and blue, respectively, in the figures.

RNA sequencing

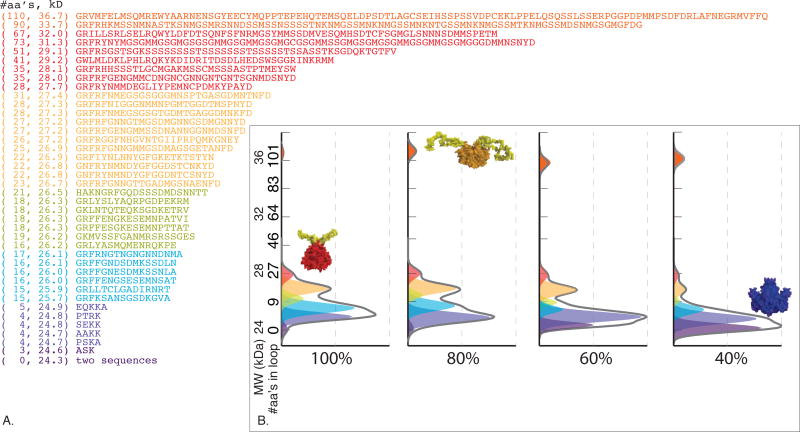
Given the age of extant S-crystallin studies and subsequent improvements in sequencing technologies, it was important to ensure we had captured the full range of S-crystallin genetic diversity expressed in the squid lens (17–19). Therefore, we sequenced transcriptomes of mature lens tissue from Doryteuthis pealeii. Our Illumina RNAseq resulted in 65.8 million paired-end reads for the 100% layer and 88.6 million paired-end reads for the 60% layer. After assembly, we found 53 unique S-crystallins transcripts. The predicted protein sequences are very similar to known S-crystallin sequences, with 52.0% ± 15.0% amino acid identity and 60.9% ± 12.9% similarity to Lops8, an archived S-crystallin from L. opalescens chosen for comparison (Genbank U19296.1) (18). In the 53 unique S-crystallins in the transcriptome, we identified 43 unique loop sequences that varied in length from 3 to 110 amino acids (Fig. 2A). 90% of the residues within the set of unique loops are algorithmically predicted to be disordered in solution, and are likely to encode an unstructured region of the protein polymer extending from the folded body of the homodimeric protein (8, 19–20).

Figure 2.

“Loop” sequences and their estimated relative abundance as a function of lens radius. A) Unique “loop”-encoding sequences as determined by lens RNA sequencing, and the relative abundance of proteins of different molecular weights. Parentheses show number of amino acids in the sequence and its molecular weight in kilodaltons. Sequence text is colored to correspond to peak decomposition in (B). B) SDS-PAGE of lens samples taken from different radial positions of the lens, and an estimated abundance of components of different loop molecular weights. The grey curve shows both the raw SDS-PAGE staining density and the sum of the curves in the fit (the two are similar to within the width of the line). The colored regions show the estimated abundance of a molecular weight component within a given sample. Images of protein show the predicted homology model structure of an S-crystallin in a given molecular weight class (long loops in red, short loops in blue, and 100-aa loops in orange).

Molecular weight characterization by gel electrophoresis

We used sodium dodecyl sulfate polyacrylamide gel electrophoresis (SDS-PAGE) to characterize the protein molecular weight distribution as a function of lens radius. At all radial positions in the lens, more than 95% of the total protein was found in two broad molecular weight classes consistent with S-crystallin monomers, one with average molecular weight ~24.5 kDa and the other with average molecular weight ~26.5 kDa (Fig. 2B). There are also two minor bands in each sample, one at 32 and another at 36 kDa, consistent with S-crystallins from our transcriptome data with ~100 residue-long loop sequences (Fig. 2B). The molecular weight differences in SDS-PAGE are consistent with translations of our lens transcriptome, such that differences in S-crystallin molecular weight with lens radius are likely due to different loop composition with lens radius.

We performed a deconvolution of our SDS-PAGE data by modeling each migration pattern as a sum of Gaussian contributions from individual proteins with molecular weights encoded by full-length sequences obtained from RNA-seq (16). This analysis shows that although the ratio of the two major peaks centered at 24.5 and 26.5 kDa (due to the presence of short and long loops, respectively) shifts continuously toward larger proteins as a function of increasing radius, the underlying mixture of protein sequences associated with this shift is complex, not the result of a binary mixture of a few long- and short-loop sequences (Fig. 2B). The third peak on the gel, due to proteins with ~100 amino-acid-long loops, is a minor constituent of the periphery, reaches a maximum of 5% total protein at a relative radial position of 0.36, and is also present as 5% of total protein in the core. Proteins with very short loops are highly abundant in the core (34% of total protein), but a minor constituent in the peripheral layer (3% of total protein).

Small-angle x-ray scattering (SAXS)

We used SAXS to understand the spatial structure of S-crystallins within the squid lens. The scattering intensity as a function of wave vector (I(q)) was found to be very similar for each layer of the lens, even though the packing fraction of the layers systematically changes from Φ = 0.05 to Φ ≈1.0 (Fig. 3A). In all samples, at small wave vector q=4π sin(θ)/λ, where θ is the half angle between the x-ray beam and the detector, the scattering intensity for all layers decreases with increasing q‥ There were three major features also observed in scattering from all radial position within the lens: a broad, low peak between 0.01 Å⁻¹ <q<0.03 Å⁻¹, a shoulder around q=0.15 Å⁻¹, and a second peak near q=0.21 Å⁻¹. The shoulder near q=0.15 Å⁻¹ has a position and shape similar to scattering from a solution of 5 nm spheres. The peak at q= 0.21 Å⁻¹ corresponds to the real-space distance between the monomers within an S-crystallin dimer of ~3 nm.

Figure 3.

SAXS, DAMMIF structures, and modeled networks of particles. <M> is the average protein coordination number. A) X-ray scattering intensity as a function of q, (I(q)). Measurements from different radial portions of the lens are indicated by color. Gray traces show the calculated form factor of isolated S-crystallin dimers. B) Structure factors of different concentric regions of the lens, calculated using I(q) and the calculated form factor shown in (A). Inset of (B): Peak position associated with particle pair-wise interactions in numerical simulation (top panel, data from [22])) and experimentally measured in this study (bottom panel). The peak associated with pairwise interactions moves toward lower q as <M> increases when Φ is held constant. C) Structure factors of simulated branching networks of particles with coordinate numbers predicted to exist in the squid lens. D) Sample of DAMMIF predictions of lens material structure, calculated using the SAXS data in (A), coordination number. Scale bar applies to all panels of (D). Individual S-crystallins are colored according to radial position while predicted links between S-crystallins are colored yellow. E) Sample of structures from network simulations, whose structure factors are shown in (C). Scale bar applies to all panels of (E). 10,000 particles were included in the calculation of structure factor; a few hundred particles from each simulation are shown here, in a box of the same volume for each simulation.

Dilution and scattering form factor

To obtain a form factor, or scattering from an isolated protein, we initially attempted to dilute lens proteins in buffer. This procedure resulted in transparent suspensions containing >95% of the lens material when using tissue from the periphery of the lens. When treated in the same manner, samples from the core resulted in an insoluble pellet comprising >95% of the lens material. Tissue from intermediate radial positions resulted in a systematic gradient between these two extremes (Figs. S1, 4A). SAXS characterization of the supernatants from each radial position revealed structures consistent with folded protein at high q, but with a relationship of S(q)∝q^−1.5 between 9e-3≥q≥4e-3, the minimum q technically accessible. (Figs. S2, S3). This result was independent of the salt content of the buffer, and the concentration of protein in the fluid in a concentration range from ~10 mg/mL (Φ = 1.4e-2) to ~0.05 mg/mL (Φ = 1.1e-4), the minimum at which SAXS data were meaningful (Fig. S4). A structural fit to these SAXS data using the algorithm AMBIMETER produced a low-ambiguity result that these solutions contain pairwise-linked chains of S-crystallin proteins (21). Patchy colloid theory gives insight to this behavior: in patchy systems, dilution will not cause a transition from glassy to isolated particles, as is the case for isotropic particles (9, 10), but instead will cause a transition from an equilibrium gel to an equilibrium percolating/cluster fluid (13).

Figure 4.

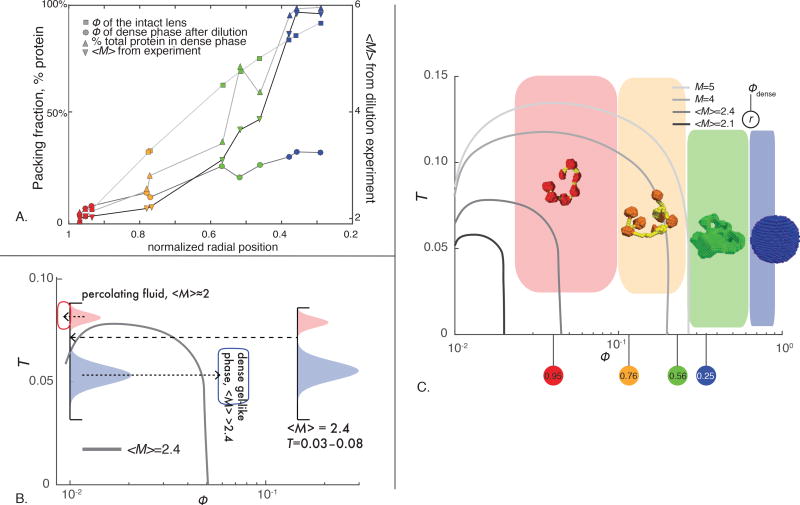
Experimental data mapped to patchy colloid theory A) Volume fraction (Φ) of the intact lens, of the dense material after dilution, percent total protein in the dense state, and calculated <M> resulting from this experiment as a function of lens radius. Each symbol represents one measurement and three lenses were sampled for each curve. B) Schematic showing how a polydisperse set of effective bond temperatures in a patchy colloidal system, when diluted, will phase separate. Vertical line indicates the likely range of effective bond temperatures (T) in a given mixture in the lens, and the filled red and blue shapes indicate a possible set of “high” and "low" effective temperature bonds in the system. Arrows indicate how “high temperature” particles in the system will re-equilibrate into a percolating fluid, while “low temperature” particles are in an unstable part of the diagram and re-equilibrate in to a dense material. C) Experimental data for the lens system plotted in context of patchy colloid theory. Likely bond temperatures for the system are shown in the height of the colored squares, while the density spanned by each experimentally characterized layer is shown in the width. Spinodal lines from theory (11) are shown in shades of grey. Circles underneath the x-axis indicate the densities of the dense material generated dilution, the radius from which samples were taken is shown inside.

This particle assembly upon dilution meant that it was not possible to measure a form factor in the usual manner. Therefore, we calculated a form factor of isolated S-crystallin dimers using atomic positions taken from S-crystallin homology models (16). The predicted form factors of all S-crystallin homodimers are similar: they are flat at small values of q < 0.05 Å⁻¹, then decrease to a minimum near q = 0.17 Å⁻¹, with a minor peak at q ≈ 0.21 Å⁻¹ (Fig. 3A).

Structure Factor, S(q)

The “structure factor” is a reciprocal-space representation of the interactions between defined particles in a sample, found by dividing the overall scattering of a sample by the form factor. The Fourier transform of the structure factor then becomes the pair-distribution function of the particles defined by the form factor. We calculated the structure factor of the lens tissue using the total SAXS scattering intensity and the average of the calculated form factors from individual S-crystallin dimers. This structure factor was also found to share a few prominent features for all radial positions of the lens: a strong peak in the structure factor at q =0.15 Å⁻¹, a trough at 0.03 Å⁻¹< q < 0.1 Å⁻¹, and at q < 0.01 Å⁻¹ a relation Δ(log I)/Δ(log q) of approximately -2.3 (Fig. 3B).

The most prominent peak in the structure factors at q ≈ 0.15 Å⁻¹ corresponds to the real-space size of the S-crystallin dimer. This suggests that the structure factor of all regions of the lens is dominated by pair-wise dimer-dimer interactions. This peak shifts toward higher q toward the center of the lens, meaning that the real-space pairwise distance decreases from the periphery to the core of the lens. Measurements on samples from different lens radii also shared a minimum in structure factor at q ≅ 0.05 Å⁻¹ that increased with decreasing lens radius. This relationship is similar to previous numerical work that found that this peak in S(q) indicating pair-wise interactions shifted to the right with increasing numbers of contacts between proteins (coordination number or <M>) (Fig. 3B, inset) (22).

The broad feature in structure factor between 0.01 Å⁻¹ < q < 0.03 Å⁻¹ could be due to a few, possibly interacting, phenomena. First, there could be local swelling of the gel due to weak van der Waals, electrostatic, hydrophobic interactions, or water migration within the lens (23). This feature could also indicate complex, multiparticle nodes within the protein network, consistent with those observed in simulations (22). Samples from all regions in the lens also had similar structure factors in the region 0.006 Å⁻¹ < q < 0.01 Å⁻¹, where the signal exhibited a slope of slightly more than -2 in a log-log plot, consistent with expectations for a percolating network (24).

Dilution and characterization of network coordination number

We observed that when tissue from different radial positions was diluted to a volume fraction of 0.01 then centrifuged, two materials formed: a protein fluid and a pellet (Fig. S1). As described above, the sparse phase is a percolating protein fluid (Figs. S2–S4). Both the relative amount of protein in and the density of the pellet increased with decreasing lens radius (Fig. 4A). In samples taken from the periphery of the lens, the pellet was a soft, volume-spanning translucent gel, while the core of the lens formed a white powder (Fig. S1). Since all S-crystallins are extremely hydrophilic (mean grand average of hydropathy index per sequence of -5.61±0.07), this variation in pellet formation is due to different protein-protein interactions at different radial positions of the lens, not differences in protein-water interactions (25). Except for at the extreme peripheral edge of the lens, the pellet that formed was always less dense than the lens tissue that went into the sample, even after accounting for pore space of volume fraction 0.35 in the powder pellets. This result suggests that a phase or state transition of S-crystallins occurs upon dilution of the native tissue (Figs. 4A–C, S1).

This phase or state transition upon dilution allowed us explore the intrinsic average coordination number, <M>, of the particles as a function of lens radius (11). Given the high sequence polydispersity present at every radial position in the lens (Fig. 2), a polydisperse set of effective protein-protein bond temperatures must also be present. If this set of effective bond temperatures spans the spinodal line for the system, the diagram predicts that upon dilution the proteins will separate into a sparse phase containing the “high temperature” (low bond energy) particles located above the spinodal line, and a dense material containing the “low temperature” (high bond energy) particles (Fig. 4B) (11). The “low temperature” particles, when relocated to the unstable region of the phase space under the spinodal line, must then re-equilibrate to a density dictated by the average valence of this subset of the original total protein mixture (Fig. 4B–C). This phenomenon allowed us to estimate <M> for the pellet material given its density. We used the measured particle density in each material, the inferred <M> of the pellet, and the fact that in the spare chain the particles are in chains with <M>=2 to calculate <M> as a function of radial position (Fig. 4A). (Fig. 4A). We found that <M> in the periphery of the lens is slightly greater than two, and increased toward the center of the lens to a maximum near six at the core (Fig. 4A).

Monte Carlo Analysis

We used the algorithm DAMMIF, a Monte Carlo approach to finding a coarse-grain realspace structure given SAXS data (26). For the outermost layer of the lens, this result shows a network of 3–5 nm diameter spheres that are connected by pairs of “arms” leaving the body of an individual sphere (Fig. 1C). Most of the ~5 nm spheres show a rotational symmetry consistent with dimers of two structurally similar monomers. The distance bridged by these arms is typically ~40 Å, and the arms leave individual ~5 nm spheres at angles ranging from 60° to 120° with respect to each other. The average nearest-neighbor distance between the centers of two bridged proteins was 75 Å in the 100% layer and 60 Å in the 80% layer. These predictions are consistent with sequencing data and homology models that S-crystallins have extended loops protruding from the two pairs of helices forming the core of the folded structure (Figs. 2B, 3D, 5), with the loops linking the bodies of the proteins into a network of spherical particles.

Figure 5.

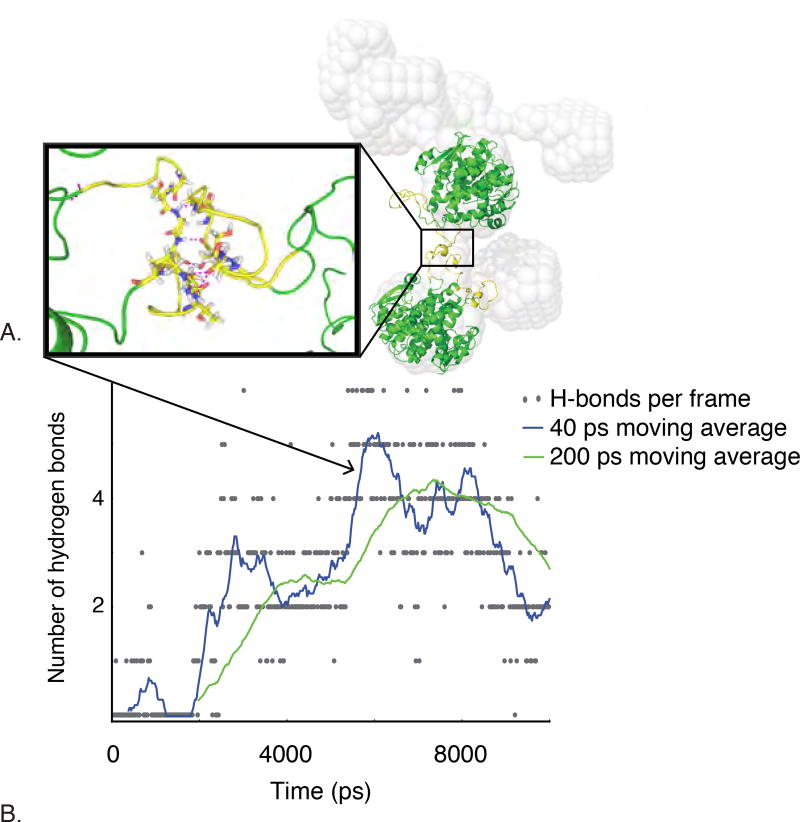
MD simulation of patch-like loop-loop interaction in low-index regions of the lens. A) Homology models of S-crystallin dimers, shown in green and yellow, with centers of mass positioned according to DAMMIF output, shown in grey. Inset shows the interaction of the two unstructured loops of proteins in this orientation after ~6,000 ps of MD simulation. Hydrogen bonds between the two loops are shown in pink. B) Number of hydrogen bonds between two loops binding together two separate S-crystallin dimers in MD simulation as a function of time. Hydrogen bonds form between the two loops after a few hundred ps and increase to a maximum of six, with a 200-ps moving average of four.

Because DAMMIF is a Monte Carlo technique, each calculation generates a likely but not unique structural fragment given a single SAXS measurement. However, the volume-spanning material in the lens is much larger than the ~300-nm real-space span accessed by SAXS. Therefore, we generated an ensemble of 100 DAMMIF outputs for each layer of the lens, and treated these as ensembles of fragments of the larger protein network forming the lens.

This approach generated an independent estimate of <M> as a function of lens radius and showed how <M> emerges from S-crystallin secondary and tertiary structure. In the ensembles from the 100% and 80% layers, we observed 5-nm proteins connected by thin bridges that vary in length from 50 Å to 400 Å, to a minimum of one and a maximum of four other dimers (Fig. 3D). In the 100% layer, the majority of particles have two contacts, with the pair of unstructured loops from an S-crystallin dimer forming contacts with loops from other dimers. A few particles have a third contact resulting from loop-body interaction with another dimer. The 80% layer had a greater proportion of M = 3 nodes in the network than the 100% layer. In the 80% layer, a second form of M=3 interactions appears: loops of length ~100 amino acids bifurcate to form a Y-shaped structure. This Y-shaped structure results in two points of contact within a single loop, each capable of contacting the end(s) of another loop (Fig. 3D).

These structural ensembles showed <M> = 2.19 for the 100% layer, and <M> = 2.45 for the 80% layer, and a permutation test showed the distribution of M to be different between the two ensembles. The dilution experiment found <M> = 2.01–2.22 for the 100% layer and <M> = 2.22–3.11 for the 80% layer (Fig. 4A), so two independent estimates of <M> agree.

At samples from lens radii of 60% and 40%, the predicted structures were dense, with contacts between particle surfaces occupying much of the surface area. The 60% layer prediction showed 5 nm-thick ramifying lamellae, consistent with interconnected sheets of S-crystallin dimers (Fig. 3D). In the 40% layer prediction, protein completely filled the volume, consistent with a solid containing little or no bulk water (Fig. 3D). The dilution analysis described above found that <M> =3.1–3.9 for the 60% layer, and <M> = 3.9–5.8 for the 40% layer (Fig. 4A), qualitatively consistent with these structural predictions.

Network-of-spheres simulations

As an aid to visualization, we simulated branching chains of particles, generating non-equilibrium structures with qualitative similarity to those in our SAXS data, and calculated the resulting structure factors. (16). We added spheres at arbitrary angles to a growing chain of spheres, with the addition of two spheres causing a bifurcation in the chain (Fig. 3E). We chose bifurcation frequencies so that average particle valences were similar to those in the lens. For all simulated <M>, there was a peak at q = 0.15 Å⁻¹ corresponding to the particle-particle nearest-neighbor distance, a minimum in structure factor between 0.03<q<0.1 Å⁻¹, and log-log slope of -2.3 for q < 0.07 Å⁻¹.

These simulations also show the origin of the local minimum in lens structure factor around q=0.10 Å⁻¹. There is systematically less spatial fluctuation at this q-range when the particles are more closely packed at higher <M>; their positions are more constrained with respect to each other, causing in a decrease in density fluctuation. The depth of the minimum at q=0.10 Å⁻¹ in the experimental data is deeper than in the simulation for radial positions less than 60%, further supporting the result that <M> at these radial positions is likely greater than three.

Molecular details of protein-protein interactions

To study the atomic origin of M=2 interactions in the lens material, we used an explicit-water molecular dynamics (MD) approach using the coarse-grained structure of the 100% layer as a starting point (16). When we positioned two long-loop S-crystallins at the DAMMIF-predicted distance and relative orientation, several hydrogen bonds formed between the two disordered loops, forming a stable bridging structure (Fig. 5A). The number of hydrogen bonds increased from zero to a maximum six, with the resulting structure resembling a metastable amyloid interaction (Fig. 5B).

We used this simulation to estimate the bond energies resulting from these loop-loop contacts. We characterized protein-protein interactions with a dimensionless temperature, T, defined as the thermal energy of the system divided by the bonding energy of a particular interaction. A previous study measured the Gibbs free energy of hydrogen bonding between hydrated strand-like peptides to average 2.6 kcal/H-bond/mol (27). For links consisting of 3–8 H-bonds at 10°C, T=0.08–0.03. This estimate of T applies to the 100% and 80% radius region of the lens where linkages between proteins are primarily between disordered loops.

At radial positions less than 60%, proteins form ramifying lamellae and then a proteinaceous material with no bulk water. These structures are consistent with patchy systems in which patches have become so large and/or numerous that their interactions approach those of isotropic, spherical particles (Figs. 3D, 4D). Here, the energies of protein-protein binding are likely similar to those involved in protein docking, in the range of 10–20 kcal/bond/mol, so the lower bound for T for these interactions is ~0.01 (28).

Discussion

Our data show that at all radial positions and every possible density, structure in the intact squid lens is dominated by attractive interactions between S-crystallin dimers, a result that is inconsistent with isotropic potentials, since these systems will undergo liquid-liquid phase separation and opacification at some point (29).

From a materials perspective, this lens could in principle be built from a single mixture of particles with M slightly greater than two, since any system to the right of the spinodal line for <M>=2.1 in the patchy colloid phase diagram may form a volumetric material with low density variation. However, our data show that <M> changes monotonically with lens radius, from a minimum near two in the periphery to a maximum near six at the core of the lens.

There is a biological rationale for the lens evolving an array of <M> rather than simply using one mixture with <M>≈2.1 at many different densities. New lens cells must be filled gradually with protein through the process of mRNAs and amino acids diffusing to large ribosomes, with full-length proteins then diffusing away from the ribosome. In any cell whose proteome-determined <M> allowed for gelation at a density lower than the appropriate endpoint for a given radial position, protein synthesis would be arrested prematurely. Patchy colloidal physics allows for a cellular mechanism by which lens cells gel near the optically appropriate endpoint density for a given radial position. The cellular transcriptome systematically titrates S-crystallin isoforms as <M> changes as a function of lens radius. We hypothesize that a cell then passively ceases protein synthesis at the appropriate density, since upon gelation, protein synthesis would simply stop due to inability of large polymers (mRNAs and newly transcribed protein) to diffuse through the material.

Given that in principle one protein sequence could encode one valence in the lens, requiring a minimum of six S-crystallin sequences, there were a large number of unique S-crystallin sequences encoded by the genome, and the loops encoded by these sequences that form the linkages between proteins also had high chemical polydispersity. We speculate that this high degree of polydispersity in loop sequence and subsequent linker interaction dynamics may both avoid kinetic traps during nucleation and reduce the entropic cost of forming a volume-spanning network (30). This set of linker sequences generated by evolution may then help inform experimental attempts to exploit the self-assembly principles revealed by patchy particle theory.

We observed that the difference between the original density of the lens and the density of the pellet formed from low effective temperature bonds increased from near zero at the periphery to a factor of two at the core (Fig. 4A–C). At the core of the lens, the pellet after a dilution-induced phase/state transition had a packing fraction near 0.5, indicating <M> for the system near six, or square-lattice-like packing, while the intact lens core has little or no bulk water and a packing fraction approaching 1.0 (consistent with M=12). We speculate that in the squid embryo, these original, most central cells in the lens structure initially gel near the lower square-lattice packing fraction of 0.5, consistent with constituent proteins of <M>≈6. Then, as new cells are added to the organ periphery during lens growth, the newer material will be both more compliant due to a lower coordination number, and have a higher charge density due to the increasingly positive surface charge of the proteins in the peripheral layers (8). Both of these factors will tend to cause water to migrate outward from the lens core as the structure grows, systematically increasing the density of central regions of the lens with the animal’s age and size, and potentially resulting in a near-dry lens core in the mature organ.

Our data also describe a gradual “inside-out” mechanism for evolving a gradient index lens from a single protein fold. In this view, an initial protein closely related to enzymatic glutathione s-transferase duplicated for lens expression and formed a high-density colloidal gel through near-isotropic interactions. Selection pressure for a gradient index then resulted in proteins with less-isotropic interactions and the resulting lamellar structures observed in extant lenses, consistent with patchy colloidal systems of intermediate average valence (31). Further selection on S-crystallins resulted in an unstructured loop encoded in a novel exon that was able to undergo flexible, non-specific hydrogen-bonding interactions with other similar loops. These loops, coupled to the increase in positive charge on the folded, spherical surfaces of the protein represent an evolutionary innovation of a protein particle able to enforce a coordinate number of M=2. With this loop-binding innovation, squid lenses were then able to exploit the entire physics of the patchy colloid phase diagram, and the thermodynamically stable materials with low density fluctuation that result from this physics. It is also possible that this patchy colloidal perspective could provide insights into still poorly understood aspects of vertebrate lens biology. In particular, the polydisperse nature of alpha crystallins in the low-density regions of the vertebrate lens have been a puzzle; even in solution, they appear to interact via “tentacles” in ways that are hard to specifically characterize (32). It is possible that they are also acting as low-valence patchy colloidal gels in vivo, as is the case for squid S-crystallins.