Abstract
Craniosynostosis is a congenital malformation of the infant skull typically treated via corrective surgery. To accurately quantify the extent of deformation and identify the optimal correction strategy, the patient-specific skull model extracted from a pre-surgical computed tomography (CT) image needs to be registered to an atlas of head CT images representative of normal subjects. Here, the authors present a robust multi-stage, multi-resolution registration pipeline to map a patient-specific CT image to the atlas space of normal CT images. The proposed registration pipeline first performs an initial optimisation at very low resolution to yield a good initial alignment that is subsequently refined at high resolution. They demonstrate the robustness of the proposed method by evaluating its performance on 560 head CT images of 320 normal subjects and 240 craniosynostosis patients and show a success rate of 92.8 and 94.2%, respectively. Their method achieved a mean surface-to-surface distance between the patient and template skull of <2.5 mm in the targeted skull region across both the normal subjects and patients.
Keywords: image registration, bone, surgery, medical image processing, computerised tomography, deformation, biomechanics, image resolution, optimisation
Keywords: robust head CT image registration pipeline, craniosynostosis skull correction surgery, congenital malformation, infant skull, corrective surgery, deformation, optimal correction strategy, patient-specific skull model extraction, presurgical computed tomography image, robust multistage multiresolution registration pipeline, patient-specihc CT image, normal CT images, initial optimisation, very low resolution, mean surface-to-surface distance, template skull, targeted skull region
1. Introduction
Craniosynostosis is the premature fusion of sutures in the infant skull that restricts the normal growth of the skull and brain. It is a congenital malformation occurring in 1 of 2500 live births [1]. Early diagnosis and surgical treatment is essential to avoid the elevated intracranial pressure that leads to respiratory and visual impairments associated with the malformation [2, 3]. Craniosynostosis treatment involves cranial surgery to provide adequate intracranial volume facilitating brain growth and to create an aesthetically normal skull shape and facial appearance. While there is no single best method for treatment, therapy is driven by the philosophy of the institution and the wishes of the parents [4]. When cranial reconstruction surgery is the selected treatment plan, careful preoperative planning is required to minimise complications and morbidity.
Computed tomography (CT) imaging is the preferred modality for diagnosis, preoperative planning and post-surgical assessment of craniosynostosis patients [2]. A high-quality 3D skull model is reconstructed from the patient's CT image and used to analyse the precise skull deformation relative to a normal skull shape [5]. Subsequently, the closest normal skull is identified to serve as the target skull shape for corrective surgery. Hence, a surgical plan to cut and reconfigure the bones is prepared using computer-aided design software or 3D-printed models, such that the pathological skull matches the target skull shape. A critical step in this pre-surgical planning is the registration of the craniosynostotic skull into the normative image space.
Various image registration techniques have been proposed in [6], yet despite their exhaustive dissemination and citation, medical image registration is seldom used in clinical practice [7]. Of the disseminated registration methods, only a few study skull registration of craniosynostotic cases. The study in [8] was limited to generating an average normative pediatric skull model from 103 normal infant skulls aged 8–12 months using point-set-based registration algorithm [9], but did not include any pathological cases. Sahilliouglu et al. [10] used PCA alignment of point sets and performed a modified iterative closest point (ICP) global registration followed by deformable volumetric registration, but evaluated their method on only five craniosynostotic patients. Therefore, a robust registration technique to map a pathological case into the normative image space would be very useful to precisely plan the corrective surgery.
Here we describe and validate a robust multi-stage, multi-resolution image registration pipeline for craniosynostotic skull registration. We propose a clinically applicable method that leverages the lower skull features not affected by the disease pathology to map the patient skull into the image space of normal skulls, despite the large deformities induced by craniosynostosis. Moreover, we implement and assess the performance of the registration on a large number of both normal (320) and pathological (240) cases.
The proposed registration pipeline, which is the focus of this paper, serves as the first step in planning the skull correction surgery. Following patient skull mapping into the normative skull space, a normal skull closest in shape to the craniosynostosis skull is identified and used as a post-surgical target. The surgery is then planned according to the estimated deformation required to correct the diseased skull shape to its desired normal shape. Fig. 1 shows how this proposed image registration pipeline fits within the larger scope of the project aimed at optimising pre-surgical planning for craniosynostotic corrective surgery.
Fig. 1.
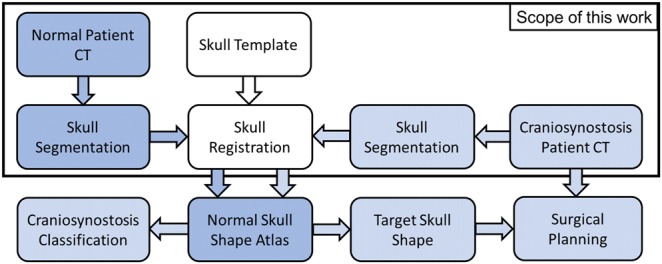
Craniosynostosis skull correction pipeline. Normal skulls segmented from CT images are registered to the template skull to create a normal skull shape atlas. Craniosynostosis patient skull is registered to the atlas to quantify skull deformity, determine the best patient-specific target skull shape after surgery, and perform the cranial deformation analysis to plan the surgical correction of skull shape as in [11]
2. Methods
Our workflow entails several stages: first we extract the head and segment the skull using fixed and adaptive thresholds, respectively. We then employ a robust five-stage multi-resolution registration pipeline to register the segmented binary skull with the template skull. Since CT image intensities are a direct measure of tissue density and standardised via the Hounsfield unit (HU) [12], a good skull segmentation is achieved by simple adaptive thresholding. We then employ a segmentation-based registration to map the normal and craniosynostosis patient skulls into the template image space.
2.1. Head segmentation
Since the Hounsfield number of air is −1000 HU and that of fat ranges between −100 and −50 HU, we select a heuristic threshold of −200 HU to delineate the structures of interest (tissues, fat, and bones) from the CT image. We then use a binary morphological opening operation to separate noisy structures attached to the patient head, followed by largest connected component extraction to retain the head segmentation as shown in Fig. 2. It is worth noting that due to the binary morphological opening operation, the obtained segmentation features holes in the nose, air tract, and ear regions that serve as landmarks for the subsequent image registration.
Fig. 2.
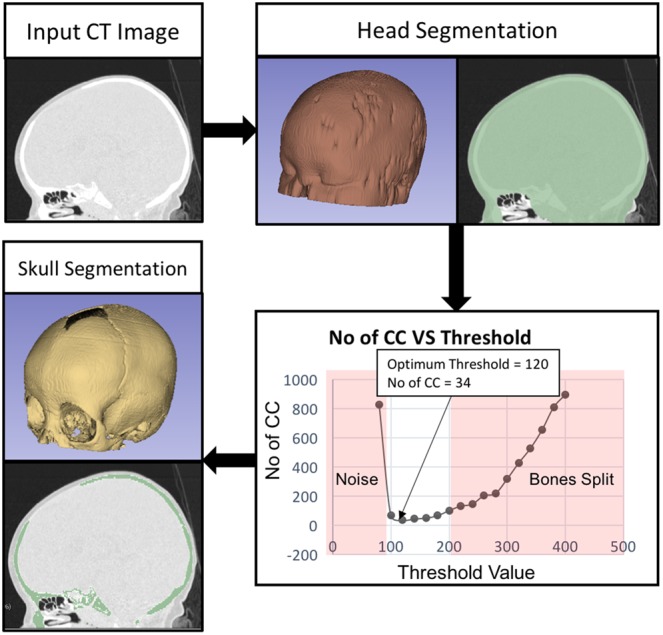
Input CT image is thresholded and cleaned to obtain the head segmentation. The optimum threshold resulting in minimum number of connected components is used to segment the skull
2.2. Skull segmentation using adaptive thresholding
Since we cannot rely on a single threshold to delineate between bone and soft tissues, we threshold the image region within the head mask (Section 2.1) using several threshold values between 60 and 300 HU at an increment of 20 HU and select the optimum threshold that yields a minimum number of connected components. A low threshold would produce high number of connected components by segmenting soft tissues as bone, while a high threshold would split bones into pieces leading to a higher number of connected components. Since the largest connected component might not include all the major bones, due to open sutures in infant skull, we retain the connected components comprising of at least 95% of the total number of segmented pixels to obtain the optimal skull segmentation as shown in Fig. 2.
2.3. Image registration
To register a patient head CT image into the normative space, we select an 8-month-old healthy patient with high CT resolution and adequate extent of imaged anatomy to serve as a template. We then segment the individual bones from the template CT image manually to generate a template skull model (Fig. 4c). Automatically segmented normal and craniosynostosis skulls are registered to the template skull space for further analysis.
Fig. 4.
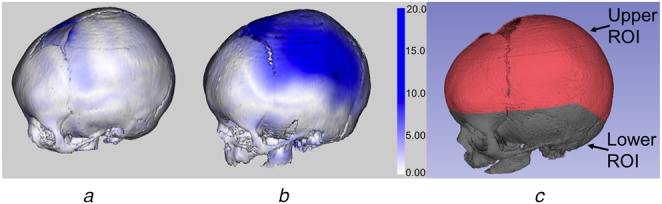
Absolute distance error between the registered subject and template skulls mapped onto the subject skull model with corresponding error bar
a Normal skull
b Craniosynostosis skull
c The lower ROI mapped onto the template skull (all 8 months old).
Highest error occurs in the fontanel region due to the anatomical mismatch between the subject and template models, hence we rely on percentile distance instead of the maximum distance. The normal skull has better alignment compared with the craniosynostosis skull. Also the errors are larger in the upper region compared with the stable lower regions which are used for registration
The skull is a rigid object and to maintain its shape proportions, we parameterise the registration using a seven degree of freedom similarity transformation – translation along and rotation about the x-, y-, and z-axes and isotropic scaling. We define a similarity function based on the sum of squared difference between the images being registered:
| (1) |
where x is a three-dimensional vector representing image space, and are Gaussian filtered fixed and moving images, respectively, is the similarity transform (with seven-parameters p) applied to , and N is the number of voxels in the image overlap domain . Hence, the image registration is formulated as a minimisation of the similarity function in a seven-dimensional parametric space p. We use the regularised gradient descent algorithm [13] implemented in the Insight Toolkit (ITK) to minimise the function using the parameter update:
| (2) |
where is the learning rate set to 0.5, which reduces by a relaxation factor of half each time the gradient of the objective function changes abruptly, facilitating the convergence of the algorithm towards the closest optimum. The algorithm converges when the step size gets very small or the parameter difference or the difference in the cost function between consecutive iterations is either very small or maximum number of iterations have been reached.
The similarity function is highly non-linear in the seven-dimensional parametric space and hence the probability of converging to a local minimum during the optimisation is very high. To avoid convergence to local minima, we employ a five-stage registration pipeline (Fig. 3) where the first three optimisations are performed at low resolution with high Gaussian blurring to obtain a coarse alignment, whereas the final two stages refine the registration results at higher resolution. The optimal transformation obtained from each stage is used as an initialisation for the subsequent stage.
Fig. 3.
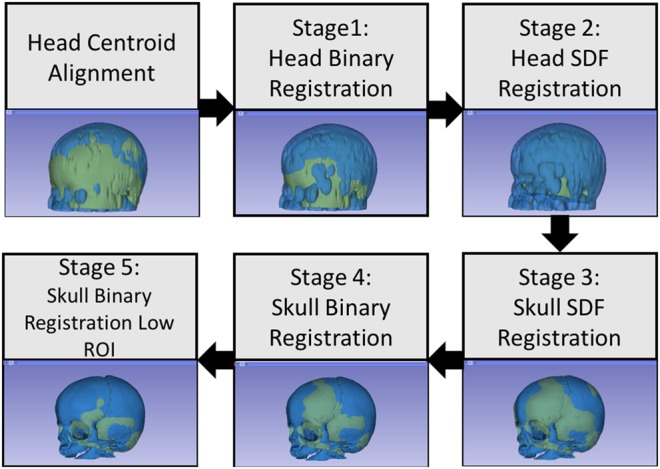
Proposed registration pipeline for aligning normal and craniosynostosis skulls to the template skull. We start by aligning the head centroids followed by three stages of optimisation performed at low-resolution to obtain a coarse initial alignment; this alignment is then refined at higher resolution in final two stages. Finally, we use the lower region to refine the registration in the final stage to obtain good alignment for highly deformed craniosynostosis skulls
2.3.1. Binary head mask registration
We recover the initial translation between the two CT images by aligning the centroids of the head masks (Section 2.1). Next, to recover the scaling between the patient and the template head, we modify the similarity metric (1) such that:
where and are Gaussian filtered binary head segmentations for template and subject CT images, respectively, and is the number of voxels in the image overlap domain . The optimisation is performed at one-fourth of the original resolution using the parameter update (2).
2.3.2. Signed distance-based head registration
The anatomical extent and orientation of a patient's head varies significantly between the images being registered. Hence, we use the holes in nose, air tract, and ear regions as landmarks to recover the accurate orientation from the head segmentations. As such, the similarity metric (1) is modified using:
where is the signed distance function (SDF) with positive values outside and negative values inside the binary object, is the truncated SDF with a fixed high value assigned to the positive distances, and N is the number of voxels in the image overlap domain within the moving image mask . Assigning high values to the distances outside restricts the to be transformed within the , forcing the orientation recovery via the landmarks in the head segmentations. The optimisation is performed at one-fourth of the original resolution.
2.3.3. Signed distance-based skull registration
To recover the appropriate scaling factor between the two skull segmentations following the rotation correction, we modify the similarity metric (1) using:
where and are the binary skull segmentations (Section 2.2) for template and subject CT images, respectively, is the SDF operator, and N is the number of voxels in the image overlap domain . The optimisation is also performed at one-fourth of the original resolution.
2.3.4. Binary skull registration
The first three low-resolution optimisation steps yield a good coarse skull alignment, which we then refine by modifying the cost function (1) using:
where is the number of voxels in the image overlap domain , within the fixed and moving image masks and , respectively. The optimisation is performed at half the original resolution.
2.3.5. Binary skull registration in low region of interest (ROI)
Since our registration algorithm is targeted for craniosynostosis application, it must retain robust and accurate alignment despite severely deformed skull shapes. Hence, we use the lower region of the skull located below four anatomical landmarks – the Opisthion, Nasion, and Left and Right Dorsum Sellae [5] – to register the skulls, since this region is not affected by the disease pathology and features low shape variability across normal and craniosynostosis patients. The final registration stage refines the skull alignment within the low ROI (Fig. 4c) using:
in (1), where is the final similarity transform between the subject and template CT images, and is the number of voxels in the image overlap domain , within the fixed and moving image masks and , respectively. The final alignment is performed at full image resolution.
3. Results
The proposed algorithm was implemented in C++ using the ITK library on a 2.4 GHz Xenon machine with 72 GB of RAM and took 450 s on average to segment a subject CT image and register it to the template skull model.
We tested our registration pipeline on 560 CT images with an age range of 1 week to 19 years ( months) and in-plane and slice resolution of 0.26–0.49 mm and 0.625–5 mm, respectively.
We quantitatively evaluate our registration accuracy by computing the mean absolute distance and percentile symmetric distance between the template skull model and the registered subject model. Fig. 4 shows the absolute distances between the registered subject and template model mapped onto the subject model for both normal and craniosynostosis cases.
Fig. 5 shows the registration accuracy of successfully registered skulls compared against the template skull model. Mean registration accuracy for the normal and craniosynostosis skulls in the lower ROI are and , whereas that for the upper ROI are and , respectively. High registration accuracy in the lower ROI region for both normal and craniosynostotic cases demonstrates the robustness of our method. As expected, registration error in upper ROI for craniosynostosis patients is high due to the deformity of the pathological skull.
Fig. 5.
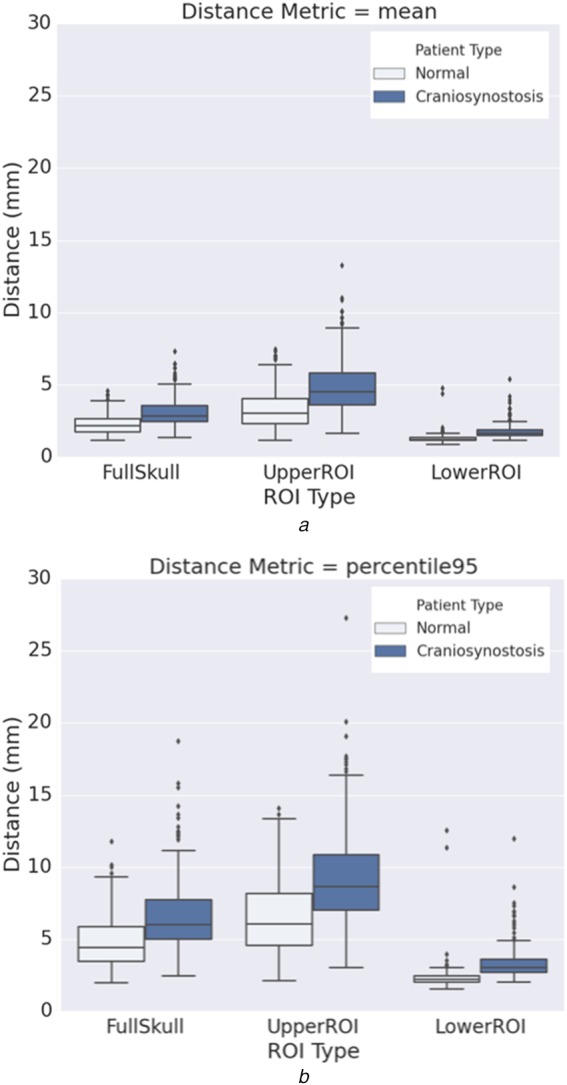
Median, inter-quartile range and outliers
a Mean absolute distance
b percentile
surface-to-surface distance between the registered patients against the template. The distance metric for full skull, upper ROI and lower ROI regions are plotted from left to right. Normal (297) and craniosynostosis (226) cases are shown in light and dark colours, respectively. The mean and percentile distances in the lower ROI are within 2.5 and 5.0 mm, respectively
A small surface-to-surface distance is a necessary condition for good registration but not sufficient. Hence, we also perform qualitative evaluation by visual inspection of the registration results. The algorithm produced visually correct results for 297 normal (out of 320) and 226 craniosynostosis (out of 240) cases as shown in Table 1.
Table 1.
Evaluation of the robustness of our registration pipeline against the baseline registration [5] for both normal and craniosynostosis skulls
| Registration method | Failed normal, N = 320 | Failed craniosynostosis, N = 240 |
|---|---|---|
| baseline method [5] | ||
| proposed method | ||
| percentage improvement, % |
A general registration approach is to align the centroids of skull segmentations and perform optimisations as described in fourth and fifth stages of Section 2.3 as employed in [5]. Here we compare the additional registration robustness introduced by the first three stages of our pipeline that perform initial alignment in low resolution, against the baseline scheme [5] in Table 1. We are able to reduce the number of registration failures from 47 to 23 for normal cases and from 30 to 14 for craniosynostosis cases, therefore leading to a 47% improvement in registration robustness on average.
4. Discussion
As evident from Fig. 1, this paper addresses the most important and difficult part of the problem of robustly registering a diseased patient skull to the ‘normative’ space of normal skulls. Although registration algorithms exist that register the image of a normal skull to another reasonably well, there are unfortunately no sufficiently robust registration methods that are specifically tailored to registering deformed skulls to normal skulls.
In the second part of the project, which is currently underway, following the accurate recovery of pose and scaling using linear registration, we perform the shape analysis using non-rigid registration algorithms to quantify the amount and nature of deformity associated with the diseased skull and hence to determine the closest normal skull shape to serve as target during corrective surgery.
Briefly, our proposed strategy is to use non-rigid registration to compute the closest normal target skull shape based on the deformation of the diseased patient's skull with respect to the unbiased, average skull shape obtained by co-registering normal skulls, therefore removing the bias towards a single subject.
The goal of this first stage is to remove the pose and scale variation in the normal and diseased patients and bring them all into the same coordinate space. Existing alternative solutions for linear registrations can be broadly classified as point-set-based algorithms and image-based algorithms. The ICP algorithm is a popular point-set-based algorithm where the point sets are initially aligned using the principal component directions. Due to the deformations induced by the premature fusion of the sutures, the structure of the skull changes significantly, rendering the principal components-based initial alignment highly susceptible to error, and, as a result, the final registration result is highly inaccurate and unrealistic. Although the image-based linear registration algorithms are computationally demanding, they have more flexibility in implementation. Here we alternate between the binary image and distance maps to carefully guide the registration towards the appropriate solution and compare our results against a standard image-based registration algorithm. Moreover, by selecting and optimising the registration parameters, we demonstrate that our method performs well on registering both the normal subjects and diseased patients.
Specifically, we demonstrated the robustness of our algorithm by evaluating its performance on 360 image datasets of normal subjects and 240 image datasets of diseased patients. The age of the normal subjects and diseased patients is summarised in Table 2: normal subjects were months (1 week to 24 months), and the diseased patients were months (1 week to 228 months). While the early diagnosis and treatment of the patients occurs within the first 2 years of age and considering that there is minimal skull growth beyond 6 years of age, the normal subjects used to create an atlas are in the representative age range of 1 week to 24 months. Nevertheless, eight patients above 84 months old who underwent craniosynostosis correction surgery at Children's National Medical Center were included in our study to demonstrate that our registration method is robust across a wide variety of patient populations, clinical data, and disease characteristics (Table 3).
Table 2.
Age of the subjects used in the study
| Subject | Mean std. dev. | Range |
|---|---|---|
| normal, months | 1 week–24 | |
| craniosynostosis, months | 1 week–228 | |
| all, months | 1 week–228 |
Table 3.
Type of craniosynostosis patients used in the study
| Craniosynostosis type | Number of patients |
|---|---|
| coronal | |
| sagittal | |
| metopic | |
| pansynostosis | |
| frontal sphenoid | |
| coronal-sagittal | |
| coronal-lamboidal | |
| unknown | |
| total |
Moreover, the radiation exposure to the patients should be minimised, and hence the CT scans are acquired with a limited anatomical coverage, mostly including the regions affected by the malformation. Our approach focuses on registering the malformed patient to the normal template by excluding the regions significantly affected by the disease from the registration in the final stage. As evident from the registration accuracy in the lower stable parts of the skull, the algorithm performs reasonably well even for the malformed patients.
5. Conclusion
We presented a robust multi-stage, multi-resolution pipeline for registration of both normal and craniosynostosis skulls and conducted an exhaustive evaluation on 560 clinical CT images with success rates of 92.8 and 94.2% across 320 normal and 240 craniosynostosis patients, respectively. We evaluated our registration success using surface-to-surface distance accompanied by a visual inspection. Our method reduced the registration failure in both normal and craniosynostosis cases by 47% compared with a baseline registration algorithm employed in [5]. Finally, this registration yielded an accuracy within 2.5 and 5.0 mm for mean absolute and percentile surface-to-surface distance across the lower skull ROI for both normal and craniosynostosis cases, respectively. Hence, this registration pipeline can be reliably used to map craniosynostotic skulls into the normative skull space to help identify the closest normal skull shape that serves as post-procedural target during corrective surgery planning.
6. Acknowledgment
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
7. Funding and Declaration of interests
Research reported in this publication was supported by the Eunice Kennedy Shriver National Institute Of Child Health & Human Development of the National Institutes of Health under Award Number R42HD081712.
8 References
- 1.Lajeunie E., Merrer M.L., Binaiti-Pellie C., et al. : ‘Genetic study of nonsyndromic coronal craniosynostosis’, Am. J. Med. Genet., 1995, 55, (4), pp. 500–504 (doi: 10.1002/ajmg.1320550422) [DOI] [PubMed] [Google Scholar]
- 2.Nagaraja S., Anslow P., Winter B.: ‘Craniosynostosis’, Clin. Radiol., 2013, 68, (3), pp. 284–292 (doi: 10.1016/j.crad.2012.07.005) [DOI] [PubMed] [Google Scholar]
- 3.Kirmi O., Lo S.J., Johnson D., et al. : ‘Craniosynostosis: a radiological and surgical perspective’, In: Seminars in Ultrasound, CT and MRI, 2009, vol. 30, Elsevier, pp. 492–512 [DOI] [PubMed] [Google Scholar]
- 4.Szpalski C., Weichman K., Sagebin F., et al. : ‘Need for standard outcome reporting systems in craniosynostosis’, Neurosurgical Focus, 2011, 31, (2), pp. E1 (doi: 10.3171/2011.6.FOCUS1192) [DOI] [PubMed] [Google Scholar]
- 5.Mendoza C.S., Safdar N., Okada K., et al. : ‘Personalized assessment of craniosynostosis via statistical shape modeling’, Med. Image Anal., 2014, 18, (4), pp. 635–646 (doi: 10.1016/j.media.2014.02.008) [DOI] [PubMed] [Google Scholar]
- 6.Maintz J.A., Viergever M.A.: ‘A survey of medical image registration’, Med. Image Anal., 1998, 2, (1), pp. 1–36 (doi: 10.1016/S1361-8415(01)80026-8) [DOI] [PubMed] [Google Scholar]
- 7.Viergever M.A., Maintz J.A., Klein S., et al. : ‘A survey of medical image registration - under review’, Med. Image Anal., 2017, 33, pp. 140–144 (doi: 10.1016/j.media.2016.06.030) [DOI] [PubMed] [Google Scholar]
- 8.Saber N.R., Phillips J., Looi T., et al. : ‘Generation of normative pediatric skull models for use in cranial vault remodeling procedures’, Child’s Nervous Syst., 2012, 28, (3), pp. 405–410 (doi: 10.1007/s00381-011-1630-7) [DOI] [PubMed] [Google Scholar]
- 9.Myronenko A., Song X.: ‘Point set registration: coherent point drift’, IEEE Trans. Pattern Anal. Mach. Intell., 2010, 32, (12), pp. 2262–2275 (doi: 10.1109/TPAMI.2010.46) [DOI] [PubMed] [Google Scholar]
- 10.Sahillioglu Y., Kavan L.: ‘Skuller: a volumetric shape registration algorithm for modeling skull deformities’, Med. Image Anal., 2015, 23, (1), pp. 15–27 (doi: 10.1016/j.media.2015.03.005) [DOI] [PubMed] [Google Scholar]
- 11.Porras A.R., Zukic D., Equobahrie A., et al. : ‘Personalized optimal planning for the surgical correction of metopic craniosynostosis’. In: Workshop on Clinical Image-Based Procedures, 2016, Springer, pp. 60–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Goldman L.W.: ‘Principles of CT and CT technology’, J. Nucl. Med. Technol., 2007, 35, (3), pp. 115–128 (doi: 10.2967/jnmt.107.042978) [DOI] [PubMed] [Google Scholar]
- 13.Avants B.B., Tustison N.J., Stauffer M., et al. : ‘The insight toolkit image registration framework’, Front. Neuroinform., 2014, 8, pp. 44 (doi: 10.3389/fninf.2014.00044) [DOI] [PMC free article] [PubMed] [Google Scholar]


