Estimation of surgical tool-tip tracking error distribution in coordinate reference frame involving pivot calibration uncertainty

Abstract

Accurate understanding of surgical tool-tip tracking error is important for decision making in image-guided surgery. In this Letter, the authors present a novel method to estimate/model surgical tool-tip tracking error in which they take pivot calibration uncertainty into consideration. First, a new type of error that is referred to as total target registration error (TTRE) is formally defined in a single-rigid registration. Target localisation error (TLE) in two spaces to be registered is considered in proposed TTRE formulation. With first-order approximation in fiducial localisation error (FLE) or TLE magnitude, TTRE statistics (mean, covariance matrix and root-mean-square (RMS)) are then derived. Second, surgical tool-tip tracking error in optical tracking system (OTS) frame is formulated using TTRE when pivot calibration uncertainty is considered. Finally, TTRE statistics of tool-tip in OTS frame are then propagated relative to a coordinate reference frame (CRF) rigid-body. Monte Carlo simulations are conducted to validate the proposed error model. The percentage passing statistical tests that there is no difference between simulated and theoretical mean and covariance matrix of tool-tip tracking error in CRF space is more than 90% in all test cases. The RMS percentage difference between simulated and theoretical tool-tip tracking error in CRF space is within 5% in all test cases.

1. Introduction

Surgical tool-tip tracking is an essential technique in image-guided surgery (IGS) [1, 2]. On the one hand, it can be used to provide the real-time surgical tool-tip position in tracking system frame during surgery. On the other hand, it can also be adopted to acquire fiducials' positions in patient space for an image-to-patient registration [3]. Statistics of surgical tool-tip tracking error can provide real-time feedback to help surgeons make correct decisions (e.g. avoiding potentially dangerous tool movements) during surgery [4]. Among various tracking systems, optical tracking system (OTS) is most commonly adopted because of its robustness and high accuracy. OTS frame is usually set as a frame whose x- and y-axis are in the image plane while the z-axis is pointing outwards the stereo camera.

Before surgical tool-tip tracking, an important procedure called pivot calibration usually has to be done to determine the tool-tip position in tool reference frame (TRF), i.e. ${}^{\mathrm{trf}}\mathit{r}$ [5]. TRF is the local coordinate frame of a surgical tool determined by the relative positions of markers attached to the surgical tool with the frame's origin being the centroid of markers' locations. During pivot calibration, the surgical tool is pivoted around a fixed point. During surgical tool-tip tracking process, to acquire the pose of surgical tool ${}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{R}$ and ${}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{t}$, measured positions of tool-attached fiducials (markers) in OTS frame have to be registered to corresponding ones in TRF frame.

Assuming that the pivot calibration is perfect, surgical tool-tip tracking error is actually target registration error (TRE) in the above paired-point rigid registration (PPRR). Paired-point indicates the correspondences between points in two spaces are known. Extensive efforts have been made to estimate or model TRE statistics when fiducial localisation error (FLE) distribution is known [6–13]. FLE is produced when OTS locates the three-dimensional (3d) coordinates of fiducials/markers. TRE statistical model was first formally adopted in the scenario of surgical tool-tip tracking by West and Maurer [14]. FLE distribution was assumed to be isotropic (the same in all directions) and homogenous (the same for all fiducials) in [14]. Anisotropic FLE was later considered in [8, 15]. All of above work shares one assumption that pivot calibration is perfect.

In surgical tool-tip tracking, two issues exist: (i) The surgical tool-tip position is usually reported relative to a CRF. The CRF rigid body also consisting of fiducials is usually attached to the patient to compensate the patient's motion during surgery [16]. Like TRF, CRF is determined by the relative positions of markers attached to the CRF rigid-body. (ii) Pivot calibration is in fact not perfect [17, 18]. As physical measurements in real world cannot be perfect, there exists inevitable error in pivot calibration as well. It is of great value to consider pivot calibration uncertainty in order to estimate tool-tip tracking error more accurately. To summarise, both FLEs in locating CRF-attached fiducials and pivot calibration uncertainty have to be considered. FLEs of TRF-attached and CRF-attached fiducials can be determined from fiducial registration error (FRE) during tracking [19] or through other methods [20]. If the ‘true’ tool-tip position in TRF, ${}^{\mathrm{trf}}{\mathit{r}}^{\ast }$, is known, the calibration error is easily calculated: ${\mathit{E}}_{\mathrm{cal}}{=}^{\mathrm{trf}}\mathit{r}{-}^{\mathrm{trf}}{\mathit{r}}^{\ast }$. However, without loss of generality, since ground truth of ${}^{\mathrm{trf}}{\mathit{r}}^{\ast }$ is not available due to financial costs [17]. Fortunately, statistics (e.g. covariance matrix) of pivot calibration uncertainty can be estimated during the calibration process [4, 21].

Recently, the covariance propagation techniques are adopted to incorporate uncertainties from tool pose estimation, pivot calibration, image-to-patient registration [4, 21]. While their method can model the tool-tip tracking error distribution in computed tomography (CT) frame quite well, the numerical computation of Jacobians involved in their methods may be a potential drawback for its easy implementation. The purpose of this Letter is to describe and validate a closed-form solution to surgical tool-tip tracking error model problem in CRF while pivot calibration uncertainty is considered. To do this, we first define and develop a new type of error metric called total target registration error (TTRE) in a single rigid registration. Target localisation error (TLE) in two spaces to be registered is considered in the formulation of TTRE. Tool-tip tracking error in OTS frame is represented by TTRE where TLE in TRF space is caused by pivot calibration. Then TTRE model is extended to the case where an optically tracked tool's pose is measured relative to a CRF. A closed-form formulation of statistics (i.e. mean, covariance matrix, RMS (root-mean-square)) of surgical tool-tip tracking error in CRF is then derived. Simulation results show that the proposed model can (i) predict the mean and covariance matrix of tool-tip tracking error in CRF well (at least 90% of test cases accepting the null-hypothesis of hypothesis tests); and (ii) predict RMS value of tool-tip tracking error in CRF well (RMS percentage difference between predicted and simulated data is within 5% for all test cases). We summarise our contributions as follows: (i) A new type of error related to target called TTRE is proposed in a paired-point rigid registration; (ii) TTRE statistical model is derived when first-order approximation in FLE or TLE magnitude is made; (iii) TTRE model is applied to surgical tool-tip tracking scenario; and (iv) simulations are conducted to validate the effectiveness of proposed error model.

2. Method

The coordinate frames and transformation matrices involved in this Letter are first defined for clarity:

• OTS – optical tracking system;

• TRF – tool reference frame;

• CRF – coordinate reference frame;

• ${}_A^B\mathit{T}$ – measured transformation matrix relating frames A and B;

• ${\mathit{T}}^{\ast }$ or ${\mathit{R}}^{\ast }$ – true transformation or rotation matrix;

• ${}^A{\mathit{p}}^{\ast }$ – true value of vector $\mathit{p}$ in frame A;

• ${}^A\mathit{p}$ – measured value of vector $\mathit{p}$ in frame A.

2.1. PPRR problem

The PPRR problem is to determine the rigid transformation $\mathit{T}\in SE(3)$ composed of a rotation matrix $\mathit{R}\in SO(3)$ and a translation vector $\mathit{t}\in {\mathbb{R}}^3$ which minimise the following term [10]:

$$\begin{array}{c}\mathrm{FR}{\mathrm{E}}^2=\sum _{i=1}^N|{\mathit{W}}_i(\mathit{R}({\mathit{x}}_i+\mathrm{\Delta }{\mathit{x}}_i)+\mathit{t}-({\mathit{y}}_i+\mathrm{\Delta }{\mathit{y}}_i{))|}^2\end{array}$$ (1)

where FRE is the weighted fiducial registration error, $N\ge 3$ is the number of fiducials, $X=\{{\mathit{x}}_1,\dots ,{\mathit{x}}_N\}\in {\mathbb{R}}^{3\times N}$ and $Y=\{{\mathit{y}}_1,\dots ,{\mathit{y}}_N\}\in {\mathbb{R}}^{3\times N}$ represent corresponding fiducials' position sets in X (e.g. TRF) and Y (e.g. OTS frame) spaces to be registered, $\{\mathrm{\Delta }{\mathit{x}}_1,\dots ,\mathrm{\Delta }{\mathit{x}}_N\}\in {\mathbb{R}}^{3\times N}$ and $\{\mathrm{\Delta }{\mathit{y}}_1,\dots ,\mathrm{\Delta }{\mathit{y}}_N\}\in {\mathbb{R}}^{3\times N}$ represent FLE vector sets in X and Y spaces, ${\mathit{W}}_i\in {\mathbb{R}}^{3\times 3}$ is a non-singular weighting matrix of the ith fiducial. Without loss of generality, $\mathrm{\Delta }{\mathit{x}}_i$ and $\mathrm{\Delta }{\mathit{y}}_i$ are modelled as independent zero-mean random variables (only reasonable for passive OTS [5]) satisfying $\mathrm{\Delta }{\mathit{x}}_i\sim N(\mathbf{0},\mathrm{cov}[{\mathit{x}}_i])$ and $\mathrm{\Delta }{\mathit{y}}_i\sim N(\mathbf{0},\mathrm{cov}[{\mathit{y}}_i])$, where $\mathrm{cov}[\mathit{v}]$ denotes the covariance matrix of one random variable v with itself.

2.2. Total target registration error

A new type of error metric that is referred to as total target registration error at a given ‘nominal’ target point r is proposed and defined as follows:

$$\begin{array}{rl}\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})& =\mathit{R}(\mathit{r}+\mathrm{\Delta }{\mathit{r}}_x)+\mathit{t}+\mathrm{\Delta }{\mathit{r}}_y-({\mathit{R}}^{\ast }\mathit{r}+{\mathit{t}}^{\ast })\\ & =\mathit{R}\mathit{r}+\mathit{t}-({\mathit{R}}^{\ast }\mathit{r}+{\mathit{t}}^{\ast })+\mathit{R}\mathrm{\Delta }{\mathit{r}}_x+\mathrm{\Delta }{\mathit{r}}_y\\ & =\stackrel{\mathrm{TRE}(\mathit{r})}{\overbrace{\mathrm{\Delta }\mathit{R}{\mathit{R}}^{\ast }\mathit{r}+\mathit{t}-{\mathit{t}}^{\ast }}}+\mathit{R}\mathrm{\Delta }{\mathit{r}}_x+\mathrm{\Delta }{\mathit{r}}_y\end{array}$$ (2)

where ${\mathit{R}}^{\ast }\in SO(3)$ and ${\mathit{t}}^{\ast }\in {\mathbb{R}}^3$ are the ‘true’ rotation matrix and translation vector relating X and Y spaces, $\mathit{r}\in {\mathbb{R}}^3$ is the ‘true’ target location in X space, $\mathrm{\Delta }{\mathit{r}}_x\in {\mathbb{R}}^3\sim N(\mathbf{0},\mathrm{cov}[\mathrm{\Delta }{\mathit{r}}_x])$ and $\mathrm{\Delta }{\mathit{r}}_y\in {\mathbb{R}}^3\sim N(\mathbf{0},\mathrm{cov}[\mathrm{\Delta }{\mathit{r}}_y])$ are independent TLE vectors in X and Y spaces. $\mathrm{TLE}=(\mathit{R}\mathrm{\Delta }{\mathit{r}}_x+\mathrm{\Delta }{\mathit{r}}_y)\sim N(\mathbf{0},\mathit{R}\mathrm{cov}[\mathrm{\Delta }{\mathit{r}}_x]{\mathit{R}}^T+\mathrm{cov}[\mathrm{\Delta }{\mathit{r}}_y])$ is the ‘two-space’ TLE vector. The concept of TTRE is illustrated in Fig. 1. Two assumptions are now made to simplify (2): (a) both FLE and TLE magnitudes are small; (b) approximation to first-order in FLE or TLE magnitude is utilised. It was proved in [10] that $\mathrm{\Delta }\mathit{R}=\mathit{R}({\mathit{R}}^{(\ast )}{)}^T-{\mathit{I}}_{3\times 3}$ is of first-order in FLE or TLE magnitude. With the two assumptions, we can see TTRE equals the following:

$$\begin{array}{rl}\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})& =\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})+\mathrm{\Delta }\mathit{R}{\mathit{R}}^{\ast }\mathrm{\Delta }{\mathit{r}}_x+{\mathit{R}}^{\ast }\mathrm{\Delta }{\mathit{r}}_x+\mathrm{\Delta }{\mathit{r}}_y\\ & \simeq \mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})+{\mathit{R}}^{\ast }\mathrm{\Delta }{\mathit{r}}_x+\mathrm{\Delta }{\mathit{r}}_y\end{array}$$ (3)

where the term $\mathrm{\Delta }\mathit{R}{\mathit{R}}^{\ast }\mathrm{\Delta }{\mathit{r}}_x$ disappears in last line of (3) as it is of second order in FLE.

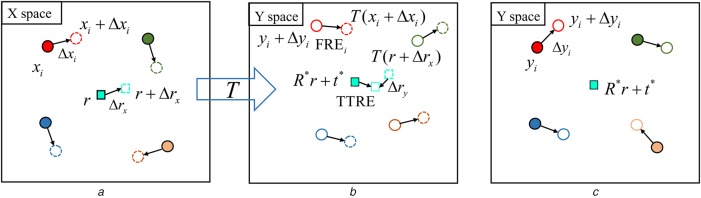
Fig. 1.

Illustrations of TTRE in a rigid registration

a X space: before registration, solid circles $\{{\mathit{x}}_i{\}}_{i=1}^N$ and open dashed circles $\{{\mathit{x}}_i+\mathrm{\Delta }{\mathit{x}}_i{\}}_{i=1}^N$ are ‘true’ and localised/measured fiducial sets, respectively. Solid square r and open dashed square $\mathit{r}+\mathrm{\Delta }{\mathit{r}}_x$ represent ‘true’ and localised target, respectively. $\{\mathrm{\Delta }{\mathit{x}}_i{\}}_{i=1}^N$ are FLE vectors and $\mathrm{\Delta }{\mathit{r}}_x$ is the TLE vector in X space

b Y space: before registration, solid circles $\{{\mathit{y}}_i{\}}_{i=1}^N$ and open circles $\{{\mathit{y}}_i+\mathrm{\Delta }{\mathit{y}}_i{\}}_{i=1}^N$ are ‘true’ and localised fiducial sets, respectively. $\{\mathrm{\Delta }{\mathit{y}}_i{\}}_{i=1}^N$ are FLE vectors in Y space

c Y space: after registration, open dashed circles $\{\mathit{T}({\mathit{x}}_i+\mathrm{\Delta }{\mathit{x}}_i){\}}_{i=1}^N$ is set of the transformed localised fiducials from X space where T is the estimated/calculated rigid transformation matrix, $\mathbf{F}\mathbf{R}{\mathbf{E}}_i$ is the FRE vector between corresponding ith fiducials after registration, open dashed square $\mathit{T}(\mathit{r}+\mathrm{\Delta }{\mathit{r}}_x)$ is the transformed localised target from X space, $\mathrm{\Delta }{\mathit{r}}_y$ is TLE vector in Y space, solid square ${\mathit{R}}^{\ast }\mathit{r}+{\mathit{t}}^{\ast }$ is ‘true’ target in Y space, $\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}$ is the distance between ‘true’ and ‘localised’ target denoted by open square

2.2.1. Mean of TTRE

The mean of TTRE is calculated by taking the expectation of TTRE vector in (3)

$$\begin{array}{rl}⟨\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})⟩& =⟨\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})⟩+⟨{\mathit{R}}^{\ast }\mathrm{\Delta }{\mathit{r}}_x⟩+⟨\mathrm{\Delta }{\mathit{r}}_y⟩\\ & =⟨\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})⟩+⟨{\mathit{R}}^{\ast }⟩⟨\mathrm{\Delta }{\mathit{r}}_x⟩+⟨\mathrm{\Delta }{\mathit{r}}_y⟩={\mathbf{0}}_{3\times 1}\end{array}$$ (4)

where we have adopted the property that ${\mathit{R}}^{\ast }$ is a constant matrix in going from the first to second line of (4).

2.2.2. Covariance matrix of TTRE

The covariance matrix of TTRE is calculated using the expected value of the outer product of TTRE vector with itself

$$\mathrm{cov}[\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})]=⟨\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})\cdot (\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r}){)}^T⟩$$ (5)

Substitute (3) into (5), together with (4), the following holds:

$$\begin{array}{rl}\mathrm{cov}[\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})]& =\mathrm{cov}[\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})]+\mathrm{cov}[{\mathit{R}}^{\ast }\mathrm{\Delta }{\mathit{r}}_x]+\mathrm{cov}[\mathrm{\Delta }{\mathit{r}}_y]\\ & =\mathrm{cov}[\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})]+{\mathit{R}}^{\ast }\cdot \mathrm{cov}[\mathrm{\Delta }{\mathit{r}}_x]\cdot ({\mathit{R}}^{\ast }{)}^T+\mathrm{cov}[\mathrm{\Delta }{\mathit{r}}_y]\end{array}$$ (6)

where we have utilised the property that terms $\mathrm{TRE}$, $\mathrm{\Delta }{\mathit{r}}_x$ and $\mathrm{\Delta }{\mathit{r}}_y$ are co-independent and thus uncorrelated with each other. The expression of $\mathrm{cov}[\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})]$ was developed in [10].

2.2.3. RMS of TTRE

The TTRE RMS value is acquired by calculating the trace of TTRE covariance matrix

$$⟨\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r}{)}^2⟩=\mathrm{trace}(\mathrm{cov}[\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}(\mathit{r})]).$$ (7)

2.3. Surgical tool-tip tracking

Two paired-point rigid registrations are involved in determining the tool-tip position in CRF space (denoted by ${}^{\mathrm{crf}}\mathit{r}$): (i) TRF-attached fiducials' measured positions in OTS frame are registered to corresponding fiducials' calibrated positions in TRF and ${}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{T}$ is acquired; (ii) CRF-attached fiducials' measured positions in OTS frame are registered to corresponding fiducials' calibrated positions in CRF and ${}_{\mathrm{crf}}^{\mathrm{ots}}\mathit{T}$ is acquired. After the two registrations, ${}^{\mathrm{crf}}\mathit{r}$ can be calculated as: ${}^{\mathrm{crf}}\mathit{r}{=}_{\mathrm{ots}}^{\mathrm{crf}}\mathit{T}{(}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{T}{(}^{\mathrm{trf}}\mathit{r}))$, where we defined ${}_A^B\mathit{T}{(}^A\mathit{r}){=}_A^B\mathit{R}\cdot {}^A\mathit{r}{+}_A^B\mathit{t}$. The above two registrations are denoted as ‘to’ and ‘oc’ hereafter, respectively. It is worth mentioning that we still assume that both TRF-attached and CRF-attached fiducials' positions in their own respective local coordinate frames (i.e. TRF and CRF) are well calibrated. Mathematically, let ${\{}^{\mathrm{trf}}{\mathit{x}}_i{\}}_{i=1}^N$ be the TRF-attached N fiducials's calibrated positions in TRF, we assume ${\{}^{\mathrm{trf}}{\mathit{x}}_i{\}}_{i=1}^N={\{}^{\mathrm{trf}}{\mathit{x}}_i^{\ast }{\}}_{i=1}^N$. Likewise, we assume ${\{}^{\mathrm{crf}}{\mathit{c}}_i{\}}_{i=1}^N={\{}^{\mathrm{crf}}{\mathit{c}}_i^{\ast }{\}}_{i=1}^N$ if we let ${\{}^{\mathrm{trf}}{\mathit{c}}_i{\}}_{i=1}^N$ denote the CRF-attached N fiducials's calibrated positions in CRF.

2.3.1. Surgical tool-tip tracking error in OTS frame

In surgical tool-tip tracking, tool-tip tracking error in OTS frame is actually an adapted version of TTRE in (2)

$$\begin{array}{rl}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r})& ={}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{R}\cdot {(}^{\mathrm{trf}}{\mathit{r}}^{\ast }+\mathrm{\Delta }{\mathit{r}}_x){+}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{t}-{(}_{\mathrm{trf}}^{\mathrm{ots}}{\mathit{R}}^{\ast }{\cdot }^{\mathrm{trf}}{\mathit{r}}^{\ast }{+}_{\mathrm{trf}}^{\mathrm{ots}}{\mathit{t}}^{\ast })\end{array}$$ (8)

where TRF is X space and OTS frame is Y space in (8), target (tool-tip) localisation error $\mathrm{\Delta }{\mathit{r}}_x$ in TRF space is caused by pivot calibration. Notice $\mathrm{\Delta }{\mathit{r}}_y$ disappears in (8) as the tracking system does not make any direct localisation of the tool-tip in OTS frame.

2.3.2. Surgical tool-tip tracking error in CRF space

We shift back to use term $\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{comb}}{(}^{\mathrm{crf}}\mathit{r})$ to represent surgical tool-tip tracking error vector in CRF

$$\begin{array}{rl}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{comb}}{(}^{\mathrm{crf}}\mathit{r})& ={}^{\mathrm{crf}}\mathit{r}{-}^{\mathrm{crf}}{\mathit{r}}^{\ast }\\ & ={}_{\mathrm{ots}}^{\mathrm{crf}}\mathit{T}{(}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{T}{(}^{\mathrm{trf}}\mathit{r})){-}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{T}}^{\ast }{(}_{\mathrm{trf}}^{\mathrm{ots}}{\mathit{T}}^{\ast }{(}^{\mathrm{trf}}{\mathit{r}}^{\ast }))\\ & ={}_{\mathrm{ots}}^{\mathrm{crf}}\mathit{T}{(}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{T}{(}^{\mathrm{trf}}\mathit{r})){-}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{T}}^{\ast }{(}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{T}{(}^{\mathrm{trf}}\mathit{r}){-}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r}))\\ & {=}^{\mathrm{crf}}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r}){+}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{T}}^{\ast }{(}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r}))\\ & {=}^{\mathrm{crf}}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r}){+}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{R}}^{\ast }\cdot {}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r})\end{array}$$ (9)

where

$${}^{\mathrm{crf}}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r})={}_{\mathrm{ots}}^{\mathrm{crf}}\mathit{T}{(}^{\mathrm{ots}}\mathit{r}){-}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{T}}^{\ast }{(}^{\mathrm{ots}}\mathit{r})$$ (10)

$${}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r})={}_{\mathrm{trf}}^{\mathrm{ots}}\mathit{T}{(}^{\mathrm{trf}}\mathit{r}){-}_{\mathrm{trf}}^{\mathrm{ots}}{\mathit{T}}^{\ast }{(}^{\mathrm{trf}}{\mathit{r}}^{\ast })={}^{\mathrm{ots}}\mathit{r}{-}^{\mathrm{ots}}{\mathit{r}}^{\ast }$$ (11)

Notice since ${}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r})$ represents a difference vector and is not a spatial position, the transformation ${}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{T}}^{\ast }$ can be reduced to the rotation matrix ${}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{R}}^{\ast }$ in the last line of (9) [15].

2.3.3. Mean, covariance matrix and RMS of tool-tip tracking error in CRF space

The mean of TRE in CRF space is a zero vector

$$⟨\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{comb}}{(}^{\mathrm{crf}}\mathit{r})⟩={\mathbf{0}}_{3\times 1}$$ (12)

The covariance matrix of TRE in CRF space is the following:

$$\mathrm{cov}[\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{comb}}{(}^{\mathrm{crf}}\mathit{r})]=⟨\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{comb}}{(}^{\mathrm{crf}}\mathit{r})\cdot (\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{comb}}{(}^{\mathrm{crf}}\mathit{r}){)}^T⟩$$ (13)

Substitute the last expression of (9) into (13), with some expansions, we can obtain

$$\begin{array}{rl}& \mathrm{cov}{[}^{\mathrm{crf}}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{comb}}{(}^{\mathrm{crf}}\mathit{r})]={⟨}^{\mathrm{crf}}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r})\cdot {(}^{\mathrm{crf}}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r}){)}^T⟩\\ & {+}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{R}}^{\ast }{⟨}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r})\cdot {(}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r}){)}^T⟩{(}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{R}}^{\ast }{)}^T\\ & +2{⟨}^{\mathrm{crf}}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r})\cdot {(}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r}){)}^T⟩\cdot {(}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{R}}^{\ast }{)}^T\end{array}$$ (14)

Due to the two registrations, respectively, denoted by ‘oc’ and ‘to’ are independent, the two random variables ${}^{\mathrm{crf}}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r})$ and ${(}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r}){)}^T$ are uncorrelated. Thus, the last term in (14) disappears and together with (4), we obtain a more concise expression of $\mathrm{cov}[\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{comb}}{(}^{\mathrm{crf}}\mathit{r})]$:

$$\mathrm{cov}{[}^{\mathrm{crf}}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r})]{+}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{R}}^{\ast }\cdot \mathrm{cov}{[}^{\mathrm{ots}}\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r})]\cdot {(}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{R}}^{\ast }{)}^T$$ (15)

where ${}^{\mathrm{crf}}\mathrm{cov}[\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r})]$ can be computed using the expression developed in [10], ${}^{\mathrm{ots}}\mathrm{cov}[\mathbf{T}\mathbf{T}\mathbf{R}{\mathbf{E}}_{\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r})]$ is calculated using (9). The RMS value of surgical tool-tip tracking error in CRF space is further calculated as the following:

$$\mathrm{RM}{\mathrm{S}}_{\mathrm{tre},\mathrm{comb}}{(}^{\mathrm{crf}}\mathit{r})=\sqrt{{(\mathrm{RM}{\mathrm{S}}_{\mathrm{tre},\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r}))}^2+{(\mathrm{RM}{\mathrm{S}}_{\mathrm{ttre},\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r}))}^2}$$ (16)

where ${(\mathrm{RM}{\mathrm{S}}_{\mathrm{tre},\mathrm{oc}}{(}^{\mathrm{crf}}\mathit{r}))}^2$ and ${(\mathrm{RM}{\mathrm{S}}_{\mathrm{ttre},\mathrm{to}}{(}^{\mathrm{ots}}\mathit{r}))}^2$ can be computed using (7).

3. Experiments

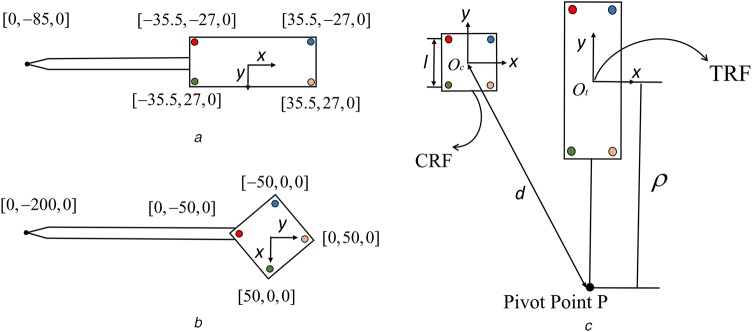
We conducted extensive simulations using two different surgical tool configurations. The two surgical tool configurations are shown clearly in Figs. 2a and b. In all simulations, the number of TRF-attached or CRF-attached fiducials N is 4. More specifically, for the first kind of surgical tool, the coordinates of fiducials in TRF, ${\{}^{\mathrm{trf}}{\mathit{x}}_i{\}}_{i=1}^4$, are: $[35.5,27,0{]}^T$, $[-35.5,27,0{]}^T$, $[-35.5,-27,0{]}^T$, $[35.5,-27,0{]}^T$ mm [19]. For the second kind of surgical tool, the coordinates of fiducials in TRF, ${\{}^{\mathrm{trf}}{\mathit{x}}_i{\}}_{i=1}^4$, are: $[0,-50,0{]}^T,[-50,0,0{]}^T,[0,50,0{]}^T,[50,0,0{]}^T\mathrm{mm}$ [21]. As it is shown in Fig. 2c, the CRF rigid-body is a square centred at $O_c$ with side length l being 32 or 64 mm. The coordinates of CRF-attached fiducials in CRF, ${\{}^{\mathrm{crf}}{\mathit{c}}_i{\}}_{i=1}^4$, are $[l/2,l/2,0{]}^T$, $[l/2,-l/2,0{]}^T$, $[-l/2,-l/2,0{]}^T$, $[-l/2,l/2,0{]}^T$ mm. The distance d between CRF origin $O_c$ and pivot point or tool-tip position P was set to be 100, 200, 300 or 400 mm. For the first kind of tool, the distance $\rho$ between tool tip P and marker centroid $O_t$ was 85 mm; for the second kind of tool, $\rho$ equals 200 mm. The FLE covariance matrix ${\mathbf{\Sigma }}_{\mathrm{FLE}}$ in OTS frame was set to be identical for all TRF-attached and CRF-attached fiducials: ${\mathbf{\Sigma }}_{\mathrm{FLE}}=\mathrm{diag}([{0.02}^2,{0.02}^2,{0.2}^2{]}^T)$ [20]. The pivot calibration uncertainty covariance matrix ${\mathbf{\Sigma }}_{\mathrm{pivot}}$ was set to be a matrix whose eigenvalues' square roots were $[0.31,0.40,0.91{]}^T$ [4]. For all simulated cases, the rotation matrix between CRF and OTS stays the same and is denoted as ${}_{\mathrm{crf}}^{\mathrm{ots}}{\mathit{R}}^{\ast }$.

Fig. 2.

Two surgical tool configurations

a Fiducials' configuration and tool-tip position of the first surgical tool

b Fiducials' configuration and tool-tip position of the second surgical tool. Notice that the two fiducial configurations are planar which means these fiducials lie on one plane

c CRF and TRF are indicated by the x and y axes, l is the side length of CRF rigid body, d is the distance between CRF origin $O_c$ and the pivot point P, $\rho$ is the distance from TRF origin $O_t$ to the tip position P. z axis is perpendicular to both x and y axes. CRF-attached and TRF-attached fiducials are denoted as coloured solid circles

For each simulated case with certain values of l and d, $M=100$ random orientations of surgical tool ${\{}_{\mathrm{trf}}^{\mathrm{ots}}{\mathit{R}}_j^{\ast }{\}}_{j=1}^M$ were generated while the tool-tip was fixed at the pivot point P. For the jth tool orientation ${}_{\mathrm{trf}}^{\mathrm{ots}}{\mathit{R}}_j^{\ast }$, $N_s=2000$ samples of $2N$ FLE vectors and pivot calibration uncertainty vectors $\mathrm{\Delta }{\mathit{r}}_x$ are generated independently according to ${\mathbf{\Sigma }}_{\mathrm{FLE}}$ and ${\mathbf{\Sigma }}_{\mathrm{pivot}}$, respectively. Let $k=1,\dots ,N_s$ denotes the index of $N_s$ error samples. For the kth sample, the generated $2N+1$ vectors were added to ‘true’ transformed fiducials' positions in OTS frame ${}_{\mathrm{trf}}^{\mathrm{ots}}{\mathit{R}}_j^{\ast }\cdot {\{}^{\mathrm{trf}}{\mathit{x}}_i{\}}_{i=1}^4$ and ${}_{\mathrm{crf}}^{\mathrm{ots}}{\mathit{R}}^{\ast }\cdot {\{}^{\mathrm{crf}}{\mathit{c}}_i{\}}_{i=1}^4$, and the ‘real’ tip position in TRF ${}^{\mathrm{trf}}{\mathit{r}}^{\ast }$. In this way, the kth measured TRF-attached and CRF-attached positions in OTS frame ${\{}^{\mathrm{ots}}{\mathit{x}}_i^k{\}}_{i=1}^4$ and ${\{}^{\mathrm{ots}}{\mathit{c}}_i^k{\}}_{i=1}^4$ and ‘disturbed’ tool-tip position in TRF ${}^{\mathrm{trf}}{\mathit{r}}^k$ were acquired. Then ${\{}^{\mathrm{ots}}{\mathit{x}}_i^k{\}}_{i=1}^4$ and ${\{}^{\mathrm{ots}}{\mathit{c}}_i^k{\}}_{i=1}^4$ were registered to their corresponding calibrated ones in TRF and CRF spaces ${\{}^{\mathrm{trf}}{\mathit{x}}_i{\}}_{i=1}^4$ and ${\{}^{\mathrm{crf}}{\mathit{c}}_i{\}}_{i=1}^4$, respectively. The registration algorithm introduced in [22] was used in the above two registrations with the weighting matrix ${\mathit{W}}_i$ being $({\mathrm{\Sigma }}_{\mathrm{FLE}}{)}^{-1/2}$ for all the fiducials. After the two registrations, ${}_{\mathrm{trf}}^{\mathrm{ots}}{\mathit{R}}_j^k$ and ${}_{\mathrm{crf}}^{\mathrm{ots}}{\mathit{R}}^k$ were acquired. So for jth tool orientation, ${\{}_{\mathrm{trf}}^{\mathrm{ots}}{\mathit{R}}_j^k{\}}_{k=1}^{N_s}$ and ${\{}_{\mathrm{crf}}^{\mathrm{ots}}{\mathit{R}}^k{\}}_{k=1}^{N_s}$ were calculated in all. For each tool orientation, TRE statistics of tool-tip in CRF space were calculated using above simulated data and (8), (9). At the same time, for each tool orientation, the predicted TRE statistics in CRF were computed using (5)–(7), (12), (15) and (16).

Two Wishart distribution hypothesis tests ($\alpha =0.05$) similar to those in [6] were conducted for each simulation case (with the null hypothesis stating that there was no difference between simulated and theoretical TRE covariance matrix (or mean and covariance matrix)). For each simulated case, the percentage passing the M Wishart distribution hypothesis tests was recorded. The percentage difference between simulated and theoretical TRE RMS was also calculated for each tool orientation [$\text{\%}\mathrm{diff}=100(\mathrm{RM}{\mathrm{S}}_{\mathrm{pre}}-\mathrm{RM}{\mathrm{S}}_{\mathrm{sim}})/\mathrm{RM}{\mathrm{S}}_{\mathrm{sim}}$.]. Statistics (mean, standard deviation, maximum and minimum) of RMS percentage difference were further calculated for each simulated case.

4. Results and discussion

Simulation results are summarised in Tables 1 and 2. The worst cases in each column are emphasised using black bold texts. For the first kind of tool, at least 93 and 94% accept the null hypothesis of first and second hypothesis test, respectively. The RMS percentage difference is within $\pm 2.78\text{\%}$ (95% confidence interval (CI)) with maximum and minimum values being 4.41 and −4.23%. For the second kind of tool, at least 93 and 95% accept the null hypothesis of first and second hypothesis tests, respectively. The RMS percentage difference is within $\pm 2.60\text{\%}$ (95% CI) with maximum and minimum values being 4.33 and −3.71%. Thus, we can conclude proposed error model can well predict the simulated/measured tool-tip tracking error magnitudes. With FLE RMS and pivot calibration uncertainty vector RMS being 0.20 and 1.27 mm, respectively, the model's performance varies little with respect to different side lengths l of CRF and working distances d.

Table 1.

Monte Carlo simulation results for first kind of surgical tool with various reference tool size l and working distance d. Null hypothesis for test 1 is ${\mathbf{\Sigma }}_{\mathrm{sim}}={\mathbf{\Sigma }}_{\mathrm{pre}}$ and test 2 is $H_0:{\mu }_{\mathrm{sim}}={\mu }_{\mathrm{pre}},{\mathbf{\Sigma }}_{\mathrm{sim}}={\mathbf{\Sigma }}_{\mathrm{pre}}$

Case	Ref. size	Working distance	Accepted		RMS percent difference summary statistics
	l, mm	d, mm	1, %	2, %	Mean, %	Std. dev, %	Max, %	Min, %
1	32	100	93.00	97.00	0.04	1.28	3.10	−2.94
2	32	200	95.00	99.00	−0.06	1.39	3.75	−4.23
3	32	300	95.00	95.00	−0.01	1.16	3.41	−3.36
4	32	400	97.00	94.00	0.07	1.23	3.09	−2.67
5	64	100	97.00	100.00	0.14	1.11	3.43	−2.05
6	64	200	97.00	99.00	0.02	1.01	2.13	−3.24
7	64	300	95.00	96.00	0.08	1.26	4.41	−3.02
8	64	400	98.00	100.00	0.06	1.22	3.38	−2.68

Table 2.

Monte Carlo simulation results for second kind of surgical tool with various reference tool size l and working distance d. Null hypothesis for test 1 is: ${\mathbf{\Sigma }}_{\mathrm{sim}}={\mathbf{\Sigma }}_{\mathrm{pre}}$ and test 2 is $H_0:{\mu }_{\mathrm{sim}}={\mu }_{\mathrm{pre}},{\mathbf{\Sigma }}_{\mathrm{sim}}={\mathbf{\Sigma }}_{\mathrm{pre}}$

Case	Ref size	Working distance	Accepted		RMS percent difference summary statistics
	l, mm	d, mm	1, %	2, %	Mean, %	Std. dev, %	Max, %	Min, %
1	32	100	94.00	96.00	−0.12	1.30	2.74	−3.71
2	32	200	95.00	99.00	−0.01	1.16	3.28	−3.13
3	32	300	93.00	98.00	0.04	1.06	3.36	−2.28
4	32	400	95.00	95.00	−0.03	1.21	3.18	−2.98
5	64	100	96.00	100.00	0.10	1.15	3.06	−2.46
6	64	200	97.00	100.00	0.09	1.12	3.23	−2.48
7	64	300	95.00	99.00	0.01	1.16	3.04	−2.97
8	64	400	96.00	100.00	0.07	1.21	4.33	−3.58

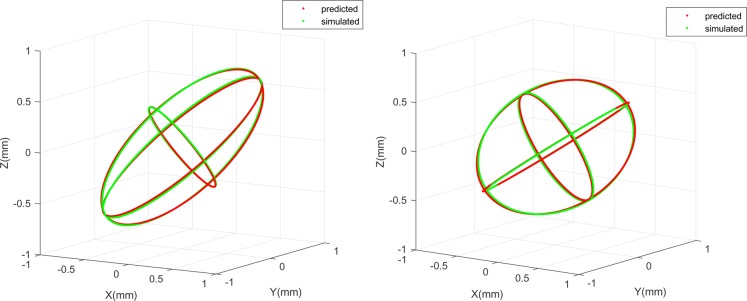
The 95% CI boundary of predicted (red) and simulated (green) covariance matrices are visualised in Fig. 3. The three ellipses in each plot represent the three principal directions of tool-tip tracking error covariance matrices in CRF. As it is shown in the plots of Fig. 3, predicted covariance matrices agree very well with the simulated ones. It is worth mentioning the tool-tip tracking error distribution is anisotropic in CRF. More specifically, we are more uncertain of tool-tip position in the direction with larger ellipse.

Fig. 3.

(Left) Predicted (red) and simulated (green) tool-tip tracking error covariance matrix (95% CI boundary) in CRF for one simulation case using first kind of surgical tool; (Right) similar statistics are visualised for one simulation case using the second kind of surgical tool

One issue in applying the error model to real surgical tool tracking scenario is that the ‘true’ rotation matrix ${}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{R}}^{\ast }$ in (6), (15) is not known. In real implementations, ${}_{\mathrm{ots}}^{\mathrm{crf}}{\mathit{R}}^{\ast }$ can be approximated using measured rotation matrix${}_{\mathrm{ots}}^{\mathrm{crf}}\mathit{R}$. Another one is the choice of visualisation methods in order to better convey the information of tool-tip tracking uncertainty to surgeon [4]. One potential advantage of our method over those in [4, 21] is that more realistic or vivid geometry rendering technique can be used for uncertainty visualisation. This is due to that there needs no expensive calculations like Jacobian computation and Cholesky decompositions involved in [4, 21], which cost much time.

As indicated in [2], TRE vectors of optically tracked tool-tip may be used as FLEs for an image-to-patient registration of an IGS procedure. The acquired FLE can be utilised to estimate the TRE of a surgical target after the image-to-patient registration [23] or be adopted as weightings to improve the accuracy of an image-to-patient registration. Moreover, the TRE vectors of optically tracked tool-tip can also be used to update the pre-operative surgical plan to decrease the probability of the surgical tool touching critical structures [24, 25].

5. Conclusions

In this Letter, we have presented a closed-form formulation of surgical tool-tip tracking error distribution in CRF. Pivot calibration uncertainty is included in the proposed error model. Results show that the proposed model can predict tool-tip tracking error statistics in a precise way for all test cases. More specifically, the magnitude (RMS), position (mean) and shape (covariance matrix) of surgical tool-tip tracking error are very well modelled for two kinds of surgical tools.

Future extensions include incorporating the proposed error model into a commercial surgical navigation system to provide useful feedback for surgeon during surgery. The proposed model will also be extended to the case where a multi-camera tracking system is adopted to eliminate the occlusion problem of existing stereo-camera tracking system. In a multi-camera tracking system, FLEs of TRF-attached and CRF-attached fiducials should be considered to be inhomogeneous and anisotropic. The inhomogeneity of FLE is partly caused by different number of cameras seeing each fiducial.

6. Funding and declaration of interests

This work was supported by RGC GRF grants CUHK 415512 and CUHK 415613, CRF grant CUHK 6CRF13G, and CUHK VC discretional fund #4930765, awarded to Prof. Max Q.-H. Meng. The authors thank Singapore Academic Research Fund under grant R-397-000-227-112 and NMRC Bedside & Bench under grant R-397-000-245-511 and Singapore Millennium Foundation awarded to Prof. Hongliang Ren.