Abstract
We report the detection of linear and cyclic isomers of C3H and C3H2 towards various starless cores and review the corresponding chemical pathways involving neutral (C3Hx with x=1,2) and ionic (C3Hx+ with x = 1,2,3) isomers. We highlight the role of the branching ratio of electronic Dissociative Recombination (DR) reactions of C3H2+ and C3H3+ isomers showing that the statistical treatment of the relaxation of C3H* and C3H2* produced in these DR reactions may explain the relative c,l-C3H and c,l-C3H2 abundances. We have also introduced in the model the third isomer of C3H2 (HCCCH). The observed cyclic-to-linear C3H2 ratio vary from 110 ± 30 for molecular clouds with a total density around 1×104 molecules.cm-3 to 30 ± 10 for molecular clouds with a total density around 4×105 molecules.cm-3, a trend well reproduced with our updated model. The higher ratio for low molecular cloud densities is mainly determined by the importance of the H + l-C3H2 → H + c-C3H2 and H + t-C3H2 → H + c-C3H2 isomerization reactions.
Keywords: ISM: abundances, ISM: clouds, ISM: molecules, astrochemistry
1. Introduction
The C3H and C3H2 species are observed in two isomeric forms, cyclic and linear, in various interstellar environments, the cyclic isomers being the most stable isomer in both cases. The ring molecule cyclopropynylidyne (c-C3H) has been widely observed in the galaxy (Turner et al. 2000, Fossé et al. 2001, Pety et al. 2012a, Liszt et al. 2014) after its discovery by (Yamamoto et al. 1987). The linear counterpart, propynylidyne (l- C3H), was discovered in TMC-1 and IRC+10216 by Thaddeus et al. (1985) and is also widely present in the galaxy (Turner et al. 2000, Fossé et al. 2001, Pety et al. 2012a, McGuire et al. 2013), associated to the cyclic isomer but in general with a notably smaller abundance. The cyclopropenylidene (c-C3H2) has been also observed in many environements (Turner et al. 2000, Fossé et al. 2001, Pety et al. 2012a, McGuire et al. 2013, Liszt et al. 2014, Sakai et al. 2010) after its discovery by (Thaddeus et al. 1985). The linear isomer, propadienylidene (l-C3H2), a cumulene carbon chain (H2C=C=C:), was discovered in TMC-1 by (Cernicharo et al. 1991) and in other sources (Cernicharo et al. 1999, Turner et al. 2000, Fossé et al. 2001, Pety et al. 2012a, Liszt et al. 2012) despite the fact that it is always much less abundant than the cyclic isomer. The linear l-C3H2 isomer has been proposed as a potential carrier of the 4881 and 5450 Å DIBs (Maier et al. 2011), this attribution being finally discarded considering the column densities required to reproduce the DIBs, ranging from two to three orders of magnitude higher than the values measured in the diffuse medium at radio frequencies in absorption (Krełowski et al. 2011, Liszt et al. 2012).
The presence of these isomers raises various key questions about their chemistry. In particular, as cyclic and linear C3H and C3H2 are not well reproduced by usual models (Agúndez & Wakelam 2013, Sipilä et al. 2016), are rings and chains formed from the same progenitors? Also, is there a relation between the abundance ratio of the most stable isomer to the other isomers and their energy differences, relation which is believed to follow the “minimum energy principle” (Lattelais et al. 2009) despite some counter examples (Loomis et al. 2015, Loison et al. 2016)? Moreover, can we explain the fact that, as already noted by (Fossé et al. 2001), the abundance ratio of cyclic to linear isomer is not constant across the galaxy? In addition to these questions, we emphasize the specific behavior of C3H+ which is found only in 2 PDRs (Pety et al. 2012b, McGuire et al. 2014), and nowhere else despite thorough searches in other interstellar environments (McGuire et al. 2013, McGuire et al. 2015). To get a better picture of C3Hx chemistry, we performed an extensive and systematic review and update of the KIDA chemical network (Wakelam et al. 2015b) using the methodology presented in (Loison et al. 2014a) and in Appendix A of this paper, including specific theoretical calculations presented in Appendix B. We have in particular introduced the third isomer of C3H2, (t-C3H2: H-CCC-H), a quasi linear species (Nguyen et al. 2001, Aguilera-Iparraguirre et al. 2008), which may play a non-negligible role as it has a different chemistry than the other C3H2 isomers. The thermochemical properties of the C3Hx=0-3 neutral and ionic isomers are summarized in Table 1. It should be noted that the geometry of l-C3H2+ corresponds to that of t-C3H2, i.e., HCCCH+. We did not introduce the cyclic isomer of C3H+ nor the third isomeric form of C3H2+ (H2CCC+), which are notably less stable than the other isomers and, considering the chemistry, are not supposed to play an important role.
Table 1.
C3Hx=1-3 neutral and ionic isomers characteristics
| species | ΔHf298 kJ/mol | µ (Debye) |
|---|---|---|
| c-C3H cyclopropynylidyne | 715 ± 8 kJ/mol (Costes et al. 2009) | 2.30 (experimental) (Lovas et al. 1992) |
| l-C3H propynylidyne | 727 ± 8 kJ/mol (Costes et al. 2009) |
3.55 (theory) (Woon 1995) |
| l-C3H+ | 1591 kJ/mol (Costes et al. 2009, Wang et al. 2007) |
3.06 (theory) (Huang et al. 2013) |
| c-C3H+ | 1661 kJ/mol (Costes et al. 2009, Wang et al. 2007) |
1.49 (theory) (This work) |
| c-C3H2 cyclopropenylidene | 497 ± 4 kJ/mol (Vazquez et al. 2009) |
3.27 (experimental) (Lovas et al. 1992) |
| t-C3H2 (HCCCH) Propynylidene | 543 ± 8 kJ/mol (Aguilera-Iparraguirre et al. 2008) |
0.51 (Nguyen et al. 2001) |
| l-C3H2 (H2CCC) propadienylidene (vinylidencarbene) | 557 ± 4 kJ/mol (Vazquez et al. 2009) |
4.16 (theory) (Wu et al. 2010). |
| c-C3H2+ | 1382.8 ± 9.2 kJ/mol (C. Lau & Ng 2006) |
1.2 (theory) (this work) |
| l-C3H2+ (HCCCH+) | 1396 ± 16 kJ/mol (Prodnuk et al. 1990) |
0 (theory) (Wong & Radom 1993, Taatjes et al. 2005) |
| l-C3H2+,b (H2CCC+) | 1565 kJ/mol (C. Lau & Ng 2006) |
3.0 (theory) (this work) |
| C3H3 (CH2CCH) 2-propynyl (propargyl) | 352 ± 4 kJ/mol (Vazquez et al. 2009) |
0.14 (theory) (this work) |
| c-C3H3+ | 1076 ± 6 kJ/mol (CCSD(T)-F12/aug-cc-pVQZ calculations by comparison with l-C3H3+, this work) |
0 (theory) (This work) |
| l-C3H3+ | 1191 ± 4 kJ/mol (ΔHf298(C3H3) + IE(C3H3) = 839.5 ± 0.1 kJ/mol (Jacovella et al. 2013)) |
0.524 (theory) (Huang et al. 2011) |
We present our observations in section 2 and our chemical model including various updates in Section 3. Our conclusions are presented in Section 4. This study is the last part of a large review of C3Hx=0-8Oy=0-1 chemistry in cold interstellar media (Loison et al. 2016, Hickson et al. 2016b, Wakelam et al. 2015a).
2. Observations
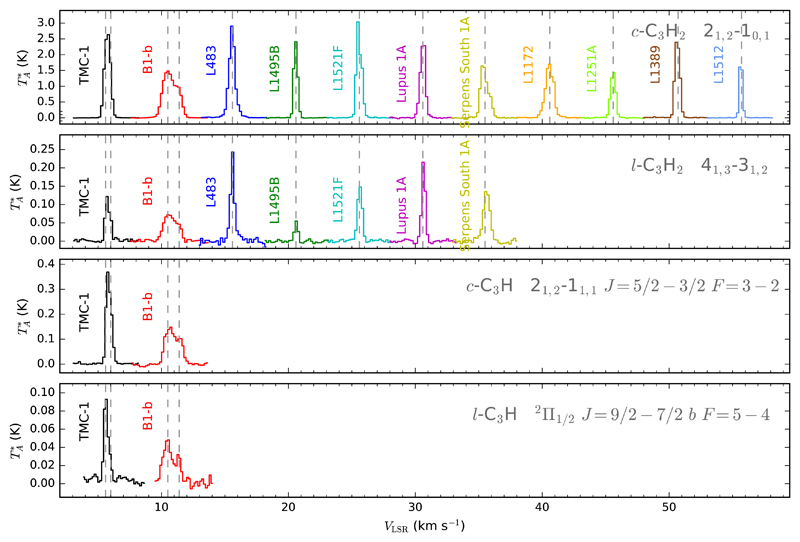
We have carried out observations of cyclic and linear C3H and C3H2 toward various cold dark clouds. The observations were done with the IRAM 30m telescope using the frequency-switching technique and the EMIR 3 mm receiver connected to a fast Fourier transform spectrometer providing a spectral resolution of 50 kHz. At the IRAM 30m telescope, spectra are calibrated by comparing the sky emissivity with that of hot and cold loads and using the ATM program (Cernicharo 1985, Pardo et al. 2001). The uncertainty in the calibration in the 3 mm band is ~10 %. Pointing was checked on nearby planets and quasars. The error in the pointing is 3'' at most. Data reduction, carried out using the software CLASS within the package GILDAS1, consisted in the subtraction of a baseline generated by smoothing the spectral regions free of lines. The observations of TMC-1 and B1-b are part of a 3 mm line survey (Marcelino et al. 2009), a good part of which was observed between January and May 2012 (see details in (Cernicharo et al. 2012)). In the cases of L483, Lupus-1A, L1495B, L1521F, and Serpens South 1a, the observations were carried out from September to November 2014 in selected frequency ranges across the 3 mm band (Agúndez et al. 2015). Examples of the observed spectra are shown in Fig. 1. The line parameters given in Tables 2, 3, and 4 were obtained by Gaussian fitting to the observed line profiles. In some sources, lines were simultaneously fitted to two Gaussian components because this resulted in a better fit. For example, in B1-b there are two velocity components at VLSR +6.5 and +7.4 km s-1. In TMC-1 the existence of the two velocity components is less obvious, but still the lines of some molecules can be decomposed into two velocity components at VLSR +5.7 and +6.0 km s-1.
Figure 1.
Sample of lines of c-C3H2, l-C3H2, c-C3H, and l-C3H observed in the cold dense clouds, where lines of each source have been shifted by fixed amounts along the velocity axis for a better visualization. Dashed vertical lines indicate the position of the VLSR of each source. Note that for TMC-1 and B1-b lines can be fitted to two velocity components. Transition frequencies and quantum numbers of the observed lines are listed in Tables 2, 3 and 4.
Table 2.
Observed line parameters of c-C3H2 and l-C3H2 in TMC-1 and B1-b.
| Molecule | Transition | Frequency (MHz) |
Eup (K) |
Aul (s−1) |
HPBW (″) |
VLSR (km s−1) |
Δv (km s−1) |
(K km s−1) |
|
|---|---|---|---|---|---|---|---|---|---|
| TMC-1 | |||||||||
| c-C3H2 | 31,2 – 30,3 (ortho) | 82966.196 | 13.7 | 9.91 × 10−6 | 29.3 | 0.86 | +5.83(2) | 0.46(1) | 0.279(2) |
| 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10−5 | 28.5 | 0.86 | +5.82(1) | 0.56(1) | 1.659(1) | |
| 43,2 – 42,3 (ortho) | 85656.415 | 26.7 | 1.52 × 10−5 | 28.4 | 0.86 | +5.81(1) | 0.49(5) | −0.013(1)a | |
| 32,2 – 31,3 (para) | 84727.687 | 16.1 | 1.04 × 10−5 | 28.7 | 0.86 | +5.78(2) | 0.50(2) | 0.078(2) | |
| l-C3H2 | 41,3 – 31,2 (ortho) | 83933.699 | 9.1 | 4.96 × 10−5 | 29.0 | 0.86 | +5.65(2) | 0.24(5) | 0.033(4) |
| +5.94(2) | 0.27(6) | 0.024(4) | |||||||
| 51,5 – 41,4 (ortho) | 102992.379 | 13.8 | 9.60 × 10−5 | 23.6 | 0.84 | +5.70(4) | 0.45(3) | 0.022(2) | |
| +6.01(10) | 0.25(10) | 0.002(1) | |||||||
| 51,4 – 41,3 (ortho) | 104915.583 | 14.1 | 1.02 × 10−4 | 23.2 | 0.84 | +5.65(3) | 0.27(5) | 0.010(2) | |
| +5.93(6) | 0.35(11) | 0.009(2) | |||||||
| 40,4 – 30,3 (para) | 83165.345 | 10.0 | 5.15 × 10–5 | 29.2 | 0.86 | +5.69(2) | 0.31(4) | 0.018(2) | |
| +5.94(4) | 0.46(8) | 0.015(2) | |||||||
| 50,5 – 40,4 (para) | 103952.926 | 15.0 | 1.03 × 10−4 | 23.4 | 0.84 | +5.70(5) | 0.36(4) | 0.009(1) | |
| B1-b | |||||||||
| c-C3H2 | 31,2 – 30,3 (ortho) | 82966.196 | 13.7 | 9.91 × 10−6 | 29.3 | 0.86 | +6.49(1) | 0.88(2) | 0.289(6) |
| +7.39(1) | 0.58(3) | 0.100(5) | |||||||
| 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10−5 | 28.5 | 0.86 | +6.55(1) | 0.92(1) | 1.492(9) | |
| +7.4 1(1) | 0.66(1) | 0.597(9) | |||||||
| 43,2 – 42,3 (ortho) | 85656.415 | 26.7 | 1.52 × 10−5 | 28.4 | 0.86 | +6.54(2) | 0.67(5) | 0.020(1) | |
| +7.45(7) | 0.30(14) | 0.002(1) | |||||||
| 32,2 – 31,3 (para) | 84727.687 | 16.1 | 1.04 × 10−5 | 28.7 | 0.86 | +6.50(2) | 0.86(3) | 0.087(3) | |
| +7.38(3) | 0.55(5) | 0.025(3) | |||||||
| l-C3H2 | 41,3 – 31,2 (ortho) | 83933.699 | 9.1 | 4.96 × 10−5 | 29.0 | 0.86 | +6.56(4) | 0.95(7) | 0.075(5) |
| 51,5 – 41,4 (ortho) | 102992.379 | 13.8 | 9.60 × 10−5 | 23.6 | 0.84 | +6.54(2) | 0.84(5) | 0.054(3) | |
| +7.39(2) | 0.41(5) | 0.017(2) | |||||||
| 51,4 – 41,3 (ortho) | 104915.583 | 14.1 | 1.02 × 10−4 | 23.2 | 0.84 | +6.53(2) | 0.80(4) | 0.046(2) | |
| +7.47(2) | 0.55(5) | 0.023(2) | |||||||
| 40,4 – 30,3 (para) | 83165.345 | 10.0 | 5.15 × 10−5 | 29.2 | 0.86 | +6.54(3) | 0.92(9) | 0.043(2) | |
| 50,5 – 40,4 (para) | 103952.926 | 15.0 | 1.03 × 10−4 | 23.4 | 0.84 | +6.54(3) | 0.89(6) | 0.034(2) | |
| +7.42(4) | 0.50(7) | 0.011(2) | |||||||
Numbers in parentheses are I σ uncertainties in units of the last digits. Antenna temperature can be converted to main beam brightness temperature (TMB) by dividing by (Beff/Feff).
Line in absorption against cosmic microwave background.
Table 3.
Observed line parameters of c-C3H2 and l-C3H2 in various cold dense clouds.
| Molecule | Transition | Frequency (MHz) |
Eup (K) |
Aul (s−1) |
HPBW (″) |
VLSR (km s−1) |
Δv (km s−1) |
(K km s−1) |
|
|---|---|---|---|---|---|---|---|---|---|
| L483 | |||||||||
| c-C3H2 | 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10−5 | 28.5 | 0.86 | +5.26(1) | 0.55(1) | 1.637(9) |
| 43,2 – 42,3 (ortho) | 85656.415 | 26.7 | l.52 × 10−5 | 28.4 | 0.86 | +5.28(2) | 0.58(6) | 0.069(5) | |
| 32,2 – 31,3 (para) | 84727.687 | 16.1 | l.04 × 10−5 | 28.7 | 0.86 | +5.29(1) | 0.39(1) | 0.165(2) | |
| l-C3H2 | 41,3 – 31,2 (ortho) | 83933.699 | 9.1 | 4.96 × 10−5 | 29.0 | 0.86 | +5.30(1) | 0.36(1) | 0.091(3) |
| 51,5 – 41,4 (ortho) | 102992.379 | 13.8 | 9.60 × 10−5 | 23.6 | 0.84 | +5.25(1) | 0.35(2) | 0.055(2) | |
| 40,4 – 30,3 (para) | 83 165.345 | 10.0 | 5.15 × 10−5 | 29.2 | 0.86 | +5.30(1) | 0.34(2) | 0.054(2) | |
| Lupus-1A | |||||||||
| c-C3H2 | 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10−5 | 28.5 | 0.86 | +5.00(1) | 0.47(1) | 1.259(6) |
| 32,2 – 31,3 (para) | 84727.687 | 16.1 | 1.04 × 10−5 | 28.7 | 0.86 | +5.06(1) | 0.36(1) | 0.112(2) | |
| l-C3H2 | 41,3 – 31,2 (ortho) | 83933.699 | 9.1 | 4.96 × 10−5 | 29.0 | 0.86 | +5.05(1) | 0.33(1) | 0.078(1) |
| 51,5 – 41,4 (ortho) | 102992.379 | 13.8 | 9.60 × 10−5 | 23.6 | 0.84 | +5.01(1) | 0.33(1) | 0.044(1) | |
| 51,4 – 41,3 (ortho) | 104915.583 | 14.1 | 8.74 × 10−5 | 23.2 | 0.84 | +5.06(2) | 0.27(4) | 0.039(5) | |
| 40,4 – 30,3 (para) | 83165.345 | 10.0 | 5.15 × 10−5 | 29.2 | 0.86 | +5.06(1) | 0.35(2) | 0.042(2) | |
| 50,5 – 40,4 (para) | 103952.926 | 15.0 | 1.03 × 10−4 | 23.4 | 0.84 | +5.07(4) | 0.41(9) | 0.039(7) | |
| L1521F | |||||||||
| c-C3H2 | 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10 −5 | 28.5 | 0.86 | +6.36(1) | 0.50(1) | 1.491(9) |
| 43,2 – 42,3 (ortho) | 85656.415 | 26.7 | 1.52 × 10−5 | 28.4 | 0.86 | +6.56(3) | 0.32(6) | 0.017(3) | |
| 32,2 – 31,3 (para) | 84727.687 | 16.1 | 1.04 × 10−5 | 28.7 | 0.86 | +6.43(1) | 0.39(1) | 0.101(2) | |
| l-C3H2 | 41,3 – 31,2 (ortho) | 83933.699 | 9. 1 | 4.96 × 10−5 | 29.0 | 0.86 | +6.44(1) | 0.43(1) | 0.071(1) |
| 51,5 – 41.4 (ortho) | 102992.379 | 13.8 | 9.60 × 10−5 | 23.6 | 0.84 | +6.41(1) | 0.40(2) | 0.039(1) | |
| 40,4 – 30,3 (para) | 83165.345 | 10.0 | 5.15 × 10−5 | 29.2 | 0.86 | +6.46(1) | 0.43(2) | 0.039(1) | |
| Serpens South la | |||||||||
| c-C3H2 | 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10 −5 | 28.5 | 0.86 | +7.33(1) | 0.73(1) | 1.246(12) |
| 32,2 – 31,3 (para) | 84727.687 | 16.1 | 1.04 × 10−5 | 28.7 | 0.86 | +7.56(1) | 0.64(1) | 0.146(3) | |
| l-C3H2 | 41,3 – 31,2 (ortho) | 83933.699 | 9. 1 | 4.96 × 10−5 | 29.0 | 0.86 | +7.53(1) | 0.61 (2) | 0.090(2) |
| 51,5 – 41,4 (ortho) | 102992.379 | 13.8 | 9.60 × 10−5 | 23.6 | 0.84 | +7.51(1) | 0.59(3) | 0.050(2) | |
| 40,4 – 30,3 (para) | 83165.345 | 10.0 | 5.15 × 10−5 | 29.2 | 0.86 | +7.57(2) | 0.71(4) | 0.054(2) | |
| L1495B | |||||||||
| c-C3H2 | 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10−5 | 28.5 | 0.86 | +7.57(1) | 0.37(1) | 0.975(3) |
| 32,2 – 31,3 (para) | 84727.687 | 16.1 | 1.04 × 10−5 | 28.7 | 0.86 | +7.63(1) | 0.29(1) | 0.033(1) | |
| l-C3H2 | 41,3 – 31,2 (ortho) | 83933.699 | 9.1 | 4.96 × 10−5 | 29.0 | 0.86 | +7.62(1) | 0.32(2) | 0.019(1) |
| 51,5 – 41,4 (ortho) | 102992.379 | 13.8 | 9.60 × 10-5 | 23.6 | 0.84 | +7.60(2) | 0.36(6) | 0.010(1) | |
| 40,4 – 30,3 (para) | 83165.345 | 10.0 | 5.15 × 10−5 | 29.2 | 0.86 | +7.68(1) | 0.18(9) | 0.007(1) | |
| L1172 | |||||||||
| c-C3H2 | 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10−5 | 28.5 | 0.86 | +2.68(1) | 0.75(1) | 1.358(6) |
| L1251A | |||||||||
| c-C3H2 | 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10−5 | 28.5 | 0.86 | -4.02(1) | 0.47(1) | 0.753(7) |
| L1389 | |||||||||
| c-C3H2 | 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10−5 | 28.5 | 0.86 | -4.76(1) | 0.47(1) | 1.280(12) |
| L1512 | |||||||||
| c-C3H2 | 21,2 – 10,1 (ortho) | 85338.900 | 4.1 | 2.32 × 10−5 | 28.5 | 0.86 | +7.05(1) | 0.28(1) | 0.601 (6) |
Numbers in parentheses are 1σ uncertainties in units of the iast digits. Antenna temperature () can be convert.ed to main beam brightness temperature (TMB) by dividing by (Beff/Feff).
Table 4.
Observed line parameters of c-C3H and l-C3H in TMC-1 and BI-b.
| Molecule | Transition | Frequency (MHz) |
Eup (K) |
Aul (s−1) |
HPBW (″) |
VLSR (km s−1) |
Δv (km s−1 |
(K km s−1) |
|
|---|---|---|---|---|---|---|---|---|---|
|
TMC-1 | |||||||||
| c-C3H | 21,2 − 11,1 J=5/2-3/2 F=3-2 | 91494.349 | 4.4 | 1.46 × 10−5 | 26.6 | 0.86 | +5.70(6) | 0.27(2) | 0.080(1) |
| +5.96(16) | 0.41 (3) | 0.110(1) | |||||||
| 21,2 − 11,1 J=5/2-3/2 F=2-1 | 91497.608 | 4.4 | 1.26 × 10−5 | 26.6 | 0.86 | +5.79(2) | 0.28(2) | 0.057(1) | |
| +6.05(4) | 0.48(5) | 0.063(1) | |||||||
| 21,2 − 11,1 J=5/2-3/2 F=2-2 | 91512.969 | 4.4 | 1.61 × 10−6 | 26.6 | 0.86 | +5.74(10) | 0.30(15) | 0.009(1) | |
| +5.95(20) | 0.46(13) | 0.010(1) | |||||||
| 21,2 − 11,1 J=3/2-1/2 F=1-1 | 91681.696 | 4.4 | 2.85 × 10−6 | 26.5 | 0.85 | +5.72(4) | 0.44(4) | 0.019(1) | |
| 21,2 − 11,1 J=3/2-1/2 F=1-0 | 91692.752 | 4.4 | 8.15 × 10−6 | 26.5 | 0.85 | +5.63(2) | 0.38(4) | 0.033(3) | |
| +5.92(7) | 0.34(10) | 0.019(3) | |||||||
| 21,2 − 11,1 J=3/2-1/2 F=2-1 | 91699.471 | 4.4 | 1.26 × 10−5 | 26.5 | 0.85 | +5.75(2) | 0.34(9) | 0.085(2) | |
| +6.05(2) | 0.31(20) | 0.032(2) | |||||||
| 21,2 − 11,1 J=3/2-3/2 F=1-1 | 91747.372 | 4.4 | 3.27 × 10−6 | 26.5 | 0.85 | +5.69(4) | 0.43(9) | 0.017(3) | |
| +6.06(15) | 0.68(19) | 0.016(3) | |||||||
| 21,2 − 11,1 J=3/2-3/2 F=2-2 | 91780.518 | 4.4 | 2.05 × 10−6 | 26.5 | 0.85 | +5.79(2) | 0.34(5) | 0.018(2) | |
| +6.16(6) | 0.32(10) | 0.005(1) | |||||||
| l-C3H | 2Π1/2 J=9/2-7/2 b F=5-4 | 97995.166 | 12.5 | 6.12 × 10−5 | 24.8 | 0.85 | +5.59(2) | 0.30(2) | 0.030(3) |
| +5.89(5) | 0.33(7) | 0.010(3) | |||||||
| 2Π1/2 J=9/2-7/2 b F=4-3 | 97995.913 | 12.5 | 5.95 × 10−5 | 24.8 | 0.85 | +5.59(2) | 0.34(2) | 0.028(3) | |
| +5.94(2) | 0.23(7) | 0.005(3) | |||||||
| 2Π1/2 J=9/2-7/2 a F=5-4 | 98011.611 | 12.5 | 6.13 × 10−5 | 24.8 | 0.85 | +5.62(3) | 0.36(2) | 0.036(2) | |
| +6.00(6) | 0.25(7) | 0.006(1) | |||||||
| 2Π1/2 J=9/2-7/2 a F=4-3 | 98012.524 | 12.5 | 5.96 × 10−5 | 24.8 | 0.85 | +5.54(4) | 0.36(6) | 0.028(2) | |
| +5.90(10) | 0.34(14) | 0.009(1) | |||||||
| B1-b | |||||||||
| c-C3H | 21,2 − 11,1 J=5/2-3/2 F=3-2 | 91494.349 | 4.4 | 1.46 × 10−5 | 26.6 | 0.86 | +6.46(2) | 0.88(4) | 0.143(10) |
| +7.31(2) | 0.60(5) | 0.060(6) | |||||||
| 21,2 − 11,1 J=5/2-3/2 F=2-1 | 91497.608 | 4.4 | 1.26 × 10−5 | 26.6 | 0.86 | +6.70(5) | 0.90(10) | 0.104(10) | |
| +7.58(5) | 0.55(8) | 0.033(4) | |||||||
| 21,2 − 11,1 J=5/2-3/2 F=2-2 | 91512.969 | 4.4 | 1.61 × 10−6 | 26.6 | 0.86 | +6.79(6) | 0.43(14) | 0.006(2) | |
| 21,2 − 11,1 J=3/2-1/2 F=1-1 | 91681.696 | 4.4 | 2.85 × 10−6 | 26.5 | 0.85 | +6.60(9) | 0.74(20) | 0.010(2) | |
| 21,2 − 11,1 J=3/2-1/2 F=1-0 | 91692.752 | 4.4 | 8.15 × 10−6 | 26.5 | 0.85 | +6.64(5) | 1.25(11) | 0.049(4) | |
| 21,2 − 11,1 J=3/2-1/2 F=2-1 | 91699.471 | 4.4 | 1.26 × 10−5 | 26.5 | 0.85 | +6.57(3) | 0.70(5) | 0.076(6) | |
| +7.38(4) | 0.72(8) | 0.048(6) | |||||||
| 21,2 − 11,1 J=3/2-3/2 F=1-1 | 91747.372 | 4.4 | 3.27 × 10−6 | 26.5 | 0.85 | +6.49(9) | 0.60(15) | 0.008(2) | |
| 21,2 − 11,1 J=3/2-3/2 F=2-2 | 91780.518 | 4.4 | 2.05 × 10−6 | 26.5 | 0.85 | +6.79(9) | 1.03(16) | 0.016(2) | |
| l-C3H | 2Π1/2 J=9/2-7/2 b F=5-4 | 97995.166 | 12.5 | 6.12 × 10−5 | 24.8 | 0.85 | +6.47(2) | 0.82(5) | 0.040(2) |
| +7.36(2) | 0.40(6) | 0.013(2) | |||||||
| 2Π1/2 J=9/2-7/2 b F=4-3 | 97995.913 | 12.5 | 5.95 × 10−5 | 24.8 | 0.85 | +6.49(3) | 0.84(7) | 0.030(2) | |
| +7.44(6) | 0.43(13) | 0.006(2) | |||||||
| 2Π1/2 J=9/2-7/2 a F=5-4 | 98011.611 | 12.5 | 6.13 × 10−5 | 24.8 | 0.85 | +6.51(2) | 0.73(5) | 0.036(2) | |
| +7.36(4) | 0.54(9) | 0.013(2) | |||||||
| 2Π1/2 J=9/2-7/2 a F=4-3 | 98012.524 | 12.5 | 5.96 × 10−5 | 24.8 | 0.85 | +6.40(3) | 0.69(7) | 0.027(2) | |
| +7.24(8) | 0.47(10) | 0.008(2) | |||||||
Numbers in parentheses are lσ uncertainties in units of the last digits. Antenna temperature can be converted to main beam brightness temperature (TMB) by dividing by (Beff/Feff).
2.1. Observed abundances of c/l-C3H2 and c/l-C3H
From the observed line intensities, we determined column densities of c/l-C3H2 and c/l-C3H in the different sources, averaged over the beam of the IRAM 30-m telescope, which, at the observed frequencies, ranges from 23” to 29”. These column densities are given in Table 5 as well as the physical conditions corresponding to the various sources.
Table 5.
Physical properties, and derived column densities and cyclic-to-linear column density ratios.
| Source |
Tk (K) |
n(H2) (cm−3) |
N(c-C3H)a (cm−2) |
N(l-C3H)a (cm−2) |
N(c-C3H2)b (cm−2) |
N(l-C3H2)a (cm−2) |
R1c | R2c |
|---|---|---|---|---|---|---|---|---|
| TMC-1 | 10 | 3.0 × 104 | 6.1 × 1012 | 1.1 × 1012 | 1.2 × 1014 | 1.8 × 1012 | 5.5 | 67 |
| B1-b | 12 | 4.0 × 105 | 6.2 × 1012 | 1.2 × 1012 | 1.8 × 1013 | 6 × 1011 | 5.2 | 30 |
| L483 | 10 | 3.0 × 105 | 4.0 × 1013 | 7 × 1011 | 57 | |||
| Lupus-1A | 14 | 4.0 × 105 | 1.4 × 1013 | 3.5 × 1011 | 40 | |||
| L1521F | 10 | 4.0 × 105 | 1.5 × 1013 | 4 × 1011 | 38 | |||
| Serpens South la | 11 | 4.0 × 105 | 1.4 × 1013 | 5 × 1011 | 28 | |||
| L1495B | 10 | 1.1 × 104 | 2.0 × 1014 | 1.8 × 1012 | 111 | |||
| L1172 | 10 | 7.5 × 104 | 1.4 × 1013 | |||||
| L1251A | 10 | 2.1 × 104 | 2.2 × 1013 | |||||
| L1389 | 10 | 5.2 × 104 | 2.2 × 1013 | |||||
| L1512 | 10 | 2.6 × 104 | 1.7 × 1013 |
Estimated error is a factor of 2.
Estimated error is 50 % for the first 7 sources and a factor of 2 for L1172, L1251A, L1389, and L1512.
R1 = N(c-C3H)/N(l-C3H) and R2 = N(c-C3H2)/N(l-C3H2). Estimated uncertainties in R1 and R2 are 30 %.
The error estimates and the assumed parameters are described in the text.
2.1.1. Statistical equilibrium: c-C3H2 and l-C3H2
In the cases of cyclic and linear C3H2 we carried out statistical equilibrium calculations using the LVG method and assuming a medium with uniform volume density of H2 and gas kinetic temperature. These two physical parameters were taken from the literature for each source, and, when possible (i.e., when multiple lines of c-C3H2 or l-C3H2 were available), additional constraints were provided by the line intensity ratios observed in this study. The adopted values of Tk and n(H2) are given in Table 5. The gas kinetic temperature in most sources is around 10 K, whereas densities span over almost two orders of magnitude in the range 104 − 106 cm−3. It is important to note that the column densities of cyclic and linear C3H2 derived are very sensitive to the adopted volume density (the higher the density the lower the column density needed to reproduce the observed line intensities), although the cyclic-to-linear ratios show little dependence with n(H2). The ortho and para species of both c-C3H2 and l-C3H2 were considered independently in the statistical equilibrium calculations and the statistical ortho-to-para ratio of 3 was assumed for both isomers, which is consistent with the intensity ratios between ortho and para lines observed. To derive the column densities, we carried out various LVG models in which the column density of C3H2 was varied (for those sources for which multiple lines were available the volume density was also varied) and selected the model that results in the best overall agreement between observed and calculated velocity-integrated intensities. When some of the lines were calculated to be optically thick, as occurs for the 21,2 −10,1 line of c-C3H2 in most sources, we prioritized to reproduce the intensities of those lines that are optically thin.
For c-C3H2, level energies were computed from the rotational constants derived by Bogey et al. (1987) and line strengths were computed from the dipole moment of 3.27 debye measured by Lovas et al. (1992), slightly lower than the value of 3.43 debye previously measured by Kanata et al. (1987). Rate coefficients for de-excitation of c-C3H2 through inelastic collisions with He have been calculated by Avery & Green (1989) including 16 and 17 levels for ortho and para c-C3H2, respectively, and covering the temperature range 10-30 K, and by Chandra & Kegel (2000) accounting for 47 and 48 levels for ortho and para c-C3H2, respectively, and covering the temperature range 30-120 K. Unfortunately, Chandra & Kegel (2000) did not extend their calculations down to 10 K. Therefore, here we adopted the values of Avery & Green (1989). We note however that by comparing the rate coefficients calculated in both studies at 30 K the values of Avery & Green (1989) are systematically higher (by up to a factor of 2) than those of Chandra & Kegel (2000), and thus at low densities it may lead to column densities of c-C3H2 significantly lower than those obtained using the coefficients of Chandra & Kegel (2000). In this study the collision rate coefficients of Avery & Green (1989) at 10 K were adopted, scaled up by a factor of 1.38 to account for H2 instead of He as collider. In the case of l-C3H2, level energies were computed from the CDMS archive2 (Müller et al. 2005), which is based on the experimental data of Vrtilek et al. (1990), and a dipole moment of 4.16 debye was adopted, based on the ab initio calculations of Wu et al. (2010). As rate coefficients for de-excitation of l-C3H2 through inelastic collisions with H2 and He we adopted those calculated for H2CO by Green (1991).
The density of H2 at the position of the cyanopolyyne peak in TMC-1 has been estimated as (3 − 8) × 104 cm−3 by Pratap et al. (1997), based on observations of three transitions of HC3N, and around 3 × 104 cm−3 by Lique et al. (2006), based on the observations of multiple transitions of SO. Here we adopt this latter value, which was also adopted by Fossé et al. (2001) in their study of c/l-C3H2 in TMC-1. The fact that the 43,2 − 42,3 transition at 85.6 GHz, with an upper level energy of 26.7 K, is observed in absorption against the cosmic microwave background (see Table 1) indicates that this transition has an excitation temperature below 2.7 K and that c-C3H2 is not thermalized in TMC-1, which is consistent with the adopted value of n(H2). From the intensities of the 4 lines of c-C3H2 observed in TMC-1 we derive a column density of 1.2 × 1014 cm−2. This value is twice higher than that derived by Fossé et al. (2001) based on the observation of the 11,0 − 10,1 transition at 18.3 GHz with the Effelsberg 100-m telescope, probably due to optical depth effects and to the different beam sizes of the Effelsberg 100-m and IRAM 30-m telescopes. Our analysis indicates that the 21,2 −10,1 line at 85.3 GHz is optically thick (τ ≈ 10), and thus the derived c-C3H2 column density relies heavily on the other, optically thinner, observed transitions. The column density of l-C3H2 derived in TMC-1 is 1.8×1012 cm−2, in agreement with values derived by Cernicharo et al. (1991) and Fossé et al. (2001), and the cyclic-to-linear C3H2 ratio is 67.
The source Barnard 1b is a dense core with a steep density gradient, with values ranging from a few 106 cm−3 at the center to a few 105 cm−3 at angular scales of the order of the IRAM 30-m beam, according to the modelling of the continuum emission at 350 μm and 1.2 mm by Daniel et al. (2014). Based on this latter study, here we adopt a mean gas kinetic temperature of 12 K and n(H2) = 4 × 105 cm−3, physical parameters that result in line intensity ratios in good agreement with the observed ones. The column densities we derive in B1-b are N(c-C3H2) = 1.8×1013 cm−2 and N(l-C3H2) = 6 × 1011 cm−2, which results in a cyclic-to-linear C3H2 ratio of 30.
The dense core L483 hosts a Class 0 source and shows evidences of infall motions and a density gradient (Tafalla et al. 2000). The gas kinetic temperature has been estimated as 10 K (Anglada et al. 1997). Densities of H2 around 3 × 104 cm−3 are derived by Anglada et al. (1997), based on NH3 observations, and by Jørgensen et al. (2002), based on the modelling of continuum observations at 450 μm and 850 μm, while Tafalla et al. (2000) derive a mean density of H2 of 3 × 105 cm−3 over a size ≈20” in radius, based on the analysis of CH3OH emission. Here we adopt this latter value because at a gas kinetic temperature of 10 K, the 43,2 − 42,3 transition of c-C3H2 can only be excited up to the level observed in L483 at densities well above 105 cm−3.
In the starless core Lupus-1A, the kinetic temperature has been estimated as 14 ± 2 K (Agúndez et al. 2015), the value adopted here, and as 12.6 ± 1.5 K at a position 2.8’ away from Lupus-1A (Sakai et al. 2009). The density of H2 has not been accurately estimated but Sakai et al. (2009) point to densities as high as 106 cm−3, while the observed intensity ratio between the 21,2 − 10,1 and 32,2 − 31,3 transitions of c-C3H2 points as well to densities above 105 cm−3. The value of n(H2) adopted here, 4 × 105 cm−3, results in line intensity ratios for cyclic and linear C3H2 in reasonable agreement with the observed ones. The column densities derived are N(c-C3H2) = 1.4 × 1013 cm−2 and N(l-C3H2) = 3.5 × 1011 cm−2, which results in a cyclic-to-linear C3H2 ratio of 40.
In L1521F the volume density of H2 has been estimated as 1.1 × 106 cm−3, based on observations of the continuum at 1.2 mm, and in the range (1.3 − 4.5) × 105 cm−3 from observations of N2H+ and N2D+ (Crapsi et al. 2005). These authors derive a rotational temperature of 4.8 K for N2H+, which is consistent with a gas kinetic temperature of 10 K. We find that a density of H2 of 4 × 105 cm−3 results in line intensity ratios for cyclic and linear C3H2 in agreement with the observed ones, in particular as concerns the intensity ratio between the 21,2 − 10,1 and 43,2 − 42,3 transitions of c-C3H2. The column densities we derive are N(c-C3H2) = 1.5 × 1013 cm−2 and N(l-C3H2) = 4 × 1011 cm−2, which results in a cyclic-to-linear C3H2 ratio of 38.
In the clump 1a of the Serpens South complex, Friesen et al. (2013) derive a gas kinetic temperature of 11 K through observations of NH3. The density of H2 has not been accurately determined but Friesen et al. (2013) suggest a volume density around 104 cm−3 based on timescale arguments. However, on the assumption that the ortho-to-para ratio is 3 for c-C3H2, the observed intensity ratio between the 21,2 − 10,1 and 32,2 − 31,3 transitions requires gas densities above 105 cm−3. Adopting n(H2) = 4 × 105 cm−3, the column densities we derive are N(c-C3H2) = 1.4 × 1013 cm−2 and N(l-C3H2) = 5 × 1011 cm−2, which results in a cyclic-to-linear C3H2 ratio of 28.
The physical conditions in the sources L1495B, L1172, L1251A, L1389, and L1512 have been taken from the study by Cordiner et al. (2013). These authors adopt a common gas kinetic temperature of 10 K and derive the volume density from the observation of a couple of lines of HC3N, which are in the range (1 − 10) × 104 cm−3. In 4 of these sources, observations are restricted to just one line, the 21,2 − 10,1 transition of c-C3H2, and thus it is not possible to put additional constraints on the volume density. Moreover, according to our statistical equilibrium calculations, this line is optically thick (τ = 2 − 6) in these sources, which introduces a higher degree of uncertainty in the column densities of c-C3H2 derived.
The column densities derived for c-C3H2 and l-C3H2 have uncertainties coming from the observations (line fitting plus telescope calibration), although the main source of error arises in the conversion of line intensities into column densities, with uncertainties in the kinetic temperature, gas density, collisional rate coefficients, and the probable lack of uniformity of the physical conditions of the cloud within the telescope beam. We estimate that the column densities derived for c-C3H2 have an uncertainty of 50 % in those sources in which the availability of multiple lines permit to set constraints on the gas density (TMC-1, B1-b, L483, Lupus-1A, L1521F, Serpens South 1a, L1495B) and an error of a factor of 2 in those sources in which only the 21,2 − 10,1 line was observed (L1172, L1251A, L1389, L1512). In the case of l-C3H2, in those sources in which this isomer was observed, multiple lines were available. However, the adopted collision rate coefficients were not specifically computed for this molecule but for formaldehyde, and thus we estimate uncertainties of a factor of 2 for the column densities of l-C3H2. Systematic errors in the kinetic temperature and gas density would tend to cancel when computing cyclic-to-linear column density ratios, and thus we estimate errors of 30 % for the cyclic-to-linear C3H2 ratios derived.
2.2.1. Local thermodynamic equilibrium: c-C3H and l-C3H
For cyclic and linear C3H local thermodynamic equilibrium was assumed (e.g. Turner (1991)) due to the lack of adequate collision rate coefficients for these two isomers. The spectroscopy of c-C3H was taken from JPL database3 (Pickett et al. 1998), which is based on the experimental study by Yamamoto et al. (1994), and the adopted dipole moment is 2.30 debye, the value measured by Lovas et al. (1992). For l-C3H, level energies were taken from the CDMS database (Müller et al. 2005), which is based on laboratory work by Yamamoto et al. (1990) plus some further studies, and we adopted a dipole moment of 3.55 debye based on ab initio calculations by Woon (1995). In this study, observations of c-C3H and l-C3H were restricted to various hyperfine components of a single rotational transition in TMC-1 and B1-b. Column densities were derived by assuming a rotational temperature of 5 K for the two isomers in both TMC-1 and B1-b, which is consistent with values from the literature (Mangum & Wootten 1990, Fossé et al. 2001). The column densities derived imply that the cyclic isomer of C3H is ≈5 times more abundant than the linear one in both TMC-1 and B1-b. We estimate uncertainties of a factor of 2 for the column densities of c-C3H and l-C3H in TMC-1 and B1-b, while the cyclic-to-linear C3H ratios are estimated to have errors of 30 %.
3. The chemical model
3.1. Model description
To calculate the abundances we use the chemical model Nautilus in its 3-phase version from (Ruaud et al. 2016). The Nautilus code computes the gas-phase and dust ice composition as a function of time taking into account reactions in the gas-phase, sticking on grains and desorption from grain surfaces, and reactions at the surface. The ice is decomposed into a surface (the two most external monolayers of molecules) and a bulk. Both the surface and the bulk are chemically active based on the Langmuir-Hinshelwood mechanism with the formalism of Hasegawa et al. (1992). In the bulk though the diffusion of species is much less efficient as compared to the surface. All the details and surface parameters for diffusion are the same as in Ruaud et al. (2016). For the desorption from the surface (only), we consider thermal desorption and desorption induced by cosmic-rays (Hasegawa & Herbst 1993) as well as by exothermic chemical reactions (exothermicity of surface chemical reactions allows for the species to be desorbed after their formation) (Garrod et al. 2007). The Garrod et al. (2007) chemical desorption mechanism leads to approximately that 1% of the newly formed species desorb and 99% remain on the grain surfaces (this correspond to a factor of 0.01 in (Garrod et al. 2007)). The binding energies of the species to the surface have been updated from Wakelam et al. (submitted to Molecular Astrophysics) and the atomic oxygen is allowed to diffuse by tunneling (see Wakelam et al. submitted for discussion on this point).
The gas-phase network is based on kida.uva.20144 (Wakelam et al. 2015b)), with the modifications described in section 3. The surface network and parameters are the same as in (Ruaud et al. 2015) with some updates from Wakelam et al. (submitted). Following (Hincelin et al. 2015), the encounter desorption mechanism is included in the code. This mechanism accounts for the fact that the H2 binding energy on itself is much smaller than on water ices and prevents the formation of several H2 monolayers on grain surfaces.
The chemical composition of the gas-phase and the grain surfaces is computed as a function of time. The gas and dust temperatures are equal to 10 K, the total H2 density is equal to 3×104 cm-3 (various runs have been performed with total H density been varied between 1×104 cm-3 and 2×105 cm-3). The cosmic-ray ionization rate is equal to 1.3×10-17 s-1 and the total visual extinction is set equal to 10. All elements are assumed to be initially in atomic form (elements with an ionization potential below the maximum energy of ambient UV photons (13.6 eV, the ionization energy of H atoms) are initially in a singly ionized state, i.e., C, S, Si, Fe, Na, Mg, Cl, and P), except for hydrogen, which is entirely molecular. The initial abundances are similar to those of Table 1 of Hincelin et al. (2011), the C/O elemental ratio being equal to 0.7 in this study. The grains are considered to be spherical with a 0.1µm radius, a 3 g.cm-3 density and about 106 surface sites, all chemically active. The dust to gas mass ratio is set to 0.01.
3.2. Update of the chemistry
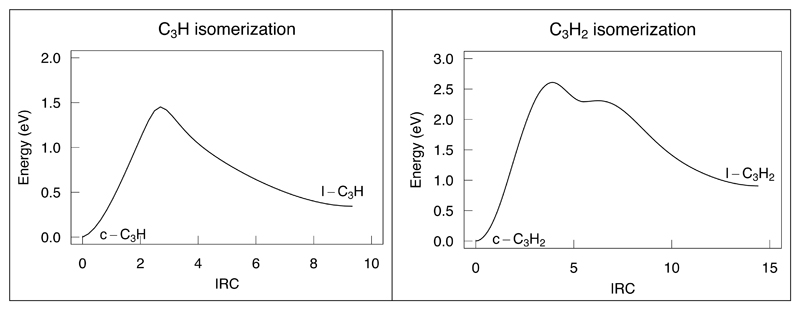
To determine the unknown rate constant which will be used in the network, we use a methodology developed in previous articles (Loison et al. 2014a, Loison et al. 2014b, Loison et al. 2015) and summarized in appendix A. This methodology includes extensive literature review, various DFT and ab-initio calculations for critical gas phase reactions, namely H + l-C3H2, H + t-C3H2, O + c-C3H2, O + l-C3H2, N + C3, N + c-C3H2, N + l-C3H2, H + C3O, O + C3O, O + c-C3H3+, OH + C3, OH + c-C3H2, H2 + l-C3H and H2 + c-C3H, to determine the presence, or not, of barrier. When there is no barrier in the entrance valley and exothermic bimolecular exit channels, we choose to use capture rate constant or sometimes a fraction of the capture rate constant by comparison with similar reactions (capture rate is the upper limit of the rate constants for barrierless reactions). Dissociative Recombination (DR) of c,l-C3H2+ and c,l-C3H3+ is an important source of c,l-C3H and is the main source c,l,t-C3H2 in our network. The first step of c,l-C3H2+ and c,l-C3H3+ DR is the formation of highly excited C3H2** and C3H3**, which leads to bond fragmentation. Angelova et al. (2004) have shown that the DR of c-C3H2+ leads to 87.5 % of C3Hx and 12.5 % of C2Hy + CHz, and the DR of c-C3H3+ leads to 90.7% of C3Hx and 9.3% of C2Hy + CHz. Moreover, in DR processes, the H ejection is in general favored than H2 ejection (Plessis et al. 2012, Plessis et al. 2010, Janev & Reiter 2004). Considering the exothermicty for the ejection of two hydrogen atoms (endothermic for c-C3H3+ DR and only slightly exothermic for l-C3H2+, c-C3H2+ and l-C3H3+ DR, see annex B) this process will have low branching ratio. Then, dissociation of C3H2** and C3H3** will mainly produce C3H + H and C3H2 + H, both C3H and C3H2 species being also excited considering the exothermicity of the DR and the fact that hydrogen atom will carry only a limited part of the available energy through kinetic energy. Part of the excited C3H and C3H2 will lead to dissociation when they are populated above the dissociation limit, but most of them will relax through radiative emission of an infrared photon. As noted by Herbst et al (2000), the typical time-scales for isomeric conversion is much shorter than for relaxation by one infrared photon. Thus, as radiative relaxation occurs slowly, isomeric conversion leads to equilibrated isomeric (c-C3H ⇆ l-C3H, c-C3H2 ⇆ l-C3H2) abundances at each internal energy. The final balance is determined at or near the effective barrier to isomerization, which corresponds to the energy of the transition state. The ratio between the isomeric forms are then approximated by the ratio of the rovibrational densities of states of the isomers at the barrier to isomerization calculated using MESMER program (Glowacki et al. 2012). Figure 2 shows the isomerization pathway calculated at DFT level. The calculated geometries of the stationary point can be found in appendix A. The t-C3H2 has a triplet ground stateand its production in excited singlet ground state is neglected here. The production of t-C3H2 from DR of c,l-C3H3+ is supposed to come from the c,l-C3H3+ + e- → c,l-C3H3 → t-C3H2 + H which is supposed to be a minor channel versus c,l-C3H3+ + e- → c,l-C3H3 → c,l-C3H2 + H (t-C3H2 has a ground triplet state contrary to c,l-C3H2 which have a ground singlet state).
Figure 2.
Intrinsic Reaction Coordinate pathway for the isomerization of c,l-C3H and c,l-C3H2 in their ground state calculated at M06-2X/aug-cc-pVTZ level.
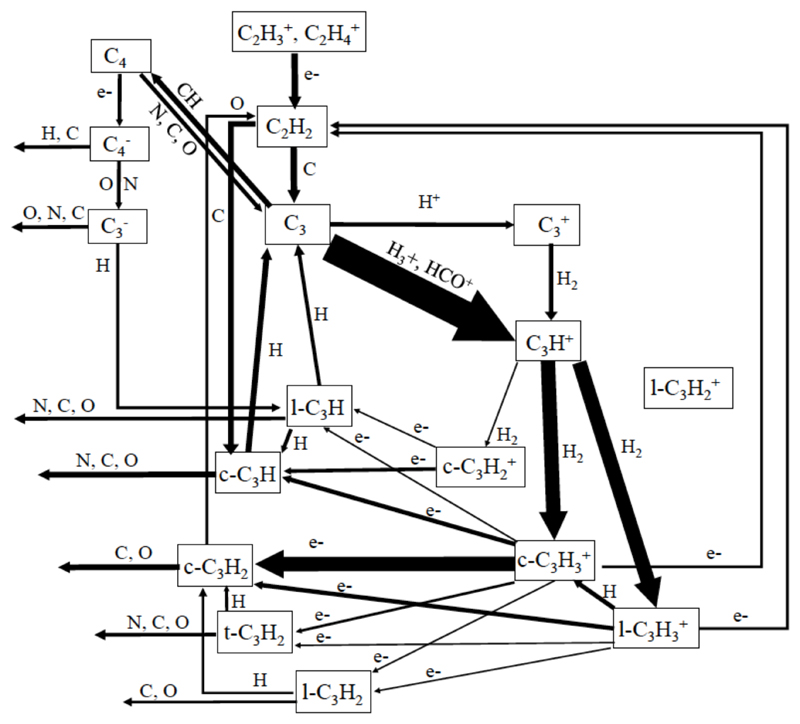
Then, contrary to usual astrochemical models where it is assumed that the cyclic ions leads to cyclic neutral, and linear ions leads only to linear neutral, we consider that c,l-C3H2+ DR leads mainly to cyclic c-C3H and c,l-C3H3+ DR leads mainly to cyclic c-C3H2, with, in both cases, cyclic to linear branching ratio given by the rovibrational densities of states of the isomers at the barrier to isomerization. The reactions involving C3Hx chemistry, including c,l-C3H2+ and c,l-C3H3+ DR, are represented displayed Figure 3. It should be noted that if c,l,t-C3H2 are produced almost exclusively from c,l-C3H3+ DR, the c,l-C3H are produced not only from c,l-C3H2+ and c,l-C3H3+ DR, but also through the C + C2H2 reaction as well as H + C3– reaction.
Figure 3.
Schematic diagram highlighting the important pathways for C3Hx chemistry in dense molecular cloud for a typical age (between 1×105 and 6×105 years). The thickness of each arrow is proportional to the fluxes (the very minor fluxes are not represented).
4. Results and comparison with observations
With our network and the physical conditions relevant to the various molecular clouds, the main formation pathways for c,l,t-C3H2 is through DR of c,l-C3H3+, these ions being formed mainly through C3 + H3+, HCO+, HCNH+ → C3H+ reactions followed by C3H+ + H2 reaction, the C3H+ being also produced through the C+ + C2H2 reaction, and the main consumption is with atoms: O, C for the four isomers, H for c,l-C3H and l,t-C3H2 and N for c,l-C3H and t-C3H2, most of these reactions are introduced for the first time in astrochemical network thanks to new ab-initio calculations. For a typical dense cloud age (time between 105 years and 106 years), the c-C3H2+ and c,l-C3H3+ DR is an important source of c,l-C3H, but the main c-C3H formation pathway is the C + C2H2 reaction. Considering the importance of c-C3H2+ and c,l-C3H3+ DR, the branching ratio of the C3H+ + H2 reaction, particularly between c,l-C3H3+ and c-C3H2+ + H, may have some importance. The rate constant measurements at room temperature for the C3H+ + H2 reaction clearly show a rate constant function of the pressure leading only to C3H3+, the nature of the isomer being not clearly identified (Raksit & Bohme 1983, Smith & Adams 1987). A more recent experimental study (Savic & Gerlich 2005) leads to a high rate constant for the radiative association at low temperature with however a non-negligible branching ratio toward c-C3H2+. A global theoretical analysis, including branching ratio calculation using RRKM theory, has been performed by (Maluendes et al. 1993b, Maluendes et al. 1993a) leading to the formation of both c,l-C3H3+ isomers in roughly equal abundances. We adopt their rate constant expressions for these channels and we also consider some c-C3H2+ production with a high uncertainty factor. To estimate the importance of the uncertainties in these branching ratios we performed various runs considering only c-C3H3+ or l-C3H3+ production showing that the nature of the C3H3+ isomer is not negligible (up to 20% for the cyclic-to-linear C3H2 ratio) but not critical, the key point being the relaxation of the C3H3** and C3H2* produced. It should be noted also that the low branching ratio for c-C3H2+ + H channel considered in this study leads to a negligible importance for this channel.
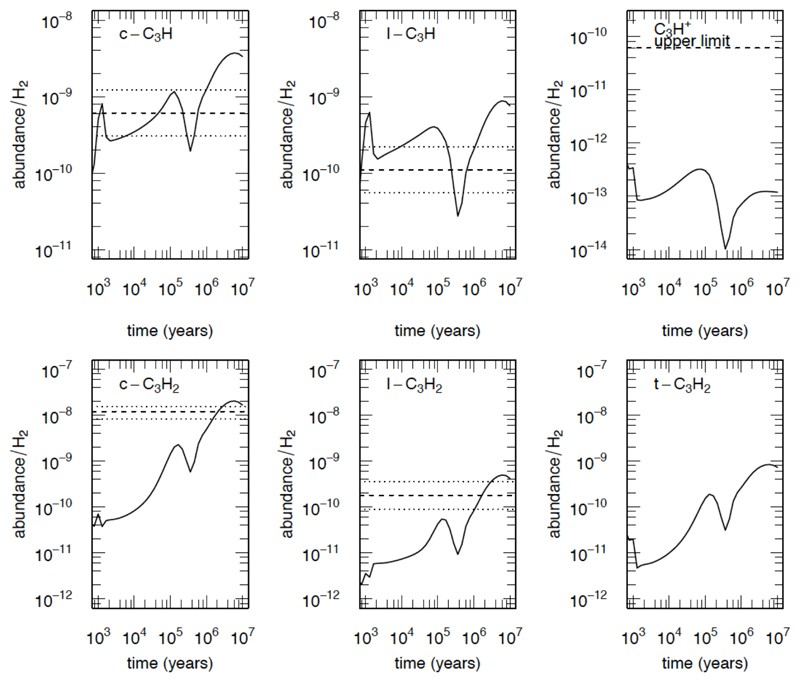
The results of the simulation for the various species studied here and for typical molecular cloud conditions (n(H2) = 3×104 cm-3, T = 10K) are shown Figure 4 as well as observations for TMC-1.
Figure 4.
Abundances of C3Hx gas phase species studied in this work as a function of time predicted by our model (n(H2) = 3×104 cm-3, T = 10K). The dashed horizontal lines represent the abundances observed for TMC-1 (this work, see Table 5). The dotted lines correspond to the uncertainties (see text).
c-C3H and l-C3H:
The C3H isomers have been detected in this study only in two molecular clouds, TMC-1 and B1-b. The agreement between observations in TMC-1 and the model is good for a cloud time age between 105 and 106 years (see Figure 4), the age being not critical in that case. For TMC-1 and B1-b, the c-C3H/l-C3H ratio is close to 5. It is worth noting that as shown on Figure 5, the c-C3H/l-C3H ratio given by our model is almost independent of the total density of the molecular cloud in the range of H2 between 1×104 and 2×105 molecule.cm-3 in good agreement with observations (see table 5) (measured only for two molecular clouds however). In our model, c-C3H and l-C3H are produced not only from c,l-C3H2+ and c,l-C3H3+ DR, but also through the C + C2H2 reaction as well as H + C3− reaction. The larger amount of cyclic isomer is due to the fact that both C + C2H2 reaction and DR of c,l-C3H3+ and c,l-C3H2 favor c-C3H. In the Horsehead PDR, the cyclic isomer is also favored with a slightly smaller ratio equal to 1.92 (Pety et al. 2012b). In IRC+10216 however, the linear isomer is more abundant with a c-C3H/l-C3H ratio equal to 0.38. In his simulation, Agúndez (2009) reproduces the fact that l-C3H is more abundant than c-C3H using the theoretical results from (Buonomo & Clary 2001) for the C + C2H2 reaction favoring l-C3H production contrary to the more recent experimental results from (Costes et al. 2009). However, the result of (Costes et al. 2009) involves complex fitting leading to large uncertainty. Considering our chemical network and the photodissociation cross sections from van Hemert & van Dishoeck (2008), there is no alternative to the C + C2H2 reaction to form l-C3H in circumstellar envelopes. Note that this reaction is the most important formation channel to l-C3H in IRC+10216, but it is of little importance in molecular clouds. It can be noticed that c-C3H is supposed to be mainly produced through c-C3H2 photodissociation in IRC+10216 (there is no experimental or theoretical data on c-C3H2 photodissociation branching ratio). There is then a crucial need to study the products of the photodissociations as well as for the C + C2H2 reaction despite the considerable amount of work already performed on it (Bergeat & Loison 2001, Buonomo & Clary 2001, Clary et al. 2002, Leonori et al. 2008, Costes et al. 2009, Hickson et al. 2016a).
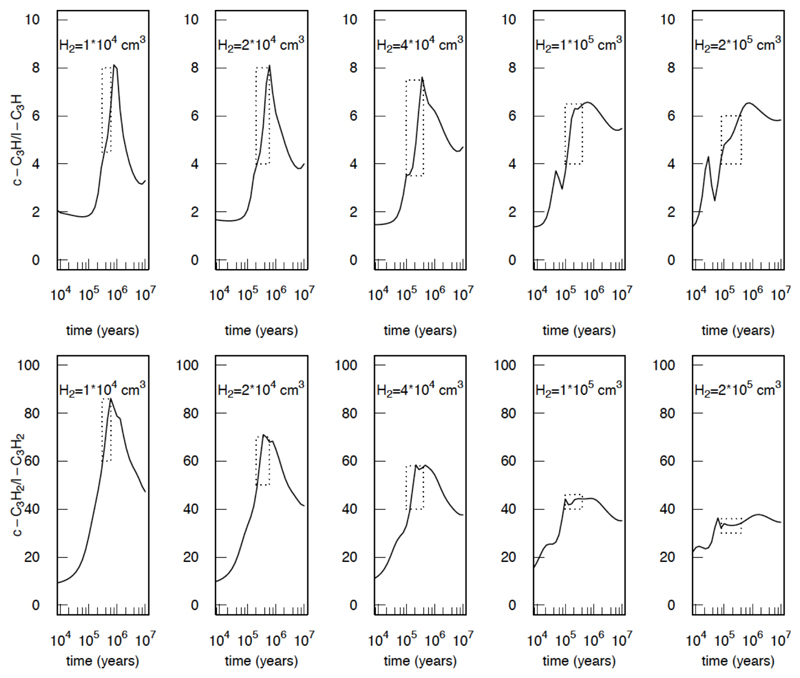
Figure 5.
c-C3H/l-C3H and c-C3H2/l-C3H2 ratios given by our model in function of the total density of the molecular cloud. Dotted rectangles correspond to the possible values at chemical cloud age given by the so-called distance of disagreement (Wakelam et al. 2006) at the given total densities.
c-C3H2 and l-C3H2:
The C3H2 isomers have been detected in this study in most of the molecular clouds. The agreement between observations in TMC-1 and the model is notably less good for c,l-C3H2 than for c,l-C3H for an early cloud age (few 105 years). At late time (after 106 years) the grain chemistry leads to relatively large s-CH4 abundance (few %, compatible with observations on Ice in YSO (Boogert et al. 2015)). As CH4 is not strongly bond to the ice (Raut et al. 2007), the release of CH4 into the gas phase trigger an intensive hydrocarbon chemistry. Moreover, as for these clouds ages, oxygen and nitrogen atoms are depleted on grain leading mainly to H2O, CO2, NH3 and HCN, all strongly bond to the ice with low desorption rate. Then, the hydrocarbons produced in the gas phase do not react with O and N atom but with C, others hydrocarbons neutral and ions leading to rich hydrocarbon chemistry and large C3Hx abundances. Among the various reactions, the C + C2H2 and C+ + C2H2 reactions are of a particular importance. The most efficient c-C3H2 destruction pathway in dense molecular clouds is the O + c-C3H2 reaction which shows no barrier at various theoretical levels (DFT, MP2, CCSD(T), MRCI+Q detailed in Appendix A). Products and branching ratio for this reaction are not fully studied here but HC3O should be a non-negligible product of the O + c-C3H2 reaction.
The cyclic-to-linear C3H2 ratio observed here in 7 molecular clouds vary between 111 and 28 with decreasing values when the total density of the cloud increase. As the uncertainties for the observed cyclic-to-linear C3H2 ratios is estimated around 30%, these uncertainties cannot explain the difference between the various molecular clouds. In Figure 5, we have plotted the c-C3H2/l-C3H2 ratio evolution with the total density given by our model. The trend of the c-C3H2/l-C3H2 ratio is in good agreement with observations (see Table 5), for a chemical cloud age given by the so-called distance of disagreement (Wakelam et al. 2006) (minimum average difference (in magnitude) between modeled and observed abundances) represented with dotted rectangle on the Figure 5. As C3H2 isomers are mostly coming from DR of c,l-C3H3+, DR independent of the total density of the molecular clouds, the main reaction impacting the cyclic to linear C3H2 ratio is supposed to be the l-C3H2 + H → c-C3H2 + H reaction. We have then performed a run suppressing the l-C3H2 + H → c-C3H2 + H reaction (presented in Appendix A). This suppression strongly reduce the cyclic-to-linear C3H2 ratio which become close to the ratio given by the cyclic-to-linear C3H2 ratio of the c,l-C3H3+ DR and also close to the cyclic-to-linear C3H2 ratio of the most dense molecular clouds. This clearly shows that the high value of the cyclic-to-linear C3H2 ratio of low density molecular clouds such as TMC-1 and L1495B (see Table 5) is due to the l-C3H2 + H → c-C3H2 + H reaction which convert efficiently the linear l-C3H2 into the cyclic c-C3H2. This reaction becomes less efficient when the total density increase because the H atoms density is almost constant with the total density of the cloud contrary to the fluxes of the C3Hx and C3Hx+ chemistry (for example the C3 + H3+ flux increase with the total density for typical molecular cloud age).
In the Horsehead Nebula PDR, the cyclic isomer is also favored but with a smaller ratio equal to 3.4 (Pety et al. 2012b). In IRC+10216, the cyclic-to-linear C3H2 ratio is ≈19 (Agúndez 2009), i.e., close to the values found in dense molecular clouds. It seems clear that, contrary to C3H, the chemistry is comparable in all these objects, the formation of C3H2 isomers being mainly due to DR of C3H3+, the photodissociation of C3H3 and CH3CCH playing a minor role. In PDR regions, the lower cyclic-to-linear C3H2 ratio may be due to the fact that c-C3H2 is supposed to be notably more photodissociated than l-C3H2 (van Hemert & van Dishoeck 2008). In diffuse clouds, where atomic H can be significant, the H + l-C3H2 → H + c-C3H2 reaction (introduced in this study) may strongly enhance the cyclic-to-linear C3H2 ratio and compensate the photodissociation effects.
t-C3H2:
We have introduced the third isomer of C3H2: t-C3H2 (HCCCH). This isomer, almost symmetric, has a stability between the cyclic and the linear isomer. It has a triplet ground state and it is reactive with H, C, O and also with N atom (cyclic and the linear isomer show barrier for reaction with N atoms). It should be noted that there is no measurement of the dipole moment of t-C3H2 and that the structure is not well defined, the C2, Cs and C2v structures being very close in energy (Aguilera-Iparraguirre et al. 2008). The dipole moment calculated by Nguyen et al. (2001) and equal to 0.51 D corresponds to the C2 structure compatible with EPR spectroscopy (Seburg et al. 2009). Its introduction doesn’t change notably the C3H and C3H2 chemistry but the reaction with N atom is a new pathway toward HC3N production, minor but non-negligible.
C3H+:
C3H+ has been detected only in three objects: the Orion Bar PDR, the Horsehead PDR, and Sgr B2(N) (Pety et al. 2012b, McGuire et al. 2013, McGuire et al. 2015). The lack of detection of l-C3H+ in cold dense molecular clouds (upper limit of 6×10-11×[H2] in TMC-1 from (McGuire et al. 2013)) is in agreement with our calculations where l-C3H+ abundance is around few 10-13 to 10-12 relative to H2 for typical dense molecular cloud ages (few 105 years). The formation of l-C3H+ is relatively well known through the reaction of C+ with C2H2 and the reaction of C3 with H3+, HCO+ and HCNH+. However, its main destruction rate via reaction with molecular hydrogen is not so well known despite the fact that the rate constant has been measured several times at various temperatures and pressures (Savic & Gerlich 2005, Raksit & Bohme 1983, Smith & Adams 1987). We use the global analysis performed by (Maluendes et al. 1993b, Maluendes et al. 1993a) leading to high rate constant at low temperature, which strongly limit the l-C3H+ abundance but has no, or very small, effect on c,l-C3H3+ abundance and then almost no effect on c,l-C3H and c,l-C3H2, as long as the l-C3H+ consumption is dominated by reaction with H2 instead of DR. The amount of l-C3H+ in the gas phase can be notably higher than the one given in our model if l-C3H+ reacts little bit more slowly with H2 at low temperature which will have no, or small, effect on c,l-C3H and c,l-C3H2 abundances.
l-C3H3+, c-C3H2+:
Both l-C3H3+ and c-C3H2+ reach a non-negligible abundance in our calculation for typical dense molecular clouds (around few 10-11 and up to 10-10 versus H2) and both have non-zero dipole moments (see Table 1). As already pointed out by Huang & Lee (2011) for l-C3H3+, it may be detectable. However, it should be noted that the main formation pathway is the C3H+ + H2 reaction for which the branching ratios toward l-C3H3+ and c-C3H2+ are not well known.
The C3 + O reaction
As already highlighted in (Hickson et al. 2016b), C3 is abundant in the gas phase as a result of various efficient neutral pathways producing C3 and very few destruction mechanisms. The low reactivity of C3 allows it to reach high abundance levels, which is at the origin of the rich C3H4, C3H6 and C3H8 production on grains through H addition reactions. To evaluate the role of the O + C3 reaction, which has been studied only theoretically by (Woon & Herbst 1996) finding a small barrier in the entrance valley, we performed a run considering no barrier for this reaction and a rate constant equal to 2.0×10-10 cm3 s-1 molecule-1 (close to the capture rate constant) which considerably reduce the C3 abundance. The introduction of O + C3 reaction decreases all C3Hx abundances the agreement being notably less good, for typical dense cloud age, than considering a barrier for the O + C3 reaction particularly for 1-C3H2 and c-C3H2. At late time (after 106 years) the release of CH4, produced on grains, into the gas phase trigger an intensive hydrocarbon chemistry allowing to reproduce most of the observations. Considering the large uncertainty of grain reactions (most of the reactions on grain surface are not well characterized) and the large variability of the results with the description of the physic of the grains (for example induced by the new three phases model introduced by Ruaud et al. (2016)), the good agreement between observations and calculations at late age, considering no barrier for the O + C3 reaction, may be fortuitous. It clearly shows the need to perform experimental measurement of the O + C3 rate constant which will be a way to constraint the CH4 formation on grains and its release in gas phase.
5. Conclusion
We have detected both cyclic and isomers C3H and C3H2 towards several molecular clouds using the IRAM 30m telescope. We have introduced in our gas-grain chemical model NAUTILUS new branching ratio of DR deduced from statistical theory with a relative amount of c-C3H/l-C3H and c-C3H2/l-C3H2 being proportional to the density of vibrational states of each isomer near the effective barrier to isomerization, and not, as assumed in usual astrochemical models, that the cyclic ions lead only to cyclic neutral, and linear ions lead only to linear neutral. We have also introduced the third isomer of C3H2, t-C3H2 which play a minor but non-negligible role due to specific reactivity. Our model allows to reproduce the observations for c-C3H, l-C3H and c-C3H2/l-C3H2 ratio in dense molecular clouds despite a notable underestimation for c-C3H2 and l-C3H2. In particularly the cyclic-to-linear C3H2 ratio given by our model is in good agreement with observations of the 7 molecular clouds studied in this paper, with a ratio value decreasing when the total density of the cloud increase. This decrease is due to the l-C3H2 + H → c-C3H2 + H reaction which is important for low density molecular cloud.
We also highlight the role of the O + C3 reaction which is likely to possess a substantial barrier, in good agreement with the calculations of Woon & Herbst (1996) leading to a high C3 abundance in dense molecular clouds.
Another critical point is the branching ratio of the C+ C2H2 reaction, the amount of 1-C3H produced being critical to reproduce the linear to cyclic ratio in IRC+10216.
Acknowledgments
This work was supported by the program “Physique et Chimie du Milieu Interstellaire” (PCMI) funded by CNRS and CNES. VW researches are funded by the ERC Starting Grant (3DICE, grant agreement 336474).
M.A., N.M. and J.C. thanks the ERC for support under grant ERC-2013-Syg-610256 NANOCOSMOS. They also thank Spanish MINECO for funding support under grants AYA2012-32032, and from the CONSOLIDER Ingenio program “ASTROMOL” CSD 2009-00038. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
This work received financial support from the French Agence Nationale de la Recherche (ANR) under grant ANR-13-BS05-0008 (IMOLABS : Molecules interstellaires : spectroscopie et synthèse en laboratoire)
We also thank the anonymous reviewer for his useful comments to improve the manuscript, particularly the suggestion to study more in detail the relation between c-C3H2/l-C3H2 ratio and the total H2 density of the molecular cloud.
Footnotes
References
- Aguilera-Iparraguirre J, Daniel Boese A, Klopper W, Ruscic B. Chem Phys. 2008;346:56. [Google Scholar]
- Agúndez M. PhD Thesis; Universidad Autónoma de Madrid: 2009. [Google Scholar]
- Agúndez M, Cernicharo J, Guélin M. A&A. 2015;577:L5. doi: 10.1051/0004-6361/201526317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agúndez M, Wakelam V. Chem Rev. 2013;113:8710. doi: 10.1021/cr4001176. [DOI] [PubMed] [Google Scholar]
- Angelova G, Novotny O, Mitchell JBA, Rebrion-Rowe C, Le Garrec JL, Bluhme H, Svendsen A, Andersen LH. Int J Mass Spectrom. 2004;235:7. [Google Scholar]
- Anglada G, Sepúlveda I, Gómez JF. Astron Astrophys Suppl Ser. 1997;121:255. [Google Scholar]
- Avery LW, Green S. ApJ. 1989;337:306. [Google Scholar]
- Bergeat A, Loison J-C. PCCP. 2001;3:2038. [Google Scholar]
- Bogey M, Demuynck C, Destombes JL, Dubus H. J Mol Spectr. 1987;122:313. [Google Scholar]
- Boogert ACA, Gerakines PA, Whittet DCB. Annual Review of Astronomy and Astrophysics. 2015;53:541. [Google Scholar]
- Buonomo E, Clary DC. J Phys Chem A. 2001;105:2694. [Google Scholar]
- Lau KC, Ng CY. Chinese Journal of Chemical Physics. 2006;19:29. [Google Scholar]
- Cernicharo J. IRAM Internal Report No. 52. 1985 [Google Scholar]
- Cernicharo J, Cox P, Fossé D, Güsten R. A&A. 1999;351:341. [Google Scholar]
- Cernicharo J, Gottlieb CA, Guélin M, Killian TC, Paubert G, Thaddeus P, Vrtilek JM. ApJ. 1991;368:L39. [Google Scholar]
- Cernicharo J, Marcelino N, Roueff E, Gerin M, Jiménez-Escobar A, Caro GMM. ApJ Lett. 2012;759:L43. [Google Scholar]
- Chandra S, Kegel WH. Astron Astrophys Suppl Ser. 2000;142:113. [Google Scholar]
- Clary DC, Buonomo E, Sims IR, Smith IWM, Geppert WD, Naulin C, Costes M, Cartechini L, et al. J Phys Chem A. 2002;106:5541. [Google Scholar]
- Cordiner MA, Buckle JV, Wirström ES, Olofsson AOH, Charnley SB. ApJ. 2013;770:48. [Google Scholar]
- Costes M, Halvick P, Hickson KM, Daugey N, Naulin C. ApJ. 2009;703:1179. [Google Scholar]
- Crapsi A, Caselli P, Walmsley CM, Myers PC, Tafalla M, Lee CW, Bourke TL. ApJ. 2005;619:379. [Google Scholar]
- Daniel F, Gérin M, Roueff E, Cernicharo J, Marcelino N, Lique F, Lis DC, Teyssier D, et al. A&A. 2014;560:A3. [Google Scholar]
- Fossé D, Cernicharo J, Gerin M, Pierre C. ApJ. 2001;552:168. [Google Scholar]
- Friesen RK, Medeiros L, Schnee S, Bourke TL, Francesco JD, Gutermuth R, Myers PC. MNRAS. 2013;436:1513. [Google Scholar]
- Garrod RT, Wakelam V, Herbst E. A&A. 2007;467:1103. [Google Scholar]
- Glowacki DR, Liang C-H, Morley C, Pilling MJ, Robertson SH. J Phys Chem A. 2012;116:9545. doi: 10.1021/jp3051033. [DOI] [PubMed] [Google Scholar]
- Green S. ApJS. 1991;76:979. [Google Scholar]
- Hasegawa TI, Herbst E. MNRAS. 1993;261:83. [Google Scholar]
- Hasegawa TI, Herbst E, Leung CM. ApJS. 1992;82:167. [Google Scholar]
- Herbst E, Terzieva R, Talbi D. MNRAS. 2000;311:869. [Google Scholar]
- Hickson KM, Loison J-C, Wakelam V. Chem Phys Lett. 2016a;659:70. [Google Scholar]
- Hickson KM, Wakelam V, Loison J-C. Mol Astroph. 2016b;3–4:1. [Google Scholar]
- Hincelin U, Chang Q, Herbst E. A&A. 2015;574:A24. [Google Scholar]
- Hincelin U, Wakelam V, Hersant F, Guilloteau S, Loison JC, Honvault P, Troe J. A&A. 2011;530:61. [Google Scholar]
- Huang X, Fortenberry RC, Lee TJ. ApJL. 2013;768:L25. [Google Scholar]
- Huang X, Lee TJ. ApJ. 2011;736:33. [Google Scholar]
- Huang X, Taylor PR, Lee TJ. J Phys Chem A. 2011;115:5005. doi: 10.1021/jp2019704. [DOI] [PubMed] [Google Scholar]
- Jacovella U, Gans B, Merkt F. J Chem Phys. 2013;139:084308. doi: 10.1063/1.4818982. [DOI] [PubMed] [Google Scholar]
- Janev RK, Reiter D. Physics of Plasmas (1994-present) 2004;11:780. [Google Scholar]
- Jorgensen JK, Schoier FL, Dishoeck EFv. A&A. 2002;389:908. [Google Scholar]
- Kanata H, Yamamoto S, Saito S. Chem Phys Lett. 1987;140:221. [Google Scholar]
- Krełowski J, Galazutdinov G, Kołos R. ApJ. 2011;735:124. [Google Scholar]
- Lattelais M, Pauzat F, Ellinger Y, Ceccarelli C. ApJ. 2009;696:L133. [Google Scholar]
- Leonori F, Petrucci R, Segoloni E, Bergeat A, Hickson KM, Balucani N, Casavecchia P. J Phys Chem A. 2008;112:1363. doi: 10.1021/jp0776208. [DOI] [PubMed] [Google Scholar]
- Lique F, Cernicharo J, Cox P. ApJ. 2006;653:1342. [Google Scholar]
- Liszt H, Sonnentrucker P, Cordiner M, Gerin M. ApJL. 2012;753:L28. [Google Scholar]
- Liszt HS, Pety J, Gerin M, Lucas R. A&A. 2014:564. [Google Scholar]
- Loison J-C, Agúndez M, Marcelino N, Wakelam V, Hickson KM, Cernicharo J, Gerin M, Roueff E, et al. MNRAS. 2016;456:4101. doi: 10.1093/mnras/stv2866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loison J-C, Wakelam V, Hickson KM, Bergeat A, Mereau R. MNRAS. 2014a;437:930. [Google Scholar]
- Loison JC, Hébrard E, Dobrijevic M, Hickson KM, Caralp F, Hue V, Gronoff G, Venot O, et al. Icarus. 2015;247:218. [Google Scholar]
- Loison JC, Hickson KM, Wakelam V. MNRAS. 2014b;443:398. [Google Scholar]
- Loomis RA, McGuire BA, Shingledecker C, Johnson CH, Blair S, Robertson A, Remijan AJ. ApJ. 2015;799:34. [Google Scholar]
- Lovas FJ, Suenram RD, Ogata T, Yamamoto S. ApJ. 1992;399:325. [Google Scholar]
- Maier JP, Walker GAH, Bohlender DA, Mazzotti FJ, Raghunandan R, Fulara J, Garkusha I, Nagy A. ApJ. 2011;726 [Google Scholar]
- Maluendes SA, McLean AD, Herbst E. ApJ. 1993a;417:181. doi: 10.1086/173301. [DOI] [PubMed] [Google Scholar]
- Maluendes SA, McLean AD, Yamashita K, Herbst E. J Chem Phys. 1993b;99:2812. doi: 10.1063/1.465190. [DOI] [PubMed] [Google Scholar]
- Mangum JG, Wootten A. A&A. 1990;239:319. [Google Scholar]
- Marcelino N, Cernicharo J, Tercero B, Roueff E. ApJ. 2009;690:L27. [Google Scholar]
- McGuire BA, Carroll PB, Dollhopf NM, Crockett NR, Corby JF, Loomis RA, Burkhardt AM, Shingledecker C, et al. ApJ. 2015;812:76. [Google Scholar]
- McGuire BA, Carroll PB, Ryan AL, Geoffrey AB, Jan MH, Frank JL, Philip RJ, Anthony JR. ApJ. 2013;774:56. [Google Scholar]
- McGuire BA, Carroll PB, Sanders JL, Weaver SLW, Blake GA, Remijan AJ. MNRAS. 2014;442:2901. [Google Scholar]
- Müller HSP, Schlöder F, Stutzki J, Winnewisser G. J Mol Struct. 2005;742:215. [Google Scholar]
- Nguyen TL, Mebel AM, Lin SH, Kaiser RI. J Phys Chem A. 2001;105:11549. [Google Scholar]
- Pardo JR, Cernicharo J, Serabyn E. IEEE Transactions on Antennas and Propagation. 2001;49:1683. [Google Scholar]
- Pety J, Gratier P, Guzman V, Roueff E, Gerin M, Goicoechea JR, Bardeau S, Sievers A, et al. A&A. 2012a;548:A68. [Google Scholar]
- Pety J, Gratier P, Guzmán V, Roueff E, Gerin M, Goicoechea JR, Bardeau S, Sievers A, et al. A&A. 2012b;548 [Google Scholar]
- Pickett HM, Poynter IRL, Cohen EA. J Quant Spect Rad Trans. 1998;60:883. [Google Scholar]
- Plessis S, Carrasco N, Dobrijevic M, Pernot P. Icarus. 2012;219:254. [Google Scholar]
- Plessis S, Carrasco N, Pernot P. J Chem Phys. 2010;133:134110. doi: 10.1063/1.3479907. [DOI] [PubMed] [Google Scholar]
- Pratap P, Dickens JE, Snell RL, Miralles MP, Bergin EA, Irvine WM, Schloerb FP. ApJ. 1997;486:862. doi: 10.1086/304553. [DOI] [PubMed] [Google Scholar]
- Prodnuk SD, Depuy CH, Bierrbaum VM. Int J Mass Spectrom. 1990;100:693. [Google Scholar]
- Raksit AB, Bohme DK. Int J Mass Spectrom Ion Proc. 1983;55:69. [Google Scholar]
- Raut U, Famà M, Teolis BD, Baragiola RA. J Chem Phys. 2007;127:204713. doi: 10.1063/1.2796166. [DOI] [PubMed] [Google Scholar]
- Ruaud M, Loison JC, Hickson KM, Gratier P, Hersant F, Wakelam V. MNRAS. 2015;447:4004. [Google Scholar]
- Ruaud M, Wakelam V, Hersant F. MNRAS. 2016;459:3756. [Google Scholar]
- Sakai N, Sakai T, Hirota T, Burton M, Yamamoto S. ApJ. 2009;697:769. [Google Scholar]
- Sakai N, Sakai T, Hirota T, Yamamoto S. ApJ. 2010;722:1633. [Google Scholar]
- Savic I, Gerlich D. Phys Chem Chem Phys. 2005;7:1026. doi: 10.1039/b417965j. [DOI] [PubMed] [Google Scholar]
- Seburg RA, Patterson EV, McMahon RJ. JACS. 2009;131:9442. doi: 10.1021/ja901606a. [DOI] [PubMed] [Google Scholar]
- Sipilä O, Spezzano S, Caselli P. A&A. 2016;591:L1. [Google Scholar]
- Smith D, Adams NG. Int J Mass Spectrom. 1987;76:307. [Google Scholar]
- Taatjes CA, Klippenstein SJ, Hansen N, Miller JA, Cool TA, Wang J, Law ME, Westmoreland PR. Phys Chem Chem Phys. 2005;7:806. doi: 10.1039/b417160h. [DOI] [PubMed] [Google Scholar]
- Tafalla M, Myers PC, Mardones D, Bachiller R. Astron Astrophys. 2000;359:967. [Google Scholar]
- Thaddeus P, Gottlieb CA, Hjalmarson A, Johansson LE, Irvine WM, Friberg P, Linke RA. ApJ. 1985;294:L49. doi: 10.1086/184507. [DOI] [PubMed] [Google Scholar]
- Turner BE. ApJS. 1991;76:617. [Google Scholar]
- Turner BE, Herbst E, Terzieva R. ApJS. 2000;126:427. [Google Scholar]
- van Hemert MC, van Dishoeck EF. Chem Phys. 2008;343:292. [Google Scholar]
- Vazquez J, Harding ME, Gauss J, Stanton JF. J Phys Chem A. 2009;113:12447. doi: 10.1021/jp9029908. [DOI] [PubMed] [Google Scholar]
- Vrtilek JM, Gottlieb A, Gottlieb EW, Killian TC, Thaddeus P. ApJ. 1990;364:L53. [Google Scholar]
- Wakelam V, Herbst E, Selsis F. A&A. 2006;451:551. [Google Scholar]
- Wakelam V, Loison J-C, Hickson KM, Ruaud M. MNRAS. 2015a;453:L48. [Google Scholar]
- Wakelam V, Loison JC, Herbst E, Pavone B, Bergeat A, Béroff K, Chabot M, Faure A, et al. ApJ, Supp Series. 2015b;217:20. [Google Scholar]
- Wang Y, Braams BJ, Bowman JM. J Phys Chem A. 2007;111:4056. doi: 10.1021/jp0676787. [DOI] [PubMed] [Google Scholar]
- Wong MW, Radom L. JACS. 1993;115:1507. [Google Scholar]
- Woon DE. Chem Phys Lett. 1995;244:45. doi: 10.1016/0009-2614(95)00906-k. [DOI] [PubMed] [Google Scholar]
- Woon DE, Herbst E. ApJ. 1996;465:795. [Google Scholar]
- Wu Q, Cheng Q, Yamaguchi Y, Li Q, Schaefer HF. J Chem Phys. 2010;132:044308. doi: 10.1063/1.3273321. [DOI] [PubMed] [Google Scholar]
- Yamamoto S, Saito S. J Chem Phys. 1994;101:5484. [Google Scholar]
- Yamamoto S, Saito S, Ohishi M, Suzuki H, Ishikawa S, Kaifu N, Murakami A. ApJ. 1987;322 [Google Scholar]
- Yamamoto S, Saito S, Suzuki H, Deguchi S, Kaifu N, Ishikawa S, Ohishi M. ApJ. 1990;348:363. [Google Scholar]