Measuring arithmetic: A psychometric approach to understanding formatting effects and domain specificity

Abstract

Using multitrait, multimethod data, and confirmatory factor analysis, the current study examined the effects of arithmetic item formatting and the possibility that across formats, abilities other than arithmetic may contribute to children’s answers. Measurement hypotheses were guided by several leading theories of arithmetic cognition. With a sample of 1314 3rd grade students (age M=103.24 months, SD=5.41 months), Abstract Code Theory, Encoding Complex Theory, Triple Code Theory, and the Exact versus Approximate Calculations Hypothesis were evaluated, using 11 measures of arithmetic with symbolic problem formats (e.g., Arabic numeral and language-based formats) and various problem demands (e.g., requiring both exact and approximate calculations). In general, results provided support for both Triple Code Theory and Encoding Complex Theory. As predicted by Triple Code Theory, arithmetic outcomes with language formatting, Arabic numeral formatting, and estimation demands (across formats) were related but distinct from one another. As predicted by Encoding Complex Theory, executive attention was a direct predictor of all arithmetic outcomes. Language was no longer a direct predictor of arithmetic outcomes when executive attention was accounted for in the model; however, a strong and enduring relationship between language and executive attention suggested that language may play a facilitative role in reasoning during numeric processing. These findings have important implications for assessing arithmetic in educational settings and suggest that in addition to arithmetic-focused interventions, interventions targeting executive attention, language, and/or the interplay between them (i.e., internal speech during problem-solving) may be a promising avenues of mathematical problem-solving intervention.

Introduction

Arithmetic mastery is essential for successful daily living and is foundational for advanced-level participation in STEM disciplines (AAIDD, 2010; STEM Coalition, 2000). Despite decades of mathematics education reform, children in the U.S. continue to struggle with math achievement, and this is true of both basic arithmetic skills and more advanced problem solving (National Center for Education Statistics, 2013; Woodward, 2004). This study explored the possibility that problem formatting, the manner in which problems are conveyed during testing, may be an important factor for understanding arithmetic cognition and achievement.

Format-Based Concerns for Word Problems

Formatting of assessment stimuli is an important consideration for the measurement of arithmetic ability (Ansari, 2007; Campbell, 1994; Dehaene, Piazza, Pinel, & Cohen, 2003; Lourenco, Bonny, Fernandez, & Rao, 2012; McCloskey, 1992; Piazza, Pinel, Le Bihan, & Dehaene, 2007). Symbolic formats (e.g., Arabic numerals, spoken language, written language) are usually used for teaching and testing arithmetic ability in formal educational settings; however, research has suggested that different symbolic formats may lead to different sorts of mental representation and processing of numerical information (Ansari, 2007; Campbell, 1994; Dehaene et al., 2003).

In the realm of educational testing, linguistic formats serve an important purpose for testing arithmetic ability. Language formats are often used to convey everyday “word problems” in a variety of testing scenarios. For example, both the National Assessment of Educational Progress (NAEP) and the Program for International Student Assessment (PISA) use “word problems” to assess students’ understandings of real-world mathematics (Kelly et al., 2013; National Center for Education Statistics, 2013). Word problems are generally thought to go beyond basic arithmetic knowledge, testing students’ abilities to apply their conceptual knowledge and strategic competence to problem-solving situations they encounter in and outside of the classroom (Greer, 1997; National Academy of Sciences, 2001; Verschaffel, De Corte, & Lasure, 1994). Ideally word problems require students to both decide upon strategies for problem-solving and apply their arithmetic and procedural knowledge in order to execute those strategies. Thus, linguistic formats represent a valuable means of surmising how students will perform arithmetic in their daily lives.

Despite their importance for assessing arithmetic ability, word problems have been the subject of measurement controversy, perhaps since they became common as indicators of mathematical ability on popular standardized testing instruments. They have been criticized for the extent to which they fail to encourage students to apply common-sense to mathematical problem-solving (Baranes, Perry, & Stigler, 1989; Verschaffel, Greer, & de Corte, 2000), conversely for the extent to which they may penalize students with less world or situational knowledge (Chipman, Marshall, & Scott, 1991; Davis-Dorsey, Ross, & Morrison, 1991; Stern & Lehrndorfer, 1992), and perhaps most notably for penalizing students with lower reading ability (Ballew & Cunningham, 1982; Helwig, Rozek-tedesco, & Tindal, 2002; Helwig, Rozek-tedesco, Tindal, Heath, & Almond, 1999; Muth, 1984).

Efforts in test reform have largely acknowledged these concerns about content, design, and administration of linguistically formatted items (American Educational Research Association, American Psychological Association, & National Council on Measurement in Education, 1985, 1999, 2014; National Research Council Committee on Appropriate Test Use, 1999). However, more recently, a number of researchers have suggested that linguistic formats may unintentionally tap executive abilities (e.g., working memory) and language ability, particularly when examinees are unfamiliar with the language system utilized in test formatting (Abedi & Lord, 2001; Martiniello, 2009; Rhodes, Branum-Martin, Morris, Romski, & Sevcik, 2015; Shaftel, Belton-Kocher, Glasnapp, & Poggio, 2006; Terry, Hendrick, Evangelou, & Smith, 2010). This line of research is focused on the idea that the very formatting of word problems may be a source of inherent testing bias.

To be clear, the newer line of research focused on issues of testing bias for linguistically formatted mathematics problems is not the only research tradition to implicate domain general abilities as important to arithmetic cognition. Several educational and developmental researchers have implicated executive abilities and language in arithmetic performance (e.g., Bull, Espy, & Wiebe, 2008; Bull & Scerif, 2001; Cummins, Kintsch, Reusser, & Weimer, 1988; Hecht, Torgesen, Wagner, & Rashotte, 2001; Lefevre et al., 2013; Mazzocco & Kover, 2007; Passolunghi, Vercelloni, & Schadee, 2007; Zheng, Swanson, & Marcoulides, 2011). Furthermore, the idea that both conceptual knowledge and procedural/strategic ability contribute to successful performance on word problems is not new (see for example Nesher, 1986; Riley, Greeno, & Heller, 1983; Siegler & Shrager, 1984; Siegler, 1991). However, the question of domain general testing bias is distinct from the question of domain general contributions. This difference is subtle but important. From the valid measurement / testing bias perspective, the issue is not whether domain general abilities are important contributors to arithmetic development. Rather, the issue is whether commonly used measures of arithmetic ability are actually also measures of domain general abilities and should be interpreted as such (in which case it would not be surprising that measures of “arithmetic ability” correlate with or can be linearly regressed upon measures of domain general abilities).

Detecting Format-Based “Bias” in Arithmetic Problems

Even with careful design of problem content, formatting may pose a hidden threat to the validity of a measure (Messick, 1989, 1996). Though “bias” is a term that usually means “unfair” or “discriminatory” in popular speech, it generally refers to the underlying issue of construct validity in psychometric contexts (Crocker & Algina, 2008; Hambleton, Swaminathan, & Rogers, 1991; Reynolds & Suzuki, 2012). A test item is biased when two examinees with the same level of ability would not have the same probabilities of correctly answering (often called “differential item functioning” or DIF; see for example Borsboom et al., 2002; Hambleton et al., 1991). The unequal probability of correct answers is always because the item is unintentionally measuring some dimension other than the one intended by test developers (i.e., it is not unidimensional). When the bias is an artifact of the way test items are formatted, it can more specifically be referred to as common method variance (CMV; Cote & Buckley, 1987, 1988; Messick, 1989, 1996; Podsakoff, MacKenzie, Lee, & Podsakoff, 2003). In this case, the linguistic formatting of word problems may lead to the unintentional measurement of language and executive abilities in addition to the intentional measurement of arithmetic abilities, and the interpretation of test scores as indicators of math ability regardless of formatting would be invalid.

Detecting common method variance requires a specific measurement methodology, which ideally is guided by a strong theoretical foundation. Potential confounding dimensions of language and executive abilities must be measured along with arithmetic, in a variety of formats (i.e., a multitrait, multimethod methodology). Then measures of arithmetic ability and potential confounding dimensions must be included in statistical models of responses, which evaluate not only mean structures but also variance structures. This can be accomplished with statistical models capable of allowing for the possibility that multiple abilities may predict behaviors (see for example Cote & Buckley, 1987; Eid, Lischetzke, & Nussbeck, 2006; Marsh, Beard, & Bailey, 2002; Maul, 2013). These statistical models fall under the broad umbrella of factor analysis, and in the case where they are theoretically guided and specified by a priori hypotheses about construct measurement, they may be more specifically referred to as “confirmatory factor analysis.”

Forming Measurement Hypotheses with Leading Theories of Arithmetic Cognition

Four leading theories of arithmetic cognition, Abstract Code Theory, Encoding Complex Theory, Triple Code Theory, and Exact versus Approximate Calculations, provide the theoretical basis for forming confirmatory factor models of arithmetic cognition in the current study. Each of these theories attempts to explain (1) how we encode numerical information and represent numerical information mentally, (2) how we retrieve math facts from memory, process the information, or operate upon numerical representations to achieve solutions to problems, (3) how we recode our mental, numerical representations of solutions into output and report our answers, and (4) which cognitive domains are involved in these activities and how they may interact with one another, if at all. In general, these four facets define the process of “arithmetic” for theories of arithmetic cognition, and each of these facets of arithmetic are areas in which theories of arithmetic cognition may diverge from each other, sometimes irreconcilably.

One consequence of this theoretical divergence has been that there is no consensus assessment of numeric processing. Cognitive research on arithmetic has considered any number of calculation demands represented in a variety of formats as potentially valid measures of arithmetic. Across various arithmetic tasks, dominant theories of arithmetic cognition offer different accounts of how people do arithmetic, what mental processes are involved in arithmetic, and why people exhibit individual differences in arithmetic ability. The following section considers each theory with regard to its specifications for the process and measurement of arithmetic, with special attention as to how it attempts to explain language-formatting effects and the roles that language and executive abilities may play in arithmetic performance.

Abstract Code Theory

Abstract Code Theory stipulates that a single, abstract code is used to mentally represent all numeric information, regardless of input format (e.g., Arabic numerals; McCloskey, Caramazza, & Basili, 1985; McCloskey, 1992). Because this abstract, semantic code is the object of numeric processing, formatting exerts no effect on numeric processing (McCloskey, 1992). Differences in reaction time seen with language-formatted arithmetic stimuli can be attributed to increased encoding time necessary for mental representation of language input (McCloskey, Macaruso, & Whetstone, 1992). The extent to which a language domain may be involved in aiding numeric comprehension or production is unclear and not specified by the theory, but rather addressed as an area for future investigation (McCloskey, 1992). Similarly, the theory does not specify the extent to which some executive system of control (regulation, attention, inhibition, working memory) is responsible for coordinating numeric comprehension, processing, and production. Rather, Abstract Code Theory tends to allow for a specialized numeric processing module to facilitate the execution of arithmetic operations. McCloskey (1992) notes that the roles of general processing abilities (e.g., working memory) are issues for future investigation.

Encoding Complex Theory

Encoding Complex Theory stipulates that the presentation of numerical stimuli activates an associative network of format-specific numerical “codes” or mental representations (Campbell, 1994; Campbell & Clark, 1988; Clark & Campbell, 1991). Mental representations of number can be verbal (e.g., articulatory, orthographic) or nonverbal (e.g., visual, motor, analog magnitude; Campbell, 1994; Campbell & Clark, 1988; Clark & Campbell, 1991). The mental representations or “codes” are associatively connected within a complex network, called the encoding complex, and as such, they are assumed to stimulate each other in complex patterns of activation without the use of a common, abstract code (Campbell & Clark, 1988; Clark & Campbell, 1991). Successful numeric processing (number comprehension, calculation, comparison, parity judgment) requires enhancing relevant association patterns and inhibiting interfering association patterns within the encoding complex network, and this is particularly true for calculation activities (Campbell & Clark, 1988; Clark & Campbell, 1991).

Encoding Complex Theory does not specify a specific quantitative domain as responsible for numeric processing. Instead, Campbell and Clark (1988; Clark & Campbell, 1991) have implicated a number of domain general cognitive capacities in resolving the complex network of associations activated during numeric processing. These domains include executive systems of control (inhibition, problem-solving, attention, working memory, specifically, Baddeley and Hitch’s 1974 model of working memory), the motor domain, the language domain, and the visuo-spatial domain. Though executive systems of control are implicated across problem-solving activities and language ability is implicated in language formatted problems, the roles of motor and visuo-spatial abilities in predicting outcomes across various formats and relating to other cognitive domains during problem-solving is unclear.

Triple Code Theory

According to Triple Code Theory, stimulus format affects encoding and mental representation of number. The format in which number stimuli are presented will determine the type of mental representation encoded for them. Arabic numeral input is represented by the visual Arabic number form; language-based numeral input is represented by the verbal word frame; sets of objects are represented by the analogical magnitude representation (Dehaene, 1992; Dehaene & Cohen, 1995; Dehaene et al., 2003). Although each of these factors is allowed to communicate directly with one another via transcoding, problem demands influence the way in which numerical processing is conducted. Under Triple Code Theory, format-based differences in arithmetic performance are thus attributed to issues of efficiency in the transcoding process (Campbell & Epp, 2005).

The cognitive factors responsible for encoding and mentally representing numeric information are not the only cognitive domains involved in Triple Code Theory’s arithmetic. The language domain supports the recognition of spoken and written number input, the production of spoken and written number output, and the retrieval of number facts (e.g., two plus two equals four) from memory (Dehaene, 1992; Dehaene & Cohen, 1995). The role of executive systems in coordinating the functions of arithmetic is unclear in Triple Code Theory. Although the three factors for the mental representation of number are assumed to cooperate with one another and with the language domain in carrying out numeric processing, the extent to which their cooperation is self-directed as opposed to organized by a super ordinate system of attention, inhibition, working memory, and regulation is not specified by the theory.

Exact versus approximate calculations, an extension of Triple Code Theory

Unlike the other theories of arithmetic cognition, exact versus approximate calculations theory pertains specifically to the numeric processing task of calculations. It is an extension of Triple Code Theory, supporting the idea that distinct neural networks contribute to (1) approximate calculation tasks involving semantic representations of quantity, comparison, and estimation versus (2) exact calculation tasks involving the retrieval of rote, verbal, numerical facts about quantity to compute exact arithmetic solutions (Dehaene et al., 1999; Stanescu-Cosson et al., 2000). The analogical magnitude representation domain is hypothesized to be supported by the neural network for approximate calculations, and the verbal word frame domain is hypothesized to be supported by the neural network for exact calculations. These domains appear to be integrated, and they may both be recruited for difficult, exact calculation problems involving large quantities (Stanescu-Cosson et al., 2000).

Other assumptions of Triple Code Theory, including the possible cognitive domains involved in numeric processing are generally not addressed in the empirical literature supporting exact versus approximate calculations. The focus of this empirically generated theory is specifying the roles of the analogical magnitude representation domain and the verbal word frame domain on approximate and exact calculation activities. The visual Arabic number form domain is largely absent from this specification of Triple Code Theory; however, spatial attention networks, possibly representing some of the predictive power of the visual Arabic number form domain and possibly representing some form of executive control for attention, may contribute to coordinating both types of task.

Summary: Comparing and Contrasting Theories of Arithmetic Cognition

Although Abstract Code, Encoding Complex, Triple Code, and Exact versus Approximate Calculations Theories overlap in many areas, they also diverge in their explanations of mental representation of quantity and cognitive domains responsible for numeric processing. Encoding Complex and Triple Code Theories both agree that stimulus formatting can largely influence both mental representation of quantity and subsequent numeric processing; however, Abstract Code Theory stipulates that regardless of stimulus format, mental representations are amodal abstract codes and subsequent numeric processing relies on these abstract codes. Triple Code and Abstract Code Theories both agree that numeric processing relies on cognitive domains specialized for processing quantity; however, Encoding Complex Theory stipulates that numeric processing relies on cognitive domains which are not modular and not unique to processing quantity. Clearly, encoding (forming mental representations) and cognitive dimensionality of numeric processing are major areas of departure for these theories.

In terms of specifying domains which may help to facilitate numeric processing, both Encoding Complex and Triple Code Theories suggest that the language domain (retrieving verbal information about number facts) may contribute to numeric processing. Encoding Complex Theory is perhaps the most prescriptive in specifying additional domain general contributions to numeric processing. Encoding Complex Theory suggests that working memory, domain general reasoning, and attention/inhibition are all important for successful numeric processing. Pieces of these domain general capacities are reflected in other theories of cognitive arithmetic (e.g., Abstract Code Theory mentions that working memory is of interest to numeric processing; Triple Code Theory mentions that executive domains involving coordinating attention are of interest to numeric processing). However, the centrality of all of these domain general capacities is made clear in Encoding Complex Theory, as well as the stipulation that they work in concert to perform a variety of problem-solving activities (i.e., that arithmetic cognition is simply one form of problem-solving which happens to involve operating on quantities).

From a larger cognitive theoretical position, working memory, domain general reasoning, and attention/inhibition are three separate but related constructs that form the basis for executive attention, the ability to form and maintain mental representations of problems and problem-solving goals robust to distractions during problem-solving activities (Engle, Kane, & Tuholski, 1999; Engle & Oransky, 1999; Engle & Kane, 2004; Kane & Engle, 2002). Executive attention is distinct from general intelligence, though executive attention is related to the larger idea of general intelligence via the importance that the construct of fluid intelligence serves for each. Executive attention is thought to be carried out by distinct neural substrates in the pre-frontal cortex (particularly the dorsolateral PFC), and behaviorally, is typically measured by fluid intelligence, working memory capacity, and attention/inhibition (Engle & Kane, 2004; Kane & Engle, 2002). Though the theory of executive attention allows for these three capacities to be distinct (i.e., to maintain distinct variance), their overlapping contributions to complex problem-solving tasks that demand sustained attention and goal maintenance in the face of distraction (i.e., their covariance) is thought to reflect the larger executive attention construct (Kane & Engle, 2002). Notably, for the purposes of the current study, Encoding Complex Theory views arithmetic cognition as one example of a complex problem-solving task. Thus, Encoding Complex Theory’s hypothesized, joint contributions of working memory, domain general reasoning, and attention/inhibition may be best represented by the larger cognitive construct of executive attention.

Measurement Hypotheses for the Current Study

Given these varying theoretical accounts of arithmetic cognition, the purpose of the current study was to examine arithmetic cognition on symbolically formatted measurement instruments, with attention to potential formatting effects and possible contributions from cognitive abilities other than a quantitative domain that is specialized for numeric processing. Each leading theory of arithmetic cognition was used to formulate a series of measurement hypotheses, and a multitrait, multimethod methodology was used in conjunction with confirmatory factor analysis to examine each set of hypotheses. The architecture of an arithmetic domain(s), implications of that architecture for measuring various problem formats, and contributions of language and executive attention domains were simultaneously specified and estimated in the larger measurement models for each theory under investigation.

Method

Participants

Participants were drawn from public schools in a metropolitan school district in the Southeastern United States. During the fall of each third-grade school year, students who assented to participate and whose parents consented to participate in the study were included in assessment (and instructional intervention for the purposes of a parent study focused on testing the effects of an experimental instructional program for mathematics problem solving and its cognitive correlates; see for example (Fuchs et al., 2008). An initial 2,023 students across 120 classrooms had consent to participate in the parent study. A subset of N=1320 children were randomly selected for full participation in the parent study and received the full testing battery (including screening measures, the full mathematics battery, cognitive measures, and demographic reports from teachers). A final sample of 1314 children was selected for the current study.

The final sample had a mean age of 103.24 months (SD=5.41, range = 89 – 142), was approximately 50% female (n=661 females, n=652 males), and was ethnically and racially diverse (43% African American, 40% White, 10% Hispanic, 1% Kurdish, 4% other not specified, and 1% missing). Approximately 56% of the children in the sample qualified for free or reduced lunch. Teachers reported that approximately 5% of the children in the parent study sample were receiving special education services. Of those 67 children whose teachers reported receiving special education services, most were receiving services for learning disabilities (N=22), speech/hearing/language (N=21), ADHD (N=7), or giftedness (N=4).

Procedures

The parent study was designed to sample four, consecutive cohorts of third grade students, following each cohort for three academic years spanning from the fall of third grade until the spring of fifth grade. The current analysis, however, relies only on baseline testing for each of these four cohorts of students (i.e., all measures in the current study were administered before the sample cohorts received any intervention in the parent study). Table 1 displays cohort sampling information.

Table 1.

Cohort Measurement Information

Measures	Cohort 1 Received	Cohort 2 Received	Cohort 3 Received	Cohort 4 Received
Mathematics Measures:
WJ-III Applied Problems	X	X	X	X
Single Digit Story Problems	X	X	X	X
Vanderbilt Complex Story Problems				X
Basic Facts Addition	X	X	X	X
Basic Facts Subtraction	X	X	X	X
WRAT Written Arithmetic		X	X	X
Test of Computational Fluency	X	X	X	X
Double Digit Addition	X
Double Digit Subtraction	X
Double Digit Addition Estimation	X
Double Digit Subtraction Estimation	X
Language Measures:
WASI Vocabulary	X	X	X	X
WDRB Listening Comprehension	X	X	X	X
TOLD Grammatic Closure	X	X	X	X
Executive Attention Measures:
SWAN teacher survey	X	X	X	X
WMTB Listening Recall	X	X	X	X
WJ-III Numbers Reversed	X	X	X	X
WASI Matrix Reasoning	X	X	X	X
WJ-III Concept Formation	X	X	X	X
Cohort Sampling Information	N=491 stud. N=30 class. N=7 school.	N=485 stud. N=30 class. N=8 school.	N=452 stud. =29 class. N=8 school.	N=531 stud. N=31 class. N=9 school.
Total Sample for the Current Study	N=1959 students N=120 classrooms (classrooms do not overlap) N=16 schools (schools do overlap across cohorts)

During September and October of each year of the study, (1) a demographic questionnaire was completed by teachers, (2) students’ mathematical skills were assessed in three sessions lasting 30–60 minutes each, and (3) students’ cognitive abilities were assessed in two sessions lasting 45 minutes each. Total testing span from first assessment to last was approximately one month.

The cognitive battery (described below) was administered individually by trained assessment professionals in quiet testing locations within schools. Standardized mathematics assessments were administered using recommended test developer procedures, and non-standardized mathematics assessments were administered to students using a whole classroom assessment methodology. Students received individual stimulus papers and pencils. Trained assessment professionals read questions aloud while students followed along on their own paper copies. Students were given time to respond to each question, and the next question was not administered until all students or all but two students had put their pencils down. Students were not permitted to communicate answers or disrupt the testing of the whole class. Table 2 presents descriptive statistics for mathematics, language, and executive attention measures.

Table 2.

Descriptive Statistics for All Measures

Measure	N	Mean (SD)	Range: Min - Max
Mathematics Measures:
WJ-III Applied Problems	1302	29.15 (4.32)	2 – 48
Single Digit Story Problems	1307	9.96 (3.46)	0 – 14
Vanderbilt Complex Story Problems	324	8.31 (6.11)	0 – 34
Basic Facts Addition	1309	11.90 (4.99)	0 – 25
Basic Facts Subtraction	1310	6.97 (5.03)	0 – 25
WRAT Written Arithmetic	957	23.73 (2.51)	15 – 34
Test of Computational Fluency	1312	12.07 (6.06)	0 – 25
Double Digit Addition	339	17.12 (4.24)	0 – 20
Double Digit Subtraction	339	11.51 (5.82)	0 –20
Double Digit Addition Estimation	340	8.65 (7.11)	0 –20
Double Digit Subtraction Estimation	339	6.53 (5.90)	0 – 20
Language Measures:
WASI Vocabulary	1314	27.35 (6.45)	5 – 51
WDRB Listening Comprehension	1302	21.12 (4.29)	0 – 33
TOLD Grammatic Closure	1303	18.78 (6.60)	0 – 30
Executive Attention Measures:
SWAN teacher survey	1258	75.71 (23.47)	18 – 126
WMTB Listening Recall	1302	9.97 (3.58)	0 – 63
WJ-III Numbers Reversed	1302	9.37 (2.85)	1 – 26
WASI Matrix Reasoning	1314	15.51 (6.45)	0 – 30
WJ-III Concept Formation	1302	15.64 (7.07)	1 – 39

Measures

For each measure, correct items were scored “1,” and incorrect items as “0” unless otherwise noted. Total raw score was the number of correct items (or partially correct items in noted instances), and this score was used in analyses. We report model-based reliability, in the form of R².

Mathematics achievement measures with language formatting

WJ III Applied Problems

This measure consists of 60 orally presented word problems designed to represent every day, practical math problems (McGrew & Woodcock, 2001). Items require examinees to count, perform simple arithmetic operations, tell time, tell temperature, or problem-solve by eliminating extraneous information (McGrew & Woodcock, 2001). It is important to note that some of the WJ III Applied Problems items do not represent the traditional word problems that students typically encounter in school curricula. These items represent a mixture of traditional word problems and applied problems.

Single digit story problems

This measure consists of 14 word problems (adapted from Jordan & Hanich, 2000), read aloud while students follow along on their own written copies. Each item could be solved in one step with sums or minuends of 9 or less.

Complex story problems

This measure consists of 18 word problems, read aloud while students follow along on their own written copies (Fuchs, Hamlett, & Powell, 2003). Each item involves one to four steps for solution. Nine items are more complex and require students to eliminate extraneous information from the problem, solve problems involving novel contexts using real-world information and their own problem-solving experiences, and apply information and solutions generated in previous segments of the complex problem. Students could earn a total of 2 points per item, 1 point for correctly calculating intermediate steps in the problem, and 1 point for correctly labeling the final answer.

Mathematics achievement measures with Arabic numeral formatting

Basic facts addition

This measure consists of 25 addition fact items (Fuchs et al., 2003). Each item involves addends of 9 or less and sums of 12 or less. Students are provided with the stimulus paper and a pencil and permitted one minute to complete as many items as possible.

Basic facts subtraction

This measure consists of 25 subtraction fact items (Fuchs et al., 2003). Each item involves minuends of 18 or less and answers of 12 or less. Students are provided with the stimulus paper and a pencil and were permitted one minute to complete as many items as possible.

WRAT Written Arithmetic

The WRAT-3 Written Arithmetic subtest (Blue form; Wilkinson, 1993) consists of 40 computation problems. Students are provided a pencil and asked to produced written responses to as many items as possible within 15 minutes. Items contain a variety of arithmetic content including basic facts, arithmetic involving multiple operands, arithmetic operations with proportions, and reducing and evaluating algebraic expressions (Wilkinson, 1993).

Second grade computational fluency

This measure consists of 25 items and is designed for second grade addition, subtraction, number combinations, and procedural computation problems (Fuchs, Hamlett, & Fuchs, 1990). Examinees are given 3 minutes to complete as many problems as possible.

Double digit addition

This measure consists of 20 2-digit by 2-digit addition items with and without regrouping (Fuchs et al., 2003). Students are provided a written protocol, pencil, and 5 minutes to complete as many problems as possible.

Double digit subtraction

This measure consists of 20 2-digit by 2-digit subtraction items with and without regrouping (Fuchs et al., 2003). Students are provided a written protocol, pencil, and 5 minutes to complete as many problems as possible.

Mathematics achievement measures involving estimation or analog magnitude

Double digit estimation addition

This measure consists of 20 symbolic 2-digit by 2-digit addition items in which students are instructed to estimate answers to the nearest ten (Fuchs et al., 2003). Examiners complete a sample problem in order to demonstrate estimation and to remind students that they are not computing exact answers to problems. Students are provided with a written protocol and pencil, and given 5 minutes to complete as many problems as possible. Exact calculated answers were scored as incorrect.

Double digit estimation subtraction

This measure consists of 20 symbolic 2-digit by 2-digit subtraction items in which students are instructed to estimate answers to the nearest ten (Fuchs et al., 2003). Examiners complete a sample problem in order to demonstrate estimation and to remind students that they are not computing exact answers to problems. Students are provided with a written protocol and pencil, and given 5 minutes to complete as many problems as possible. Exact calculated answers were scored as incorrect.

Language measures

Three measures of language were used. Language is commonly defined an integration of form, use, and content, a combination of skills in the areas of phonology, syntax, morphology, lexical knowledge, semantics, pragmatics, and prosody (Bloom & Lahey, 1978). Among these possible indicators of language ability, it appears that capturing listening comprehension, vocabulary knowledge, and grammatical comprehension may be essential for accurately measuring language ability (Carroll, 1993), and thus, for the purpose of this analysis, these key components of language ability were the focus of measurement.

WASI Vocabulary

The Vocabulary subtest of the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999) consists of 42 items, assessing expressive vocabulary. The initial four items require students to view a picture display and provide a verbal label for the object in each picture. Remaining items require students to provide definitions for vocabulary prompts given by examiners. Responses to all items were scored “0” if incorrect, “1” if partially correct, or “2” if the targeted response was present (Wechsler, 1999).

WDRB Listening Comprehension

The Listening Comprehension subtest of the Woodcock Diagnostic Reading Battery (WDRB; Woodcock, 1997) consists of 38 sentences or passages, read aloud to examinees who are then prompted to supply the missing word at the end of each prompt. Initial items require students to complete simple verbal analogies and word associations, and as the test continues, items become more complex and require students to discern implications of the passages they have just heard (Woodcock, 1997).

TOLD Grammatic Closure

The Grammatic Closure subtest of the Test of Language Development (TOLD-Revised edition; Newcomer & Hammill, 1988) consists of 30 sentences, assessing ability to recognize, understand, and express English morphology. Students are prompted with a sentence that is missing a word and respond verbally to supply the missing word and complete the sentence (Newcomer & Hammill, 1988).

Executive attention measures

Five measures of executive attention were used. These measures emphasize the three, domain general abilities whose coordination is theorized to allow maintenance of mental representations of problems, attention, and problem-solving goals, in the face of distraction during problem-solving activities: working memory, attention/inhibition, and fluid intelligence or inductive reasoning.

SWAN

The SWAN (Swanson et al., 2012) is a teacher survey with 18 items measuring attention, inhibition, and self-regulation. This instrument is used to measure the inattentive behavior, distractibility, impulsivity, and hyperactivity characteristic of Attention-Deficit/Hyperactivity Disorder (ADHD) while also capturing the normal distribution of nonclinical behavior. On the first nine items, teachers rate students for various types of inattentive behavior and distractibility; on the next nine items, teachers rate students for various types of impulsive and hyperactive behaviors. Teachers respond on a seven point Likert-type scale (7 “far above average,” 6 “above average,” 5 “slightly above average,” 4 “average,” 3 “slightly below average,” 2 “below average,” 1 “far below average).”

WMTB Listening Recall

The Listening Recall subtest of the Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001) consists of sequences of sentences, assessing verbal working memory. Examiners read aloud a series of short sentences to students. After listening to each sentence, the student evaluates the sentence as true or false. Finally, after evaluating all of the sentences in a trial, the student is asked to recall, in order, the last word of each sentence in the trial (Pickering & Gathercole, 2001).

WJ III Numbers Reversed

The Numbers Reversed subtest of the WJ-III (Test of Cognitive Abilities; Woodcock, McGrew, & Mather, 2001) consists of 30 items, assessing working memory. On each item, students listen to orally presented, random spans of digits, and upon completion of the span, students are prompted to orally list the digits they have just heard in reversed order. As students progress through the test, digit spans increase, ranging from two to eight digits (McGrew & Woodcock, 2001).

WASI Matrix Reasoning

The Matrix Reasoning subtest of the WASI is designed to measure nonverbal problem-solving or induction (Wechsler, 1999). This assessment requires examinees to view visual displays of matrices from which a section is missing and to use pattern completion, classification, analogy, and serial reasoning to induct the rule in the matrix and predict the next item in the sequence. Examinees complete the matrix using one of five possible response choices from a multiple choice array beneath the matrix prompt. Responses are identified verbally or with pointing (Wechsler, 1999).

WJ III Concept Formation

The Concept Formation subtest of the WJ-III (Test of Cognitive Abilities; Woodcock et al., 2001) consists of 40 items, assessing fluid intelligence and induction. On each item, students are shown illustrations which demonstrate instances and non-instances of a concept and are asked to identify the rules for concepts by inducting or inferring the rules (McGrew & Woodcock, 2001).

Design

The full mathematics assessment battery involved 11 measures total, and therefore, the mathematics assessments also were delivered using a planned missing design such that not all measures were administered to the random subset of children selected to receive the full battery every year of the study (for more information on planned missing designs, see for example Graham, Hofer, & MacKinnon, 1996). Because of the planned missingness inherent in this design, cohorts which have unavailable data on certain measures are assumed to have data that are missing completely at random, or MCAR.

Results

Planned analyses were executed in two phases of model testing. Phase one began by examining measurement models for arithmetic measures using confirmatory factor analysis with maximum likelihood estimation in MPlus 7 (Muthén & Muthén, 2012). Next measurement models for language and executive attention were examined using confirmatory factor analysis with maximum likelihood estimation in MPlus 7 (Muthén & Muthén, 2012). Phase two examined full measurement models, incorporating all constructs of interest (mathematics, language, and executive attention as outlined in the introduction). Missing data were estimated using full information maximum likelihood estimation (see for example Enders & Bandalos, 2001) in MPlus 7 (Muthén & Muthén, 2012). Note that because hypothesized model testing was extensive and included examination of 11 models, full model results are presented only for a select few of the tested models. The model results presented in text are highlighted because of their relevance to the current study’s overall conclusions about the structure of arithmetic cognition, including possible formatting effects and domain specificity. However, full model testing results, including standardized and unstandardized factor loadings and intercepts as well as indicator residuals and corresponding commonalities, are available in the supplementary materials for this article.

Phase 1: Measurement Models for Arithmetic, Language, and Executive Attention

This phase of model testing began with an examination of the arithmetic portions of measurement for each of the four theories considered in this study. Figure 1 displays diagrams for each model tested, global fit statistics (exact and approximate), and completely standardized indicator factor loadings. The abstract semantic representations measurement model tested the extent to which the 11 mathematics indicators measure a unitary, underlying, common form of mental representation upon which all factors of numeric processing operate, in predicting mathematics outcomes. The seemingly-modular encoding complex model tested the extent to which 11 arithmetic indicators measure a unitary, underlying, encoding complex factor, which appears to be modular with practice. It should be noted that this factor is being called “seemingly-modular encoding complex” here, but in actuality is the same measurement model as the abstract semantic representations measurement model because from a measurement standpoint, the same factor structure can be used to represent these hypotheses (though the implications and interpretations of that factor structure would be conceptually distinct across the two theories). This limitation of the factor analytic framework is considered in more detail in the Discussion section.

Figure 1.

Summary of Phase 1 Testing. The highlighted Triple Code Theory model represented the best fitting model of arithmetic measurement for this phase of testing.

The Triple Code Theory model of arithmetic tested the extent to which arithmetic behavioral outcomes could be explained by three, latent factors with format and problem demand specific responsibilities in numeric processing, a visual Arabic factor (indicated by 6 mathematics measures), an auditory verbal factor (indicated by 3 mathematics measures), and an analog magnitude factor (indicated by 2 mathematics measures). The Exact versus Approximate Calculations Theory tested the extent to which arithmetic behavioral outcomes could be explained by two, latent factors, an analog magnitude factor (indicated by 2 mathematics measures), and an auditory verbal factor (indicated by 9 mathematics measures). Of these models, the Triple Code Theory model of arithmetic was an approximate good fit for the data, while the other three models of arithmetic measurement were not. These results support Triple Code Theory’s specification that three, separate but mutually informed, format-specific factors predict arithmetic cognition outcomes.

Measurement models for language and executive attention also were examined during this phase of model testing. The language measurement model tested the extent to which three indicators (vocabulary, listening comprehension, and grammatical closures) measure a unitary, latent language ability. With three observed indicators, this latent language ability factor model is just-identified (i.e., has zero degrees of freedom), meaning that tests of global fit such as the Chi-square test of model fit, the root mean squared error of approximation (RMSEA), or the comparative fit index (CFI) are trivial (Brown, 2006). Though global fit could not be examined for this model, factor loadings indicated that these three indicators were reasonable measures of the same underlying dimension.

The executive attention measurement model tested the extent to which five indicators measure a unitary, underlying, executive attention ability which was hypothesized to be indicated by a measure of attention and inhibition (the SWAN teacher survey), two measures of verbal working memory (the WJ-III Numbers Reversed and the WMTB-C Listening Recall subtests), and two measures of fluid intelligence and inductive reasoning (the WASI Matrix Reasoning and the WJ-III Concept Formation subtests). Though this model was an approximate good fit for the data, all indicators in this model demonstrated relatively high residuals. The executive attention model, though adequate for the purposes of the current study, evidenced issues of fit that could be interpreted to mean that important complexity in this construct was not being modeled with a unitary conceptualization.

These results were not surprising given that theoretically, executive attention is a construct that represents hierarchical overlap between the three separable abilities of working memory, fluid intelligence, and attention/inhibition. Their covariance represented coordination and joint contributions to sustained attention and goal maintenance during problem-solving. As the current study was focused on their overlap in predicting arithmetic performances across various formats, and because the model was an approximate good fit for the data, this model of executive attention was ultimately retained for further testing.

Phase 2: Full Measurement Models for Each Theory

The next phase of model testing examined each of the four theories of arithmetic cognition with the inclusion of language and executive attention abilities in full measurement models. Figure 2 displays diagrams for each model tested, global fit statistics (exact and approximate), and completely standardized indicator factor loadings. Each model is briefly presented in the sections that follow.

Figure 2.

Summary of Phase 2 Testing. The highlighted Encoding Complex Theory model represented the best fitting model of arithmetic measurement for this phase of testing.

Abstract Code model

The full measurement model of Abstract Code Theory was represented with a one factor model of abstract semantic representation, which at a minimum, was allowed to correlate with other cognitive domains (e.g., language, executive attention). Global fit statistics indicated that this factor model was not an approximate good fit for the data, (χ² (141) = 1204.93, p < .001, RMSEA = .08, CFI = .87). Completely standardized factor loadings ranged from .49 to .78; indicator residual variances ranged from .39 to .77; and model R² ranged from .24 to .61. Although the correlation between language and abstract semantic representations was moderate, r=.56, the correlations between executive attention and abstract semantic representations and executive attention and language were quite high (r=.81 and r=.82 respectively). Although both the abstract semantic representations and executive attention measurement model results suggest that both of these factors are contributing to the model misfit for the Abstract Code Theory full measurement model, the patterns of factor correlation would suggest that the relationships between executive attention and other constructs in the model were also important sources of model misspecification.

Encoding Complex model

The full measurement model of Encoding Complex Theory allowed language and executive attention to directly predict arithmetic outcomes along with the seemingly modular encoding complex for arithmetic. Executive attention was allowed to predict arithmetic behavioral outcomes across various formats and problem demands; however, language was allowed to predict arithmetic behavioral outcomes for language-formatted problems. Global fit statistics indicated that this factor model was an approximate good fit for the data, (χ² (128) = 465.40, p < .001, RMSEA = .05, CFI = .96). Completely standardized factor loadings ranged from .05 (non-significant) to .74; indicator residual variances ranged from .24 to .77; and model R² ranged from .23 to .76. As mentioned in the executive attention measurement model results, the residuals for this factor were high. However, executive attention was a significant and salient predictor of all arithmetic outcomes, and language was a significant predictor of WJ Applied Problems and Single Digit Story Problems, though these loadings were quite low.

Allowing for direct prediction of arithmetic outcomes by executive attention and language left little unique predictive power for the seemingly modular encoding complex; however, each arithmetic outcome was still significantly predicted by something other than executive attention and language (represented here by the seemingly modular encoding complex). Three outcomes in particular (Basic Facts Addition, Basic Facts Subtraction, and Computational Fluency, all of which were formatted with Arabic numerals and involved relatively small problem sizes) had high encoding complex factor loadings despite the addition of executive attention as a predictor.

Because executive attention was a direct predictor of arithmetic outcomes in this model, the correlation between executive attention and the seemingly modular encoding complex was restricted to zero for the purpose of model specification. The correlation between executive attention and language was large and positive, r=.78; however, the correlation between language and the encoding complex was small and negative, r=−.12. These results indicate that although language is a small but significant predictor of outcomes in language-formatted problems, it is not a predictor of outcomes in Arabic numeral formatted problems or estimation problems.

Triple Code model

The full measurement model for Triple Code Theory allowed a latent language factor and an executive attention factor to correlate with the auditory verbal, visual, and analog magnitude factors of Triple Code Theory. Global fit statistics indicated that this factor model was an approximate good fit for the data, (χ² (134) = 501.35, p < .001, RMSEA = .05, CFI = .95). Completely standardized factor loadings ranged from .49 to .92; indicator residual variances ranged from .16 to .76; and model R² ranged from .24 to .84. As in the Triple Code Theory arithmetic measurement model, the arithmetic portion of this full model was very strong. Completely standardized factor loadings ranged from .54 to .92, and factor correlations for this portion of the model ranged from r=.68 to r=.76, indicating that each of Triple Code Theory’s arithmetic cognition factors were separable but highly related. Again the executive attention measurement model results demonstrated high residuals. However, executive attention factor loadings indicated that the selected outcomes were all significant and salient indicators of this factor. The executive attention factor correlated highly with all other factors in the Triple Code Theory model.

The addition of executive attention raised some structural questions for the arithmetic portion of the Triple Code Theory model. Specifically, the relationship between executive attention and the auditory verbal factor was nearly at singularity, r=.94, and the relationship between language and the auditory verbal factor was also quite high, r=.78. Taken together, these results indicate that (1) problem formatting should be explicitly accounted for in modeling arithmetic outcomes, (2) executive attention and language may both play important roles in facilitating arithmetic cognition across various problem formats, but (3) language-formatted items in particular may be predicted by domains other than a specialized quantitative domain.

Exact versus approximate model

The full measurement model of Exact versus Approximate Calculations Theory allowed a latent language factor and an executive attention factor to correlate with the both the analogical magnitude representation factor (predicting tasks requiring approximate calculations) and an auditory verbal factor (predicting tasks requiring exact calculations). Global fit statistics indicated that this factor model was not an approximate good fit for the data, (χ² (138) = 1076.75, p < .001, RMSEA = .07, CFI = .88). Completely standardized factor loadings ranged from .48 to .91; indicator residual variances ranged from .17 to .77; and model R² ranged from .23 to .83. Although both the exact versus approximate calculations and executive attention measurement model results suggest that all of these factors are contributing to the model misfit for the Exact Versus Approximate Calculations full measurement model, the patterns of factor correlation would suggest that the relationships between executive attention and other constructs in the model may also be important sources of model misspecification.

Executive attention correlated significantly and strongly with all other factors in the model, indicating that executive systems of control may indeed play a role in facilitating both exact and approximate calculations. Language, however, correlated only moderately with the auditory verbal and analog magnitude factors, but it correlated highly with executive attention. Taken together, this pattern of correlations would seem to suggest that language is separable from traits predicting arithmetic outcomes across exact and approximate problem demands, which are in turn both highly related and separate from each other (auditory verbal and analog magnitude factors correlated at r=.76).

Summary of Model Testing Results

Results from the arithmetic only measurement models indicated that the Triple Code Theory model of arithmetic was the best fitting model; however, the Triple Code Theory full measurement model displayed some structural problems, namely a correlation between executive attention and the auditory verbal factor that was near singularity and very high correlations between executive attention and the other factors of arithmetic in the model.

Conversely, results from the Encoding Complex full measurement model indicated that this model of arithmetic (and its relationships with other cognitive domains) was the best fitting model; however, the architecture for arithmetic in the Encoding Complex Theory model was unidimensional, and results from the arithmetic only measurement models indicated that a unidimensional arithmetic was not a good fit for the data.

Given that (1) a three-factor model of arithmetic presented by Triple Code Theory was an excellent fit for the data and (2) a direct prediction of executive attention and language on math outcomes presented by Encoding Complex Theory was an excellent fit for the data, results supported both Encoding Complex Theory and Triple Code Theory. Thus, a final, unplanned, post-hoc model, incorporating key measurement hypotheses of each theory, was examined.

Post-hoc Testing: Hybrid Full Measurement Model

The post-hoc model represents the three-factor arithmetic (only) portion of Triple Code Theory with Encoding Complex Theory’s specification that executive attention could be a direct predictor of all arithmetic outcomes and that language could be a direct predictor of outcomes on language-formatted arithmetic problems. A visual Arabic factor processes digital input and output as well as multi-digit operations. An auditory verbal factor processes simple mathematical facts, language-based input and output, and language-based memory for numbers. An analog magnitude factor processes semantic information for number and is responsible for performing comparison, estimation, approximate calculation, and subitizing tasks across various formats of input and output. Transcoding allows for these factors to inform one another directly during numeric processing tasks. The post-hoc hybrid model represents each of these factors as a latent factor and transcoding as the correlation between these factors.

Global fit statistics indicated that this factor model was an approximate excellent fit for the data, (χ² (124) = 327.82, p < .001, RMSEA = .04, CFI = .97). Across outcomes, completely standardized factor loadings ranged from −.003 (non-significant) to .74; indicator residual variances ranged from .22 to .76; and model R² ranged from .24 to .78. As mentioned in the executive attention measurement model results, the residuals for this factor were high and among the highest in the model. Table 3 presents completely standardized results for the Hybrid full measurement model. Figure 3 displays a model schematic with completely standardized factor loadings, indicator residuals, and latent factor correlations.

Table 3.

Post Hoc Hybrid Full Measurement Model Completely Standardized CFA Results

Indicator	Intercepts (SE)	Factor Loadings (SE) by Factor					Residual Variance	R2
		Auditory Verbal	Visual Ab. Nm.	Analog Mag.	Language	Exec. Attn.
Arithmetic Measures
App. Prb.	6.71 (.14)	.32 (.05)			.04 (.06)NS	.67 (.06)	.40	.60
Story Prb.	2.89 (.06)	.21 (.04)			.09 (.06)NS	.65 (.06)	.43	.57
VU Story Prb.	1.33 (.07)	.28 (.08)			−.003 (.13)NS	.64 (.12)	.52	.49
Basic Add.	2.39 (.05)		.67 (.02)			.42 (.03)	.37	.63
Basic Sub.	1.39 (.04)		.61 (.02)			.46 (.03)	.42	.58
WRAT Arth.	9.42 (.21)		.38 (.03)			.62 (.02)	.47	.53
Comp Fluency	1.99 (.05)		.70 (.02)			.52 (.03)	.23	.77
DD Add.	4.04 (.16)		.24 (.06)			.48 (.04)	.71	.29
DD Sub.	1.98 (.09)		.18 (.05)			.61 (.04)	.60	.40
DD Add. Est.	1.21 (.06)			.53 (.06)		.71 (.03)	.22	.78
DD Sub. Est.	1.09 (.06)			.60 (.06)		.64 (.04)	.23	.77
Language Measures
Voc	4.24 (.09)				.74 (.02)		.45	.55
List	4.88 (.10)				.71 (.02)		.50	.50
Gram	2.82 (.06)				.72 (.02)		.49	.51
Exec. Attn. Measures
Att.	3.20 (.07)					.59 (.02)	.65	.35
Recall	2.78 (.06)					.49 (.02)	.76	.24
Num. Rev.	3.28 (.07)					.49 (.02)	.76	.24
Matrix Reason.	2.41 (.05)					.57 (.02)	.68	.32
Con. Form.	2.20 (.05)					.67 (.02)	.55	.45

Figure 3.

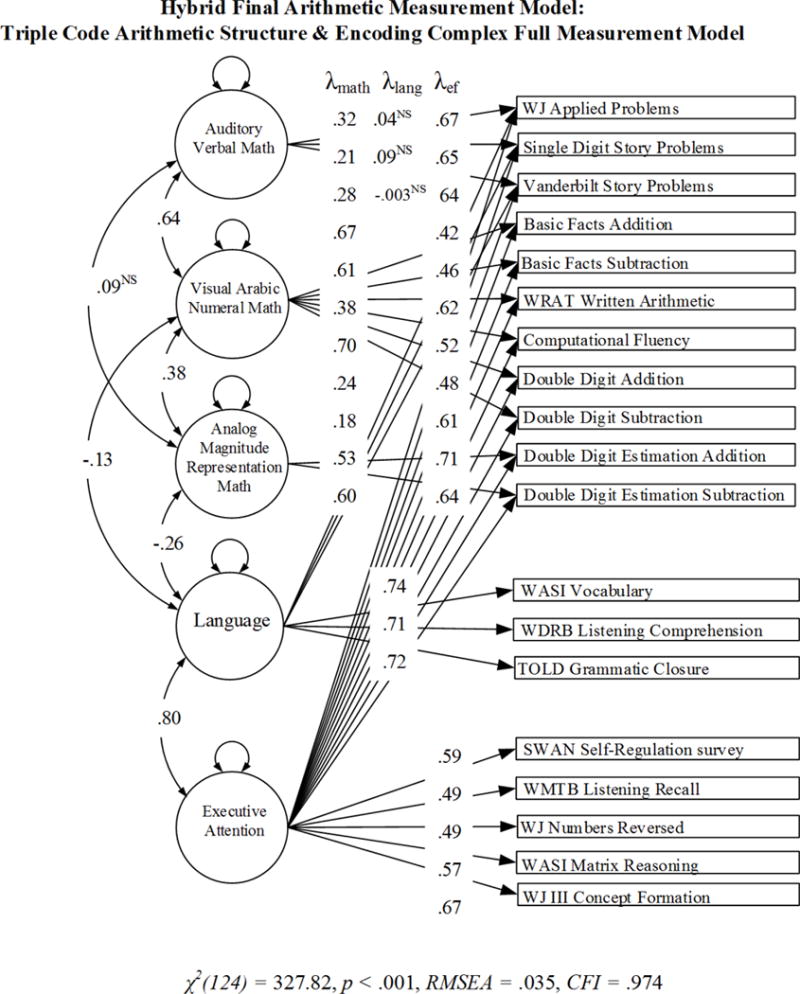
Hybrid final arithmetic measurement model: Triple code arithmetic structure and encoding complex measurement model.

More specifically, for the arithmetic outcomes across the three Triple Code factors, completely standardized factor loadings ranged from .18 to .70. All of these loadings were significant, but only the factor loadings for the following five arithmetic outcomes were salient: Basic Facts Addition, Basic Facts Subtraction, and Computational Fluency (all Arabic numeral formatted and all involving relatively small problem sizes), as well as Double Digit Estimation Addition and Double Digit Estimation Subtraction (both involving estimation). For the language outcomes, completely standardized factor loadings were all significant and salient, ranging from .71 to .74; however, none of the language-formatted arithmetic outcomes were significant indicators of language, meaning that the auditory verbal factor is distinct from language. For the executive attention outcomes, completely standardized factor loadings were all significant and salient, ranging from .49 to .67. The arithmetic outcomes were all significantly and saliently indicated by the executive attention factor. Completely standardized factor loadings ranged from .42 to .70, and they were lowest for the three aforementioned Arabic numeral formatted / small problem size outcomes.

Allowing for direct prediction of arithmetic outcomes by executive attention and language left little unique predictive power for the three Triple Code Theory factors of arithmetic; however, all of the arithmetic outcomes were still significantly predicted by its corresponding Triple Code Theory factor. This pattern of results indicates that something other than executive attention and language (represented here by the visual Arabic number form factor, auditory verbal factor, and analog magnitude factor) was predicting performance for each of these problem formats or analogical magnitude demands. The auditory verbal factor loadings were all particularly low with executive attention in the model, which would seem to indicate that language-formatted problems, in particular, are largely executive attention tasks.

Because executive attention was a direct predictor of arithmetic outcomes in this model, the correlations between executive attention and the visual Arabic number form factor, the auditory verbal factor, and the analog magnitude factor were restricted to zero for the purpose of model specification. Similarly, the correlation between language and the auditory verbal factor was also restricted to zero. The correlation between executive attention and language was large and positive, r=.80; however, the correlations between language and both the visual Arabic number form and analog magnitude factors were small and negative, r=−.13 and r=−.26 respectively. Among the Triple Code Theory factors, auditory verbal arithmetic and visual Arabic number form arithmetic were moderately and positively related, r=.64, and analog magnitude arithmetic and visual Arabic number form arithmetic were slightly and positively related, r=.38. However, the auditory verbal and analog magnitude factors were not significantly related.

This model was an approximate good fit for the data, and Chi-square difference testing indicated that this model significantly improved fit as compared to all other full measurement models tested (see Table 4). This model represented a synthesis of hypotheses from two theories of arithmetic cognition that were supported by patterns of results from all model testing, and as such, this model was ultimately retained as the most parsimonious presentation of results.

Table 4.

Summary of Model Testing Results

Initial Measurement Models	χ2	df	p	CFI	RMSEA	Note
Abstract Code Arithmetic	555.19	36	<.001	.88	.11
Encoding Complex Arithmetic	555.19	36	<.001	.88	.11	Structurally Identical to Abstract Code Arithmetic
Triple Code Arithmetic	214.66	33	<.001	.96	.07
Exact V. Approximate Arithmetic	421.24	35	<.001	.91	.09
Language	0.00	0	N/A	1.00	.00	Model is just-identified
Executive Attention	31.57	5	<.001	.97	.06
Full Measurement Models	χ2	df	p	CFI	RMSEA	Note
Abstract Code Theory	1204.93	141	<.001	.87	.08	Δχ2 (17) = 877.11, p < .001
Encoding Complex Theory	465.40	128	<.001	.96	.05	Δχ2 (4) = 137.58, p < .001
Triple Code Theory	501.35	134	<.001	.95	.05	Δχ2 (10) = 173.53, p < .001
Exact V. Approximate Theory	1076.75	138	<.001	.88	.08	Δχ2 (14) = 748.93, p < .001
Post Hoc Hybrid	327.82	124	<.001	.97	.04	Baseline Model for χ2 Difference Testing

Discussion

The purpose of this study was to evaluate the effects of item formatting and to explore the possibility that language and executive systems of control contribute to solving various formats of arithmetic problems. This research was approached using multitrait, multimethod data, and confirmatory factor analysis. Four leading theories of arithmetic cognition were used to guide measurement hypotheses about the (1) structure of mathematics abilities involved in arithmetic cognition, (2) roles of symbolic problem formatting (language versus Arabic numeral formats) and calculation demands (exact versus approximate) in predicting arithmetic outcomes, and (3) possible contributions of language and executive attention in predicting arithmetic outcomes.

Summary of Major Findings

As predicted by Triple Code Theory, the structure of arithmetic cognition was best supported by several latent factors of quantitative ability with specialization for particular formats and problem demands. Put in terms of psychometric theory, similarly formatted problems displayed common method variance that was explained by unique factors of arithmetic ability. An auditory verbal factor was largely responsible for problems that were language-formatted. A visual Arabic number form factor was largely responsible for problems that were formatted with Arabic numerals. An analog magnitude factor was largely responsible for problems that involved estimation across formats. This three-factor architecture of arithmetic cognition was valuable for explaining arithmetic outcomes across the models tested in the current study.

Abstract Code Theory’s stipulation that abstract semantic codes predict arithmetic outcomes across various formats of problem was not supported, nor was a specification of Encoding Complex Theory in which a unitary, seemingly modular encoding complex predicts arithmetic outcomes across formats. Exact Versus Approximate Calculations Theory’s specification that exact and approximate problem demands would be predicted by separable cognitive architectures was somewhat supported. Among calculation demands, exact and approximate calculations were distinct but related; however, within exact problems, those problems with language formatting were separable from problems with Arabic numeral formatting.

As predicted by Encoding Complex Theory, executive attention was a major predictor of all arithmetic outcomes. The inclusion of executive attention as a direct predictor of arithmetic outcomes overwhelmed the arithmetic-only models of cognition. Little variance remained for factors of arithmetic cognition to explain; however, each retained some unique predictive value.

Interestingly, executive attention left no predictive value for language on language-formatted problems. Language-formatted problems were explained mostly by executive attention and somewhat by the auditory verbal factor of arithmetic, and language evidenced a negative relationship with Arabic numeral formatted problems and estimation problems. This outcome suggested that language was not directly contributing to arithmetic cognition. However, the lingering, large correlation between language and executive attention suggested that language had some role to play in arithmetic cognition. Taken together, these findings raise questions about the possibility that language may play a facilitative role in reasoning, particularly for language-formatted problems.

Explaining the relationship between language ability and executive attention in a theoretical model of arithmetic cognition will be a challenge for future research. Because language was not positively associated with factors of arithmetic, because language was not a direct predictor of language-formatted arithmetic, and because executive attention was a direct predictor of arithmetic outcomes across factors of cognition, this study suggests that language may play an indirect role in helping executive systems of control to predict arithmetic outcomes.

Several theories have implicated language as a facilitator of systems of executive control. Most often, this relationship has been conceptualized in terms of the construct of internal speech, also called self-directed speech or private speech. Internal speech is not directed socially toward communication partners other than the self, for the purpose of facilitating cognition and behavioral control (see for example, Berk, 1999). In Baddeley’s (see for example Baddeley & Logie, 1999; Baddeley, 1992, 2000) model of working memory, internal speech may play a critical role in helping to maintain mental representations of stimuli via an articulatory rehearsal system. In Barkley’s (1997) model of self-regulation, internal speech helps to regulate inhibitory control by guiding rule-governed behaviors and self-evaluation during problem-solving. Similarly, in Zelazo’s (see for example Zelazo & Frye, 1998) model of problem-solving, self-directed, internal speech plays a crucial role in problem-solving, particularly during planning, inhibition, and evaluation.

Measuring internal speech may require methods that use careful behavioral observation and self-reporting during and after the performance of problem-solving tasks (Berk, 1999). Though this was beyond the scope of the current study, future research should investigate the construct of internal speech as an indirect predictor of arithmetic problem-solving.

The addition of executive attention as a direct predictor of arithmetic outcomes not only impacted the relations between factors of arithmetic and language, but also executive attention impacted the relationships between the three factors of arithmetic cognition. Although the three factors of Triple Code Theory evidenced a pattern of strong, positive relationships when modeled in isolation, this was no longer true when executive attention was explicitly modeled. Problems involving exact calculations remained highly related across language formats (on the auditory verbal factor) and Arabic numeral formats (on the visual Arabic number form factor); however, the relationships of these factors with the analog magnitude factor changed when executive attention was included. With explicit modeling of executive attention in arithmetic outcomes, the visual Arabic number form factor was only slightly related to the analog magnitude factor, and the auditory verbal factor was no longer related to the analog magnitude factor.

These correlations represented Triple Code Theory’s specification of transcoding, or direct communication between factors of arithmetic cognition during numeric processing, and it is this notion of transcoding that allows Triple Code Theory’s arithmetic factors to avoid necessarily communicating via abstract semantic codes. Though direct communication between Triple Code Theory’s factors is assumed during numeric processing, only the analog magnitude factor is hypothesized to contain semantic information about number. These findings suggest that when the role of executive attention in arithmetic cognition is directly modeled, transcoding with the analog magnitude factor may be minimal or non-existent. Perhaps numeric processing for problems involving language-formats, Arabic numeral formats, multi-digit operations, and language-based memory for numbers relies more heavily on temporarily maintained mental representations of problems in a coordinated system of executive attention than it does on semantic information about number.

Implications for Measuring Arithmetic

The findings from the current study raise important questions about the inferences that can confidently be made from various formats of arithmetic tests. The assumption that all assessments that involve arithmetic are inherently measures of arithmetic ability, and only arithmetic ability, may not be warranted. Features of problem formatting and problem demands may influence the extent to which measurement instruments capture arithmetic ability, and even when measures appear to reliably and validly capture arithmetic skill, they may also be measures of executive systems of control.

When attempting to measure arithmetic cognition, measurement formatting and problem demands are important, but all of the arithmetic outcomes in the current study were largely predicted by domain general capacities in executive attention. Despite the overwhelming effect of executive attention, several measures of arithmetic did retain unique predictive value that was salient. These measures either involved Arabic numeral formatting and small problem sizes or estimation problem demands. Such formats and problem demands may be promising methods of assessing basic conceptual competence because these types of problems remained strong predictors of arithmetic cognition despite the contributions of executive attention.

Conversely, language-formatted arithmetic items may yield results with dubious inferential value for assessing some “pure” construct of arithmetic cognition. Language-formatted items retained little unique predictive value once executive attention was added as a direct predictor of arithmetic outcomes, suggesting that language-formatted items may be mostly measures of executive attention and, by extension, the role of language ability in facilitating linguistic problem-solving. Thus, language-formatted “arithmetic items,” may more accurately be labeled “linguistically formatted problem-solving tasks that involve some arithmetic”.

Given prior research findings and the fact that word problems are intentionally designed to reflect real-world problem-solving experiences, it is not surprising that word problems exhibited these patterns of multidimensionality (indicated by both executive attention and arithmetic ability); however, if they are multidimensional measures of both executive attention and arithmetic abilities, they should be interpreted as such as opposed to being collapsed into interpretations of mathematical ability based on other problem formats and demands. In other words, arithmetic word problems do not appear to be measures of a “pure” arithmetic ability; they also largely appear to be measures of the ability to form and maintain mental representations of problems and problem-solving goals robust to distractions during problem-solving activities. For interpretations of examinee performances on word problems to be accurate and valid, the multidimensional nature of these problems should not be ignored, and the elements of sustained and coordinated attention that they require (i.e., not just conceptual knowledge, but also strategic and procedural competence) should be acknowledged.

Limitations and Future Directions

Adapting theories toward specific measurement hypotheses

The specificity required by the factor analytic framework is a limitation of the current project. Factor models represent abilities or commonalities between various measures, but they do not represent processes unless a process is specifically being modeled (Carroll, 1993). Such a model would necessitate structural hypotheses among traits, with the specific allowance for traits to influence one another in the time-scale specified by the process (e.g., over seconds, minutes, days, years). Arithmetic cognition, executive attention, and self-directed speech are processes. Inferences in the current study are limited to traits, but the relationships among traits at a single time point can give important clues about underlying processes, and factor analysis can help to answer important questions about the properties of measurements.

It is important to note that these theories of arithmetic cognition were not specified with factor analysis methodologies in mind, and so, translation into factor analytic frameworks becomes difficult when theories of arithmetic cognition do not provide explicit measurement parameters. For example, “contributions” could be conceptualized as direct predictions of latent factors, correlations between latent factors, or perhaps residual error terms. Some specific aspects of each theory lend themselves to formulations with factor models, while other aspects were not necessarily testable with this method. For example, modeling Abstract Code Theory’s highly complex mechanism of numeric processing was beyond the scope of the current study. Measurement hypotheses in the current study were carefully constructed with the aim of striking a balance between faithfully representing theoretical postulates and holding the research to the methodological rigor demanded by factor analysis. Still, the measurement hypotheses for theories of arithmetic cognition are open to other interpretations. Future research should explore alternate measurement hypotheses with these theories of arithmetic cognition.

Adapting theories toward developmental hypotheses

The second limitation of the current project lies in the generalization of theory to a population at an earlier developmental stage. This project aimed to understand the arithmetic cognition of school-aged children and the facets of numerical cognition that may predict their development into skilled adults. Although some theories of arithmetic cognition make specifications about growth and the ways in which one might become a skilled adult, others do not. Invariance testing (testing the hypothesis that the same cognitive architecture specified for adults can be assumed for children) is implicit in the current project. However, extant neuroimaging research has indicated that quantitative cognition of children and adolescents may be qualitatively different from that of skilled adults (e.g., Cantlon et al., 2006). Future research should examine the development of arithmetic cognition in children, adolescents, and adults utilizing a longitudinal design and explicit testing of longitudinal measurement invariance. Indeed, the measurement findings of the current study may not generalize to adolescents, adults, or even children at earlier or later developmental stages than those included in the current study, and it would not be surprising to find age-related changes in the roles of language and executive attention in various arithmetic tasks. A line of developmental research with explicit focus on longitudinal measurement invariance should inform theoretical extensions of existing theories of arithmetic cognition, addressing hypotheses about the developmental continuum of quantitative cognition and its ideal measurement.

Generalizability of symbolic formatting

Another limitation of the current project is that it is exclusively focused on numeric processing with symbolically formatted measures of arithmetic (e.g., language or Arabic numeral formats) and does not include non-symbolically formatted measures of arithmetic (e.g., dot arrays). Although the arithmetic that children will encounter in most formalized assessment settings is symbolically formatted, developmental research on the quantitative domain is focused largely on children’s performance with non-symbolically formatted measures (e.g., Feigenson, Carey, & Hauser, 2002; Starkey & Cooper, 1980; Wynn, 1992; Xu & Spelke, 2000). Including non-symbolically formatted measures of arithmetic in measurement batteries will be essential for establishing common scaling and examining developmental continuity in the quantitative domain, and may very well provide a more “pure” measure of numerical cognition than symbolic formats. Future research should explore arithmetic cognition, formatting effects, and domain specificity with the inclusion of non-symbolically formatted arithmetic items in the measurement battery.

Similarly, many other aspects of item modality (e.g., timed/untimed, problem size, number of steps required to solve a problem) as well as item content (e.g., arithmetic, algebraic reasoning, geometry) are often controlled or varied in order to approximate item difficulty across various types of mathematics tasks. The purpose of the current study was to examine symbolically formatted arithmetic items with regard to theoretical specifications of the cognitive abilities involved in solving them; however, future research should examine other aspects of item modality and their effect(s) on the measurement of cognitive abilities across a variety of tasks involving differing mathematical content.

Overlap in features of item modality

Although children were instructed to use estimation to solve the double digit estimation problems, and although these items were speeded in order to encourage the use of the most efficient strategy for solution, it should be noted that these problems could have been solved by using the strategy of calculating the exact answer and then rounding. In other words, depending upon the strategies employed by children during numeric processing, the double digit estimation problems may have been solved using a combination exact calculations and approximation. Unfortunately, the strategy usage employed by children during numeric processing was beyond the scope of the current study. It is indeed probable that certain formats may be better suited for eliciting certain problem-solving strategies (e.g., nonsymbolic formats may be better suited to eliciting approximate calculation strategies; see for example Siegler & Shrager, 1984).

Similarly, the WJ Applied Problems subtest items are language-formatted problems designed to measure children’s knowledge of and ability to solve everyday problems (e.g., telling time). These problems served different roles in different models in the current study. They were alternately loaded onto unitary factors (abstract semantic representations or a seemingly modular encoding complex), an exact calculations factor, and an auditory verbal factor. Their treatment as exact calculation items was perhaps the most questionable. Problems on the WJ Applied Problems subtest require children to produce exact answers, but they do not necessarily require children to perform exact calculations. Of the 39 problems designed for examinees who are not above average adults or who are below college-level in education, most require knowledge of numbers and operations; however, 12 items (approximately 31%) involve the production of exact answers requiring specific, applied knowledge of telling time, recognizing American money, or reading a thermometer. Thus, unfortunately, the WJ Applied Problems subtest represented a mixture of traditional word problems and applied problems. Though this subtest was consistently significant and salient as an indicator in the models tested for the current study, generalizing of the WJ Applied Problems subtest as a test of traditional word problems requiring exact calculations is limited by the extent to which it includes applied problems.

In both the case of the double digit estimation problems and the WJ Applied Problems, issues of item-formatting overlapped with issues of item calculation demands in ways that may have led to model misfit. This caveat is particularly relevant to the exact versus approximate calculations model. This research found some support for a central tenet of exact versus approximate calculations theory; problems requiring the production of exact solutions appeared to be separable from problems requiring the production of approximate solutions. Symbolic formatting was also an important contributor to the dimensionality of arithmetic measures. However, examination of the possibility that item features may interact to predict examinee responses was beyond the scope of the current study. Future research should examine the relationship between item modality and the measurement of arithmetic cognition with explicit control in the design of item features (e.g., formatting, calculation demands), observation of children’s strategy usage during numeric problem-solving, and allowances for the possibility that features of item modality may interact to predict children’s responses.

Measuring and modeling executive attention

For the purposes of the current study, executive attention was indicated by a combination of measures of working memory, inhibition and attention, and fluid intelligence (inductive reasoning or problem-solving). These measures were combined in an a priori specified, latent factor model with the aims of (1) synthesizing important facets of executive attention, while (2) explicitly accounting for measurement error. However, it should be noted that across all of the full measurement models and in the executive attention-only measurement model, the executive attention factor evidenced some problems.

Although this unitary executive attention factor displayed good model fit in most ways, patterns of residual variance indicated that much of the complexity of these indicators was not accounted for by a single factor. The single factor called executive attention likely represented a hierarchical construct, which would help to explain the variance unaccounted for in fluid intelligence, working memory, and attention/inhibition indicators. For the purposes of the current study, executive attention was interpreted as an overall relationship between these key systems of control in coordinating problem-solving activity; however, future research should investigate the extent to which fluid intelligence, working memory, and attention/inhibition may make shared and unique contributions to arithmetic (e.g., a bi-factor model).

Summary and Conclusions

Because this study aimed to examine the construct of arithmetic cognition by examining the formatting and dimensionality of arithmetic measures, a factor analytic framework in conjunction with a multi-trait, multi-method approach was appropriate. The factor analytic framework requires explicit statements of hypotheses about model parameters, which can reveal areas of theoretical misspecification, implications of measurement techniques for construct-level inferences, as well as areas of theoretical ambiguity. Though the specificity required by a factor analytic framework can be challenging, this approach is a promising method for evaluation of the construct of arithmetic cognition and its potential measures.

Four leading theories of arithmetic cognition were used to guide measurement hypotheses in the current study. Each of the theories was designed to explain the arithmetic cognition of skilled adults. This study sought to understand the arithmetic cognition of developing children who have some formal education and exposure to arithmetic, but are still actively engaged in mathematics education. Describing a developmental continuum that links the arithmetic cognition of developing children to the cognition of skilled adults will be a crucial next step for researchers and theoreticians.

In general, results from this study provided support for both Triple Code Theory and Encoding Complex Theory, and to some extent, Exact Versus Approximate Calculations Theory was also supported. As predicted by Triple Code Theory, arithmetic outcomes with language formatting, Arabic numeral formatting, and estimation demands across formats were related but distinct from one another. This finding is also compatible with Encoding Complex Theory’s stipulation that formatting effects exist for arithmetic cognition. The large and enduring relationship between problems that required exact calculations (across formats) also provides support for Exact Versus Approximate Calculations Theory’s stipulation that exact calculation problems may draw from the same cognitive processes.

Executive attention was a direct predictor of all arithmetic outcomes. This finding is compatible with Triple Code Theory’s stipulation that other cognitive domains, in particular domains responsible for coordinating visuospatial attention, may contribute to arithmetic cognition. Executive attention is complex, and modeling that complexity was beyond the scope of the current study; however, the facets of working memory, inhibition and attention, and induction and reasoning ability shared a unitary predictive power in explaining arithmetic.

Given the strong and enduring relationship between executive attention and language ability, and the fact that language ability was not a direct predictor of arithmetic performances, this synthesized executive attention may have been facilitated by language ability in a collaborative relationship that was beyond the scope of the current study. Future research should investigate the extent to which internal or self-directed speech may facilitate executive attention and indirectly predict performance on arithmetic problem-solving tasks. This pattern of results may be particularly pertinent for language-formatted arithmetic items.

Results from the current study support the growing body of literature indicating that caution should be used in interpreting the results from language-formatted arithmetic items (e.g., Abedi & Lord, 2001; Martiniello, 2009; Rhodes, Branum-Martin, Morris, Romski, & Sevcik, 2015). These items may have little construct validity as pure measures of mathematics ability, but rather appear to be largely executive attention tasks which also involved some arithmetic ability. Though problems formatted with Arabic numerals or involving approximate calculations were also multidimensional measures of both executive attention and arithmetic abilities, these measures retained far more predictive power for measuring arithmetic abilities than language-formatted problems. When executive attention was allowed to directly predict arithmetic outcomes on language-formatted problems, arithmetic abilities had either no significant or no salient predictive power. Thus, difficulties with linguistically-formatted arithmetic problems likely largely indicate problems with domain general problem solving capacities, and to a lesser extent may also indicate some domain specific arithmetic ability. Inferences about “pure” mathematical ability should be made with caution when they are based on results from language-formatted testing instruments, and this caution is particularly relevant to national achievement assessments that utilize language-formatting in their assessment of mathematical competence.

The notion of “pure” mathematical abilities raises a fundamental, ontological question for researchers and practitioners who are designing, administering, and interpreting educational assessments of basic mathematical competence: What is meant by “pure mathematical ability,” and is it possible to design a symbolically-formatted, educational assessment of the most basic, arithmetic skills involved in such a construct? The current study found evidence that various types of symbolically-formatted arithmetic problems (1) demonstrated unique clusters of quantitative skills depending upon their designs of problem formats and calculation demands, and (2) also measured domain general executive attention ability, particularly when problems were linguistically formatted. Taken together, these findings imply that (1) different types of symbolically-formatted arithmetic problems measure different constellations of skills, and (2) symbolic formats may not be appropriate for measuring some construct that is purely mathematical.

Thus, measures of arithmetic should be designed, selected, and interpreted differently with respect to their formats and problem demands. For example, if one is interested in obtaining a strong measure of conceptual number knowledge, Arabic numeral formats and problems with approximate calculation demands may be more desirable than language-formatted problems. Students experiencing difficulty with Arabic numeral formats or approximate calculation problems may be struggling with understanding concepts like place-value (i.e., the visuo-spatial strings of digits represented by the visual Arabic number form) or numerosity (i.e., the semantic understanding of a number’s cardinality and ordinality represented by the analog magnitude form), and to a lesser extent, may also be struggling with executive attention required during problem-solving. If one is interested in understanding the roles that strategic and procedural competence play in the realm of arithmetic problem-solving, word problems may provide a more desirable measure of arithmetic. Students experiencing difficulty with word problems are likely struggling with understanding concepts like selecting appropriate strategies for problem-solving and executing the procedural steps of the strategies they select, and to a lesser extent may also be struggling with concepts like interpreting number words (i.e., the syntactic, phonological, and/or graphemic understanding of number represented by the auditory verbal word frame).

Regardless of the measurement technique selected for assessing arithmetic skill, researchers and practitioners should also be aware that language may be playing a crucial, indirect, and internal role in facilitating children’s mathematical problem-solving. The findings of the current study suggest that language ability is not a direct predictor of arithmetic performance for many students, but rather may help students to maintain attention and coordinate problem-solving procedures. More research is needed to determine the role that internal speech may play in arithmetic problem-solving; however, the strong and enduring relationship between language and executive attention in the current study suggests that targeting executive attention or helping children to moderate their internal speech during mathematical problem-solving may be promising avenues of intervention.

Educational Impact and Implications Statement.

Symbolic formats (e.g., Arabic numerals, spoken language, written language) are usually used for teaching and testing arithmetic ability in formal educational settings; however, research has suggested that different symbolic formats may lead to different sorts of arithmetic problem-solving. Using a large sample of elementary school-aged children, this study explored the possibility that the manner in which problems are conveyed during testing may be an important factor for understanding arithmetic cognition and achievement. Findings suggested that (1) different types of symbolically-formatted arithmetic problems measure different constellations of skills, and (2) symbolic formats may not be appropriate for measuring an ability that is purely mathematical. Executive attention was a significant and direct predictor of arithmetic performance across problem formats. Language ability was not a direct predictor of arithmetic performance, but rather appeared to facilitate executive attention, helping students maintain attention and coordinate problem-solving procedures.

These findings have important implications for the selection and interpretation of arithmetic assessments that are commonly used in educational settings. For example, students experiencing difficulty with word problems are likely struggling with understanding concepts like selecting appropriate strategies and executing the procedural steps of the strategies they select, and to a lesser extent may also be struggling with concepts like interpreting number words. Findings also suggest that targeting executive attention and/or language-facilitated executive attention (i.e., internal speech) during mathematical problem-solving may be promising avenues of intervention.