Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2017 Nov 15;28(24):3480–3488. doi: 10.1091/mbc.E17-05-0282

Membrane mechanics govern spatiotemporal heterogeneity of endocytic clathrin coat dynamics

N M Willy a,†, J P Ferguson a,†, S D Huber a, S P Heidotting a, E Aygün b, S A Wurm c, E Johnston-Halperin a, M G Poirier a,c, C Kural a,c,*
Editor: Alex Mogilnerd
PMCID: PMC5683759  PMID: 28904210

Cellular processes associated with spatiotemporal changes in membrane mechanics induce significant alterations in clathrin-mediated endocytosis dynamics. This phenomenon is also observed during morphological changes shaping embryo development.

Abstract

Dynamics of endocytic clathrin-coated structures can be remarkably divergent across different cell types, cells within the same culture, or even distinct surfaces of the same cell. The origin of this astounding heterogeneity remains to be elucidated. Here we show that cellular processes associated with changes in effective plasma membrane tension induce significant spatiotemporal alterations in endocytic clathrin coat dynamics. Spatiotemporal heterogeneity of clathrin coat dynamics is also observed during morphological changes taking place within developing multicellular organisms. These findings suggest that tension gradients can lead to patterning and differentiation of tissues through mechanoregulation of clathrin-mediated endocytosis.

INTRODUCTION

Clathrin-mediated endocytosis (CME) is the most prominent internalization mechanism of membrane lipids and proteins from the cell surface. The major building blocks of endocytic clathrin coats, that is, clathrin triskelions, can assemble into (complete or partial) polyhedral cages in a seemingly infinite number of geometries (Heuser et al., 1987; Heuser, 1989). The dynamic properties of clathrin-coated structures can be strikingly diverse as well. Lifetime, the time it takes for formation and internalization of endocytic clathrin coats, can be an order of magnitude disparate within the same cell (Ferguson et al., 2016). Here we show that cellular processes associated with membrane tension gradients, that is, spreading and migration, result in increased spatiotemporal heterogeneity of endocytic clathrin coat dynamics. The variations in clathrin coat dynamics coincide with the gradients in plasma membrane tension, which is a potent regulator of endocytic processes (Dai and Sheetz, 1995). We also show that spatiotemporal changes in clathrin coat dynamics take place during developmental processes shaping Drosophila melanogaster embryos.

RESULTS AND DISCUSSION

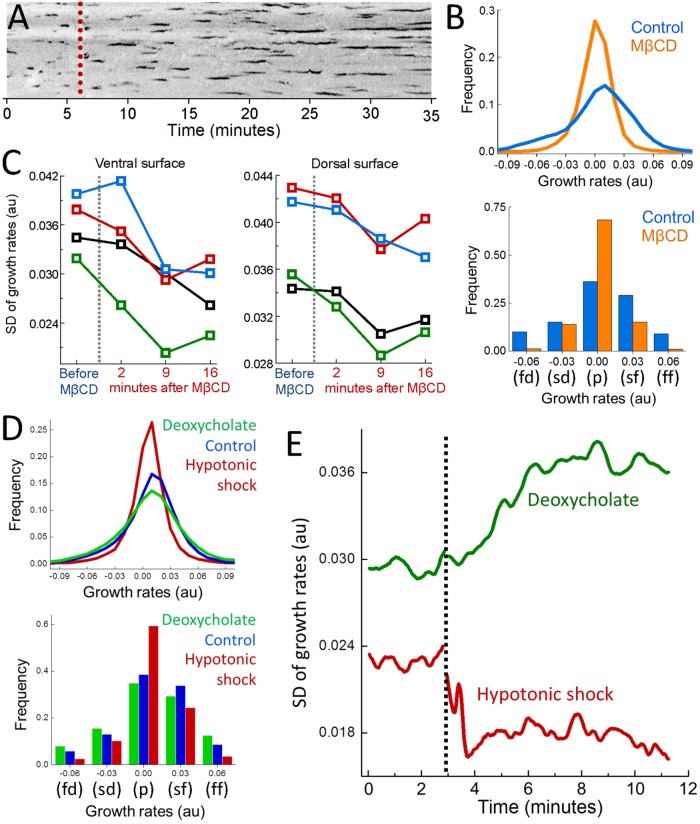
Physical factors that increase the energy cost of curvature generation on the plasma membrane slow down formation of clathrin-coated vesicles. Using quantitative imaging of fluorescently tagged clathrin coat components (clathrin or AP2) within live cells, this phenomenon can be observed as elongated coat lifetime (Figure 1A) (Boulant et al., 2011). Alternatively, mechanoregulation of CME dynamics can be monitored at distinct surfaces of a cell through growth rate distributions which are assembled by quantifying the changes in the fluorescence signal of individual clathrin coats within short time windows (Ferguson et al., 2016). High magnitude growth rates, that is, rapid changes in the clathrin coat intensity corresponding to fast formation and fast dissolution of the coat, diminish with increasing plasma membrane tension. Therefore, the standard deviation (SD) of the growth rate distributions reduces when the effective membrane tension is increased by cholesterol depletion or hypotonic swelling (Figure 1, B–E) (Dai et al., 1998; Khatibzadeh et al., 2012; Diz-Muñoz et al., 2016; Sun et al., 2007). Conversely, SD of growth rate distributions increases when tension is reduced on deoxycholate treatment (Figure 1, D and E) (Raucher and Sheetz, 1999; Batchelder et al., 2011).

FIGURE 1:

FIGURE 1:

Open in a new tab

Monitoring mechanoregulation of clathrin coat dynamics in real time. (A) Depletion of plasma membrane cholesterol by methyl-β-cyclodextrin (MβCD) increases the adhesion energy between membrane and the cytoskeleton and, thereby, inhibits curvature formation by clathrin-coats (Subtil et al., 1999; Sun et al., 2007; Khatibzadeh et al., 2012). A 35-min-long kymograph shows clathrin coat dynamics at the ventral surface of a BSC1 cell stably expressing the σ2 subunit of AP2 fused with enhanced green fluorescent protein (EGFP). The dashed line marks the addition of MβCD. The traces corresponding to individual clathrin-coated structures elongate as clathrin pits are gradually replaced by less dynamic flat arrays (plaques). (B) For the cell in A, growth rate distributions are assembled using the traces detected before cholesterol depletion (Control; the first 5 min of the acquisition) and after (MβCD; the last 5 min of the acquisition). As clathrin coat dynamics slow down, growth rate distribution gets narrower (top). The distribution is also displayed using five bins corresponding to five growth phases (bottom; fd: fast dissolution, sd: slow dissolution, p: plateau, sf: slow formation, ff: fast formation). High-magnitude slopes, corresponding to fd and ff phases, diminish due to inhibition of CME. (C) SD of clathrin growth rate distributions are shown for the ventral and dorsal surfaces of four BSC1 cells before and after MβCD treatment. (D) Growth rate distributions are assembled using AP2 traces detected in SUM159 cells under different conditions (top; Ncells = 4). With application of hypotonic shock (Dai et al., 1998; Diz-Muñoz et al., 2016), CME slows down due to increasing in-plane tension. Deoxycholate treatment reduces membrane tension (Raucher and Sheetz, 1999; Batchelder et al., 2011) and results in increased clathrin coat dynamics. The distributions are also displayed using five bins corresponding to distinct growth phases (bottom). (E) Temporal change in the SD of clathrin coat growth rates is plotted for two SUM159 cells. The dashed line marks the application of hypotonic shock and deoxycholate.

Clathrin coat dynamics in spreading and migrating cells

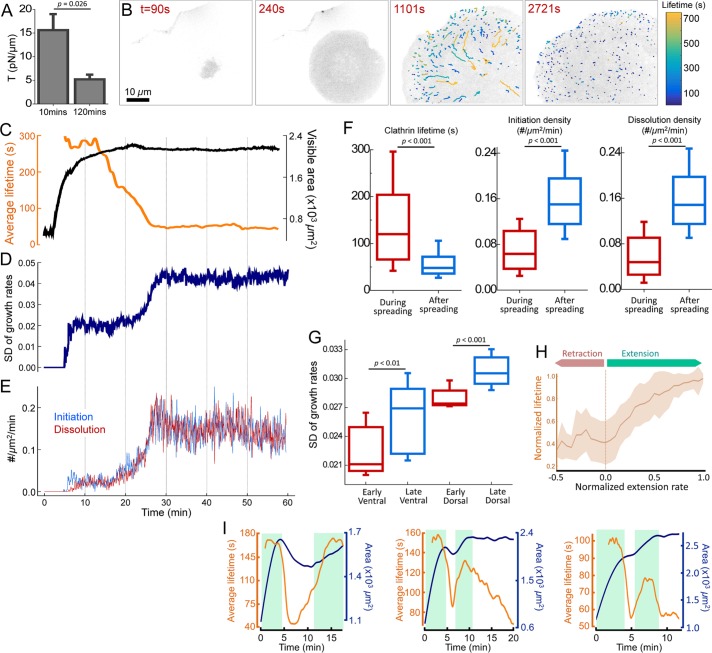
Membrane tension reduces gradually during cell spreading (Gauthier et al., 2009). Rounded-up cells have approximately threefold greater membrane tension compared with well-spread cells (Figure 2A) (Gauthier et al., 2012). We found that the factors defining CME dynamics change significantly in the course of spreading. Figure 2B shows the ventral (adherent) surface of a BSC1 cell at different time points of its spreading. AP2 traces are color coded according to the lifetime to illustrate the changes in density and dynamics of clathrin coats throughout spreading. Decreasing membrane tension results in gradual shortening of the average clathrin coat lifetime (Figure 2C and Supplemental Movie 1). Changes in the SD of growth rates in both ventral and dorsal surfaces demonstrate that clathrin coat dynamics increase across the entire cell (Figure 2, D and G). We also found that initiation and dissolution densities of clathrin-coated structures increase significantly with the completion of spreading (Figure 2, E and F).

FIGURE 2:

FIGURE 2:

Open in a new tab

Clathrin coat dynamics reflect changing membrane tension throughout cell spreading. (A) Optically trapped beads are used to measure membrane tether forces of BSC1 cells at early and late stages of spreading. Membrane tension values (mean + standard error) are shown for cells plated for 10 and 120 min (Ncells = 12). (B) Snapshots show spreading of a BSC1 cell expressing AP2-EGFP. Detected clathrin coat traces are colored according to the lifetime (Supplemental Movie 1). (C) Time variations of the average clathrin coat lifetime (orange) and visible spreading area (black) of the cell in B. SD of growth rates (D), and initiation and dissolution densities of clathrin coats (E) are plotted for the same cell. Shortening of lifetimes, increasing SD of growth rates, and increased initiation and dissolution rates establish increased endocytosis rates with the completion of spreading. (F) Box plots show the cumulative comparison of the clathrin coat lifetime and initiation/dissolution densities obtained during and after spreading of BSC1 cells (Ncells = 24, Ntraces = 41,989). (G) SD of growth rates are calculated for the ventral and dorsal surfaces of BSC1 cells at early and late stages of spreading (measurements are separated by 30–40 min; Ncells = 11). Boxes extend to the quartiles, with a line at the median. Whiskers extend from the 10th to 90th percentiles. (H) The plot shows the normalized clathrin coat lifetime (mean ± SD) vs. normalized extension rate of the ventral surface (area/time) obtained from 24 spreading cells. (I) Spreading area (blue) and average clathrin coat lifetime (orange) in cells featuring periods of spreading (shaded green regions) as well as retraction or pause. p values were obtained using the two-tailed t test.

Extension of the cell surface area is associated with increasing membrane tension (Gauthier et al., 2011; Houk et al., 2012; Masters et al., 2013). In good agreement with this observation, we detected a strong correlation between the rate of area extension and average clathrin coat lifetime in spreading cells (Pearson’s r = 0.67; Figure 2H). This phenomenon is particularly conspicuous in cells that undergo multiple rounds of extension. When spreading is interrupted temporarily, clathrin coat lifetimes converge to the values observed during low tension phases. Lifetimes elongate back to the values observed under high tension as soon as the cells start to spread again (Figure 2I and Supplemental Movie 2). Together, our findings show that temporal variations in tension have direct effects on dynamics and distribution of endocytic clathrin coats in cells.

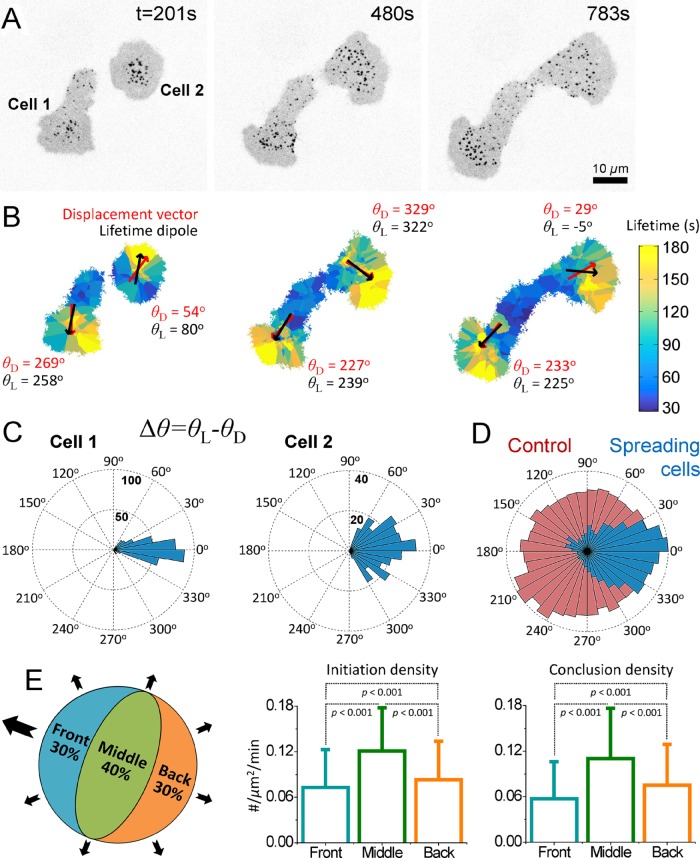
Polarization of cells induces spatial heterogeneity in effective membrane tension (Dai and Sheetz, 1999; Lieber et al., 2015). Theoretical studies predict a strong front-to-rear tension gradient at the ventral surface of protruding cells (Fogelson and Mogilner, 2014). We found that the spatial heterogeneity in clathrin coat dynamics outlines the predicted tension gradient at the ventral surface of asymmetrically spreading cells (Figure 3). Figure 3B shows clathrin lifetime maps of two spreading cells in which every data point is given the average value of the closest three clathrin coats’ lifetime. We found that long-lived clathrin-coated structures are predominantly located in the vicinity of the leading edge. To better quantify this trend, for each time point of spreading, we calculated the lifetime dipole moment, which is a vector pointing in the direction of increasing clathrin coat lifetime. We detected a significant correlation between the direction of the lifetime dipole and the cells’ center-of-mass displacement even when cells change directions (Pearson’s r = 0.53; Figure 3, B–D, and Supplemental Movie 3). As a control, we randomly exchanged the lifetime values between clathrin coats and recalculated the dipoles. The rose diagrams generated using the angular separation between the simulated lifetime dipoles and cells’ original displacement directions were omnidirectional, indicating that the control analyses had no preference for the correct direction (Figure 3D). We also found that clathrin coat distribution is significantly heterogeneous even when the net cellular displacement is due to slight asymmetry of the spreading. Initiation and dissolution densities are the lowest within cellular regions with the highest extension rate (Figure 3E).

FIGURE 3:

FIGURE 3:

Open in a new tab

Heterogeneous clathrin dynamics maps the tension gradient in protruding cells. (A) Snapshots show two asymmetrically spreading BSC1 cells expressing AP2-EGFP. (B) Lifetime maps of the cells in A. This representation allows analyzing the local lifetime and density information by the color and size of the domains, respectively, that is, the domain sizes are inversely related to the local density of clathrin coats. The clathrin coat lifetime dipole moments are shown by black vectors for each cell. The displacement directions of the cellular centers of mass for the given frames are shown by red vectors. θ L and θ D represent the angles of the lifetime dipoles and displacement vectors, respectively (Supplemental Movie 3). (C) Rose plots are assembled using the angular separation between the lifetime dipole vectors and the displacement vectors (Δθ = θ L – θ D) for the two spreading cells in A and B. (D) The blue angular histogram shows Δθ values obtained from 15 spreading cells (total spreading time is 123 min). The red histogram shows the cumulative result of five simulations (using the same 15 cells) in which θ L values are determined after clathrin coat lifetimes are randomly exchanged within a cell. (E) Asymmetrically spreading cells are sectioned into three regions (front: 30% of the cell area next to the leading edge; back: 30% of the cell area at the opposite side of the leading edge; middle: the remaining 40% of the cell area in between the front and back regions) in each frame of spreading movies. Both the front and back are extending regions. However, initiation and conclusion densities (shown as bar plots; mean + SD) are the lowest at the front region, which has the highest extension rate. p values were obtained using the two-tailed t test.

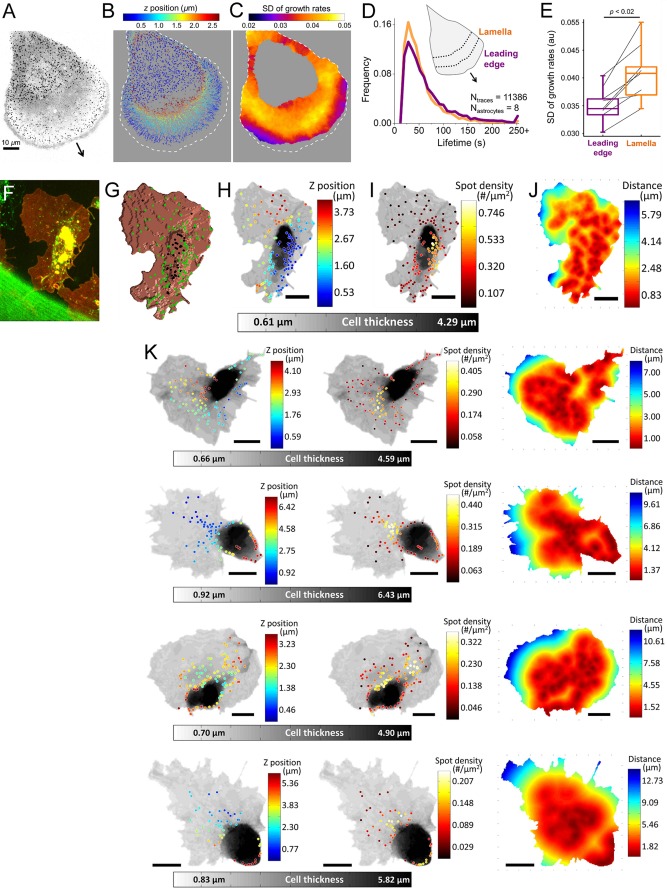
Tether force measurements revealed a significant front-to-rear tension gradient at the lamellipodial fragments of migrating keratocytes (Lieber et al., 2015). Such fragments cannot be isolated from migrating astrocytes for tension measurements. However, at the dorsal surface of these cells, we detected significant spatial heterogeneity in CME dynamics accompanying the expected tension gradient. Clathrin coats originating in the proximity of the leading edge have longer lifetimes (69 ± 51 s [leading edge] vs. 58 ± 39 s [lamella], p < 0.001; Figure 4D) and narrower growth rate distributions (0.035 ± 0.003 [leading edge] vs. 0.041 ± 0.005 [lamella], p < 0.02; Figure 4E). As a visualization tool for the spatial distribution of the clathrin dynamics, we generated growth rate maps in which each pixel is given the value of the SD of the growth rates detected in a circular neighborhood. In this representation, regions of the cell that have slower clathrin dynamics have smaller SD values (Figure 4C). A comparative analysis of clathrin coat initiation and dissolution densities at the two regions is infeasible due to the complex three-dimensional (3D) geometries of the membrane ruffles appearing at the leading edge (Kural et al., 2015). Collectively, our results demonstrate that the cellular processes associated with spatial divergences in plasma membrane tension increase the heterogeneity of CME in cells.

FIGURE 4:

FIGURE 4:

Open in a new tab

Heterogeneous CME during in vitro and in vivo cell migration. (A) Maximum z-projection image shows clathrin-coated structures at the ventral and dorsal surfaces of an U373 astrocyte expressing AP2-GFP. The arrow points toward the direction of extension. (B) Clathrin coat traces obtained from the cell in A are color-coded according to their z-position relative to the substrate. (C) Growth rate map of the dorsal surface is created by calculating the SD of clathrin growth rates within a 4.8-µm radius. SD values are lower in the vicinity of the leading edge due to slower clathrin dynamics. Dashed lines represent the cell boundary. (D) Normalized distributions show lifetimes of dorsal clathrin coats positioned within an 8-µm neighborhood of the leading edge (indigo) and the dorsal coats positioned in the lamellar region between 8 and 16 µm from the leading edge (orange). (E) Box plots show the SD of growth rate distributions assembled using the leading edge and lamellar clathrin coat populations from eight astrocytes (Ntraces = 11,386). Connected lines indicate the values obtained from the same astrocyte. The narrower distribution obtained for the leading edge group (indigo) indicates slower clathrin dynamics at this region. Boxes extend to the quartiles, with a line at the median. Whiskers extend from the 10th to 90th percentiles. p value was obtained using the two-tailed t test. (F) Hemocytes expressing clathrin-GFP (green) and CD4-tdTomato (red) are imaged at the ventral surface of late Drosophila embryos. (G) CD4 signal is used to generate a 3D mask representing the surface of the hemocyte. Positions of the clathrin coats within 320-nm neighborhood of the surface are shown with green dots. (H, I) Grayscale represents the thickness of the hemocyte. Endocytic clathrin coats are color coded according to their z-positions in H and local density of clathrin spots calculated within a 5-µm cube in I. (J) Each pixel in the hemocyte image is color coded according to its average distance to the three closest clathrin coats. (K) Examples of hemocyte images highlighting the heterogeneous distribution of endocytic clathrin-coated structures. Scale bars in F–K are 8 μm.

Spatiotemporal variations in clathrin dynamics of Drosophila embryos

We expect spatiotemporal heterogeneity in clathrin coat dynamics to be prominent during developmental processes associated with dynamic tissue mechanics. It was previously shown that tension-based regulation of receptor endocytosis have important functions in development of Drosophila embryos (Pouille et al., 2009). Since quantification of clathrin lifetimes is error prone within tissue contexts, we used growth rates and spatial distribution of clathrin-coated structures to probe CME in this system (Ferguson et al., 2016). During late stages of Drosophila embryogenesis, hemocytes migrate along the ventral nerve cord to populate the entire embryo. Unlike in vitro migration systems, embryonic hemocytes are physically constrained by the 3D environment and therefore do not form membrane ruffles at their lamellipodial extensions (Tucker et al., 2011). Figure 4F shows the maximum z-projection image of a hemocyte expressing fluorescently tagged clathrin and CD4 (membrane marker). We assessed the 3D positions of clathrin structures to distinguish the endocytic coats, which are in the vicinity of the cell surface (Figure 4, G and H) (Kural et al., 2012), and used alternative visualization tools to analyze the spatial distribution of endocytic clathrin coats. In Figure 4I, positions of endocytic clathrin coats are color coded according to the density of neighboring coats within the 5-µm neighborhood. In Figure 4J, the heat map shows each pixel’s average distance to the three closest clathrin coats. Both representations illustrate that the density of endocytic clathrin coats are the lowest at the thin lamellipodial extensions of hemocytes (Figure 4K).

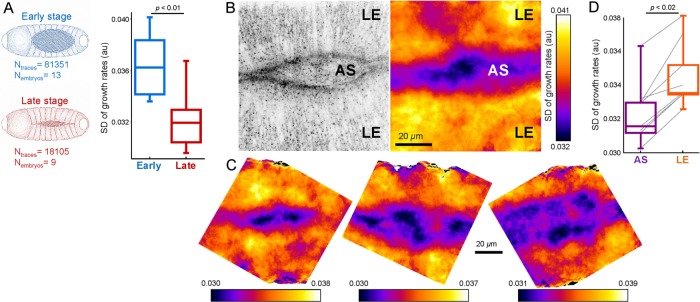
During dorsal closure of the Drosophila embryo, tension on the amnioserosa (AS) tissue increases and the tissue volume reduces gradually (Ma et al., 2009; Saias et al., 2015). As expected, we detected significant reduction in clathrin dynamics at later stages of the dorsal closure (SD: 0.036 ± 0.003 [early] vs. 0.032 ± 0.002 [late], p < 0.01; Figure 5A). Using SD maps, we also discovered that CME dynamics is spatially heterogeneous at the dorsal surface of the embryo (Figure 5, B and D). The growth rate analysis revealed that clathrin dynamics are markedly slower at the AS compared with the two flanks of the lateral epidermis (LE) tissue (SD: 0.032 ± 0.002 [AS] vs. 0.035 ± 0.002 [LE], p < 0.02; Figure 5C). Such a divergence in endocytic dynamics was anticipated, considering the distinct physical properties of AS and LE cells and the mechanical roles they play during dorsal closure (Brodland et al., 2014; Ducuing and Vincent, 2016; Pasakarnis et al., 2016).

FIGURE 5:

FIGURE 5:

Open in a new tab

Spatiotemporal variations in clathrin dynamics can be detected within tissues of Drosophila embryo. (A) Clathrin dynamics slow down with increasing tension during late stages of the dorsal closure. Box plots show the SD of clathrin growth rate distributions obtained from early and late stage AS tissues. Reduced SD is a hallmark of slowed-down endocytosis (Ferguson et al., 2016). (B) Left, clathrin-coated structures at the dorsal surface of a Drosophila embryo. AS appears as narrow opening between the two flanks of lateral epidermis (LE). Right, SD map of the clathrin growth rates obtained from the same area. The map is created by calculating the SD of apical clathrin growth rates within an 8-µm radius. Lower SD values in the AS region display slower clathrin dynamics with respect to the neighboring LE. (C) More examples demonstrating the heterogeneous clathrin dynamics at the dorsal surface of late Drosophila embryos. (D) Box plots show the SD of clathrin growth rate distributions obtained from LE and AS of eight embryos. Connected lines indicate the values obtained from the same embryo. Boxes extend to the quartiles, with a line at the median. Whiskers extend from the 10th to 90th percentiles. p values were obtained using the two tailed t test.

In this study, we show that spatial and temporal variations in cell membrane tension dominate the dynamics of clathrin-coated structures. Endocytic machinery must overcome the major constituents of the effective membrane tension, that is, in-plane tension and membrane-cytoskeleton adhesion, to deform the plasma membrane (Sheetz, 2001). In-plane tension is assumed to be in equilibrium across the entire plasma membrane due to fast flow of membrane lipids. However, membrane-cytoskeleton adhesion can be heterogeneous and induce stark differences in the clathrin dynamics between distinct surfaces of a cell (Dai and Sheetz, 1999; Boulant et al., 2011). Similarly, adhesion to the substrate can inhibit curvature formation and slow down clathrin coat dynamics locally. Therefore, nonuniform adhesion of a cell to the substrate creates another layer of heterogeneity in clathrin dynamics (Batchelder and Yarar, 2010; Ferguson et al., 2016).

We believe that spatiotemporal heterogeneity in clathrin coat dynamics plays important roles in central cellular processes. Mechanoinhibition of endocytosis at early stages of cell spreading might elevate the rate of extension of the plasma membrane area (Gauthier et al., 2009, 2011). Inhibition of endocytosis at the leading edge of migrating cells may facilitate cell protrusion by allowing net membrane deposition to this region (Bretscher, 2014). Similarly, increased tension at the amnioserosa tissue of developing embryos may account for the gradual reduction of the cell volume through inhibition of endocytosis in the late stages of the dorsal closure. Future studies should be directed toward investigating the mechanoregulation of endocytosis in situ and elucidating the roles it plays at the organismal level.

MATERIALS AND METHODS

Cell culture and fluorescence microscopy

BSC1 and U373 cells stably expressing σ2-EGFP were cultured in DMEM (Life Technologies) containing penicillin/streptomycin and 10% fetal bovine serum (FBS). Gene-edited SUM159 cells were grown in F-12 medium containing 5% FBS and 1 µm/ml hydrocortisone (Aguet et al., 2016). Live cells and embryos are imaged using a Nikon Eclipse (TI-E) microscope equipped with a 100× objective lens (Nikon CFI Plan-Apochromat Lambda, NA 1.45), a CSU-W1 spinning disk confocal head (Yokogawa Electric Corporation) and an electron-multiplying charge-coupled device (EMCCD) camera (iXon DU897 Ultra; Andor Technology). Sample temperature and z-position are stabilized using a temperature controlled chamber and perfect focusing system (PFS), respectively. NIS Elements software is used for image acquisition.

Spreading cells were imaged on glass bottom dishes (Greiner Bio-One) directly after plating. The plating time prior to astrocyte migration experiments was 8–24 h. Live cell imaging is performed at 37°C ambient temperature within L15 (Thermo Fisher Scientific) supplemented with 10% FBS. Images were acquired at 0.25–0.5 Hz, and laser exposure lasted for 50–300 ms per frame. The final concentrations of MβCD and deoxycholic acid (Sigma-Aldrich) were 10 and 0.4 mM in serum-free L15, respectively. Hypotonic shock was performed using 1:5 dilution of the imaging medium using deionized water. In the figures and movies fluorescence acquisitions are inverted to increase visibility.

Fly strains and in vivo imaging

We used the UAS/GAL4 system to monitor clathrin dynamics in Drosophila embryos. Arm-GAL4, CLC-GFP, and CD4-tdTom strains were provided by the Bloomington Drosophila Stock Center. srpHemo-GAL4 was a gift from Norbert Perrimon (Harvard Medical School). Embryos were collected and aged for 11–13 h at 25°C. After dechorionation, embryos were mounted on coverslips and immersed in halocarbon oil. Clathrin dynamics at the dorsal and ventral surfaces were imaged at 22°C using 3D time-lapse acquisitions. In amnioserosa, apical clathrin coats were determined by filtering out the bright puncta corresponding to organelle-bound clathrin-coated structures as described earlier (Ferguson et al., 2016). In Figure 5A, maximum amnioserosa openings for the early- and late-stage embryos were 81.5 ± 13.0 and 28.2 ± 10.6 μm, respectively.

To analyze hemocyte images, clathrin coats were found using a simple threshold of the clathrin channel and localized using the center of intensity of the fluorescence signal (Kural et al., 2012). Similarly, the membrane was identified using a threshold on the CD4 channel. Using the built-in MATLAB function, isosurface, a triangular mesh of the membrane surface was generated. Clathrin coats were defined to be endocytic if they were <320 nm from the nearest surface voxel. The spot density was determined by counting all endocytic coats around a spot within a 5-µm cube and then dividing that by the sum of the area from the triangulated mesh found within the cube. The distance map was generated by determining the average distance of the three closest endocytic clathrin spots for each pixel on the surface.

Two-dimensional tracking of clathrin-coated structures

We used cmeAnalysis software for 2D single particle tracking (Aguet et al., 2013). We used a previously developed trace rejection scheme to filter traces that do not follow a characteristic clathrin coat intensity profile (Ferguson et al., 2016). We used the traces that pass the rejection scheme in the calculation of lifetime distributions, growth rate distributions, initiation/dissolution densities and lifetime dipoles.

To determine the temporal evolution of the average clathrin coat lifetime, for each frame of a movie, we added together the lifetime of each trace that exists in that frame and divided by the number of traces considered.

Three-dimensional tracking of clathrin-coated structures

We used the z-position information to distinguish the dorsal and ventral clathrin coats in cells (Figures 1C, 2G, and 4B). cmeAnalysis software was used to analyze each z-plane of 3D time-lapse movies (followed by the trace rejection scheme detailed above). The resulting data were combined to link traces which occur at the same lateral position in two adjacent z-planes. Coincident traces had to remain within one pixel (160 nm) x–y distance for at least three frames. The resulting trace was assigned the maximum intensity value among all traces considered for combination. Axial positions were calculated using the intensity-weighted mean z-position of all traces considered. The algorithm for trace combination ran from the outermost z-planes to the innermost, alternating between the top and the bottom to ensure that there was no directional bias and all possible trace combinations were considered.

Growth rate distributions

Clathrin coat intensity traces were normalized by subtracting a global minimum and dividing by the resulting maximum. From this normalized trace, each 12-s interval was used in a least-squares fit to determine the growth rate of each interval. A trace had to be at least 12 s long to be included in the distribution. An arbitrary bin width (0.03) was found to delineate five distinct growth phases (fast dissolution, slow dissolution, plateau, slow formation, and fast formation) (Ferguson et al., 2016).

To determine the SD of the growth rates per frame, we generated a list of the intensity slope of each trace within that frame and took the SD of that list. When the data are sparse, we used the walking average of three adjacent frames. We used PFS to eliminate sample defocusing triggered by the squeezing procedure. We found that the adjustment of the PFS resulted in a single frame of artificial growth rate values due to abrupt changes in the clathrin coat fluorescence intensities. Those frames are excluded from the analyses.

SD maps of clathrin coat growth rates in Figures 4 and 5 are made by, for each pixel within the cell, calculating the SD of all growth rates within 4.8 and 8 μm, respectively.

Lifetime maps and dipole vectors

Lifetime maps in Figure 3 and Supplemental Movie 3 are made of a given frame by calculating the average lifetime of the three closest clathrin-coated structures for each pixel within the cell. Patches of color are regions where the set of closest clathrin coats are the same, so color is an indication of local lifetime and the size of the patch is an indication of local clathrin coat density (larger patches indicates lower density).

Lifetime dipoles were calculated using the equation 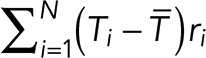Inline graphic, where Ti and ri are the lifetime and the position of the ith clathrin-coated structure and 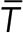Inline graphic is the average lifetime of all clathrin-coated structures in the frame. Abortive clathrin coats with lifetimes less than 20 s, hotspots, and clathrin-coated plaques that do not disappear until the end of the acquisitions were excluded from the calculation of lifetime dipoles. In the randomization scheme used for the control analyses, the positions of clathrin-coated structures remained untouched to validate that the reciprocity between the lifetime dipole and cell displacement is due only to the spatial distribution of lifetimes within the cell.

Tether force measurements

We used optically trapped beads to quantify membrane tether forces. An optical tweezers system was built based on a previous design; however; only one of the two traps was used in this application (Bustamante et al., 2009). Polystyrene beads (1 μm; Spherotech) were coated with fibronectin (Sigma-Aldrich) before the experiments. Cells were incubated for 10 min or 2 h before the experiments for measuring membrane tension at different stages of spreading. Membrane tension values (T) are calculated using 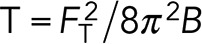Inline graphic, where FT is the measured membrane tether forces and B is the bending modulus of the plasma membrane, and the value is assumed to be 0.27 pN μm (Hochmuth et al., 1996).

Statistics

All of the p values were obtained using the two-tailed t test. All of the r values correspond to Pearson’s correlation coefficient.

Supplementary Material

Supplemental Materials
supp_28_24_3480__index.html (2.1KB, html)

Acknowledgments

We thank Steeve Boulant, Tomas Kirchhausen, and Norbert Perrimon for the cell and fly lines.

This work was supported by National Institutes of Health Grant No. R01 AI121124.

Abbreviations used:

3D

three-dimensional

AS

amnioserosa

CLC

clathrin light chain

CME

clathrin-mediated endocytosis

EGFP

enhanced green fluorescent protein

EMCCD

electron-multiplying charge-coupled device

FBS

fetal bovine serum

LE

lateral epidermis

MβCD

methyl-β-cyclodextrin

PFS

perfect focus system.

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E17-05-0282) on September 13, 2017.

REFERENCES

  1. Aguet F, Antonescu CN, Mettlen M, Schmid SL, Danuser G. Advances in analysis of low signal-to-noise images link dynamin and AP2 to the functions of an endocytic checkpoint. Dev Cell. 2013;26:279–291. doi: 10.1016/j.devcel.2013.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Aguet F, Upadhyayula S, Gaudin R, Chou Y, Cocucci E, He K, Chen B-C, Mosaliganti K, Pasham M, Skillern W, et al. Membrane dynamics of dividing cells imaged by lattice light-sheet microscopy. Mol Biol Cell. 2016;27:3418–3435. doi: 10.1091/mbc.E16-03-0164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Batchelder EL, Hollopeter G, Campillo C, Mezanges X, Jorgensen EM, Nassoy P, Sens P, Plastino J. Membrane tension regulates motility by controlling lamellipodium organization. Proc Natl Acad Sci USA. 2011;108:11429–11434. doi: 10.1073/pnas.1010481108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Batchelder EM, Yarar D. Differential requirements for clathrin-dependent endocytosis at sites of cell-substrate adhesion. Mol Biol Cell. 2010;21:3070–3079. doi: 10.1091/mbc.E09-12-1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Boulant S, Kural C, Zeeh J-C, Ubelmann F, Kirchhausen T. Actin dynamics counteract membrane tension during clathrin-mediated endocytosis. Nat Cell Biol. 2011;13:1124–1131. doi: 10.1038/ncb2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bretscher MS. Asymmetry of single cells and where that leads. Annu Rev Biochem. 2014:1–15. doi: 10.1146/annurev-biochem-060713-035813. [DOI] [PubMed] [Google Scholar]
  7. Brodland GW, Veldhuis JH, Kim S, Perrone M, Mashburn D, Hutson MS. CellFIT: a cellular force-inference toolkit using curvilinear cell boundaries. PLoS One. 2014;9:e99116. doi: 10.1371/journal.pone.0099116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bustamante C, Chemla YR, Moffitt JR. High-resolution dual-trap optical tweezers with differential detection: instrument design. Cold Spring Harb Protoc. 2009;2009 doi: 10.1101/pdb.ip73. pdb.ip73. [DOI] [PubMed] [Google Scholar]
  9. Dai J, Sheetz MP. Regulation of endocytosis, exocytosis, and shape by membrane tension. Cold Spring Harb Symp Quant Biol. 1995;60:567–571. doi: 10.1101/sqb.1995.060.01.060. [DOI] [PubMed] [Google Scholar]
  10. Dai J, Sheetz MP. Membrane tether formation from blebbing cells. Biophys J. 1999;77:3363–3370. doi: 10.1016/S0006-3495(99)77168-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dai J, Sheetz MP, Wan X, Morris CE. Membrane tension in swelling and shrinking molluscan neurons. J Neurosci. 1998;18:6681–6692. doi: 10.1523/JNEUROSCI.18-17-06681.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Diz-Muñoz A, Thurley K, Chintamen S, Altschuler SJ, Wu LF, Fletcher DA, Weiner OD. Membrane tension acts through PLD2 and mTORC2 to limit actin network assembly during neutrophil migration. PLoS Biol. 2016;14:1–30. doi: 10.1371/journal.pbio.1002474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ducuing A, Vincent S. The actin cable is dispensable in directing dorsal closure dynamics but neutralizes mechanical stress to prevent scarring in the Drosophila embryo. Nat Cell Biol. 2016;18:1149–1160. doi: 10.1038/ncb3421. [DOI] [PubMed] [Google Scholar]
  14. Ferguson JP, Willy NM, Heidotting SP, Huber SD, Webber MJ, Kural C. Deciphering dynamics of clathrin-mediated endocytosis in a living organism. J Cell Biol. 2016;214:347–358. doi: 10.1083/jcb.201604128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fogelson B, Mogilner A. Computational estimates of membrane flow and tension gradient in motile cells. PLoS One. 2014;9:e84524. doi: 10.1371/journal.pone.0084524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gauthier NC, Fardin MA, Roca-Cusachs P, Sheetz MP. Temporary increase in plasma membrane tension coordinates the activation of exocytosis and contraction during cell spreading. Proc Natl Acad Sci USA. 2011;108:14467–14472. doi: 10.1073/pnas.1105845108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gauthier NC, Masters TA, Sheetz MP. Mechanical feedback between membrane tension and dynamics. Trends Cell Biol. 2012;22:527–535. doi: 10.1016/j.tcb.2012.07.005. [DOI] [PubMed] [Google Scholar]
  18. Gauthier NC, Rossier OM, Mathur A, Hone JC, Sheetz MP. Plasma membrane area increases with spread area by exocytosis of a GPI-anchored protein compartment. Mol Biol Cell. 2009;20:3261–3272. doi: 10.1091/mbc.E09-01-0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Heuser J. Effects of cytoplasmic acidification on clathrin lattice morphology. J Cell Biol. 1989;108:401–411. doi: 10.1083/jcb.108.2.401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Heuser JE, Keen JH, Amende LM, Lippoldt RE, Prasad K. Deep-etch visualization of 27S clathrin: a tetrahedral tetramer. J Cell Biol. 1987;105:1999–2009. doi: 10.1083/jcb.105.5.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hochmuth FM, Shao JY, Dai J, Sheetz MP. Deformation and flow of membrane into tethers extracted from neuronal growth cones. Biophys J. 1996;70:358–369. doi: 10.1016/S0006-3495(96)79577-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Houk AR, Jilkine A, Mejean CO, Boltyanskiy R, Dufresne ER, Angenent SB, Altschuler SJ, Wu LF, Weiner OD. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell. 2012;148:175–188. doi: 10.1016/j.cell.2011.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Khatibzadeh, N, Gupta S, Farrell B, Brownell WE, Anvari B. Effects of cholesterol on nano-mechanical properties of the living cell plasma membrane. Soft Matter. 2012;8:8350–8360. doi: 10.1039/C2SM25263E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kural C, Akatay AA, Gaudin R, Chen B-C, Legant WR, Betzig E, Kirchhausen T. Asymmetric formation of coated pits on dorsal and ventral surfaces at the leading edges of motile cells and on protrusions of immobile cells. Mol Biol Cell. 2015;26:2044–2053. doi: 10.1091/mbc.E15-01-0055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kural C, Tacheva-Grigorova SK, Boulant S, Cocucci E, Baust T, Duarte D, Kirchhausen T. Dynamics of intracellular clathrin/AP1- and clathrin/AP3-containing carriers. Cell Rep. 2012;2:1111–1119. doi: 10.1016/j.celrep.2012.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lieber AD, Schweitzer Y, Kozlov MM, Keren K. Front-to-rear membrane tension gradient in rapidly moving cells. Biophys J. 2015;108:1599–1603. doi: 10.1016/j.bpj.2015.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ma X, Lynch HE, Scully PC, Hutson MS. Probing embryonic tissue mechanics with laser hole drilling. Phys Biol. 2009;6:36004. doi: 10.1088/1478-3975/6/3/036004. [DOI] [PubMed] [Google Scholar]
  28. Masters TA, Pontes B, Viasnoff V, Li Y, Gauthier NC. Plasma membrane tension orchestrates membrane trafficking, cytoskeletal remodeling, and biochemical signaling during phagocytosis. Proc Natl Acad Sci USA. 2013;110:11875–11880. doi: 10.1073/pnas.1301766110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Pasakarnis L, Frei E, Caussinus E, Affolter M, Brunner D. Amnioserosa cell constriction but not epidermal actin cable tension autonomously drives dorsal closure. Nat Cell Biol. 2016;18:1161–1172. doi: 10.1038/ncb3420. [DOI] [PubMed] [Google Scholar]
  30. Pouille P-A, Ahmadi P, Brunet A-C, Farge E. Mechanical signals trigger Myosin II redistribution and mesoderm invagination in Drosophila embryos. Sci Signal. 2009;2:ra16. doi: 10.1126/scisignal.2000098. [DOI] [PubMed] [Google Scholar]
  31. Raucher D, Sheetz MP. Membrane expansion increases endocytosis rate during mitosis. J Cell Biol. 1999;144:497–506. doi: 10.1083/jcb.144.3.497. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Saias L, Swoger J, D’Angelo A, Hayes P, Colombelli J, Sharpe J, Salbreux G, Solon J. Decrease in cell volume generates contractile forces driving dorsal closure. Dev Cell. 2015;33:611–621. doi: 10.1016/j.devcel.2015.03.016. [DOI] [PubMed] [Google Scholar]
  33. Sheetz MP. Cell control by membrane-cytoskeleton adhesion. Nat Rev Mol Cell Biol. 2001;2:392–396. doi: 10.1038/35073095. [DOI] [PubMed] [Google Scholar]
  34. Subtil A, Gaidarov I, Kobylarz K, Lampson MA, Keen JH, McGraw TE. Acute cholesterol depletion inhibits clathrin-coated pit budding. Proc Natl Acad Sci USA. 1999;96:6775–6780. doi: 10.1073/pnas.96.12.6775. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Sun M, Northup N, Marga F, Huber T, Byfield FJ, Levitan I, Forgacs G. The effect of cellular cholesterol on membrane-cytoskeleton adhesion. J Cell Sci. 2007;120:2223–2231. doi: 10.1242/jcs.001370. [DOI] [PubMed] [Google Scholar]
  36. Tucker PK, Evans IR, Wood W. Ena drives invasive macrophage migration in Drosophila embryos. Dis Model Mech. 2011;4:126–134. doi: 10.1242/dmm.005694. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Materials
supp_28_24_3480__index.html (2.1KB, html)
supp_E17-05-0282v1_CombinedSupMats.pdf (36.5KB, pdf)
Download video file (7.3MB, avi)
Download video file (20.7MB, avi)
Download video file (15.8MB, avi)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES