Abstract.
A three-dimensional (3-D) convolutional neural network (CNN) trained from scratch is presented for the classification of pulmonary nodule malignancy from low-dose chest CT scans. Recent approval of lung cancer screening in the United States provides motivation for determining the likelihood of malignancy of pulmonary nodules from the initial CT scan finding to minimize the number of follow-up actions. Classifier ensembles of different combinations of the 3-D CNN and traditional machine learning models based on handcrafted 3-D image features are also explored. The dataset consisting of 326 nodules is constructed with balanced size and class distribution with the malignancy status pathologically confirmed. The results show that both the 3-D CNN single model and the ensemble models with 3-D CNN outperform the respective counterparts constructed using only traditional models. Moreover, complementary information can be learned by the 3-D CNN and the conventional models, which together are combined to construct an ensemble model with statistically superior performance compared with the single traditional model. The performance of the 3-D CNN model demonstrates the potential for improving the lung cancer screening follow-up protocol, which currently mainly depends on the nodule size.
Keywords: three-dimensional convolutional neural network, three-dimensional convolutional neural network, pulmonary nodule classification, low-dose chest CT, lung cancer screening
1. Introduction
Annual lung cancer screening with low-dose chest CT has recently been approved in the United States for the early detection and treatment of lung cancer for people at high risk, with million Americans eligible for the screening.1 The costly follow-up procedures provide motivation for the development of systems for establishing the malignancy status of pulmonary nodules from low-dose chest CT images. The purpose of this paper is to determine the benefits of applying a machine learning approach, three-dimensional (3-D) convolution neural network (CNN) to the task of pulmonary nodule classification from low-dose chest CT scans obtained from lung cancer screening, through the performance comparison with traditional machine learning approaches. In addition, the classifier ensembles of the different combinations of the 3-D CNN and traditional machine learning classifiers based on handcrafted 3-D image features are also explored to study the key to the success of the ensembles.
A typical automated system for lung cancer diagnosis generally consists of two stages: pulmonary nodule detection and pulmonary nodule malignancy classification. This paper focuses on the latter stage, namely the discrimination between benign pulmonary nodules and malignant pulmonary nodules given the nodule location and size from the volumetric low-dose chest CT scans acquired during the lung cancer screening.
The conventional automated approaches to the discrimination between benign pulmonary nodules and lung cancer generally consist of four major stages:2 (1) nodule segmentation, (2) image feature extraction from the segmented nodules, (3) feature selection based on the discriminative power of the features, and (4) machine learning classifier training given the selected features. A wide range of image features, such as gray-level distribution, size, morphology, and texture description, and various types of machine learning models, including linear discriminant analysis,3,4 support vector machines (SVM),5,6 massive training artificial neural network,7 random forest,2 and distance-weighted nearest neighbor (NN),6,8 have been explored in the literature2,3,4,5,6,8 to address the problem of pulmonary nodule classification. The fast volume growth rate of a nodule9 serves as a reliable indicator for malignancy; however, it usually requires more accurate image segmentation for the nodule volume measurement and at least two CT scans, which prolongs diagnosis and exposes the patient to possible unnecessary radiation exposure.5,6,8
The astounding revival of convolutional neural networks (CNNs)10,11 since 2012, owing to the availability of large-scale annotated image datasets12 and affordable parallel computing resources,13 has led to remarkable advances11,14–16,17 in several computer vision applications of natural images and the birth of deep learning, a new area of machine learning research. The application of deep learning techniques to various automated medical imaging analysis problems has also been explored in a large number of published works,18 which can be summarized in the following three primary categories.19 First, off-the-shelf deep features can be extracted directly from pretrained deep learning networks and then fed into traditional machine learning models, such as SVM and random forest, to address the detection or classification problems.20–23 Although the performance of using only off-the-shelf deep features is normally inferior to the traditional state-of-the-art features acquired by careful feature engineering,20–23 the ensemble of both can result in substantial improvement.20–22 Second, fine-tuning deep learning models pretrained on irrelevant and, typically, nonmedical images has been demonstrated to outperform the state-of-the-art traditional approaches.24,19 Third, effective deep learning models can also be trained from scratch. It can be used either from end-to-end13,19,25–27,28–34 or as a feature extractor,35,26,36,37 which requires succeeding traditional approaches such as the conventional classifier for classification applications or the deformable shape model for segmentation applications.
Pulmonary nodule detection and classification from CT scans is a 3-D problem, whereas most of the published work on deep learning still adopts a two-dimensional (2-D) approach13,38 since the CNNs were originally proposed for 2-D natural images with RGB color channels. To utilize the established network architectures and pretrained network weights, the most common solution is to map each 3-D volumetric CT scan into a three-channel 2-D image by assigning three-orthogonal planes, which can be axial, coronal, and sagittal slices20,23,24 or even planes with random orientations13,19,25 to three different channels. It effectively reduces the network complexity, in terms of the number of trainable weights and the required memory for the computation as well as data storage, and reduces the amount of the training data needed to avoid overfitting; however, the concern of the loss of 3-D information still exists.38 A number of recent publications have started to employ 3-D CNNs in various types of medical imaging applications, including pulmonary nodule28 and cerebral microbleed29 detection, prostate finding30 and breast mass31 classification, and different types of anatomy segmentations.32–36 A 3-D CNN has been shown to achieve significant performance enhancement attributed to the consideration of contextual information along the third-spatial dimension, compared with the corresponding 2-D CNN, by Çiçek et al.32 for the segmentation of xenopus kidney, Dou et al.29 for the detection of cerebral microbleeds, and Li et al.31 for the classification of breast masses. For the application of pulmonary nodule classification, no published work has been found on the employment of a 3-D CNN, which may potentially provide benefits due to the consideration of the full 3-D data.5 In the CNN proposed by Shen et al.,26,27 although 3-D image patches around the nodules are directly fed into the input layer, the network is still not completely 3-D because no convolution operation or pooling operation is performed along the third-spatial dimension, which is treated as the channel dimension.
The matching of size distribution for malignant and benign nodules in the validation set is necessary for a meaningful assessment of automated systems for pulmonary nodule classification as first noted in 20078 and also in Refs. 2 and 6. Datasets with benign nodules dominating the small size range and malignant nodules dominating the large size range are very common in the published studies39,3,4,7,40 since the nodule malignancy is highly correlated to nodule size. However, algorithm performance evaluated on such a dataset can be misleading and overly optimistic2,6,8 because a simple size classifier that is based on nodule size thresholding only may achieve promising performance due to correctly classifying very large and very small nodules. However, such a classifier would not be effective for classifying the malignancy status of nodules of intermediate sizes, which are the most frequent in lung cancer screening and of most interest to clinical practice.
A balanced class distribution (i.e., an approximately equal number of benign and malignant nodules in our case) is another favorable property of the validation set for a classification problem evaluated using receiver operating characteristic (ROC) curves. A large skew in class distribution in the validation set can lead to an overly optimistic view of an algorithm’s performance based on ROC curves.41 Therefore, it can be unfair to directly compare the ROC curves of the algorithms evaluated on the datasets with different amounts of skewness.
The reported performance of automated nodule classification systems spans a very large range,2,3–8,24,35,26,27 with area under the ROC curve (AUC) ranging from 0.502 to 0.93.27 However, the performance of studies is generally not comparable due to two primary reasons.2 First, different datasets were employed for the evaluation of each study; therefore, direct comparison is meaningless.42 Additionally, as discussed above, a biased validation set may lead to an unfair assessment of its performance.19 Moreover, studies3,4,6,7,8 that focus on pulmonary nodule classification from low-dose CT images acquired during lung cancer screening are considered more challenging6,8 compared with other studies2,5,24,35,26,27 that include standard-dose CT images acquired during clinical practice due to the small size of the present nodules and the high level of image noise.6,7 The current scan protocol in lung cancer screening (fixed CT scan resolution of 512 pixels across lungs) limits the number of pixels available for analysis, especially for nodules of small size, which are the most clinically relevant nodules for early detection of lung cancer. Second, different evaluation schemes were used. For instance, the malignancy status is confirmed by biopsy outcome in some studies,2,3,4,6,7,8,35 whereas, in other studies,5,24,26,27 the malignancy status is established purely based on malignancy ratings of radiologists after reviewing the CT scans, where interobserver differences can be significant.2,24 In addition, the cross-validation strategy, such as leave-one-out compared with fivefold cross-validation, may have a significant impact on the resulting performance.19
In this paper, we applied a 3-D CNN trained from scratch to the classification of pulmonary nodule malignancy using a class-balanced and size-matched low-dose chest CT dataset, where the malignancy status is pathologically confirmed. Since the exact same training and validation dataset as well as the evaluation scheme were employed in a previous study based on handcrafted features and traditional machine learning models by Reeves et al.,6 a direct performance comparison between the 3-D CNN and the conventional approaches to the pulmonary nodule classification is possible. The ensemble models of the different combinations of the 3-D CNN and traditional machine learning models were also explored. Our hypothesis is that the CNN can learn the 3-D image features automatically and achieve at least the same classification performance compared with the conventional approaches that are based on handcrafted image features and traditional machine learning classifiers. In addition, since the features learned by a 3-D CNN should be complementary to the handcrafted features, the ensembles should achieve further performance improvement.
2. Methods
In this study, we applied a 3-D CNN to a class balanced and size matched low-dose chest CT dataset for the classification of pulmonary nodule malignancy. The 3-D CNN was trained and tested in the context of a fivefold cross-validation and was evaluated based on the ROC curves. Several ensembles of the 3-D CNN and traditional models were constructed to explore the potential performance gain resulting from the combination of complementary features and classifiers.
2.1. Nodule Image Preprocessing
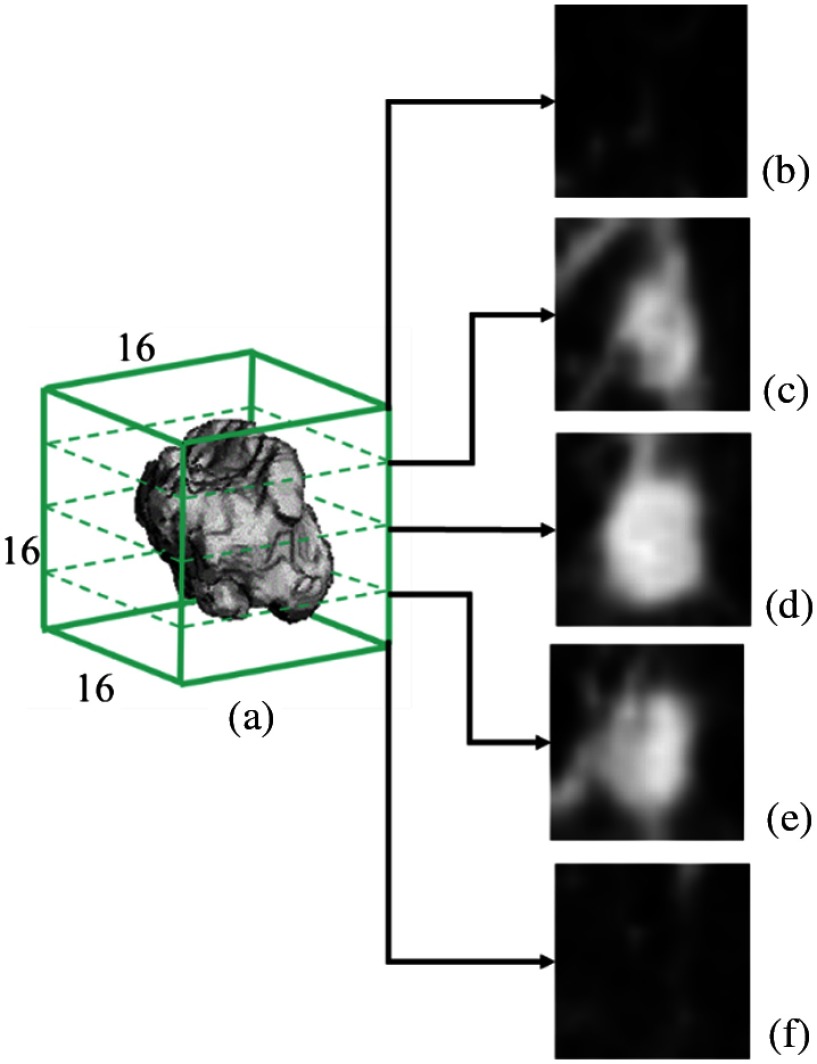
Each nodule CT volume is cropped into a real space cube around the nodule center with a margin of 20% of the nodule radius as shown in Fig. 1 to include approximately the same volume for background context as the nodule itself. The nodule location (center) and size (radius) are calculated from automated nodule segmentation.6,9 The cropped 3-D image region is then resampled using tricubic interpolation to an isotropic fixed size 3-D image.
Fig. 1.
Cropped 3-D CT volume used as the input to the CNN. (a) resampled isotropic CT volume centered at a nodule and (b–f) five axial slices at the corresponding axial level.
For these CT images, the - and -dimensions have the same resolution and the -dimension (slice spacing) usually has a lower resolution. As detailed in Sec. 3.1, the pixels in the dataset, in general, varied in a size range from 0.5 to 0.85 mm in the - and -dimensions and from 1.0 to 2.5 mm in the -dimension. Two different resampled image sizes were independently explored for the CNN network: and . For the image size, oversampling occurred in all three dimensions since none of the cropped image regions had any dimension with in the original CT scan. For the image size, 27.6% of the cropped image regions (corresponding to the largest nodules) had an -dimension ; no cases had in the -dimension (the largest cropped region dimension was 31 pixels () and the largest -dimension was 15 pixels). Therefore, for these 27.6% cases, there was some amount of undersampling (possible information loss), although oversampling always occurred in the -dimension.
The image pixel values are first converted to the Hounsfield unit (HU) scale, then clipped between considering the common image intensity distribution of pulmonary nodules, and scaled by 1/200. The resulting image intensity distribution is in the range with most of the nodule pixels approximately zero-centered in the range .
2.2. Convolutional Neural Network Architectures
A CNN10 is a specialized type of feedforward neural network (or multilayer perceptrons), which incorporates convolution operations in at least one of its computational layers and is typically applied to input data with grid-like topology, such as image data.43 A feedforward neural network is made up of a number of concatenated computational layers, where the computational outcome, namely the feature map, of each layer is simply a mathematical mapping of the output of the previous layer. The composition of all computational layers contained in the network together defines a mapping from the input tensor (3-D image matrix in our study here) to the output tensor (1-D class vector in our study here), where is a set of mapping parameters (or weights) to be learned during the training process.43
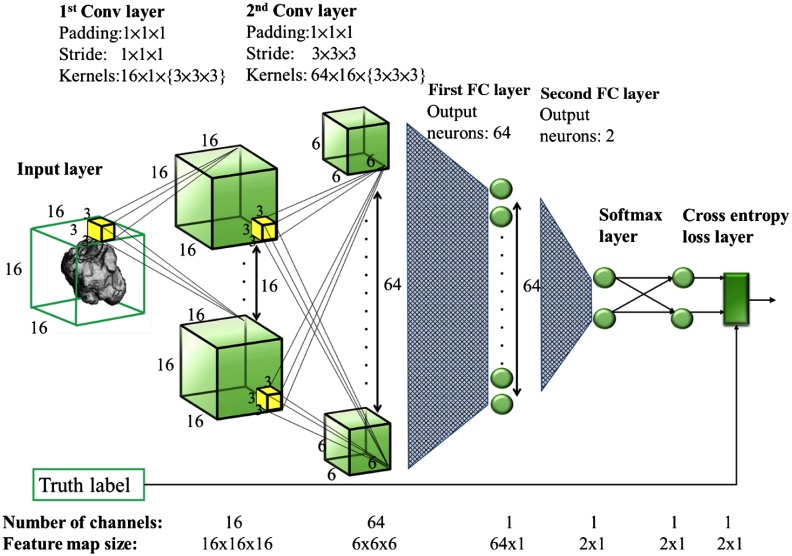
Two 3-D CNN architectures, CNN1 and CNN2, are considered in this paper. CNN1 takes an input image of size and consists of two 3-D convolutional (conv) layers followed by two fully connected (FC) layers with one rectified linear units (ReLU) layer inserted between each pair of adjacent hidden layers as shown in Fig. 2. The spatial dimension and the number of channels of the feature map in each hidden layer are denoted at the bottom of the figure. The dimension and the number of kernels as well as the size of padding and stride used in each conv layer and the number of output neurons in each FC layer are denoted at the top of the figure. CNN2 takes an input image of size and correspondingly employs a deeper (one additional convolutional layer) and wider network as shown in Table 1.
Fig. 2.
The presented CNN1 architecture. The spatial dimension and the number of channels of the feature map in each hidden layer are denoted on the bottom. The dimension and the number of kernels as well as the size of padding and stride used in each conv layer and the number of output neurons in each FC layer are denoted on the top.
Table 1.
Description of two 3-D CNN models. The kernel size, padding size, and stride size are the same for all spatial dimensions; thus, only one number is specified in the table, e.g., kernel size of 3 indicates for 3-D network. A conv layer with kernels is denoted as conv-, with default kernel size of 3, padding of 1, and stride of 1. An FC layer with output neurons is denoted as FC-. A ReLU nonlinearity layer is inserted after each conv layer and the first FC. All parameter values other than the default are specified explicitly below. The same output layer Softmax + Cross entropy is used for both models and not shown below.
| CNN models | Input | Architecture |
|---|---|---|
| CNN1 | Size: | conv-16 + conv-64 (stride of 3) + FC-64 + FC-2 |
| Channels: 1 | ||
| CNN2 | Size: | conv-32 + conv-64 (kernel of 4 and stride of 2) + conv-64 (stride of 3) + FC-64 + FC-2 |
| Channels: 1 |
The presented CNN architecture, including the input volume size, types of layers, network depth, kernel size, and the number of kernels and neurons, was based on the architectures proposed in several recent studies,13,19,27,28,29,36 taking into consideration the size of the input image volume and the training set to avoid overfitting. It is infeasible to employ many layers of feature abstractions as discussed by Dou et al.29 since our task is a binary classification problem with a relatively small size of input or . Moreover, less complicated CNN architectures are better suited due to the small scale of the training dataset. In fact, in several recent studies13,27,28,29,36 using CNN trained from scratch for discrimination task in medical imaging processing, no more than three-convolutional layers are used and the maximal number of convolutional kernels is 64.
2.3. Ensembles of Convolutional Neural Network and Traditional Models
Classifier ensembles have been shown to consistently outperform a single best classifier,20,44,45 assuming sufficient diversity among the included classifiers. The presented CNN model can be considered complementary to the conventional machine learning models20,24 because of two main reasons. First, traditional models are built upon handcrafted features that were designed empirically with respect to gray-level distribution, size, morphology, and texture pattern, whereas the features employed by the CNN are learned by the network automatically. Second, the design of the two types of classifiers is also different, namely, they target optimizing different types of loss functions with CNN potentially providing significantly increased model capacity. Therefore, ensembles of CNN and traditional models have the potential to give rise to remarkable performance enhancement.
Two types of traditional nodule classification models, the size-universal model and size-binned model presented by Reeves et al.,6 are used in combination with the CNN model to construct ensemble models in this paper. The size-universal model consists of one classifier that is trained in the class-balanced and size-matched dataset and is applicable to classifying nodules of any size. The size-binned model consists of several classifiers, each of which is trained with and applicable to nodules of a specific size range. Both the three-bin model [including B6 for diameter of (5, 7) mm, B8 for diameter of (7, 9) mm, and B12 for diameter of (9, 14) mm] and the two-bin model [including B6 for diameter in (5, 7) mm and B8 + 12 for diameter in (7, 14) mm] were presented in Ref. 6.
The same set of handcrafted image features is used in the aforementioned two types of traditional nodule classification models. The feature set consists of 46 3-D image descriptors in terms of morphology, density, curvature, and margin gradient. The details on the definition and generation of the image features are described by Reeves et al.6 Four traditional classifiers, including distance-weighted NN,46 logistic regression (LOG),47 support vector machine with polynomial function kernel (SVMp), and support vector machine with radial basis function kernel (SVMr),48 were explored for each of the two models.
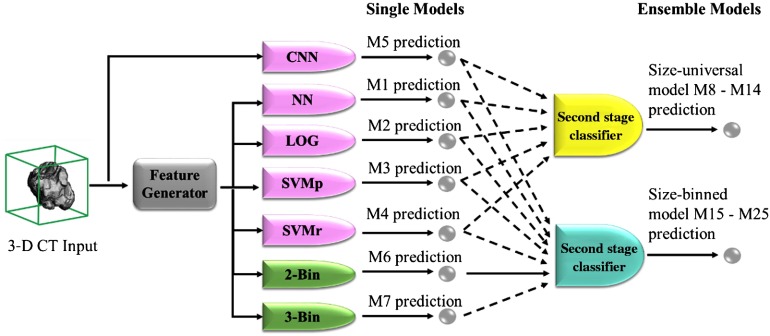
The CNN model and the traditional models are combined into ensemble models by a second-stage classifier20,23 as shown in Fig. 3. Before the combination, the classification scores predicted by each single model are first standardized to zero-mean and unit-variance. A second-stage classifier then takes the standardized scores as input features and generates classification scores to serve as the final prediction of the ensemble model.
Fig. 3.
The construction of the ensemble models. Models of four different categories are differentiated by colors: size-universal single models (pink), size-binned single models (green), size-universal ensemble models (yellow), and size-binned ensemble (blue) models. For the inputs to the second-stage classifiers, the dashed line indicates the respective input may or may not be used.
3. Experiments
For the verification of the proposed hypothesis stated at the end of the introduction, three primary experiments were conducted. First, the two CNN models were trained and evaluated using fivefold cross-validation. Second, the 3-D CNN1 model was then compared with the four size-universal traditional models presented by Reeves et al.6 Since exactly the same training–validation–testing partition and evaluation schemes were employed, the effectiveness and strength of the 3-D CNN model can be demonstrated. Third, the classifier ensembles constructed with different combinations of single classifiers were compared to explore the key to performance enhancement in classifier ensembles.
3.1. Dataset Description
The dataset was constructed by combining CT scans from two large lung cancer screening studies, the National Lung Cancer Screening Trial (NLST)40 and Early Lung Cancer Action Program (ELCAP).39 Only one instance of a nodule was used per subject. The status of malignant nodules was confirmed by either biopsy or histology of resected tissue, while the status of benign nodules was established based on a negative outcome of the biopsy or histology of resected tissue or by 2 years of no clinical change determined by a board certified radiologist.
The dataset is class-balanced with equal size distribution for benign and malignant nodules. The same number of benign and malignant nodules, namely 163 of each, was included. The size distribution for the benign nodules is the same as that for the malignant nodules: 44.79% nodules with a diameter between 5.0 and 7.0 mm, 28.22% nodules with a diameter between 7.0 and 9.0 mm, and 26.99% nodules with a diameter between 9.0 and 14.0 mm. Only solid nodules and solid components of part-solid nodules are considered, as in the study by Reeves et al.6 A summary of the distribution of the nodule sizes and classes is given in Table 2.
Table 2.
The distribution of nodule sizes and classes.
| Number of nodules | Min. size (diameter in mm) | Max. size (diameter in mm) | Average size (diameter in mm) | Median size (diameter in mm) | |
|---|---|---|---|---|---|
| Malignant | 163 | 5.01 | 14.00 | 8.05 | 7.21 |
| Benign | 163 | 5.02 | 13.91 | 8.01 | 7.27 |
| All | 326 | 5.01 | 14.00 | 8.03 | 7.22 |
The CT scans were obtained using a wide range of scanners, including Siemens, GE medical systems, Philips and Toshiba scanners, and image resolutions, where 95.4% CT scans have in-plane resolution in the range of [0.5, 1.0] mm and 98.2% CT scans have vertical resolution in the range of [1.0, 2.5] mm. More details about the process of dataset construction are described in Ref. 6.
3.2. Training and Testing
The dataset is randomly divided into five approximately equal-sized folds with balanced size and class distribution. The fivefold partition is the same as that used by Reeves et al.6 to ensure fair comparison. During the fivefold cross-validation, each fold is iteratively tested while the other four folds are further split to be used for the training set (85%) and validation set (15%). The performance of the five testing folds is averaged and considered the overall performance of the testing model.
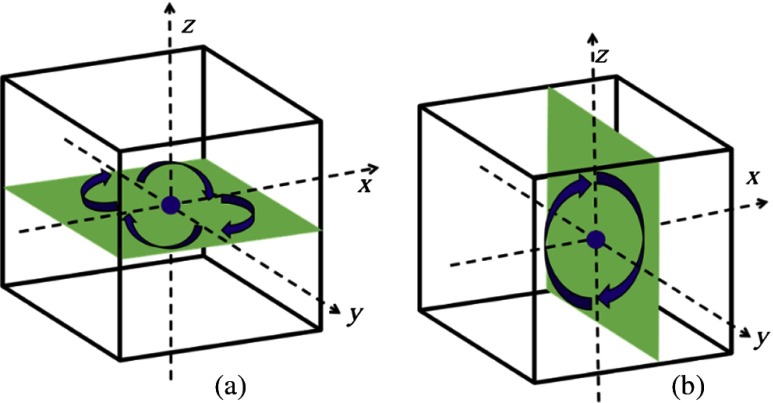
Data augmentation is employed during the training of CNN models to reduce overfitting. Each nodule volume is rotated into eight different orientations, including four rotations by 90 deg about the -axis and two rotations by 180 deg about the -axis (in this case, it can also be viewed as rotation about the -axis) as indicated in Fig. 4, which results in an augmented dataset of nodule volumes. Many additional augmentations through other angle rotations or mirroring are possible. Rotations of 90 deg about the - or -axes were avoided due to the difference in resolution between the -, -, and -dimensions; - and -resolutions of all scans are , while -resolution of all scans is and 60% scans are . The augmented data are not used during the testing.
Fig. 4.
Data augmentation by rotation. (a) Four orientations on the axial () plane and (b) two orientations along the vertical () direction.
The weights in the conv layers are initialized using random Gaussian distributions with a standard deviation of 0.01, and the weights in the FC layers are initialized according to the Xavier algorithm as suggested by Glorot and Bengio.49 In each round of the fivefold cross-validation, the network is trained up to 6000 epochs with the mini-batch size of 16 nodule image volumes. Early termination is adopted to reduce overfitting based on the performance tested in the validation set.
Stochastic gradient descent with a moment of 0.9 is used for the training. To avoid overfitting, L2 regularization and dropout (only for the first FC layer) with a dropout ratio of 0.5 are incorporated. The initial learning rate and weight decay parameter are hyperparameters tuned by random search in the range and based on the performance tested in the validation set. The learning rate is decreased according to the strategy defined as
| (1) |
where is the learning rate at training iteration of .
The CNN is implemented and evaluated using Caffe framework50 on 5 Intel(R) CPUs 2.6 GHZ with CentOS Linux OS and 2 NVIDIA Tesla K40c GPUs.
3.3. Ensembles
As is summarized in Table 3 and Fig. 3, 18 ensemble models are constructed using different combinations of seven single models (M1 to M7). To demonstrate the benefits resulting from the incorporation of the 3-D CNN model into the ensembles of other traditional models, the ensemble models are constructed in pairs, one with 3-D CNN and the other without 3-D CNN, as in M8 versus M9, M10 versus M11, M12 versus M13, M3 versus M14, M15 versus M16, M17 versus M18, M19 versus M20, M21 versus M22, M23 versus M24, and M6 versus M25. Different combinations of the single models are explored with gradual exclusion of models with inferior performance, such as LOG, SVMr, and NN, to illustrate the effects of the number and quality of single models on the overall ensemble performance.
Table 3.
The summary of 25 models M1 to M25. The classifiers included in each model are marked by “+.” Each model belongs to one of the four different categories indicated in the leftmost column: size-universal single model (M1 to M5), size-binned single model (M6 to M7), size-universal ensemble model (M8 to M14), and size-binned ensemble model (M15 to M25). The results for each model are shown in the six rightmost columns. The overall AUC and AUC for each size bin are averaged over fivefolds with corresponding standard deviation () reported below. The two rightmost columns are the -values for the difference of ROC compared with the M3 (SVMp) and M6 (two-bin), respectively. AUC shown in bold indicates the largest in each category. -values show in bold indicate it is below the significant level (0.05), thus statistically significant.
| Size-universal | Size-binned | Results | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NN | LOG | SVMp | SVMr | CNN | Two-bin | Three-bin | AUC for | AUC for | AUC for | Overall | -value compared to M3 (SVMp) | -value compared to M6 (two-bin) | ||
| Size-universal single | M1 | + | 0.862 | 0.160 | ||||||||||
| M2 | + | 0.289 | 0.014 | |||||||||||
| M3 | + | 0.494 | ||||||||||||
| M4 | + | 0.639 | 0.213 | |||||||||||
| M5 | + | 0.256 | 0.444 | |||||||||||
| Size-binned single | M6 | + | 0.494 | |||||||||||
| M7 | + | 0.956 | 0.451 | |||||||||||
| Size-universal ensemble | M8 | + | + | + | + | 0.650 | 0.219 | |||||||
| M9 | + | + | + | + | + | 0.028 | 0.859 | |||||||
| M10 | + | + | + | 0.499 | 0.399 | |||||||||
| M11 | + | + | + | + | 0.740 | |||||||||
| M12 | + | + | 0.482 | 0.384 | ||||||||||
| M13 | + | + | + | 0.788 | ||||||||||
| M14 | + | + | 0.818 | |||||||||||
| Size-binned ensemble | M15 | + | + | + | + | + | + | 0.816 | 0.644 | |||||
| M16 | + | + | + | + | + | + | + | 0.078 | 0.359 | |||||
| M17 | + | + | + | + | + | 0.688 | 0.627 | |||||||
| M18 | + | + | + | + | + | + | 0.040 | 0.144 | ||||||
| M19 | + | + | + | + | 0.679 | 0.533 | ||||||||
| M20 | + | + | + | + | + | 0.026 | 0.153 | |||||||
| M21 | + | + | + | 0.571 | 0.599 | |||||||||
| M22 | + | + | + | + | 0.030 | 0.032 | ||||||||
| M23 | + | + | 0.572 | 0.622 | ||||||||||
| M24 | + | + | + | 0.015 | 0.017 | |||||||||
| M25 | + | + | 0.013 | |||||||||||
For the selection of the second-stage classifier, nine different classifiers including KNNs,46 LOG, linear SVM,51 SVMp, SVMr, decision tree, random forest,52 AdaBoosted tree,53 and Gaussian naive Bayes54 are explored, with hyperparameters in each classifier tuned using the validation set. For each ensemble model, the classifier that achieved the best performance (averaged over fivefolds) in the validation set is selected as the second-stage classifier. The training and evaluation of the classifier ensembles are implemented using the Scikit-learn python package.55
3.4. Evaluation
The ROC curve averaged over five cross-validation folds for each classifier is plotted, and the respective area under the curve (AUC) and standard deviation () are reported. As a measure of the difference between a pair of ROC curves, the statistical significance -value (with significance level of 0.05) of the difference is computed based on the DeLong test.56 The -values for five cross-validation folds are combined using Fisher’s method.57,58 The statistical tests on ROC curves are implemented using pROC R package.59
4. Results
The performance comparison for two presented 3-D CNN models, CNN1 and CNN2, is summarized in Table 4. CNN1 outperforms CNN2; thus, it is used in the construction of ensemble models listed in Table 3. The performance of 7 single models and 18 ensemble models is summarized in Table 3. The columns marked by “+” indicate the classifiers included in the respective model on each row. The performance of each model is summarized in six rightmost columns, including overall , for each size bin and the -values for the ROC difference compared with M3 (SVMp) and M6 (two-bin). M3 and M6 are selected as references because they are the best traditional size-universal single model and the best traditional size-binned model, respectively.
Table 4.
The summary of performance of two 3-D CNN models, CNN1 and CNN2. The overall AUC and AUC for each size bin are averaged over fivefolds with corresponding standard deviation () reported below.
| CNN models | AUC for | AUC for | AUC for | Overall |
|---|---|---|---|---|
| CNN1 | ||||
| CNN2 |
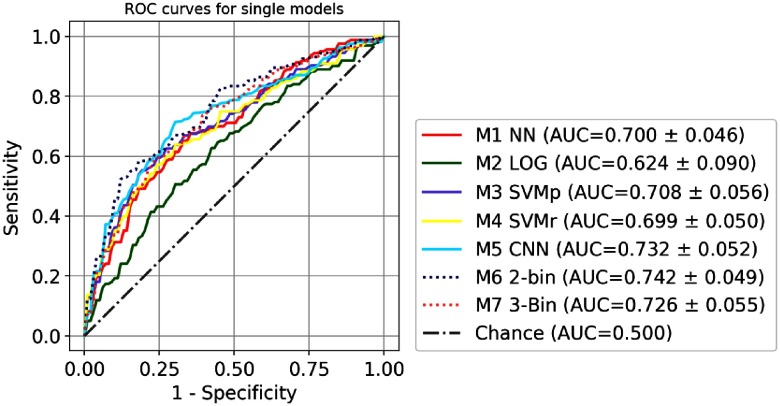
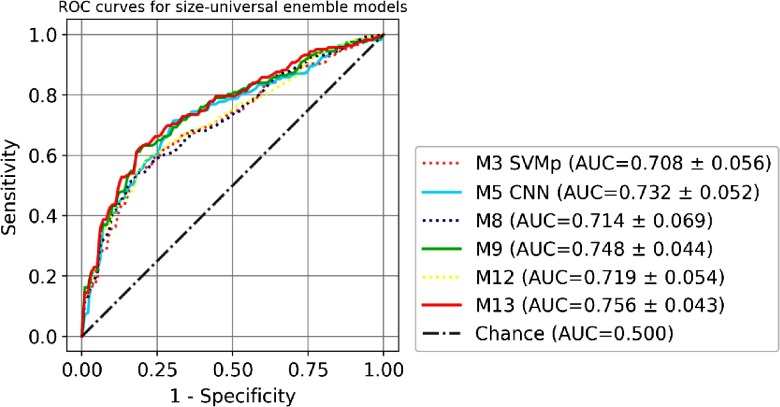
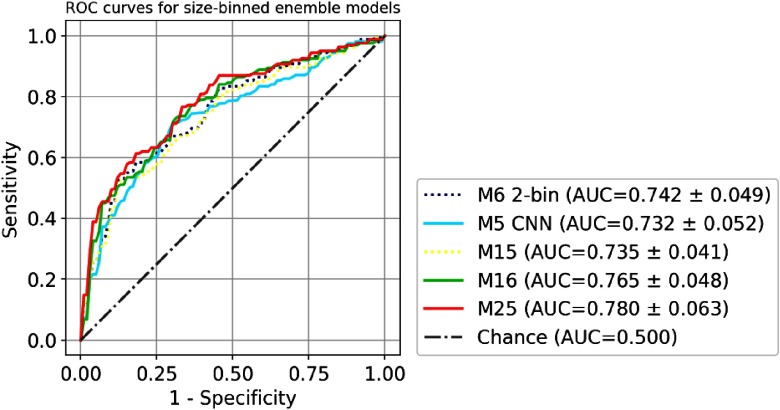
The comparison of the ROC curves of seven single models (M1 to M7) is shown in Fig. 5. Size-universal models (M1 to M5) are plotted in a solid line, and size-binned models (M6 to M7) are plotted in a dashed line. The comparison of the ROC curves of four size-universal ensemble models (M8, M9, M12, and M13) is shown in Fig. 6. Two single models M3 SVMp and M5 CNN are also shown for reference since they are the best traditional size-universal single model and the best size-universal single model, respectively. The models (M5, M9, and M13) that include CNN are plotted in solid lines, and the models (M3, M8, and M12) that are built only with traditional models are plotted in dashed lines. The comparison of the ROC curves of three size-binned ensemble models (M15, M16, and M25) is shown in Fig. 7. Two single models M6 two-bin and M5 CNN (size-universal) are also shown for reference since they are the best traditional single model and the best size-universal model, respectively. The models (M5, M16, and M25) that include CNN are plotted in solid lines, and the models (M6 and M15) that are built only with traditional models are plotted in dashed lines. For the clarity of the figures, not all ensemble models in Table 3 are included in the plots.
Fig. 5.
The comparison of ROC of single models M1 to M7. The size-universal models (M1 to M5) are plotted in solid lines, and the size-binned models are plotted in dashed lines (M6 to M7).
Fig. 6.
The comparison of ROC of size-universal ensemble models M8, M9, M12, and M13. Two single models M3 SVMp and M5 CNN are also shown for reference. Models that include CNN are plotted in solid lines, and the models that are built only with traditional models are plotted in dashed lines.
Fig. 7.
The comparison of ROC of size-binned ensemble models M15, M16, and M25. Two single models M6 2-bin and M5 CNN (size-universal) are also shown for reference. Models that include CNN are plotted in solid lines, and the models that are built only with traditional models are plotted in dashed lines.
5. Discussion
The task of 3-D nodule analysis in lung cancer screening differs from the traditional tasks in 2-D imaging in that there is a very wide range of nodule sizes, resulting in the number of pixels on target for a nodule varying by a factor of 57 in our dataset. The difference in resolution is shown in Figs. 8(g) and 8(n). With the CNN1 () model, the largest 27.6% of the nodules were slightly under-sampled, with most of these nodules in the B12 group, while there was no under-sampling for the CNN2 () model. This may account for the difference in performance between the two models as shown in Table 4. The CNN1 model had better performance for the smaller nodules in the B6 and B8 groups, while the CNN2 model exhibited better performance for the larger and more detailed nodules in the B12 group. A better classification model can be constructed without any retraining by simply using CNN1 for nodules in B6 and B8 and using CNN2 for nodules in B12, and it achieves overall as , although the ROC difference is not statistically significant with respect to CNN1.
Fig. 8.
(a–e) Five axial CT slices sampled from the input 3-D volume of a nodule (nodule 1) with diameter of 5.1 mm, (f) the segmentation of nodule 1 shown in 3-D axial view, (h–l) five axial CT slices sampled from the input 3-D volume of a nodule (nodule 2) with diameter of 12.09 mm, (m) the segmentation of nodule 2 is shown in 3-D axial view, (g, n) axial slices cropped from original CT before rescaling, corresponding to (c, j) respectively. Since the nodules are first cropped based on nodule size and then scaled to the same image size, the image appearance of the nodule and nearby structures (such as vessels) can be rather different.
The size-universal single classification model of 3-D CNN (M5) has been shown to achieve better AUC compared with the size-universal single models (M1 to M4) constructed using handcrafted features and traditional machine learning approaches as shown in Fig. 5 and Table 3, although the ROC difference between the 3-D CNN model and the best traditional model M3 is not statistically significant (-value 0.256). Since the exact same fivefold training and testing partition and evaluation scheme were used, the direct performance comparison demonstrates the strength of the 3-D CNN approach with the benefits of eliminating manual feature design and selection, which relies on task-specific expert knowledge and can be rather time consuming. Moreover, due to the much smaller scale of available training examples compared with computer vision applications in natural images,11,14,15,16 it is reasonable to hypothesize that better performance can be obtained by the 3-D CNN model if more training examples are available, and, thus, deeper network architectures can be utilized, based on the relation between the performance and the dataset size observed in other studies.60,27
The size-binned single models (M6 and M7) outperform all the size-universal single models (M1 to M5) as shown in Fig. 5 and Table 3, although the ROC difference between the best size-binned model M6 and the best size-universal model 3-D CNN M5 is not statistically significant (-value 0.444). It suggests that, given more training examples, a size-binned 3-D CNN model may potentially achieve better performance than its size-universal counterpart because of the advantage of considering the nodules of different size ranges separately. Additionally, in the presented size-universal 3-D CNN model, to ensure a uniform target object scale that is usually considered helpful for the training of CNNs, nodules of different sizes are scaled to image volumes of the same size in pixels. This results in very different image representations of nodules and nearby structures, such as more blurring effect and larger scale of the attached vessels for small nodules, as shown in Fig. 8, and, thus, has a potential negative effect on the final classification performance. Unfortunately, due to the limited size of current dataset, a size-binned 3-D CNN cannot be trained to converge, as only 44.79% of the training set can be used to train a 3-D CNN for size bin B6, 28.22% of the training set for bin size B8, and 26.99% of the training set for bin size B12. Finally, for all models shown in Table 3, the best overall AUC is 0.735 for B6, 0.823 for B8, and 0.830 for B12, which is consistent with the classification of small nodules being more challenging6,8 due to the larger number of target pixels for larger nodules.
The incorporation of the 3-D CNN model into the ensembles of other traditional models always leads to performance enhancement compared with the ensemble counterparts without the 3-D CNN as shown in Table 3 and Figs. 6 and 7 (solid lines versus dashed lines). The models with the best performance in each of the three categories shown in Table 3, including M5 for size-universal single model, M13 for size-universal ensemble model, and M25 for size-binned ensemble model, all include 3-D CNN in its composition, whereas the simple combination of traditional models, such as M8, M10, M12, M15, M17, M19, M21, and M23, can only lead to negligible performance improvement compared with the best single model, with no statistical significance, as shown in Table 3. The ROC differences between the best performance ensemble models and the respective best performance traditional single model, i.e., M13 versus M3, and M25 versus M6, are statistically significant (-values ).
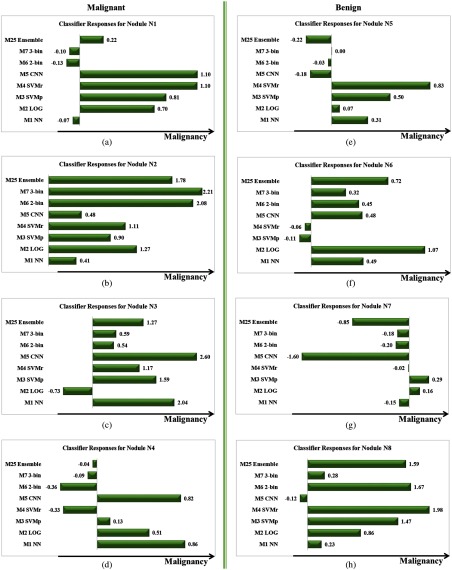
The results of the ensemble models demonstrate that the diversity among the individual models in the composition is the key to the success of the ensembles, which is consistent with the discussion by Kittler et al.44 and Kuncheva and Whitaker.45 As illustrated in the examples given in Figs. 9 and 10, misclassifications by different single classifiers (M1 to M7) often do not overlap; consequently, different single classifiers usually exhibit complementary advantages in recognizing different image patterns, leading to an optimized classifier ensemble. Since all of the traditional models explored in this paper are built upon the same set of handcrafted image features and trained with the same training data, the diversity among them is limited. On the contrary, the 3-D CNN model takes the raw image volumes as inputs and learns the features automatically by the network itself, which often provides complementary information about the image patterns to be classified compared with the traditional models,20,24 and, thus, can potentially be harnessed to improve the overall ensemble performance.
Fig. 9.
Examples of malignant nodules N1 to N4 (a–h) shown on the first row and benign nodules N5 to N8 (i–p) shown on the second row. For each nodule, the central axial slice from the CT scan is shown on the left, and the segmentation of each nodule is shown in 3-D axial view on the right.
Fig. 10.
The model response output by seven single models (M1 to M7) and the best ensemble model (M25) for nodules N1 to N8 as defined in Fig. 9. Malignant nodules N1 to N4 (a–d) are shown in the left column and benign nodules N5 to N8 (e–h) are shown in the right column. For the purpose of direct comparison, the classifier response output by each model has been normalized to zero mean and unit standard deviation. A larger value of response indicates a higher probability for malignancy predicted by the model.
Excluding single models with inferior performance from the ensemble models can also be beneficial to the ensemble performance as can been seen in the comparison of M13 versus M9 and M25 versus M16 in Table 3. On the other hand, excluding more single classifiers with inferior performance may be detrimental to the ensemble performance due to the decreased diversity as can been seen in the comparison of M14 versus M13 in Table 3. Therefore, the number of single models to be included needs to be optimized in the construction of ensemble models.
This paper is the first study to employ a 3-D CNN trained from scratch to address pulmonary nodule classification from low-dose chest CT. Due to the consideration of the full 3-D image volume, it has the potential for better performance32,31,29 compared with other work based on 2-D CNN.35,24 In addition, unlike using a pretrained CNN in the study by Buty et al.,24 training a CNN from scratch eliminates the constraint on using the same network architecture as the pretrained CNN, which may be suboptimal for the specific task of interest.21,22 However, in the situation where the computation resource is limited and the training data are insufficient to train a deep neural network, which is often true for automated applications in medical imaging,21 the use of 2-D CNN becomes attractive because it avoids the need for training from scratch and allows the utilization of off-the-shelf deep features and fine-tuning from pretrained networks that were trained with large-scale annotated natural image datasets.12,21
To quantify the benefit of using a 3-D CNN architecture for pulmonary nodule classification, a 2-D CNN model, CNN3, with comparable network architecture to the best performing 3-D CNN model, CNN1, was also evaluated. The 2-D network maps each 3-D volumetric image into a three-channel 2-D image by assigning three orthogonal views (axial, coronal, and sagittal views centered at the nodule) to different input channels following the approach used in Refs. 20, 23, and 24. Thus, the 2-D architecture is described by: conv-16 (stride of 1) + conv-64 (stride of 3) + FC-64 + FC-2, which compares with CNN1 as described in Table 1. The same dataset (including the same image preprocessing, data augmentation, and cross-validation split) and the training strategy as described in the Secs. 2 and 3 were used for the 2-D model. The hyperparameters, including the initial learning rate and weight decay parameter , were retuned for the 2-D model based on the performance tested in the validation set. The 2-D network achieved an overall AUC of 0.688, which is less than the overall AUC for the 3-D network of 0.732; a difference of 0.44. CNN3 may not be the optimal 2-D architecture for this task; other 2-D architectures were considered, but none of them outperformed the 3-D model CNN1.
The malignancy status of nodules was established in this paper by either biopsy or histology of resected tissue, which should be considered a much more reliable truth reference compared with the subjective malignancy ratings of radiologists. The nodules exhibit a significant intraclass variation in image appearance on CT scans, i.e., a wide variation among the same class (benign or malignant), as demonstrated by the examples listed on the same row in Fig. 9, whereas the interclass variations can be small, i.e., the appearance of the benign and malignant nodules can be rather similar, which makes the visual discrimination between benign and malignant nodules challenging, as demonstrated by the examples listed in the same column in Fig. 9. As shown in the observer study in LUNGx challenge,2 the interobserver variations among experienced thoracic radiologists in the task of malignancy rating even on diagnostic chest CT are significant, with AUC ranging from 0.70 to 0.85. As a result, the presented study cannot be directly compared with the studies using subjective malignancy ratings as the truth reference.5,24,26,27
In future work, there are two possible extensions to consider. First, different ensemble classifiers can be trained for nodules of different size ranges to take advantage of the fact that the performance for some single classifier is superior for one size bin but inferior for another size bin. Second, the complementary information learned by conventional classifiers can be incorporated into the CNN by feeding predictions of conventional models or handcrafted features as input to the FC layers and then trained from end-to-end to replace the use of ensemble classifiers.
6. Conclusion
This paper presents a 3-D CNN trained from scratch for the challenging task of classifying pulmonary nodule malignancy from low-dose chest CT obtained from the annual screening of lung cancer. The dataset consisting of 326 nodules is constructed with balanced size and class distribution with the malignancy status pathologically confirmed. The experiments were designed to replicate those in the study by Reeves et al.6 using the exact same fivefold training and testing partition, truth definition, and evaluation scheme for the direct performance comparison of the 3-D CNN and conventional approaches. The results demonstrate three primary advantages of applying 3-D CNN to pulmonary nodule classification. First, both the 3-D CNN single model (AUC of 0.732) and the ensemble models with 3-D CNN (AUC of 0.780) outperform the respective counterparts constructed using only traditional machine learning models (AUC of 0.708 for the best single traditional model and AUC of 0.748 for the best ensemble model constructed without CNN). Second, 3-D CNN models eliminate the procedure of manual feature design and selection that are required by the traditional machine learning models and rely heavily on domain-specific expert knowledge. Third, complementary information of nodules can be learned by the 3-D CNN and the conventional models, which together are combined to construct an ensemble model with statistically significant performance improvement (-value ) compared with any single traditional model in its composition. Although the current best performance model with AUC of 0.780 is insufficient for direct diagnosis in the clinical practice, the automated prediction outcome may be useful in improving the lung cancer screening follow-up protocol, which currently mainly depends on the nodule size.
Acknowledgments
We gratefully acknowledge the contributions of Robert Gillies and Yoganand Balagurunathan of the Moffitt Cancer Center and support by U01 CA143062-04 in the preparation of the NLST image dataset. We gratefully acknowledge the support of Claudia Henschke and David Yankelevitz of the Icahn School of Medicine at Mount Sinai for making the Weill Cornell dataset available to this project. This work was funded in part by the Flight Attendants’ Medical Research Foundation (FAMRI) and NSF award CBET-1014813.
Biographies
Shuang Liu is currently a PhD candidate in the School of Electrical and Computer Engineering, Cornell University, Ithaca, New York. She received her BS degree in electrical engineering from Zhejiang University, China, in 2011 and her MS degree in electrical engineering from Stanford University, Stanford, California, in 2013. Her research interests are in the areas of fully automated medical image analysis, computer-aided diagnosis, computer vision, and machine learning.
Yiting Xie is currently pursuing a PhD at Cornell University Vision and Image Analysis Group advised by Dr. Anthony P. Reeves. Her research mainly focuses on the automated quantitative analysis of CT images in the cardiac and lung regions. Before coming to Cornell, she worked in the CyLab Biometrics Center at Carnegie Mellon University advised by Dr. Marios Savvides.
Artit Jirapatnakul is an assistant professor in the Department of Radiology at the Ichan School of Medicine at Mount Sinai. He holds a PhD in electrical and computer engineering from Cornell University. His research interests include medical imaging and machine learning, particularly as applied to detecting and diagnosing disease from low-dose chest CT scans. His work includes the development of algorithms, software, and databases to support CAD research.
Anthony P. Reeves is a professor in the School of Electrical and Computer Engineering and director of the Vision and Image Analysis (VIA) Group at Cornell University. His research interests include computer methods for analyzing digital images with a focus on accurate image measurements and biomedical applications. The VIA group in collaboration with the Early Lung Action Program (ELCAP) pioneered volumetric growth rate analysis for pulmonary nodules. He is a senior member of SPIE.
Disclosures
Shuang Liu, Yiting Xie, and Artit Jirapatnakul declare that they have no conflict of interest. Anthony Reeves financial and research disclosures: Financial: (1) General Electric: Dr. Reeves is a coinventor on a patent and other pending patents owned by Cornell Research Foundation (CRF), which are nonexclusively licensed and related to technology involving computer-aided diagnostic methods, including measurement of pulmonary nodules in CT images. (2) D4Vision Inc.: Dr. Reeves is the owner of D4Vision Inc., a company that licenses software for image analysis. Research: Dr. Reeves receives research support in the form of grants and contracts from NSF and the Flight Attendants’ Medical Research Institute.
References
- 1.Rose V. P. D., et al. , “Use of lung cancer screening tests in the United States: results from the 2010 National Health Interview Survey,” Cancer Epidemiol. Prev. Biomarkers 21(7), 1049–1059 (2012). 10.1158/1055-9965.EPI-12-0343 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Armato S. G., et al. , “LUNGx challenge for computerized lung nodule classification,” J. Med. Imaging 3(4), 044506 (2016). 10.1117/1.JMI.3.4.044506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Aoyama M., et al. , “Computerized scheme for determination of the likelihood measure of malignancy for pulmonary nodules on low‐dose CT images,” Med. Phys. 30(3), 387–394 (2003). 10.1118/1.1543575 [DOI] [PubMed] [Google Scholar]
- 4.Armato S. G., et al. , “Automated lung nodule classification following automated nodule detection on CT: a serial approach,” Med. Phys. 30(6), 1188–1197 (2003). 10.1118/1.1573210 [DOI] [PubMed] [Google Scholar]
- 5.Han F., et al. , “Texture feature analysis for computer-aided diagnosis on pulmonary nodules,” J Digit Imaging 28(1), 99–115 (2015). 10.1007/s10278-014-9718-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Reeves A. P., Xie Y., Jirapatnakul A., “Automated pulmonary nodule CT image characterization in lung cancer screening,” Int. J. Comput. Assisted Radiol. Surg. 11(1), 73–88 (2016). 10.1007/s11548-015-1245-7 [DOI] [PubMed] [Google Scholar]
- 7.Suzuki K., et al. , “Computer-aided diagnostic scheme for distinction between benign and malignant nodules in thoracic low-dose CT by use of massive training artificial neural network,” IEEE Trans. Med. Imaging 24(9), 1138–1150 (2005). 10.1109/TMI.2005.852048 [DOI] [PubMed] [Google Scholar]
- 8.Jirapatnakul A. C., et al. , “Pulmonary nodule classification: size distribution issues,” in 4th IEEE Int. Symp. on Biomedical Imaging: From Nano to Macro (SBI 2007), pp. 1248–1251, IEEE; (2007). 10.1109/ISBI.2007.357085 [DOI] [Google Scholar]
- 9.Reeves A. P., et al. , “On measuring the change in size of pulmonary nodules,” IEEE Trans. Med. Imaging 25(4), 435–450 (2006). 10.1109/TMI.2006.871548 [DOI] [PubMed] [Google Scholar]
- 10.LeCun Y., et al. , “Backpropagation applied to handwritten zip code recognition,” Neural Comput. 1(4), 541–551 (1989). 10.1162/neco.1989.1.4.541 [DOI] [Google Scholar]
- 11.Krizhevsky A., Sutskever I., Hinton G. E., “ImageNet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems, pp. 1097–1105 (2012). [Google Scholar]
- 12.Deng J., et al. , “ImageNet: a large-scale hierarchical image database,” in IEEE Conf. on Computer Vision and Pattern Recognition (CVPR 2009), pp. 248–255, IEEE; (2009). 10.1109/CVPR.2009.5206848 [DOI] [Google Scholar]
- 13.Setio A. A. A., et al. , “Pulmonary nodule detection in CT images: false positive reduction using multi-view convolutional networks,” IEEE Trans. Med. Imaging 35(5), 1160–1169 (2016). 10.1109/TMI.2016.2536809 [DOI] [PubMed] [Google Scholar]
- 14.Sermanet P., et al. , “Overfeat: integrated recognition, localization and detection using convolutional networks,” arXiv:1312.6229 (2013).
- 15.Simonyan K., Zisserman A., “Very deep convolutional networks for large-scale image recognition,” arXiv:1409.1556 (2014).
- 16.Szegedy C., et al. , “Going deeper with convolutions,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, pp. 1–9 (2015). 10.1109/CVPR.2015.7298594 [DOI] [Google Scholar]
- 17.He K., et al. , “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, pp. 770–778 (2016). 10.1109/CVPR.2016.90 [DOI] [Google Scholar]
- 18.Litjens G., et al. , “A survey on deep learning in medical image analysis,” arXiv:1702.05747 (2017). [DOI] [PubMed]
- 19.Shin H. C., et al. , “Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning,” IEEE Trans. Med. Imaging 35(5), 1285–1298 (2016). 10.1109/TMI.2016.2528162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.van Ginneken B., et al. , “Off-the-shelf convolutional neural network features for pulmonary nodule detection in computed tomography scans,” in IEEE 12th Int. Symp. on Biomedical Imaging (ISBI 2015), pp. 286–289, IEEE; (2015). 10.1109/ISBI.2015.7163869 [DOI] [Google Scholar]
- 21.Huynh B. Q., Li H., Giger M. L., “Digital mammographic tumor classification using transfer learning from deep convolutional neural networks,” J. Med. Imaging 3(3), 034501 (2016). 10.1117/1.JMI.3.3.034501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Antropova N., Huynh B., Giger M., “Performance comparison of deep learning and segmentation-based radiomic methods in the task of distinguishing benign and malignant breast lesions on DCE-MRI,” Proc. SPIE 10134, 101341G (2017). 10.1117/12.2255582 [DOI] [Google Scholar]
- 23.Ciompi F., et al. , “Automatic classification of pulmonary peri-fissural nodules in computed tomography using an ensemble of 2D views and a convolutional neural network out-of-the-box,” Med. Image Anal. 26(1), 195–202 (2015). 10.1016/j.media.2015.08.001 [DOI] [PubMed] [Google Scholar]
- 24.Buty M., et al. , “Characterization of lung nodule malignancy using hybrid shape and appearance features,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 662–670, Springer International Publishing; (2016). [Google Scholar]
- 25.Roth H. R., et al. , “A new 2.5 D representation for lymph node detection using random sets of deep convolutional neural network observations,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 520–527, Springer International Publishing, Vancouver: (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shen W., et al. , “Multi-scale convolutional neural networks for lung nodule classification,” in Int. Conf. on Information Processing in Medical Imaging, pp. 588–599, Springer International Publishing; (2015). [DOI] [PubMed] [Google Scholar]
- 27.Shen W., et al. , “Multi-crop convolutional neural networks for lung nodule malignancy suspiciousness classification,” Pattern Recognit. 61, 663–673 (2017). 10.1016/j.patcog.2016.05.029 [DOI] [Google Scholar]
- 28.Hamidian S., et al. , “3D convolutional neural network for automatic detection of lung nodules in chest CT,” Proc. SPIE 10134, 1013409 (2017). 10.1117/12.2255795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dou Q., et al. , “Automatic detection of cerebral microbleeds from MR images via 3D convolutional neural networks,” IEEE Trans. Med. Imaging 35(5), 1182–1195 (2016). 10.1109/TMI.2016.2528129 [DOI] [PubMed] [Google Scholar]
- 30.Mehrtash A., et al. , “Classification of clinical significance of MRI prostate findings using 3D convolutional neural networks,” Proc. SPIE 10134, 101342A (2017). 10.1117/12.2277123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Li J., et al. , “Discriminating between benign and malignant breast tumors using 3D convolutional neural network in dynamic contrast enhanced-MR images,” Proc. SPIE 10138, 1013808 (2017). 10.1117/12.2254716 [DOI] [Google Scholar]
- 32.Çiçek Ö., et al. , “3D u-net: learning dense volumetric segmentation from sparse annotation,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 424–432, Springer International Publishing; (2016). [Google Scholar]
- 33.Kleesiek J., et al. , “Deep MRI brain extraction: a 3D convolutional neural network for skull stripping,” NeuroImage 129, 460–469 (2016). 10.1016/j.neuroimage.2016.01.024 [DOI] [PubMed] [Google Scholar]
- 34.Patel A., et al. , “Automatic cerebrospinal fluid segmentation in non-contrast CT images using a 3D convolutional network,” Proc. SPIE 10134, 1013420 (2017). 10.1117/12.2254022 [DOI] [Google Scholar]
- 35.Kumar D., et al. , “Lung nodule classification using deep features in CT images,” in 12th Conf. on Computer and Robot Vision (CRV 2015), pp. 133–138, IEEE; (2015). 10.1109/CRV.2015.25 [DOI] [Google Scholar]
- 36.Korez R., et al. , “Intervertebral disc segmentation in MR images with 3D convolutional networks,” Proc. SPIE 10133, 1013306 (2017). 10.1117/12.2254069 [DOI] [Google Scholar]
- 37.Korez R., et al. , “Model-based segmentation of vertebral bodies from MR images with 3D CNNs,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 433–441, Springer International Publishing; (2016). [Google Scholar]
- 38.Zheng Y., et al. , “3D deep learning for efficient and robust landmark detection in volumetric data,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 565–572, Springer International Publishing; (2015). [Google Scholar]
- 39.International Early Lung Cancer Action Program Investigators, “Survival of patients with stage I lung cancer detected on CT screening,” N. Engl. J. Med. 2006(355), 1763–1771 (2006). 10.1056/NEJMoa060476 [DOI] [PubMed] [Google Scholar]
- 40.National Lung Screening Trial Research Team, “Reduced lung-cancer mortality with low-dose computed tomographic screening,” N. Engl. J. Med. 2011(365), 395–409 (2011). 10.1056/NEJMoa1102873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Davis J., Goadrich M., “The relationship between precision-recall and ROC curves,” in Proc. of the 23rd Int. Conf. on Machine Learning, pp. 233–240, ACM; (2006). [Google Scholar]
- 42.van Ginneken B., et al. , “Comparing and combining algorithms for computer-aided detection of pulmonary nodules in computed tomography scans: the ANODE09 study,” Med. Image Anal. 14(6), 707–722 (2010). 10.1016/j.media.2010.05.005 [DOI] [PubMed] [Google Scholar]
- 43.Goodfellow I., Bengio Y., Courville A., Deep Learning, MIT Press, Cambridge, Massachusetts: (2016). [Google Scholar]
- 44.Kittler J., et al. , “On combining classifiers,” IEEE Trans. Pattern Anal. Mach. Intell. 20(3), 226–239 (1998). 10.1109/34.667881 [DOI] [Google Scholar]
- 45.Kuncheva L. I., Whitaker C. J., “Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy,” Mach. Learning 51(2), 181–207 (2003). 10.1023/A:1022859003006 [DOI] [Google Scholar]
- 46.Dudani S. A., “The distance-weighted k-nearest-neighbor rule,” IEEE Trans. Syst. Man Cybern. SMC-6(4), 325–327 (1976). 10.1109/TSMC.1976.5408784 [DOI] [Google Scholar]
- 47.Le Cessie S., Van Houwelingen J. C., “Ridge estimators in logistic regression,” Appl. Stat. 41, 191–201 (1992). 10.2307/2347628 [DOI] [Google Scholar]
- 48.Suykens J. A., Vandewalle J., “Least squares support vector machine classifiers,” Neural Process. Lett. 9(3), 293–300 (1999). 10.1023/A:1018628609742 [DOI] [Google Scholar]
- 49.Glorot X., Bengio Y., “Understanding the difficulty of training deep feedforward neural networks,” in Proc. of the Thirteenth Int. Conf. on Artificial Intelligence and Statistics, Vol. 9, pp. 249–256 (2010). [Google Scholar]
- 50.Jia Y., et al. , “Caffe: convolutional architecture for fast feature embedding,” in Proc. of the 22nd ACM Int. Conf. on Multimedia, pp. 675–678, ACM; (2014). [Google Scholar]
- 51.Cortes C., Vapnik V., “Support-vector networks,” Mach. Learn. 20(3), 273–297 (1995). [Google Scholar]
- 52.Ho T. K., “The random subspace method for constructing decision forests,” IEEE Trans. Pattern Anal. Mach. Intell. 20(8), 832–844 (1998). 10.1109/34.709601 [DOI] [Google Scholar]
- 53.Freund Y., et al. , “An efficient boosting algorithm for combining preferences,” J. Mach. Learn. Res. 4(Nov), 933–969 (2003). [Google Scholar]
- 54.John G. H., Langley P., “Estimating continuous distributions in Bayesian classifiers,” in Proc. of the Eleventh Conf. on Uncertainty in Artificial Intelligence, pp. 338–345, Morgan Kaufmann Publishers Inc. (1995). [Google Scholar]
- 55.Pedregosa F., et al. , “Scikit-learn: machine learning in python,” J. Mach. Learn. Res. 12(Oct), 2825–2830 (2011). [Google Scholar]
- 56.DeLong E. R., DeLong D. M., Clarke-Pearson D. L., “Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach,” Biometrics 44, 837–845 (1988). 10.2307/2531595 [DOI] [PubMed] [Google Scholar]
- 57.Birnbaum A., “Combining independent tests of significance,” J. Am. Stat. Assoc. 49(267), 559–574 (1954). 10.1080/01621459.1954.10483521 [DOI] [Google Scholar]
- 58.Fisher R. A., Statistical Methods for Research Workers, 4th ed., Oliver and Boyd, Edinburgh and London: (1932). [Google Scholar]
- 59.Robin X., et al. , “pROC: an open-source package for R and S+ to analyze and compare ROC curves,” BMC Bioinf. 12(1), 77 (2011). 10.1186/1471-2105-12-77 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Fotin S. V., et al. , “Detection of soft tissue densities from digital breast tomosynthesis: comparison of conventional and deep learning approaches,” Proc. SPIE 9785, 97850X (2016). 10.1117/12.2217045 [DOI] [Google Scholar]