Alzheimer’s Disease Diagnosis using Landmark-based Features from Longitudinal Structural MR Images

Abstract

Structural magnetic resonance imaging (MRI) has been proven to be an effective tool for Alzheimer’s disease (AD) diagnosis. While conventional MRI-based AD diagnosis typically uses images acquired at a single time point, a longitudinal study is more sensitive in detecting early pathological changes of AD, making it more favorable for accurate diagnosis. In general, there are two challenges faced in MRI-based diagnosis. First, extracting features from structural MR images requires time-consuming nonlinear registration and tissue segmentation, whereas the longitudinal study with involvement of more scans further exacerbates the computational costs. Moreover, the inconsistent longitudinal scans (i.e., different scanning time points and also the total number of scans) hinder extraction of unified feature representations in longitudinal studies. In this paper, we propose a landmark-based feature extraction method for AD diagnosis using longitudinal structural MR images, which does not require nonlinear registration or tissue segmentation in the application stage and is also robust to inconsistencies among longitudinal scans. Specifically, 1) the discriminative landmarks are first automatically discovered from the whole brain using training images, and then efficiently localized using a fast landmark detection method for testing images, without the involvement of any nonlinear registration and tissue segmentation; 2) high-level statistical spatial features and contextual longitudinal features are further extracted based on those detected landmarks, which can characterize spatial structural abnormalities and longitudinal landmark variations. Using these spatial and longitudinal features, a linear support vector machine (SVM) is finally adopted to distinguish AD subjects or mild cognitive impairment (MCI) subjects from healthy controls (HCs). Experimental results on the ADNI database demonstrate the superior performance and efficiency of the proposed method, with classification accuracies of 88.30% for AD vs. HC and 79.02% for MCI vs. HC, respectively.

I. Introduction

Dementia is a clinical syndrome that encompasses neurological disorders characterized by memory loss and cognitive impairment [1]. It is estimated that the global economic costs of dementia are more than US $818 billion in 2015 [2]. Being the most common cause of dementia in elderly people, Alzheimer’s disease (AD) accounts for up to 70% of all dementia cases, and is now estimated to be the third-leading cause of death, after heart disease and cancer [3]. Thus, in order to delay disease progression and take therapeutic measures, early diagnosis of AD, especially at its early prodromal state, such as mild cognitive impairment (MCI), is especially imperative.

In the literature, structural magnetic resonance imaging (MRI) has been proven to be an effective tool for AD diagnosis because of its capability to visualize brain anatomical structures [4], [5]. Extensive studies have focused on AD diagnosis based on cross-sectional analysis using MRI data from one single time point. In these methods, various features are extracted based on gray matter (GM) [6], [7], [8], cortical thickness [9], [10], as well as shape and volume measurement of hippocampus [11], [12]. Recently, longitudinal studies have shown more attractive clinical assessment of biomarkers [13], [14], [15]. Compared with cross-sectional study at a single time point, a longitudinal study is more sensitive to early pathological changes by focusing on both the spatial structural abnormalities and the longitudinal variations of tissues.

Generally, existing longitudinal studies largely focus on the degeneration of well-known representative biomarkers, which include hippocampal volume, ventricular volume, whole brain volume, and cortical thickness. For example, Chincarini et al. proposed four image analysis strategies based on hippocampal volume by integrating longitudinal atrophy rate as a measurement for AD diagnosis [16]. Jack et al. investigated the changing rates of four structures (i.e., hippocampus, entorhinal cortex, whole brain, and ventricle), and supported the idea of using changing rates as biomarkers for AD diagnosis [17]. Aguilar et al. analyzed the longitudinal atrophy changes in cortical thickness measures and subcortical volumes, and pointed out that using the data from two time points yielded better index results than only using one time-point data(such as cross-sectional data) [18]. Farzan et al. [19] adopted longitudinal percentage of brain volume changes and principal component analysis (PCA) [20] based feature selection strategy for AD diagnosis. The results suggested that the use of intermediate atrophy rates and their principal components improved diagnostic accuracy.

However, there are still several challenges in existing longitudinal data based analysis. 1) Time-consuming nonlinear registration or tissue segmentation step is usually required, whereas the longitudinal study with involvement of more scans further exacerbates the computational time; 2) Limited measurements may be incapable of capturing the full pattern of morphological abnormalities of the whole brain; 3) Longitudinal scans across subjects are usually inconsistent, since the scans at some time points might be missing during the data collection process.

In this study, a landmark-based feature extraction framework is proposed for AD diagnosis using longitudinal structural MR images. Different from traditional longitudinal studies, our method 1) does not require the time-consuming nonlinear registration and tissue segmentation, 2) can cover the representative morphological abnormalities from the whole brain, and 3) is able to handle the inconsistency among longitudinal scans. Specifically, the discriminative landmarks with significant morphological group differences are automatically discovered from the whole brain. By using a regression forest-based landmark detection method, these landmarks can be efficiently detected in the application stage without using conventional steps of nonlinear registration and tissue segmentation. Based on these detected landmarks, high-level spatial features and contextual longitudinal features are further extracted, respectively. Specifically, a bag-of-words strategy is used to extract high-level spatial features, by calculating the frequency of low-level landmark-based morphological features from different scanning time points. In this way, the significant spatial abnormalities from all scanning time points are aggregated together, thus also invariant to the number of longitudinal scans. In addition, to extract contextual longitudinal features, an interpolation step is first used to generate a Jacobian map from longitudinal landmark displacements. Then, contextual features can be extracted around the landmarks from the Jacobian map. Finally, a linear support vector machine (SVM) classifier [21] is adopted to perform AD/MCI classification using these spatial and longitudinal features.

Note, this work is different from our early work in [22]. Specifically, our early work [22] focused on proposing an anatomical landmark discovery approach, while in this paper we mainly propose a new feature extraction method based on anatomical landmarks, where both spatial and longitudinal feature representations are extracted from longitudinal MR images. In particular, the major contributions of this paper can be summarized as follows. First, we adopt a bag-of-words strategy to generate high-level spatial features for MR images. Second, we propose using the normalized longitudinal deformations to generate the contextual longitudinal features for MR images. Importantly, both types of features are invariant to inconsistent longitudinal scans (i.e., different scanning time points and also different numbers of total scanned MRI images in individuals) in the longitudinal studies.

The remaining sections are organized as follows. Section II first introduces the data used in this study, and then presents the image processing step in detail for identifying the discriminative landmarks. Section III describes the proposed landmark-based feature extraction procedures for both high-level spatial features and contextual longitudinal features. Section IV gives the experimental results by comparing the proposed method with competing methods, and further analyzes the influences of parameters on the performance of the proposed method. In Section V, we discuss those important components in the proposed method. Finally, the conclusion is given in Section VI.

II. Materials and Image Processing

A. Dataset

The Alzheimer’s Disease Neuroimaging Initiative (ADNI-1)¹ is a 5-year public-private partnership to test whether serial MRI, positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment and early Alzheimer’s disease. One goal of ADNI is to develop improved methods that will lead to uniform standards for acquiring longitudinal, multi-site MRI and PET data on subjects with AD, MCI, and elderly healthy controls (HCs). Subjects used in this study are from the ADNI-1 database.

In our study, the basis longitudinal scanning interval is 0.5 year. The scanning step is starting from 0 to 3 years, but some of the subjects have missing canning time points. That is, all subjects may have scans from different time points and different numbers of total scans. We selected the subjects which have at least 3 scanning time points in our experiments. Thus, there are a total of 207 age-matched HCs, 154 AD, and 346 MCI subjects. The demographic information (i.e., gender, age, and education) of the studied subjects used in this study are summarized in Table I. The statistics of scans for the studied subjects is summarized in Table II.

TABLE I.

Demographic information of selected subjects in the ADNI-1 database

	Male/Female	Age (years) (Mean±SD)	Edu. (years) (Mean±SD)
AD	81/73	75.10 ± 7.50	14.82 ± 3.08
MCI	219/127	74.33 ± 9.91	15.53 ± 3.29
HC	111/96	75.83 ± 4.98	16.10 ± 2.86

TABLE II.

Number of scans for the selected subjects in the ADNI-1 database

	3 scans	4 scans	5 scans	6 scans
AD	63	91	-	-
MCI	57	97	170	22
HC	46	145	16	-

B. Image Processing

In this paper, we adopt a data-driven landmark discovery algorithm to obtain our landmarks [22]. The image processing includes two major steps: linear alignment and landmark discovery. In the following, we describe details about the two steps.

1) Linear Alignment

All MR images are linearly aligned to a common template, namely Colin27, which was created by averaging 27 registered scans of a single subject [23]. Since the template only provides a common space for us to compare different brain images, other templates (e.g., MNI) can also be used in this case. In order to achieve high efficiency, we adopt a landmark-based affine registration method. Specifically, five pre-defined landmarks (i.e., anterior commissure (AC) and posterior commissure (PC) landmarks, and the other three representative landmarks in the mid-sagittal plane) are automatically detected by a pre-trained regression forest-based landmark detection model [24]. A global similarity transformation matrix, which encodes 7 degrees of freedom (DOF), can be estimated to model the transformation of the landmarks from the moving image to the template [25]. Since each landmark has three coordinate values, five landmarks are enough to estimate the transformation matrix.

2) Landmark Discovery based on Training Data

Our target is to identify the regions with group differences in local structures between patients and HCs in the training set. To this end, we intend to perform a voxel-wise group comparison between these two groups, following our previous work [22]. However, the linearly aligned images are not voxel-wisely comparable. In order to build the correspondences among voxels from different images, in the training stage, all training images are nonlinearly aligned to the Colin27 template after linear alignment. In general, the warped images are very similar to each other so that the subject-specific structural information in different images may not be sufficiently significant. Therefore, we extract patch-based morphological features (i.e., the 3D histogram of oriented gradients (HOG) features [26]) from linearly aligned images to describe local brain structures. By using the deformation field from nonlinear image registration, we can build correspondences between voxels in the template and all linearly-aligned images [27], [28], [29]. Therefore, for each voxel in the template, we can extract two groups of HOG features from its corresponding voxels in all training patients and HCs, respectively. We can then perform a multivariate test (i.e., Hotelling’s T² statistic [30]) on the two groups, through which a p-value can be calculated for each voxel in the template. Accordingly, a p-value map can be obtained according to the template. Finally, the local minima in the p-value map are identified as locations of discriminative landmarks in the template space. These landmarks, which are located in the template space, can be directly projected to all training images using their own deformation fields. It is worth noting that we use both baseline and longitudinal MR images in the training set for landmark detection in the training stage.

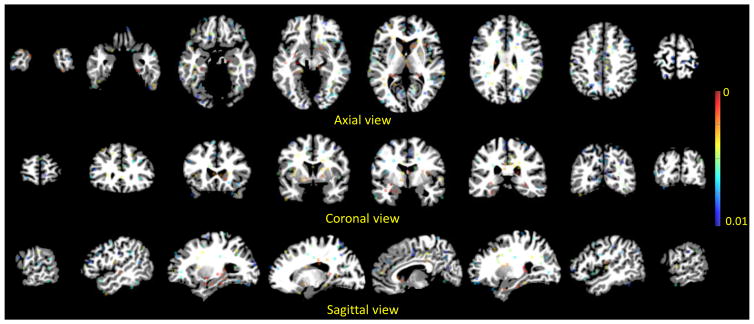
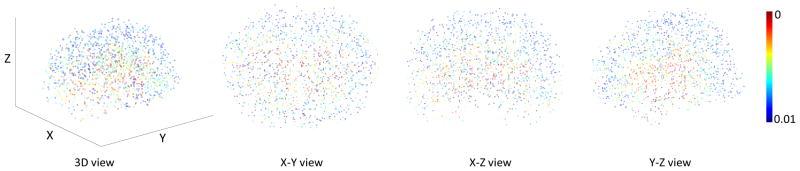
Figure 1 shows our identified landmarks via performing group comparison between AD subjects and HCs. As can be seen from this figure, the landmarks that have significant group difference (i.e., small p-values) are most located in the ventricles and hippocampus, and such phenomenon coincides with previous findings of the potential pathologic regions of AD subjects. In addition, we also illustrate the 3D distribution of our identified landmarks in Fig. 2. We can see the possible locations and distribution of all landmarks in the whole brain. From this figure, we can also discover that the landmarks close to ventricles and hippocampus have significant group difference. In addition, we further show the identified landmarks in MCI vs. HC classification in Fig. S1 in the Suppmentary Materials.

Fig. 1.

2D slice illustration of the identified landmarks in AD vs. HC classification with AD and HC subjects from ADNI-1. The color illustrates the corresponding p-value in group comparison.

Fig. 2.

3D Illustration of the identified landmarks in AD vs. HC classification with AD and HC subjects from ADNI-1. The color illustrates the corresponding p-value in group comparison.

3) Landmark Detection for Testing Data

We further train a regression-forest-based landmark detector [22] using all training images in the training stage, and apply this model to detect the respective landmarks for each testing image in the testing stage. In this way, we do not need to perform nonlinear registration for testing images. Recently, regression learning has been broadly used in detecting anatomical landmarks in 3D medical images [31], [32], [33], [34]. Particularly, regression forest is most popular due to its high efficiency, robustness, and accuracy. Specifically, the proposed regression forest in [22] is used to learn a non-linear mapping between a voxel’s local appearance and its 3D displacement to the target landmark. Therefore, by using the learned regression forest, each sampled voxel can predict a 3D displacement based on its local appearance, and then votes for a potential landmark position. The landmark position can be determined by gathering all votes and selecting the position with the most votes. Specifically, in our method, we jointly detect multiple landmarks using a multivariate regression forest [35]. In order to avoid overly strong correlations among all landmarks, the landmarks are clustered into different groups, and then landmarks in each group are detected separately. Here, landmark clustering is performed based on a dissimilarity matrix, where each entry is the variance of pairwise landmark distances across subjects. Then, we adopt normalized cuts [36] to implement final clustering. In doing so, the correlations for each group is considered relatively stable, thus the regression forest model could be accurately constructed. In this way, both training images and testing images have the same landmarks, and particularly, the landmarks for each testing image can be obtained efficiently, thanks to the fast landmark detector. More details can be found in our previous work in [22].

III. Feature Extraction and Classification

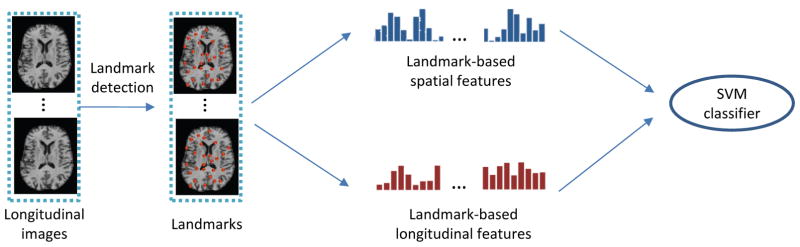
Based on the identified landmarks, we propose a landmark-based framework for extracting features from longitudinal MR images. As shown in Fig. 3, two types of landmark-based features, i.e., spatial features and longitudinal features, are extracted to describe the spatial structural abnormalities and longitudinal landmark variations, respectively. In the following, we explain details about the feature extraction process.

Fig. 3.

Framework of our efficient AD/MCI diagnosis method, including landmark detection, spatial feature and longitudinal feature extraction, and SVM-based AD classification/diagnosis.

A. Landmark-based Spatial Feature Extraction

Intuitively, in the cross-sectional study with only a single time point, the morphological features (e.g., 3D HOG, local energy pattern [37], and curvature features [38]) for all landmarks can be extracted and concatenated as strong features for classification. However, there are two challenges in the longitudinal study: 1) The numbers of scanning time points across subjects are often inconsistent due to missing time points during longitudinal study for some subjects, which makes it difficult to extract a unified feature representation for these subjects with different numbers of scans. 2) It is also difficult to identify the corresponding baseline images across different subjects, which means that a baseline scanning time point of one subject may not correspond to that of another subject. Thus, how to extract a unified spatial feature representation from subjects with inconsistent longitudinal scans is a very challenging task.

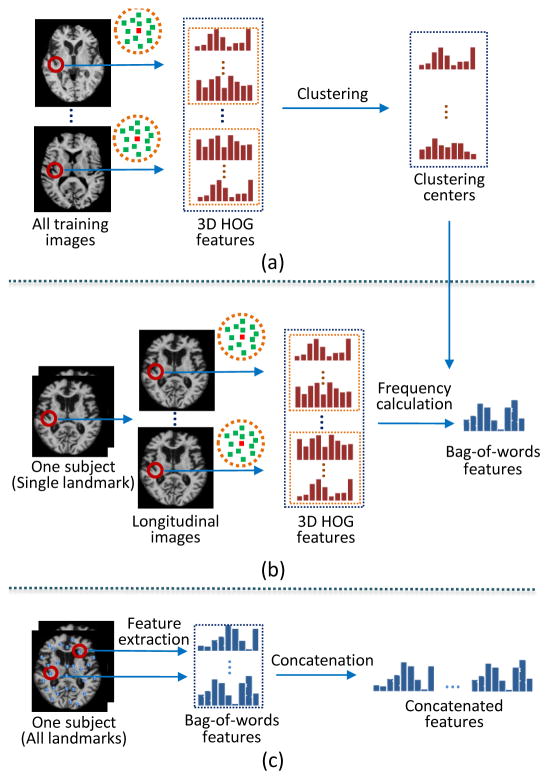
To address these two problems, we propose to use a bag-of-words strategy to extract statistical high-level spatial features. The bag-of-words strategy has demonstrated impressive performance on text, language, and image classification [39], [40], [41], [42]. Specifically, Figure 4 shows the procedure of our spatial feature extraction method, where each landmark is treated independently. As shown in Fig. 4(a), we first extract the 3D HOG feature vector for each landmark, as well as 3D HOG feature vectors for the supplementary voxels (i.e., the neighboring voxels within a small spherical patch of the landmark). After extracting features from all training images and aggregating them together, we have a set of 3D HOG feature vectors. Then, we perform K-means clustering [43] on this set of feature vectors, and build a dictionary (i.e., 𝒟) with its words (i.e., w₁, w₂, …, w_M) being the clustering centers. In the Supplementary Materials, we further show the a part of visual words learned in AD vs. HC classification and MCI vs. HC classification in Fig. S4 and Fig. S5, respectively. Then, for each individual subject, we can first extract the 3D HOG feature vectors (denoted by a feature set ℱ) for each landmark and its supplementary voxels in all longitudinal scans. The statistical histogram representation is then calculated by counting the occurrence frequencies of the clustering centers in these HOG features (i.e., ℱ), as shown in Fig. 4(b). Mathematically, the histogram representation (i.e., R) for one landmark can be defined as

Fig. 4.

Steps of extracting the high-level spatial features based on discriminative landmarks. (a) Generating the dictionary (words) by clustering the 3D HOG features from training images. (b) Counting the appearing frequency of words in a 3D HOG feature set from the longitudinal images of one subject. (c) Concatenating bag-of-words features from all landmarks of one subject.

$$R(j)=\sum _{\mathbf{f}\in ℱ}\delta ((\underset{i\in \{1,\dots ,M\}}{\text{argmin}}{\Vert \mathbf{f}-{\mathbf{w}}_i\Vert }_2^2)=j),j=1,\dots ,M,$$ (1)

where δ(·) is the Kronecker delta function defined as

$$\delta (A)=\{\begin{array}{cc}1& ifAis\mathit{true};\\ 0& \mathit{otherwise}.\end{array}$$ (2)

In order to achieve the invariance to the number of longitudinal scans, the histogram representation is ℓ₁ normalized. Finally, we extract the statistical features for all landmarks, regardless of differences in the number of scanning time points, as shown in Fig. 4(c). Here, the reasons for using supplementary voxels in the neighborhood of landmarks are two-fold: 1) The HOG feature set can be expanded to get statistical features by using the bag-of-word strategy; 2) It is also helpful to relieve potential errors in localizing landmark positions.

B. Landmark-based Longitudinal Feature Extraction

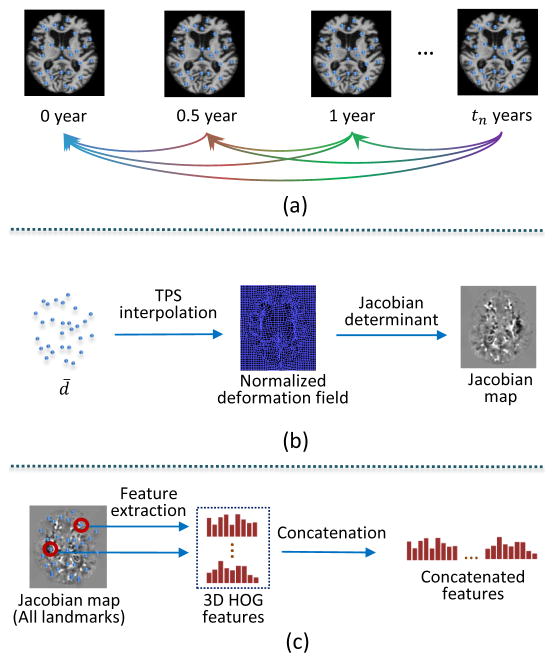
To address the inconsistent number of longitudinal scans in different subjects, we generate a normalized 3D longitudinal displacement at the beginning of feature extraction. Specifically, we first define the longitudinal displacement between two scans for one specific landmark by

$$d_{p,q}=L_{t_p}-L_{t_q},$$ (3)

where L_tp is the landmark location of the p-th scan from all longitudinal scans and t_p is the corresponding relative scanning time point with respect to the first scan. Then, the normalized 3D displacement d̄ (mean displacement per year) is calculated from all possible combinations between two scans at different scanning time points, as shown in Fig. 5. Mathematically, d̄ is defined as follows:

$$\overline{d}=\frac{1}{{\sum }_{1\le q<p\le n}1}\sum _{1\le q<p\le n}\frac{d_{p,q}}{t_p-t_q},$$ (4)

where n is the number of existing scans. As shown in Fig. 5(b), a normalized deformation field can be built by applying thin plate splines (TPS) interpolation [44] to the normalized 3D longitudinal displacement d̄ of all landmarks. Based on this normalized deformation field, a Jacobian map is further calculated to capture longitudinal volume changes. Finally, as shown in Fig. 5(c), we can extract morphological features (i.e., 3D HOG) for landmarks in the Jacobian map. Therefore, the longitudinal volume changes on these discriminative landmarks can be captured by these morphological features. It is worth noting that, instead of treating each landmark individually, the neighboring landmarks are jointly considered during the generation of the normalized deformation field. In this way, although the morphological features in the Jacobian map are extracted for each landmark individually, the contextual information about the neighboring landmarks is automatically embedded into the calculated features.

Fig. 5.

Steps of extracting the contextual longitudinal features based on discriminative landmarks. (a) An example of calculating longitudinal displacements among longitudinal images. (b) Generating a Jacobian map from the normalized deformation field interpolated by the mean longitudinal displacements. (c) Concatenating 3D HOG features from all landmarks in the Jacobian map.

C. Classification with SVM Classifier

Recently, the support vector machine (SVM) classifier [21], [45], [46], [47], [48] has been proved to be effective in distinguishing patients (AD/MCI) from HCs [49], [50], [51], [52]. Therefore, in this study, using the concatenated spatial and longitudinal landmark-based features, we adopt the linear SVM as the classifier to identify AD/MCI patients from HCs, since the linear SVM is capable of tackling our high dimensional features and has good generalization ability (due to its max-margin classification characteristic). Specifically, we first normalize those landmark-based features using the conventional z-score normalization method [53]. Then, these normalized features are fed into a linear SVM classifier for AD/MCI diagnosis.

IV. Experiments

A. Parameter Setup

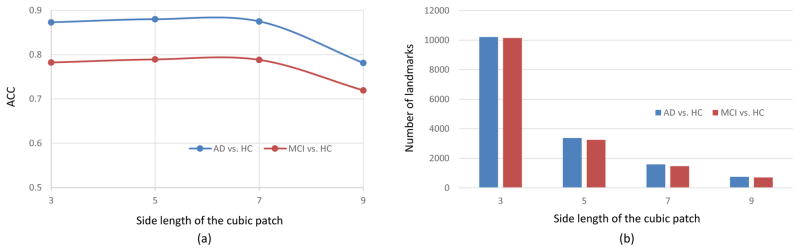
Using a 10-fold cross-validation strategy, we conduct experiments for two classification tasks, i.e., AD vs. HC and MCI vs. HC. The parameter values used in our approach are summarized as follows: For extraction of 3D HOG features, we use 9 orientations, 2 × 2 × 2 cells, and a size of 8 × 8 × 8 for each cell. Therefore, the dimensionality of 3D HOG features is 72. In the bag-of-words strategy, the number of clustering centers is set to 50, and thus the dimensionality of spatial features for each landmark is 50. The radius of the spherical region for sampling supplementary voxels around each landmark is 5. For the SVM classifier, we fix the margin parameter C = 1. Due to the data-driven property of our method, the number of landmarks is determined by the training images. In our experiment, we search the local minima within a 7 × 7 × 7 cubic patch, and obtain roughly 1500 identified landmarks for each fold of cross-validation process.

B. Experimental Results

Five classification performance measures are used, namely 1) accuracy (ACC): the number of correctly classified samples divided by the total number of samples; 2) sensitivity (SEN): the number of correctly classified positive samples (patients) divided by the total number of positive samples; 3) specificity (SPE): the number of correctly classified negative samples (controls) divided by the total number of negative samples; 4) balanced accuracy (BAC): the mean value of sensitivity and specificity; and 5) area under receiver operating characteristic (ROC) curve (AUC).

For comparison, we also report the classification results of two baseline strategies based on our landmarks. The baseline spatial features are the HOG features that are directly extracted according to the landmarks from the baseline (i.e., first scan) MR image only. The baseline longitudinal features refer to features obtained by directly using normalized displacements (i.e., d̄) of the landmarks. It is worth noting that these two baseline methods adopt a similar classification strategy as our method, i.e., using a linear SVM with C=1 as the classifier.

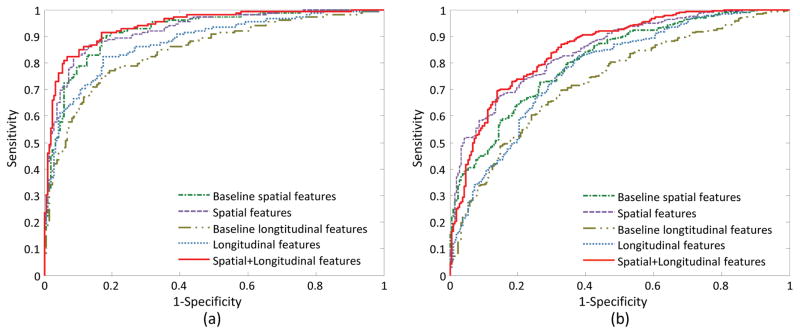
Table III reports the classification results, and Fig. 6 shows their corresponding ROC curves. These results demonstrate that, in both classification tasks, the proposed spatial features consistently outperform the baseline spatial features, and our longitudinal features generally achieve better performance than the baseline longitudinal features. Moreover, the combination of the proposed spatial and longitudinal features can further improve the classification performance.

TABLE III.

Classification results achieved by methods using different feature representations.

	AD vs. HC (%)				MCI vs. HC (%)
	ACC	SEN	SPE	BAC	AUC	ACC	SEN	SPE	BAC	AUC
Baseline spatial features	84.40	74.34	91.79	83.06	91.98	74.86	84.68	58.45	71.5	80.78
Spatial features	86.35	77.63	92.75	85.19	92.52	76.49	86.13	60.39	73.26	84.57
Baseline longitudinal features	78.83	72.37	83.57	77.97	84.64	69.08	78.32	53.62	65.97	73.04
Longitudinal features	80.78	77.63	83.09	80.36	87.69	72.88	85.55	51.69	68.62	77.26
Spatial+Longitudinal features	88.30	79.61	94.69	87.15	94.01	79.02	90.46	59.90	75.18	85.19

Fig. 6.

ROC curves achieved by five methods using different feature representations in the tasks of (a) AD vs. HC classification, and (b) MCI vs. HC classification.

C. Comparison with State-of-the-art Feature Representations

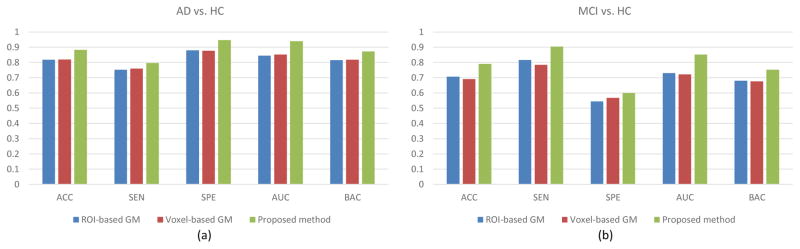
We further compare our method with two cross-sectional feature extraction methods based on GM, i.e., the ROI-based GM and the Voxel-based GM methods that share the same data with our proposed method. In ROI-based GM method, we extract GM concentrations based on 90 ROIs and perform classification using SVM classifier. Specifically, for partitioning a brain MR image into 90 ROIs, we use the Automated Anatomical Labeling (AAL) map. The AAL map is originally defined on the Montreal Neurological Institute (MNI) single subject brain MR image [54]. In our implementation, we use HAMMER [55] for nonlinear image alignment, and then map the GM tissue and ROIs to the template image. In Voxel-based GM method, we implement the classification method in [49], which successfully distinguishes AD cases from HCs using voxel-based GM features and the linear SVM classifier. To make a fair comparison, the same registration and segmentation methods, as used in the ROI-based GM method, are adopted in Voxel-based GM method. The classification results are shown in Fig. 7, from which we can see that our method consistently outperforms the other two GM-based features in both classification tasks. The superior classification performance of our method is mainly coming from the combination of spatial and longitudinal features.

Fig. 7.

Comparisons with two types of GM-based features. (a) ACC of AD vs. HC. (b) ACC of MCI vs. HC.

In addition, we compare the proposed method with a recent work [16] that adopted longitudinal data for AD classification. Specifically, Chincarini et al. [16] used hippocampal volume and hippocampal volume atrophy rate as measurements for representing longitudinal MRI data in the task of AD classification. There are 96 AD patients and 148 healthy control (HC) subjects used in [16]. The reported AUC for AD vs. HC on ADNI-1 is 93.00%, which is slightly lower than ours (94.01%). Moreover, they used multi-atlas based method to obtain hippocampal segmentations, which is very time-consuming. For example, it usually takes hours to obtain an accurate hippocampal segmentation. On the other hand, for our landmark-based method (e.g., using four longitudinal scans), it requires less than 3 minutes to complete all feature extraction steps, including linear registration, landmark detection, and the spatial and the longitudinal feature extraction.

D. Parameter Analysis

In this part, we investigate the effects of several important parameters on the classification performance of the proposed method. In this group of experiments, we simply fix half of the data as training data and the remaining as testing data, in order to save the computational time.

During the discovery of landmarks, we define the landmarks by identifying the local minima within a cubic patch in the p-value map. Since the size of the cubic patch directly affects the number of landmarks, we conduct an experiment using different size of the cubic patch. That is, a smaller cubic patch will lead to a relatively larger number of landmarks. The experimental results for the two classification tasks are shown in Fig. 8. As can be seen from Fig. 8, using too many landmarks (> 2000) will lead to very high dimensional features, with a limited improvement of classification performance. The possible reason could be that many redundant features are included when using too many landmarks. In general, the size of 7×7×7 with roughly 1500 landmarks provides satisfactory performance.

Fig. 8.

Effect of using different sizes of the cubic patch for selecting local minima. (a) Classification accuracy. (b) Number of landmarks.

In the spatial feature extraction step, the number of words in the dictionary (i.e., clustering centers) affects the accuracy and dimensionality of representation. Figure 9 shows the classification results of using our high-level spatial features for classification. From the figure, we can observe that the classification accuracy gradually increases with the use of more words, such as in a range from 10 to 50 words. Generally, when the number of words is 50, a good compromise between classification accuracy and representation dimensionality is achieved.

Fig. 9.

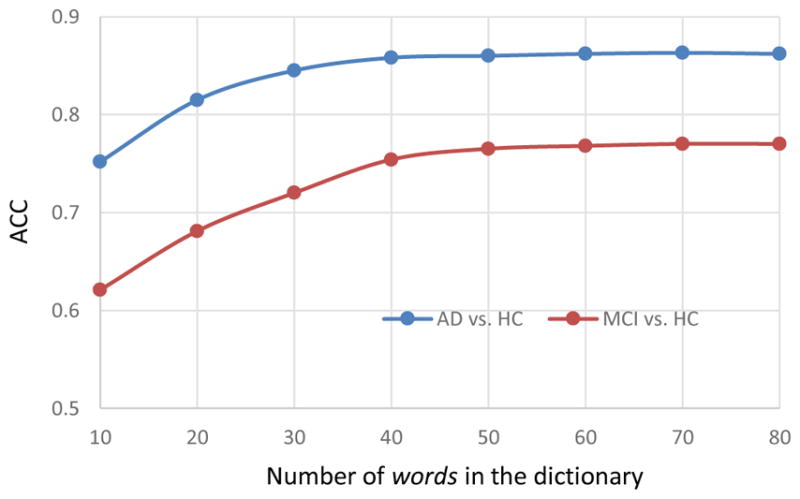
Classification accuracy with respect to the number of words used in the dictionary for calculation of spatial features.

In addition, we further report the landmark detection accuracy achieved by the method proposed in [22] adopted in this study, and analyze the influence of landmark detection accuracy on the performance of our proposed method. The experimental results can be found in Table S1 and Fig. S3 in the Supplementary Materials.

V. Discussion

A. Landmark-based Framework

The major advantages of using landmark-based framework are two-fold: 1) The identified discriminative landmarks can cover all possible abnormalities from the whole brain without using several pre-defined biomarkers; 2) The use of landmarks makes it possible to integrate a fast landmark detection model into the diagnosis framework, such that both time-consuming nonlinear registration and tissue segmentation can be avoided. It is worth noting that, although each landmark is a weak descriptor that only covers limited information from a small local patch, a large number of landmarks (such as thousands of landmarks) can well describe the brain structure, thus leading to a satisfactory classification performance.

B. Spatial Features

In the bag-of-words representation, words in the dictionary can be regarded as representative local spatial structures. Thus, the calculation of their occurrence frequency can be regarded as labeling the spatial structure of each landmark with its similarities to all words. Moreover, such high-level statistics are robust to both numbers and orders of scanning time points, and can capture unified spatial features for identifying structural abnormalities, even for the cases with variable longitudinal scans. As can be seen from both Table III and Fig. 6, the method of using bag-of-words based spatial features achieves better classification performance than that of using just baseline spatial features.

C. Longitudinal Features

Intuitively, one type of longitudinal information is the trajectory of each landmark over time. However, this ignores the coherence among all neighboring landmarks, if just simply using the mean longitudinal displacements (d̄) as features. In our method, we generate a normalized deformation field by interpolation, through which we can extract contextual information by jointly using the neighboring landmarks. Moreover, it is also well known that the Jacobian determinants can indicate the local volume changes. Therefore, the local morphological features from the Jacobian map can comprehensively capture longitudinal volume changes around landmarks. The experimental results show that using longitudinal features from Jacobian map achieves 2% to 4% accuracy improvement, as compared with the methods using baseline longitudinal features.

D. Limitations and Future Work

In the proposed method, each landmark has 72 spatial features and 50 longitudinal features. Given thousands of landmarks, the concatenation of all these features from all landmarks would lead to high feature dimension, compared with the number of training subjects. Also, there are always some redundant or noisy features that can adversely affect the learning performance of the subsequent classification model. Therefore, selecting the most informative landmarks and features is important and can provide a reasonable solution for further performance improvement, which will be included in our future work. On the other hand, the proposed feature extraction framework may be also applied to multi-modal data (e.g., MRI, PET and functional MRI), which could further improve the accuracy of the brain disease diagnosis. In addition, besides the landmarks identified by the data-driven algorithm, there could be missing or spurious landmarks that are not considered in this study. A reasonable solution is to perform manual correction by adding more discriminative landmarks or removing those unreliable or redundant landmarks based on expert knowledge.

VI. Conclusion

In this paper, we have presented a landmark-based feature extraction method using longitudinal structural MR images. Compared with previous approaches, our method avoids the time-consuming steps of both nonlinear registration and tissue segmentation in the application stage. In addition, our method can also extract unified feature representations for subjects with different numbers of longitudinal scans, which is typical in the longitudinal studies. These two merits make our method suitable for clinical practice, where efficient diagnosis with the capability of dealing with the problem of inconsistent scan numbers is desired. To validate the effectiveness of our method, we have evaluated it extensively with the ADNI database, and achieved superior classification performance in both AD vs. HC and MCI vs. HC classifications, compared with several other benchmark methods.