Virtual Interactive Suturing for the Fundamentals of Laparoscopic Surgery (FLS)

Abstract

Background

Suturing with intracorporeal knot-tying is one of the five tasks of the Fundamentals of Laparoscopic Surgery (FLS), which is a pre-requisite for board certification in general surgery. This task involves placing a short suture through two marks in a penrose drain and then tying a double-throw knot followed by two single-throw knots using two needle graspers operated by both hands. A virtual basic laparoscopic skill trainer (VBLaST^©) is being developed to represent the virtual versions of the FLS tasks, including automated, real time performance measurement and feedback. In this paper, we present the development of a VBLaST suturing simulator (VBLaST-SS^©). Developing such a simulator involves solving multiple challenges associated with fast collision detection, response and force feedback.

Methods

In this paper, we present a novel projection-intersection based knot detection method, which can identify the validity of different types of knots at haptic update rates. A simple and robust edge-edge based collision detection algorithm is introduced to support interactive knot tying and needle insertion operations. A bimanual hardware interface integrates actual surgical instruments with haptic devices enabling not only interactive rendering of force feedback but also realistic sensation of needle grasping, which realizes an immersive surgical suturing environment.

Results

Experiments on performing the FLS intracorporeal suturing task show that the simulator is able to run on a standard personal computer at interactive rates.

Conclusions

VBLaST-SS^© is a computer-based interactive virtual simulation system for FLS intracorporeal knot-tying suturing task that can provide real-time objective assessment for the user’s performance.

Graphical abstract

1. Introduction

With reduced surgical invasion and faster recovery, minimally invasive surgery (MIS) has rapidly evolved over the past couple of decades as a technique of choice for an increasingly large number of surgical procedures. However, the complexity of MIS exceeds that of traditional open surgery as long slender surgical tools inserted through trocars into the abdominal cavity are used to perform the procedures with a two-dimensional field of view captured by a wide-angle camera. The complexity of the eye-hand coordination necessary in laparoscopic surgery and the occurrence of adverse events in the early days of its introduction have led to increased emphasis on psychomotor skill training using simulations and models outside the operating room (OR).

Virtual reality (VR) is of growing interest in medical training, especially in surgery [1][2]. With the advance of VR techniques, considerable effort has been dedicated to the development of VR-based surgical training simulators, which provides both visual and force feedbacks to users when they interact with virtual environment. VR-based simulators offer many advantages over the traditional training method by teaching surgical skills in a safe and controlled environment, ensuring repeatable conditions, offering automated assessment, and often without the need for supervision. The simulators provide a computer-generated realistic environment where surgeons can be trained with no risk to patients. The repeatability and reusability offered by VR-based simulators can improve surgical skills by allowing repetitive practice on different scenarios. In addition, these simulators can also provide objective evaluation of task performance and assessment of competency, and those may be unmeasurable via traditional means. For instance, a simulator has the potential to record the motion of virtual surgical instruments or detect whether a damaging contact with nearby anatomy has been made by the user. With rapid advances in hardware and software capabilities, VR-based simulators are also becoming increasingly affordable.

Laparoscopic suturing is one of the most commonly performed tasks in MIS, that requires significant practice to master as a curved needle is used to close a tissue defect with a knot that is neither too loose nor too tight. In open surgery, suturing is much less complicated as full articulation of the needle can be achieved. Using needle drivers in laparoscopic surgery deprives the surgeon of this natural wrist articulation, increasing the difficulty level of the procedure. A simple suturing task is included in the Fundamentals of Laparoscopic Surgery (FLS) [3], which is now a pre-requisite for board certification in general surgery. In the FLS intracorporeal suturing task, one needs to place a thread through two dots marked on either side of defect in a penrose drain using a surgical needle, and then tie a double-throw knot followed by two single-throw knots using two needle graspers operated by both hands. The task is designed to test multiple skills including hand-eye coordination, bimanual operation and precision. A proctor must be present to score the procedure and the system suffers from multiple other drawbacks of a physical simulator pointed out earlier. A virtual basic laparoscopic skill trainer (VBLaST) is being developed to represent the FLS tasks, including automated real-time performance measurement and feedback [4]. In this paper, we present the development of a VBLaST suturing simulator (VBLaST-SS^©). A VR-based suturing simulator is expected to be able to simulate the deformation of thread and penrose drain, knot detection and tying, as well as interactions between needle, thread, penrose drain, surgical needle graspers and the environment, which require intensive computations for collision detection and dynamic response between the virtual tools and the models. As a high update rate of 1 kHz is necessary for the haptic servo loop to be stable, designing an interactive suturing simulator allowing for these features while providing force feedback in real time is a challenging task.

Virtual suturing techniques have been extensively explored by others. A thread is often modeled as a sequence of nodes connected by either rigid links or springs. For rigid links, a kinematic scheme such as “follow the leader” has been used while the force between adjacent nodes is not considered [5]. The use of elastic springs is more physically realistic [6]–[13]. Le Duc et al. [13] modeled the thread using a simple linear mass-spring system to achieve good computational performance. Jia and Pan [7] simulated interaction and deformation of the thread and tissue. However, these algorithms lack detection of self-collision and knot-tying, nor can they be used for more complex suturing tasks. Payandeh and Shi [8] presented a suturing platform to teach basic stitching on a pre-wound tissue with only one tool provided to perform suturing. Some recent work [9]–[11] explored the feasibility of utilizing a physics engine, NIVIDIA PhysX [32], to develop a suturing simulator that can take advantage of hardware acceleration. As the force data is not available from the PhysX engine, the computation of force feedback is not straightforward [9] for those methods. Furthermore, none of the above simulators integrate real surgical suturing instruments with haptic devices as hardware interfaces to improve the fidelity of suturing sensation which includes the feeling of picking up a rigid needle and orienting it appropriately to achieve the right bite angle. There are some commercial virtual surgical training systems have been developed, such as LAP Mentor [35], Lap-X [36], LapVR [37] and Lapsim [38]. These training systems are able to simulate basic suturing skills, such as stitching a pre-wound tissue, but they generally differ from the actual FLS intracorporeal suturing task. In addition, in order to operate all the training modules of the system, they all customize their own user interfaces which deviate from the tools specified by FLS.

Robust handling of self-collision is critical to prevent the thread from passing through itself. Early work on collision detection based on one instance of geometry [14] led to missed detection in high speed contact. Initial work on continuous collision detection (CCD) was based on formulating and solving a cubic equation with time-to-collision of edges [15] accounting for multiple time frames. Several enhancements on this approach for reducing missed collisions, false-negatives and improving performance have been developed. For instance, ExactCCD [16] involves analysis of the roots of the equations to achieve geometrically exact detection in cloth simulation. In FastCCD [17], analytical reformulation of the approach led to more efficient and robust detection. SafeCCD [18] improves safety through analysis of numerical and rounding errors while TightCCD [19] uses Bernstein sign classifications to significantly enhance performance and reduce false-negatives.

In these approaches, as the underlying initial computation is to find roots of a cubic equation, extensive arithmetic and choice-making (Boolean) operations are involved, leading to propagating floating point errors and performance degradation. In addition, failures to handle scenarios such as parallel segments and geometrically degenerate cases have been reported [16].

Methods to robustly handle self-collision of suture thread in real-time simulation environment is challenging [20] [21]. In [22], collision is handled by resolving thread penetration considering the current geometry. An energy based approach for self-collision of tentacles in a squishy-ball is developed in [23]. In the work on collision detection of deforming cables, a sweep-and-prune [24] algorithm is employed for simulation of cable assembly operations. Most of the above approaches are developed for simulation of cloth or hair and are used for aesthetic appeal where missed collisions are not very critical, while in suturing simulation, missed self-collisions can lead to loss of the knot. The key here is to simulate simultaneous collision of thread segments accurately.

In this paper, we present an algorithm for robust handling of self-collision, which can be applied for general edge-edge collision, based on a simple distance calculation of the line segments. The method is conducive to early elimination of collision and the data from collision detection can be used to handle collision response. The time-to-collision can be easily derived. Furthermore, we extend the concept to triangle-point collision to handle the piercing (or puncturing) of the surgical needle through the penrose drain.

Knot tying is an essential component in suturing simulation [5], [6], [8]–[12]. Knot identification is useful to evaluate the quality of the suturing operation, for instance, double-throw knot (square knot) is often considered to be more secure than a single-throw knot. For some surgical suturing training programs [3], the skill of tying certain types of knots is usually required to be mastered. The user must be allowed to commit errors including incorrect knots or missed knots. Considering that collisions need to be updated at haptic rendering rates, the knot detection routine must be performed in real-time as well. Existing methods [5], [25] identify a knot using the knot theory, where a knot needs to be tied up first and frozen for evaluation of its topology. In knot theory [26], a knot is topologically represented by projecting onto a plane and labeling the crossing order in the planar diagram. For the same knot, choosing different planes can lead to different planar diagrams, though those planar diagrams may be reached from one another based on a sequence of three manipulations known as the Reidemeister moves [27]. Moreover, incorrect result may be generated by this method in the case of multiple crossings projecting to the same point in the diagram [5].

In this work, we propose a novel projection-intersection based knot detection method, which can interactively evaluate the validity of a knot on the basis of two criteria: 1) closed loop around the tool; 2) loop penetration. Different types of knot (e.g., single-throw or double-throw) can be identified using the same criteria. During the knot tying process, these two criteria are checked respectively using simple projection and intersection tests, and a knot can be detected when both criteria are satisfied. The basic idea is as follows.

To identify if there exists a closed thread loop around the tool, the thread line segments are projected onto a plane that is perpendicular to the tool being looped around. A closed loop can be recognized when any two of the projected line segments intersect (closed loop around the tool). To complete the knot, the thread end must pass through the loop, which is determined by checking whether there is a thread line segment penetrates the loop (loop penetration).

Our method is also robust for detecting a knot made of multiple loops, where more than two projected line segments may intersect at the same point – multiple overlapping crossings [5]. Simply detecting all loops at once could lead to incorrect result. To solve that, we identify each loop one after another by traversing the thread line segment from the beginning. Once the first intersection between the inquired line segment and its subsequent line segment is found, a loop is identified; and the searching for the next loop starts from the line segment next to the ending line segment of its prior loop by following the same manner. Once there is a thread line segment passes all loops at the same time, a multiple-throw knot is identified.

Finally, in this paper, a unique hardware interface that is designed for providing realistic surgical suturing experience. This includes not only haptic feedback during tool manipulation and interaction, but also the sense of needle grasping, which commercially available haptic devices do not provide.

In what follows, an overview of the system framework with four major modules designed for building the virtual suturing simulator is presented in section 2. The physics-based modeling of virtual objects (i.e., thread, penrose drain, needle, and needle graspers) as well as the collision detection and interactions between them are discussed in section 3 and section 4 respectively. Our knot detection method is presented in section 5. The automatic data recording and measurement and hardware interface are introduced in section 6 and 7 respectively. Finally, numerical results pertaining to the performance of the suturing simulator are presented in section 8 followed by concluding remarks in section 9.

2. VBLaST-SS^© Overview

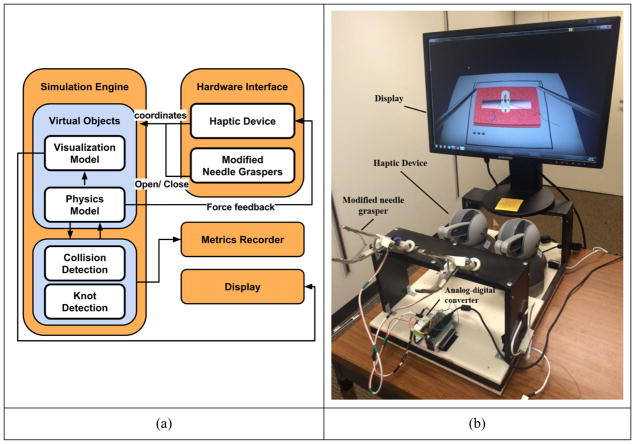
The VBLaST-SS^© framework consists of four major components: simulation engine, hardware interface, automated metrics recording and measurement module and display (Figure 1(a)). The physical hardware setup is shown in Figure 1(b).

Figure 1.

The VBLaST-SS^© (a) architecture and (b) hardware setup.

In the simulation engine, the virtual scenarios include models of the needle, suture thread, penrose drain and two needle graspers. These virtual objects are modeled from both graphical and physical aspects. To simulate the interactions between the virtual objects and their dynamics in real-time, simpler geometries (physics model) are constructed for fast collision detection and physics-based deformation. For better rendering effect, finer mesh models with textures are used for visualization (visualization model). The physics models can drive the movements of their coupled visualization models in the simulator. To enable knot-tying, the thread self-collision must be detected and handled properly. Meanwhile, the knot detection routine running at haptic update rates can detect the correctness and type of the knot (double-throw or single throw) in real-time.

For the hardware interface, a pair of surgical needle graspers, which are used in surgical suturing, are attached to the styluses of a pair of Geomagic Touch^™ haptic devices. Each haptic device provides 6 degree of freedom (DOF) position/orientation input, and 3 DOF force feedback. The angular motion of each needle grasper handle is captured by a 10K Ohm Breadboard potentiometer and interpreted as an analog voltage signal. An analog-to-digital converter, NI USB-6008 data acquisition device (NI-DAQ) from National Instrument, is utilized to digitize the analog signal and fed to the simulation engine, thus allowing the jaws of the virtual needle grasper to open and close, to pick up or release a virtual object. The forces computed based on the real-time interactions between virtual objects can be fed back to user through the haptic devices.

An automated data recording module has been developed to collect user data and compute performance in real-time, based on the scoring metrics developed for FLS intracorporeal suturing task. These metrics are IP protected and have been obtained with a memorandum of understanding with the Society of American Gastrointestinal and Endoscopic Surgeons. Hence, details regarding them cannot be presented in this paper.

3. Modeling of virtual objects

For interactive simulation involving multiple objects and their interactions in real-time, simple yet robust physics based models for each of the objects in the virtual workspace, and algorithms for appropriately handling their interactions, are necessary. In this section, the geometric and physics-based modeling details of the suture thread, penrose drain, needle and needle graspers are presented.

3.1. Suture thread

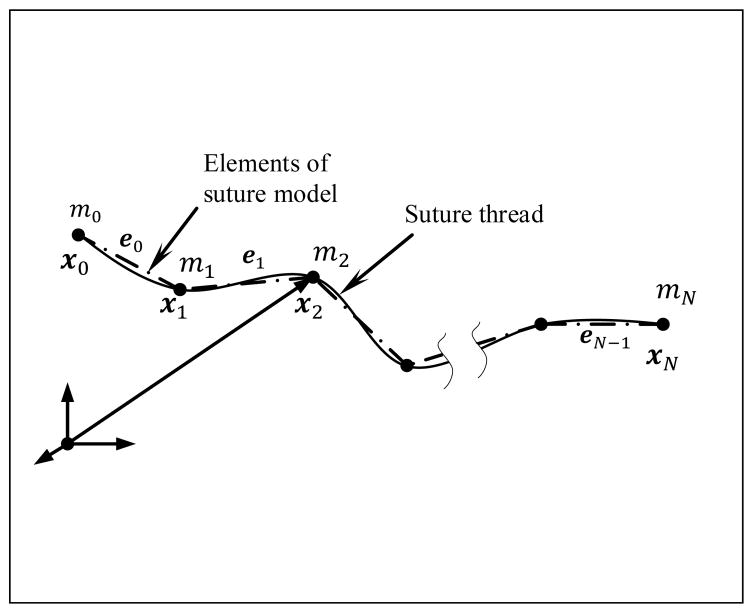
The suture thread forms the central part of the suturing task and capturing its realism plays an important role in the simulation of the task. In the FLS suturing task, a suture thread of length 150 mm and diameter 0.25 mm is used. The virtual thread, as shown in Figure 2, is modeled with N particles at equally spaced positions x_i, i = 0,1, … N connected by line segments denoted by vectors e_i, i = 0,1..N − 1 where e_i = x_i+1 − x_i. The particle masses are evaluated based on linear mass density of silk suture.

Figure 2.

Model of the suture thread

The constrained particle system model of the suture thread is formulated using the augmented Lagrangian equation $L(\mathbf{x},\mathbf{v})=\frac{1}{2}{\mathbf{v}}^T\mathbf{Mv}-V(\mathbf{x})-\mathbf{C}{(\mathbf{x})}^T\mathbf{\lambda }$ in which $\mathbf{x}={[\begin{array}{cccc}{\mathit{x}}_0^T& {\mathit{x}}_1^T& \dots & {\mathit{x}}_N^T\end{array}]}^{\mathit{T}}$ and $\mathbf{v}={[\begin{array}{cccc}{\mathit{v}}_0^T& {\mathit{v}}_1^T& \dots & {\mathit{v}}_N^T\end{array}]}^{\mathit{T}}$ where v_i is the velocity of particle i; M is the mass matrix of the system; V(x) is the potential energy; C(x) is the vector of constraints; and λ is the vector of Lagrange multipliers. The dynamics of the suture thread is computed by solving the corresponding Euler-Lagrange equations: Mv̇ = −F(x) − ∇C(x)^Tλ and C(x) = 0, where F(x) represent the external forces acting on the particles and ∇C(x) is the Jacobian of constraints.

3.1.1 Internal forces

The internal forces due to deformation of the suture thread are modeled from two contributions: viz. extensional and bending. The former is handled with each segment e_i being treated as a linear spring of stiffness k_s. Thus, the extensional force contribution from segment e_i at point x_i is given by ${\mathit{F}}_i^s=k_s(\mid {\mathit{x}}_{i+1}-{\mathit{x}}_i\mid -l_i){\widehat{\mathit{e}}}_i$ where l_i denotes the rest length of segment e_i and ê_i is the unit vector along e_i. The bending force in the thread is modeled using the theory of discrete Kirchhoff rods [28] which relies on discrete definition of the curvature vector κ_i at vertex x_i sharing elements e_i−1 and e_i, given by

$${\mathit{\kappa }}_i=\frac{2{\mathit{e}}_{i-1}\times {\mathit{e}}_i}{\mid {\mathit{e}}_{i-1}\mid \mid {\mathit{e}}_{i-1}\mid +{\mathit{e}}_{i-1}·{\mathit{e}}_i}.$$

The internal force due to bending ${\mathit{F}}_i^b$ at vertex x_i is given by

$${\mathit{F}}_i^b=\frac{2\alpha }{\overline{l}}{\left({\nabla }_i{\mathit{\kappa }}_j\right)}^T{\mathit{\kappa }}_j$$

where l̄ is a measure of length pertaining to vertex x_i and α is the bending modulus of the suture thread. Definition of the gradient of the curvature vector ∇_iκ_j and further details may be found in [28]. The total force ${\mathit{F}}_i^{st}$ at vertex x_i on the suture thread is ${\mathit{F}}_i^{st}={\mathit{F}}_i^b+{\mathit{F}}_i^s-{\mathit{F}}_i^g$, where ${\mathit{F}}_i^g$ is the external force due to gravity acting on the particle.

3.1.2 Sections of the suture thread

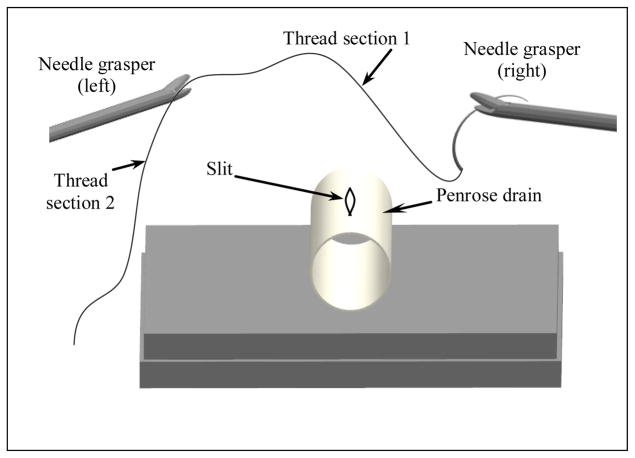
Before proceeding to the treatment of time integration and constraints, we note here that the suture thread is divided into sections based on the way in which the thread is held in space (by the tools and knots) during the simulation, for the purpose of efficient handling of constraints and damping. For instance, in Figure 3, the thread is (notionally) divided into two sections separated by the points constrained by the tools. Thus, each section has particle positions (possibly) constrained only at the end of the sections and no constrained points inside. The sections of suture thread are dynamically determined in each time step during the simulation.

Figure 3.

Sections of suture thread for efficient handling of constraints

3.1.3 Time integration and damping

The unconstrained and un-damped velocity v_i of particle i due to the action of forces can be written as ${\mathit{v}}_i(t_{i+1})={\mathit{v}}_i(t_i)+\frac{\mathrm{\Delta }t}{m_i}{\mathit{F}}_i^{st}$. For damping, we utilize an adapted version of the viscous damping scheme introduced in [29] for particle based systems, where the individualized “deviations” of particle velocities are damped with respect to the total linear and angular momentum of the system of particles. In our treatment, we consider each section of the thread as a system for this purpose, because each section of the thread can have largely independent motion depending on the nature of constraints imposed at the ends of the sections.

The velocity of the particle i is damped using

$${\mathit{v}}_i(t_{i+1})\leftarrow {\mathit{v}}_i(t_{i+1})-c_s\mathrm{\Delta }{\mathit{v}}_i(t_{i+1})$$

where c_s is the damping coefficient and Δv_i(t_i+1) is the individual difference in the particle velocity with respect to the velocity of the thread section and is given by [29]

$$\mathrm{\Delta }{\mathit{v}}_i(t_{i+1})={\mathit{v}}_i(t_{i+1})-({\overline{\mathit{v}}}_s+{\overline{\mathit{\omega }}}_s\times {\mathit{r}}_i)$$

where v̄_s and ω_s are the angular velocity of the section of the thread and r_i = x_i − x̄_s is the relative position of point x_i with respect to the center of gravity (x̄_s) of the section of the thread. Positions are updated using the damped velocities as follows:

$${\mathit{x}}_i(t_{i+1})={\mathit{x}}_i(t_i)+\mathrm{\Delta }t{\mathit{v}}_i(t_{i+1}).$$

3.1.4 Constraints

Interaction of the suture thread with the needle and the tools such as while the tools manipulating the suture thread, or being attached to the penrose drain after the formation of the knots, are handled by constraints. Moreover, inextensibility of the suture thread is handled through constraints. We use the fast projection method [30] to enforce constraints to solve for constrained positions and velocities by projecting the unconstrained positions. Addition of the stretching term in the forces aids in finding a closer unconstrained position to the projection manifold corresponding to inextensibility enforcement, thus enhancing convergence.

The constraint for inextensibility in segment e_i is $C_i^{\mathit{inext}}({\mathit{x}}_i,{\mathit{x}}_{i+1})=\frac{1}{l_i}\Vert {\mathit{x}}_{i+1}-{\mathit{x}}_i\Vert -l_i$ where l_i is the original length of the segment. The gradient of the constraint is given by $\nabla C_i^{\mathit{inext}}({\mathit{x}}_i,{\mathit{x}}_{i+1})=\frac{2}{l}({\mathit{x}}_{i+1}-{\mathit{x}}_i)$. Utilizing the fact that the sections are divided into sections based on constraints, each section is considered individually for enforcement of constraints. This is done to improve the efficiency, by limiting the size of the Jacobian, without affecting the accuracy of the simulation. We use Newton iterations [30] to solve for the constrained positions. If the constraint iterations fail to converge for any section, especially during the formation of knots, only the point constraints are applied without inextensibility for the corresponding section in that time step.

3.2. Penrose drain

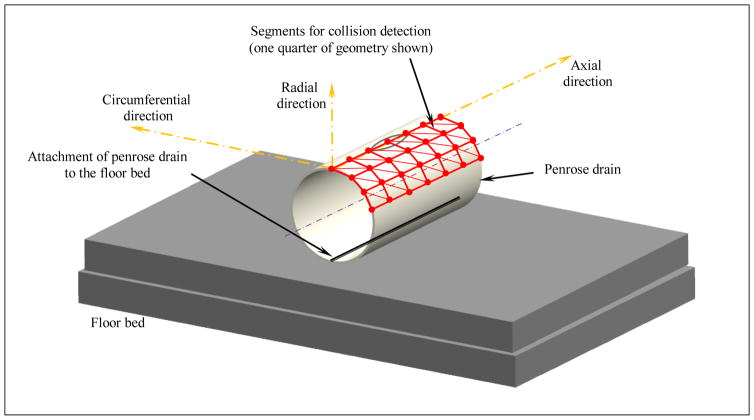
The penrose drain is a thin elastomeric object of cylindrical shape of radius 6.5 mm, length 32 mm and thickness 1.0 mm with a longitudinal slit of about 10 mm in length as shown in Figure 3. The formulation for deformation behavior of the penrose drain is similar to that of the suture thread with the exception of derivation of the internal forces. The virtual object is modeled with a mesh of grid of mass points (particles) connected by elements. Internal forces are handled using a method where the spring elements are connected between the original and current positions of the vertex points in the penrose drain [13]. Damping and time integration are performed as presented in the section 3.1. Collision detection for the penrose drain is handled with edge-edge collision. For this purpose, a mesh of segments aligned in circumferential and longitudinal (axial) directions on the mid-surface, in addition to diagonal segments, one per rectangular grid, are used, as shown in Figure 4. The number of axial divisions is 6 and circumferential is 12.

Figure 4.

Penrose-drain model showing partial internal view

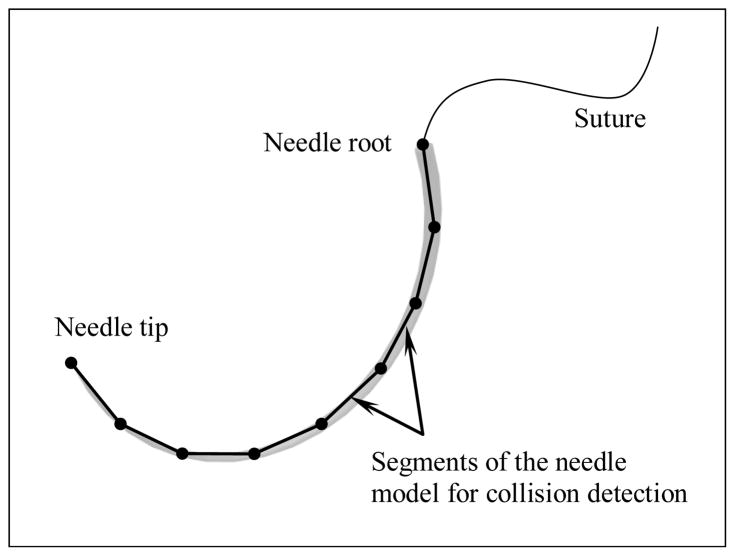
3.3. Needle

The needle used in the FLS suturing task is semi-circular in geometry with a radius of 10.5 mm. For collision detection and response, the needle skeleton is divided into 8 segments as shown in Figure 5.

Figure 5.

Needle skeleton is modeled as line segments

The needle has three states, (i) unconstrained, (ii) grasped by one tool and (iii) grasped by both tools. In the unconstrained state, the needle is governed by rigid body dynamics. When grasped, the degrees of freedom of the needle, which are the global positions and rotations, are controlled by the position and rotation of the (first) tool holding the needle. The rotation is represented using quaternions. When the needle is interacting with the penrose drain, it is acted upon by the forces from the elements of the penrose drain. The first node of the suture thread is constrained to the rear end of the needle.

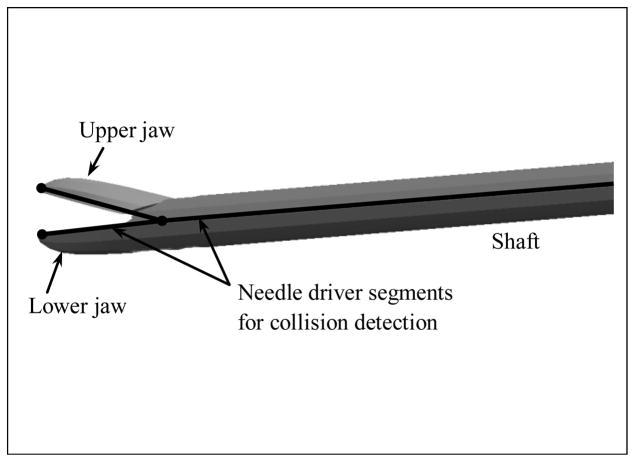
3.4. Needle graspers

The needle graspers are modeled with three rigid straight segments, two of which represent the grasping jaws and the third, the shaft. The inlay of the segments on the needle-grasper geometric model is shown in Figure 6. The motion is captured from the translation and rotational movements of the pair of haptic devices attached to the physical needle grasping handles which are manipulated by the user.

Figure 6.

Needle grasper skeleton modeled as line segments for collision detection

The jaw movements are captured using potentiometers fixed on the grasping handles in the hardware interface as detailed in section 7. The sensation of grasping the needle is provided using solenoid switches fixed on each of the needle grasping handles. The shears, for cutting the thread at the end of the simulation, are modeled in an identical fashion, in which case, the grasping jaws are replaced by the shearing scissors.

4. Collision detection and interactions between objects

The FLS suturing simulation involves real-time interactions between different virtual objects viz. needle, suture thread, needle graspers, penrose drain and the floor-bed. In this section, we discuss the collision detection and response between combinations of such objects. The floor bed is considered as a rigid, flat surface, and thus handling collision detection and response with other objects (e.g., needle, suture thread and needle graspers) is straightforward. The needle and the needle graspers are treated as rigid bodies, while the suture thread and the penrose drain are treated as deformable objects. We use edge-edge collision extensively as most objects in the scene are modeled as one-dimensional or as line segments for the purpose of collision detection. Details of the edge-edge continuous collision detection technique are provided below in the context of thread self-collisions. We extend the technique to continuous collision detection of point-triangle, which is used to handle penetration detection of the needle into the penrose drain.

4.1. Detection of self-collisions in suture thread

The suturing task involves thread self-interaction scenarios such as performing a double-throw loop where each thread segment may contact multiple others simultaneously, increasing the complexity of detection and response of self-collisions in comparison to normal edge-edge collisions. Here we present a simple geometry based continuous collision algorithm for detecting and handling self-collision of the suture thread in real-time.

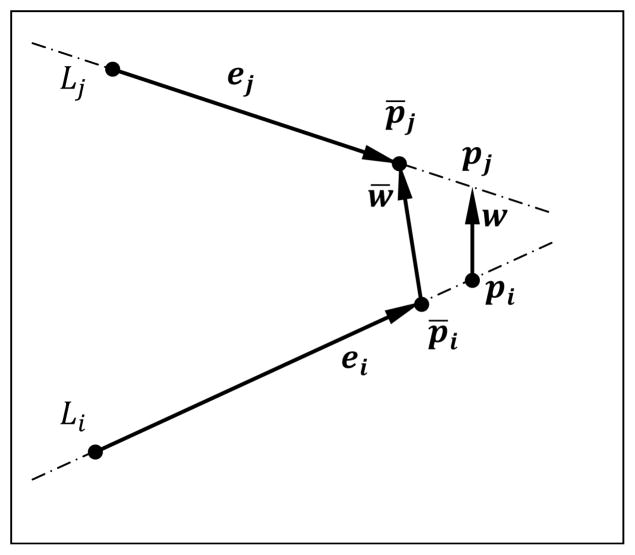
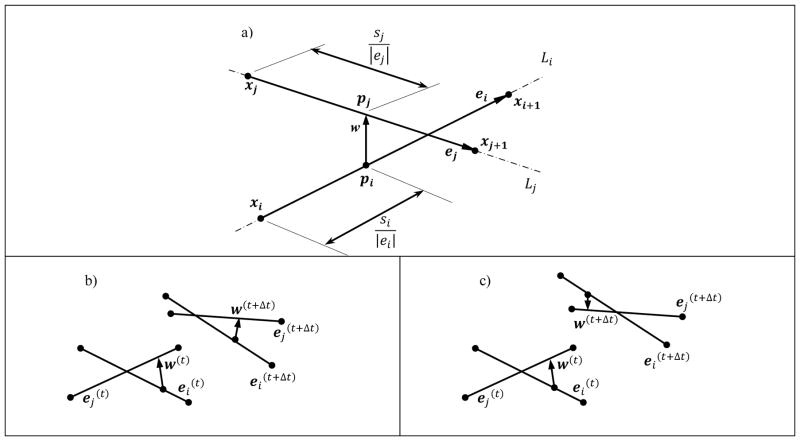
Consider any two non-adjacent segments of the suture thread defined by the vectors e_i = x_i+1 − x_i and e_j = x_j+1 − x_j at any given instance of time, where x_i, x_i+1, x_j, and x_j+1 are vertices defining the segments. Given the position of the vertices between two instances of time t and t + Δt and assuming that each vertex moves at constant velocity in the interval, we are interested in finding whether the segments e_i and e_j collide between the time instances. Let $\widehat{\mathit{n}}=\frac{\left({\mathit{e}}_i\times {\mathit{e}}_j\right)}{\left|{\mathit{e}}_i\times {\mathit{e}}_j\right|}$ be the unit vector perpendicular to both the line segments. Then, the shortest distance between two line rays L_i and L_j, defined respectively along vectors e_i and e_j, can be written as d = w₀ · n̂, where w₀ = x_j − x_i. Thus, the shortest distance vector between the rays is w = dn̂.

Using the dot product between the shortest distance vectors at the two instances of time w^(t) and w(^t+Δt), one can detect the collision of the line rays, i.e. m = sign(w^(t).w^(t+Δt)) ≤ 0 implies that the line rays have collided (or crossed each other) in the interval. Here, the superscripts (t) and (t + Δt) denote quantities calculated from configurations in previous and current time instances, respectively. Moreover, negative values of |w^(t)| − m| w^(t+Δt)| indicate that the segments are moving away from each other, whereas, when the quantity is zero, the segments stay at constant distance with respect to each other. Both these cases imply no collision.

The time for the line rays to collide (Δt_c) from the previous configuration, assuming constant velocities of the vertices, can be evaluated using the relation

$$\frac{\mathrm{\Delta }{t}_c}{\mathrm{\Delta }t}=\frac{\left|{\mathit{w}}^{(t)}\right|}{\mid {\mathit{w}}^{(t)}\mid -m\mid {\mathit{w}}^{(t+\mathrm{\Delta }t)}\mid }$$

Now, let p_i and p_j denote the respective intersecting points of w with the line rays L_i and L_j. Thus, p_i = x_i + s_i e_i, where s_i is a scalar signifying the fraction that locates the point p_i in the ray L_i in terms of e_i.

Notice that the shortest distance vector w is defined between the line rays and might fall outside the limits of either of the line segments in either or both of the time instances (t) and (t + Δt). But for the segments to collide, the vector (which reduces to a zero vector) must fall inside both the segments. In other words, the collision point (the intersection point of line rays at the instance of collision) must be inside both the line segments: i.e., $0\le \frac{{s_i}^{(t+\mathrm{\Delta }{t}_C)}}{\mid {\mathit{e}}_i\mid },\frac{{s_j}^{(t+\mathrm{\Delta }{t}_C)}}{\mid {\mathit{e}}_j\mid }\le 1$.

Summarizing, collision is detected between two line segments, when either of the following two conditions is true:

1. if the magnitude of shortest distance vector in the current configuration is less than a specified distance, i.e. |w^t+Δt| < D (OR)

2.  

   1. if the line rays have crossed each other sign(w^(t).w^(t+Δt)) < 0 (AND)

   2. the collision point falls within line segments $0\le \frac{{s_i}^{(t+\mathrm{\Delta }{t}_C)}}{\mid {\mathit{e}}_{\mathit{i}}\mid },\frac{{s_j}^{(t+\mathrm{\Delta }{t}_C)}}{\mid {\mathit{e}}_{\mathit{j}}\mid }\le 1$.

Here, the distance D is twice the radius of the suture thread (r) plus a chosen tolerance (ε_D), i.e. D = 2r + ε_D. The first condition checks for collision considering the proximity of segments at the current configuration accounting for the thickness of the thread and is specific for treating collisions of reduced dimensional objects (such as threads, rods etc.). Part (a) of the second condition checks for crossing of line rays through one another, while part (b) checks whether the collision point falls inside the entities and is performed only when the rays have crossed.

In the case when w(^t+Δt) falls outside either of the line segments as shown in Figure 8 (i.e. the end points of vector w(^t+Δt) lies outside the line segments), we compute w̄(^t+Δt), which is the closest vector to w(^t+Δt), and use this in place of w(^t+Δt) in the first condition. This is done for accounting for thickness at the end points of segments in scenarios of corner collisions and is applicable for collision of segments with thickness (as in the case of suture threads).

Figure 8.

The closest vector w̄ to the shortest distance vector w between the line rays L_i and L_j in the case when w falls outside both the line segments e_i and e_j.

The procedure for contact detection is given in Algorithm 1.

Algorithm 1.

Edge-edge continuous collision detection for thread self-collision

1:	procedure selfCollisionDetection
2:	for each line segment i = 1 → N do
3:	for each proximate line segment j (found in broad phase) do
4:	compute w(t+Δt) from current positions
5:	compute [or retrieve] w(t) from previous positions
6:	compute |w(t)|, |w(t+Δt)|, m = sign(w(t).w(t+Δt))
7:	if |w(t+Δt)| − m|w(t+Δt)| ≤ 0 then
8:	return false; (no collision)
9:	else
10:	if si(t+Δt) < 0 or si(t+Δt) > 1 or si(t+Δt) < 0 or si(t+Δt) > 1 then
11:	(case when w(t+Δt) lies outside any of line segment)
12:	compute w̄(t+Δt)
13:	else
14:	set w̄(t+Δt) = w(t+Δt)
15:	end if
16:	if |w̄(t+Δt)| < D then
17:	return true; (collision)
18:	else
19:	if sign(w(t).w(t+Δt) < 0 and 0 ≤ si(t+Δt), sj(t+Δt) ≤ 1 then
20:	return true; (collision)
21:	else
22:	return false; (no collision)
23:	end if
24:	end if
25:	end if
26:	end for
27:	end for
28:	end procedure

In practice, we use the following relations to find the fractions: s_i = be − cd, s_j = ae − bd, where a = e_i.e_j, b = e_i.e_j, c = e_j.e_j, d = e_i.w₀ and e = e_j.w₀. Parallel segments are identified using ac − b² < ε_E, where ε_E is a suitable tolerance (e.g., 10⁻⁶) and are accounted by setting s_i = 0 and s_j = d/b [33].

Extension to point-triangle case

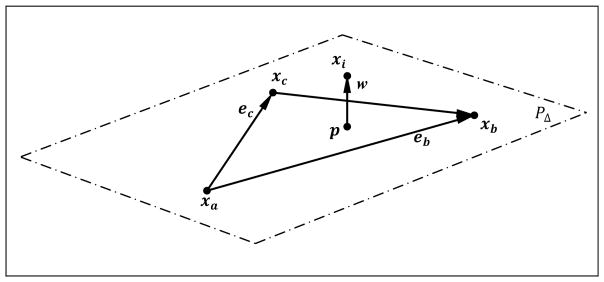
The concepts and the algorithm detailed above for edge-edge continuous collision detection can be directly extended to point-triangle continuous collision detection. In this case, w is the shortest (perpendicular) distance vector between a given point x_i and the plane containing any two edges e_a and e_b of the given triangle. In case where the entities represent reduced dimensional objects, w̄ is the closest vector from the point x_i to any point in the triangle. If p_i defines the projected point of x_i in the plane, one can check whether p_i falls inside the triangle at the time of collision using linear interpolation of the area co-ordinates of p_i. As before, penetration can be captured when m = sign(w^(t).w^(t+Δt)) is negative.

4.2. Response for self-collisions in suture thread

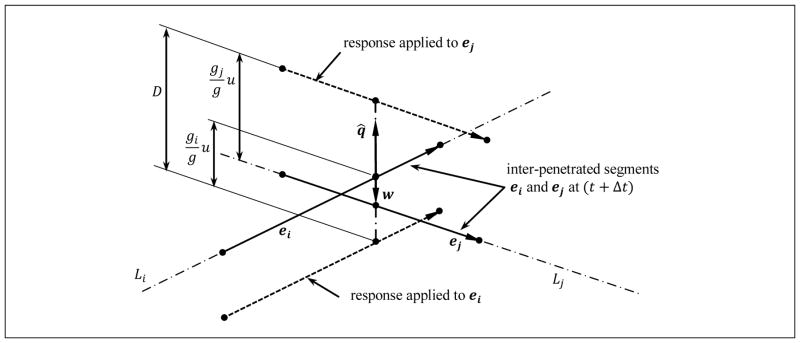
In handling the response of self-collision in the suture thread, the intended goal is to keep the segments away by a specified minimum distance by setting them apart in the direction of shortest separation ${\widehat{\mathit{w}}}^{(\mathrm{t}+\mathrm{\Delta }\mathrm{t})}=\frac{{\mathit{w}}^{t+\mathrm{\Delta }t}}{\left|{\mathit{w}}^{t+\mathrm{\Delta }t}\right|}$ (directed from segment e_i to e_j). The direction of movement of the segments for collision response is thus defined as

$$\widehat{\mathit{q}}=\mathit{sign}({\mathit{w}}^{(t)}.{\mathit{w}}^{(\mathrm{t}+\mathrm{\Delta }\mathrm{t})}){\widehat{\mathit{w}}}^{(t+\mathrm{\Delta }t)}$$

which is directed along the shortest distance vector in the current configuration and taking into account whether the segments have inter-penetrated or not by using the sign of the dot product. The total relative distance to move the segments apart is

$$u=D-\mathit{sign}({\mathit{w}}^{(t)}.{\mathit{w}}^{(\mathrm{t}+\mathrm{\Delta }\mathrm{t})})\left|{\mathit{w}}^{(t+\mathrm{\Delta }t)}\right|$$

where the distance of current separation is |w^(t+Δt)|.

With the direction and magnitude of relative movement defined, it remains to arrive at the proportion of movement between the segments (for deformable-deformable collision such as self-collisions). For the suture thread self-collision response, we choose the proportion based on the relative velocities of segments along the shortest separation unit vector q̂ i.e. segments are moved apart proportionally based on their normal relative velocities. This will ensure correct response in instances such as while tightening the loops, where a segment on the knot-making-loop slide or roll against a segment on the straighter portion of the thread.

In this work, we choose to use quantities at the current configuration for collision response. One has the option of choosing the quantities at the instance of collision or at the current configuration for treating collision response. For instance, the separation vector can be chosen at the instance of collision as n̂^(t+Δt_c) and in this case, u = D as the magnitude of separation at the instance of collision is zero, i.e. |w^(t+Δt_c) = 0|. Nevertheless, the treatment detailed here is general and can be applied to corresponding quantities at the instance of collision, or at any instance in the open interval (t,t + Δt based on the requirement.

Let Δp̄_i and Δp̄_j be the displacement of the points corresponding to end points ${\overline{\mathit{p}}}_i^{(\mathrm{t}+\mathrm{\Delta }\mathrm{t})}$ and ${\overline{\mathit{p}}}_j^{(\mathrm{t}+\mathrm{\Delta }\mathrm{t})}$ of w̄^(t+Δt) vector in the given interval of time respectively. Then, the magnitudes of relative normal displacements are g_i = −Δp̄_i · q̂ and g_j = −Δp̄_j · q̂ respectively. Negative sign in the first relation is because of the chosen convention that getting closer is positive and that the separation vector q̂ is oriented from segment e_i to e_j (at time instance t). Thus, the proportion of movement for segment can be written as $\frac{g_i}{g}$ and $\frac{g_j}{g}$ where g = g_i + g_j. The segments are set apart using the vectors $\frac{g_i}{g}u\widehat{\mathit{q}}$ and $\frac{g_j}{g}u\widehat{\mathit{q}}$. The procedure for collision response of suture thread is presented in Algorithm 2.

Algorithm 2.

self-collision response

1:	procedure selfCollisionResponse
2:	for each pair of line segments i, j do
3:	evaluate direction to move q̂= sign(w(t).w(t+Δt)).ŵ(t+Δt)
4:	evaluate distance to move u = D − sign(w(t).w(t+Δt))|w(t+Δt)|
5:	compute displacements Δp̄i and Δp̄j
6:	evaluate ${\overline{\mathbf{p}}}_i^{(t+\mathrm{\Delta }t)}$ and ${\overline{\mathbf{p}}}_j^{(t+\mathrm{\Delta }t)}$ (points at the end of w̄(t+Δt))
7:	compute gi = −Δp̄iq̂, gj = Δp̄jq̂ and g = gi + gj
8:	compute vectors $\frac{g_i}{g}u\widehat{\mathbf{q}}$ and $\frac{g_j}{g}u\widehat{\mathbf{q}}$
9:	apply response to line segnrents i,j
10:	end for
11:	end procedure

Consider the case when both the segments move in the same direction with different velocities with decreasing relative distance. The response algorithm, as is in our case, should account for this scenario, without adversely affecting the nature of motions of the segments. This is crucial in applications like suture thread simulation.

4.3. Piercing of needle through penrose drain

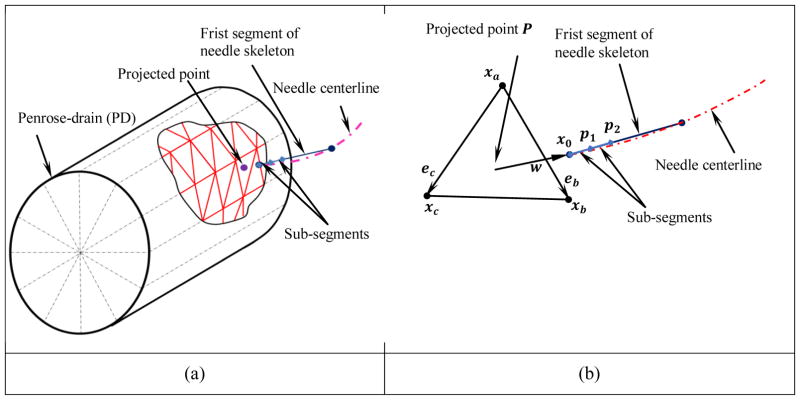
Another important aspect in simulating the FLS suturing task is to consistently capture the penetration of the needle into the penrose drain. One way to detect penetration utilizing the above geometric collision detection method is by computing the dot product of vectors of the needle tip point in previous and current configurations with its projected point on to the penrose drain surface (triangle). If the dot-product is non-positive and the collision point of the needle tip falls inside the triangle, the needle can be treated as penetrated the triangle. But since the needle tip displacement between two consecutive frames is miniscule and minute variations in the hand-movements lead to needle tip going back and forth between the triangle causing multiple penetration capture or loss of capture, causing occasional false artifacts. Also, penetration capture through thin object (as in our case of penetration capture of needle across the thickness of penrose drain) needs different treatment when compared to detection of penetration of vertices or edges of a solid inside the triangulated mesh of another solid. Thus, the general point-triangle collision is not robust enough for the purpose of needle penetration capture for the above-mentioned reasons. In this work, we present an algorithm based on the same concepts of collision detection described above, but adapted to capture the penetration of needle through the penrose drain using a simple and robust algorithm by extending the geometric method in Algorithm 1.

Let x₀ be the position vector defining the tip of the needle at any given instance in time. Let the first segment of the needle be denoted as vector e₀. Consider two points p₁ and p₂ on the segment e₀ of the needle close the needle tip x₀ such that p₁ = x₀ + s₁e₀ and p₂ = x₀ + s₂e₀, where s₁ is small fraction (which corresponds to the thickness of the penrose drain) and s₂ = 2 s₁. Thus, vectors z₀ = p₁ − x₀ and z₁ = p₂ − p₁ form tiny sub-segments near the tip of the needle as shown in Figure 11.

Figure 11.

Detection of penetration of needle through the triangles of the penrose drain

Now, let x_a, x_b, and x_c be the position vectors that define the triangle on the surface of the penrose drain and let e_b = x_b − x_a and e_c = x_c − x_a be the two edges of the triangle.

Let w,w₁ and w₂ be the perpendicular distance vectors from the points x₀, p₁ and p₂ to the plane containing the triangle respectively. Then, penetration of the first sub-segment can be captured when sign(w · w₁) < 0, and similarly for the second sub-segment when sign(w₁ · w₂) < 0. We set a toggle on while capturing initial penetration of the first sub-segment, and confirm penetration of needle into the penrose drain when second sub-segment penetrates. The above procedure of capturing penetration spans multiple frames (time steps). This arrangement eliminates occasional problems arising due to minute reciprocation in hand movements caused by the user, which will otherwise erroneously cause multiple penetration captures in the virtual environment. The algorithm for penetration captures is as detailed in Algorithm 3.

Algorithm 3.

Capturing needle penetration of penrose drain

1:	procedure captureNeedlePenetration
2:	set toggle = 0 at start of simulation
3:	if toggle == 0 then
4:	for each surface triangle of penrose drain do
5:	find vector w0 = x0 − xa
6:	if |w0| > DT then
7:	continue to next triangle (broad phase elimination)
8:	end if
9:	find outward normal n̂ of the triangle
10:	find projected penetration point P = xa + (w0.n̂)n̂
11:	if P lies outside the triangle then
12:	continue to next triangle
13:	end if
14:	compute vectors w and w1
15:	if w.w1 < 0 then
16:	set toggle = 1
17:	identify triangle
18:	initiate penetration
19:	end if
20:	end for
21:	end if
22:	if toggle == 1 then
23:	compute vectors w w1 and w2 in identified triangle
21:	if w1.w2 ≤ 0 then
25:	set toggle = 0
26:	confirm penetration
27:	end if
28:	if w.w1 ≥ 0 and w1.w2 ≥ 0 then
29:	set toggle = 0
30:	no penetration
31:	end if
32:	end if
33:	end procedure

4.4. Rigid-deformable collisions

Collision detection and response between deformable objects such as the suture thread and the penrose drain and rigid objects such as needle segments and jaws and shaft of the tool are handled using Algorithm 1 and Algorithm 2, respectively. For such case of deformable-rigid collisions, the response is applied only to the deformable segment. The surface springs of the penrose drain are treated as deformable segments when determining collision and response with the needle and needle-graspers.

5. Projection-intersection based Knot Detection Method

Knot tying is an essential procedure in the FLS suturing task. Three knots are required to be tied in sequence: a double-throw knot followed by two single-throw knots. The existing methods identify a knot by checking the order of the crossings in the planar diagram, where a knot needs to be tied up first and frozen for evaluation [5], [25]. In this paper, we propose a new method where the validity and the type (single-throw or double-throw) of a knot can be detected interactively using simple projection and intersection tests.

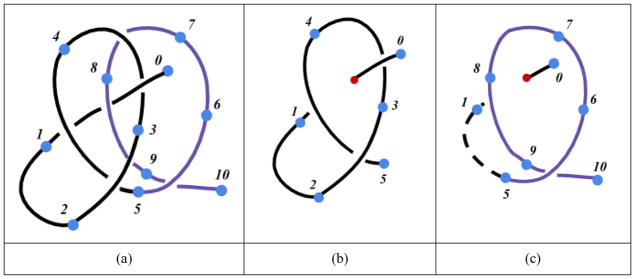
As illustrated in Figure 12, in practice, a knot is tied by looping the thread around one needle grasper, passing the thread end through the loop, and pulling both ends. Based on that, a knot can be identified based on two criteria:

Figure 12.

Knot tying process in the simulator. (a) Looping the thread around the tool. (b) Passing the thread end through the loop to apply a knot.

• Closed loop around the tool: whether the thread is twining around the tool and forming a closed loop;

• Loop penetration: whether the loop is penetrated by a thread end.

In line with these criteria, the proposed knot detection algorithm comprises two major steps: loop projection and detection and thread-loop intersection. During the knot tying process, those two criteria are checked within the two steps respectively for each time step. A knot is identified when both criteria are satisfied.

5.1. Loop projection and detection

The process of determining a complete thread loop around the tool can be simplified by 1) projecting the line segments of the thread onto a plane, P, which is perpendicular to the tool being looped around, and 2) checking if the thread line segments form a closed loop in P.

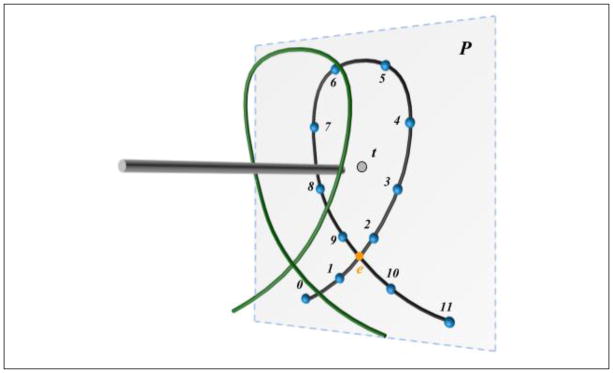
As shown in Figure 13, the projection of the thread (in black) on P, referred to as the projected thread, is shown as a set of line segments, 1–2, 2–3, …, 10–11. A closed loop is formed when any two of the line segments intersect. In this example, as 1–2 and 9–10 intersect at point e, the closed loop, denoted loop_P, can be expressed as: e-2-3-4-5-6-7-8-9-e. In addition, since the projection of the tool, t, locates inside of loop_P, which indicates the thread is looping around the tool, and the first criterion (Closed loop around the tool) is fulfilled. loop_P and the intersecting line segments, named intersecting pair, are then recorded for checking loop penetration in the thread-loop intersection step. The algorithm for the loop detection is as follows:

Figure 13.

Loop projection and detection. Each line segment forming the thread (curve in green) is first projected onto P. A thread loop is determined by checking whether there are two line segments (1–2 and 9–10) intersecting with each other at e (point in orange), and form a closed loop loop_P: e-2-3-4-5-6-7-8-9-e. The thread is looping around the tool when the projection of the tool (i.e., t) is inside the loop_P.

Algorithm 4.

Loop Detection Algorithm

	thread:{l(0,1), l(1, 2), … l(N − 1, N)} ▷ N num projected line segments
	t:	▷ tool projection
1:	procedure loopDetection(thread, t)
2:	for i = 0 to N − 1 do
3:	for j = i+2 to N do
4:	e ← line-line-intersection(l(i, i + 1), l(j, j + 1))
5:	if (e ≠ null) then
6:	loopp ← e, i + 1, … j, e
7:	intersection pair ← l(i, i + 1), l(j, j + 1)
8:	if (point-polygon-Inclusion(t, loopp)) then
9:	record loopp, intersection pair
10:	i ← j+ 1
11:	break
12:	end if
13:	end if
14:	end for
15:	end for
16:	end procedure

Given a set of thread line segments projected on P, to identify a loop, we traverse each line segment from the beginning, and determine the intersection between the current inquired segment l(i, i + 1) and each of its following line segment l(j, j + 1) in sequence by checking the intersection between them (line 4). If no intersection is found, we then move on to the next line segment and repeat the process until the first intersection (e) is found. The line segments in between form the loop, loop_P. In line 8 we then determine whether the projection of the tool, t, is inside of loop_P (polygon), based on the widely used even-odd rule [31], where a ray is shot from t to a random direction along P: if the ray interests the polygon (loop_P) in odd times (e.g., once), t is inside of loop_P; otherwise, it is outside. We only record the closed loop around the tool (line 9). Line 10 indicates the searching for the next loop, whose starting line segment is next to the ending line segment of its prior loop. The multiple-loop detection scenario will be discussed in detail in section 5.3. The algorithm will be end when all line segments in the first for-loop (l(i, i + 1)) are traversed, and all closed loops can be identified.

5.2. Thread-loop intersection

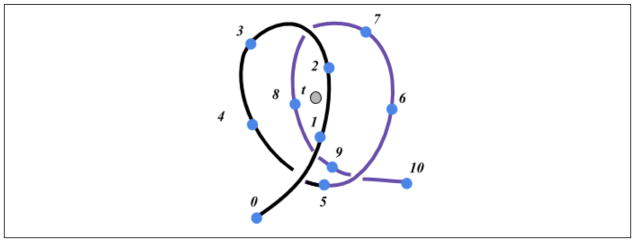
As illustrated in Figure 12(b), to complete the knot, the thread end must pass through the loop, which can be determined by checking whether there is a thread line segment, denoted penetrating line segment (e.g., 2–3 in Figure 14(a)), passes through the closed loop (loop_P) identified from loop projection and detection.

Figure 14.

Thread-loop intersection. A line segment penetrates the closed loop identified from loop projection from (a) inside out and (b) outside in.

It can be seen from Figure 14, there are two types of loop penetration: (a) inside-out and (b) outside-in. To determine the loop penetration type, the “above” and “below” relationship of intersecting pair (e.g., 5–6 and 11–12 in (a)) need to be introduced first.

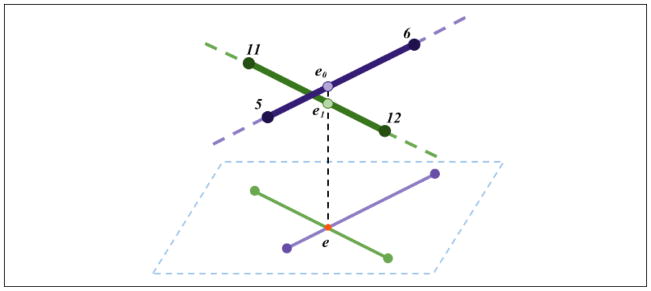
Above and below – the relative position between two line segments of the intersecting pair with respect to P, i.e., which line segment is above (or below) the other one, can be determined as following. As shown in Figure 15, the intersection point of the intersecting pair, e, is mapped back to their corresponding thread line segments, 5–6 and 11–12, and two mapping points, e₀ and e₁, can be identified using the barycentric coordinate method. The line segment (e.g., 5–6) whose mapping point (e.g., e₀) with larger distance to e is identified as above, and the other one is below.

Figure 15.

Determining “above” and “below” relationship between the line segments of intersecting pair. e (in orange) is the intersection point of intersecting pair on P. As the corresponding point of e on 5–6, e0, has a larger distance to the plane compared to e1, 5–6 is identified as above 11–12.

The above and below relationship of the intersecting pair can be further used to determine the penetration type when the penetrating line segment passes the loop:

• If the penetrating line segment is closer to the above line segment of the intersecting line segment pair, it must penetrate the loop from the inside out (Figure 14(a)).

• If the penetrating line segment is closer to the below line segment of the intersecting line segment pair, it must penetrate the loop from the outside in (Figure 14(b)).

In Figure 14(a), thread line segments 5–6 and 11–12 comprise the intersecting pair, where 5–6 is above 11–12. Since the penetrating line segment 2–3 is closer to 5–6 than 11–12, when it passes through the loop from the inside out, a knot can be tied. However, if line segment 2–3 penetrates the loop from the outside in instead, the knot is undone in the end. Similarly, in Figure 14(b), as the penetrating line segment 11–12 which is closer to the below part (i.e., 8–9) of the intersecting pair, penetrates the loop from the outside in, a knot can also be made.

5.3. Knot detection for multiple loops

The proposed method can detect a knot not only made with single loop (single-throw knot), but also with more than one loop (e.g., double-throw knot) based on the same criteria described in section 5.1.

Loop projection and detection – the loop detection algorithm described in Algorithm 4 is still applicable to multiple-loop scenario.

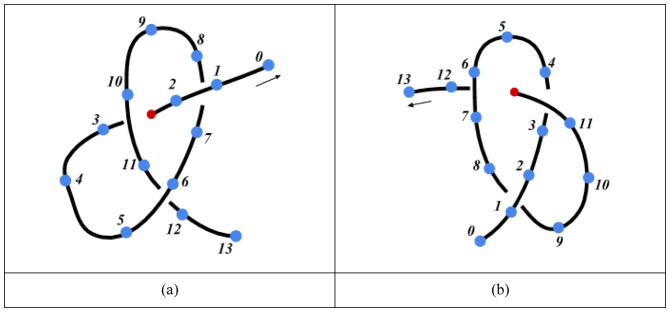
As shown in Figure 16, loops are made of consecutive line segments, and can be identified one after another by traversing the thread line segments from the beginning. Once the first intersection between two line segments is found, the first loop (in black) is detected. The searching for the next loop starts from the line segment (5–6) next to the last segment of the first loop. Once the first intersection is found between the current inquired line segment (5–6) and its following segment (9–10), the second loop (in purple) is determined. All loops can be identified in such manner. Meanwhile, when the tool projection (t) is inside of both loops at the same time, two throws around the tool can be identified based on the first criterion (Closed loop around the tool).

Figure 16.

Detection for multiple-loops of a thread. A double-throw is made when the tool projection, t, is inside of the first loop (in black) and second loop (in purple) at the same time.

Thread-loop intersection – as shown in Figure 17, to tie a multiple-loop knot, all closed loops detected in the previous step need to be penetrated by the penetrating line segment at the same time. we first check whether the penetrating line segment (0–1) intersects with the projection plane (P), and whether the intersection point is inside of both loops concurrently, using the same point-polygon inclusion algorithm mentioned in Algorithm 4 (line 8). Since the penetrating line segment penetrates both loops from the inside out, a double-throw knot can therefore be made based on the loop penetration criterion. An example of tying a double-throw knot is demonstrated in Figure 22(a–c).

Figure 17.

Thread-loop intersection for multiple loops. The penetrating line segment (0–1) should penetrate all closed loops at the same time.

Figure 22.

Double-throw knot tying in VBLaST-SS^© (a–c) and FLS (d–f).

6. Automatic metrics recording and measurement

A major advantage of VR-based surgical training simulator is the ability to automate measure and record user performance on the fly. In our suturing simulator, a user’s performance is measured in real-time by the metrics recording module developed on the basis of the assessment metrics devised by FLS committee, including:

• The deviation of the suture thread from the two marks on the penrose drain (in millimeter)

• Knot tightness (0, 10, 20)

• Gap of the slit in the penrose drain (in millimeter)

• Overall time to complete the task (in seconds)

These metrics are computed in the simulator as following.

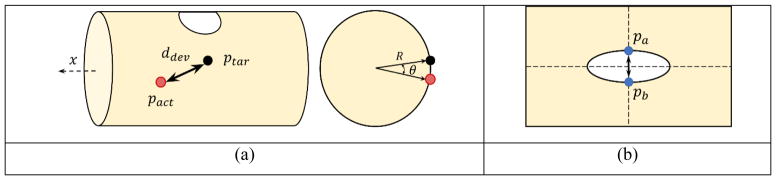
Deviation from the two marks (mm) – as illustrated in Figure 18(a), the penrose drain is a cylinder-shaped model, the deviation of the actual penetrate position (p_act) to a mark (p_tar) can be measured by computing the geodesic distance between two points on a cylinder:

$$d_{\mathit{dev}}=\sqrt{R^2{\theta }^2+x^2}$$

Figure 18.

Metric measurement. (a) Deviation of the actual penetration position, p_act, to the mark, p_tar, on the penrose drain. (b) Gap of the slit in the penrose drain is evaluated by measuring the distance between p_a and p_b.

Where, R is the radius of the cylinder (penrose drain), θ is the angular displacement (in radians) and x is the axial displacement between the two points.

Knot tightness – the knot tightness can be measured based on the tension applied to the thread when pulling its ends from both sides. In the simulator, the tension is evaluated by measuring the stretching distance of the thread when it is being pulled. Since the thread can only have limited stretch, when the tension reaches a pre-defined threshold, the knot is considered as tight (0); otherwise it is slipping (10). For an untied knot, the metric is set to 20.

Gap of the slit (mm) – the gap of the slit in the penrose drain can be determined by measuring the distance between the two pre-identified points along the boundary of the slit, p_a and p_b, as shown in Figure 18(b), which shows the initial gap of the slit before a knot is made.

Completion time (seconds) - Timing for the task starts when the needle appears in the simulator, and ends when all three knots are tied and the thread is cut from both sides.

These quantitative metrics provide objective measure to study the proficiency of a user and the effectiveness of the virtual simulator on real suturing performance.

7. Hardware interface and haptic rendering

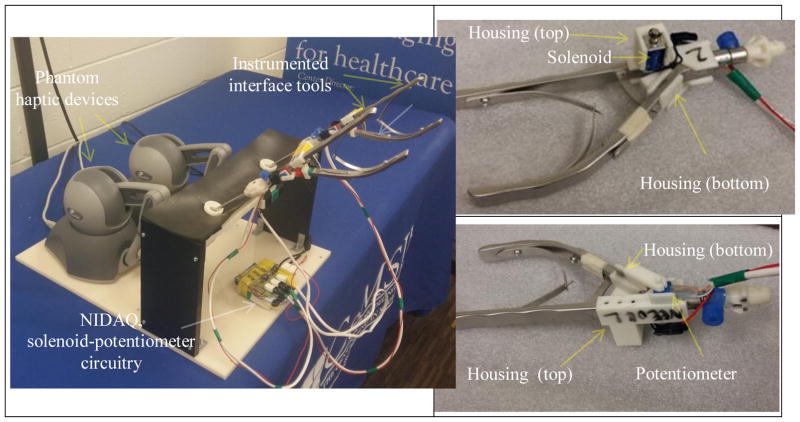
The user interacts with the simulation environment through a custom designed haptic hardware interface which consists of a pair of instrumented suture tools (needle drivers/shears) connected to pair of Geomagic Touch^™ haptic devices.

The tools are instrumented for capturing the user hand actions, which involves two components: (i) the motion of the needle-graspers in the task space (ii) action of grasping (or releasing). The former is captured through the Phantom haptic device connected at the grasper end of the needle grasper tool. The latter action is captured through rotary potentiometers (10 KΩ) installed in the housing on each of the tools. The housing consists of two parts (top and bottom) and are mounted on to each arm near the junction of the handles as shown in Figure 19. As the handles are compressed (for grasping) or released (for ungrasping), the change in voltage signal from the potentiometer is processed using NI-DAQ® (National Instruments Data Acquisition) device for appropriately displaying the action of the tool by the simulation software.

Figure 19.

(a) The hardware interface (b) & (c) Needle grasper handles with the potentiometer and solenoid mounted on the housing

The feedback offered to the user through the tools interface are (i) force feedback while manipulating the suture thread and the penrose drain and (ii) sensation for needle grasping. The interface offers force feedback while the user manipulates the suture thread. The forces are evaluated when a section of thread is stretched beyond its original length. For instance, if a section between the knot and the tool is stretched (as shown in Figure 20), the tool which causes the action is provided with force feedback so as to resist the stretching. The magnitude of force feedback given to the tool is k_s(l_s − L_s), where l_s and L_s are respectively, original and stretched lengths of the section of the suture thread. The direction of force feedback is along the fully stretched section of the thread.

Figure 20.

Force feedback on the stretched section of the suture thread.

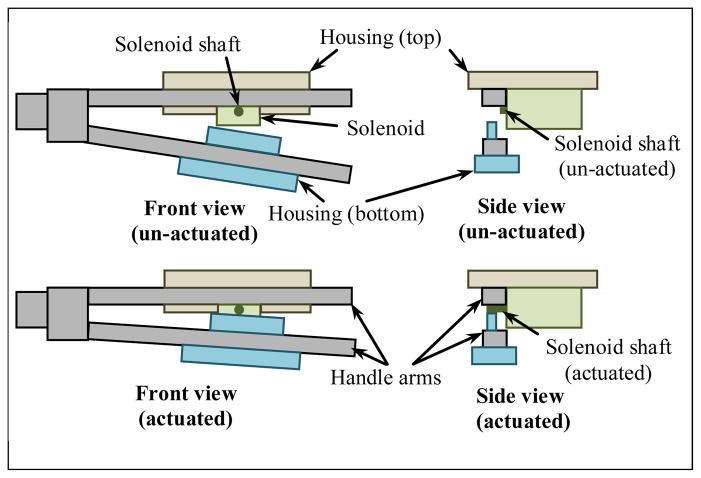
Another aspect of feedback is the sensation of needle grasping, i.e. when the user operates the handles to grasp the needle, a feedback is provided to the user on successful grasping. This is accomplished by triggering a solenoid switch (5.0V DC 4.5Ω miniature) when the user compresses the handle arms while having the grasper jaws proximate and appropriately placed for the needle to be grasped. The design of the housing and placement of the solenoid is such that, under the circumstances of actuation, the shaft of the solenoid (as shown in the Figure 21) is inserted inside the contraption between the arms of the handles for the user to feel a small restriction in the operating span of the handles. The input signal from the simulation software to the circuitry is provided using the NI-DAQ controller.

Figure 21.

Schematic diagram describing the feedback for needle sensation using solenoid switch.

8. Results and Discussion

The VBLaST-SS^© has been implemented on a standard desktop computer with an Intel Core i7-4930K, 3.4GHz CPU and 16.0 GB RAM.

The suturing simulator can be used to simulate the whole procedure of FLS intracorporeal knot-tying process, which involves placing a suture thread through two marks in a penrose drain, typing a double-throw knots followed by two single-throw knots, and finally cutting the thread ends from both sides. A video that demonstrates this procedure performed in our simulator as well as in the FLS box can be found at this link. Our simulator runs at interactive frame rates of 150 frames per second (FPS) during the simulation.

A series of snapshots of key stages in suturing is presented in Figure 22(a–c), with a user holding the needle with the right needle grasper, (a) twining the thread around the left tool to make double loops; (b) tying a double-throw knot; (c) closing the slit of the penrose drain by pulling the thread from both side to tighten the knot. The same suturing procedure has been done in the FLS box, and the captures of tying a double-throw knot can be found in (d-f) for reference.

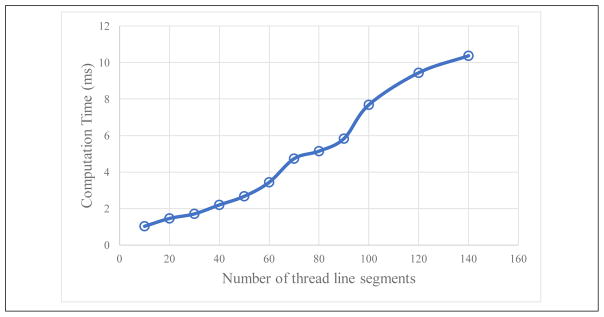
To test the simulation speed by changing the number of line segments used for modeling the thread, we conducted the same suturing task, i.e., tying a double-throw knot, with increasing number of line segments. Figure 23 shows the average computation time with increase in number of thread line segments. To maintain 30 frames per second (FPS) real-time rendering speed, the computation for the whole simulator including collision detection and knot detection needs to be done in under 33.3 milliseconds (ms). It can be observed that the computation time is under 10 ms when 120 line segments are involved, and the thread can still be operated freely in the simulator. In the suturing simulator, the number of line segments chosen to model the suture thread is 30, and its length is maintained to be 150 millimeters, which is the length of the thread used in the FLS intracorporeal suturing task.

Figure 23.

Average computation time per simulation time step for a thread modeled with increasing number of line segments.

For evaluating our collision detection method against the traditional approach of continuous collision detection (CCD) methods, we compare the operations involved in the detection process in both the methods. The existing CCD methods essentially involve the following steps that are common to both edge-edge and point-triangle cases viz. (i) formulating a cubic polynomial equation in time considering co-planarity of entities (ii) solution of the cubic equation for time-to-collision (iii) verification of the root and computation of interpolated geometry and (iv) performing an inside test (i.e. test whether the intersection point falls during collision falls inside the limits of the colliding entities). Cost-wise, the first step (in the case of edge-edge collision for instance) needs 10 vector subtractions, 2 vector cross products, a scalar triple product and 6 vector dot products given the coordinates of positions in the previous and current configurations, while the second step involves the cost of solving a cubic equation. On completion of the above mandatory steps, validity of root (time-of-collision) is checked, the geometry of the entities is interpolated at the time of collision and the inside test is performed, which involves 4 scalar-vector multiplications and 4 vector additions (for the edge-edge case).

In comparison, our approach of continuous collision detection involves the following steps (i) finding the shortest (perpendicular) distance between entities at previous and current configurations and evaluate dot product of minimum distance vectors, (ii) if collision is possible, evaluate time to collision, (iii) if collision is possible, interpolate the geometry and (iv) the inside test. The cost of step (i) and (ii) in our approach is 6 vector subtractions, 2 vector cross product and 5 vector dot products and 4 scalar-vector operations and 3 scalar operations. Further computation is avoided in (eliminated) cases when the dot product is positive. It is worth noting that, after step (i), we are sure about the existence of a root inside the interval, signifying the effectiveness of the elimination. The step of solving a cubic polynomial equation is completely avoided. The interpolation of geometry and the inside tests are common for both methods, though, in our case, these steps are performed only for more probable cases. In addition to the above aspects contributing to the efficiency, the quantities computed during collision detection are directly used to evaluate the collision response. More specifically, computing collision-response specific quantities such as the normal approach velocities, the tangential components for treating restitution and friction, depth of penetration etc. can be quickly evaluated from quantities computed for collision detection (as demonstrated in the treatment of self-collision response) depending on the nature of application. The detection and response algorithms, demonstrated in the context of reduced dimensional objects, can easily be applied for treatment of collisions of rigid or deformable triangulated bodies (by skipping the steps associated with bared quantities such as w̄ for example).

Moreover, in the case when the segments align parallel in the given interval without colliding, the traditional approach falsely captures this as collision as the cubic equation results in a valid root inside the interval, whereas our approach accounts for this scenario, contributing towards more robust simulations.

9. Conclusion

This study presents the development of a computer-based interactive virtual simulation system for FLS intracorporeal knot-tying suturing task. The system incorporates a realistic graphics and novel bimanual haptic hardware interface to provide an immersive FLS suturing environment. The unique design of integrating real surgical instruments with haptic devices enables not only interactive rendering of force feedback but also realistic sensation of needle grasping.

We present a novel projection-intersection based knot detection method, which can identify the validity of different types of knots at haptic update rates. We also introduce a simple and robust edge-edge based self-collision detection and response algorithm which allows for operations like knot-tying and needle-insertion in the interactive and real-time suturing environment. Based on the advancements of the proposed knot detection and collision handling techniques, our simulator is capable of running on a standard personal computer in real time at interactive rates.

The simulator has been reviewed by clinical experts in the FLS committee. Future work will involve subjective validation studies of our suturing system. A trainee’s performance can be measured by a scoring system on the fly on the basis of the assessment metrics [34], such as completion time and knot tightness. These quantitative data provide objective assessment to study the effectiveness of the virtual training system on the real suturing performance.

Figure 7.

(a) Segments e_i and e_j with shortest distance vector at any instance in time. (b) Segments in two different time steps t and t + Δt. (c) Penetrated (crossed over) segments.

Figure 9.

Extension of the method to point-triangle continuous collision detection: The shortest distance vector w from a point x_i to the plane P_Δ containing the triangle defined by vectors e_b and e_c at any instance in time.

Figure 10.

Collision response applied to inter-penetrated segments e_i and e_j.

Highlights.

• The development of a virtual simulator for the suturing with intracorporeal knot-tying is presented.

• A novel projection-intersection based knot detection method, which can identify the validity of different types of knots at haptic update rates is proposed.

• A simple and robust edge-edge based collision detection algorithm is introduced to support interactive knot tying and needle insertion operations.

• The simulator can provide real-time objective assessment for the user’s performance.

• A bimanual hardware interface integrates actual surgical instruments with haptic devices enabling not only interactive rendering of force feedback but also realistic sensation of needle grasping.