Abstract
Vascular networks in cancers usually fail to develop a mature organization, resulting in chaotic dynamics with stochastic variations that include slowing, cessation, and even reversal of flow and will result in substantial spatial and temporal heterogeneity in oxygen concentration. Here, we consider the evolutionary stresses placed on tumor cells subject to these profound, frequent, but stochastic variations in oxygen.
Normal mammalian cells employ fermentative glucose metabolism only under aerobic conditions because it is markedly inefficient compared to oxidative respiration, generating 2 ATP/glucose compared to ~36 ATP/glucose. Furthermore, this inefficiency requires increased glucose flux, which results in greater acid production leading to a toxic acidic local environment. In contrast, cancer cells generally ferment glucose even in normoxic conditions - termed the “Warburg effect”.
Warburg physiology is often viewed as a metabolic defect. Indeed, this metabolic “hallmark” of cancer is termed “energy dysregulation.” However, if cancers arise through an evolutionary optimization process, we hypothesize any commonly observed property must confer an adaptive advantage. Here, we investigate the hypothesis that aerobic glycolysis represents a successful adaptation to stochastic variations in oxygen concentration stemming from chaotic intratumoral blood flow. Using mathematical models, we demonstrate that the Warburg effect evolves as a conservative metabolic bet-hedging strategy in response to stochastic fluctuations of oxygen. Specifically, the Warburg effect sacrifices fitness in physoxia but preemptively adapts cells to survive during sudden decreases in oxygen concentration. We conclude the Warburg phenotype represents an optimal bet-hedging evolutionary strategy in an environment with stochastic fluctuations of oxygen.
Keywords: Tumor metabolism, Intermittent hypoxia, bet hedging
Introduction
Cancers are open, complex, adaptive, dynamic systems. “Complex” because they contain a large number of components linked through mostly nonlinear interactions. “Adaptive” because the tumor cells evolve phenotypic strategies in response to their micro-environmental circumstance, each other, and eventually to therapy. “Dynamic” because the elements of the tumor and their interactions with each other and the selecting environment change over space and time. “Open” because the tumor continuously interacts with normal tissue in large part through its vascular network. Similar to riparian ecosystems, blood vessels provide nutrients and growth factors to and remove metabolites from the surrounding cancer population.
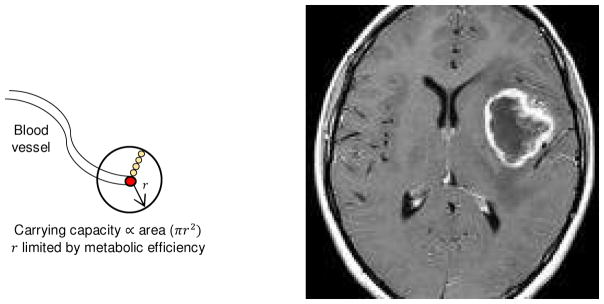
The complex eco-evolutionary dynamics of cancer are particularly evident in the spatial and temporal consequences of disordered blood flow. Spatially heterogeneous perfusion is frequently and readily observed as areas of poor enhancement and necrosis in routine cross sectional imaging (Figure 1). This significantly contributes to micro-environmental, cellular, and molecular heterogeneity within tumors1–4 and its clinical consequences are well recognized5–7. However, it is also clear from a number of in vivo studies8,9 that blood flow within many regions of a tumor varies with time. Some of these changes can be monotonic with, for example, progressive loss of blood flow in the tumor core as the overall tumor size increases (Figure 1). Importantly, however, blood flow can also vary stochastically or cyclically with temporal dynamics ranging from seconds to hours, as disordered vascular organization results in transient periods in which blood vessels can be dilated, occluded, or experience flow reversal.
Figure 1.
Local diffusion reaction kinetics around a blood vessel allow microscopic-scale spatial gradients in oxygen, glucose, and H+. Although not spatially explicit, the model equates carrying capacity with the cross-sectional area of a tumor cord growing around a centrally located blood vessel (right panel). At macroscopic scale, the spatial density of blood vessels can vary. The most common pattern is high vascular density in the tumor periphery and low blood flow with tumor necrosis centrally (right panel, ring-enhancing glioblastoma).
A consequence of temporal variations in blood flow is episodic hypoxia, which has been documented in a number of animal models and some human studies10–14. Similar to blood flow, changes in local oxygen concentration can be stochastic or cyclical with periodicities ranging from a few cycles per hour to cycle times of days. Yet, hypoxia is only the “tip of the iceberg” as blood flow also delivers multiple other substrates including serum growth factors and hormones (e.g. estrogen) and removes cellular metabolites (e.g. acid). This results in complicated diffusion-reaction kinetics in peri-vascular tissue as molecules diffuse to or from the local blood vessel along concentration gradients while often being either consumed or produced by the cells along the diffusion path. Therefore, when a vessel is transiently occluded, the perivascular tissue will undergo complex temporal and spatial gradients in virtually every component of the microenvironment, eliciting a wide range of tumor cell responses from death to increased motility. The formation of an irregular vasculature and its impact on the tumor microenvironment have been investigated using a number of sophisticated mathematical models15–19, which demonstrate spatial heterogeneity in vascular density and flow based on distance from the tumor-host interface, as well as dynamic changes in oxygenation as angiogenesis, vascular remodeling, and invasion proceed. Such dynamics have been shown to have significant clinical implications; for instance, in vivo studies have demonstrated that cyclical hypoxia is associated with greater metastatic potential than chronic hypoxia20,21. Both acute and chronic hypoxia result in resistance to radiation therapy and vascular occlusion will reduce local delivery of systemic therapies.
Constitutively elevated glycolysis is commonly observed in malignancy and forms the basis for 18F-FDG-PET imaging. Ordinarily, mammalian cells downregulate glycolysis in aerobic conditions, preferring to maximize the efficiency of energy extraction through cellular respiration, which generates more ATP/glucose than fermentation. This stereotyped metabolic response to oxygen is termed the Pasteur effect22. Conversely, high aerobic glycolysis with persistent fermentation of pyruvate to lactate is termed the Warburg effect23. Fermentation is markedly inefficient compared to cellular respiration, generating just 2 ATP/glucose while respiration generates 38 ATP/glucose, implying the Warburg effect should limit the Darwinian fitness of cancer cells. But, if cancers progress by somatic evolution, then common features of the malignant phenotype such as the Warburg effect result from natural selection and are expected to confer a fitness advantage. How, then, does the Warburg effect benefit cancer cells, either intrinsically or competitively?
Variations in environmental conditions over time impose strong evolutionary selective pressures quite different from constant conditions, no matter how harsh. That is, stochastic variations in environment result in phenotypic and genotypic properties that are specifically adapted to survive and even proliferate in a very wide range of micro-environmental conditions. While there has been extensive investigation of cancer cells subjected to fixed non-physiological environments (e.g. hypoxia) there has been virtually no effort to understand tumor cell adaptive strategies selected by rapid cyclical or stochastic variations. Some environmental perturbation will simply require acclimation - minor phenotypic changes such as the stabilization of HIF-1a in acute hypoxia. However, other changes may threaten cell survival and thus elicit complex Darwinian adaptive dynamics.
We hypothesize that the Warburg effect evolves as a conservative metabolic bet-hedging strategy in response to stochastic fluctuations of oxygen. In ecology, bet-hedging refers to traits or behaviors which adapt the organism to an unpredictable environment by spreading risk, such that population loss resulting from environmental shifts is generally reduced24,25. This requires a population to sacrifice its fitness under ideal conditions and, therefore, the arithmetic mean fitness across generations is less. Bet-hedging strategies enhance geometric mean fitness, however, and are evolutionarily successful because biological populations grow geometrically rather than arithmetically. Consequently, all bet-hedging strategies satisfy three mathematically explicit criteria: 1) reduced population variance, 2) lesser arithmetic mean fitness, and 3) greater geometric mean fitness when compared to the equivalent non bet-hedging phenotype.
Methods
Bet-Hedging Strategies
Three types of bet-hedging have been described in the ecology literature. Here, we borrow descriptions quite similar ones presented by Olofsson, Ripa and colleagues26,27. Adaptive coin-flipping is any strategy that adapts the organism to stochastic variations in environmental conditions by predicting future conditions based on present conditions. For example, the parthenogenetic aphid Rhopalosiphum padi generates either cold-tolerant sexual offspring or cold-sensitive parthenogenetic females during reproduction and its investment in cold-tolerant offspring reflects the severity of winter28. Next, diversified bet-hedging means to simultaneously employ a variety of strategies; a tactic embodied by the idiom “don’t place all your eggs in one basket.” For instance, the fairy shrimps Streptocephalus woottoni and Branchinecta sandiegonensis live in pools of rainwater and produce eggs which hatch at staggered times. Shrimp born into short-lived pools are likely to perish once the pool evaporates. However, delayed hatching permits a subset of eggs to survive the dry period and hatch once another pool forms, thereby preventing extinction29. Diversified bet-hedging is analogous to diversified investing: at least a subset of investments should be successful regardless of market trends, reducing risk to the investor.
Lastly, conservative bet-hedging means to persistently employ the same strategy irrespective of environmental conditions. One example is the monocarpic plant Lobelia inflata, which guarantees wintertime survival through size- and season-dependent bolting30. In accordance with the criteria for bet-hedging, Lobelia inflata curtails its reproductive capacity by hesitating to bolt during mild winters, thereby lessening its own arithmetic mean fitness. However, the plant boosts its geometric mean fitness by preventing death in harsher winters when premature bolting would prove fatal. We propose that the Warburg effect represents this type of strategy because cancer cells persistently display a glycolytic metabolic phenotype irrespective of oxygen concentration, although glycolysis is significantly less efficient than cellular respiration and should consequently reduce arithmetic mean fitness. Herein, the Warburg effect is framed as a conservative bet-hedging strategy using a discrete-time population dynamic model with the major determinants of growth set via metabolic arguments. If truly a bet-hedging strategy, the Warburg effect is expected to reduce population variance, lessen arithmetic mean fitness, and enhance geometric mean fitness with respect to more metabolically efficient cell phenotypes. Indeed, the model confirms these predictions and demonstrates that the success of Warburg metabolism increases alongside the magnitude of environmental chaos.
Model
Carbohydrate metabolism is modelled as parallel first-order chemical reactions, fermentation and respiration, with cellular glucose allocated to each pathway according to a fraction 0 ≤ φ ≤ 1 whereby fermentation receives φ of cellular glucose and respiration receives the remainder, or 1 − φ. The steady state concentration of intracellular glucose is proportional to a parameter, C, called the transport capacity. High grade malignancies are observed both clinically and experimentally to internalize glucose at rates much greater than healthy tissues31–33, therefore, the model assumes that Cw = 10 for Warburg cells and Cp = 1 for Pasteur cells. Hereafter, the subscript ‘w’ denotes ‘Warburg’ cells and the subscript ‘p’ denotes ‘Pasteur’ cells. Warburg cells are persistently glycolytic, in contrast to Pasteur cells which prefer cellular respiration when adequate oxygen is present. In general, malignant cells display a Warburg phenotype whereas healthy tissues display a Pasteur phenotype, although “Pasteur cells” may also represent an oxidative intratumoral subpopulation. Because of this, the distinction of Warburg vs. Pasteur is preferred to malignant vs. nonmalignant, allowing the model to be generalized to competition between tumor and host tissue, as well as between metabolically distinct intratumoral subpopulations. In other words, the key distinction is not whether a cell is malignant or nonmalignant, but whether or not it is persistently glycolytic.
Fermentation generates x ATP and respiration generates y ATP per molecule of glucose. The results presented here correspond to x = 2 and y = 38, meaning cellular respiration is nearly 20 times more efficient than fermentation in terms of ATP yield. However, fermentation generates ATP nearly 100 times faster than respiration, making Warburg metabolism highly advantageous during competition for shared resources34. This is represented in the model using rate constants, k1 = 100 and k2 = 1, which describe the relative kinetics of fermentation and respiration, respectively. Thus, cells are faced with a classic thermodynamic tradeoff between one pathway with superior kinetics (fermentation) and another with superior efficiency (respiration). The fraction φ describes a cell’s investment in each pathway and is the primary determinant of a cell’s metabolic phenotype.
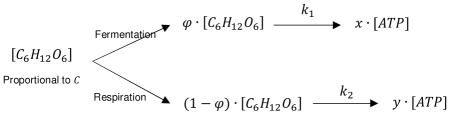
Importantly, φ varies as a function of oxygen concentration (% O2). The form of the relationship between φ and O2 is exponential decay, based on experimental measurements of HIF1α, a major transcriptional upregulator of glycolysis having expression levels which increase exponentially as oxygen levels decline, causing a commensurate increase in fermentative metabolism. Using μ as the decay constant:
| (1) |
Warburg cells are assigned a decay constant of μ = 0.005, mandating that upwards of 90% of glucose is fermented despite normoxia, which has been observed in glioblastoma cell culture using 13C-nuclear magnetic resonance spectroscopy35. Pasteur cells are assigned a larger decay constant, μ = 0.347, and route glucose mostly to respiration except in severe hypoxia. This particular value of μ is based on HIF1α expression in HeLa cell culture subjected to various levels of oxygen36. The value 0.347 fits equation (1) to the data presented by Jiang and colleagues, such that the fraction φ mirrors changes in HIF1a expression. Although HeLa cells are malignant, they demonstrate appropriate HIF1α degradation in response to rising oxygen tension, whereas glioblastoma cells tend to constitutively overexpress HIF1α through mechanisms such as inactivating mutations of isocitrate dehydrogenase-1 37.
Population dynamics are governed by a system of discrete-time two species competition equations conceived by ecologists Hassell and Comins38. The equations resemble the classical Lotka-Volterra model and have similar dynamics and requirements for coexistence, however, a discrete-time model is better suited to the stochastic nature of the present application than a continuous-time Lotka-Volterra system. In this case, the competitors are distinct populations of Warburg and Pasteur cells, each containing N members growing at an intrinsic rate λ equal to 2 daughter cells per day. Growth is limited by a parameter A equal to the reciprocal of the carrying capacity (K), expressed in number of cells. The model incorporates competition using Lotka-Volterra coefficients, α. For instance, αpw describes the effect that Warburg cells have on Pasteur cell growth. αpw = 2 indicates that the presence of each Warburg cell contributes the equivalent of 2 cells toward the Pasteur population’s carrying capacity. The complete system of two equations is given below, where t is the time in days. Recall that the subscripts ‘w’ and ‘p’ denote ‘Warburg’ (predominantly glycolytic) and ‘Pasteur’ (predominantly respiratory) populations.
| (3) |
| (4) |
Carrying capacities and competition coefficients are defined using metabolic arguments. A population’s carrying capacity is determined by the ATP extracted per glucose, or metabolic efficiency, equal to xφ + y(1 − φ). This value is measured relative to the metabolic efficiency of the competing population (see equations 5 and 6) and is independent of kinetics, therefore, C, k1, and k2 do not influence carrying capacity. Then, the relative carrying capacity Aw/Ap is proportional to the ratio of metabolic efficiencies squared, adding spatial significance to the model, which is intended to describe a cord of cells growing around a centrally located blood vessel. The radial growth attained by a tumor cord is determined by the rate of nutrients diffusing outward from the central vessel and also by the rate of nutrient consumption by cells along the diffusion path. Metabolically efficient populations presumably consume less nutrients, permitting members to survive farther from the central vessel. Therefore, the maximum radius of a tumor cord is proportional to the metabolic efficiency and the cross-sectional area is proportional to its square. Similar conclusions have been drawn in other mathematical models of the Warburg effect, including that by Astanin and Preziosi, which found the stationary thickness of a tumor cord is dependent on the rate of cellular oxygen consumption39. In our implicit two-dimensional representation, cross-sectional area is equated with carrying capacity (Figure 1).
| (5) |
| (6) |
Competition coefficients are determined by relative rates of glucose consumption. The rate of glucose consumption is influenced by transport capacity and also by φ, k1, and k2 because fermentation and respiration create the gradient for glucose transport. Assuming first-order kinetics for both pathways, the competition coefficient is defined as:
| (7) |
| (8) |
Stochastic fluctuations of oxygen are modelled as a Gaussian random walk with minimum value of 0% O2 and maximum value of 7% O2. Interstitial oxygen concentrations in most human tissues fall within this range. The initial oxygen concentration is selected randomly from a uniform distribution spanning 0–7% O2. Then, the magnitude of each fluctuation is selected from a normal distribution with mean of 0 and standard deviation of σ. If the fluctuation should cause the % O2 to be negative or exceed 7%, then the oxygen concentration is reset to either 0% or 7%, whichever is nearest. The stability of the random walk is manipulated via the standard deviation of fluctuations in oxygen concentration, σ.
Results
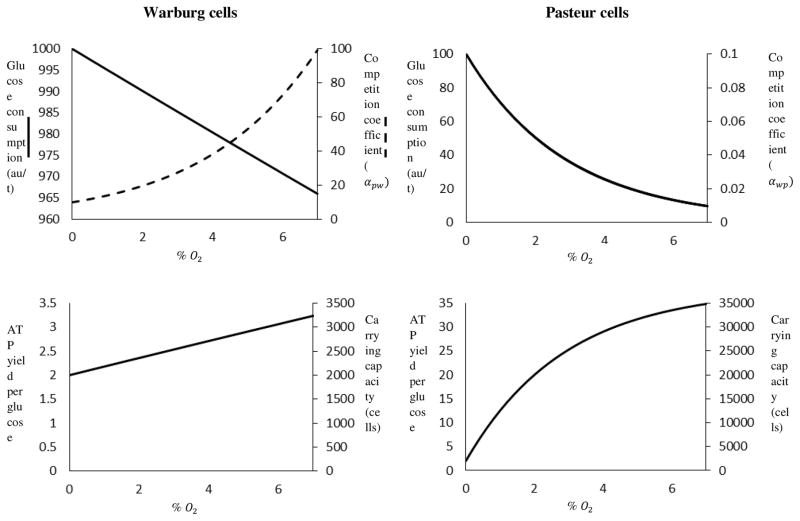
Warburg cell glucose consumption, which in truth decays exponentially as oxygen levels rise, appears to have a linear relationship with oxygen concentrations in the physiological range (Figure 2). The vanishingly small magnitude of μw is responsible for this behavior. In comparison, Pasteur cell glucose consumption decays rapidly as oxygen levels rise because μp ≫ μw and this has an unanticipated consequence: αpw grows exponentially with oxygen concentration. As a result, the competitive advantage conferred by the Warburg effect is, unexpectedly, much greater in physoxia than in hypoxia. This competitive edge is largely offset, however, by the Pasteur population’s superior carrying capacity in aerobic conditions. Likewise, the metabolic efficiency of Warburg cells grows linearly with oxygen concentration, whereas the metabolic efficiency of Pasteur cells increases rapidly in the form of a saturating curve. All cells have the same metabolic efficiency in anoxia because fermentation is the only route available for ATP synthesis in such conditions. Thus, except in anoxia, the carrying capacity of the Pasteur population exceeds that of the Warburg population .αwp < 1< αpw for all values of O2 and Ap < Aw for nonzero values of O2.
Figure 2.
The metabolisms of Warburg (glycolytic) and Pasteur (normal) cells are compared graphically (left axes) alongside competition coefficients and carrying capacities (right axes). Data for Warburg cells are displayed in the left column and data for Pasteur cells are displayed in the right column. Warburg cells consume more glucose than Pasteur cells, but generally yield less ATP/glucose. The result is that αpw > 1 > αwp for all values of O2 and Kp > Kw, except in anoxia. Unexpectedly, the competitive advantage endowed by Warburg metabolism rises alongside oxygen levels.
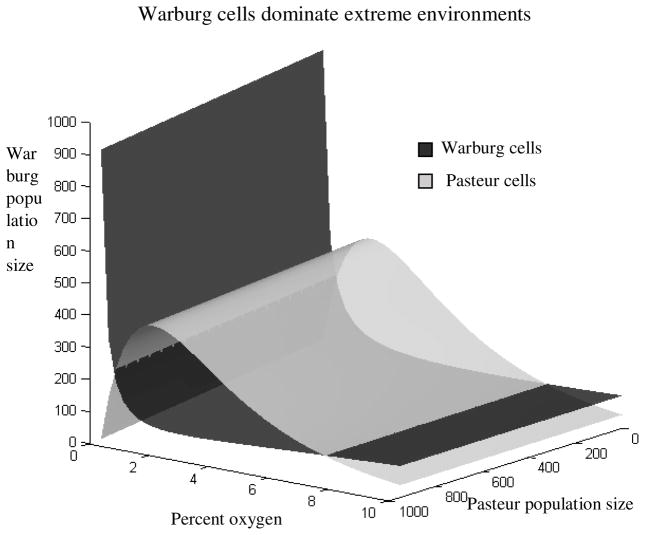
Phase space analysis demonstrates that stable equilibrium (coexistence) between the Warburg and Pasteur populations cannot exist except at specific oxygen concentrations (Figure 3); however, oxygen concentrations are not themselves stable, therefore, the populations cannot coexist. Warburg cells dominate in “extreme” conditions of low or high oxygen concentration, while Pasteur cells dominate the intermediate conditions ranging from approximately 1% to 8% O2. Pasteur cells have a maximum competitive advantage at approximately 2% oxygen, but this advantage surprisingly erodes as oxygen levels rise because 1) the carrying capacity of Pasteur cells saturates, and 2) αpw increases exponentially. Although oxygen concentrations were capped at 7% during our simulations, the model suggests Warburg cells should dominate at higher oxygen concentrations, which correlates with increased resistance to oxidative stress observed in actual malignancies.
Figure 3.
Phase space analysis using isocline surfaces reveals that Warburg cells dominate Pasteur cells in select for Pasteur cells. The populations cannot coexist extreme environments, while moderate levels of O2except at specific oxygen concentrations where their isocline surfaces intersect.
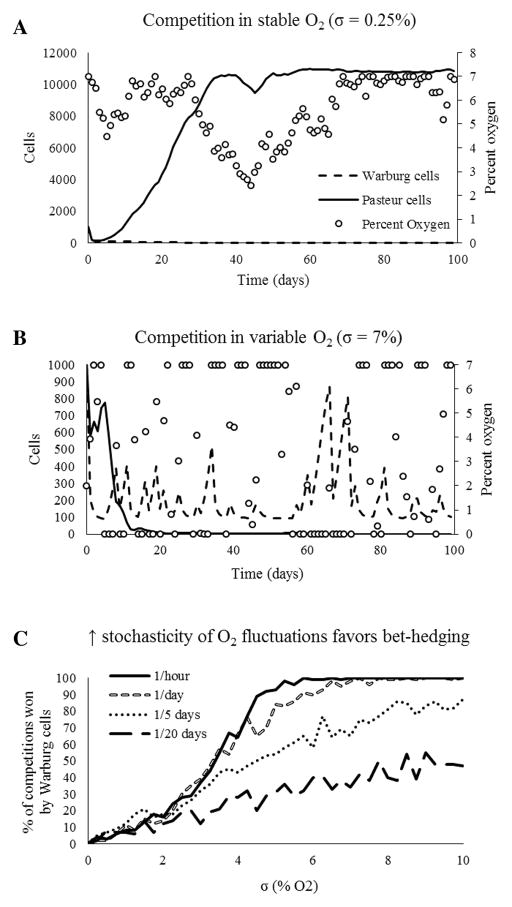
The simulations predict that the outcome of competition depends on the standard deviation of fluctuations in oxygen concentration, or σ (Figure 4). High amplitude fluctuations (high σ) favor the glycolytic (Warburg) phenotype by generating episodes of severe hypoxia. High frequency fluctuations also favor the glycolytic phenotype by causing stochastic drift in the oxygen concentration which may lead to hypoxia. Most importantly, sufficiently large and frequent fluctuations of oxygen consistently select for Warburg cells, despite their random nature (Figure 4).
Figure 4.
Simulated competitions between Warburg and Pasteur cells subjected to stochastic temporal variations in oxygen concentration demonstrate that increasing both the amplitude (σ) and frequency of oxygen fluctuations favors the Warburg (bet-hedging) phenotype. In panel C, each data point represents an average of 100 simulated competitions, each lasting 100 days. Pasteur cells dominate competition in an environment with stable oxygen concentrations (panel A), while Warburg cells dominate more variable environments (panel B).
Three predictions of bet-hedging theory were described previously: a bet-hedging strategies 1) reduce population variance, 2) lessen the arithmetic mean fitness, and 3) enhance the geometric mean fitness. The simulations demonstrate that the Warburg effect meets all 3 criteria, but this is depenent on a threshold amplitude and frequency of fluctuations in oxygen concentration. The geometric mean fitness of the Warburg and Pasteur populations does not significantly diverge until σ ≈ 3% O2 (Figure 5). Warburg cells consistently dominate stochastic environments with σ > 3% O2.
Figure 5.
Homogeneous (either Warburg or Pasteur) populations grown to carrying capacity were simulated in environments with temporally varying oxygen, then the population variance, AMF, and GMF were calculated after 100 days. Warburg cells have reduced population variance and AMF, but enhanced GMF when compared to Pasteur cells, consistent with bet-hedging theory. These effects grow as oxygen fluctuations become more chaotic (↑σ, panel C).
Discussion
Cancer cells are often subjected to harsh, non-physiological environmental conditions. In large part, this is due to spatial and temporal variations in blood flow. Tumor growth beyond a volume of a few mm3 requires tumor cells to evolve strategies to promote angiogenesis. However, because the unit of selection in intratumoral Darwinian dynamics is the individual cell, the angiogenic process can be complicated by “cheaters” who do not actually make angiogenic factors, but still benefit from the vascular ingrowth stimulated by other cells. As a result, cancer populations cannot typically perform the coordinated signal process that permits organs to form well-regulated, mature vascular networks. The resulting vascular network is usually significantly less organized than those found in normal tissues and this is readily visible in many cancers as regions of little or no blood flow, often resulting in extremely low cell densities (i.e. necrosis). In contrast, temporal variations in blood flow cannot be readily visualized using conventional imaging. Still, chaotic flow in intratumoral vessels has been observed microscopically and fluctuating oxygen concentrations have been measured in a number of in vivo tumor models.
Here, we investigated stochastically fluctuating blood flow as a Darwinian selection pressure with the primary focus being the cellular effects of environmental oxygen fluctuations from normoxia to hypoxia and even anoxia. Importantly, glucose concentrations in blood are much higher than oxygen concentrations and, as a result, glucose is typically present in relatively high concentrations even during periods of anoxia. But, depending on the environment, optimal metabolism of glucose through oxidative or glycolytic pathways will vary. Bet-hedging strategies are one means of evolving optimal fitness in a temporally varying and unpredictable environment. Using a population dynamic model, we conclude that the Warburg effect (i.e. persistent fermentative metabolism of glucose even in the presence of normoxia) evolves as a conservative metabolic bet-hedging strategy in an environment with temporally varying oxygen concentration. The success of the Warburg phenotype is dependent on a threshold level of stochasticity which produces hypoxia frequently enough to permit the selection of more glycolytic cells. The result is a paradox for cancer treatment: therapies that inhibit angiogenesis in an attempt to starve the tumor have the unfortunate effect of selecting more glycolytic metabolic phenotypes, despite transiently suppressing tumor growth. An analogous phenomenon is the spread of an invasive plant during drought conditions40.
It is important to note, however, that the representation of all malignant cells as “Warburg cells” and all host cells as “Pasteur cells” is an oversimplification of competition between the tumor and host. Both populations are, in truth, composed of a vast array of cell phenotypes with metabolisms ranging from predominantly glycolytic to predominantly respiratory. Indeed, nonmalignant cells such as thymocytes are known to adopt a Warburg glycolytic phenotype during periods of rapid proliferation41. As well, malignant cells exist that rely on lactate as fuel for their predominantly oxidative metabolism42. Therefore, the conclusions of the model are rightly applied to competition between cells based on metabolic differences rather than differing malignant potential, although malignancies adopt a more glycolytic metabolic phenotype than normal tissues, in general. Additionally, the model is not spatially explicit and is thus lacking complexity that may influence the outcome of competition. The predictions of game theoretical models can change completely when spatial considerations are incorporated, as demonstrated by Nowak and May43,44. The present model implies homogeneous mixing of the competing populations, which in reality is highly unlikely whether the competition is considered to take place between malignant intratumoral subpopulations or between the tumor and host at their interface.
An alternative to treatment using angiogenesis inhibitors would be to promote tumor blood flow in order to stabilize oxygen concentrations. Of course, this strategy carries the risk of enhancing the overall tumor growth by increasing the delivery of nutrients and, therefore, requires accompaniment by chemotherapy that is sufficient to subdue progression without disrupting the tumor vasculature. There are other concerns as well, including the accelerated development of drug resistance due to improved drug delivery. We do not advocate this strategy without a better understanding of its unique evolutionary consequences. Still, manipulating the intratumoral microenvironment to resemble the stable oxygenation of healthier tissues should, according to the model, select for non-Warburg metabolic phenotypes. As well, a mature vasculature is expected to remove acid generated by glycolytic cells and temper acid-mediated tissue invasion. Furthermore, as long as the growth stimulated by improved blood flow is offset by an effective chemotherapeutic regimen, an abundance of nutrients will favor non-Warburg phenotypes limited glucose supplies create a tragedy of the commons wherein cells that consume glucose fastest (Warburg cells) receive the most benefit34.
The competition between Warburg cells and those with normal glucose metabolism reflects the evolutionary trade-off between generalist and specialist adaptive strategies. As generalists, Warburg cells are capable of colonizing habitats with a variety of oxygen concentrations and tend to be acid-adapted via mechanisms such as chronic autophagy45, permitting survival in a large range of pH. In contrast, Pasteur cells (i.e. healthy tissues) are specialists that require a narrow range of oxygen concentration and pH to survive. Habitat variability has a deeper impact on specialists than on generalists because of a specialists’ more stringent growth requirements, an observation already well established among plants and animals46–49. Therefore, locally chaotic environments favor generalists such as the Warburg phenotype. Moreover, generalist tumor cells are likely more successful at adapting to “foreign” tissue habitats, which may explain experimental findings that normoxia-hypoxia cycles are associated with greater metastatic potential than temporally stable environments20,21.
Often, it is unclear if an invasive species is the driver or passenger of habitat change50. In the case of cancer, the environmental stochasticity that selects for malignant cells is likely driven by the cancer itself through disordered growth and secreted factors. For instance, the secretion of vascular endothelial growth factor (VEGF) by a variety of tumor types has been shown to not only stimulate endothelial proliferation and enhance blood flow, but also to paradoxically induce the production of procoagulant molecules including tissue factor which interrupt blood flow51. Generally, wildlife management strategies focus on eliminating an invasive species when it is the driver of habitat change. Cancer treatment currently mirrors this paradigm. However, in the case of cancer, malignant cells should additionally be considered passengers of habitat change because the chaotic, nonphysiological environment that cancers foster directly contributes to their capacity for tissue invasion. For example, acid-adapted cancer cells benefit from Warburg metabolism because it fosters a low pH microenvironment through acid secretion, which disrupts surrounding healthy tissue and permits local extension of the tumor. Thus, cancer begins with the evolution of a generalist phenotype such as Warburg effect and progresses through the propagation of environmental variability that favors malignant generalists. This perspective emphasizes the importance of regulating the tumor environment, in addition to targeting the cancer itself.
Previous mathematical modelling of bet-hedging has demonstrated that a combination of adaptive coin-flipping, diversified and conservative strategies may be required to achieve optimal fitness in a temporally varying and unpredictable environment26. While the Warburg effect represents a purely conservative strategy, other aspects of the cancer cell phenotype may qualify as diversified bet-hedging or adaptive coin-flipping, thereby contributing to a combination of strategies that optimizes growth. It has recently been proposed that cancer cells bet-hedge via stochastic state transitions, or random switching between phenotypes with different functional attributes52. This capability is evidenced by the persistence of specific phenotypic equilibria in cell culture after the isolation of a unique surface phenotype using flow cytometry53. Stochastic state transitions likely represent a mixture of diversified bet-hedging and adaptive coin-flipping. The random transitions are diversifying because they directly enforce intratumor phenotypic heterogeneity. Adaptive coin-flipping is present as well, because the probabilities with which specific transitions occur may be tuned to the distribution of environmental conditions due to natural selection resulting from temporal variations. The tuning of stochastic phenotypic transitions to match environmental variations has already been demonstrated in the budding yeast, Saccharomyces cerevisiae54. Given exposure to significant spatial and temporal micro-environmental variation throughout tumorigenesis, we predict that many traits common to cancer cells represent bet-hedging strategies, including the Warburg effect.
Acknowledgments
This work was supported by the James S. McDonnell Foundation grant, the V Foundation, Cancer therapy: Perturbing a complex adaptive system, NIH/National Cancer Institute (NCI) R01CA170595, Application of Evolutionary Principles to Maintain Cancer Control (PQ21), and NIH/NCI U54CA143970-05 [Physical Science Oncology Network (PSON)] Cancer as a complex adaptive system. CG was supported by an Alpha Omega Alpha Carolyn L. Kuckein Fellowship
References
- 1.Helmlinger G, Yuan F, Dellian M, Jain RK. Interstitial pH and pO2 gradients in solid tumors in vivo: high-resolution measurements reveal a lack of correlation. Nat Med. 1997;3:177–182. doi: 10.1038/nm0297-177. [DOI] [PubMed] [Google Scholar]
- 2.Sottoriva A, et al. Intratumor heterogeneity in human glioblastoma reflects cancer evolutionary dynamics. Proc Natl Acad Sci. 2013;110:4009–4014. doi: 10.1073/pnas.1219747110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Marusyk A, Almendro V, Polyak K. Intra-tumour heterogeneity: a looking glass for cancer? Nat Rev Cancer. 2012;12:323–334. doi: 10.1038/nrc3261. [DOI] [PubMed] [Google Scholar]
- 4.Gerlinger M, et al. Intratumor heterogeneity and branched evolution revealed by multiregion sequencing. N Engl J Med. 2012;366:883–892. doi: 10.1056/NEJMoa1113205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lloyd MC, et al. Darwinian dynamics of intratumoral heterogeneity: not solely random mutations but also variable environmental selection forces. Cancer Res. 2016;76:3136–3144. doi: 10.1158/0008-5472.CAN-15-2962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gerlinger M, Swanton C. How Darwinian models inform therapeutic failure initiated by clonal heterogeneity in cancer medicine. Br J Cancer. 2010;103:1139–1143. doi: 10.1038/sj.bjc.6605912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Grove O, et al. Quantitative computed tomographic descriptors associate tumor shape complexity and intratumor heterogeneity with prognosis in lung adenocarcinoma. PloS One. 2015;10:e0118261. doi: 10.1371/journal.pone.0118261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brurberg KG, Gaustad JV, Mollatt CS, Rofstad EK. Temporal heterogeneity in blood supply in human tumor xenografts. Neoplasia. 2008;10:727–735. doi: 10.1593/neo.08388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fisher DT, et al. Intraoperative intravital microscopy permits the study of human tumour vessels. Nat Commun. 2016;7 doi: 10.1038/ncomms10684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Brown J. Evidence for acutely hypoxic cells in mouse tumours, and a possible mechanism of reoxygenation. Br J Radiol. 1979;52:650–656. doi: 10.1259/0007-1285-52-620-650. [DOI] [PubMed] [Google Scholar]
- 11.Chaplin DJ, Olive PL, Durand RE. Intermittent blood flow in a murine tumor: radiobiological effects. Cancer Res. 1987;47:597–601. [PubMed] [Google Scholar]
- 12.Cardenas-Navia LI, et al. The pervasive presence of fluctuating oxygenation in tumors. Cancer Res. 2008;68:5812–5819. doi: 10.1158/0008-5472.CAN-07-6387. [DOI] [PubMed] [Google Scholar]
- 13.Pigott K, Hill S, Chaplin D, Saunders M. Microregional fluctuations in perfusion within human tumours detected using laser Doppler flowmetry. Radiother Oncol. 1996;40:45–50. doi: 10.1016/0167-8140(96)01730-6. [DOI] [PubMed] [Google Scholar]
- 14.Hill S, et al. Microregional blood flow in murine and human tumours assessed using laser Doppler microprobes. Br J Cancer Suppl. 1996;27:S260. [PMC free article] [PubMed] [Google Scholar]
- 15.Owen MR, Alarcon T, Maini PK, Byrne HM. Angiogenesis and vascular remodelling in normal and cancerous tissues. J Math Biol. 2009;58:689–721. doi: 10.1007/s00285-008-0213-z. [DOI] [PubMed] [Google Scholar]
- 16.Macklin P, et al. Multiscale modelling and nonlinear simulation of vascular tumour growth. J Math Biol. 2009;58:765–798. doi: 10.1007/s00285-008-0216-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Boujelben A, et al. Multimodality imaging and mathematical modelling of drug delivery to glioblastomas. Interface Focus. 2016;6:20160039. doi: 10.1098/rsfs.2016.0039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Welter M, Fredrich T, Rinneberg H, Rieger H. Computational Model for Tumor Oxygenation Applied to Clinical Data on Breast Tumor Hemoglobin Concentrations Suggests Vascular Dilatation and Compression. PloS One. 2016;11:e0161267. doi: 10.1371/journal.pone.0161267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Welter M, Bartha K, Rieger H. Emergent vascular network inhomogeneities and resulting blood flow patterns in a growing tumor. J Theor Biol. 2008;250:257–280. doi: 10.1016/j.jtbi.2007.09.031. [DOI] [PubMed] [Google Scholar]
- 20.Cairns RA, Kalliomaki T, Hill RP. Acute (cyclic) hypoxia enhances spontaneous metastasis of KHT murine tumors. Cancer Res. 2001;61:8903–8908. [PubMed] [Google Scholar]
- 21.Rofstad EK, Gaustad J, Egeland TA, Mathiesen B, Galappathi K. Tumors exposed to acute cyclic hypoxic stress show enhanced angiogenesis, perfusion and metastatic dissemination. Int J Cancer. 2010;127:1535–1546. doi: 10.1002/ijc.25176. [DOI] [PubMed] [Google Scholar]
- 22.Pasteur L. Mémoire sur la fermentation applée lactique. Mémoire sur la fermentation alcoolique. Mallet-Bachelier; 1857. [Google Scholar]
- 23.Warburg O. Experiments on surviving carcinoma tissue. Methods Biochem. 1923:317–333. [Google Scholar]
- 24.Slatkin M. Hedging one’s evolutionary bets. Nature. 1974;250:704–705. [Google Scholar]
- 25.Philippi T, Seger J. Hedging one’s evolutionary bets, revisited. Trends Ecol Evol. 1989;4:41–44. doi: 10.1016/0169-5347(89)90138-9. [DOI] [PubMed] [Google Scholar]
- 26.Olofsson H, Ripa J, Jonzen N. Bet-hedging as an evolutionary game: the trade-off between egg size and number. Proc R Soc Lond B Biol Sci. 2009 doi: 10.1098/rspb.2009.0500. rspb20090500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ripa J, Olofsson H, Jonzen N. What is bet-hedging, really? Proc R Soc Lond B Biol Sci. 2009 doi: 10.1098/rspb.2009.2023. rspb20092023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Halkett F, et al. Dynamics of Production of Sexual Forms in Aphids: Theoretical and Experimental Evidence for Adaptive ‘Coin-Flipping’ Plasticity. Am Nat. 2004;163:E112–E125. doi: 10.1086/383618. [DOI] [PubMed] [Google Scholar]
- 29.Simovich MA, Hathaway SA. Diversified bet-hedging as a reproductive strategy of some ephemeral pool anostracans (Branchiopoda) J Crustac Biol. 1997;17:38–44. [Google Scholar]
- 30.Simons A, Johnston MO. Suboptimal timing of reproduction in Lobelia inflata may be a conservative bet-hedging strategy. J Evol Biol. 2003;16:233–243. doi: 10.1046/j.1420-9101.2003.00530.x. [DOI] [PubMed] [Google Scholar]
- 31.Warburg O. The metabolism of carcinoma cells. J Cancer Res. 1925;9:148–163. [Google Scholar]
- 32.Cori CF, Cori GT. The Carbohydrate Metabolism of Tumors II. Changes in the sugar, lactic acid, and CO2-Combining Power of Blood Passing through a tumor. J Biol Chem. 1925;65:397–405. [Google Scholar]
- 33.Gambhir SS. Molecular imaging of cancer with positron emission tomography. Nat Rev Cancer. 2002;2:683–693. doi: 10.1038/nrc882. [DOI] [PubMed] [Google Scholar]
- 34.Pfeiffer T, Schuster S, Bonhoeffer S. Cooperation and competition in the evolution of ATPproducing pathways. Science. 2001;292:504–507. doi: 10.1126/science.1058079. [DOI] [PubMed] [Google Scholar]
- 35.DeBerardinis RJ, et al. Beyond aerobic glycolysis: transformed cells can engage in glutamine metabolism that exceeds the requirement for protein and nucleotide synthesis. Proc Natl Acad Sci. 2007;104:19345–19350. doi: 10.1073/pnas.0709747104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jiang BH, Semenza GL, Bauer C, Marti HH. Hypoxia-inducible factor 1 levels vary exponentially over a physiologically relevant range of O2 tension. Am J Physiol-Cell Physiol. 1996;271:C1172–C1180. doi: 10.1152/ajpcell.1996.271.4.C1172. [DOI] [PubMed] [Google Scholar]
- 37.Zhao S, et al. Glioma-derived mutations in IDH1 dominantly inhibit IDH1 catalytic activity and induce HIF-1α. Science. 2009;324:261–265. doi: 10.1126/science.1170944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hassell M, Comins H. Discrete time models for two-species competition. Theor Popul Biol. 1976;9:202–221. doi: 10.1016/0040-5809(76)90045-9. [DOI] [PubMed] [Google Scholar]
- 39.Astanin S, Preziosi L. Mathematical modelling of the Warburg effect in tumour cords. J Theor Biol. 2009;258:578–590. doi: 10.1016/j.jtbi.2009.01.034. [DOI] [PubMed] [Google Scholar]
- 40.Everard K, Seabloom EW, Harpole WS, de Mazancourt C. Plant water use affects competition for nitrogen: why drought favors invasive species in California. Am Nat. 2010;175:85–97. doi: 10.1086/648557. [DOI] [PubMed] [Google Scholar]
- 41.Hedeskov CJ. Early effects of phytohaemagglutinin on glucose metabolism of normal human lymphocytes. Biochem J. 1968;110:373–380. doi: 10.1042/bj1100373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sonveaux P, et al. Targeting lactate-fueled respiration selectively kills hypoxic tumor cells in mice. J Clin Invest. 2008;118:3930–3942. doi: 10.1172/JCI36843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. [Google Scholar]
- 44.Nowak MA, May RM. The spatial dilemmas of evolution. Int J Bifurc Chaos. 1993;3:35–78. [Google Scholar]
- 45.Wojtkowiak JW, et al. Chronic autophagy is a cellular adaptation to tumor acidic pH microenvironments. Cancer Res. 2012;72:3938–3947. doi: 10.1158/0008-5472.CAN-11-3881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wilson SK, et al. Habitat utilization by coral reef fish: implications for specialists vs. generalists in a changing environment. J Anim Ecol. 2008;77:220–228. doi: 10.1111/j.1365-2656.2007.01341.x. [DOI] [PubMed] [Google Scholar]
- 47.Devictor V, Julliard R, Jiguet F. Distribution of specialist and generalist species along spatial gradients of habitat disturbance and fragmentation. Oikos. 2008;117:507–514. [Google Scholar]
- 48.Marvier M, Kareiva P, Neubert MG. Habitat destruction, fragmentation, and disturbance promote invasion by habitat generalists in a multispecies metapopulation. Risk Anal. 2004;24:869–878. doi: 10.1111/j.0272-4332.2004.00485.x. [DOI] [PubMed] [Google Scholar]
- 49.Wilson DS, Yoshimura J. On the coexistence of specialists and generalists. Am Nat. 1994;144:692–707. [Google Scholar]
- 50.MacDougall AS, Turkington R. Are invasive species the drivers or passengers of change in degraded ecosystems? Ecology. 2005;86:42–55. [Google Scholar]
- 51.Zucker S, et al. Vascular endothelial groth factor induces tissue factor and matrix metalloproteinase production in endothelial cells: Conversion of prothrombin to thrombin results in progelatininase a activation and cell proliferation. Int J Cancer. 1998;75:780–786. doi: 10.1002/(sici)1097-0215(19980302)75:5<780::aid-ijc19>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- 52.Brutovsky B, Horvath D. Structure of Intratumor Heterogeneity: Is Cancer Hedging Its Bets? 2013 ArXiv Prepr. ArXiv13070607. [Google Scholar]
- 53.Gupta PB, et al. Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell. 2011;146:633–644. doi: 10.1016/j.cell.2011.07.026. [DOI] [PubMed] [Google Scholar]
- 54.Acar M, Mettetal JT, van Oudenaarden A. Stochastic switching as a survival strategy in fluctuating environments. Nat Genet. 2008;40:471–475. doi: 10.1038/ng.110. [DOI] [PubMed] [Google Scholar]