Role of digit placement control in sensorimotor transformations for dexterous manipulation

This study was designed to understand the sensorimotor mechanisms underlying digit force-to-position modulation required for manipulation. Surprisingly, estimation of relative digit position and force-to-position modulation was accurate regardless of whether the digits were passively or actively positioned. Therefore, accurate estimation of digit position does not require an efference copy of active digit positioning, and the hypothesized advantage of active over passive movement on estimation of end-point position appears to be task and effector dependent.

Abstract

Dexterous manipulation relies on the ability to modulate grasp forces to variable digit position. However, the sensorimotor mechanisms underlying such critical ability are not well understood. The present study addressed whether digit force-to-position modulation relies entirely on feedback of digit placement and force, or on the integration of such feedback with motor commands responsible for digit positioning. In two experiments, we asked 25 subjects to estimate the index fingertip position relative to the thumb (perception test) or to grasp and lift an object with an asymmetrical mass distribution while preventing object roll (action test). Both tests were performed after subjects’ digits were placed actively or passively at different distances (active and passive condition, respectively) and without visual feedback. Because motor commands for digit positioning would be integrated with position and force feedback in the active condition, we hypothesized this condition to be characterized by greater accuracy of digit position estimation and digit force-to-position modulation. Surprisingly, discrimination of digit position and force-to-position modulation was statistically indistinguishable in the active and passive conditions. We conclude that voluntary commands for digit positioning are not essential for accurate estimation of finger position or modulation of digit forces to variable digit position. Thus digit force-to-position modulation can be implemented by integrating sensory feedback of digit position and voluntary commands of digit force production following contact.

NEW & NOTEWORTHY This study was designed to understand the sensorimotor mechanisms underlying digit force-to-position modulation required for manipulation. Surprisingly, estimation of relative digit position and force-to-position modulation was accurate regardless of whether the digits were passively or actively positioned. Therefore, accurate estimation of digit position does not require an efference copy of active digit positioning, and the hypothesized advantage of active over passive movement on estimation of end-point position appears to be task and effector dependent.

dexterous object manipulation requires coordination of digit forces (Johansson and Flanagan 2009; Johansson and Westling 1988) and position on an object (Crajé et al. 2011; Fu et al. 2010, 2011; Lukos et al. 2007, 2008; Zhang et al. 2010). When subjects are asked to grasp objects that allow choice of digit placement (i.e., “unconstrained” grasp), trial-to-trial variability in digit placement prevents subjects from using the same digit force distribution used in previous manipulations. We found that subjects modulate, on a trial-to-trial basis, digit force distribution as a function of digit position before object lift-off to compensate for digit placement variability (Fu et al. 2010). This phenomenon, which we refer to as “digit force-to-position modulation,” is found not only in response to small trial-to-trial digit placement variability but also when subjects change the number of digits involved in the grasp (Fu et al. 2011). This behavior is critically important for attaining the manipulation task goal, i.e., lifting the object straight by countering external torques, despite changes in digit force and position distributions. Importantly, digit force-to-position modulation suggests that the central nervous system (CNS) integrates feedback of relative location of digit contact points with motor commands responsible for distributing forces among the digits before initiating the manipulation. However, the sensorimotor mechanisms underlying humans’ ability to estimate digit position and change digit forces as a function of digit placement are not well understood.

Estimation of contact points on the object could theoretically evolve throughout the reach, during which fingertip trajectories are actively controlled to contact the object at planned locations. Thus visual and proprioceptive feedback of fingertips could then be potentially combined with tactile feedback elicited by object contact, culminating with a final estimation of digit placement. Work aimed at quantifying subjects’ ability to estimate relative fingertip position have shown that human subjects can better match the perceived distance between fingertips for larger vertical fingertip separations and when matching with the same hand and posture used to sense fingertip distance (Shibata et al. 2013). Furthermore, isometric digit forces exerted in opposite directions (e.g., as found when generating a torque on the object) negatively affects the accuracy with which subjects can match fingertip distance (Shibata et al. 2014). Nevertheless, these psychophysical studies were designed to isolate factors that may affect the acuity of haptic feedback required for fingertip distance matching rather than modulation of manipulative forces.

Another major difference separating the above psychophysical studies and object manipulation is that psychophysical protocols generally require subjects to indicate the sensed limb or fingertip position after these have been passively placed to a given position by the experimenter. Conversely, in object manipulation, subjects actively place their digits on the object for manipulation. This is an important distinction, because it has been suggested that subjects can predict sensory consequences of active movements through internal forward models using a copy of the motor commands (Kawato 1999; Wolpert et al. 1995). Therefore, the extent to which the results of the above psychophysical studies may apply to tasks where subjects actively position their fingertips and modulate forces accordingly remains to be investigated. In particular, the open question is whether active control of digit placement might contribute to estimation of digit position, and therefore accuracy of force-to-position modulation.

In the present work, we focus on sensorimotor mechanisms underlying estimation of fingertip position and how position feedback may affect digit force control. Specifically, we quantified the role of voluntary commands of digit placement on 1) estimation of fingertip distance and 2) digit force-to-position modulation required to perform a dexterous manipulation task. We designed two experiments to isolate the perceptual component from the perception-to-action continuum (perception and action tests, respectively). For each study, we addressed the question of whether active digit placement improves accuracy of perception of digit position and force modulation as a function of digit placement. This question was addressed by having subjects’ digits placed on the object either actively or passively by an experimenter (active and passive conditions, respectively). We hypothesized that 1) during the perceptual task, subjects would discriminate the relative digit position more accurately after active than passive digit placement, and 2) during the motor task, digit forces would be more accurately modulated as a function of digit position in the active than passive condition.

MATERIALS AND METHODS

Subjects

We tested 25 subjects who were assigned to 2 groups: group 1 (10 men and 5 women, age 23.4 ± 5.8 yr, mean ± SD) and group 2 (8 men and 2 women, age 24.3 ± 4.0 yr.). Group 2 was included to assess the extent to which the results obtained from group 1 would also apply to smaller vertical separation of the digits (this rationale is further described below). All subjects were classified as right-handed on the basis of the mean laterality quotient and standard deviation (80.8 ± 14.1) based on the 10-item Edinburgh Handedness Inventory (Oldfield 1971). All subjects were naïve to the purpose of the study. Subjects gave their written informed consent according to the Declaration of Helsinki, and the protocols were approved by the Office of Research Integrity and Assurance at Arizona State University.

Apparatus

A custom-made grip object was used for all experimental conditions to measure digit forces and center of pressure (CoP) of the thumb and index finger pad (Fig. 1B). The sensorized object has been described in detail elsewhere (Fu et al. 2010; Shibata et al. 2013). Briefly, two six-component force/torque sensors were mounted on each side of the object (ATI Nano-25 SI-125-3; ATI Industrial Automation, Garner, NC; force range: 125, 125, and 500 N for x-, y-, and z-axes, respectively; force resolution: 0.06 N; torque range: 3,000 N·mm; torque resolution: 0.378 N·mm; Fig. 1B). The vertical coordinate (y) of the CoP of each digit on the contact surface was computed from the force-torque sensor output. To prevent the digits from slipping when subjects applied tangential forces, the contact surfaces of the handles were covered with 100-grit sandpaper (static friction coefficient range: 1.4–1.5). The location of center of mass of the object was adjusted by adding a mass (400 g) in the slot at the base of the object on the index finger side (Fig. 1B). The object’s center of mass was fixed throughout the experiment. The total mass of the object was 915 g. This additional mass created an asymmetrical mass distribution and introduced a torque on the frontal plane of 230 N·mm toward the index finger. Object position was recorded using an active marker three-dimensional motion capture system (PhaseSpace; frame rate: 480 Hz; spatial accuracy: ~1 mm; spatial resolution: 0.1 mm) with eight cameras. Two markers were placed on the lateral extremities of the object (Fig. 1B, green dots).

Fig. 1.

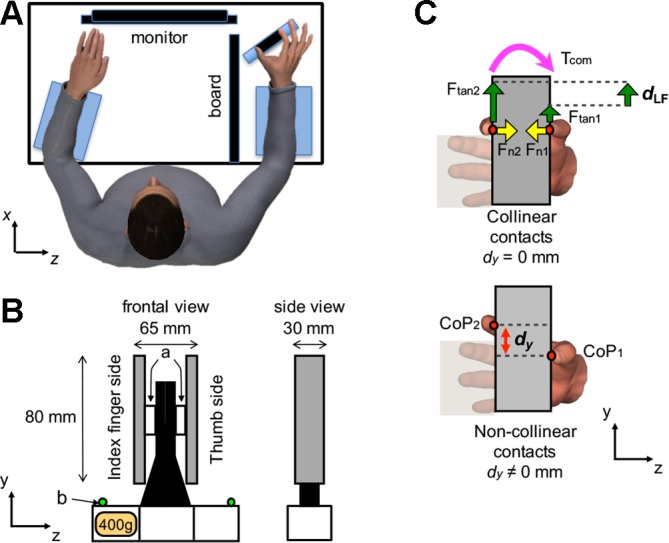
Experimental setup. A: top view of the experimental setup. The subject is shown contacting the handle with the right thumb and index fingertip while the left hand is kept flat on the table. When the subject relaxed between trials, both hands were kept flat and relaxed. Note that the board was placed so as to prevent subjects from seeing their right forearm and hand. Foam cushions were placed underneath the forearms and wrist for subjects’ comfort. B: front and side views of the grip device; a and b denote force/torque sensors and active markers for motion tracking, respectively. A mass (400 g) was added to the slot at the bottom of the device on the index finger side. C: front views of the object showing the thumb and index fingertip center of pressure (CoP; red circles) of the hand located at the same (collinear contacts; top) or different y-coordinates (non-collinear contacts; bottom). The vertical distance between thumb and index fingertip CoP is denoted by d_y. Top panel also shows normal and tangential forces generated by each digit (F_n and F_tan) and the torque generated by the digits (T_com) to compensate the torque caused by the object’s asymmetrical mass distribution (mass added to the index finger side of the object).

Experimental Procedures

We designed our experiments to quantify subjects’ ability to perceive the vertical distance between thumb and index fingertip (perception test) and to use haptic feedback to modulate digit forces to position (action test). For each of these tests, thumb and index fingertip were placed on the grip device by either the experimenter or the subject (passive and active condition, respectively).

Perception test.

Subjects grasped the object with the thumb and index fingertip of the right hand while sitting on an adjustable chair with both forearms resting on a table or foam cushion (Fig. 1A). The left hand rested on the table throughout the experiment with all digits straight, adducted, and in a pronated position. Vision of the right forearm, hand, and object was prevented by a board placed between the subject’s arm and the computer monitor (Fig. 1A).

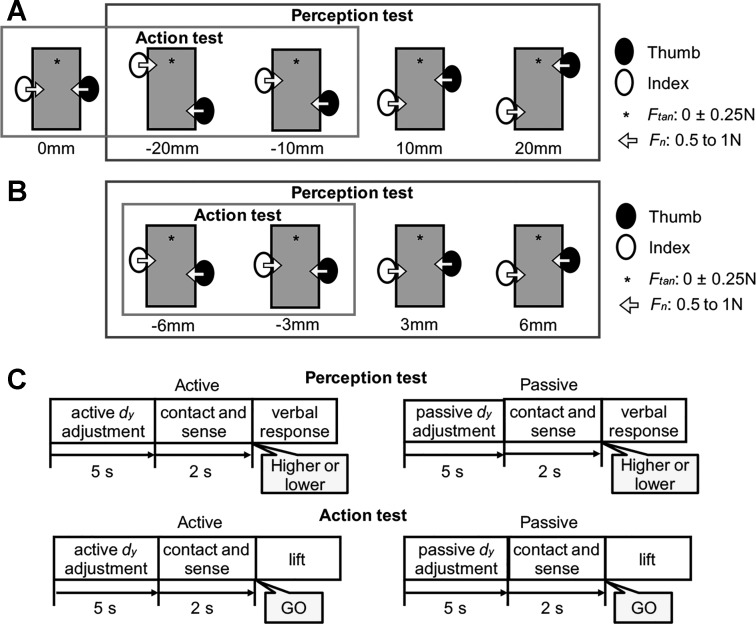
We used a two-alternative forced-choice paradigm through which subjects had to verbally report whether the index finger CoP was perceived as being higher or lower than the thumb CoP. We tested four relative vertical distances between the digits (group 1: thumb CoP higher than index finger CoP: 20 and 10 mm; thumb CoP lower than index finger CoP: −10 and −20 mm; Fig. 2A, black box). When subjects actively placed their digits on the object, feedback of the relative fingertip position (vertical distance between fingertip CoPs, d_y) was shown as a cursor on the computer monitor. Subjects were required to move the cursor to the target area by adjusting digit position (Fig. 2C, “active d_y adjustment” phase). Subjects were allowed to slide the finger pads over the contact surface and to release and reposition them within a maximum time limit of 5 s. Note that visual feedback of cursor and target areas did not provide subjects with information about the relative digit position. Specifically, the cursor could move up and down over the target horizontal line, thus displaying mismatches between actual and target d_y. However, regardless of the actual d_y, location of the target area and the excursion of the cursor was always kept the same by adjusting the gain of the relation between actual d_y and cursor position for each target d_y. This visual feedback of d_y was removed when subjects’ digits were passively placed on the grasped object by an experimenter at the designated target digit positions (Fig. 2C, “passive d_y adjustment” phase).

Fig. 2.

Tests (perception, action), experimental conditions (active, passive), and protocols. A and B: relative digit positions and force requirements for perception and action tests in group 1 and group 2. We tested 4 relative digit positions (A: group 1, d_y = −20, −10, 10, and 20 mm; B: group 2, d_y = −6, −3, 3, and 6 mm) for the perception test (black box) and 3 and 2 positions (A: group 1, d_y = 0, −10, and −20 mm; B: group 2, d_y = −3 and −6 mm, respectively) for the action test (gray box). Subjects were asked to exert negligible tangential and normal digit forces. C: experimental protocols. In the passive d_y adjustment phase of the perception and action tests, the subject’s thumb and index fingertip were passively placed by an experimenter to a given digit position. In contrast, subjects actively placed the center of pressure of the thumb and index finger to a given d_y in the active d_y adjustment phase of the perception and action tests. Once the desired d_y and target digit forces were reached, subjects were asked to sense d_y while maintaining the digit contacts and forces for ~2 s (contact and sense phase). In the perception test, subjects were cued to verbally report whether the index finger CoP was higher or lower than thumb CoP (verbal response phase). In the action test, a “Go” signal was given to subjects to lift the object while preventing it from tilting (lift phase).

After the active or passive digit placement, we asked subjects to sense the d_y while exerting very low forces (see below) with thumb and index fingertip on the vertical surfaces of the grip device (Fig. 2C, “contact and sense” phase). Once the experimenter visually confirmed compliance of the desired d_y, subjects were given a verbal cue to exert negligible normal and tangential forces with each digit (0.5–1 N and 0 ± 0.25 N, respectively; Fig. 2A). The same monitor that provided feedback of the digit position was used to provide feedback of digit forces. After sensing the d_y for 2 s, subjects were asked to verbally report whether the index finger CoP was higher or lower than the thumb CoP (Fig. 2C, “verbal response” phase). Subjects released their digits after providing an answer and then rested and prepared for the following trial.

Action test.

For this test we asked subjects to grasp and lift the same sensorized object used for the perception test with the thumb and index finger. As for the perception test, vision of the right forearm, hand, and object was prevented by a board (Fig. 1A). Each trial started with active or passive d_y adjustment on the grip device (Fig. 2C, “active d_y adjustment” or “passive d_y adjustment” phase) at one of three d_y values for group 1 (−20, −10, and 0 mm; Fig. 2A, gray box). We then asked subjects to sense the d_y while maintaining the given d_y with negligible forces (the same as those described above for the perception test; Fig. 2A) for a maximum of 2 s (Fig. 2C, “contact and sense” phase). For the action test, we provided the same feedback of digit forces and position, and the same temporal constraints, as described for the perception test. Once the experimenter visually confirmed compliance of the desired d_y, a visual “Go” signal was displayed on the monitor to cue subjects to lift the grasped object. We instructed subjects to lift the object vertically to a comfortable height at a natural speed while trying to maintain its vertical alignment, hold it for ~1 s, and replace it on the table.

A second group of subjects (group 2, 10 subjects) was tested using the same protocols described above but on smaller d_y. For this group, we tested four d_y values (−6, −3, 3, and 6 mm; Fig. 2B, black box) for the perception test and two d_y values (−6 and −3 mm; Fig. 2B, gray box) for the action test. Experimental setup, apparatus, and procedures were identical to those for group 1. The rationale for testing this second group of subjects was to assess the extent to which results obtained from group 1 generalized to smaller vertical distances between thumb and index finger pads. Specifically, we reasoned that smaller d_y might challenge subjects’ ability to perceive d_y or integrate d_y feedback with motor commands to a greater extent than larger d_y. Furthermore, this design was preferred to presentation of all d_y levels in one experimental session to one group of subjects to avoid fatigue and fluctuations in attention.

Familiarization with perception and action tests.

To familiarize subjects with the tests and task conditions, all subjects practiced the perception and action tests, as well as lifting the object while minimizing the object roll at all d_y, before starting the experiment. This familiarization phase lasted ~30 min. For the action test, visual feedback of manipulation performance (object tilt minimization) was provided only during this familiarization phase to facilitate learning of the torque that had to be generated at object lift onset to compensate the external torque. Note that for the perception test, feedback of task performance was not given to subjects during the familiarization phase.

Each group was presented with two tests (perception, action), and each of these tests consisted of two experimental conditions (active, passive). The perception test of group 1 (Fig. 2A, black box) consisted of 6 trials per d_y (−20, −10, 10, and 20 mm) per condition (active, passive) for a total of 48 trials (6 × 4 × 2). The action test of group 1 (Fig. 2A, gray box) consisted of 6 trials per d_y (−20, −10, and 0 mm) per condition (active, passive) for a total of 36 trials (6 × 3 × 2). The total number of trials performed by subjects in group 1 was 84 trials (48 + 36). The perception test of group 2 (Fig. 2B, black box) consisted of 6 trials per d_y (−6, −3, 3, and 6 mm) per condition (active, passive) for a total of 48 trials (6 × 4 × 2). The action test of group 2 (Fig. 2B, gray box) consisted of 6 trials per d_y (−6 and −3 mm) per condition (active, passive) for a total of 24 trials (6 × 2 × 2). The total number of trials performed by subjects in group 2 was 72 trials (48 + 24). Within each group and test type, the order of presentation of the active and passive conditions was counterbalanced. The order of presentation of the active and passive was counterbalanced across subjects.

Data Processing

Force and torque data were acquired with a 12-bit analog-to-digital converter board (PCI-6225; National Instruments, Austin, TX; sampling frequency: 1 kHz) through a custom data acquisition interface (LabVIEW version 8.0; National Instruments) and stored in a computer for off-line analysis. During data collection, force data were filtered online using a moving average filter every 50 samples over the 5-s duration of data recording. The filtered force data were then used for computing and displaying online normal and tangential digit forces and d_y using LabVIEW.

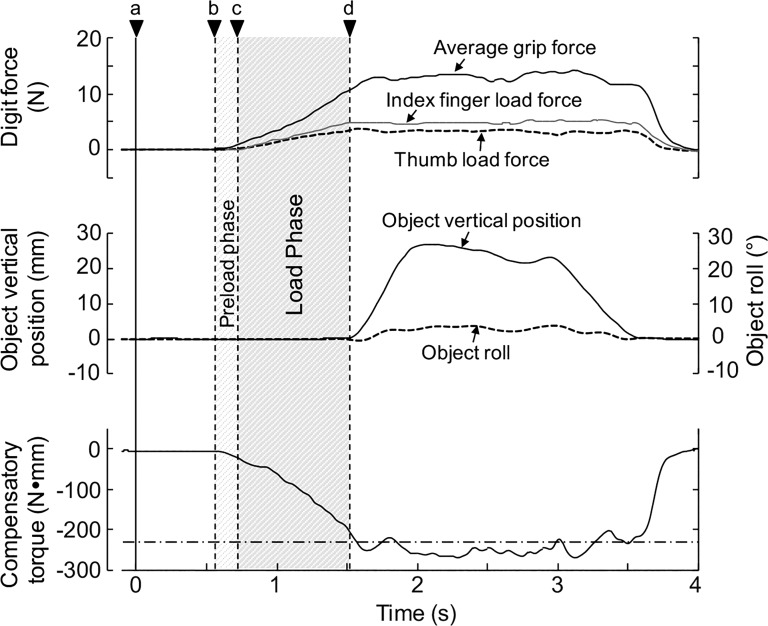
After data collection, force and position data were temporally aligned off-line with custom-written software (MATLAB; The MathWorks, Natick, MA). Analyses focused on the following variables: 1) digit CoP, the vertical coordinates of the CoP of the contact between each finger pad and the graspable surface relative to the center of the sensor (Fig. 1C); 2) digit force normal and tangential to the grip surface (grip force, GF, and load force, LF, respectively; Figs. 1C and 3); 3) object lift onset, defined as the time at which the vertical position of one of the active markers on the object exceeded the threshold of 2 mm for 5 ms (Fig. 3, d); 4) object roll, defined as the angle between the gravitational vector and the vertical axis of the grip device, and peak object roll, defined as the peak of object roll occurring shortly (~500 ms) after object lift onset (Fig. 3); and 5) peak object velocity, defined as the peak velocity of the grip device during the lift.

Fig. 3.

Experimental variables and grasp phases. The time courses of the experimental variables and grasp phases are shown for 1 representative trial. Shown from top to bottom are grip force averaged across thumb and index fingers and load forces exerted by the thumb and index finger (dashed and gray solid lines, respectively), vertical height of the object, and object roll; the solid line denotes compensatory torque, whereas the dashed horizontal line denotes the target torque subjects had to exert to counter the external torque caused by the added mass at the bottom of the object. Time epochs shown are “Go” signal (a), grip force onset (b), load force onset (c), and lift onset (d) (see text for details). The “Go” signal was given to subjects 2 s after the contact and sense phase (see Fig. 2C) to cue the subject to initiate object lift.

Digit forces and CoP were used to compute the following variables: 1) d_y, defined as the difference between the vertical coordinates of thumb CoP and index finger CoP (Fig. 1C); 2) the average of the normal forces exerted by thumb and index finger (F_GF; Figs. 1C and 3); and 3) the difference between the tangential forces exerted by thumb and index finger (d_LF; Fig. 1C). In our previous work (Fu et al. 2010), we described that learning to minimize object roll depends on coordinating, on a trial-to-trial basis, d_y, F_GF, and d_LF to generate a compensatory torque (T_com) at object lift onset that matches the external torque caused by mass added to one side of the inverted-T object. However, two significant differences exist between how we studied this task in our previous work and the present study. First, in reach-to-grasp tasks, d_y is characterized by trial-to-trial variability, whereas in the present study the experimenter ensured that a given d_y would be invariant across trials (regardless of whether the digits were actively or passively positioned on the object). Second, in the present study we eliminated visual feedback throughout the entire duration of the action test, whereas in our previous work subjects had visual feedback of their hand and the object. Regardless of these two differences, however, in the present study subjects were still required to modulate digit forces as a function of d_y to generate the desired T_com to counter the external torque (Fig. 3, dashed horizontal line, bottom trace).

We used GF, LF, and object lift onset to determine grasp phases (Fig. 3). The time at which GF and LF exceeded the threshold of 0.4 N for 50 ms was defined as GF and LF onset, respectively (Fig. 3, b and c). The time between GF onset and LF onset was defined as “preload phase,” whereas the time between the LF onset and lift onset was defined as “load phase” (Fig. 3, shaded areas).

Statistical Analysis

For the perception test, probability of trials perceived as “lower” across subjects per d_y were analyzed using analysis of variance (ANOVA) for each group with repeated measures with within-subject factors of condition (2 levels: active and passive) and digit position (4 levels: −20, −10, 10, and 20 mm in group 1; −6, −3, 3, and 6 mm in group 2). Although the main focus of our study was to quantify the effect of active vs. passive digit placement, we added d_y to the ANOVA model for completeness and to allow comparison with a previous study (Shibata et al. 2013).

For the action test, we performed ANOVA with repeated measures to assess the effects of within-subject factors of condition (2 levels: active and passive) and digit position (3 levels: −20, −10, and 0 in group 1; 2 levels: −6 and −3 in group 2) on the following manipulation performance variables: F_GF, d_LF, T_com, peak object roll, peak object velocity, preload and load phase durations, peak load and grip force rates, and the difference between d_y at contact and object lift onset (d_y shift). We performed linear regression analyses to quantify the relation between d_LF and d_y, as well as F_GF and d_y, at object lift onset over all trials from all subjects. To compute the coefficient of determination (R²), each data point was normalized for each subject by removing the mean of all trials from the value of each trial and dividing the result by the standard deviation of the mean. Analyses within each group were identical. Post hoc tests were run using paired-sample t-tests with Bonferroni corrections when appropriate. Sphericity assumptions were tested for all analyses (Mauchly’s sphericity test). When the sphericity assumptions were violated, we used Greenhouse-Geisser analysis (P < 0.01). All tests were performed at the P ≤ 0.05 significance level. Values in the text are means ± SE unless otherwise noted.

RESULTS

Perception Test

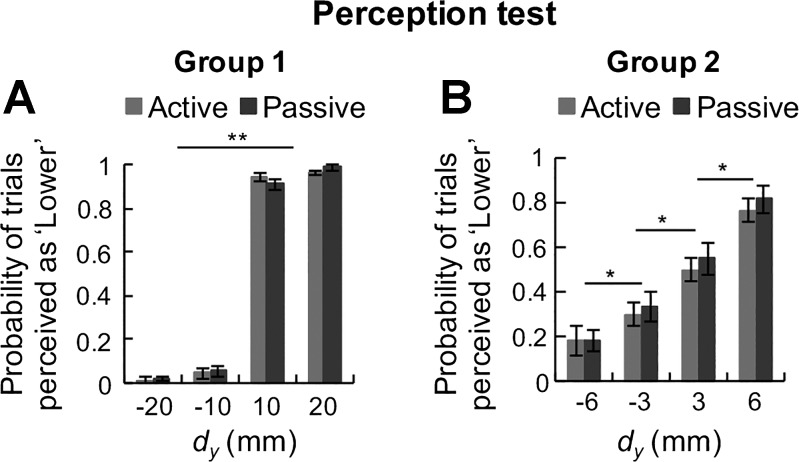
Subjects could accurately estimate the relative digit position of the fingertips in 96% of the trials in both the active and passive conditions in group 1 and in 70% of the trials in both conditions in group 2. A repeated-measures ANOVA on probability of trials perceived as “lower” across subjects per d_y for both groups revealed no significant difference between the active and passive digit placement conditions [condition: group 1, F_(1,14) = 1.094, P > 0.05, Fig. 4A; group 2, F_(1,9) = 0.629, P > 0.05, Fig. 4B]. These findings indicate that subjects’ ability to perceive the index finger CoP with respect to the thumb CoP was not affected by whether the digits were placed actively or passively.

Fig. 4.

Perception test: probability of “lower” response. Probability of trials perceived as “lower” across all subjects in the perception test are plotted for each vertical distance between digits’ center of pressure (d_y) for group 1 (A) and group 2 (B). Data are mean values averaged across all subjects (vertical lines denote SE).

However, there was a significant difference in the probability of accurate estimation of relative vertical digit distances [main effect of digit position: group 1, F_(1,14) = 1,325.112, P < 0.001, Fig. 4A; group 2, F_(1,9) = 39.437, P < 0.001, Fig. 4B]. Post hoc paired t-tests with Bonferroni corrections revealed that in group 1, the probability of a “lower” response when the index finger CoP was lower than the thumb CoP (d_y = 10, 20 mm) was significantly greater than when the index finger CoP was higher than the thumb CoP [d_y = −20, −10 mm; t₍₁₄₎ = 41.190, P < 0.001, Fig. 4A]. In group 2, the probability of a “lower” response was significantly different across pairs of d_y values [6 vs. 3 mm: t₍₉₎ = 2.449; 3 vs. −3 mm: t₍₉₎ = 3.478; −3 vs. −6 mm: t₍₉₎ = 4.147; P < 0.05 for all comparisons; Fig. 4B]. Thus, when fingertip distance was 3 mm, subjects were not as accurate as when fingertip distance was 6 mm. Furthermore, when the index finger CoP was higher than the thumb CoP (d_y = −20, −10, −6, −3 mm), the probability of a “lower” response was significantly higher in the smaller than in the larger d_y group [−20, −10 vs. −6, −3 mm: t₍₉₎ = 4.770; P < 0.05]. Similarly, when the index finger CoP was lower than the thumb CoP (d_y = 3, 6, 10, 20 mm), the probability of a “lower” response was significantly higher in the larger than in the smaller d_y group [6, 3 vs. 20, 10 mm: t₍₉₎ = 6.249; P < 0.05]. Thus the percentage of trials when subjects erroneously perceived the index fingertip to be lower than the thumb was greater for d_y = −3 and −6 mm than for d_y = −10 and −20 mm. In sum, our first hypothesis was not supported, because accuracy of relative fingertip distance estimation was the same regardless of whether the digits were positioned actively or passively. Additionally, we found that fingertip distance estimation decreased as a function of vertical relative digit distance, but only below a given distance threshold.

Action Test

Measurements of actual d_y values averaged across the last 50 ms of the 2 s within the “contact and sense” phase (Fig. 2C) revealed that the digits were positioned precisely to each target digit position (d_y = 0: −0.47 ± 1.4 mm; d_y = −10: −10.35 ± 1.0 mm; d_y = −20: −20.03 ± 1.1 mm; d_y = −3: −3.15 ± 0.7 mm; d_y = −6: −6.15 ± 0.7 mm). These actual d_y values were significantly different across the target d_y values [0 vs. −10 mm: t₍₁₇₉₎ = 296.97; 0 vs. −20 mm: t₍₁₇₉₎ = 615.69; −10 vs. −20 mm: t₍₁₇₉₎ = 677.17; −3 vs. −6 mm: t₍₁₁₉₎ = 288.99; P < 0.001 for all comparisons].

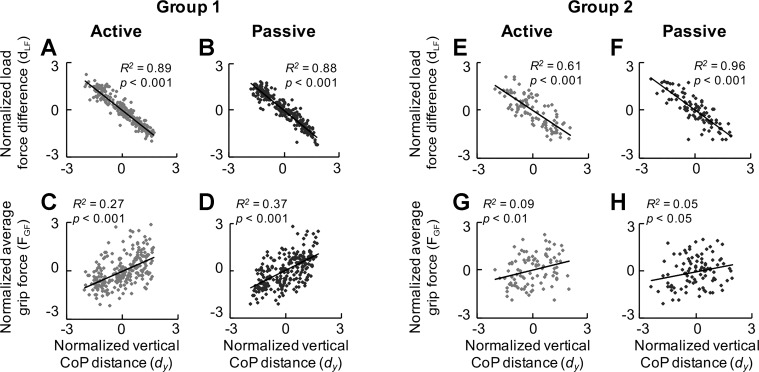
We first examined whether subjects could appropriately lift an object and minimize its roll by modulating digit forces as a function of position at object lift onset as found for self-paced dexterous manipulation tasks (Fu et al. 2010). There was no difference between the active and passive conditions in average grip force (F_GF), digit load force difference (d_LF), and compensatory torque (T_com) at object lift onset, as well as peak object roll and peak object velocity after object lift onset, in group 1 and group 2 (Table 1). Moreover, d_LF and relative digit position (d_y) negatively covaried in a similar fashion for the active and passive conditions in both subject groups, as indicated by similar coefficients of determination (Fig. 5, A and B, and E and F). A similar positive correlation between F_GF and d_y was also found for both conditions in group 1 and group 2 (Fig. 5, C and D, and G and H). Contrary to our second hypothesis, these findings indicate that the accuracy of sensorimotor transformations responsible for modulating digit forces as a function of position was not affected by whether digits were placed on the object in an active or passive fashion.

Table 1.

Summary of lifting performance variables in action test across all subjects

	FGF, N	dLF, N	Tcom, N·mm	Peak Roll, deg	Peak Object Velocity, cm/s
Group 1
dy = 0 mm
Active	12.2 ± 1.2	–5.0 ± 0.2	–227.7 ± 4.5	2.0 ± 0.3	10.4 ± 1.0
Passive	13.3 ± 1.4	–5.0 ± 0.3	–225.8 ± 3.0	1.5 ± 0.3	9.3 ± 0.9
dy = –10 mm
Active	11.3 ± 1.2	–2.6 ± 0.3	–222.7 ± 4.1	1.6 ± 0.2	10.1 ± 0.9
Passive	12.2 ± 1.3	–2.1 ± 0.3	–223.2 ± 3.2	1.3 ± 0.2	9.6 ± 1.0
dy = –20 mm
Active	10.4 ± 1.1	–0.1 ± 0.5	–219.9 ± 5.7	1.8 ± 0.2	10.0 ± 0.9
Passive	11.1 ± 1.2	0.4 ± 0.5	–225.0 ± 4.0	1.3 ± 0.3	9.6 ± 1.2
Group 2
dy = –3 mm
Active	14.1 ± 2.4	–4.1 ± 0.5	–244.2 ± 9.1	2.6 ± 0.4	20.8 ± 2.7
Passive	15.5 ± 2.1	–3.8 ± 0.5	–242.4 ± 5.2	1.7 ± 0.3	21.3 ± 3.4
dy = –6 mm
Active	13.9 ± 2.5	–3.7 ± 0.4	–236.5 ± 9.4	2.2 ± 0.3	20.1 ± 2.4
Passive	13.7 ± 2.4	–3.2 ± 0.4	–242.9 ± 3.6	1.5 ± 0.3	20.9 ± 3.4

Data are means ± SE of average grip force (F_GF), load force difference (d_LF), compensatory torque (T_com), peak roll of object, and peak object velocity per vertical distance between digit center of pressure (d_y) averaged across all subjects for the active and passive conditions.

Fig. 5.

Action test: relations between digit forces and center of pressure. A, B, E, F: correlations between the difference in digit load force (d_LF) and relative digit positions (d_y) for active (A and E) and passive conditions (B and F). C, D, G, H: correlations between average grip force (F_GF) and d_y for active (C and G) and passive conditions (D and H). Data from all trials and subjects are plotted for each condition (group 1: 18 trials × 15 subjects = 270; group 2: 18 trials × 8 subjects = 144) and expressed in normalized form (see text for details). Larger values of d_LF and d_y correspond to the larger normalized values within the condition per digit position, and vice versa for the smaller values. The coefficient of determination (R²) and corresponding P value are shown in each plot.

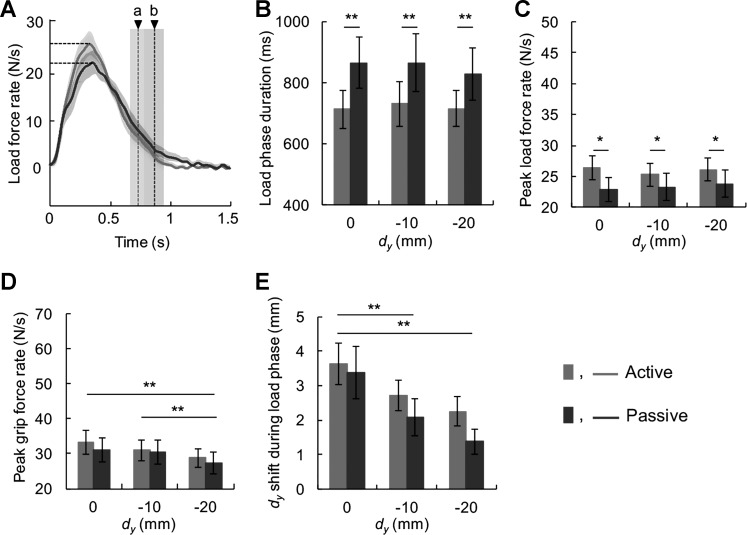
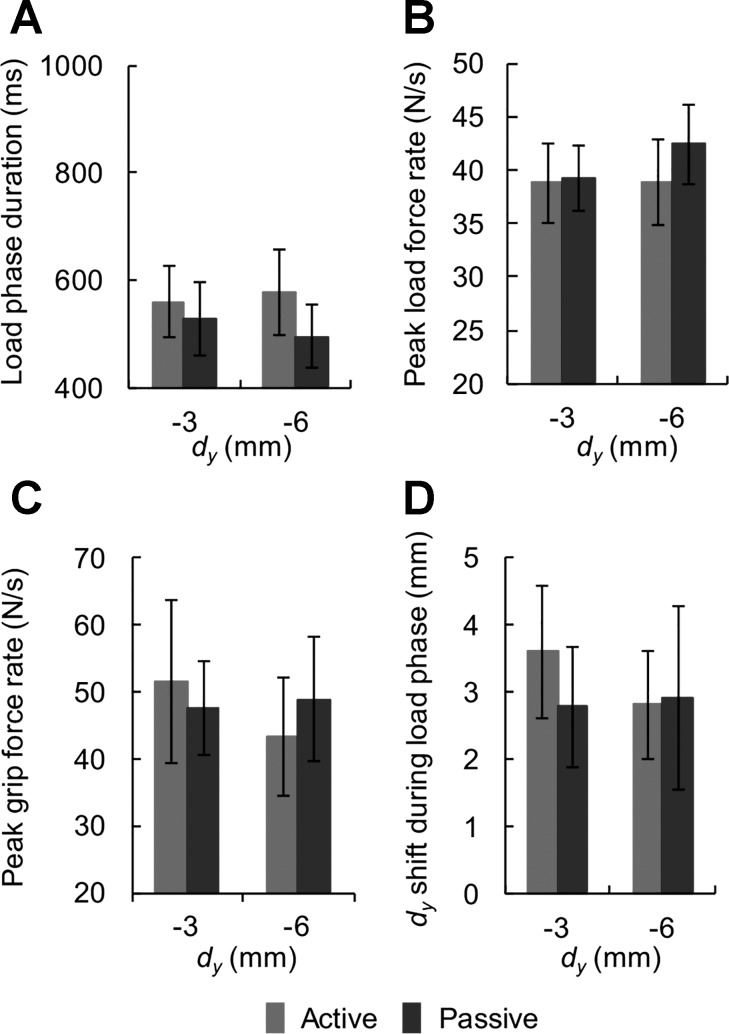
Although force-to-position coordination, which is measured at the instant of object lift-off, was similar in the active and passive conditions, we further analyzed the data by examining the temporal evolution of forces by quantifying load phase duration and force rates. This analysis revealed that the time from the “Go” signal to object lift onset was longer in the passive condition than in the active condition in group 1. We therefore performed separate analyses of the duration of preloading phase (from GF onset to LF onset) and loading phase (from LF onset to object lift onset) (Fig. 3). We found no significant difference between active and passive conditions in the preloading phase duration [9 ms on average across subjects; t₍₁₄₎ = −0.792, P > 0.05]. In contrast, the loading phase duration was consistently longer in the passive condition on average by 136 ms (active: 733 ± 59 ms; passive: 869 ± 84 ms) and across all digit positions (Fig. 6, A and B). The effect of condition was statistically significant [F_(1,14) = 12.005, P < 0.01], whereas that of digit position was not [F_(2,28) = 0.991, P > 0.05; Fig. 6B]. We also found a main effect of digit position on peak grip force rate [F_(2,28) = 11.910, P < 0.01], but no effect of condition [F_(1,14) = 1.519, P > 0.05; Fig. 6D]. Therefore, the longer load phase duration could not be accounted for by a difference in grip force rates. However, we found that subjects in group 1 developed load force faster in the active condition than in the passive condition [main effect of condition: F_(1,14) = 6.568, P < 0.05]. In contrast, for group 2, the comparison of active vs. passive condition revealed no significant differences in temporal or force variables [load phase duration: F_(1,7) = 3.408; peak load force rate: F_(1,7) = 1.099; peak grip force rate: F_(1,7) = 0.035; shift of d_y during the load phase: F_(1,7) = 2.216; all P > 0.05; Fig. 7]. Furthermore, d_y had no significant effect on temporal or force variables for either group (all P > 0.05).

Fig. 6.

Load phase duration, load and grip force rate, and shift in digit center of pressure during the load phase of group 1. A: load force rate plotted from load force onset from a representative trial. The horizontal dashed lines denote peak load force rates, whereas the gray and black vertical dashed lines denote object lift onset for the active and passive conditions (a and b, respectively). B: average load phase duration as a function of initial vertical distance between digits center of pressure (d_y). C: average peak load force rate as a function of d_y. D: average peak grip force rate as a function of d_y. E: shift of d_y during the load phase as a function of d_y. Data are mean values averaged across all subjects (vertical lines and shaded areas denote SE). *P < 0.05; **P < 0.01, statistically significant difference.

Fig. 7.

Load phase duration, load and grip force rate, and shift in digit center of pressure during the load phase of group 2. A: average load phase duration as a function of initial vertical distance between digits center of pressure (d_y). B: average peak load force rate as a function of d_y. C: average peak grip force rate as a function of d_y. D: shift of d_y during the load phase as a function of d_y. Data are mean values averaged across all subjects (vertical lines and shaded areas denote SE).

Last, we examined the magnitude of d_y changes during the load phase to quantify a possible contribution of different amount of skin deformation of the finger pads to the longer load phase duration in the passive condition found in group 1. Shift of d_y during the load phase was significantly different as a function of d_y [main effect of digit position: F_(2,28) = 16.587, P < 0.01], but not between the active and passive condition [main effect of condition: F_(1,14) = 1.470, P > 0.05; Fig. 6E]. Thus the longer loading phase duration in the passive condition can be accounted for by a lower peak load force rate relative to the active condition.

DISCUSSION

The present study was designed to quantify the role of voluntary motor commands responsible for digit placement in sensing relative digit position and subsequent modulation of digit forces to position. Our main findings are that, regardless of whether subjects actively positioned their fingertips or had their fingertips passively moved by an experimenter, 1) subjects could accurately discriminate index fingertip position relative to thumb and 2) modulate fingertip forces to variable digit position. These findings indicate that perception of relative fingertip position and accuracy of force modulation as a function of sensed fingertip position was similar regardless of how digit placement was controlled. We discuss these results in the context of perception-action coupling involved with dexterous manipulation and underlying neural mechanisms.

Role of Active Digit Movement in Estimation of Digit Relative Position and Force-to-Position Modulation

Contrary to our first hypothesis, active digit placement and motor commands responsible for digit placement and force production did not improve the accuracy of digit position estimation compared with passive digit placement (Fig. 4). This finding rules out voluntary commands of digit placement as an important contributor to feedback-mediated mechanisms for fingertip position estimation and is therefore important in refining our theoretical framework of neural control of dexterous manipulation (Fu et al. 2010, 2011; Mojtahedi et al. 2015). Subjects could rely on visual and somatosensory feedback of digit placement during the reach to plan digit force distribution following object contact. However, the fact that corrective force responses often occur shortly after contact in unconstrained grasps suggests a mismatch between planned and actual digit placement, and the need for adjustment of forces to actual, rather than planned, digit placement (Mojtahedi et al. 2015). Importantly, the present data emphasize the role of object contact as the key event after which processing of sensed digit placement occurs. Experimental evidence from a transcranial magnetic stimulation study is consistent with this proposition by revealing a significant modulation of corticospinal excitability for unconstrained grasping only shortly after contact, but not during the reach (Davare et al. 2013). Modulation of corticospinal excitability has also been documented for constrained grasping (Lemon et al. 1995).

The similarity of fingertip distance estimation in the active and passive conditions is not consistent with previous observations that static limb end-point estimation is more accurate after active than passive reaching movements (Adamovich et al. 1998; Bhanpuri et al. 2013; Gritsenko et al. 2007). This discrepancy suggests task- or effector-specific differences in the extent to which voluntary motor commands might facilitate perception of fingertip position. Specifically, control of shoulder and elbow joint rotation associated with reaching are negligible in our task, and thus motor commands are mostly limited to small digit movements (Fig. 1A). Therefore, the discrepancy between the present and previous findings may be due to a higher “signal-to-noise” ratio in motor commands involved for large upper limb joint excursion and trajectory control for reaching than for small digit movements. However, further work is needed to validate this interpretation.

Contrary to our second hypothesis, the accuracy of digit force modulation to position was the same for active and passive conditions (Fig. 5), thus suggesting similar underlying neural mechanisms. This finding suggests that the sensorimotor transformation is reliable upon the production of manipulative forces and regardless of the availability of an efference copy of digit placement motor commands. These results also underscore the exquisite ability of the CNS to implement accurate sensorimotor transformations that are critical to the performance of skilled manipulation within a wide range of task constraints.

Effect of Fingertip Distance on Perception and Sensorimotor Transformations for Manipulation

We found that accuracy of perception of fingertip relative position, but not sensorimotor transformations, was sensitive to fingertip distance (Fig. 4, A and B, and Fig. 5, respectively). Specifically, as the digits were placed closer to each other, subjects’ ability to distinguish the position of the index finger relative to the thumb declined (Fig. 4). This phenomenon is consistent with our previous work showing greater accuracy of matching fingertip distance for non-zero than zero d_y levels (Shibata et al. 2013). Interestingly, however, the effect of d_y on estimation accuracy of relative fingertip position did not affect the accuracy with which subjects could modulate force as a function of small or large fingertip distances (Fig. 5). We should note that d_y = 0 mm in group 1 led to a longer load phase duration, whereas d_y = –3 and –6 mm did not. Therefore, we interpret the effect of d_y on load phase duration as being due to trial-to-trial changes in d_y rather than on the magnitude of d_y per se. Specifically, larger changes in d_y from one trial to the next (group 1) would require subjects to perform a greater change in force and underlying motor commands. Thus removal of an efference copy would penalize these larger trial-to-trial changes to a greater degree than smaller trial-to-trial d_y changes.

Role of Active vs. Passive Movement for Motor Control: Neural Mechanisms

Relative digit position was estimated without applying significant digit forces after the digits were actively or passively placed on an object. This design was motivated by the results of our previous study showing that estimation of digit position can be biased by the congruence of digit force directions (Shibata et al. 2014). We interpreted this finding as evidence for predicted sensory consequences arising from motor commands overriding estimation of fingertip position through haptic sensory feedback. Results reported by Bhanpuri et al. (2013) are consistent with this theoretical framework. When a physical contact with the limb was predictable, subjects could accurately estimate the end point of active limb movement, whereas accuracy was lower for cerebellar patients (Bhanpuri et al. 2013). These findings suggest that the cerebellum uses predicted sensory feedback through internal forward models by comparing it with proprioceptive feedback during voluntary movement. A major difference between our study and Bhanpuri et al.’s (2013) work is that in our task, proprioceptive and tactile feedback is present throughout our active and passive conditions. Furthermore, both of these conditions resulted in similar digit positions and finger pad deformation, thus eliciting similar proprioceptive and tactile inputs, respectively, as suggested by similar estimation errors (Figs. 4 and 6E).

We conclude that proprioceptive and tactile feedback during force production is sufficient to enable appropriate force modulation to digit placement. For the passive condition, sensory feedback about digit placement after force production onset would be integrated with an efferent copy of force motor commands. For the active condition, subjects might have integrated predicted sensory feedback from active digit placement before contact with digit position sensed after contact.

Conclusions

Our findings demonstrate that the phenomenon of digit force-to-position modulation underlying dexterous manipulation does not require an efferent copy of digit position derived from active digit placement. When this efferent copy is available, it can be readily used for appropriate digit force modulation as a function of digit position to accurately manipulate an object. These results underscore the remarkable ability of the CNS to retain accuracy of sensorimotor transformations across a wide range of task conditions, even when penalized in terms of the speed at which these transformations can occur. Our data further indicate that the advantage of active over passive movement on psychophysical estimation of end-point position that has been reported for arm movements does not apply to fingertip position estimation and control of dexterous manipulation. Therefore, this difference between our findings and literature on arm movements suggests that the extent to which active movement may benefit sensorimotor transformations is task and effector dependent.

GRANTS

This research was partially supported by National Science Foundation (NSF) Collaborative Research Grant BCS-1455866. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of NSF.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

D.S. and M.S. conceived and designed research; D.S. performed experiments; D.S. and M.S. analyzed data; D.S. and M.S. interpreted results of experiments; D.S. and M.S. prepared figures; D.S. and M.S. drafted manuscript; D.S. and M.S. edited and revised manuscript; D.S. and M.S. approved final version of manuscript.