The thermodynamic efficiency of computations made in cells across the range of life

Abstract

Biological organisms must perform computation as they grow, reproduce and evolve. Moreover, ever since Landauer’s bound was proposed, it has been known that all computation has some thermodynamic cost—and that the same computation can be achieved with greater or smaller thermodynamic cost depending on how it is implemented. Accordingly an important issue concerning the evolution of life is assessing the thermodynamic efficiency of the computations performed by organisms. This issue is interesting both from the perspective of how close life has come to maximally efficient computation (presumably under the pressure of natural selection), and from the practical perspective of what efficiencies we might hope that engineered biological computers might achieve, especially in comparison with current computational systems. Here we show that the computational efficiency of translation, defined as free energy expended per amino acid operation, outperforms the best supercomputers by several orders of magnitude, and is only about an order of magnitude worse than the Landauer bound. However, this efficiency depends strongly on the size and architecture of the cell in question. In particular, we show that the useful efficiency of an amino acid operation, defined as the bulk energy per amino acid polymerization, decreases for increasing bacterial size and converges to the polymerization cost of the ribosome. This cost of the largest bacteria does not change in cells as we progress through the major evolutionary shifts to both single- and multicellular eukaryotes. However, the rates of total computation per unit mass are non-monotonic in bacteria with increasing cell size, and also change across different biological architectures, including the shift from unicellular to multicellular eukaryotes.

This article is part of the themed issue ‘Reconceptualizing the origins of life’.

1. Introduction

At the centre of understanding the evolution of life is identifying the constraints faced by biological systems and how those constraints have varied across evolutionary epochs. For example, a question that often arises in evolutionary theory is how relevant the contingent constraints faced by modern life are for understanding early life or even the origin of life. Another example is the question of how organisms cope with the constraints of distinct physical scales—a dependence that by definition does not change across evolutionary epochs.

The laws of thermodynamics restrict what biological systems can do on all physical scales and in all evolutionary epochs (e.g. [1–12]). In addition, all known living systems perform computations. Accordingly, the deep connection between computation and the laws of thermodynamics are a fundamental constraint operating on life across all physical scales and evolutionary epochs [2–11,13–18]. This implies that, by analysing the thermodynamic properties of biological computation, and in particular, the efficiency of those computations, we may gain insight into the changing constraints that have governed the evolution of life.

A deeper understanding of the thermodynamics of biological systems may also help to address a question that pervades almost all of biology: how to quantify the fitness of organisms in a more nuanced way than by their instantaneous relative reproduction rates. One way to make progress on this question is to understand the more fundamental processes that govern reproduction rates. In this regard, it is worth noting that recent research has derived reproduction rates (growth rates) of organisms from their metabolic power budgets, thus illustrating the deep connection between energetic efficiency, the cost of organism functions and reproductive success (e.g. [19,20]). Another way to make progress is to analyse other important organism functionalities in addition to reproduction rate. Here too thermodynamics is vitally important. For example, important organism features, such as the tapering of vascular network structure, can be predicted from considerations of minimizing energy dissipation [21,22]. Clearly then, analysing biological systems in terms of their thermodynamic efficiency can provide insight on how to quantify the fitness of organisms. This approach to defining ‘fitness’ is analogous to recent efforts that have defined the concept of ‘genes’ and ‘functionality’ in terms of chemical computations [23].

In this paper, we extend previous work on thermodynamics in biological systems in several ways. We begin by discussing the surprising ways that the overall thermodynamic efficiency of different biological architectures, quantified as power per unit mass, varies across both physical scale and the age of first appearance. These shifts in overall thermodynamic efficiency provide the backdrop against which we compare shifts in the computational thermodynamic efficiency within the cell across biological architectures. First, we consider the thermodynamic efficiency of the cellular computation of copying symbolic strings during translation in a single ribosome. We then consider the useful thermodynamic efficiency of this computation at the whole cell level, i.e. the total energy rate for all translation, including protein replacement, divided by the rate of translation done for replication. This calculation requires consideration of intracellular decay processes and ribosome and protein scaling. After a consideration of the computation of translation, we consider the efficiency both of the computation of DNA replication and of maintaining storage capacity, from the scale of cells up to the biosphere.

2. Power usage across biological scales

In this paper, we frequently investigate features of efficiency by using power laws of the form Y =Y ₀X^β, where Y ₀ is a normalization constant, β is the scaling exponent and X represents the scale of the system. This type of equation makes it easy to relate behaviours at different scales. For example, if β=1 then all changes in Y are simply proportional to changes in X. Similarly, for β≠1 the ratio Y/X will not be constant and will either increase or decrease with increasing X.

Before turning to the thermodynamics of biological computation specifically, it is useful to consider the scaling of total organismal power usage in order to gain insight on the bulk thermodynamic efficiency of distinct biological architectures. This perspective will allow us to separate total power usage from the cost of computational rates within cells and to distinguish which features are changing (or not) across the evolution of life.

A surprising feature of life at the multicellular scale is that overall metabolic rate does not simply scale linearly with total body size. This is traditionally know as Kleiber’s Law [21,24], expressed as a power law with 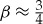. This value of β implies that multicellular life obeys a certain economy of scale: as organisms grow larger, the metabolic rate required to support a unit of mass is decreasing and larger mammals support more tissues for the same amount of energy (e.g. [21]). More recently, it has been observed that this scaling relationship is not preserved across all the taxa of life [25]. In bacteria β is greater than 1 and in unicellular eukaryotes the exponent is close to, but slightly smaller than, 1 [25]. These relationships imply fundamentally different scaling behaviour for each taxa, and are complementary to recent arguments that the epochs of life bring the ability to harness novel energy sources [26]. The relationships have also been used to derive interspecific growth trends and the limits for the smallest possible bacterium and largest unicellular eukaryote [20,27].

Other work has extended a consideration of power usage from the scales of life to comparisons with astronomical objects. This work has argued that a characteristic of the ageing Universe is the appearance of structures with ever higher power density (power per unit mass) [28,29]. (We will return to this specific claim below.)

The scaling relationships mentioned above can also be used to analyse power density across the epochs of life, since the noted differences in scaling relationships imply very different power efficiency across each form of life. For example, bacteria require an increasing amount of power to support a unit of mass with increasing cell size, but are able to reproduce more quickly as a consequence [20,25]. More generally, in the evolution of life, power density first increases with increasing size (bacteria), then saturates for unicellular eukaryotes and then decreases with size for multicellular organisms. It also decreases with size in astronomical systems such as the Sun and Milky Way (figure 1a). The surprising features here are:

• (i) the opposing power density relationships for bacteria compared with multicellular life;

• (ii) multicellular organisms fall along a power density curve that would fall below astronomical systems at the same scale, implying they would be more efficient (in the sense of requiring less power density to maintain themselves);

• (iii) human societies are well above the average curve for multicellular organisms implying a possible inefficiency—humanity is extremely profligate, using power for more than simple maintenance.

Figure 1.

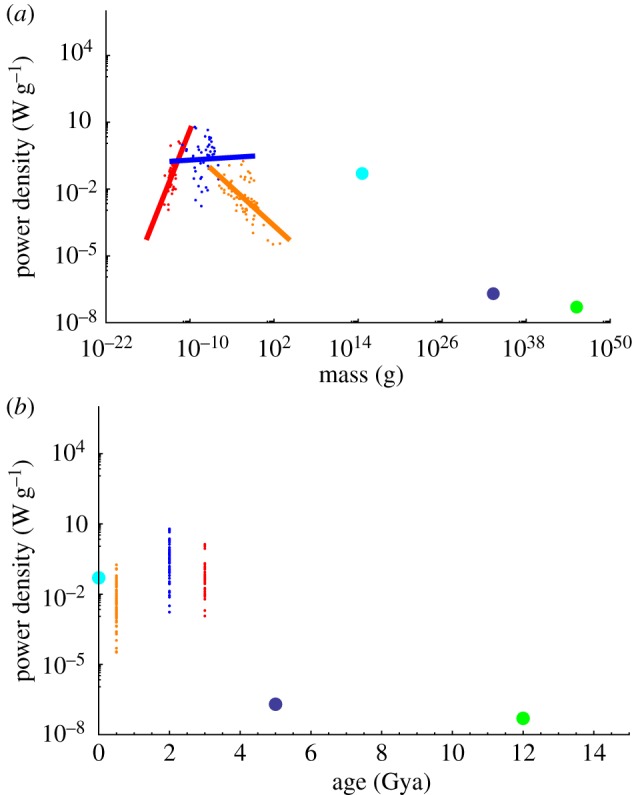
(a) The overall power density of various systems in the Universe. The red points and associated red power-law curve are bacteria, the blue points and curve are unicellular eukaryotes and the orange is for small multicellular eukaryotes, cyan is modern human society followed by the Sun in purple and the Milky Way in green. (b) Power density as a function of the age (years before the present) of first appearance of each system. The data shown are a reanalysis of [20,25,28,29], where the time of first appearance and masses were supplemented by [30–33].

In addition, figure 1b provides the power density as a function of the estimated time when each group of systems arose (in the same way as in [28,29]) and reveals that the biological groups largely overlap independent of the time of first appearance. Considering the averages of each group, the surprising feature is that the evolution of biological architecture first increased and then decreased the power density as a function of first appearance.

These observations highlight a critical question: How should we interpret power density? Phrased informally, should a species be proud or ashamed of its power density? The answer ultimately comes down to how effectively power density is converted into functionality. This is a challenging question to address, both because function is often hard to quantify in terms of increased survival, and because it varies widely across species. In bacteria, we know that the overall power usage predicts the appropriate growth rates from a partitioning between biosynthesis and repair costs [20]. However, it has been previously noted that this comes at the cost of a lower efficiency of biomass production [25] compared with unicellular and multicellular eukaryotes. More generally, organisms with a wide variety of growth rates and biomass production efficiencies exist in nature. This either highlights very different selective pressures in different environments (e.g. classic r/K selection theory [34,35]), or shows that there are other quantifications of functionality that are more uniform across diverse species.

The thermodynamics of computation, which we consider in the rest of this paper, provides a potential starting place for analysing this issue of function.

3. The thermodynamics of computation

In this section, we first provide background on the modern understanding of the thermodynamics of computation, grounded in non-equilibrium statistical physics. We then discuss the different kinds of computation that take place in biological systems, clarifying the (very narrow) set of computations that we consider in this paper.

(a). Formalizing and generalizing Landauer’s bound

There has been great interest for over a century in the relationship between thermodynamics and computation [36–51]. A breakthrough was made with the semi-formal arguments of Landauer, Bennett and co-workers that there is a minimal thermodynamic cost of 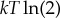required to run a 2-to-1 map like bit erasure on any physical system [44,49,52–63]. A related conclusion was that a 1-to-2 map can act as a refrigerator rather than a heater, removing heat from the environment [44,52,56,57]. For example, this occurs in adiabatic demagnetization of an Ising spin system [52].

More recently, there has been dramatic progress in our formal understanding of non-equilibrium statistical physics and its relation to information processing, in general [61,62,64–78]. In particular, to focus on the specifically computation-based thermodynamic cost of a process, suppose that at any given time t all states x have the same energy. It is now known that in this situation the minimal work required to transform a distribution P₀(x) at time 0 to a distribution P₁(x) at time 1 is exactly

3.1

where S(.) is Shannon entropy and x lives in a countable space X. This lower bound on the work is achieved if and only if the process implementing the transformation is thermodynamically reversible [58,73,78]. This theoretical result is now being confirmed experimentally [79–83]. (If the Hamiltonians are not uniform at both times, then the change in expected value of the Hamiltonian must be added to equation (3.1).)

This recent work—and in particular (3.1)—has fully clarified the early reasoning of Landauer et al. To see how, suppose that the state space X is binary, P₀(x) is uniform and P₁(x) is a delta function about x=0. So the transformation is bit erasure, with a uniform initial distribution of the state of the bit. For this special case, the bound in (3.1) giving the minimal work is just 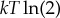, Landauer’s bound. Note that for a different initial distribution P₀(x), the minimal work will be less than 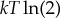. More importantly, note that the bound in (3.1) is achieved with a thermodynamically reversible process; in general, logical irreversibility and thermodynamic irreversibility need not imply one another [84]. (Indeed, if we use a thermodynamically irreversible process to implement the logically irreversible map from uniform P₀(x) to delta function P₁(x), then the total work used exceeds Landauer’s bound of .)

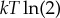Viewed as a computation, bit erasure has the very special property that its output (namely the value 0) is independent of its input. Obviously, this is not true for the vast majority of computations that we might wish to implement in the real world; in almost all computations of interest the output depends crucially on the input. Moreover, the analyses that have been used to derive (3.1) implicitly exploited this feature of bit erasure; they only work for physical processes in which the output is independent of the input. This restriction means we cannot use those analyses to analyse more general types of computation.

To rectify this, in [85] a physical process was analysed that can implement an arbitrary computation in a thermodynamically reversible way, even a computation whose output depends on its input [58,86]. That analysis established that (3.1) still applies for arbitrary computations. Importantly, this result—which we call the generalized Landauer bound—holds even if the conditional distribution P(x₁|x₀) is not a single-valued map. Indeed, that conditional distribution is not directly relevant; only the resultant marginal distribution 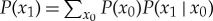arises in the generalized Landauer bound.

(b). Thermodynamics of biological computation

In artificial digital computers, there is no uncertainty about what precise dynamical process constitutes a ‘computation’. Things are not so clear-cut with biological systems, however. One natural criterion is to characterize a biological process as a ‘computation’ if it is reliable and repeatable, and especially if it can clearly be modelled as a digital operation [86,87]. We adopt this criterion here, viewing any system that meets these criteria as performing a ‘computation’. (At a minimum, we feel that such systems perform ‘computation’ at least as much as does a binary system undergoing a 2-to-1 map, which ever since Landauer has been viewed as a canonical model of a computation.)

However, even having settled on a clear criterion for what constitutes a biological computation, there is still a major challenge in accurately identifying and then counting all the computation operations in a biological system. This is because so many computational processes operate at so many levels of biological organization (e.g. [88–90] for a review, discussion and formalism). For example, simply counting the number of bit operations in the multiple interactions of any given chemical in a metabolic network is quite difficult, let alone the bit operations involved in controlling all cellular processes such as uptake rates, chemotaxis and metabolic regulation. Similarly, for human cognition it is necessary to consider not only the input–output operations of each separate neuron, but also the ‘software’ of overall human cognition, which of course involves vast numbers of neurons and is yet to be fully understood.

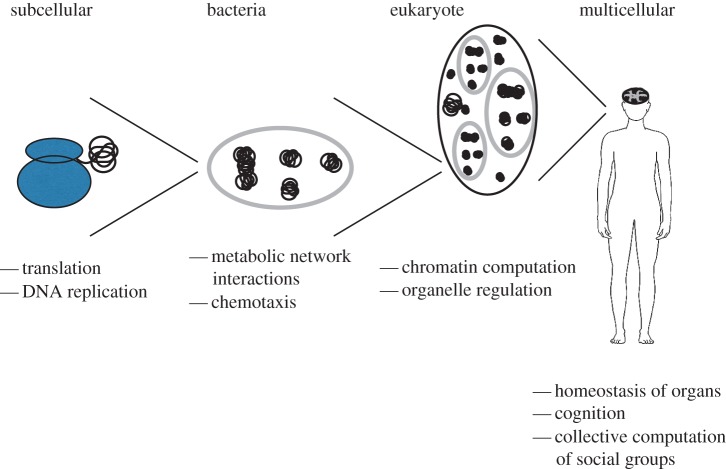
Adopting a broad perspective, we can loosely think of each organism as having their own biological computational hierarchy, where each level in the hierarchy contains all of the lower levels of computation, combining them to form unique higher-level computations. For example, the bacterial cell not only contains the basic computations of the ribosome, but also combines the produced proteins to run more advanced computations at the level of metabolic networks. Similarly, a mammal contains computations ranging from translation within its individual eukaryotic cells up to signalling networks coupling those cells, and at a higher level, participates in social organization [88–90]. Thus, a full treatment of the energetics of computation requires not only understanding how power usage varies over different levels of biological organization (as we addressed above), but understanding the associated hierarchy of computations straddling those levels. Figure 2 illustrates this nesting and gives examples of the new types of computation at each level of biological organization.

Figure 2.

The hierarchies of biological computation ranging from subcellular processes to interactions within collections of multicellular organisms. At each level of biological organization, a few examples of the dominant computational processes are provided, where it should be noted that the highest levels of biological computation integrate the lower levels [88,89]. For example, while neurons are integrated into a complicated cognitive process they also contain the string writing processes of basic protein translation.

A full treatment of this nested computation is a huge task, which will be central to future work in the emerging field of biological computation [88–90]. Here we only present results based on the most conservative counting of the number of bit operations performed by several of the simplest biological processes, focusing on translation and replication. These results are meant to provide intuition on the overall efficiency of the cell, but by no means account for all bit operations in the cell. In addition, our approach only provides a lower bound on the thermodynamic expenditures of those processes that we do consider, modelling those processes as the writing of one-dimensional strings, without considering the additional thermodynamic costs of those processes associated with changes in particle number or positional entropies.

4. Efficiency of cellular computation

In this section, we start by considering the thermodynamic efficiency of translation, first by analysing the efficiency of the ribosome as the basic unit for translation, and then by analysing the efficiency of translation for replication at the level of the entire cell, which includes the overhead costs of protein replacement. We pay particular attention to how these efficiencies vary with the size of the cell, and therefore across evolutionary scales. We then broaden our scope to consider other ways of measuring how the amount of computation varies with size. We conclude by scaling up our analysis to consider the thermodynamic efficiency of the translational computation performed by the biosphere.

(a). Thermodynamic efficiency of computation of translation

First, we consider the energetic efficiency of translation, which represents the simple computation of writing free-floating amino acids into distinct strings. Translation is a particularly well-defined biological computation because it produces a repeatable output (the polymerized amino acid chain) from a given input (mRNA) with a high degree of reliability, which as we argued above qualifies it as a computation. (It also should be noted that this computation is more complex than the simple bit erasure considered in analyses of the Landauer bound.)

We have long known that it takes four ATP equivalents for the ribosome to add an amino acid to the growing protein chain [9,91,92]. There has been much past theoretical and empirical work on the energetics of translation, ranging from arguments of kinetic proof reading [92] to the ratio of forward and backward reaction rates [7]. However, each of these contexts relies on knowledge of the actual chemical process of translation in terms of either natural reaction time scales or the free energy change of certain reactions [7,92]. Our goal here is to compare translation to any physical process performing the same abstract operation. It should be noted though that the expenditure of these four ATP equivalents is partitioned into two key steps: charging the tRNA, which requires two ATP, and forming the peptide bond between amino acids, which requires another two ATP equivalents (e.g. [9,91]). These two chemical processes are used together to take the amino acids out of solution and bind them together.

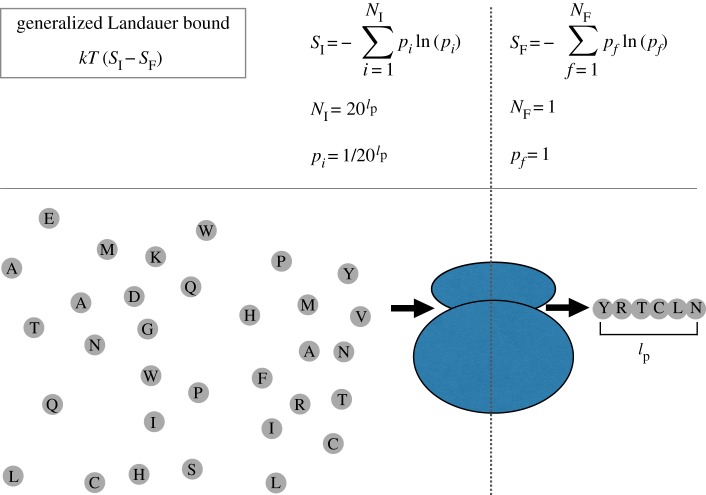
Biological translation is a computation that writes a specific string of length l_p using a 20 letter alphabet (figure 3 and table 1). It is achieved with a specific chemical process involving tRNA, mRNA, amino acids and the ribosome. We are interested in quantifying how thermodynamically efficient this chemical process is by comparing its thermodynamic cost to the smallest possible thermodynamic cost that would be incurred by any physical process that performs the same computation. The generalized Landauer bound provides us with precisely such a ‘scale’ for assessing the thermodynamic efficiency of biological translation compared with all possible processes performing the same operation.

Figure 3.

Minimal free energy required for the string writing process of protein translation, taking a uniform bath of amino acids to a specific protein. The formula for the generalized Landauer bound is given, along with the initial and final entropies of writing a specific string of length l_p (the average length of a protein in amino acids) from a set of 20 objects (amino acids).

Table 1.

Definitions of parameters and constants.

parameter	units	definition
td	s	division time
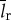	bp	length of all ribosomal proteins
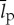	bp	the average length a protein
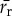	bp ⋅ s−1	ribosomal base pair processing rate
η	s−1	specific ribosome degradation rate
ϕ	s−1	specific protein degradation rate
μ	s−1	specific growth rate
Np		total number of proteins
Nr		total number of ribosomes
γ		fraction of translation dedicated to making ribosomes
Vc	m3	cell volume
Rt	amino acids ⋅ s−1	repair translation
Tt	amino acids ⋅ s−1	total translation
Ut	amino acids ⋅ s−1	useful translation
Et	J ⋅ amino acids−1	energy per amino acid polymerization

We can apply equation (3.1) to calculate the minimal free energy required to implement the many-to-one mapping that transforms a pool of free-floating amino acids (a bath of a large number of uniformly distributed amino acid abundances) into the prescribed amino acid sequence of a particular protein. Since there is only one final state, the final entropy is S_F=0, and if we generalize slightly to a scenario of C possible amino acids, we get

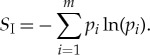4.1

In particular, if we have a uniform p_i, i.e. p_i=p=1/C^l_p, then there are a total of m=C^l_p states, and 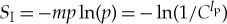. In many of the calculations below, C is taken to be 20, the actual number of amino acids; we have left the value general in some of our formulae so that considerations of a reduced amino acid pool, although unlikely, could be considered.

Given that the average protein length is 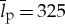aa (see [27] for a review of values), for 20 unique amino acids, we have that p_i=p=1/20³²⁵=1.46×10⁻⁴²³, where there are 20³²⁵ states, such that the initial entropy is 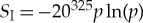, which gives the free energy change of kT(S_I−0)=4.03×10⁻¹⁸ (J) or 1.24×10⁻²⁰ (J per amino acid). This value provides a minimum for synthesizing a typical protein. We can also calculate the biological value from the fact that if four ATP equivalents are required to add one amino acid to the polymer chain with a standard free energy of 47.7 (kJ mol⁻¹) for ATP to ADP, then the efficiency is 1.03×10⁻¹⁶ (J) or 3.17×10⁻¹⁹ (J per amino acid). This value is about 26 times larger than the generalized Landauer bound.

It should be noted that the efficiency of the translation system is much closer to the Landauer bound than estimates for other biological processes. For example, synapses have been estimated to be 10⁵ to 10⁸ times worse than the Landauer bound [93].

These results illustrate that translation operates at an astonishingly high efficiency, even though it is still fairly far away from the Landauer bound. To put these results in context, it is interesting to note that the best supercomputers perform a bit operation at approximately 5.27×10⁻¹³ (J per bit) [94,95]. In other words, the cost of computation in supercomputers is about eight orders of magnitude worse than the Landauer bound of 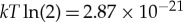(J) for a bit operation, which is about six orders of magnitude less efficient than biological translation when both are compared to the appropriate Landauer bound. Biology is beating our current engineered computational thermodynamic efficiencies by an astonishing degree.

As elaborated in the appendix, to focus solely on the cost of the computation, we only calculate changes in the Shannon information contribution to the thermodynamic work. We do not account for changes in the chemical binding energies during the copying process, changes in momentum degrees of freedom, energy levels of the vibrational modes of the folded protein, etc. Our focus is on estimating the computational part of the string writing process in isolation. As such it is also worth noting that two ATP are being spent to pull the amino acid out of solution and bind it to the tRNA and two are being spent to actually polymerize the amino acid once the tRNA has docked via random processes. Thus, if we focus purely on the computational process of string writing, the cost is only two ATP equivalents; the other two ATP equivalents can be seen as an upstream process, whose efficiency we are not analysing. This would halve the biological cost calculated above and bring it closer to the Landauer bound for the idealized string writing process.

There are several other subtleties in our analysis, concerning the choice for how to define the set of states of the system undergoing translation, and therefore, the cost of the associated changes in entropy. The calculation above of the change in entropy during string writing is based on the specific situation of an infinite bath of uniformly distributed amino acids. We note that, although this is a reasonable zeroth-order approximation of the cellular environment, it is an underestimate of the thermodynamic efficiency of translation, since only some of the entropic costs of translation have been accounted for. In particular, the entropic cost to pull amino acids from a three-dimensional bath into a one-dimensional string is neglected. Thus, there are other entropy accountings that are worth investigating, including one that begins to approximate the three-dimensional problem. Below we provide a few of these alternatives.

First, consider the case where a particular protein is being written from a pool of only the exact amino acids (both number and composition) required for that protein. In this case, the number of distinguishable states is given by

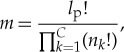4.2

where C is the number of distinct amino acids used, n_k is the number of amino acid of type k and 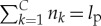. The initial entropy is then calculated using 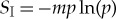with p=1/m. In the case where all amino acids are used in equal proportion, this alternative would be m=l_p!/[(l_p/20)!]²⁰, which, using the values above, gives a Landauer bound of 3.86×10⁻¹⁸. This value is very close to the bound calculated above for the case of an infinite uniform bath. The maximal thermodynamic cost in equation (4.2) decreases as the number of amino acid types employed decreases. The smallest non-zero value is given by employing two amino acid types with only a single amino acid from one of the types, in which case m=l_p!/[(l_p−1)!]. This gives a Landauer bound of 2.40×10⁻²⁰, which is about two orders of magnitude smaller than the original bound above.

As we have mentioned, this process of string writing underestimates the change in entropy because it does not account for the three-dimensional positional entropies of each amino acid. One way to start to address this challenge, which still underestimates the positional entropy, is to consider each individual amino acid as distinguishable from the others regardless of type. Under this condition m=n!, and the Landauer bound would be 6.46×10⁻¹⁸, which is about 1.6 times the original estimate from the uniform bath.

The energetics of copying a polymer have been considered before [12,16–18,96]. These earlier analyses choose different subsystems of a cell to identify as the ‘computer’, and/or different times to identify as ‘initial’ and ‘final’ moments of the computation. These different choices alter both what we calculate as the actual thermodynamic cost in a real cell and what we calculate as the minimal cost over all possible physical systems. So they change the thermodynamic efficiency calculated.

As an example, in our calculation, we choose to analyse the thermodynamics with a fixed mRNA rather than a distribution over mRNAs. Specifically, as elaborated in the appendix, we calculate the free energy needed to remove the set of amino acids specified by that fixed mRNA from a (random) bath of amino acids inside the cell. By contrast, in [16], there is a distribution over the mRNAs. As a result their calculation of thermodynamic cost involves the mutual information between the mRNA and the protein. However, this choice implicitly sets the ‘ending moment’ of the computation as occurring before a subsequent step in which the cell decomposes the mRNA (to re-use those nucleotides), a step which zeroes out that mutual information contribution. In addition, the analysis [16] only considers the subsystem of the cell that produces the protein from the mRNA, and so does not consider the cost of changing the distribution of amino acids in the bath of amino acids—the very cost that we concentrate on.

More generally, it has also been pointed out that the full string writing process goes from the DNA ‘tape’ to the protein string [2,13]. In this case, the full four ATP equivalents described above should be used, plus an additional one or two ATP per nucleotide to polymerize the mRNA transcript [9,91,97], and this would add an additional three to six ATP per amino acid to the full string writing processes. This would double the above biological cost estimate—although the Landauer bound would remain unchanged (see appendix A). Thus, the value for the thermodynamic efficiency would be halved.

Likewise, the costs we tally do not include all of the upstream costs of preparing the amino acid and nucleotide pools in the cell in the first place, before modifying subsets of them to form strings (of proteins and of RNA, respectively). Here we have focused on the maximum efficiency of the ribosome in isolation, as a system where a well-defined computation can be quantified, and compared this to the thermodynamic lower bound for the same computation, performed with arbitrary (possibly non-biological) processes. In our calculation we sidestep all the details of the biochemistry. We do this on purpose, since we are concerned with the thermodynamic efficiency of string writing as an idealized computer. We are calculating the minimal thermodynamic work that would need to be expended to do the copying for any physical process, not just the kind of stepwise construction considered, e.g. [16].

We emphasize that there is no right or wrong choice of which subsystem of the cell to identify as ‘the computer’, or of which moments to identify as the ‘beginning and ending moments’ of the computation. Rather, different choices answer different scientific questions. Here we concentrate on the thermodynamic efficiency of one particular subset of the entire translation process, as discussed in detail in appendix A.

These calculations we perform (and the variations of them discussed above) do not prove that evolutionary fitness is highly dependent on thermodynamic efficiency; conceivably, the majority of chemical processes that perform an analogous computation have such an efficiency. Indeed, the specific energetics of translation are tied to the precise processes operating in the ribosome. It is at least conceivable that evolution, or an alternative origin of life, could have found an even more efficient chemical process that operates even closer to the Landauer bound. Nonetheless, these calculations are at least consistent with the hypothesis that the evolutionary fitness of cells has been highly dependent on the thermodynamic efficiency with which they perform the computation of translation.

(b). Thermodynamic efficiency of useful translation

The calculations in §4a do not involve the size of a cell, nor any of the cellular functions beyond the operation of a single ribosome. If we are interested in the computational efficiency of an entire cell we must consider other features of the cell as well. In particular, we must consider cellular functions that maintain information. To do this requires an assessment of the rate of information damage. Specifically, we need to assess the rate of loss of proteins due to damage.

Building on previous efforts which describe the general trends in cellular rates and composition [20,27], bacteria provide an ideal case for understanding the trends in computational efficiency across a range of biological scales. A review of analyses of this issue can be found in the Material and methods section (§6). The key result [27] is that the number of ribosomes required for the cell to be able to divide, N_r, is bound by the inequality

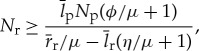4.3

where both the specific growth rate, μ, and number of proteins, N_p, have been shown to scale with overall cell volume, V _c [20,25,27] (see the Material and methods section (§6), table 1 and [27] for definitions and values of the constants in equation (4.3)). The number of proteins is given by

4.4

where, empirically, β_p=0.70±0.06 [27]. In addition, the cross-species trends in ribosomes have been shown to follow the lower bound on N_r described above [27], and this is the relationship that we use here for all further calculations.

This same approach allows us to quantify the total translational computation being performed by the cell (defined here as writing the amino acid pool within a cell to specific protein sequences) as

4.5

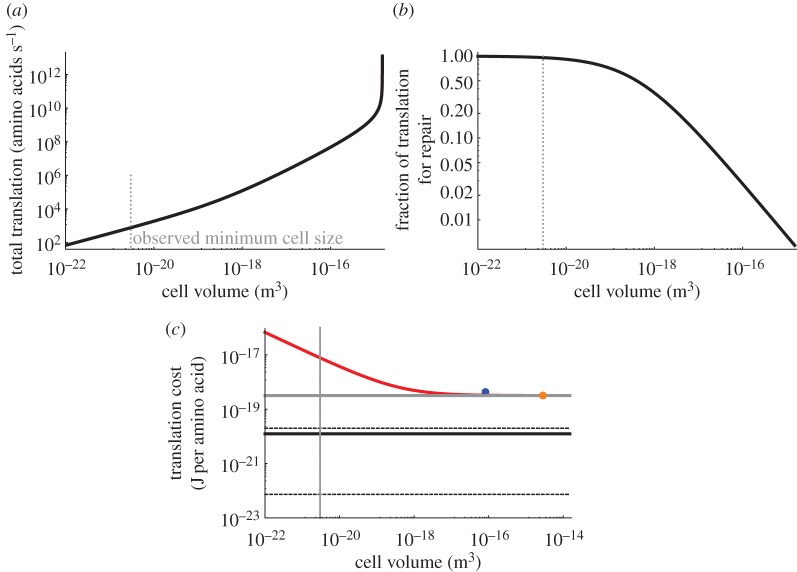
(measured in amino acids per second; note the division by 3 to convert from base pairs to amino acids), where r_r is the maximum base pair processing rate of the ribosome (bp per second). This is plotted in figure 4a. The asymptotic behaviour for the largest bacteria is due to the ‘ribosome catastrophe’ [27], the point where the scaling of growth rate (as determined by metabolic rate [20]) demands a greater ribosomal capacity than can fit in the cell, or equivalently, the point where cellular division rate becomes faster than the rate at which a ribosome can replicate even the ribosomal proteins.

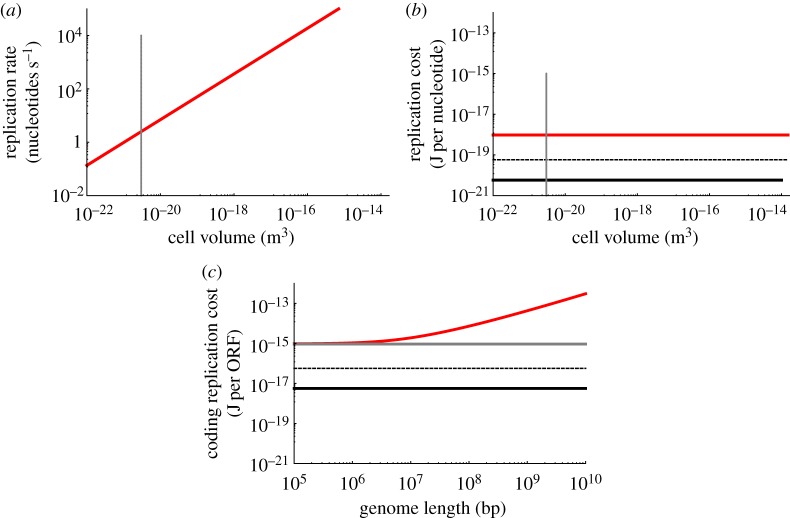
Figure 4.

(a) The total translation rate as a function of bacterial cell volume. The smallest observed bacterial species is indicated with the dotted grey line. (b) The fraction of translation activity that is dedicated to repairing damaged proteins. (c) The useful translation cost, defined as the total energy expended on all translation divided by the number of proteins synthesized for replication rather than for the repair of damage. The red curve is bacteria, the blue point is for unicellular eukaryotes and the orange point is a single mammalian cell. The black curve is the Landauer bound for translating a protein scaled to a single amino acid addition, and the grey curve is the known energetic cost per amino acid for a single ribosome given the ATP costs. The dashed black lines are the range of Landauer estimates given different accountings of the entropy discussed in the text. For example, the upper dashed line is the case where every amino acid is distinguishable. The discrepancy between the red and grey curves at the small end of bacteria is the result of the high fraction of total translation spent on repair for the smallest cells as shown in (b).

We can build off these previous analyses, to analyse the rate of translation that is used to replace damaged proteins (measured in amino acid units), 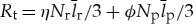. Combining with equation (4.5), the fraction of total translation that is used for such repair is

4.6

The dependence of this ratio on cell size provides a perspective on the limits of cell size (figure 4b). At the smallest end of life, cellular translation is dominated by the replacement of proteins. This should be compared with previous results which found that total metabolism is dominated by maintenance processes at the small end of bacteria [20]. Here we tease apart that earlier result to show that even the individual process of translation becomes dominated by maintenance (protein replacement) at the small end of the scale.

As a complement to analysing the fraction of translation dedicated to repair, we can analyse the useful translation, which we define as the accumulated translation that will eventually allow the cell to divide, 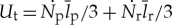. A convenient way to quantify the overall energetic efficiency of translation is the ratio of the total energetic cost of translation relative to the useful translation (J per non-degraded amino acid),

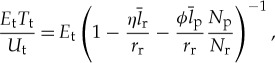4.7

where E_t is the energy to polymerize one amino acid (four ATP equivalents at 47.7 (kJ mol⁻¹) of ATP). In figure 4c, we have plotted this overall efficiency of translation based on the known scaling of N_r and N_p across bacteria. We find that the smallest cells are over an order of magnitude less energetically efficient than the largest cells at performing the operation of adding an amino acid to the protein chain. The largest cells converge to the energetic efficiency of the ribosome itself, which is still about 26 times larger than the Landauer bound as discussed earlier (figure 4c).

Another interesting question is how the translational efficiency changes across diverse biological architectures. We find that the translational efficiency of single-cell eukaryotes (considering values for yeast; see Material and methods (§6)) and single mammalian cells does not significantly deviate from the efficiency of a single ribosome (figure 4c), which is also the efficiency of the largest bacteria. Life quickly converges to the efficiency of the ribosome as cells become larger, and maintains that efficiency at the cellular level across the diversity of both free-living and multicellular eukaryotes. It should be noted that a critical feature of both equation (4.6) and equation (4.7) is the ratio of N_p to N_r. In particular, the global cost of useful translation and the fraction of translation dedicated to repair are minimized by N_p/N_r=0. Our results show that, after a sufficient cell size, life has been able to adjust this ratio such that the effective translational cost is only negligibly larger than that of the ribosome. A surprising result here is that, while the bulk power consumption of organisms dramatically shifts across major evolutionary transitions, the unit costs of translation are held constant once cells reach a sufficiently large size.

(c). Rates of cellular computation measured in oklos

So far, we have only considered one aspect of the thermodynamic cost of cellular computation, namely energy spent per amino acid operation, measured either using the Landauer bound or the efficiency achieved by a single ribosome. However, there are other important metrics for analysing cellular computation. One that was recently introduced is the oklo, defined as the number of bit operations per gram per second [94].

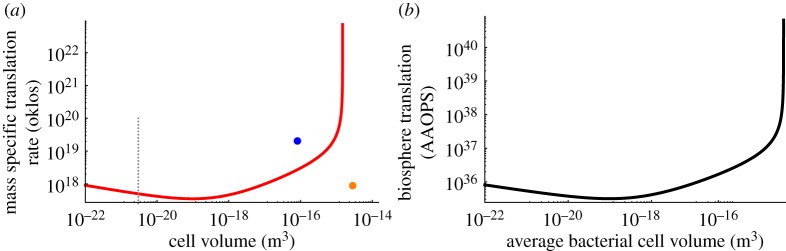
Our analysis above allows us to calculate one component of the number of oklos expended in cellular computation: the rate of amino acid bit operations per unit of bacterial mass. We plot this as a function of the overall size of the bacterial species in figure 5a. We find a non-monotonic function for bacteria with a minimum in the mid range of bacterial sizes, and a rapid increase for the largest bacteria due to the increased number of ribosomes [27]. However, it should be noted that for most bacterial sizes the oklos curve is surprisingly flat and ranges within an order of magnitude. The unicellular eukaryote value from yeast is significantly larger than that of bacteria of the same size, and is about an order of magnitude larger than the value for bacteria of average cell size. However, the mammalian cell values appear to be indistinguishable from the value for a bacterium of average size. In contrast with the energetic efficiency of translation, which appears to saturate at the ribosome minimum and be held constant across evolutionary transitions, the oklos found within different biological architectures have significant shifts across diverse life, where unicellular eukaryotes are able to achieve the highest rate of bit operations per unit mass.

Figure 5.

(a) The mass specific translation rate of individual cells of different size in oklos (here considering amino acid operations per gram per second). The red curve is the average cross-species relationship calculated for bacteria, the blue point is for yeast and the orange point is a mammalian cell. The dotted grey line indicates the smallest observed bacterial species. (b) The total amino acid operations per second (AAOPS) of all the bacteria in the biosphere as a function of the average bacterial cell volume.

(d). Translational computation by the biosphere

Known cellular rates of the amount of computation per unit mass have recently been scaled up to analyse the rate of translational computation performed by the biosphere [94]. Having done this, one can then divide by total solar flux to calculate the thermodynamic efficiency of translation at the scale of the biosphere [94]. However, given the strong scaling relationships demonstrated both in this paper and in previous work [20,25,27], it is important to note that any such estimates depend strongly on how we model cell size distributions in different environments. In addition, we have seen that growth rate plays an important role in determining the overall computational efficiency of translation, and it should be noted that large amounts of the biomass on Earth is growing at rates close to zero [98]. These low growth rates will not affect the assessment of the information stored in the biosphere in DNA [95], but will matter for assessing the overall rates of computation.

To begin to address these subtleties we have plotted (figure 5b) the total translation of bacteria (at maximum growth rate; measured in amino acid operations per second ‘AAOPS’) based on the previous estimate of total bacterial cells in the biosphere [95]. These results show that the total computation rate of translation in the biosphere could range over many orders of magnitude depending on average cell size and growth rate (which scales with cell volume in these calculations). Nonetheless, the estimate of the amount of computation occurring in translation (measured in AAOPS) greatly exceeds previous estimates of the nucleotide operations per second, which range between 10²⁴ and 10²⁹ [94,95]. However, it should be noted that this estimate is based on the scaling of cells growing at maximum rate, which does not represent most of the Earth’s biomass [98]. Following Laughlin [94], and considering the slowest growing bacteria [98], we can calculate an extreme lower bound on the computational efficiency of the biosphere by assuming that all usable sunlight is dedicated to the total translation. We find that the biosphere would have a total of 1.86×10³⁰ (AAOPS per biosphere) leading to an efficiency of 3.65×10¹³ (AAOPS per J of sunlight). This value is close to but exceeds the estimate of 2×10¹² (bit operations per J of sunlight) from [94] for DNA replication.

(e). DNA replication efficiency

As noted above, much of the previous work on biological computation has focused on the process of DNA replication [94,95]. Accordingly, in parallel to our analysis of translation, we consider how the total computations and efficiencies of DNA replication shift across bacteria of different size. In figure 6a, we have plotted the total nucleotide replication rate for bacterial species of different size (to form this figure we multiply overall genome size by division rate, each of which follows a known scaling relationship with cell volume [20,27]). We find that the rate of nucleotide copying varies by several orders of magnitude across the range of bacteria.

Figure 6.

(a) The total DNA replication rate as a function of bacterial cell volume. The smallest observed bacterial species is indicated with the grey dotted line. (b) The DNA replication efficiency compared with the Landauer bound for copying a single nucleotide. (c) The DNA replication efficiency for open reading frames (ORFs) considering the total cost of replication. The Landauer bound for copying a single nucleotide has been scaled up using the average length of a gene.

Paralleling our calculations of string writing during translation we can use similar entropic considerations to estimate the Landauer bound in DNA replication. For a uniform nucleotide bath, the number of states is m=4^G, where G is the length of a genome, and the corresponding Landauer bound is 1.86×10⁻¹⁴ (J) for a typical bacterial genome size, which can more meaningfully be converted to 5.74×10⁻²¹ (J per nucleotide), a value that will not vary with genome size. The known value of 12 ATP equivalents per nucleotide copying in cells gives a value of 9.50×10⁻¹⁹ (J per nucleotide), which is 165 times larger than the Landauer bound. Thus, bacteria consume about two orders of magnitude more energy than the Landauer bound for DNA replication.

However, just as we saw with translation, there is a broad range of possibilities for the details of the string writing that affect the associated calculations of the entropies. This is particularly relevant for DNA replication, where it is much more likely that the string is written from a pool of nucleotides that approximately match the length and composition of the genome. As described earlier, this scenario would give m=G!/[(G/4)!]⁴, leading to a Landauer bound of 5.74×10⁻²¹ (J per nucleotide), which is indistinguishable from the value above. For a set of completely distinguishable nucleotides, we would have m=G!, giving 5.80×10⁻²⁰ (J per nucleotide), which is an order of magnitude larger than the other thermodynamic cost estimates for DNA replication. This range of Landauer bound estimates is shown in figure 6b,c.

(f). Thermodynamic efficiency of gene replication

While the unit costs of replicating a nucleotide are not changing across cells of different size, it should be noted that across unicellular bacteria and eukaryotes the percentage of the genome dedicated to coding regions is decreasing with increasing genome size [99,100]. Specifically, it has been shown that a good empirical fit to the number of open reading frames (ORFs) is given by

4.8

where A=4016±280 ORF, B=4106±680 kbp and G=cDNA+ncDNA, with cDNA and ncDNA denoting the coding and non-coding fractions of the genome [100]. This relationship makes it possible to quantify the cost of replicating a coding nucleotide relative to the Landauer bound. Figure 6c shows that the total cost for replicating a gene is increasing as genomes become larger. This result is the opposite of what we found in protein translation, where the smallest and simplest cells are the least efficient at translation at a whole cell level because of the high overhead of protein replacement.

There has been recent interest in understanding how the energetics of single genes change across the range of life [9,27,97,101]. For example, it has been shown that the fraction of the total energy budget spent on DNA replication is decreasing with increasing cell size [9]. However, the results here show that, compared with an absolute unit efficiency, the replication cost for a single nucleotide from a coding region is increasing. It is possible that the decreasing relative cost of replication compared to total metabolism as cell size increases allows for this potential inefficiency (‘potential’ because we have not quantified the utility of the non-coding DNA). It has also been proposed that the underlying distribution leading to equation (4.8) is a Benford distribution, and that this gives genomes the following properties: (i) upon combination of genes the minimal error possible is made (maximum fidelity) and (ii) the information contained in the genes is transferred at the maximum possible rate (minimizing distortion) [100,102,103]. Thus far, in this paper we have analysed the thermodynamic efficiency of the computational processes; however, the above connection opens up important future efforts which should focus on the connection between the thermodynamic efficiency of both computation and communication within cells.

(g). DNA computation and storage of the biosphere

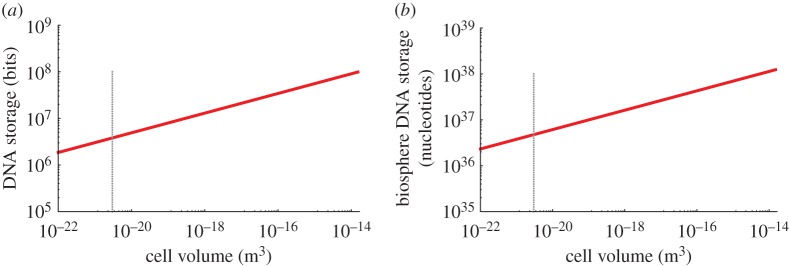
In addition to the overall computational rate in DNA replication, another important characteristic of naturally occurring DNA computation is the total storage capacity of DNA, both within a single cell and within the biosphere as a whole. We find that these values again depend strongly on assumptions about average bacterial size. In figure 7a,b, we have plotted the storage both of a single cell and of the total bacterial biomass in the biosphere as a function of cell size. Each varies over about an order of magnitude. We note that the calculation for the biosphere would agree with the previous estimate of 1.6×10³⁷ bp [95] only for an assumption that most of the biomass in the biosphere is small bacteria. Similar to our calculation of the amino acid operations per total energy of the biosphere, above we calculate that there are 2.54×10²⁹ (nucleotide operations/s/biosphere) or 4.98×10¹² (nucleotide operations per J), which agrees well with the independent estimate from [94].

Figure 7.

(a) The storage capacity of the DNA in a single cell as a function of total cell size and (b) these same values scaled up to the biosphere.

5. Discussion

Here we have shown that life maintains a roughly constant power usage as a function of the age of the system’s evolutionary arrival, yet the overall scale and type of system have strong implications for power usage: bacteria increase in power usage per unit mass for larger cells, whereas multicellular life has a decreasing power expenditure per unit mass for larger systems. In fact, multicellular life would be surprisingly more efficient than astronomical objects if extrapolated to the same scales.

Despite these shifts across the architectures of life, we find surprising consistency in the efficiency of translation, one of the most universal types of computation carried out in biological systems. Our analyses show that as bacteria become larger their overall translational efficiency converges on that of a single ribosome. In addition, this efficiency is maintained for unicellular eukaryote and mammalian cells. Astonishingly, this efficiency is only about an order of magnitude larger than the Landauer bound, and is an impressive feat of biology, as it far exceeds modern computers. However, to properly ‘calibrate’ this efficiency we would need to know how close to the Landauer bound biology could have gotten using alternative biochemical processes (arrived at via alternative evolutionary histories) to perform translation. On the other hand, it is important to note that the processes considered here represent only a fraction of the total computations of the cell. In the future, it will be important to quantify the computational efficiency of various levels of biological physiology. These additions should range from metabolic networks in bacteria, to chromatin computations in unicellular eukaryotes (e.g. [104]), to information encoded over evolutionary search (e.g. [11,14] and references therein), to the social computations of multicellular mammals [88–90], where each new level of hierarchy integrates the computations of the lower levels [88,89]. In addition, we note that our calculations underestimate the full computational cost of translation, since they treat amino acids as one-dimensional strings, ignoring the computational cost of reducing the three-dimensional positional entropy of amino acids into a single string. Accordingly, they underestimate the thermodynamic efficiency of biological computation, which is already impressively close to the lower bounds considered here. It should also be noted that ATP are used for many cellular processes in addition to those considered here. Understanding the thermodynamic efficiency for these other enzymatic and metabolic processes will require quantifying the computations being performed, and this represents a major challenge of future interest for the community.

Furthermore, we have shown how the overall computational efficiency of translation in the biosphere greatly depends on how much of the total biomass is partitioned into organisms of different size. This type of analysis of the biosphere, similar to previous efforts [94,95], provides new ways to quantify ecological efficiency. Yet it should be noted that a huge fraction of biomass on Earth is partitioned into the smallest cells, which are the least computationally efficient from the perspective of translation. This implies that, despite the evident efficiency of the biosphere, it could have been higher, and is clearly not the dominant force for evolutionary selection in some systems. On the other hand, it may well be that it is not possible to maintain an entire biosphere without maintaining a level of diversity that results in lots of organisms with inefficient computation. Under that hypothesis, it may well be that the biosphere as a whole computes with close to the maximal possible thermodynamic efficiency.

6. Material and methods

(a). Review of ribosome requirements

Previous analyses have shown that the number of ribosomes can be predicted based on the overall growth rate of cells and the total protein content [27]. These analyses were based on the translation and degradation dynamics given by

6.1

and

6.2

where it has been shown [27] that the partitioning of translation between ribosomal and non-ribosomal proteins is bounded by

6.3

where 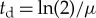is the division time, 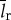is the total length of all ribosomal proteins in base pairs as a cross-species average, 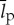(bp) is the average length of all other cellular proteins, 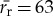(amino acids s⁻¹) [105] is the maximum base pair processing rate of the ribosome, η (s⁻¹) and ϕ (s⁻¹) are specific degradation rates for ribosomes and proteins, respectively (both taken to be 6.20×10⁻⁵ [27]), μ is the specific growth rate and N_p is the total number of proteins (table 1).

(b). Parameter values

In figure 1, the lines represent transformations (division by cell volume) of the best ordinary least squares fits of metabolic rate against cell volume (compared with the RMA (reduced major axis) fits carried out in [25]). The large scatter in the data for unicellular eukaryotes is due to the fact that the metabolic rate scaling is approximately linear with cell volume, and thus power density is effectively just the residual values around this linear scaling relationship.

For the translational efficiency in unicellular eukaryotes, we combined values for yeast, and for multicellular eukaryotes, we used values for mammalian cells. The equations for bacteria are general provided that we can accurately estimate the number of ribosomes and proteins, and the overall time to divide for a given cell volume. For yeast, we use a value of N_r=1.87×10⁵ [106], N_p=5×10⁷ [107] and a division time of t_d=7561.6 (s) [108]. For mammalian cells, we use N_r=1.27×10⁷ [109], N_p=1.70×10⁵ [110] and a division time of t_d=1.71×10⁵ (s) [111].

Appendix A

In this appendix, we elaborate our calculation of the minimal amount of thermodynamic work that would be required to construct a copy of a single, pre-specified sequence of amino acids. In other words, we calculate the amount of work that would be used in a semi-static, thermodynamically reversible process to construct such a copy. For simplicity, we assume that the process proceeds in continual contact with an infinite heat bath at equilibrium at a constant temperature T. We also choose units so that Boltzmann’s constant equals 1.

(a) The copying process

Let the total number of types of amino acid be C (e.g. 20). We suppose that before the copy operation, in addition to the single, pre-fixed protein we wish to copy, we also have a soup of amino acids accessible within the cell. That soup was formed by IID (independent and identically distributed) sampling a distribution p(i) over amino acid of type i a total of N times. (In general, N itself will be a random variable reflecting differences in the size of the amino acid pool, but we ignore that for now.) Let n⁰ be the resultant (random) vector of counts of amino acids in the pre-copy soup, and n⁰(i) be the number of amino acids of type i in the pre-copy soup of amino acids. So n⁰ has C components, and the probability of a particular n⁰ is

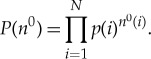A 1

We then remove a set of k amino acids from that soup, and arrange them in the precise order specified by the protein being copied (this is our definition of the ‘copying process’). Let σ be the output string of amino acids, where for all i∈1,…,k, σ(i) has one of C values, and σ has k components in all (this is the protein length l_p in the main text). We write the count vector of amino acids in σ as ν(i). Note that whereas count vectors like ν have C components, strings like σ have k components.

For simplicity, we suppose that the thermal equilibrium distribution is the same before and after copying. This means that the change in non-equilibrium free energy of the system that occurs in this copying process gives the minimal thermodynamic work required to perform the copying.

As is conventional, to focus on the exclusively ‘computational’ contribution to the change in non-equilibrium free energy, we take the energy levels of all possible states of the system to be the same. This means that there is no change in expected energy of the system in the copying process, so that the change in non-equilibrium free energy during that process reduces to (T times) the change in Shannon entropy of the distribution over possible states of our system. Equivalently, if there are differences in energy levels, we ignore them, to focus on the computational contribution, which again leads us to consider only the change in Shannon entropy.

(b) The state space

Before calculating the change in entropy, we first need to precisely specify the system’s state space that the (probability distribution defining the) entropy is defined over. Obviously, to perform our statistical physics calculations, we do not want to choose the state space to be the precise joint quantum state of all the quarks, gluons, etc. that comprise the cell. But what should we choose it to be instead? Phrased differently, what is the appropriate coarse-graining to adopt for our analysis?

Here we answer this question by building on the insight of Jaynes in his famous analysis of the Gibbs paradox [112]. Formulating this in fully general terms (extending beyond the special case of calculating changes in entropy when forming an amino acid string), write the microstate space of the system as Y . For example, y∈Y could specify the joint state of all the quarks and so on in the system. In addition to the system with state space Y , we also have a physical work-extraction device for manipulating the system. Let X be (the set of elements of) some partition of Y , where each x∈X is called a macrostate. Now suppose we are told the distribution P_X(x) and nothing more. For completeness, we could suppose that for each x∈X, the associated distribution P(y|x) of microstates within the macrostate x is an appropriately masked and renormalized Boltzmann distribution. We can use that distribution P_X to choose the initial state of the device. Suppose that after this initialization of the device by us (using only P_X), the device is coupled to the system and extracts thermodynamic work from it. (To fix thinking, we could suppose that the work is extracted by the device by relaxing the system to thermal equilibrium over X.)

Let Ω(X,P_X) be the maximum work we can extract for partition X and distribution P_X using the device, by appropriate choice of the initial state of the device. Similarly, for any partition 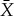that is a refinement of X, let be the maximum work we can extract for partition and distribution 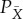, by appropriate choice of the initial state of the device. Note that P_X is a marginalization of 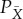. Then following the insight of Jaynes, we should choose X—choose our coarse-graining of the system—to be the coarsest partition of Y such that there is no refinement of X, 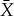, where for some 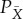and associated marginalization P_X, .

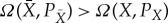This is an operational definition of ‘coarse-graining’. It says that if we cannot exploit knowledge of P(y|x), the distribution of states within some x∈X, to extract more work than we can just by knowing P_X(x), then there is no operational sense in which the statistical physics occurs over a finer coarse-graining than X. To paraphrase Jaynes, a scientist Jane who has finer tools to use to extract work from the distribution over the states of the system can appear to violate the second law to a scientist Bob who only has crude tools for extracting work from the system. Specifically, Jaynes analysed the case where Jane can exploit information about whether a gas particle at a given location in a cylinder is one of two types, while to Dick all particles are interchangeable, and so Dick cannot exploit such information.¹

Here, for simplicity, we assume that our device is not able to exploit any property of the protein being copied. We also assume it not able to exploit the distribution over momentum degrees of freedom of each amino acid (in either the bath or the final amino acid string produced by the copying). We also assume our device cannot exploit the distribution over two out of three positional degrees of freedom of the amino acids. In other words, for simplicity we are reducing the bath (both pre-copy and post-copy) to a one-dimensional string, just like the amino acid sequence that is produced by the copy process. Finally, because we assume for simplicity that the string being copied is unique (i.e. has a delta function probability distribution), our state space reduces to the set of one-dimensional strings of amino acids in the bath. So the change in entropy in the copying process is the change in the entropy over possible strings of amino acids in the bath.

(c) The change in entropy

In the light of the foregoing, our state space X consists of all strings of amino acids (explicitly excluding the protein that is being copied). The initial state is the string x of length N characterizing the pre-copy state of the bath. To begin, assume that the count vector n⁰ is fixed. Then the distribution over initial states is

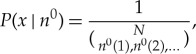A 2

if we assume that all orderings of the N amino acids with count vector n⁰ have equal probability.

After the copy operation, we remove amino acids from components of x, until we get exactly the amino acids needed to form σ. This results in a new state (i.e. new amino acid string in the bath) of length N−k. The distribution over the possible post-copy states of the bath—which is all that matters for our calculation—is

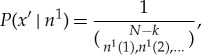A 3

where in vector notation, n¹=n⁰−ν. (Note the precise amino acids that were removed from x to form x′ are irrelevant, since our state space cannot distinguish two amino acids of the same type that could have been removed from x to form the copy of σ.)

So the drop in entropy in the copy process is

A 4

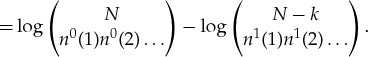A 5

Using Stirling’s formula to lowest order, we can approximate this drop in entropy as

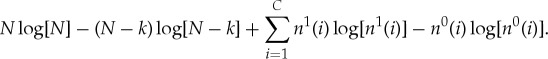A 6

If we take N≫k, then we can approximate the first two terms by expanding to lowest order in k/N, where we obtain

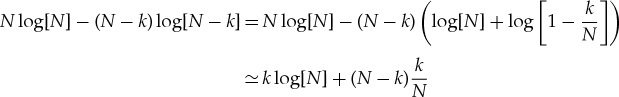A 7

A 8

If we also take each n⁰(i)≫ν(i), the remaining terms can be similarly approximated as

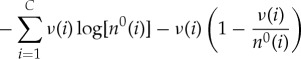A 9

and the total entropy change can be approximated as

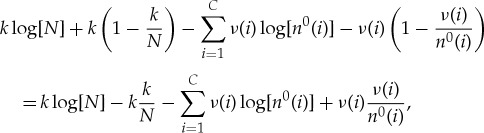A 10

where we have used the fact that .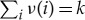

In the limit where the bath becomes large, i.e. 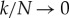, 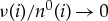for all i. This gives our final answer that the total entropy is approximately

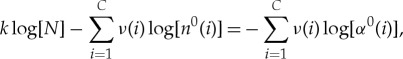A 11

where

A 12

is the fraction of amino acids of type i that are actually in the pre-copy bath. Equation (A 11) recovers the result in the main text, if we take ν and α⁰ to be uniform. In this case ν(i)=k/C and n⁰(i)=N/C, and α⁰(i)=1/C implying that equation (A 11) reduces simply to 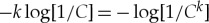which, noting that k=l_p, agrees exactly with the simplifications following equation (4.1).

Note that this entire analysis was conditioned on the specified n⁰. So strictly speaking, we need to average this result over all possible n⁰(i) (and therefore over all possible α⁰(i)) to get the expected drop in entropy. However, for N large enough, by the asymptotic equipartition property [114], we can simply fix α⁰(i)=p(i) for all i. Since (A 11) only depends on ν (which is fixed by σ and α⁰), this means that we can ignore the averaging step, for large enough N.

(d) Alternative accounting of free energy change

In any analysis of the thermodynamic efficiency of a computer, we need to specify what exactly the computer is, i.e. we need to choose both what physical processes we are including as part of our ‘computer’, and what events signal that the computer is in its initial and final states. There is nothing sacrosanct about the choice we have made here. In general, making different choices will both change the amount of work done by the cell, and the theoretical minimum that could be achieved with a thermodynamically reversible process. Interestingly, often the theoretical minimum of amount of required work will not change if we change our precise choice of ‘what the computer is’, even when the actual amount of work expended by the cell grows when we make such a change in our analysis.

As an example, as an alternative to the calculation we performed here, we could have considered the entire composite map comprising translation and then transcription, i.e. the map taking {DNA, bath of nucleotides to make RNAs, bath of amino acids}{DNA, bath of nucleotides to make RNAs, smaller bath of amino acids, a protein}. There is some actual amount of thermodynamic work used to run this composite map in actual cells. To calculate the minimal possible work, we can decompose the composite map into any sequence of thermodynamically reversible maps that achieves the same thing. So we can start with a (thermodynamically reversible) map (1) taking {a sequence of nucleotides in a DNA string plus a bath of nucleotides}{that same DNA string, plus a specific sequence of nucleotides in an mRNA that is a copy of the DNA string, plus the remaining nucleotides in the bath}. We can suppose that after this map (1), there is a (many-to-one) thermodynamically reversible map (2) taking the codons in the mRNA to a (fictional) sequence of amino acids, formed from the amino acid bath. After this there is a map (3) copying that sequence of amino acids to produce our protein. Our analysis above considers the minimal work needed to achieve map (3).

At this point we actually have four copies of the information giving the protein; the DNA segment, the mRNA, the ‘fictional sequence of amino acids’ and the actual protein. Next, the ‘fictional sequence of amino acids’ is broken back down into its constituent amino acids (leaving us with the DNA, mRNA and protein, along with the baths) in a thermodynamically reversible map (2′) that recovers the thermodynamic cost of map (2). After that the mRNA is broken down into its constituent nucleotides in a map (1′) that (in an idealized process) recovers the thermodynamic cost of map (1). So all we are left with is the cost of map (3)—which is what we calculate above.

Data accessibility

All the data used in this paper can be found as compilations in [20,25,28,29], where [20,25] provide online data files as supplementary information. Other key values, which are either directly quoted or used for the calculations within this article, can be found in [2,9,13,27,30–33,91–95,100,106–111] as indicated in the text.

Authors' contributions

C.P.K. conceived of and designed the study, performed the mathematical analyses, calculated values, compiled biological data and values, and drafted the manuscript. D.W. conceived of and designed the study, performed the mathematical analyses and drafted the manuscript. Z.C. contributed initial calculations and discussions of translational trade-offs. J.P.-M. contributed analyses and helped draft the manuscript. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This paper was made possible through the support of grant no. TWCF0079/AB47 from the Templeton World Charity Foundation, grant no. FQXi-RHl3-1349 from the FQXi Foundation, and grant no. CHE-1648973 from the U.S. National Science Foundation. C.P.K. acknowledges the support of the Omidyar Fellowship at the Santa Fe Institute.

Disclaimer

The opinions expressed in this paper are those of the authors and do not necessarily reflect the view of Templeton World Charity Foundation.