Conceptualizing the origin of life in terms of evolution

Abstract

In this opinion piece, we discuss how to place evolution in the context of origin-of-life research. Our discussion starts with a popular definition: ‘life is a self-sustained chemical system capable of undergoing Darwinian evolution’. According to this definition, the origin of life is the same as the origin of evolution: evolution is the ‘end’ of the origin of life. This perspective, however, has a limitation, in that the ability of evolution in and of itself is insufficient to explain the origin of life as we know it, as indicated by Spiegelman’s and Lincoln and Joyce’s experiments. This limitation provokes a crucial question: What conditions are required for replicating systems to evolve into life? From this perspective, the origin of life includes the emergence of life through evolution: evolution is a ‘means’ of the origin of life. After reviewing Eigen’s pioneering work on this question, we mention our ongoing work suggesting that a key condition might be conflicting multi-level evolution. Taken together, there are thus two questions regarding the origin of life: how evolution gets started, and how evolution produces life. Evolution is, therefore, at the centre of the origin of life, where the two lines of enquiry must meet.

This article is part of the themed issue ‘Reconceptualizing the origins of life’.

1. Introduction

How does life originate (or did originate)? To answer this question requires answering another question: What do we mean by life? Although it would be pointless to insist on the ultimate definition of life, it would be equally futile to study the origin of life without any idea about what life is. Thus, understanding the origin of life entails attempts to conceptualize life.

Different ways of conceiving life imply different ways of answering the origin-of-life question. The aim of this opinion piece is to conceptualize the origin of life in terms of evolution. Accordingly, we consider two common conceptions of life that not only set different agendas for research on the origin of life, but also provide distinct perspectives on what evolution is for the origin of life. Specifically, we first consider the idea that life is that which evolves [1]—an intensional definition of life. Second, we consider the idea that life is bacteria, animals, plants, etc.—the extensional definition of life. To explore what questions these conceptions imply in terms of the origin of life, we briefly review the classical studies of Spiegelman, Eigen and Maynard Smith, and put them in a respective context. Then, we also touch on a few recent theoretical and experimental studies building on these fundamental forerunners in order to indicate connections between the above discussion and ongoing efforts to synthesize protocells. Finally, by combining these perspectives, we propose a way to conceptualize the origin of life with evolution at the centre.

Since our focus is on evolution, which implies replication, we shall not discuss the other major conceptions of life, such as autopoiesis [2], chemoton [3] and garbage-bag world [4], which put more emphasis on metabolism, except for noting that these conceptions and our discussion below both converge on the importance of spatial structuring for life.

2. Evolution as the ‘end’ of the origin of life

An often-quoted definition of life reads: ‘life is a self-sustained chemical system capable of undergoing Darwinian evolution’ [1]. Whether or not this definition is valid is less important than the question it raises about the origin of life. According to this definition, the origin of life is basically the same as the origin of evolution [5]—hence, evolution is the ‘end’ of the origin of life. Thus, the crucial question is how evolution gets started (or got started). Indeed, Orgel writes, ‘it may be claimed, without too much exaggeration, that the problem of the origin of life is the problem of the origin of the RNA world, and that everything that followed is in the domain of natural selection’ (emphasis added) [6].

(a). Spiegelman’s experiments

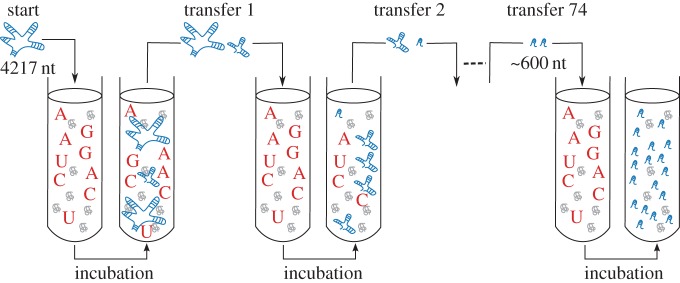
If life is conceived as such, it is natural to search for the simplest possible system capable of undergoing Darwinian evolution. This challenge was taken up by Spiegelman about 50 years ago [7] (reviewed in [8]). He thought RNA molecules were a good candidate because they are capable of instructing their own replication. The important question, however, was whether RNA molecules could display any selectable phenotypes without translation into proteins, the molecules ordinarily considered responsible for phenotypes. To address this issue, Spiegelman et al. inoculated the genomic RNA of Qβ bacteriophage into a reaction medium containing mononucleotides and replicases [7]. After incubation, an aliquot was transferred to a fresh medium, and such transfer was repeated many times (figure 1). The result was the first-ever in vitro evolution performed by humans (‘to play God’ as Spiegelman is said to have put it [10]). RNA molecules evolved 15-fold faster replication, the acceleration largely achieved by the drastic shortening of genome sizes (approx. 85% shorter than the original). Consequently, the molecules lost information required to infect bacteria. Spiegelman et al. also tried exposing RNA molecules to various hazards, such as nutrient limitation and inhibitory analogues, and successfully obtained variants showing improved replication under those conditions, demonstrating that RNA molecules can evolve specific adaptations to different environments [8].

Figure 1.

Schematic of Spiegelman’s experiment. Test tubes contain Qβ replicases (grey globules) and activated mononucleotides (red letters). RNA molecules (blue ladders, branched or non-branched) are inoculated at the start of an experiment and serially transferred. RNA molecules evolve faster replication and shorter lengths. (Adapted from Eigen et al. [9]. The original figure, however, depicts RNA molecules evolving longer lengths in opposition to what actually happened in Spiegelman’s experiment.) (Online version in colour.)

Spiegelman’s experiments have provided two important insights. First and foremost, ‘naked’ RNA molecules can evolve, provided their replication is sustained by the environment they are in (note that this condition applies to many organisms, e.g. humans would not last long without any living microbes). Second, however, evolution does not necessarily increase the amount of information contained in the molecules, but can actually decrease it. It is hardly conceivable that continuing Spiegelman’s experiment eventually produces a system as complex as the simplest life we know. Therefore, the capability of undergoing evolution in and of itself falls short of explaining the origin of life as we know it.

The limitation of regarding evolution as the end of the origin of life is reinforced by the work of Lincoln & Joyce [11]. Lincoln and Joyce have artificially synthesized ‘a self-sustained chemical system capable of undergoing Darwinian evolution’. Their system is considerably simpler than that of Spiegelman, in that it does not contain any externally supplied enzymes. However, in their system, only 12 bp are subject to evolution, so that the total number of possible genotypes is bounded above by 4¹²∼10⁷. In fact, the maximum amount of information that can accumulate (i.e. 24 bits) is smaller than that required to get evolution started (namely, 84 bits) [12]. Whether or not their system should be called life is only a matter of definition.

3. Evolution as the ‘means’ of the origin of life

The above discussion ends in an alternative conception of life: life is bacteria, archaea, plants, animals and so forth, all of which possess genes, enzymes, membranes and so forth (i.e. the extensional definition of life). According to this definition, the origin of life is not the same as the origin of evolution, but includes the emergence of life through evolution. In this sense, evolution is a ‘means’ of the origin of life.

(a). Eigen’s theory

With life conceived as such, it is compelling to ask what sort of replicating system has a potential to evolve into life, a field of enquiry pioneered by Eigen [13]. Stimulated by Spiegelman’s experiments, Eigen constructed a model of replicating sequences as follows:

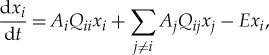3.1

where x_i is the concentration of sequence i in a reaction vessel; A_i is the replication rate (the complementarity of replication is ignored); Q_ij is the probability that the replication of sequence j results in the production of sequence i, thus Q_ii is the probability of no mutation; and E is the rate of outflow keeping the total concentration constant (defined as the average replication rate). This outflow imposes natural selection by decreasing sequences produced at below-average rates.

Using the above model, Eigen discovered that there is an upper limit to the amount of information that can be stably maintained through evolution in a population of replicating sequences [13] (reviewed, for example, in [14–16]). This limit, often called the error threshold or information threshold, is expressed by the following inequality:

3.2

where ν is the length of a sequence, q is the probability of error-free replication per digit (i.e. q^ν≡Q_ii) and σ indicates the selective advantage of the sequence carrying information (see below for the definition). The important point is that σ appears in a logarithmic term—a surprising result because it means that natural selection does not have much impact! Therefore, ν(1−q) is basically bounded above by ∼1. If ν(1−q) is greater than the threshold given by equation (3.2), the sequence carrying information practically goes extinct owing to replication errors, even if it has a selective advantage. More precisely, the concentration of this sequence becomes not much different from that expected from random synthesis; for example, if ν=100, the probability of producing any RNA sequence by chance is 1/4¹⁰⁰≈10⁻⁶⁰, which is practically zero. The bottom line is that the amount of information that can be maintained by evolution (ν) depends heavily on mutation rate (1−q), but not much on natural selection (σ)—a conclusion casting doubt on Orgel’s statement quoted above. (σ is defined as the replication rate of the sequence carrying information divided by the average replication rate of all the other sequences.)

Now suppose that replication involves no enzymes—more precisely, base-pair recognition is a thermodynamically equilibrated process—as is likely to have been the case under prebiotic conditions. Under such conditions, the value of q cannot be much greater than 0.99, given the free energy differences between the correct and mismatched base pairs [13]. Therefore, ν cannot be much greater than 100 according to equation (3.2). The amount of information exceeding this value cannot evolve owing to replication errors. To increase this amount, that is, to give replicating sequences a possibility of evolving into life as we know it, q must be somehow increased.

Eigen thought that increasing the value of q would require specific enzymes, which in turn would require translation [17] (note that his study preceded the discovery of ribozymes). Translation, however, would require much more information than possible with ν<100—hence, the catch-22 of the origin of life: ‘No large genome without enzymes, and no enzymes without a large genome’ [18] (also known as Eigen’s paradox [14]).

Increasing q most likely requires some specific catalysts. In order for such catalysts to be produced continuously, the information about the catalysts must be contained in replicating sequences. The sequences themselves may act as catalysts like ribozymes, or they may be somehow translated into enzymes as presumed by Eigen. In either case, the concentration of catalysts is expected to be approximately proportional to that of sequences if the production of catalysts is in quasi-equilibrium [13]. If sequence j (or its translation product) catalyses the replication of sequence i, A_i is proportional to x_j, assuming that catalysts are abundant (otherwise, Michaelis–Menten kinetics can be employed). By such an argument, Eigen constructed an alternative model of replicating sequences [13,19],

3.3

where F_i is a phenomenological rate constant. For simplicity, mutation is ignored, a simplification that turns out to involve a serious oversight as described in the next section.

Using the above model, Eigen and Schuster discovered that multiple distinct sequences can stably coexist (i.e. can survive without out-competing each other), even if they are not coupled via mutations (i.e. not similar in their sequences), provided they form a specific network of mutual catalysis called a ‘hypercycle’ (figure 2) [19]. Eigen and Schuster suggested that the hypercycle overcomes the limitation imposed by erroneous replication (equation (3.2)) because, even if each member of a hypercycle can contain only a limited amount of information (e.g. ν_i<100), the hypercycle as a whole can contain much more () [19]. Increased information capacity would raise the possibility of increasing q, which in turn would further increase the information capacity. Eigen and Schuster thus proposed that the hypercycle has the potential to evolve into life as we know it [19].

Figure 2.

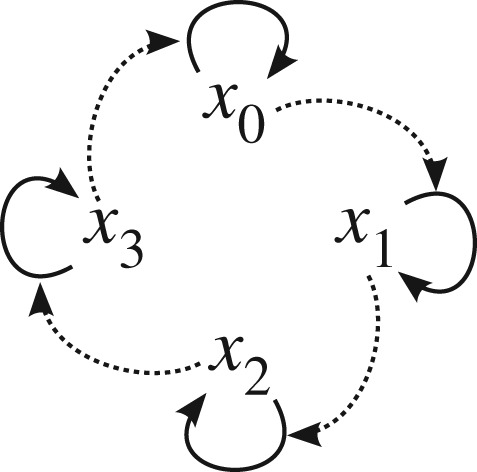
Schematic of a four-member hypercycle. x_i denotes sequence i. Sequence i (or its translation product) catalyses the replication of sequence i+1 (mod n), where ‘mod n’ denotes taking the remainder after division by n. n is the number of members constituting a hypercycle (n=4 above). The essence of the hypercycle is that a catalytic network forms a closed cycle, with each node being a cycle in itself due to replication, hence hyper-cycle.

(b). The problem of parasites

Eigen and Schuster’s proposal was soon followed by the discovery of a fundamental problem inherent in the hypercycle. Maynard Smith [20] considered how a hypercycle would evolve through mutation and selection. There are two possible kinds of mutations that can improve the replication of a hypercycle (see figure 2 for notation):

• — mutations improving sequence i as a template for replication catalysed by sequence i−1;

• — mutations improving sequence i as a catalyst replicating sequence i+1.

The former increases the replication rate of a mutant. Thus, the mutant can spread through a population. By contrast, the latter increases the replication rate of sequence i+1, but not of a mutant itself. Thus, the mutant is not selected (i.e. selectively neutral). To sum up: selection favours better templates, but is indifferent to better catalysts [20]. Therefore, if a mutant appears that serves as a better template, but provides no catalysis, it will out-compete the wild-type providing catalysis and thereby drive the entire hypercycle to extinction. That is, the hypercycle is unstable against the invasion of ‘parasites’ (see also [21,22]).

The situation is actually even worse: if one takes into account the fact that replication consumes a finite amount of time, it can be shown that sequences providing catalysis are at a selective disadvantage rather than being selectively neutral [23]. Thus, selection favours better templates, but acts against better catalysts.

The pioneering work of Eigen and Schuster, combined with the fundamental issue raised by Maynard Smith, has set a specific agenda for research on the origin of life: assume a system of replicating molecules that compete and interact with each other, and investigate what conditions are required for the system to have a potential to evolve into life as we know it. It is not the purpose of this opinion piece to review the studies done since the above pioneering work, for which the reader is referred to the reviews [15,16,24–27]. Here, we only touch on our own recent work in order to connect the above discussion to ongoing experimental work on synthetic protocells.

(c). Multi-level evolution

One way to alleviate the problem of parasites is to assume that replicating molecules are compartmentalized by vesicles (protocells) whose growth and division are coupled to the replication of internal molecules [28–30] (another way is to consider spatial self-organization [31–35]). Recently, we investigated a theoretical model incorporating a dynamic feedback between the evolution of protocells and that of replicating molecules within protocells [36]. The model assumes a population of protocells, each containing a population of replicating catalytic molecules (namely, a hypercycle with n=1). This hierarchical organization causes evolution to operate at two levels with conflicting tendencies: protocells tend to evolve towards maximizing the catalytic activity of internal molecules in order to maximize their growth rates (cellular-level evolution, for short), whereas molecules tend to evolve towards minimizing their catalytic activity in order to maximize their relative chance of replication within protocells, i.e. to evolve into parasites (molecular-level evolution, for short).

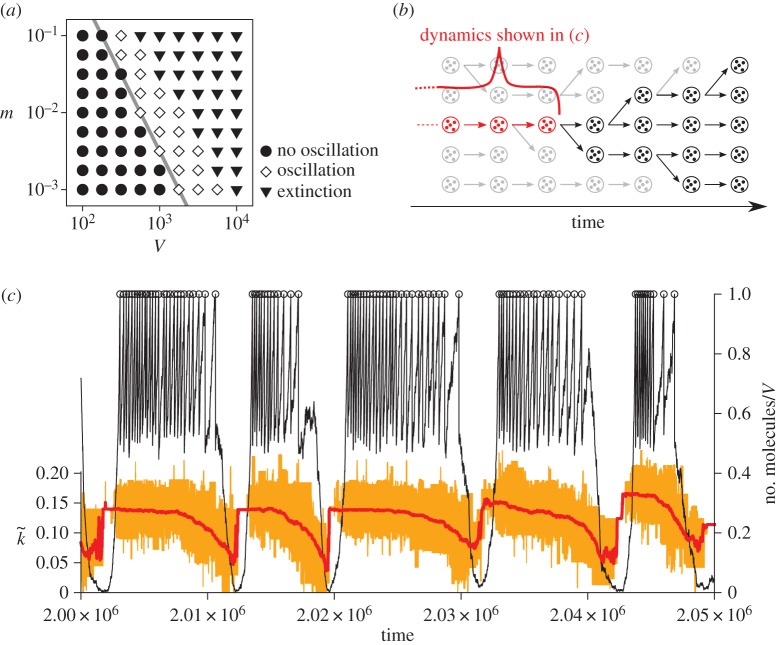
Using the above model, we computed a condition required for the survival of protocells in terms of the mutation rate per molecule per replication m and the number of molecules per protocell V (more precisely, a protocell divides when the number of its internal molecules exceeds V). The result indicates that m and V must be sufficiently small for protocells to survive as depicted in figure 3a. This condition bears some similarity to the error threshold described by equation (3.2), in that m (mutation rate per molecule) and V (number of molecules per cell) are analogous to 1−q (mutation rate per digit) and ν (number of digits per molecule), respectively, although the mechanisms by which the two limits arise are different [36] (see also [37]).

Figure 3.

(a) Phase diagram of the protocell model with respect to m (mutation rate) and V (a protocell divides when the number of its internal molecules exceeds V). The boundary between the parameter regions where the oscillation occurs (diamonds) and where it does not occur (filled circle) has approximately the same slope as that of mV ∝1/V (grey line). (Reproduced from Takeuchi et al. [36].) (b) Schematic of ancestor tracking (the method employed to obtain the data plotted in (c). A circle enclosing dots denotes a protocell. Ancestor tracking detects the lineage of the common ancestors of all surviving protocells (red). The dynamics of this lineage along its line of descent is plotted in (c). Extinct lineages are in grey. (c) The oscillatory dynamics of a protocell lineage along its line of descent (see also (b)). The displayed lineage was the common ancestors of a population at time 2.5×10⁶. Colour coding: the number of molecules in a protocell normalized by V (thin black line); cell division (open circle); the average catalytic activity of molecules within a protocell (thick red line); the range of catalytic activities of molecules within a protocell (orange region around ). V =1000, m=0.01. (Reproduced from Takeuchi et al. [36].) (Online version in colour.)

Furthermore, the detailed analysis of the model shows that, when V or m is sufficiently large, the system gets evolutionarily destabilized, and the lineages of protocells start to oscillate ceaselessly between high and low intracellular catalytic activity, i.e. high and low fitness, along their lines of descent (figure 3b,c) [36]. The onset of this oscillation is demarcated by an approximate scaling relationship (figure 3a),

3.4

This relationship permits the following interpretation. The left-hand side (mV) is proportional to the amount of mutational input per protocell and, therefore, to the rate of molecular-level evolution, which tends to turn molecules into parasites. The right-hand side (1/V) is proportional to the amount of variation among protocells in growth rates and, therefore, to the rate of cellular-level evolution, which counters the tendency of molecular-level evolution. The oscillation is triggered when the rate of molecular-level evolution is comparable to that of cellular-level evolution, hence mV ∝1/V (figure 3a, diamonds). When the rate of molecular-level evolution is much higher than that of cellular-level evolution, protocells go extinct (figure 3a, inverted triangles).

The results described above are partially supported by the experiments done by Bansho et al. [38,39]. Bansho et al. inoculated RNA molecules encoding the Qβ replicase in a reaction medium containing a cell-free translation system and activated mononucleotides. In this medium, the inoculated templates are translated into Qβ replicases, which in turn replicate the templates. A reaction mixture was compartmentalized with a water-in-oil emulsion. Varying the average size of compartments (i.e. protocells), Bansho et al. monitored the amplification of the inoculated templates. Their results show that, as the average size of compartments increases, the amplification declines, and the amount of parasitic templates commensurately increases, indicating that protocells become unstable as their size increases [38], in partial agreement with the result shown in figure 3a.

Furthermore, Bansho et al. [39] conducted serial transfer experiments that involved the mixing and reassortment of compartments in every generation (in their experiments, protocells do not maintain genealogical identity, unlike protocells envisaged in the model mentioned above). Their results indicate that the populations of replicase-encoding templates and parasites undergo oscillation. Unlike the typical host–parasite population dynamics, which also exhibits oscillation, the oscillation observed in their experiments occurs only under a compartmentalized condition, and not under a bulk condition. The necessity of compartmentalization suggests that the smallness of the number of RNA molecules per protocell plays an important role for the sustained oscillation. Interestingly, the oscillation displayed by the model of protocells mentioned above also hinges on the smallness of the number of molecules in a protocell [36].

We are currently investigating an extension of the aforementioned theoretical model by incorporating complementary replication. We observe that, when V and m are sufficiently large, the complementary strands of replicating molecules undergo spontaneous symmetry breaking, whereby one strand remains catalytically active and increases its copy number (enzyme-like molecules), whereas the other strand loses catalytic activity and decreases its copy number (genome-like molecules). This symmetry breaking between ‘templates’ and ‘catalysts’ substantially increases the stability of protocells against the evolution of parasites. An interesting aspect of this result is that there is no apparent selection pressure imposed for the symmetry breaking. That is, both molecular- and cellular-level evolution are directed along the single axis, either minimizing or maximizing the catalytic activity of both strands of molecules. Evolution at a single level, therefore, cannot cause the symmetry breaking; nevertheless, evolution at multiple levels can. Therefore, multi-level evolution opens up a new dimension to evolution that goes beyond the simple maximization of replication rates at single levels—a situation contrasting with Spiegelman’s experiments. Thereby, multi-level evolution potentially bridges the gap between the origin of evolution and the evolution of life. The results will be reported in detail elsewhere 40. The potential of multi-level evolution has been observed in different models, where multi-level evolution occurs either as a result of protocell compartmentalization or as a result of spatio-temporal self-organization of replicators [34,41–43]. In particular, multi-level evolution might be responsible for the evolution of the central dogma of molecular biology [41].

4. Conclusion: evolution as the centre of the origin of life

Answering what life is is useful, not for its own sake but for the questions it raises about the origin of life. A diversity of answers helps if it leads to novel approaches to the origin-of-life question(s).

Above, we considered two ways of conceiving life: life is that which evolves; life is bacteria, animals, etc. These two perspectives lead to two distinct questions about the origin of life: how evolution gets started; how evolution produces life as we know it. These two perspectives are complementary, as they lead to the questions both of which must be answered in order to address the origin of life. Combining these perspectives, we can conceptualize the origin of life as the origin of evolution and the evolution of life. Therefore, evolution is at the centre of the origin of life, where the two lines of enquiry must meet.

With the origin of life conceptualized as such, the central question is about the evolvability of a system [44]. The degree of evolvability might be gauged by the types of major evolutionary transitions a system can undergo [15]. Alternatively, it might be gauged by the amount of information that can accumulate subtracted by the amount required to get evolution started [12] or by the time required for the emergence of a system scaled by individuals’ lifetimes [45]. At any rate, what is interesting is that evolvability itself is subject to evolution. Therefore, perhaps, life ‘is what it is not, and it is not what it is’ (Jean-Paul Sartre).

Data accessibility

This article has no supporting data.

Authors' contributions

N.T. drafted the manuscript. All authors read, revised and approved the manuscript.

Competing interests

The authors declare that they have no competing interests.

Funding

N.T. and K.K. are supported by the Dynamic Approaches to the Living Systems from MEXT, Japan. P.H. is supported by the EU FP7 EVOEVO project (ICT-610427). N.T. is supported by JSPS KAKENHI (grant no. JP17K17657).