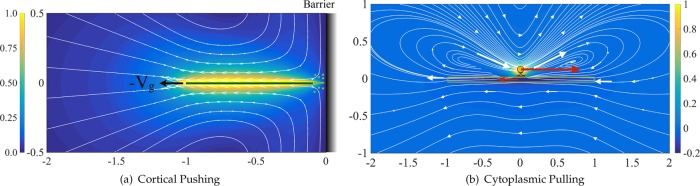
Interactions of astral microtubules (MTs), the pronuclear complex, and the cell cortex with the cytoplasm during pronuclear migration in the first cell division of Caenorhabditis elegans have two key consequences: cytoplasm-filled astral MTs behave as a porous medium, and different mechanisms result in different cytoplasmic flows.
Abstract
The proper positioning of mitotic spindle in the single-cell Caenorhabditis elegans embryo is achieved initially by the migration and rotation of the pronuclear complex (PNC) and its two associated astral microtubules (MTs). Pronuclear migration produces global cytoplasmic flows that couple the mechanics of all MTs, the PNC, and the cell periphery with each other through their hydrodynamic interactions (HIs). We present the first computational study that explicitly accounts for detailed HIs between the cytoskeletal components and demonstrate the key consequences of HIs for the mechanics of pronuclear migration. First, we show that, because of HIs between the MTs, the cytoplasm-filled astral MTs behave like a porous medium, with its permeability decreasing with increasing the number of MTs. We then directly study the dynamics of PNC migration under various force-transduction models, including the pushing or pulling of MTs at the cortex and the pulling of MTs by cytoplasmically bound force generators. Although achieving proper position and orientation on reasonable time scales does not uniquely choose a model, we find that each model produces a different signature in its induced cytoplasmic flow. We suggest that cytoplasmic flows can be used to differentiate between mechanisms.
INTRODUCTION
The cytoskeleton is an ensemble of filaments and molecular motors immersed in the cytoplasmic fluid and is involved in cellular processes such as cell division and migration. The energy required for the rearrangement of cytoskeletal components and organelle transport is typically provided by the force exchange between the cytoskeletal filaments—including microtubules (MTs) and actin fibers—and motor proteins. These interactions are local, that is, they occur over the length scales of the molecular motors, which are significantly smaller than the length of the filaments. Nevertheless, because the structures are embedded in the cytoplasmic fluid, their motion can instantaneously induce flows on the scale of the cell (Shelley, 2016). These nonlocal interactions between the cytoplasmic fluid and the structures within (fibers, nuclei, the cell cortex, etc.) are referred to as hydrodynamic interactions (HIs). Previous theoretical and computational studies of the mechanics of cytoskeleton mostly ignore HIs, often arguing that HIs are screened in the dense network/suspension of filaments (Broedersz and MacKintosh, 2014). The purpose of this work is to revisit this assumption and use detailed simulations to demonstrate the importance of HIs in determining the mechanics of cytoskeletal assemblies.
For this purpose, we developed a versatile and highly efficient numerical platform for studying the dynamics of active and flexible filaments in cellular assemblies (Nazockdast et al., 2017). This method offers a major improvement from our earlier numerical study (Shinar et al., 2011), which did not explicitly model HIs between MTs and their mechanical flexibility. This is, to our knowledge, the first attempt to incorporate many-body HIs between MTs and other intracellular bodies with the cytoplasmic fluid while also accounting for the flexibility of MTs, their dynamic instability, and interactions with motor proteins. By accounting for HIs, we can also compute the large-scale cytoplasmic flows generated by the movements of MTs and other immersed bodies within the cell.
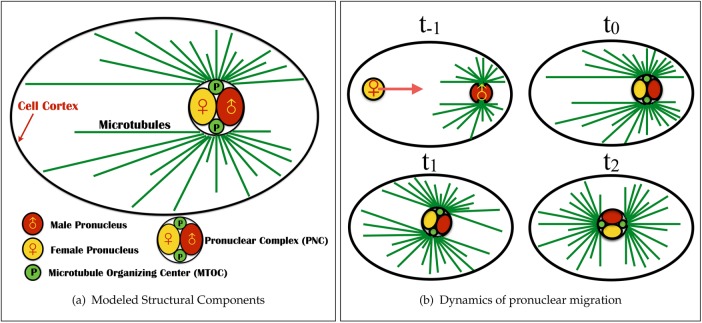
As an example, we study pronuclear migration before the first cell division of the Caenorhabditis elegans embryo (see the schematic in Figure 1). Proper positioning of the mitotic spindle is indispensable to the successful segregation of chromosomes and to the generation of cell diversity in early development (Cowan and Hyman, 2004). Before mitosis and after fertilization, the female pronucleus migrate toward (at t = t−1 in the schematic) and meets the male pronucleus (t = t0) and its associated astral array of MTs at the cell posterior to form the pronuclear complex (PNC). The PNC then moves toward and centers at the cell center (t = t1) and rotates 90° (t = t2) to align the axis between its two associated centrosomes with the cell’s anterior–posterior (AP) axis. The mitotic spindle then forms, and the chromatid pairs are pulled toward the opposite sides of the cell (t > t2).
FIGURE 1:
The modeled structural components and dynamics of pronuclear migration in the single-cell C. elegans embryo. (a) Structural components. The pronuclear complex—here modeled as a rigid sphere—contains the male (red) and female (yellow) pronuclei and is attached to two arrays of MTs (green lines) that polymerize from two centrosomes (green bodies). These structures are immersed in the cellular cytoplasm (light blue) and confined within an ellipsoidal eggshell. (b) The dynamics of pronuclear migration and positioning. At t = t−1, the female pronucleus moves to the posterior to combine with the male pronucleus (t = t0) to form the PNC. This initial period of female nuclear migration is not modeled here (Payne et al., 2003). Between t = t0 and t1, the PNC moves anteriorwise to the center while rotating into “proper position” with the centrosomal axis along the AP axis (t = t2).
HIs arise from several features of PNC migration. Centering and rotating the PNC will push and rotate the cytoplasm, as well as the astral MT arrays. Hence each structure moves against the backdrop of flows produced by the other. Further, because the PNC and its associated MT arrays are on the scale of the cell itself, the confinement of the cell will have a very strong effect on the nature of the cytoplasmic flows. Finally, as we will show, the mechanisms of force transduction that position the PNC can have a qualitative—and in principle experimentally measurable—effect on these flows.
To start, we study the flow induced by the motion of the PNC and its attached astral MTs, irrespective of the force transduction mechanisms. For this, we perform the numerical experiment of pulling the PNC, and its astral MT array, with an externally applied force from the posterior to the center of the cell and aligning it with AP axis with an externally applied torque. By studying the resulting flows, we establish, as a consequence of HIs, that the cytoplasm-filled astral MTs behave like a porous medium surrounding the PNC, where the permeability of the medium decreases with increasing number of MTs. To quantify the effect of HIs, we compare the computed translational and rotational drag on the PNC/MT-array complex with other estimates, including those based on the radius of the aster formed by the MTs (Reinsch and Gönczy, 1998; Kimura and Onami, 2005, 2007), those using a local drag model (Nedelec and Foethke, 2007), and our previous study, which ignored the MT drag altogether (although not PNC drag or the effect of confinement; Shinar et al., 2011). We find in each case that these estimates drastically overestimate or underestimate this drag by a large factor. We also find that confinement has a much stronger effect on translational than on rotational drag, meaning that HIs cannot be lumped into a modified viscosity.
We next establish that the cytoplasmic flows induced by HIs can be used as a diagnostic tool to differentiate between different active mechanisms for pronuclear migration. For this, we instantiate three proposed mechanisms for pronuclear migration in C. elegans. 1) The cortical pulling model, in which MTs impinging on the cortex are pulled on by dynein motors that are attached to the plasma membrane, in particular by association to the protein complex formed by the Gα subunits, GPR-1/2, and LIN-5. An asymmetric distribution of PAR and LET-99 proteins on the cortex in prophase then produces an asymmetric association of dyneins with the protein complex and larger pulling forces on the anterior, and so the pronuclear complex moves in that direction (Grill et al., 2001; Tsou et al., 2002; Labbé et al., 2004; Goulding et al., 2007; Kimura and Onami, 2007; Siller and Doe, 2009; McNally, 2013). 2) The cortical pushing model, in which the growth of astral MTs against the cell periphery induces repulsive forces on MTs that move the complex away from the periphery and thus opens space for further polymerization (Holy et al., 1997; Reinsch and Gönczy, 1998; Tran et al., 2001). Perhaps the strongest evidence in support of the cortical pushing mechanism being involved in the positioning of the mitotic spindle in C. elegans comes from the recent study by Garzon-Coral et al. (2016), in which the magnetic tweezers are used to directly measure the forces involved in the positioning of the mitotic spindle. Using these force measurements in different molecular and geometrical perturbations, Garzon-Coral et al. (2016) argue that the cortical pushing forces maintain the position of the mitotic spindle during metaphase. 3) The cytoplasmic pulling model, in which forces are applied by cargo-carrying dyneins attached on MTs and walking toward the centrosomes (Kimura and Onami, 2007). As a consequence of Newton’s third law, the force applied by dynein on MTs is equal and opposite to the force required to move the cargo through the cytoplasm (Shinar et al., 2011; Longoria and Shubeita, 2013). Because longer MTs carry more dyneins and produce larger pulling forces, the PNC moves in the direction of longer MTs, that is, anteriorwise.
First, we show that all three mechanisms can center and rotate the PNC on a reasonable time scale, and so proper positioning alone cannot choose a unique model. However, we demonstrate that each mechanism produces its own fingerprint in the generated cytoplasmic flows, which can be used to differentiate between them. These flow signatures are generic features of each mechanism and do not depend on the details of its biochemical regulation and molecular pathways. Specifically, we show that the cytoplasmic flow generated in the cortical pulling model is analogous to the flow that arises from pushing a porous object with an external force. In the cortical pushing model, the cytoplasmic flow is the combination of that same driven porous object flow with that produced by MT deformations induced by compressive polymerization forces at the periphery. Finally, we demonstrate that the flow induced by a cytoplasmic pulling model is fundamentally different because it can be interpreted as a porous structure that is moved by internal force generators, with its early time flows in the class of self-propelled puller particles (Saintillan and Shelley, 2013).
Although this study focuses on the pronuclear migration process in the C. elegans embryo, the active mechanisms discussed here, including the polymerization forces and forces from cortically or cytoplasmically bound dyneins, are used in other stages of cell division and in other organisms (Howard, 2001). Thus the generic features of these mechanical models, including their flow signatures, can be useful in identifying or differentiating between force transduction mechanisms in other instances.
RESULTS
A few remarks on the scale of single-microtubule drags and flows
The microscopic size of subcellular structures and the large viscosity of cytoplasm yield inertial forces of the cytoplasm negligible compared with viscous forces. Assuming for simplicity that the response of the cytoplasm is Newtonian, we find the force balance in the fluid phase to be governed by the incompressible Stokes equations (Happel and Brenner, 1965):
|
|
where µ is the viscosity of the cytoplasm and u and p are the fluid velocity and pressure fields, respectively. Owing to the linearity of the Stokes equation, the induced velocity of the PNC is related to the net force on it by an instantaneous drag coefficient, γ, of the structure composed of the PNC and its attached astral MTs.
An important consequence of being in the Stokesian regime is that the drag coefficients of the immersed objects scale with their longest dimensions, making the drag of very thin individual MTs nonetheless comparable to the drag on the PNC. To see this, consider an MT of length L = 10 µm, which is about the diameter of the PNC and on the scale of astral MT lengths, being moved transversely to itself at a constant speed, U. Slender body theory (Tornberg and Shelley, 2004) estimates the drag force on the MT as 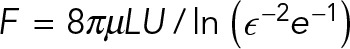 , where ɛ is the aspect ratio of the MT (∼1/400). The classical Stokes formula estimates the drag force on a spherical PNC moving at the same speed and diameter L as
, where ɛ is the aspect ratio of the MT (∼1/400). The classical Stokes formula estimates the drag force on a spherical PNC moving at the same speed and diameter L as 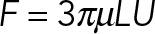 . The ratio of these two drags (MT to PNC) is given by
. The ratio of these two drags (MT to PNC) is given by 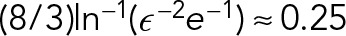 . Hence, despite having a diameter of only 24 nm, a single MT has 25% of the PNC’s drag. This can be seen more clearly by noting that the drag coefficient has only a weak logarithmic dependence,
. Hence, despite having a diameter of only 24 nm, a single MT has 25% of the PNC’s drag. This can be seen more clearly by noting that the drag coefficient has only a weak logarithmic dependence, 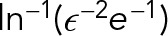 , on the thickness of the MT.
, on the thickness of the MT.
The large drag of a single MT is associated with the large volume of fluid that is transported by the motion of that MT. To visualize this long-range nature of the induced flows, in Figure 2a we show the fluid velocity vectors around a single fiber (thick black line) being pulled in the transverse direction and the variations of the magnitude of the fluid velocity induced by this motion. The generated flow is three dimensional, but for visualization, we present only the results in the plane of the fiber (and of the force). The solid white line is the contour line that corresponds to |u| = 0.20U, where |u| is the magnitude of the induced fluid velocity. We can see that at distances comparable to the length of the MT, the fluid velocity remains significant. In other words, as long as the separation distance between the astral MTs is less than or comparable to their length, as it typically is in cytoskeletal assemblies, the motion of an individual MT is strongly coupled to the other MTs through the cytoplasmic flows.
FIGURE 2:
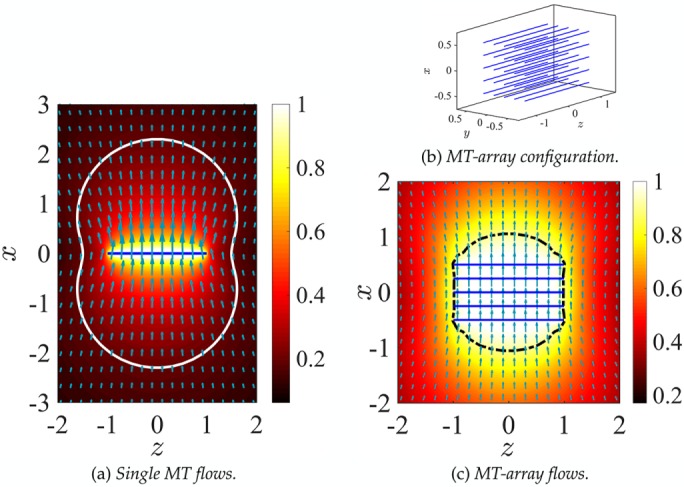
The 3D cytoplasmic flow induced by moving (a) a single MT and (c) a MT array in their transverse direction (x-axis) and with a net velocity U = 1, projected in the plane of the motion of the MT xz-plane. The arrows show the fluid velocity vectors. The size of the arrows and the background color plots correspond to the local magnitude of the fluid velocity. (b) The 3D configuration of the MT array. The solid white line in a corresponds to the contour with velocity magnitude |u| = 0.20U. The dark dashed line in c is the contour with |u|= 0.90U, roughly corresponding to the effective hydrodynamic size of the MT array.
Cytoplasm-filled astral microtubules behave as a porous medium
The mechanical role of astral MTs in all three pronuclear positioning mechanisms is to transfer the force applied either on their plus ends (by cortical pushing or pulling) or along their lengths (by cytoplasmic pulling) to their minus ends anchored in the centrosomes, themselves attached to the PNC. This results in active forces and torques acting on the PNC. Thus the feature of the cytoplasmic flow that is common in all of the cortically based mechanisms—the cortical pushing and cortical pulling mechanisms—is the flow generated by the motion of the PNC and its anchored astral MTs under a given external force and/or torque. To understand the effect of HIs between MTs, we first study the flow induced by a much simpler MT assembly: a 5 × 5 microtubule array that moves with velocity U = 1 along the transverse direction of MTs (x-axis) in free space (Figure 2b). Figure 2c shows the resulting fluid velocity field and the spatial variations of its magnitude in the xz-plane. Again, the fluid flow is three dimensional, and the results are projected into the xz-plane for visualization. The enclosed surface illustrated by a dashed line is the fluid velocity magnitude contour corresponding to |u| = 0.9U. Hence those fluid elements within this surface move roughly with the velocity of the MT array. In other words, HIs between the MTs significantly reduce the convective penetration of the fluid between the MTs and result in an effective hydrodynamic surface that is much larger than the total surface area of all MTs. The microtubule array, therefore, can be seen as a porous volume in which the fluid permeability is decreased as more MTs are included in the array. The HIs also affect the drag on the MT array. As we showed earlier, the drag of a single MT moving transversely is roughly 1/4 of a sphere with the same diameter as the MT length, 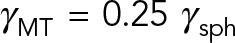 . If HIs are neglected, the total drag on the MT array is the summation of the drag on the individual MTs:
. If HIs are neglected, the total drag on the MT array is the summation of the drag on the individual MTs: 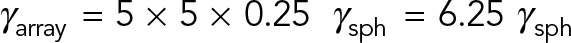 . However, when HIs are accounted for, the computed drag of the MT array is only
. However, when HIs are accounted for, the computed drag of the MT array is only 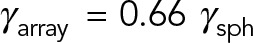 , which is ∼10 times smaller than the local drag prediction. Of interest, increasing the number of MTs in the array to 10 × 10 increases the total drag by <4%, to
, which is ∼10 times smaller than the local drag prediction. Of interest, increasing the number of MTs in the array to 10 × 10 increases the total drag by <4%, to 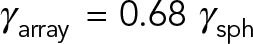 . The computed drag for a 15 × 15 remains almost unchanged from that for a 10 × 10 array, as if the entire volume in the MT array was filled with MTs. Note that if HIs are ignored, the predicted drag for 15 × 15 MT-array is
. The computed drag for a 15 × 15 remains almost unchanged from that for a 10 × 10 array, as if the entire volume in the MT array was filled with MTs. Note that if HIs are ignored, the predicted drag for 15 × 15 MT-array is 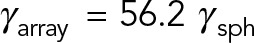 , which is ∼85 times larger than the computed value; see Table 1.
, which is ∼85 times larger than the computed value; see Table 1.
TABLE 1:
Predicted drag on the MT-array, γarray, in the presence and absence of HIs.
| Drag on MT array without HIs | Drag on MT array with HIs | |
|---|---|---|
| 3 × 3 | 2.25 | 0.63 |
| 5 × 5 | 6.25 | 0.66 |
| 10 × 10 | 25 | 0.68 |
| 15 × 15 | 56.25 | 0.68 |
The values are normalized by the drag on a sphere with a diameter equal to the length of the MTs in the array.
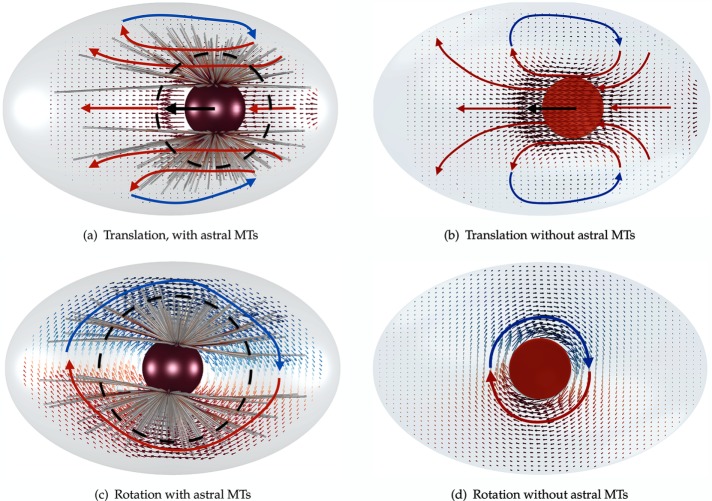
With that in hand, we now explore the flows generated by translation and rotation of the PNC and its associated astral MT arrays, first by pulling it with a given external force from the cell posterior to its center, and then rotating it to proper alignment by applying an external torque. The resulting flows are illustrated in Figure 3 using NMT = 600 astral MTs. Flows in the absence of astral MTs are also shown for comparison. Again, the flow is three dimensional and is projected to the plane of the applied force and AP axis to aid visualization. The simulation parameters are given in Table 2. Two main translational flow features that are apparent in the presence and the absence of MTs are 1) fluid flows in the direction of motion of the PNC and along the AP axis, and 2) reversed flows induced by cellular confinement. Comparing Figure 3a and Figure 3b shows that the presence of the MT array reduces the size of the reversing flow zone. In other words, the presence of MTs increased the effective hydrodynamic radius of the PNC (dashed circle). This increase in hydrodynamic radius is also apparent in rotational motion (Figure 3, c and d) by noting that the magnitude of the bulk velocity decays much more slowly away from the PNC when the astral MTs are present.
FIGURE 3:
The cytoplasmic flows induced by (a) translational and (c) rotational motion of the PNC and its attached astral MTs. (b, d) Translational and rotational flows in the absence of astral MTs.
TABLE 2:
The biophysical parameters used in our simulations.
| Parameter | Value used in simulations |
|---|---|
| MT growth velocity (Vg0) | 0.12 µ·s–1 |
| MT shrinkage velocity (Vs) | 0.288 µ·s–1 |
| MT rate of catastrophe (fcat0) | 0.014 µ·s–1 |
| MT rate of rescue (fres) | 0.014 µ·s–1 |
| MT bending modulus (E) | 10 pN·m2 |
| MT stall force for polymerization reaction (FSP) | 4.4 pN |
| Cytoplasmic dynein’s stall force (Fstall) | 1 pN |
| Viscosity of the cytoplasm (µ) | 1 pa·s |
| Long axis of the cell | 50 µm |
| Short axis of the cell | 30 µm |
| Radius of the pronuclear complex (aPNC) | 5 µm |
These values are taken from Table 1 of Kimura and Onami (2005). The references related to each measurement are given in that article.
We observed the same trend in the earlier example of MT arrays (Figure 2c), which can be described as follows. In pronuclear migration, the astral MTs act as a comoving porous layer that surrounds the PNC and abuts the cell periphery. In particular, the HIs between the MTs reduce the convective penetration of fluid into the porous layer and creates an effectively larger object moving through (or rotating in) the fluid. Note that the relevant dimension of MTs that defines the strength of HIs and the fluid flow into the astral MTs is the length of the MTs and not their thickness. Thus, as we saw in the earlier example of the MT array, a small number of astral MTs can substantially increase the effective volume of the PNC and reduce the permeability of the fluid into the volume filled with astral MTs. See Nazockdast et al. (2017) for a more quantitative study of the cytoplasm-filled astral MTs behaving as a porous medium.
Neglecting hydrodynamic interactions produces wrong estimates of pronuclear migration force magnitudes
To provide a more quantitative analysis of the effect of the astral MTs on the dynamics of pronuclear migration, we compute the translational, 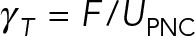 , and rotational,
, and rotational, 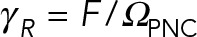 , drag coefficients as a function of the number of MTs. Here UPNC and ΩPNC are the computed translational and angular velocities of the PNC under external force F and torque T, respectively. We consider three different conditions or models. In model 1, we neglect all HIs and calculate drag on MTs using a local slender-body drag formula (Tornberg and Shelley, 2004) and drag on the PNC using Stokes’ drag formula. This approximation closely follows the Brownian dynamics simulation techniques used for modeling cellular assemblies, such as Cytosim (Nedelec and Foethke, 2007). In model 2, we include HIs among the MTs and with the PNC but neglect the backflow generated by the cell periphery through the no-slip boundary condition. That is, in model 2, cytoplasm flows in and out of the cell periphery without impedance. The confining presence of the cell wall is partially maintained by having MTs depolymerize upon reaching it. In model 3, we include all HIs—in particular, those that arise from applying the no-slip boundary condition at the periphery. A comparison between models 2 and 3 model allows us to separate the effect of confinement flows induced by the cell wall from those induced by the aster.
, drag coefficients as a function of the number of MTs. Here UPNC and ΩPNC are the computed translational and angular velocities of the PNC under external force F and torque T, respectively. We consider three different conditions or models. In model 1, we neglect all HIs and calculate drag on MTs using a local slender-body drag formula (Tornberg and Shelley, 2004) and drag on the PNC using Stokes’ drag formula. This approximation closely follows the Brownian dynamics simulation techniques used for modeling cellular assemblies, such as Cytosim (Nedelec and Foethke, 2007). In model 2, we include HIs among the MTs and with the PNC but neglect the backflow generated by the cell periphery through the no-slip boundary condition. That is, in model 2, cytoplasm flows in and out of the cell periphery without impedance. The confining presence of the cell wall is partially maintained by having MTs depolymerize upon reaching it. In model 3, we include all HIs—in particular, those that arise from applying the no-slip boundary condition at the periphery. A comparison between models 2 and 3 model allows us to separate the effect of confinement flows induced by the cell wall from those induced by the aster.
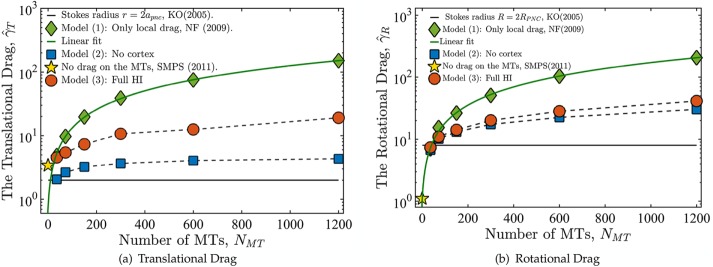
Figure 4 shows the variation of computed translational and rotational drag coefficients with the number of MTs for models 1–3. The values are normalized, respectively, by the drag coefficients of a rigid spherical PNC, 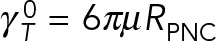 and
and 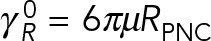 . The black reference lines at
. The black reference lines at 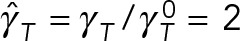 and
and 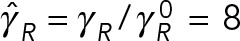 are estimates that assume that PNC drag can be modeled using Stokes’ formula with an effective sphere of radius
are estimates that assume that PNC drag can be modeled using Stokes’ formula with an effective sphere of radius 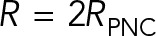 , as used by Kimura and Onami (2005, 2007) in their modeling of pronuclear rotation and centering.
, as used by Kimura and Onami (2005, 2007) in their modeling of pronuclear rotation and centering.
FIGURE 4:
(a) Normalized translational, 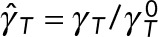 , and rotational,
, and rotational, 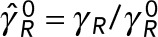 , drag coefficients vs. number of MTs, where
, drag coefficients vs. number of MTs, where  and
and 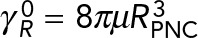 are the translational and rotation drag coefficients, respectively, of a rigid spherical PNC in the absence of MTs. The solid straight lines correspond to the estimates used in Kimura and Onami (2005, 2007); ◊, predictions of model 1, in which only the local drag coefficient of individual MTs is accounted for, as used by Cytosim (Nedelec and Foethke, 2007); □, predictions of model 2, in which HIs with the cell cortex (hydrodynamic confinement) is neglected; *, our previous study, which neglects the drag on the MTs (Shinar et al., 2011); ○, simulation result of model 1, which fully accounts for all HIs. The solid lines going through the prediction of model 2 are linear fits to the data. These equations are
are the translational and rotation drag coefficients, respectively, of a rigid spherical PNC in the absence of MTs. The solid straight lines correspond to the estimates used in Kimura and Onami (2005, 2007); ◊, predictions of model 1, in which only the local drag coefficient of individual MTs is accounted for, as used by Cytosim (Nedelec and Foethke, 2007); □, predictions of model 2, in which HIs with the cell cortex (hydrodynamic confinement) is neglected; *, our previous study, which neglects the drag on the MTs (Shinar et al., 2011); ○, simulation result of model 1, which fully accounts for all HIs. The solid lines going through the prediction of model 2 are linear fits to the data. These equations are 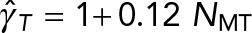 and
and 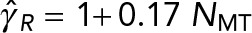 for translational and rotational drag, respectively.
for translational and rotational drag, respectively.
As expected for model 1, having no HIs between MTs, both drag coefficients increase linearly with NMT, showing no saturation. For model 2, 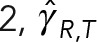 increases monotonically with NMT, with
increases monotonically with NMT, with 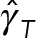 saturating as
saturating as 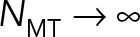 This behavior can be explained through our earlier finding that the astral MTs and cytoplasm form a porous medium. As the number of MTs is increased, the permeability of the porous medium is decreased, while the effective hydrodynamic dimensions of the PNC are increased. In the limit of
This behavior can be explained through our earlier finding that the astral MTs and cytoplasm form a porous medium. As the number of MTs is increased, the permeability of the porous medium is decreased, while the effective hydrodynamic dimensions of the PNC are increased. In the limit of 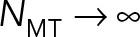 the flow cannot penetrate the porous layer, which fills the cell volume. Because in model 2 the back flows induced by the cell confinement are neglected, in this limit, the drag coefficients asymptote to those of a solid object filling the cell and moving in free space.
the flow cannot penetrate the porous layer, which fills the cell volume. Because in model 2 the back flows induced by the cell confinement are neglected, in this limit, the drag coefficients asymptote to those of a solid object filling the cell and moving in free space.
When confinement-induced back flows are included by accounting for HIs with the periphery (model 3), the drag coefficients again show monotonic increase with NMT. However, for 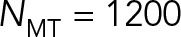 , the
, the 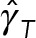 of model 3 is sixfold larger than that for model 2, severalfold smaller than for model 1, and sixfold smaller than for model 3 with
of model 3 is sixfold larger than that for model 2, severalfold smaller than for model 1, and sixfold smaller than for model 3 with 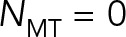 (the red star), which corresponds roughly to our previous modeling (Shinar et al., 2011) of pronuclear migration in which MT drag was not included. Now, as
(the red star), which corresponds roughly to our previous modeling (Shinar et al., 2011) of pronuclear migration in which MT drag was not included. Now, as 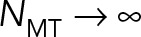 , the effective hydrodynamic dimensions of PNC approaches the size of cell periphery, and we expect
, the effective hydrodynamic dimensions of PNC approaches the size of cell periphery, and we expect 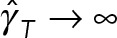 due to the no-slip condition.
due to the no-slip condition.
Rotational dynamics of the PNC
Figure 4b shows that the rotational drag coefficient qualitatively follows the same trend as the translational coefficient, with one key difference. Comparing models 2 and model 3 in Figure 4, a and b, shows that confinement has a much smaller effect on the dynamics of rotation than on translational motion. This is expected because rotation of the PNC and the astral MTs involves sliding an effectively larger PNC tangentially to the cell periphery, whereas translation involves moving the effective surface of the PNC and the astral MTs normal to the cell periphery’s surface, which induces larger resistance to motion (Happel and Brenner, 1965).
We can use the predictions of model 2, shown in Figure 4, a and b, to study a more fundamental question: can the mixture of cytoplasm and astral MTs be modeled as a fluid with a simple effective viscosity? If that is true, then we expect the ratios of the translational drag coefficient to the rotational drag coefficient to be independent of the number of MTs i.e., 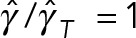 . Our model 2 predictions, however, show that
. Our model 2 predictions, however, show that 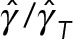 increases from 1 at
increases from 1 at 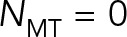 to 7 at
to 7 at 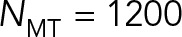 . This simple example demonstrates that HIs cannot be coarse grained through a single effective viscosity because HIs do not have the same dynamical effect on rotational and translational motions. Instead, our simulations show generally that the entire cytoplasm-filled MT array acts as a porous medium whose permeability decreases with increasing number of MTs, thus giving an increased effective size of the PNC in response to an applied force (at least in the absence of force generators within the astral MT array producing active flows). The different scaling of translational and rotational drag coefficients with the effective radius of the PNC (γ T scales with R, whereas γ R scales with R3) causes
. This simple example demonstrates that HIs cannot be coarse grained through a single effective viscosity because HIs do not have the same dynamical effect on rotational and translational motions. Instead, our simulations show generally that the entire cytoplasm-filled MT array acts as a porous medium whose permeability decreases with increasing number of MTs, thus giving an increased effective size of the PNC in response to an applied force (at least in the absence of force generators within the astral MT array producing active flows). The different scaling of translational and rotational drag coefficients with the effective radius of the PNC (γ T scales with R, whereas γ R scales with R3) causes 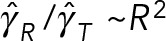 to increase, as the effective radius of the PNC and its astral MTs increases with the number of MTs.
to increase, as the effective radius of the PNC and its astral MTs increases with the number of MTs.
Three mechanisms of pronuclear migration yield proper positioning of the pronuclear complex
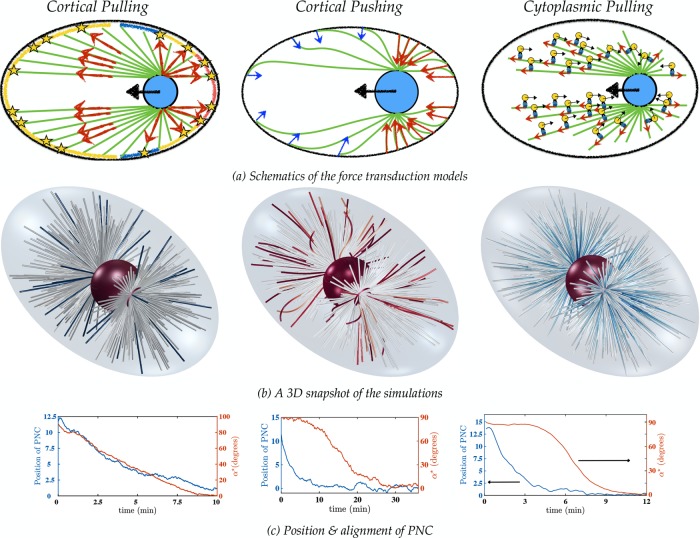
We now investigate the mechanics of pronuclear migration and positioning using three proposed positioning mechanisms in C. elegans embryo; namely the cortical pulling, cortical pushing, and cytoplasmic pulling models. To start, within our framework, we instantiated a cortical pulling model that Kimura and Onami (2007) developed for their study of pronuclear migration. Figure 5a shows a schematic of this model, which was motivated by experimental observations of Tsou et al. (2002). In this model, pulling forces on astral MTs are generated by the asymmetric attachment of astral MTs to cortically bound dyneins, whose activation probability is inhomogeneously distributed along the posterior cortex, with the greatest probability of attachment at the posterior pole and the least to the immediate posterior of the midplane. Attached MTs are pulled upon, and simultaneously depolymerized, at the cortex; see the Supplemental Materials for details. A snapshot of the simulation at long times is shown in Figure 5b, left. It demonstrates that this mechanism leads to centering and rotation to the proper position. In this simulation, PNC translation and rotation are in temporal register, and proper position is achieved on a reasonable time scale (Figure 5c, left). Because the cortically bound force generators in this model put the MTs under an extensional load, MT deformations are small and remain relatively straight (Figure 5b, left). For the parameters used in this simulation (motor attachment distribution and number density, MT attachment and detachment rates, etc.), we find that the PNC robustly finds the proper position. These chosen parameters were physiologically reasonable but also narrowly constrained, as other, seemingly reasonable choices of these parameters can lead to lack of centering. More details are given in the Supplemental Materials; the biophysical parameters corresponding to the figures are given in Table 2.
FIGURE 5:
(a) The force transduction mechanisms. Left, cortical pulling model, in which the blue, yellow and red strips on the cortex correspond to the lowest, average, and highest density, respectively, of the cortical force generators. See the Supplemental Materials for details. Middle, the cortical pushing model. The larger number of MTs polymerizing against the cortex on the posterior side and their shorter lengths (corresponding to larger bending forces) result in larger pushing forces on the posterior pole (compared with the anterior) and pronuclear migration from posterior to the center of the cell. Right, the length-dependent cytoplasmic pulling mechanism, in which cargo-carrying dynein motors apply pulling forces on the astral MTs. Longer MTs have more dyneins attached to them, which result in pronuclear migration toward the longest MT, that is, from posterior to the center of the cell. (b) Long-time 3D snapshots of the simulations in the three mechanisms (Supplemental Movies S1–S3). The fibers are color coded with respect to the local tension; red, blue, and white denote compressional, extensional, and no forces, respectively. In the cortical and cytoplasmic pulling models, the MTs are under extensile forces and thus remain straight; in the cortical pushing simulations, the MTs are buckled due to the compressional forces from their polymerization against the cortex. (c) Variations of the PNC position and angle between the intercentrosomal axis and the AP axis vs. time.
Next we consider a variation of the cortical pushing model. In this model, we constrain the position of the MT plus ends, which reach and polymerize at the cortex to remain fixed (and hinged) at the cortex as long as they are in growing state (see the Supplemental Materials). In an idealized system in which the PNC is pushed by an up–down symmetric set of astral MTs, the intercentrosomal axis would remain orthogonal to the AP axis throughout the centering process (having started that way). However, a combination of dependence of polymerization forces on MT length (shorter MTs are harder to deform, resulting in larger polymerization forces) and the elongated shape of the cell periphery makes this orientation mechanically unstable and susceptible to the fluctuations that MT dynamic instability can provide. Once seeded, this “torque instability” produces a self-reinforcing, rotating torque on the PNC, moving it toward the proper position, which is a mechanically stable equilibrium (see the Supplemental Materials).
As shown in Figure 5c, middle, this model results in proper centering and rotation of the PNC on a reasonable time scale. In addition, Figure 5b, middle, shows that for this particular instantiation of the cortical pushing model, the MTs are substantially buckled near the cortex. We also considered another variation of cortical pushing in which, rather than fixing the plus ends of MTs, pushing forces are applied in the normal direction to the cell boundary (pointing inward) so that MT plus ends cannot penetrate the boundary. MTs are nonetheless allowed to grow or slide freely tangentially. Our simulations show that, although the PNC properly centers in this model, it fails to rotate the PNC to the proper alignment with the AP axis; this variation of the model is discussed in detail in the Supplemental Materials.
Finally, Figure 5a, right, shows a schematic of the cytoplasmic pulling model. This model was initially proposed to explain observations in newly fertilized sand-dollar eggs (Hamaguchi and Hiramoto, 1986). Later, via modeling and experimental study, this was proposed as a mechanism for pronuclear positioning in the C. elegans embryo (Kimura and Onami, 2005; Kimura and Kimura, 2011). This model was studied in our earlier work on pronuclear migration (Shinar et al., 2011), in which minus end–directed cargo-carrying dyneins walk on MTs and thus apply a pulling force on them toward their plus end. Applying proper force balance (Shinar et al., 2011), the cargo exerts an equal and opposite force on the fluid. If dyneins are uniformly distributed along the MTs, as is assumed here, the PNC moves in the direction of the longest MTs, as these contribute the greatest pulling forces; see the Supplemental Materials for details. As shown in Figure 5c, right, this model can yield both centering and rotation on a time-scale comparable to experimental observations (Kimura and Onami, 2005). Similarly to the cortical pulling model, the MTs are under extension, and their deformations are small, which is evident in the long-time three-dimensional (3D) snapshot of the simulation in Figure 5b, right.
Cytoplasmic flows during pronuclear migration
Our simulation results thus far show that all three positioning mechanisms can produce the expected alignment and position of the pronuclear complex within a reasonable time scale and choice of biophysical parameters. We now discuss their induced cytoplasmic flows and the generic features specific to each. Our motivation is that different mechanisms of force transduction will exert different forces on MTs and hence should be associated with generically different cytoplasmic flows. To demonstrate these differences, we start by studying the flows induced by a single MT growing against a barrier and by a single cargo-carrying dynein motor walking along a MT. These are the simplest representations of cortical pushing and cytoplasmic pulling flows, respectively. These flows are shown in Figure 6. The flow induced by a MT being pulled by cortical force generators—the simplest model of the cortical pulling mechanism—is the same as in Figure 6a but in the opposite direction, and thus is not presented here.
FIGURE 6:
(a) Flow induced by MT growing against a barrier and (b) flow induced by a cargo-carrying dynein walking on a MT as simple representations of the cortical pushing and cytoplasmic pulling mechanisms. The induced flows are all three dimensional and are presented only in the plane of the MT and the direction of its motion for visualization. The solid curved lines are the flow streamlines. The arrows tangent to the streamlines are the velocity vectors. The size of the arrows and the background contour plot correspond to the magnitude of fluid velocity. The vectors with only an arrowhead in b correspond to nearly zero fluid velocity, as evident from the contour plot. The maximum and minimum in the color bar in b correspond to the velocity of the cargo and the MT in the x-direction, respectively.
General physical principles underlie the gross cytoplasmic flow structures that we observe for the different models. In both cortically based models, the MTs are pushing or being pulled against a fixed boundary (cell periphery) while an opposite force is applied from the cell boundary or the cortically bound dynein motors to the MTs. In such a case, because the force on the outer boundary does not generate any internal flows, the cytoplasmic flows are associated with the motion of the MT under an external force within the cellular confinement. In the case of the cortical pushing mechanism, because the MT plus end is fixed at the cortex, the polymerization forces push the MT away from the cortex to open space for adding the newly formed microtubule materials. This outward flux creates a flow by dragging cytoplasm from the cell periphery into the cell volume (Figure 6a). In the case of the cortical pulling mechanism, the applied force and the resulting cytoplasmic flows are in the opposite direction.
In the cytoplasmic pulling model, the pulling force applied on the MTs by a dynein motor is balanced by the equal and opposite force applied by that motor’s cargo onto the cytoplasm through which it is being dragged. Unlike the cortical models, in which the applied forces at the cell boundary do not induce internal flows, the force applied by the dynein motors to the cargo generates a flow in the opposite direction of the MT motion. The flow is then a combination of the flow induced by the motion of the MT and the flow induced by the cargo transport. Because equal and opposite forces are applied to the cargo and the MT, the flow roughly corresponds to the flow induced by a force dipole (Happel and Brenner, 1965). Figure 6b shows the 3D velocity streamlines and spatial variations of velocity magnitude induced by a single dynein motor carrying a 0.1-µm spherical cargo along a 2-µm-long microtubule. The results are projected to the plane of motion of the MT. Note that the flow strength in this model decays much faster than the flow induced by growing/shrinking MTs against barriers and becomes negligible at distances less than the length of the MT.
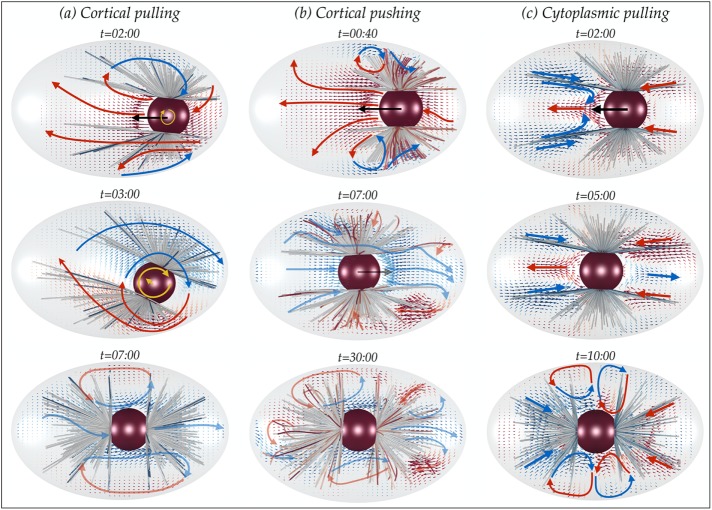
With these simple examples in hand, we now discuss the computed cytoplasmic flows during pronuclear migration in complete instantiations of the three mechanisms. We start with the cortical pulling mechanism. Because the MTs are hardly deformed in this model, the motion of the entire PNC/MT-array complex generates cytoplasmic flows similar to that of a porous body towed through a confined space. Figure 7a, top, shows a snapshot of the cytoplasmic velocity field at early times, which, at this instant, is dominated by translation and bears a striking resemblance to that shown in Figure 3a, where the PNC/MT array is translated by an external force. At an intermediate time, the cytoplasmic flow has become primarily rotational (Figure 7a, middle). In these conditions, the flow begins to resemble that seen in Figure 3c, where the centered PNC/MT array is rotated by an external torque. At late times (e.g., Figure 7a, bottom), the cytoplasmic flows are weak and arise from fluctuations in PNC position due to the stochastic attachment and detachment of MTs from the cortex. As the MTs remain straight under their extensive loading from cortical force generators, the cytoplasmic velocity fields arise almost entirely from the translations and rotations of the PNC/MT array complex.
FIGURE 7:
Snapshots of cytoplasmic flows at different stages of pronuclear migration: the (a) cortical pulling, (b) cortical pushing, and (c) cytoplasmic pulling mechanisms. Numbers denote time in minutes:seconds after the nuclei meeting. The results are projected onto the xy-plane to aid visualization, where the AP axis is the x-axis and the intercentrosomal axis is initially aligned with the y-axis. Note that both the shape of the MTs and the flow are defined in three dimensions. The faint colors of the velocity vectors in the bottom panel of the cortical pulling flows and the middle and bottom panels of the cortical pushing flows represent the “weakness” of the cytoplasmic flows in those instances compared to the flow strength at the initial stages of the PNC migration. In contrast, the flows in the cytoplasmic pulling model remain “strong” throughout the entire migration process.
For the cortical pushing model shown in Figure 7b, the cytoplasmic flow is a combination of the flows generated by the motion of the PNC/MT-array complex (similar to the flow shown in Figure 3a) and flows due to MT deformations near the periphery. After the MTs reach the cortex and continue polymerizing, they are pushed away from the boundaries with the same speed as they grow. Thus the generated flows near the cortex scale with the plus-end polymerization rate and are primarily in the direction opposite the polymerization direction (Figure 6a). (The generated flows near the cortex can be quite involved: the growth of the buckling amplitude, which is orthogonal to the direction of MTs, also contributes to the flow, as does the relaxation of the MTs switching to catastrophe.) For the range of biophysical parameters used in our simulations, see Table 2. The flow induced by MT deformation near the periphery is comparable in magnitude to that induced by the PNC motion for most of the migration process. Figure 7b, middle and bottom, shows that the same flow patterns are also observed near the periphery after completion of PNC centering and rotation.
Finally, we discuss the flows in the cytoplasmic pulling mechanism. Unlike the cortical pushing and pulling models, which use the cell periphery as the mechanical substrate against which to exert forces through MTs, the force substrate is now the cytoplasm in which the cargoes are immersed. Hence the generated flow arises from two sources: 1) the flow induced by the motion of the PNC/MT-array, and 2) the flow generated by the motion of cargoes toward the minus ends of MTs. Figure 7c shows that the cytoplasmic flows thus produced are fundamentally different than those observed in the two previous models. The key flow signature that is present in all stages of migration is that, unlike the cortical pushing and pulling mechanisms, the cytoplasmic flow in the anterior is in the opposite direction of the motion of the PNC and is along the direction of cargo transport toward the centrosomes in the volume occupied by the astral MTs. The strength of the flow in the cytoplasmic pulling model is determined by the total active force applied by the dynein motors, which in our model scales with the total length of the MTs. Consequently the strength of flow throughout and after the migration process does not change significantly. On the other hand, the velocity of the PNC monotonically decreases as it approaches the center of the cell. Hence, as we see in Figure 7c, middle and bottom, after centering, the strength of cytoplasmic flows is much stronger than the small fluctuating velocity of the PNC. This leads us to another key difference between the cytoplasmic pulling and cortically based models: in the cytoplasmic pulling model, the fluid velocity magnitude is much larger than that of velocity fluctuations of the PNC after centering, whereas for the other mechanisms, the fluid velocity is similar in magnitude to that of the PNC velocity fluctuations.
The flows arising from cytoplasmic pulling resemble those generated by “puller” microswimmers (Saintillan and Shelley, 2013) such as Chlamydomonas reinhardtii (Drescher et al., 2010). The reason lies in the ensemble behavior of the PNC/MT array and the immersed dynein motors. As shown in Figure 7a, for any force applied by the attached dynein motors on the MTs, there is an equal and opposite force applied by the cargoes to the cytoplasmic fluid. Thus, whereas the force on the PNC/MT array is not zero, the net force on the PNC/MT array and the cytoplasmic fluid is identically zero. In particular, the motion of each cargo on the MT array generates a force dipole described by a tensor whose symmetric part gives the net stress on the system, which, unlike the net force, is not zero. For straight MTs and a uniform distribution of the motors, the net stress tensor induced by motor activity is
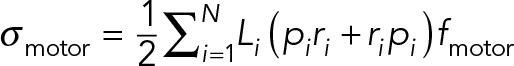 (2) (2)
|
where Li and pi are the length and unit tangent vector of the ith MT, respectively, and ri, taken as orthogonal to pi, gives the relative position of the cargo with respect to its attachment point on the ith MT. The antisymmetric part of the force dipole determines the net torque on the system, which is also zero. Zero net force and torque and a finite active stress are the two hallmarks of active, self-propelled particles (Saintillan and Shelley, 2013). As a result, the flow far from such particles is that generated by the symmetric part of a force dipole. Whereas in our system the size of the “active particle” —the PNC/MT-array—is similar to the scale of its confinement, the flow still closely resembles that generated by a puller particle in an open flow (see Figure 5 of Saintillan and Shelley, 2013).
The cortically based models both generate grossly similar cytoplasmic flows (albeit different MT deformations) because they share the feature that the force is transduced to the PNC by MT pushing/pulling on/from an immobile cell boundary. In these conditions, the net force on the PNC/MT arrays and the cytoplasm is nonzero. The cytoplasmic flows then resemble those generated by a force monopole, or a Stokeslet, within a confinement.
DISCUSSION
The motion of cytoskeletal components and payloads within the cytoplasm can generate global flows and long-range HIs between them. Most previous studies related to the mechanics of cytoskeleton ignore the effect of HIs; see Shinar et al. (2011) for an exception. In this study, we used detailed dynamic simulations that explicitly account for many-body HIs to demonstrate several important consequences of HIs in the mechanics of the pronuclear migration stage of the first cell division in C. elegans embryo. Nevertheless, the findings of this study are quite generic and extendable to other cytoskeletal assemblies.
First, through direct simulation, we showed that the most fundamental effect of HIs in pronuclear migration is that the astral MTs array behaves effectively as a porous medium; see Nazockdast et al. (2017) for a more quantitative study. Increasing the number of astral MTs reduces the permeability of the fluid, resulting in larger hydrodynamic dimensions of the PNC and a larger net force/torque associated with moving the PNC to the proper position/orientation. We showed that previous approximations of the PNC drag coefficient, which either ignore HIs or include them partially, overpredict or underpredict active forces by a large factor. By comparing the translational and rotational motion of the PNC and its astral MTs, we showed that the effect of astral MTs cannot be simply reduced to an effective viscosity. This observation has important consequences that go beyond the pronuclear migration problem. For example, consider measuring the effective viscosity of the cell’s interior using active microrheology, in which a probe is externally driven through the cytoplasm using magnetic forces and/or optical tweezers with a given force or torque (Wirtz, 2009). The measured translational or angular velocity of the probe is then used to compute the effective viscosity. For a spherical probe, the viscosity is computed using µ = F/(6πUa) or µ = F/(6πΩa3) for cases of applying a fixed external force F or torque L, respectively. If the cellular interior acts as a porous medium—because the hydrodynamic effect of the astral MTs cannot be modeled with an effective viscosity—the computed viscosities from these two models (applying a force vs. a torque) may yield viscosities that differ considerably. Instead, if the astral MTs were not attached to the PNC and were freely suspended in the cytoplasm, these two experiments would be expected to give similar results for the viscosity.
We studied the dynamics of PNC/MT-array positioning using simple instantiations of the cortical pulling, cortical pushing, and cytoplasmic pulling mechanisms. Our results show that all three mechanisms can center and rotate the PNC within reasonable times and range of biophysical parameters. Thus proper positioning alone cannot identify the main mechanism of PNC migration. We propose that the structure of cytoplasmic flows may select between the different possible active mechanisms involved in cellular processes such as pronuclear migration. We show, through simulation, that each of these force transduction mechanisms leaves its specific fingerprint in the generated cytoplasmic flows; these features are directly related to how the force is transferred from molecular motors and cell boundaries to the MTs. Specifically, we show that when the active forces are applied from an immobile substrate to the MTs, such as in the cortical pushing and pulling mechanisms, the basic feature of the cytoplasmic flows is that of the flow generated by a point force (Stokeslet) in a confined geometry. In the cytoplasmic pulling mechanism, in which the substrate is mobile (cargo-carrying dynein), the generated flow is the combination of the flow generated by the average motion of the PNC/astral MT and flow induced by cargo transport, which resembles the flows induced by a force dipole.
These aspects of flow signatures are generic features of each active mechanism and do not depend on details such as the value of the shear viscosity of the cytoplasm, the MT bending rigidity, the stall force of the molecular motors, or their force–velocity relationship. Thus they can be used to study the possible contributions of these differing force transduction mechanisms in other stages of cell division and possibly other cytoskeletal structures. We are following up on these ideas by directly measuring the cytoplasmic flows by particle-tracking methods.
Supplementary Material
Acknowledgments
We thank Sebastian Füerthauer, Hassan Masoud, Tong Gao, Michael O’Neal, and Carlos Garzon-Coral for helpful discussions. We acknowledge support from National Institutes of Health Grant 1R01GM104976-01. E.N. and M.S. acknowledge support from National Institutes of Health Grant 1R01GM104976-01 and National Science Foundation Grants DMS 1463962 and DMS-1620331. A.R. acknowledges the support of the National Science Foundation through Grant DMS-1320621.
Abbreviations used:
- AP
anterior–posterior
- HIs
hydrodynamic interactions
- MTs
microtubules
- PNC
pronuclear complex.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E16-02-0108) on March 22, 2017.
REFERENCES
- Broedersz CP, Mackintosh FC. Modeling semiflexible polymer networks. Rev Mod Phys. 2014;86:995. [Google Scholar]
- Cowan CR, Hyman AA. Asymmetric cell division in C. elegans: cortical polarity and spindle positioning. Annu Rev Cell Dev Biol. 2004;20:427–453. doi: 10.1146/annurev.cellbio.19.111301.113823. [DOI] [PubMed] [Google Scholar]
- Drescher K, Goldstein RE, Michel N, Polin M, Tuval I. Direct measurement of the flow field around swimming microorganisms. Phys Rev Lett. 2010;105:168101. doi: 10.1103/PhysRevLett.105.168101. [DOI] [PubMed] [Google Scholar]
- Garzon-Coral C, Fantana HA, Howard J. A force-generating machinery maintains the spindle at the cell center during mitosis. Science. 2016;352:1124–1127. doi: 10.1126/science.aad9745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goulding MB, Canman JC, Senning EN, Marcus AH, Bowerman B. Control of nuclear centration in the C. elegans zygote by receptor-independent Gα; signaling and myosin II. J Cell Biol. 2007;178:1177–1191. doi: 10.1083/jcb.200703159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grill SW, Gönczy P, Stelzer EH, Hyman AA. Polarity controls forces governing asymmetric spindle positioning in the Caenorhabditis elegans embryo. Nature. 2001;409:630–633. doi: 10.1038/35054572. [DOI] [PubMed] [Google Scholar]
- Hamaguchi MS, Hiramoto Y. Analysis of the role of astral rays in pronuclear migration in sand dollar eggs by the colcemid-uv method. Dev Growth Differ. 1986;28:143–156. doi: 10.1111/j.1440-169X.1986.00143.x. [DOI] [PubMed] [Google Scholar]
- Happel J, Brenner H. Low Reynolds Number Hydrodynamics. Leiden, Netherlands: Martinus Nijhoff; 1965. [Google Scholar]
- Holy TE, Dogterom M, Yurke B, Leibler S. Assembly and positioning of micro- tubule asters in microfabricated chambers. Proc Natl Acad Sci USA. 1997;94:6228–6231. doi: 10.1073/pnas.94.12.6228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J. Mechanics of Motor Proteins and the Cytoskeleton. Sunderland, MA: Sinauer; 2001. [Google Scholar]
- Kimura A, Onami S. Computer simulations and image processing reveal length-dependent pulling force as the primary mechanism for C. elegans male pronuclear migration. Dev Cell. 2005;8:765–775. doi: 10.1016/j.devcel.2005.03.007. [DOI] [PubMed] [Google Scholar]
- Kimura A, Onami S. Local cortical pulling-force repression switches centrosomal centration and posterior displacement in C. elegans. J Cell Biol. 2007;179:1347–1354. doi: 10.1083/jcb.200706005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura K, Kimura A. Intracellular organelles mediate cytoplasmic pulling force for centrosome centration in the Caenorhabditis elegans early embryo. Proc Natl Acad Sci USA. 2011;108:137–142. doi: 10.1073/pnas.1013275108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labbé JC, Mccarthy EK, Goldstein B. The forces that position a mitotic spindle asymmetrically are tethered until after the time of spindle assembly. J Cell Biol. 2004;167:245–256. doi: 10.1083/jcb.200406008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longoria RA, Shubeita GT. Cargo transport by cytoplasmic dynein can center embryonic centrosomes. PLoS One. 2013;8:e67710. doi: 10.1371/journal.pone.0067710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNally FJ. Mechanisms of spindle positioning. J Cell Biol. 2013;200:131–140. doi: 10.1083/jcb.201210007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nazockdast E, Rahimian A, Zorin D, Shelley MJ. A fast platform for simulating semi-flexible fiber suspensions applied to cell mechanics. J Comput Phys. 2017;329:173–209. [Google Scholar]
- Nedelec F, Foethke D. Collective Langevin dynamics of flexible cytoskeletal fibers. New J Phys. 2007;9:0–24. [Google Scholar]
- Payne C, Rawe V, Ramalho-Santos J, Simerly C, Schatten G. Preferentially localized dynein and perinuclear dynactin associate with nuclear pore complex proteins to mediate genomic union during mammalian fertilization. J Cell Sci. 2003;116:4727–4738. doi: 10.1242/jcs.00784. [DOI] [PubMed] [Google Scholar]
- Reinsch S, Gönczy P. Mechanisms of nuclear positioning. J Cell Sci. 1998;111:2283–2295. doi: 10.1242/jcs.111.16.2283. [DOI] [PubMed] [Google Scholar]
- Saintillan D, Shelley M. Active suspensions and their nonlinear models. CR Phys. 2013;14:497–517. [Google Scholar]
- Shelley MJ. The dynamics of microtubule/motor-protein assemblies in biology and physics. Annu Rev Fluid Mech. 2016;48:487–506. [Google Scholar]
- Shinar T, Mana M, Piano F, Shelley MJ. A model of cytoplasmically driven microtubule-based motion in the single-celled Caenorhabditis elegans embryo. Proc Natl Acad Sci USA. 2011;108:10508–10513. doi: 10.1073/pnas.1017369108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siller KH, Doe CQ. Spindle orientation during asymmetric cell division. Nat Cell Biol. 2009;11:365–374. doi: 10.1038/ncb0409-365. [DOI] [PubMed] [Google Scholar]
- Tornberg A-K, Shelley MJ. Simulating the dynamics and interactions of flexible fibers in Stokes flows. J Comput Phys. 2004;196:8–40. [Google Scholar]
- Tran PT, Marsh L, Doye V, Inoue S, Chang F. A mechanism for nuclear positioning in fission yeast based on microtubule pushing. J Cell Biol. 2001;153:397–412. doi: 10.1083/jcb.153.2.397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsou M-FB, Hayashi A, Debella LR, Mcgrath G, Rose LS. LET-99 determines spindle position and is asymmetrically enriched in response to PAR polarity cues in C. elegans embryos. Development. 2002;129:4469–4481. doi: 10.1242/dev.129.19.4469. [DOI] [PubMed] [Google Scholar]
- Wirtz D. Particle-tracking microrheology of living cells: principles and applications. Annu Rev Biophys. 2009;38:301–326. doi: 10.1146/annurev.biophys.050708.133724. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.