An essential feature of healthy axons is the development of a uniform microtubule (MT) polarity pattern. Computational simulations support a model in which MTs are polarity sorted in the axon by dynein-based gliding, occasionally opposed by plus-directed motors. We predict that cross-linking proteins limit the mobility of longer MTs.
Abstract
We present a computational model to test a “polarity sorting” mechanism for microtubule (MT) organization in developing axons. We simulate the motor-based axonal transport of short MTs to test the hypothesis that immobilized cytoplasmic dynein motors transport short MTs with their plus ends leading, so “mal-oriented” MTs with minus-end-out are transported toward the cell body while “correctly” oriented MTs are transported in the anterograde direction away from the soma. We find that dynein-based transport of short MTs can explain the predominately plus-end-out polarity pattern of axonal MTs but that transient attachments of plus-end-directed motor proteins and nonmotile cross-linker proteins are needed to explain the frequent pauses and occasional reversals observed in live-cell imaging of MT transport. Static cross-linkers increase the likelihood of a stalled “tug-of-war” between retrograde and anterograde forces on the MT, providing an explanation for the frequent pauses of short MTs and the immobility of longer MTs. We predict that inhibition of the proposed static cross-linker will produce disordered transport of short MTs and increased mobility of longer MTs. We also predict that acute inhibition of cytoplasmic dynein will disrupt the polarity sorting of MTs by increasing the likelihood of “incorrect” sorting of MTs by plus-end-directed motors.
INTRODUCTION
Microtubules (MTs) align in axons and dendrites to create long parallel bundles with distinct polarity patterns. While dendrites have a mixed polarity pattern, axons have a nearly uniform plus-end-out organization of the MT array (Heidemann et al., 1981; Baas et al., 1988; Baas and Lin, 2011) (Figure 1A). The establishment and maintenance of a uniform polarity pattern in axons are essential for organized trafficking of organelles. Corruption of the MT polarity pattern can lead to loss of axonal and dendritic identity and is associated with degeneration of the neuron in response to injury and disease (Chevalier-Larsen and Holzbauer, 2006). Therefore, it is of critical importance to develop an understanding of the detailed molecular mechanisms involved in the development and maintenance of MT polarity patterns in the axon.
FIGURE 1:
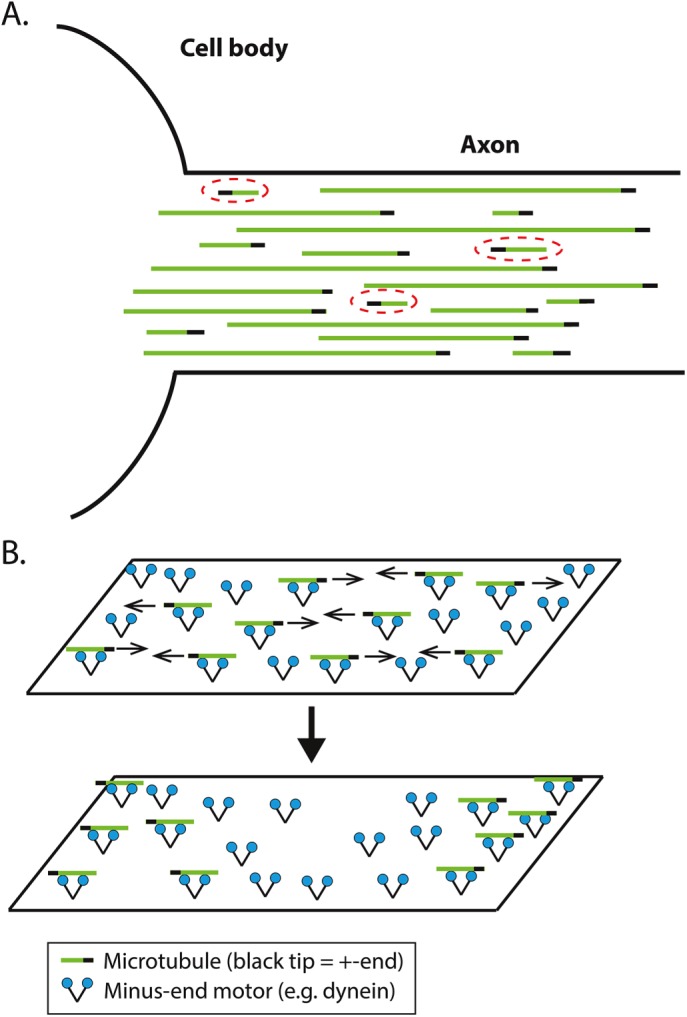
(A) Schematic of MT polarity pattern in the axon. Green lines represent MTs and black tips represent the plus-end. Long MTs have a nearly uniform plus-end-out polarity pattern, while short MTs are occasionally oriented with minus-end-out (highlighted with red dashed line). (B) Schematic of motor-based polarity sorting of MTs in vitro. A minus-directed motor such as dynein transports MTs with their plus ends leading, giving rise to regions of uniform MT polarity.
A growing body of evidence supports a “polarity sorting” model in which minus-end-directed motor proteins slide short MTs with their plus-ends leading, resulting in anterograde motion of plus-end-out MTs and retrograde motion of minus-end-out MTs (Baas and Mozgova, 2012; Rao et al., 2017) (Figure 1B). Live-cell imaging reveals rapid movement of short MTs (less than 10 μm in length), interspersed by frequent pauses and occasional reversals of motion (Wang and Brown, 2002; Rao et al., 2017). The ratio of anterograde to retrograde transport events is around 3:1, depending on the developmental stage and conditions of the axon (Wang and Brown, 2002; He et al., 2005; Myers and Baas, 2007). We posit that the observed movement of short MTs is the result of an ongoing polarity sorting mechanism, in which minus-end-out MTs are cleared from the axon into the cell body to prevent corruption of the axonal polarity pattern and plus-end-distal MTs are moved forward in the axon where they can eventually incorporate into the array of longer MTs.
Cytoplasmic dynein is a minus-end-directed motor protein that has been implicated as the principal driver of short MT transport in axons (Vallee et al., 2004; Ahmad et al., 2006). In vitro gliding assays provide a proof of principle for cytoplasmic dynein as a polarity-sorting motor protein in the axon: When MTs in a random orientation are applied to a lawn of motors adhered to a glass coverslip by their cargo domains, the motor proteins sort the MTs into regions of uniform polarity (Shima et al., 2006; Yokokawa et al., 2008; Alper et al., 2013) (Figure 1B). This is possible because the motor domain is able to swivel (Tanenbaum et al., 2013). Cytoplasmic dynein has a role in organizing the MT cytoskeleton in a variety of cell types (Ahmad et al., 2006; Zheng et al., 2008; Tanenbaum et al., 2013; Mazel et al., 2014).
Here we introduce a computational model of polarity sorting of MTs in the axon. We build on previous models that describe emergent organization of the cytoskeleton from motor-filament interactions (Mogilner and Zemel, 2008; Craig et al., 2011) to develop a computational framework for describing the essential mechanical components of the polarity sorting machinery in the axon. We predict the movement of individual MTs along an axon using stochastic simulations based on force-dependent binding and unbinding rates of cytoplasmic dynein. We expand the model to consider other possible contributors to short MT transport in the axon, including the plus-end-directed motor, kinesin-1, and hypothetical transient cross-links that resist relative sliding between parallel MTs. Following the approach of Müller et al. (2008), we assume that multiple motors pulling the MT in the same direction share the mechanical load equally. When opposing motors simultaneously attach and pull the MT in opposite directions, the resulting motion of the MT depends on the number of attached motors and the load-dependent properties of the motors. While many mechanical parameters of these motors have been measured in vitro (Kunwar et al., 2011), we can further constrain the model by comparing our simulated MT trajectories with live-cell imaging of motile axonal MTs (Wang and Brown, 2002; He et al., 2005; Myers and Baas, 2007).
We describe several mechanistic insights gained from this study: 1) A model in which dynein motors drive short MTs in a direction determined by the orientation of the MT can explain how mal-oriented MTs are cleared from the axon to avoid organization flaws in the MT array; 2) competition between molecular motors of opposite polarities can account for the rapid asynchronous movement observed experimentally; and 3) nonmotile protein cross-linkers between parallel MTs provide an effective viscous drag that gives rise to the inverse relationship between MT transport and MT length that has been observed experimentally. We predict that loss of cross-linker function would lead to disorganized MT transport and polarity flaws in the axonal MT bundle. These insights build on our recently published experimental and modeling work (Rao et al., 2017).
RESULTS
Mechanical model for filament sliding
Figure 2 illustrates key features of our model. We simulate the time-dependent trajectory of an individual MT transported along the axon by a sliding filament mechanism (see Materials and Methods). We assume there are three populations of proteins that can stochastically bind and unbind to the MT: 1) Cytoplasmic dynein, which is a minus-end-directed motor (i.e., “walks” toward the minus end of MTs) and therefore slides MTs with their plus ends leading; 2) kinesin-1, which is a plus-end-directed motor (i.e., “walks” toward the plus end of MTs) and therefore slides MTs with their minus ends leading; and 3) nonmotile cross-linking proteins, which provide an effective viscous drag opposing the motion of the MT. In the case of cytoplasmic dynein and kinesin-1, we assume that the motors are immobilized by interactions between their cargo domains and longer stationary MTs in the axon. We assume that cross-linking proteins transiently interact with parallel MTs of any length and resist relative motion between them. For brevity, we will refer to cytoplasmic dynein and kinesin-1 as dynein and kinesin, respectively.
FIGURE 2:
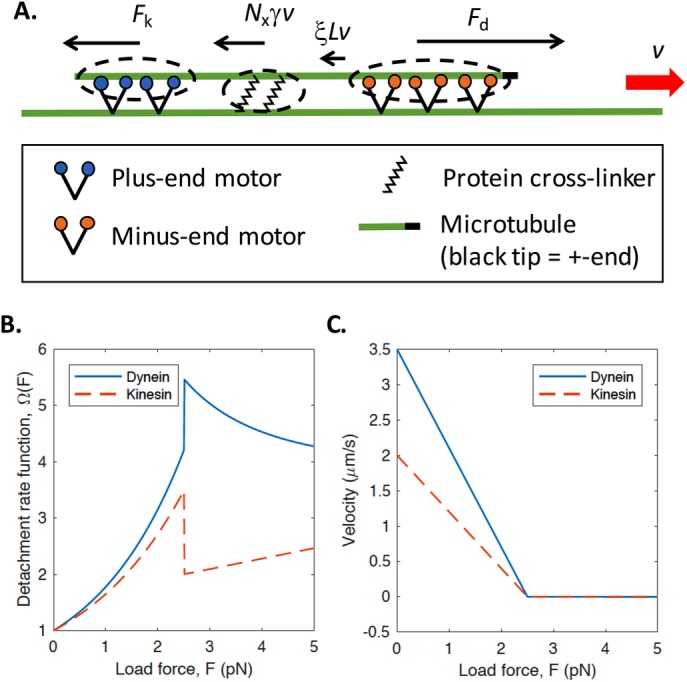
Mechanical model of axonal MT motility. (A) Schematic of the molecular components of our computational model. Minus-end-directed motors such as cytoplasmic dynein (orange) are immobilized via their cargo domains to long axonal MTs (longer green line) and apply a force that slides a shorter MT in the direction with its plus end leading (plus-end indicated by black tip). Plus-end-directed motors such as kinesin-1 (blue) apply a force to the short MT in the opposite direction. Static cross-linkers (black, zigzag lines) stochastically cross-link MTs, increasing the effective viscous drag force opposing the motion of the short MT. When NdFsd > NkFsk, dynein motors are the primary drivers of motion, siding the MT with its plus end leading as illustrated here (red arrow). Black arrows indicate the direction and relative magnitude of forces acting on the MT, corresponding to the terms in Eq. 12. (B) Characteristic detachment rate functions described in Eqs. 4 and 8. (C) Linear load-velocity function as described in Eq. 11.
The number of engaged dynein motors, Nd, is given by
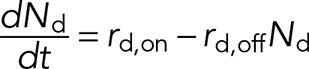 (1) (1)
|
where
|
|
and
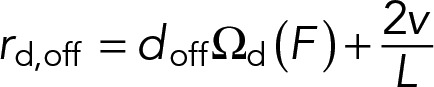 (3) (3)
|
Equation 2 describes the rate of dynein attachment, where don is the attachment rate per available binding sites, Ntot is the total number of possible binding sites on the MT, and the number of attached dynein, kinesin, and cross-linkers are Nd, Nk, and Nx, respectively. As an upper bound, we assume that the number of attached motors is limited by the periodic spacing of 8 nm between motor domain binding sites on MTs (Song and Mandelkow, 1993; Svoboda et al., 1993), such that the maximum linear density of attached motors is λ = (1/8 nm) = 125 μm−1, and the maximum number of attachments is Ntot = λL, where L is the length of the MT.
The first term of Eq. 3 describes the rate at which dynein motors detach from the MT, where doff represents the load-free detachment rate, Ωd(F) is a function that characterizes the force dependence of the detachment rate of individual motors, and F = Fd/Nd is the load force per motor, where Fd is the total force applied to all attached dynein motors. The second term of Eq. 3 gives the average rate of motor dissociation as a result of the MT sliding past immobilized motors, where v is the instantaneous sliding rate of the MT. We assume that a motor has equal probability to attach anywhere along the MT, and therefore the average distance the MT can slide before passing the motor is L/2, giving rise to an average rate of sliding-based dissociation of 2v/L.
In vitro measurements of motor dissociation rates under load imposed by an optical trap revealed that single cytoplasmic dynein motors exhibit a catch-bond behavior for superstall loads (Kunwar et al., 2011). We adopt the load-dependent detachment function obtained in this study (Kunwar et al., 2011) (shown in Figure 2B):
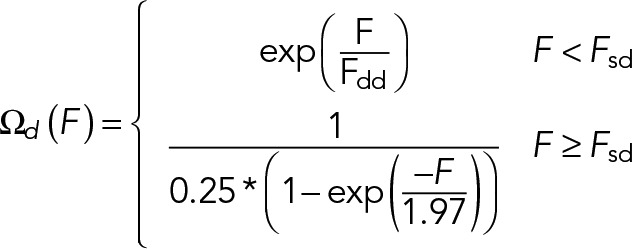 (4) (4)
|
Here Fsd is the stall force of cytoplasmic dynein, defined as the mean load force at which the motor stops moving. The characteristic detachment force for cytoplasmic dynein, Fdd, is defined as the mean value of the force at which a single motor detaches from the MT. We use values for both of these parameters obtained from in vitro optical trap-based experiments (summarized in Table 1).
TABLE 1:
Input parameters used in simulations, constrained based on experimental measurements.
| Parameter | Meaning | Value | Reference |
|---|---|---|---|
| ξ | Viscous drag coefficient per unit length for longitudinal free diffusion of a MT | 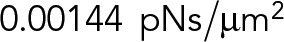 |
Imafuku et al. (1996) |
| γ | Effective viscous drag coefficient per attached cross-linker |  |
Pringle et al. (2013) (We use measurements for MAP65 for an order-of-magnitude estimate of the mechanical features of the cross-linker proposed in this model.) |
| λ | Maximum linear density of motor attachment to MT | 125 µm-1 | Song and Mandelkow (1993) |
| doff | Cytoplasmic dynein unbinding rate under zero load | 0.37 s-1 | Kunwar et al. (2011) |
| koff | Kinesin-1 unbinding rate under zero load | 0.35 s-1 | Kunwar et al. (2011) |
| Fdd | Cytoplasmic dynein detachment force | 1.74 pN | Kunwar et al. (2011) |
| Fdk | Kinesin-1 detachment force | 2.0 pN | Kunwar et al. (2011) |
| Fsd | Cytoplasmic dynein stall force | 2.5 pN | Kunwar et al. (2011) |
| Fsk | Kinesin-1 stall force | 2.5 pN | Kunwar et al. (2011) |
| vbd | Characteristic velocity parameter for cytoplasmic dynein under superstall loads | 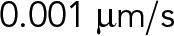 |
Kunwar et al. (2011) |
| vbk | Characteristic velocity parameter for kinesin-1 under superstall loads | 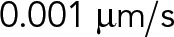 |
Kunwar et al. (2011) |
| vfd | Cytoplasmic dynein velocity under zero load | 3.5 µm | Ahmad et al. (2006) (parameter tuned to match velocity histograms of short axonal MTs in Ahmad et al., 2006). |
| vfk | Kinesin-1 velocity under zero load | 1.0 µm | Ahmad et al. (2006) |
Likewise, the number of engaged kinesin motors is given by
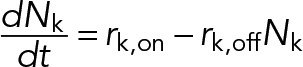 (5) (5)
|
where
|
|
and
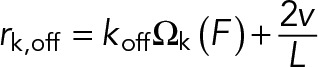 (7) (7)
|
Here kon is the attachment rate per available binding site for kinesin-1 and koff is the dissociation rate at zero load. We use the load-dependent dissociation function, Ωk(F), measured in Kunwar et al. for kinesin-1 (shown in Figure 2B):
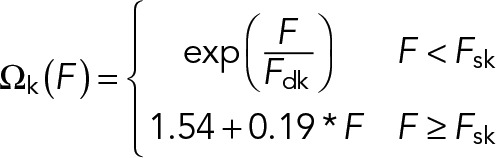 (8) (8)
|
Here Fsk and Fdk are the stall force and detachment force, respectively, for kinesin-1, which we constrain based on in vitro measurements (Table 1) (Kunwar et al., 2011). For kinesin, the load force per motor is F = Fk/Nk, where Fk is the total force applied to all attached kinesin motors.
We also consider the possibility that transient attachment of nonmotile cross-linking proteins produces protein friction that resists relative sliding between MTs. The number of cross-linker attachments, Nx, is given by
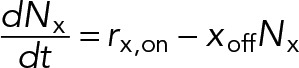 (9) (9)
|
where xoff is a constant detachment rate per cross-linker and the overall cross-linker attachment rate is given by
|
|
We use a linear force-velocity curve for individual motors (Figure 2C):
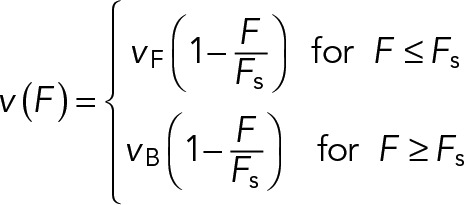 (11) (11)
|
Here vF represents the unloaded velocity of the motor, vB is the characteristic velocity for a motor under superstall loads, and Fs is the characteristic stall force of the motor. Experimentally measured values of these parameters are summarized in Table 1 (denoted as vF = vfd, vB = vbd, and Fs = Fsd for dynein; and vF = vfk, vB = vbk, and Fs = Fsk for kinesin). The load force per motor, F, is equal to Fd/Nd for dynein and Fk/Nk for kinesin. Following the approach of Müller et al. (2008), we assume that when motors of opposite polarity interact with the same object, the load is shared equally among motors pulling in the same direction. Although there is evidence suggesting that motors attached to a cargo via flexible connections experience an uneven distribution of the load force (Kunwar et al., 2011), we expect equal load sharing to be a reasonable approximation in the case of motor-based gliding of MTs, due to the high tensile rigidity of a MT (Brangwynn et al., 2006).
In the case of dynein-driven sliding of a plus-end-out MT, NdFsd > NkFsk, the overdamped motion of the MT is described by the force-balance condition (illustrated in Figure 2A):
|
|
The total force between the MT and dynein motors, Fd, is resisted by the force, Fk, applied by kinesin motors to the MT, the protein friction resulting from cross-linker attachments, Nxγv, and the viscous drag force of the surrounding fluid on the MT, ξLv, where v is the instantaneous velocity of the MT. The parameter γ represents the effective viscous drag per attached cross-linker, and ξ represents the drag coefficient per unit length of the MT.
Most of the model parameters can be constrained based on experimental measurements (see Table 1 and Materials and Methods). In this study, we vary the rates at which dynein, kinesin, and cross-linkers attach to the MT (don, kon, and xon, respectively) and the MT length L to elucidate how each of the molecular players impacts the quantitative characteristics of MT transport. Note that the attachment rates incorporate two unknown characteristics for each protein population: the local concentration of available protein and the characteristic binding affinity to MTs. We build the model up one layer at a time, first characterizing a “dynein-only” model over a broad range of the dynein attachment rate, don. Next, we simulate MT movement arising from competition between dynein and kinesin, characterizing how the motion depends on the ratio of kinesin and dynein attachment rates, kon/don. Finally, we add a population of nonmotile cross-linkers to the system and investigate MT transport for a variety of kon/don and xon/don ratios. By characterizing each layer of the model over a broad parameter range, we identify the minimal model components necessary to reproduce qualitative features of experimental data, such as the relationship between velocity and MT length and the prevalence of pauses and reversals in motion. We then numerically constrain the input parameters to recapitulate quantitative features of MT transport in live axons, such as the fraction of time spent paused. With a constrained model, we make new experimentally testable predictions. Our methods for obtaining analytical solutions for the “dynein-only” model and our numerical simulation methods are described in more detail under Materials and Methods.
Inherent in our modeling is the presumption that the short mobile MTs are moving via a sliding-filament mechanism in which the cargo domain of the motor protein interacts with the longer stationary microtubule while the motor domain interacts with the shorter microtubule. This mechanism has also been referred to as “crowd surfing,” because the short microtubule would have to be handed off from one motor protein to another for the short microtubule to display concerted movement. The question arises as to why the short microtubules do not simply move as cargo along the microtubule, as membranous vesicles do. If that were to happen, then microtubules of both polarity orientations would be conveyed in the retrograde direction by cytoplasmic dynein, or in the anterograde direction by kinesin-1, in a nonpolarity-sorting manner. We hypothesize that the sliding-filament mechanism is the predominant driver of MT movement based on the ability of this form of transport to promote polarity sorting. A possible mechanism for the predominance of the filament-sliding mechanism over the cargo-transport mechanism is that short axonal MTs are unusually stable, and their composition of post-translationally modified tubulin renders them poorly suited for interaction with the cargo domain and better suited for interaction with the motor domain of cytoplasmic dynein (Baas, 2013). Furthermore, each short MT is surrounded by long MTs (and/or cortical actin cytoskeleton) with motor proteins bound via their cargo domains (Hasaka et al., 2004), so a large population of immobilized motors is available to promote filament sliding. The short MTs may have cargo domains of motor proteins associated with them as well, but we suspect that they will be much more likely to encounter motor domains rather than cargo domains due to the large number of surrounding MTs (and/or cortical actin cytoskeleton) coated with immobilized motors. While future experimental investigation may reveal additional complexity, we limit our model to motor-based forces arising from the filament-sliding mechanism for simplicity.
We will use the following terminology throughout the manuscript to refer to direction of transport and polarity orientation of MTs (Figure 1A): A MT oriented with its plus end away from the cell body will be referred to as “plus-end-out,” while a MT with its minus end oriented away from the cell body is “minus-end-out.” We will refer to MT transport away from the cell body as “anterograde” and toward the cell body as “retrograde.” We adopt a sign convention in which anterograde movement has a positive velocity.
Dynein-only filament sliding model does not explain immobility of longer MTs
Previous modeling (Mogilner and Zemel, 2008; Craig et al., 2011) and in vitro experiments (Shima et al., 2006; Yokokawa et al., 2008) have demonstrated that a single type of motor is sufficient to sort cytoskeletal filaments into regions of uniform polarity using a sliding filament mechanism (Figure 1B). A single-motor polarity sorting mechanism works by sliding MTs across a “lawn” of immobilized motor proteins in a direction that depends on the polarity orientation of the MT. For example, a motor such as cytoplasmic dynein that normally moves toward MT minus ends would slide MTs with their plus-ends leading if the motor itself is immobilized. This provides an intuitive mechanism for polarity sorting of axonal MTs in which “correctly oriented” plus-end-out MTs are transported in the anterograde direction, allowing them to eventually incorporate into the MT array and contribute to the elongation of the axon, while “mal-oriented” minus-end-out MTs are transported in the retrograde direction and cleared from the axon. Acute inhibition of cytoplasmic dynein in axons decreases short MT transport in both directions and leads to an accumulation of minus-end-out MTs in the axon (Rao et al., 2017), suggesting this motor as a likely candidate for the primary driver of MT polarity sorting.
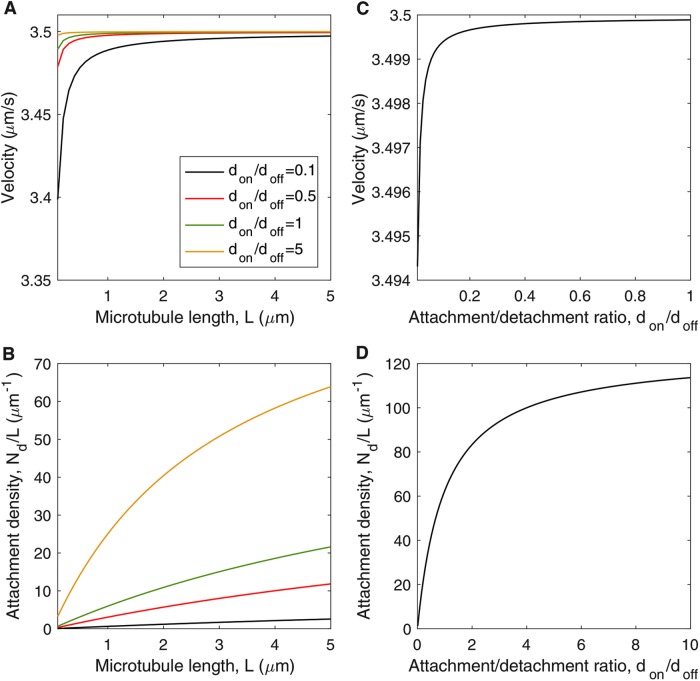
To determine whether axonal MT transport can be explained by dynein-based sliding alone, we examine analytical solutions of the model (Eqs. 16–18; Materials and Methods) and relevant limiting cases (Eqs. 19 and 20; Materials and Methods). Figure 3A shows the MT sliding velocity v as a function of MT length for several values of the ratio (Eq. 18). Figure 3B shows the corresponding steady-state dynein attachment density, Nd/L, as a function of MT length (Eq. 17). The sliding velocity, v, and the attachment density, Nd/L, both increase and then level off as a function of L (Figure 3, A and B). For shorter MTs, the length dependence of v and Nd/L arises from motor dissociation that occurs when MTs slide past immobilized motors (represented by the second term, 2v/L, in Eq. 3). The average rate of sliding-based dissociation is inversely proportional to MT length, resulting in a smaller steady-state motor attachment density for short MTs (Eq. 17; Figure 3B). The reduced motor attachment density for short MTs gives rise to a higher load force per motor and, therefore, a lower average sliding velocity (Eq. 16; Figure 3A).
FIGURE 3:
Dynein-based sliding of MTs: analytical solutions with input parameters from Table 1. (A) MT sliding velocity v as a function of MT length L, based on the positive root of Eq. 18 for several values of the dynein attachment ratio don/doff. (B) Steady-state dynein attachment density, Nd/L, as a function of MT length L corresponding to the velocity plots in A. (C) MT sliding velocity as a function of dynein attachment ratio don/doff, in the limit that sliding-based dissocation is negligible (L ≪ 2vfd / doff ≈ 19 μm; Eq. 20). (D) Steady-state dynein attachment density, Nd/L, as a function of attachment ratio don/doff in the limit that sliding-based dissociation is negligible (Eq. 19).
The predicted length independence of MT sliding velocity for large L (Eq. 20; Figure 3A) arises from the cancelation of two competing factors: The steady-state motor attachment number, Nd (Eq. 19), and the filament drag force, ξvL, are both directly proportional to MT length. For this reason, the drag force per attached motor (ξvL/Nd), and the resulting sliding velocity (Eq. 20), are independent of microtubule length for large L. Examination of Eqs. 19 and 20 reveals that the dynein attachment density and MT sliding velocity both increase and then level off with motor attachment ratio a = don/doff (Figure 3, C and D). The velocity reaches half its maximum value for a = b / (1 - b) = 1.6 × 10-5, suggesting that the sliding velocity is insensitive to the attachment ratio over a broad range of values (Figure 3C). The dynein attachment density reaches half its maximum value for a = don/doff = 1 (Figure 3D).
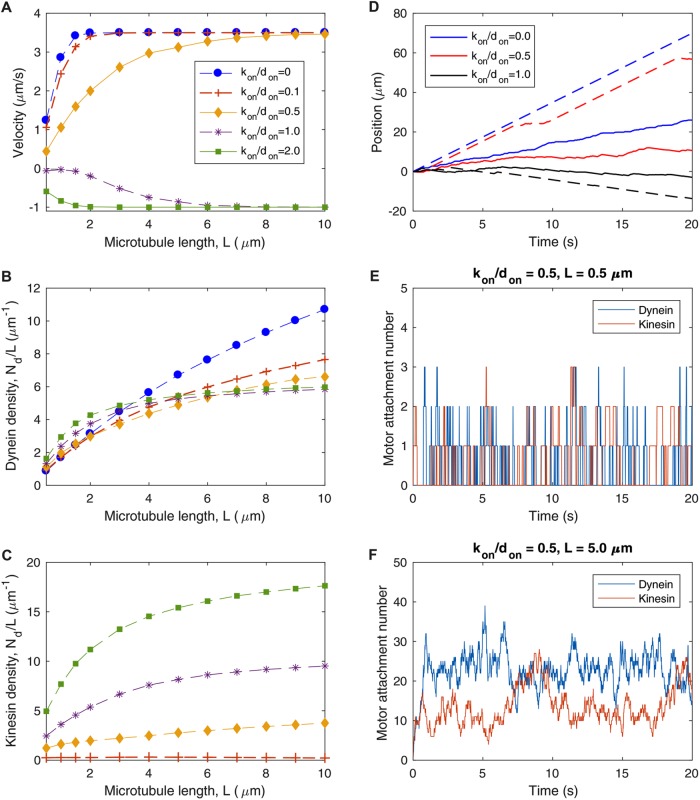
Computational simulations of a “dynein-only” model (with don = 0.1 s−1, kon = 0, and xon = 0) (Figure 4A, blue dots) confirm the velocity versus MT length trend predicted analytically (Figure 3A), providing a consistency check between the analytical predictions of the model and the stochastic simulations. Sample simulated trajectories illustrate measurable characteristics of the dynein-only model (Figure 4D): For a short MT (L = 0.5 μm), rapid fluctuations in attachment number lead to frequent pauses in motion (Figure 4D, solid blue line). For a longer MT (L = 5 μm), fast processive motion arises from a large number of attached motors sharing the load (Figure 4D, dashed blue line).
FIGURE 4:
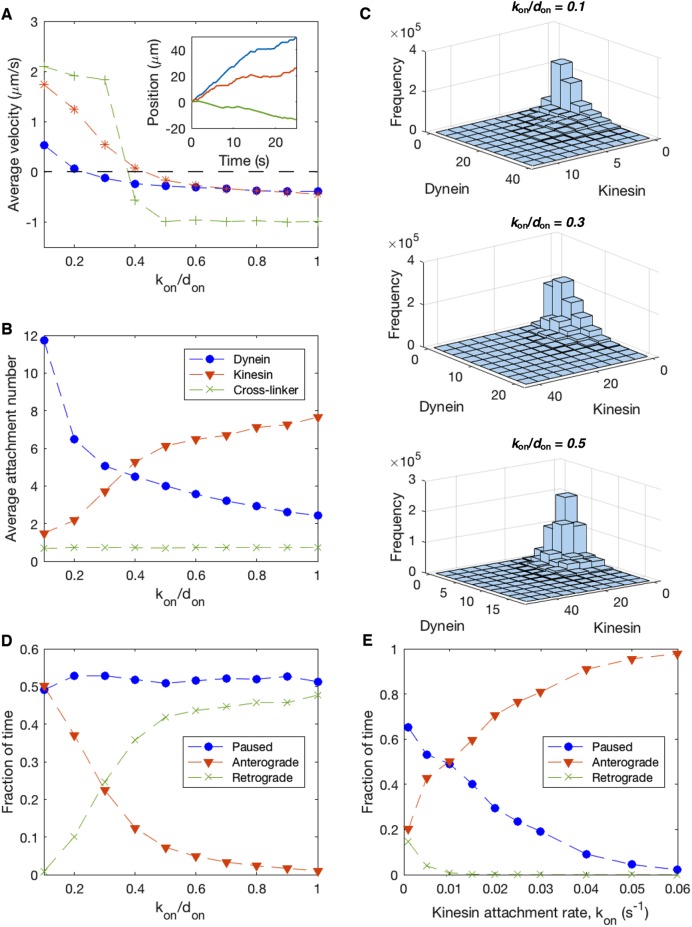
Competition between cytoplasmic dynein and kinesin-1 does not explain immobility of long axonal MTs. Parameters in Table 1, don = 0.1 s−1, and xon = 0 are used for all simulations. (A) Time-averaged velocity of MT transport as a function of MT length for various values of the ratio of kinesin attachment rate to dynein attachment rate, kon/don. (B) Average dynein attachment density, Nd/L, as a function of MT length L, for the same values of kon/don as in A. (C) Average kinesin attachment density, Nk/L, as a function of MT length L, for the same values of kon/don as in A. (D) Sample trajectories for several values of kon/don, with solid lines corresponding to short MTs of length L = 0.5 μm and dashed lines corresponding to longer MTs of length L = 5.0 μm. Solid lines and dashed lines of the same color correspond to the same kon/don, as specified in the legend. (E) Dynein and kinesin motor attachment numbers as a function of time for kon/don = 0.5 and L = 0.5 μm, corresponding to the solid red line in D. (F) Dynein and kinesin motor attachment numbers as a function of time for kon/don = 0.5 and L = 5.0 μm, corresponding to the dashed red line in D.
In vitro gliding assays, in which MTs slide over a surface coated with immobilized dynein motors, exhibit velocity that increases and then levels off as a function of MT length (Alper et al., 2013), in close agreement with our dynein-only model predictions (Figures 3A and 4A). In contrast, observations of motile MTs in live axons have been limited to short filaments (L < 10 μm) (Wang and Brown, 2002; He et al., 2005; Rao et al., 2017). Furthermore, the occasional reversals of motion observed for axonal MTs (Wang and Brown, 2002; He et al., 2005; Myers and Baas, 2007) are not readily explained by a dynein-only sliding model. For this reason, we next consider additional molecular players that may be involved in MT transport in axons.
Filament sliding model with opposing motors exhibits “winner-takes-all” dynamics
Next, we consider the possibility that opposition between competing classes of motors could account for the immobility of longer MTs observed in the axon. While ongoing experimental investigation will be needed to identify which motors compete with cytoplasmic dynein to drive MT movement in axons, we consider kinesin-1 to be a reasonable candidate based on observations of kinesin-1-based transport in cultured insect neurons (Lu et al., 2015). In principle, two “teams” of motors pulling the same object in opposite directions can give rise to a stalled “tug-of-war” in which all motors experience a load force close to their stall force while remaining attached to the object (Müller et al., 2008). Another possibility is that the class of motors with fewer initial attachments will undergo a cascade of load-dependent detachment, leaving the “winning team” of motors to drive fast processive transport (Müller et al., 2008) in what we will refer to as a “winner-takes-all” scenario. The outcome of a competition between motors attached to the same object depends on the mechanical characteristics of the motors (load-velocity curves, stall forces, and load-dependent dissociation rates), which we base on in vitro measurements for cytoplasmic dynein and kinesin-1 (Eqs. 4, 8, and 11; Table 1).
To determine whether competition between cytoplasmic dynein and kinesin-1 produces a stalled “tug-of-war” for longer MTs, we simulate MT trajectories as a function of MT length for several values of the kinesin attachment rate, kon, with a fixed value of the dynein attachment rate, don = 0.1 s−1 (Figure 4). The sliding velocity as a function of MT length (Figure 4A) depends on the kinesin-to-dynein attachment ratio, kon/don, which determines the average attachment densities of each population of motor (Figure 4, B and C).
For low kon/don (see kon/don = 0.1, red “+” symbols in Figure 4, A–C), the average kinesin attachment density is much smaller than the average dynein attachment density (Figure 4, B and C). As a result, the average load force per attached dynein is only slightly higher than in the dynein-only case, and the average velocity approaches vfd with increasing L in a similar manner to the kon = 0 case (Figure 4A).
For an intermediate attachment ratio of kon/don = 0.5, the average attachment density is only slightly higher for dynein than kinesin (Figure 4, B and C, yellow diamond symbols). For shorter MTs (<2 μm), continual fluctuations in the kinesin and dynein attachment numbers (Figure 4E) lead to frequent pauses and brief reversals in motion (Figure 4D; solid red line). As a result, the average velocity of short MTs is lower, but in the same direction, as the kon = 0 case (Figure 4A; yellow diamond symbols). For longer MTs, we observe fast processive movement primarily driven by dynein, with infrequent pauses occurring when fluctuations in attachment number cause kinesin to briefly outnumber dynein (Figure 4, D, dashed red line, and F).
For high kon/don, predominantly kinesin-driven transport results in retrograde movement of plus-end-out MTs (Figure 4A). In the kon/don = 1.0 case, where the unloaded kinetic rates are the same for both types of motor, comparable dynein and kinesin attachment numbers lead to an average sliding velocity close to zero for short MTs (Figure 4, A–C, purple “*” symbols). For longer MTs, with larger overall attachment numbers producing larger total forces on the MT, dynein and kinesin behave differently under load (Eqs. 4, 8, and 11): Based on in vitro measurements of the load-dependent characteristics of each type of motor (Table 1 and Figure 2, B and C), dynein motors are more prone to detachment under load force, leading to higher average attachment numbers for kinesin than dynein (Figure 4, B and C). As a result, MTs have an average velocity in the retrograde direction, at a speed that approaches the unloaded kinesin velocity vfk at large L (Figure 4A). For kon/don = 2.0 (Figure 4, A–C, green squares), the model exhibits retrograde velocity primarily driven by kinesin-1 for all MT lengths, approaching vfk with increasing L (Figure 4A).
Taken together, these results suggest that an opposing motor such as kinesin-1 does not explain the immobility of longer MTs in the axon and in fact could lead to disruption of the MT polarity pattern due to occasional reversals of motion that occur when fluctuating attachment numbers lead to kinesin-driven motion. In contrast to observations of MT movement in live axons, a two-motor model predicts that longer MTs move more rapidly than shorter MTs (Figure 4A). While it is possible in principle to fine-tune the motor attachment ratio to achieve zero average velocity, this would constitute an unstable balance in which a small deviation in attachment rate for either motor would tip the system toward a “winner-takes-all” scenario with net transport in one direction. We expect that the regulation of MT transport in axons relies on a mechanism that is robust enough to allow consistent directional transport of short MTs, and immobility of longer MTs, despite the likelihood of local fluctuations in the pool of available motors. In summary, these model predictions suggest that competition between oppositely oriented motors does not fully explain the transport mechanism for axonal MTs.
Static cross-linkers limit movement of longer MTs in axon
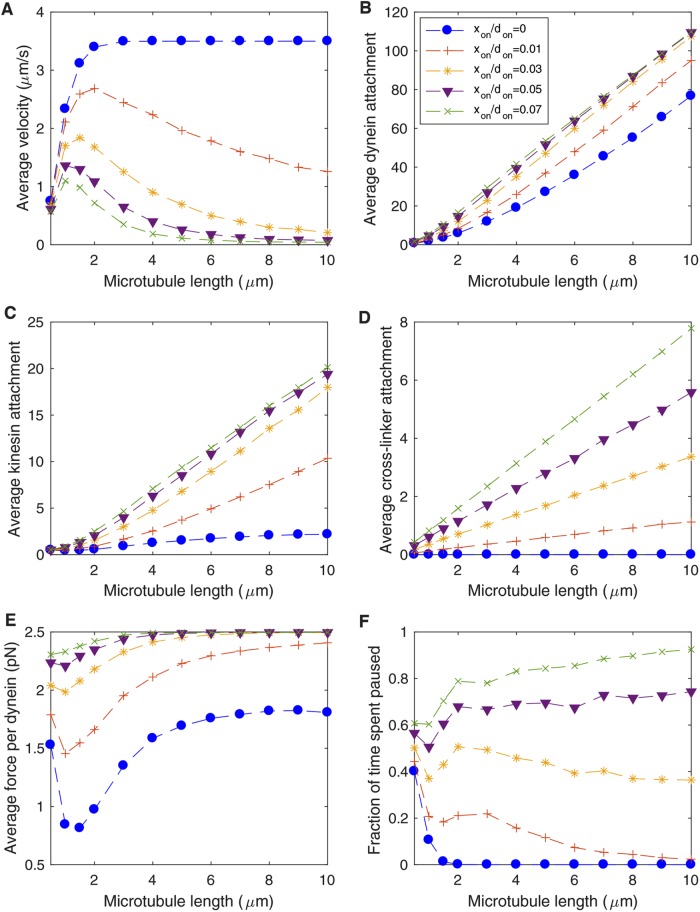
Next, we consider the possibility that a small population of nonmotile proteins can stochastically cross-link MTs, giving rise to viscous friction that opposes MT movement. In contrast to the “dynein-only” and “dynein + kinesin” scenarios discussed above, when nonmotile cross-linkers are included in the model, we find that the average velocity of MT transport decreases with MT length (Figure 5A), in agreement with live cell imaging demonstrating that movement of axonal MTs is limited to short filaments (Wang and Brown, 2002; He et al., 2005; Rao et al., 2017).
FIGURE 5:
Static cross-linkers limit transport of longer MTs in the axon. Parameters in Table 1, don = 0.1 s−1, and kon = 0.01 s−1 are used for all simulations. Legend in B applies to all panels. (A) Time-averaged velocity of MT transport as a function of MT length for several values of the ratio of cross-linker attachment rate to dynein attachment rate xon/don. (B) Average number of cytoplasmic dynein motors attached to the MT as a function of MT length. (C) Average number of kinesin-1 motors attached to the MT as a function of MT length. (D) Average number of static cross-linkers attached to the MT as a function of MT length. (E) Average load force experienced by each of the attached cytoplasmic dynein motors as a function of MT length. Note that the dynein stall force in the simulations is 2.5 pN (Table 1). (F) Fraction of the time the MT spends paused as a function of MT length. A MT is considered “paused” if it moves less than 0.65 μm/s. This criterion for pauses is chosen to facilitate comparison between the model and fluorescence imaging of axonal MTs in photobleach experiments, where typical experimental resolution limits do not allow detection of movement below this threshold.
To better understand the mechanism by which static cross-linkers limit the movement of longer MTs, we examine the average attachment numbers of dynein, kinesin, and cross-linkers as a function of length (Figure 5, B and C). In the absence of cross-linkers (blue dots), the dynein attachment number increases in proportion with MT length (Figure 5B), while the kinesin attachment number never exceeds one to two motors (Figure 5C). This is due to a “winner-takes-all” effect in which a large number of attached dynein motors share the load, while each kinesin that attaches experiences a relatively large load and detaches rapidly. However, when nonmotile cross-linkers are included in the model, kinesin attachment numbers (Figure 5C) and cross-linker attachment numbers (Figure 5D) both increase with MT length, because the cross-linkers bear some of the load force and reduce the average force applied to each kinesin. This, in turn, increases the average load force applied to each dynein motor (Figure 5E), with the average force per motor approaching the stall force with increasing MT length. As a result, the fraction of time a MT spends paused increases as a function of cross-linker attachment rate (Figure 5F), in particular for longer MTs where it becomes more rare for transient bursts of motion to take place in response to stochastic cross-linker detachment.
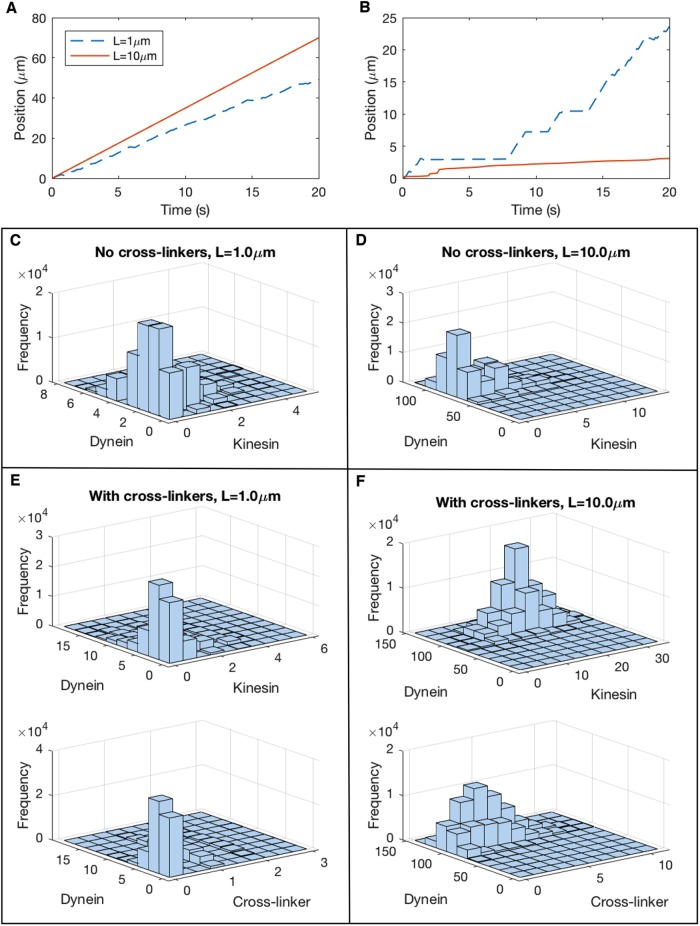
The velocity-versus-length predictions of the model when cross-linkers are included (Figure 5A) point to a fundamental change in the mechanical behavior of the system: The inclusion of cross-linkers triggers a shift from a scenario in which one type of motor drives largely unopposed movement (“winner-takes-all”) to a situation in which the dominant motors frequently experience a stalled “tug-of-war” in response to oppositional motors and cross-linkers. We illustrate this point with sample MT trajectories without cross-linkers (xon = 0; Figure 6A) and with cross-linkers (xon = 0.0003 s−1; Figure 6B). We also show bivariate histograms of the simultaneous protein attachment numbers corresponding to each sample trajectory (Figure 6, C–F) to illustrate how the combination of dynein, kinesin, and cross-linker attachment give rise to qualitatively distinct patterns of movement under each condition.
FIGURE 6:
Static cross-linkers increase likelihood of stalled “tug-of-war” between opposing motors. (A) Sample MT trajectories in the absence of static cross-linkers (xon = 0), showing position as a function of time. Parameters: don = 0.1 s−1, kon = 0.01 s−1, Table 1. Legend applies to A and B. (B) Sample MT trajectories in the presence of static cross-linkers (xon = 0.003 s−1). (C) Bivariate histogram of the attachment numbers of cytoplasmic dynein and kinesin-1 for a 1 μm MT in the absence of cross-linkers (corresponding to the dashed blue line in A). (D) Bivariate histogram of the attachment numbers of cytoplasmic dynein and kinesin-1 for a 10-μm MT in the absence of cross-linkers (corresponding to the solid red line in A). (E) Top: Histogram of dynein and kinesin attachment numbers for a 1-μm MT in the presence of cross-linkers (corresponding to the dashed blue line in B). Bottom: Histogram of dynein and cross-linker attachment numbers for the same trajectory. (F) Histogram of dynein and kinesin attachment (top) and corresponding histogram of dynein and cross-linker attachment (bottom) for a 10-μm MT in the presence of cross-linkers (corresponding to the solid red line in B)
In the absence of cross-linkers, dynein-driven transport of short MTs is punctuated by short pauses (Figure 6A, blue dashed line), which occur when kinesin and dynein attachment numbers are comparable (Figure 6C). For the same motor attachment rates, but longer MTs, the number of dynein attachments increases significantly while the typical kinesin attachment remains fewer than five (Figure 6D), producing steady MT transport at a velocity close to the maximum, vfd (Figure 6A, red line).
For a nonzero rate of cross-linker attachment, simultaneous attachment of kinesin and dynein becomes more prevalent (Figure 6, E and F), because cross-linkers bear some of the mechanical load, allowing kinesin motors to stay attached longer. The movement of short MTs alternates between bursts of fast motion when only dynein is attached to pauses in motion when dynein is opposed by forces from kinesin or cross-linkers (Figure 6B, blue dashed line). For a longer MT, the overall attachment numbers increase for dynein, kinesin, and cross-linkers, making it increasingly rare for one class of motor to drive MT sliding in the absence of load forces from the opposing class of motor (Figure 6F). As a result, the average velocity approaches zero with MT length (Figure 5A), as a stalled “tug-of-war” becomes less sensitive to fluctuations in attachment number at large L (Figure 6, B and F)
In summary, we have demonstrated that a model with three molecular components (dynein, kinesin, and cross-linkers) is capable of explaining the following qualitative features of MT transport in axons: 1) short MTs undergo fast transport in the axon, while longer MTs are immobile (Figure 5A), and 2) short MTs move in an asynchronous, saltatory manner, characterized by frequent pauses (Figure 6B). Our data suggest that nonmotile cross-linkers may play an important role in maintaining an organized polarity pattern in the axonal MT array by limiting movement of longer MTs (Figure 5A) and preventing shorter MTs from being transported with minus-end leading by competing plus-end-directed motors such as kinesin-1 (compare Figures 4A and 5A).
Having established a minimal model to reproduce qualitative characteristics of the system, we can constrain unfixed parameters by further requiring quantitative agreement with experimental data. If we set the dynein attachment rate to don = 0.1 s−1 (corresponding to average dynein attachment density on the order of 10 μm−1), then we can constrain the kinesin and cross-linker attachment ratios to kon/don = 0.1 and xon/don = 0.3, respectively, to limit MT transport to MTs shorter than ∼10 μm (Figure 5A) and to match the experimental observation that short axonal MTs spend ∼ 50% of the time paused (Figure 5F) (Wang and Brown, 2002). In the next section, we will use these attachment ratios as a starting point from which to make experimentally testable predictions.
Dynein inhibition disrupts polarity sorting of axonal MTs
Because the polarity sorting mechanism described in this model relies on primarily dynein-driven transport of MTs, we next investigate the predictions of the model when dynein activity is depleted. We reduce don, and thus increase the ratio of kinesin to dynein attachment rates, kon/don, to mimic experiments in which dynein is pharmacologically inhibited (Figure 7). As this ratio increases, the time-averaged velocity of MT transport decreases and eventually reverses direction (Figure 7A). For low kon/don, we predict fast anterograde motion interspersed with occasional pauses (Figure 7A inset, blue line), consistent with live-cell imaging of MT transport in axons under control conditions (Wang and Brown, 2002; He et al., 2005; Rao et al., 2017). For intermediate levels of kon/don (simulating partial dynein inhibition), we observe more frequent pauses and occasional reversals in the direction of motion following a pause (Figure 7A, inset, red line). For higher kon/don, we observe primarily retrograde motion interspersed with pauses (Figure 7A, inset, green line). This is because reducing the level of dynein activity allows a larger relative number of kinesin motors to attach to the MT (Figure 7, B and C), producing transport in both directions for intermediate kon/don and primarily kinesin-driven retrograde transport for higher kon/don. Taken together, these simulations suggest that inhibition of cytoplasmic dynein disrupts the predominant dynein-based polarity sorting mechanism by increasing the likelihood that a MT will be transported by kinesin with its minus end leading.
FIGURE 7:
Inhibition of dynein allows kinesin to play more prominent role in MT transport. Parameters from Table 1, L = 2 μm, xon = 0.003 s−1, and kon = 0.01 s−1 except where indicated otherwise. (A) Time-averaged velocity as a function of the ratio of kinesin attachment rate to dynein attachment rate (kon/don) for several values of the kinesin attachment rate: kon = 0.1 s−2 (green “+” symbols), kon = 0.01 s−1 (red “*” symbols), and kon = 0.001 s−1 (blue circles). For each data set, the kon/don ratio is increased by reducing the dynein attachment rate, don, while keeping kon constant, mimicking experimental inhibition of cytoplasmic dynein activity. Inset: Sample trajectories corresponding to kon = 0.01 s−1 are shown for kon/don = 0.1 (blue), kon/don = 0.3 (red), and kon/don = 0.5 (green). (B) Average attachment numbers of cytoplasmic dynein, kinesin-1, and static cross-linkers as a function of kon/don. (C) Histogram of instantaneous attachment numbers of dynein and kinesin. (D) Fraction of time MT spends paused, moving in the anterograde direction, and moving in the retrograde direction as a function of kon/don, with a fixed kinesin attachment rate, kon = 0.01 s−1. (E) Fraction of time MT spends paused, moving in the anterograde direction, and moving in the retrograde direction as a function of kon, with a fixed ratio kon/don = 0.1.
We predict several quantitative features of individual MT trajectories that could allow the model to be tested by high-resolution imaging of axonal MTs. If don is reduced while holding kon constant, simulating dynein inhibition experiments, then the fraction of time spent paused is independent of kon/don, and a plus-end-out MT becomes more likely to move in the retrograde direction as kon/don increases (Figure 7D). On the other hand, if the overall rate of motor activity is varied by changing kon and don while maintaining a constant kon/don ratio, we find that high motor attachment rates produce “winner-takes-all” behavior, in which the MT moves rapidly in the direction driven by the dominant motor, while low motor attachment rates correspond to more frequent pauses induced by stalled “tug-of-wars” (Figure 7E).
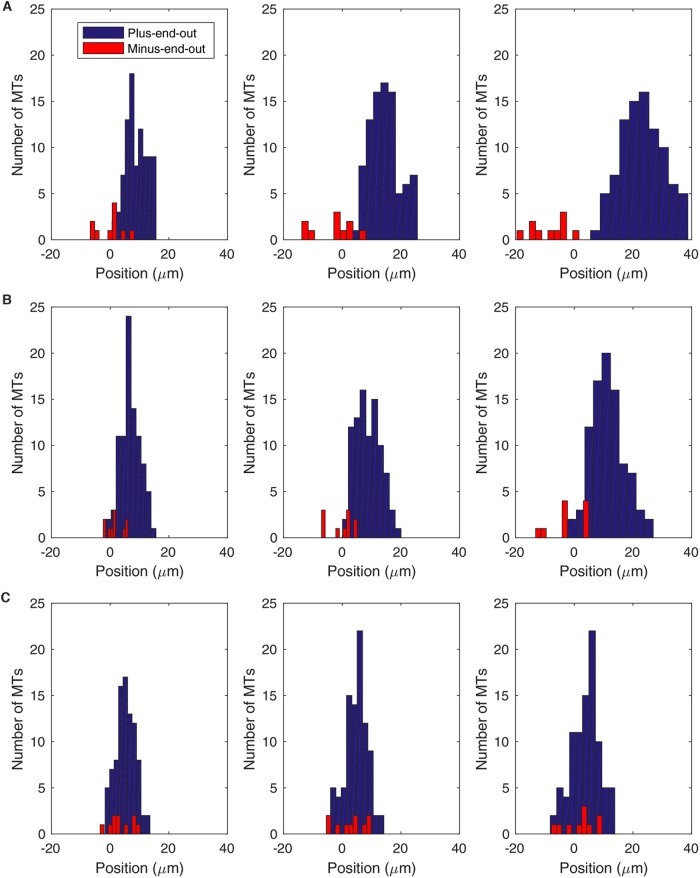
To illustrate how a reduction in cytoplasmic dynein activity level can disrupt the axonal MT polarity pattern, we simulate the movement of 100 MTs initially distributed evenly across a 10-μm segment of the axon, with 90 MTs in a plus-end-out orientation and the other 10 MTs oriented with minus-end-out (Figure 8). For high levels of dynein activity (kon/don = 0.1), the MT distribution is completely sorted on the basis of polarity by t = 10 s, with no remaining overlap between plus-end-out and minus-end-out MTs (Figure 8A). For intermediate levels of dynein activity (kon/don = 0.3), we observe some reduction in the effectiveness of polarity sorting (Figure 8B), and for even further reduced dynein activity (kon/don = 0.5) we predict disorganized polarity patterns resulting from the competition between dynein and kinesin (Figure 8C). These predictions are consistent with recent experiments in which acute inhibition of cytoplasmic dynein with ciliobreven D led to accumulation of minus-end-out MTs in the axon (Rao et al., 2017).
FIGURE 8:
Dynein inhibition disrupts the establishment of plus-end-out MT polarity pattern. Parameters from Table 1, L = 2 μm, xon = 0.003 s−1, kon = 0.01 s−1. Distributions of plus-end-out MTs (blue) and minus-end-out MTs (red) for several values of kon/don evolve over time. Each simulation has an initial distribution of 90 plus-end-out MTs and 10 minus-end-out MTs evenly distributed between x = 0 and x = 10 μm at time t = 0. (A) MT distribution for high dynein activity level (kon/don = 0.1) at times t = 2 s (left), t = 5 s (middle), and t = 10 s (right). (B) MT distribution for kon/don = 0.3 at times t = 2 s (left), t = 5 s (middle), and t = 10 s (right). (C) MT distribution for kon/don = 0.5 at times t = 2 s (left), t = 5 s (middle), and t = 10 s (right).
DISCUSSION
The axon’s plus-end-out MT polarity pattern is an essential characteristic that distinguishes axons from dendrites (Figure 1A). This pattern must be established and maintained for proper axon function throughout the life of the neuron. Inspired by the ability of cytoskeletal elements to self-organize in vitro (Figure 1B), we propose that the polarity pattern of axonal MTs is established through a “polarity sorting” mechanism in which molecular motors slide MTs in a direction based on their polarity orientation. We posit that immobilized cytoplasmic dynein transports axonal MTs with their plus-ends leading, resulting in minus-end-out MTs being transported toward the cell body and “cleared” from the axon, while plus-end-out MTs move distally and populate the growing axon (Figure 9A).
FIGURE 9:

Schematic summarizing current model of polarity sorting mechanism in axons. (A) Control conditions. We predict that when dynein is the primary driver of MT movement, MTs are sorted according to their polarity orientation with plus-end-out MTs usually moving distal (to the right in the figure) and minus-end-out MTs (indicated with red dashed circles) being transported toward the cell body and cleared from the axon. We posit that static cross-linkers prevent movement of longer MTs, and that MTs are occasionally mis-sorted by plus-directed motors. (B) Dynein inhibition. Inhibition of dynein disrupts the polarity sorting mechanism by increasing the likelihood that a plus-directed motor such as kinesin-1 transports an MT in the “incorrect” direction, with its minus end leading (indicated with yellow dashed circles). (C) Cross-linker inhibition. When the density of static cross-linkers is depleted, this leads to increased mobility of longer MTs (indicated with orange dashed circles).
Our computational model establishes proof of principle for dynein-mediated polarity sorting as a primary mechanism for MT organization in the axon. Based on comparison between our model and features of experimentally observed MT motion, we conclude that additional molecular components must also play a role in driving or regulating the axonal transport of short MTs. We demonstrate that competition between cytoplasmic dynein and a plus-end-directed motor such as kinesin-1 can explain the frequent pauses and occasional reversals that have been observed in live-cell imaging of MT movements along the axon (Wang and Brown, 2002; Rao et al., 2017). Our model predicts disruption in the plus-end-out polarity pattern when dynein is partially inhibited, allowing other types of motors to play a more prominent role, in agreement with experimental observations of reduced anterograde transport when dynein heavy chain was partially depleted by RNA interference (He et al., 2005). Acute dynein inhibition by Ciliobrevin D, a specific inhibitor of cytoplasmic dynein, produced immediate reduction of MT transport in both directions along the axon and an increase in minus-end-out MTs in the axon (Rao et al., 2017), confirming key predictions of the dynein-based polarity sorting model. These observations suggest that while dynein is a primary driver of MT transport in axons, other types of motors can transport MTs in the absence of robust dynein activity (Figure 9B).
A long-standing puzzle of the axon cytoskeleton has been the observation that short MTs undergo rapid bidirectional movement along the axon, while MTs longer than several microns are immobile, in contrast to the length-independent gliding of MTs in vitro. We consider two hypothetical explanations: Motors of competing directionality could simultaneously bind to a long MT, locking the MT into a stalled “tug-of-war.” On the other hand, the immobility of longer MTs could arise from transient cross-linking that creates passive resistance to relative sliding between MTs. Our simulations of competition between cytoplasmic dynein and kinesin-1 do not support the “tug-of-war” mechanism and instead predict that competition between opposing motors is more likely to produce a “winner-takes-all” scenario in which one type of motor drives the motion while opposing motors undergo rapid load-dependent detachment. The addition of a hypothetical static cross-linking protein to the computational model qualitatively changes the predicted length dependence of MT transport: For short MTs, rapid transport takes place in bursts when the MT is not cross-linked to another MT. Longer MTs are effectively immobilized due to the increased likelihood of having at least one cross-linker attachment at all times (Figure 9, A and C). When mechanical parameters of the motor proteins are experimentally constrained, we can tune the attachment rate of hypothetical cross-linkers to reproduce the observed length dependence of MT movement in the axon.
Taken together, our results support a model in which axonal MTs are sorted into regions of uniform polarity by dynein-based gliding, occasionally punctuated by competition from plus-end-directed motors such as kinesin-1. We predict that competition between plus-end-directed and minus-end-directed motors could lead to incorrectly sorted MTs, but that static cross-linking proteins play an essential role in maintaining the MT polarity pattern in the axon by limiting MT transport by incorrect motors. A possible candidate for a cross-linker in vertebrate neurons is TRIM46, a protein that has been shown to cross-link MTs and that, when depleted, leads to flaws in MT polarity (van Beuningen et al., 2015). More recently, partial depletion of TRIM46 from cultured rat sympathetic neurons led to increased mobility of MTs (Rao et al., 2017), lending further support to the potential role of TRIM46 in maintaining the polarity pattern of axonal MTs. We suspect that TRIM46 is one cross-linker, but that others exist as well, possibly with a sophisticated division of labor. We also suspect that the ability of kinesin-1 to promote MT sliding in a manner that opposes dynein reflects a functional role for kinesin-1-based MT sliding in discrete locales of the axon, up-regulated during morphogenetic transitions such as axogenesis, branch formation, or regeneration after injury (Lu et al., 2015; Lee et al., 2017).
MATERIALS AND METHODS
Computational simulation methods
The force Fd is determined by the condition that all of the engaged motors move at the same velocity, v, obtained by combining the characteristic load–velocity curves for each type of motor (Eq. 11) and the force-balance condition (Eq. 12):
 (13) (13)
|
Solving for Fd and v yields the following:
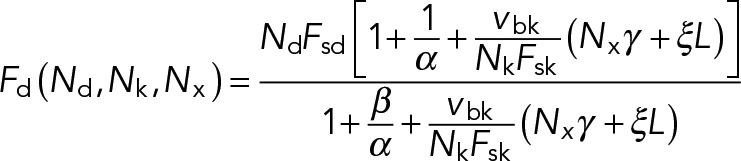 (14) (14)
|
and
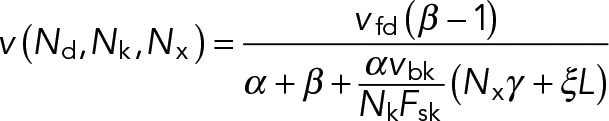 (15) (15)
|
where we define the dimensionless parameters: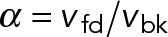 and
and 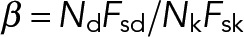 . Expressions of the same form, but exchanging the parameters associated with dynein and kinesin, can be obtained for the kinesin-driven retrograde movement of a plus-end-out MT that takes place when NkFsk > NdFsd. A minus-end-out MT would move at the same average speed but in the opposite direction than a plus-end-out MT, because the direction of applied forces is reversed.
. Expressions of the same form, but exchanging the parameters associated with dynein and kinesin, can be obtained for the kinesin-driven retrograde movement of a plus-end-out MT that takes place when NkFsk > NdFsd. A minus-end-out MT would move at the same average speed but in the opposite direction than a plus-end-out MT, because the direction of applied forces is reversed.
When additional molecular players are included, the model is no longer analytically tractable, but MT sliding trajectories can be predicted using computational simulations. In each time step of the simulation, the attachment numbers Nd, Nk, and Nx are stochastically updated based on Eqs. 1, 5, and 9, respectively, and the instantaneous velocity is updated based on the number of attached motors and cross-linkers using Eq. 15. The center-of-mass position of the MT is then updated according to x(t + dt) = x(t) + vdt, where the program time step, dt, is kept much smaller than the characteristic time scale of dynein-based sliding of the MT (dt ≪ L / vfd).
Analytical solutions of dynein-only model
When MT transport is driven by dynein alone (Nk = Nx = 0; kon = xon = 0), we can obtain analytical expressions for the sliding velocity and dynein attachment density in certain limits. In the absence of kinesin and cross-linkers, dynein motors experience a total load force of Fd = ξLv (Eq. 12). For realistic values of the drag coefficient ξ (Table 1), the maximum load force experienced per motor, ξLvfd, is below the cytoplasmic dynein stall force for relevant values of L (ξLvfd < Fsd or, equivalently, L < Fsd / ξvfd ≈ 5 × 102 µm), allowing Eq. 11 to be reexpressed as
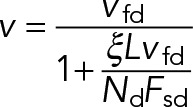 (16) (16)
|
Furthermore, if the maximum load force per motor is much less than the motor detachment force (ξLvfd ≪ Fdd; equivalently, L ≪ Fdd /ξvfd ≈ 3.5 × 102 µm), the load-dependent dissociation rate function (Eq. 4) is approximately Ωd(F) ≈ 1, and the motor detachment rate (Eq. 3) can be approximated as 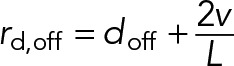 . We can then obtain the steady-state dynein attachment number by solving Eq. 1 for
. We can then obtain the steady-state dynein attachment number by solving Eq. 1 for 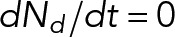 :
:
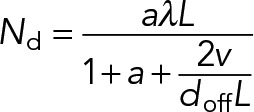 (17) (17)
|
Here we denote the unloaded attachment/detachment ratio for dynein as a = don / doff. Note that the coupled equations 16 and 17 reflect the interdependency of MT sliding velocity and motor attachment number: As more motors attach, thus reducing the load experienced by individual motors, the velocity approaches vfd (Eq. 16). However, as the sliding velocity increases, MTs slide past immobilized motors more rapidly (at an average rate of 2v/L), which in turn decreases the steady-state motor attachment number (Eq. 17). To obtain steady-state values of the variables v and Nd, as a function of system parameters, we can combine Eqs. 16 and 17, yielding the following quadratic equation:
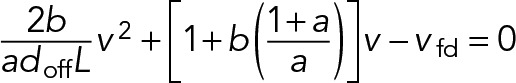 (18) (18)
|
Here the dimensionless parameter 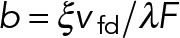 is a characteristic measure of the ratio of drag force to stall force at saturating levels of motor attachment and can be constrained based on experimental measurements (Table 1; b ≈ 1.6 × 10-5). In the limit that the maximum rate of dissociation due to sliding, 2vfd / L is much smaller than the rate of dissociation due to motor detachment (2vfd / L ≪ doff or, equivalently, L ≪ 2vfd / doff ≈ 19 µm), the steady-state attachment number (Eq. 17) reduces to a Michaelis-Menton-style equation:
is a characteristic measure of the ratio of drag force to stall force at saturating levels of motor attachment and can be constrained based on experimental measurements (Table 1; b ≈ 1.6 × 10-5). In the limit that the maximum rate of dissociation due to sliding, 2vfd / L is much smaller than the rate of dissociation due to motor detachment (2vfd / L ≪ doff or, equivalently, L ≪ 2vfd / doff ≈ 19 µm), the steady-state attachment number (Eq. 17) reduces to a Michaelis-Menton-style equation:
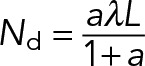 (19) (19)
|
and the steady-state sliding velocity becomes
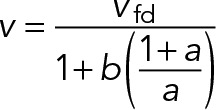 (20) (20)
|
Acknowledgments
This work was supported by a grant to P.W.B. from the National Institute of Neurological Disorders and Stroke (NINDS) (R01 NS28785). A.N.R. is supported by an National Research Service Award (1F31NS093748-01A1) from the NINDS.
Abbreviation used:
- MT
microtubule
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E17-06-0380) on October 4, 2017.
REFERENCES
- Ahmad FJ, He Y, Myers KA, Hasaka TP, Francis F, Black MM, Baas PW. Effects of dynactin disruption and dynein depletion on axonal microtubules. Traffic. 2006;7:524–537. doi: 10.1111/j.1600-0854.2006.00403.x. [DOI] [PubMed] [Google Scholar]
- Alper JD, Tovar M, Howard J. Displacement-weighted velocity analysis of gliding assays reveals that Chlamydomonas axonemal dynein preferentially moves conspecific microtubules. Biophys J. 2013;104:1989–1998. doi: 10.1016/j.bpj.2013.03.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baas PW. Microtubule stability in the axon: new answers to an old mystery. Neuron. 2013;78:3–5. doi: 10.1016/j.neuron.2013.03.012. [DOI] [PubMed] [Google Scholar]
- Baas PW, Lin S. Hooks and Comets: The story of microtubule polarity orientation in the neuron. Devel Neurobiol. 2011;71:403–418. doi: 10.1002/dneu.20818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baas PW, Mozgova OI. A novel role for retrograde transport of microtubules in the axon. Cytoskeleton. 2012;69:416–425. doi: 10.1002/cm.21013. [DOI] [PubMed] [Google Scholar]
- Baas PW, Deitch JS, Black MM, Banker GA. Polarity orientation of microtubules in hippocampal neurons: uniformity in the axon and nonuniformity in the dendrite. Proc Natl Acad Sci USA. 1988;85:8335–8339. doi: 10.1073/pnas.85.21.8335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brangwynne CP, Mackintosh FC, Kumar S, Geisse NA, Talbot J, Mahadevan L, Parker KK, Ingber DE, Weitz DA. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J Cell Biol. 2006;173:733–741. doi: 10.1083/jcb.200601060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevalier-Larsen E, Holzbauer ELF. Axonal transport and neurodegenerative disease. Biochim Biophys Acta. 2006;1762.11:1094–1108. doi: 10.1016/j.bbadis.2006.04.002. [DOI] [PubMed] [Google Scholar]
- Craig EM, Dey S, Mogilner A. Emergence of sarcomeric, graded-polarity and spindle-like patterns in bundles of short cytoskeletal polymers and two opposite molecular motors. J Phys: Condens Matter. 2011;23:374102. doi: 10.1088/0953-8984/23/37/374102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Francis F, Myers KA, Yu W, Black MM, Baas PW. Role of cytoplasmic dynein in the axonal transport of microtubules and neurofilaments. J Cell Biol. 2005;168:697–703. doi: 10.1083/jcb.200407191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heidemann SR, Landers JM, Hamborg MA. Polarity orientation of axonal microtubules. J Cell Biol. 1981;91:661–665. doi: 10.1083/jcb.91.3.661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasaka TP, Myers KA, Baas PW. Role of actin filaments in the axonal transport of microtubules. J Neurosci. 2004;24:11291–11301. doi: 10.1523/JNEUROSCI.3443-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imafuku Y, Toyoshima YY, Tawada K. Fluctuation in the microtubule sliding movement driven by kinesin in vitro. Biophys J. 1996;70:878–886. doi: 10.1016/S0006-3495(96)79631-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunwar A, Tripathy SK, Xu J, Mattson MK, Anand P, Sigua R, Vershinin M, McKenney RJ, Yu CC, Mogilner A, Gross SP. Mechanical stochastic tug-of-war models cannot explain bidirectional lipid-droplet transport. Proc Natl Acad Sci USA. 2011;108:18960–18965. doi: 10.1073/pnas.1107841108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee TJ, Lee JW, Haynes EM, Eliceiri KW, Halloran MC. The kinesin adaptor Calsyntenin-1 organizes microtubule polarity and regulates dynamics during sensory axonarbor development. Front Cell Neurosci. 2017;11:107. doi: 10.3389/fncel.2017.00107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu W, Lakonishok M, Gelfand VI. Kinesin-1 powered microtubule sliding initiates axonal regeneration in Drosophila cultured neurons. Mol Biol Cell. 2015;26:1296–1307. doi: 10.1091/mbc.E14-10-1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazel T, Biesemann A, Krejczy M, Nowald J, Muller O, Dehmelt L. Direct observation of microtubule pushing by cortical dynein in living cells. Cell. 2014;25:95–106. doi: 10.1091/mbc.E13-07-0376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogilner A, Zemel A. Expansion and polarity sorting of microtubule-dynein bundles. Prog Theor Phys Suppl. 2008;173:17–20. [Google Scholar]
- Muller MJI, Klumpp S, Lipowsky R. Tug-of-war as a cooperative mechanism for bidirectional cargo transport by molecular motors. Proc Natl Acad Sci USA. 2008;105:4609–4614. doi: 10.1073/pnas.0706825105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers KA, Baas PW. Kinesin-5 regulates growth of the axon by acting as a brake on its microtubule array. J Cell Biol. 2007;178:1081–1091. doi: 10.1083/jcb.200702074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pringle J, Muthukumar A, Tan A, Crankshaw L, Conway L, Ross JL. Microtubule organization by kinesin motors and microtubule crosslinking protein MAP65. J Phys Condens Matter. 2013;25:374104. doi: 10.1088/0953-8984/25/37/374103. [DOI] [PubMed] [Google Scholar]
- Rao AN, Patil A, Black MM, Craig EM, Meyers KA, Yeung HT, Baas PW. Cytoplasmic dynein transports axonal microtubules in a polarity-sorting manner. Cell Rep. 2017;19:1–10. doi: 10.1016/j.celrep.2017.05.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shima T, Kon T, Imamula K, Ohkura R, Sutoh K. Two modes of microtubule sliding driven by cytoplasmic dynein. Proc Natl Acad Sci USA. 2006;103:17736–17740. doi: 10.1073/pnas.0606794103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Y-H, Mandelkow E. Recombinant kinesin motor domain binds to b-tubulin and decorates microtubules with a B-surface lattice. Proc Natl Acad Sci USA. 1993;90:1671–1675. doi: 10.1073/pnas.90.5.1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svoboda K, Schmidt CF, Schnapp BJ, Block SM. Direct observation of kinesin stepping by optical trapping interferometry. Nature. 1993;365:721–727. doi: 10.1038/365721a0. [DOI] [PubMed] [Google Scholar]
- Tanenbaum ME, Vale RD, McKenney RJ. Cytoplasmic dynein crosslinks and slides anti-parallel microtubules using its two motor domains. eLife. 2013;2:e00943. doi: 10.7554/eLife.00943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallee RB, Williams JC, Varma D, Barnhart LE. Dynein: an ancient motor protein involved in multiple modes of transport. J Neurobiol. 2004;58:189–200. doi: 10.1002/neu.10314. [DOI] [PubMed] [Google Scholar]
- van Beuningen SF, Will L, Harterink M, Chazeau A, van Battum EY, Frias CP, Franker MA, Katrukha EA, Stucchi R, Vocking K, et al. TRIM46 controls neuronal polarity and axon specification by driving the formation of parallel microtubule arrays. Neuron. 2015;88:1208–1226. doi: 10.1016/j.neuron.2015.11.012. [DOI] [PubMed] [Google Scholar]
- Wang L, Brown A. Rapid movement of microtubules in axons. Curr Biol. 2002;12:1496–1501. doi: 10.1016/s0960-9822(02)01078-3. [DOI] [PubMed] [Google Scholar]
- Yokokawa R, Murakami T, Sugie T, Kon T. Polarity orientation of microtubules utilizing a dynein-based gliding assay. Nanotechnology. 2008;19:125505. doi: 10.1088/0957-4484/19/12/125505. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Wildonger J, Ye B, et al. Dynein is required for polarized dendritic transport and uniform microtubule orientation in axons. Nat Cell Biol. 2008;10:1172–1180. doi: 10.1038/ncb1777. [DOI] [PMC free article] [PubMed] [Google Scholar]