A model of the core of the yeast spindle pole body (SPB) was created by a Bayesian modeling approach that integrated a diverse data set of biophysical, biochemical, and genetic information. The model led to a proposed pathway for the assembly of Spc110, a protein related to pericentrin, and a mechanism for how calmodulin strengthens the SPB during mitosis.
Abstract
Microtubule-organizing centers (MTOCs) form, anchor, and stabilize the polarized network of microtubules in a cell. The central MTOC is the centrosome that duplicates during the cell cycle and assembles a bipolar spindle during mitosis to capture and segregate sister chromatids. Yet, despite their importance in cell biology, the physical structure of MTOCs is poorly understood. Here we determine the molecular architecture of the core of the yeast spindle pole body (SPB) by Bayesian integrative structure modeling based on in vivo fluorescence resonance energy transfer (FRET), small-angle x-ray scattering (SAXS), x-ray crystallography, electron microscopy, and two-hybrid analysis. The model is validated by several methods that include a genetic analysis of the conserved PACT domain that recruits Spc110, a protein related to pericentrin, to the SPB. The model suggests that calmodulin can act as a protein cross-linker and Spc29 is an extended, flexible protein. The model led to the identification of a single, essential heptad in the coiled-coil of Spc110 and a minimal PACT domain. It also led to a proposed pathway for the integration of Spc110 into the SPB.
INTRODUCTION
The centrosome is the primary hub for microtubule nucleation in most animal cells (Lüders and Stearns, 2007; Conduit et al., 2015; Petry and Vale, 2015). By imposing polarity on the microtubule cytoskeleton, it coordinates the many cellular processes that are dependent on directed transport by microtubules or microtubule-based motors (Hirokawa, 1998; Howard and Hyman, 2003; Bornens, 2012). Yet, despite its importance, our understanding of the centrosome is incomplete. Proteins assigned to the human centrosome currently number 1053, with 324 having evidence from more than one source (Alves-Cruzeiro et al., 2014). However, few of these proteins are annotated with a molecular function. The molecular mechanisms that regulate microtubule nucleation are largely unknown (Petry and Vale, 2015).
Despite its complexity, an outline of the molecular structure of the centrosome is beginning to emerge (Jana et al., 2014; Mennella et al., 2014; Winey and O’Toole, 2014; Feng et al., 2017). Centrosomes are composed of two centrioles surrounded by pericentriolar material (PCM). Proteins and interactions that drive the ninefold symmetry at the core of the centriole have been identified in a number of eukaryotes. Some components of the PCM are layered, extending away from the centriole, and organized into apparent fibers and matrices. Recently an in vitro reconstitution of a stable network of SPD-5 from Caenorhabditis elegans suggests that SPD-5 serves as the structural foundation of the PCM and forms a scaffold onto which other proteins assemble and that concentrates tubulin, allowing microtubule nucleation (Woodruff et al., 2015, 2017). In Drosophila, Cnn and DSpd-2 together form a dynamic scaffold that initially forms near the centrioles and then spreads outward. Despite these insights, our understanding of the structure and molecular interactions of the centrosome, and the PCM in particular, is still in its infancy.
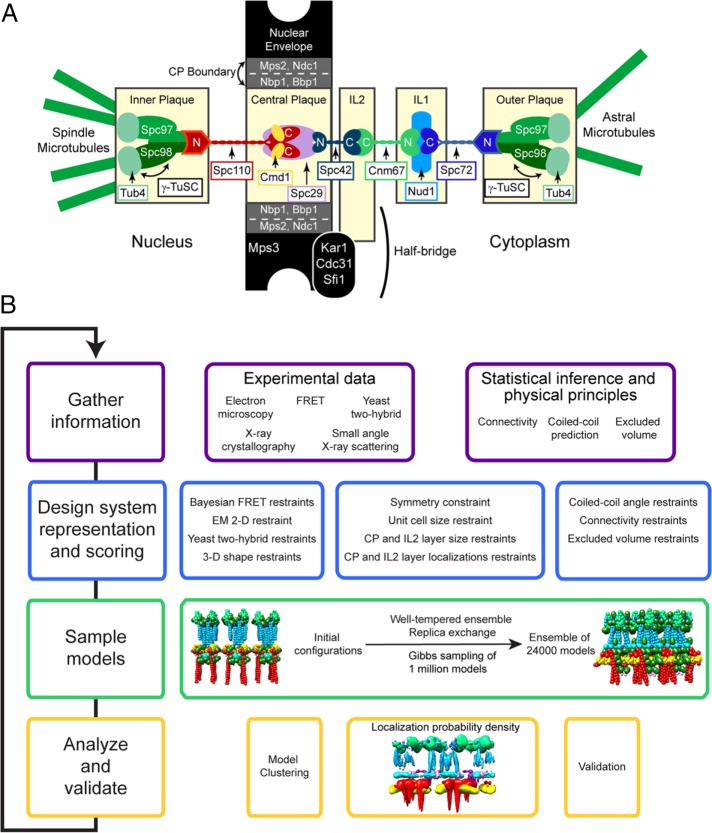
The spindle pole body (SPB) of Saccharomyces cerevisiae offers many advantages as a simple model for the centrosome (Figure 1A) (Jaspersen and Winey, 2004). Foremost, it contains only 18 proteins (Burns et al., 2015). Although the SPB does not contain centrioles, at its core it does contain a lattice formed by the protein Spc42 (Bullitt et al., 1997; Muller et al., 2005). This lattice is a scaffold on which the SPB core is assembled. Spc42 interacts with Spc29 to anchor the SPB in the nuclear envelope during a closed mitosis. It also interacts with Spc110 and Cnm67, two proteins that extend from the core in opposite directions toward the sites of mitotic and astral microtubule formation.
FIGURE 1:
Schematic outlines of the basic organization of the S. cerevisiae SPB and the experimental approach. (A) The SPB contains five layers: the inner, central, and outer plaques and the IL1 and IL2 layers. Each one is composed of large multimeric complexes of the indicated proteins. Adjacent layers are linked by coiled-coil proteins that extend between layers with their N- and C-termini in opposing layers. The inner and outer plaques are the sites of nuclear and cytoplasmic microtubule nucleation, respectively. They contain γ-tubulin (Tub4) complexes anchored to the SPB by Spc110 and Spc72. The CP is surrounded by a ring of boundary proteins that are embedded in the nuclear membrane. The half-bridge is a unique asymmetric protrusion where SPB duplication is initiated. (B) Integrative structure determination proceeds through four stages: 1) gathering of data; 2) representation of subunits and translation of the data into spatial restraints; 3) configurational sampling to produce an ensemble of structures consistent with the input information; and 4) analysis and validation of the ensemble structures. The process is iterative until an acceptable model is obtained. Further details are provided in Supplemental Tables S1 and S2 and Materials and Methods.
On the nuclear face of the SPB, the protein Spc110 shares structural similarities with the centrosomal proteins pericentrin and centrosomin (Lin et al., 2014). Spc110 serves many functions. At its N-terminus, it binds the γ-tubulin small complex (γ-TuSC) (Knop and Schiebel, 1997; Nguyen et al., 1998) and directs the oligomerization of γ-TuSC to form a ring (Kollman et al., 2008, 2011, 2015; Lyon et al., 2016). This ring then acts as a template for microtubule nucleation in a mechanism proposed to be highly conserved (Kollman et al., 2011). The C-terminus of Spc110 is anchored to the SPB via a conserved PACT domain and, like human pericentrin, binds calmodulin (Geiser et al., 1993; Stirling et al., 1994). Connecting the N- and C-terminal domains is a central coiled region of ∼800 Å in length. Spc110, like many pericentriolar proteins (Conduit et al., 2014), is dynamic, with half the Spc110 exchanging in a cell cycle–dependent manner (Yoder et al., 2003).
Given the conservation of critical components, the structure of the SPB is likely to share fundamental features common to all microtubule-organizing centers (MTOCs). To assemble a structural model of the SPB core, we developed and applied a Bayesian modeling approach (Rieping et al., 2005) to properly integrate data from different types of experiments. This Bayesian approach addresses the challenges presented by data sparseness, noise, and ambiguity. Similar integrative Bayesian techniques have been successfully used to determine the structure of a number of other large biomolecular assemblies (Erzberger et al., 2014; Molnar et al., 2014; Street et al., 2014; Robinson et al., 2015; Fernandez-Martinez et al., 2016). The data used here embrace both sources from the literature and novel data acquired from x-ray crystallography on the structure of calmodulin bound to Spc110, SAXS analysis of Spc29, and in vivo fluorescence resonance energy transfer (FRET) data. The novel integration of the FRET data took advantage of a new Bayesian approach to compute FRETR values from a model (Bonomi et al., 2014).
The model predicted the region of Spc110/calmodulin that bound the SPB. This insight was validated by genetic analysis that identified a single heptad of the coiled-coil of Spc110 that was essential for viability and further narrowed the essential region of its PACT domain. The model also offers a possible mechanism for how calmodulin and the calmodulin-binding domain (CBD) of Spc110 strengthens the SPB during mitosis (Fong et al., 2017). The results led to a proposed model for the assembly of Spc110 into the SPB.
RESULTS
Structural models of the SPB core were obtained using an integrative Bayesian approach (Rieping et al., 2005) that properly combines all the available data by weighting each piece of information based on its level of noise. In general, the integrative modeling approach consists of four basic steps (Alber et al., 2007a,b) (Figure 1B): 1) gather information; 2) design the system representation and scoring function; 3) sample models; and 4) analyze and validate the resulting models.
Gathering of data
First, published structural information from the literature on the SPB core was gathered. The data include data from genetic and biochemical approaches, cryo-electron microscopy (cryo-EM), tomography, and the high-resolution x-ray crystal structure of the C-terminal domain of Cnm67 (see Supplemental Table S4 and Materials and Methods: Stage 1). Next new data were acquired on the structure of the central plaque (CP).
Calmodulin (Cmd1) and Spc110.
Crystallographic data for the structure of the S. cerevisiae calmodulin bound to the C-terminus of Spc110 could not be obtained. However, calmodulin from Kluyveromyces lactis did productively cocrystalize with Spc110891-944 (Figure 2, A and B, and Supplemental Materials). K. lactis calmodulin is 95% identical in sequence to S. cerevisiae calmodulin. There are two notable differences. Calmodulin from S. cerevisiae binds three Ca2+ ions (Geiser et al., 1991; Starovasnik et al., 1993; Ogura et al., 2012). However, in K. lactis, Gln63, which participates in the coordination of Ca2+ in site 2, is replaced with alanine. Thus K. lactis calmodulin only binds two Ca2+ ions per peptide chain, one each in the N- and C-terminal globular lobes (Figure 2A). The other difference is that Ser79 is replaced with cysteine. This position sits at the center flex point between the helices connecting the two lobes of calmodulin (Kursula, 2014; Villarroel et al., 2014).
FIGURE 2:
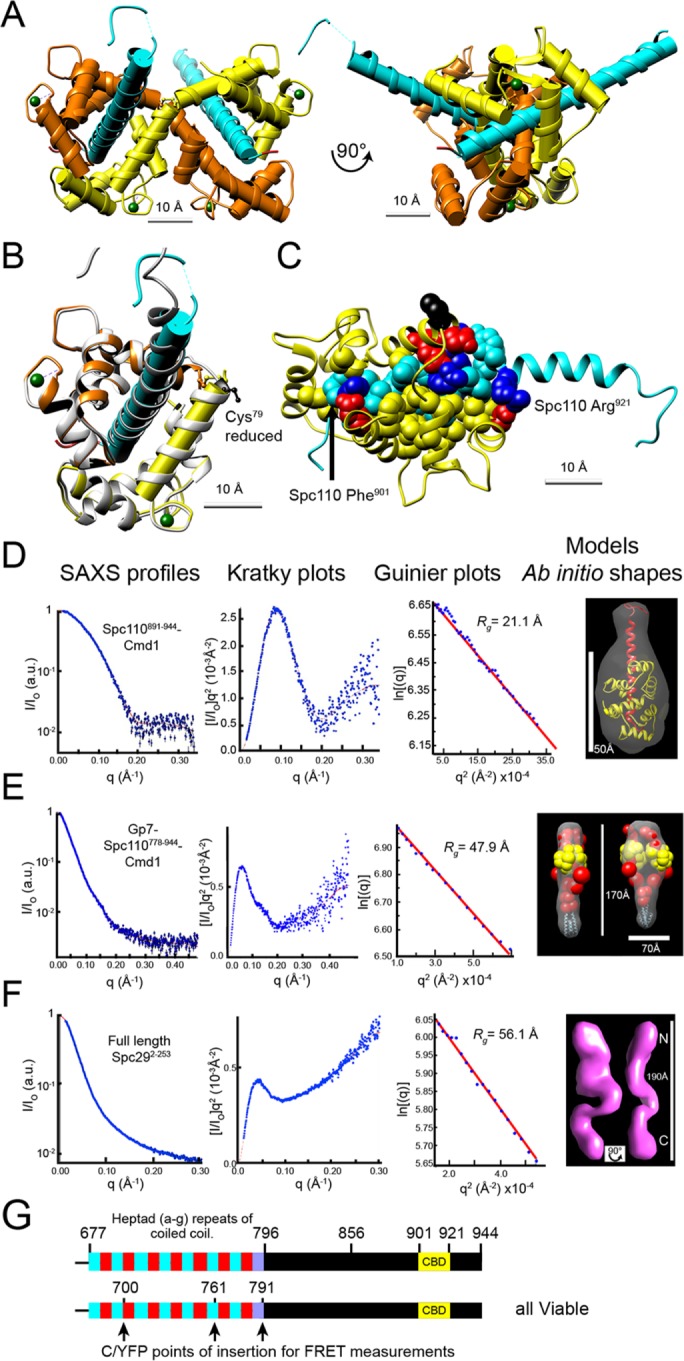
Analysis of the structures of calmodulin, Spc110, and Spc29. (A) Ribbon model of the crystal structure of Spc110891-944 in complex with K. lactis calmodulin. The complex crystallized as interlocking dimers connected by a disulfide bond between Cys79. The two calmodulins are shown in yellow and orange. Each calmodulin bound only two calcium atoms (green), in loops I and III. Spc110 is colored cyan. Cylinders show the helices. (B) Comparison of crystal structure with an atomistic model used in modeling. A ribbon for the atomistic model, in gray, is overlaid upon the left half of the crystal structure as shown in A. The fourth helix (D) of calmodulin and the helix of Spc110 are highlighted with cylinders. Cys79 is black. The atomistic model fits well with the crystal structure. In particular, the crossing angle between the Spc110 helix and calmodulin helix E (which ends with Cys79) in the crystal structure (55.7°) is preserved in the model (55.6°). (C) Nonpolar and charged polar amino acid residues anchor Sp110 CBD in the crystal structure. A modified ribbon structure of Spc110891-944 in cyan, with the nonpolar residues of the CBD shown as cyan spheres and the basic residues in gray with nitrogen atoms blue. The ribbon structure of calmodulin (Chain B:Met1-Cys79 in orange, Chain A:Cys79-Lys147 in yellow) and the acidic residues that bind the peptide in gray with oxygen atoms in red. The nonpolar residues of calmodulin that bind the peptide are not highlighted to better view the CBD. (D–F) SAXS profiles (first column; blue dots with black error bars), Kratky plots (second column; blue dots), and Guinier plots (third column; blue dots) are shown along with the extrapolation curves (red) for Spc110891-944-Cmd1 (D), Gp7-Spc110778-944-Cmd1 (E), and full-length Spc292-253 (F). (G) The position of internal FPs in Spc110 used for FRET measurements. The schematic shows the predicted coiled-coil (heptad repeats in alternating cyan and red) and CBD (in yellow) structure of the portion of Spc110 included in the model. CFP and YFP were inserted at the positions indicated in the full-length, lone genomic copy of Spc110. The last heptad with diminishing probability is shown in purple.
The CBD of Spc110 is FKTVALLVLACVRMKRIAFYR (positions 901–921) (Figure 2B). It represents a classic calmodulin target, with basic residues located at either end of nonpolar residues and position 1 anchored with phenylalanine. The peptide forms a helix in the bound state and binds to nonpolar and acidic residues in calmodulin.
The most striking feature of the crystal structure is the 2:2 stoichiometry of the Spc110 CBD with calmodulin and a domain swap (Figure 2, A and B). Unlike canonical binding, in which a single calmodulin wraps around the CBD, in this structure, the central helices of the two calmodulins remain extended and cross in an antiparallel manner. The crossover point is at a disulfide formed between the corresponding Cys79 in the two calmodulins. The CBD is still enwrapped by calmodulin, but the N-lobe of one calmodulin works in concert with the C-lobe of the other calmodulin. The conformation links two Spc110 CBDs in an antiparallel arrangement. The two helices of the CBDs cross with an angle of 46°, spaced 26.8 Å apart.
The SAXS profile of Spc110891-944 and K. lactis calmodulin shows that they are in a 1:1 complex in solution (Figure 2D, Supplemental Figure S1A, and Supplemental Table S1). The sharp peak of the Kratky plot suggests a low level of flexibility, while the linearity of the Guinier plot confirms a high degree of homogeneity. For modeling, we used an atomistic model of a 1:1 complex to allow more freedom in its position (Figure 2C). The atomistic model was developed using the high-resolution crystal structure (Materials and Methods: Stage 2). For verification, we calculated a SAXS profile for our atomistic model and found it agrees well with the experimental curve (Supplemental Figure S1A).
Our model of Spc110 extends from Spc110K680, which is within the long coiled-coil, to Spc110W944 at the C-terminus. We had previously shown that in S. cerevisiae Spc110736-944 is a stable domain that binds calmodulin to form a heterodimer (Muller et al., 2005). This result was confirmed by SAXS analysis of MBP-Spc110736-944/calmodulin (S. cerevisiae) (Supplemental Table S1, fraction B, and Supplemental Figure S1B).
Spc29.
Recombinant Spc29 was purified and subjected to SAXS analysis (Figure 2F and Supplemental Table S1). Phosphomimetic mutations were introduced (Supplemental Methods) to reflect the phosphomodifications present in yeast (Keck et al., 2011). The monotonous increase in the Kratky plot of the SAXS analysis shows that the purified Spc29 is largely disordered, while the linearity of the Guinier plot predicts a high degree of homogeneity. Thus the purified protein is not globular or compact but flexible, with a maximum length of 188 Å (Supplemental Table S1). For modeling, the distance between the beads representing the N- and C- termini of Spc29 is restrained to the range of 130–173 Å based on the SAXS-derived radius of gyration and bead dimensions (Table 1, Supplemental Table S1, and Supplemental Methods).
TABLE 1:
Restraints used for integrative structure modeling of the SPB core.
| Restraints | Restrained feature | Functional form and parameters | Ref.a |
|---|---|---|---|
| Bayesian FRET | Distances between termini of SPB proteins and Spc110 coiled-coil | See Bonomi et al., 2014 | 1 |
| Cryo-EM density | Position of Spc42 | See Velazquez-Muriel et al., 2012; Materials and Methods | 3 |
| Unit-cell size and shape | Dimensions of the rhomboid primitive unit cell | Uniform distribution with bounds 9 to 13.5 nm | 3 |
| Planar Spc42 | Position of Spc42 | Harmonic bound on the z-axis distance between every pair of N-terminal beads (and separately, every pair of C-terminal beads) of Spc42 copies, with mean 0 nm and spring constant 1 kBT | 3, 6 |
| Coiled-coil angle | Orientations of coiled-coil domains of Spc42, Spc110, and Cnm67 | Harmonic upper bound on the tilt angle between the coiled-coil domain and the z-axis, with threshold of 0° for Spc110 and Cnm67 and 20° for Spc42; spring constant 100 kBT | 3, 6 |
| CP-layer localization | Position of CP layer protein domains |
|
2, 3, 4 |
| SAXS shape | Structure of the Spc110-Cmd1 dimer |
|
1 |
| Distance restraints for unstructured domains |
|
Likelihood: Lognormal distribution with mean d and width 0.001 Prior: Uniform distribution for d between 13-17.3 nm (Spc29) and 0–6.44 nm (Spc42) |
1 |
| Yeast two-hybrid | Proximities between interacting SPB protein domains | Harmonic bounds on the minimum distances between all pairs of the beads representing the two interacting domains, with mean 0 nm and spring constant of 1 kBT | 4, 5 |
| Cnm67-Spc42 binding site | Proximity between Cnm67 C-terminus and Spc42 | Harmonic bound on the minimum distance between all pairs of beads representing Spc42 and beads corresponding to residues 503–514 of Cnm67 with mean 0 nm and spring constant of 1 kBT | 8 |
| Excluded volume | Distances between SPB components | Harmonic lower bound with mean 0 nm, spring constant 0.1 kBT | 1, 7 |
| Sequence connectivity | Distances between consecutive beads of SPB components and between SPB components and FPs | Harmonic bound on the surface distance between consecutive beads, with mean 0 nm, spring constant 1 kBT | 1, 7 |
aReferences are as follows: 1. this study; 2. Rout and Kilmartin, 1990; 3. Bullitt et al., 1997; 4. Adams and Kilmartin, 1999; 5. Elliott et al., 1999; 6. O’Toole et al., 1999; 7. Alber, 2007a.
In vivo FRET.
We re-collected in vivo FRETR data (Supplemental Table S2) from yeast strains that had previously been used to derive a simple model of the yeast SPB core based on coarse classifications of the FRETR values and Euclidean geometry (Muller et al., 2005). The recollection allowed us to take advantage of a new Bayesian approach to compute FRETR values from a model (Bonomi et al., 2014). This novel approach rigorously addresses uneven fluorophore brightness, signal contributions from multiple donors and acceptors, photobleaching, and flexibility of the linker connecting the fluorophore to the tagged protein, as well as cross-talk and spectral bleed-through of donor and acceptor fluorescence.
In addition, preliminary models (unpublished data) suggested that part of the coiled-coil region of Spc110 was embedded in the CP. To both validate and extend this preliminary result, the fluorescent proteins (FPs) cyan fluorescent protein (CFP) and yellow fluorescent protein (YFP) were inserted in frame in three positions within the last dozen heptad repeats (Figure 2G) and used for FRET measurements with CFP and YFP tags at the C-termini of calmodulin, Spc29 and the N-terminus of Spc42 (Supplemental Table S2).
Representations and restraints
The structural information used to model the core of the SPB was obtained from approaches that yielded data at dramatically different resolutions. Thus the SPB components are represented at resolutions ranging from a few residues per bead, when crystallographic structures or comparative models were available, to coarse grained, with tens of residues per bead (Supplemental Table S3 and Figure 3A). Atomic structures for Cnm67, fluorescent proteins and calmodulin, and predicted coiled-coil regions in Cnm67, Spc42, and Spc110 are modeled as rigid bodies, while the remaining beads in a protein are represented as a flexible chain of beads. For Spc29 and the C-terminal domain of Spc42, only the termini are represented to increase the efficiency of configurational sampling in the absence of any knowledge of the intervening structure. Protein stoichiometry was initially based on a previous study (Muller et al., 2005).
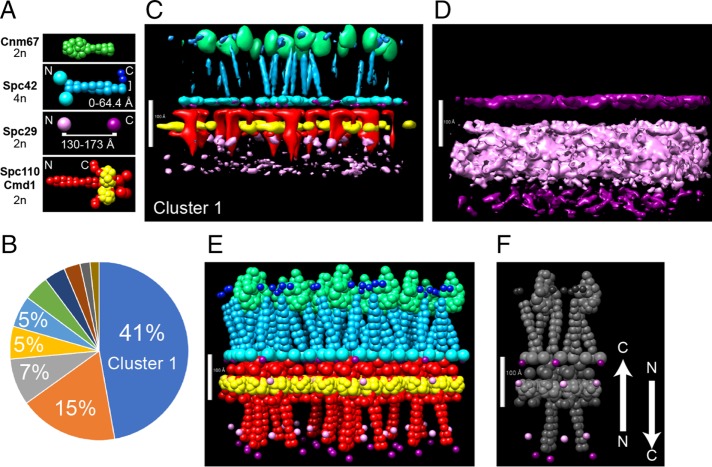
FIGURE 3:
Integrative structure modeling of the SPB core. There are two copies of Spc29 per unit cell. (A) Representations of proteins (not to scale). Distance restraints for Spc42 C-terminus and Spc29 and protein stoichiometry are shown. Detailed descriptions of all representations are in Supplemental Table S3, and restraints are listed in Table 1 and Supplemental Table S1. Note that modeling of the FRET data explicitly included the structure of fluorescent proteins, but they are not shown for clarity. (B) The distribution of clusters. All models were clustered as described in Materials and Methods. The percentages of models in the largest clusters are shown in the pie chart. (C–F) Different representations of cluster 1. Models in cluster 1 were combined to create a probability-density map of all proteins (C) and Spc29 alone (D). The color scheme reflects the representations in A. To display the distribution, a 50% threshold was used in C and a 75% threshold was used in D. The highest-scoring model is shown in E, with the positions of the termini of Spc29 highlighted in F. Scale bars: 100 Å.
The gathered data were translated by our Bayesian method into spatial restraints that were subsequently used to help define the positions of the SPB components (Table 1, Supplemental Table S4, and Materials and Methods: Stage 2). The relative weights of these restraints were not set a priori but were automatically determined by our Bayesian approach, dependent on the quantified level of noise in the data. Low-noise data resulted in stronger structural restraints, whereas high-noise data were down-weighted in the construction of structural models.
Initial models
The architecture of the SPB core layers was modeled using the open-source Integrative Modeling Platform (IMP) package (Russel et al., 2012), version 2.3 (Materials and Methods). IMP produced an ensemble of models that were subsequently grouped into clusters of structurally similar models. Similarity between two models was measured by the distance root-mean-square deviation for bead coordinates (Materials and Methods: Stage 4). A cutoff radius of 15 Å was chosen to define a cluster and thus set the precision of our models (Materials and Methods: Stage 4). The size of a cluster (Figure 3B) is proportional to its posterior probability and thus quantifies the confidence assigned to the cluster given all the available information.
Several visualizations are presented of the most populated cluster, cluster 1 at 42% of the total (Figure 3, C–F). The localization–probability density maps define the probability of any voxel being occupied by a specific protein in a set of models (Materials and Methods: Stage 4).
Cnm67 is deeply embedded within the IL2 layer, with a fraction of its lower surface below the C-terminus of Spc42 and in a position to bind the coiled-coils of Spc42 (region Spc42138-353 is not represented in our models for the same reasons Spc2911-243 was omitted, because of lack of structural information, as discussed earlier).
The CP is a densely packed region ∼100 Å thick with a sparse region beneath it (Figure 3, C and E). The probability density of Spc110 shows a hooklike shape rising to an interface with the Spc42 N-terminus before curling back to bind to calmodulin. The calmodulin probability density is well defined and somewhat exposed to the nucleoplasm. The probability-density map of Spc29 has a broad distribution that is clearer when the probability threshold is reduced to 75% (Figure 3D). The localization of the N-terminus is spread over an area spanning more than 100 Å, and there are two widely separated regions for the C-terminus. One is a more probable position in the area of the Spc42/Spc110 interface, and a second one in a region near the furthest limit of the CP, below the start of the coiled-coil of Spc110.
The prominent features of cluster 1 are as follows: The coiled-coils of Spc42 and Spc110 are bundled into trimers of dimers (Figure 3, D–F). The end of the Spc4260-137 coiled-coil is proximal to Cnm67. The end of the Spc110 coiled-coil is part of the interface with Spc42. Calmodulins are positioned tightly together with adjacent chains almost in contact. The unique feature of cluster 1 is two antiparallel populations of Spc29 (Figure 3F): one with the C-terminus embedded in the CP, and one with the C-terminus ∼230 Å away and far down along the coiled-coil of Spc110. The N-termini are sandwiched between these extremes. Both copies lay perpendicular to the plane of the CP. This unique feature was shared among the top 10 clusters produced by this initial modeling run (Figure 3B).
The C-termini of Spc29 are in a single layer
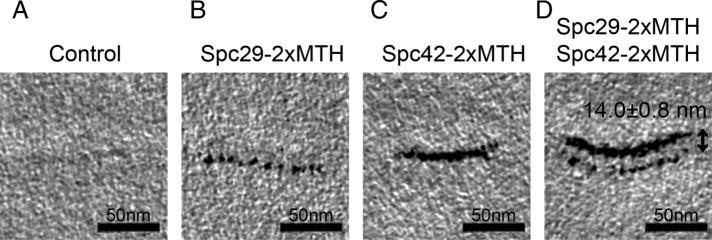
For testing the two-layer organization of C-termini of Spc29, the SPB was imaged by electron tomography of high-pressure freezing/freeze substitution–prepared cells with the C-termini of Spc29 tagged with metallothionein (MTH) (Figure 4) (Supplemental Materials and Methods). This technique can resolve layers separated by at least ∼80 Å and thus would be able to determine whether the two layers of Spc29 are separated by ∼230 Å. However, the images clearly show a single layer of Spc29 (Figure 4B). Based on a dual-labeled experiment in which both Spc42 and Spc29 were tagged with MTH, the C-termini of Spc29 are ∼140 ± 8 Å from the C-termini of Spc42 in the CP (Figure 4D). Thus the electron tomography invalidated the two-layer organization of Spc29 seen in the initial models.
FIGURE 4:
Tomographic slices of MTH-tagged proteins precisely localize Spc29 and Spc42. (A) In an untagged control strain, the SPB is faintly visible. (B) Spc29 tagged with two copies of MTH localizes to one layer of the SPB. (C) Spc42 tagged with two copies of MTH is also localized to a single layer of the SPB. (D) Spc29 and Spc42 localize to discrete layers of the SPB. The MTH tags on their C-termini are 14.0 ± 0.8 nm apart in a strain expressing both tagged proteins.
Molecular architecture of the SPB core with reduced Spc29
The cryo-electron tomography of Spc29-MTH, showed that the initial modeling had inaccurately positioned the C-terminus of Spc29. Some aspect of either our representation of the SPB or the restraints must be incorrect. One feature of the model we explored was the assumption that Spc29 was in a single uniform population in the SPB. Perhaps there were two pools with different conformations and contacts. In a sense this must be true, because Spc29 is the only CP component known to interact with Bbp1, part of a protein complex at the periphery of the SPB that anchors the SPB to the nuclear membrane (Schramm et al., 2000; Kupke et al., 2017). This peripheral pool of Spc29 would plausibly have different conformations than the pool at the core of the SPB, which interacts with CP proteins.
Modeling with half the amount of Spc29.
To account for two distinct functional and structural pools of Spc29, we decided to reduce by half the amount of Spc29 in the unit cell of our model. We modeled using a core stoichiometry of 4:1:2:2:2 for Spc42:Spc29:Spc110:Cmd1:Cnm67. The resulting model is discussed in the rest of the paper. The MTH tomogram test discussed earlier is passed by construction, because one Spc29 in the unit cell forces Spc29 to have identical orientations, and so a priori, the C-termini of Spc29 will be in one layer.
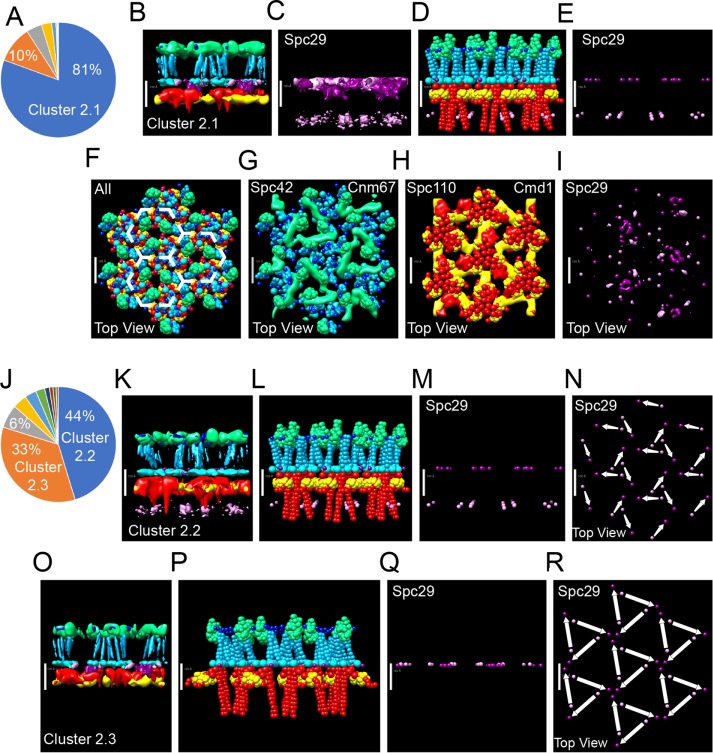
We clustered the models both excluding (Figure 5, A–I) and including (Figure 5, J–R) the positions of Spc29. At the precision of 15 Å and excluding Spc29, the majority (81%) of the models generated by our approach (Figure 5A) are classified into a single structural cluster, cluster 2.1.
FIGURE 5:
Integrative structure modeling of the SPB core. There is one copy of Spc29 per unit cell. All other restraints, protein representations, and the color schemes of the probability-density maps are the same as in Figure 3. In A–I, clustering did not include the positions of Spc29. (A) The percentages of models in the largest clusters are shown in the pie chart. (B–I) Different representations of cluster 2.1. Models in cluster 2.1 were combined to create a probability-density map of the locations of the proteins. To display the distribution, a 50% threshold was used in B and G–I, and a 75% threshold was used in C. The highest-scoring model is shown in D–I, with the positions of the termini of Spc29 highlighted in E. (D) Side view and (F) top (cytoplasmic) view of the top-scoring model. The probability-density maps are overlaid with the positions of the proteins in the top-scoring model as indicated (G–I). In J–R, clustering did include the positions of Spc29. (J) The percentage of the largest clusters. (K) The probability-density map (50% threshold) and highest-scoring model (L–N) of cluster 2.2. (M) Side view and (N) top view of the positions of the Spc29 termini. (N) Arrows show the connections between the termini of individual proteins. (O) The probability-density map (50% threshold) and highest-scoring model (P–R) of cluster 2.3. (Q) Side view and (R) top view of the positions of the Spc29 termini. (R) Arrows show the connections between the termini of individual proteins. The model is built on P3 symmetry and created a hexagonal array outlined in F. Scale bars: 100 Å.
To see whether clusters 1 and 2.1 were similar in their placement of all proteins except Spc29, we computed the distribution of distances between the top 10% of models in both clusters, excluding Spc29. The distances between proteins in the two clusters were of the same magnitude (mean = 12.9 Å) as the variability within an individual cluster (15 Å cutoff) (Supplemental Figure S2 and Materials and Methods). Therefore the two sets of models are similar in their placement of all proteins except Spc29.
All the main clusters lead to a single unified model for the organization of Spc42, Cnm67, Spc110, and Cmd1. Their organization will be described in detail first, before describing the variability of Spc29.
The organization of the IL2 layer.
The most striking feature of the IL2 layer is again the trimeric bundles of Spc42 coiled-coils seen in an en face view of the cytoplasmic face of the IL2 layer (Figure 5, F and G). Each coiled-coil dimer of Spc42 forms the vertex of a hexagonal lattice with an average spacing of 125 Å in cluster 2.1. The bead representing the C-terminal 10 amino acid residues of Spc42 sits near the end of the Spc42 coiled-coil. Therefore the rest of the C-terminal domain of Spc42, which was not modeled, must either loop around from the top of the coils back to the top of the same coils or stretch to adjoining coils.
Three homomeric dimers of Cnm67 line the interior of the Spc42 hexagonal array formed by 12 Spc42 chains. In Figure 5G, the 50% probability-density map is superimposed with the position of Cnm67 in the top-scoring model. With three dimers within the interior of the hexagon, the probability density has a triangular shape that may reflect either heterogeneity in the structure or a lack of sufficient input information to locate it more precisely (Figures 5, B, D, K, L, O, and P, and 3C). The C-terminal domain of Cnm67 is positioned to interact with the coiled-coil of Spc42.
Inter–IL2-CP distance.
The coiled-coil of Spc42 was not forced to be perpendicular to the CP (Supplemental Table S4) and was given the freedom to tilt as much as 20°. In addition, the distance between the IL2 and CP was only defined to have a maximum of 300 Å with a minimum of 0 Å. The coiled-coils are slightly tilted in our ensemble of models (Figure 5, B, D, K, L, O, and P). The distance between the base of Cnm67 and the bead representing the N-terminus of Spc42 is ∼94 Å, in close agreement with the 108 Å (O’Toole et al., 1999) determined by EM for the IL2-CP distance.
CP: Calmodulin, Spc110, and the N-terminus of Spc42.
Calmodulin is exposed to the nucleoplasm (Figure 5, B, D, K, L, O, and P). A layer of calmodulin sits under the interface between Spc110, Spc42, and Spc29. It is tightly packed, close enough to support a domain swap of adjacent calmodulin lobes as seen in the crystal structure but not used as a modeling restraint.
Figure 5H shows the en face view from the cytoplasmic side of the CP of just the Spc110/calmodulin layer, peeling away Spc42 and Cnm67. As in Spc42, the coiled-coils of Spc110 are in trimeric bundles of coiled-coil dimers. The region of Spc110 that links the coiled-coil and the calmodulin-binding motif is exposed and sits in juxtaposition to the N-terminus of Spc42 and the probable location of the C-terminus of Spc29. This exposed region represents the start of the PACT domain that binds Spc110 to the CP (Lin et al., 2014).
Spc29.
In cluster 2.1 (Figure 5, A–I), Spc29 was not considered in the clustering. Nevertheless, the probability-density map for Spc29 in cluster 2.1 suggests that the N- and C-termini had a higher probability of comingling in a broad layer with the N-terminus of Spc42 in CP (Figure 5C). There was still a significant probability that the N- and C-termini were apart and perpendicular to the plane of the CP, as shown for the top-scoring model in Figure 5, E and I.
Including the positions of Spc29 in the clustering process yielded two clusters, clusters 2.2 and 2.3. Representing 44% and 33% of the total populations, respectively, they describe two configurations for Spc29 (Figure 5, K–R).
In both clusters 2.2 and 2.3, Spc29 assumed an elongated conformation with the average distance between N- and C-terminus equal to 145 Å. In cluster 2.2, Spc29 is positioned along the axis perpendicular to the CP. The elongated Spc29 proteins create an interlocking matrix (Figure 5K). Trimeric bundles of N-termini on the nuclear side of the CP spread out and up to connect to trimeric bundles of the C-termini from neighboring proteins at the more cytoplasmic side of the CP. This arrangement is the same as in the top-scoring model in cluster 2.1 (Figure 5, E and I)
In cluster 2.3, the N- and C-termini of Spc29 are in a single plane on the cytoplasmic side of the CP (Figure 5, O–Q). Again, an interlocking matrix is formed, and the N-termini spread out to connect adjoining trimeric bundles of C-termini. However, here the N-termini appear to surround the C-terminal bundles.
In conclusion, our modeling finds the more probable position for the C-terminus of Spc29 is adjacent to the N-terminus of Spc42, consistent with the cryo-EM of Spc29-MTH. However, the position of the N-terminus is unresolved. The models computed for each of the two stoichiometries satisfy the FRET data comparably well; therefore our FRET data cannot be used to discriminate between the two stoichiometries. However, the initial models are not consistent with the MTH-tagged cryo-electron tomograms, which are consistent with the final model, albeit by construction. Additionally, the final models are consistent with the trimerization of Spc29 seen in vitro (see SAXS analysis under Model validation).
Model validation
Four key aspects of the model were assessed. First, we ensured that the sampling was exhaustive at the precision of the final model. Second, we showed that the model fits the data used to compute it. Third, we demonstrated that the model is robust with respect to omitting small subsets of the data used to construct the model (sensitivity analysis). Fourth, we showed that the model is consistent with the data not used in modeling. Specifically, a hypothesis based on the model, that the region at the end of the coiled-coil of Spc110 is critical for binding to the CP, was subsequently validated by genetic analysis. The agreements between the model and data not used to construct the model are particularly powerful validations of the model.
Sampling exhaustiveness.
The final clustering described earlier was performed on a merge of ensembles from two independent sampling runs initiated from different random configurations. First, when the runs were clustered independently (excluding Spc29), the population size of the largest cluster converges to 89% and 72% (runs 1 and 2, respectively) as the simulation progressed (Supplemental Figure S3A). Second, we applied a statistical test verifying that the two independent runs generate the same ensemble of models (Materials and Methods: Stage 4). Third, we visually inspected the probability-density maps of the main clusters from the two different runs and confirmed that they are similar, except for the position of Spc29 (Supplemental Figure S3B). These three tests indicate that the two runs converge to the same ensemble of models. The sampling was exhaustive and results in a single model at the precision of 15 Å (threshold for clustering). This precision is sufficiently high to pinpoint the locations and orientations of all components except Spc29.
Because sampling is exhaustive at 15 Å precision, overfitting (i.e., proposing only one or a few models consistent with the input information as the “correct models,” while there could potentially be many others equally consistent) is not a problem at this precision; all models at this precision that are consistent with the data are provided in the ensemble.
Fit to data used in modeling.
The computed FRET values for cluster 1 and clusters 2.1, 2.2, and 2.3 were compared with each other and to the input experimental values. The derived FRETR values for cluster 1 (Supplemental Figures S4A and S5A) and clusters 2.1, 2.2, and 2.3 (Supplemental Figures S4B and S5B, cluster 2.1 shown) are on average within 4% of the experimental data, which is significantly smaller than the standard deviations for the experimental data (13% of the FRETR value). Therefore the models are in excellent agreement with the FRETR data. This validation also demonstrates the strength of our method for converting distances in the model to FRETR values (Bonomi et al., 2014).
The three least-satisfied FRET pairs include Spc42-CFP/Spc29-YFP (17% lower than experimental), Spc29-CFP/Spc42-YFP (11% lower), and CFP-Spc42-YFP (15% lower). This difference is seen in all the clusters. In addition, for cluster 1, the FRET pair CFP-Spc42/Spc29-YFP is 34% higher than the experimental data. The CFP-Spc42/Spc29-YFP pair was the one example in which the reduced stoichiometry of Spc29 significantly improved the fit, as the model values are only 7%, 10%, and 3% higher in clusters 2.1, 2.2, and 2.3, respectively. The violations of the data by the model are in general due to error in the model and/or noise in the data; the most parsimonious explanation of the current violations is that they are likely due to the noise in the data, because the violations are so small (not larger than approximately 1 SD).
In conclusion, the overall agreement among the FRETR values is high and remarkably independent from the two Spc29 stoichiometries used. The Bayesian approach automatically down-weighs outliers, which contributes to the final accuracy of the model and the estimate of its precision.
The models also fit the two-hybrid data used in modeling well (Supplemental Figure S6A), in that the interactions implied by the data are present in the models.
Finally, the models and probability density indicate a hexagonal lattice of Spc42 (Figure 5, O and Q) as seen in the EM map, with an average lattice spacing of 125 Å, in agreement with the 126 Å spacing of the semicrystalline lattice of Spc42 in vivo (Bullitt et al., 1997).
Sensitivity analysis.
We assessed that our ensemble of models was robust with respect to the amount of data used, by means of a sensitivity analysis test (Materials and Methods: Stage 4) (Robinson et al., 2015). In three trials, the models generated when we randomly removed 5% of the FRET data were in good agreement with those obtained with the entire data set (Supplemental Figure S7, A–C) and fit the 5% unused FRETR data points (Supplemental Figure S7, D–F).
Fit to data not used in modeling
IL2-CP gap and lattice size.
As mentioned earlier, the existence of two distinct layers, IL2 and CP, and the exact sizing of the hexagonal lattice of Spc42 were not specified in modeling. Nevertheless, the model reproduced the gap between the IL2 and CP layers, in agreement with EM data (O’Toole et al., 1997). Moreover, the size of the hexagonal Spc42 lattice in the model (125 Å) reproduces the experimentally measured one (126 Å) (Bullitt et al., 1997) very precisely, even though the size of the lattice was restrained very weakly via soft cryo-EM density and unit cell size restraints.
Yeast two-hybrid data.
The models were assessed against the two yeast-two hybrid data points not used in modeling (Supplemental Figure S6B). The models show a contact between fragments 823 and 944 of two Spc110 copies, in agreement with one of the yeast two-hybrid data points (Adams and Kilmartin, 1999). A two-hybrid assay detected an interaction between Spc29 and fragment 811–898 of Spc110 (Elliott et al., 1999) that is also predicted by our models in cluster 2.1. Thus our models are validated by these yeast two-hybrid data points.
SAXS analysis.
As mentioned earlier, Spc110736-944 is a stable domain that binds calmodulin to form a heteromeric dimer (Muller et al., 2005), a result confirmed by SAXS analysis (Supplemental Table S1, fraction B). However, in gel filtration, a second fraction (Supplemental Figure S1B, fraction A) was also detected and subjected to SAXS analysis. This fraction scattered with a mass corresponding to a trimeric bundle of dimers, suggesting a stable hexameric complex (Table 1 and Supplemental Table S1). As visualized in Figure 5H for cluster 2.1, but observed in all clusters examined, the arrangement of Spc110680-944/calmodulin in the CP is also a bundle of three dimers (i.e., a hexamer). Therefore the gel filtration and SAXS analysis support the presentation of Spc110/calmodulin as a trimer of dimers found in the model.
In both clusters 2.2 and 2.3, three C-termini of Spc29 are in close proximity, suggesting trimerization. In cluster 2.2, the N-termini are clustered in groups of three, although not to the same peptide chains clustered at the C-termini. In agreement, the SAXS analysis of Spc29 showed that it formed a trimer (Supplemental Table S1). Spc29129-174 has also been shown to form a homotrimeric coiled-coil by circular dichroism and FRET in solution (Zizlsperger et al., 2008). Thus the tendency to form trimers is consistent with the ensemble of structures found when stoichiometry of Spc29 was reduced.
Genetic analysis.
Our models predict that the region of Spc110 from position 788 (which includes the last heptad repeat of the coiled-coil) to the start of the CBD interacts with Spc42 and Spc29 and binds Spc110 to the CP. The granularity of the model limited the precision of the prediction, but this prediction changes the limits of the PACT domain proposed to bind Spc110 to the SPB (Lin et al., 2014). To validate the model and refine the proposed binding region, we undertook a genetic analysis.
Prior genetic studies of Spc110 guided our approach. The C911R mutation in the CBD causes a temperature-sensitive loss of calmodulin binding, a loss of viability, and a failure of Spc110 to incorporate into the SPB (Sundberg et al., 1996). However, the binding of calmodulin to Spc110 is not essential. In a screen for extragenic suppressors of the temperature-sensitive cmd1-1 allele, five dominant alleles of Spc110 containing C-terminal truncations that removed the CBD were isolated (Geiser et al., 1993). In the largest viable truncation, S857 is mutated to an amber stop codon. A still larger truncation, Spc1101-827, could not support growth. Internal deletions also defined a region from R710 to R824 as being essential (Kilmartin et al., 1993). These prior results are summarized in Figure 6, b–f.
FIGURE 6:

The essential region of the C-terminal domain of Spc110. Row 1 diagrams the arrangement of the C-terminal region. Cyan and red depict locations of alternating heptad repeats with >90% probability of forming a dimeric coiled-coil, whereas purple indicates a drop in probability to 60% (Delorenzi and Speed, 2002; Alva et al., 2016). Viability was assessed as described in the Supplemental Methods. Information from the literature is indicated: 1. Sundberg et al., 1996; 2. Kilmartin and Goh, 1996; 3. Stirling et al., 1996; 4. Geiser et al., 1993; 5. Kilmartin et al., 1993; 6. Sundberg and Davis, 1997.
The earlier extragenic suppressor screen of cmd1-1 generated viable, dominant truncations of Spc110. To see whether longer, novel truncations could be found that narrowed the essential region for binding of Spc110 to the SPB, we mutated the C-terminal region of Spc110 and again screened for cmd1-1 suppressors.
We obtained a suppressor mutant allele, SPC110-230 (S809I, L813stop), that truncated 131 amino acids from the end (Figure 6, g and h). This removed the CBD and most of the PACT domain. S809I was necessary to maintain viability. The truncation did not affect the ratio of Spc29 to Spc42 nor their amounts (Supplemental Figure S8). Thus the majority of the C-terminal domain was not necessary for binding of Spc110 or Spc29 to the SPB. The requirement of S809I suggested that S809 participates in binding.
The well-characterized temperature-sensitive spc110-226 allele (Sundberg and Davis, 1997; Yoder et al., 2005) has point mutations in the area where Spc110-230 is truncated (L772M, R795L, D797V, N823S, L836P) (Figure 6i). We dissected the mutations and found that the N823S/L836P pair of mutations yielded a fully functional Spc110 protein. The model predicted that the last heptads of the coiled-coil participated in binding, but we found mutations N782G/ L785G, predicted to disrupt the last heptad of the predicted coiled-coil, yield a functional protein. However, one heptad repeat mutation, L785G, combined with the N823S/L836S pair of mutations, yields a temperature-sensitive Spc110 protein (Figure 6, j–m).
To further test the importance of the last heptad, we created an Spc110 mutant with an internal deletion, ΔN782-R788. This deletion creates a nonfunctional protein and, when integrated into the genome, leads to a loss of viability. Deletion of the penultimate heptad repeat (ΔI775-R781) leads to a functional protein able to support growth (Figure 6, n and o).
In sum, the genetic analysis strongly supports the proposed hooked conformation of Spc110 and the overall structure of the SPB core. The region of Spc110 facing and in closest contact with Spc42 (and likely the C-terminus of Spc29) in the model is shown to be essential (ΔN782-R788 is not viable) and sufficient (Spc110-230 is functional) for binding. The essential region includes the last heptad repeat of the coiled-coil, N782, and ends between L836 and S857. There is redundancy between the binding at L785 and N823/L826.
DISCUSSION
The relevance of coiled-coil domains
Centrosomes and SPBs are replete with coiled-coil proteins. Many of the coiled-coil domains of the yeast SPB have been characterized, which led to a model of SPB assembly (Zizlsperger and Keating, 2010). In our model of the CP/IL2 core layers, we include three coiled-coils in Spc110, Spc42, and Cnm67. Our model places the Spc110 coiled-coil at the interface with Spc42. Indeed, we find that a deletion of the most C-terminal high-probability heptad repeat is lethal. In addition, a point mutation in this heptad, coupled with point mutations in a nearby part of the PACT domain, confers a temperature-sensitive growth phenotype. Clearly, a high-resolution structure of the region of Spc110 from this heptad to residue L838 in the PACT domain would greatly enhance our understanding of how proteins containing PACT domains are recruited to centrosomes. In addition, the trimeric bundles of coils of Spc110 align with coils of Spc42, opening the possibility that they interact. Finally, Cnm67 is positioned to interact with the Spc42 coils region in the IL2 layer. The proposed structure suggests that the coils are more than inert spacers and may provide binding interfaces.
An unstructured structure
Spc29 is a major component of the CP, with four times the mass of the N-terminal, CP domain of Spc42. Spc29 is predicted to be 8% disordered (protein binding), 33% helical, and the rest unknown (PSIPRED; Buchan et al., 2013). It has two predicted coiled-coils, one of which, Spc29129-174, forms a homotrimeric coiled-coil in solution (Zizlsperger et al., 2008). We show by SAXS analysis that the full-length purified protein is highly flexible and confirm a trimer conformation.
Quantitative fluorescence microscopy of fluorescent protein–tagged SPB components showed a 2:1 stoichiometry of Spc42 to Spc29 at the SPB (Muller et al., 2005). However, our models generated with this stoichiometry are inconsistent with EM–tomography of Spc29 that was labeled and visualized with an MTH tag. Better agreement with the EM and the trimerization of Spc29 arise from models in which the stoichiometry of Spc29 is reduced by half. Even then, a single dominant conformation did not appear.
It is possible that, with more restraints, a single conformation would emerge. But it is also possible that the flexibility of Spc29 allows it to adopt multiple conformations. Spc29 does interact with Bbp1 at the periphery of the SPB (Schramm et al., 2000; Kupke et al., 2017), and this may represent a distinct pool of Spc29 with a different conformation. The models that arose when the amount of Spc29 was reduced by half, clusters 2.2 and 2.3, both suggest that Spc29 forms an interconnected matrix. Such a matrix might not have a unique configuration and perhaps resembles the gel-like properties of SPD-5, the PCM scaffold of the C. elegans centrosome (Woodruff et al., 2017).
The assembly of Spc110
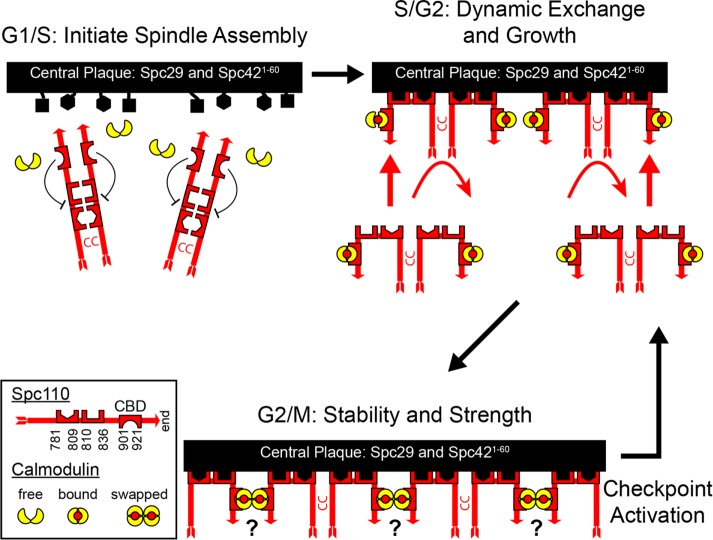
During cell division, the centrosome nucleates and organizes the microtubules necessary for proper chromosome segregation. In mammalian cells, it is difficult to determine how tightly the cell regulates the number of microtubules, given the size and complexity of the mitotic spindle. However, in S. cerevisiae, the number is clearly tightly controlled: one for each chromosome and two to six interpolar, interdigitated core microtubules are reproducibly found in the mitotic spindle (Winey and O’Toole, 2001). The mechanism by which this control is exerted is largely unknown (Storchova et al., 2006). A priori, because Spc110 anchors and activates the γ-TuSC at the SPB (Lyon et al., 2016), the regulation of the integration of Spc110 must be part of the process for controlling the number of microtubules. Here the structure predictions and genetic analysis presented in this paper, combined with information in the literature, allowed us to formulate a model for the assembly of Spc110 into the SPB (Figure 7).
FIGURE 7:
Model for the assembly of Spc110 into the SPB. The process is depicted as having three phases. During the initial phase, Spc110 is synthesized and binding sites in Spc42 and Spc29 become accessible in both the old and new poles. The second phase is a period of dynamic exchange and growth. The third phase ends exchange and strengthens the pole to withstand the pulling forces in the spindle. Checkpoint activation renews a period of expansion that later contracts when the checkpoint is satisfied.
Calmodulin binding to Spc110 is required for its recruitment to the SPB (Sundberg et al., 1996). Spc110 binds to the SPB via two redundant binding regions, one at N782-Y811 and a second between K812-Y838. The models predict that both are exposed to a layer of Spc42, and perhaps Spc29, at the CP. The canonical Pfam PACT domain, a conserved centrosomal targeting motif (Gillingham and Munro, 2000), begins at M802 (Lin et al., 2014). Residues Y811 and Y838 are highly conserved in all PACT domains. Here we have expanded the PACT domain to include a heptad repeat on the N-terminal side of the PACT motif.
In the early stages of spindle formation, Spc110 undergoes dynamic exchange (Yoder et al., 2003). At the old pole, 50% of the Spc110 exchanges with protein in the nucleoplasm, and as the new pole grows, exchange is also presumed to occur there. The exchange might be part of the process that insures that the size of the pole is sufficient to nucleate the required spindle microtubules. Once the mitotic spindle is fully formed, exchange is terminated, and Spc110 is stable.
During metaphase, the strength of the pole is challenged by the pulling forces in the spindle. Temperature-sensitive mutations in the PACT domain lead to delamination of the CP (Sundberg and Davis, 1997; Yoder et al., 2005; Shimogawa et al., 2006). Recently it was shown by direct-force measurements that removing the calmodulin binding site from Spc110 (and therefore removing calmodulin from the SPB) weakens the SPB–microtubule attachment (Fong et al., 2017). Thus calmodulin binding is important to maintain the high tensile strength of the SPB.
A hypothesis consistent with our model and data is that the CP is stabilized and reinforced by calmodulins undergoing a domain swap to create lateral cross-links between neighboring Spc110/calmodulin complexes. The high-resolution x-ray structure of calmodulin with the Spc110 peptide showed that it crystallized as a 2:2 domain-swapped heterotetramer. The only other example of a calmodulin domain swap is in complex with calcineurin (Ye et al., 2008). That result remains controversial (Dunlap et al., 2014). However, at the SPB, the tight protein packing along with cell cycle–regulated modifications could promote the domain swap. The stabilization must be reversible, because activation of the mitotic checkpoint stimulates growth of the pole, which then shrinks once the checkpoint is satisfied (O’Toole et al., 1997; Yoder et al., 2005).
Many of the general features of Spc110 assembly might be conserved in centrosomes. For example, like Spc110, calmodulin binding to the PACT domain protein AKAP450 is calcium independent (Geiser et al., 1991; Gillingham and Munro, 2000). Recruitment of AKAP450 to the centrosome involves subsets of the PACT domain (Gillingham and Munro, 2000). Calmodulin is a conserved element of centrosomes (Firat-Karalar et al., 2014). Finally, in a reconstituted minimal centrosome, the PCM scaffold evolves and becomes less dynamic with time (Woodruff et al., 2017). Our model for Spc110 assembly is a guide for future research on the control of centrosome assembly, size, and dynamics.
Modeling the structure of the SPB
Our model refines prior information about SPB structure gathered over decades by multiple groups using a variety of approaches (Kilmartin, 2014). It provides an important extension to these studies as well, leading to insights into the mechanism of Spc110 assembly, the role of coiled-coil domains, and the structure of Spc29. Importantly, it provides a framework for further analysis of the SPB structure and could be applied to other MTOCs as well. The Bayesian integrative structure-modeling approach (Rieping et al., 2005; Erzberger et al., 2014; Molnar et al., 2014; Street et al., 2014; Robinson et al., 2015; Fernandez-Martinez et al., 2016), as implemented in the IMP package (Russel et al., 2012), is a powerful tool, able to combine biophysical, biochemical, biological, and genetic data into a coherent, predictive model.
MATERIALS AND METHODS
Strains and plasmids used in this study are listed in Supplemental Tables S5 and S6. Integrative structure determination of the yeast SPB core proceeded through four stages (Alber et al., 2007a, b) (Figure 1B): 1) gathering data; 2) representing subunits and translating data into spatial restraints; 3) configurational sampling to produce an ensemble of structures consistent with the input information; and 4) analyzing and validating the ensemble of structures and data. The modeling protocol (i.e., stages 2, 3, and 4) was implemented using our open-source IMP package (Russel et al., 2012), version 2.3 (http://integrativemodeling.org). Files containing the input data, scripts, and output results are available at https:/salilab.org/spb/DOI: 10.5281/zenodo.838791, and will also be deposited at the nascent Protein Data Bank archive for integrative structures (https://pdb-dev.rcsb.rutgers.edu).
Stage 1: Gathering data
Composition and stoichiometry of SPB subunits.
The identity of the proteins in the CP and IL2 layers is known via electron microscopy and immunoelectron microscopy (Rout and Kilmartin, 1990; Adams and Kilmartin, 1999): the C-terminus and the coiled-coil domain of Spc110, Spc29, Cmd1, and the N-terminus of Spc42 are in the CP layer; the C-terminus of Cnm67 and the C-terminus of Spc42 are in the IL2 layer. Spc42 is present in the 2:1 ratio with respect to Cmd1, Spc110, Spc29, and Cnm67 (Muller et al., 2005).
In vivo FRET.
A total of 41 FRETR data points (32 between the N- and C-termini of all pairs of CP and IL2 proteins and an additional nine between the coiled-coil of Spc110 and termini of CP proteins) were identified by in vivo FRET spectroscopy (Bonomi et al., 2014), informing the spatial proximities of the termini of the SPB proteins.
Cryo-EM.
A low-resolution density map of overexpressed Spc42 was determined by cryo-EM at a resolution of 36 Å (Bullitt et al., 1997). The map informed the P3 symmetry of the Spc42 lattice in the IL2 layer, the boundaries of the size of the primitive unit cell, the thickness of the CP layer, and the maximum tilt angle for coiled-coil domains of Spc42, which was based on the minimum and maximum distances between the CP and IL2 layers.
SAXS.
SAXS profiles of Spc110/calmodulin complexes and full-length Spc29 (Figure 2 and Supplemental Table S3) informed their shapes and the distance between the N- and C- termini for Spc29. Protocols for sample preparation and SAXS analysis are outlined in the Supplemental Experimental Methods.
Yeast two-hybrid interactions.
Five published yeast two-hybrid data points (Spc421-141/Spc110781-944, Spc421-138/Spc29, Cnm67442-573/Spc4249-363, Spc29/Spc110811-898, and Spc110823-944/Spc110823-944) (Adams and Kilmartin, 1999; Elliott et al., 1999) informed the spatial proximities of the interacting domain pairs. The first three were used for building the model, and the last two were used for testing it.
Cnm67 binding-site localization.
The site in Cnm67 that binds Spc42 (residues 503–514) was identified by a biochemical analysis (Klenchin et al., 2011). This established the close proximity of these Cnm67 residues to Spc42.
Stage 2: Representing subunits and translating data into spatial restraints
The gathered data were used for defining the representation of the model, defining the scoring function that guides sampling of alternative models, limiting sampling, filtering of good-scoring models obtained by sampling, and final validation of the models. The SPB representation relies on stoichiometry, atomic structures, and models of subcomplexes (Supplemental Table S3). The scoring function relies on in vivo FRET data, cryo-EM density map, three yeast two-hybrid interactions, Cnm67-Spc42 binding-site localization, SAXS shapes of subcomplexes, excluded volume, and sequence connectivity. The sampling benefits from symmetry constraints. The validation of the final model relies on EM, the remaining yeast two-hybrid interactions, SAXS analysis of Spc110-Cmd1 dimer and Spc29, and genetic analysis of Spc110. This stage is next described in detail.
System representation.
To improve computational efficiency and avoid too coarse a representation, we represented the SPB in a multiscale manner.
A rigid body consisting of multiple beads is defined for each crystal structure, comparative model, and coiled-coil model (Supplemental Table S3). Rigid bodies were coarse-grained using two resolutions: 50 residues per bead for CFP and YFP or 10 residues per bead for all proteins. The coordinates of the beads correspond to the center of mass of the 10 constituent residues (FPs principal axis of inertia). The radius of each bead is just large enough to include all constituent atoms (∼10 Å [15 Å for fluorescent proteins]).
The Cnm67 dimer was represented by its crystal structure, PDB 3OA7 (Klenchin et al., 2011). A model of calmodulin with fragment Spc110896-944 was constructed with MODELLER 9, version 8 (Sali and Blundell, 1993), based on the crystal structure PDB 4DS7 (Supplemental Computational Methods).
The structures of the coiled-coil domains of Spc110679-798 and Spc4260-137 were generated by the CCCP server (Grigoryan and DeGrado, 2011) with the default Crick parameters (Crick, 1953) for coiled-coil dimers. YFP and CFP were represented by a crystal structure of green fluorescent protein (GFP) (PDB 1EMA) (Ormo et al., 1996).
Unstructured regions without an atomic model (Supplemental Table S3) or not in rigid bodies are represented as a flexible string of beads. One bead represents ∼60 residues, with bead radius calculated from an approximate protein density (Fischer et al., 2004). An alternate representation was used for domains whose structure is unknown but expected to be extended. Spc29 was represented by a bead at the N- and C- termini, with 10 residues per bead. A similar representation was used for the Spc42 C-terminus, with one 10-residue bead representing the C-terminus.
With this representation in hand, we encoded the spatial restraints based on the information gathered in stage 1, as follows (Supplemental Table S4).
Integrative Bayesian scoring function.
The Bayesian approach (Rieping et al., 2005) estimates the probability of a model, given information available about the system, including prior knowledge, and newly acquired experimental data. In modeling a macromolecular system, the model M consists of a set X of N modeled states X = {Xk}, their population fractions in the sample {wk}, and extra parameters, such as the parameters  quantifying the magnitude of noise in data point n in experiment E. Here we model the SPB in a single structural state (i.e., N = 1). Using Bayes theorem, the posterior probability p(M | D,I) of model M, given data D and prior information I, is
quantifying the magnitude of noise in data point n in experiment E. Here we model the SPB in a single structural state (i.e., N = 1). Using Bayes theorem, the posterior probability p(M | D,I) of model M, given data D and prior information I, is
where the likelihood function p(M | D,I) is the probability of observing data D given M and I; and the prior p(M | I) is the probability of model M, given I. Data 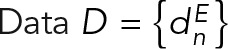 is the set of measured values for an experimental observable. To define the likelihood function, one needs a forward model
is the set of measured values for an experimental observable. To define the likelihood function, one needs a forward model 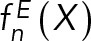 that predicts the data point that would have been observed for structure(s) X in a noise-free experiment and a noise model that quantifies the deviation between the predicted and observed data points. When several kinds of independent experimental data are simultaneously considered, the joint likelihood p(M | D,I) can be modeled as the product of individual likelihoods
that predicts the data point that would have been observed for structure(s) X in a noise-free experiment and a noise model that quantifies the deviation between the predicted and observed data points. When several kinds of independent experimental data are simultaneously considered, the joint likelihood p(M | D,I) can be modeled as the product of individual likelihoods 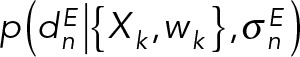 , one for each experiment E and data point n. The joint prior p(M | I) is a product of priors p(Xk), p(wk), and
, one for each experiment E and data point n. The joint prior p(M | I) is a product of priors p(Xk), p(wk), and 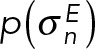 defined on the coordinates of the structures, the population fractions, and the uncertainties, respectively, as well as the forward model parameters (see Bayesian FRET restraints). The integrative Bayesian scoring function is defined as the negative logarithm of the posterior probability p(M | D,I):
defined on the coordinates of the structures, the population fractions, and the uncertainties, respectively, as well as the forward model parameters (see Bayesian FRET restraints). The integrative Bayesian scoring function is defined as the negative logarithm of the posterior probability p(M | D,I):
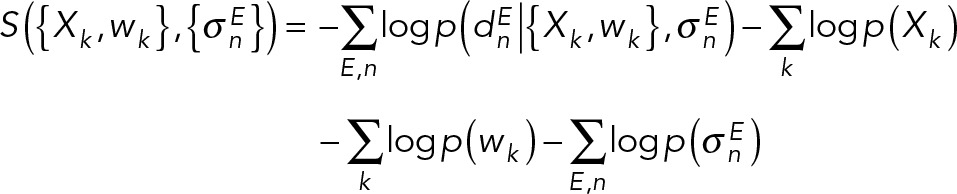 |
In the Bayesian approach, the weights for the data terms are automatically determined by the consistency among data points and with the priors, while the priors are weighted uniformly (i.e., weight is 1.0).
Next we define the scoring-function terms used to model SPB.
Bayesian FRET restraints.
Forty-one in vivo FRET data points were used to restrain the distances between the SPB core protein termini and Spc110 coiled-coil. The FRET distance restraint relies on a Bayesian scoring function (Bonomi et al., 2014) based on FRETR, a quantitative measure of FRET (Muller et al., 2005). The multistate forward model for FRETR can be written as
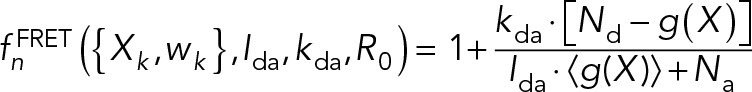 |
where
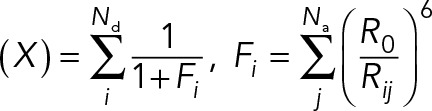 |
R0 is the Förster radius, and kda is the ratio of donor and acceptor excitation rates at 430 nm. Nd and Na are the number of donors and acceptors, respectively. Ida is the ratio of fluorescence intensities in the FRET channel, which is experimentally measured when CFP and YFP are individually expressed at equal concentration. The average for g(X) was calculated over all possible acceptor photobleaching states, each with weight 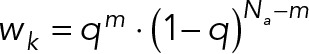 , where m is the number of acceptors alive and q is the probability of an acceptor to be alive during imaging of the CFP channel. The distance Rij between donor i and acceptor j was calculated considering all copies of the donor and acceptor. The likelihood of data point n is a log-normal distribution with individual noise level
, where m is the number of acceptors alive and q is the probability of an acceptor to be alive during imaging of the CFP channel. The distance Rij between donor i and acceptor j was calculated considering all copies of the donor and acceptor. The likelihood of data point n is a log-normal distribution with individual noise level 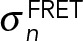 . Priors were defined on all forward model parameters (Ida, kda, R0, and q) and on the uncertainties
. Priors were defined on all forward model parameters (Ida, kda, R0, and q) and on the uncertainties 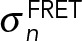 . In particular, the priors
. In particular, the priors 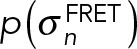 were unimodal distributions (Sivia and Skilling, 2006) with a heavy tail to account for outliers.
were unimodal distributions (Sivia and Skilling, 2006) with a heavy tail to account for outliers.
Cryo-EM density restraint.
The restraint for the position of the C-terminus of Spc42 is the posterior model density given the EM map of overexpressed Spc42 (Bullitt et al., 1997). The likelihood function was defined as a normal distribution truncated to the interval 0–1:
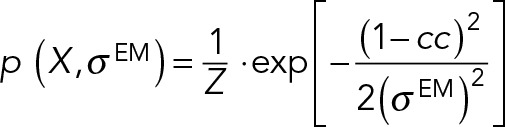 |
where cc is the cross-correlation between a projection of the experimental map and a low-resolution two-dimensional map calculated from a model using the EM2D approach (Velazquez-Muriel et al., 2012), in the x, y plane. Z is a normalization factor, and 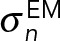 is the uncertainty associated with the EM map. The prior
is the uncertainty associated with the EM map. The prior 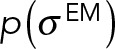 was a Jeffrey’s function:
was a Jeffrey’s function: 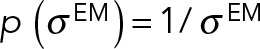 .
.
Unit-cell size restraint.
The size and shape of the rhomboid primitive unit cell, s, was restrained based on the EM map (Bullitt et al., 1997) and sampling considerations. s was treated as an unknown parameter to account for an increase of the unit-cell size due to the presence of FPs and the uncertainty in the size of the EM map. A uniform distribution p(s) bounded between 9 and 13.5 nm was used to sample s. The positions and orientations (i.e., configurations) of components in all copies of the rhomboid primitive unit cells were by construction identical.
Planar restraint for Spc42.
The planar restraint was used to enforce the symmetric lattice of Spc42 seen in the EM map (Bullitt et al., 1997). Specifically, the N terminus beads of all copies of Spc42 in the primitive unit cell were restrained to be on the same z-axis level. A similar restraint was applied on the C-terminal bead of Spc42. This goal was achieved by imposing harmonic bounds on the z-axis distances between every pair of Spc42 N-terminus beads (or equivalently, every pair of Spc42 C-terminus beads), with equilibrium distance and spring constant of 0 Å and 1 kBT, respectively.
Coiled-coil angle restraints.
The coiled-coils of Spc42, Spc110, and Cnm67 were maintained normal to the CP and IL2 layers (z-axis) by applying a harmonic upper bound on the tilt angle between the coiled-coil domain and the z-axis. The threshold angle was 0° for Spc110 and Cnm67 and 20° for Spc42; the spring constants were set to 102 kBT in all cases. The tilt-angle restraints were enforced to provide flexibility for coiled-coil proteins spanning layers that are under great stress in the SPB. These restraints were designed based on EM data that indicate a range of values for the CP-IL2 layer gap (Bullitt et al., 1997) and therefore restrict the range of tilt angles allowed to the spanning coiled-coil domains.
CP-layer localization restraints.
The CP-layer localization restraint was used to position Spc110, Spc29, Cmd1, and the N-terminus of Spc42 based on EM (Bullitt et al., 1997) and immuno-EM (Rout and Kilmartin, 1990; Adams and Kilmartin, 1999), The restraint was implemented in the Bayesian manner with a likelihood and a prior. Specifically, the CP layer was defined as a slab between two planes parallel to the x, y plane. The likelihood 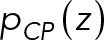 was used to confine the CP components inside the CP layer:
was used to confine the CP components inside the CP layer:
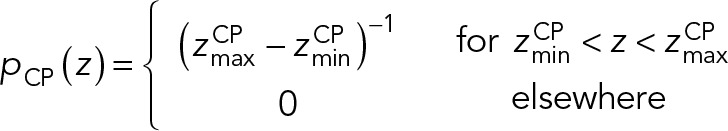 |
where the parameters 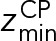 and
and 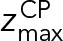 define the CP boundaries and z is the z-coordinate of the center of each bead in each CP component. To account for errors in the measurements of the CP thickness by electron tomography and EM, we treated
define the CP boundaries and z is the z-coordinate of the center of each bead in each CP component. To account for errors in the measurements of the CP thickness by electron tomography and EM, we treated 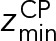 as an unknown parameter. A uniform distribution bounded between −30.0 nm and −28.6 nm was used as a prior for
as an unknown parameter. A uniform distribution bounded between −30.0 nm and −28.6 nm was used as a prior for 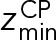 ;
; 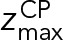 was set to 0 nm.
was set to 0 nm.
SAXS shape restraints.
SAXS shape restraints were applied to the Spc110788-944/calmodulin dimer to maintain its structure close to the ab initio shape calculated from SAXS data (Figure 2E and Supplemental Table S1). This goal was achieved by 1) applying a harmonic bound on the minimum distance between all pairs of beads representing the two calmodulins in the primitive unit cell, 2) applying a harmonic bound on the z-axis distance between the two beads representing residue 900 of Spc110 in the primitive unit cell, and 3) applying the same bound as in (2) for the two beads representing residue 940 of Spc110. In all cases, equilibrium distance and spring constant of 0 Å and 1 kBT, respectively, were used.
Distance restraints for unstructured domains.
The SAXS shape of Spc29 was used to restrain the distance between its termini. A similar restraint was applied between the C-terminal bead of Spc42 and the C-terminal bead of its coiled-coil domain, based on the distance between residues in a random coil (Kohn et al., 2004). The distance restraints were implemented by a Bayesian scoring function, with a lognormal likelihood on the distance between the corresponding beads in the model, with a mean of dref (the reference distance) and a fixed uncertainty (σ) of 0.001. The prior on dref was a uniform distribution in the ranges of 130–173 Å (Spc29) and 0–64.4 Å (Spc42) (see System representation and Supplemental Computational Methods).
Yeast two-hybrid restraints.
The distance restraints based on the interacting protein domains in two-hybrid assays were encoded as harmonic bounds on the minimum distance among all pairs of the beads representing the two interacting domains, centered at 0 Å and with the spring constant of 1 kBT.
Cnm67-Spc42 binding-site restraint.
A basic patch of Cnm67 (residues 503, 505, 506, 507, and 514) binds to Spc42 (Klenchin et al., 2011). This information was encoded in a restraint similar in manner to the yeast two-hybrid restraints, with a harmonic bound on the minimum distance between all pairs of beads representing Spc42 and the beads corresponding to residues 503–514 of Cnm67, centered at 0 Å and with the spring constant of 1 kBT.
Sequence-connectivity restraints.
We applied sequence-connectivity restraints to enforce intrachain connectivity, using a harmonic bound on the distances between the surfaces of consecutive beads in a protein. The equilibrium distance and spring constant were set to 0 Å and 1 kBT, respectively. The same restraints were used to link CFP and YFP to the N- or C-termini of each protein.
Excluded-volume restraints.
The protein excluded-volume restraint was applied to the distance between the surfaces of all pairs of beads, except for pairs of beads representing FPs attached to nonidentical proteins that were never simultaneously present in actual samples. It was implemented as a harmonic lower bound with an equilibrium distance of 0 Å, and a spring constant of 0.1 kBT.
Stage 3: Sampling
Sampling space with symmetry constraints.
We aimed to maximize the efficiency of the configurational sampling. Therefore we reduced the number of independently moving parts in the SPB model by explicitly considering the symmetries of the SPB as follows. It has been shown by EM that the IL2 layer consists of hexagonal supercells, each with P6 symmetry (Bullitt et al., 1997). However, the efficiency of computational sampling can be improved by relaxing the P6 symmetry to the rhomboid P3 symmetry within each supercell. Thus we modeled each hexagonal supercell as a triple of rhomboid primitive unit cells. The central supercell and the surrounding six hexagonal supercells were modeled in effect as an infinite lattice. This approach is more accurate than modeling only a single primitive cell or supercell, because some input information reflects interactions across unit cells (e.g., FRET, yeast two-hybrid, and excluded volume).
With these symmetries in hand, we sampled only the positions and orientations of rigid bodies and beads corresponding to a single rhomboid primitive unit cell. The equivalent components in all copies of the rhomboid primitive unit cell were by construction identical.
Sampling algorithm.
Given the size of the system and the rugged nature of the posterior probability landscape, we used a Gibbs sampler based on Monte Carlo (MC) enhanced by parallel tempering (PT) (Sugita and Okamoto, 1999) to generate a sample of coordinates X as well as of the parameters Ida, kda, R0, q,  , s, and
, s, and  from the posterior distribution. The coordinates X include positions and orientations for the rigid bodies and positions for beads in the flexible parts of the system. The moves for X included random translation and rotation of rigid parts (2 Å and 0.4 rad maximum, respectively), random translation of individual beads in the flexible segments (2 Å maximum), and normal perturbation of Ida, kda, R0, q,
from the posterior distribution. The coordinates X include positions and orientations for the rigid bodies and positions for beads in the flexible parts of the system. The moves for X included random translation and rotation of rigid parts (2 Å and 0.4 rad maximum, respectively), random translation of individual beads in the flexible segments (2 Å maximum), and normal perturbation of Ida, kda, R0, q,  , s, and
, s, and  . As indicated above, these operations were only applied to the sampled rigid bodies and beads. The remaining symmetry-constrained rigid bodies and units were moved in lockstep to maintain the exact P3 symmetry at each sampling step, as described above. For computational efficiency, the EM map was not used during sampling, but only in the analysis stage. Eight replicas were used, with temperatures distributed following a geometric progression over the range 1–5 kBT. To enhance diffusion across temperatures, PT was carried out in the well-tempered ensemble (WTE) (Bonomi and Parrinello, 2010), with a bias factor γ = 9. A total of 6 × 107 MC steps were performed per replica, each step consisting of a cycle of MC steps that moved every rigid body and flexible bead once. Exchanges between replicas were attempted every 500 MC steps. Models were saved every 2500 MC steps for further analysis. A total of 24,000 models were generated in one PT run. Two independent PT runs were performed starting from two different sets of random conformations. These 48,000 models from two independent runs were considered for further analysis.
. As indicated above, these operations were only applied to the sampled rigid bodies and beads. The remaining symmetry-constrained rigid bodies and units were moved in lockstep to maintain the exact P3 symmetry at each sampling step, as described above. For computational efficiency, the EM map was not used during sampling, but only in the analysis stage. Eight replicas were used, with temperatures distributed following a geometric progression over the range 1–5 kBT. To enhance diffusion across temperatures, PT was carried out in the well-tempered ensemble (WTE) (Bonomi and Parrinello, 2010), with a bias factor γ = 9. A total of 6 × 107 MC steps were performed per replica, each step consisting of a cycle of MC steps that moved every rigid body and flexible bead once. Exchanges between replicas were attempted every 500 MC steps. Models were saved every 2500 MC steps for further analysis. A total of 24,000 models were generated in one PT run. Two independent PT runs were performed starting from two different sets of random conformations. These 48,000 models from two independent runs were considered for further analysis.
Stage 4: Analyzing and validating the ensemble structures and data
Input information and output structures need to be analyzed to estimate structure precision and accuracy, detect inconsistent and missing information, and suggest more informative future experiments. Assessment began with a test of the thoroughness of structural sampling, including structural clustering of the models, estimating model precision, and visualizing the variability in the ensemble of structures using localization-probability-density maps. Next both the models and the data were validated by assessing the degree of consistency between them, in three ways: first, by quantification of the structure fit to the input information; second, structure assessment by cross-validation; and third, structure assessment by data not used to compute it. These validations are based on the nascent worldwide Protein Data Bank effort on archival, validation, and dissemination of integrative structural models (Berman et al., 2003). We now discuss each of these validations in turn.
Exhaustiveness of the configurational sampling.
Before the models can be analyzed, we have to ensure that the posterior probability distribution was sampled exhaustively (i.e., commensurate with the precision of the final models). Therefore sampling was assessed by comparing the two independently generated samples (i.e., sets of 24,000 models) each. Sampling exhaustiveness was monitored by first confirming that the population of the major cluster (considering all components except Spc29) does not change as a function of the number of sampled models, for two independent runs initiated from different random configurations (Supplemental Figure S3A).
Next we assessed whether models from each sample are present in each structural cluster in approximately even proportions (Viswanath et al., 2017) by clustering (see Clustering and sampling precision) all 48,000 models. To assess the significance and magnitude of the difference between the proportions of each sample in the clusters, we use the χ2 test for homogeneity of proportions. This test evaluates the null hypothesis that the two model samples are distributed nearly equally in all major clusters. The contribution to the population of each cluster by each sample was defined as the number of models in the cluster from the sample. The χ2 test indicated that the difference between the models from the two runs is significant (p < 0.05). However, the magnitude of the difference is small, as demonstrated by the effect size Cramer’s V of 0.08. Thus the two distributions of models are effectively equal.
Finally, we visually compared the probability-density maps of the most populated cluster in the two samples, which showed that the probability-density maps are identical, except for the position of Spc29 (Supplemental Figure S3B).
The caveat is that passing these tests is only necessary but not sufficient as evidence of thorough sampling; a positive outcome of the tests may be misleading if, for example, the landscape contains only a narrow, and thus difficult to find, pathway to the pronounced minimum corresponding to the correct structure.
Clustering and sampling precision.
To identify the most likely models in a given set of models, it is generally not appropriate to select models with the highest posterior probability density (i.e., the best-scoring models), just like the most stable conformations are not necessarily those with the lowest potential energy but those with the lowest free energy. Instead, it is necessary to identify broad and deep maxima in the posterior probability density. Thus the models need to be clustered. To do so, one first compares the models with one other by a distance metric that minimizes the root-mean-square deviation between two models by considering alternative assignments of equivalent distances given multiple copies of identical particles and periodic boundary conditions. The resulting matrix of pairwise distances is then used to cluster the input models by a modified GROMOS clustering algorithm (Daura et al., 1999). This modified algorithm generates clusters iteratively until all models are clustered. In each iteration, for each unclustered model, the sum of its weight and the weights of unclustered neighbors within a specified cutoff (15 Å) is calculated; the model with the largest sum and its neighbors are then defined as the current cluster. Because we are interested in identifying the broad and deep maxima in the posterior model probability distribution as opposed to the probability distribution used for sampling, the appropriate weight depends on how the input models were sampled. Specifically, the weights correspond to the ratio between the posterior probability distribution and the probability distribution actually used for sampling (umbrella-sampling reweighting) (Torrie and Valleau, 1977):
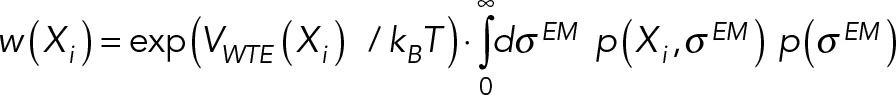 |
where  is the WTE bias at the end of the simulation (Bonomi and Parrinello, 2010).
is the WTE bias at the end of the simulation (Bonomi and Parrinello, 2010).
An ensemble of structures needs to be analyzed in terms of the precision of its structural features. The precision of a component position is defined by its variation in an ensemble of superposed structures, as quantified, for example, by the threshold distance root mean-square deviation used to define a cluster (above), which is the radius of a cluster, that is, the maximum distance from the cluster center to a cluster member. As described earlier, the precision for integrative structural modeling of the SPB core was 15 Å, with all components localized, except for Spc29.
Localization-density maps.
The precision of an ensemble of models can also be visualized by a localization–probability density map, which we calculate in five steps. Here the models are already sufficiently superposed by construction, because of the symmetry constraints, the restraints on the z-coordinates, and two-dimensional EM projection reweighting. First, we partitioned the space into a cubic grid with the spacing of 3 Å. Second, for each model and each component, we calculated the probability-density map by annotating each bin with the number of beads in the bin (model component map). Third, we defined the reference model map (for all components) as the model map of the model with the highest weight. Fourth, we aligned each model component map with the reference map by minimizing its distance to the reference over all allowed symmetry operations. Fifth, the probability-density map was obtained by summing the aligned model component maps, weighted by their model weights. The resulting probability density visualizes the marginal posterior probability in which all parameters but the model coordinates X were marginalized. In particular, we calculate a probability-density map separately for each cluster; the sum of all cluster maps is equal to the map of the entire ensemble.
Validation by fit to input data
FRET.
We computed the fit of the model to FRET data in two ways. First, by examining the average FRETR value for the models in a cluster and comparing them to the experimental average and experimental standard error (e.g., Supplemental Figure S4). Second, by comparing the distributions of FRETR data predicted by our ensemble of models to those observed experimentally (e.g., Supplemental Figure S5).
EM.
The agreement between our ensemble of models and the EM map of IL2 (Bullitt et al., 1997) was quantified by the value of 0.63 for the experimental map with the map simulated from models. The relatively moderate agreement can be explained by the absence of a major portion of the C-terminal region of Spc42 (residues 138–353), whose structure is unknown, from the SPB model.
Yeast two-hybrid.
Agreement with yeast two-hybrid data was computed by examining the distances between the two-hybrid interacting domain pairs in the ensemble of models. For domain pair (A, B), two distance distributions were obtained: 1) The minimum distance from a bead of domain A to a bead of domain B, considering all copies of domains A and B; and 2) the minimum distance from a bead of domain B to a bead of domain A over all copies of the two domains.
All other harmonic restraints (planar restraint for Spc42, coiled-coil angle restraint, SAXS shape restraint, Cnm67-Spc42 binding-site restraint) are satisfied by the ensemble of models.
Sensitivity analysis.
We modeled the SPB based on three different FRETR data sets, each time randomly selecting 95% of the data, and checking whether 1) the resulting models agreed with those obtained using the entire data set, and 2) they fit the unused FRETR data points.
Fit to data not used in modeling.
The most direct test of a modeled structure is by comparing it with the data that were not used to compute it (a generalization of cross-validation). We validated the integrative structural model of the SPB core by using 1) IL2-CP gap and hexagonal lattice spacing of Spc42 from EM (Bullitt et al., 1997), 2) yeast two-hybrid data not used in modeling (Supplemental Figure S6; see also Results), 3) molecular weight estimations of Spc110-Cmd1 dimer and Spc29 from SAXS (Supplemental Table S1; see also Results), and 4) genetic analysis of Spc110 (Figure 6; see also Results).
Supplementary Material
Acknowledgments
We thank R. Pellarin, B. Webb, David Agard, and Sue Jaspersen for useful discussions and Sue Jaspersen for suggestions on the article. This work was supported by the National Institutes of Health (NIH P01 GM105537 to M.W.). We thank T. Matsui and T.M. Weiss at the Stanford Linear Accelerator Center (SLAC) for assistance in collecting SAXS data. Use of the Stanford Synchrotron Radiation Lightsource (SSRL), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research and by the National Institutes of Health, National Institute of General Medical Sciences (including P41GM103393).
Abbreviations used:
- γ-TuSC
γ-tubulin small complex
- CBD
calmodulin-binding domain
- CP
central plaque
- cryo-EM
cryo-electron microscopy
- FPs
fluorescent proteins
- FRET
fluorescence resonance energy transfer
- IMP
Integrative Modeling Platform
- MC
Monte Carlo
- MTH
metallothionein
- MTOC
microtubule-organizing center
- PCM
pericentriolar material
- PT
parallel tempering
- SAXS
small-angle x-ray scattering
- SPB
spindle pole body
- WTE
well-tempered ensemble
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E17-06-0397) on August 16, 2017.
REFERENCES
- Adams IR, Kilmartin JV. Localization of core spindle pole body (SPB) components during SPB duplication in Saccharomyces cerevisiae. J Cell Biol. 1999;145:809–823. doi: 10.1083/jcb.145.4.809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alber F, Dokudovskaya S, Veenhoff LM, Zhang W, Kipper J, Devos D, Suprapto A, Karni-Schmidt O, Williams R, Chait BT, et al. Determining the architectures of macromolecular assemblies. Nature. 2007a;450:683–694. doi: 10.1038/nature06404. [DOI] [PubMed] [Google Scholar]
- Alber F, Dokudovskaya S, Veenhoff LM, Zhang W, Kipper J, Devos D, Suprapto A, Karni-Schmidt O, Williams R, Chait BT, et al. The molecular architecture of the nuclear pore complex. Nature. 2007b;450:695–701. doi: 10.1038/nature06405. [DOI] [PubMed] [Google Scholar]
- Alva V, Nam SZ, Soding J, Lupas AN. The MPI bioinformatics toolkit as an integrative platform for advanced protein sequence and structure analysis. Nucleic Acids Res. 2016;44:W410–W415. doi: 10.1093/nar/gkw348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alves-Cruzeiro JMDC, Nogales-Cadenas R, Pascual-Montano AD. CentrosomeDB: a new generation of the centrosomal proteins database for human and Drosophila melanogaster. Nucleic Acids Res. 2014;42:D430–D436. doi: 10.1093/nar/gkt1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H, Henrick K, Nakamura H. Announcing the worldwide Protein Data Bank. Nat Struct Biol. 2003;10:980–980. doi: 10.1038/nsb1203-980. [DOI] [PubMed] [Google Scholar]
- Bonomi M, Parrinello M. Enhanced sampling in the well-tempered ensemble. Phys Rev Lett. 2010;104:190601. doi: 10.1103/PhysRevLett.104.190601. [DOI] [PubMed] [Google Scholar]
- Bonomi M, Pellarin R, Kim SJ, Russel D, Sundin BA, Riffle M, Jaschob D, Ramsden R, Davis TN, Muller EG, Sali A. Determining protein complex structures based on a Bayesian model of in vivo Forster resonance energy transfer (FRET) data. Mol Cell Proteomics. 2014;13:2812–2823. doi: 10.1074/mcp.M114.040824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bornens M. The centrosome in cells and organisms. Science. 2012;335:422–426. doi: 10.1126/science.1209037. [DOI] [PubMed] [Google Scholar]
- Buchan DW, Minneci F, Nugent TC, Bryson K, Jones DT. Scalable Web services for the PSIPRED protein analysis workbench. Nucleic Acids Res. 2013;41:W349–W357. doi: 10.1093/nar/gkt381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullitt E, Rout MP, Kilmartin JV, Akey CW. The yeast spindle pole body is assembled around a central crystal of Spc42p. Cell. 1997;89:1077–1086. doi: 10.1016/s0092-8674(00)80295-0. [DOI] [PubMed] [Google Scholar]
- Burns S, Avena JS, Unruh JR, Yu Z, Smith SE, Slaughter BD, Winey M, Jaspersen SL. Structured illumination with particle averaging reveals novel roles for yeast centrosome components during duplication. Elife. 2015;4:e08586. doi: 10.7554/eLife.08586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conduit PT, Feng Z, Richens JH, Baumbach J, Wainman A, Bakshi SD, Dobbelaere J, Johnson S, Lea SM, Raff JW. The centrosome-specific phosphorylation of Cnn by Polo/Plk1 drives Cnn scaffold assembly and centrosome maturation. Dev Cell. 2014;28:659–669. doi: 10.1016/j.devcel.2014.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conduit PT, Wainman A, Raff JW. Centrosome function and assembly in animal cells. Nat Rev Mol Cell Biol. 2015;16:611–624. doi: 10.1038/nrm4062. [DOI] [PubMed] [Google Scholar]
- Crick FH. The Fourier transform of a coiled coil. Acta Cryst. 1953;6:685–689. [Google Scholar]
- Daura X, Gademann K, Jaun B, Seebach D, van Gunsteren WF, Mark AE. Peptide folding: when simulation meets experiment. Angew Chem Int Edit. 1999;38:236–240. [Google Scholar]
- Delorenzi M, Speed T. An HMM model for coiled-coil domains and a comparison with PSSM-based predictions. Bioinformatics. 2002;18:617–625. doi: 10.1093/bioinformatics/18.4.617. [DOI] [PubMed] [Google Scholar]
- Dunlap TB, Guo HF, Cook EC, Holbrook E, Rumi-Masante J, Lester TE, Colbert CL, Vander Kooi CW, Creamer TP. Stoichiometry of the calcineurin regulatory domain-calmodulin complex. Biochemistry. 2014;53:5779–5790. doi: 10.1021/bi5004734. [DOI] [PubMed] [Google Scholar]
- Elliott S, Knop M, Schlenstedt G, Schiebel E. Spc29p is a component of the Spc110p subcomplex and is essential for spindle pole body duplication. Proc Natl Acad Sci USA. 1999;96:6205–6210. doi: 10.1073/pnas.96.11.6205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erzberger JP, Stengel F, Pellarin R, Zhang S, Schaefer T, Aylett CH, Cimermancic P, Boehringer D, Sali A, Aebersold R, Ban N. Molecular architecture of the 40SeIF1eIF3 translation initiation complex. Cell. 2014;158:1123–1135. doi: 10.1016/j.cell.2014.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng Z, Caballe A, Wainman A, Johnson S, Haensele AFM, Cottee MA, Conduit PT, Lea SM, Raff JW. Structural basis for mitotic centrosome assembly in flies. Cell. 2017;169:1078–1089. doi: 10.1016/j.cell.2017.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez-Martinez J, Kim SJ, Shi Y, Upla P, Pellarin R, Gagnon M, Chemmama IE, Wang J, Nudelman I, Zhang W, et al. Structure and function of the nuclear pore complex cytoplasmic mRNA export platform. Cell. 2016;167:1215–1228. doi: 10.1016/j.cell.2016.10.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Firat-Karalar EN, Sante J, Elliott S, Stearns T. Proteomic analysis of mammalian sperm cells identifies new components of the centrosome. J Cell Sci. 2014;127:4128–4133. doi: 10.1242/jcs.157008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer H, Polikarpov I, Craievich AF. Average protein density is a molecular-weight-dependent function. Protein Sci. 2004;13:2825–2828. doi: 10.1110/ps.04688204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fong KK, Sarangapani KK, Yusko EC, Riffle M, Llauro A, Graczyk B, Davis TN, Asbury CL. Direct measurement of microtubule attachment strength to yeast centrosomes. Mol Biol Cell. 2017;28:1853–1861. doi: 10.1091/mbc.E17-01-0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiser JR, Sundberg HA, Chang BH, Muller EG, Davis TN. The essential mitotic target of calmodulin is the 110-kilodalton component of the spindle pole body in Saccharomyces cerevisiae. Mol Cell Biol. 1993;13:7913–7924. doi: 10.1128/mcb.13.12.7913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiser JR, van Tuinen D, Brockerhoff SE, Neff MM, Davis TN. Can calmodulin function without binding calcium. Cell. 1991;65:949–959. doi: 10.1016/0092-8674(91)90547-c. [DOI] [PubMed] [Google Scholar]
- Gillingham AK, Munro S. The PACT domain, a conserved centrosomal targeting motif in the coiled-coil proteins AKAP450 and pericentrin. EMBO Rep. 2000;1:524–529. doi: 10.1093/embo-reports/kvd105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grigoryan G, DeGrado WF. Probing designability via a generalized model of helical bundle geometry. J Mol Biol. 2011;405:1079–1100. doi: 10.1016/j.jmb.2010.08.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirokawa N. Kinesin and dynein superfamily proteins and the mechanism of organelle transport. Science. 1998;279:519–526. doi: 10.1126/science.279.5350.519. [DOI] [PubMed] [Google Scholar]
- Howard J, Hyman AA. Dynamics and mechanics of the microtubule plus end. Nature. 2003;422:753–758. doi: 10.1038/nature01600. [DOI] [PubMed] [Google Scholar]
- Jana SC, Marteil G, Bettencourt-Dias M. Mapping molecules to structure: unveiling secrets of centriole and cilia assembly with near-atomic resolution. Curr Opin Cell Biol. 2014;26:96–106. doi: 10.1016/j.ceb.2013.12.001. [DOI] [PubMed] [Google Scholar]
- Jaspersen SL, Winey M. The budding yeast spindle pole body: structure, duplication, and function. Annu Rev Cell Dev Biol. 2004;20:1–28. doi: 10.1146/annurev.cellbio.20.022003.114106. [DOI] [PubMed] [Google Scholar]
- Keck JM, Jones MH, Wong CC, Binkley J, Chen D, Jaspersen SL, Holinger EP, Xu T, Niepel M, Rout MP, et al. A cell cycle phosphoproteome of the yeast centrosome. Science. 2011;332:1557–1561. doi: 10.1126/science.1205193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilmartin JV. Lessons from yeast: the spindle pole body and the centrosome. Philos Trans R Soc Lond B Biol Sci. 2014;369:20130456. doi: 10.1098/rstb.2013.0456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilmartin JV, Dyos SL, Kershaw D, Finch JT. A spacer protein in the Saccharomyces cerevisiae spindle poly body whose transcript is cell cycle-regulated. J Cell Biol. 1993;123:1175–1184. doi: 10.1083/jcb.123.5.1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilmartin JV, Goh PY. Spc110p: assembly properties and role in the connection of nuclear microtubules to the yeast spindle pole body. EMBO J. 1996;15:4592–4602. [PMC free article] [PubMed] [Google Scholar]
- Klenchin VA, Frye JJ, Jones MH, Winey M, Rayment I. Structure-function analysis of the C-terminal domain of CNM67, a core component of the Saccharomyces cerevisiae spindle pole body. J Biol Chem. 2011;286:18240–18250. doi: 10.1074/jbc.M111.227371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knop M, Schiebel E. Spc98p and Spc97p of the yeast gamma-tubulin complex mediate binding to the spindle pole body via their interaction with Spc110p. EMBO J. 1997;16:6985–6995. doi: 10.1093/emboj/16.23.6985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohn JE, Millett IS, Jacob J, Zagrovic B, Dillon TM, Cingel N, Dothager RS, Seifert S, Thiyagarajan P, Sosnick TR, et al. Random-coil behavior and the dimensions of chemically unfolded proteins. Proc Natl Acad Sci USA. 2004;101:12491–12496. doi: 10.1073/pnas.0403643101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kollman JM, Greenberg CH, Li S, Moritz M, Zelter A, Fong KK, Fernandez JJ, Sali A, Kilmartin J, Davis TN, Agard DA. Ring closure activates yeast γTuRC for species-specific microtubule nucleation. Nat Struct Mol Biol. 2015;22:132–137. doi: 10.1038/nsmb.2953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kollman JM, Merdes A, Mourey L, Agard DA. Microtubule nucleation by γ-tubulin complexes. Nat Rev Mol Cell Biol. 2011;12:709–721. doi: 10.1038/nrm3209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kollman JM, Zelter A, Muller EGD, Fox B, Rice LM, Davis TN, Agard DA. The structure of the gamma-tubulin small complex: implications of its architecture and flexibility for microtubule nucleation. Mol Biol Cell. 2008;19:207–215. doi: 10.1091/mbc.E07-09-0879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kupke T, Malsam J, Schiebel E. A ternary membrane protein complex anchors the spindle pole body in the nuclear envelope in budding yeast. J Biol Chem. 2017;292:8447–8458. doi: 10.1074/jbc.M117.780601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kursula P. The many structural faces of calmodulin: a multitasking molecular jackknife. Amino Acids. 2014;46:2295–2304. doi: 10.1007/s00726-014-1795-y. [DOI] [PubMed] [Google Scholar]
- Lin TC, Neuner A, Schlosser Y, Scharf A, Weber L, Schiebel E. Cell-cycle dependent phosphorylation of yeast pericentrin regulates γ-TUSC-mediated microtubule nucleation. eLife. 2014;3:e02208. doi: 10.7554/eLife.02208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lüders J, Stearns T. Microtubule-organizing centres: a re-evaluation. Nat Rev Mol Cell Biol. 2007;8:161–167. doi: 10.1038/nrm2100. [DOI] [PubMed] [Google Scholar]
- Lyon AS, Morin G, Moritz M, Yabut KCB, Vojnar T, Zelter A, Muller E, Davis TN, Agard DA. Higher-order oligomerization of Spc110p drives gamma-tubulin ring complex assembly. Mol Biol Cell. 2016;27:2245–2258. doi: 10.1091/mbc.E16-02-0072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mennella V, Agard DA, Huang B, Pelletier L. Amorphous no more: subdiffraction view of the pericentriolar material architecture. Trends Cell Biol. 2014;24:188–197. doi: 10.1016/j.tcb.2013.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molnar KS, Bonomi M, Pellarin R, Clinthorne GD, Gonzalez G, Goldberg SD, Goulian M, Sali A, DeGrado WF. Cys-scanning disulfide crosslinking and Bayesian modeling probe the transmembrane signaling mechanism of the histidine kinase, PhoQ. Structure. 2014;22:1239–1251. doi: 10.1016/j.str.2014.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller EG, Snydsman BE, Novik I, Hailey DW, Gestaut DR, Niemann CA, O’Toole ET, Giddings TH, Jr, Sundin BA, Davis TN. The organization of the core proteins of the yeast spindle pole body. Mol Biol Cell. 2005;16:3341–3352. doi: 10.1091/mbc.E05-03-0214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen T, Vinh DBN, Crawford DK, Davis TN. A genetic analysis of interactions with Spc110p reveals distinct functions of Spc97p and Spc98p, components of the yeast γ-tubulin complex. Mol Biol Cell. 1998;9:2201–2216. doi: 10.1091/mbc.9.8.2201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogura K, Kumeta H, Takahasi K, Kobashigawa Y, Yoshida R, Itoh H, Yazawa M, Inagaki F. Solution structures of yeast Saccharomyces cerevisiae calmodulin in calcium- and target peptide-bound states reveal similarities and differences to vertebrate calmodulin. Genes Cells. 2012;17:159–172. doi: 10.1111/j.1365-2443.2012.01580.x. [DOI] [PubMed] [Google Scholar]
- Ormo M, Cubitt AB, Kallio K, Gross LA, Tsien RY, Remington SJ. Crystal structure of the Aequorea victoria green fluorescent protein. Science. 1996;273:1392–1395. doi: 10.1126/science.273.5280.1392. [DOI] [PubMed] [Google Scholar]
- O’Toole E, Mastronarde D, Giddings TJ, Winey M, Burke D, McIntosh J. Three-dimensional analysis and ultrastructural design of mitotic spindles from the cdc20 mutant of Saccharomyces cerevisiae. Mol Biol Cell. 1997;8:1–11. doi: 10.1091/mbc.8.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Toole ET, Winey M, McIntosh JR. High-voltage electron tomography of spindle pole bodies and early mitotic spindles in the yeast Saccharomyces cerevisiae. Mol Biol Cell. 1999;10:2017–2031. doi: 10.1091/mbc.10.6.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petry S, Vale RD. Microtubule nucleation at the centrosome and beyond. Nat Cell Biol. 2015;17:1089–1093. doi: 10.1038/ncb3220. [DOI] [PubMed] [Google Scholar]
- Rieping W, Habeck M, Nilges M. Inferential structure determination. Science. 2005;309:303–306. doi: 10.1126/science.1110428. [DOI] [PubMed] [Google Scholar]
- Robinson PJ, Trnka MJ, Pellarin R, Greenberg CH, Bushnell DA, Davis R, Burlingame AL, Sali A, Kornberg RD. Molecular architecture of the yeast Mediator complex. Elife. 2015;4:e08719. doi: 10.7554/eLife.08719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rout MP, Kilmartin JV. Components of the yeast spindle and spindle pole body. J Cell Biol. 1990;111:1913–1927. doi: 10.1083/jcb.111.5.1913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russel D, Lasker K, Webb B, Velazquez-Muriel J, Tjioe E, Schneidman-Duhovny D, Peterson B, Sali A. Putting the pieces together: integrative modeling platform software for structure determination of macromolecular assemblies. PLoS Biol. 2012;10:e1001244. doi: 10.1371/journal.pbio.1001244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- Schramm C, Elliott S, Shevchenko A, Schiebel E. The Bbp1p-Mps2p complex connects the SPB to the nuclear envelope and is essential for SPB duplication. EMBO J. 2000;19:421–433. doi: 10.1093/emboj/19.3.421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimogawa MM, Graczyk B, Gardner MK, Francis SE, White EA, Ess M, Molk JN, Ruse C, Niessen S, Yates Iii JR, et al. Mps1 Phosphorylation of Dam1 couples kinetochores to microtubule plus ends at metaphase. Curr Biol. 2006;16:1489–1501. doi: 10.1016/j.cub.2006.06.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivia DS, Skilling J. Data Analysis: A Bayesian Tutorial. Oxford, UK: Oxford University Press; 2006. [Google Scholar]
- Starovasnik MA, Davis TN, Klevit RE. Similarities and differences between yeast and vertebrate calmodulin: an examination of the calcium-binding and structural properties of calmodulin from the yeast Saccharomyces cerevisiae. Biochemistry. 1993;32:3261–3270. doi: 10.1021/bi00064a008. [DOI] [PubMed] [Google Scholar]
- Stirling DA, Rayner TF, Prescott AR, Stark MJ. Mutations which block the binding of calmodulin to Spc110p cause multiple mitotic defects. J Cell Sci. 1996;109:1297–1310. doi: 10.1242/jcs.109.6.1297. [DOI] [PubMed] [Google Scholar]
- Stirling DA, Welch KA, Stark MJ. Interaction with calmodulin is required for the function of Spc110p, an essential component of the yeast spindle pole body. EMBO J. 1994;13:4329–4342. doi: 10.1002/j.1460-2075.1994.tb06753.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storchova Z, Breneman A, Cande J, Dunn J, Burbank K, O’Toole E, Pellman D. Genome-wide genetic analysis of polyploidy in yeast. Nature. 2006;443:541–547. doi: 10.1038/nature05178. [DOI] [PubMed] [Google Scholar]
- Street TO, Zeng X, Pellarin R, Bonomi M, Sali A, Kelly MJ, Chu F, Agard DA. Elucidating the mechanism of substrate recognition by the bacterial Hsp90 molecular chaperone. J Mol Biol. 2014;426:2393–2404. doi: 10.1016/j.jmb.2014.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem Phys Lett. 1999;314:141–151. [Google Scholar]
- Sundberg HA, Davis TN. A mutational analysis identifies three functional regions of the spindle pole component Spc110p in Saccharomyces cerevisiae. Mol Biol Cell. 1997;8:2575–2590. doi: 10.1091/mbc.8.12.2575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sundberg HA, Goetsch L, Byers B, Davis TN. Role of calmodulin and Spc110p interaction in the proper assembly of spindle pole body components. J Cell Biol. 1996;133:111–124. doi: 10.1083/jcb.133.1.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torrie GM, Valleau JP. Non-Physical sampling distributions in Monte-Carlo free-energy estimation—umbrella sampling. J Comput Phys. 1977;23:187–199. [Google Scholar]
- Velazquez-Muriel J, Lasker K, Russel D, Phillips J, Webb BM, Schneidman-Duhovny D, Sali A. Assembly of macromolecular complexes by satisfaction of spatial restraints from electron microscopy images. Proc Natl Acad Sci USA. 2012;109:18821–18826. doi: 10.1073/pnas.1216549109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villarroel A, Taglialatela M, Bernardo-Seisdedos G, Alaimo A, Agirre J, Alberdi A, Gomis-Perez C, Soldovieri MV, Ambrosino P, Malo C, Areso P. The ever changing moods of calmodulin: how structural plasticity entails transductional adaptability. J Mol Biol. 2014;426:2717–2735. doi: 10.1016/j.jmb.2014.05.016. [DOI] [PubMed] [Google Scholar]
- Viswanath S, Chemmama IE, Cimermancic P, Sali A. Assessing exhaustiveness of stochastic sampling for integrative modeling of macromolecular structures. Biophys J. 2017;113 doi: 10.1016/j.bpj.2017.10.005. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winey M, O’Toole E. The spindle cycle in budding yeast. Nat Cell Biol. 2001;3:E23–E27. doi: 10.1038/35050663. [DOI] [PubMed] [Google Scholar]
- Winey M, O’Toole E. Centriole structure. Philos Trans R Soc Lond B Biol Sci. 2014;369:20130457. doi: 10.1098/rstb.2013.0457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodruff JB, Ferreira Gomes B, Widlund PO, Mahamid J, Honigmann A, Hyman AA. The centrosome is a selective condensate that nucleates microtubules by concentrating tubulin. Cell. 2017;169:1066–1077. doi: 10.1016/j.cell.2017.05.028. [DOI] [PubMed] [Google Scholar]
- Woodruff JB, Wueseke O, Viscardi V, Mahamid J, Ochoa SD, Bunkenborg J, Widlund PO, Pozniakovsky A, Zanin E, Bahmanyar S, et al. Regulated assembly of a supramolecular centrosome scaffold in vitro. Science. 2015;348:808–812. doi: 10.1126/science.aaa3923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye Q, Wang H, Zheng J, Wei Q, Jia Z. The complex structure of calmodulin bound to a calcineurin peptide. Proteins. 2008;73:19–27. doi: 10.1002/prot.22032. [DOI] [PubMed] [Google Scholar]
- Yoder TJ, McElwain MA, Francis SE, Bagley J, Muller EG, Pak B, O’Toole ET, Winey M, Davis TN. Analysis of a spindle pole body mutant reveals a defect in biorientation and illuminates spindle forces. Mol Biol Cell. 2005;16:141–152. doi: 10.1091/mbc.E04-08-0703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoder TJ, Pearson CG, Bloom K, Davis TN. The Saccharomyces cerevisiae spindle pole body is a dynamic structure. Mol Biol Cell. 2003;14:3494–3505. doi: 10.1091/mbc.E02-10-0655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zizlsperger N, Keating A. Specific coiled-coil interactions contribute to a global model of the structure of the spindle pole body. J Struct Biol. 2010;170:246–256. doi: 10.1016/j.jsb.2010.01.022. [DOI] [PubMed] [Google Scholar]
- Zizlsperger N, Malashkevich VN, Pillay S, Keating AE. Analysis of coiled-coil interactions between core proteins of the spindle pole body. Biochemistry. 2008;47:11858–11868. doi: 10.1021/bi801378z. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.