A combination of quantitative imaging, modeling, and genetics has been used to test a proposed mechanism for measuring the size of an organelle. One way to measure distance is to send a clock out on a train and measure the elapsed time when the train returns. We tested a molecular version of this model as a possible regulator of intraflagellar transport by altering the return speed of the transport machinery and probing the effect on a known length-dependent process.
Abstract
Cilia and flagella are microtubule-based organelles that protrude from the surface of most cells, are important to the sensing of extracellular signals, and make a driving force for fluid flow. Maintenance of flagellar length requires an active transport process known as intraflagellar transport (IFT). Recent studies reveal that the amount of IFT injection negatively correlates with the length of flagella. These observations suggest that a length-dependent feedback regulates IFT. However, it is unknown how cells recognize the length of flagella and control IFT. Several theoretical models try to explain this feedback system. We focused on one of the models, the “time-of-flight” model, which measures the length of flagella on the basis of the travel time of IFT protein in the flagellar compartment. We tested the time-of-flight model using Chlamydomonas dynein mutant cells, which show slower retrograde transport speed. The amount of IFT injection in dynein mutant cells was higher than that in control cells. This observation does not support the prediction of the time-of-flight model and suggests that Chlamydomonas uses another length-control feedback system rather than that described by the time-of-flight model.
INTRODUCTION
How cells regulate the size of their organelles is currently an unanswered question in cell biology. Eukaryotic cilia and flagella (the two terms describe the same organelle) provide an excellent model system in which to investigate size-control mechanisms because of the fact that the organelle maintains a constant diameter as it elongates and shortens, thus representing a one-dimensional size-control problem. Cilia and flagella generally grow to a cell type–specific length, which is stably maintained. For example, when the flagella of the biflagellate green alga Chlamydomonas are severed, they will regrow back to their pre-severing length in ∼90 min. This regrowth occurs with decelerating kinetics such that the flagella asymptotically restore to their normal length (Rosenbaum et al., 1969). This slowdown in growth as the flagella reach the correct length suggests some mechanism that adjusts the growth rate as a function of length. Flagella are dynamic structures, with flagellar microtubules undergoing continuous turnover (Stephens, 1997, 1999; Marshall and Rosenbaum, 2001; Song and Dentler, 2001). The rate of microtubule disassembly appears to be independent of length (Marshall and Rosenbaum, 2001), suggesting that the gradual slowing of net assembly as flagella reach their final length must reflect a length dependence in the rate of assembly.
Flagellar assembly relies on an active transport process known as intraflagellar transport, or IFT (Rosenbaum and Witman, 2002; Ishikawa and Marshall, 2011), in which a heterotrimeric kinesin-2 motor drags a complex of at least 22 polypeptides, known as an IFT particle, from the cell body out to the tip of the flagellum. These IFT particles associate into linear arrays known as trains. The IFT particle proteins are not, themselves, structural components of the flagellum but instead serve as adaptors that bind cargo proteins such as tubulin (Hao et al., 2011; Wren et al., 2013; Craft et al., 2015) and bring them out to the tip, which is the site of tubulin incorporation during growth (Rosenbaum and Child, 1967; Johnson and Rosenbaum, 1992). At the tip, the kinesin motor is released from the IFT particles, which are then brought back to the cell body by cytoplasmic dynein (Ishikawa and Marshall, 2011). The IFT particles thus undergo a cyclical movement from the cell body, out to the tip, and then back again. Motion in both the anterograde (from cell body to tip) and retrograde (from tip to cell body) directions is highly processive (Kozminski et al., 1993; Iomini et al., 2001; Dentler, 2005).
A pool of IFT protein resides at the basal body (Deane et al., 2001). Photobleaching studies show that IFT exchanges between the flagellum and the basal body–associated pool (Buisson et al., 2013; Ludington et al., 2015), hence some mechanism must exist to regulate entry of IFT from this pool into the flagellum. The process by which IFT particles from the basal body–associated pool enter the flagellar compartment will be termed “injection.” Quantitative live-cell imaging has shown that the rate of IFT injection is length dependent (Engel et al., 2009; Ludington et al., 2013), with the injection rate scaling approximately as 1/L (Ludington et al., 2013). The decrease in injection rate as length increases is the product of two length-dependent changes: as length increases, the frequency with which IFT trains are injected increases, but the size of the trains decreases such that longer flagella inject a large number of smaller trains. The train size decreases faster than the frequency increases, thus leading to a net decrease in injection (Engel et al., 2009).
How does this length dependence arise? Evidently, cells have some way of measuring the length of flagella and adjusting IFT injection accordingly. How then might the cell sense flagellar length? In Ludington et al. (2015), we examined a series of different mathematical models for length sensing. Of the models examined in that study, one model that was consistent with measured data on injection versus length based on model selection criteria was the “time-of-flight” model (Sloboda and Rosenbaum, 2007). This was an abstract model in which it is imagined that the IFT particle contains a molecular clock in the form of a chemical modification that requires a specific length of time to take place. The longer the flagellum, the more time the IFT particle would spend in transit, and hence the more likely it would be to become modified.
In this article, we examine the time-of-flight model in more detail and attempt to test it. One approach to testing the time-of-flight model is to attempt to guess what molecular component is serving as the clock. For example, small GTPases are well known to function as molecular timers in many different contexts (Bourne, 1995). For a particle moving at the standard IFT rate of 1–3 µm/s within a flagellum of length 10 µm, the time constant of the IFT clock would need to be on the order of 10 s, potentially in the range achievable by a small GTPase (Rybin et al., 1996; Simon et al., 1996). Consistent with this suggestion, it is notable that two components of the IFT complex, IFT22 and IFT27, are small GTPases (Qin et al., 2007; Qin, 2012). If one of these proteins were the timer, we could test the time-of-flight model by mutating the active site, thus changing the turnover rate. However, there is no reason to assume that the timer has to be a GTPase. For example, there could be some phosphorylatable residue that is modified by a kinase localized within the flagellum. The phosphorylation state of this residue would thus increase the longer the particle stayed inside the flagellum. Indeed, several flagellar proteins have been described whose phosphorylation appears to be length dependent (Luo et al., 2011; Cao et al., 2013), although the association of these proteins with the IFT machinery is not known. Within the IFT complex, the GTPase interactor IFT25 is a phosphoprotein (Wang et al., 2009). Could one of these phosphoproteins serve as a time-of-flight sensor by accumulating more phosphorylation, or experiencing more dephosphorylation, during its transit through the flagellar space? Perhaps, but for all we know, the sensor might not involve guanosine 5′-triphosphate (GTP) or phosphorylation. Any one of a number of alternative posttranslational modifications could take place at an appropriate timescale to serve as a length sensor. For that matter, even a slow conformational change in a key protein could serve as a timer to measure time of flight. A protein might be injected into the flagellum in one conformation and then undergo a stochastic switch to a different, more stable conformation en route, and thus the proportion of proteins in the two conformations could serve as a time-of-flight indicator. The ability to implement a time-of-flight mechanism through many different molecular means is a strength of the model in terms of evolvability because such a scheme could easily evolve in many different ways, but this same feature poses a challenge for testing the model since we cannot know a priori which molecule in the highly complex IFT system is playing the role of timer. If we knew which molecule were the timer, we could attempt to mutate it in such a way as to change the timescale on which it switches between states. But how can we test the time-of-flight model without knowing the molecular identity of the timer?
Here we test the time-of-flight model, not by targeting the unknown timer itself, but by changing the speed of retrograde IFT. A decrease in retrograde IFT velocity increases the time of flight for the particles and should thus be interpreted by the cell as an increase in flagellar length. Increased length should lead to a decreased injection rate. In fact, we observed the opposite result—when retrograde IFT is reduced using mutations in the IFT dynein complex, the result is that IFT injection is actually increased, not decreased. This result argues against the time-of-flight model and suggests that some other mechanism may be used to sense length. However, the fact that IFT injection increases when retrograde speed is reduced suggests that the injection is sensing retrograde return rates in some way.
RESULTS
Model for time-of-flight sensing using a GTPase
First we asked whether the time-of-flight model could work in principle, taking into account specific features of IFT. Although an abstract version of the time-of-flight model has been shown capable of producing length-dependent IFT injection (Ludington et al., 2015), several details of actual IFT dynamics were not included, namely the difference between anterograde and retrograde IFT velocity and the fact that IFT particles require a finite length of time to remodel from anterograde to retrograde motion at the flagellar tip. Also, our previous analysis did not consider flagellar length dynamics but rather only the behavior of the time-of-flight model for fixed flagellar lengths. Before performing any experimental tests of the time-of-flight mechanism, we first tested whether the time-of-flight model would still produce length-dependent injection when these additional details were added and also whether the injection rate would be predicted to be sensitive to the velocity of retrograde particle motion.
We thus began by testing whether one particular proposed molecular mechanism, based on small GTPases, could work in the sense of providing a measure of flagellar length with sufficient dynamic range. More importantly, we wanted to use this model to establish whether changes in retrograde velocity could in fact produce a large enough change in signal output within the model to substantially affect injection.
As a model framework (Figure 1), we assumed that a molecular timer in the form of a GTPase is set (loaded with GTP) and then sent out with each IFT particle during injection. These particles transit through the flagellum, return via retrograde IFT, and then upon return, the GTP state of the timer is detected and used to control the injection rate of new particles. We assumed first-order decay of the GTP state, as expected for an enzyme with a single GTP bound acting independently of any other enzymes. On the basis of this assumption, we inferred that lifetimes of GTP-bound protein are exponentially distributed with some mean time tm. For convenience, we define the rate constant kcat as the reciprocal of the mean lifetime. The faster the enzyme converts GTP to guanosine 5′-diphosphate (GDP), the larger kcat would be.
FIGURE 1:
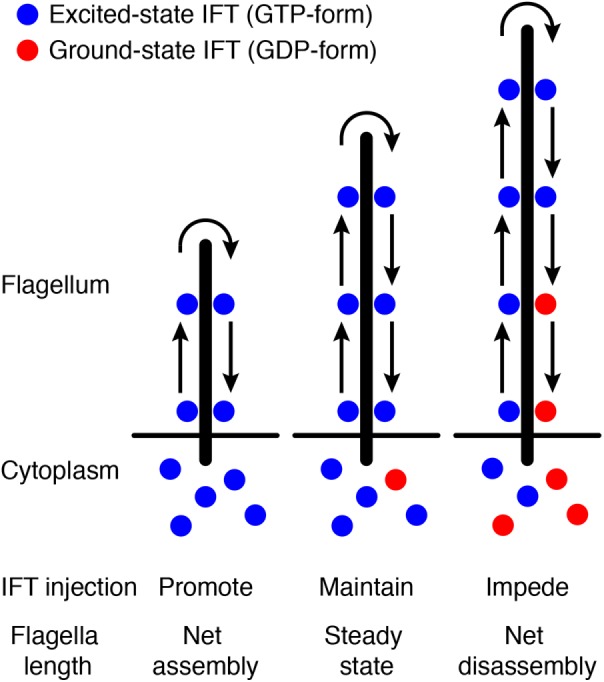
Schematic of the time-of-flight model. See the main text for details.
The cumulative distribution function of an exponential distribution is
|
|
which gives the probability that the enzyme has converted GTP to GDP at some point in time before the time T. So, if an ensemble of particles is loaded with GTP and injected into the flagellum, and then the particles spend a total time T inside the flagellum, and when they come back to the base, the fraction for which the GTP had turned over to GDP will be given by 1 – exp(–kcatT), and the fraction that still have GTP bound would just be exp(–kcatT). So, if we know the “time-of-flight” T, then we can calculate the fraction of molecules that would return with GTP on them.
If we start with the assumption that anterograde and retrograde speeds are the same, then the time-of-flight T is just given by 2L/v, where v is the speed of the particle and L is the length. We can thus find the probability of finding a GTP still on the GTPase in terms of the flagellar length and mean IFT velocity: P(GTP) = exp(–2 kcatL/v).
We next assumed that the rate of injection of new anterograde particles depends on the fraction of returning particles that have GTP bound. Presumably, the GTPase that comes back has to interact with some molecular machinery that gates the entry of new particles. We made the assumption that the injection rate for new IFT particles is proportional to the fraction of returning particles that still have a GTP on them. So, if all the GTP turned over to GDP, then nothing would get injected, and if none of the GTP turned over, injection would be at some maximum injection rate M.
Under these assumptions, the injection rate r is given by the product of the maximum injection rate and the probability that a returning particle has a GTP on it:
|
|
Thus the model predicts an exponentially decreasing dependence of injection on length: as the length increases, the injection rate decreases. This corresponds to qualitative trends seen in the data (Ludington et al., 2013, 2015) and also makes sense in terms of feedback control. Because injections lead to elongation, negative feedback control would require that there be fewer injections as the length increases. The length dependence predicted by the model is exponential rather than a 1/L as reported by Ludington et al. (2013), but this difference might be very hard to discriminate in actual measurements.
Can such a length sensor, based on the time of flight, account for the decelerating kinetics of flagellar growth? We invoke a simple model for flagellar length dynamics in which disassembly is length independent and assembly is mediated by anterograde particles carrying material from a total precursor pool. This gives us the differential equation:
|
|
where D is the disassembly rate, r is the injection rate, P is the total pool size, and δ is a proportionality constant that tells how much the flagellum elongates for each injected particle.
We next substituted the expression derived above for the injection rate r given by the time-of-flight model:
|
|
and simplify by lumping the parameters δ and M together into a lumped parameter A = δΜ:
|
|
We could also write this equation in terms of the GTP lifetime:
|
|
The model developed thus far makes several unrealistic assumptions that may be relevant to our proposed experiments. First, it assumes that anterograde and retrograde velocities are the same. In actuality, the anterograde velocity is slower than retrograde (2.5 vs. 3.5 µm/s, respectively). Because our experimental approach was to alter the retrograde velocity, it was important for us to know whether altering just this one velocity would have a substantial effect if we left the anterograde velocity unaltered. For this reason, we needed to modify the model to include both velocities explicitly. A second complication is that once IFT particles reach the tip of the flagellum, they do not immediately return but instead must spend some time remodeling into retrograde trains. Because this dwell time at the tip will affect the time of flight in a manner that does not depend on the retrograde velocity, it may have impacted our ability to test the model if we had just changed the retrograde velocity. To represent these effects, we specified anterograde and retrograde velocities va and vr and the remodeling time lag τ, which yields the more realistic equation for injection rate r and growth rate dL/dt as follows:
|
|
|
|
The numerical solution of Eq. 8 shows that it is possible to recapitulate the growth kinetics seen in Chlamydomonas flagella. As shown in Figure 2A, the model predicts that flagella would grow with decelerating kinetics, reaching half their final length in ∼20 min and leveling off at ∼13 µm. Given that the goal of this analysis was simply to test plausibility, we did not conduct a systematic fitting to actual data. A plot of injection rate versus length in this model (Figure 2B) shows that as length increases, the injection rate decreases. This is the key goal of a length sensor and confirms that the time-of-flight model could, at least in principle, provide enough information to regulate IFT as a function of length. This establishes plausibility of the model.
FIGURE 2:
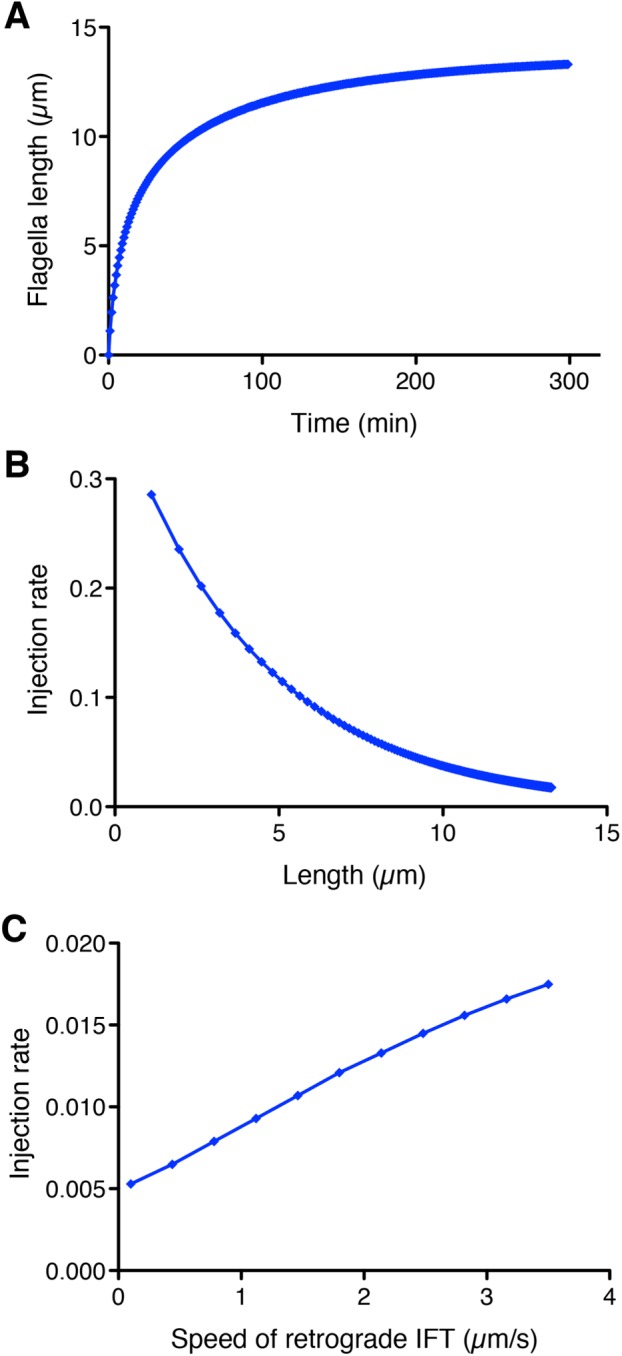
Modeling the time-of-flight length-sensing mechanism. (A) The time-of-flight model can produce stable length control and recapitulates decelerating growth kinetics seen in Chlamydomonas flagella. Plot shows a numerical solution of flagellar length vs. time according to Eq. 8 with the following parameter values: A = 0.0015 s–1, D = 0.0003 µm/s (based on shortening rate of flagella in absence of IFT; see Marshall and Rosenbaum, 2001), lifetime = 3 s, va = 2.5 µm/s (Engel et al., 2012), τ = 3 s (Chien et al., 2017), vr = 3.5 µm/s, and P = 40 (Marshall et al., 2005). (B) IFT injection rate is a decreasing function of flagellar length. Plot is based on the numerical solution of panel A and depicts injection rate as a function of length. (C) Dependence of injection rate on retrograde IFT velocity. Numerical solutions were determined for a range of retrograde velocities, keeping all other parameters the same as in the solution shown in A. Plot demonstrates that a reduction in retrograde IFT velocity is predicted to yield a reduction in the IFT injection rate.
Next we asked whether a reduction in retrograde IFT speed could, in principle, produce a detectable alteration in injection rate. Inspection of Eq. 7 indicates that decreasing the rate of retrograde IFT (decreasing vr) is expected to reduce the injection rate r. The question is how large of an effect on retrograde velocity would be needed to see a response. To answer this question, we systematically varied the retrograde speed over a range of values up to normal speed of 3.5 µm/s. As plotted in Figure 2C, the model predicts that the injection rate should decrease when retrograde velocity decreases. With this particular set of parameters, a twofold decrease in retrograde speed should reduce the injection rate by 30%, an effect that would be within our abilities to detect in our measurements. The conclusion of this modeling study is that a more-detailed model of the time-of-flight mechanism, taking into account distinct anterograde and retrograde velocities as well as a finite remodeling time of IFT particles at the tip, is able to produce decelerating flagellar growth kinetics and an injection rate that is a decreasing function of length. Most importantly, reduction in retrograde IFT velocity can potentially produce a detectable reduction in IFT injection rates. On the basis of this analysis, we therefore proceeded to develop an experimental approach to testing the time-of-flight model by manipulating retrograde IFT. We note that the velocities given in Eqs. 7 and 8 are effective velocities that represent the averaged effect of large numbers of individual steps by the dynein motor. Mutations could reduce the average velocity by either altering the stepping frequency, for example by changing the catalytic efficiency of the dynein motor domain, or time spent in a moving state, for example by altering dynein attachment efficiency to the microtubule—any of these would have the same effect on the effective velocity and would thus allow us to test the model in the same way.
IFT dynein mutants show slower retrograde IFT speed during flagellar regeneration
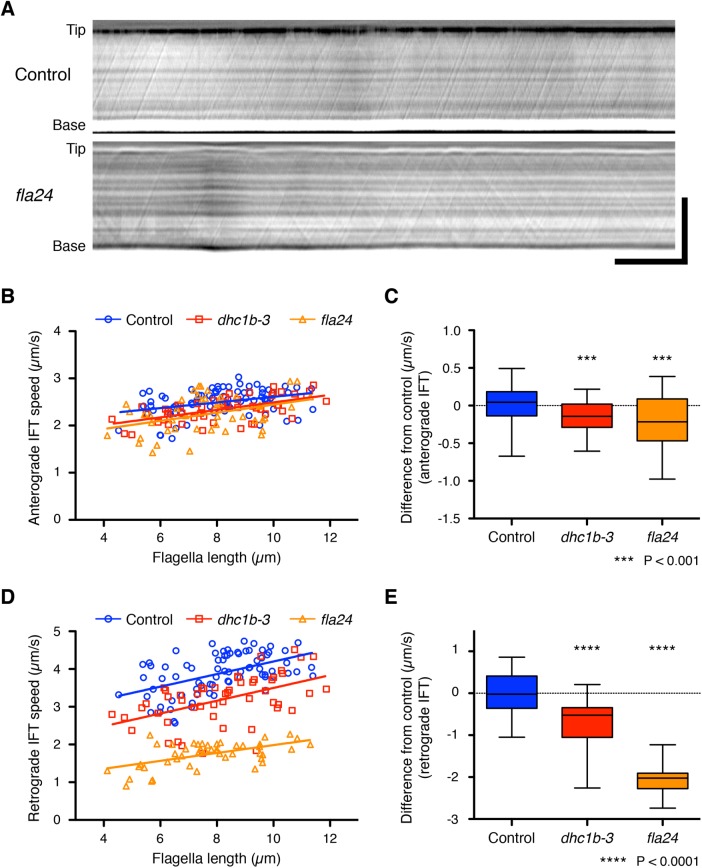
To change the IFT speed, we used Chlamydomonas temperature-sensitive cytoplasmic dynein 1b (also known as cytoplasmic dynein 2) mutant strains, dhc1b-3 and fla24. The dhc1b-3 and fla24 mutant strains carry distinct point mutations in the motor domain of the dynein heavy chain and show slower retrograde IFT speed at nonrestrictive temperatures (Iomini et al., 2001; Engel et al., 2012; Lin et al., 2013). To confirm these dynein mutant strains show slower IFT speed during flagella regeneration, we observed IFT using high-resolution differential interference contrast (DIC) microscopy and recorded our observations as movies (Supplemental Videos S1 and S2). We developed a method to measure average IFT speed automatically and quantitatively from kymographs (see Materials and Methods). DIC movies of flagella were converted into kymographs to measure the speed of IFT (Figure 3A). Because IFT speed can be calculated from the angle of the IFT trajectory against the axis of time in the kymograph (Ishikawa and Marshall, 2015), we measured the average angle of the trajectories from entire kymographs using the two-dimensional fast Fourier transform (2D FFT). During flagellar regeneration, anterograde IFT speed-of-control cells slightly increased as flagellar length increased (Figure 3B). Because this increasing trend and the speed of anterograde IFT were consistent with the previous report (Engel et al., 2009), the IFT speed–measuring method using 2D FFT was validated. Both dhc1b-3 and fla24 strains showed slightly slower anterograde IFT speed than control (0.15 ± 0.21 and 0.23 ± 0.36 µm/s slower than control, respectively; Figure 3, B and C). Meanwhile, both dynein mutant strains showed much slower retrograde IFT speed than control during flagella regeneration (0.71 ± 0.55 and 2.07 ± 0.30 µm/s slower than control, respectively; Figure 3, D and E). Because the fla24 mutant has a mutation in the AAA domain, a core of the motor, of the dynein heavy chain, it is perhaps not unexpected that it shows a slower retrograde IFT speed (more severe phenotype) than the dhc1b-3 mutant, in which the mutation is outside the motor core. High-resolution DIC imaging of IFT thus confirmed that the dynein mutant cells show constantly slower retrograde IFT speed during flagella regeneration.
FIGURE 3:
IFT speed during flagella regeneration in dynein mutant strains. (A) Representative DIC kymographs of Chlamydomonas flagella in control (fla3 KAP-GFP) and fla24 strains. These kymographs were assembled from Supplemental Videos S1 and S2. The horizontal axis is time, and the vertical axis is position along the flagellum. Horizontal bar: 5 s; vertical bar: 5 µm. (B, D) Average speeds of anterograde and retrograde IFT were measured from each kymograph and plotted against their flagellar length. Control (blue circles, n = 76 flagella), dhc1b-3 (red squares, n = 52 flagella), and fla24 (orange triangles, n = 47 flagella). (C, E) The differences of anterograde and retrograde IFT speed from the control regression line. The distances from the control regression line to each data point for each sample were calculated and shown as a box-and-whisker plot. Significance was determined by unpaired two-tailed t test (***P < 0.001 and ****P < 0.0001).
To relate experimental results to our model predictions, it is crucial that the behavior of the mutant motors can be described by an effective velocity. The mutations in the dynein motors could, in principle, alter the directional persistence of the dynein motion. This would pose difficulties for testing the time-of-flight model because if directional persistence were lost, the motion would become effectively diffusive and therefore the dwell time inside the flagella would no longer be linearly proportional to length. However, we do not think this happens to an appreciable extent with our mutants because the retrograde traces are still straight lines and thus can be described by an effective velocity.
Prediction of the time-of-flight model for dynein mutant flagella
Interestingly, retrograde as well as anterograde IFT speed increased as flagellar length increased (Figure 3D). The time-of-flight model measures the length of flagella based on the travel time of IFT in the flagellar compartment. However, travel time of IFT might decrease as flagellar length increases because both anterograde and retrograde IFT speeds increase as flagellar length increases. To confirm that longer flagella still show longer IFT travel time, we estimated the travel time corresponding to flagella length based on our observation. Both anterograde and retrograde IFT speeds during flagella regeneration were calculated from the regression lines in Figure 3. The remodeling time lag τ at the tip of flagella was estimated to be 3 s on the basis of our photobleaching assays (unpublished data), and this estimation was consistent with reported measurements from Chien et al. (2017). Travel time of IFT versus flagella length was calculated from anterograde and retrograde IFT speeds and the remodeling time lag (Figure 4A). We found that even though IFT speed increases slightly with the increasing flagella length, it is still the case that longer flagella have a longer IFT travel time (Figure 4A). Thus the time-of-flight model is still potentially viable as a length-sensing model.
FIGURE 4:
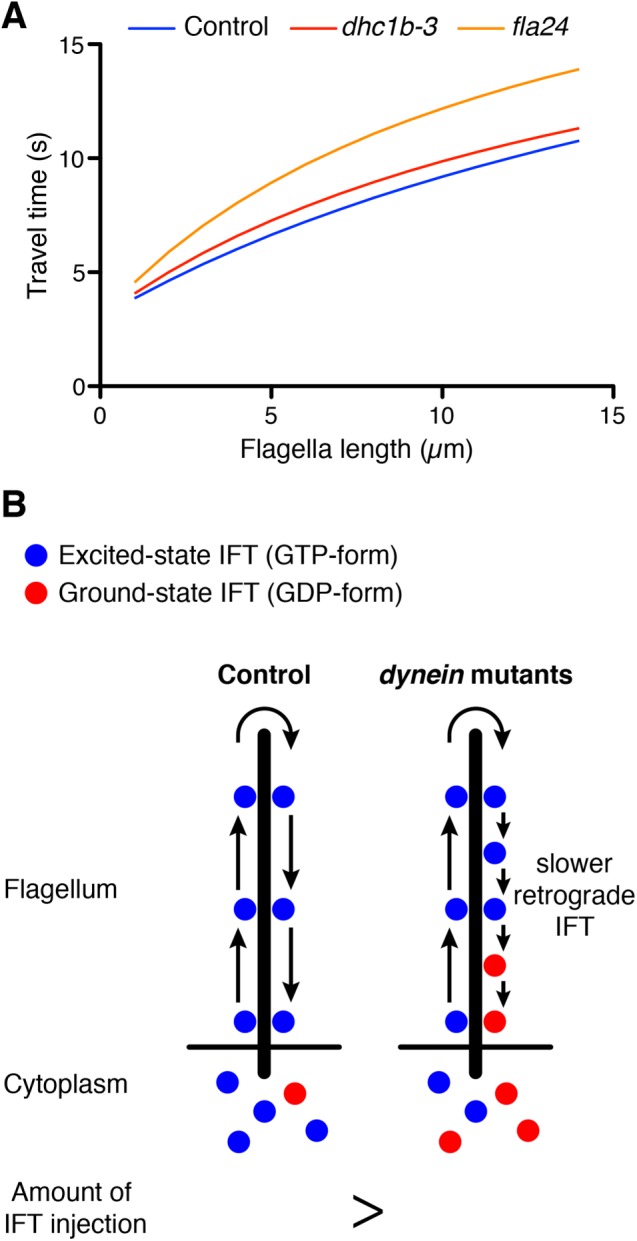
Prediction of the time-of-flight model for dynein mutant flagella. (A) Estimation of travel time of IFT in control and dynein mutant cells. The speeds of anterograde and retrograde IFT were based on our observation (Figure 3). Remodeling time at the tip of flagella was estimated as 3 s on the basis of our photobleaching assay and published results (Chien et al., 2017). Longer flagella still show longer IFT travel time. (B) Prediction for the time-of-flight model of dynein mutant flagella. Dynein mutant cells show slower retrograde IFT speed than control. When dynein mutant cells have same flagella length as control cells, dynein mutant cells should inject a lesser amount of IFT into flagella than control cells because slower retrograde IFT mimics the effect of longer flagella.
Because dynein mutant cells have slower retrograde IFT, they take more time to travel to the tip and back (Figure 4A). In the time-of-flight model, this increased travel time in the dynein mutant cells would be interpreted as an increase in flagellar length. For example, when flagella length is 5 µm, travel time in control cells is around 6.6 s, but the fla24 mutant takes 8.9 s in the same length of flagella (Figure 4A). This travel time is comparable to that for 9.4 µm of flagella in control cells. Because longer flagella inject a lesser amount of IFT into flagella (Engel et al., 2009; Ludington et al., 2013), dynein mutant cells should inject a lesser amount of IFT than the control cells, whose flagella are same length as those of dynein mutants (Figure 4B).
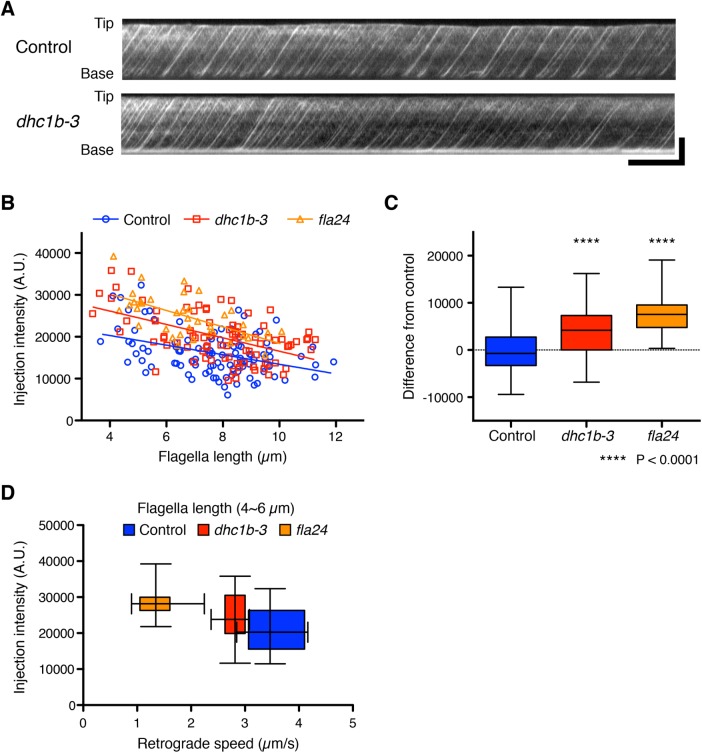
IFT injection intensity increased in IFT dynein mutants
To test our prediction, we measured the intensity of kinesin-associated protein (KAP), which is a subunit of the heteromeric kinesin-2 motor, tagged with green fluorescent protein (GFP). Because KAP-GFP was expressed in the fla3 (KAP) mutant cell and rescues the phenotype of the fla3 mutant (Mueller et al., 2005), the intensity of GFP reflects the amount of functional KAP in the cell. This fla3 KAP-GFP strain was also used in previous studies for measuring IFT injection intensity (Engel et al., 2009; Ludington et al., 2013). We used the fla3 KAP-GFP strain as a control. The dhc1b-3 and fla24 mutants expressing KAP-GFP were generated by mating with the fla3 KAP-GFP strain. To measure the intensity of KAP-GFP in control and dynein mutant cells, we performed total internal refection fluorescence (TIRF) microscopy (Supplemental Videos S3 and S4). TIRF movies of KAP-GFP were converted into kymographs to measure the IFT intensity (Figure 5A). Injection intensity of KAP-GFP in control cells increases as flagella length decreases (Figure 5B). This result is consistent with previous reports (Ludington et al., 2013). Injection intensities of KAP-GFP in both dynein mutant cells showed a linear dependence on length with a similar slope as control cells but shifted to higher average values compared with control cells (Figure 5, B and C). By considering only flagella in the 4- to 6-µm length range and plotting average injection intensity versus average retrograde speed for all three genotypes (Figure 5D), we found that as retrograde velocity decreases in the mutants, injection intensity increases. This observation is the opposite result from the prediction based on the time-of-flight model that slower retrograde IFT in the dynein mutants should lead to reduced IFT injection (Figure 2C). Finally, to determine how slower retrograde IFT combined with higher IFT injection intensity affects actual flagella regeneration, we checked the kinetics of flagella regeneration of dynein mutant cells (Figure 6). We found that the kinetics of flagella regeneration in dynein mutant cells are comparable with control cells (Figure 6). This result suggested that the higher IFT injection intensity in dynein mutant cells may compensate for slower retrograde IFT by another length-control mechanism.
FIGURE 5:
IFT injection intensities were increased in dynein mutant cells. (A) Representative kymographs of Chlamydomonas flagella in control (fla3 KAP-GFP) and dhc1b-3 (dhc1b-3 fla3 KAP-GFP) strains. These kymographs were assembled from Supplemental Videos S3 and S4. Horizontal bar: 5 s; vertical bar: 5 µm. (B) The mean injection intensity of each flagellum was calculated from kymographs and plotted against flagella length. Control (blue circles, n = 103 flagella), dhc1b-3 (red squares, n = 85 flagella), and fla24 (orange triangles, n = 37 flagella). (C) A box-and-whisker plot shows the mean difference of injection intensity from the control regression line. Both dynein mutant cells inject more IFT into flagella than control cells. Significance was determined by unpaired two-tailed t test (****P < 0.0001). (D) Relationship between injection rate and retrograde speed, derived by taking all flagella in the length range 4–6 µm for all three genotypes and plotting their average injection intensity (as in B) on the vertical axis and their average retrograde speed (as in Figure 3D) on the horizontal axis as a two-dimensional box-and-whisker plot. Control (blue, n = 18 flagella), dhc1b-3 (red, n = 13 flagella), and fla24 (orange, n = 12 flagella).
FIGURE 6:
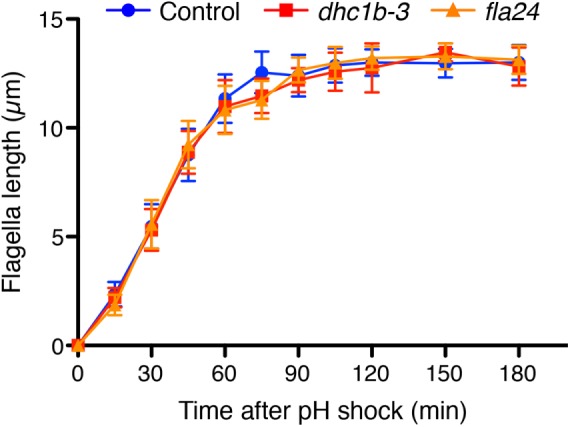
The kinetics of flagella regeneration of control (wild-type CC-125, blue circles) and dynein mutant (dhc1b-3 and fla24, red squares and orange triangles, respectively) cells. n = 20 cells per strain and time point.
DISCUSSION
The strategy reported here for testing the time-of-flight model relies on using mutations in dynein to slow down retrograde velocity. However, Eq. 7 relating injection rates to length involves several parameters, and it is worth considering whether alterations in other parameters might be confusing the results. We know that there is little change in anterograde velocity in the mutants based on direct measurements (Figure 3B). Because tip remodeling involves dynein altering its interactions with the rest of the IFT particle, we were concerned by the possibility that the dynein mutations might alter not only the retrograde velocity but also the tip remodeling time. Considering Eq. 7, it is evident by inspection that a decrease in tip remodeling time τ would lead to an increase in injection rate. This raises the possibility that our dynein mutations might not only slow retrograde velocity vr but also decrease the remodeling time τ to such an extent that we observe an overall increase in injection rates, even though the time-of-flight model holds true. We can estimate how large an effect on remodeling time τ could be. By inspecting Eq. 7, it can be seen that in order to cause increased injection rate, τ would have to decrease compared with the wild type. Specifically, the sum (τ + L/vr) would have to be smaller for the mutant than for the wild type (based on our measurement that va does not change in the mutants). Given a wild-type length of 10 µm, and given retrograde velocities of 3.5 and 1.5 µm/s for the wild type and mutant, respectively, we find that the ratio of L/vr increases by a total of 3.8 s in the mutant compared with the wild type. To cause injection rates to increase, rather than decrease as expected for the time-of-flight model, the mutation would thus need to cause a compensatory change in τ of at least 3.8 s. This value of 3.8 s would be enough to eliminate the change in injection. Increasing injection would require a decrease of >3.8 s. But τ has been reported to be 3 s in wild-type cells (Chien et al., 2017). The remodeling time cannot be negative, and hence the most that could happen is to reduce it to zero, and this would thus only be a 3-s change, not the 3.8-s change required to eliminate the change in length. Thus the possible range of variation of τ does not seem to be sufficient to account for our observed results even in the extreme case in which τ was reduced entirely to zero. Moreover, chemical inhibition of dynein has recently been reported to slightly increase, rather than decrease, the tip remodeling time τ (Chien et al., 2017), further arguing against the idea that a compensatory change in remodeling time is masking the decrease in injection predicted by the time-of-flight model.
Our results thus suggest that a time-of-flight mechanism is unlikely to be the basis for length-dependent control of IFT injection. Other potential mechanisms, such as length sensing by ion currents or diffusion-based gradients of signaling molecules, have been shown capable of producing a length-dependent molecular signal that could be used to modulate IFT injection (see Ludington et al., 2015). These alternative models are not tested by the present data, and thus they remain viable options. Alternative experimental approaches will be required to test these other classes of models. For example, one of the models we previously analyzed was a calcium ion current model in which a constant density of calcium channels in the flagellar membrane produces a current proportional to flagellar length. Higher current, leading to greater calcium influx, would reduce IFT injection, which is potentially consistent with published results that calcium-induced phosphorylation of the IFT kinesin-2 can impede its entry into flagella (Liang et al., 2014). Mutations in retrograde dynein such as those used here would not allow us to test such a model, in which retrograde speeds play no obvious role. Instead, a calcium current model would need to be tested by altering either calcium concentrations or channel activity. Depletion of calcium from the medium, or blocking the current with appropriate calcium channel blockers, would lead to reduced calcium influx, which would mimic the current normally seen in a short flagellum. Hence the prediction is that reducing calcium current should lead to an increase in IFT injection. To interpret such an experiment, intracellular calcium reporters would be needed to measure the effect of any perturbation, especially given that at this point, the molecular identity of the putative calcium channel is not known. Testing models based on diffusion of a signaling molecule will require a method to alter the diffusion constant of the molecule in question. It should be possible to use osmotic stress to lower diffusion constants globally, but as with the calcium current model, using such perturbations to assess the model requires methods for measuring the effect of the perturbation; for example, in the case of the diffusion model, methods are required to measure the diffusion of the signal in vivo, which requires us to know the identity of the signaling molecule.
In the course of testing the time-of-flight model, our experiments revealed two novel observations. First, we found that the speed of retrograde IFT motion is a function of length, with retrograde speed being higher in long flagella than in short flagella. We previously showed that anterograde speed is also higher in longer flagella than in shorter flagella (Engel et al., 2009). It thus appears that motion in both directions is higher in longer flagella, a result that we do not fully understand. One possibility, based on the fact that anterograde trains are smaller in longer flagella (Engel et al., 2009), is that longer anterograde trains move slowly because they contain more kinesin motors, and the trains can move only when all motors are actively stepping; otherwise bound but nonstepping motors should slow the movement down. However, the latter possibility seems less likely in light of studies showing that two or more kinesin motors attached to the same cargo cause the cargo to move at a speed similar to that of a single motor (Rogers et al., 2009; Derr et al., 2012). An alternative possibility is that longer trains experience increased drag forces due to friction. Although in some cases the force exerted by multiple kinesins is additive, in other cases it is less than additive (Furuta et al., 2013) such that the additional motors on a longer train might not be able to overcome the additional frictional forces. In either case, the effect on speed is thought to reflect the increased size of trains in shorter flagella. Our present measurements allow us to measure the speed of retrograde trains but not their size; hence we do not know whether a similar type of train-size effect can account for the length dependence of retrograde speed.
A second unexpected finding is that injection of IFT particles increases when retrograde speed is reduced. At the start of these experiments, we had envisioned two possibilities: either the time-of-flight model was correct, in which case injection would decrease when retrograde speed was reduced, or else injection would not be affected at all. The observation that injection actually increases when retrograde speed drops was not anticipated, and we do not currently have an explanation for this new phenomenon. We speculate that some form of compensation mechanism may be at work, such that the cell is able to detect impairment of retrograde IFT and injects additional IFT particles to compensate. The question is, what aspect of the system is impaired? Although the mutants considered here slow down retrograde return, we know the IFT trains eventually do make it back to the base since we do not see them accumulating inside the flagellum. Perhaps one or more proteins dissociate from the retrograde trains during their slower return to the base, and the resulting incomplete trains trigger a compensatory response by which the cells inject new trains into the flagellum. At the very least, these results suggest a previously unsuspected link between retrograde IFT and anterograde IFT. Dissecting the mechanism of this link requires future studies.
A third finding of this work is that regeneration kinetics are unaffected by mutations that reduce retrograde IFT speed. This observation is consistent with the idea that retrograde IFT mainly functions to return IFT proteins to the cytoplasm, rather than playing a direct role in modulating flagellar doublet dynamics. Such a result is consistent with previous results that complete blockage of retrograde IFT has very little effect on flagellar length for long periods of time (Engel et al., 2012). However, it is quite striking that injection can increase without a concomitant increase in growth rates. Previous studies have found that an increase in injection rates, caused by the lf4 mutation or by treatment with lithium, corresponds to increased length (Ludington et al., 2013). Why does the increased injection seen in the retrograde mutants not lead to increased assembly? One possibility might be that the injected trains are carrying less cargo such as tubulin. It has been reported that tubulin association with anterograde trains is length dependent (Craft et al., 2015), which might predict that injection could be increased without an increase in assembly. The potential influence of retrograde transport on tubulin loading would be an interesting question to explore in future investigations. Indeed, one possibility is that tubulin cargo loading is regulated by a time-of-flight mechanism. Our results thus conclusively rule out the time-of-flight mechanism as a means of controlling injection as a function of length, suggesting that some other length-measuring mechanism must be at work, but they do not rule out the possibility that a time-of-flight scheme might regulate cargo loading or other aspects of length control besides IFT injection.
MATERIALS AND METHODS
Strains and culture conditions
Chlamydomonas reinhardtii strains, wild-type 137c (CC-125), the fla3 mutant expressing KAP-GFP (CC-4296), and the fla24 mutant (CC-3866), were obtained from the Chlamydomonas Resource Center (University of Minnesota, St. Paul, MN). The dhc1b-3 mutant (CC-4422) was previously generated by UV mutagenesis (Engel et al., 2012). We mated dhc1b-3 or fla24 mutant strains with the fla3 KAP-GFP strain to generate dhc1b-3 fla3 and fla24 fla3 double-mutant strains expressing KAP-GFP. Chlamydomonas cells were grown in liquid Tris-acetic acid-phosphate (TAP) medium at room temperature with constant aeration.
Flagella regeneration assay
Chlamydomonas flagella were amputated by the pH shock method (Lefebvre, 1995). The pH of TAP cell cultures was adjusted to pH 4.5 with 0.5 M acetic acid and incubated for 1 min to amputate flagella, and then the pH was returned to pH 7.0 with 0.5 M KOH. The pH-shocked cells were pelleted by a centrifuge and resuspended with fresh TAP media. Cells were cultured at room temperature with constant aeration in light. Aliquots of cells were taken from the culture and fixed with 2.5% glutaraldehyde every 15 min after pH shock. Fixed cells were imaged by DIC microscopy using an inverted microscope (AxioVert 200M; Zeiss) with an air objective (Plan Apo 40×/numerical aperture [NA] 0.75; Zeiss) and a charge-coupled device (CCD) camera (Axiocam MRm; Zeiss). The lengths of 20 biflagellated cells at each time point and each sample were measured using ImageJ (National Institutes of Health [NIH]).
Live-cell imaging of IFT
All live-cell imaging was performed during regeneration of flagella. High-resolution DIC imaging was performed for visualizing IFT as previously described (Dentler et al., 2009). Flagella-regenerating cells were
placed on a #0 (22 × 22 mm) coverslip, immobilized with 2% agarose/TAP, and then covered with another #0 (24 × 60 mm) coverslip. The coverslips were sealed with VALAP (1:1:1 vaseline, lanolin, and paraffin). Movies were acquired at 25 frames per second (fps) at room temperature on an inverted microscope (Eclipse Ti; Nikon) with an oil objective (Apo TIRF 100 ×/NA 1.49; Nikon), a DIC oil condenser (NA 1.4; Nikon), and a scientific complementary metal-oxide-semiconductor (sCMOS) camera (ORCA-Flash4.0; Hamamatsu). Cells were selected for the presence of both flagella and the orientation of at least one of their flagella relative to the shear axis.
TIRF imaging was performed essentially as previously described (Engel et al., 2012; Ludington et al., 2013). Images were acquired at ∼20 fps at room temperature on an inverted microscope (Eclipse Ti; Nikon) with an oil objective (Apo TIRF 100 ×/NA 1.49; Nikon) and an electron-multiplying CCD (EM-CCD) camera (iXon Ultra 897; Andor).
Imaging analysis
For IFT speed analysis, kymographs were generated from DIC image sequences with ImageJ (NIH). IFT speed was calculated from DIC kymographs as follows. We calculated the 2D FFT of DIC kymographs. IFT trajectories resulted in skewed transforms, where the direction of skews was directly related to the angle of both anterograde and retrograde IFT trajectories. The average orientation of the IFT trajectories in the kymographs was orthogonal to the principle direction of the skewed transforms in the frequency space of the 2D FFT. The principle direction of the skewed transform was determined by calculating the orientation distribution at the center of the frequency space of the 2D FFT.
For IFT injection intensity analysis, anterograde directional kymographs were generated using Kymograph Clear (Mangeol et al., 2016). Kymographs were convolved with a Gaussian filter to remove noise. To extract KAP-GFP trajectories, peak detection was performed along the position axis of the kymograph, and then peaks were connected using the location and intensity of the peak. IFT injection intensity was calculated as the total intensity of KAP-GFP trajectories per unit length and unit time. All calculations were performed using custom-written routines in MATLAB (MathWorks).
Supplementary Material
Acknowledgments
We thank members of the Marshall laboratory for helpful discussions. We also thank Kurt Thorn, DeLaine Larsen, and the Nikon Imaging Center at the University of California, San Francisco, for invaluable microscopy resources and assistance. This work was supported by NIH Grant no. R01 GM097017 (to W.F.M.).
Abbreviations used:
- DIC
differential interference contrast
- fps
frames per second
- GDP
guanosine 5’-diphosphate
- GFP
green fluorescent protein
- GTP
guanosine 5’-triphosphate
- IFT
intraflagellar transport
- KAP
kinesin-associated protein
- NA
numerical aperture
- TAP
Tris-acetic acid-phosphate
- TIRF
total internal refection fluorescence
- 2D FFT
two-dimensional fast Fourier transform.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E17-06-0384) on September 20, 2017.
REFERENCES
- Bourne HR. GTPases: a family of molecular switches and clocks. Philos Trans R Soc Lond B Biol Sci. 1995;349:283–289. doi: 10.1098/rstb.1995.0114. [DOI] [PubMed] [Google Scholar]
- Buisson J, Chenouard N, Lagache T, Blisnick T, Olivo-Marin J-C, Bastin P. Intraflagellar transport proteins cycle between the flagellum and its base. J Cell Sci. 2013;126:327–338. doi: 10.1242/jcs.117069. [DOI] [PubMed] [Google Scholar]
- Cao M, Meng D, Wang L, Bei S, Snell WJ, Pan J. Activation loop phosphorylation of a protein kinase is a molecular marker of organelle size that dynamically reports flagellar length. Proc Natl Acad Sci USA. 2013;110:12337–12342. doi: 10.1073/pnas.1302364110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chien A, Shih SM., Bower R, Trischler D, Porter ME, Yildiz A. Dynamics of the IFT machinery at the ciliary tip. bioRxiv. 2017 doi: 10.7554/eLife.28606. doi:10.1101/156844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craft JM, Harris JA, Hyman S, Kner P, Lechtreck KF. Tubulin transport by IFT is upregulated during ciliary growth by a cilium-autonomous mechanism. J Cell Biol. 2015;208:223–237. doi: 10.1083/jcb.201409036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deane JA, Cole DG, Seeley ES, Diener DR, Rosenbaum JL. Localization of intraflagellar transport protein IFT52 identifies basal body transitional fibers as the docking site for IFT particles. Curr Biol. 2001;11:1586–1590. doi: 10.1016/s0960-9822(01)00484-5. [DOI] [PubMed] [Google Scholar]
- Dentler W. Intraflagellar transport (IFT) during assembly and disassembly of Chlamydomonas flagella. J Cell Biol. 2005;170:649–659. doi: 10.1083/jcb.200412021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dentler W, Vanderwaal K, Porter ME. Recording and analyzing IFT in Chlamydomonas flagella. Methods Cell Biol. 2009;93:145–155. doi: 10.1016/S0091-679X(08)93008-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derr ND, Goodman BS, Jungmann R, Leschziner AE, Shih WM, Reck-Peterson SL. Tug-of-war in motor protein ensembles revealed with a programmable DNA origami scaffold. Science. 2012;338:662–665. doi: 10.1126/science.1226734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel BD, Ishikawa H, Wemmer KA, Geimer S, Wakabayashi KI, Hirono M, Craige B, Pazour GJ, Witman GB, Kamiya R, et al. The role of retrograde intraflagellar transport in flagellar assembly, maintenance, and function. J Cell Biol. 2012;199:151–167. doi: 10.1083/jcb.201206068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel BD, Ludington WB, Marshall WF. Intraflagellar transport particle size scales inversely with flagellar length: revisiting the balance-point length control model. J Cell Biol. 2009;187:81–89. doi: 10.1083/jcb.200812084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furuta K, Furuta A, Toyoshima YY, Amino M, Oiwa K, Kojima H. Measuring collective transport by defined numbers of processive and nonprocessive kinesin motors. Proc Natl Acad Sci USA. 2013;110:501–506. doi: 10.1073/pnas.1201390110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao L, Thein M, Brust-Mascher I, Civelekoglu-Scholey G, Lu Y, Acar S, Prevo B, Shaham S, Scholey JM. Intraflagellar transport delivers tubulin isotypes to sensory cilium middle and distal segments. Nat Cell Biol. 2011;13:790–798. doi: 10.1038/ncb2268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iomini C, Babaev-Khaimov V, Sassaroli M, Piperno G. Protein particles in Chlamydomonas flagella undergo a transport cycle consisting of four phases. J Cell Biol. 2001;153:13–24. doi: 10.1083/jcb.153.1.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishikawa H, Marshall WF. Ciliogenesis: building the cell’s antenna. Nat Rev Mol Cell Biol. 2011;12:222–234. doi: 10.1038/nrm3085. [DOI] [PubMed] [Google Scholar]
- Ishikawa H, Marshall WF. Efficient live fluorescence imaging of intraflagellar transport in mammalian primary cilia. Methods Cell Biol. 2015;127:189–201. doi: 10.1016/bs.mcb.2015.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson KA, Rosenbaum JL. Polarity of flagellar assembly in Chlamydomonas. J Cell Biol. 1992;119:1605–1611. doi: 10.1083/jcb.119.6.1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozminski KG, Johnson KA, Forscher P, Rosenbaum JL. A motility in the eukaryotic flagellum unrelated to flagellar beating. Proc Natl Acad Sci USA. 1993;90:5519–5523. doi: 10.1073/pnas.90.12.5519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefebvre PA. Flagellar amputation and regeneration in Chlamydomonas. Methods Cell Biol. 1995;47:3–7. doi: 10.1016/s0091-679x(08)60782-7. [DOI] [PubMed] [Google Scholar]
- Liang Y, Pang Y, Wu Q, Hu Z, Han X, Xu Y, Deng H, Pan J. FLA8/KIF3B phosphorylation regulates kinesin-II interaction with IFT-B to control IFT entry and turnaround. Dev Cell. 2014;30:585–597. doi: 10.1016/j.devcel.2014.07.019. [DOI] [PubMed] [Google Scholar]
- Lin H, Nauman NP, Albee AJ, Hsu S, Dutcher SK. New mutations in flagellar motors identified by whole genome sequencing in Chlamydomonas. Cilia. 2013;2:14. doi: 10.1186/2046-2530-2-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludington WB, Ishikawa H, Serebrenik YV, Ritter A, Hernandez-Lopez RA, Gunzenhauser J, Kannegaard E, Marshall WF. A systematic comparison of mathematical models for inherent measurement of ciliary length: how a cell can measure length and volume. Biophys J. 2015;108:1361–1379. doi: 10.1016/j.bpj.2014.12.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludington WB, Wemmer KA, Lechtreck KF, Witman GB, Marshall WF. Avalanche-like behavior in ciliary import. Proc Natl Acad Sci USA. 2013;110:3925–3930. doi: 10.1073/pnas.1217354110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo M, Cao M, Kan Y, Li G, Snell W, Pan J. The phosphorylation state of an aurora-like kinase marks the length of growing flagella in Chlamydomonas. Curr Biol. 2011;21:586–591. doi: 10.1016/j.cub.2011.02.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangeol P, Prevo B, Peterman EJG. KymographClear and KymographDirect: two tools for the automated quantitative analysis of molecular and cellular dynamics using kymographs. Mol Biol Cell. 2016;27:1948–1957. doi: 10.1091/mbc.E15-06-0404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall WF, Qin H, Rodrigo Brenni M, Rosenbaum JL. Flagellar length control system: testing a simple model based on intraflagellar transport and turnover. Mol Biol Cell. 2005;16:270–278. doi: 10.1091/mbc.E04-07-0586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall WF, Rosenbaum JL. Intraflagellar transport balances continuous turnover of outer doublet microtubules: implications for flagellar length control. J Cell Biol. 2001;155:405–414. doi: 10.1083/jcb.200106141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller J, Perrone CA, Bower R, Cole DG, Porter ME. The FLA3 KAP subunit is required for localization of kinesin-2 to the site of flagellar assembly and processive anterograde intraflagellar transport. Mol Biol Cell. 2005;16:1341–1354. doi: 10.1091/mbc.E04-10-0931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin H. Regulation of intraflagellar transport and ciliogenesis by small G proteins. Int Rev Cell Mol Biol. 2012;293:149–168. doi: 10.1016/B978-0-12-394304-0.00010-5. [DOI] [PubMed] [Google Scholar]
- Qin H, Wang Z, Diener D, Rosenbaum J. Intraflagellar transport protein 27 is a small G protein involved in cell-cycle control. Curr Biol. 2007;17:193–202. doi: 10.1016/j.cub.2006.12.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers AR, Driver JW, Constantinou PE, Kenneth Jamison D, Diehl MR. Negative interference dominates collective transport of kinesin motors in the absence of load. Phys Chem Chem Phys. 2009;11:4882–4889. doi: 10.1039/b900964g. [DOI] [PubMed] [Google Scholar]
- Rosenbaum JL, Child FM. Flagellar regeneration in protozoan flagellates. J Cell Biol. 1967;34:345–364. doi: 10.1083/jcb.34.1.345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum JL, Moulder JE, Ringo DL. Flagellar elongation and shortening in Chlamydomonas. The use of cycloheximide and colchicine to study the synthesis and assembly of flagellar proteins. J Cell Biol. 1969;41:600–619. doi: 10.1083/jcb.41.2.600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum JL, Witman GB. Intraflagellar transport. Nat Rev Mol Cell Biol. 2002;3:813–825. doi: 10.1038/nrm952. [DOI] [PubMed] [Google Scholar]
- Rybin V, Ullrich O, Rubino M, Alexandrov K, Simon I, Seabra MC, Goody R, Zerial M. GTPase activity of Rab5 acts as a timer for endocytic membrane fusion. Nature. 1996;383:266–269. doi: 10.1038/383266a0. [DOI] [PubMed] [Google Scholar]
- Simon I, Zerial M, Goody RS. Kinetics of interaction of Rab5 and Rab7 with nucleotides and magnesium ions. J Biol Chem. 1996;271:20470–20478. doi: 10.1074/jbc.271.34.20470. [DOI] [PubMed] [Google Scholar]
- Sloboda RD, Rosenbaum JL. Making sense of cilia and flagella. J Cell Biol. 2007;179:575–582. doi: 10.1083/jcb.200709039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song L, Dentler WL. Flagellar protein dynamics in Chlamydomonas. J Biol Chem. 2001;276:29754–29763. doi: 10.1074/jbc.M103184200. [DOI] [PubMed] [Google Scholar]
- Stephens RE. Synthesis and turnover of embryonic sea urchin ciliary proteins during selective inhibition of tubulin synthesis and assembly. Mol Biol Cell. 1997;8:2187–2198. doi: 10.1091/mbc.8.11.2187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens RE. Turnover of tubulin in ciliary outer doublet microtubules. Cell Struct Funct. 1999;24:413–418. doi: 10.1247/csf.24.413. [DOI] [PubMed] [Google Scholar]
- Wang Z, Fan Z-C, Williamson SM, Qin H. Intraflagellar transport (IFT) protein IFT25 is a phosphoprotein component of IFT complex B and physically interacts with IFT27 in Chlamydomonas. PloS One. 2009;4:e5G84. doi: 10.1371/journal.pone.0005384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wren KN, Craft JM, Tritschler D, Schauer A, Patel DK, Smith EF, Porter ME, Kner P, Lechtreck KF. A differential cargo-loading model of ciliary length regulation by IFT. Curr Biol. 2013;23:2463–2471. doi: 10.1016/j.cub.2013.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.