Abstract
Measures of brain changes can be computed from sequential MRI scans, providing valuable information on disease progression for neuroscientific studies and clinical trials. Tensor-based morphometry (TBM) creates maps of these brain changes, visualizing the 3D profile and rates of tissue growth or atrophy. In this paper, we examine the power of different nonrigid registration models to detect changes in TBM, and their stability when no real changes are present. Specifically, we investigate an asymmetric version of a recently proposed unbiased registration method, using mutual information as the matching criterion. We compare matching functionals (sum of squared differences and mutual information), as well as large deformation registration schemes (viscous fluid registration versus symmetric and asymmetric unbiased registration) for detecting changes in serial MRI scans of 10 elderly normal subjects and 10 patients with Alzheimer’s Disease scanned at 2-week and 1-year intervals. We demonstrated that the unbiased methods, both symmetric and asymmetric, have higher reproducibility. The unbiased methods were also less likely to detect changes in the absence of any real physiological change. Moreover, they measured biological deformations more accurately by penalizing bias in the corresponding statistical maps.
1. Introduction
In recent years, computational neuroimaging has become an exciting interdisciplinary field with many applications in functional and anatomic brain mapping, image-guided surgery, and multimodality image fusion [1, 4, 7, 8]. The goal of image registration is to align, or spatially normalize, one image to another. In multi-subject studies, this reduces subject-specific anatomic differences by deforming individual images onto a population average brain template. When applied to serial scans of human brain, image registration offers tremendous power in detecting the earliest signs of illness, understanding normal brain development or aging, and monitoring disease progression. Recently, there has been an expanding literature on various nonrigid registration techniques, with different image matching functionals, regularization schemes, and numerical implementations. In [6, 9], the authors systematically examined the statistical properties of Jacobian maps (the determinant of the local Jacobian operator applied to the deformations), and proposed an unbiased large-deformation image registration approach. In this context, unbiased means that the Jacobian determinants of the deformations recovered between a pair of images follow a log-normal distribution, with zero mean after log-transformation. The authors argued that this distribution is beneficial when recovering change in regions of homogeneous intensity, and in ensuring symmetrical results when the order of two images being registered is switched. The authors applied this method to a longitudinal MRI dataset from a single subject, and showed promising results in eliminating spurious signals. They also noticed that different registration techniques, when applied to the same longitudinal dataset, may sometimes yield visually very different Jacobian maps, causing problems in interpreting local structural changes. Given this ambiguity and the increasing use of registration methods to measure brain change, more information is required concerning the baseline stability, reproducibility, and statistical properties of signals generated by different nonrigid registration techniques.
In this paper, we introduce a novel Asymmetric Unbiased model (by contrast with the Symmetric Unbiased model) and, for the first time, we analyze unbiased models with mutual information based matching functionals (prior work has focused on the case where the summed squared intensity difference is used as the criterion for registration). Most importantly, we aim to provide quality calibrations for different non-rigid registration techniques in TBM. In particular, we compare two common matching functionals: L2, or the sum of squared intensity differences, versus mutual information, and three regularization techniques (fluid registration versus the Asymmetric Unbiased and Symmetric Unbiased techniques). Our experiments are designed to decide which registration method is more reproducible, more reliable, and offers less artifactual variability in regions of homogeneous image intensity. The foundation of our calibrations is based on the assumption that, by scanning healthy normal human subjects twice over a 2-week period using the same protocol, serial MRI scan pairs should not show any systematic biological change. Therefore, any regional structural differences detected using TBM over such a short interval may be assumed to be errors. We apply statistical analysis to the profile of these errors, providing information on the reliability, reproducibility and variability of different registration techniques. Moreover, serial images of 10 subjects from the ADNI follow-up phase (images acquired one year apart) were analyzed in a similar fashion and compared to the ADNI baseline data. In images collected one year apart, real anatomical changes are present; neurobiological changes due to aging and dementia include widespread cell shrinkage, regional gray and white matter atrophy and expansion of fluid-filled spaces in the brain. Thus, a good computational technique should be able to differentiate between longitudinal image pairs collected for the ADNI baseline (2-week) and follow-up (1-year) phases.
At this point, we would like to motivate the unbiased approach, which couples the computation of deformations with statistical analyses on the resulting Jacobian maps. As a result, the unbiased approach ensures that deformations have intuitive axiomatic properties by penalizing any bias in the corresponding statistical maps. In the following sections, we describe the mathematical foundations of this approach, define energy functionals for minimization, and perform thorough statistical analyses to demonstrate the advantages of the unbiased registration models.
2. Unbiased Image Registration
Let Ω be an open and bounded domain in ℝn, for arbitrary n. Without loss of generality, assume that the volume of Ω is 1, i.e. |Ω| = 1. Let I1 : Ω → ℝ and I2 : Ω → ℝ be the two images to be registered. We seek to find the transformation g : Ω → Ω that maps the source image I2 into correspondence with the target image I1. In this paper, we will restrict this mapping to be differentiable, one-to-one, and onto. We denote the Jacobian matrix of a deformation g to be Dg, with Jacobian denoted by |Dg(x)| ≔ det(Dg(x)). The displacement field u(x) from the position x in the deformed image I2 ◦ g(x) back to I2(x) is defined in terms of the deformation g(x) by the expression g(x) = x − u(x) at every point x ∈ Ω. Thus, we consider the problems of finding g and u to be equivalent.
We now describe the construction of the Unbiased Large-Deformation Image Registration. We associate three probability density functions (PDFs) to g, g−1, and the identity mapping id: Pg(x) = |Dg(x)|, Pg−1 (x) = |Dg−1(x)|, Pid(x) = 1. By associating deformations with their corresponding global density maps, we can now apply information theory to quantify the magnitude of deformations. In our approach, we choose the Kullback-Leibler (KL) divergence and symmetric Kullback-Leibler (SKL) distance. The KL divergence between two probability density functions, p1(x) and p2(x), is defined as
We define the SKL distance as SKL(p1(x), p2(x)) = KL(p1(x), p2(x)) + KL(p2(x), p1(x)).
The Unbiased method solves for the deformation g (or, equivalently, for the displacement u) minimizing the energy functional E, consisting of the image matching term F and the regularizing term R which is based on KL divergence or SKL distance. The general minimization problem can be written as
| (1) |
Here, λ > 0 is a weighting parameter.
2.1. Asymmetric Unbiased Registration
To quantify the magnitude of deformation g, in this paper we introduce a new regularization term RKL, which is an asymmetric measure between Pid and Pg:
This regularization term can be shown to be
| (2) |
2.2. Symmetric Unbiased Registration
We also examine the regularization functional based on the symmetric KL distance between Pid and Pg:
As shown in [6, 9], the regularization term is linked to statistics on Jacobian maps as follows
| (3) |
Notice that the symmetric unbiased regularizing functional is pointwise nonnegative, while the asymmetric unbiased regularizer in (2) can take either positive or negative values locally.
3. Fidelity Metrics
In this paper, the matching functional F takes two forms: the L2 norm (the sum of squared intensity differences) and MI (mutual information). We briefly describe both distances in this section.
3.1. L2-norm
The L2-norm matching functional is suitable when the images have been acquired through similar sensors and thus are expected to present the same intensity range and distribution. The L2 distance between the deformed image I2 ◦ g(x) = I2(x − u) and target image I1(x) is defined as
3.2. Mutual Information
One of the main advantages of using mutual information is that it can be used to align images of different modalities, without requiring knowledge of the relationship (joint intensity distribution) of the two registered images. To define the mutual information between the deformed image I2(x − u) and the target image I1(x), we denote by pI1 and the intensity distributions estimated from I1(x) and I2(x − u), respectively. An estimate of their joint intensity distribution is denoted as . We also let i1 = I1(x), i2 = I2(x − u(x)) denote intensity values at point x ∈ Ω. Given the displacement field u, the mutual information computed from I1 and I2 is provided by
We seek to maximize the mutual information between I2(x − u) and I1(x), or equivalently, minimize the negative of , i.e. .
4. Minimization of Energy Functionals
In general, we expect minimizers of the energy functional E(u) to exist. Computing the first variation of the functional in (1), we obtain the gradient of E(u), namely ∂uE(u). We define the force field f, which drives I2 into registration with I1, as
| (4) |
Here, R(u) is either RKL(u) or RSKL(u). We minimize (1) using the fluid flow proposed in [1]. Given the velocity field v, the following partial differential equation can be solved to obtain the displacement field u:
| (5) |
Here, τ is an artificial time variable. The instantaneous velocity as in [3] is obtained by convolving f with Gaussian kernel Gσ of variance σ2, v = Gσ * f (x, u).
To avoid possible confusion, we summarize the methods we will be referring to in our subsequent analyses. In later discussions, minimization of the following energies
| (6) |
| (7) |
using equations (4), (5) will be referred to as L2-Asymmetric Unbiased and L2-Symmetric Unbiased models, respectively. The model above, provided λ = 0, will be referred to as the L2-Fluid model.
Similarly, minimization of
| (8) |
| (9) |
will be referred to as the MI-Asymmetric Unbiased and MI-Symmetric Unbiased models, respectively. Such models, with λ = 0, define the MI-Fluid model.
5. Statistical Analysis
5.1. Statistical testing on the deviation of log Jacobian maps in the absence of changes
Based on the authors’ approach in [6], we observe that, given that there is no systematic structural change within two weeks, any deviation of the Jacobian map from one should be considered error. Thus, we expect that a better registration technique would yield log |Dg| values closer to 0 (i.e., smaller log Jacobian deviation translates into better methodology). Mathematically speaking, one way to test the performance is to consider the deviation map dev of the logged (i.e., logarithmically transformed) Jacobian away from zero, defined at each voxel as dev(x) = | log |Dg(x)||. For two different registration methods A and B, we define the voxel-wise deviation gain of A over B (denoted by SA,B) as SA,B(x) = devA(x) − devB(x).
For the ADNI baseline dataset (in which patients are scanned twice with MRI, two weeks apart), we perform a group paired t test across subjects, by computing a voxel-wise t-map of deviation gains. In order to statistically compare the performance of two registration methods, we rely on the standard t test on the voxel mean of S. To construct a suitable null hypothesis, we notice that the following relation would hold, assuming B outperforms A: SA,B > 0. Thus, the null hypothesis in this case would be testing if the mean deviation gain is zero: H0 : μSA,B = 0. To determine the ranking of A and B, we have to consider one-sided alternative hypotheses. For example, when testing if B outperforms A, we use the following alternative hypothesis: H1 : μSA,B > 0. The voxel-wise T statistic, defined as
| (10) |
where , and , thus follows the Student’s t distribution under the null hypothesis and may be used to determine the p-value that the null hypothesis is true. If the alternative hypothesis is accepted, we confirm that sequence B outperforms A at point x. Otherwise, we would rank A and B equally if the null hypothesis is not rejected.
5.2. Detecting Real Changes - Statistical testing on the mean log Jacobian
For both the ADNI follow-up dataset (in which patients are scanned twice with MRI, one year apart) and ADNI baseline dataset, we create a voxel-wise t map using the local log Jacobian values of the ten subjects, allowing us to test the validity of the zero mean assumption. To simplify the notation, we introduce J to denote J = |Dg|. The following voxel-wise T statistic compared to a two-tailed Student’s t distribution may then be used to test the above null hypothesis
| (11) |
where , and . We reject the null hypothesis if the p value calculated above exceeds a pre-set threshold based on a suitable confidence interval.
5.3. Permutation Testing to Correct Multiple Comparisons
To determine the overall global effects of different registration methods on the deviation of log Jacobian maps throughout the brain, we performed permutation tests to adjust for multiple comparisons. Following the analyses in [5], we resampled the observations by randomly flipping the sign of under the null hypothesis. For each permutation, voxelwise t tests are computed. We then compute the percentage of voxels inside the chosen ROI (in this case the ICBM mask) with T statistics exceeding a certain threshold. The multiple comparisons- corrected p value may be determined by counting the number of permutations whose above-defined percentage exceeds that of the un-permuted observed data. For example, we say that sequence B outperforms A on the whole brain if this corrected p value is smaller than 0.05 (that is, less than 5% of all permutations have the above-defined percentage greater than that of the original data). All possible (210 = 1024) permutations were considered in determining the final corrected p value.
5.4. Cumulative Distribution Function (CDF)
To visually assess the global significance level of the voxel-wise t tests on deviation gains and log-Jacobian values, we also employed the cumulative distribution function (CDF) plot. In brief, we plot observed cumulative probabilities against the theoretical distribution under the null hypothesis. In the case of deviation gains S of a worse technique A over a better technique B in the ADNI baseline data, we expect a CDF curve to lie above the Null line (y = x), in the sense that a better technique exhibits less systematic changes. In the case of log-Jacobian values, a better registration technique, on the other hand, should be able to separate the CDF curves between ADNI baseline and follow-up phases (this is what we refer to as the separation of CDF curves in the presence of real physiological changes).
6. Results
In this section, we tested the Asymmetric Unbiased and Symmetric Unbiased models and compared the results to those obtained using the Fluid registration model [1, 3]. Of note, even though Asymmetric Unbiased and Symmetric Unbiased methods minimize different energy functionals, our experiments showed that they generate very similar maps. For each regularization technique, we employed both L2 and mutual information matching functionals (see (6)–(9)). In order to obtain a fair comparison, re-gridding was not employed.
6.1. ADNI Baseline Scans
In this section, nonlinear registration was performed on a dataset that we shall refer to as the “ADNI Baseline” dataset, which includes serial MRI images of ten normal elderly subjects acquired two weeks apart. Each of the ten pairs of scans is represented on a 128 × 160 × 128 grid. Here, the foundation of calibrations is based on the assumption that, by scanning normal control human subjects serially within a two-week period using the same MRI protocol, no systematic structural changes should be recovered.
Here, we compared Fluid, Asymmetric Unbiased, and Symmetric Unbiased methods coupled with both L2 and mutual information matching. Uniform values of λ = 500 and λ = 1000 were used for all deformations using L2-Symmetric Unbiased and L2-Asymmetric Unbiased algorithms, respectively. Also, λ = 5 and λ = 10 were used for deformations using MI-Symmetric Unbiased and MI-Asymmetric Unbiased methods. Since the Asymmetric Unbiased model quantifies only the forward deformation, the weight of the corresponding regularization functional is half the magnitude of that of the Symmetric Unbiased model, and hence, a weighting parameter twice as large should be used.
Figures 1–3 show the results of registering a pair of serial MRI images for one of the subjects. The deformation was computed in both directions (time 2 to time 1, and time 1 to time 2) using all three regularization methods based on L2 and mutual information matching. Results indicate the Asymmetric Unbiased and Symmetric Unbiased methods outperform Fluid method, generating more stable inverse consistent maps [2] with less variability.
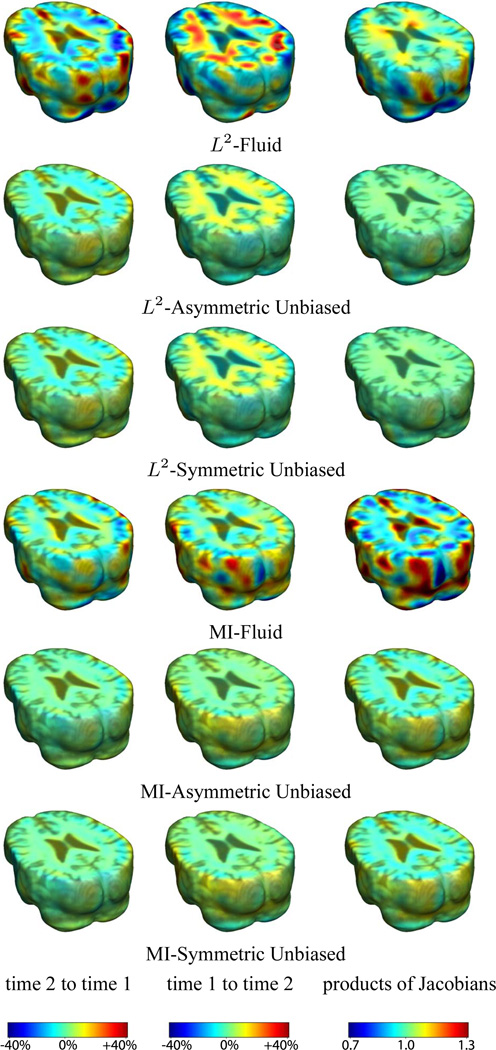
Figure 1.
Nonrigid registration was performed on an image pair from one of the subjects from the ADNI Baseline study (serial MRI images acquired two weeks apart) using L2-Fluid, L2-Asymmetric Unbiased, L2-Symmetric Unbiased, MI-Fluid, MI-Asymmetric Unbiased, and MI-Symmetric Unbiased registration methods. Jacobian maps of deformations from time 2 to time 1 (column 1) and time 1 to time 2 (column 2) are superimposed on the target volumes. The unbiased methods generate less noisy Jacobian maps with values closer to 1; this shows the greater stability of the approach when no volumetric change is present. Column 3 examines the inverse consistency of deformation models. Products of Jacobian maps are shown for the forward and backward directions. For the unbiased methods, the products of the Jacobian maps are less noisy, with values closer to 1, showing better inverse consistency.
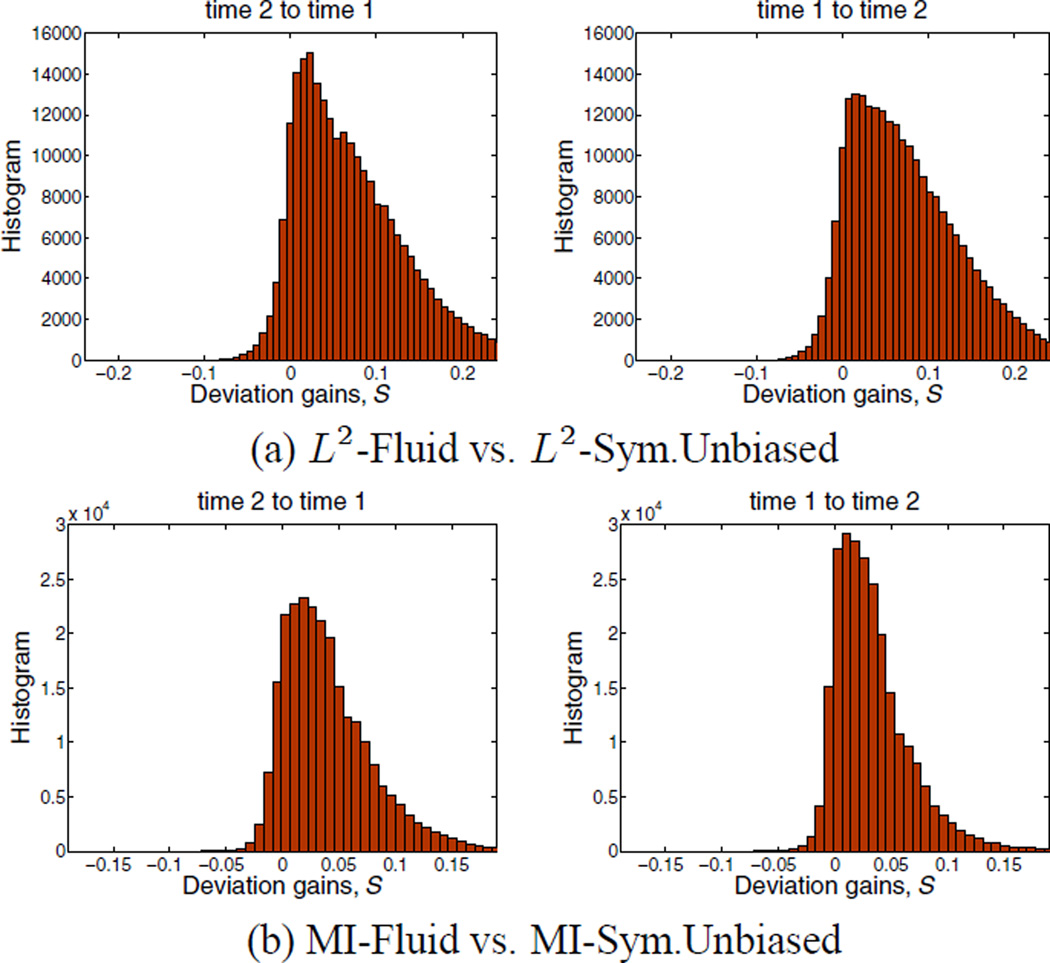
Figure 3.
Histograms of voxel-wise deviation gains (a) L2-Fluid over L2-Symmetric Unbiased, and (b) MI-Fluid over MI-Symmetric Unbiased for one of the subjects, for the forward direction (time 2 to time 1) and backward direction (time 1 to time 2). The histograms are skewed to the right, indicating the superiority of Symmetric Unbiased registration method over Fluid registration. Since the results obtained using the Asymmetric Unbiased method are similar to those obtained using the Symmetric Unbiased method, they are not shown here.
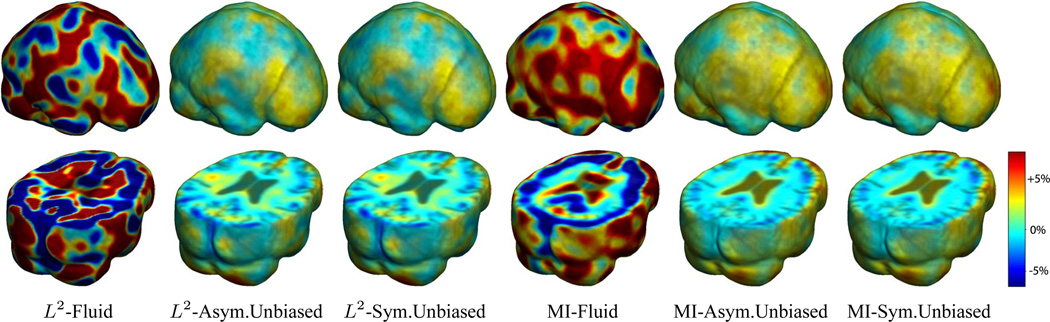
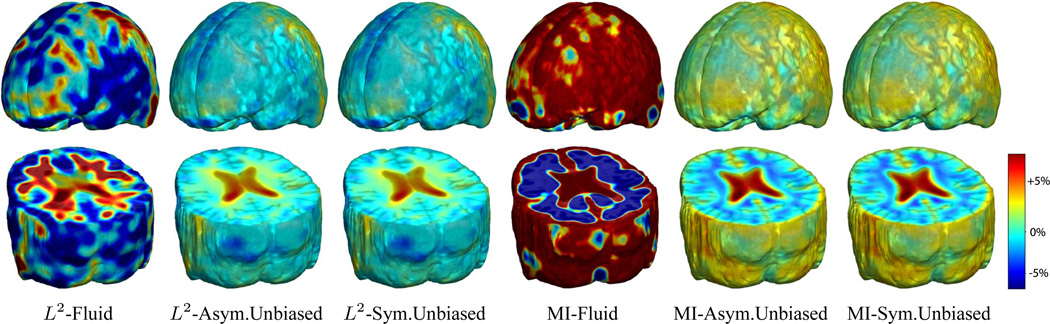
Figure 4 shows the mean Jacobian maps of ten subjects obtained using Fluid, Asymmetric Unbiased, and Symmetric Unbiased registration algorithms coupled with both L2 and mutual information matching. Jacobian maps generated using unbiased models have values closer to 1, whereas Fluid model generated noisy mean maps. Figures 5 and 6(a,b) demonstrate the Unbiased regularization technique outperforming Fluid registration with statistical significance.
Figure 4.
Nonrigid registration was performed on the ADNI Baseline study (serial MRI images acquired two weeks apart) of ten normal elderly subjects using L2-Fluid, L2-Asymmetric Unbiased, and L2-Symmetric Unbiased, MI-Fluid, MI-Asymmetric Unbiased, and MI-Symmetric Unbiased registration methods. For each method, the mean of the resulting 10 Jacobian maps is superimposed on one of the brain volumes. Visually, Fluid registration generates noisy mean maps, while maps generated using the Asymmetric Unbiased and Symmetric Unbiased methods are less noisy with values closer to 1. For all deformation models, regions with least stability, due to both spatial distortion and intensity inhomogeneity, are the brain stem, thalamus, and ventricles.
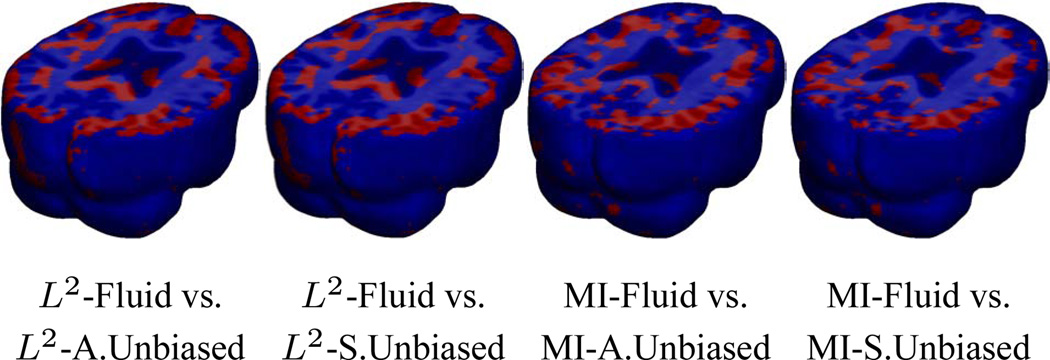
Figure 5.
Voxel-wise paired t test for the deviation gain S empirically thresholded at 2.82 (p = 0.005 on the voxel level with 9 degrees of freedom), showing where Asymmetric Unbiased and Symmetric Unbiased registration outperform Fluid registration (regions in red) with statistical significance on a voxel level. Regularization methods are coupled with L2 and MI matching.
Figure 6.
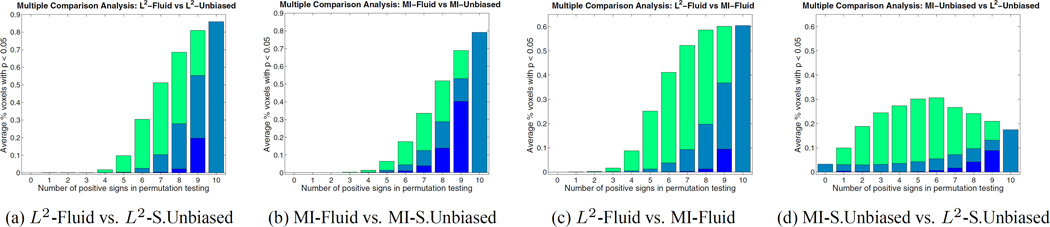
Multiple Comparison Analysis using permutation testing on the deviation gain S of (a) L2-Fluid over L2-Symmetric Unbiased, (b) MI-Fluid over MI-Symmetric Unbiased, (c) L2-Fluid over MI-Fluid, and (d) MI-Symmetric Unbiased over L2-Symmetric Unbiased, all for ADNI baseline dataset. Each permutation randomly assigns a positive or negative sign to each of the 10 log-Jacobian maps. Here, results are plotted with respect to the number of positive signs (from 0 to 10) with 10 positive signs indicating the observed data. Dark blue, light blue, and green colors indicate the minimum, average, and maximum percentage of voxels with p < 0.05 of all possible permutations with a given number of positive signs. Experiments in (a) and (b) are designed to compare Fluid and Symmetric Unbiased regularization techniques. The result shows that out of 1024 permutations, no permutation gives a greater percentage of voxels with p < 0.05 than the observed data does, which indicates that unbiased regularization technique outperforms Fluid methods with p < 0.001. Results in (c) and (d) compare L2 and mutual information matching functionals. In (c), we observe that MI-Fluid method outperforms L2-Fluid method with p < 0.001. However, the comparison of MI-Symmetric Unbiased and L2-Symmetric Unbiased in (d) is inconclusive. Since the results obtained using Asymmetric Unbiased method are similar to those obtained using Symmetric Unbiased method, they are not shown here.
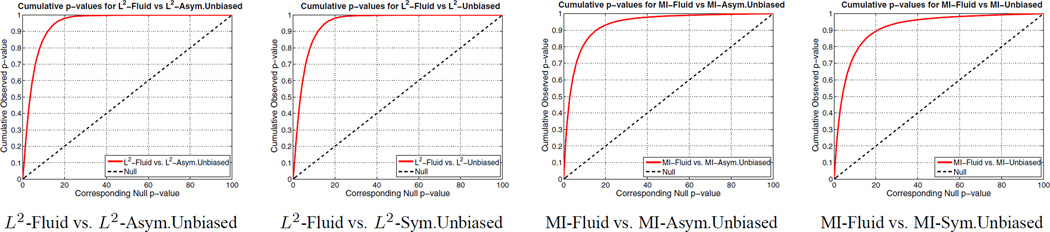
To emphasize the differences between the distributions of log Jacobian values for Fluid and unbiased (both asymmetric and symmetric) methods, in Figure 7, we plotted the cumulative distribution function of the p-values in deviation gains (SA,B). For a null distribution, this cumulative plot falls along the line y = x. Larger upward inflections of the CDF curve near the origin are associated with significant deviation gains, indicating that both Asymmetric Unbiased and Symmetric Unbiased methods outperform Fluid method in being less likely to exhibit structural changes in the absence of systematic biological changes.
Figure 7.
Cumulative distribution of p-values for the deviation gain S of L2-Fluid over L2-Asymmetric Unbiased, L2-Fluid over L2-Symmetric Unbiased, MI-Fluid over MI-Asymmetric Unbiased, and MI-Fluid over MI-Symmetric Unbiased. Here, the ADNI baseline dataset is used. The CDFs lines are well above the Null line (y = x), indicating that both asymmetric and symmetric unbiased methods outperform Fluid method (i.e. less deviation) in being less likely to exhibit structural change in the absence of biological change.
We also compared L2 and mutual information cost functionals for both Fluid and Symmetric Unbiased regularization. (Since Asymmetric Unbiased and Symmetric Unbiased regularizations produce similar results, we do not show the results for the asymmetric version). We showed that MI-Fluid outperforms L2-Fluid with statistical significance (Figure 6(c)). However, the result of the comparison of L2-Symmetric Unbiased and MI-Symmetric Unbiased is inconclusive (Figure 6(d)). In other words, mutual information performs better (than L2) when coupled with Fluid registration, but there is no statistical difference between mutual information and L2 when the Symmetric Unbiased method is used. To explain this result, we postulate that by constraining the deformations less (i.e., as in Fluid registration), assuming intensity 1-to-1 correspondence (i.e., matching using L2) may lead to local oscillations of the deformation maps, as minimizing L2 forces a local search for the smallest intensity differences. One result of this is a Jacobian map with locally extreme values, translating into spurious signals and, in our case, less reproducibility. On the other hand, the Symmetric Unbiased method eliminates local oscillations, allowing globally better matching when intensity 1-to-1 correspondence can be assumed (i.e., when L2 is applicable as a data fidelity term).
6.2. ADNI Follow-up Scans
In this section, we analyze a dataset we shall call the “ADNI Follow-up” phase dataset, which includes serial MRI images (220 × 220 × 220) of ten subjects acquired one year apart. As the images are now one year apart, real anatomical changes are present, which enables the comparison of methods in the presence of true biological changes.
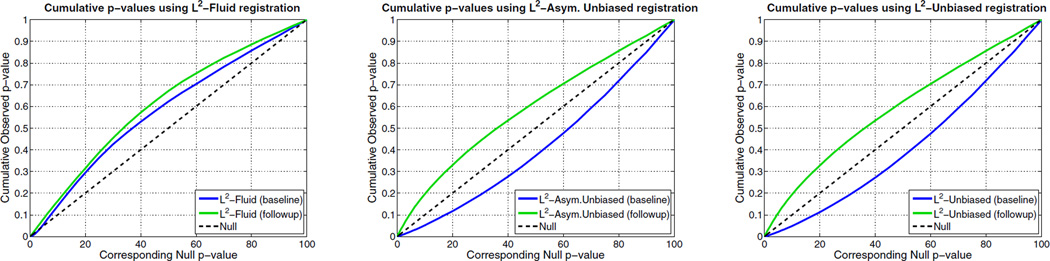
In Figure 8, nonlinear registration was performed using Fluid, Asymmetric Unbiased, and Symmetric Unbiased methods coupled with both L2 and mutual information matching. Visually, the Fluid method generates noisy mean Jacobian maps, while maps generated using unbiased methods suggest a volume reduction in gray matter as well as ventricular enlargement. Here, both Asymmetric Unbiased and Symmetric Unbiased methods perform equally well. Figure 9 displays the cumulative distribution of p-values for the voxel-wise log Jacobian t-maps for both ADNI Baseline and ADNI Follow-up datasets. We expect a better method to separate these two CDF curves, indicating that a real biological change has occurred between the two time points. A greater separation is accomplished when Unbiased methods are used, while the Fluid method does not differentiate between the two datasets.
Figure 8.
Nonrigid registration was performed on the ADNI Follow-up study (serial MRI images acquired 12 months apart) using L2-Fluid, L2-Asymmetric Unbiased, L2-Symmetric Unbiased, MI-Fluid, MI-Asymmetric Unbiased, and MI-Symmetric Unbiased registration methods. For each method, the mean of the resulting 10 Jacobian maps is superimposed on one of the brain volumes. Visually, Fluid registration generates noisy mean maps, while maps generated using the Asymmetric Unbiased and Symmetric Unbiased methods suggest a volume reduction in gray matter as well as ventricle enlargement.
Figure 9.
Cumulative distribution of p-values for the voxelwise log Jacobian t-maps (as defined in Equation (11)) for both ADNI Baseline (in blue) and Follow-up (in green) using L2-Fluid, L2-Asymmetric Unbiased, and L2-Symmetric Unbiased methods. A better method should separate these two CDF plots (see Section 5.4) with the Null line in between, indicating a real biological change has occurred between these two time points. Hence, L2-Asymmetric Unbiased and L2-Symmetric Unbiased methods outperform L2-Fluid method.
7. Conclusion
This paper is the first work to systematically investigate the reproducibility and variability of different registration methods in TBM. We showed that Asymmetric Unbiased and Symmetric Unbiased models perform significantly better than the fluid registration technique. Although various techniques have been extensively applied to detect disease effects and monitor brain changes with TBM, this paper is the first calibration study to compare registration models for tensor-based morphometry. We believe our results are important, as they provide greater insight into the interpretation of TBM results in the future.
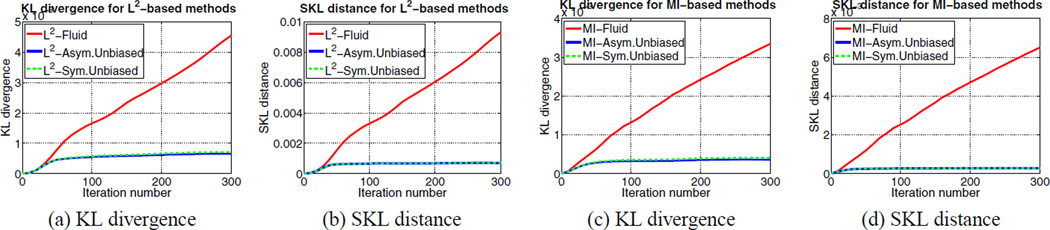
Figure 2.
(a) KL divergence and (b) SKL distance per iteration are shown for L2-Fluid (solid red), L2-Asymmetric Unbiased (solid blue), and L2-Symmetric Unbiased (dashed green) methods. (c) KL divergence and (d) SKL distance per iteration are shown for MI-Fluid, MI-Asymmetric Unbiased, and MI-Symmetric Unbiased methods. For Fluid regularization technique, both KL and SKL measures increase. Even though the Asymmetric Unbiased method explicitly minimizes the KL distance, and the Symmetric Unbiased model minimizes the SKL distance, both of the KL and SKL measures stabilize for unbiased methods.
Acknowledgments
This work was supported in part by the National Institutes of Health under Grant U54 RR021813 NIH/NCRR, Grant U01 AG024904, Grant P41 RR13642, and Grant R21 EB001561. The work of Igor Yanovsky was also supported by NSF VIGRE Grant DMS-0601395 and CCB-NIH Grant 30886. The work of Paul Thompson was also supported in part by the National Center for Research Resources, the National Institute for Biomedical Imaging and Bioengineering, the National Institute of Aging, and the National Institute for Neurological Disorders and Stroke, Grant R21 RR019771, Grant EB01651, Grant AG016570, Grant NS049194.
References
- 1.Christensen G, Rabbitt R, Miller M. Deformable templates using large deformation kinematics. IEEE Transactions on Image Processing. 1996;5(10):1435–1447. doi: 10.1109/83.536892. [DOI] [PubMed] [Google Scholar]
- 2.Christensen GE, Johnson HJ. Consistent image registration. IEEE Trans. Med. Imag. 2001;20(7):568–582. doi: 10.1109/42.932742. [DOI] [PubMed] [Google Scholar]
- 3.D’Agostino E, Maes F, Vandermeulen D, Suetens P. A viscous fluid model for multimodal non-rigid image registration using mutual information. Medical Image Analysis. 2003;7:565–575. doi: 10.1016/s1361-8415(03)00039-2. [DOI] [PubMed] [Google Scholar]
- 4.Grenander U, Miller MI. Computational anatomy: An emerging discipline. Quarterly of Applied Mathematics. 1998;56:617–694. [Google Scholar]
- 5.Leow A, et al. Longitudinal stability of MRI for mapping brain change using tensor-based morphometry. NeuroImage. 2006;31(2):627–640. doi: 10.1016/j.neuroimage.2005.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Leow A, Yanovsky I, Chiang M-C, Lee A, Klunder A, Lu A, Becker J, Davis S, Toga A, Thompson P. Statistical properties of Jacobian maps and the realization of unbiased large-deformation nonlinear image registration. IEEE Trans. Med. Imaging. 2007;26(6):822–832. doi: 10.1109/TMI.2007.892646. [DOI] [PubMed] [Google Scholar]
- 7.Miller MI. Computational anatomy: shape, growth, and atrophy comparison via diffeomorphisms. NeuroImage. 2004;23(suppl. 1):S19–S33. doi: 10.1016/j.neuroimage.2004.07.021. [DOI] [PubMed] [Google Scholar]
- 8.Thompson PM, Toga AW. A framework for computational anatomy. Comp. Vis. Science. 2002;5:13–34. [Google Scholar]
- 9.Yanovsky I, Thompson P, Osher S, Leow A. Topology preserving log-unbiased nonlinear image registration: Theory and implementation. IEEE CVPR. 2007 [Google Scholar]