Abstract
To obtain a patient-specific cardiac electrophysiological (EP) model, it is important to estimate the three-dimensionally distributed tissue properties of the myocardium. Ideally, the tissue property should be estimated at the resolution of the cardiac mesh. However, such high dimensional estimation face major challenges in identifiability and computation. Most existing works reduce this dimension by partitioning the cardiac mesh into a pre-defined set of segments. The resulting low-resolution solutions have a limited ability to represent the underlying heterogeneous tissue properties of varying sizes, locations and distributions. In this paper, we present a novel framework that, going beyond a uniform low-resolution approach, is able to obtain a higher resolution estimation of tissue properties represented by spatially non-uniform resolution. This is achieved by two central elements: 1) a multi-scale coarse-to-fine optimization that facilitates higher resolution optimization using the lower resolution solution, and 2) a spatially adaptive decision criterion that retains lower resolution in homogeneous tissue regions and allows higher resolution in heterogeneous tissue regions. The presented framework is evaluated in estimating the local tissue excitability properties of a cardiac EP model on both synthetic and real data experiments. Its performance is compared with optimization using pre-defined segments. Results demonstrate the feasibility of the presented framework to estimate local parameters and to reveal heterogeneous tissue properties at a higher resolution without using a high number of unknowns.
Index Terms: Parameter estimation, Cardiac electrophysiological model, Multi-Scale optimization, Gaussian Process
I. Introduction
CARDIAC disease is the leading cause of mortality worldwide [1]. To determine treatments for cardiovascular disease, traditional medicine typically relies on prior experiences and empirical data from similar patients. However, this ‘one-size-fit-all’ strategy is often sub-optimal partly owing to large anatomical and physiological variations among individuals [2]. Recent advances in mathematical modeling and medical imaging technologies have facilitated the use of multi-scale cardiac models as patient-specific predictive and prognostic tools. Promising examples include the design of cardiac resynchronization therapy for ventricular dysynchrony [1], the design of ablation therapy for atrial fibrillation [3], and risk stratification of sudden cardiac death for the insertion of implantable cardioverter defibrillator [2].
Owing to the advances in medical imaging technologies, high-fidelity patient-specific anatomical models have become possible [2]. However, an accurate physiological model requires more than an accurate geometry: it is also important to obtain patient-specific tissue properties (in the form of model parameters). However, these model parameters have to be inferred from sparse and indirect measurements. This often involves a challenging optimization problem to match the output of a sophisticated physiological model to the measurement data. Moreover, material properties of the heart are spatially varying, with local abnormality and heterogeneity bearing important physiopathological implications. This means that an accurate characterization of patient-specific material properties involves a high dimension of unknowns.
Numerous approaches have been developed to estimate patient-specific model parameters, mostly tackling the challenge of having a physiological model in the objective function. These include derivative-free optimization [1], [4], [5], Bayesian estimation by building surrogates using Polynomial chaos [6] or Gaussian process [7], and Bayesian filtering [8]. Essentially, all these methods involve a non-intrusive, repeated evaluation of the physiological model. However, none of the existing methods can be directly applied to estimate high-dimensional model parameters corresponding to the spatially-varying material properties. This is because the increased dimension of unknowns: 1) increases the ill-posedness of the problem, where estimation of parameters at the resolution of the discrete cardiac mesh is likely to be unidentifiable given limited indirect measurements, and 2) leads to an exponential increase in the number of model evaluations, where each model evaluation itself is computationally intensive.
As a result, most previous works resort to the estimation of parameters at a reduced spatial dimension. Many works focus on the estimation of a global parameter [9], [10] by assuming uniform tissue property throughout the myocardium. Although such estimation allows a fast model calibration, it does not capture the locally varying tissue properties. Another approach is to reduce the dimension of the unknowns by partitioning the cardiac mesh into pre-defined segments and to assume uniform parameter value within each segment. This reduces the spatial field of tissue properties to a low-resolution representation (in the range of 3-26 segments) [1], [4], [7], [11]. As a result of this drastically decreased resolution, the solution has limited ability to reflect different levels of tissue heterogeneity, or the existence of local abnormal tissue with various sizes and distributions. Additionally, as the number of pre-defined segments increases, a good initialization is shown to become critical to the accuracy of parameter estimation [4]. This unfortunately relies on the availability of measurement data that can reveal diseased regions a priori. Therefore, a critical gap remains in personalized modeling between the needs for a high resolution estimation of spatially-varying parameters and the difficulty to accommodate such high dimensionality by existing optimization methods.
To bridge the above gap, the central aim of this study is to develop an optimization framework that, instead of a uniform low-resolution representation of the parameter field, can obtain a higher resolution non-uniform representation consisting of higher resolution in heterogeneous regions and lower resolution in homogeneous regions. It is based on the key assumption that not all spatial dimensions corresponding to individual nodes in the cardiac mesh are independent; rather, dimensions corresponding to the neighboring nodes maybe correlated. By automatically dedicating higher resolution to more informative regions, the presented framework allows us to maximize the knowledge of tissue properties we can obtain from limited data, given a limited budget of dimensionality any optimization method can handle. The key contributions of this work are as follows:
A multi-scale optimization framework that progressively optimizes from lower resolution to higher resolution, where a lower resolution solution is used to facilitate the higher resolution optimization.
An adaptive decision criterion that allocates higher resolution to regions with heterogeneous tissue properties, allowing a higher resolution parameter estimation without using a large number of unknowns.
Development of the presented framework with two optimization methods: 1) Gaussian process (GP) surrogate based optimization (GPO) [12], and 2) Bound Optimization BY Quadratic Approximation (BOBYQA) [13]; and comparison with standard BOBYQA carried out on a predefined division of cardiac mesh into 26 segments.
Evaluation of the presented framework in the estimation of local tissue excitability in a 3D cardiac EP model, using several measurement data including 120-lead ECG, 12-lead ECG, and epicardial action potentials. It is noteworthy that limited work has been done on estimating local electrophysiological properties using non-invasive ECG data [14], [11].
We tested the performance of the presented framework on three categories of experiments. First, on synthetic experiments, we evaluated the presented method in estimating local tissue excitability: 1) in the presence of infarcted tissues of varying sizes and locations, and 2) using 120-lead ECG vs. using 12-lead ECG. Second, we applied the presented method to estimate local tissue excitability on seven patients with prior myocardial infarction, where a subset of epicardial potentials simulated from a high-resolution ionic EP model binded to the parameter estimation framework is used as measurement data. Finally, we conducted two pilot studies on patients who underwent catheter ablation of ventricular tachycardia due to prior tissue infarction by using non-invasive 120-lead ECG as measurement data. Results show that the presented framework is able to characterize local abnormal infarct tissues without using any knowledge of the abnormal tissue derived from other data modalities.
II. Models of Cardiac Electrophysiology
A. Cardiac Electrophysiological Model
Over the last few decades, a wide range of computational models of cardiac electrophysiology varying in the level of complexity and detail have been developed [15]. These models can be broadly classified into three types: biophysical, Eikonal and phenomenological. Biophysical models capture the microscopic level ionic interactions within the cardiac cell and through the cell membrane. Because these models typically consist of a large number of parameters and are computationally intensive, they have found limited application in local parameter estimation. In contrast, the Eikonal models focus only on the propagation of the electrical wave-front and cannot accurately describe the action potential. Phenomenological models offer a level of detail that lies in between these two types of models. They capture the key macroscopic dynamical properties such as the inward and outward current. Because these models have a small number of parameter and a faster execution time compared to the biophysical models [16], they offer a practical balance between model plausibility and computational feasibility for local parameter estimation.
Without the loss of generality, in this study we consider local parameter estimation for the two-variable Aliev-Panfilov (AP) [17] model:
| (1) |
where u is the normalized transmembrane action potential ([0, 1]), z is the recovery current and ε = e0+ (μ1z)/(u + μ2) controls the coupling between the transmembrane action potential and the recovery current. Parameter D is the diffusion tensor, c controls the repolarization, and a controls the excitability of the cell.
To select the parameter to be estimated in the AP model, we conduct a one-factor-at-a-time sensitivity analysis of the AP model. As a baseline, we use the values of the parameters as documented in literature [17]: a=0.15, c = 8, e0 = 0.002, μ1 = 0.2, and μ2 = 0.3. The shaded blue region in Fig. 1 shows the standard deviation of u throughout the action potential duration resulting from the variations in each model parameter. As shown, the average of these standard deviations is the highest as a result from the variations in parameter a (tissue excitability). Furthermore, tissue excitability is documented to be closely associated with the ischemic severity of the myocardial tissue [16]. Therefore, in this study, we will consider the application of the presented framework in estimating parameter a of the AP model. The physiological bounds on the value of parameter a is [0, 0.5] in which a ∼ 0.15 represents normal excitability and an increase in the value represents an increase in the severity of tissue infarct until a ∼ 0.5 represents necrotic tissue. For the rest of the parameters, their values are fixed to standard values as specified above. We also fix the values of longitudinal conductivity to 0.24Sm−1 and transversal conductivity to 0.024Sm−1 [18]. The EP model is solved on 3D myocardium discretized using the meshfree method [19].
Fig. 1.
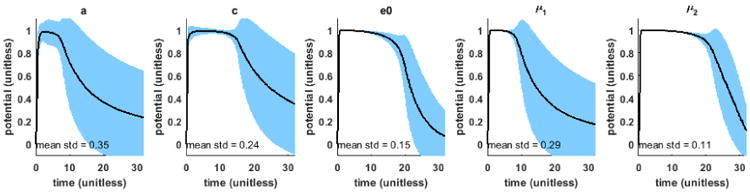
Result of one-factor-at-a-time sensitivity analysis of the AP model. Mean (solid black) and standard deviation (std) (shaded blue) throughout the action potential duration resulting from the variation in each model parameter.
B. ECG Measurement Model
Action potential inside the heart produces potential on the body surface that is measured as time-varying ECG signals. The relationship can be described by the quasi-static approximation of the electromagnetic theory [20]. Solving the governing equations on the discrete mesh of heart and torso, a linear biophysical relationship between the ECG and action potential can be obtained [19] as: Φ = Hu(θ), where Φ is the discrete time ECG signals from all the leads on the body surface, H is the transfer matrix unique to patient-specific heart and torso geometry, u(θ) is the transmembrane action potential as a function of θ, and θ is the spatially-varying local parameters a of the AP model (1) at the dimensionality determined by the discrete cardiac mesh.
III. Spatially-Adaptive Multi-Scale Optimization
Estimation of the three dimensionally distributed tissue excitability in a cardiac mesh with m nodes can be formulated as an optimization problem:
| (2) |
with bounds constraint: Ω = {θ ∈ ℝm|lb ≤ θ ≤ ub}. The objective function J could be any measure of similarity between the model output Φ and the measured ECG Y, such as a measure of the similarity in signal magnitude by squared error, or a measure of the similarity in signal morphology by correlation coefficient. Because the measurement ECG data tend to be noisy and there is often a scale difference between the measured and simulated data, we use an objective function consisting of correlation coefficient and squared error term.
| (3) |
where l is the number of body surface leads, t is the number of discrete time samples, and Φ̄i and ȳi are respectively the mean of simulated and measured ECG on the ith body surface lead. The correlation coefficient takes value in the range [−1, 1] and the value of the squared error mainly depends on the unit of measurement data. Parameter λ is empirically adjusted using the knowledge of the two.
The direct estimation of θ involves a high-dimensional optimization that is infeasible due to high ill-posedness and prohibitively large computation. To maximize the resolution of local parameter estimation using a limited dimensionality of unknowns, we present a spatially-adaptive multi-scale scheme that can be used in conjunction with any optimization method. This framework consists of three key components: 1) a multi-scale hierarchical representation of the spatial domain, 2) a coarse-to-fine optimization, and 3) a criterion for adaptive spatial resolution adjustment that favors higher resolution in heterogeneous regions. The flowchart in Fig. 2 shows how each of the key components work together in the presented framework. Given a discrete cardiac mesh, we first construct the multi-scale representation of the spatial domain. Parameter estimation is then carried out as an iterative procedure of coarse-to-fine optimization with an adaptive adjustment of spatial resolution, until further refinement does not produce major improvement in the global optimum. Individual components of the framework are detailed in the following sections.
Fig. 2.
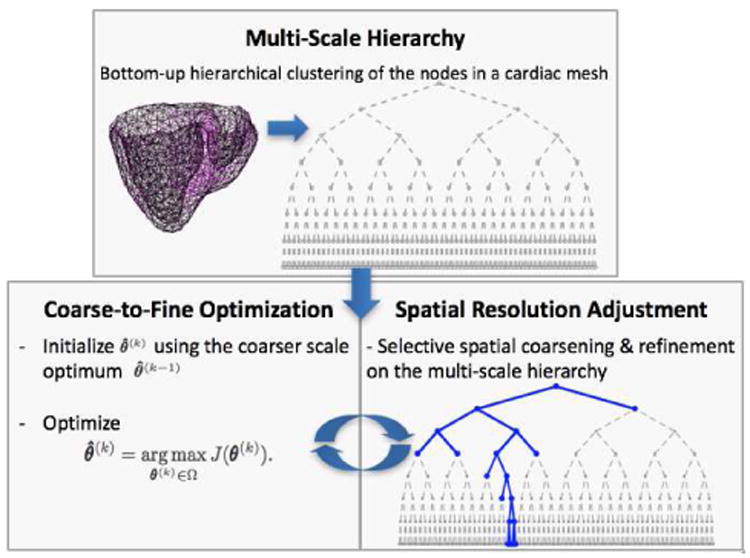
A work-flow diagram of the presented framework.
A. Multi-Scale Hierarchy
To facilitate a coarse-to-fine optimization, a multi-scale representation of the cardiac mesh is needed. By exploiting the spatial smoothness of tissue properties (i.e., neighboring tissues have similar material properties), we adopt a bottom-up agglomerative hierarchical clustering [21]. It begins with every node in the cardiac mesh as separate clusters. As one moves up the hierarchy, a pair of the closest clusters is merged until all the nodes belong to a single cluster. The distance between two clusters is measured by the average of the pairwise Euclidean distance between every node in the two clusters. Fig. 3 shows the clusters of this multi-scale hierarchy at several scales, illustrating (from left to right) how two clusters at a lower scale is merged into a cluster at a higher scale. The finest level in the multi-scale hierarchy corresponds to the beginning stage of the clustering. At this stage parameter estimation would correspond to a direct high-dimensional local parameter estimation at the resolution of the cardiac mesh. The coarsest level in the multi-scale hierarchy corresponds to the end stage of the clustering where all the nodes belong to the same cluster. At this stage, parameter estimation would correspond to a global parameter estimation.
Fig. 3.

Multi-Scale hierarchy with 20, 15, 10, 5, and 1 final clusters (left to right); color is repeated for unconnected clusters.
B. Coarse-to-Fine Optimization
In optimizing a highly detailed objective function, a coarse-to-fine optimization may: 1) facilitate faster convergence by exploiting coarser-scale information in finer-scale optimization, and 2) decrease the risk of being stuck in a bad local minimum by optimizing a cascade of increasingly complex objective functions over a gradually increasing resolution.
The optimization starts from the coarsest scale of the multi-scale hierarchy. It then progressively optimizes the parameters at a higher resolution that is determined by the adaptive spatial resolution adjustment criterion (section III-C). For clarity, in this paper, we represent the change in resolution during the coarse-to-fine optimizations using a tree, in which the leaf nodes represent the clusters in the present resolution. At the kth iteration, we consider the optimization of θ(k) corresponding to the parameter values on the leaf nodes:
| (4) |
In the presented framework, any optimization method that can handle the objective function (3) can be used. As an example, below we present the presented framework with GPO [22]. The use of the presented framework with BOBYQA [13] follows the same line and will be discussed in the experiment section.
A GP is first used to approximate the objective function (4). The GP assumes a smoothness property of the objective function which is mainly determined by its co-variance function. Because the most commonly used squared exponential kernel is known to enforce a large smoothness property, we take the “Mátern 5/2” kernel that enables less smooth function [23]:
where , and γ and α are kernel parameters. Because no prior knowledge about the objective function (4) is available, we use a zero mean function for simplicity.
A typical surrogate based optimization consists of two major ingredients: 1) using the current surrogate of the objective function, find out points in the solution space that can improve the approximation of the objective function well especially in the region of global maximum, and 2) evaluate the objective function at the point determined in the previous step and update the surrogate. Because the initial knowledge of the GP plays an important role in determining how fast a good GP can be obtained in the subsequent updates, here we introduce an additional step to initialize the GP using the coarser-scale optimum. Below we describe each of these major steps:
1) Initialize Using the Coarser-Scale Optimum
Depending on the optimization method used, different strategies can be used. If the optimization starts with a single point, such as the BOBYQA used here, the lower resolution optimum can be used as initialization. If the optimization can start with multiple points, such as the GPO used here, a set of higher resolution points derived from the lower resolution optimum can be used. For two sibling leaf nodes obtained by recent refinement, a set of two values whose average equals to the value on the parent node (lower resolution optimum) are generated. This is done by first uniformly sampling a set of values from the parameter bound [lb, ub] for one of the leaf nodes. Then, corresponding set of values for the second leaf node are generated by subtracting previous samples from twice the value on the parent node. For leaf nodes that did not undergo resolution change, their parameter values are equal to their current optimum. These points are used to obtain an initial GP surrogate.
2) Determine the Next Query Point
In the context of optimization, a good surrogate should both approximate the objective function well globally, and have higher accuracy in the region of global maximum. For the former, the query point is determined to explore the solution space where the predictive uncertainty σ(θ(k)) of the current GP is high. For the latter, the query point is determined to exploit the current GP at the solution space where the predictive mean μ(θ(k)) is high. Overall, this nth query point is obtained by maximizing the upper confidence bound (UCB) of the GP using BOBYQA.
| (5) |
where the parameter β = 2 log(π2n2/6η), η ∈ (0, 1) balances between exploitation and exploration. The predictive mean and uncertainty in (5) is evaluated by using the Sherman-Morrison-Woodbury formula [23]:
| (6) |
Where and K is the positive definite co-variance matrix . A small noise ζ is added for numerical stability during matrix inversion.
|
| |
| Algorithm 1 Spatially-Adaptive Multi-Scale Optimization | |
|
| |
| 1: | H ← multi-scale hierarchy of cardiac nodes |
| 2: | k = 1 |
| 3: | T(k) ← root node, |
| 4: | do |
| 5: | θ̂(k) = arg maxθ(k) ∈ ΩJ(θ(k)) ▷ optimize |
| 6: | T(k) ← update leaf nodes values using θ̂(k) |
| 7: | loop (leaf nodes in T(k)) ▷ calculate gain |
| 8: | If sibling nodes with parent : |
| 9: | |
| 10: | If nodes without sibling : |
| 11: | , where (k – k′) |
| 12: | is the iteration when was coarsened |
| 13: | |
| 14: | end loop |
| 15: | T(k+1) ← split node/s with maximum r(k) ▷ refine |
| 16: | T(k+1) ← merge node pairs if r(k) < ∊ ▷ coarsen |
| 17: | For sibling nodes ( ) split from : |
| 18: | ; ▷ initialize |
| 19: | k = k + 1 |
| 20: | while (J(θ(k–1)) – J(θ(k–2)) ≥ ∊) |
|
| |
3) Update the GP
Once a new query point is obtained, the objective function (4) is evaluated at this point. GP is updated at the new point-objective function value pair { , Jn}.
| (6) |
This provides an updated GP. These steps are run in iteration until the query points do not change significantly over several iterations. In this way, a GP surrogate of the objective function along with the optimum at a given resolution is obtained. In this study, we empirically set the values of the kernel parameters. The optimization of the kernel parameters is discussed in section VII-D.
C. Adaptive Spatial Resolution Adjustment
If coarse-to-fine optimization is done on the full multi-scale hierarchy, the number of unknowns will again quickly become too high in dimension to be effectively optimized. To overcome this, we aim for a non-uniform resolution with higher resolution in heterogeneous regions and lower resolution in homogeneous regions. To achieve this, instead of refinement of all the leaf nodes after optimization at each scale, we selectively refine the leaf nodes that are heterogeneous and coarsen those that are homogeneous.
To identify the clusters that are heterogeneous versus homogeneous in tissue properties, we propose a greedy criterion based on gain in the global optimum. Intuitively, if a cluster is homogeneous, its refinement is expected to yield children clusters with similar parameter values; as a result, there will be a minimal gain in the objective function in representing this region with higher resolution. The contrary is true for heterogeneous clusters. For each pair of sibling leaf nodes ( ) that share the common parent node , we evaluate the gain resulting from the refinement as the change in the objective function value on θ̂(k) (current optimum) versus replacing the values of the children nodes ( ) with the value of their parent node :
| (8) |
where is the parameter vector obtained by replacing and with in the current optimum θ̂(k). For leaf nodes that do not have a sibling due to previous coarsening, no resolution change has occurred but their value may have changed as a result of resolution-change elsewhere. For such nodes , the gain equals the change in the objective function due to the change in during the coarsening and after the optimization.
Based on , two actions are taken. For the leaf node or the pair of leaf nodes that has the maximum gain , we hypothesize that they represent highly heterogeneous regions and allow a higher resolution representation (i.e., refinement). For the pair of leaf nodes that bring negligible or negative gain ( ), we assume that the refinement suggested in the previous scale is not beneficial and thus retract the refinement (i.e., coarsening). The refinement and coarsening is done by using the multi-scale hierarchy (section III-A) as a reference.
D. Algorithm Summary
The overall procedure of the presented framework is summarized in Algorithm 1. First, a multi-scale hierarchy of the cardiac mesh is obtained. Using a random initial value, the optimization starts at the coarsest scale in the multi-scale hierarchy as a 1D global optimization. Then, it proceeds in a coarse-to-fine manner along the multi-scale hierarchy, iterating between the following two steps First, the step of adaptive spatial resolution adjustment determines the refinement and coarsening on the present resolution using the full multi-scale hierarchy as a baseline. Second, the optimization proceeds by optimizing the parameters values on the clusters of the updated resolution. These two steps iterate until the improvement in the global optimum is not significant (≤ ∊).
IV. Synthetic Experiments
In synthetic experiments, we evaluate the performance of the presented framework in combination with the GPO and the BOBYQA (termed as adaptive GPO and adaptive BOBYQA respectively for the remainder of this paper) in the presence of infarcts of varying sizes and locations. We also compare the presented framework with optimization using 26 pre-defined segments of ventricles, with 17 segments on the left ventricle (LV) based on the AHA standard and 9 segments on the right ventricle (RV) as shown in Fig. 4. Finally, we study the identifiability of local tissue excitability with respect to: 1) the size of the infarct, and 2) the amount of measurement data.
Fig. 4.
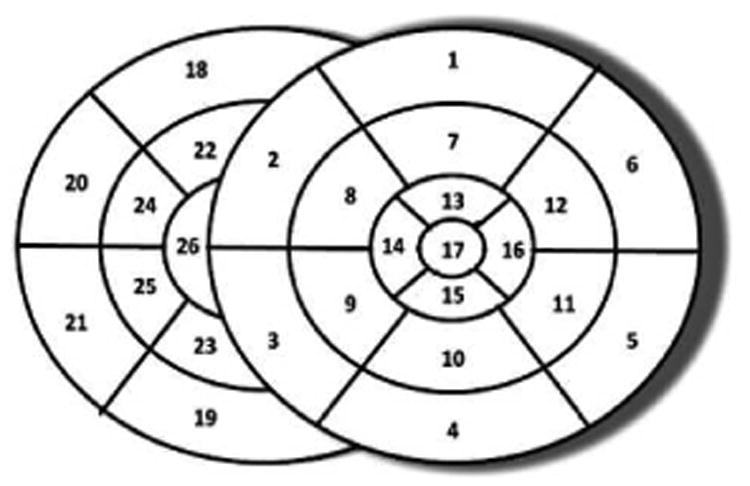
Schematics of 26 pre-defined ventricular segments for optimization with uniform resolution.
In total, we consider 35 synthetic cases with different settings of infarcts on three realistic CT-derived human heart-torso geometrical models. We set infarcts of sizes varying from 1% to 65% of the ventricles at different LV and RV locations by using various combinations of the pre-defined segments, or random locations when the size is smaller than one pre-defined segment. To represent healthy and infarcted tissues, the parameter a of the AP model (1) is uniformly sampled from [0.149, 0.151] and [0.399, 0.501] respectively. For each infarct case, the action potentials are first simulated using the AP model. 120-lead ECG is then generated using the forward model and corrupted with 20dB Gaussian noise. The admissible range of tissue excitability parameter for the optimization is set to [0, 0.52]. To evaluate the accuracy of the estimated local parameters, we use two metrics: 1) root mean squared error (RMSE) = ‖θ̂ – θ‖2 between the true and estimated parameter values, and 2) dice coefficient (DC) = , where S1 and S2 are the sets of nodes in the true and estimated regions of the infarct; these regions are determined for each infarct case by calculating a threshold value that minimizes the intra-region variance [24] on the estimated parameter values. Both metrics are evaluated at the resolution of the cardiac mesh.
A. Performance Based on the Size and Location of the Infarct
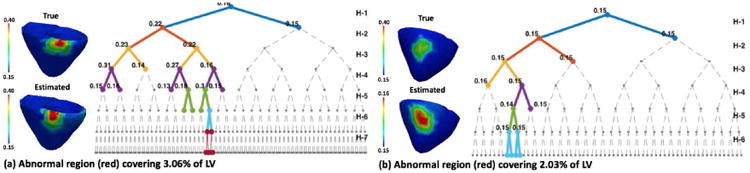
We first summarize the performance of the presented framework in the presence of infarcts of varying sizes using three representative examples. Fig. 5(a) shows an example of estimation on a small infarct (3.6%). The tree shows that once a homogeneous healthy region is found in stage 1, the optimization keeps the entire region at a very low resolution and refines only along the heterogeneous region that contains the infarct. It continues narrowing down the infarct with higher resolution, generating a narrow yet deep tree. The final result shown in stage 3 of Fig. 5(a) is achieved with only a dimension of 10 unknowns. In comparison, if a uniform resolution is used, a dimension of 128 would be needed to achieve an estimation at the same resolution. Fig. 5(b) shows another example with a medium sized infarct (28.7%). Since the infarct spans a larger number of clusters, it is not until stage 2 before the tree can be split along one major branch. In addition, because both normal and infarcted tissues are large enough to be represented by low-resolution homogeneous clusters, an overall lower resolution solution is obtained with a wider yet shallower tree. While the presented method converges at a dimension of 7, a uniform resolution would require a dimension of 16 for an estimation at similar resolution. Finally, Fig. 5(c) shows an example with a larger sized infarct (62.4%). A larger sized infarct can be represented by big clusters at low resolution and has a boundary that needs to be represented by a larger number of smaller clusters. Therefore, until stage 2 the large homogeneous regions (both normal and infarcted) are split into major clusters. In the following stages, the border region is split into multiple branches increasing the resolution along the border yielding a wider tree in the first a few steps and narrow branches in later stages. In this case, while the presented method converges at a dimension of 13, a uniform resolution estimation would require a dimension of 64.
Fig. 5.
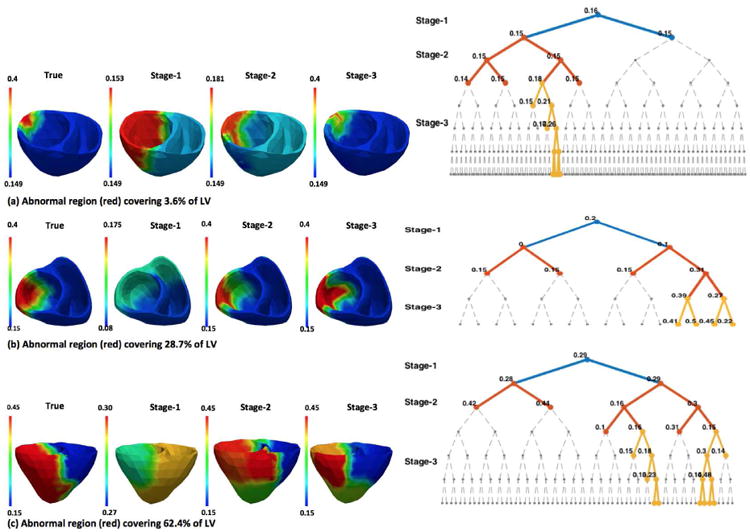
Synthetic experiments. Examples of the progression of the presented spatially-adaptive multi-scale optimization. Left: true parameter settings vs. estimation results improved over 3 successive stages of the optimization (red: infarcted tissue, blue: healthy tissue). Right: the corresponding structure of the tree at each stage. The value on each node of the tree represents the optimized parameter value for that node.
Additional examples of the estimated tissue excitability for different infarcts are provided in Fig. 6. Fig. 7 summarizes the accuracy in estimation of the presented adaptive BOBYQA (magenta bar) and adaptive GPO (blue bar) with respect to the size and location of the infarct. In specific, as shown in Fig. 7, while both the presented methods are in general able to identify infarcted tissues at various locations and of various sizes, the accuracy in the presence of septal infarcts show a noticeable decrease. As shown in an example of septal infarct in Fig. 6(c), this drop in accuracy is associated with the presence of false positives at the lateral ventricular walls. This implies the existence of multiple parameter configurations that fit the measurement data well. The challenge in dealing with septal infarcts is consistent with that reported in literature [19]. Interestingly, in the presence of septal infarct, adaptive GPO shows higher accuracy than the adaptive BOBYQA (Fig. 7). This could be because adaptive GPO was able to avoid local minima owing to the initialization with multiple points. The adaptive BOBYQA, however, in general has higher efficiency, especially in the estimation of higher dimension of unknowns. Because both presented methods show similar performance, in the remaining sections of this paper, we consider performance analysis of the presented framework using adaptive GPO only unless explicitly stated otherwise.
Fig. 6.
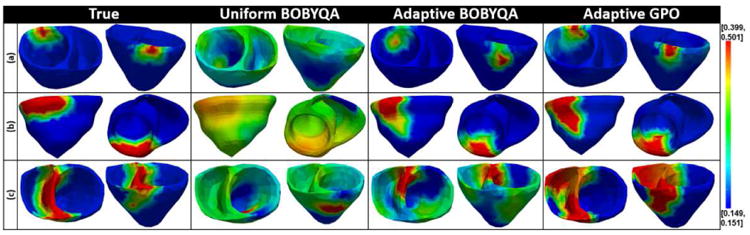
Synthetic experiments. Examples of tissue excitability estimated using: 1) uniform BOBYQA, 2) adaptive BOBYQA, and 3) adaptive GPO in the presence of infarcts of varying sizes and locations (red: infarcted tissue, blue: healthy tissue). Infarct locations and sizes (in percentage ventricles covered) from top to bottom: anterior (3.17%), inferior (9.84%), and septal (24.31%).
Fig. 7.
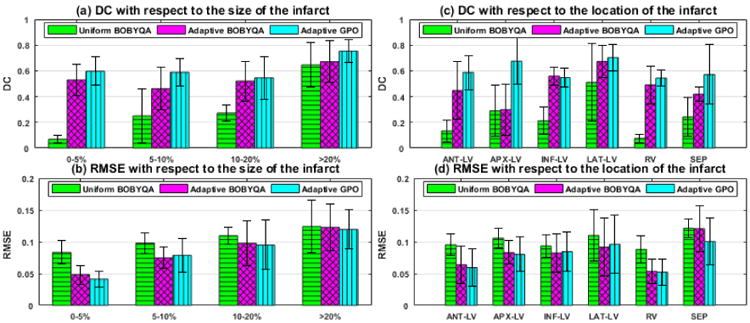
Synthetic experiments. Comparison of uniform BOBYQA, adaptive BOBYQA, and adaptive GPO in terms of DC and RMSE based on 35 different infarct cases of varying sizes and locations (bar: mean, line: standard deviation).
B. Comparison with Optimization using Uniform Resolution
We compare the performance of the presented adaptive methods with the state-of-the-art BOBYQA using 26 predefined segments (termed as uniform BOBYQA for the remainder of this paper). We do not include comparison with GPO using 26 pre-defined segments because it performs poorly for a dimension higher than 20 both as reported in literature [22] and as observed in our experiments. Experimental setup as described in section IV is used. Because uniform BOBYQA is sensitive to initialization, each experiment case is run twice using random initialization and the better result is picked for comparison. The summary statistics of accuracy as shown in Fig. 7 demonstrates that the presented adaptive methods are more robust to infarcts of various sizes and locations. This improvement is statistically significant in both DC and RMSE (paired-t tests on 35 synthetic experiments, p < 0.0025). In particular, using uniform BOBYQA, it is difficult to estimate an infarct of size equal to or less than a single segment. In comparison, the presented methods are able to identify infarcts smaller than a single segment with a small number of unknowns (10-14). Furthermore, as shown in Fig. 6, uniform BOBYQA tends to show false-positives across multiple segments, failing to accurately reveal the spatial distribution of the infarcted tissues. The major computational cost in local parameter estimation comes from the repeated evaluation of the CPU-intensive simulation model. We compare the computational cost of the presented adaptive methods and uniform BOBYQA in terms of the computation time and the number of model evaluations used. This is based on 35 synthetic experiments conducted on a computer with Xeon E5 2.20GHZ processor and 128 GB RAM. In summary, uniform BOBYQA takes on average 3.33±0.83hrs for convergence, while the presented methods take on average 6.07±3.02hrs for convergence. Because, in the presented methods, the tree varies with varying infarct sizes leading to a significant difference in the number of model evaluations, we summarize the comparison of the number of model evaluations by grouping the experiments into two types by infarct size. For smaller and larger infarcts, the trees are deeper involving multiple coarse-to-fine optimizations and an average of 10-12 final dimensions of unknowns (Fig. 8). Such cases in general require a larger number of model evaluations. Our experiments show that the presented methods take at most twice as many model evaluations. However, it should be noted that uniform BOBYQA for such cases as shown in Fig. 6 and 7 suffer from limited accuracy in estimation. For average sized infarcts, the trees are shallower and end up with an average of 7-8 unknown dimensions (Fig. 8), resulting in a fewer number of coarse-to-fine optimizations of a smaller number of unknowns. Compared to uniform BOBYQA, the presented methods require a similar number of model evaluations. In the presented methods, the adaptive spatial resolution adjustment step also necessitates model evaluations. Supposing that at a stage there are 2n leaf nodes, a minimum of n model evaluations (when all nodes have sibling) and a maximum of 2n model evaluations (when no nodes have sibling) are needed. At the current stage where the number of leaf nodes are typically < 20, the number of model evaluations needed for spatial resolution adjustment is insignificant in comparison to that needed for optimization (at a range thousands).
Fig. 8.
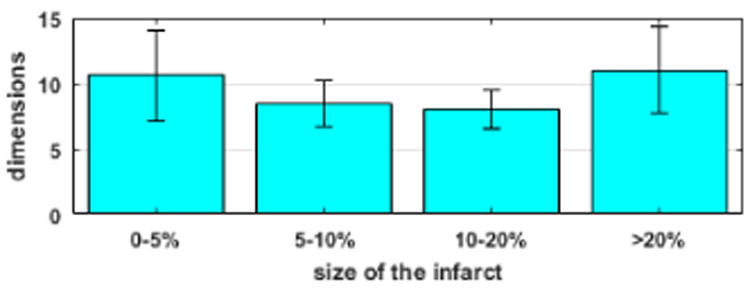
Synthetic experiments. Comparison of the final dimensions of unknowns obtained by using presented methods based on 35 infarct cases of various sizes (bar: mean, line: standard deviation).
C. Identifiability Based on the Size of the Infarct
To investigate the limit of the presented method in terms of the smallest size of the infarct that can be identified, we conduct a set of experiments by gradually decreasing the size of an infarct until a size that cannot be identified is found. For such a size of infarct, six different experiments are repeated. In summary, an infarct of size ≥ 3% can be estimated with good accuracy, ∼ 2% can be identified with lower accuracy, and ∼ 1% cannot be identified. Fig. 9 shows two examples of estimation for infarcts of different sizes. For an infarct of size 3.6%, the tree progressively branches by allocating higher resolution along the infarct and lower resolution along the homogeneous normal regions. However, for an infarct of size 2.0%, the tree branches along the infarct only for first a few steps (until H-3) and later branches along the homogeneous normal tissue. This shows that no significant gain in objective function was obtained by dividing the heterogeneous regions containing the infarct. Rather, the gain in objective function by refining the homogeneous regions (fine tuning of parameter values) is comparable to that by refining the heterogeneous region. Hence, in this case the infarct was not observable given the current data and the objective function used.
Fig. 9.
Synthetic experiments. Left: tree narrows down along the infarct region showing that the infarct is identified. Right: tree takes first a few steps along the infarct region, but later splits along homogeneous healthy region showing that the infarct is not identified.
D. Identifiability Based on the Amount of Measurement Data
We investigate the change in the performance of the presented method when the amount of measurement data is decreased from 120-lead ECG to 12-lead ECG on 35 synthetic experiments. Experimental setup as described in section IV is used. In addition, 12-lead ECG is extracted from the simulated and noisy 120-lead ECG. As summarized in Fig. 10, an overall decrease in the accuracy across both metrics is observed. This is mainly due to larger false positive regions and sometimes non-unique solutions. The accuracy in estimation when infarcts are located at inferior LV and RV regions shows major decline. Fig 11 shows an example of estimation when an infarct is present in the inferior LV. Using 120-lead ECG, the presented method is able to progressively narrow down to the infarct region. Using 12-lead ECG, all the nodes in the tree take the value of 0.15 showing that the infarct is not identified. The drop in accuracy, especially in the RV and inferior LV, could be explained by the limited presence of leads in the inferior and RV side in the 12-lead ECG set.
Fig. 10.
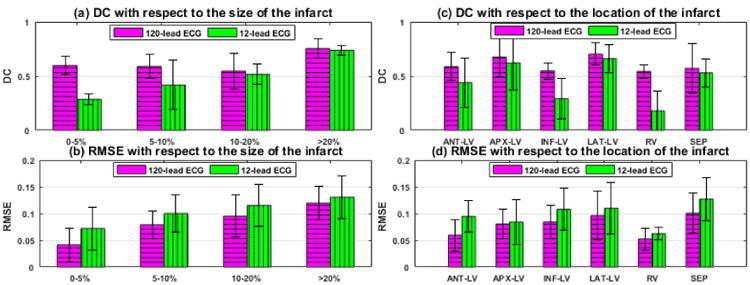
Synthetic experiments. Performance of the presented method using 12-lead ECG in comparison to that using 120-lead ECG in terms of DC and RMSE. Comparison is based on 35 different infarct cases of varying sizes and locations (bar: mean, line: standard deviation).
Fig. 11.
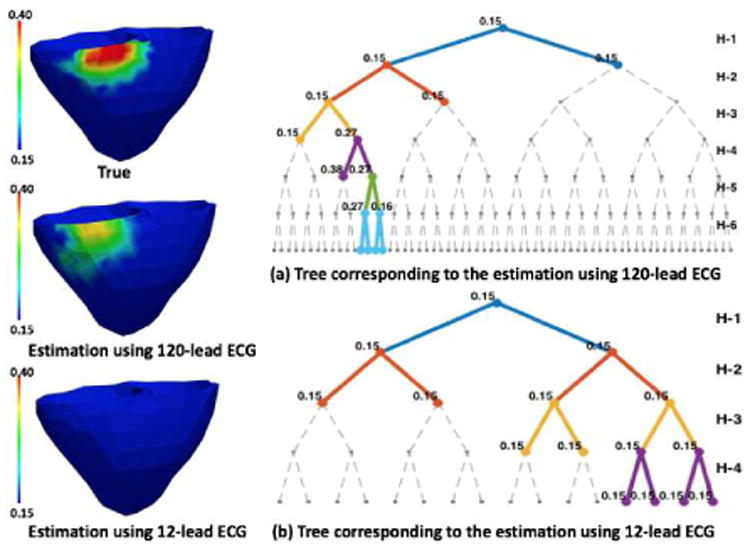
Synthetic experiments. Estimation using 120-lead ECG shows good accuracy with splits along the infarct region, whereas using 12-lead ECG is unable to identify the infarct.
V. Experiments Using a Blind EP Model and In-vivo MRI Scar Data
We next test the performance of the presented method in estimating tissue property of 3D myocardial infarct delineated from high resolution in-vivo magnetic resonance (MR) images. Compared to the settings in synthetic experiments, these MRI-derived 3D infarcts have the following characteristics that can be expected to increase the difficulty of local parameter estimation: 1) heterogeneous tissues due to the presence of both dense scar core and gray zone, 2) the presence of a single or multiple scars with complex spatial distribution and irregular boundary, and 3) the presence of both transmural and non-transmural scars. Due to the lack of in-vivo electrical mapping data, here measurement data for parameter estimation are generated by a high resolution (average resolution of 350 μm), multi-scale (sub-cellular to organ scale) in-silico ionic EP model on the MRI-derived patient-specific ventricular models as detailed in [2]. Data are extracted from 300-400 epicardial sites, temporarily down-sampled to a 5ms resolution, and corrupted with 20dB Gaussian noise. Note that although no in-vivo electrical data were available for parameter estimation, the experiments are designed to mimic a real-data scenario because: 1) the 3D EP model used to generate the measurement data is known to be capable of generating high-fidelity EP simulation of patient-specific heart [2], 2) this model is unknown to the framework of parameter estimation and thus no “inverse crime” is involved, and 3) only a subset of epicardial surface data corrupted with noise is used as measurement data. Fig. 12 shows the local tissue excitability estimated using the presented method on 7 cases. Based on the fundamental assumption of the presented method (higher resolution in heterogeneous regions), we expect that its performance will be closely tied to the underlying heterogeneity of the tissue property. Therefore, we analyze the performance of the presented method with respect to the following two factors that affect the heterogeneity of the scar:
Fig. 12.
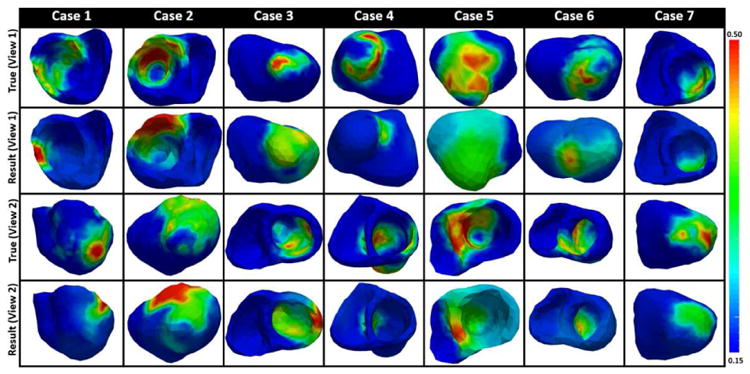
Results of local parameter estimation using the presented method, where measurement data is generated from epicardial potentials simulated by a multi-scale ionic EP model blinded to the presented estimation method. Infarct from 3D-MRI is used as the ground-truth.
1) Scar Transmurality
Because scar non-transmurality increases tissue heterogeneity across the myocardial wall, it is expected that the estimation accuracy in the presence of dense transmural scars would be higher than that in the presence of non-transmural scars. In specific, cases 4-7 have some dense transmural scars surrounded by gray zone. In these cases, the location of the dense transmural scar is accurately identified with the estimated parameter value close to the documented parameter value for infarct core (i.e., 0.5) [16]. In comparison, the non-transmural scars in case 1 anterior-septal region and case 4 apical region are missed. The tissue property for the non-transmural scar in case 3 apical region and case 5 inferior region, although identified, are not accurately estimated. Overall, in the presence of non-transmural scars, the estimation either misses the scar, or produces regions of abnormal tissues larger than the scar with parameter value in between the values for healthy and infarct core.
2) Dense vs. Gray Zone
The presence of gray zone is also expected to increase the difficulty in parameter estimation. For example, tissue property in dense scar in cases 4, 6 apical region and case 2 anterior region are correctly estimated, whereas the gray zone in case 1 septal region is missed. Additionally, as shown in Fig. 12 case 5 view 1, the presence of gray zone within the dense scar decreases the estimation accuracy. In these cases, the location of scar is identified, but the value of the parameter does not accurately reflect the heterogeneous presence of the dense scar and the gray zone.
VI. Experiments Using In-vivo 120-lead ECG and Catheter Mapping Data
A real-data study is conducted on two patients who underwent catheter ablation of ventricular tachycardia due to prior tissue infarction as described in [25]. The patient-specific heart-torso geometry is constructed from 3D CT images. The tissue excitability is estimated from 120-lead ECG using adaptive GPO, adaptive BOBYQA, and uniform BOBYQA. Because uniform BOBYQA is sensitive to initialization, we use the result of the global parameter estimation to initialize this optimization. For validation of the result, we consider: 1) the relation between the estimated tissue excitability and in-vivo epicardial bipolar voltage data obtained from catheter mapping, and 2) the similarity between the real ECG data and those simulated with the estimated tissue excitability. Note that voltage data can be used only as a reference and not the gold standard for the estimated tissue excitability.
Fig. 13 shows a comparison between the estimated tissue excitability and the bipolar voltage data, in which the first column shows the original catheter maps (red: dense scar, pink: healthy tissue), the second column shows the catheter mapping registered to the CT-derived cardiac mesh (red: dense scar ≤0.5mV, green: scar border = 0.5 – 1.5mV, blue: normal > 1.5mV). The catheter maps from patient case 1 reveal a dense scar on the basal lateral region of the LV. As shown in Fig. 13, tissue excitability estimated using the presented adaptive methods reveal abnormal tissues in the same region. In this case, tissue excitability estimated using the uniform BOBYQA does not align with the catheter maps. Similarly, the catheter maps from patient case 2 reveal a dense infarct distributed across the lateral and inferior LV regions. As shown in Fig. 13, the tissue excitability estimated from the presented methods and uniform BOBYQA successfully reveal the dense abnormal tissues in this region. However, the estimation results from uniform BOBYQA also shows some dense abnormal tissues in the apical region.
Fig. 13.
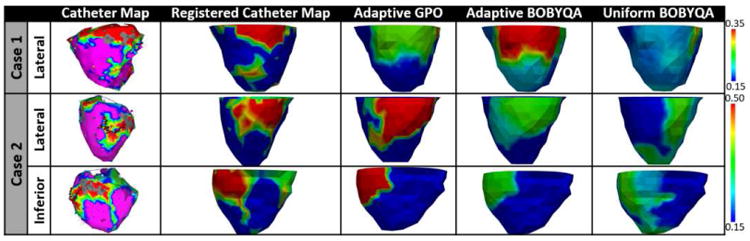
Real-data experiments. Estimated tissue excitability using the presented adaptive methods and uniform BOBYQA. In-vivo voltage maps are used as reference data.
Fig. 14 shows a comparison of the real ECG data and those simulated with the estimated tissue excitability on a few example leads. In patient case 1, the simulated ECG fits the real ECG data on majority of the leads, although the fit is poor on a few leads (see an example of a good and a poor fit in Fig. 14(a)). The average RMSE between the simulated and real ECG across all the leads is 0.2133mV. As shown in Fig. 14(b), in patient case 2, the simulated ECG fits the real ECG data with lower accuracy: RMSE 0.4388mV. The limited data-fitting accuracy suggests the existence of modeling errors in addition to that in the tissue excitability.
Fig. 14.
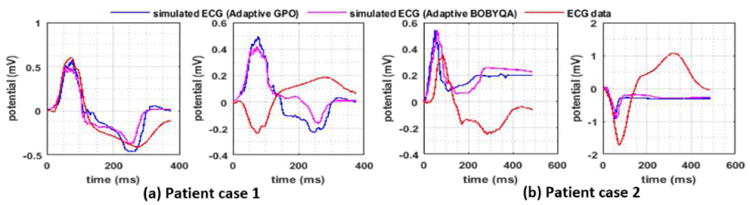
Real-data experiments. Comparison of the real ECG data and the simulated ECG with estimated tissue excitability.
VII. Discussion
A. Relation to the Existing Works
This paper extends our previous work [26] as follows: 1) development of the presented framework with BOBYQA, 2) detailed quantitative evaluation of the presented framework and comparison with standard BOBYQA optimization carried out on a pre-defined 26-segment model of the heart, 3) a study of the identifiability of local tissue excitability when 12-lead ECG is used as measurement data, and 4) a study of the performance of the presented framework in the presence of highly heterogeneous tissue properties on a new set of experiments that uses scar obtained from high resolution MR images and measurement data generated from an EP model blinded to parameter estimation framework.
The presented framework shares an important intuition with [5], [27] where a coarse-to-fine optimization is used to estimate local conductivity parameters using endocardial electrical potential measurements. In brief, the approach in [27], [5] first obtains a global estimate of the parameter using the bisection method. Local adjustments are then made to the parameter by iteratively subdividing the spatial region that has a mismatch between regional measurement data and simulation outcome. Despite the common intuition of a coarse-to-fine optimization, the presented method and the work in [5] differ in several ways. First, the criteria for adaptive spatial resolution (refinement or coarsening) in the presented framework is based on the gain in the global cost function that encourages the division of regions with heterogeneity; in [5], the adaptive criteria favors the division of regions that have the highest regional data fitting error. Second, by design, the method in [5] relies on the availability of regional measurement data on the heart; in contrast, our method by design is applicable to a wide variety of measurement data. Finally, in [5] during the local adjustment, the parameter for each subdivisions is sequentially optimized using the 1D-Brent optimizer while the parameter values of the remaining subdivisions are fixed. As a result, as noted in [5], it is important for the order of this sequential optimization to follow the order of depolarization time measured on the vertices of the cardiac mesh. The presented framework is not subject to this constraint as all parameter values in a resolution are optimized together.
The estimation of the size and location of the infarct is also presented in [28]. In brief, an Artificial Neural Network is first used to predict the segment that contains the infarct out of the 53 pre-defined segments. Local adjustments to the initial size and location of the infarct is then done in two steps. First, the optimal location of the infarct is searched by considering the neighboring segments of the current best segment. Second, the optimal size is searched by slowly growing and shrinking the units around the optimal segment. The presented method is fundamentally different from the work in [28] in several ways. First, the presented framework is based on a coarse-to-fine optimization on a multi-scale hierarchy of the parameter space, whereas the work in [28] does not take a coarse-to-fine approach. At most, the method in [28] can be regarded as a two-scale approach with the first scale being the initialization step and the second scale being the optimization step. Second, as noted by the authors, in [28] the parameter search space is reduced by using the knowledge of the initial location of the infarct; in contrast our method reduces the parameter search space by allocating lower resolution to regions with homogeneous tissues and higher resolution to regions with heterogeneous tissues. Finally, the presented method obtains local parameters on an estimated non-uniform resolution of the spatial parameter field; in contrast the work in [28] obtains local parameters on an estimated two regions of the spatial parameter field: the infarct region and the non-infarct region.
B. Threshold for Adaptive Coarsening
In the presented framework, if the refinement of a parent node into two leaf nodes does not yield a significant gain in the objective function, such refinements are retracted. To do this, a threshold value in the gain of the objective function must be pre-determined. We study the influence of this threshold value using synthetic experiments on 5 different infarct cases. On each case parameter estimation is done with the following values of the threshold: 0.1%, 0.5%, 1%, 5%, 10% and 20% of the maximum gain in global optimum at the present resolution. The following observations are made: When a small value of the threshold is used (0.1%), the refinements that contribute small gain to the global optimum are retained, resulting in a large number of unknowns in the higher levels of the multi-scale hierarchy and a decreased ability to go deeper into the multi-scale hierarchy. As a result, wider but shallower trees are obtained. Alternatively, when a large value of the threshold is used (20%), only those refinements that contribute a large gain in the global optimum are retained, resulting in an increased ability to go deeper in the multi-scale hierarchy but at the cost of accuracy. As a result, the final tree is narrower and deeper. In overall, as shown in Fig. 15 left, a threshold value of 5% resulted in good accuracy consistently.
Fig. 15.
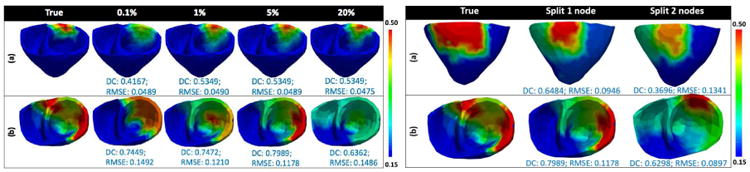
Performance analysis of the presented framework: when threshold for spatial coarsening changes from 0.1% to 20% of the maximum gain in global optimum (left), and when two nodes vs. one node is split for spatial refinement (right).
C. Effect of Refining Multiple Nodes Versus a Single Node
Because an optimization method can accurately estimate only a limited dimensions of unknowns in local parameter estimation, we choose to create spatial partitions in the cardiac mesh sparingly. Thus, we refine a single node at each scale. Alternatively, the refinement of more than one node could result in a different final resolution of the cardiac mesh, and consequently different parameter values. On 8 synthetic experiments, we test the performance of the presented method when one node is refined vs. when two nodes are refined. As shown in Fig. 15 right, because the refinement of two nodes results in a need to optimize a larger number of unknowns at each scale, there is a decrease in the accuracy. The ability of the presented framework to go deeper into the multi-scale hierarchy is also impacted.
D. Parameters of the GPO
The GPO is dependent on three kernel parameters: 1) the length scale ‘γ’, 2) the covariance amplitude ‘α’, and 3) the observation noise ‘ζ’ as described in section III-B. The optimization of these kernel parameters along with each update of the GP could result in higher accuracy. The most commonly used approach is to maximize the marginal likelihood under the current GP, p(J|θ1:n, α, γ, ζ) = 𝒩(J|μ1, Kα,γ + ζI). As shown in Fig. 16 left, adaptive GPO with kernel parameter optimization does achieve higher accuracy compared to that without. Therefore, we will include kernel parameter optimization in the future development of the presented method.
Fig. 16.
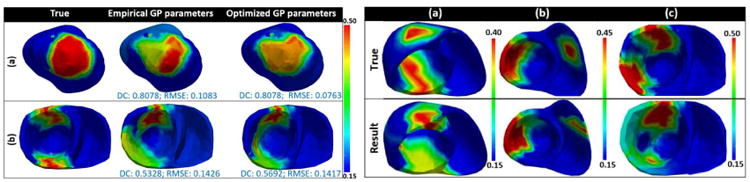
Left: comparison of the performance of the presented method when empirical kernel parameters are used vs. when optimized kernel parameters are used. Right: examples of estimation results using the presented method in the presence of two infarcted tissue regions.
E. Performance in the Presence of Two Infarcts
On 6 synthetic experiments, we test the performance of the presented framework in the presence of two infarcts. As shown in Fig. 16 right, both the infarcts are revealed. However, when two infarcts are spatially close some false positives might be obtained at the narrow healthy tissue region separating the two infarcts (Fig. 16 right case (c)). A large number of studies will be carried out in future to investigate the performance of the presented framework in the presence of multiple infarcts.
VIII. Conclusion
This paper presents a novel framework that is able to estimate spatially-varying parameters using a small number of unknowns, achieved through a coarse-to-fine optimization and a spatially-adaptive resolution that is higher at heterogeneous regions. This is demonstrated on the estimation of local tissue excitability in a cardiac EP model on both synthetic and real-data experiments. Our future step is to integrate the presented framework with a probabilistic estimation to quantify the uncertainties in local parameters. Another future step is to improve the ability of the presented framework to go deeper and wider into the multi-scale hierarchy. While experiments in this study consider the estimation of the tissue excitability represented by a single parameter a in the AP model, future work will also study the estimation of multiple parameters at once.
Contributor Information
Jwala Dhamala, B. Thomas Golisano College of Computing and Information Sciences, Rochester Institute of Technology, Rochester, NY, USA.
Hermenegild J. Arevalo, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, USA
John Sapp, Department of Medicine, Dalhousie University, Halifax, NS, Canada.
Milan Horacek, Physiology and Biophysics Department, Dalhousie University, Halifax, NS, Canada.
Katherine C. Wu, Department of Medicine, Division of Cardiology, Johns Hopkins Medical Institutions, Baltimore, MD, USA
Natalia A. Trayanova, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, USA
Linwei Wang, B. Thomas Golisano College of Computing and Information Sciences, Rochester Institute of Technology, Rochester, NY, USA.
References
- 1.Sermesant M, Chabiniok R, Chinchapatnam P, Mansi T, Billet F, Moireau P, Peyrat JM, Wong K, Relan J, Rhode K, et al. Patient-specific electromechanical models of the heart for the prediction of pacing acute effects in crt: a preliminary clinical validation. Medical image analysis. 2012;16(no. 1):201–215. doi: 10.1016/j.media.2011.07.003. [DOI] [PubMed] [Google Scholar]
- 2.Arevalo HJ, Vadakkumpadan F, Guallar E, Jebb A, Malamas P, Wu KC, Trayanova NA. Arrhythmia risk stratification of patients after myocardial infarction using personalized heart models. Nature communications. 2016;7 doi: 10.1038/ncomms11437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zahid S, Whyte KN, Schwarz EL, Blake RC, Boyle PM, Chrispin J, Prakosa A, Ipek EG, Pashakhanloo F, Halperin HR, et al. Feasibility of using patient-specific models and the minimum cut algorithm to predict optimal ablation targets for left atrial flutter. Heart Rhythm. 2016 doi: 10.1016/j.hrthm.2016.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wong KC, Sermesant M, Rhode K, Ginks M, Rinaldi CA, Razavi R, Delingette H, Ayache N. Velocity-based cardiac contractility personalization from images using derivative-free optimization. Journal of the mechanical behavior of biomedical materials. 2015;43:35–52. doi: 10.1016/j.jmbbm.2014.12.002. [DOI] [PubMed] [Google Scholar]
- 5.Chinchapatnam P, Rhode KS, Ginks M, Rinaldi CA, Lambiase P, Razavi R, Arridge S, Sermesant M. Model-based imaging of cardiac apparent conductivity and local conduction velocity for diagnosis and planning of therapy. Medical Imaging, IEEE Transactions on. 2008;27(no. 11):1631–1642. doi: 10.1109/TMI.2008.2004644. [DOI] [PubMed] [Google Scholar]
- 6.Konukoglu E, Relan J, Cilingir U, Menze BH, Chinchapatnam P, Jadidi A, Cochet H, Hocini M, Delingette H, Jaïs P, et al. Efficient probabilistic model personalization integrating uncertainty on data and parameters: Application to eikonal-diffusion models in cardiac electrophysiology. Progress in biophysics and molecular biology. 2011;107(no. 1):134–146. doi: 10.1016/j.pbiomolbio.2011.07.002. [DOI] [PubMed] [Google Scholar]
- 7.Lê M, Delingette H, Kalpathy-Cramer J, Gerstner ER, Batchelor T, Unkelbach J, Ayache N. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2015. Bayesian personalization of brain tumor growth model; pp. 424–432. [Google Scholar]
- 8.Moireau P, Chapelle D. Reduced-order unscented kalman filtering with application to parameter identification in large-dimensional systems. ESAIM: Control, Optimisation and Calculus of Variations. 2011;17(no. 2):380–405. [Google Scholar]
- 9.Marchesseau S, Delingette H, Sermesant M, Rhode K, Duckett SG, Rinaldi CA, Razavi R, Ayache N. Cardiac mechanical parameter calibration based on the unscented transform. International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer. 2012. pp. 41–48. [DOI] [PubMed] [Google Scholar]
- 10.Moreau-Villéger V, Delingette H, Sermesant M, Faris O, Mcveigh E, Ayache N. Global and local parameter estimation of a model of the electrical activity of the heart. 2004 [Google Scholar]
- 11.Zettinig O, Mansi T, Georgescu B, Kayvanpour E, Sedaghat-Hamedani F, Amr A, Haas J, Steen H, Meder B, Katus H, et al. Fast data-driven calibration of a cardiac electrophysiology model from images and ecg. International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer. 2013. pp. 1–8. [DOI] [PubMed] [Google Scholar]
- 12.Brochu E, Cora VM, De Freitas N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. arXiv preprint arXiv:1012 2599. 2010 [Google Scholar]
- 13.Powell MJ. Cambridge NA Report NA2009/06. University of Cambridge; Cambridge: 2009. The bobyqa algorithm for bound constrained optimization without derivatives. [Google Scholar]
- 14.Dössel O, Krueger MW, Weber FM, Schilling C, Schulze WH, Seemann G. Engineering in Medicine and Biology Society, EMBC. IEEE; 2011. A framework for personalization of computational models of the human atria; pp. 4324–4328. [DOI] [PubMed] [Google Scholar]
- 15.Clayton R, Bernus O, Cherry E, Dierckx H, Fenton F, Mirabella L, Panfilov A, Sachse F, Seemann G, Zhang H. Models of cardiac tissue electrophysiology: progress, challenges and open questions. Progress in biophysics and molecular biology. 2011;104(no. 1):22–48. doi: 10.1016/j.pbiomolbio.2010.05.008. [DOI] [PubMed] [Google Scholar]
- 16.Clayton R, Panfilov A. A guide to modelling cardiac electrical activity in anatomically detailed ventricles. Progress in biophysics and molecular biology. 2008;96(no. 1):19–43. doi: 10.1016/j.pbiomolbio.2007.07.004. [DOI] [PubMed] [Google Scholar]
- 17.Aliev RR, Panfilov AV. A simple two-variable model of cardiac excitation. Chaos, Solitons & Fractals. 1996 Mar;7(no. 3):293–301. [Google Scholar]
- 18.Fischer G, Tilg B, Modre R, Huiskamp G, Fetzer J, Rucker W, Wach P. A bidomain model based bem-fem coupling formulation for anisotropic cardiac tissue. Annals of biomedical engineering. 2000;28(no. 10):1229–1243. doi: 10.1114/1.1318927. [DOI] [PubMed] [Google Scholar]
- 19.Wang L, Zhang H, Wong KC, Liu H, Shi P. Physiological-model-constrained noninvasive reconstruction of volumetric myocardial transmembrane potentials. Biomedical Engineering, IEEE Transactions on. 2010;57(no. 2):296–315. doi: 10.1109/TBME.2009.2024531. [DOI] [PubMed] [Google Scholar]
- 20.Plonsey R. Bioelectric phenomena. Wiley Online Library; 1969. [Google Scholar]
- 21.Hastie T, Tibshirani R, Friedman J. Unsupervised learning. Springer; 2009. [Google Scholar]
- 22.Shahriari B, Swersky K, Wang Z, Adams RP, de Freitas N. Taking the human out of the loop: A review of bayesian optimization. Proceedings of the IEEE. 2016;104(no. 1):148–175. [Google Scholar]
- 23.Rasmussen CE. Gaussian processes for machine learning. 2006 [Google Scholar]
- 24.Otsu N. A threshold selection method from gray-level histograms. Automatica. 1975;11(no. 285-296):23–27. [Google Scholar]
- 25.Sapp J, Dawoud F, Clements J, Horáček M. Inverse solution mapping of epicardial potentials: Quantitative comparison to epicardial contact mapping. Circulation: Arrhythmia and Electrophysiology. 2012:CIRCEP–111. doi: 10.1161/CIRCEP.111.970160. [DOI] [PubMed] [Google Scholar]
- 26.Dhamala J, Sapp JL, Horacek M, Wang L. Spatially-adaptive multi-scale optimization for local parameter estimation: Application in cardiac electrophysiological models. International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer. 2016. pp. 282–290. [Google Scholar]
- 27.Relan J, Pop M, Delingette H, Wright GA, Ayache N, Sermesant M. Personalization of a cardiac electrophysiology model using optical mapping and mri for prediction of changes with pacing. IEEE Transactions on Biomedical Engineering. 2011;58(no. 12):3339–3349. doi: 10.1109/TBME.2011.2107513. [DOI] [PubMed] [Google Scholar]
- 28.Li G, He B. Non-invasive estimation of myocardial infarction by means of a heart-model-based imaging approach: a simulation study. Medical and Biological Engineering and Computing. 2004;42(no. 1):128–136. doi: 10.1007/BF02351022. [DOI] [PubMed] [Google Scholar]


