StreamQRE: Modular Specification and Efficient Evaluation of Quantitative Queries over Streaming Data

Abstract

Real-time decision making in emerging IoT applications typically relies on computing quantitative summaries of large data streams in an efficient and incremental manner. To simplify the task of programming the desired logic, we propose StreamQRE, which provides natural and high-level constructs for processing streaming data. Our language has a novel integration of linguistic constructs from two distinct programming paradigms: streaming extensions of relational query languages and quantitative extensions of regular expressions. The former allows the programmer to employ relational constructs to partition the input data by keys and to integrate data streams from different sources, while the latter can be used to exploit the logical hierarchy in the input stream for modular specifications.

We first present the core language with a small set of combinators, formal semantics, and a decidable type system. We then show how to express a number of common patterns with illustrative examples. Our compilation algorithm translates the high-level query into a streaming algorithm with precise complexity bounds on per-item processing time and total memory footprint. We also show how to integrate approximation algorithms into our framework. We report on an implementation in Java, and evaluate it with respect to existing high-performance engines for processing streaming data. Our experimental evaluation shows that (1) StreamQRE allows more natural and succinct specification of queries compared to existing frameworks, (2) the throughput of our implementation is higher than comparable systems (for example, two-to-four times greater than RxJava), and (3) the approximation algorithms supported by our implementation can lead to substantial memory savings.

1. Introduction

The last few years have witnessed an explosion of IoT systems in applications such as smart buildings, wearable devices, and healthcare [9]. A key component of an effective IoT system is the ability to make decisions in real-time in response to data it receives. For instance, a gateway router in a smart home should detect and respond in a timely manner to security threats based on monitored network traffic, and a healthcare system should issue alerts in real-time based on measurements collected from all the devices for all the monitored patients. While the exact logic for making decisions in different applications requires domain-specific insights, it typically relies on computing quantitative summaries of large data streams in an efficient and incremental manner. Programming the desired logic as a deployable implementation is challenging due to the enormous volume of data and hard constraints on available memory and response time.

The motivation for our work is to assist IoT programmers: the proposed language StreamQRE (pronounced Stream-Query) makes the task of specifying the desired decision-making logic simpler by providing natural and high-level declarative constructs for processing streaming data, and the proposed compiler and runtime system facilitates deployment with guarantees on memory footprint and per-item processing time. The StreamQRE language extends quantitative regular expressions—an extension of classical regular expressions for associating numerical values with strings [11], with constructs typical in extensions of relational query languages for handling streaming data [5, 7, 15, 17, 34, 36, 38, 45]. The novel integration of linguistic constructs allows the programmer to impart to the input data stream a logical hierarchical structure (for instance, view patient data as a sequence of episodes and view network traffic as a sequence of Voice-over-IP sessions) and also employ relational constructs to partition the input data by keys (e.g., patient identifiers and IP addresses).

The basic object in our language is a streaming function, a partial function from sequences of input data items to an output value (which can be a relation). We present the syntax and formal semantics of the StreamQRE language with type-theoretic foundations. In particular, each streaming function has an associated rate that captures its domain, that is, as it reads the input data stream, the prefixes that trigger the production of the output. In our calculus, the rates are required to be regular, captured by symbolic regular expressions, and the theoretical foundations of symbolic automata [47] lead to decision procedures for constructing well-typed expressions. Regular rates also generalize the concept of punctuations in the streaming database literature [36].

The language has a small set of core combinators with formal semantics. The atomic query processes individual items. The operators split and iter are quantitative analogs of concatenation and Kleene-iteration, and integrate hierarchical pattern matching with familiar sequential iteration over a list of values. The global choice operator allows selection between two expressions with disjoint rates. The output composition allows combining output values produced by multiple expressions with equivalent rates processing input data stream in parallel. The key-based partitioning operator map-collect is a generalization of the widely used map-reduce construct that partitions the input data stream into a set of substreams, one per key, and returns a relation. Finally, the streaming composition streams the sequence of outputs produced by one expression as an input stream to another, allowing construction of pipelines of operators.

Modular declarative specifications

The core StreamQRE combinators can be used to define a number of derived patterns, such as tumbling and sliding windows [36], selection, and filtering, that are useful in practice. We have implemented the language as a Java library that supports basic and derived combinators, and a number of built-in quantitative sequential iterators such as sum, maximum, minimum, average, linear regression, discounted sum, standard deviation, and linear interpolation. We show how to program in StreamQRE using an illustrative example regarding monitoring patient measurements, the recent Yahoo Streaming Benchmark for advertisement-related events [22], and the NEXMark benchmark for auction bids [43]. These examples illustrate how hierarchically nested iterators and global case analysis facilitate modular stateful sequential programming, and key-based partitioning and relational operators facilitate traditional relational programming. The two styles offer alternatives for expressing the same query in some cases, while some queries are best expressed by intermingling the two views.

Compilation into streaming processor with guaranteed complexity bounds

The StreamQRE compiler translates a query to a single-pass streaming algorithm. The regular operators associate an unambiguous parse tree with every prefix of the input stream. The typing rules allow the algorithm to maintain only a constant (in the length of the data stream) number of potential parse tree alternatives. The hierarchical sequential iterators can be evaluated naturally and efficiently using a stack. Since exact computation of operations such as the median of a sequence of values and computing sum over sliding windows requires linear space for exact computation [39], we show (with supporting implementation) how to integrate approximate computation of subexpressions in the query evaluation. Implementing the synchronization semantics of multiple threads of computation created during the evaluation of key-based partitioning also requires care. For a subclass of StreamQRE expressions, we give a theoretical guarantee of O(1) memory footprint and O(1) per-item processing time.

Experimental performance evaluation

We compared our StreamQRE implementation with three open-source popular streaming engines RxJava [3], Esper [2], and Flink [1], and found that the theoretical guarantees of our compiler indeed translate to better performance in practice: the throughput of the StreamQRE engine is 2 to 4 times higher than RxJava, 6 to 75 times higher than Esper, and 10 to 140 times higher than Flink. We also show that the approximation algorithms supported by our implementation can lead to substantial memory savings. Finally, StreamQRE supports both sequential iteration and key-based partitioning as high-level programming constructs leading to alternative expressions of the same query with substantially different performance, thus opening new opportunities for query optimization, even beyond those used in database and stream processing engines.

Organization

The remaining paper is organized as follows. §2 informally introduces the key StreamQRE constructs using an illustrative example regarding monitoring patient measurements. The language definition is presented in §3. The StreamQRE compiler is described in §4. Experimental evaluation of the Java implementation of StreamQRE is given in §5. Section §6 describes related work, and the contributions and future work are summarized in §7.

2. Overview

As a motivating example, suppose that a patient is being monitored for episodes of a physiological condition such as epilepsy [37], and the data stream consists of four types of events: (1) An event B marking the beginning of an episode, (2) a time-stamped measurement M(ts, val) by a sensor, (3) an event E marking the end of an episode, (4) and an event D marking the end of a day. Given such an input data stream, suppose we want to specify a policy f that outputs every day, the maximum over all episodes during that day, of the average of all measurements during an episode. A suitable abstraction is to impart a hierarchical structure to the stream:

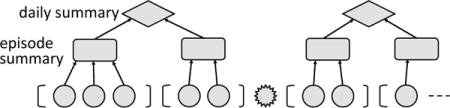
The data stream is a sequence of days (illustrated as diamonds), where each day is a sequence of episodes (illustrated as rectangles), and each episode is a sequence of corresponding measurements (shown as circles) between a begin B marker (shown as an opening bracket) and an end E marker (shown as a closing bracket). The regular expression ((B · M* · E)* · D)* over the event types B, M, E and D specifies naturally the desired hierarchical structure. For simplicity, we assume that episodes do not span day markers.

The policy f thus describes a hierarchical computation that follows the structure of this decomposition of the stream: the summary of each episode (pattern B · M* · E) is an aggregation of the measurements (pattern M) it contains, and similarly the summary of each day (pattern ( B · M* · E)* · D) is an aggregation of the summaries of the episodes it contains.· In order for the policy to be fully specified, the hierarchical decomposition (parse tree) of the stream has to be unique. Otherwise, the summary would not be uniquely determined and the policy would be ambiguous. To guarantee uniqueness of parsing at compile time, each policy f describes a symbolic unambiguous regular expression, called its rate, which allows for at most one way of decomposing the input stream. The qualifier symbolic means that the alphabets (data types) can be of unbounded size, and that unary predicates are used to specify classes of letters (data items) [47]. The use of regular rates implies decidability of unambiguity. Even better, there are efficiently checkable typing rules that guarantee unambiguity for all policies [19, 26, 40].

Existing query languages such as CQL [15] and CEDR [18] indeed use regular expressions, and other complex forms of pattern matching and sliding windows, to select events. However, the selected events are collected as a set without any intrinsic temporal ordering. If the desired summary of an episode is a set-aggregator (such as the average of all measurements), then the relational languages suffice. But suppose the diagnosis depends on the average value of the piecewise-linear interpolation of the sampled measurements. Such a computation is easy to specify as a stateful streaming algorithm that iterates over the sequence of data items, but cannot be expressed directly in existing relational query engines (and would instead need to be specified by a user-defined aggregate function that cannot be optimized by the compiler). The list-iteration scheme provided by the combinator fold : B × (B × A → B) × A* → B (where B is the aggregate type, and A is the type of the elements of the list), which is very common in functional programming languages, is sufficient for expressing iterative computations.

State can be introduced in relational languages using recursion, but this is neither natural, nor necessary, nor conducive to efficient compilation to a streaming algorithm. Recent work on quantitative regular expressions (QRE) [11] shows how to tightly integrate regular expressions with numerical computations, and allows a natural expression of sequential iterators. QREs and other such proposals in runtime monitoring and quantitative formal verification, however, do not provide relational abstractions.

In our example, suppose now the data stream consists of measurements for multiple patients, hence every episode marker and measurement has a patient identifier:

$$\mathrm{B}(\mathit{pId})\mathsf{M}(\mathit{pId},ts,\mathit{val})\mathrm{E}(\mathit{pId})\mathrm{D}$$

where pId is the unique identifier for a patient. Suppose we have written a query f processing the data stream for a single patient that outputs the desired quantitative summary at the end of each day as discussed earlier. If the daily summary computed by f exceeds a fixed threshold value, then we say that the patient has had a critical day. Suppose we want to output each day the set of patients for whom the two past consecutive days have been critical. Given f, we can first construct the query g which partitions the input stream by patient identifiers, applies f to each sub-stream, collects the results of the form (pId, daySummary) in a set, and selects those patients whose daily summary indicates a critical day. The high-level query then can be specified by supplying the input stream both to g and a version of g shifted by a day, and intersect the outputs of the two. Such computation can be most naturally specified in existing relational query languages, but not in state-based formalisms. This key-based partitioning operation is our analog of the map-reduce operation [27, 28], but it raises semantic and implementation questions that have to do with the sequential nature of the data stream: reducing must be sequence-aware, and we need a mechanism to indicate when to emit the output.

The proposed query language StreamQRE draws upon features of relational languages for continuous query processing and quantitative extensions of regular expressions and related formalisms. Unlike previous proposals, it allows the arbitrary mixing of relation-based and sequence-based operations.

3. The StreamQRE Language

In this section we introduce the formal syntax and semantics of the core StreamQRE language. Figure 1 summarizes the formalism, which we will use to program several common stream transformations, such as stream filtering, projection, and windowing. Several detailed examples that illustrate the use of StreamQRE can be found in [12].

Figure 1.

Streaming Quantitative Regular Expressions (QREs): Syntax and denotational semantics with streaming functions.

Basic types & operations

Since our query language combines regular expressions with quantitative operations, we first choose a typed signature which specifies the basic data types and operations for manipulating them. We fix a collection of basic types, and we write A, B, … to range over them. This collection contains the type Bool of boolean values, and the unit type Ut whose unique inhabitant is denoted by def. It is also closed under the cartesian product operation × for forming pairs of values. Typical examples of basic types are the natural numbers Nat, the integers Int, and the real numbers R. We also fix a collection of basic operations on the basic types, for example the k-ary operation op : A₁ × ⋯ × Ak → B. The identity function on D is written as id_D : D → D, and the operations π₁ : A × B → A and π₂ : A × B → B are the left and left projection respectively. We assume that the collection of operations contains all identities and projections, and is closed under pairing and function composition. We write !_A : A → Ut for the unique function from A to Ut.

Predicates

For every basic type D, we fix a collection of atomic predicates, so that the satisfiability of their Boolean combinations is decidable. We write φ : D → Bool to indicate that φ is a predicate on D, and we denote by true_D : D → Bool the always-true predicate. The requirement for decidability of satisfiability for predicates is necessary for the query typing rules that we will present later. The satisfiability checks can be delegated to an SMT solver [26].

Example 1

For the example stream of monitored patients described in §2, the data type DP is the tagged (disjoint) union:

$$\mathsf{\text{DP}}=\left\{\mathsf{D}\right\}\cup \{\mathsf{B}(p),\mathsf{E}(p)|p\in \mathsf{PID}\}\cup \{\mathsf{M}(p,t,v)|p\in \mathsf{\text{PID}},t\in \mathsf{T},v\in \mathsf{V}\},$$

where PID is the set of patient identifiers, T is the set of timestamps, and V is the set of scalars for the measurements.

Relational types and operations

We consider relation types of the form Rel(A), where A is a basic type. The elements of Rel(A) are multisets over A. To express the well-known operations select, project and join from relational algebra [6], it suffices to consider the operation of cartesian product and the higher-order functions map and filter.

$$\mathit{pro}{d}_{A,B}:\mathsf{\text{Rel}}(A)\times \mathsf{\text{Rel}}(B)\to \mathsf{\text{Rel}}(A\times B)$$

$$\mathit{map}(op):\mathsf{\text{Rel}}(A)\to \mathsf{\text{Rel}}(B),\text{where}op:A\to B$$

$$\mathit{filter}(\phi ):\mathsf{\text{Rel}}(A)\to \mathsf{\text{Rel}}(A),\text{where}\phi :A\to \mathsf{\text{Bool}}$$

We also consider standard set-aggregators of relational query languages (e.g., sum, count, minimum, maximum, average), which we model as operations of type Rel(A) → A. We write Map〈K, V〉 for the subtype of Rel(K × V) which consists of (partial) maps from K to V.

Symbolic Regexes

For a type D, we define the symbolic regular expressions over D [46], denoted RE〈D〉, as

$$r\colon\colon =\phi |r\bigsqcup r|r\cdot r|r^{\ast },$$

where φ ranges over predicates on D. The concatenation symbol · is sometimes omitted, i.e. we write rs instead of r · s. The expression r⁺ (iteration at least once) abbreviates r · r*.We interpret an expression r : RE〈D〉 as a set 〚r〛 ⊆ D* of strings over D. We put 〚φ〛 = {d ∈ D | φ(d)} is true}, and this extends to all expressions in the usual way.

The notion of unambiguity for regular expressions [19] is a way of formalizing the requirement of uniqueness of parsing. The languages L₁ and L₂ are said to be unambiguously concatenable if for every word w ∈ L₁ · L₂ there are unique w₁ ∈ L₁ and w₂ ∈ L₂ with w = w₁w₂. The language L is said to be unambiguously iterable if for every word w ∈ L* there is a unique integer n ≥ 0 and unique w_i ∈ L with w = w₁ ⋯ w_n. The definitions of unambiguous concatenability and unambiguous iterability extend to regular expressions in the obvious way. Now, a regular expression is said to be unambiguous if it satisfies the following: (1) r, s are disjoint for every subexpression r ⊔ s, (2) r, s are unambiguously concatenable for every subexpression rs, and (3) r is unambiguously iterable for every subexpression r*.

Observation 2

Suppose r and s are unambiguous symbolic regexes over D. Let Σ be the set of truth assignments for the base predicates of r and s. Assuming that satisfiability of the predicates can be decided in unit time, the problems

1. Are r and s disjoint?

2. Are r and s unambiguously concatenable?

3. Is r unambiguously iterable?

4. Is r contained in s?

are decidable in polynomial time in |r|, |s|, |Σ| [19, 26, 40]. In particular, checking weather a regular expression is unambiguous can be done in polynomial time.

Remark 3

Witnesses of Ambiguity

Consider the computation: “summarize a patient episode with at least one high-risk measurement”. This computation is analogous to the regex-matching problem: “identify sequences over a and b with at least one occurrence of b”. The regex (a⊔b)*b(a⊔b)* is very natural to write, but is ambiguous. The procedure for checking unambiguity (see Observation 2) can flag it as ambiguous, and it can also give a minimum-length trace witnessing the ambiguity: the sequence bb can be parsed in two ways, either as ε · b · b or as b · b · ε. Generally, this procedure can pinpoint both the ambiguous subexpression and the smallest examples that prove ambiguity. For the given example, the expression is equivalent to the unambiguous a*b(a + b)*.

Streaming functions

The basic semantic object in our calculus is a partial map f of type D* ⇀ C (we use the arrow ⇀ to indicate partiality), where D is the type of the input elements and C the type of the outputs. We call these objects streaming functions. They describe general transformations of unbounded streams by specifying the output f(w) (if any) on the stream w seen so far. For example, suppose we want to describe a filtering transformation on streams of scalars of type V, where only the nonnegative scalars are retained and the negative ones are filtered out. The streaming function f : V* ⇀ V that describes this transformation is defined on the sequences {v₁v₂ … v_n | n ≥ 1 and v_n ≥ 0} and the value is the last scalar of the sequence, i.e. the current item.

Streaming Queries

We now introduce formally the language of Streaming Quantitative Regular Expressions (QREs) for representing stream transformations. For brevity, we also call these expressions queries. A denotational semantics will be given in terms of streaming functions. The denotations satisfy the additional property that their domains are regular sets over the input data type. The rate of a query f, written R( f), is a symbolic regular expression that denotes the domain of the interpretation of f, that is, the set of stream prefixes for which f is defined:〚 R( f)〛= dom(〚 f〛). We say that a sequence w of data items matches the query f if it belongs to dom(〚 f〛). The definition of the query language has to be given simultaneously with the definition of rates (by mutual induction), since the query constructs have typing restrictions that involve the rates. We annotate a query f with a type QRE〈D,C〉 to denote that the input stream has elements of type D and the outputs are of type C. The full formal definition of the syntax and semantics of streaming queries is given in Figure 1. The decidability of type checking is established in Observation 2.

Example 4

Rate of a Query

In the patient monitoring example, the statistical summary of a patient’s measurements should be output at the end of each day, and thus, depends only on the types of events in a regular manner. The rate in this case is the regular expression (( B · M* · E)* · D)*.

Atomic queries

The basic building blocks of queries are expressions that describe the processing of a single data item. Suppose φ : D → Bool is a predicate over the data item type D and op : D → C is an operation from D to the output type C. Then, the atomic query atom(φ, op) : QRE〈D, C〉, with rate φ, is defined on single-item streams that satisfy the predicate φ. The output is the value of op on the input element. It is common for op to be the identity function, and φ to be the always-true predicate. So, we abbreviate the query atom(φ, id_D) by atom(φ), and atom(true_D) by atom().

Iteration

Suppose the query f : QRE 〈D, A〉 describes a computation that we want to iterate over consecutive non-overlapping subsequences of the input stream, in order to aggregate the produced values (of type A) sequentially using an aggregator op : B × A → B. More specifically, we split the input stream w into subsequences w = w₁ w₂ … w_n, where each w_i matches f. We apply the computation f to each of the w_i, thus producing the output values a₁ a₂ ⋯ a_n with a_i = 〚 f〛w_i. Finaly, we combine these results using the list iterator left fold with start value init ∈ B and aggregation operation op : B × A → B by folding the list of values a₁ a₂ ⋯ a_n. This can be formalized with the combinator fold : B × (B × A → B) × A* → B, which takes an initial value b ∈ B and a stepping map op : B × A → B, and iterates through a sequence of values of type A:

$$\mathsf{\text{fold}}(b,op,\mathrm{\epsilon })=b$$

$$\mathsf{\text{fold}}(b,op,\gamma a)=op(\mathsf{\text{fold}}(b,op,\gamma ),a)$$

for all sequences γ ∈ A* and all values a ∈ A. For example, fold(b, op, a₁a₂a₃) = op(op(op(b, a₁), a₂), a₃).

The query h = iter( f, init, step) : QRE〈D, B〉 describes the computation of the previous paragraph. In order for h to be well-defined as a function, every input stream w that matches h must be uniquely decomposable into w = w₁w₂ …w_n with each w_i matching f. This requirement can be expressed equivalently as: the rate R( f) is unambiguously iterable.

These sequential iterators can be nested imparting a hierarchical structure to the input data stream facilitating modular programming. In the single-patient monitoring stream, for example, we can associate an iterator with the episode nodes to summarize the sequence of measurements in an episode, and another iterator with the day nodes to summarize the sequence of episodes during a day.

Combination and application

Assume the queries f and g describe stream transformations with outputs of type A and B respectively that process the same set of input sequences, and op is an operation of type A × B → C. The query combine( f, g, op) describes the computation where the input is processed according to both f and g in parallel and their results are combined using op. Of course, this computation is meaningful only when both f and g are defined on the input sequence. So, we demand w.l.o.g. that the rates of f and g are equivalent. This binary combination construct generalizes to an arbitrary number of queries. For example, we write combine( f, g, h, op) for the ternary variant. In particular, we write apply( f, op) for the case of one argument.

Quantitative concatenation

Suppose that we want to perform two streaming computations in sequence on consecutive non-overlapping parts of the input stream: first execute the query f: QRE〈D, A〉, then execute the query g: QRE〈D, B〉, and finally combine these two intermediate results using the operation op : A×B → C. More specifically, we split the input stream into two parts w = w₁w₂, process the first part w₁ according to f with output 〚 f〛w₁, process the second part w₂ according to g with output 〚 g〛w₂, and produce the final result op( f(w₁), g(w₂)) by applying op to the intermediate results. The query split( f, g, op) : QRE〈D, C〉 describes this computation. In order for this construction to be well-defined as a function, every input w that matches split( f, g, op) must be uniquely decomposable into w = w₁w₂ with w₁ matching f and w₂ matching g. In other words, the rates of f and g must be unambiguously concatenable. The binary split construct extends naturally to more than two arguments. For example, the ternary version would be split( f, g, h, op).

Global choice

Given queries f and g of the same type with disjoint rates r and s, the query or( f, g) applies either f or g to the input stream depending on which one is defined. The rate of or( f, g) is the union r ⊔ s. This choice construction allows a case analysis based on a global regular property of the input stream. In our patient example, suppose we want to compute a statistic across days, where the contribution of each day is computed differently depending on whether or not a specific physiological event occurs sometime during the day. Then, we can write a query summarizing the daily activity with a rate capturing good days (the ones without any significant event) and a different query with a rate capturing bad days, and iterate over their disjoint union.

Key-based partitioning

The input data stream for our running example contains measurements from different patients, and suppose we have written a query f that computes a summary of data items corresponding to a single patient. Then, to compute an aggregate across patients, the most natural way is to partition the input stream by a key, the patient identifier in this case, supply the corresponding projected sub-streams to copies of f, one per key, and collect the set of resulting values. In order to synchronize the per-key computations, we specify a predicate φ_S : D → Bool which defines the synchronization elements. The rest of the elements, which satisfy the negation ¬φ_S, are the keyed elements. We typically write K for the set of keys, and κ : D → K for the function that projects the key from an item (the value of κ on synchronization items is irrelevant). For the patient input data type of Example 1 we choose: φ_S = D(i.e., φ_S(x) is true when x is a day marker) and K = PID. The partitioning ensures that the synchronization elements are preserved so that the outputs of different copies of f are synchronized correctly (for example, if each f outputs a patient summary at the end of the day, then each sub-stream needs to contain all the end-of-day markers). Note that the output of such a composite streaming function is a mapping T : Map〈K, C〉 from keys to values, where C is the output type of f and T(k) is the output of the computation of f for key k. This key-based partitioning operation is our analog of the map-reduce operation [27, 28].

The details of this construction are subtle, and we have to introduce more notation to present the semantics precisely. We describe the partitioning of the input stream using terminology from concurrent programming. For every key k, imagine that there is a thread that receives and processes the sub-stream with the data items that concern k. This includes all synchronization items, and those keyed data items x for which κ(x) = k. So, an item satisfying ¬φ_S is sent to only one thread (as prescribed by the key), but an item satisfying φ_S is sent to all threads. See Figure 2 for an illustration of the partitioning into sub-streams. For a sequence w of data items, we write Keys(w) to denote the set of keys that appear in w, and w|_k for the subsequence of w that corresponds to the key k. Each thread computes independently, and the synchronization elements are used for collecting the results of the threads. We specify a symbolic regular expression r : RE〈D〉, which enforces a rate of output for the overall computation. For example, if r = (((¬ D)* · D)²)* then we intend to have output every other day. The rate should only specify sequences that end in a synchronization item.

Figure 2.

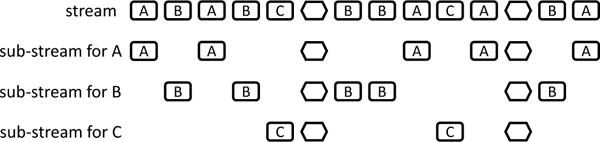
Partitioning a stream into several parallel sub-streams according to a key (letter in box).

Suppose f : QRE〈D, C〉 is a query that describes the per-key (i.e., per-thread) computation, and r is the overall output rate that we want to enforce. Then, the query

$$\mathsf{\text{map}}-\mathsf{\text{collect}}({\phi }_S,\kappa ,\mathsf{f},r):\mathsf{\text{QRE}}\langle D,\mathsf{\text{Map}}\langle K,C\rangle \rangle$$

describes the simultaneous computation for all keys, where the overall output is given whenever the stream matches r. The overall output is the map obtained by collecting the outputs of all threads that match. W.l.o.g. we assume that the rate of f is contained in r, and that it only contains streams with at least one occurrence of a keyed data item. This can be expressed as the regex inclusion $\mathsf{R}(\mathsf{f})\subseteq r\backslash {\phi }_S^{\ast }$, which is equivalent to ${\phi }_S^{\ast }\cdot (\neg {\phi }_S)\cdot \mathit{tru}{e}_D^{\ast }\subseteq \mathsf{R}(\mathsf{f})\subseteq r$. The rate r should only depend on the occurrence of synchronization elements, a requirement that can be expressed syntactically:

$$r=s[(\neg {\phi }_S)\ast {\phi }_S/{\phi }_S]$$

for some expression s : RE〈D〉, where the only predicate that s is allowed to contain is φ_S. We write s[ψ/φ] to denote the result of replacing every occurrence of φ in s with ψ. When r satisfies this condition we say that it is well-formed w.r.t. φ_S. For example, if s = D* (indicating output at every day marker) and φ_S = D, then r = s[(¬φ_S)* φ_S/φ_S] = ((¬ D)* D)* is well-formed w.r.t. φ_S. All these restrictions that we have imposed on the rates do not affect expressiveness, but are useful for efficient evaluation and type-checking.

Remark 5

The operation of key-based partitioning raises significant challenges for the efficiency of type-checking. In the context of pure regex matching, one could consider either an existential or a universal notion of key-based partitioning:

$$\frac{\kappa :D\to Kr:\mathsf{\text{RE}}\langle D\rangle }{{\mathsf{\text{partition}}}_{\exists }(\kappa ,r),{\mathsf{\text{partition}}}_{\forall }(\kappa ,r):\mathsf{\text{RE}}\langle D\rangle }.$$

The expression partition_∃(κ,r) accepts nonempty words w with w|_k ∈ 〚r〛, where k is the key of the last element of w. Similarly, the expression partition_∀(κ; r) accepts nonempty words w with w|_k ∈ 〚r〛 for every key k that appears in w. Notice that partition_∃(κ; r) is the standard construct of disjoint partitioning used in streaming systems (see, for example, the “partition-by” clause in the languages of [49] and [33]). Unfortunately, these natural notions of partitioning and matching give rise to decision problems (such as nonemptiness and unambiguity) that are not easy to compute. The introduction of synchronization elements for the map-collect construct of StreamQRE is meant to solve this problem by enforcing a rate of output that depends only on the occurrence of synchronization elements in a regular way. This simplifies the description of the domain of a map-collect query, and the typing checks become easy.

Streaming composition

A natural operation for query languages over streaming data is streaming composition: given two streaming queries f and g, f ≫ g represents the computation in which the stream of outputs produced by f is supplied as the input stream to g. Such a composition is useful in setting up the query as a pipeline of several stages. We allow the operation ≫ to appear only at the top-level of a query. So, a general query is a pipeline of ≫-free queries. At the top level, no type checking needs to be done for the rates, so we do not define the function R for queries f ≫ g. With streaming composition we can express non-regular patterns, such as a sequence of increasing numbers.

The semantics of streaming composition involves a lifting operator on streaming functions. For a function f : D* ⇀ * C we define the partial lifting lift(f) : D* ⇀ C*, which generates sequences of output values. The domain of lift(f) is equal to the domain of f, but lift(f) returns the sequence of all outputs that have been emitted so far.

3.1 Derived stream transformations

The core language of Figure 1 is expressive enough to describe many common stream transformations. We present below several derived patterns, including filtering, mapping, and aggregation over windows.

Iteration (at least once)

Let f : QRE〈D, A〉 be a query with output type A, init : B be the initialization value, and op : B × A → B be the aggregation function. The query iter₁( f, init, op), with output type B, splits the input stream w unambiguously into consecutive parts w₁ w₂ … w_n each of which matches f, applies f to each w_i producing a sequence of output values a₁ a₂ … a_n, i.e. a_i = f(w_i), and combines the results a₁ a₂ … a_n using the list iterator left fold with start value init and accumulation operation op. The construct iter₁ can be encoded using iter as follows:

$${\mathsf{\text{iter}}}_1(\mathsf{f},\mathit{init},op)\triangleq \mathsf{\text{split}}(\mathsf{\text{iter}}(\mathsf{f},\mathit{init},op),\mathsf{f},op).$$

The type of the query is QRE〈D, B〉 and its rate is R( f)⁺.

Iteration exactly n times

Let n ≥ 0 and f : QRE〈D, A〉 be a query to iterate exactly n times. The aggregation is specified by the initialization value init : B and the aggregation function op : B × A → B. The construct iterⁿ describes iteration (and aggregation) exactly n times, and can be encoded as follows: iter⁰( f, init, op) = init and

$${\mathsf{\text{iter}}}^{\mathrm{n}+1}(\mathsf{f},\mathit{init},op)\triangleq \mathsf{\text{split}}({\mathsf{\text{iter}}}^{\mathrm{n}}(\mathsf{f},\mathit{init},op),\mathsf{f},op).$$

The type of iterⁿ( f, init, op) is QRE〈D, B〉 and its rate it R( f)ⁿ (n-fold concatenation).

Matching without output

Suppose r is an unambiguous symbolic regex over the data item type D. We want to write a query whose rate is equal to r, but which does not produce any output. This is essentially the same as returning def. So, we define the regex to query translation function match:

$$\mathsf{\text{match}}(\phi )\triangleq \mathsf{\text{atom}}(\phi ,{!}_D)$$

$$\mathsf{\text{match}}(r_1\bigsqcup r_2)\triangleq \mathsf{\text{or}}(\mathsf{\text{match}},(r_1),\mathsf{\text{match}},(r_2))$$

$$\mathsf{\text{match}}(r_1\cdot r_2)\triangleq \mathsf{\text{split}}(\mathsf{\text{match}},(r_1\text{),match},(r_2),{!}_{\mathsf{\text{Ut}}\times \mathsf{\text{Ux}}}\text{)}$$

$$\mathsf{\text{match}}(r\ast )\triangleq \mathsf{\text{ilter}}(\mathsf{\text{match}}(r),{!}_{\mathsf{\text{Ut}}\times \mathsf{\text{Ux}}}\text{)}$$

An easy induction establishes that R( match(r)) = r.

Stream filtering

Let φ be a predicate over the type of input data items D. We want to describe the streaming transformation that filters out all items that do not satisfy φ. We implement this with the query filter(φ), which matches all stream prefixes that end with an item satisfying φ.

$$\mathsf{\text{filter}}(\phi )\triangleq \mathsf{\text{split}}(\mathsf{\text{match}}(\mathit{tru}{e}_D^{\ast }),\mathsf{\text{atom}}(\phi ),{\pi }_2)$$

The type of filter(φ) is QRE〈D, D〉 and its rate is $\mathit{tru}{e}_D^{\ast }\cdot \phi$.

Stream mapping

The mapping of an input stream of type D to an output stream of type C according to the operation op : D → C is given by the following query:

$$\mathsf{\text{map}}(\mathit{\text{op}})\triangleq \mathsf{\text{split}}(\mathsf{\text{match}}(\mathit{tru}{e}_D^{\ast }),\mathsf{\text{atom}}(\mathit{tru}{e}_D,op),{\pi }_2)$$

The type of the query is QRE〈D, C〉 and its rate is $\mathit{tru}{e}_D^{+}$.

Pattern-based tumbling windows

The term tumbling windows is used to describe the splitting of the stream into contiguous non-overlapping regions [36]. Suppose we want to describe the streaming function that iterates f: QRE〈D, C〉 at least once and reports the result given by f at every match. The following query expresses this behavior:

$$\mathsf{\text{iter}}-\mathsf{\text{last}}(\mathsf{f})\triangleq \mathsf{\text{split}}(\mathsf{\text{match}}(\mathsf{R}(\mathsf{f})\ast ,\text{f,}{\pi }_2)).$$

The type of the query is QRE〈D, C〉 and its rate is R(f)⁺.

Sliding windows (slide by pattern)

To express a policy such as “output the statistical summary of events in the past ten hours every five minutes” existing relational query languages provide an explicit sliding window primitive [36]. We can support this primitive, which can be compiled into the base language by massaging the input data stream with the introduction of suitable tags (marking five-minute time intervals in this example). The insertion of the tags then allows to express both the window and the sliding using very general regular patterns. Let n ≥ 1 be the size of the window, and f : QRE〈D, A〉 be the query that processes a unit pattern. The aggregation over the window is specified by the value init : B for initialization and the aggregation function op : B × A → B. We give a query that computes the aggregation over the last n units of the stream (or over all units if the stream has less than n units):

$$\mathsf{g}=\mathsf{\text{or}}({\mathsf{\text{iter}}}^1(\mathsf{f},\mathit{init},op),\dots ,{\mathsf{\text{iter}}}^{\mathrm{n}-1}(\mathsf{f},\mathit{init},op))$$

$$\mathsf{h}=\mathsf{\text{split}}(\mathsf{\text{match}}(\mathsf{R}(\mathsf{f})\ast ),{\mathsf{\text{iter}}}^{\mathrm{n}}(\mathsf{f},\mathit{init},op),{\pi }_2)$$

Event counting in sliding windows

Consider the sliding window computation that counts the number of occurrences of an event. For a query f : QRE〈D, C〉, a window size n, and a predicate φ : C → Bool that indicates the occurrence of the event, we define:

$$\mathsf{\text{wnd}}-\mathsf{\text{count}}(\mathsf{f},n,\phi )\triangleq \mathsf{\text{wnd}}(\mathsf{f},n,0,op),\text{where }op(x,c)\triangleq \text{if}\phi (c)\text{then}x+1\text{else }x.$$

The type of the query is $\mathsf{\text{QRE}}\langle D,\mathbb{N}\rangle$ and its rate is R(f)⁺.

Remark 6 (Sliding Windows)

We defined earlier an encoding of sliding windows using the derived construct iterⁿ, which correponds to iterated concatenation n times. This encoding causes an exponential blowup in the size of the query, and is therefore an inefficient way to implement sliding windows. The purpose of describing this encoding, however, is to illustrate the expressiveness of regular parsing, namely that sliding windows are a special case of regular decomposition and therefore fit naturally in the StreamQRE framework.

Our implementation, which is benchmarked in Section 5, provides a specialized treatment of sliding windows without using the expensive encoding with iterⁿ. In particular, we allow plugging in arbitrary code for handling the insertion of new elements in the window and the eviction of expiring elements. So, all algorithmic techniques proposed in the literature for sliding-window aggregation [16, 41, 42] can be seamlessly integrated in StreamQRE. The main point here is that efficient sliding-window aggregation algorithms can be nested arbitrarily with the regular constructs of StreamQRE without incurring any additional computational overhead.

4. Compilation Algorithm

In this section we will describe the compilation of a query f: QRE〈D, C〉 into a streaming algorithm that computes the intended function. Before presenting the compilation procedure, we should describe more precisely the streaming model of computation. The input stream is a potentially unbounded sequence of elements, and a streaming algorithm computes by consuming the elements of the stream in order, as they become available. The input stream is read incrementally in one pass, which means that past input elements cannot be accessed again. A streaming algorithm $\mathcal{A}$ consists of: (1) a possibly infinite state space S, which is the set of all possible internal configurations of the algorithm (i.e., its memory), (2) an initial state init ∈ S, and (3) a transition function next : S × D → S × C, which consumes the next input element, mutates the current state, and produces an output.

We say that the streaming algorithm $\mathcal{A}$ implements the query f: QRE〈D, C〉 if for every input w ∈ D*: the output of $\mathcal{A}$ after consuming w is equal to 〚 f〛w (when defined), and equal to nil when 〚 f〛w is undefined. The space and time requirements of a streaming algorithm are typically given as functions of the size n of the stream consumed so far, and possibly also in terms of other significant parameters of the input (e.g., range of numerical values).

The goal of the compilation procedure is to generate an algorithm that uses a small amount of space and processes fast each newly arriving element. Ideally, both the space and time requirements are independent of the length of the data stream. Conceptually, the computation of 〚 f〛w, where f is a query and w is an input stream, amounts to evaluating an expression tree that is of size linear in the length of w. This expression tree mirrors the parse tree that corresponds to the the rate of f, so one crucial challenge is the online computation of the split points in the stream to match the pattern. Suppose we process the query split( f, g, op) on w₁w₂w₃w₄, where the prefixes w₁ and w₁w₂ match f and the subsequences w₂w₃ and w₃w₄ match g. After having seen the prefix w₁w₂, we need to maintain the parallel computation of two expression trees, since f has matched twice. The insight is that the number of these parallel computations is bounded and depends only on the size of the query (see also [10] and [11]). The computation of 〚 f〛w involves, however, more than just parsing: to compute efficiently the intermediate expression trees, they must have a compact representation. Indeed, the intermediate results can be represented by stacks of values, whose size is bounded by the size of the query. This is a crucial part of establishing the efficiency of the proposed evaluation algorithm.

Generalized evaluation problem

We proceed now with some technical details of our approach. In order to define the compilation procedure by recursion on the structure of the query f : QRE〈D, C〉, we have to generalize the problem. Let Stack be the type of finite stacks that can contain any value of any basic type, and [] be the empty stack. We assume that Stack is equipped with the following standard operations:

$$\mathit{pus}{h}_A:\text{Stack}\times A\to \text{Stack}\mathit{pop}:\text{Stack}\to \text{Stack}$$

and the operation getTop_A : Stack → A∪{nil}, which maps a stack to the value on the top of it (or nil if the stack is empty). Instead of just input streams d₁d₂d₃ … of data items, we consider streams that also contain non-consecutive occurrences of stacks. For example, s₁ d₁ d₂ d₃ s₂ d₄ d₅ s₃ d₆ d₇ d₈ … is such a stream. Informally, we think that every stack item marks the beginning of a thread of execution that processes all the data items that follow. Our example stream involves the parallel threads shown on the left. We want an algorithm that simulates the parallel computation of f on the threads. The output on a thread s w must be defined when 〚 f〛w is defined, and it has to be equal to the stack s.push(〚 f〛w). In order for the overall output to be well-defined, we require that at most one active thread gives output. We say that a sequence w ∈ (D∪Stack)* is well-formed for f if for every prefix of w there is at most one thread for which 〚 f〛 is defined. So, we describe for every query f an algorithm that solves this generalized problem on well-formed inputs from (D ∪ Stack)*.

$$s_1{d}_1{d}_2{d}_3{d}_4{d}_5{d}_6{d}_7{d}_8$$

$$s_2{d}_4{d}_5{d}_6{d}_7{d}_8$$

$$s_3{d}_6{d}_7{d}_8$$

There are four components to specify: the state space State_f, the initial state init_f, the function start_f that consumes stack items, and the function next_f that consumes data items (elements of D). Figures 3 and 4 show this construction (by recursion on f) for the base queries and the constructs iteration, concatenation, and map-collect. We write ${\mathcal{A}}_{\mathsf{f}}$ to denote the streaming generalized evaluation algorithm for f. The other constructs are easier to handle, and hence omitted.

Figure 3.

Compilation for atomic queries, quantitative iteration, and quantitative concatenation.

Figure 4.

Compilation for key-based partitioning queries.

Split

To see why this generalization of the problem is necessary, let us consider the evaluation of h = split( f, g, op) on a single thread [] d₁ d₂ d₃ d₄ d₅ d₆ d₇ d₈. The algorithm ${\mathcal{A}}_{\mathsf{h}}$, described in Figure 3, forwards every data item to both ${\mathcal{A}}_{\mathsf{f}}$ and ${\mathcal{A}}_{\mathsf{g}}$. Suppose that there are two prefixes of the input that match f: d₁ d₂ d₃ and d₁ d₂ d₃ d₄ d₅, for which ${\mathcal{A}}_{\mathsf{f}}$ reports outputs a₁ and a₂ respectively. Recall that all queries are unambiguous, therefore it is not possible for both suffixes d₄ d₅ d₆ d₇ d₈ and d₆ d₇ d₈ to match g. We use the stacks of values as a mechanism to propagate the intermediate results of the computations. For our particular example stream, the evaluator ${\mathcal{A}}_{\mathsf{h}}$ ensures that the sequence of items fed to ${\mathcal{A}}_{\mathsf{g}}$ is d₁ d₂ d₃ [a₁] d₄ d₅ [a₂] d₆ d₇ d₈. This means that ${\mathcal{A}}_{\mathsf{g}}$ has to simulate the concurrent evaluation of multiple suffixes of the data stream. After reading the stream, suppose ${\mathcal{A}}_{\mathsf{g}}$ accepts the suffix d₆ d₇ d₈ and reports the value b₂ = 〚 g〛d₆d₇d₈. The output of ${\mathcal{A}}_{\mathsf{g}}$ is then [b₂, a₂], that is, the result of pushing the value b₂ on the stack [a₂] that started the accepting thread. Finally, ${\mathcal{A}}_{\mathsf{h}}$ uses the output stack [b₂, a₂] to compute the answer op(a₂, b₂). This stack-based mechanism of propagating values is crucial for matching the outputs of f and g and computing the final value.

Atomic

It is instructive to see how the query atom(φ, op) is implemented in order to satisfy the contract of the generalized evaluation problem. The crucial observation is that there should only be output on consecutive occurrences of the form s d, where s is a stack and d is an item that satisfies the predicate φ. To achieve this, we have to record the stack s given with a start(s) invocation, and with the following next(d) invocation we return the stack s.push(op(d)) as output. As seen in Figure 3, the state space of the algorithm consists of elements L(in), where in is the stack that initiated the current thread of execution. The initial state is L( nil), since in the beginning there is no active thread. The function start sets the stack for the active thread, and returns nil because the empty sequence ε does not match the query atom(φ, op). The transition function next checks if there is an active thread and if the current item d satisfies the formula φ. If so, it returns the active stack after pushing the result on it.

Iteration

Consider now the generalized evaluation algorithm for iter( f, b₀, σ), shown in Figure 3. The state space consists of elements I(child), where child is a state of ${\mathcal{A}}_{\mathsf{f}}$. The initial state is I(init_f), where init_f is the initial state of ${\mathcal{A}}_{\mathsf{f}}$. The idea of the algorithm is to use the stack to store the intermediate results of the aggregation. When start_h is invoked with the stack s, we propagate the start call to the algorithm for f with the stack s.push(b₀), since the initial value b₀ is the first intermediate result. Now, the transition on a data item d involves first sending the item to ${\mathcal{A}}_{\mathsf{f}}$. The interesting case is when ${\mathcal{A}}_{\mathsf{f}}$ gives output. The stack s that it returns contains the value a given by f as well as the previous intermediate result b that we pushed on the stack. From these we can compute the next intermediate result σ(b, a), which we place again on the stack in order to restart ${\mathcal{A}}_{\mathsf{f}}$.

Map-Collect

Suppose that the predicate φ : D → Bool specifies the synchronization elements, K is a finite set of keys, κ : D → K extracts a key from an element, f describes the per-key processing, and r : RE〈D〉 is the rate of output that we want to enforce. In Figure 3 we describe the compilation of h = map-collect(φ, κ, f, r). Each state of ${\mathcal{A}}_{\mathsf{h}}$ is a pair: the first component is a key-indexed map of states of ${\mathcal{A}}_{\mathsf{f}}$, and the second component is a state of ${\mathcal{A}}_r$. The implementation of the function next is noteworthy. If the data item is a synchronization element, then it is propagated to all key-threads. If the data item specifies a key, then it is propagated only to the key-thread that it is meant for. The rate determines when to collect the outputs of the key-threads. When the rate accepts, then we collect in a relation the outputs of all key-threads that have available output. A crucial optimization that we have implemented is the collapsing of key-threads that have only seen synchronization elements so far, hence these threads have identical state.

Theorem 7

Let f be a query which involves only finite sets of keys for the occurrences of map-collect in it. Then, the streaming algorithm ${\mathcal{A}}_r$ that implements f (as described in Figure 3) satisfies the following:

1. Assume that the values of the basic types appearing in f require unit space to be stored. Then, ${\mathcal{A}}_{\mathsf{f}}$ requires space that depends only on the size of f, independent of the length of the stream.

2. Suppose additionally that the basic operations that appear in f require unit time to be performed. Then, the processing time per element for ${\mathcal{A}}_{\mathsf{f}}$ depends only on the size of f, and is independent of the length of the stream.

Remark 8 (Map-Collect)

When the map-collect construct is used at the top level of a query, it is easy to implement key-based partitioning so that the space requirements are |K| · (space needed for f), where K is the set of keys appearing in the stream. The situation is much more complicated when map-collect is nested beneath several regular operators, because then the evaluation algorithm has to explore the possibility of matching it against several (possibly overlapping) subsequences of the stream. Putting a constant bound (on the length of the input stream) on the several concurrent possibilities of matching a nested map-collect hinges on the carefully chosen typing restrictions of Figure 1.

The assumptions of Theorem 7 for the basic types and operations are satisfied by standard constant-size data types: unsigned and signed integers, booleans, characters, floating-point numbers. For such types Theorem 7 guarantees the compilation of a query into an efficient streaming algorithm. However, if the types appearing in the query involve unbounded data structures (such as sets, maps, multisets, and so on), then the total space and time-per-element accounting has to account for the storage and manipulation of these complex data structures. The literature on database systems addresses the problem of efficient processing with relational data structures (e.g., for selecting, filtering, joining, etc.), and this issue is orthogonal to our investigations. Theorem 7 assures us that even when computing with relational data structures, the parsing of the stream and the combination of the intermediate results incur very little additional computational overhead.

4.1 Approximation

Theorem 7 states space and time guarantees for our evaluation algorithm that are applicable only when the basic data values have a constant-size encoding, and the basic operations can be computed in constant time. One very important statistic that does not fit these assumptions is median, the computation of which requires recording multisets of values (hence, linear space is required). We will see that using approximation we can overcome this barrier. It is known that an exact computation of the median of a stream of n positive integers requires Ω(n) space [31]. So, any small space computation of median must allow some error. We get around this barrier by using the idea of a geometric discretization of the range of possible values, and rounding down each element in the stream to its nearest discrete value.

At a high level, the idea is to use a data structure of approximate histograms, which maintain counts for the discretized values. This idea applies to all real numbers (negative, zero, and positive), but for the sake of simplicity we assume that the range is (0, +∞). We first choose an approximation constant ε ∈ (0, 1). For x ≥ 1, define its ε-approximation as apx(x) = (1 + ε)ⁱ, where i = ⌊log_1+ε x⌋. For x ∈ (0, 1) we put apx(x) = (1 + ε)⁻ⁱ⁻¹, where i = ⌊log_1+ε(1/x)⌋. For x ∈ (0, ∞), the inequality apx(x) ≤ x ≤ apx(x)(1 + ε) holds. The implies, for example, that if ε = 0.01 then the approximation error is at most 1% of the actual value.

Our streaming algorithm for computing median queries maintains a summary $\mathscr{H}$, which is an integer-indexed array of counts (for discretized values). For an integer i, the entry $\mathscr{H}[i]$ is the count of values in the interval [(1+ε)ⁱ, (1+ε)ⁱ⁺¹) that we have seen so far. From this summary, any rank query can be answered approximately with relative error ε. Suppose that U is the largest value and L is the smallest (positive) value appearing in the stream. For asymptotic analysis, we assume w.l.o.g. that U ≫ 1 and L ≪ 1. Then, the array $\mathscr{H}$ requires log_1+ε U + log_1+ε L⁻¹ ≤ ε⁻¹. log₂(U/L) entries.

We write M_ε( V) for the type of ε-approximate histograms over scalars V, and ∅_ε for the empty histogram. We support the operations ins_ε : M_ε( V)× V→M_ε( V) for value insertion and mdn_ε : M_ε( V) → V for obtaining the approximate median. Choosing between exact or approximate computation amounts to simply using the appropriate data structure. The approximation guarantees are given concisely as follows:

Theorem 9

For every nonempty sequence w of scalars, we have that 〚 f_ε-apx〛w ≤ 〚 f_exact〛w ≤ (1+ε) · 〚 f_ε-apx〛w, where

$${\mathsf{f}}_{\mathrm{\text{exact}}}=\mathsf{\text{apply}}(\mathsf{\text{iter}}(\mathsf{\text{atom}}(),\mathrm{\varphi },\mathit{ins}),\mathit{mdn})$$

$${\mathsf{f}}_{\epsilon -\text{apx}}=\mathsf{\text{apply}}(\mathsf{\text{iter}}(\mathsf{\text{atom}}(),{\mathrm{\varphi }}_{\epsilon },in{s}_{\epsilon }),md{n}_{\epsilon })$$

Assuming that constant space is enough for storing the size of the stream, the space used by the evaluation algorithm for f_ε-apx is linear in ε⁻¹ and in log(U/L), where U (L) is the largest (smallest) absolute value appearing in the stream.

When the computation of medians is mixed with other numerical operations, providing a global approximation guarantee is more subtle. If we restrict attention to non-negative numbers and the numerical operations +, min, max, avg and mdn_ε, then the guarantees of Theorem 9 can be lifted to all queries involving these operations. However, adding an ε-approximately computed positive number and an ε-approximately computed negative number can result in unbounded relative error for the result.

Another useful computation that benefits tremendously from approximation is sliding-window event counting (described in §3.1). To count the number of events exactly, it can be shown that space linear in the size of the window is necessary. The work of [25] shows that a (1+ε)-approximate estimate can be obtained using space that is linear in ε⁻¹ and logarithmic in the size of the window. We have incorporated the approach of [25] in our implementation.

5. Experiments

We have implemented StreamQRE as a Java library in order to facilitate the easy integration with user-defined types and operations. Our implementation covers all the core combinators of Figure 1, and provides optimizations for the derived operations (stream filtering, mapping, windowing, event counting, etc.). We have already discussed in Remark 6 that our implementation of sliding windows does not use the expensive encoding of §3.1, but instead allows the use of efficient algorithms for the manipulation of the window. The data structure of approximate histograms and the algorithm for approximate event counting, as described in §4.1, are also supported.

The goals of our experimental evaluation are the following: (1) examine if the language constructs of StreamQRE are sufficiently expressive and flexible to describe useful stream transformations on realistic workloads, (2) check whether our compilation procedure produces efficient code that can achieve high performance, and (3) evaluate whether approximation can provide substantial space benefits for some realistic but expensive computations.

We have chosen the widely used Yahoo and NEXMark benchmarks [22, 43], which describe realistic workloads and suggest complex and useful queries. We evaluate StreamQRE by comparing it against three other streaming engines: RxJava [3], Esper [2] and Flink [1]. We have picked these popular engines because they offer rich sets of high-level stream manipulation operations, and they all have actively maintained open-source implementations in Java that can be deployed on a single machine (in fact, on a single JVM).

Figure 5 lists some useful stream transformations and the engines that directly support them. For the QREs of [11], no implementation was given. The streaming operations marked with - in Figure 5 can be encoded using the core regular constructs, but an efficient engine would require additional optimizations, especially for the expensive windowing operations. The operations (2)–(6) from Figure 5 are used in every query of both benchmarks, while a few of the queries require time-based tumbling/sliding windows. As we will discuss later, the regular constructs of StreamQRE prove especially useful for some of the queries of NEXMark. Finally, we use the features (11) and (12) of StreamQRE to program two queries inspired from the patient monitoring example of §2.

Figure 5.

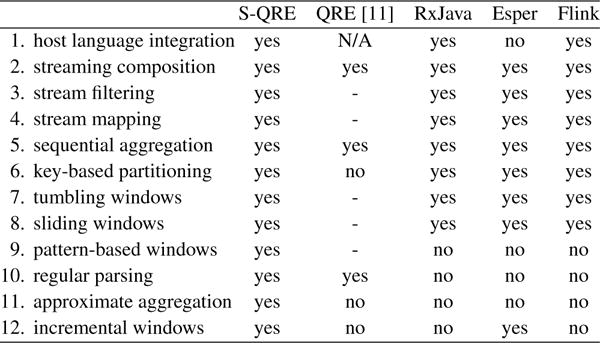
Some of the features and stream transformations supported by StreamQRE, RxJava, Esper and Flink.

Yahoo Benchmark

The Yahoo Benchmark [22] specifies a stream of advertisement-related events for an analytics pipeline. It specifies a set of campaigns and a set of advertisements, where each ad belongs to exactly one campaign. The static map from ads to campaigns is computed ahead-of-time and stored in memory. Each element of the data stream is of the form ( userId, pageId, adId, eventType, eventTime), indicating the interaction of a user with an advertisement, where eventType is one of { view, click, purchase}. The component eventTime is the timestamp of the event.

Query Y1

The basic benchmark query (described in [22]) computes, at the end of each second, a map from each campaign to the number of views associated with that campaign within the last second. For each event tuple, this involves a lookup to determine the campaign associated with the advertisement viewed. The reference implementation published with the Yahoo benchmark involves a multi-stage pipeline: (a) stage 1: filter view events, (b) stage 2: project the ad id from each view tuple, (c) stage 3: lookup the campaign id of each ad, (d) stage 4: compute for every one-second window the number of events (views) associated with each campaign. The query involes key-based partitioning on only one property, namely the derived campaign id of the event.

Query Y2

We extend the Yahoo benchmark with a more complex query. An important part of organizing a marketing campaign is quantifying how successful ads are. We define success as the number of users who purchase the product after viewing an ad for it. Our query outputs, at the end of every second, a map from campaigns to the most successful ad of the campaign so far, together with its success score.

NEXMark benchmark

The Niagara Extension to XMark benchmark (NEXMark) [43] concerns the monitoring of an on-line auction system such as eBay. Four kinds of events are recorded in the event stream: (a) Person events, which describe the registering of a new person to the auction system, (b) Item events, which mark the start of an auction for a specified item, (c) Close events, which mark the end of an auction for a specified item, and (d) Bid events, which record the bids made for items that are being auctioned.

$$\mathsf{\text{Person}}(\mathsf{\text{personaId}},\mathsf{\text{name}},\mathsf{\text{ts}})\mathsf{\text{Close}}(\mathsf{\text{itemId}},\mathsf{\text{ts}})$$

$$\mathsf{\text{Item}}(\mathsf{\text{itemId}},\mathsf{\text{sellerId}},\mathsf{\text{initPrice}},\mathsf{\text{ts}},\mathsf{\text{dur}},\mathsf{\text{category}})$$

$$\mathsf{\text{Bid}}(\mathsf{\text{itemId}},\mathsf{\text{bidderId}},\mathsf{\text{bidIncrement}},\mathsf{\text{ts}})$$

Every event contains the field ts, which is the timestamp of when the event occurred. Every new auction event (of type Item) specifies an initial price initPrice for the item, the duration dur of the auction, and the category to which the item belongs. Every bid event contains the bid increment, that is, the increment by which the previous bid is raised. So, to find the current bid for an item we need to add the initial price of the item together with all the bid increments for the item so far. We have chosen five queries, which are minor variants of some of the queries of the NEXMark benchmark: (N1) Output at every auction start or close the number of currently open auctions. (N2) Output at every auction close the average closing price of items sold so far. (N3) Output at every auction close the average closing price of items per category. (N4) Output every 10 minutes the highest bid within the last 10 minutes. (N5) Output every 10 minutes the item with the most bids in the last 24 hours.

Queries N2 and N3 involve identifying for every item a pattern-based window that spans all events relating to the auction for that item. These windows are naturally specified by the regular pattern Item· Bid*· Close. The constructs of StreamQRE are very well suited for this purpose, whereas the encoding of these queries in RxJava, Esper and Flink is arguably awkward and error-prone.

Results

Figure 6 summarizes the throughput results for the queries of the Yahoo and NEXMark benchmark. Every experiment was repeated 100 times and we report the arithmetic mean, together with an error bar that indicates the standard deviation of the samples. All experiments were run on a typical contemporary laptop, with an Intel Core i7-4710HQ CPU running at 2.5 GHz and with 12 GB of RAM (Windows 8.1 with Oracle JDK 1.8.0_111-b14). Both StreamQRE and RxJava, which are relatively lightweight libraries, achieve significantly higher throughputs for these sequential workloads than Esper and Flink. Moreover, StreamQRE is two to four times faster than RxJava for all queries. Both the Yahoo and NEXMark benchmarks specify random stream generators that create timestamped events. In order to get meaningful throughput measurements, we have modified the stream generators so that the event generation is not throttled. This means that event time, i.e. the time dimension of the timestamps, is not the same as real time. The queries describe the computations in event time, so we can “replay” the execution at higher actual speeds.

Figure 6.

Yahoo and NEXMark benchmarks: results for the queries Y1, Y2, and N1–N5 (from left to left). Every bar chart shows the throughput (in millions of events per second) for StreamQRE (Q), RxJava (R), Esper (E) and Flink (F).

Approximation

To measure the benefit of approximation we have implemented a random stream generator for the patient monitoring example of §2, and have written the following two queries in StreamQRE: (P6) Report at the end of every day, the median over all previous days of the count of measurements per day. (P7) Report at every new event arrival, the number of atypical measurements, i.e. those that exceed a threshold T, that have occurred over the last W events, where we vary the size W of the sliding window.

We report the results in Table 1: the throughput is in million events per second, and the space usage is in 1000 bytes. We have computed queries P6 and P7 using both an exact and approximate evaluation algorithm. We set the approximation constant at ε = 0.01, which means that the approximate results have relative error at most 1%. For query P7 we vary the window size from 10⁴ to 10⁷ elements. Memory usage was measured by serializing the evaluator state using Java’s default serializer. Note that for both queries P6 and P7, the approximate evaluator consumes significantly less memory than the exact query evaluation algorithm. For query P7, the approximate evaluator is generally slower than the exact evaluator, because the processing of each element requires the updating of a small but complicated data structure [25]. However, for a massive sliding window of 10⁷ elements the exact query becomes noticeably slower, because memory starts becoming scarce. For query P6, the approximate evaluator is slightly faster than the exact evaluator, in spite of the overhead of performing floating-point arithmetic to maintain approximate histograms. For both P6 and P7, the actual error in output is less than the stated threshold limit of 1%. In summary, if small errors are permissible in the computation, then approximate QRE evaluation has the potential to significantly reduce memory usage by an exponential.

Table 1.

Performance for queries with approximation.

	Throughput		Space (1000 bytes)		Error
	Exact	Approx	Exact	Approx
P6	8.208	8.643	1,458	25.3	0.14%
P7 (w = 104)	6.747	3.221	151	9.9	0.09%
P7 (w = 105)	5.100	2.067	1,501	14.9	0.52%
P7 (w = 106)	4.030	1.863	15,001	19.4	0.19%
P7 (w = 2 · 106)	3.411	1.857	30,001	20.9	0.24%
P7 (w = 4 · 106)	2.050	1.871	60,001	22.3	0.30%
P7 (w = 6 · 106)	1.434	1.876	90,001	23.2	0.34%
P7 (w = 8 · 106)	1.028	1.864	120,001	23.7	0.03%
P7 (w = 107)	0.826	1.841	150,001	24.3	0.36%

Why regular parsing?

We have already mentioned that regular patterns facilitate the implementation of N2 and N3. The ability to extract pattern-based windows of interest from a stream and compute incrementally with their elements distinguishes StreamQRE from other engines. For example, for the patient stream of §2, we can easily extract episodes with at least one extreme measurement and return the average of the measurements after the last occurrence of an extreme one. Programming such realistic queries in RxJava, Esper or Flink would be extremely cumbersome.

6. Related work

Streaming databases

There is a large body of work on streaming database languages and systems such as Aurora [5], Borealis [4], STREAM [14], and StreamInsight [7, 18]. The query language supported by these systems (for example, CQL [15]) is typically a version of SQL with additional constructs for sliding windows over data streams. This allows for rich relational queries, including set-aggregations (e.g. sum, maximum, minimum, average, count) and joins over multiple data streams. Such SQL-based languages are, however, severely limited in their ability to express properties and computations that rely on the sequence of the events such as: sequence-based pattern-matching, and numerical computation based on list-iteration when the order of the data items is significant (e.g., average of piecewise-linear interpolation). In contrast, our query language allows the combination of relational with sequence-based operations, which poses unique technical challenges that are not addressed in the aforementioned works. Of particular relevance are engines such as IBM’s Stream Processing Language (SPL) [34, 45], ReactiveX [3], Esper [2] and Flink [1], which support user-defined types and operations, and allow for both relational and stateful sequential computation. However, none of these engines provides support for decomposing the stream in a regular fashion and performing incremental computations that reflect the structure of the parse tree, a useful and challenging feature (especially when combined with key-based partitioning) that is central in our work. Another aspect not addressed in any of the aforementioned systems is approximate query evaluation with strong guarantees, for example approximate medians and approximate event-counting over sliding windows. Our use of synchronization elements bears resemblance to the punctuations of [36, 44], which are used to trigger the closing of windows. The setting here is much more general since we allow arbitrary regular patterns of synchronization elements.

Complex Event Processing (CEP)

The literature on CEP [20, 21, 23, 32, 33, 48, 49] is concerned with the recognition of complex patterns over streaming data. The patterns are typically given as queries that resemble regular expressions or as automata-based models. In some of these proposals a pattern can depend on the evolution of values: for example, a pattern where the price of a stock is constantly increasing. While CEP languages offer powerful event-selection capabilities, they cannot express the hierarchical computations that StreamQRE specifies.

String transformations

The language of StreamQRE is closely related to automata- and transducer-based formalisms for the manipulation of strings. There have been several recent works on the subject [10, 13, 24, 29, 35]. The current work draws especially from [11], where the language of Quantitative Regular Expressions (QREs) is proposed. It is a language based on regular expressions, intended for describing simple numerical calculations over streaming data. There are several crucial differences between [11] and the current work. The most important one is that we consider here relational structures and operations, including an explicit construct map-collect for building relations by partitioning the stream on keys and collecting the outputs of the sub-streams. The map-collect combinator presents significant new challenges, both for defining its semantics and for efficient type-checking and evaluation (Remarks 5 and 8). The lack of such a construct from the QREs of [11] implies that the benchmark queries of §5 are inexpressible. Another important technical difference between the present work and [11] is that our iteration scheme is based on list-iteration (the fold combinator), as opposed to a complicated parameter-passing scheme involving variables and algebraic terms. This makes the language much simpler and easier to use. Moreover, it enables efficient evaluation using small stacks of values, as opposed to the arithmetic terms of [11], which require some kind of compression that is dependent on the nature of the primitive operations. Using approximation, we also handle here the challenging median operation, as well as sliding-window event counting [25].

Streaming algorithms

Our work addresses issues of streaming computation that are complementary to the algorithmic questions that are tackled by the work on data stream algorithms. The seminal paper of Alon, Matias and Szegedy [8] on the streaming computation of frequency moments gave enormous momentum to the area and spawned a lot of subsequent research. See [39] for a broad exposition of the area. Of particular relevance is the work on the approximate computation of quantile queries (see [30] for a survey). The goal is to return an element of rank r, and the ε-approximation relaxation is that the algorithm is allowed to return an element of rank $\widehat{r}$ satisfying the guarantee: $r-\epsilon n\le \widehat{r}\le r+\epsilon n$, where n is the length of the stream. For our application, even if we had an element of rank r − 1 or r + 1 (exactly adjacent to r), its value could be arbitrarily far from the exact value. This means that the above approximation notion is not appropriate for our work. Instead, we want an ε-approximate answer that is guaranteed to be close in value to the exact answer. Much of the work within the streaming algorithms literature has focused on approximating specific functions in small space, whereas we investigate here is a wide class of queries with hierarchical nesting of several numerical operations, and we provide a general framework for dealing with such queries.

7. Conclusion

We have introduced the StreamQRE language, a high-level formalism for processing streaming data. Our query language integrates two paradigms for programming with streams: streaming relational languages with windowing constructs, and state-machine-based models for pattern-matching and performing sequence-aware computations. We have presented a small but powerful core language, which has a formal denotational semantics and a decidable type system. The expressiveness of the language has been illustrated by encoding common patterns and programming significant examples. A compilation procedure has been described that translates a query into a streaming algorithm with precise space and time usage guarantees. We have also shown how to incorporate efficient approximation algorithms in our framework, e.g. for computing the median of a collection of numbers and for counting the number of events occurring over large windows of time. A Java implementation of StreamQRE has been provided, and it has been evaluated using two benchmarks: Yahoo [22] and NEXMark [43].