Temporal Envelope Coding by Inferior Colliculus Neurons with Cochlear Implant Stimulation

Abstract

Modulations in temporal envelopes are a ubiquitous property of natural sounds and are especially important for hearing with cochlear implants (CIs) because these devices typically discard temporal fine structure information. With few exceptions, neural temporal envelope processing has been studied in both normal hearing (NH) and CI animals using only pure sinusoidal amplitude modulation (SAM) which poorly represents the diversity of envelope shapes contained in natural sounds because it confounds repetition rate and the width of each modulation cycle. Here, we used stimuli that allow independent manipulation of the two parameters to characterize envelope processing by inferior colliculus (IC) neurons in barbiturate-anesthetized cats with CIs. Specifically, the stimuli were amplitude modulated, high rate pulse trains, where the envelope waveform interleaved single cycles (“bursts”) of a sinusoid with silent intervals. We found that IC neurons vary widely with respect to the envelope parameters that maximize their firing rates. In general, pure SAM was a relatively ineffective stimulus. The majority of neurons (60 %) preferred a combination of short bursts and low repetition rates (long silent intervals). Others preferred low repetition rates with minimal dependence on envelope width (17 %), while the remainder responded most strongly to brief bursts with lesser sensitivity to repetition rate (23 %). A simple phenomenological model suggests that a combination of inhibitory and intrinsic cellular mechanisms suffices to account for the wide variation in optimal envelope shapes. In contrast to the strong dependence of firing rate on envelope shape, neurons tended to phase lock precisely to the envelope regardless of shape. Most neurons tended to fire specifically near the peak of the modulation cycle, with little phase dispersion within or across neurons. Such consistently precise timing degrades envelope coding compared to NH processing of real-world sounds, because it effectively eliminates spike timing as a cue to envelope shape.

Introduction

The amplitude envelopes of most natural sounds, including speech, fluctuate in time (Houtgast and Steeneken 1973; Nelken et al. 1999; Escabí et al. 2003; Singh and Theunissen 2003). Consequently, temporal envelope processing by the auditory system is important for communication in particular and environmental awareness in general. This is especially true in the context of cochlear implants (CI), whose processors encode the amplitude envelopes of sounds but generally discard temporal fine structure information.

Neural coding of temporal envelopes has been studied extensively in normal hearing animals at all levels of the auditory system (Frisina et al. 1990; Joris and Yin 1992; Eggermont 1994; Grothe 1994; Krishna and Semple 2000; Joris et al. 2004). Envelope coding is most often quantified using two metrics, the degree of spike synchrony to the envelope and overall firing rate, each measured as a function of modulation frequency (i.e., the modulation transfer function, MTF) in response to pure sinusoidal amplitude modulation (SAM) of tone or noise carriers (Joris et al. 2004).

The inferior colliculus (IC) is of particular interest because the responses of its neurons show important transformations in temporal envelope processing relative to subcollicular levels (Rees and Moller 1987; Langner and Schreiner 1988; Rees and Palmer 1989; Krishna and Semple 2000). Spike synchrony is enhanced and more sharply tuned to modulation frequency in the IC compared to lower centers. In addition, rate-tuning to modulation frequency is sharper and much more common in the IC. Cutoff modulation frequencies quantified with either metric are generally lower in the IC than in the auditory nerve and brainstem (Joris et al. 2004).

The neural representation of envelopes has also been measured in response to intracochlear electric stimulation comprising sinusoidally modulated pulse train carriers delivered to deaf animals (Snyder et al. 1995, 2000; Litvak et al. 2001; Middlebrooks 2008; Smith and Delgutte 2008; George et al. 2016). Similar to normal hearing animals, neurons in the IC of electrically stimulated animals show both good synchrony to the envelope and significant rate-tuning to modulation frequency, though band pass rate-tuning may be somewhat less prevalent compared to normal hearing (Snyder et al. 1995, 2000). Unlike normal hearing, however, IC neurons in electrically stimulated animals often respond only to the onset of unmodulated carriers, specifically high-rate pulse trains similar to those used in clinical CI processors (Snyder et al. 2000; Smith and Delgutte 2008; Hancock et al. 2012; Chung et al. 2014). Many IC neurons, especially in anesthetized preparations, discharge at the onset of such stimuli and are thereafter completely adapted; amplitude modulation of some kind is essential to elicit ongoing firing in these neurons.

Despite the usefulness of SAM in revealing the emergence of parallel synchrony and rate codes for modulation frequency in the IC, this modulation waveform is limited because the duration of each envelope cycle covaries with the modulation frequency. The inability to separate the shape of the envelope per se from the repetition rate renders SAM a poor model for the diversity of envelopes contained in natural stimuli. For example, natural stimuli typically have broadband modulation spectra and often contain significant periods of silence (Singh and Theunissen 2003), a feature not present in SAM.

Stimulation with SAM in normal hearing animals fails to capture nonlinearities in the responses of IC neurons, such as asymmetries in the response to rising and falling phases of the envelope (Møller and Rees 1986). As a result, MTFs computed from responses to SAM do not accurately predict responses to stimuli with more complex envelopes, including speech and reverberation (Delgutte et al. 1998; Slama and Delgutte 2015). Moreover, MTFs measured using SAM differ significantly from MTFs measured using short sound bursts separated by periods of silence (Sinex et al. 2002; Krebs et al. 2008; Zheng and Escabí 2008). Neural sensitivity to other stimulus parameters, such as interaural time differences, also depends on envelope shape and in general cannot be predicted from SAM responses alone (Dietz et al. 2016).

In contrast to normal hearing, there are as yet no data describing the response of IC neurons to CI stimulation using modulation waveforms other than SAM. In particular, the envelope shapes and modulation rates capable of evoking ongoing firing in IC neurons have not been characterized. Nor has the dependence of synchrony on modulation parameters been studied. In practice, these issues bear on the kinds of envelope fluctuations in natural sounds that can be represented with fidelity in the brain in response to CI stimulation.

Here, we used modulation waveforms that allow independent manipulation of the envelope cycle duration and repetition rate to study temporal envelope coding in the IC of anesthetized, acutely-deafened cats with CIs. SAM generally elicited weak responses, and significant silent periods were required to produce ongoing firing. Synchrony to the modulation waveforms was generally quite high and did not vary with modulation parameters to the same extent as comparable responses to acoustic stimulation in normal hearing animals. A simple phenomenological model suggested that differing contributions of inhibitory inputs and excitatory properties may underlie the wide variation across neurons with respect to the most effective envelope parameters.

Methods

Experiments were performed on six anesthetized adult cats (five male and one female, aged 4.5–9 months), who received cochlear implants bilaterally at the time of experimentation. All procedures were approved by the Massachusetts Eye and Ear animal care and use committee.

Deafening Procedures

About 1 week before each experiment, cats were deafened by injection of kanamycin (300 mg/kg, s.c.) and ethacrynic acid (25 mg/kg, i.v.) while under ketamine anesthesia (33 mg/kg, i.m.) (Xu et al. 1993). In four cats, hearing loss was confirmed at the time of the experiment by the absence of click-evoked auditory brainstem responses (ABRs) for intensities up to 100 dB SPL (see Hancock et al. 2010 for ABR methods). In two animals, ABR data showed incomplete deafening. A second administration of ototoxic drugs was made in one case, with deafening confirmed a few hours later. In the other case, no second injection was made, but distilled water was injected into each cochlea at the time of implantation to evoke deafness through hypotonic stress (Ebert et al. 2004). This, in conjunction with the trauma associated with the implantation itself, resulted in a 50–70 dB increase in click-evoked thresholds after ~7 h. The data obtained from this animal were neither qualitatively nor quantitatively different from the others and so are included here.

Surgery and Cochlear Implantation

For electrophysiological recordings, all surgical and experimental procedures were performed under anesthesia induced by separate injections of Nembutal (37 mg/kg, i.p.) and urethane (300 mg/kg, i.p.). Supplemental doses (~10 % of initial dose) were given as needed to maintain areflexia to strong toe pinches. Dexamethasone (0.2 ml, i.m.) was given every 4 h to minimize brain swelling. The trachea was cannulated to maintain airway patency, and body temperature was maintained at 37 °C using a feedback-controlled heating blanket. Heart rate, respiration rate, and expired CO₂ were monitored continuously throughout the experiment. The typical experiment duration was 3–4 days.

The lateral and dorsal aspects of the skull were exposed by reflecting the overlying tissue, and the pinnae were transected to facilitate placement of closed acoustic systems for measuring acoustic ABRs. On each side, the tympanic bulla was opened, and a cochlear implant with eight contacts (Cochlear Ltd., Z60274 or HL8, 0.75 mm spacing between contacts) was inserted through a small cochleostomy near the round window. An opening was made in the skull; then, the dorsal surface of the IC was exposed by aspirating the overlying occipital cortex and removing a portion of the bony tentorium.

Stimuli

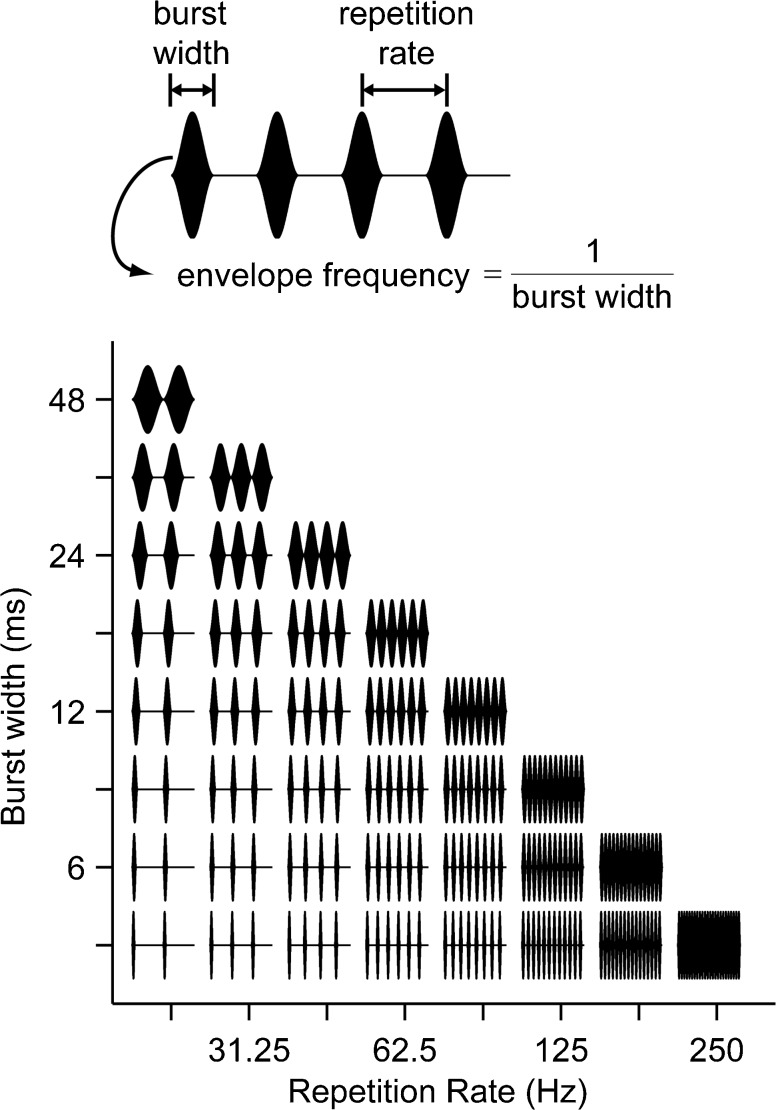
The main stimulus set comprised a family of amplitude-modulated, high-rate (1000 pulses/s) pulse trains (cathodic-leading biphasic pulses, 50 μs/phase). The envelope waveform interleaved single cycles of a sinusoid with silent intervals (Fig. 1a). Both the duration (“width”) of each sinusoidal modulation burst and the repetition rate of the modulation bursts were systematically varied (Fig. 1b, range: from 20 to 250 Hz for rate and from 4 to 48 ms for width). Conventional sinusoidal amplitude modulation corresponds to the diagonal in Fig. 1b, where the burst width is the reciprocal of the repetition rate. Stimuli were 288 ms in duration (giving 6 modulation cycles at the lowest rate) and were presented once every 600 ms. The phase of the carrier was constant with respect to the envelope for all stimulus presentations. About half of the neurons were also stimulated with low-rate, unmodulated pulse trains for which the pulse rates were varied over the same range as the repetition rates of modulated stimuli, and the timing parameters were identical.

FIG. 1.

Stimuli were amplitude-modulated trains of biphasic pulses. Individual pulses cannot be resolved because of the high carrier rate (1000 pps). Top, envelopes comprised single cycles of sinusoidal modulation interleaved with silent intervals. Bottom, envelope burst width and modulation rate were independently varied as shown in the grid. For clarity, the first 96 ms of each waveform is shown; actual stimulus duration was 288 ms.

The stimuli were digitally synthesized at a sampling rate of 100 kHz, generated using 16-bit D/A converters (National Instruments PXI-6221), and delivered to each cochlear implant through a pair of custom built, wide-bandwidth, isolated current sources. Stimulation was between the most apical and most basal intracochlear electrodes in the array (separation = 5.25 mm). This wide bipolar electrode configuration allows stimulation of auditory-nerve fibers innervating the entire length of the cochlea while minimizing stimulus artifacts as compared to monopolar stimulation (Litvak et al. 2001).

Single-Unit Recording

Recordings were made from well-isolated single units using 16-site silicon electrode arrays (Neuronexus, 177-μm² sites, 150-μm separation). The electrode was advanced dorsoventrally into the IC to a maximum depth of 4.5 mm. Electrode signals were acquired with a unity gain headstage (Plexon HST/16o50), then filtered (100–8000 Hz), and amplified (×1000) using an analog amplifier (Plexon PBX2). The recording was typically made differentially between adjacent electrodes in the array in order to minimize the amplitudes of stimulus artifacts and local field potentials. The conditioned signals were sampled at 100 kHz using a high-speed A/D converter (National Instruments PXI-6123).

Artifact cancelation and spike detection were performed online using custom software. Stimulus artifacts were canceled using a gate-and-interpolate technique for artifact cancelation (Heffer and Fallon 2008); this technique makes it possible to estimate the time of threshold crossing even when the artifact gate occurs during the rising phase of a spike.

The search stimulus was a sequence of three pulses (binaural, ipsilateral, and contralateral) separated by 100 ms and presented once every 400 ms. Upon isolating a single unit, we first measured thresholds for each of the three pulses by increasing the level in 1-dB steps and presenting 10 stimulus repetitions at each level.

Neural sensitivity to envelope parameters was then characterized by presenting bilaterally 10 repetitions of each stimulus waveform illustrated in Figure 1. The stimulus level was typically 1–5 dB above the binaural single-pulse threshold, and burst width and repetition rate were randomly interleaved across stimulus presentations.

Responses to SAM Tones in the IC of NH Animals

We compared the phase locking produced in IC neurons by CI stimulation to the phase locking produced by SAM tones in NH animals. The methods were similar between the CI and NH experiments, except for the few exceptions noted below. Neural recordings were made from 10 cats anesthetized with Dial-in-urethane (initial dose 75 mg/kg, i.p, supplemental dose 7.5 mg/kg). The IC was accessed from the caudal direction by performing a posterior fossa craniectomy and aspirating the overlying cerebellum. The bullae were vented through 30-cm lengths of plastic tubing to maintain ambient pressure in the middle ear. Parylene-insulated tungsten electrodes were used to record neural action potentials from isolated neurons.

Acoustic stimuli were generated by a 16-bit digital-to-analog converter (Concurrent DA04H) at a sampling rate of either 20 or 50 kHz and delivered through closed acoustic assemblies driven by a headphone (Realistic 40-1377). The search stimulus was a sinusoidally amplitude-modulated (40 Hz) pure tone whose carrier frequency was swept from 0.2 to 10 kHz.

Threshold and characteristic frequency were measured for each neuron using an automated tracking procedure (Kiang et al. 1970). Binaural interactions for each neuron were assessed by turning the stimulus in each ear on and off. Subsequent measures for the neuron were made with the most responsive binaural condition (monaural or diotic).

Modulation transfer functions were measured using 100 % sinusoidally modulated tones at the neuron characteristic frequency by varying the modulation frequency from 1 to 512 Hz in octave steps. Stimuli were 20 s in duration and usually presented at 60 dB SPL with a few additional measurements made at stimulus levels ranging from 20 to 80 dB SPL.

Data Analysis

Single-Pulse Thresholds

Thresholds to binaural, ipsilateral, and contralateral single electric pulses were quantified by the minimum level of the search stimulus that evoked significantly pulse-locked firing (Hancock et al. 2012). At each level and for each of the three pulses, a peristimulus time histogram (PSTH) was computed using 0.1-ms bins. Confidence bounds were assigned to identify significant peaks in the PSTH. Specifically, synthetic random spike trains were used to generate an additional 1000 PSTHs, where the number of synthetic spikes was equal to the number of spikes in the actual neural response. The confidence bound on each bin in the neural PSTH was the 99th percentile of the synthetic PSTHs. A phase-locked response was deemed to exist when two consecutive bins of the neural PSTH exceeded the 99 % confidence bounds. Interpolation was used to find the lowest level where this criterion was met.

Mean Firing Rate Vs. Envelope Shape

Firing rate was computed as a function of envelope shape (burst width and repetition rate) by counting spikes over the 288-ms stimulus duration, excluding the first period of the repetition rate to avoid onset effects. Firing rates were normalized between the minimum and maximum rates across envelope shapes (in practice, the minimum was almost always zero) and visualized using heat maps (e.g., Fig. 2b). To improve the clarity of the visualization relative to the coarse sampling of the parameter space, the normalized firing rates were interpolated on a 4× finer scale (griddata, MATLAB). The interpolation does not change the value of the original firing rates; it serves only to guide the eye, in the same manner as the line connecting data points on a line plot.

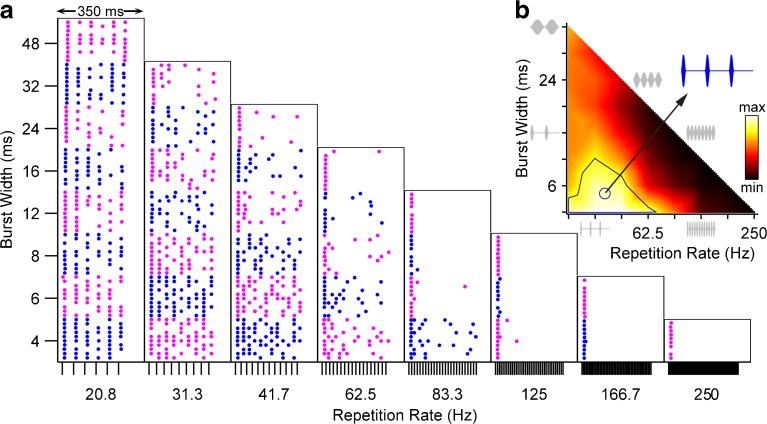
FIG. 2.

Responses of one IC neuron as a function of envelope burst width and modulation rate. a Dot rasters show spike times relative to stimulus onset. Alternating colors distinguish blocks of trials at different burst widths. Ticks at bottom of each column mark the start of each modulation cycle. b Corresponding heat map showing normalized firing rate as a function of envelope shape. Solid line: contour enclosing firing rates ≥75 % of maximum. Circle: centroid of 75 % contour. Blue inset: best envelope shape (waveform corresponding to centroid). Gray: waveforms illustrating subset of envelope shapes on perimeter of heat map.

The contour corresponding to 75 % of the maximum firing rate was computed (contour, MATLAB) and used to characterize the region of the envelope shape parameter space to which the neuron was best tuned. The burst width/repetition rate combination at the centroid of this region was taken as the “best envelope.” The centroid is a less noisy and less discretized measure of central tendency than simply taking the point with the maximum firing rate.

Clustering Analysis

The variability across neurons with respect to the most effective envelope shape was summarized by plotting best envelope shape (i.e., the centroid of each 75 % contour) in the burst width-repetition rate space. A k-means clustering analysis (kmeans, MATLAB) was applied to this scatterplot to objectively segregate neurons into groups based on most effective envelope shape. Centroids are initially grouped at random into k clusters. The k-means procedure then iteratively re-clusters the centroids to minimize the summed Euclidean distance between each centroid and its cluster centroid. The entire clustering procedure was repeated 10 times with different random initial clusters to increase the likelihood of finding the global maximum. The number of clusters k is an independent variable that was systematically varied from 1 to 10.

Phase Locking to the Envelope

Period histograms were constructed by binning neural spike times modulo the period of the envelope repetition rate. For ease of comparison, the time axes were rotated to center each envelope burst within the repetition rate cycle. We subtracted the first spike latency to a single pulse from each spike time so that the period histogram indicates more directly the phase of the envelope responsible for triggering spikes.

The first spike latency was estimated for each neuron from its responses to the search stimulus (single bilateral, contralateral, and ipsilateral pulses varied in level). Specifically, the latency was computed individually from the responses to single bilateral, contralateral, and ipsilateral pulses measured at the same levels as used to acquire the envelope shape data and the level 1 dB higher. The overall first spike latency was taken as the mean of those six latencies. In rare cases when this method did not provide a reliable estimate (11/121 units), the first spike latency was instead estimated from the envelope data set itself, specifically the response to the 4-ms burst width (shortest burst width) presented at the lowest repetition rate. In those cases, it was assumed that the first spike was elicited by the peak of the burst which occurs 2 ms after stimulus onset, and this additional delay was subtracted from the computed latency.

Phase locking was quantified using vector strength (Goldberg and Brown 1969). The preferred or “best phase” was computed as a fraction of the repetition rate period in the usual way, but then scaled relative to the burst width to allow direct comparison of response phase across envelope parameters. Thus, best phases of 0, 0.5, and 1 correspond to the beginning, peak, and end of the burst, even if the burst is followed by a silent interval. Best phases <0 or >1 indicate spikes elicited during the silent portion of the repetition rate cycle, when present.

Envelope Coding Model

A simple phenomenological model of envelope coding involving an interplay between excitation and feedforward inhibition was fit to the neural responses. It closely follows the model of Smith and Delgutte (2008) for interaural time difference coding of amplitude-modulated CI stimulation, except here it is diotic in form, rather than binaural. The model is also similar to the SFIE model of Nelson and Carney (2004) used to describe response of IC neurons to AM in NH animals. To compute model responses, a threshold was applied to the pulse train stimuli used in the experiment which were then convolved with a positive-going alpha function simulating an excitatory postsynaptic potential (EPSP) with strength α and time constant τ:

$$\mathit{\text{EPSP}}\left(t\right)={\alpha }_{\mathit{\text{EPSP}}}t{e}^{-\frac{t}{{\tau }_{\mathit{\text{EPSP}}}}}\mathrm{u}\left(t\right)$$

where u(t) is the unit step function. The threshold was fixed at −3 dB re: peak to produce stimulus levels comparable to the experimental data. Feedforward inhibition was implemented by convolving the excitatory waveform with a negative-going alpha function:

$$\mathit{\text{IPSP}}\left(t\right)=-{\alpha }_{\mathit{\text{IPSP}}}\left(t-t_d\right)e^{-\frac{t-t_d}{{\tau }_{\mathit{\text{IPSP}}}}}\mathrm{u}\left(t\right)$$

where the term t _d indicates a synaptic delay. The excitatory and inhibitory waveforms were then summed and half-wave rectified, yielding an instantaneous probability of firing which was integrated over time to compute a mean firing rate. This was repeated for every envelope in the parameter space (Fig. 1) to generate data sets in the same form as the experimental data.

The model nominally has five free parameters: α _EPSP, α _IPSP, τ _EPSP, τ _IPSP, and t _d. However, the excitatory and inhibitory strengths, α _EPSP and α _IPSP, trade directly for one another, so the excitatory strength was fixed to 1. To a lesser extent, the inhibitory strength also trades with the synaptic delay (not shown), so t _d was fixed to 1 ms. The remaining three free parameters (α _IPSP, τ _EPSP, and τ _IPSP) were fit to experimental data sets using a gradient descent algorithm (lsqcurvefit, MATLAB).

Results

A full set of responses to the complete envelope shape parameter space (Fig. 1) was obtained from 121 single neurons in the IC of 6 cats. The firing rates of most neurons were maximal for shapes containing at least some silent interval between bursts, though there was considerable variability across neurons with respect to the best envelope shape. Neural spiking tended to be precisely phase locked near the peak of the modulation burst, regardless of the envelope shape.

Dependence of Firing Rate on Envelope Shape

Figure 2 shows the responses of a representative IC neuron as a function of envelope shape. The dot rasters are arranged in parallel with the waveform diagram in Figure 1 and show the spike patterns as a function of time following stimulus onset. At low repetition rates, the spiking is well-timed with respect to the modulation cycle, producing conspicuous regular spacing of the dots in each raster. The corresponding heat map (Fig. 2b) plots the normalized firing rate as a function of envelope shape and shows that the strongest spiking is elicited by repetition rates <62.5 Hz and burst widths <12 ms. The best envelope (the centroid of the 75 %-contour: width = 5.4 ms, rate = 35.1 Hz) emphasizes that a rather long off-time between cycles is needed to maximize firing. In general, the neuron responded comparatively poorly to pure sinusoidal modulation (dark region along the diagonal) except at the lowest repetition rates. In this region, the neuron tended to fire a single spike at the onset of each stimulus presentation and was thereafter strongly adapted.

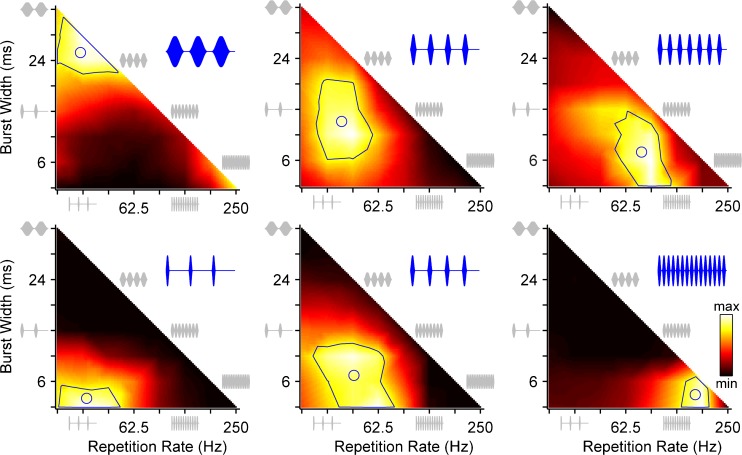
The firing rate heat maps of six additional neurons (Fig. 3) show considerable variability with respect to the envelope shape that maximized firing rate. In both rows, the preferred repetition rate increases from left to right. The neurons in the bottom row prefer shorter burst widths (longer off times).

FIG. 3.

Sensitivity of firing rate to envelope shape varies widely across IC neurons. Heat maps plot normalized firing rate as a function of envelope burst width and modulation rate for six neurons. Solid lines: contour enclosing firing rates ≥75 % of maximum. Circles: centroid of 75 % contour. Blue insets: stimulus waveform corresponding to centroid. Gray: waveforms illustrating subset of envelope shapes on perimeter of heat map.

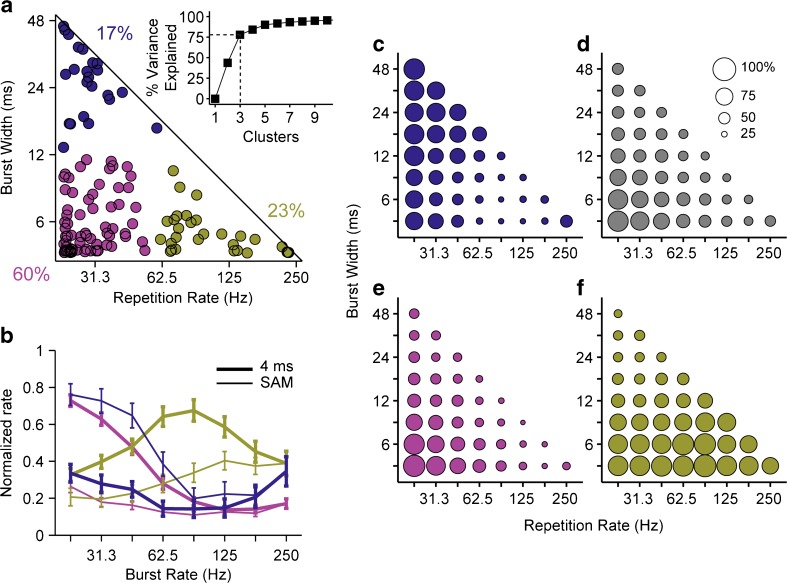
The sensitivity to envelope shape is further summarized in Figure 4. For each of the 121 neurons, the burst width and repetition rate of the “best envelope” are plotted as a point in the envelope parameter space (Fig. 4a). In general, for most parts of the envelope shape parameter space, a neuron could be found that was maximally driven there. A notable exception is the area along the diagonal (pure SAM). Few neurons were well-driven by pure SAM for repetition rates >~40 Hz; the insertion of silent time between bursts enhanced the responsiveness of the vast majority of neurons.

FIG. 4.

Sensitivity to envelope shape varies widely across IC neurons, but a majority prefers the shortest bursts and lowest modulation rates. a Scatterplot of centroids of 75 % contours from firing rate heat maps (N = 121 neurons). Colors segregate the centroids into three (k-means) clusters, which account for ~80 % of the variance (bottom). The majority of the neurons fall in the cluster preferring bursts <12 ms and rates <62.5 Hz (red). b Comparison of normalized rate modulation transfer functions across clusters shown in a, and between pure SAM (thin lines) and 4-ms bursts (thick lines). Rate is normalized for each neuron by its maximum firing rate across the entire parameter space. Curves show mean ± std. err for neurons in each cluster. c–f: Bubble plots show fraction of neurons that fire >1 spike/stimulus to each envelope shape. Colored bubbles correspond to clusters in a. Gray bubbles show data pooled across all neurons.

A k-means clustering analysis was applied to the scatter plot of Figure 4a to segregate the neurons into groups based on the best envelope shape. Three clusters form a natural breakpoint—the variance explained increases steeply (to ~80 %) up to k = 3 after which the slope clearly flattens. The majority (60 %) of the neurons fall in the cluster in the lower left of the parameter space (red), meaning they prefer both the lowest repetition rates and shortest bursts (longest off times). Neurons in the other clusters preferred either high repetition rates (lower right, green, 23 %) or more sustained bursts (upper left, blue, 17 %). We analyzed the spatial distribution of the clusters with respect to depth from the surface of the IC and with respect to medial-lateral and rostral-caudal position using penetration maps made during the experiments, but found no underlying spatial organization in any dimension.

Neurons maximally sensitive to narrow bursts and low repetition rates (Fig. 4a lower left, magenta cluster) tend to have low-pass rate MTFs in response to 4-ms bursts and very low firing rates in response to pure SAM (Fig. 4b). Neurons sensitive to wide bursts and low repetition rates (Fig. 4a upper left, blue cluster) generally respond to both pure SAM and 4-ms bursts with largely low-pass MTFs. Sometimes, these neurons show a second region of excitation at higher repetition rates, reminiscent of IC responses to pure SAM in NH animals (Krishna and Semple 2000). Finally, neurons sensitive to high repetition rates (Fig. 4a right, gold cluster) tend to have band-pass MTFs, with slightly higher best modulation frequencies but lower firing rates in response to pure SAM as compared to 4-ms bursts. Thus, with CI stimulation, only about a quarter of the neurons have bandpass rate MTFs in response to pure SAM, in contrast to NH where the majority of neurons have band-pass tuning (Langner and Schreiner 1988; Krishna and Semple 2000).

Another way to summarize the overall sensitivity of the IC to envelope shape is to compute the fraction of the neurons that respond to each envelope parameter pair (Fig. 4c–f). We counted a neuron as responsive if its average steady-state firing rate was at least 1 spike/trial. The neurons most sensitive to long bursts and low rates (Fig. 4c) also tend to respond to short bursts as long as the repetition rate is still low, indicated by the relatively large bubbles along the left edge of the triangle in Fig. 4c. These neurons are thus comparatively duration-tolerant but rate-sensitive. Conversely, the neurons most sensitive to short bursts and high rates (Fig. 4f) tend to fire at all of the tested repetition rates as long as the burst duration is short (large bubbles along the bottom edge of Fig. 4f), and in this sense are rate-tolerant but width-sensitive. Neurons in the most populous cluster (Fig. 4a, magenta cluster) tend to respond only to a combination of short bursts and low rates (Fig. 4e). The overall sensitivity to envelope shape across all IC neurons largely reflects the behavior of this largest cluster (Fig. 4d).

In summary, as a whole, IC neurons are most strongly responsive to CI stimulation when the stimulus envelope has a relatively low duty cycle (short bursts and low repetition rates). However, there is considerable variability across neurons, such that envelope shape could in principle be determined by reading out the activity of specific subsets of neurons maximally sensitive to particular envelope shapes.

Temporal Coding

The highly regular spacing apparent in the dot raster of Fig. 2 reflects strong phase locking to the envelope rate by that neuron. This is shown more directly by replotting the rasters with spike times expressed relative to the repetition rate cycle, after subtracting the first spike latency (Fig. 5a). For all envelope shapes, the spikes are tightly confined to a narrow window of the modulation cycle, especially where the spike rate was highest (lower left corner: burst width ≤ 12 ms, repetition rate ≤ 62.5 Hz). The corresponding vector strengths were near 1 (Fig. 5b); even where the spike rate was low, the vector strength was still >0.75. Modulation of high-rate pulse trains generally produced vector strengths comparable in magnitude to low-rate unmodulated pulse trains (UPT, black line).

FIG. 5.

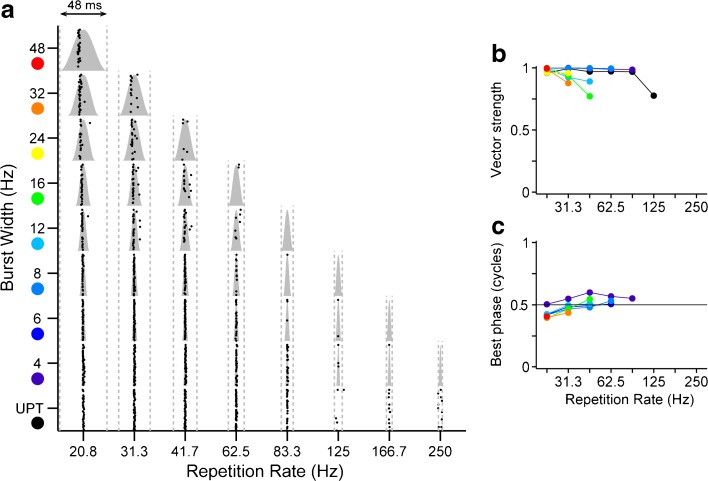
Response of one IC neuron demonstrates precise phase locking near the peak of the stimulus envelope. Same neuron as in Fig. 2. a Period dot rasters show spike times relative to modulation period. Times are shifted to position the peak of the burst in the center of the period and first spike latency is removed. Gray shading, envelope burst shape. Gray dotted lines, modulation period. b Vector strength vs. modulation rate. c Response phase relative to burst width vs. modulation rate. b, c: Colors indicate different burst widths (as shown in a). UPT low-rate unmodulated pulse train.

The first spike latency was subtracted before constructing the period histograms, so that the best phase corresponds to the portion of the modulation cycle triggering the response (see “Methods”). The best phase is just below 0.5 cycles for the neuron of Fig. 5 for all envelope shapes to which it responds (Fig. 5c), indicating that it is specifically the portion of the envelope burst just preceding the peak that tends to evoke firing.

For the neuron in Figure 5, most envelope shapes that elicited firing also produced strong phase locking, comparable in strength to that produced by low-rate unmodulated pulse trains. This was generally true of IC neurons, as shown in Figure 6a, which compares the weighted mean vector strength vs. repetition rate for two cross-sections of the envelope shape parameter space, the diagonal (pure SAM) and the base (4-ms bursts varied in rate), and for unmodulated pulse trains (UPT) at the same rates. The mean was computed by weighting the vector strength for each neuron and envelope shape by the spike count to minimize the contribution of vector strengths based on small numbers of spikes.

FIG. 6.

Electrical stimulation produces comparable phase locking between modulated high-rate pulse trains and unmodulated low-rate pulse trains and produces stronger phase locking than acoustic stimulation with pure SAM. a Firing rate-weighted mean vector strength as a function of modulation rate for all CI-stimulated neurons in this study. Red line, pure SAM stimulation (diagonal of envelope shape triangle, inset, N = 121). Blue line, narrowest burst width (4 ms, base of envelope shape triangle, N = 121). Black line, unmodulated pulse trains (N = 65). b Comparison to IC responses in NH cats using acoustic stimulation. Gray line: weighted mean vector strength combined across CI responses to pure SAM and 4-ms bursts. Thick red line: pure SAM of tone carrier (N = 92). Dotted red line: pure SAM of a noise carrier, and dotted blue line: trains of 250-μs periodic noise bursts (PNB) (N = 135, Zheng and Escabí 2013). Error bars and gray shading: 95 % confidence intervals based on bootstrap analysis.

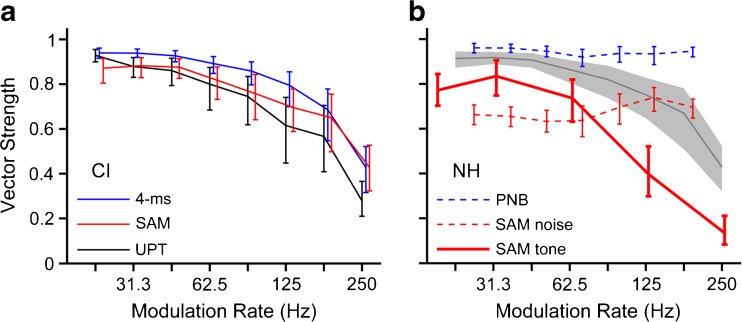
Nearly perfect phase locking was produced by the 4-ms modulated pulse trains for repetition rates up to ~80 Hz, above which rate vector strengths decreased. Phase locking followed the same trend for pure SAM and UPT. The mean vector strength for these stimuli was consistently lower as compared to the vector strength for 4-ms modulation, although there is considerable overlap in the bootstrapped confidence intervals among the three stimulus types.

Figure 6b compares phase locking to modulated CI stimulation to that obtained with modulated acoustic stimuli in anesthetized NH cats. To this end, we analyzed modulation transfer functions we previously recorded from 92 IC neurons in anesthetized NH cats using pure SAM of sinusoidal carriers. The vector strength vs. modulation rate trend for CI stimulation parallels that for pure SAM tones in NH, but the vector strengths are consistently larger in magnitude for CI stimulation (compare solid red line to shaded area in Figure 6b).

We further compared our CI results to previously published responses of IC neurons to modulated broadband noise in barbiturate-anesthetized NH cats. Specifically, Zheng and Escabí (2013) identified distinct coding schemes for envelope shape and repetition rate by comparing responses to pure SAM, for which shape and rate naturally covary, and responses to periodic trains of noise bursts, for which the shape was held constant (250-μs bursts, 50-μs rise/fall times) as the rate varied. In contrast to CI stimulation and SAM tones in NH, mean vector strength varied only modestly with modulation rate for noise carriers (Fig. 6b, dashed lines). Whereas CI stimulation produces similar phase locking between pure SAM, 4-ms bursts, and UPT, for acoustic stimulation with noise carriers, pure SAM yields significantly lower vector strengths than the narrow envelopes.

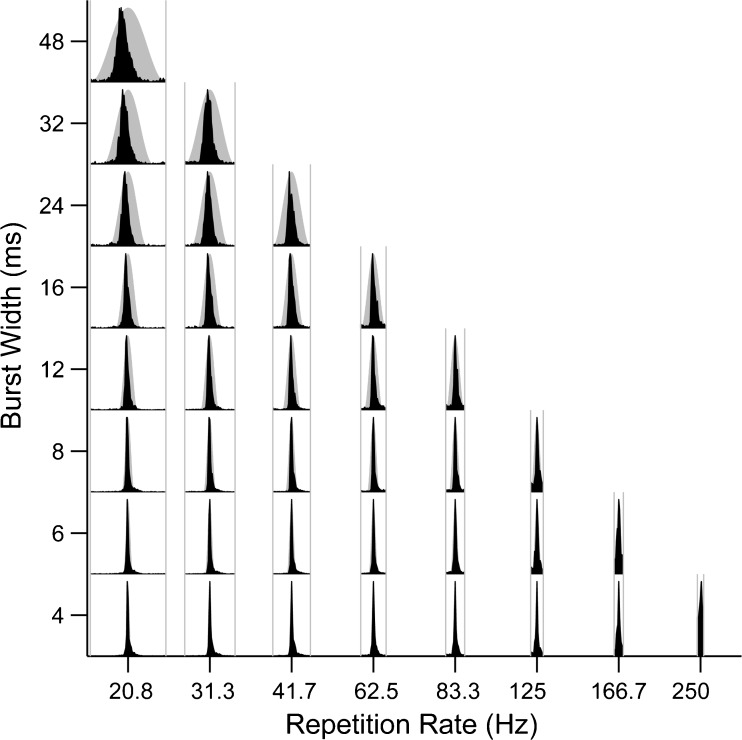
The example shown in Figure 5 is representative of IC neurons as a whole, in that they consistently showed strong phase locking and a tendency to fire near the peak of the envelope for all envelope shapes. This is illustrated in Figure 7, which shows average period histograms computed by pooling spikes across all 121 neurons. The first spike latency was subtracted from the spike times for each neuron as before. The pooled period histograms are narrow, occupying only a small fraction of the modulation cycle, even at the largest burst widths. This shows that IC neurons are not only generally strongly phase-locked to the envelope, but they also tend to respond at similar phases close to the envelope maximum.

FIG. 7.

IC neurons are strongly phase locked near the peak of the envelope in response to CI stimulation. Period histograms pooled across all IC neurons as a function of burst width and modulation rate. Gray shading, envelope burst shape. Gray lines, modulation period.

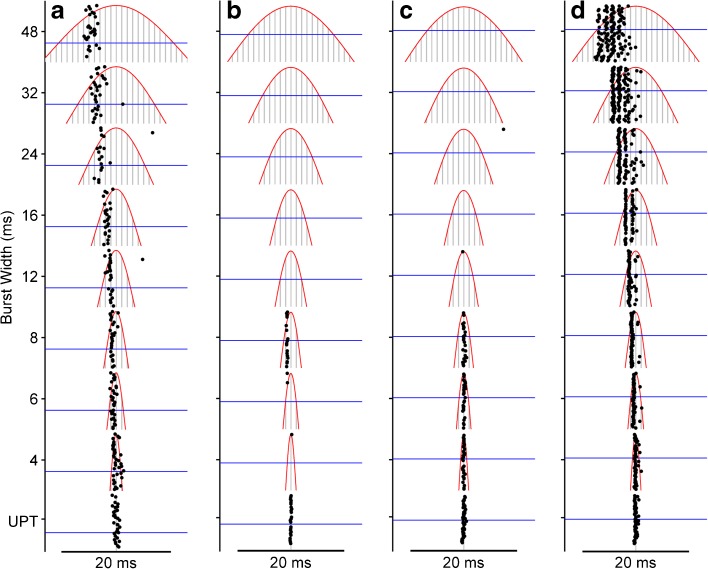
A concern is that the stimulus level in these experiments was typically within a few dB of threshold, so that a substantial portion of the stimulus waveform was below threshold. In the extreme case, if only the single electrical pulse at the peak of the envelope is suprathreshold, then there is only one point in the cycle that can elicit spikes and our findings with respect to strong phase locking have a trivial explanation. However, close inspection of the firing patterns makes it clear that the phase locking seen here is even more precise than would be expected on the basis of the relatively low stimulus levels relative to threshold. Responses of four neurons are used to illustrate this point in Figure 8. Specifically, Figure 8 shows raster plots for spike times expressed relative to the repetition rate cycle, as in Figure 5 except responses are shown only for the lowest repetition rate. Superimposed on the raster are the stimulus waveforms (gray lines) and the single-pulse threshold (blue line). The axes are scaled to focus specifically on the activity around threshold. In general, as burst width increases, more and more pulses exceed threshold. But the neuron of Figure 8a failed to respond to the first suprathreshold pulse for all burst widths ≥12 ms. Instead, it responded as many as four or five pulses later by firing only one or two spikes, and was silent thereafter. It appears that the strongly phase-locked response of this neuron results from an interaction between subthreshold pulses which elevated the threshold, delaying the onset of the spiking, followed by adaptation to the subsequent barrage of high-rate, suprathreshold pulses which prevented further spiking.

FIG. 8.

IC neurons typically respond only to select suprathreshold electrical pulses at a specific phase of the envelope burst. Period dot rasters show responses of four example neurons to the lowest repetition rate (20.8 Hz) as a function of burst width. Red lines, envelope. Gray lines, individual stimulus pulses. Axes are scaled to focus on portion of the modulation burst near single-pulse threshold (blue line). UPT: 20.8-Hz unmodulated pulse train. a Neuron consistently fires ~1 spike/burst but for the widest bursts, spikes occur several pulses after the first suprathreshold pulse. Same as neuron in Fig. 5. b, c Neurons fail to respond to any suprathreshold pulse for burst widths ≥12 ms. d Rare neuron that responds to first suprathreshold pulse at all burst widths. The response adapts such that the neuron does not respond after the peak of the modulation burst. Stimulus levels re threshold: a 4.5 dB, b 2.5 dB, c 1.8 dB, d 2 dB.

The neurons shown in Figure 8b, c are typical of the majority of neurons in this study in that they did not respond at all to the widest burst widths, despite the presence of many nominally suprathreshold pulses, indicating that the subthreshold and suprathreshold interactions are so potent as to suppress firing altogether. Figure 8b also shows effects of subthreshold interactions for short burst widths. Specifically, the unmodulated low-rate pulse train (UPT) and the high-rate pulse train modulated with a 4-ms envelope (bottom two rasters) are identical except for two additional pulses per cycle in the modulated stimulus, one on either side of the peak and 6 dB lower in amplitude (off the scale in the figure). The neuron responds strongly to the central pulse of the modulated stimulus in isolation (UPT), but the presence of just one preceding subthreshold pulse is sufficient to abolish the response almost entirely.

The vast majority of IC neurons in this study responded in the manner illustrated in Figure 8a–c, which stands in contrast to the comparatively rare example shown in Figure 8d. This neuron responds consistently to the first suprathreshold pulse at every burst width and to one or more of the following pulses. Nevertheless, there is conspicuous adaptation to the ongoing barrage of high-rate pulses. We found only two neurons that responded throughout the suprathreshold portion of the waveform.

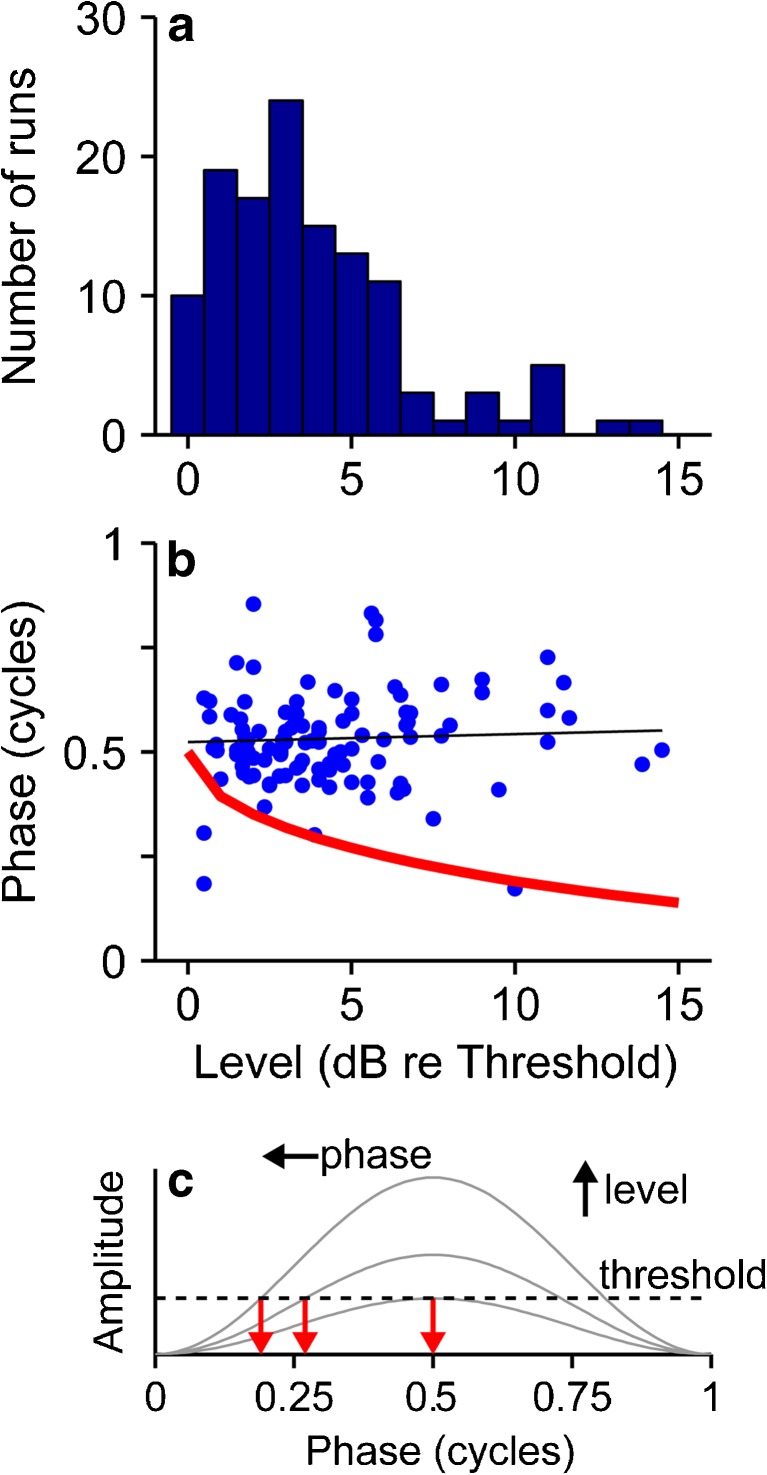
To summarize these findings across neurons, we assessed, within the limits of our data, the effect of level on sensitivity to envelope shape. Only a few neurons were tested at multiple levels, and so we compared across neurons with respect to the stimulus level re threshold of a binaural single pulse (see “Methods”). Figure 9a shows the distribution of these relative levels. The median was 3.5 dB re threshold, but there was a sufficient range to support a preliminary assessment of level effects. Figure 9b plots the best phase as a function of stimulus level re threshold. If spikes were triggered at a fixed threshold amplitude, then as level re threshold goes up, the threshold pulse amplitude would be reached earlier in the envelope burst, and the best phase would be correspondingly smaller (Fig. 9c). If anything, the data show the opposite trend, a slight increase in best phase as level increases.

FIG. 9.

Relationship between stimulus level and phase locking. a Distribution of stimulus levels (re binaural single pulse threshold) at which envelope shape characterization was performed. b Best phase (mean phase of period histogram for the shape that evoked the largest firing rate) vs. stimulus level. Red line: trend predicted if phase simply corresponds to the point in the envelope burst that equals the single pulse threshold, as illustrated in c. For a fixed threshold, as level increases, threshold is attained earlier in the burst (i.e., at a smaller phase).

Model

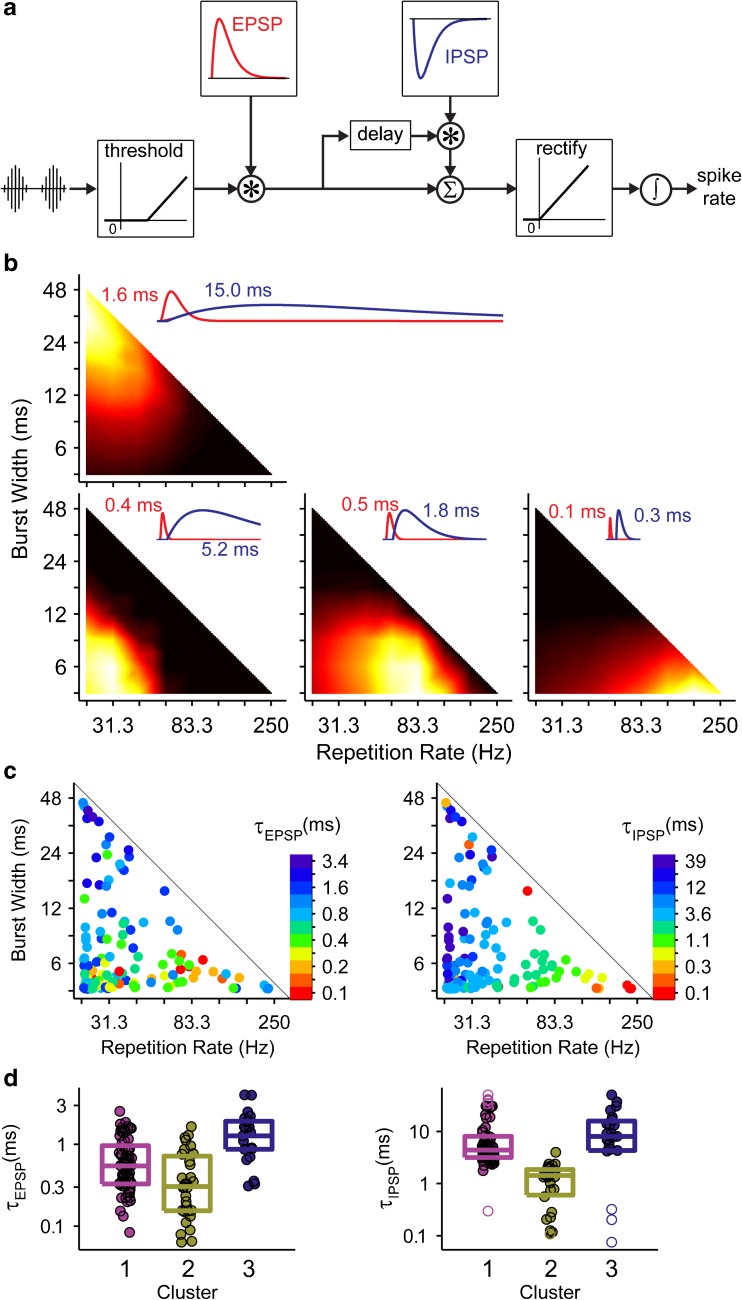
We used a phenomenological model of envelope coding with CI (Smith and Delgutte 2008) to gain insight into the basis of the diverse dependency of neural firing rate on envelope parameters. The core of the model is the summation of an excitatory potential and an inhibitory potential, where the inhibition is itself driven by the excitatory potential, after a short “synaptic” delay (Fig. 10a). The relative dynamics of excitation and inhibition determine the model sensitivity to envelope parameters. This is illustrated in Figure 10b, which shows model fits to rate responses in representative data sets whose best envelopes span the triangular envelope parameter space. These representative data sets were obtained by dividing the neurons into four clusters (instead of three as in Fig. 4) and computing the mean response of each cluster. A combination of fast excitation and fast inhibition (<1 ms each) produces strong sensitivity to short bursts and high repetition rates (lower right). At the other end of the spectrum, slow excitation (>1 ms) combined with even slower inhibition (>10 ms) produces strong sensitivity to long bursts and low repetition rates (upper left). In between, lengthening the inhibition decreases the repetition rate to which the model is most sensitive. The most commonly observed pattern (lower left) is obtained with short excitation and relatively long inhibition.

FIG. 10.

Smith and Delgutte (2008) model of envelope coding can reproduce diverse sensitivities to envelope shape. a Block diagram of model. See text for details. Asterisk convolution. sigma waveform sum. integral sum over time. b Best fit of model to four representative data sets. Data were divided into four clusters (instead of three as in Fig. 4), and the model was fit to the mean heat map in each cluster. Insets show EPSPs and IPSPs of each fit labeled with the corresponding time constant. c Model was also fit to the heat maps of every single unit. Dots are plotted at the optimal width/rate combination for each neuron. The excitatory (left) and inhibitory (right) time constants of each best fit are indicated using a log color scale. d Box plots show distributions of best-fit excitatory and inhibitory parameters for the neurons clustered as in Fig. 4. Rectangle indicates interquartile range. Center line indicates median value. Unfilled symbols indicate outliers.

Similar trends are apparent in model fits to responses of individual neurons (Fig. 10c, d). Inhibitory time constants are shortest for neurons with best envelopes in the lower right corner of the parameter space (short bursts, low rates, and cluster 2) and systematically increase moving left and up (to longer bursts and lower rates) (Kruskal-Wallis test, p = 6.99 × 10⁻¹³). The excitatory time constants are shortest along the bottom of the triangle (short bursts, clusters 1 and 2) and increase towards the top (longer bursts, cluster 3) (Kruskal-Wallis test, p = 7.09 × 10⁻⁷). In general, order of magnitude variations in both excitatory and inhibitory time constants was required to account for the diversity of best envelope parameters exhibited by IC neurons in this study.

Discussion

We recorded responses of single units in the IC of deaf cats to CI stimulation with amplitude-modulated, high-rate electric pulse trains, to better understand how complex envelope fluctuations in CI stimulation are represented in the brain. We found considerable variation across neurons with respect to the envelope shape that maximized firing rate, but most responded more strongly when there was a silent interval between modulation cycles as compared to pure SAM. Responses were precisely phase locked, regardless of envelope shape, and tended to fire at a consistent phase across neurons and envelope widths.

Effect of Modulation Shape on Firing Rate

In anesthetized animals, unmodulated CI pulse trains elicit spikes from IC neurons only at stimulus onset when delivered at high rates comparable to those used as carriers in clinical devices (~1000 pps) (Snyder et al. 1995; Smith and Delgutte 2007; Hancock et al. 2012, 2013; Chung et al. 2014). Though ongoing firing can be restored by imposing SAM on a high-rate carrier (Snyder et al. 2000; Smith and Delgutte 2008), we have shown here that pure SAM was relatively ineffective for this purpose as compared to modulation waveforms comprising shorter bursts separated by periods of silence (Fig. 4). For a majority of neurons, firing rates were maximized by bursts shorter than 12 ms delivered at rates slower than 60 Hz (Fig. 4a).

Only 62 % of IC neurons responded to pure SAM at any of the rates tested (where the existence of a response was determined using a relatively lenient criterion of 1 spike/stimulus). Previous studies using CI stimulation did not report on the incidence of IC neurons not responding to SAM in an ongoing fashion (Snyder et al. 2000; Smith and Delgutte 2008; George et al. 2016). There are several reasons why the failure rate of ~40 % seen here might not have been noted in earlier studies. George et al. (2016) primarily analyzed multiunit data which were appropriate for studying the effects of electrode configuration on envelope coding in the IC, but which necessarily mask the existence of unresponsive neurons. Smith and Delgutte (2008) used continuous “binaural beat” stimuli to characterize interaural time difference (ITD) sensitivity; consequently, they may have preferentially sampled neurons less prone to adaptation and hence more likely to respond to SAM. On the other hand, our stimulus paradigm (Fig. 1) might have exaggerated the number of neurons unresponsive to SAM, if the interleaving of more effective modulation waveforms produced a general adaptation that suppressed the responses to SAM below what would be produced by SAM stimuli presented in isolation. Nevertheless, it seems likely that the use of SAM limited previous studies to submaximal IC firing rates and may have led to oversampling the minority of neurons that respond vigorously to pure SAM (upper left cluster Fig. 4a).

In normal hearing (NH) animals, quantitative estimates of the fraction of neurons that do not respond to SAM tones range from 18 % in bat (Condon et al. 1996) to 40 % in rat (Shaddock Palombi et al. 2001). Neurons that respond poorly to SAM tones or noise consistently exhibit onset-type responses to unmodulated stimuli (Condon et al. 1996; Krishna and Semple 2000; Shaddock Palombi et al. 2001; Sinex et al. 2002).

A few studies in NH animals have sought to disambiguate the contributions of modulation burst duration and repetition rate on the responses of IC neurons (Sinex et al. 2002; Krebs et al. 2008; Zheng and Escabí 2008). Sinex et al. (2002) found that neurons giving sustained responses to unmodulated tones tended to fire at higher rates to SAM than to trains of brief tone pips at the same repetition rate, while the reverse was true for units with transient response patterns. Krebs et al. (2008) reported that IC neurons in the gerbil form discrete classes sensitive to different combinations of burst duration and repetition rate. Our results are broadly consistent with those from NH animals in that IC neurons are sensitive to modulation properties beyond just the repetition rate and differ widely with respect to the combination of parameters that maximizes firing rate. The comparatively high fraction of neurons unresponsive to pure SAM suggests the need for some silence between modulation bursts may be more acute with CI than in NH.

An important question is how other stimulus parameters interact with the dependence of firing rate on modulation waveform. For example, there is current interest in improving perceptual interaural time difference (ITD) sensitivity in CI users by enhancing appropriate features of the envelope (Smith 2010; Klein-Hennig et al. 2011; Laback et al. 2011; Noel and Eddington 2013). Neural envelope ITD sensitivity in NH animals depends on envelope shape in a manner that varies across classes of neurons with different response properties (D’Angelo et al. 2003; Sterbing et al. 2003; Dietz et al. 2016). While Smith and Delgutte (2008) showed that ITD sensitivity of IC neurons with CI stimulation is greater when the ITD is applied to the carrier rather than the envelope of SAM stimuli (for the half of their sample sensitive to both carrier and envelope ITD), they did not explore the effects of other modulation shapes.

Effect of Modulation Waveform on Temporal Coding

We found that IC neurons fire consistently and precisely (vector strengths typically >0.9) at specific phases of the envelope, usually near the peak. Similarly, auditory nerve fibers show phase locking to both sinusoidal and pulsatile intracochlear electrical stimulation (van den Honert and Stypulkowski 1987; Dynes and Delgutte 1992). The strength of phase locking in IC is only slightly greater for short envelope bursts compared to pure SAM and low-rate unmodulated pulse trains. Phase locking degrades with increasing repetition rate in a manner that parallels the response to SAM tones in NH animals. While vector strengths appear to be larger for CI stimulation than in NH, it is not clear to what extent the stimulus levels are comparable between the two conditions.

In contrast, IC neurons in NH animals respond to SAM noise with greater phase dispersion (lower vector strengths) and, as compared to CI stimulation, a much greater difference in phase locking strength between pure SAM and narrow modulation bursts (Zheng and Escabí 2013). That the phase locking trend with CI stimulation tends to parallel SAM tones in NH is perhaps unsurprising, because in each case, the carrier is temporally regular, whereas fluctuations in the fine structure of noise carriers would tend to degrade temporal precision (Zheng and Escabí 2013). Thus, to the extent that real-world sounds have temporally fluctuating fine structure, the superior temporal precision produced by CI stimulation represents a degradation of neural envelope coding because it minimizes the difference in the temporal patterns evoked by envelopes with different cycle durations but similar repetition rates, effectively leaving firing rate as the only means of encoding envelope cycle duration. In NH animals, the repetition rate and burst shape of modulated noise stimuli are to a large extent separately encoded by variations in firing rate and temporal pattern, respectively (Zheng and Escabí 2013).

Such consistently high temporal precision may underlie the finding that envelope sharpening does not improve modulation rate discrimination in CI subjects (Landsberger 2008; Kreft et al. 2010). In NH listeners, sharpening the envelope of high-frequency carriers improves performance compared to pure SAM on tasks involving temporal processing, including ITD discrimination (Bernstein and Trahiotis 2002) and pitch discrimination (Oxenham et al. 2004). On this basis, Kreft et al. (2010) hypothesized that half-wave rectified sinusoidal modulation would produce finer temporal information compared to SAM and improve discrimination of modulation rate in CI listeners, but in fact found no difference between the two envelope types. Our results suggest that this occurs because phase locking is already nearly maximal for SAM stimuli and can be little improved by sharpening the envelope.

On the other hand, Noel and Eddington (2013), using envelope shapes similar to those used here (Fig. 1), showed that ITD thresholds in CI subjects decrease as burst duration decreases but are relatively constant across repetition rates, which would seem to require some variation in timing information with envelope shape. ITD coding occurs at an earlier stage than the IC and so it is not clear to what extent it is shaped by the effects described here for IC neurons. More work is needed to better understand how envelope shape affects neural ITD coding.

Interestingly, a recent study has shown that while NH listeners are most sensitive to ITD during the rising phase of a modulated stimulus, CI listeners are maximally sensitive at the peak of the modulation (Hu et al. 2017). This is broadly consistent with our finding that IC neurons also tend to phase lock to CI stimulation near the peak of the modulation burst.

Overall, the lack of variation in temporal patterns within and across neurons represents a diminished ability to encode stimulus properties using timing information and underscores the potential utility of a mechanism for producing phase dispersion with CI stimulation. It is unclear what form such a mechanism might take, as simply desynchronizing auditory nerve fibers using high-rate pulse trains (Rubinstein et al. 1999; Litvak et al. 2003a,b) has so far not led to improvements in performance by CI users (Galvin and Fu 2005).

Mechanisms

We used a simple excitatory-inhibitory model (Nelson and Carney 2004; Smith and Delgutte 2008) to replicate the wide variation across neurons with respect to the modulation parameters that maximized firing rate (Fig. 10). The model had three free parameters: the excitatory and inhibitory time constants and the relative amplitude of the two “synaptic potentials.” The inhibitory time constant was the most important parameter, varying by nearly two orders of magnitude across the optimal modulation shapes (Fig. 10c). This extreme range of values suggests that synaptic inhibition is unlikely to be the sole underlying mechanism. However, this component of the model can more generally represent any mechanism that tends to hyperpolarize the membrane potential, such as the effects of membrane conductances. For example, the neurons most sensitive to short bursts and high rates (Fig. 4a, lower right corner) are characterized by very brief inhibition and excitation. Such fast dynamics could include low-threshold potassium conductances, which are expressed at every level of the auditory brainstem, including the IC (Sivaramakrishnan and Oliver 2001) and which might underlie the recovery from adaptation associated with jittering inter-pulse intervals in high-rate CI stimulation (Hancock et al. 2012).

At the other extreme, neurons most sensitive to long bursts and low rates (Fig. 4a, upper left corner) are characterized by very long “inhibitory” time constants (~50 ms). Suppression on this time scale is consistent with the slow after hyperpolarizations exhibited by many IC neurons (Sivaramakrishnan and Oliver 2001). Similar properties were previously used to model the directional sensitivity of IC neurons to time-varying ITDs (Cai et al. 1998).

Between these extremes lie the majority of IC neurons whose firing rates are maximized by a combination of short bursts and low rates (Fig. 4a, lower left corner). In the model, these responses comprise a heterogeneous mixture of inhibitory time constants, suggesting that they may arise from multiple mechanisms.

The variability in optimal envelope shape shown in Fig. 4a may thus represent the relative contributions of inhibitory inputs, intrinsic cellular mechanisms, and other forms of neural modulation. One broad class of neurons, putatively dominated by fast effects resembling those of low-threshold potassium currents, prefers short bursts but is relatively rate-tolerant (Fig. 4f). Another, putatively dominated by slow hyperpolarizing effects, prefers low rates but is relatively tolerant to burst width (Fig. 4c). The majority of neurons, perhaps subject to multiple mechanisms, is sensitive to both burst width and rate (Fig. 4e).

The contribution of distinct mechanisms to differential sensitivity to envelope burst width and rate is consistent both with the correlation between temporal response patterns and sensitivity to envelope shape observed in NH animals (Sinex et al. 2002; Krebs et al. 2008) and with model results demonstrating a correlation between inferred neural circuitry and the dependence of ITD sensitivity on envelope shape (Dietz et al. 2016). A shift in the balance of excitatory and inhibitory gain has been implicated in age-related changes in the coding of modulation rate and envelope shape in rats (Herrmann et al. 2016).

CI processing strategies involving envelope enhancement, for example to improve ITD sensitivity, may preferentially activate neurons dominated by one particular mechanism, which in turn may not be well-suited for transmitting other important stimulus properties, such as speech envelopes. Further study is required to fully characterize the coding capabilities of neurons sensitive to different envelope shapes.

Limitations

The distribution of optimal burst width/repetition rate combinations summarized in Figure 4 is limited by two factors. First, compared to unanesthetized preparations, barbiturate anesthesia significantly lowers the range of pulse rates over which IC neurons show sustained responses to CI stimulation with unmodulated pulse trains (Chung et al. 2014). Thus, it seems likely that we have underestimated the maximum repetition rate to which IC neurons can respond. Second, to arrive at a stimulus paradigm of reasonable duration, we arbitrarily limited the maximum burst width to 48 ms and the minimum repetition rate to 20.83 Hz. It is likely that some of the neurons represented in the lower left of Figure 4a would have responded more strongly to even lower repetition rates.

Time considerations also precluded systematically varying other important modulation parameters, including modulation depth and stimulus level. In particular, the fact that most of the stimulus levels here were within a few dB of threshold affects the findings regarding the strength of phase locking. But as shown in Figure 8, responses are more temporally precise than can be accounted for by simple threshold effects. There appears to be a combination of subthreshold interactions and suprathreshold adaptation, between which lies a narrow window where spiking is possible. We hypothesize that raising the stimulus level may simply shift this window earlier in the envelope burst, but preserve temporally precise firing. Alternatively, given the potency of adaptation to high-rate stimulation in these neurons, raising the stimulus level might simply suppress firing altogether.

Conclusion

IC neurons vary widely with respect to the envelope parameters that maximize their firing rates. Different combinations of inhibitory and intrinsic mechanisms may determine the relative sensitivity to envelope burst duration and repetition rate. Regardless of envelope shape, phase locking is so precise and so consistent across neurons that the saliency of temporal information about envelope shape is effectively reduced compared to normal hearing. Further work is needed to characterize the interaction between envelope shape and other stimulus parameters, including ITD.

Compliance with Ethical Standards

All procedures were approved by the Massachusetts Eye and Ear animal care and use committee.

Conflict of Interest

The authors declare that they have no conflict of interest.