Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Sep 12;13(11):5697–5708. doi: 10.1021/acs.jctc.7b00706

Simulation of Reversible Protein–Protein Binding and Calculation of Binding Free Energies Using Perturbed Distance Restraints

Jan Walther Perthold 1, Chris Oostenbrink 1,*
PMCID: PMC5688412  PMID: 28898077

Abstract

graphic file with name ct-2017-00706c_0007.jpg

Virtually all biological processes depend on the interaction between proteins at some point. The correct prediction of biomolecular binding free-energies has many interesting applications in both basic and applied pharmaceutical research. While recent advances in the field of molecular dynamics (MD) simulations have proven the feasibility of the calculation of protein–protein binding free energies, the large conformational freedom of proteins and complex free energy landscapes of binding processes make such calculations a difficult task. Moreover, convergence and reversibility of resulting free-energy values remain poorly described. In this work, an easy-to-use, yet robust approach for the calculation of standard-state protein–protein binding free energies using perturbed distance restraints is described. In the binding process the conformations of the proteins were restrained, as suggested earlier. Two approaches to avoid end-state problems upon release of the conformational restraints were compared. The method was evaluated by practical application to a small model complex of ubiquitin and the very flexible ubiquitin-binding domain of human DNA polymerase ι (UBM2). All computed free energy differences were closely monitored for convergence, and the calculated binding free energies had a mean unsigned deviation of only 1.4 or 2.5 kJ·mol–1 from experimental values. Statistical error estimates were in the order of thermal noise. We conclude that the presented method has promising potential for broad applicability to quantitatively describe protein–protein and various other kinds of complex formation.

Introduction

Virtually all biological processes rely on the interaction between macromolecules at some point. While the number of experimentally determined protein structures grows rapidly, it has been proven difficult to obtain experimental structures of protein–protein complexes. Moreover, a single protein might have multiple interaction partners, which is further increasing the number of desired complex structures. In the field of drug design, the computational modeling of macromolecular interactions can give insight into the mode of action of biological therapeutics like antibodies and aid the development thereof. Methods like protein–protein docking attempt to overcome the mismatch between the number of available complex structures and single protein structures by the prediction of binding interfaces. However, the binding free energy estimates given by the scoring algorithms used in such approaches show only poor correlation with experimentally determined binding free energies.1 It is moreover noted that thermodynamic properties are intrinsically determined by ensembles of microstates and not from single structures.2 If a precise binding free energy estimate should be calculated from a complex structure by computational means, molecular dynamics (MD) simulations are the method of choice, given the efficient sampling of macromolecular phase-space. Because of the large phase-space and the possible conformational changes accompanying binding reactions, different approaches to the efficient calculation of protein–protein binding free energies have been proposed.

While more recent approaches all employ methods to enforce a reaction along a geometrical pathway of some kind, Gohlke et al. attempted more than a decade ago to calculate the binding free energies of protein–protein complexes by the difference in solvation free energy of the complex and the single proteins obtained from implicit solvent models. The binding free energy estimates obtained by this approach showed poor correlation with experimentally determined values, and error estimates were in the order of 15–25 kJ·mol–1, which might be due to rather short trajectory lengths from today’s viewpoint.3,4 At the same time, computational studies of protein–protein complexes employing nonequilibrium simulations were described.5 However, a more recent attempt to calculate binding free energies from many nonequilibrium simulations using Jarzynski’s equality6 largely overestimated the binding strengths of the modeled proteins.7 Later, stabilities of different amyloid fibers were studied employing atomistic explicit solvent MD simulations and a combination of umbrella sampling at different distances of the molecular center of masses (COMs) and the weighted histogram analysis method.8−10 Dadarlat and Skeel demonstrated the calculation of binding free energies of small proteins that were in agreement with experimental values using the same general approach and additional restraints on the relative orientation and conformations of the proteins.11 The method was later generalized by Gumbart et al., who successfully calculated the binding free energy of the Barnase-Barstar complex.12 In a different approach, restraints on the number of native contacts between proteins were applied.13 Bidirectional nonequilibrium simulations using multiple fixed steering centers have also been used to calculate protein–protein binding free energies.14 Furthermore, coarse-grained models have been employed to calculate the binding strengths of proteins from MD simulations,15,16 with a very recent proposal to rank docking structures employing umbrella sampling in combination with mean-force integration.17

While the calculation of standard-state protein–protein binding free energies that are quantitively comparable to experimentally determined values has already been demonstrated,11−14 error estimates for the computed values were either still in the order of 6–9 kJ·mol–1,11,12,14 or lacking completely.13 Moreover, it has been shown that it is important to consider the dissipation of work that leads to irreversibilities, i.e. hysteresis effects, also in equilibrium approaches like umbrella sampling.18 Closely related to the phenomenon of hysteresis is the convergence of thermodynamic properties resulting from simulations. While in general convergence relies on the sufficient sampling of phase-space, it has been shown that nonequilibrated trajectory regions can contribute to poor convergence of calculated properties,19,20 which in turn leads to hysteresis. Irreversibility, hysteresis, and convergence of the resulting binding free energy values have not been thoroughly discussed in recent literature on protein–protein binding.11−14 For sufficiently converged free-energy calculations, the accuracy will be mostly dependent on the force field used to describe the molecular interactions. However, the lack of a proper discussion of the convergence, and hence the precision of the methods, hampers a fair comparison and represents a significant drawback in recent literature.

Approach

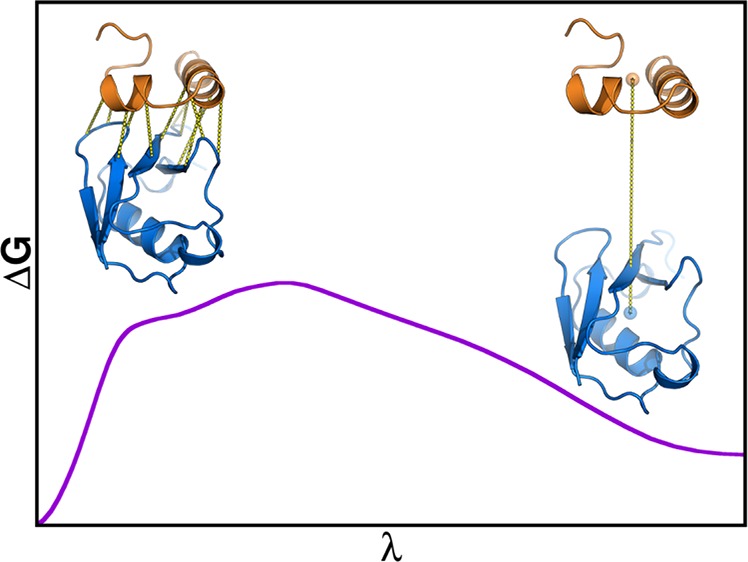
The aim of this work is to introduce a relatively simple method with broad applicability for the calculation of protein–protein binding free energies using perturbed distance restraints with special emphasis on reversibility and convergence. The general approach is similar to the work described in refs (11) and (12). The methodology will be applied to the complex of ubiquitin (UBI) and the ubiquitin-binding domain of the human DNA polymerase ι (UBM2) and of a mutant (P692A) of the latter protein. The calculation of the binding free energy was split into three different steps, as depicted in the thermodynamic cycle given in Figure 1. For the simulation of binding and unbinding (calculation of ΔGunbindres), both proteins were restrained to a bound conformation using an elastic network (EN) approach, i.e. through intramolecular Cα–Cα distance restraints. Moreover, in the bound state, additional intermolecular Cα–Cα distance restraints were used to ensure a canonical binding mode of the proteins during the simulation of binding. The intermolecular restraints were turned off during unbinding to allow free rotation of the unbound molecules. To keep the proteins in a defined volume with respect to each other and to limit sampling of phase-space in the unbound state, a single distance restraint between the COMs of both proteins was introduced during unbinding. Different approaches to restrain the proteins to bound conformations and orientations during the simulation of binding and unbinding have already been discussed in recent literature11−14 and were used to facilitate the simulation of protein binding and to shift the computationally expensive sampling of conformational changes accompanying binding reactions to separate simulations which can be performed in smaller simulation boxes. The free-energy contributions of releasing the applied ENs in the unbound state (ΔGen,1,ΔGen,2u) were calculated for each protein alone, and the contributions of releasing the ENs and the intermolecular Cα–Cα distance restraints in the bound state (ΔGen,dr) were also calculated in a separate simulation. Following the thermodynamic cycle, the binding free energy of the unrestrained proteins can be calculated according to

graphic file with name ct-2017-00706c_m001.jpg 1

To compare the resulting binding free energy with experimental values, a standard-state correction must be added. The standard-state correction terms used will be discussed in the Methods section below.

Figure 1.

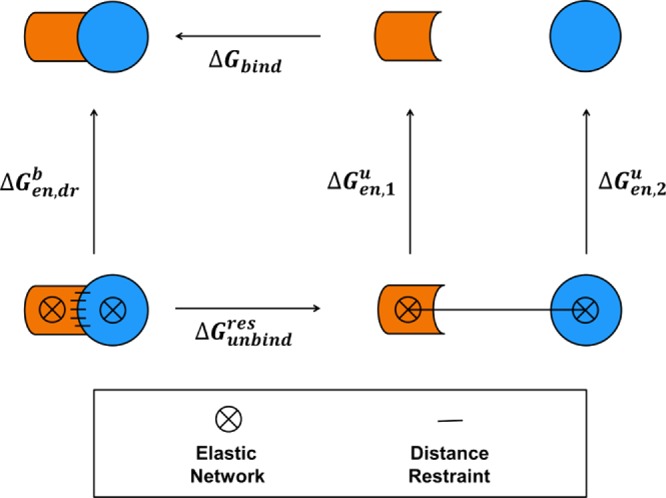
Figure 1

Open in a new tab

Thermodynamic cycle of protein–protein binding used for the calculation of the binding free energy (ΔGbind) in this work. Orange and blue cartoons represent the binding partners for which a binding free energy is calculated. Arrows indicate the direction of the considered reaction for which a free-energy difference is calculated. Restraints used to keep the molecules in a defined conformation (ENs) are indicated by circles filled with a cross. Distance restraints are indicated by black lines.

The processes for which the free-energy contributions to the binding free energy were calculated were defined using perturbed distance restraint potentials. A harmonic potential energy restraint function for a distance r with a force constant k was coupled linearly to a coupling parameter λ. The coupling parameter can take values between zero and one, thereby connecting two distinct states A and B:

graphic file with name ct-2017-00706c_m002.jpg 2

The free-energy difference for an arbitrary process involving both the modification of the force constant and the restrained distance for multiple restraining potentials can be simply obtained for such λ-coupled potentials by, for example, thermodynamic integration (TI)21 or Bennett’s acceptance ratio (BAR).22 Note that this approach differs from the more typically used umbrella sampling technique, where a potential of mean force along a (geometrical) reaction coordinate is computed.9−14,23 By using perturbed distance restraints, multiple distance restraints can be coupled elegantly to a single parameter λ. We do not unbias a set of restrained simulations but compute the free-energy difference between two end-states in which some intermolecular restraints remain and compute the free-energy contribution of the restraints explicitly. However, the introduction or complete removal of restraining potentials by setting the force constant of one end-state to zero can be problematic in practice, as sampling of (almost) unrestrained regions of the reaction coordinate will be required to cover a very large conformational space, leading to high numerical errors and uncertainties. This issue is often referred to as “end-state problem”. Approaches in which the protein conformation is restrained through alternative methods (for example RMSD restraints discussed in refs (11) and (12)) will invariably suffer from similar end-state problems. Different approaches to counteract this issue for distance restraints have been proposed in the literature, the first being so-called “hidden restraints” (HR), where the potential energy function given in eq 2 is modified with an additional prefactor including two selectable parameters n and m to smoothen the free-energy contribution near the affected end-state:24,25

graphic file with name ct-2017-00706c_m003.jpg 3

A second approach proposed very recently aims at “softening” the harmonic potential energy function toward greater distance deviations and has been shown to be efficient for the simulation of chemical bond formation and breaking.26 For this “soft-core” potential energy restraint (SCR), again a prefactor is introduced to eq 2, with a selectable parameter α, here given for a restraint that is being turned off toward state B (i.e., kB = 0):

graphic file with name ct-2017-00706c_m004.jpg 4

While turning off the intermolecular Cα–Cα distance restraints during the simulation of protein binding and unbinding (ΔGunbindres) was only performed using HR potentials, the contributions of the intermolecular Cα–Cα distance restraints in the bound state and the ENs in the bound (ΔGen,dr) and unbound (ΔGen,1u,ΔGen,2) states were both calculated using HR and SCR potential energy functions. A more detailed description of the simulation setups is given in the Methods section below.

As discussed above, the convergence of the computed free-energy values was of major importance for this work. In particular, both the forward and reverse cumulative average of the free energies over the trajectories were monitored to identify the equilibrated region of the trajectory and to increase confidence in the numerical correctness of the result.19,20

Methods

Simulation Settings

Standard-state binding free energies of a wild-type (wt) UBI domain to the wt UBM2 domain and to a mutant (P692A) UBM2 domain were calculated using the approach described above. All MD simulations were started from the first complex structure provided in the PDB entry 2KTF, which was calculated from nuclear magnetic resonance (NMR) observables.27 Despite a complex structure of wt UBI and P692A UBM2 also being available in the PDB, for simulations of P692A UBM2 the structure of the mutated domain was prepared from the wt complex structure using the mutagenesis wizard of PyMOL, given the high structural similarity to the complex of the wt proteins27 and the unequal number of residues in both structures.

Proteins were parametrized using the GROMOS 54A8 force field28 with the GROMOS++ software package29 followed by a conversion to the GROMACS topology format. All MD simulations were performed with the GROMACS 5.1.2 software package,30 which was modified to allow for the use of the HR and SCR potential energy functions given in eqs 3 and 4, respectively. After initial energy minimization for 2000 steps in vacuo using a steepest descent algorithm, proteins were solvated with SPC water31 in a 3D PBC rhombic dodecahedral box with a minimum protein-to-wall distance of 1.0 nm. Sodium and chloride ions were added to reach a concentration of 0.15 mol·L–1 and to make the system charge neutral. The ion concentration was chosen to approximately reproduce the physiological ionic strength and the ionic strength used in the experimental determination of the binding affinity in ref (47). Subsequently, systems were energy minimized again for 2000 steps using a steepest descent algorithm. For initial equilibration, random velocities from a Maxwell–Boltzmann distribution at 60 K were assigned to all atoms, and the system was simulated in a NVT ensemble using a velocity-rescaling thermostat32,33 with a relaxation time of 0.1 ps at 60 K for 20 ps. The system was then heated by increasing the temperature of the external heat bath by 60 K every 20 ps to reach a final temperature of 300 K. Initial equilibration to a constant pressure of 1 bar was then performed for 50 ps using a weak-coupling barostat32 with isotropic pressure scaling, a relaxation time of 0.5 ps, and an isothermal compressibility of 4.5·10–5 bar–1. Until this point, position restraints with force constants of 1000 kJ·mol–1·nm–2 in the x-, y-, and z-coordinates on all non-hydrogen protein atoms were used. Constant pressure equilibration was then continued for 50 ps with the same parameters but without position restraints. Production runs were performed in an NPT ensemble using a Parrinello–Rahman barostat34,35 with isotropic pressure scaling, a relaxation time of 2.0 ps, and an isothermal compressibility of 4.5·10–5 bar–1. For all MD simulations, a leapfrog integration scheme36 with a time-step of 2 fs was used, and covalent bonds were constrained to a constant distance using the LINCS algorithm.37 Neighbor searching was performed using a group-based cutoff scheme every 5 steps with a cutoff sphere of 1.4 nm. Calculation of nonbonded electrostatic and Lennard-Jones interactions was done within a cutoff sphere of 1.4 nm. For the calculation of electrostatic interactions, a reaction-field contribution38 with a relative dielectric permittivity of 6139 beyond the cutoff sphere was added.

Structures of the bound wt and P692A complexes and of the individual proteins were simulated for 30 ns in an NPT ensemble after equilibration. After 5 ns, a snapshot of the wt complex simulation was taken to define the ENs used for restraining the proteins to a bound conformation. Before the calculation of the EN, the structure was energy minimized in vacuo for 2000 steps using a steepest descent algorithm to remove possible high-energy conformations. Intramolecular harmonic EN distance restraints were defined for Cα–Cα distances between a lower cutoff of 0.4 nm and a higher cutoff of 0.9 nm with the restrained distance being the Cα–Cα distance in the energy-minimized snapshot and a force constant of 250 kJ·mol–1·nm–2. For UBI, 352 unique intramolecular distance restraints and for UBM2, 108 unique intramolecular distance restraints were formulated. While previous work focused on the tuning of EN parameters,40−42 preliminary simulations revealed that the method is relatively robust against the use of slightly different definitions of the ENs regarding the choice of the force constant and the cutoff distances. The specific intermolecular Cα–Cα distance restraints and COM–COM distance restraint in the bound state were also defined from the energy-minimized snapshot taken after 5 ns. The same distances were used for the complex of UBI with wt UBM2 and P692A UBM2. In total 12 specific intermolecular Cα–Cα distance restraints were used to defined the bound, restrained state.

For the simulation of protein binding and unbinding (ΔGunbindres), complex structures taken from the snapshots of unrestrained simulations at 5 ns were re-equilibrated in bigger simulation boxes allowing for the increase of the intermolecular distance. Minimum protein-to-wall distances were either 2.5 nm for binding and unbinding in a 3D PBC rhombic dodecahedral box (radial COM–COM distance restraint, system RS) or 1.0 nm in the x- and y-coordinates based on the dimensions of the bigger UBI protein and 2.5 nm (system ZS) or 7.5 nm (system ZL) in the z-coordinate for binding and unbinding in a 3D PBC rectangular box in which the COM–COM vector was aligned along the z-coordinate. Different box sizes for the latter were chosen to test whether the calculation of specific Cα–Cα distances in the unbound regions, where proteins can freely rotate, are prone to periodicity effects. Intramolecular EN distance restraints and specific intermolecular Cα–Cα distance restraints were already applied during equilibration. For systems ZS and ZL, additional COM–COM distance restraints to zero distance in the x- and y-components were applied with a force constant of 3000 kJ·mol–1·nm–2 to keep the COM–COM vector aligned along the z-axis. To equilibrate the different simulated λ points from the bound to the unbound state, the system was changed from λ = 0 (bound state) to λ = 1 (unbound state) in 54 unequally spaced discrete steps with a simulation time of 100 ps per λ point. The number and spacing of the used λ points (see Table S1 in the Supporting Information) was optimized in preliminary simulations to allow reversible binding and unbinding of molecules in a Hamiltonian replica exchange setup and to minimize errors during numerical TI. During unbinding, the distances of the specific intermolecular Cα–Cα distance restraints were increased linearly by a maximum of 2.5 nm in the unbound state, while the force constant was turned off from effectively 250 to 0 kJ·mol–1·nm–2 with hidden restraints parameters n = 0, m = 2, and kA = 62.5 kJ·mol–1·nm–2. The radial COM–COM distance restraint in the system RS or the COM–COM distance restraint in the z-component in the systems ZS and ZL was also increased linearly during unbinding by a maximum of 2.5 nm in the unbound state, and the force constant was increased linearly from 0 to 3000 kJ·mol–1·nm–2. The dependence of the scaling factors of the restraining potential functions on λ is given in Figure 2, and a detailed description of the intermolecular distance restraint parameters is given in Table S2 in the Supporting Information. For the simulations used for the free energy calculations, a Hamiltonian replica exchange MD (HREMD) scheme was employed to enhance sampling.48 Every 20 ps, an exchange of the coordinates and momenta of neighboring λ points was attempted. The potential energy difference of the applied λ-dependent restraints between the original and exchanged coordinates was calculated, and the exchange was accepted under the Metropolis criterion which ensures detailed balance. Simulations of all systems were performed for 50 ns per λ point.

Figure 2.

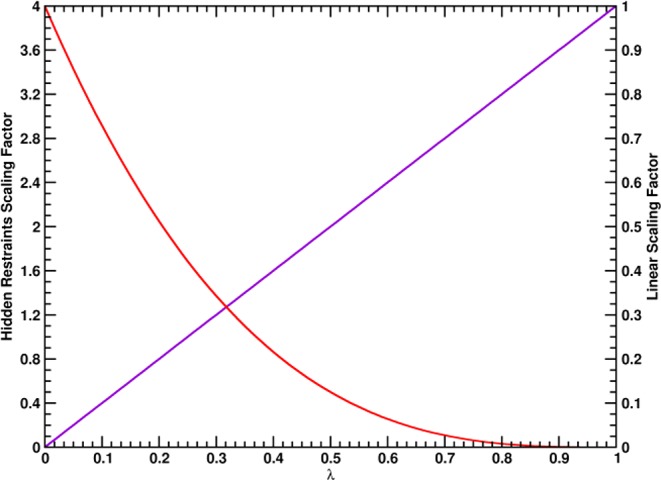
Figure 2

Open in a new tab

Scaling prefactors f(λ) for the potential energy functions of the different intermolecular distance restraints along λ used for the simulation of protein binding and unbinding. The potential energy functions used in eqs 2 and 3 are formulated as 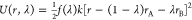Inline graphic. The scaling factor for the intermolecular Cα–Cα distance restraints are indicated with a red line (HR, f(λ) = 4(1 – λ)3) and the linear scaling factor for the radial COM–COM distance restraint or linear COM–COM distance restraint in the z-component is indicated with a violet line (f(λ) = λ).

For the calculation of the free energy contributions of the applied ENs in the unbound state (ΔGen,1u,ΔGen,2) and the ENs and the specific intermolecular Cα–Cα distance restraints in the bound state (ΔGen,drb), similar simulation setups were used. The structures of the single proteins were taken from the snapshot of the free complex simulation at 5 ns and solvated in 3D PBC rhombic dodecahedral boxes with a minimum protein-to-wall distance of 1 nm. All structures were then simulated after equilibration in an NPT ensemble without restraints for 30 ns. The Cα–Cα distance restraints were subsequently turned on from λ = 1 (unrestrained state) to λ = 0 (restrained state) in 31 equally spaced steps for 100 ps to generate the starting configurations of the λ points used in subsequent HREMD simulations for the calculation of the restraint free energy contributions. With the HR potential function given in eq 3, restraints were turned off to λ = 1 from an effective force constant of 250 kJ·mol–1·nm–2 with hidden restraints parameters n = 0, m = 2, and kA = 62.5 kJ·mol–1·nm–2. With the SCR potential energy function given in eq 4, restraints were turned off from a force constant of kA = 250 kJ·mol–1·nm–2 with a soft-core parameter α = 5 nm−2. All production simulations were performed again in a HREMD setup with a time interval between exchange attempts of 100 ps. Simulations were run for 50 ns per λ point and in selected cases continued for another 50 ns per λ point.

Standard-State Corrections

To compare binding free energies calculated according to the scheme given in Figure 1 and eq 1 with experimentally determined values, the restrained unbinding free energy (ΔGunbindres) needs to be corrected for the fact that in the unbound state, the protein molecules are not present at a standard-state concentration for solutes of 1 mol·L–1. The correction term describes the free-energy contribution of bringing one molecule from the available volume in the unbound state to the standard-state volume of V⊖ = 1.661 nm3. For a radial unbinding coordinate as used in system RS, the unbound volume is the volume of the hollow sphere given by the difference in the minimum and maximum COM–COM distance sampled in the unbound state, ru and rumax, and the correction reads

graphic file with name ct-2017-00706c_m005.jpg 5

If protein binding and unbinding is simulated only in one component of the Cartesian coordinate system (as done for systems ZS and ZL), the unbound volume is the volume of the cuboid given by the minimum and maximum COM–COM distances in the x-, y-, and z-components in the unbound state (Δrx,u, Δry,u, and Δrz,u).43 Furthermore, an additional correction term has to be introduced to account for the rotational restriction of the complex in the bound state. This term describes the change in the bound area available to the restrained and unrestrained complexes, respectively. The bound area of the restrained complex is calculated from the maximum deviations of the COM–COM restraints in the x- and y-components in the bound state (Δrx,b and Δry,b). The bound area of the unrestrained complex is calculated from the average radial COM–COM distance in the unrestrained state (Inline graphic) of the simulation used to calculate the free-energy contribution of the ENs and intermolecular distance restraints in the bound state. Note that it would also be possible to calculate the free-energy contribution of the rotational restriction from the ratio of the angular volume in the unrestrained state and the restrained (cuboid) volume in the restrained state. However, both approaches can be considered almost equivalent as in the restrained state, the protein–protein distance fluctuates mainly in the z-component, and the freedom in this dimension would approximately cancel with the freedom of the radial protein–protein distance in the unrestrained state.

graphic file with name ct-2017-00706c_m007.jpg 6

For simulation setups RS, eq 5 was used to obtain a standard-state binding free energy, and for simulation setups ZS and ZL, eq 6 was used. The standard-state binding free energy of the proteins accordingly becomes

graphic file with name ct-2017-00706c_m008.jpg 7

Trajectory Analysis and Evaluation

All free-energy differences of the processes given in Figure 1 were computed using the BAR program of the GROMACS software package. Error estimates were calculated using the same program: The trajectories were split into 5 blocks, and error estimates for the free-energy differences were calculated from standard errors of the mean of the individual free-energy differences of those blocks, which were assumed to be independent. All calculated free energies were closely monitored for convergence, i.e. the forward and reverse cumulative averages over the trajectories were calculated and compared. If both forward and reverse cumulative averages were constant and equal, the calculations were considered converged. Moreover, nonequilibrated data from the beginnings of the trajectories were discarded to improve convergence.19,20 Additionally, diffusion of the different replicas in HREMD simulations through the reaction coordinate λ was monitored as a measure for reversibility of the simulated reactions. In particular, the average number of uniquely visited λ-points per replica, the number of full-trips (all λ-points were visited at least once by one replica), and the number of round-trips (after all λ-points were visited at least once, the replica diffused to its starting λ-point again) were calculated for each trajectory. Example replica trajectories that were classified as round-trip, full-trip, or none of those are given in Figure 3.

Figure 3.

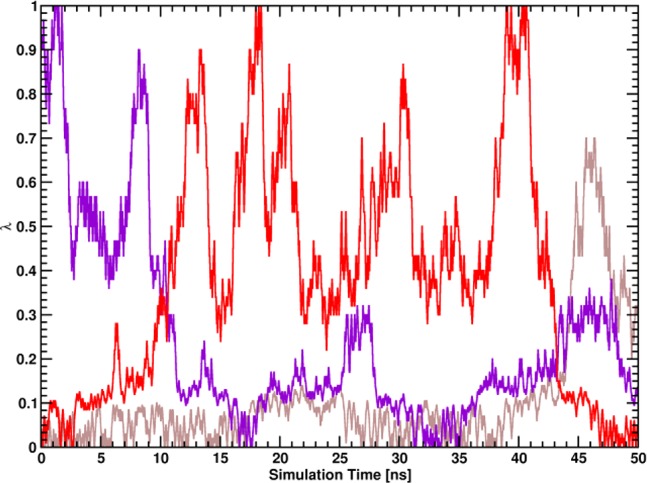
Figure 3

Open in a new tab

Examples for classifications of replica trajectories along the coupling parameter λ: round-trip (red line), full-trip (violet line), and no special classification (brown line).

For structural analysis of the generated trajectories of the bound complexes, the number of intermolecular hydrogen bonds and the buried surface area of the proteins were calculated. Hydrogen bonds were defined using a geometric criterion, with a maximum hydrogen−donor–acceptor angle of 30° and a maximum donor–acceptor distance of 0.35 nm. The buried surface area was defined by the difference in the surface area44 of both single proteins and the bound proteins. Additionally, the α-helical and β-strand secondary structure content of both the simulated bound and unbound proteins was monitored using the DSSP algorithm.45

In addition to the structural analyses described above, ensembles generated in the end-states of the simulations of both the bound and unbound wt proteins were tested for agreement with experimentally determined hydrogen–hydrogen distances using NMR nuclear Overhauser effect spectroscopy (NOESY). As many ambiguous NOE assignments were present in the available NOESY data downloaded from the PDB, ⟨r–3⟩–1/3 averaged distances from the generated trajectories were compared with experimental upper bounds for interatomic distances that were not violated in the first structure of the respective structure bundle. NOE analyses were performed both for the whole trajectories and for trajectory blocks with a length of 1 ns to investigate the time-dependence of NOE upper bound violations.

Results and Discussion

Calculation of Standard-State Binding Free Energies and Convergence

For the calculation of the unbinding free energy of the proteins restrained to their bound conformations (ΔGunbindres), the binding and unbinding process was simulated in a HREMD setup with 54 unequally spaced replicas. While the distance of all restraints was increased by up to 2.5 nm in the unbound state, specific intermolecular distance restraints, used to restrain the proteins to a canonically bound orientation in the bound state, were turned off in the unbound state (λ = 1) with hidden restraints, while a single distance restraint connecting both COMs of the proteins was turned on linearly toward the unbound state. The exact definitions of the distance restraints in the bound and unbound states are given in Table S2 in the Supporting Information, and the dependence of the scaling factors of the distance restraint potential functions on λ is given in Figure 2.

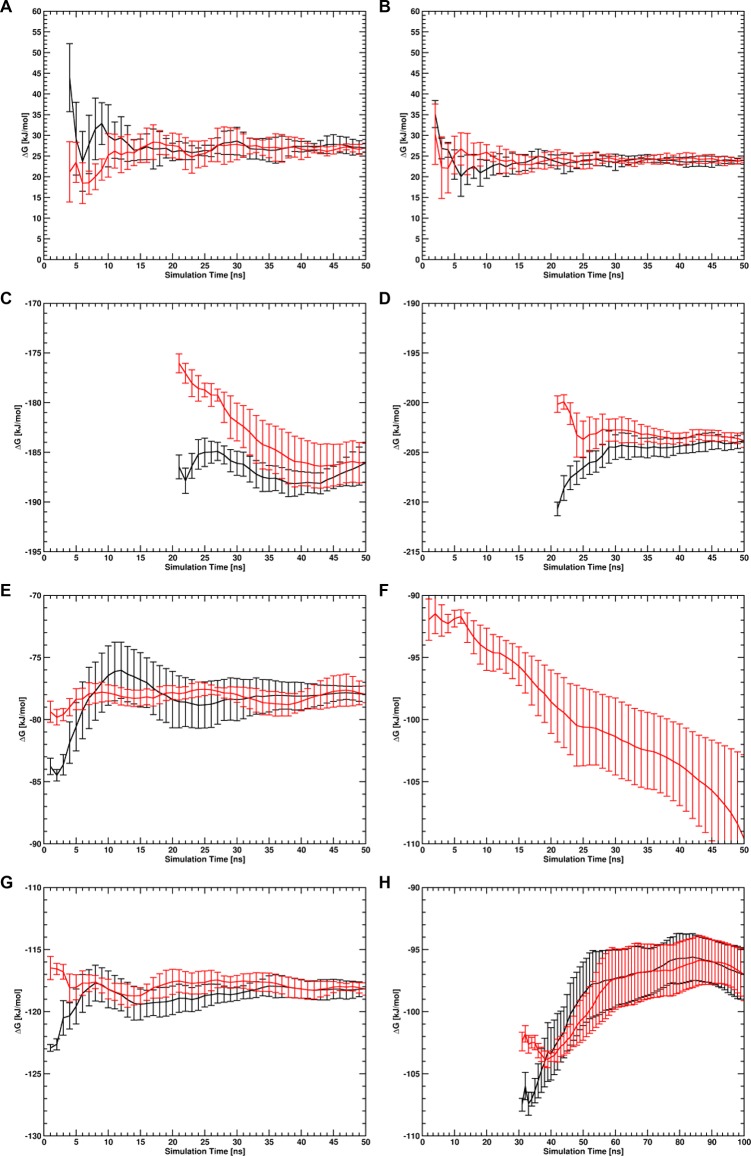
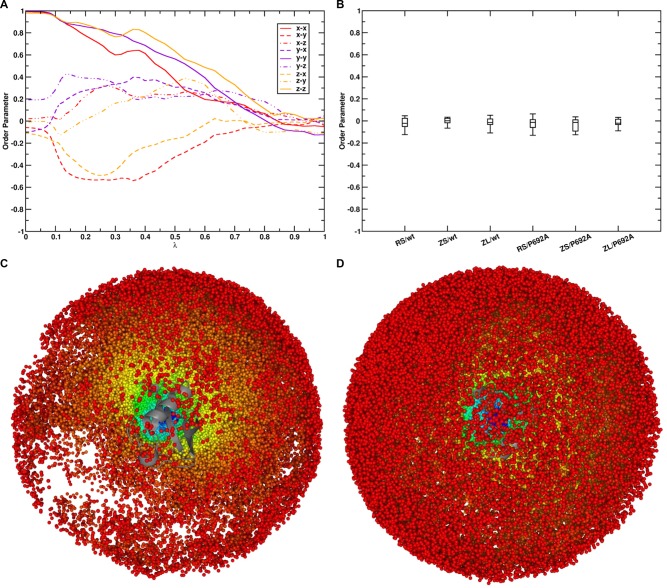
Forward and reverse cumulative averages of ΔGunbindres of both the complex involving wt UBM2 and P692A UBM2 calculated with BAR for systems RS (radial COM–COM distance restraint) are given in Figure 4 (panels A and B). It can be seen that, both for the wt complex (panel A) and the complex with P692A UBM2 (panel B), calculated ΔGunbind values converged very well within the given simulation time of 50 ns after small regions at the beginning of the free-energy trajectories were discarded as nonequilibrated region (the first 3 ns for the wt complex and the first 1 ns for the complex with P692A UBM2). Figure S2 in the Supporting Information shows the λ-dependent free energy profiles for all performed simulations. To ensure sufficient orientational sampling in the unbound state, the average order parameter ⟨cos θαβ⟩ was computed. Here, θαβ is the angle between two vectors α and β, of which three were defined in each protein to construct a system of orthogonal axes that were parallel in the two bound proteins. The computed order parameters indicated that both proteins sample random orientations with respect to each other in the unbound state, as all nine order parameters had values close to zero in the unbound state (see Figure 5, panels A and B). Also inspection of the sampled COM positions of one protein with respect to the other protein showed that both proteins sample almost the complete spherical shell around the other protein in the unbound state. The sampled relative COM positions of both UBI and wt UBM2 in the unbound state are given in Figure 5, panels C and D.

Figure 4.

Figure 4

Open in a new tab

Forward (black lines) and reverse (red lines) cumulative averages along the trajectories of the free-energy differences calculated with BAR for protein binding and unbinding (ΔGunbindres) in system RS of the wt UBM2 domain (A) and the P692A UBM2 domain (B), for the free-energy contribution of the ENs and specific intermolecular distance restraints in the bound state (ΔGen,dr) of the wt complex (C) and the complex involving P692A UBM2 (D), for the free-energy contributions of the ENs in the unbound state (ΔGen,1u,ΔGen,2) of wt UBM2 (E), P692A UBM2 up to 50 ns total simulation time (F), P692A UBM2 up to 100 ns total simulation time (H) and UBI (G). Simulations of the processes used to obtain (C–H) were performed using SCR potential energy functions. Note that in panel F the forward cumulative average falls off the scale of the plot.

Figure 5.

Figure 5

Open in a new tab

Order parameters ⟨cos θαβ⟩, where θαβ is the angle between two vectors α and β, anchored to each protein. Three orthogonal vectors were defined in each protein to construct a system of orthogonal axes that were parallel in the bound proteins. (A) shows the development of all nine order parameters along λ for the simulation of protein binding and unbinding with the wt UBM2 domain and system setup RS. (B) shows the values of the same order parameters in the unbound state (λ = 1) for all performed simulations of protein binding and unbinding. (C) COM positions of wt UBM2 sampled around UBI shown in gray cartoon representation and (D) COM positions of UBI sampled around wt UBM2 shown in gray cartoon representation in the simulation of protein binding and unbinding with the wt UBM2 domain and system setup RS. In (C) and (D), the sampled COM positions are colored according to their λ point: λ = 0 (bound state) corresponds to blue, λ = 1 (unbound state) corresponds to red.

Resulting values for ΔGunbindres for all simulated systems including setups ZS and ZL are given in Table 1 together with the standard-state corrections ΔGcorr and the resulting standard-state restrained binding free energies, ΔGbind⊖,res. The values of ΔGbind should be the same for all simulations of the wt complex or the complex involving the P692A UBM2 domain, respectively. It is noted that the same ΔGcorr⊖ values were used for systems RS and ZL or ZS, respectively, as they are expected to be the same but also expected to converge slowly, as they depend on the extreme distances sampled during the simulations. For both the wt and the P692A complex, resulting ΔGbind were within the associated error estimates, indicating that the geometry of the used simulation box and the chosen reaction coordinate has no influence on the resulting free-energy value. However, simulations with setup RS had generally lower error estimates and seemed to converge better than simulations with setups ZS or ZL. Forward and reverse cumulative averages of ΔGunbindres calculated from systems ZS and ZL are given in Figure S2 in the Supporting Information. While the difference in convergence behavior cannot be explained by a difference in replica diffusion properties (see Table 2), we suspect that the different reaction coordinate geometries (radial COM–COM distance restraint versus COM–COM distance restraint linear in the Cartesian coordinates) can lead to differently sampled binding and unbinding paths that are sampled with different efficiencies.

Table 1. Restrained Unbinding Free Energies, Standard-State Corrections, and Resulting Restrained Standard-State Binding Free Energies for wt UBM2 and P692A UBM2 Binding to UBI in Systems RS, ZS, and ZL, Respectivelya.

system ΔGunbindres ΔGcorr⊖ ΔGbind⊖,res
RS/wt 27.0 ± 1.1 –9.2 –36.2 ± 1.1
ZS/wt 27.2 ± 2.8 –5.4 –32.6 ± 2.8
ZL/wt 30.1 ± 2.1 –5.4 –35.5 ± 2.1
RS/P692A 24.0 ± 0.6 –9.2 –33.2 ± 0.6
ZS/P692A 26.2 ± 1.8 –5.4 –31.6 ± 1.8
ZL/P692A 28.5 ± 1.9 –5.4 –33.9 ± 1.9
Open in a new tab
a

All free-energy values are in kJ·mol–1.

Table 2. Number of Round-Trips, Full-Trips and Average Number of Unique λ-Point Visits of the Replica Trajectories of All Performed HREMD Simulations.

free-energy term simulation no. of round-trips no. of full-trips average unique visits
ΔGbind⊖,res RS/wt 0 4 37.1
  ZS/wt 2 12 39.9
  ZL/wt 2 11 39.1
  RS/P692A 2 15 41.8
  ZS/P692A 3 6 40.1
  ZL/P692A 0 6 39.2
ΔGen,drb complex/HR/wt 0 3 19.7
  complex/HR/P692A 0 3 21.2
  complex/SCR/wt 0 1 22.4
  complex/SCR/P692A 1 2 21.1
ΔGen,1u UBM2/HR/wt 0 3 20.0
  UBM2/HR/P692A 0 2 19.6
  UBM2/SCR/wt 0 4 24.3
  UBM2/SCR/P692A 1a 4a 22.6a
ΔGen,2u UBI/HR 12 19 27.7
  UBI/SCR 3 11 28.6
Open in a new tab
a

Total simulation time of 100 ns instead of the 50 ns considered by default.

The calculation of the free energy contributions of the applied ENs in the unbound state (ΔGen,1u,ΔGen,2) and the ENs and the specific intermolecular Cα–Cα distance restraints in the bound state (ΔGen,drb), i.e. the simulations of turning off the restraints to λ = 1, were performed either using HR or SCR potential energy functions. The processes were simulated as well using a HREMD setup, here using 31 equally spaced replicas.

Forward and reverse cumulative averages of the free-energy differences of the processes simulated with SCR potential energy functions are given in Figure 4. For both the bound wt complex (panel C) and the complex with P692A UBM2 (panel D), the first 20 ns of the trajectories were identified as nonequilibrated region and discarded. However, both calculations then converged reasonably well up to a total simulation time of 50 ns per λ-point. While for the unbound wt UBM2 domain (panel E) and unbound UBI (panel G), no data from the beginning of the trajectories were discarded and calculations converged very well, the calculation of the EN contribution in unbound P692A UBM2 did not converge within 50 ns simulation time, and no distinct equilibrated region was found (panel F). The simulation was therefore continued for another 50 ns per λ-point. From the total trajectory with a length of 100 ns, the first 30 ns were discarded as nonequilibrated region, and convergence of the calculated free-energy difference was reached (panel H).

The free energy contributions of the applied ENs in the unbound state (ΔGen,1u,ΔGen,2), the ENs and the specific intermolecular Cα–Cα distance restraints in the bound state (ΔGen,drb), and the final calculated values for the standard-state binding free energy of the unrestrained proteins (ΔGbind) are given in Table 3 for both HR and SCR potential energy functions. Calculations of the free-energy contributions performed with HR potential energy functions converged to similar values as obtained with SCR potential energy functions for the complex with wt UBM2. For the bound complex with P692A UBM2 and unbound P692A UBM2 however, calculated free-energy differences between the restrained and unrestrained state did not converge with HR, neither within a simulation of 50 ns nor within a total simulation time of 100 ns as seen from the agreement between the forward and reverse cumulative free-energy differences. Where sufficiently converged data was available, the calculated values of ΔGbind⊖ for both the complex with the wt UBM2 domain and the complex with the P692A UBM2 domain were compared to the two sets of experimental data that were available (Table 3). The agreement with the experimental data of ref (27) was excellent, with a mean unsigned error of only 1.4 kJ·mol–1 over the 9 different calculations that were converged. For 8 of these calculations, the small statistical uncertainty was larger than the deviation from the experiment, while for simulation ZS/wt with HR it was 0.3 kJ·mol–1 smaller. The agreement with experimental data reported in ref (47) was very similar, with a mean unsigned error of 2.3 kJ·mol–1 and 7 of the calculations showing a deviation from experiment that was within the statistical uncertainty. Compared to recently published calculations of protein–protein binding free energies, deviations from experimentally determined binding free energy values were comparable or lower, with previously reported errors being in the range of 2.1 to 8.4 kJ·mol–1.11−14 Moreover, our statistical uncertainties of 2.2 to 3.5 kJ·mol–1 are lower than the previously reported values of 5.9 to 8.8 kJ·mol–1.11,12,14

Table 3. All Calculated Free-Energy Contributions of Restrained Standard-State Binding (ΔGbind⊖,res), of the Applied ENs in the Unbound State (ΔGen,1,ΔGen,2u) and the ENs and the Specific Intermolecular Cα–Cα Distance Restraints in the Bound State (ΔGen,dr) to the Calculated Unrestrained Standard-State Binding Free Energy ΔGbind⊖a.

    simulation system
restraint setup free-energy term RS/wt ZS/wt ZL/wt RS/P692A ZS/P692A ZL/P692A
HR ΔGbind⊖,res –36.2 ± 1.1 –32.6 ± 2.8 –35.5 ± 2.1 –33.2 ± 0.6 –31.6 ± 1.8 –33.9 ± 1.9
HR ΔGen,drb –180.7 ± 1.5 –180.7 ± 1.5 –180.7 ± 1.5 n/a n/a n/a
  ΔGen,1u –76.5 ± 1.0 –76.5 ± 1.0 –76.5 ± 1.0 n/a n/a n/a
  ΔGen,2u –115.4 ± 0.5 –115.4 ± 0.5 –115.4 ± 0.5 –115.4 ± 0.5 –115.4 ± 0.5 –115.4 ± 0.5
  ΔGbind⊖ –25.0 ± 2.2 –21.4 ± 3.4 –24.3 ± 2.8 n/a n/a n/a
SCR ΔGen,drb –186.1 ± 2.0 –186.1 ± 2.0 –186.1 ± 2.0 –203.8 ± 0.7 –203.8 ± 0.7 –203.8 ± 0.7
  ΔGen,1u –78.0 ± 0.7 –78.0 ± 0.7 –78.0 ± 0.7 –97.0 ± 2.1b –97.0 ± 2.1b –97.0 ± 2.1b
  ΔGen,2u –118.2 ± 0.5 –118.2 ± 0.5 –118.2 ± 0.5 –118.2 ± 0.5 –118.2 ± 0.5 –118.2 ± 0.5
  ΔGbind⊖ –26.1 ± 2.4 –22.5 ± 3.5 –25.4 ± 3.0 –21.8 ± 2.3 –20.2 ± 2.9 –22.5 ± 3.0
experiment ΔGbind⊖ –25.1,(27)–28(47) –20.4,(27)–21(47)
Open in a new tab
a

Experimentally determined standard-state binding free energies are given for comparison from two different references. All free-energy values have units [kJ·mol–1].

b

Total simulation time of 100 ns instead of the 50 ns considered by default.

Structural Trajectory Analysis

Different structural analyses and tests for agreement with experimentally determined NOE distances of the ensembles generated in the simulations were performed to demonstrate the similarity of configurational ensembles generated in different simulations at the same thermodynamic state. In particular, the structural ensembles generated in free MD trajectories without applied restraints and in the unrestrained state of the simulations used to calculate the free-energy contribution of the specific intermolecular distance restraints and ENs are expected to be similar. Moreover, also the ensembles of the unbound state of the binding and unbinding simulation and the restrained state of the simulations used to calculate the free-energy contribution of the specific intermolecular distance restraints and ENs are expected to be similar for the single proteins. Where applicable, the number of intermolecular hydrogen bonds, the buried surface area, the number of NOE distance upper bound violations, and the secondary structure content of the proteins were calculated.

The results of the analyses for the bound complexes with the wt UBM2 domain or the P692A UBM2 domain are given in Table 4. It can be seen that the structural properties of the simulated complexes were similar where expected. Only the α-helical content of the wt complex in the unrestrained state of the simulation to compute ΔGen,drb seems to be somewhat reduced, compared to the other simulations. Comparable structural properties of the unbound proteins in simulations that represent the same thermodynamic states were also obtained (see Table S3 and Table S4 in the Supporting Information), except for the unrestrained wt and P692A UBM2 domains, where larger differences were present. Especially in the simulation used to calculate the free-energy contribution of the EN in the unbound state, very diverse sets of conformations of UBM2 and P692A UBM2 were sampled, and partial unfolding of the wt UBM2 and P692A domains was observed. Figure 6 depicts the number of NOE violations and secondary structure along the trajectories of unbound wt UBM2 for simulations employing SCR or HR potential energy functions. It can be seen that the number of NOE violations increases, and the secondary structure elements are highly dynamic. The α-helical secondary structure content of the protein in the unrestrained trajectory was roughly 32%, compared to a secondary structure content in the experimentally determined structure of about 59%. These findings agree with the findings of a recent computational study in which the conformational entropy of the bound and unbound UBM2 domain was calculated. The authors of this study described the unbound wt UBM2 domain to be behaving similar to an intrinsically disordered protein (IDP) in simulations with time scales of several μs.46 Moreover, in the P692A domain, the secondary structure content was even reduced to 12%. A more flexible behavior of the P692A domain could be explained by the replacement of the rigid proline in the kink between the two α-helices of UBM2 by a more flexible alanine residue. While experimentally determined structures of bound P692A UBM2 domains are very similar to the bound structures of wt UBM2,27 there is no structural data available of unbound P692A UBM2. These findings also provide a reasonable explanation for the necessity of simulating the restraining process of unbound P692A UBM2 to a bound conformation for the determination of ΔGen,1 for a longer time, as the sampling of very diverse conformations requires a longer simulation time. The difficulty of calculating ΔGen,1u for P692A UBM2 is also reflected by the fact that the restrained standard-state binding free energies ΔGbind for both the wt and the P692A UBM2 domain are very similar (the same EN was used to restrain both proteins to a bound conformation), but the unrestrained standard-state binding free energies ΔGbind⊖ are not.

Table 4. Different Structural Properties and Number of NOE Distance Upper Bound Violations of the Generated Ensembles or Experimentally Determined Structures of the Bound Complexes.

    no. of interprotein H-bonds buried surface area [nm2] no. of NOE violations > 0.0 nm/> 0.3 nm % DSSP α-helix/β-sheet
wt complex straight MD 7.4 13.8 245/9 26.1/20.9
  bound, unrestrained 6.4 11.7 299/22 22.7/21.0
  bound, restrained 4.6 13.4 353/36 27.6/20.7
  bound, binding (restrained) 5.2 11.9 367/42 27.8/20.6
  experimental bundle (PDB-ID 2KTF) 3.5 15.5 4/0 29.3/23.8
P692A straight MD 7.6 12.1 n/a 24.6/20.7
complex bound, unrestrained 8.6 12.9 n/a 24.3/20.7
  bound, restrained 5.7 12.2 n/a 27.1/20.6
  bound, binding (restrained) 4.9 11.7 n/a 27.4/20.7
  experimental bundle (PDB-ID 2L0F) 4.0a 14.2a n/a 29.5/23.2a
Open in a new tab
a

As experimental structures contained additional N- and C-terminal residues in P692A UBM2 that were not simulated but were expected to influence the calculated properties, additional residues were removed prior to analysis.

Figure 6.

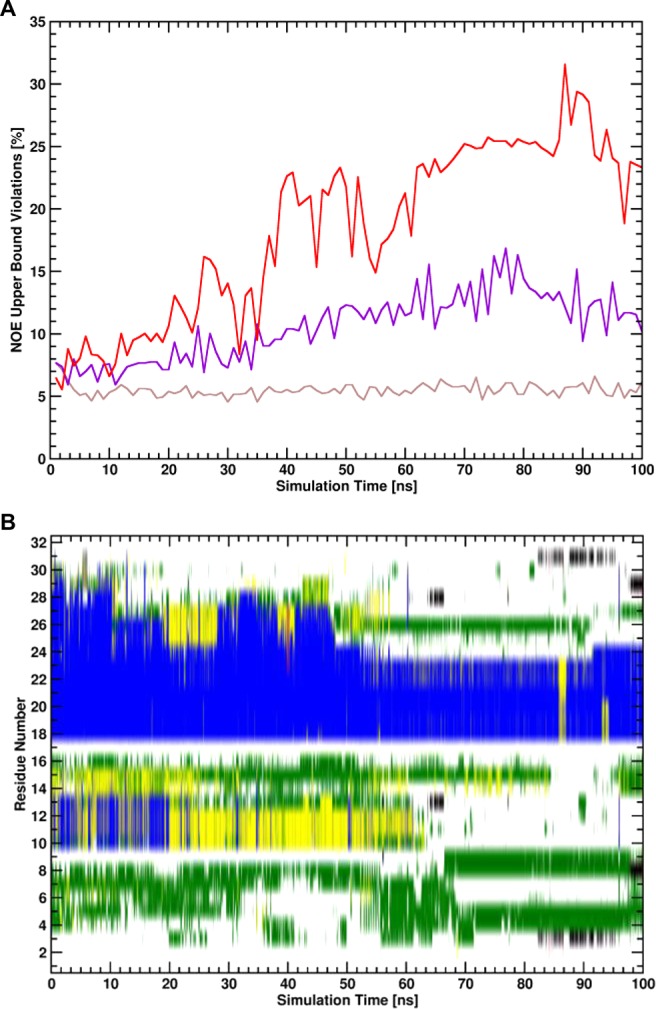
Figure 6

Open in a new tab

(A) Percentages of NOE upper bound violations of structural ensembles of trajectory windows with a simulation length of 1 ns for the unrestrained state of unbound wt UBM2 of the simulation employing SCR potential functions (red line), for the unrestrained state of unbound wt UBM2 of the simulation employing HR potential functions (violet line), and the restrained state of unbound wt UBM2 of the simulation employing SCR potential functions (brown line). (B) Secondary structure trajectory (blue: α-helical, red: β-strand, yellow: turn, green: bend, black: β-bridge, gray: 3-helix, white: coil) calculated with the DSSP algorithm45 for the unrestrained state of unbound wt UBM2 of the simulation employing SCR potential functions.

Continuation of Restraining Simulations up to 100 ns

Because a total simulation time of 100 ns was necessary to reach convergence of the calculation of the free-energy contribution of the EN of P692A UBM2 in the unbound state, also all other simulations were continued for another 50 ns up to a total simulation time of 100 ns. The forward and reverse free-energy cumulative averages of the continued simulations employing SCR potential energy functions are given in Figure S3 in the Supporting Information. While the free-energy contributions of the restraints remained constant and converged for the unbound proteins, the calculated free-energy values diverged for both the wt complex and the complex involving the P692A UBM2 domain. The effect of nonconverged calculated free-energy differences was even more pronounced for the simulation of the wt complex with the HR potential energy function (see Figure S4 in the Supporting Information). For this simulation, an obvious shift of the UBM2 domain to a noncanonically bound orientation was observed (panel D in Figure S4). It is noted that unbinding of the proteins in the unrestrained state of the simulation is allowed, since the proteins are free to sample the entire available phase-space and may even be expected to do so for a process with a binding free energy of approximately 10 kT, as the probability ratio of the bound to the unbound state is 2.2·104. However, an ensemble in which the unrestrained proteins unbind is not desired, as the thermodynamic cycle requires the proteins to remain in the bound state. Clearly, any method that (correctly) includes extensive simulations of the unrestrained state runs the risk of observing deviations from a defined bound state. Therefore, only the trajectories up to a total simulation length of 50 ns were used for the calculation of ΔGen,drb.

Comparison of SCR and HR Potential Energy Functions

The calculation of the free-energy contributions of the specific intermolecular distance restraints and the ENs in the bound state (ΔGen,drb) and the ENs in the unbound states (ΔGen,1 and ΔGen,2u) were performed both with SCR and HR potential energy functions. As already mentioned previously, the calculation of the contributions of the restraints for the bound complex with P692A UBM2 and unbound P692A UBM2 did not converge for simulations employing HR potential energy functions. In contrast, it was possible to calculate ΔGen,dr and ΔGen,1u for P692A UBM2 using SCR potential energy functions.

The difference in convergence behavior can possibly be explained by the nature of the “soft” potential energy function of the SCR. As discussed above, the unbound UBM2 domains sample a very diverse set of conformations in the unbound and unrestrained state, similar to the behavior of an IDP. Hence, it can be expected that the intramolecular distances sampled in the trajectories are very diverse and the distributions of the distances difficult to converge. In BAR or TI however, restrained energies (or derivatives) are computed from the unrestrained snapshots, leading to noise in the calculations. In contrast to the HR potential energy function, different intramolecular distances will lead to the same restrained potential energy if distance deviations are large if the SCR potential energy function is used. The SCR potential energy function therefore makes the calculation of the EN free-energy contribution easier, as sampling of the completely unrestrained state is less important for the calculation of the free-energy contribution. The diversity in the structural ensembles for wt UBM2 is shown in Figure 6. While the structural ensemble of unbound UBM2 in the simulation employing SCR violates experimentally determined NOE distances more than the structural ensemble generated in the simulation employing HR and the domain partially unfolds, the calculation of the free-energy contribution is still converged well as can be seen in Figure 4. From Figure S1, it can be seen that the largest contribution to the work of releasing the EN restraints takes place at different values of λ for HR or SCR.

Total Simulation Time

The total simulation times spent for the calculation of the presented standard-state binding free energies were 7.4 μs for the complex of wt UBM2 and UBI and 8.9 μs for the complex of P692A UBM2 and UBI. Other published calculations of protein–protein binding free energies employing MD simulations used simulations times of less than 1 μs.11,12,14 While the aim of this work was not to optimize the simulation protocol for computational efficiency but to demonstrate convergence and reliability of the calculated free-energy values, the complex nature of protein–protein binding reactions obviously still requires extensive simulation time in the order of μs to sample the phase-space of such reactions sufficiently, especially if extensive conformational changes accompany the binding reaction.

Conclusion

While the calculation of protein–protein binding free energies that are comparable with experimentally determined values has been reported previously, the lack of discussed convergence and reversibility of the described processes represents a significant drawback in previous literature. We introduced a relatively simple approach employing perturbed distance restraints for the simulation of reversible protein–protein binding and the calculation of the standard-state free energy of the binding process. The method was demonstrated at the hand of calculation of the binding free energy of UBI and the wt UBM2 domain or the P692A mutant UBM2 domain. The calculated standard-state binding free energies of both protein complexes were converged and in very good agreement with experimentally determined values. Moreover, error estimates of the computed binding free energies were in the order of thermal noise, and the reversibility of the simulated processes was illustrated with the replica diffusion properties of the performed HREMD simulations.

Furthermore, we discussed the use of two different potential energy functions for the calculation of the free-energy contributions of conformational changes associated with the binding processes. It was only possible to calculate the free-energy of the EN corresponding to the bound conformation in the unbound state of P692A UBM2, which is very flexible and behaves like an IDP in the simulations, with the SCR potential energy function26 proposed very recently. Hence, we think that SCR are better suited for such free-energy calculations.

While the calculation of the EN free-energy contributions was found to be difficult in some cases, also given the necessity to monitor the unrestrained, bound states of the complex simulations for possible noncanonically bound configurations, we demonstrated the applicability of the methodology for proteins which at least partially unfold in the unbound state and sample a very diverse conformational ensemble. Hence, we are confident that our proposed method has broad applicability which, however, remains to be further demonstrated in practice. We are planning to extend the application of the protocol not only to other protein complexes but also to complexes involving other macromolecular species like small peptides, carbohydrates, and DNA.

Supporting Information Available

This material is available free of charge at The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b00706.

  • Derivatives of the free energy with respect to λ and free-energy differences along λ calculated with BAR for all performed free-energy calculations (Figure S1); forward and reverse cumulative averages of the restraint unbinding free energies for the wt UBM2 and P692A UBM2 complexes calculated with system setups ZS or ZL (Figure S2); forward and reverse cumulative averages of restraining free energies along the continued trajectories with a total simulation time of 100 ns per λ-point (Figure S3); forward and reverse cumulative average of ΔGen,drb, RMSD trajectory of the UBM2 domain after a fit to the UBI domain and examples of canonically and noncanonically bound proteins from a simulation where bound and unrestrained proteins partially moved to noncanonically bound configurations (Figure S4); number and spacing of the used λ points for the simulation of reversible protein binding (Table S1); parameters for intermolecular distance restraints between UBI and UBM2 used for the simulation of reversible protein–protein binding (Table S2); different structural properties and number of NOE upper bound distance violations of the generated ensembles of unbound UBI and wt UBM2 (Table S3); structural properties of the generated ensembles of unbound P692A UBM2 (Table S4) (PDF)

We gratefully acknowledge financial support of the Austrian science fund (FWF) grant number I 1999-N28. The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC).

The authors declare no competing financial interest.

Supplementary Material

ct7b00706_si_001.pdf (993KB, pdf)

References

  1. Kastritis P. L.; Bonvin A. M. Are Scoring Functions in Protein-Protein Docking Ready to Predict Interactomes? Clues from a Novel Binding Affinity Benchmark. J. Proteome Res. 2010, 9 (5), 2216–25. 10.1021/pr9009854. [DOI] [PubMed] [Google Scholar]
  2. van Gunsteren W. F.; Bakowies D.; Baron R.; Chandrasekhar I.; Christen M.; Daura X.; Gee P.; Geerke D. P.; Glattli A.; Hunenberger P. H.; Kastenholz M. A.; Oostenbrink C.; Schenk M.; Trzesniak D.; van der Vegt N. F.; Yu H. B. Biomolecular Modeling: Goals, Problems, Perspectives. Angew. Chem., Int. Ed. 2006, 45 (25), 4064–92. 10.1002/anie.200502655. [DOI] [PubMed] [Google Scholar]
  3. Gohlke H.; Kiel C.; Case D. A. Insights into Protein-Protein Binding by Binding Free Energy Calculation and Free Energy Decomposition for the Ras-Raf and Ras-RalGDS Complexes. J. Mol. Biol. 2003, 330 (4), 891–913. 10.1016/S0022-2836(03)00610-7. [DOI] [PubMed] [Google Scholar]
  4. Gohlke H.; Case D. A. Converging Free Energy Estimates: MM-PB(GB)SA Studies on the Protein-Protein Complex Ras-Raf. J. Comput. Chem. 2004, 25 (2), 238–50. 10.1002/jcc.10379. [DOI] [PubMed] [Google Scholar]
  5. Bayas M. V.; Schulten K.; Leckband D. Forced Detachment of the CD2-CD58 Complex. Biophys. J. 2003, 84 (4), 2223–33. 10.1016/S0006-3495(03)75028-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Jarzynski C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78 (14), 2690–3. 10.1103/PhysRevLett.78.2690. [DOI] [Google Scholar]
  7. Cuendet M. A.; Michielin O. Protein-Protein Interaction Investigated by Steered Molecular Dynamics: The TCR-pMHC Complex. Biophys. J. 2008, 95 (8), 3575–90. 10.1529/biophysj.108.131383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Lemkul J. A.; Bevan D. R. Assessing the Stability of Alzheimer’s Amyloid Protofibrils using Molecular Dynamics. J. Phys. Chem. B 2010, 114 (4), 1652–60. 10.1021/jp9110794. [DOI] [PubMed] [Google Scholar]
  9. Torrie G. M.; Valleau J. P. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella sampling. J. Comput. Phys. 1977, 23 (2), 187–199. 10.1016/0021-9991(77)90121-8. [DOI] [Google Scholar]
  10. Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R. H.; Kollman P. A. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992, 13 (8), 1011–21. 10.1002/jcc.540130812. [DOI] [Google Scholar]
  11. Dadarlat V. M.; Skeel R. D. Dual Role of Protein Phosphorylation in DNA Activator/Coactivator Binding. Biophys. J. 2011, 100 (2), 469–77. 10.1016/j.bpj.2010.11.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gumbart J. C.; Roux B.; Chipot C. Efficient Determination of Protein-Protein Standard Binding Free Energies from First Principles. J. Chem. Theory Comput. 2013, 9 (8), 3789–98. 10.1021/ct400273t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Barducci A.; Bonomi M.; Prakash M. K.; Parrinello M. Free-Energy Landscape of Protein Oligomerization from Atomistic Simulations. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (49), E4708–13. 10.1073/pnas.1320077110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Rodriguez R. A.; Yu L.; Chen L. Y. Computing Protein-Protein Association Affinity with Hybrid Steered Molecular Dynamics. J. Chem. Theory Comput. 2015, 11 (9), 4427–38. 10.1021/acs.jctc.5b00340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Stark A. C.; Andrews C. T.; Elcock A. H. Toward Optimized Potential Functions for Protein–Protein Interactions in Aqueous Solutions: Osmotic Second Virial Coefficient Calculations Using the MARTINI Coarse-Grained Force Field. J. Chem. Theory Comput. 2013, 9 (9), 4176–85. 10.1021/ct400008p. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. May A.; Pool R.; van Dijk E.; Bijlard J.; Abeln S.; Heringa J.; Feenstra K. A. Coarse-Grained versus Atomistic Simulations: Realistic Interaction Free Energies for Real Proteins. Bioinformatics 2014, 30 (3), 326–34. 10.1093/bioinformatics/btt675. [DOI] [PubMed] [Google Scholar]
  17. Hou Q.; Lensink M. F.; Heringa J.; Feenstra K. A. CLUB-MARTINI: Selecting Favourable Interactions amongst Available Candidates, a Coarse-Grained Simulation Approach to Scoring Docking Decoys. PLoS One 2016, 11 (5), e0155251. 10.1371/journal.pone.0155251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Velez-Vega C.; Gilson M. K. Overcoming Dissipation in the Calculation of Standard Binding Free Energies by Ligand Extraction. J. Comput. Chem. 2013, 34 (27), 2360–71. 10.1002/jcc.23398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Yang W.; Bitetti-Putzer R.; Karplus M. Free Energy Simulations: Use of Reverse Cumulative Averaging to Determine the Equilibrated Region and the Time Required for Convergence. J. Chem. Phys. 2004, 120 (6), 2618–28. 10.1063/1.1638996. [DOI] [PubMed] [Google Scholar]
  20. Klimovich P. V.; Shirts M. R.; Mobley D. L. Guidelines for the Analysis of Free Energy Calculations. J. Comput.-Aided Mol. Des. 2015, 29 (5), 397–411. 10.1007/s10822-015-9840-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kirkwood J. G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3 (5), 300–13. 10.1063/1.1749657. [DOI] [Google Scholar]
  22. Bennett C. H. Efficient Estimation of Free Energy Differences from Monte Carlo Data. J. Comput. Phys. 1976, 22 (2), 245–68. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
  23. Roux B. The Calculation of the Potential of Mean Force using Computer Simulations. Comput. Phys. Commun. 1995, 91 (1–3), 275–82. 10.1016/0010-4655(95)00053-I. [DOI] [Google Scholar]
  24. Christen M.; Kunz A. P.; van Gunsteren W. F. Sampling of Rare Events Using Hidden Restraints. J. Phys. Chem. B 2006, 110 (16), 8488–98. 10.1021/jp0604948. [DOI] [PubMed] [Google Scholar]
  25. Christen M.; Kunz A. P.; van Gunsteren W. F. Sampling of Rare Events Using Hidden Restraints. J. Phys. Chem. B 2008, 112 (36), 11446. 10.1021/jp806613d. [DOI] [PubMed] [Google Scholar]
  26. Wang L.; Deng Y.; Wu Y.; Kim B.; LeBard D. N.; Wandschneider D.; Beachy M.; Friesner R. A.; Abel R. Accurate Modeling of Scaffold Hopping Transformations in Drug Discovery. J. Chem. Theory Comput. 2017, 13 (1), 42–54. 10.1021/acs.jctc.6b00991. [DOI] [PubMed] [Google Scholar]
  27. Cui G.; Benirschke R. C.; Tuan H. F.; Juranic N.; Macura S.; Botuyan M. V.; Mer G. Structural Basis of Ubiquitin Recognition by Translesion Synthesis DNA Polymerase Iota. Biochemistry 2010, 49 (47), 10198–207. 10.1021/bi101303t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Reif M. M.; Hunenberger P. H.; Oostenbrink C. New Interaction Parameters for Charged Amino Acid Side Chains in the GROMOS Force Field. J. Chem. Theory Comput. 2012, 8 (10), 3705–23. 10.1021/ct300156h. [DOI] [PubMed] [Google Scholar]
  29. Eichenberger A. P.; Allison J. R.; Dolenc J.; Geerke D. P.; Horta B. A.; Meier K.; Oostenbrink C.; Schmid N.; Steiner D.; Wang D.; van Gunsteren W. F. GROMOS++ Software for the Analysis of Biomolecular Simulation Trajectories. J. Chem. Theory Comput. 2011, 7 (10), 3379–90. 10.1021/ct2003622. [DOI] [PubMed] [Google Scholar]
  30. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  31. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Hermans J.. Interaction Models for Water in Relation to Protein Hydration. In Intermolecular Forces; Pullman B., Ed.;. Springer: Netherlands, 1981; Vol. 14, pp 331–42, DOI: 10.1007/978-94-015-7658-1_21. [DOI] [Google Scholar]
  32. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81 (8), 3684–90. 10.1063/1.448118. [DOI] [Google Scholar]
  33. Bussi G.; Donadio D.; Parrinello M. Canonical Sampling Through Velocity Rescaling. J. Chem. Phys. 2007, 126 (1), 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  34. Parrinello M.; Rahman A. Polymorphic Transitions in Single Crystals: A new Molecular Dynamics Method. J. Appl. Phys. 1981, 52 (12), 7182–90. 10.1063/1.328693. [DOI] [Google Scholar]
  35. Nosé S.; Klein M. L. Constant Pressure Molecular Dynamics for Molecular Systems. Mol. Phys. 1983, 50 (5), 1055–76. 10.1080/00268978300102851. [DOI] [Google Scholar]
  36. Hockney R. W.The Potential Calculation and some Applications; Academic Press Inc.: New York, 1970; p 77. [Google Scholar]
  37. Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18 (12), 1463–72. . [DOI] [Google Scholar]
  38. Tironi I.; Sperb R.; Smith P.; van Gunsteren W. F. A Generalized Reaction Field Method for Molecular Dynamics Simulation. J. Chem. Phys. 1995, 102, 5451. 10.1063/1.469273. [DOI] [Google Scholar]
  39. Heinz T. N.; van Gunsteren W. F.; Hünenberger P. H. Comparison of Four Methods to Compute the Dielectric Permittivity of Liquids from Molecular Dynamics Simulations. J. Chem. Phys. 2001, 115 (3), 1125–36. 10.1063/1.1379764. [DOI] [Google Scholar]
  40. Hinsen K.; Petrescu A.-J.; Dellerue S.; Bellissent-Funel M.-C.; Kneller G. R. Harmonicity in slow protein dynamics. Chem. Phys. 2000, 261 (1), 25–37. 10.1016/S0301-0104(00)00222-6. [DOI] [Google Scholar]
  41. Periole X.; Cavalli M.; Marrink S. J.; Ceruso M. A. Combining an Elastic Network With a Coarse-Grained Molecular Force Field: Structure, Dynamics, and Intermolecular Recognition. J. Chem. Theory Comput. 2009, 5 (9), 2531–43. 10.1021/ct9002114. [DOI] [PubMed] [Google Scholar]
  42. Moreth J.; Kroker K. S.; Schwanzar D.; Schnack C.; von Arnim C. A.; Hengerer B.; Rosenbrock H.; Kussmaul L. Globular and protofibrillar abeta aggregates impair neurotransmission by different mechanisms. Biochemistry 2013, 52 (8), 1466–76. 10.1021/bi3016444. [DOI] [PubMed] [Google Scholar]
  43. Fukunishi H.; Watanabe O.; Takada S. On the Hamiltonian replica exchange method for efficient sampling of biomolecular systems: Application to protein structure prediction. J. Chem. Phys. 2002, 116, 9058–9067. 10.1063/1.1472510. [DOI] [Google Scholar]
  44. Doudou S.; Burton N. A.; Henchman R. H. Standard Free Energy of Binding from a One-Dimensional Potential of Mean Force. J. Chem. Theory Comput. 2009, 5 (4), 909–18. 10.1021/ct8002354. [DOI] [PubMed] [Google Scholar]
  45. Eisenhaber F.; Lijnzaad P.; Argos P.; Sander C.; Scharf M. The double cubic lattice method: Efficient approaches to numerical integration of surface area and volume and to dot surface contouring of molecular assemblies. J. Comput. Chem. 1995, 16 (3), 273–284. 10.1002/jcc.540160303. [DOI] [Google Scholar]
  46. Kabsch W.; Sander C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features. Biopolymers 1983, 22 (12), 2577–637. 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
  47. Polyansky A. A.; Kuzmanic A.; Hlevnjak M.; Zagrovic B. On the Contribution of Linear Correlations to Quasi-harmonic Conformational Entropy in Proteins. J. Chem. Theory Comput. 2012, 8 (10), 3820–9. 10.1021/ct300082q. [DOI] [PubMed] [Google Scholar]
  48. Bomar M. G.; D’Souza S.; Bienko M.; Dikic I.; Walker G. C.; Zhou P. Unconventional Ubiquitin Recognition by the Ubiquitin-binding Motif within the Y Family DNA Polymerases Iota and Rev1. Mol. Cell 2010, 37 (3), 408–17. 10.1016/j.molcel.2009.12.038. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct7b00706_si_001.pdf (993KB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES