Abstract
In the past decades, hundreds of articles have explored the mechanisms underlying priming. Most researchers assume that masked and unmasked priming are qualitatively different. For masked priming, the effects are often assumed to reflect savings in the encoding of the target stimulus, whereas for unmasked priming, it has been suggested that the effects reflect the familiarity of the prime-target compound cue. In contrast, other researchers have claimed that masked and unmasked priming reflect essentially the same core processes. In this article, we use the diffusion model (Ratcliff, 1978) to account for the effects of masked and unmasked priming for identity and associatively related primes. The fits of the model lead us to the following conclusion: masked related primes give a head start to the processing of the target compared to unrelated primes, while unmasked priming affects primarily the quality of the lexical information.
In visual-word recognition laboratory tasks (e.g., lexical decision, naming), the response to a target stimulus can be influenced by the previous presentation of a related item – the so-called prime (e.g., the response to the string “DOCTOR” is faster and/or more accurate when following a related prime like “nurse” than when following an unrelated prime like “horse”). Priming effects can occur in the absence of explicit instruction to use the prime’s information when responding to the target. Early research in visual-word recognition focused on visible, unmasked primes, and the potential role of participants’ strategies under these circumstances led a number of researchers to manipulate the stimulus-onset asynchrony (SOA) between prime and target (e.g., Neely, 1977) to explore issues around automatic vs controlled processes (Posner & Snyder, 1975). Along these lines, the introduction of masked priming (Forster & Davis, 1984) was an important development; the assumption behind masked priming was that the results would reflect early automatic processes. This article uses an explicit modeling method (Ratcliff’s diffusion model) to examine the differences among masked vs. unmasked priming in the most popular laboratory word identification task: lexical decision (e.g., see Dufau et al., 2011).
The masked priming paradigm has been used to examine the initial stages of visual-word recognition (Forster & Davis, 1984; see also Forster, Mohan, & Hector, 2003; Kinoshita & Lupker, 2003; Grainger, 2008, for recent reviews). The typical trial in a masked priming experiment consists of a mask (e.g., #####) which is presented for 500 ms, which is followed by a briefly presented lowercase prime (for around 30–60 ms) and is subsequently replaced by an uppercase target (e.g., the target word TRIAL may be preceded by the identity prime trial or by an unrelated prime like ocean). Under these conditions, participants are not only not aware of the prime’s identity, but are often also unaware of its existence.
One basic tenet in masked priming studies is that the obtained priming effects are qualitatively different from priming effects in standard (unmasked) priming paradigms (Forster et al., 2003; Grainger, 2008). Indeed, fMRI evidence has revealed that masked primes produce some activation in the so-called “visual word form area”, while activation is negligible in frontal and parietal areas; in contrast, unmasked primes produce a much larger activity at parietal, prefrontal and cingulate areas (see Dehaene et al., 2001). Unlike unmasked priming, which can be mediated by an episodic memory trace of the prime, masked priming effects are supposed to reflect a transitory change in the accessibility of lexical/semantic information. However, work by Bodner and Masson (2003; see also Bodner & Masson, 2001) has called into question the alleged qualitative difference between masked and unmasked priming. Bodner and Masson suggested that, for both masked and unmasked priming, “a prime event creates a memory resource that can be recruited during target presentation to aid in the encoding of the target” (p. 646). Bodner and Masson’s account is supported by a key finding: the size of the masked identity priming effect in lexical decision is greater when the proportion of identity trials in the stimulus list is high (0.80) rather than low (0.20) (Bodner & Masson, 2001; see also Bodner & Masson, 2003 for a parallel effect with associative/semantic primes; cf. Perea & Rosa, 2002). This finding matches the usual result from the standard long-term priming with visible stimuli. Bodner and Masson argue that this is so because the masked prime establishes an episodic record, just like the unmasked prime (i.e., conscious awareness would not be a prerequisite for establishing an episodic record).
The dissociation of different processing mechanisms in behavioral experiments is often contentious, especially when the mean latency is the sole dependent variable. Here we contrast two views of masked/unmasked priming using Ratcliff’s diffusion model (Ratcliff, 1978, 1981, 1985, 1988; Ratcliff, Van Zandt, & McKoon, 1999) in an experiment that compares masked versus unmasked priming. Ratcliff’s diffusion model has been successfully applied to lexical decision data (Ratcliff, Gomez, & McKoon, 2004; see also Gomez, Ratcliff, & Perea, 2007; Ratcliff, Perea, Colangelo, & Buchanan, 2004; Ratcliff, Thapar, Gomez, & McKoon, 2004; Wagenmakers, Ratcliff, Gomez, & McKoon, 2008; see Norris, 2009 for a complete model of lexical access that shares assumptions with the diffusion model). Importantly, the model allows cognitive processing to be divided into several components: the rate of evidence accumulation (which reflects the goodness of match between the test string and lexical memory); the decision criteria (i.e., how much information must be accumulated before a decision can be made); the non-decision components of processing (both encoding and response execution); and variabilities in the various components. In the following paragraphs, we will first describe the diffusion model, and then we will indicate what components could be affected in masked vs. unmasked priming depending on whether or not the priming effects originate from the same sources. In particular, we will examine two of the most studied types of relationships between primes as targets: identity priming and associative/semantic priming.
The diffusion model and the lexical decision
The diffusion model was developed to account for those decisions that involve a two-alternative choice and take less than a few seconds (Ratcliff, 1978; Ratcliff & Rouder, 1998). In the model, the decision-relevant information is accumulated over time in a noisy manner (see Figure 1). A response is initiated when the noisy accumulation of evidence reaches one of the two decision boundaries. The location of the decision boundaries is related to the amount of evidence needed to make a response. The two parameters of the model that describe the boundary positions are z: the location of the starting point1, and a, the distance between the decision boundaries (with the location of the negative boundary assumed to be set at 0). The values of a and z reflect speed-accuracy tradeoffs and response biases2. In the present study, two aspects of the diffusion model are of particular interest because they most likely capture the observed priming effects: the encoding of the perceptual information and the quality of such information.
Figure 1.
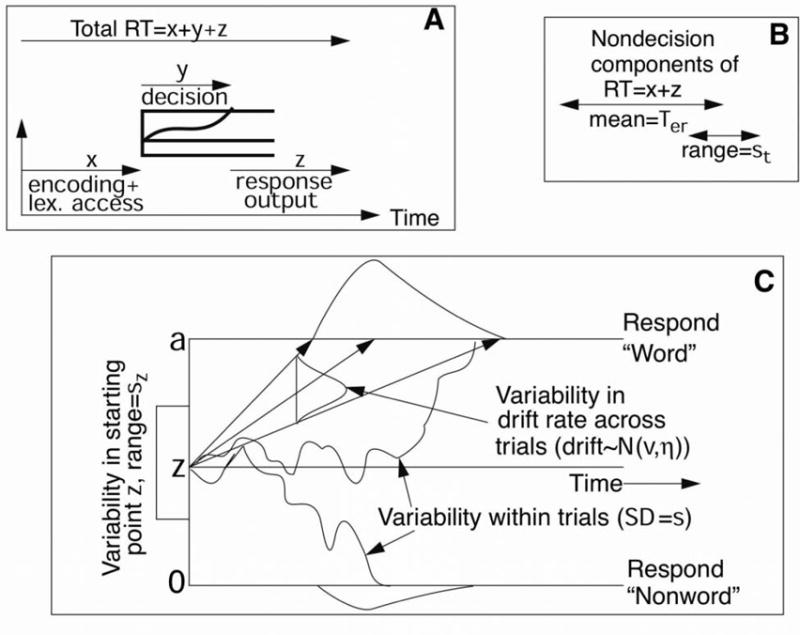
Representation of the diffusion model. Panel A shows a representation of the sequence of events in a trial of a lexical decision task. Panel B represents the nondecisional components of the response time (RT), which have a mean expressed by the Ter parameter and a range expressed by the st parameter. Panel C illustrates the diffusion model. The parameters represented in Panel C are a: boundary separation; z: starting point; sz: variability in starting point across trials; v: drift rate; η: variability in the drift rate across trials; and s: variability in drift rate within a trial.
Encoding and response execution time
The diffusion model assumes that the RT for a given trial is a sum of three components: (1) the encoding time; (2) the time taken by the accumulation of evidence process; and (3) the time taken by the response execution stage. The sum of components (1) and (3) is represented by the non-decision parameter Ter. Note that encoding and response execution cannot be separated in the model. This non-decision time is assumed to be uniformly distributed with range st. Of particular interest here is the possible contribution of the masked and unmasked primes to the encoding process. Some verbally formulated explanations of priming posit that the presentation of a related prime provide with a head-start in the processing of the target (see Forster, 1998), which can be implemented in a diffusion model framework as affecting the encoding time (Ter parameter). We must note here that the term encoding has a specific interpretation within the diffusion model. It represents processes that terminate before the beginning of the accumulation of evidence in the decision process (i.e., the decision process itself, represented by the jagged lines in Panel C of Figure 1). This might not be the same as other processes that are also termed encoding processes in other models and theories.
Drift Rate
The average rate of accumulation of evidence is termed drift rate. It can be thought of as a quality of the extraction of evidence. Easy stimuli, such as high frequency words in a lexical decision task, are associated with large positive drift rates (Ratcliff et al., 2004a). Similarly, non-wordlike nonwords are associated with large but negative drift rates. Within a trial, the accumulation of evidence has variability that is reflected in the jagged line in Figure 1. In addition to the within-trial variability, there is normally distributed variability in the drift rate from trial to trial (parameter η). This is so because all trials that nominally are in the same category (e.g., high frequency words) cannot be expected to have exactly the same discriminability.
On the qualitative differences between masked vs. unmasked priming
In Forster’s view, masked priming would reflect a savings effect, in which some of the processing carried out on the prime is transferred to the word target (see Forster et al., 2003; Forster, 2008). Specifically, Forster (1999) indicated that the magnitude of masked identity priming “ought to be equal to the duration of the prime (assuming that the target appears immediately after the prime)” (p. 10) and he provided data supporting this view. If this interpretation is correct, masked identity priming should be revealed as a shift in the entire RT distribution, without any change in spread. Thus, if we implement Forster’s verbal explanation within a diffusion model framework, the effect of the masked identity prime would be reflected as a change in the nondecision component (Ter), whereas the rate of accumulation of information would be the same across conditions. With respect to masked associative/semantic priming, Forster (2009) indicated that the “semantic evaluation of the target is completed more rapidly because the relevant semantic information retrieved by the prime is still stored in the semantic buffer” (p. 46). We believe that this latter verbal description does not have a clear translation into the diffusion model parameters. One could imagine that this buffer provides a head start (i.e., a change in Ter), but it could also cascade into the evidence being accumulated in the diffusion process (i.e., a change in drift rate). Similar views of masked priming are used in the Spatial Coding model (Davis, 2010) and in the LTRS model (Adelman, 2011). In the Spatial Coding model, the mechanism at play during masked priming is that the letter units are reset with the presentation of a new stimulus (e.g., when the prime is removed to give place to the target). When this happens, if there is lexical activation already in course, this activation is not reset and produces the advantage of the identity condition over the unrelated condition. Similarly, in the LTRS model, priming is considered as a savings effect or a headstart that takes place during the time in which the target is a candidate for lexical identification of the prime (Adelman, 2011).
To explain unmasked priming effects, one influential view is that when the prime is visible, prime and target are merged in short-term memory to form a compound cue (see Ratcliff & McKoon, 1988, for further details).3 More specifically, Ratcliff and McKoon indicated that “the familiarity value given by the computation of the strength of the compound cue is used as the drift rate in a diffusion (random walk) decision process” (p. 388) (i.e., rate of accumulation of information). This implies that the RT distribution in the related condition would be less skewed than in the unrelated condition. We should stress that this mechanism would apply similarly to associative priming and identity priming –with the (obvious) difference that the familiarity of the compound-cue of two identical words would be stronger than that of two semantically related words (i.e., identity priming implies not only semantic overlap but also form/phonological overlap). Therefore, both unmasked identity and unmasked associative priming would reflect changes in drift rate across conditions in a diffusion model.
Alternatively, in Bodner and Masson’s view (see also Plaut & Booth, 2000), both masked and unmasked primes would form an episodic trace independently of the visibility and the awareness of the prime. The explanation proposed by Bodner and Masson is similar to that of Ratcliff and McKoon for unmasked priming. The only difference is that, unlike Ratcliff and McKoon, the compound cue would be created regardless of the participant’s awareness of the prime. Therefore, the prediction is clear: the compound cue of the event would determine drift rate (i.e., rate of accumulation of information). In a diffusion model, this would imply that priming effects would be reflected in terms of drift rate for both unmasked and masked primes.
Previous research comparing masked vs. unmasked priming from an explicit model perspective is very scarce. In a recent study, Balota, Yap, Cortese, and Watson (2008) compared the RT distributions of semantic priming effects with masked vs. unmasked primes –using the estimates from the ex-Gaussian distribution rather than fits from the diffusion model. Using a masked priming paradigm at a 42-ms SOA, Balota et al. (2008; Experiment 7) found a nonsignificant 13-ms effect of semantic priming –note that the size of this effect is in line with previous masked semantic priming experiments (e.g., Perea & Lupker, 2003). In addition, using visible primes at a 200-ms SOA, Balota et al. (2008, Experiments 2 & 3) found that the semantic priming effect was larger at the higher quantiles; unexpectedly, this pattern was not reflected in ex-Gaussian fits in which only the μ and σ parameters were affected by priming, but not the τ parameter (which has been traditionally been related to changes in spread). The presence of an increasing associative/semantic priming effect at the higher quantiles is consistent with a compound-cue model (see above), whereas the apparent mismatch with the fits might be due to misspecification of the ex-Gaussian parameters.
With respect to unmasked identity priming, previous applications of the diffusion model to the lexical decision task suggest that it might affect drift rates (and consequently the spread of the RT distribution). In a long-term (unmasked) identity priming experiment in which items were presented more than once in the experiment, Ratcliff, Gomez and McKoon (2004) found that the item identity yielded changes in the drift rate. To our knowledge, very few published studies have analyzed the differences between masked and unmasked priming from a modeling perspective; nonetheless we would like to note that Pollatsek, Perea, and Carreiras (2005) reported that form-related priming produced a shift in the RT distribution relative to an unrelated priming condition. Similarly, Kinoshita, Mozer and Forster (2011) examined the prime proportion effects on masked and unmasked priming and showed that visible primes (but not masked primes) showed adaptation to the prime-target contingency. Taken together, these data suggest that the mechanism underlying masked and unmasked priming might be different.
In addition, previous research has tried to account for priming from a modeling perspective. Notably, Jacobs and Grainger (1992) were the first to simulate the masked (form) priming task with a quantitative model of visual-word recognition – the interactive-activation (IA) model (see also Perea & Rosa, 2000, for simulations of masked identity priming with this model). In these simulations, the prime is presented for a short number of processing cycles and then it is replaced by the target (see also Davis, 2010, for a similar logic for the simulations with the spatial coding model). That is, masked priming simulations with the interactive activation model and the spatial coding model assume that the prime offers a head start –similarly to Forster’s prediction. It is important to note, though, that the spatial coding model also employs the Rumelhart and Siple’s (1974) uppercase font. This implies that the prime and the target in the simulations would be exactly the same. As Jacobs and Grainger (1992), indicated, “a useful extension of the IA model would include a set of lowercase letters, thus allowing a more precise simulation of priming studies involving a change in case” (p. 1179). Finally, it may be worth noticing that this approach of modeling priming effects in an interactive-activation model cannot tell apart masked vs. unmasked priming effects.
Overview of the Experiment
In the present experiment, we used the diffusion model to test Forster’s vs. Bodner & Masson’s account of the differences between masked and unmasked priming. We focused on identity and associative/semantic priming, since these are the two most studies phenomena in previous priming experiments. In order to best compare the effects of the factors of interest in lexical decision performance, we performed all manipulations within subjects. In our experiment, we manipulated the relationship between the prime and the target through identity priming (prime: house; target: HOUSE) and associative priming (prime: doctor; target: NURSE). In addition, these targets could be preceded by a masked prime, or by an unmasked visible prime.
Method
Participants
Twenty DePaul University students participated for credit in an Introduction to Psychology class.
Materials
For the associative priming and the identity priming experiments, we selected 160 words for each type of stimulus. They were matched in word frequency: mean = 129 per million (Kucera & Francis, 1967), and other relevant variables (see the Tables 1 & 2). For the associative priming conditions, the items were obtained from the University of South Florida free association norms (Nelson, McEvoy, & Schreiber, 2004). The mean association for the associative priming pairs was .2824.
Table 1.
Parameters of materials for the word items obtained with N-Watch (Davis, 2005)
| CELEX | KF-FR | BNC-FR | EST-FR | FAM | LEN-L | N | AOA | AOA2 | IMG | IMG2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Identity priming targets | |||||||||||
|
| |||||||||||
| Mean | 119.1 | 129.1 | 118.7 | 271.1 | 413.1 | 4.8 | 3.8 | 208.8 | 140.9 | 350.5 | 101.1 |
| SD | 235.9 | 247.2 | 250.8 | 242.4 | 224.9 | 0.62 | 3.9 | 201.2 | 185.8 | 206.8 | 187.8 |
|
| |||||||||||
| Associative priming targets | |||||||||||
|
| |||||||||||
| Mean | 136.5 | 129.4 | 120.0 | 297.6 | 430.4 | 4.8 | 5.3 | 138.6 | 117.7 | 383.7 | 100.6 |
| SD | 278.7 | 244.2 | 236.8 | 252.4 | 240.9 | 0.6 | 4.6 | 153.0 | 150.3 | 233.4 | 197.3 |
See Davis (2005) for a full discussion of these statistics. CELEX, KR-FR and BNC-FR: word frequency counts according to the Celex, Kucera and Francis, and British National Corpus. EST-FR: Estimated word frequency (Balota et al, 2001). FAM: familiarity in a (1 to 7 scale). LEN-L: number of letters. N: Coltheart’s neighborhood size. AOA and AOA2: Age of acquisition based on Gilhooly and Logie (1980) and Bird, Franklin, and Howard (2001) respectively. IMG and IMG2: imaginability from MRC Psycholinguistic Database and Bird, et al’s respectively.
Table 2.
Parameters of materials for the nonword items obtained with N-Watch (Davis, 2005)
| BTK | BTY | TTK | TTY | N | HFMAX | NFM | |
|---|---|---|---|---|---|---|---|
| Mean | 1038.9 | 24.21 | 103.25 | 2.84 | 2.28 | 110 | 34.29 |
| SD | 992.4 | 20.52 | 220.61 | 2.33 | 3.12 | 434 | 128.81 |
See Davis (2005) for a full discussion of these statistics. BTK and BTY: bigram token and type frequencies obtained from the COBUILD/CELEX corpus. TTK and TTY: trigram token and type frequencies obtained from the COBUILD/CELEX corpus. N: Coltheart’s neighborhood size. HFMAX: Highest frequency of a neighbor. HFM: Mean frequency of neighbors
Procedure
Participants were tested in groups of one to three. PC-compatible computers controlled presentation of the stimuli and recording of response times. Stimuli were presented on a 15-in. computer monitor in 24-point BrHand font (similar to non-proportional Courier fonts). For the masked blocks, on each trial, a forward mask consisting of a row of hash marks (#’s) of equal length to the stimulus (i.e., 4, 5 or 6 character long) was presented for 500 ms in the center of the screen. Next, the prime was presented in lowercase and stayed on the computer screen for 56 ms. The prime was then followed by the presentation of the target stimulus in uppercase. Both prime and target were presented in the same screen location as the forward mask. The target stimulus remained on the screen until the participant’s response. For the unmasked blocks there was a fixation area that matched the size of the stimulus in terms of number of letters (e.g., “< >”) for 200 ms; the prime was presented in lowercase for 200ms, and then the target in uppercase was kept on the screen until a response was made. Participants were told that words and nonwords would be displayed on the monitor in front of them, and that they should press the ? key to indicate if the uppercase item was an English word, and a different key (Z) to indicate if the stimulus was not a word. They were instructed to respond as quickly as possible while trying not to make errors. Each participant received a different random order of stimuli, and half of the participants performed the masked priming trials first, followed by the unmasked priming trial. Each participant received a total of 20 practice trials prior to the experimental phase. Participants were presented with 40 items per condition (40 words preceded by an identity prime, 40 words preceded by a identity control prime, 40 words preceded by an associative prime, 40 words preceded by an associative control prime, 40 nonwords preceded by an identity primed, and 40 nonwords preceded by a control prime). There were 160 filler nonwords with word primes, and 80 filler words with unrelated nonword primes; this way, the primes were not predictive of the lexical status of the target. The experimental session lasted about 45 minutes.
Results
Responses under 250 ms or longer than 1800 ms were removed from the analyses (less than 3% of the data); in addition, one subject was removed because s/he pressed the “word” button more than 90% of the trials regardless of condition.
The results are straightforward (see Table 3 for a summary of the empirical results), and because our goal is not to establish the existence of either identity or associative priming (which are very well established), but instead to provide a diffusion model account of these phenomena, the results will be discussed only briefly. As expected, for both masked and unmasked modalities, the word targets were responded to faster when preceded by an identity prime than when preceded by an unrelated prime (for masked: priming effect = 60 ms, t(18) = 4.55, p < .001; for unmasked: priming effect = 105 ms, t(18) = 9.98, p < .001). Similarly, for the associative pairs, target words (in both the masked and unmasked conditions) were responded to faster when preceded by an associatively related prime than when preceded by an unrelated prime, although only for the unmasked condition was the priming effect significant (for masked: priming effect = 12 ms, t(18) = 1.08, p = .29; for unmasked: priming effect = 44 ms, t(18) = 4.75, p < .001). (Note that, despite being nonsignificant, the size of the masked associatively priming effect is similar to that in previous experiments in the literature; e.g., Perea & Lupker, 2003.) The priming effects for the nonword targets (i.e., identity masked priming and identity unmasked priming) did not produce any significant effects (all t′s < 1), and in fact there were very small inhibitory trends.
Table 3.
Summary of Results. The error rates are in parenthesis.
| Condition | Related | Control | Δ RT | t-value (df=18) | p |
|---|---|---|---|---|---|
| Masked Associative Words | 634 (.04) | 646 (.04) | −12 | 1.08 | .29 |
| Masked Identity Words | 604 (.04) | 665 (.05) | −60 | 4.55 | < .001 |
| Masked Nonwords | 750 (.08) | 743 (.06) | 7 | 0.55 | .59 |
| Unmasked Associative Words | 654 (.04) | 698 (.03) | −44 | 4.75 | < .001 |
| Unmasked Identity Words | 599 (.04) | 704 (.05) | −105 | 9.98 | < .001 |
| Unmasked Nonwords | 763 (.09) | 761 (.06) | 2 | 0.13 | .90 |
In terms of the accuracy data, performance for all word conditions were at a near-ceiling performance (all accuracies were at or above 95%) and none of the t-tests showed significant effects. The analysis on the nonword targets, on the other hand, showed a lower accuracy for the nonwords when preceded by an identity prime than when preceded by an unrelated prime in the masked condition (accuracy for primed = .917 vs. accuracy for control = .944; t(18) = 2.19, p = 0.04) as well as the unmasked condition (accuracy for primed = .910 vs. accuracy for control = .936; t(18) = 2.77, p = 0.01). This effect will be discussed together with the fits of the model to nonword data.
Modeling
We will use the diffusion model to test Forster’s vs. Bodner & Masson’s account of the differences between masked and unmasked priming. We fitted the data from the masked and the unmasked trials separately. We performed the fits of the model in two different ways:
For display in the figures and tables, we present the fits to the grouped data that we obtained using the fitting routines described by Ratcliff and Tuerlinckx (2002). We calculated the accuracy and latency (i.e., the RTs at the .1, .3, .6, .7, and .9 quantiles) for word and nonword responses for all conditions and for all subjects, and we obtained the group level performance by averaging across subjects (i.e., vincentizing; Ratcliff, 1979; Vincent, 1912).
For the analyses of the effects of priming on the parameters of the model, we fitted the model to each subject’s data, and then examined the difference in the Ter and drift rate parameters using standard inferential statistics techniques.
Fitting averaged data is an appropriate procedure for fitting the diffusion model. In previous research (Ratcliff et al., 2004b; Ratcliff, Thapar, & McKoon, 2001), fits to averaged data provided similar parameter values to parameter values obtained by averaging across fits to individual subjects. The quantile RTs were fed into the diffusion model.
For the two modeling methods (i.e., grouped data and subject-by-subject), the model generated for each response the predicted cumulative probability within the time frames bounded by the the five quantiles. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile yields the proportion of responses between each quantile, which are the expected values for the χ2 computation. The observed values are the empirical proportions of responses that fall within a bin bounded by the 0, .1, .3, .5, .7, .9, and 1.0 quantiles, multiplied by the proportion of responses for that choice (e.g., if there is a .965 response proportion for the word alternative, the proportions would be .965 × .1, .965 × .2, .965 × .2, .965 × .2, .965 × .2 and .965 × .1).
Masked Priming
There are two features of the masked priming data that needed to be accounted for (see Figure 2): (1) there was a shift in the RT distributions as a function of both identity and associative priming; and (2) there was a null effect of priming in the mean RT for nonwords; however, there was an effect of the RT distributions: lower quantiles the RTs were shorter for the related condition than for the unrelated condition and, at the same time, this pattern reversed in the higher quantiles.
Figure 2.
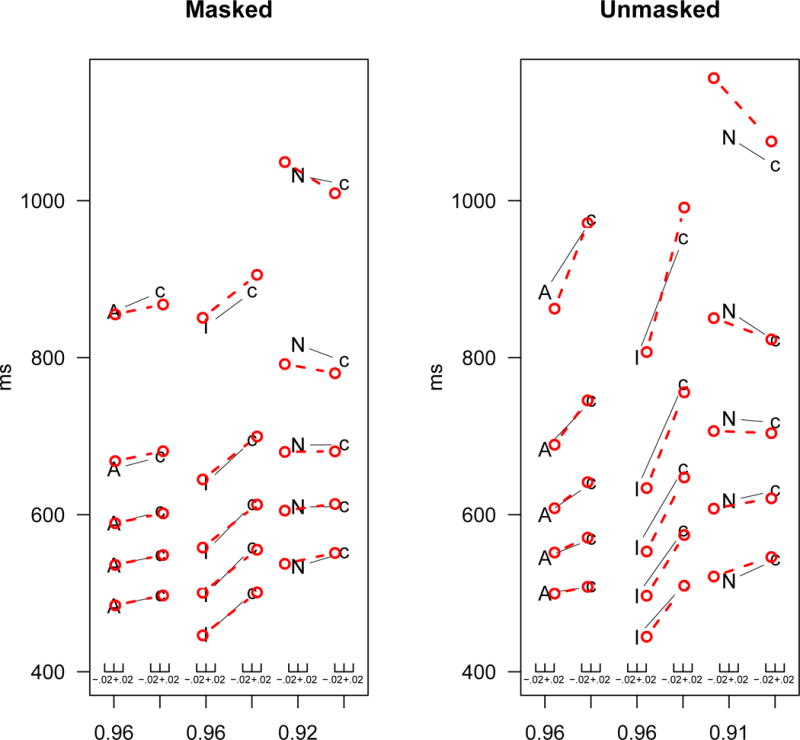
Latency-probability function for unmasked and masked priming conditions for the grouped data. The points represent (from bottom to top) the .1, .3, .5, .7 and .9 quantiles. Within each panel, from left to right, the columns of quantile RTs represent the responses associative/semantic primes (A) and their controls (c); identity primes (I) and their controls (c); and nonwords (N) and their controls (c). The light circles show the model’s fits.
Grouped data
Our model comparison strategy for the grouped data was to begin with the simplest implementation of the model (with the fewest number of free parameters) and then to add free parameters until the gain in the quality of fits did was negligible5. In other words, we looked to jointly maximize descriptive accuracy (goodness of fit) and parsimony (small number of free parameters).
Pure distributional shifts (changes in the location of the distributions) are naturally accounted for by allowing the Ter parameter to vary from the unrelated primes to the related primes. A model with a single Ter for all conditions yielded a χ2 = 362, while allowing Ter to vary yielded a χ2 = 81.3, which is 77% smaller (see Ratcliff & Smith, 2010 p. 90, Table 1, for a similar result).
A model with only Ter free to vary as a function of priming, however, could not account for the pattern of results for nonwords. Hence, we needed to allow the drift rate for the primed nonwords to be different from the drift rate for their controls, with less-negative drift rate for the primed nonwords than for their control6.
Individual subject data
Another way to analyze the effect of manipulations on the parameters of the model is by fitting a model with free parameters to data for each subject, and then to carry out standard inferential statistics on the model’s parameters. To this end, we conducted subject-by-subject fits and we obtained the drift rates and Ter parameters for each of the conditions. Planned t-test were performed to compare the parameter values for the primed conditions against the parameter values for their controls. For Ter, all effects of priming were significant: for associative priming t(18) = 2.154, p = 0.045; for identity priming t(18) = 9.749, p < .01; and for nonwords t(18) = 2.158, p = 0.045. For the drifts, neither word identity priming nor associative priming yielded significant differences (t(18) < 1); however, for nonwords there was a significant difference in drift rate between related and control items: t(18) = 2.411, p = .027.
The two fitting methods provide converging evidence: according to the diffusion model-based account, the locus of the masked priming effects for words is the encoding process (with larger effects in the Ter parameter for identity priming than for associative priming, as can be seen in Table 4). In contrast, for nonwords, identity priming seems to facilitate the encoding process (reducing the Ter value), while increasing the word-likeness of the stimuli (making the drift rate value less negative).
Table 4.
Parameters of the diffusion model
| Masked Priming | ||||||||
|---|---|---|---|---|---|---|---|---|
| a | z | sz | drift | η | Ter | st | p0 | χ2 |
| 0.136 | 0.072 | 0.001 | Words: 0.275 NW id: −0.204 NW cntrl: −0.240 |
0.094 | W assoc: 0.414 W id: 0.373 W cntrl: 0.427 NW id: 0.441 NW cntrl: 0.461 |
0.087 | .001 | 74.56 |
|
| ||||||||
| Unmasked Priming | ||||||||
| a | z | sz | drift | η | Ter | st | p0 | χ2 |
|
| ||||||||
| 0.141 | 0.075 | 0.008 | W assoc: 0.275 W id: 0.278 W ctrl: 0.217 NW id: −0.152 NW ctrl: −0.198 |
0.010 | W id: 0.364 W ctrl & assoc : 0.418 NW id: 0.401 NW ctrl: 0.434 |
0.056 | .001 | 135.69 |
Unmasked Priming
Compared to masked priming, unmasked priming produced numerically larger effects in the mean RT as a function of priming. For the nonwords, although there was no significant difference in the mean RT between the related targets and their controls, the RTs for the .1 and .3 quantiles were shorter for the related condition than for the unrelated condition. However, for the .7 and .9 quantiles, the direction of the effect reversed.
Grouped data
For unmasked priming, the first model we fit to the data was the one we used for the masked priming condition (with Ter allowed to vary as a function of priming). This model misses some important features of the data quite badly (χ2 = 246.92). Bear in mind that changes in the Ter parameter produce shifts in the RT distributions; however, in unmasked priming for word targets, the effects go beyond a shift in the distribution and include a larger spread in the higher quantiles for the unrelated conditions relative to the related conditions. In addition, for nonword targets there was a non-monotonic effect of priming as a function of quantiles. Adding a free drift rate parameter for primed nonwords improved the quality of the fits for nonwords but still misses the qualitative features of the word data (χ2 = 225.71 for the Ter + driftprimed.nonwords model). Augmenting the model by allowing not only the Ter but also the drift rates to vary as a function of primes for both word and nonwords trials improve the quality of the fits χ2 = 136.69, which is smaller by 110 from the Ter only model. We prefer this augmented model because with two extra parameters the gain in goodness of fit is quite large. Note that for the associative unmasked-priming condition, the Ter parameter has the same value as the unrelated control condition, and there is no loss in the goodness of fit if the Ter parameter is kept the same for the unrelated condition and for the associative priming condition. This finding reveals that while unmasked associative priming increases the word-likeness of the target item, it does not contribute to the encoding of the target string.
It is worth mentioning that although the focus of this research is not the effects of priming on nonwords, there is a robust debate on this issue. Our analysis suggest that the facilitatory effects on Ter and the inhibitory effects on drift rate cancel each other out, so future research might need to include a neutral condition to fully explore this issue. In any case, Kinoshita & Norris (2010) have shown robust masked priming effects for nonwords in a same-different task, which suggest a pre-lexical status of the facilitatory effect.
Individual data
The subject-by-subject fits were carried out the same way as for the masked priming data. The effects of priming on the drift rates were significant for associative priming of words: t(18) = 2.509, p = .022; for identity priming of words: t(18) = 2.134, p = .046; and also for nonwords t(18) = 2.911, p = .009. The effects of unmasked-priming on Ter were significant for all priming conditions; for word identity priming: t(18) = 7.808, p < .01; and for nonword identity priming: t(18) = 3.030, p < .01. Somewhat surprisingly we also found of effect on Ter for associative priming t(18) = 2.150, p = .045, although the effect was numerically very small.
Discussion
The empirical results of the present experiment are clear: masked identity priming effects were approximately the same at each quantile in the RT distributions (i.e., they involved a shift in the entire distribution); in contrast, unmasked priming effects (both identity priming and associative priming) involved a change in the spread of the RT distributions. More important, these findings can be accounted for by the diffusion model in a straightforward manner: on the one hand, masked identity priming affects the parameter corresponding to encoding processes (Ter), but not the parameter corresponding to the quality of information (drift rates); on the other hand, unmasked priming affects both parameters: the quality of information (drift rates) in both associative and identity priming, and also the encoding process (particularly for identity priming, note that in the subject-by-subject fits there as a fairly small but significant effect in the difference in Ter between the related and unrelated primes for associative unmasked priming). Therefore, masked priming is qualitatively different from unmasked priming. To our knowledge, this is the first dissociation between these two parameters in the model within the lexical decision task.
The diffusion model is a model of the decisional process in the lexical decision task, and is void of a lexicon or explicit word recognition processes. However, we can use the parameter behavior in the present work to deepen our understanding of the priming processes by interpreting existing models through the lens of the diffusion model. To this end, theories that have been verbally stated of even computationally implemented can be mapped into diffusion model parameters.
If we interpret the diffusion model fits in light of other theories, we find that our account of masked identity priming is compatible with a “savings” account, in which priming occurs mainly due to changes in encoding time (e.g., note that the value of Ter is close to that of the prime duration; see Forster, 1999), whereas unmasked priming is consistent with a compound-cue account in which prime-target relatedness increases the quality of the lexical information that drives the decision process. To our knowledge, this is the first dissociation between drift rate and Ter in the model within the lexical decision task.
The effect on Ter has several implications for theories of priming and for general theories of perceptual decision making. The assumption behind this parameter is non-trivial: there is a stage in the processing of perceptual information in which the incoming evidence is not used towards the accumulation of evidence driving the decision process (e.g., the “word” vs “nonword” decision in the lexical decision task). Hence, to make a decision about a string of letters, participants must first encode it, and only after that process is over, they can match the obtained perceptual representation against their lexical knowledge7. Within the context of evidence accumulation models as applied to lexical processes, two questions arise: (1) how is it that the system ends the accumulation-free encoding stage and begins the accumulation process (the diffusion per se)? and (2) what exactly do we mean by encoding in the domain of masked priming? Regarding the first question, Ratcliff and Smith (2010) offered two possible explanations in the context of a letter discrimination task; according to the first one, it is not until the stimulus is encoded in visual short term memory that the accumulation of evidence begins, while according to the second one, there is large inhibition of the accumulation of evidence process until the quality of the stimulus representation reaches a threshold. In their research, Ratcliff and Smith found that the effects in the first quantiles of the RT distributions only happened when a more abstract representation was needed to perform the task (i.e., there was an effect for letter discrimination but not for luminosity discrimination). Arguably, the lexical decision task requires an even more conceptual representation than their letter discrimination task. This leads us to the second issue: what in the nature of the encoding process in masked priming? Identity priming amounts to a head-start relative to an unrelated prime and identity priming does not seem to affect the quality of the lexical information in the decision; however, it does not seem to affect the quality of the lexical information. A number of models are compatible with this view, most notably, those that assume that there is some form of “reset” or “self-inhibition” mechanism (see Grainger & Jacobs, 1999) in which a mismatch between incoming sensory information (e.g., a prime and a target) triggers an inhibitory reset. Jacobs and Grainger (1992), had a similar intuition when they suggested that in an interactive-activation model based account, identity priming amounts to having a head start of a few cycles of processing (see also Adelman, 2011; Davis, 2010 for recent modeling efforts along the same lines). Note, however, that the mapping from an interactive activation model into a stochastic accumulation of evidence framework (e.g., the diffusion model) is not trivial. This is because activation of nodes in the interactive activation architecture is deterministic and errors only occur because of stochastic choice only at the very end of processing. The diffusion model represents noise in the decision process (within trial noise) and noise in the stimulus/lexical representation driving the decision process as across trial variability in drift rate.
The distinction between the encoding process and the evidence accumulation process is particularly clear in the case of identity priming for nonwords. Related nonwords (compared to their controls) are less accurate, have shorter RTs at .1, and .3 quantiles, but have longer RTs at .7 and .9 quantiles8. Identity priming seems to provide with time savings relative to the unrelated controls, while it makes it more difficult to correctly identify the string as a nonword. Modeling unmasked priming with drift-only and the Ter-only models does not allow us to capture a pattern like this. The interplay of these two parameters yields inconsistent effects of priming on nonword targets (see Perea, Gomez & Fraga, 2010 and Whitney, Bertrand, & Grainger, 2012, for discussion). Different studies might have elicited different proportions of facilitatory and inhibitory trials, and future research should try to dissociate the factors that may contribute to the encoding benefits, from the factors that may inhibit the identification of a nonword target.
It is important to note that our findings are consistent with the semantic priming experiments conducted by Balota et al. (2008). With unmasked primes, they found an increasing semantic priming effect at the higher quantiles (see Balota et al’s Figures 7 and 8) –note however that they failed to find a change in the τ parameter of the ex-Gaussian distribution.9 With masked primes, Balota and cols. found a small, nonsignificant masked semantic priming effect –as also occurred in the present experiment. Clearly, the small magnitude of masked semantic priming does not allow to make strong inferences on the precise nature of the underlying effects –note that previous experiments with masked associative/semantic priming have usually employed a large sample size to obtain a significant effect (e.g., see Perea & Lupker, 2003).
In summary, by using explicit modeling methods (i.e., fits from the diffusion model), the present lexical decision experiment has revealed that masked and unmasked priming involve different cognitive processes: related primes give a head start to the processing of the target compared to unrelated primes, whereas unmasked priming involves changes in the decision processes. This provides support for the use of the masked priming technique to examine the encoding mechanisms during the early stages of visual-word recognition.
Acknowledgments
This research was funded by grant PSI 2011-26924 from the Spain Ministry of Science to Manuel Perea, and by grants NIA R01-AG17083 and AFOSR FA9550-11-1-0130 to Roger Ratcliff
Footnotes
The model assumes variability in the z parameter, which is uniformly distributed with range sz.
For a comprehensive exploration of the behavior of these parameters in the lexical decision task, see Wagenmakers et al. (2008).
While we acknowledge that there are other potential explanations of unmasked priming, the compound cue model has three advantages: i) it provides a unified account of identity and associative priming; ii) it makes straightforward predictions in terms of the diffusion model; and iii) the idea of a compound cue has also been adopted (with some changes) in the competing view of Bodner and Masson.
The materials are available online at http://condor.depaul.edu/pgomez1/WNPL/Online_Appendices_files/materials.txt
The χ2 in Table 4 are based on group data, so they cannot properly be used as absolute measures of fit
For the Ter only model: χ2 = 81.30, and for the Ter + driftnonword model: χ2 = 74.55; hence , or an 8% improvement in the quality of the fit
It is important to note that during this stage, noise (without the signal from the stimulus) is most likely not accumulated either, as that would create a large proportion of fast errors
We explored if this pattern of results might have been produced by a combination of a few items producing facilitation while other items producing inhibition; to this end, we performed a multiple regression using all the orthographic variables as regressors and the priming effect as the dependent variable, but none of the effects were significant. We also wondered if this pattern was produced by just a handful of subjects, but 15 out of the 19 participants showed it.
In Balota et al.’s (2008) Experiments 2–3, the effect of semantic priming is assumed to be due to changes in the μ and σ components of the ex-Gaussian distribution, and not in the τ component – which is usually the responsible for the tail of the RT distribution.
Contributor Information
Pablo Gomez, DePaul University, Chicago, USA.
Manuel Perea, Universitat de València, Valencia, Spain.
Roger Ratcliff, The Ohio State University, Columbus, USA.
References
- Adelman J. Letters in time and retinotopic space. Psychological Review. 2011;118:570–582. doi: 10.1037/a0024811. [DOI] [PubMed] [Google Scholar]
- Balota D, Yap M, Cortese M, Watson J. Beyond mean response latency: Response time distributional analyses of semantic priming. Journal of Memory and Language. 2008;59:495–523. [Google Scholar]
- Bodner G, Masson M. Prime validity affects masked repetition priming: Evidence for an episodic resource account of priming 1. Journal of Memory and Language. 2001;45:616–647. [Google Scholar]
- Bodner GE, Masson MEJ. Beyond spreading activation: An influence of relatedness proportion on masked semantic priming. Psychonomic Bulletin and Review. 2003;10:645–652. doi: 10.3758/bf03196527. [DOI] [PubMed] [Google Scholar]
- Davis C. N-Watch: A program for deriving neighborhood size and other psycholinguistic statistics. Behavior Research Methods. 2005;37:65. doi: 10.3758/bf03206399. [DOI] [PubMed] [Google Scholar]
- Davis C. The spatial coding model of visual word identification. Psychological Review. 2010;117:713–758. doi: 10.1037/a0019738. [DOI] [PubMed] [Google Scholar]
- Davis C, Lupker S. Masked inhibitory priming in english: evidence for lexical inhibition. Journal of Experimental Psychology: Human Perception and Performance. 2006;32:668–687. doi: 10.1037/0096-1523.32.3.668. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Naccache L, Cohen L, Le Bihan D, Mangin J, Poline J, et al. Cerebral mechanisms of word masking and unconscious repetition priming. Nature Neuroscience. 2001;4:752–758. doi: 10.1038/89551. [DOI] [PubMed] [Google Scholar]
- Dufau S, Dunabeitia J, Moret-Tatay C, McGonigal A, Peeters D, Alario FX, et al. Smart phone, smart science: how the use of smartphones can revolutionize research in cognitive science. PLoS ONE. 2011;6:e24974. doi: 10.1371/journal.pone.0024974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forster K. The intervenor effect in masked priming: How does masked priming survive across an intervening word? Journal of Memory and Language. 2009;60:36–49. [Google Scholar]
- Forster K, Davis C. Repetition priming and frequency attenuation in lexical access. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1984;10:680–698. [Google Scholar]
- Forster K, Mohan K, Hector J. The mechanics of masked priming. In: Kinoshita S, Lupker S, editors. Masked priming: The state of the art. New York: Psychology Press; 2003. pp. 3–37. [Google Scholar]
- Gomez P, Ratcliff R, Perea M. Diffusion model of the go/no-go task. Journal of Experimental Psychology: General. 2007;136:389–413. doi: 10.1037/0096-3445.136.3.389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grainger J. Cracking the orthographic code: An introduction. Language and Cognitive Processes. 2008;23:1–35. [Google Scholar]
- Jacobs AM, Grainger J. Testing a semistochastic variant of the interactive activation model in different word recognition experiments. Journal of Experimental Psychology: Human Perception and Performance. 1992;18:1174–1188. doi: 10.1037//0096-1523.18.4.1174. [DOI] [PubMed] [Google Scholar]
- Kinoshita S, Lupker S. Masked priming: The state of the art. New York: Psychology Press; 2003. [Google Scholar]
- Kinoshita S, Mozer M, Forster K. Dynamic adaptation to history of trial difficulty explains the effect of congruency proportion on masked priming. Journal of Experimental Psychology: General. 2011;140:622–636. doi: 10.1037/a0024230. [DOI] [PubMed] [Google Scholar]
- Kinoshita S, Norris D. Masked priming effect reflects evidence accumulated by the prime. Quarterly Journal of Experimental Psychology. 2010;63:194–204. doi: 10.1080/17470210902957174. [DOI] [PubMed] [Google Scholar]
- Kucera H, Francis WN. Computational analysis of present-day American English. Providence, RI: Brown University Press; 1967. [Google Scholar]
- Neely JH. Semantic priming and retrieval from lexical memory: Roles of inhibitionless spreading activation and limited-capacity attention. Journal of Experimental Psychology: General. 1977;106:226–254. [Google Scholar]
- Nelson D, McEvoy C, Schreiber T. The university of south florida free association, rhyme, and word fragment norms. Behavior Research Methods. 2004;36:402–407. doi: 10.3758/bf03195588. [DOI] [PubMed] [Google Scholar]
- Norris D. Putting it all together: a unified account of word recognition and reaction-time distributions. Psychological Review. 2009;116:207–19. doi: 10.1037/a0014259. [DOI] [PubMed] [Google Scholar]
- Perea M, Gómez P, Fraga I. Masked nonword repetition effects in yes/no and go/no-go lexical decision: A test of the evidence accumulation and deadline accounts. Psychonomic Bulletin and Review. 2010;17:369–374. doi: 10.3758/PBR.17.3.369. [DOI] [PubMed] [Google Scholar]
- Perea M, Lupker SJ. Does jugde activate court? transposed-letter similarity effects in masked associative priming. Memory and Cognition. 2003;31:829–841. doi: 10.3758/bf03196438. [DOI] [PubMed] [Google Scholar]
- Perea M, Rosa E. Repetition and form priming interact with neighborhood density at a brief stimulus onset asynchrony. Psychonomic Bulletin and Review. 2000;7:668–677. doi: 10.3758/bf03213005. [DOI] [PubMed] [Google Scholar]
- Perea M, Rosa E. Does the proportion of associatively related pairs modulate the associative priming effect at very brief stimulus-onset asynchronies? Acta Psychologica. 2002;110:103–124. doi: 10.1016/s0001-6918(01)00074-9. [DOI] [PubMed] [Google Scholar]
- Plaut DC, Booth J. Individual and developmental differences in semantic priming: Empirical and computational support for a single-mechanism account of lexical processing. Psychological Review. 2000;107:786–823. doi: 10.1037/0033-295x.107.4.786. [DOI] [PubMed] [Google Scholar]
- Pollatsek A, Perea M, Carreiras M. Does conal prime canal more than cinal? masked phonological priming effects in spanish with the lexical decision task. Memory and cognition. 2005;33:557–565. doi: 10.3758/bf03193071. [DOI] [PubMed] [Google Scholar]
- Posner MI, Snyder CRR. Attention and performance V. London: Academic Press; 1975. Facilitation and inhibition in the processing of signals. [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Ratcliff R. A theory of order relations in perceptual matching. Psychological Review. 1981;88:552–572. [Google Scholar]
- Ratcliff R. Theoretical interpretations of the speed and accuracy of positive and negative responses. Psychological Review. 1985;92:212–225. [PubMed] [Google Scholar]
- Ratcliff R. Continuous vs. discrete information processing: Modeling accumulation of partial information. Psychological Review. 1988;95:238–255. doi: 10.1037/0033-295x.95.2.238. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Gomez P, McKoon G. A diffusion model account of the lexical decision task. Psychological Review. 2004;111:159–182. doi: 10.1037/0033-295X.111.1.159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G. A retrieval theory of priming in memory. Psychological Review. 1988;95:385. doi: 10.1037/0033-295x.95.3.385. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Perea M, Colangelo A, Buchanan L. A diffusion model account of normal and impaired readers. Brain and Cognition. 2004;55:374–382. doi: 10.1016/j.bandc.2004.02.051. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling response times for decisions between two choices. Psychological Science. 1998;9:347–356. [Google Scholar]
- Ratcliff R, Smith P. Perceptual discrimination in static and dynamic noise: the temporal relation between perceptual encoding and decision making. Journal of Experimental Psychology: General. 2010;139:70–94. doi: 10.1037/a0018128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, Gomez P, McKoon G. A diffusion model analysis of the effects of aging in the lexical-decision task. Psychology and Aging. 2004;19:278–289. doi: 10.1037/0882-7974.19.2.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. The effects of aging on reaction time in a signal detection task. Psychology and Aging. 2001;16:323–341. [PubMed] [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating parameters of the diffusion model: Approaching to dealing with contaminant reaction and parameter variability. Psychonomic Bulletin and Review. 2002;9:438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, McKoon G. Comparing connectionist and diffusion models of reaction time. Psychological Review. 1999;106:261–300. doi: 10.1037/0033-295x.106.2.261. [DOI] [PubMed] [Google Scholar]
- Rumelhart DE, Siple P. Process of recognizing tachistoscopically presented words. Psychological Review. 1974;81:99–118. doi: 10.1037/h0036117. [DOI] [PubMed] [Google Scholar]
- Vincent SB. The function of vibrissae in the behavior of the white rat. Behavioral Monographs. 1912;1 Whole No. 5. [Google Scholar]
- Wagenmakers EJ, Ratcliff R, Gomez P, McKoon G. A diffusion model account of crierion shifts in the lexical decision task. Journal of Memory and Language. 2008;58:140–159. doi: 10.1016/j.jml.2007.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitney C, Bertrand D, Grainger J. On coding the position of letters in words: A test of two models. Experimental Psychology. 2012;59:109–114. doi: 10.1027/1618-3169/a000132. [DOI] [PubMed] [Google Scholar]
- Yap M, Tse C, Balota D. Individual differences in the joint effects of semantic priming and word frequency revealed by RT distributional analyses: The role of lexical integrity. Journal of Memory and Language. 2009;61:303–325. doi: 10.1016/j.jml.2009.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]


