Outlier identification in radiation therapy knowledge‐based planning: A study of pelvic cases

Abstract

Purpose

The purpose of this study was to apply statistical metrics to identify outliers and to investigate the impact of outliers on knowledge‐based planning in radiation therapy of pelvic cases. We also aimed to develop a systematic workflow for identifying and analyzing geometric and dosimetric outliers.

Methods

Four groups (G1–G4) of pelvic plans were sampled in this study. These include the following three groups of clinical IMRT cases: G1 (37 prostate cases), G2 (37 prostate plus lymph node cases) and G3 (37 prostate bed cases). Cases in G4 were planned in accordance with dynamic‐arc radiation therapy procedure and include 10 prostate cases in addition to those from G1. The workflow was separated into two parts: 1. identifying geometric outliers, assessing outlier impact, and outlier cleaning; 2. identifying dosimetric outliers, assessing outlier impact, and outlier cleaning. G2 and G3 were used to analyze the effects of geometric outliers (first experiment outlined below) while G1 and G4 were used to analyze the effects of dosimetric outliers (second experiment outlined below).

1. A baseline model was trained by regarding all G2 cases as inliers. G3 cases were then individually added to the baseline model as geometric outliers. The impact on the model was assessed by comparing leverages of inliers (G2) and outliers (G3). A receiver‐operating‐characteristic (ROC) analysis was performed to determine the optimal threshold. The experiment was repeated by training the baseline model with all G3 cases as inliers and perturbing the model with G2 cases as outliers.

2. A separate baseline model was trained with 32 G1 cases. Each G4 case (dosimetric outlier) was subsequently added to perturb the model. Predictions of dose‐volume histograms (DVHs) were made using these perturbed models for the remaining 5 G1 cases. A Weighted Sum of Absolute Residuals (WSAR) was used to evaluate the impact of the dosimetric outliers.

Results

The leverage of inliers and outliers was significantly different. The Area‐Under‐Curve (AUC) for differentiating G2 (outliers) from G3 (inliers) was 0.98 (threshold: 0.27) for the bladder and 0.81 (threshold: 0.11) for the rectum. For differentiating G3 (outlier) from G2 (inlier), the AUC (threshold) was 0.86 (0.11) for the bladder and 0.71 (0.11) for the rectum. Significant increase in WSAR was observed in the model with 3 dosimetric outliers for the bladder (P < 0.005 with Bonferroni correction), and in the model with only 1 dosimetric outlier for the rectum (P < 0.005).

Conclusions

We established a systematic workflow for identifying and analyzing geometric and dosimetric outliers, and investigated statistical metrics for outlier detection. Results validated the necessity for outlier detection and clean‐up to enhance model quality in clinical practice.

1. Introduction

Knowledge‐based planning (KBP) in radiation therapy has been widely investigated.^{1, 2, 3, 4, 5, 6, 7, 8} KBP aims to provide treatment‐planning guidance, such as dose‐volume objectives and objective function weights. A recent commercial KBP software, RapidPlan (Varian Medical Systems, Palo Alto, USA), has been developed and introduced to the Eclipse treatment‐planning system. Several pre‐clinical studies have been performed to evaluate its ability in guiding treatment planning.^{9, 10} A study by Tol et al. found that plans generated with RapidPlan were comparable to clinical plans when the anatomy geometry was within range of the training cases.⁹ In addition, Fogliata et al. found that plans generated with the assistance of RapidPlan exhibited improved dosimetric performance compared to the benchmark clinically accepted plans.¹⁰ These studies confirm the feasibility of implementing KBP into the clinical environment.

To build a model that is generalizable to new cases, multiple factors need to be considered in the modeling and application process. These factors include the range of the features versus the range of the features’ potential clinical coverage, the model training data size, the existence of outliers in the training data, etc. The range of the features is the distribution of the features of all cases. This is necessary for geometric outlier detection because the model may not be applicable to a new case if its feature is out of the range. The potential clinical coverage refers to the applicable treatment site of the model. For example, “prostate model” describes models applicable to prostate cases. Boutilier et al. analyzed the minimal required training sample size for predicting dose‐volume histogram (DVH) points, DVH curves and the objective function weight.¹¹ Outlier detection has been heavily studied to identify anomalies among data.^{12, 13, 14, 15, 16, 17, 18, 19, 20, 21} Outliers deviate from other observations and may be generated by a different mechanism.^{22, 23} Due to the negative effect on the statistical analysis, such as increased error variance and reduced power of statistical tests, it is recommended to check for the existence of the outliers.²⁴

Outliers have been shown to have an effect on radiation therapy KBP. For example, Delaney et al. analyzed the effect of dosimetric outliers and demonstrated moderate degradation of model quality coinciding with the occurrence of dosimetric outliers. However, questions still remain for outlier identification in radiation therapy KBP. First, no study has been conducted so far to assess the effectiveness of outlier identification. Second, the impact of geometric outliers has not been analyzed. To answer these questions, we adopted leverage and studentized residual to aid in identifying geometric and dosimetric outliers, and analyzed how to use the metric for outlier identification. In addition, our study aimed to evaluate the impact of geometric and dosimetric outliers, respectively, and to answer the question of whether cleaning geometric or dosimetric outliers is necessary. The results of this study allow us to develop a systematic workflow for identifying and analyzing geometric and dosimetric outliers.

2. Materials and methods

2.A. Materials

Four groups of radiation therapy treatment plans in prostate regions were included in this study: group 1 (G1), with 37 low‐to‐intermediate risk prostate cases; group 2 (G2), with 37 high risk prostate cases treated with lymph node (LN) irradiation; group 3 (G3), with 37 prostate bed irradiation cases; and group 4 (G4), with 10 extra low‐to‐intermediate risk prostate cases in addition to those in G1. For G1‐G3 cases, we used the intensity modulated radiation therapy (IMRT) plans designed for clinical treatment. The G4 cases were re‐planned using the dynamic conformal arc technique (DARC). G2 and G3 represented the geometric variations relative to each other, i.e., the geometric/anatomic outliers. G2 and G3 were used to analyze geometric outliers, i.e., one group served as the inlier cases while the other group served as the outlier cases. The DARC plans in G4, which did not represent any current clinical treatment techniques, were used to simulate dosimetric outliers to G1. G1 and G4 were used to analyze dosimetric outliers, i.e., G1 served as the inlier cases while G4 served as the outlier cases. Figure 1 shows an example of the anatomy and dose distribution of four groups.

Figure 1.

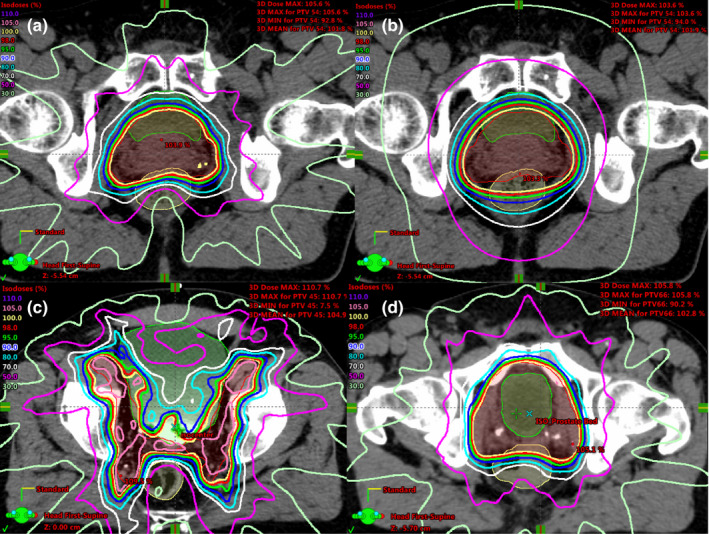
An example of the anatomy and dose distribution of G1–G4 cases: (a) a prostate case (G1) shown with the clinical IMRT dose distribution; (b) the same prostate case from (a) shown with the DARC dose distribution (G4); (c) a prostate plus LN case with the clinical IMRT dose distribution (G2); (d) a prostate bed case (G3) with the clinical IMRT dose distribution. [Color figure can be viewed at wileyonlinelibrary.com]

2.B. Model algorithm and study design

In this study, we used the KBP algorithm previously implemented by Yuan et al.⁴ This algorithm correlates the DVH (output) with geometry features (input). The algorithm uses 22 geometry features including distance‐to‐target histograms (DTH) of the first three principal components (PCs), the overlap portion of organs‐at‐risk (OARs), and organ volume. A detailed list of the features is shown in Table 1. A stepwise multiple‐regression is performed to build the model.

Table 1.

The OAR anatomical features analyzed in the algorithm implemented by Yuan et al. There were 11 features for each OAR relative to one planning target volume (PTV). One primary PTV and one boost PTV could be included. In this study, only the primary PTV was included

Anatomical features
Distance‐to‐target histogram (DTH) principal component 1 (PC1)
DTH PC2
DTH PC3
Fraction of OAR volume overlapping with the PTV
Fraction of OAR volume outside the treatment field
OAR volume
PTV volume
OAR wrap angle around the PTV
(DTH PC1)2
PTV dose volume point 1 (PTV D2%)a
PTV dose volume point 2 (PTV D50%)a

^aPTV dose volume points were included to take into consideration of the OAR sparing variation among plans, since overly spared OAR can result in less homogenous PTV dose. This variation was adjusted by standardizing the dose volume point of training cases and set 0 for the new cases.

The first part of this study focused on geometric/anatomic outliers. In particular, the statistical metric of leverage was studied for identifying the geometric outliers, and the mean Weighted Sum of Absolute Residuals (WSAR) was studied for assessing the impact of the existence of geometric outliers.

The leverage metric is used to identify geometric outliers within a training dataset during modeling. It can also be used to determine whether a new case is a geometric outlier of an existing model. The WSAR evaluates the effect of geometric outliers in a model and provides guidance whether cleaning up/excluding the outliers would be necessary to improve the modeling accuracy.

An outline of the outlier analysis is shown in Fig. 2. In the first experiment (top), each plan from the prostate plus LN group (G2) was individually added to the prostate bed model (G3) to serve as a geometric outlier. This process was repeated by individually adding each plan from the prostate bed model (G3) to the prostate plus LN group (G2). The anatomies of the G2 and G3 cases were different, mimicking the process of introducing large geometric variation in the model. The leverage was calculated for the inliers and outliers, and a receiver‐operating‐characteristic (ROC) analysis was performed to determine the optimal threshold. In the second experiment, geometric outliers were gradually added to the model to assess the impact, i.e., the prostate plus LN (G2) cases were gradually added to the prostate bed (G3) model and the prostate bed (G3) cases were gradually added to the prostate plus LN (G2) model. These models with geometric outliers were then evaluated to assess the impact on prediction accuracy from the inclusion of geometric outliers. In the third experiment, each dosimetric outlier from the DARC prostate group (G4) was added to the prostate (G1) model individually, and the model was trained with the corresponding outlier. The mean studentized residual of the dosimetric outlier from each experiment was recorded. In the fourth experiment, the DARC prostate (G4) cases were gradually added to the prostate (G1) model to assess the model quality change.

Figure 2.

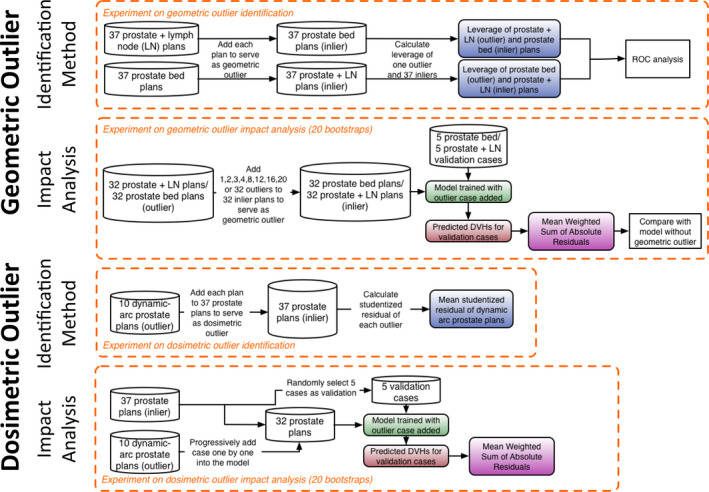
Flowchart of the experiment on the geometric outlier identification (top), geometric outlier impact analysis (second row), dosimetric outlier identification (third row), and dosimetric outlier impact analysis (bottom). [Color figure can be viewed at wileyonlinelibrary.com]

2.C. Geometric outlier identification

In this part of study, the existence of geometric outlier was simulated by adding cases from one treatment group to the model from another group. First, a base model was trained with all G3 cases. Second, a geometric outlier, i.e., the prostate plus LN (G2) case, was individually added to the base model. The leverage is used to identify geometric outliers by identifying features that are far from the population mean. The leverage score of each training case is defined as

$$h_i={(H)}_{ii}$$ (1)

where h _i is the $ith$ diagonal element of the hat matrix $H=X{(X^{T}X)}^{-1}{X}^T$, and $X$ is the feature matrix. A feature matrix is an m‐by‐n matrix where m is the number of training cases and n is the number of features. Stepwise regression was performed as part of the model training to select predictive features. The number of the selected features, n, varied between 1 and 5, and the selected feature subset was chosen as the feature matrix. Each element in the feature matrix is a scaler that quantifies a particular feature for a particular training case.

The leverage statistics of inlier cases (G3) and outlier cases (G2) were recorded and the likelihood that the leverage of a randomly selected outlier is greater than that of a randomly selected inlier was assessed via Wilcoxon Rank‐Sum test. A ROC analysis evaluated the performance of the leverage as a classifier to identify the geometric outlier. The inlier G3 cases were considered as condition negative and the outlier G2 cases were considered as condition positive. A leverage value larger than the threshold was considered as predicted condition positive while a leverage smaller than the threshold was considered as predicted condition negative. The sensitivity and specificity were calculated by varying the leverage threshold. The leverage of all inliers and outliers were pooled together and sorted ascendingly. The leverage threshold varied among the mean of two adjacent leverage values. The Youden's J index²⁵ was calculated to find the optimal threshold for differentiating the geometric inliers and outliers. The optimal threshold has the largest difference between the true positive rate and the false negative rate. This workflow was repeated by adding the prostate bed (G3) cases to the base model trained with the prostate plus LN (G2) cases. The flowchart is shown on the top row in Fig. 2.

To validate the effectiveness of using the leverage as a geometric outlier identification tool, a leave‐one‐out cross validation was performed. For each of the 37 geometric outlier cases, the optimal threshold was calculated using the other 36 cases. This threshold was then applied on this left‐out case. If the leverage of this case is larger than the calculated threshold, it is marked as “detected”. The detection rate of all 37 geometric outlier cases was reported for both the bladder and the rectum using the G2 and G3 cases as geometric outliers.

2.D. Impact on model accuracy and necessity of cleaning geometric outliers

In this part of the study, 32 cases were randomly selected from G3 to train a base model and then 1, 2, 3, 4, 8, 12, 16, 20, and 32 G2 cases were added to the base model to mimic different percentage of geometric outliers (3%, 6%, 9%, 13%, 25%, 38%, 50%, 63%, and 100%) in the modeling process and assess the impact of modeling accuracy. This resulted in nine knowledge models, in addition to the base model. Finally, five G3 cases other than the 32 cases used for training formed the validation cohort. This workflow was repeated by adding G3 cases to the base model trained with the G2 cases.

The mean WSAR of the validation cases was calculated for the base model and the nine models trained with different numbers of geometric outliers. The WSAR is given as

$$WSAR=\sum _{D=1}^{100}{w}_D·\left|V_{c,D}-V_{p,D}\right|·\mathrm{\Delta }D$$ (2)

where $V_{c,D}$ is the dose volume point for the clinical DVH at bin $D$; $V_{p,D}$ is the dose volume point for the predicted DVH at bin $D$. The factor $w_D$ is the normalized weight for each bin. Each weight varies from 50 for the 1st bin to 90 for the 100th bin, and is divided by the sum of weights of all bins. The bin width is $\mathrm{\Delta }D$. This set of weighting penalizes more toward high dose regions, which is in correspondence with the clinical focus placed on the OAR dose.

The experiment was repeated 20 times with randomly selected training and validation cases. Statistical significance of the difference between the model with and without geometric outliers was calculated using Wilcoxon Rank‐Sum test. A Bonferroni correction was applied for multiple comparisons. The significance level was adjusted as $\mathit{\alpha }=0.5/m$, where $m$ is the number of hypothesis. Since there were nine hypotheses, the significance level was set at 0.0056. The flowchart is shown in the second row in Fig. 2.

2.E. Dosimetric outlier identification

The presence of the dosimetric outliers alters the correlation between the geometry and dose distribution. The studentized residual can be used to aid the identification of dosimetric outliers. The studentized residual $r_i$ is defined as:

$$r_i=\frac{e_i}{s(e_i)}$$ (3)

where $e_i=y_i-{\tilde{y}}_i$, $y_i$ is the response variable for $i$ and $\tilde{y}$ is the regression prediction for $i$. The denominator, $s(e_i)$, is the standard deviation of the prediction error. A studentized residual of 3 was chosen as the outlier threshold. For the scenario when the model is trained but no cleaning has been performed, a studentized residual larger than 3²⁶ can signal the existence of dosimetric outliers. A new case can be added to the training cohort to train a new model and the studentized residual will be calculated to identify outliers.

The current algorithm decomposed the DVH curve into PCs and the first four PCs were used to build the model. Since the first PC of the DVH accounts for most of the variation in the DVH curve, we focus on the regression of the first PC of the DVH for the outlier analysis.

In this study, we used the prostate cases planned with DARC (G4) that did not aim to spare the OAR to simulate dosimetric outliers. The DARC plans can simulate dosimetric outliers because they do not strive to spare the dose to the OARs and often result in higher doses. The DVH of the DARC plan is higher than that of the IMRT plan for all dose regions, and therefore results in higher score in the DVH first PC.⁴ For this reason, the G4 cases simulate negative outliers (positive studentized residual) once they are added to the model. Each outlier case was individually added to the prostate case (G1) dataset to train the model and obtain the studentized residual. The mean studentized residual of the outlier cases under this simulation scenario was reported for both the bladder and rectum. The flowchart is shown in the third row in Fig. 2.

2.F. Impact of dosimetric outliers on model accuracy

The impact of dosimetric outliers was determined by gradually adding multiple DARC prostate (G4) cases into the clinical prostate IMRT cohort (G1).⁴

The base model for the dosimetric outlier analysis was trained with 32 cases from G1 with the remaining five cases from G1 reserved as the validation cases. Each of the 10 dosimetric outlier cases in G4 was then progressively added to the new base model. Since the outliers introduced were all negative, a monotonic degradation of the model quality was anticipated as the number of outlier increased. The performance of the model was evaluated by the WSAR.

The experiment was repeated 20 times via bootstrapping. The WSAR of the models with dosimetric outliers was compared to that of the base model (i.e., without outlier) via Wilcoxon Rank‐Sum test. A Bonferroni correction was applied for multiple comparisons. Since there were 10 hypotheses, the significance level was set at 0.005. The flowchart is shown in the bottom row in Fig. 2.

3. Results

3.A. Leverage of geometric outliers

The mean and standard deviation of the leverage of the inlier and outlier cases are shown in Table 2. The mean of the leverage of the inlier cases was smaller than the corresponding mean of the outlier cases. The difference between the leverage of the inlier and outlier cases was significant (P < 0.0001). Boxplots of the leverage are shown in Fig. 3. The largest separation of the leverage distributions occurred in the bladder when the prostate plus LN cases were added to the prostate bed model. This is in good agreement with the anatomical difference of the two plans. When adding the prostate bed cases to the prostate plus LN cases, the leverage distribution was less separated than adding the prostate plus LN cases to the prostate bed cases. The AUC, used to differentiate the prostate plus LN case (G2) from the prostate bed cases (G3), was 0.98 (threshold: 0.27) for the bladder, and 0.81 (threshold: 0.11) for the rectum. For differentiating the prostate bed case (G3) from the prostate plus LN cases (G2), the AUC was 0.86 (threshold: 0.11) for the bladder and 0.71 for the rectum (threshold: 0.11). The leverage could be used as a metric for identifying the geometric outlier as reflected by the AUC value.

Table 2.

The mean and standard deviation (SD) of the leverage of the inlier and outlier group for various models trained with the geometric outliers in the first experiment. The leverage of both the inlier and outlier under the scenario of adding the prostate plus LN (G2) case to the prostate bed (G3) model is shown in the first row. Addition of the prostate bed (G3) case to the prostate plus LN (G2) model is shown in the second row. The statistical significance was calculated via Wilcoxon Rank‐Sum test

	(Mean, SD)		P value		(Mean, SD)		P value
	Inlier	Outlier			Inlier	Outlier
G2 + G3 Bladder	(0.11, 0.09)	(0.62, 0.22)	<0.001	G2 + G3 Rectum	(0.09, 0.09)	(0.25, 0.26)	<0.001
G3 + G2 Bladder	(0.08, 0.11)	(0.24, 0.19)	<0.001	G3 + G2 Rectum	(0.10, 0.08)	(0.15, 0.10)	<0.001

Figure 3.

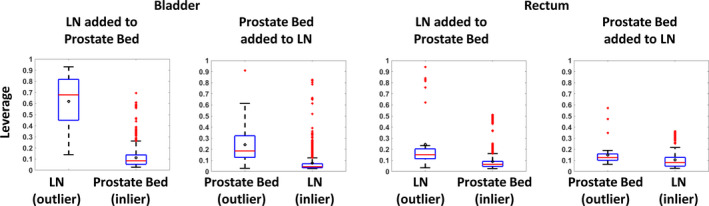
Boxplots of the leverage distribution of the outliers and inliers in the first experiment. The leverage distribution of the bladder model is shown on the left two subplots and the rectum model is shown on the right two subplots. Each geometric outlier case was added to the model and the leverage of the one geometric outlier LN/prostate bed case and the other 37 inlier prostate bed/LN cases was recorded. After adding all geometric outlier cases, the leverage statistics of the inliers and outliers were pooled to compose the boxplot. The leverage characterizes the distance of the data from the population mean and ranges from 0 to 1. The box edges bound the interquartile range. The horizontal bar in the box denotes the median. The mean is represented as the circle. The whiskers extend to the extreme data point within 1.5 times the interquartile range from the 25th/75th percentile. Data points beyond the whiskers are denoted as “+”. [Color figure can be viewed at wileyonlinelibrary.com]

The usage of the leverage as a geometric outlier identification tool was validated using leave‐one‐out cross validation. For the bladder, the sensitivity (predicted outlier cases divided by total outlier cases) of the prostate plus LN (G2) cases from the prostate bed (G3) cases was 92% (34/37), and the sensitivity of the prostate bed (G3) cases from the prostate plus LN (G2) cases was 76% (28/37). For the rectum, the sensitivity was 76% (28/37) and 73% (27/37), respectively.

3.B. Impact of geometric outliers on model accuracy

The mean WSAR for the base model and the nine models trained with 1/2/3/4/8/12/16/20/32 geometric outlier cases is plotted in Fig. 4. For the bladder, significant degradation in model accuracy was observed upon adding 16 G2 cases into the G3 model (P = 0.0080, 0.0010 for adding 12 and 16 G2 cases into the G3 model at 0.0056 significance level). Adding the G3 cases into the G2 model did not degrade the model quality at significance level (P > 0.0056 for all models). For the rectum, adding 32 G2 cases into the G3 model degraded the model quality (P < 0.0001 for adding 32 G2 cases into the G3 model). Adding the G3 cases into the G2 model did not degrade model quality. These results show a negative impact of the geometric outliers on the bladder and suggest a need to identify them to improve the model quality.

Figure 4.

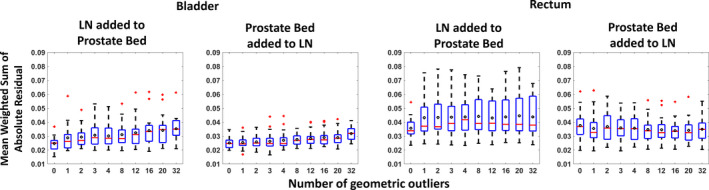
Distributions of the mean Weighted Sum of Absolute Residuals for the models versus the number of geometric outliers (LN/prostate bed) added. The WSAR distribution of the bladder model is shown on the left two subplots and the rectum model is shown on the right two subplots. The edges of the box bound the interquartile range. The horizontal bar in the box denotes the median. The mean is represented as the circle. The whiskers extend to the extreme data point within 1.5 times the interquartile range from the 25th/75th percentile. Data points beyond the whiskers are denoted as “+”. 1/2/3/4/8/12/16/20/32 geometric outliers (LN/prostate bed) were progressively added to the prostate bed/LN model with 32 cases and the model quality change was reflected by the WSAR. The WSAR was recorded for each bootstrap and the experiment was repeated 20 times. After adding 16 prostate plus LN cases into the prostate bed cases, the bladder model observed significant model quality change. Adding 32 prostate bed cases into the prostate plus LN cases degraded the model quality (P < 0.0001). Adding the prostate plus LN cases into the prostate bed model or adding the prostate bed cases into the prostate plus LN model did not change the rectum model quality at P = 0.0056. [Color figure can be viewed at wileyonlinelibrary.com]

3.C. Studentized residual of dosimetric outliers

Each of the 10 dosimetric outliers was added to the prostate model. The mean studentized residual of the dosimetric outlier cases was 10.06 for the bladder model and 9.87 for the rectum model. The corresponding mean studentized residual of the inlier cases was −0.12 for the bladder model and −0.12 for the rectum model. The positive studentized residual signals negative dosimetric outliers such that the original response variable (DVH PC1) in the model is higher than the model prediction. The negative outliers are associated with suboptimal OAR sparing while positive outliers are related to better OAR sparing than the model prediction. The positive outliers have a less detrimental clinical impact than the negative outliers, and were kept in the model.²⁷

3.D. Impact of dosimetric outliers on model accuracy

The WSAR of the validation cases is plotted in Fig. 5 with versus the number of dosimetric outlier cases introduced into the model. Increasing the number of dosimetric outlier cases increases the mean WSAR for both the bladder and rectum. For the bladder, a significant difference in the WSAR was observed for the model trained with three outliers (P = 0.0038 for three outliers; significance level of 0.005). For the rectum, a single outlier was enough to create significant difference (P = 0.0003 for 1 outlier) in the model.

Figure 5.

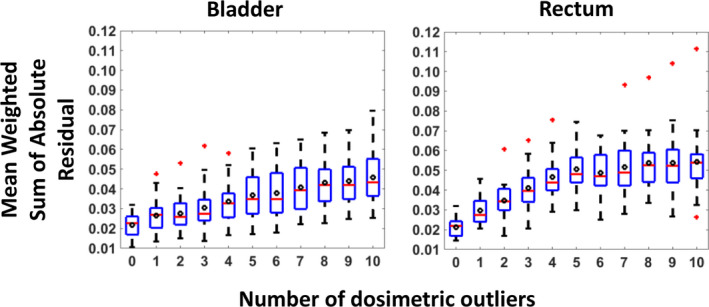
The Mean Weighted Sum of Absolute Residuals distribution of the prediction from the models trained with different numbers of outliers. The edges of the box bound the interquartile range. The horizontal bar in the box denotes the median. The mean is represented as the circle. The whiskers extend to the extreme data point within 1.5 times the interquartile range from the 25th/75th percentile. Data points beyond the whiskers are denoted as “+”. The dosimetric outlier cases were progressively added to the model until all 10 outlier cases were added. There were a total of 11 models with varying dosimetric outliers existing in the model from 0 to 10. Each model predicted the DVH curve for 5 validation prostate cases not used in the model training. The experiment was bootstrapped 20 times. At each bootstrap, the mean Weighted Sum of Absolute Residuals of the 5 validation prostate cases was recorded and all 20 bootstraps were plotted in the figure. Adding three dosimetric outlier cases affected the bladder model quality while adding only 1 dosimetric outlier case affected the rectum model quality. [Color figure can be viewed at wileyonlinelibrary.com]

4. Discussion

Careful analysis of both geometric and dosimetric outliers is an important step for maintaining and improving model quality in knowledge model development. In this study, we established a systematic workflow for identifying and analyzing geometric and dosimetric outliers. We found that the leverage can be an effective metric for identifying geometric outliers in radiation therapy knowledge‐based planning. The simulation showed negative impact of geometric outliers on the bladder model, and the dosimetric outliers on both the bladder and rectum model. The impact of dosimetric outliers is more prominent than that of geometric outliers. The regression model uses ordinary least squares (OLS) fit which fits a regression line by minimizing the sum of the squares of residuals (true observation minus regression prediction). The geometric inliers and outliers vary in the geometric feature distribution. The introduction of geometric outliers causes the regression line to pivot against the feature mean (within inlier range) to better capture the geometric outliers. However, the perturbation of the regression line within range of inliers caused by the geometric outliers is relatively small. In contrast, the dosimetric outliers introduce large prediction variation within the feature range of inliers. OLS fit tends to shift the regression line toward the dosimetric outliers to capture this variation, introducing more prominent degradation.

The results showed that the geometric outliers affected the model quality of the bladder significantly, but not that of the rectum. This is partly due to the relatively small geometrical variation between the PTV and rectum across three subsets, as well as similar plan quality of the geometric inlier and outlier cases. The existence of geometric outliers deserves attention since even small variations among the three sub‐types of pelvic cancer cases showed significant degradation in one of the OARs. The trend of the worsening model quality degradation as the number of outlier increases further indicates the need to handle geometric outliers. We identified geometric and dosimetric outliers separately in this study. Metrics that indicate both geometric and dosimetric outliers could potentially be valuable to clinical practice beyond knowledge modeling. Further research in this direction is warranted.

The KBP algorithm⁴ in this study employs a stepwise multiple‐regression to learn the relation between the anatomic and dosimetric features. A limitation of stepwise regression is the tendency of selecting inconsistent feature subset when the training sample is small.²⁸ Other regression models such as LASSO, ridge regression, and elastic nets may improve feature selection and overall prediction accuracy, and are worth investigating.

Previous studies investigated various methods for training good models.^{11, 27, 29} Wang et al. employed Pareto‐optimal prostate plans to build and validate the OVH‐based model.²⁹ This method makes it possible to develop models without the concerns of plan quality variations or dosimetric outliers. Unfortunately, routine clinical plans are known to include some that are not Pareto‐optimal. We propose a workflow to inspect the training cases made up of routine clinical plans, which could potentially include both geometric and dosimetric outliers. The result of our study agreed with Delaney et al.'s study on the deterioration effect of dosimetric outliers. Our study investigated both geometric outlier and dosimetric outliers using a statistical method. The results suggest the need to identify and clean the geometric outliers prior to treating the dosimetric outliers.

Extreme caution is recommended when predicting dose‐volume endpoints for a geometric outlier case, since the dosimetry‐anatomy relation for such geometric outlier cases may not be fully captured and represented by the model. Therefore, when implementing the model to make predictions, it is important to compare the feature of the query case with that of the training cases. If the case is indeed a geometric outlier, a different model needs to be applied. It is possible that the case shows novel geometric patterns that have never been seen by any available model. In this situation, the human planner will be required to iteratively generate a clinically acceptable plan without the model and feed this case together with the plan into the model as new knowledge. Removing geometric outliers will reduce the variation of the anatomy within a model and thus result in more models necessary to cover all cases. Building a model that can predict equally well for all cases is one possible solution and requires further study.

The clinical impact of the model degradation due to dosimetric outliers was demonstrated with one example case illustrated below. A prostate model without a dosimetric outlier and a prostate model with 10 dosimetric outliers were tested on a fresh prostate case that was not used to train the models. The predicted DVH curves from both models were used to extract the dose‐volume objectives for both the bladder and rectum to guide treatment planning.³⁰ As shown in Fig. 6, the prediction from the outlier‐added model was less favorable than that of the outlier‐free‐model which agreed better with the clinical plan DVH. The prediction guided plan DVH agreed well with the prediction for both models. The two prediction guided plan DVHs differed in the medium‐to‐high dose region. This example demonstrates that the model quality degradation could result in degradation of the final plan quality.

Figure 6.

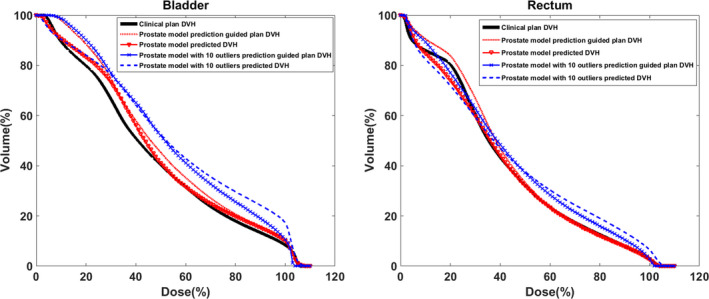
The comparison of the clinical plan DVH, model predicted DVHs, and prediction guided plan DVHs in the bladder (left) and the rectum (right) one of an example prostate case. The thick solid line is the clinical plan DVH. The triangle dotted line is the predicted DVH from the prostate model without the dosimetric outlier. The dotted line is the outlier‐free prostate model prediction guided plan DVH. The dash line is the predicted DVH from the prostate model with 10 dosimetric outliers. The “x” dotted line is the 10 outliers added prostate model prediction guided plan DVH. [Color figure can be viewed at wileyonlinelibrary.com]

There are several limitations in this study. First, the baseline KBP model was currently trained with cases from the same treatment site. To analyze the impact of geometric outliers, plans from abdominal sites other than the site(s) used to build the model were considered as geometric outliers. For example, a prostate‐bed case was a geometric outlier for a prostate plus LN model, but due to the variability of the cancer target shape and the availability of training cases, it is unclear whether it is more advantageous to build model on individual sites or on a combination of cases from some or all sites. This will affect the cases that are likely outliers or inliers. These questions are beyond the scope of this study and will require further investigation. Second, radiation therapy plans generated using DARC were treated as dosimetric outliers when added to the single‐site (prostate) model. Dosimetric outliers resulted in degraded model quality so the cleaning process is recommended. The detected dosimetric outlier case is excluded from the training cohort or a re‐plan can be ordered to improve the plan quality so that this case can be included again for model training. An outlier often arises from abnormal mechanism, e.g., treatment modality in this study, or may accumulate due to a treatment protocol change at an institution. Further investigation about updating models is warranted. Third, the dosimetric outliers introduced were all negative outliers with positive studentized residual in regression. Negative outliers often exist in the plans where the dose to the OAR is not fully minimized, such as in the DARC technology. We designed this experiment setup to answer the question whether and how insufficiently spared dosimetric outliers affect the model quality. We note that positive outliers where the OAR dose was overly minimized could also exist in the clinical cases. The positive outliers are the cases where the OAR is better spared than the model prediction. OAR over‐sparing is often related to tradeoff between multiple OARs. Although over‐sparing for such organ does not degrade the quality for this organ, the tradeoff choice may make other OAR's sparing objectives unachievable. Thus, the analysis of positive outliers requires modeling multiple OARs. Further investigation is warranted to deal with this scenario. Last, the leverage was used as the metric to identify the geometric outliers. The leverage statistic is able to reflect the distance of each datum point to the mean of the population so that the cases can be inspected according to the sequence of the leverage statistics. The leverage is able to identify geometric outlier cases one by one. Instead of leverage, a cluster‐based method could also be employed in KBP outlier detection. One cluster can be generated around the bulk of data while the observations outside the cluster frontier will be identified as the outliers. This method is capable of identifying multiple outliers at the same time.

5. Conclusions

We established a systematic workflow for identifying and analyzing geometric and dosimetric outliers. The leverage and studentized residual have demonstrated effectiveness in identifying geometric and dosimetric outliers respectively in the training datasets. Results in this study clearly illustrated that the existence of both geometric and dosimetric outliers degraded the model prediction accuracy and the process of identifying and cleaning them is necessary. The recommended workflow provides a solution to generate high quality knowledge models to improve patient care in radiation therapy.