Abstract
Purpose
In‐treatment imaging using an electronic portal imaging device (EPID) can be used to confirm patient and tumor positioning. Real‐time tumor tracking performance using current digital megavolt (MV) imagers is hindered by poor image quality. Novel EPID designs may help to improve quantum noise response, while also preserving the high spatial resolution of the current clinical detector. Recently investigated EPID design improvements include but are not limited to multi‐layer imager (MLI) architecture, thick crystalline and amorphous scintillators, and phosphor pixilation and focusing. The goal of the present study was to provide a method of quantitating improvement in tracking performance as well as to reveal the physical underpinnings of detector design that impact tracking quality. The study employs a generalizable ideal observer methodology for the quantification of tumor tracking performance. The analysis is applied to study both the effect of increasing scintillator thickness on a standard, single‐layer imager (SLI) design as well as the effect of MLI architecture on tracking performance.
Methods
The present study uses the ideal observer signal‐to‐noise ratio (d′) as a surrogate for tracking performance. We employ functions which model clinically relevant tasks and generalized frequency‐domain imaging metrics to connect image quality with tumor tracking. A detection task for relevant Cartesian shapes (i.e., spheres and cylinders) was used to quantitate trackability of cases employing fiducial markers. Automated lung tumor tracking algorithms often leverage the differences in benign and malignant lung tissue textures. These types of algorithms (e.g., soft‐tissue localization – STiL) were simulated by designing a discrimination task, which quantifies the differentiation of tissue textures, measured experimentally and fit as a power‐law in trend (with exponent β) using a cohort of MV images of patient lungs. The modeled MTF and NPS were used to investigate the effect of scintillator thickness and MLI architecture on tumor tracking performance.
Results
Quantification of MV images of lung tissue as an inverse power‐law with respect to frequency yields exponent values of β = 3.11 and 3.29 for benign and malignant tissues, respectively. Tracking performance with and without fiducials was found to be generally limited by quantum noise, a factor dominated by quantum detective efficiency (QDE). For generic SLI construction, increasing the scintillator thickness (gadolinium oxysulfide – GOS) from a standard 290 μm to 1720 μm reduces noise to about 10%. However, 81% of this reduction is appreciated between 290 and 1000 μm. In comparing MLI and SLI detectors of equivalent individual GOS layer thickness, the improvement in noise is equal to the number of layers in the detector (i.e., 4) with almost no difference in MTF. Further, improvement in tracking performance was slightly less than the square‐root of the reduction in noise, approximately 84–90%. In comparing an MLI detector with an SLI with a GOS scintillator of equivalent total thickness, improvement in object detectability is approximately 34–39%.
Conclusions
We have presented a novel method for quantification of tumor tracking quality and have applied this model to evaluate the performance of SLI and MLI EPID designs. We showed that improved tracking quality is primarily limited by improvements in NPS. When compared to very thick scintillator SLI, employing MLI architecture exhibits the same gains in QDE, but by mitigating the effect of optical Swank noise, results in more dramatic improvements in tracking performance.
Keywords: EPID, ideal observer, MTF, multi‐layer detector, NPS, portal imaging
1. Introduction
Lung tumors may exhibit substantial intrafractional respiratory motion sometimes accompanied by baseline drift.1, 2 This motion reduces the accuracy of radiotherapy delivery, necessitating the use of enlarged treatment margins to ensure adequate delivery of radiation to the target.
When deployed during radiation therapy delivery, electronic portal imaging devices (EPIDs) enable anatomical visualization from the beam's‐eye‐view.3, 4 Tumor tracking protocols designed with3 and without5, 6 fiducial markers are limited by EPID image quality. The low quantum detective efficiencies (QDE), or absorption, at megavoltage (MV) energies result in images with very high noise and low inherent contrast. Similarly, detective quantum efficiencies (DQE) for MV EPID images have been measured to be around ~2%.7
Recently, much work has been devoted to the improvement of EPID image quality through the advancement of detector design. Concepts including (but not limited to) multi‐layer imager (MLI) design, scintillator pixilation,8 and structured phosphors,9, 10 have been proposed to improve EPID DQE and image quality. Previous studies have investigated the effect of acquisition technique and detector performance on tracking quality.11, 12 In the present study, we develop a generalized platform for analyzing the relationship between image quality and tracking performance. Using standard imaging metrics, such as modulation transfer function (MTF) and noise power spectrum (NPS), the efficacy of tumor tracking either with or without the use of fiducial markers may be analyzed for clinically available and theoretical imagers. This methodology is applied to analyze detector design principles, including Gd2O2S:Tb scintillator (GOS) thickness as well as EPID architecture. In the latter analysis, we compared a conventional single‐layer imager (SLI) configuration to a novel MLI design, where four complete imager layers – consisting of copper buildup, GOS, and thin‐film transistor (TFT) readout matrix – are stacked. We compare the propagation of MTF and NPS through each detector to illuminate physical design considerations that affect the quality of tumor tracking.
2. Theory and methods
2.A. Ideal observer signal‐to‐noise ratio
To quantitate tracking performance, the ideal observer signal‐to‐noise ratio (SNR) was used as a surrogate figure‐of‐merit (FOM). Also known as the detectability index (d′), it is calculated by13, 14, 15, 16, 17, 18, 19, 20:
| (1) |
where f is the spatial frequency along the data‐ (x‐) and gate‐line (y‐) directions of the detector and SNR 2(f x ,f y ) is defined as:
| (2) |
Here, T and S denote the detector MTF and NPS. The terms task and K c define the imaging task function in question and its contrast. The task function is given by Eq. (3) as:
| (3) |
as the difference (in Fourier space) of two imaging hypotheses (hyp), that is, “A” versus “B”. While d′ is not a direct measure of tracking quality, it does provide insight into the relationship between a system's imaging performance, measured as resolution and noise, and the ability of that system to accomplish the designated task, that is, to distinguish and detect objects and image textures. Since d′ is conceptually and mathematically related to SNR and contrast‐to‐noise ratio (CNR)13, 14 and because SNR and CNR are fundamentally correlated with tracking performance,21 appropriate selection of imaging task may be reasonably equated with tracking performance.
2.A.1. Fiducial marker tracking: detection task
Tumor tracking with fiducial markers leverages the additional contrast the objects create with respect to background tissue, improving SNR of the region‐of‐interest (ROI). This effect may be modeled by employing a simple detection task, according to:
| (4) |
where the task hypothesis describes signal present, O(f x ,f y ), versus signal absent. O is defined as the object spectrum of the fiducial marker in question: in this study, either a sphere or a cylinder. The formulation of a sphere in the frequency domain is given by22:
| (5) |
where r describes the sphere radius and J 1 denotes a first‐order Bessel function of the first kind. A cylinder is given by22:
| (6) |
Here, the longitudinal axis is oriented along the y‐direction. L denotes the length of the cylinder in question. For a cylinder oriented along the x‐direction, the terms, f x and f y are interchanged.
2.A.2. Markerless tracking: discrimination task
Implantation of fiducial markers for lung tumors is associated with clinical complications such as pneumothorax,23 necessitating markerless tracking techniques and algorithms. Some automatic markerless tracking tools such as the soft‐tissue localization (STiL)24 algorithm analyze local regions of increased variance or noise to differentiate the texture in areas of interest. To provide a measure of efficacy for this type of analysis, a discrimination task may be formulated:
| (7) |
where O mal and O ben describe the object spectra (i.e., the quantified texture) of malignant and benign tissues, respectively. Human tissue (tis), both malignant and benign, as presented by X‐ray images, has often been described as following a power‐law in the frequency domain according to25, 26, 27, 28, 29, 30:
| (8) |
where κ is the measured image contrast within the tissue, f the radial frequency according to f = (f x 2 + f y 2)0.5, β is the frequency correlation due to tissue variation (i.e., texture), and α a scaling factor used to preserve units. Human tissue is often expressed as power spectra. For O tis acting as a signal (as opposed to noise or power spectra), as is the case for Eq. (7), the square‐root of the power spectrum is evaluated as in Eq. (8).
2.B. Quantification of tissue texture
Calculation of d′ using Eq. (7) requires accurate quantification of O mal and O ben . Typically, NPS analysis is performed on the tissue of interest where the lower frequency range is fitted to a power‐law: the square of Eq. (8).25, 27, 28, 29, 30, 31 However, due to the relatively large pixel sizes of both prototype and SLI EPIDs, region‐of‐interest (ROI) sizes may be composed of too few pixel elements to adequately sample the relevant frequency range of the NPS or the limited number of total realizations would result in overly noisy data. Therefore, texture was measured using a “blanket‐counting” approach32 for quantification of tissue fractal dimension (FD). Fractal analysis has been used extensively in the past to classify and quantitate tissue textures in lung,33, 34, 35, 36 breast,32, 37, 38, 39 and chest40 imaging. Furthermore, clear linear relationships have been defined between FD and β of Eq. (7), 32, 41, 42, 43:
| (9) |
To measure FD, a square (m x m) ROI was represented as a three‐dimensional (3D) contour, where pixel intensity was treated as the vertical axis. This organizes the ROI as a matrix of rectangular columns with square tops. Surface area (A), a measure related to the complexity of the image as a function of ε, the measurement precision in terms of number of pixels, was calculated according to:
| (10) |
I is the intensity or column height in terms of ε, where a pixel (p) in the vertical (z‐) direction is defined as the image dynamic range divided into m segments according to:
| (11) |
R denotes the dynamic range. A is calculated for a series of values for ε, and the relationship is fit to:
| (12) |
where λ is a simple scaling constant equal to 1.
To assess and quantitate power‐law noise, a collection of in‐treatment EPID images were used for the analysis of tissue textures. Specifically, 40 unique patients including 184 regions‐of‐interest (ROIs) of anterior‐posterior (AP) and posterior‐anterior (PA) images of healthy lung tissues were analyzed. Furthermore, a collection of 149 unique cases with 1600 ROIs were used for tumor data. All cases were imaged at an energy of 6 MV, using a Varian AS‐1200 EPID.
2.C. Monte Carlo modeling
2.C.1. Single‐layer imager model
To analyze the effect of GOS thickness on tracking performance for an SLI detector, a previously validated Monte Carlo (MC) model based on GATE is used to simulate an SLI of generic structure (seen in Fig. 1).44 Briefly, a GOS scintillator was placed between a 1 mm copper buildup layer and a 0.7 mm layer of SiO2, representing the amorphous silicon (a‐Si) TFT readout layer. A lead metal alloy was modeled below the detector to shield back‐scattered electrons.
Figure 1.

Diagram of Monte Carlo simulated SLI EPID. Radiation is incident from the top.
The MTF and normalized NPS (qNNPS) were simulated for a 6 MV X‐ray exposure via MC calculations. Cubic‐spline interpolation was performed at each modeled frequency bin to generate MTF and qNNPS curves as a function of GOS thicknesses not simulated by the MC model (Fig. 2).
Figure 2.
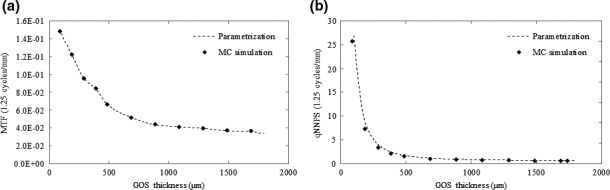
Interpolation of MTF and qNNPS as a function of GOS thickness at 1.25 cycles/mm. Interpolation was performed at each modeled frequency bin to generate MTF and qNNPS curves at GOS thicknesses not simulated by the MC model.
2.C.2. Multi‐layer imager model
The MLI was modeled with the same validated MC simulation as in Section 2.C.1. Briefly, the detector was modeled as four separate stacks, where each consisted of 1 mm of Cu buildup, GOS phosphor (either 290 μm or 430 μm in thickness), and 0.7 mm of SiO2 to model the a‐Si readout layer. A lead metal alloy was modeled below the four stacks to shield back‐scattered electrons. A comparison of the measured and modeled MTF and qNNPS may be seen in Fig. 3.
Figure 3.
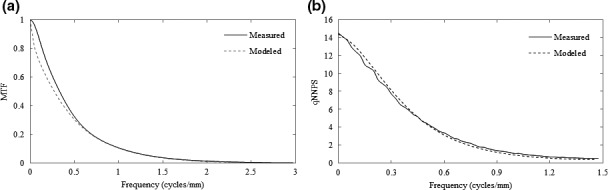
Comparison of the measured (solid lines) and modeled (dashed lines) MTF (a) and NPS (b) for the prototype (430 μm GOS) MLI detector.
3. Results
3.A. Task functions
3.A.1. Object spectra – Cartesian shapes
The evaluation of Eqs. (4) and (5) may be seen in Fig. 4, which depicts surface plots of the object spectra for a 2 mm sphere and a 5 × 0.5 mm cylinder, oriented with the long axis parallel to the y‐direction. The object spectrum of the sphere is distributed isotropically. The short axis (the diameter) of the cylinder, as seen in Fig. 4(b), results in increased signal power at higher frequencies, while the length limits the object spectra in the f x ‐direction to a lower bandwidth.
Figure 4.
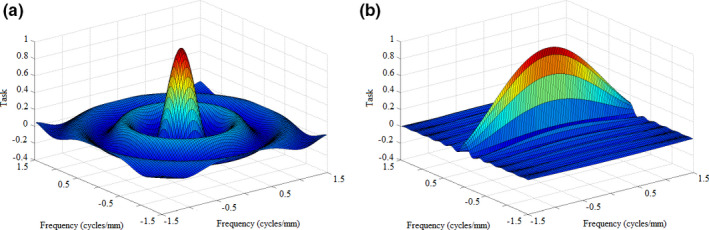
Object spectra for a 2 mm sphere (a) and a 5 × 0.5 mm cylinder (b) oriented with the long axis parallel to the x‐direction. [Color figure can be viewed at wileyonlinelibrary.com]
3.A.2. Lung tissue texture
Table 1 tabulates the fractal dimensionality (FD) results as well as the translated values for the correlative index of the power‐law, β. A two‐sample t‐test reveals that the difference in FD between benign and malignant tissue is statistically significant (P < 0.00001).
Table 1.
Measures of texture quantification for benign and malignant tissue
| Fractal dimension (FD) | β | |
|---|---|---|
| Benign tissue | 2.3534 ± 0.0044 | 3.2932 ± 0.0089 |
| Malignant tissue | 2.4445 ± 0.0016 | 3.1103 ± 0.0033 |
A comparison of the quantified textures of benign and malignant tissue may be found in Fig. 5(a). Figure 5(b) depicts a surface plot of the discrimination task as calculated by Eq. (7), assuming equivalent tissue contrast, as is reasonable for soft tissues imaged at 6 MV.
Figure 5.
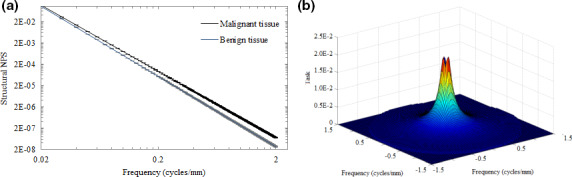
Log‐log plot of the modeled power‐law measures for benign and malignant tissue textures (a) as well as a surface plot of the tissue discrimination task for projection images (b). Error bars are plotted as horizontal lines in Fig. 6(a). [Color figure can be viewed at wileyonlinelibrary.com]
3.B. Tracking performance as a function of GOS thickness
Figure 6 plots the total noise power (a), total signal power (b), and d′ (c) as a function of GOS thickness. Total noise power and total signal power are defined as the integration of NPS and signal power over all frequencies. Total signal power and d′ are normalized to the value at which GOS is equal to 290 μm, which represents a typical, commercially available EPID.
Figure 6.
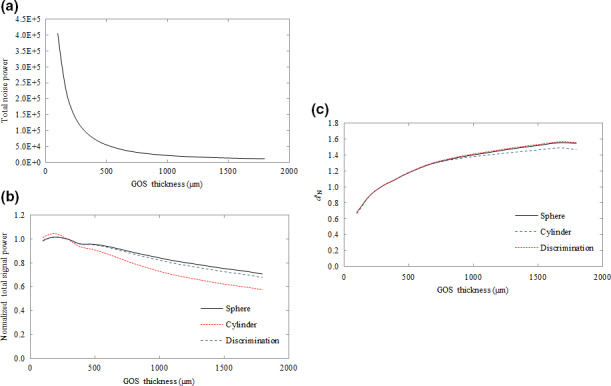
Plot of total noise power (a), normalized signal power (b) and normalized d′ N (c) as a function of GOS thickness. The plotted total signal power and d′ N represent values normalized to the value where GOS thickness was 290 μm, typical of a current state‐of‐the‐art EPID. [Color figure can be viewed at wileyonlinelibrary.com]
Total signal power is degraded as GOS thickness increases as seen in Fig. 6(b), with losses amounting to approximately 28%, 41%, and 21% for the spherical detection, cylindrical detection, and discrimination tasks, respectively, at a GOS thickness of 1720 μm in comparison to a 290 μm detector. However, at 1720 μm, total noise power is also reduced to about 10% of the value at 290 μm, resulting in improvements to d′. Although total noise power decreases monotonically with GOS thickness, the improvement tapers, improving only by 9% between values of 1000 μm and 1800 μm in comparison to an improvement of 81% between 290 μm and 1000 μm.
3.C. MLI – the effect of using multiple detector layers
Figure 7 plots a comparison of MTF (a) and qNNPS (b) for a variety of SLI and MLI detector configurations. For 290 and 430 μm SLI and MLI detectors, the MTF are essentially equivalent with the exception of an observed low‐frequency drop. An SLI equipped with a scintillator of the same thickness as the sum of all MLI layers (i.e., 1720 μm) exhibits an MTF significantly lower at all frequencies in comparison to a 290 μm SLI. Losses were most severe at 0.44 cycles/mm, representing a loss of approximately 18%.
Figure 7.
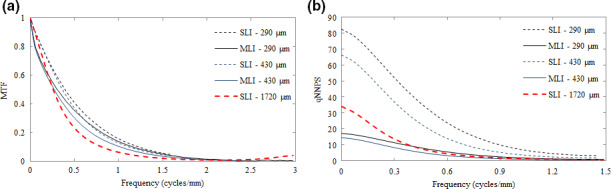
Comparison of MTF (a) and NPS (b) for SLI (dashed lines) and MLI (solid lines) detectors of varying thickness. The heavier point lines indicate the SLI with a thickness of 1720 μm. [Color figure can be viewed at wileyonlinelibrary.com]
Losses in the MTF are relatively small in comparison to the gains in the qNNPS. Increasing scintillator thickness results in lower noise in all cases, which is also illustrated by Fig. 6(a) for SLI detectors. The MLI decreases noise compared to the SLI by roughly a factor equal to the number of total layers. As a result, qNNPS for the MLI is roughly 4 times lower than that of an SLI imager with equivalent individual GOS layer thickness. For the 1720 μm SLI, above 0.3 cycles/mm, the noise performance is roughly equivalent to the 430 μm MLI. However, low‐frequency qNNPS is considerably higher.
Figure 8 plots the signal power for each studied task – the detection of a 2 mm sphere (a) and a 5 × 0.5 mm cylinder (b) as well as the discrimination of malignant from benign tissue textures (c). Losses in signal power for the MLI in comparison to the SLI are appreciated below 0.1 cycles/mm and are transferred from the low‐frequency drop observed Fig. 7(a). These losses are approximately 7% at maximum when compared to the SLI detector. The cylindrical detection task exhibits the greatest loss in signal power at all frequencies, particularly above 0.2 cycles/mm.
Figure 8.
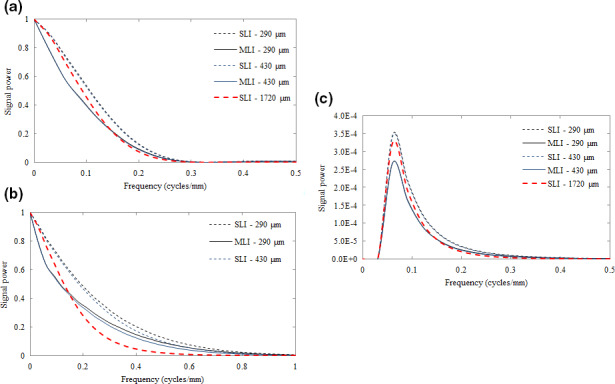
Plot of the signal power for the detection of 2 mm spherical objects (a) and 5 × 0.5 mm cylindrical objects (b), as well as for the discrimination between malignant and benign tissue textures (c) for both MLI (solid lines) and SLI (dashed lines) EPIDs. The SLI with a thickness of 1720 μm is indicated by the heavier point line. [Color figure can be viewed at wileyonlinelibrary.com]
3.D. MLI tumor tracking
3.D.1. Using fiducial markers
In Fig. 9, the SNR 2(f x ) is plotted for each fiducial shape. Employing MLI over SLI architecture results in gains of a factor of ~4 at all frequencies due to the improvement in NPS. However, as may be observed in the data tabulated in Table 2, the gain in d′ is less than 2 as would be expected strictly by improving the NPS by a factor of 4. In comparing the 430 μm MLI to the 1720 μm SLI, dividing the GOS bulk between four layers results in improvements in performance of 30–40%. In comparing the prototype (430 μm) MLI detector to a current, state‐of‐the‐art portal imager such as the Varian AS‐1200 EPID (a 290 μm SLI), improvements in detectability for all cases are greater than a factor of 2.
Figure 9.
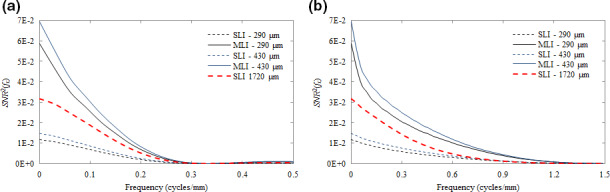
Plot of SNR 2(f x ) as a function of spatial frequency (cycles/mm) for detection tasks of 2 mm spheres (a) and 5 × 0.5 mm cylinders (b) using SLI (dashed lines) and MLI (solid lines) detectors. The SLI with a thickness of 1720 μm is indicated by the heavier point line. [Color figure can be viewed at wileyonlinelibrary.com]
Table 2.
Relative tracking performance (d′), normalized to SLI performance
|
|
|
|
|
|||||
|---|---|---|---|---|---|---|---|---|
| 2 mm sphere | 1.90 | 2.08 | 1.86 | 1.34 | ||||
| 5 × 0.5 mm cylinder | 1.89 | 2.06 | 1.84 | 1.39 | ||||
| Tissue texture | 1.90 | 2.07 | 1.85 | 1.34 |
3.D.2. Texture tracking
The SNR 2 for the discrimination task is seen in Fig. 10. Since tumor texture was implemented with the underlying assumption of image contrast being equivalent for both malignant and benign tissue, the resulting signal power of the discrimination task has no response at zero‐frequency. Again, the MLI outperforms the SLI design by a factor of four at all frequencies when the thickness of individual scintillator layers are equal. The performance of the 1720 μm SLI is exceeded by both MLI detectors.
Figure 10.
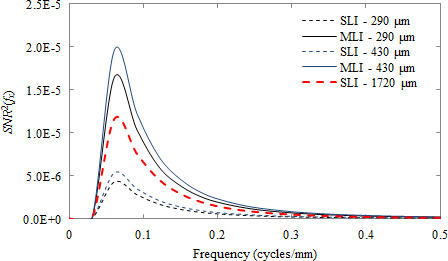
Plot of the SNR 2(f x ) as a function of spatial frequency for the discrimination between malignant and benign tissue textures for both SLI (dashed lines) and MLI (solid lines) detectors. The SLI with a thickness of 1720 μm is indicated by the heavier point line. [Color figure can be viewed at wileyonlinelibrary.com]
4. Discussion
4.A. Tracking performance as a function of GOS thickness
A summary of the effects of varying GOS thickness on image quality is plotted in Fig. 6. The monotonic decrease in signal power observed in Fig. 6(a) is explained by losses in MTF due to increased blurring from optical photon spread.45 Thicker scintillation materials afford a longer path by which optical photons may blur. This effect is particularly apparent for the modulation of a cylindrical fiducial marker, which represents the object with the highest frequency information (particularly along the short axis of the object). Since object functions for the spherical fiducial detection and discrimination tasks are largely extant below 0.3 cycles/mm, they are less affected by additional optical photon spread – which is appreciated as high‐frequency losses in the MTF – incurred by thicker GOS layers.
Despite signal power losses as a function of GOS thickness, d′ increases due to the lower total noise power, which is the result of improved QDE. Reduction of noise power tapers as a function of GOS thickness, which is explained by the increased effect of optical Swank noise from the thicker scintillator.46, 47 Briefly, the number of optical photons received by the detector readout changes as a function of depth of x‐ray interaction. Increasing the thickness of the scintillation material results in increased uncertainty of optical photon gain, resulting in increased noise.
4.B. MLI – the effect of using multiple detector layers on NPS, MTF
The issues diminishing improvements in d′ (i.e., spread of optical photons, Swank noise) are effectively reduced by implementing MLI architecture. Comparing SLI and MLI detectors of equivalent individual layer GOS thickness as well as equivalent total GOS thickness as in Fig. 7 illustrates these concepts. The changes in MTF plotted in Fig. 7(a) are relatively small when comparing 290 and 430 μm SLI and MLI detectors. However, a low‐frequency drop is observed. MLI construction necessarily involves a thicker total structure, which represents more material through which radiation can scatter and backscatter.44 Scatter and backscatter are observed as a low‐frequency drop in the MTF48, 49 and is consistent with previous validation of the MC MLI data. In general, increasing the thickness of an individual scintillator layer results in lower MTF. When each layer in the SLI and MLI are equivalent, the detectors exhibit similar high‐frequency MTF. However, an SLI equipped with a scintillator of the same thickness as the sum of all MLI layers (i.e., 1720 μm) exhibits an MTF that is significantly lower at all frequencies due to the increase in optical spread.
In comparing the NPS Fig. 7(b), increasing scintillator thickness translates to improved QDE and NPS. As was discussed in Section 4.A., optical Swank factor increases the relative amount of noise due to additional uncertainty in optical photon gain. Splitting the scintillator thickness over several readout layers results in mitigation of Swank factor by effectively reducing the uncertainty of optical gain for each layer. So, while total absorption and QDE might be equivalent – as is the case with the 430 μm MLI as compared to a 1720 μm SLI – splitting the thickness of the scintillation material decreases the low‐frequency noise.
4.C. Quality of tumor tracking
4.C.1. Using fiducial markers
Overall, as seen in Fig. 9, losses incurred in the MTF and signal power due to the additional scattered and back‐scattered radiation, are dominated by improvements in the NPS. Further Fig. 8 suggests that for the spherical object detection task (a), signal power is retained at a sufficiently low frequency (i.e., < 0.5 cycles/mm) and that MTF degradation due to greater severity of optical spread from thicker GOS layers is minor (particularly in comparison to an improvement in NPS of a factor of 4). For the cylindrical detection task (b), however, the retention of signal power above 0.3 cycles/mm furthers the significance of MTF degradation due to increased optical spread. For these higher frequency objects, MLI construction may be more beneficial.
The SNR 2 is relatively insensitive to the high‐frequency degradation of the MTF in comparison to the improvements in NPS for all studied detector configurations. Further, in comparing detectors with equivalent total scintillation material thickness (i.e., the 430 μm MLI vs. the 1720 μm SLI), where each detector should have theoretically equal X‐ray absorption, the reduction in optical Swank noise and optical photon spread achieved by MLI architecture provides further benefits in tumor tracking employing fiducial markers.
4.C.2. Texture tracking
Because there is no response observed at zero‐frequency for the discrimination task, the low‐frequency drop incurred by the MLI architecture is unappreciated. Also, since the differences in textures are most evident below 0.3 cycles/mm (Fig 8), losses in MTF, signal power, and subsequently, SNR 2 due to optical spread (which are most severe above 0.4 cycles/mm) are minimal. Thus, the effect of MTF losses incurred by very thick scintillators, as in the 1720 μm SLI, is relatively minimal in contrast to objects with non‐negligible zero‐frequency signal power and/or greater high‐frequency information. However, despite this relatively small effect of MTF degradation, texture tracking is still dominated by improvements in the NPS, resulting in improvements in d′ and SNR 2 of a factor of 4 for an MLI detector of equivalent individual layer thickness.
4.D. Implications on detector design
The results of the present study suggest that gains in tracking performance are driven primarily by improvements in NPS, which is directly affected by maximizing QDE. Losses due to MTF for the studied tasks are largely negligible. Thus, improvements in tracking performance may be most easily realized through an increase in scintillator thickness, with diminishing returns above approximately 500 μm for GOS. Generally, increasing GOS thickness may result in more severe image blur from the spread of optical photons and further degrade the MTF. However, for the studied tasks, which exhibit sufficiently low‐frequency signal power, the loss in resolution is outweighed by improvements in the QDE and subsequently the NPS. Although MTF losses may not be entirely relevant for the studied tasks, the increased effect of optical Swank noise incentivizes the use of MLI architecture. MLI construction enables an increase in effective scintillator thickness without incurring additional optical Swank noise. Furthermore, for smaller object tracking or discrimination between subtler, high‐frequency textures, losses in MTF may become a more important factor. This would suggest improvement may be best achieved by increasing the number of scintillator layers, while maintaining the thickness of each layer below a value that is adequately able to resolve the features of interest. While ideally, many thin layers may optimize imaging performance, limitations of production cost may inhibit practical implementation of such an imager.
Although the present study outlines some of the physical parameters that could improve MLI performance, some typical limitations of beam's‐eye view tracking remain unaddressed. Since the detector is based on the same platform as current, clinically available SLI, beam modulation, temporal resolution, and latency are unchanged for the prototype MLI.
4.E. Limitations and clinical implications
The present manuscript is based on linear systems assumptions and the limitations of such have been described in great detail, previously. Specifically, linear systems assume stationarity of response, which is not strictly true for analysis of tissue and tumor textures. Thus, the analysis is not applicable to measurements of absolute detectability for all patients over all regions of the lung. Further, reductions in absolute tracking performance may be observed when tumors are obstructed by overlying structures such as bony anatomy and organ tissue. However, the modeled results are a representation of a comparison of typical performance of SLI and MLI detectors when tasked with differentiating tumor textures located within primarily lung tissue.
Finally, direct correlation between d′ and absolute binary tracking ability (i.e., can the tumor be tracked or not) has not been studied. However, the analysis quantifies a global expected improvement based on image quality and detector performance for both fiducial marker tumor tracking and markerless tumor tracking performance by maximizing signal‐to‐noise ratio at relevant spatial frequencies. It should also be noted that d′ has been compared to both human observer performance as well as the Rose Criterion as a limit of system performance.13, 14 Broadly, improvements in tracking performance may eventually lead to improvements in‐treatment delivery such as reduced planned margins.
5. Conclusions
In the present manuscript, we have demonstrated a novel, generalizable method for quantification of tracking performance based on simple imaging metrics, such as MTF and NPS and applied the model to evaluate single and multi‐layer EPID designs. We showed that in general, blurring in the MTF is largely irrelevant due to the object spectra of a typical therapeutic imaging task and that decreasing noise (increasing quantum efficiency) is the primary driver for improving tracking quality. We have also shown that a MLI design can yield greater improvements in NPS than an SLI design with the same total scintillator thickness. This suggests that implementation of MLI design may offer superior performance for tracking applications when compared to typical SLI architectures.
Acknowledgments
The project was partially supported by a grant from Varian Medical Systems, Inc. and award No. R01CA188446‐01 from the National Cancer Institute. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health.
References
- 1. Shirato H, Seppenwoolde Y, Kitamura K, Onimura R, Shimizu S. Intrafractional tumor motion: lung and liver. Semin Radiat Oncol. 2004;14:10–18. [DOI] [PubMed] [Google Scholar]
- 2. Chan MKH, Kwong DLW, Tam E, Tong A, Ng SCY. Quantifying variability of intrafractional target motion in stereotactic body radiotherapy for lung cancers. J Appl Clin Med Phys. 2013;14:2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Berbeco RI, Hacker F, Ionascu D, Mamon HJ. Clinical feasibility of using an EPID in CINE mode for image‐guided verification of stereotactic body radiotherapy. Int J Radiat Oncol Biol Phys. 2007;69:258–266. [DOI] [PubMed] [Google Scholar]
- 4. Fidanzio A, Mameli A, Placidi E, et al. Epid cine acquisition mode for in vivo dosimetry in dynamic arc radiation therapy. Nucl Instrum Methods Phys Res, Sect B. 2008;266:658–666. [Google Scholar]
- 5. Rottmann J, Berbeco R. Using an external surrogate for predictor model training in real‐time motion management of lung tumors. Med Phys. 2014;41:121706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Rottmann J, Keall P, Berbeco R. Real‐time soft tissue motion estimation for lung tumors during radiotherapy delivery. Med Phys. 2013;40:091713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Rottmann J, Morf D, Fueglistaller R, Zentai G, Star‐Lack J, Berbeco R. A novel EPID design for enhanced contrast and detective quantum efficiency. Phys Med Biol. 2016;61:6297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Star‐Lack J, Shedlock D, Swahn D, et al. A piecewise‐focused high DQE detector for MV imaging. Med Phys. 2015;42:5084–5099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Zhao W, Ristic G, Rowlands JA. X‐ray imaging performance of structured cesium iodide scintillators. Med Phys. 2004;31:2594–2605. [DOI] [PubMed] [Google Scholar]
- 10. Monajemi TT, Steciw S, Fallone BG, Rathee S. Modeling scintillator‐photodiodes as detectors for megavoltage CT. Med Phys. 2004;31:1225–1234. [DOI] [PubMed] [Google Scholar]
- 11. McGarry CK, Grattan MWD, Cosgrove VP. Optimization of image quality and dose for Varian aS500 electronic portal imaging devices (EPIDs). Phys Med Biol. 2007;52:6865. [DOI] [PubMed] [Google Scholar]
- 12. Yip S, Rottmann J, Berbeco R. The impact of cine EPID image acquisition frame rate on markerless soft‐tissue tracking. Med Phys. 2014;41:061702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Vennart W. ICRU report 54: medical imaging & the assessment of image quality. Radiography. 2014;3:243–244. [Google Scholar]
- 14. Gang GJ, Lee J, Stayman JW, et al. Analysis of Fourier‐domain task‐based detectability index in tomosynthesis and cone‐beam CT in relation to human observer performance. Med Phys. 2011;38:1754–1768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Hu Y‐H, Scaduto D, Zhao W. Optimization of contrast enhanced breast imaging: analysis using a cascaded linear system model. Med Phys. 2016;44:43–56. [DOI] [PubMed] [Google Scholar]
- 16. Hu Y‐H, Zhao W. The effect of angular dose distribution on the detection of microcalcifications in digital breast tomosynthesis. Med Phys. 2011;38:2455–2466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Hu Y‐H, Zhao W. The effect of amorphous selenium detector thickness on dual‐energy digital breast imaging. Med Phys. 2014;41:111904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ikejimba L, Kiarashi N, Lin Y, et al. Task‐based strategy for optimized contrast enhanced breast imaging: analysis of six imaging techniques for mammography and tomosynthesis. 10.1117/12.913377 presented at SPIE Medical Imaging; 2012; San Diego, California, USA. [DOI] [PMC free article] [PubMed]
- 19. Richard S, Siewerdsen JH. Cascaded systems analysis of noise reduction algorithms in dual‐energy imaging. Med Phys. 2008;35:586–601. [DOI] [PubMed] [Google Scholar]
- 20. Tward DJ, Siewerdsen JH. Cascaded systems analysis of the 3D noise transfer characteristics of flat‐panel cone‐beam CT. Med Phys. 2008;35:5510–5529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Yu C, John JOC, Christine JK, Rulon RM, Arnaud B, James EM. Fiducial markers in prostate for kV imaging: quantification of visibility and optimization of imaging conditions. Phys Med Biol. 2012;57:155. [DOI] [PubMed] [Google Scholar]
- 22. Desponds L, Depeursinge C, Grecescu M, Hessler C, Samiri A, Valley JF. Image quality index (IQI) for screen‐film mammography. Phys Med Biol. 1991;36:19. [DOI] [PubMed] [Google Scholar]
- 23. Kothary N, Heit JJ, Louie JD, et al. Safety and efficacy of percutaneous fiducial marker implantation for image‐guided radiation therapy. J Vascul Intervent Radiol. 2009;20:235–239. [DOI] [PubMed] [Google Scholar]
- 24. Rottmann J, Aristophanous M, Chen A, Court L, Berbeco R. A multi‐region algorithm for markerless beam's‐eye view lung tumor tracking. Phys Med Biol. 2010;55:5585. [DOI] [PubMed] [Google Scholar]
- 25. Gang GJ, Tward DJ, Lee J, Siewerdsen JH. Anatomical background and generalized detectability in tomosynthesis and cone‐beam CT. Med Phys. 2010;37:1948–1965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Yoon S, Gang JG, Tward DJ, Siewerdsen JH, Fahrig R. Analysis of lung nodule detectability and anatomical clutter in tomosynthesis imaging of the chest. 10.1117/12.813836 presented at SPIE Medical Imaging; 2009; Lake Buena Vista, FL. [DOI]
- 27. Bochud FO, Valley J‐F, Verdun FR, Hessler C, Schnyder P. Estimation of the noisy component of anatomical backgrounds. Med Phys. 1999;26:1365–1370. [DOI] [PubMed] [Google Scholar]
- 28. Burgess AE. Mammographic structure: data preparation and spatial statistics analysis. 10.1117/12.348620 presented at SPIE Medical imaging; 1999; San Diego, CA. [DOI]
- 29. Hill ML, Mainprize JG, Carton A‐K, et al. Anatomical noise in contrast‐enhanced digital mammography. Part I. Single‐energy imaging. Med Phys. 2013;40:051910. [DOI] [PubMed] [Google Scholar]
- 30. Hill ML, Mainprize JG, Carton A‐K, et al. Anatomical noise in contrast‐enhanced digital mammography. Part II. Dual‐energy imaging. Med Phys. 2013;40:081907. [DOI] [PubMed] [Google Scholar]
- 31. Solomon J, Samei E. Quantum noise properties of CT images with anatomical textured backgrounds across reconstruction algorithms: FBP and SAFIRE. Med Phys. 2014;41:091908. [DOI] [PubMed] [Google Scholar]
- 32. Caldwell CB, Stapleton SJ, Holdsworth DW, et al. Characterisation of mammographic parenchymal pattern by fractal dimension. Phys Med Biol. 1990;35:235. [DOI] [PubMed] [Google Scholar]
- 33. Uppaluri R, Mitsa T, Galvin JR. Fractal analysis of high‐resolution CT images as a tool for quantification of lung diseases. 10.1117/12.209685 presented at SPIE Medical Imaging; 1995; San Diego, CA. [DOI]
- 34. Kido S, Kuriyama K, Higashiyama M, Kasugai T, Kuroda C. Fractal analysis of internal and peripheral textures of small peripheral bronchogenic carcinomas in thin‐section computed tomography: comparison of bronchioloalveolar cell carcinomas with nonbronchioloalveolar cell carcinomas. J Comput Assist Tomogr. 2003;27:56–61. [DOI] [PubMed] [Google Scholar]
- 35. Al‐Kadi OS, Watson D. Susceptibility of texture measures to noise: An application to lung tumor CT images. Paper presented at: BioInformatics and BioEngineering, 2008. BIBE 2008. 8th IEEE International Conference on; 8‐10 Oct. 2008; 2008.
- 36. Al‐Kadi OS, Watson D. Texture analysis of aggressive and nonaggressive lung tumor CE CT images. IEEE Trans Biomed Eng. 2008;55:1822–1830. [DOI] [PubMed] [Google Scholar]
- 37. Georgia DT, David MD, Carey EF Jr. A study on the computerized fractal analysis of architectural distortion in screening mammograms. Phys Med Biol. 2006;51:1299. [DOI] [PubMed] [Google Scholar]
- 38. Banik S, Rangayyan RM, Desautels JEL. Detection of architectural distortion in prior mammograms. IEEE Trans Med Imaging. 2011;30:279–294. [DOI] [PubMed] [Google Scholar]
- 39. Rangayyan RM, Nguyen TM. Fractal analysis of contours of breast masses in mammograms. J Digi Imaging. 2006;20:223–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Hong S, Huidong D. Fractal dimension applied in texture feature extraction in x‐ray chest image retrieval. Paper presented at: Information and Automation (ICIA), 2012 International Conference on; 6‐8 June 2012; 2012.
- 41. Lin C, Craig KA, John MB. Association between power law coefficients of the anatomical noise power spectrum and lesion detectability in breast imaging modalities. Phys Med Biol. 2013;58:1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Higuchi T. Relationship between the fractal dimension and the power law index for a time series: a numerical investigation. Phys D: Nonlin Phenom. 1990;46:254–264. [Google Scholar]
- 43. Voss RF. Fractals in nature: from characterization to simulation. In: Peitgen H‐O, Saupe D, eds The Science of Fractal Images. New York: Springer‐Verlag, Inc.; 1988:21–70. [Google Scholar]
- 44. Myronakis M, Star‐Lack J, Baturin P, et al. A novel multi‐layer MV imager computational model for component optimization. Med Phys. 2017;44:4213–4222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Lubberts G. Random noise produced by X‐ray fluorescent screens. J Optic Soc Am. 1968;58:1475–1483. [Google Scholar]
- 46. Beutel J, Kundel HL, Van Metter RL. Handbook of Medical Imaging: Physics and Psychophysics. Bellingham, WA: SPIE; 2000. [Google Scholar]
- 47. Swank RK. Absorption and noise in x‐ray phosphors. J Appl Phys. 1973;44:4199–4203. [Google Scholar]
- 48. Kyprianou IS, Rudin S, Bednarek DR, Hoffmann KR. Generalizing the MTF and DQE to include x‐ray scatter and focal spot unsharpness: application to a new microangiographic system. Med Phys. 2005;32:613–626. [DOI] [PubMed] [Google Scholar]
- 49. Salvagnini E, Bosmans H, Struelens L, Marshall NW. Quantification of scattered radiation in projection mammography: four practical methods compared. Med Phys. 2012;39:3167–3180. [DOI] [PubMed] [Google Scholar]


