Deterministic direct aperture optimization using multiphase piecewise constant segmentation

Abstract

Purpose

Direct aperture optimization (DAO) attempts to incorporate machine constraints in the inverse optimization to eliminate the post‐processing steps in fluence map optimization (FMO) that degrade plan quality. Current commercial DAO methods utilize a stochastic or greedy approach to search a small aperture solution space. In this study, we propose a novel deterministic direct aperture optimization that integrates the segmentation of fluence map in the optimization problem using the multiphase piecewise constant Mumford‐Shah formulation.

Methods

The Mumford‐Shah based direct aperture optimization problem was formulated to include an L2‐norm dose fidelity term to penalize differences between the projected dose and the prescribed dose, an anisotropic total variation term to promote piecewise continuity in the fluence maps, and the multiphase piecewise constant Mumford‐Shah function to partition the fluence into pairwise discrete segments. A proximal‐class, first‐order primal‐dual solver was implemented to solve the large scale optimization problem, and an alternating module strategy was implemented to update fluence and delivery segments. Three patients of varying complexity—one glioblastoma multiforme (GBM) patient, one lung (LNG) patient, and one bilateral head and neck (H&N) patient with 3 PTVs—were selected to test the new DAO method. For each patient, 20 non‐coplanar beams were first selected using column generation, followed by the Mumford‐Shah based DAO (DAO_MS). For comparison, a popular and successful approach to DAO known as simulated annealing—a stochastic approach—was replicated. The simulated annealing DAO (DAO_SA) plans were then created using the same beam angles and maximum number of segments per beam. PTV coverage, PTV homogeneity $\left(\frac{D95}{D5}\right)$, and OAR sparing were assessed for each plan. In addition, high dose spillage, defined as the 50% isodose volume divided by the tumor volume, as well as conformity, defined as the van't Riet conformation number, were evaluated.

Results

DAO_MS achieved essentially the same OAR doses compared with the DAO_SA plans for the GBM case. The average difference of OAR D_max and D_mean between the two plans were within 0.05% of the plan prescription dose. The lung case showed slightly improved critical structure sparing using the DAO_MS approach, where the average OAR D_max and D_mean were reduced by 3.67% and 1.08%, respectively, of the prescription dose. The DAO_MS plan substantially improved OAR dose sparing for the H&N patient, where the average OAR D_max and D_mean were reduced by over 10% of the prescription dose. The DAO_MS and DAO_SA plans were comparable for the GBM and LNG PTV coverage, while the DAO_MS plan substantially improved the H&N PTV coverage, increasing D99 by 6.98% of the prescription dose. For the GBM and LNG patients, the DAO_MS and DAO_SA plans had comparable high dose spillage but slightly worse conformity with the DAO_MS approach. For the H&N plan, DAO_MS was considerably superior in high dose spillage and conformity to the DAO_SA. The deterministic approach is able to solve the DAO problem substantially faster than the simulated annealing approach, with a 9.5‐ to 40‐fold decrease in total solve time, depending on the patient case.

Conclusions

A novel deterministic direct aperture optimization formulation was developed and evaluated. It combines fluence map optimization and the multiphase piecewise constant Mumford‐Shah segmentation into a unified framework, and the resulting optimization problem can be solved efficiently. Compared to the widely and commercially used simulated annealing DAO approach, it showed comparable dosimetry behavior for simple plans, and substantially improved OAR sparing, PTV coverage, PTV homogeneity, high dose spillage, and conformity for the more complex head and neck plan.

1. Introduction

Intensity modulated radiation therapy (IMRT) was theorized in the 1980s¹ and subsequently developed in several landmark papers.^{2, 3, 4} Since then, IMRT has been widely accepted into radiation therapy clinics as the staple approach to radiotherapy. While IMRT has been proved exceptional in controlling of dose distributions, one major weakness lies in the fluence map optimization (FMO), which does not consider machine constraints in the inverse optimization and produces optimal fluence maps that need to be converted to deliverable multileaf collimators (MLC) sequences. While several clever sequencing methods have been developed, such as sliding window or the reducing level method,⁵ this additional post processing step, separate from initial FMO inverse optimization, leads to varying degrees of degradation in the dose quality that often require plan reoptimization, which is ineffective to address the problem.

The process of converting a fluence map into deliverable apertures and be divided into two steps. First, a stratification step is performed, which bins the fluence's intensity values into patches of discrete levels. The patches are referred to as apertures in the context of IMRT. Typically, to reduce the discretization levels, the fluence maps need to be smoothed, more so for complicated and heavily modulated plans. In the second step, MLC motion trajectories are determined to efficiently deliver the apertures. Because of the modification to the optimized fluence map, the first step of stratification contributes most to the dosimetry degradation. Figure 1(a) illustrates the workflow of conventional fluence map optimization, followed by the stratification and the MLC sequencing step.

Figure 1.

Schematic of the fluence map optimization and MLC segmentation process. (a) Conventional fluence map optimization followed by smoothing and stratification. Because the smoothing is done post optimization, the plan quality degradation is often substantial. (b) Total variation regularization integrate in the fluence map optimization, resulting smaller losses in stratification and fewer intensity levels. (c) The current direct aperture optimization work flow. (d) The proposed piecewise constant Mumford‐Shah segmentation regularized fluence map optimization resulting in a few discretized patches that bypass the stratification step.

To alleviate the problem and produce simpler fluence maps that suffer a smaller loss in stratification, a total variation regularization term on the fluence maps was incorporated in the original optimization problem^{6, 7, 8, 9} to encourage piecewise smoothness. Computationally, we recently showed that a first order primal dual method is efficient to solve the large scale non‐differentiable optimization problem.⁹ However, as shown in Fig. 1(b), additional stratification is still needed to convert the piecewise smooth fluence map to apertures of uniform intensities, degrading the plan from its optimized version.

Direct aperture optimization (DAO) was invented to circumvent the stratification problem by optimizing the apertures instead of the beamlets [Fig. 1(c)]. One significant challenge with DAO is that the number of possible apertures as the combination of beamlets is mathematically intractable. To manage the challenge, stochastic and greedy approaches have been implemented. The stochastic DAO method utilizes a simulated annealing process¹⁰ to iteratively update the aperture shapes and intensity values.^{11, 12, 13, 14, 15, 16, 17, 18} Another stochastic approach of DAO employs a genetic algorithm to find a set deliverable segments with best fitness.¹⁹ Genetic algorithms, inspired by the process of natural selection, operates by having a population of solutions, and then performing genetic operations—such as crossover and mutations—on the fittest solutions in an attempt to increase the fitness value. The stochastic nature of the genetic algorithms stems from the random decisions made during the genetic operations. In the greedy approach, DAO plans are created by optimizing a predetermined library of apertures, and a column generation method to expand the aperture library until an acceptable treatment plan is acquired.^{20, 21, 22} These DAO methods result in plans that are directly deliverable by the machine without the need for a separate stratification step but there are significant limitations. Due to the computational cost, these methods can only search a small fraction of the possible apertures, which may be insufficient for complex IMRT plans.

In this study, we aim to overcome the limitations in existing fluence map and direct aperture optimization methods.^{6, 7, 8, 9} Instead of incorporating the TV regularization that encourages piecewise smoothness, we incorporate a new regularizer where the fluence map stratification problem is formulated as a piecewise constant segmentation problem. The new regularizer would encourage piecewise constant patches that are equivalent to apertures to eliminate the need for post‐optimization stratification [Figure 1(d)].

Piecewise constant segmentation is a well‐researched image processing topic, aimed at approximating an original grayscale image by a few uniform‐intensity patches. Following the original Mumford‐Shah formulation,^{23, 24, 25, 26} which was used to find the piecewise smooth approximation of grayscale images, recent developments have led to multiphase piecewise constant versions of the formulation.^{24, 25, 27, 28, 29, 30} In particular, the development of the Chan‐Vese functional and algorithm,²⁷ which used level‐set functions to define segments in the image, achieved the piecewise‐constant property by only defining one value per segment. The piecewise constant version of the Mumford‐Shah formulation, inspired by Chan‐Vese formulation, utilizes a convexly relaxed labeling array instead of level set functions. By finding the minimizer of the Mumford‐Shah formulation, an image can be segmented into multiple continuous regions, and a single value is assigned to each region during the optimization for the piecewise constant property. This is pertinent to the IMRT optimization problem, because the piecewise constant segmented regions are arbitrarily shaped, it provides a mathematically complete description of all possible MLC apertures for a specific fluence map.

In this study, we integrate the multiphase piecewise constant Mumford‐Shah function with the fluence map optimization problem into a multiconvex formulation^{31, 32}—a non‐convex problem that yields a convex subproblem when all but one block of variables are held constant. This is commonly evaluated by an alternating module scheme. We then test the feasibility of this optimization on several patient cases and compare its performance to the DAO method using simulated annealing.

2. Methods

The methods section is organized as follows. First, the novel deterministic DAO formulation is proposed. Second, a notations table of the important variables and data are presented. Third, the block alternating module approach to solving the DAO formulation is explained. Fourth, the simulated annealing DAO approach for comparison is described. Last, the evaluation details to test the performance to the Mumford‐Shah based DAO and compare it to the simulated annealing DAO are explained.

2.A. Deterministic direct aperture optimization formulation

The master optimization formulation is written as

$$\begin{array}{cc}\hfill \begin{array}{c}argmin\\ x,u,c\end{array}& \underset{Term1:DoseFidelity}{\underbrace{\frac{1}{2}\Vert {W\left(\sum _{b=1}^{n_b}\left(A_b{x}_b\right)-d\right)\Vert }_2^2}}+\underset{TermSet2:AnisotropicTVonFluence}{\underbrace{\sum _{b=1}^{n_b}\left({\mathit{\lambda }}_1\Vert D_b^{\Vert }{x_b\Vert }_1+{\mathit{\lambda }}_2\Vert D_b^{\perp }{x}_b{\Vert }_1\right)}}\hfill \\ & +\mathit{\gamma }\sum _{b=1}^{n_b}\left(\underset{MultiphasePiecewiseConstantMumford-ShahFormulation}{\underbrace{{\underbrace{\frac{1}{2}\sum _{p=1}^{n_p}\sum _{s=0}^{n_s}{u}_{bps}{|x_{bp}-c_{bs}|}^2}}_{TermSet3}+{\underbrace{\sum _{s=0}^{n_s}\left(\mathit{\omega }{\Vert }_1{D}_b^{\Vert }{u_{bs}\Vert }_1+{\mathit{\omega }}_2\Vert D_b^{\perp }{u_{bs}\Vert }_1\right)}}_{TermSet4}}}\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill subjectto& x\ge 0\hfill \\ & u\ge 0\hfill \\ & \stackrel{\rightharpoonup }{1}{}^T{u}_{bp}=1,\hfill \end{array}$$ (1)

where the notations for the data and variables used in the DAO formulation are described in Table 1.

Table 1.

Important notations and data structures used in the study

Notation	Type	Description
Indices
B	Index	Index for beam. $b\in \left\{1,2,\dots ,n_b\right\}$
P	Index	Index for beamlet. $p\in \left\{1,2,\dots ,n_p\right\}$
S	Index	Index for segment. $s\in \left\{0,1,2,\dots ,n_s\right\}$
Optimization variables
X	Vector	All beamlet intensities from all selected beams.
x b	Vector	All beamlet intensities for the bth beam. $x=\left[\begin{array}{c}{x}_{b=1}\\ ⋮\\ x_{b=n_b}\end{array}\right]$
x bp	Scalar	Intensity value for the pth beamlet of the bth beam. $x_b=\left[\begin{array}{c}{x}_{b,p=1}\\ ⋮\\ x_{b,p=n_p}\end{array}\right]$
C	Matrix	Intensity values for all segments and beams.
c b	Vector	Intensity values for all the segments of the bth beam. $c=\left[\begin{array}{c}{c}_{b=1}^T\\ ⋮\\ c_{b=n_b}^T\end{array}\right]$
c bs	Scalar	Intensity value for the sth segment of the bth beam. $c=\left[\begin{array}{ccc}{c}_{b=1,s=1}& \cdots & c_{b=1,s=n_s}\\ ⋮& \ddots & ⋮\\ c_{b=n_b,s=1}& \cdots & c_{b=n_b,s=n_s}\end{array}\right]$ $c_b=\left[\begin{array}{c}{c}_{b,s=1}\\ ⋮\\ c_{b,s=n_s}\end{array}\right]$
U	Matrix	Segmentation labeling array for all selected beams.
u b	Matrix	Segmentation labeling array for the bth beam. $u=\left[\begin{array}{c}{u}_{b=1}\\ ⋮\\ u_{b=n_b}\end{array}\right]$
u bs	Vector	Probability that the beamlets from the bth beam belong to the sth segment. $u_b=\left[\begin{array}{ccc}{u}_{b,s=1}& \cdots & u_{b,s=n_s}\end{array}\right]$
u bp	Vector	Segment probabilities for the pth beamlet of the bth beam.Lives in probability simplex. $u_b=\left[\begin{array}{c}{u}_{b,p=1}^T\\ ⋮\\ u_{b,p=n_p}^T\end{array}\right]$
u bps	Scalar	Probability that the pth beamlet of the bth beam belongs to the sth segment. $u_b=\left[\begin{array}{ccc}{u}_{b,p=1,s=1}& \cdots & u_{b,p=1,s=n_s}\\ ⋮& \ddots & ⋮\\ u_{b,p=n_p,s=1}& \cdots & u_{b,p=n_p,s=n_s}\end{array}\right]$ $u_{bs}=\left[\begin{array}{c}{u}_{b,p=1,s}\\ ⋮\\ u_{b,p=n_p,s}\end{array}\right]$ $u_{bp}=\left[\begin{array}{c}{u}_{b,p,s=1}\\ ⋮\\ u_{b,p,s=n_s}\end{array}\right]$
Other data
A	Matrix	Fluence‐to‐dose transformation matrix from all selected beams.
A b	Matrix	Fluence‐to‐dose transformation matrix for the b th beam. $A=\left[\begin{array}{ccc}{A}_{b=1}& \cdots & A_{b=n_b}\end{array}\right]$
W	Matrix	Weighting matrix for structures of interest.
D	Vector	Prescription dose the PTV and zero elsewhere.
D ∥	Matrix	Derivative matrix for all fluence maps from all beams. Takes derivative parallel to the MLC leaf motion.
$D_b^{\Vert }$	Matrix	Derivative matrix for fluence map of b th beam. Takes derivative parallel to the MLC leaf motion. $D^{\Vert }=\left[\begin{array}{ccc}{D}_{b=1}^{\Vert }& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & D_{b=n_b}^{\Vert }\end{array}\right]$
D ⊥	Matrix	Derivative matrix for all fluence maps from all beams. Takes derivative perpendicular to the MLC leaf motion.
$D_b^{\perp }$	Matrix	Derivative matrix for fluence map of b th beam. Takes derivative perpendicular to the MLC leaf motion. $D^{\perp }=\left[\begin{array}{ccc}{D}_{b=1}^{\perp }& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & D_{b=n_b}^{\perp }\end{array}\right]$
Q	Matrix	An intermediate variable that has the same structure and subscript notation as $u$. Is used in the appendix, section A3. $q_{bps}=\frac{1}{2}|x_{bp}-c_{bs}{|}^2$

Term 1 is the dose fidelity term which attempts to optimize the fluence, x, such that the projected dose, Ax, is penalized for deviations from the prescription dose, d. The structures of interest are weighted by the diagonal matrix, W. Term set 2 is the anisotropic total variation regularization on the fluence maps to promote piecewise continuous fluence maps.⁹ The matrices, D ^∥ and D ^⊥, take derivatives parallel and orthogonal to the MLC leaf direction.

Term sets 3 and 4 belong to the multiphase piecewise constant Mumford‐Shah formulation,^{23, 24, 25, 27, 28, 29, 30} which partitions each fluence map into n _s discrete segments. The function, for this study, utilizes the anisotropic version of total variation to account for the MLC leaf direction. The convexly relaxed segmentation labeling array, u, has been successfully applied to the Mumford‐Shah formulation for piecewise constant segmentation.^{25, 30} The rows of the labeling array, u _bp , are subject to the probability simplex, which is described by two constraints on u _bp —the elements of u _bp are non‐negative and their sum is equal to 1. This probability simplex constraint is applied to push u _bps to equal 1 for the segment where | x _bp  − c _bs  | ² is the smallest, but the total variation regularization term encourages each segment in u to be piecewise continuous. The index for segment, s, starts at 0, to account for a “segment” with zero fluence or completely closed MLC. By integrating MLC segmentation with FMO in a single objective function, the beam apertures become optimizable variables directly contributing to the dosimetry.

Term set 3 is not convex, rendering the whole objective formulation non‐convex. Fortunately, the formulation is multiconvex^{31, 32}—by updating one variable while holding the other two constant, we have a convex module. Similar to a previous study,³³ the algorithm is broken down into three modules, which are evaluated in an alternating block fashion.

2.A.1. Module 1

Module 1 updates x while holding u and c constant. The formulation for module 1 is written as

$$\begin{array}{cc}\underset{x}{argmin}& \frac{1}{2}\Vert W\left(\sum _{b=1}^{n_b}(A_b{x}_b)-d\right){\Vert }_2^2+\sum _{b=1}^{n_b}\left({\mathit{\lambda }}_1{\Vert D_b^{\Vert }{x}_b\Vert }_1+{\mathit{\lambda }}_2{\Vert D_b^{\perp }{x}_b\Vert }_1\right)+\frac{\mathit{\gamma }}{2}\sum _{b=1}^{n_b}\sum _{p=1}^{n_p}\sum _{s=0}^{n_s}{u}_{bps}{|x_{bp}-c_{bs}|}^2\\ subjectto& x\ge 0.\end{array}$$ (2)

The optimization formulation can be solved with a proximal‐class, first‐order primal‐dual algorithm known as the Chambolle‐Pock algorithm.^{25, 34} This study uses the overrelaxed version of the algorithm³⁵ for faster convergence rate, as well as a preconditioning process³⁴ to select the step size. A detailed explanation of the Chambolle‐Pock algorithm, as well as its application to module 1, can be found in the Appendix.

2.A.2. Module 2

Module 2 updates c, while holding x and u constant. Following the initial update of u, c is first initialized to be

$$c_{bs}=\frac{s}{n_s}max\left(x_b\right)forallb,s,$$ (3)

and the subsequent iterations will update c using a closed form solution²⁴

$$c_{bs}=\frac{u_{bs}^T{x}_b}{u_{bs}^T\stackrel{\rightharpoonup }{\mathbf{1}}}forallb,s.$$ (4)

In the case where $u_{b,s=k}^T\stackrel{\rightharpoonup }{1}=0$, its corresponding c _b,s = k takes on an average value from its neighbor values. In other words $c_{b,s=k}=\frac{1}{2}\left(c_{b,s=k-1}+c_{b,s=k+1}\right)$. If this turned off segment happens to be the last segment, meaning that $u_{b,s=n_s}^T\stackrel{\rightharpoonup }{1}=0$, then $c_{b,s=n_s}=2\ast c_{b,s=n_s-1}$. By default, c _b,s = 0 will always be set at zero to define an “off” segment. This strategy is implemented to assign an otherwise undefined c _b,s = k a unique non‐zero value, which may be effective in finding useful segments.

2.A.3. Module 3

Module 3 updates u, while holding x and c, constant. The terms in the objective setting that have u are simply the terms that belong to the Mumford‐Shah function:

$$\begin{array}{cc}\underset{u}{argmin}& \sum _{b=1}^{n_b}\left(\frac{1}{2}\sum _{p=1}^{n_p}\sum _{s=0}^{n_s}{u}_{bps}{|x_{bp}-c_{bs}|}^2+\sum _{s=1}^{n_s}({\mathit{\omega }}_1\Vert D_b^{\Vert }{u}_{bs}{\Vert }_1+{\mathit{\omega }}_2\Vert D_b^{\perp }{u}_{bs}{\Vert }_1)\right)\\ subjectto& \begin{array}{c}u\ge 0\\ \stackrel{\rightharpoonup }{1^T}{u}_{bp}=1,\end{array}\end{array}$$ (5)

where γ weighting is ignored during module 3 since it does not influence the outcome of the optimization in Eq. (5). The formulation shown in Eq. (5) can also be efficiently evaluated using the preconditioned overrelaxed Chambolle‐Pock algorithm, which is described in the Appendix.

2.A.4. Alternating module schedule and other heuristics to handle non‐convexity

To allow for a change in the fluence to immediately affect the average value of its aperture, module 1 and module 2 are alternated back‐to‐back, updating c as soon as x is updated. After the active modules 1 and 2 update x and c, module 3 will then update u. This routine would repeat until the aperture shapes converged to a constant shape. After analysis with a test case, the number of subiterations for each module was decided to be 100 for modules 1 and 2, and 1500 for module 3.

Once the aperture shapes have converged, a check is taken to see if u has converged to 1s and 0s. If not, then the u _bps with the highest value in its vector, u _bp , is assigned to 1 and the rest are assigned to 0. A polishing step is added where the intensity values are directly optimized while the apertures are locked. The polishing optimization takes the form of

$$\begin{array}{ccc}& \underset{c}{argmin}& \frac{1}{2}\Vert W\left(\sum _{b=1}^{n_b}(A_b{u}_b{c}_b)-d\right){\Vert }_2^2\\ & subjectto& c\ge 0,\end{array}$$ (6)

where the aperture intensities c are the only optimization variables. The polishing step allows for fine tuning of the aperture intensities that has been shown to improve the dosimetry. Ultimately, the aperture shapes and intensities are obtained from u and c to reconstruct the piecewise constant fluence maps.

To ensure an acceptable local minimum that emphasizes the dose fidelity, a graduated weighting technique was implemented, where γ starts at 0 and is monotonically increased over the course of the optimization, until it reaches a max value γ _max . The idea behind this technique is to start with the convex part of the objective function that includes the dose fidelity term. During the optimization, the non‐convexity is slowly introduced into the problem, ensuring that the optimized fluence segments still result in high dose fidelity. The γ was chosen to monotonically increase via the equation $\mathit{\gamma }={\mathit{\gamma }}_{max}·\text{min}\left(1,{\left(\frac{k}{\widehat{k}}\right)}^8\right)$, where k is the current subiteration number for the updates involving modules 1 and 2, and $\widehat{k}$ is a set subiteration number when γ = γ _max for the first time. For all patients in this study, $\widehat{k}$ was set to 500, which would allow for the alternating module schedule to cycle through 5 times before γ = γ _max . Note that γ is not updated while module 3 is active, since γ does not directly influence the outcome of module 3. A pseudocode is provided in (7) order to provide clarity on the update scheme:

$$\begin{array}{cc}& \widehat{k}=500\hfill \\ & k=1\hfill \\ & \mathbf{while}\mathbf{not}\mathbf{converged}\mathbf{do}\hfill \\ & \mathbf{for}\mathbf{100}\mathbf{\text{iterations}}\hfill \\ & \text{update}x(\text{Module}1)\hfill \\ & \text{update}c(\text{Module}2)\hfill \\ & \mathit{\gamma }={\mathit{\gamma }}_{max}·\text{min}\left(1,{\left(\frac{k}{\widehat{k}}\right)}^8\right)\hfill \\ & k=k+1\hfill \\ & \mathbf{end}\mathbf{for}\hfill \\ & \mathbf{for}\mathbf{1500}\mathbf{iterations}\hfill \\ & \text{update}u(\text{Module}3)\hfill \\ & \mathbf{end}\mathbf{for}\hfill \\ & \mathbf{end}\mathbf{while}\hfill \\ & \mathbf{polishing}\mathbf{step}\hfill \end{array}$$ (7)

2.B. Simulated annealing DAO

Simulated annealing is a stochastic technique developed for non‐convex optimization,¹⁰ and has been successfully used for DAO.^{11, 12, 13, 14, 15, 16, 17} We developed simulated annealing based DAO for comparison. Starting from an initial set of apertures such as the conformal aperture from beams’ eye view, the method randomly selects either to change an aperture intensity or a leaf position for modification. A random number from a Gaussian distribution is sampled to determine the size and direction of the change. The standard deviation, SD, of the Gaussian is defined as

$$\begin{array}{cc}& S{D}_{leaf}=1+\left(\mathit{\vartheta }-1\right)\frac{1}{{\left(n_{succ}+1\right)}^{1/T_0^{step}}}\hfill \\ & S{D}_{intensity}=\left(\mathit{\vartheta }-1\right)\frac{1}{{\left(n_{succ}+1\right)}^{1/T_0^{step}}}\hfill \end{array},$$ (8)

where ϑ is the initial value, n _succ is the number of successes, and $T_0^{step}$ defines the cooling rate.¹⁰ A success is defined as a change that results in a decrease of the cost function. Since the leaf position is quantized by beamlets, SD _leaf is defined such that the smallest possible value is 1 beamlet. On the other hand, SD _intensity is allowed to diminish to 0.

Once either the aperture intensity or the leaf position is randomly modified, a cost function is evaluated. For this study, the cost function used is the dose fidelity term of Eq. (1):

$$minimize\frac{1}{2}\Vert W\left(\sum _{b=1}^{n_b}(A_b{x}_b)-d\right){\Vert }_2^2,$$ (9)

where x _b a function of the leaf positions and aperture intensities—the variables that simulated annealing will be affecting directly. The theoretical leaf positions are constrained such that the two leaves on the same row will not overlap, and the aperture intensities are constrained to be non‐negative. While the cost function in Eq. (9) is convex, the conversion of the leaf positions and aperture intensity information to x _b is non‐convex. Any change that results in decreasing the cost value is accepted. If the change increases the cost value, the change can still be accepted with a probability defined as

$$P_{accept}=\mathit{\varphi }\frac{1}{{\left(n_{succ}+1\right)}^{1/T_0^{prob}}},$$ (10)

where φ is the initial probability of acceptance, and $T_0^{prob}$ defines the cooling rate. The motivation for allowing changes that increase the cost function is to allow for the jumping out of local minima.

2.C. Evaluation

Three planning cases—one glioblastoma multiforme (GBM) patient, one lung (LNG) patient, and one head and neck (H&N) patient with 3 PTVs at different prescription levels—were evaluated in this study to test the feasibility of the optimization formulation. Using a collapsed cone convolution/superposition code with a 6 MV polyenergetic kernel—with a dose array resolution of (0.25 cm)³ and a beamlet size of (0.5 cm)²—the beamlet dose was calculated for 1162 beams, evenly spaced across the 4π steradian. After beam angles that would cause gantry to couch/patient collisions were removed, a column generation and pricing approach^{22, 36, 37, 38, 39, 40, 41} was utilized to automatically select 20 beam angles for each patient. The beamlet dose of the selected beams are stored in the dose array, A, for optimization. A shell structure around the PTV and skin structure were added to every patient to reduce dose spillage outside the PTV. The thickness of the shell structure was calculated based on the equation: $thicknes{s}_{shell}=\sqrt[3]{\frac{3}{4\mathit{\pi }}TV}$, where TV is the target volume.

Patient plans were created using Mumford‐Shah based DAO (DAO_MS) and simulated annealing DAO (DAO_SA). The same beam angles and number of allowed segments per beam are used for both DAO_MS and DAO_SA for the same patient. The allowed number of segments, prescription doses and PTV volumes for three patients are shown in Table 2. To ensure an unbiased plan comparison, the weighting matrices W of DAO_MS and DAO_SA plans are iteratively updated to outperform each other in terms of OAR sparing and PTV coverage and homogeneity until further improvement in one aspect is impossible without sacrificing the other. At the end, with the same fidelity term, the structure weightings used by both the DAO_MS plans and the DAO_SA plans were found to be similar.

Table 2.

Number of allowed segments per beam, prescription dose, and PTV volume for each patient

Patient	Number of allowed segments per beam (n s )	Prescription dose (Gy)	PTV volume (cc)
Glioblastoma multiforme	10	30	57.77
Lung	10	50	47.84
Head & neck	20	54	197.54
		59.4	432.56
		69.96	254.98

For evaluation, all treatment plans were normalized such that 100% of the prescription dose is delivered to 95% of the PTV. For the H&N case, the 69.96 Gy PTV was used for normalization. PTV homogeneity $\left(\frac{D95}{D5}\right)$, D98, D99, and D_max were evaluated to assess the PTV coverage, hot spots, and homogeneity. OAR D_max and D_mean were assessed to determine dose sparing to the critical structures. D_max is defined as the dose at 2% of the structure volume, D2, which is recommended by the ICRU‐83 report.⁴² To quantitate the amount of high dose spillage to the normal tissue, R50, defined as the 50% isodose volume divided by the target volume, was determined. Last, the van't Reit conformation number (VRCN)⁴³ was also assessed. VRCN is defined as $\frac{T{V}_{RI}}{TV}\times \frac{T{V}_{RI}}{V_{RI}}$, where TV _RI is the target volume covered by the reference isodose, TV is the target volume, and V _RI is the volume of the reference isodose. van't Reit conformation number is global conformity index that takes into account both the irradiation of the target volume and healthy tissues, and ranges from 0 to 1, with 1 being the perfect case. For the H&N case, the R50 and VRCN values were calculated using the sum of all 3 PTVs as the target volume and 54 Gy as the reference dose.

The computer used to solve the optimizations has 32 GB RAM, an NVIDIA GeForce GTX 690, and an Intel Core i7‐3960X CPU, with six physical cores overclocked to 4.00 GHz.

3. Results

Figure 2 shows the DVHs of all patients. The GBM DAO_MS and DAO_SA plans are almost identical in OAR doses with difference less than 0.05% of the prescription dose. For the LNG case, the DVH shows that the DAO_MS method was able to better spare the proximal bronchus dose, but otherwise, the two methods performed similarly. On average, for the LNG case, the DAO_MS method was able to spare proximal bronchus D_max by 3.67% and D_mean by 1.08% of the prescription dose. For the more complicated H&N plan, the DAO_MS plan evidently improved OAR sparing compared to the DAO_SA plan, with as much as a 13 Gy reduction to the spinal cord. The improvement is consistent for all OARs in the H&N DAO_MS plan. On average, D_max and D_mean were reduced by 10.91% and 10.58% of the prescription dose. The OAR sparing is summarized in Table 3.

Figure 2.

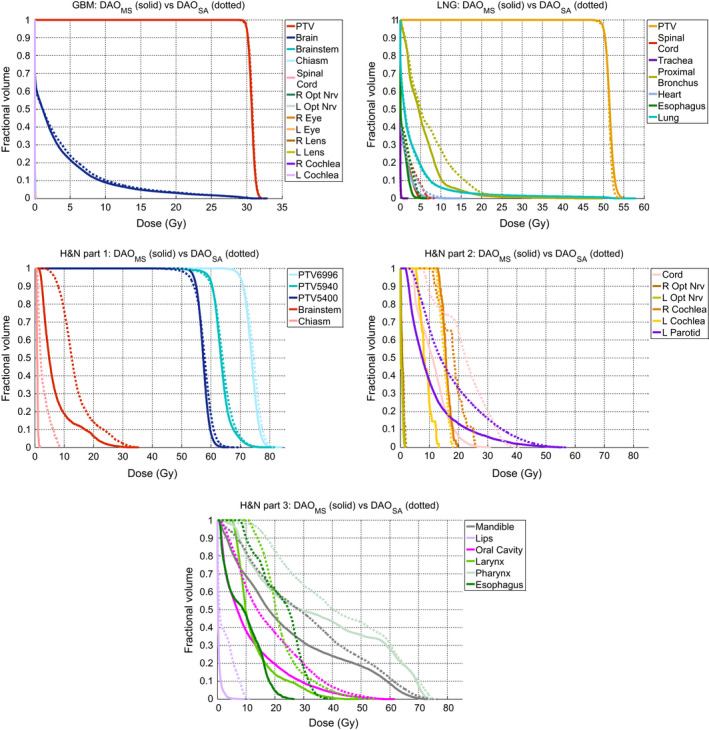
DVH comparisons of the GBM, LNG, and H&N cases. [Color figure can be viewed at wileyonlinelibrary.com]

Table 3.

Largest, smallest, and average values found for $\left({\mathrm{D}}_{\mathrm{DA}{\mathrm{O}}_{\mathrm{MS}}}-{\mathrm{D}}_{\mathrm{DA}{\mathrm{O}}_{\mathrm{SA}}}(\mathrm{Gy})\right)$ dose differences for D_max and D_mean. Negative values represent dose sparing for DAO_MS, while positive values represent dose sparing for DAO_SA. OARs that received 0 Gy in both cases are excluded in the evaluation

Dose difference $\left({\mathrm{D}}_{\mathrm{DA}{\mathrm{O}}_{\mathrm{MS}}}-{\mathrm{D}}_{\mathrm{DA}{\mathrm{O}}_{\mathrm{SA}}}(\mathrm{Gy})\right)$	Dmax			Dmean
	Largest value	Smallest value	Average value	Largest value	Smallest value	Average value
GBM	+0.021 Chiasm	−0.031 L Eye	−0.004	+0.003 Chiasm	−0.003 L Eye	−0.0004
LNG	+0.036 Trachea	−3.000 ProxBronch	−1.835	+0.004 Trachea	−1.593 ProxBronch	−0.541
H&N	−0.162 L Opt Nrv	−13.067 Spinal Cord	−5.891	−0.046 R Opt Nrv	−13.073 Esophagus	−5.714

Table 4 shows PTV dose statistics, as well the dose spillage (R50) and the conformity number (VRCN). On average, the PTV was better covered using DAO_MS. D98 and D99 was increased by 1.66% and 2.21% of the prescription dose. The H&N plan had the largest improvement in dose coverage, with an increase as large as 3.77 Gy in D99 for the 54 Gy PTV. The average homogeneity of the two planning methods is similar with DAO_MS being slightly better by 0.012. The average R50 and VRCN was more clearly improved in the H&N case using DAO_MS. The R50 for the GBM and LNG cases were similar for the two plan types, differing by 0.16. For the H&N plan, R50 was lowered by 0.826 and VRCN was increased by 1.355 using DAO_MS, indicating substantially improved dose compactness and conformality.

Table 4.

Comparison of the PTV homogeneity, D98, D99, and D_max, as well as R50 and VRCN

Patient Case		PTV Statistics					R50		VRCN
		Homogeneity		D98	D99	Dmax
		DAOMS	DAOSA	${\mathrm{D}}_{\mathrm{DA}{\mathrm{O}}_{\mathrm{MS}}}-{\mathrm{D}}_{\mathrm{DA}{\mathrm{O}}_{\mathrm{SA}}}(\mathrm{Gy})$			DAOMS	DAOSA	DAOMS	DAOSA
GBM		0.954	0.952	+0.089	+0.174	−0.047	2.553	2.712	0.816	0.847
LNG		0.938	0.951	+0.294	+0.494	+0.935	2.840	2.680	0.831	0.892
H&N	54	0.895	0.853	+2.626	+3.771	−1.595	2.248	3.074	0.748	0.607
	59.4	0.850	0.833	+1.237	+1.448	−0.483
	69.96	0.904	0.892	+0.153	−0.101	−1.054
Average		0.908	0.896	+0.880	+1.157	−0.449	2.547	2.822	0.798	0.782

Figure 3 shows the isodose comparison. The low dose cutoff for viewing was set at 10% of the prescription dose. Qualitatively, the dose distributions produced by the DAO_MS and the DAO_SA methods for GBM and LNG plans are similar. On the other hand, the dose distribution differences of the H&N plans are more compelling. The dose is visually more compact in the DAO_MS plan, with lower dose to the brainstem, spinal cord, and posterior neck region in the sagittal slice, as well as the larynx and left parotid in the coronal slice.

Figure 3.

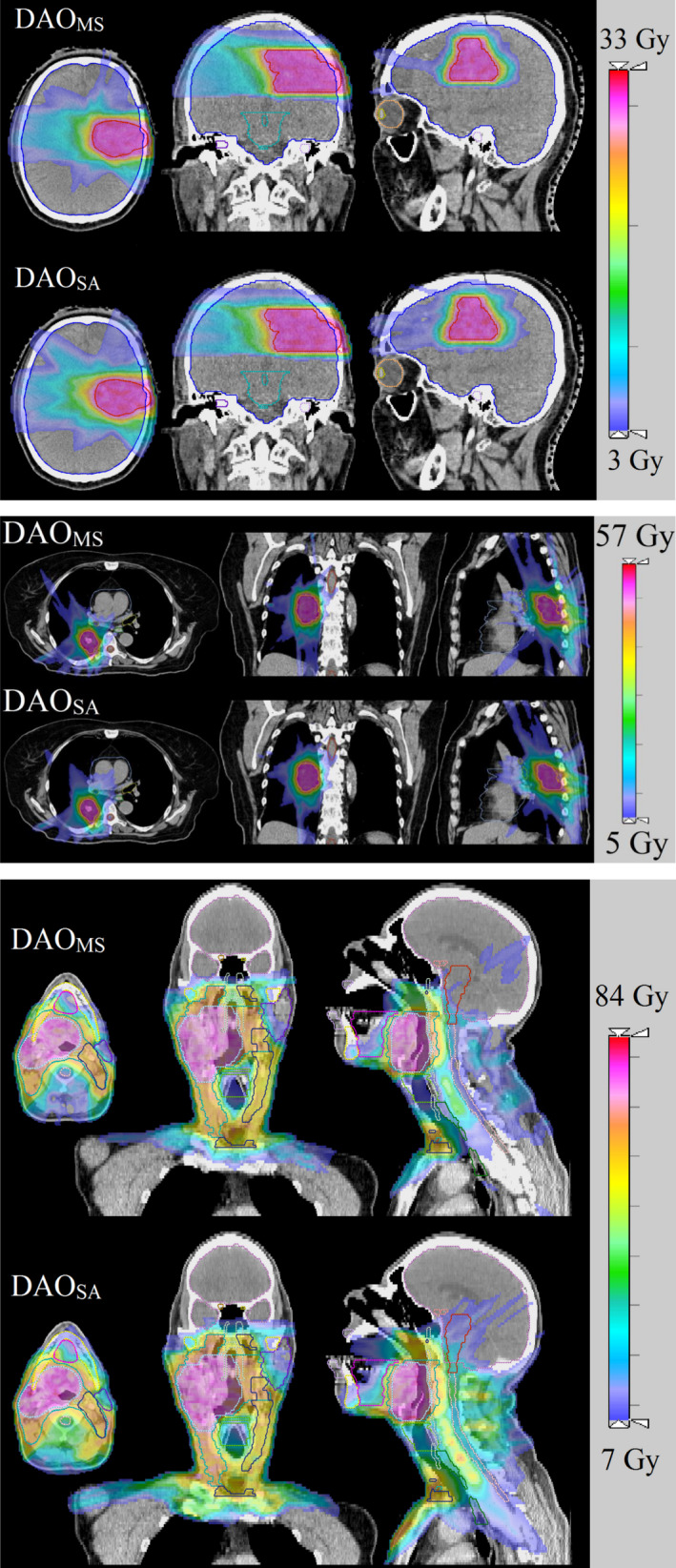
Isodose of the GBM, LNG, and H&N patients. The low dose cutoff for viewing was set to be 10% of the prescription dose. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 4 shows an example of MLC segments and resultant fluence map for the GBM patient. The pairwise disjoint nature of the piecewise constant Mumford‐Shah formulation is apparent in the segmentation results, as the DAO_MS segments do not overlap. The DAO_SA MLC segments, on the other hand, can overlap, resulting in more complex fluence. On average, the size of DAO_MS segments is smaller than that of DAO_SA. Interestingly, Table 5 shows that none of the planning methods utilized the maximal allowed segments for delivery.

Figure 4.

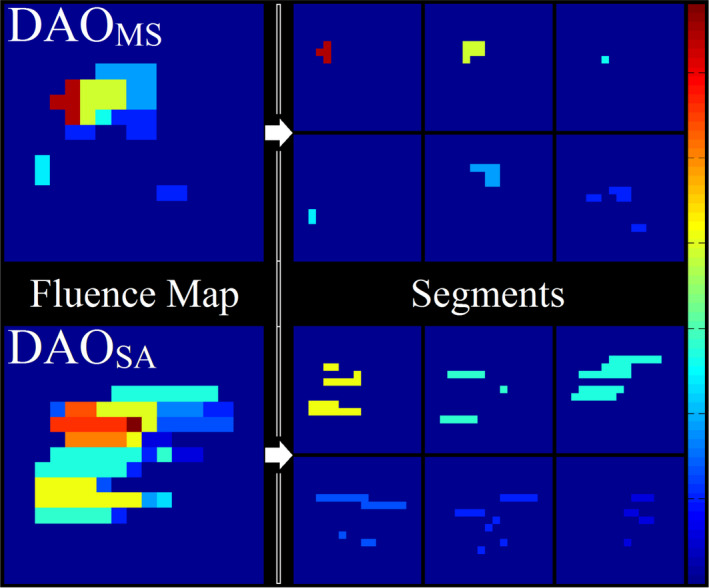
Schematic of an optimized fluence from each plan type, and the breakdown of the fluences to their segments. [Color figure can be viewed at wileyonlinelibrary.com]

Table 5.

Aperture statistics for the DAO_MS and the DAO_SA methods for the patient cases

	Allowed number of segments per beam $\left(n_s\right)$	Average number of solved segments per beam		Mean number of beamlets in a segment
		DAOMS	DAOSA	DAOMS	DAOSA
GBM	10	6.10	7.80	6.72	17.51
LNG	10	9.40	9.15	4.93	14.93
H&N	20	16.00	10.20	8.84	50.50

DAO_MS is substantially faster than DAO_SA, with a 9.5 to 40 fold decrease in total solve time. The number of times retuning the weights was greater for the DAO_MS approach because it was run 2–3 times in the beginning before the first iteration of the DAO_SA approach, which then adopted the DAO_MS weights as its starting point. Figure 5 shows example convergence plots for the GBM case. The DAO_MS approach is able to consistently lower the cost function, since each module is a convex subproblem. The stochastic property of simulated annealing causes the cost function to randomly increase at times, while attempting to escape from local minima. Figure 5 and Table 6 highlight the strengths of the multiconvex approach to quickly and deterministically reach a minimum that contains a high quality dosimetric plan.

Figure 5.

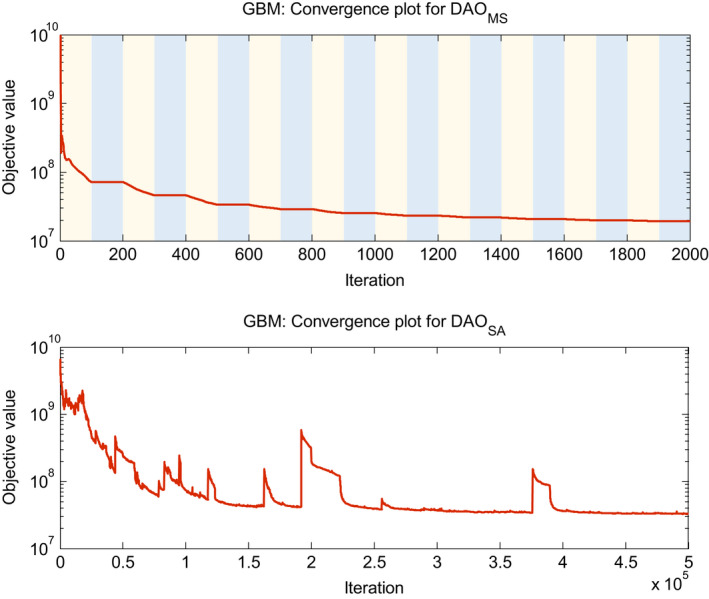
Example convergence plots for the GBM case. For DAO_MS, the light‐shaded regions represent where module 1 and module 2 are updating x and c at each subiteration. The dark‐shaded region represents where module 3 is updating u, and each data point in the blue region represents 15 subiterations. Objective value calculation for DAO_MS uses the γ _max value for all iterations. [Color figure can be viewed at wileyonlinelibrary.com]

Table 6.

Solve time for one optimization run for each case and plan type. DAO_MS solve times include the polishing step

	Solve time (s)		Number of times retuning structure weights
	DAOMS	DAOSA	DAOMS	DAOSA
GBM	599.8	5719.6	6	4
LNG	647.1	25747.7	7	4
H&N	2170.2	35682.8	11	10

4. Discussion

In this study, we developed a novel direct aperture optimization technique that integrates fluence map optimization—employing L2‐norm fidelity and L1‐norm regularization terms—with the multiphase piecewise constant Mumford‐Shah method. We utilized a first‐order primal‐dual proximal‐class algorithm, known as the Chambolle‐Pock algorithm, to solve the multiconvex direct aperture optimization problem. This novel method simultaneously solves for the fluence segments while minimizing the dose fidelity term offers a number of advantages.

Ultimately, DAO_MS result in perfectly piecewise constant fluence maps that are equivalent to apertures without additional stratification. The piecewise constancy cannot be achieved with total variation regularization alone^{6, 7, 8, 9}, because total variation energies do not differentiate piecewise smooth and piecewise constant functions.

The optimization formulation offers an elegant theoretical description of the physical problem. The fidelity term penalizes deviations from the prescription dose, the total variation term promotes piecewise smoothness on the fluence map, and the piecewise constant Mumford‐Shah formulation defines segments that constitute the fluence map. As a non‐convex optimization, this method cannot guarantee to find the global minima of the problem. However, with the graduated weighting technique on the non‐convex term, the optimization is able to find a local minimum that is biased to satisfying to dose fidelity term. By slowly introducing the non‐convexity, optimizer can begin to form segments for the fluence map that indirectly penalize deviations between the projected dose and the prescription dose.

In addition to its theoretical appeal, the deterministic multiconvex approach offers practical advantages in computational speed and dosimetric performance, compared to the existing stochastic simulated annealing method for DAO. The DAO_SA method struggled to include more apertures in the optimization but the explicit addition is heavily penalized by computational time. Given the vast number of possible apertures as a combination of beamlets, the previous methods are inherently inefficient. Our method, on the other hand, segments the MLC apertures on the fly, thus avoiding being limited to a small subset of possible apertures. As hypothesized, the advantage is shown more evident for the multilevel head and neck plan requiring complex modulation.

The Chambolle‐Pock algorithm was selected to solve the optimization problem for several reasons. As a proximal‐class algorithm, it can solve many types of non‐differentiable optimization formulations exactly, such as formulations involving the L1‐norm. The algorithm is highly efficient on memory usage and computation cost because it does not require a to solve system of linear equations involving the fluence to dose transformation matrix at every iteration, contrasting to other methods such as alternating direction method of multipliers (ADMM).⁴⁴ The computation cost of Chambolle‐Pock relies on the simple multiplication of a large matrix and its transpose at each iteration.

While the piecewise constant Mumford‐Shah term promotes apertures to be MLC deliverable, the DAO_MS method does not explicitly guarantee that the resulting aperture is MLC deliverable in 1 segment. For example, in Fig. 3, the last segment of the DAO_MS plan is not deliverable for horizontal MLCs. The simplest solution is to break down the segment into two delivery segments, which should minimally add to the treatment time since only a small fraction of the solved segments need to be further broken down.

A drawback of the current approach is that the Mumford‐Shah formulation is designed to describe non‐overlapping segments. The ability to have overlapping segments would allow for larger and fewer segments. Although the drawback did not prevent DAO_MS from outperforming the stochastic approach, particularly in complex cases, there is clearly space for improvement. As a topic of further investigation, the smaller segment size problem may be alleviated by devising an improved segmentation algorithm to divide the DAO_MS fluence into fewer and larger overlapping segments, without modifying the current fluence.

Another interesting observation one can make from the result is that both methods did not use the maximal allowed number of segments. For the DAO_MS plans, this is due to the total variation term that reduces the fluence map complexity and subsequently fewer segments. The DAO_SA method, on the other hand, is not regularized to penalize more segments. Given that DAO_SA plans are suboptimal compared to the DAO_MS plans, this reflects the weakness of using simulated annealing method to search a larger aperture solution space.

The run time of the DAO_SA method used in this study is noticeably longer than the simulated annealing implemented commercial software. The longer computational time can be attributed to the following reasons. First, the plans used 20 beams, which increased the fluence‐to‐dose transformation matrix size. Second, the fluence‐to‐dose transformation matrices in this study were not downsampled. Last, the plans allowed many more segments than what would be allowed in a commercial planning software.

5. Conclusion

A novel deterministic direct aperture optimization formulation combining fluence map optimization and multiphase piecewise constant Mumford‐Shah segmentaion into a unified framework was proposed and evaluated. The new approach enables generating MLC segments on the fly without being limited to a small subset of possible apertures as previous methods did. The non‐convex optimization formulation was split into multiple convex modules, and solved alternatingly using a first‐order primal‐dual proximal‐class algorithm. The new deterministic method solved the DAO problem is considerably faster than the simulated annealing method and is dosimetrically superior, particularly for the complex head and neck case.

Conflict of interest

There is no conflict of interest involved in the study.

Appendix 1.

1.1.

A1. The overrelaxed Chambolle‐Pock algorithm

The Chambolle‐Pock algorithm, a first‐order primal dual algorithm,²⁵, ²⁶ has previously been successfully implemented for fluence map optimization problems.⁹, ³³, ³⁶, ⁴⁵ The algorithm solves a primal problem of the canonical form

$$minimizeF\left(Kx\right)+G\left(x\right),$$ (A1)

where F and G are lower semicontinuous functions and K is a matrix. To solve an optimization problem with Chambolle‐Pock, the optimization must be rewritten to fit this canonical form. It will be seen later that all optimizations in this study that use the Chambolle‐Pock algorithm can easily be expressed in this canonical form. The overrelaxed version of the Chambolle‐Pock algorithm³⁵ solves the primal problem via the iteration

$$\begin{array}{cc}& {\overline{x}}^{n+1}=pro{x}_{\mathit{\tau }G}\left(x^n-\mathit{\tau }{K}^T{z}^n\right)\hfill \\ & {\overline{z}}^{n+1}=pro{x}_{\mathit{\sigma }{F}^{\ast }}\left(z^n+\mathit{\sigma }K\left(2{\overline{x}}^{n+1}-x^n\right)\right)\hfill \\ & x^{n+1}=\mathit{\rho }{\overline{x}}^{n+1}+\left(1-\mathit{\rho }\right)x^n\hfill \\ & z^{n+1}=\mathit{\rho }{\overline{z}}^{n+1}+\left(1-\mathit{\rho }\right)z^n\hfill \end{array},$$ (A2)

where z variable of the dual problem: $minimize{G}^{\ast }\left(-K^{T}z\right)+F^{\ast }\left(z\right)$. The Chambolle‐Pock algorithm is solving both the primal and dual problem simultaneously. The function, F*, is the convex conjugate of F, defined as $F^{\ast }\left(z\right)=\begin{array}{c}sup\\ y\end{array}\left(z^{T}y-F\left(y\right)\right)$. The overrelaxation parameter, $\mathit{\rho }\in \left[0,2\right]$, can be adjusted to control the convergence. The algorithm degenerates to the original algorithm when p = 1. As a proximal‐class algorithm,⁴⁶ the Chambolle‐Pock algorithm relies on the “proximal mapping”, or “prox operator”, defined as

$$pro{x}_{th}\left(x\right)=\begin{array}{c}argmin\\ v\end{array}\left(h\left(v\right)+\frac{1}{2t}\Vert v-x{\Vert }_2^2\right),$$ (A3)

where h is a lower semicontinous function and t is a parameter that serves as a step size. Intuitively, $pro{x}_{th}\left(x\right)$ will try to find an argument that minimizes h, without straying too far from x. The efficacy of proximal algorithms relies on that the function h has a simple evaluation with the prox operator. A useful property of the prox operator is the separable sum rule,

$$pro{x}_{\mathit{\sigma }{F}^{\ast }}\left(\left[\begin{array}{c}{z}_1\\ ⋮\\ z_n\end{array}\right]\right)=\left[\begin{array}{c}pro{x}_{\mathit{\sigma }{f}_1^{\ast }}\left(z_1\right)\\ ⋮\\ pro{x}_{\mathit{\sigma }{f}_n^{\ast }}\left(z_n\right)\end{array}\right],$$ (A4)

where $F\left(\left[\begin{array}{c}{y}_1\\ ⋮\\ y_n\end{array}\right]\right)=f_1\left(y_1\right)+\cdots +f_n\left(y_n\right)$, and this allows us to break down $F\left(Kx\right)$ into a sum of convex functions. Another valuable property is the Moreau decomposition,

$$pro{x}_{\mathit{\sigma }{F}^{\ast }}(Z)=Z-\mathit{\sigma }·pro{x}_{{\mathit{\sigma }}^{-1}F}({\mathit{\sigma }}^{-1}z),$$ (A5)

which allows us to calculated the prox operator of the convex conjugate of a function without having to evaluate the convex conjugate itself.

In the algorithm, we have the parameters τ and σ, which serve as our step sizes during the optimization. These can be selected based on a diagonal preconditioning approach³⁴:

$$\begin{array}{cc}{\mathit{\tau }}_j=\frac{1}{\sum _{i=1}^{i=n_{rows}}K(i,j)}& {\mathit{\sigma }}_i=\frac{1}{\sum _{i=1}^{i=n_{cols}}K(i,j)}\\ \mathit{\tau }=\left[\begin{array}{ccc}{\mathit{\tau }}_{j=1}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{\tau }}_{j=n_{cols}}\end{array}\right]& \mathit{\sigma }=\left[\begin{array}{ccc}{\mathit{\sigma }}_{j=1}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{\sigma }}_{i=n_{rows}}\end{array}\right],\end{array}$$ (A6)

where τ and σ. are diagonal matrices with the same number of diagonal elements as the length od x and z, respectively. The diagonal preconditioning guarantees convergence under the assumption that $F\left(Kx\right)$ and $G\left(x\right)$ have sum separable operations. In the case where these functions are not sum separable, but are block separable, it is possible to assign the block of variables the smallest step size—founduring the preconditioning process—within its block. Otherwise, τ and σ can be scalars and follow the relation, τσ||K||² ≤ 1, to guarantee convergence. The operator norm, K, can be estimated via power iteration.⁴⁷

A2. Solving Module 1 with the Chambolle‐Pock Algorithm

Module 1 updates x, while holding u and c constant. To solve module 1 with Chambolle‐Pock, which solves the optimization of the form $minimizeF\left(Kx\right)+G\left(x\right)$, we first rewrite problem 2 as:

$$\begin{array}{cc}\underset{x}{argmin}& \frac{1}{2}W\Vert \left(\sum _{b=1}^{n_b}(A_b{x}_b)-d\right){\Vert }_2^2+\sum _{b=1}^{n_b}\left({\mathit{\lambda }}_1{\Vert D_b^{\Vert }{x}_b\Vert }_1+{\mathit{\lambda }}_2{\Vert D_b^{\perp }{x}_b\Vert }_1\right)+\frac{\mathit{\gamma }}{2}\sum _{b=1}^{n_b}\sum _{s=0}^{n_s}\Vert \sqrt{diag(u_{bs})}(x_b-c_{bs}\stackrel{\rightharpoonup }{\mathbf{1}}){\Vert }_2^2\\ subjectto& x\ge 0,\end{array}$$ (A7)

where the third term is an equivalent expression to $\frac{\mathit{\gamma }}{2}\sum _{b=1}^{n_b}\sum _{p=1}^{n_p}\sum _{s=0}^{n_s}{u}_{bps}|x_{bp}-c_{bs}{|}^2$. It is written this way as a more convenient expression for updating x. We then define the matrix, K, as well as the functions, F and G, as

$$\begin{array}{cc}& K=\left[\begin{array}{c}WA\\ D_1\\ D_2\\ \sqrt{diag(u_{b=1,s=0})}\\ ⋮\\ \sqrt{diag(u_{b=n_b,s=n_s})}\end{array}\right]\hfill \\ \hfill F(y)& =\underset{f_1(y_1)}{\underbrace{\frac{1}{2}{\Vert y_1-Wd\Vert }_2^2}}+\underset{f_2(y_2)}{\underbrace{{\mathit{\lambda }}_1{\Vert y_2\Vert }_1}}+\underset{f_3(y_3)}{\underbrace{{\mathit{\lambda }}_2{\Vert y_3\Vert }_1}}\hfill \\ & +\underset{\sum _b^{n_b}\sum _{s=0}^{n_s}{f}_{bs}(y_{bs})}{\underbrace{\sum _{b=1}^{n_b}\sum _{s=0}^{n_s}\frac{1}{2}{\Vert y_{bs}-\sqrt{diag(u_{bs})}{c}_{bs}\stackrel{\rightharpoonup }{\mathbf{1}}\Vert }_2^2}}\hfill \\ & G(x)=\left\{\begin{array}{cc}0& iff\ge 0\\ \infty & otherwise\end{array}.\right.\hfill \end{array}$$ (A8)

Once K, F, and G are defined, the Chambolle‐Pock algorithm can be applied to solve the problem. The prox operator evaluations of the functions, F* and G, yield simple low cost expressions:

$$\begin{array}{cc}& pro{x}_{\mathit{\sigma }{f}_1^{\ast }}\left({\widehat{z}}_1\right)=\frac{{\widehat{z}}_1-\mathit{\sigma }Wd}{1+\mathit{\sigma }}\hfill \\ & pro{x}_{\mathit{\sigma }{f}_2^{\ast }}\left({\widehat{z}}_2\right)=P_{{\mathit{\lambda }}_{1}B}\left({\widehat{z}}_2\right)\hfill \\ & pro{x}_{\mathit{\sigma }{f_3}^{\ast }}\left({\widehat{z}}_3\right)=P_{{\mathit{\lambda }}_{2}B}\left({\widehat{z}}_3\right)\hfill \\ & pro{x}_{\mathit{\sigma }{f}_{bs}^{\ast }}\left({\widehat{z}}_{bs}\right)=\mathit{\gamma }\left(\frac{{\widehat{z}}_{bs}-\mathit{\sigma }\sqrt{diag(u_{bs})}{c}_{bs}\stackrel{\rightharpoonup }{\mathbf{1}}}{\mathit{\gamma }+\mathit{\sigma }}\right)\hfill \\ & pro{x}_{\mathit{\tau }G}\left(\widehat{x}\right)={\left(\widehat{x}\right)}_{+}\hfill \end{array},$$ (A9)

where P _λB ( · ) projects its argument onto the norm ball $\mathit{\lambda }B=\left\{{\mathit{\psi }|\Vert \mathit{\psi }\Vert }_{\infty }\le \mathit{\lambda }\right\}$, and ( · )₊ projects its argument onto the non‐negative orthant. These expressions are used at each iteration of the algorithm to update x.

A3. Solving Module 3 with the Chambolle‐Pock Algorithm

Module 3 updates u, while holding x and c constant. Since x and c are constants, Eq. (5) can be rewritten as

$$\begin{array}{cc}\underset{u}{argmin}& 〈q,u〉+\sum _{b=1}^{n_b}\pm \sum _{s=1}^{n_s}({\mathit{\omega }}_1{\Vert D_b^{\Vert }{u}_{bs}\Vert }_1+{\mathit{\omega }}_2{\Vert D_b^{\perp }{u}_{bs}\Vert }_1)\\ subjectto& \begin{array}{c}u>0\\ 1^T{u}_{bp}=1,\end{array}\end{array}$$ (A10)

where $q_{bps}=\frac{1}{2}|f_{bp}-c_{bs}{|}^2$ for all b, p, and s. The intermediate variable, q, has the same dimensions and subscript structure as u. The inner product, 〈·,·〉, takes an element‐wise product between its two arguments and sums the result. To solve problem 20 with Chambolle‐Pock, which solves an optimization of the form $F\left(Ku\right)+G(u)$, we first define our matrix, K, as well as our functions F and G as

$$\begin{array}{cc}& K=[\begin{array}{c}{D}^{\Vert }\\ D^{\perp }\end{array}]\hfill \\ & F(y)=\underset{f_1(y_1)}{\underbrace{{\mathit{\omega }}_1{\Vert y_1\Vert }_1}}+\underset{f_2(y_2)}{\underbrace{{\mathit{\omega }}_2{\Vert y_2\Vert }_1}}\hfill \\ & G(u)=〈q,u〉+{\sum }_{b=1}^{n_b}{\sum }_{p=1}^{n_p}{I}_{sp}(u_{bp}),\hfill \end{array}$$ (A11)

where I _sp is the indicator function for the probability simplex. In other words,

$$\begin{array}{cc}& I_{sp}(u_{bp})=I_{+}(u_{bp})+I_1(u_{bp})\hfill \\ & I_{+}(u_{bp})=\left\{\begin{array}{cc}0& if{u}_{bp}\ge 0\\ \infty & otherwise\end{array}\right.\hfill \\ & I_1(u_{bp})=\left\{\begin{array}{cc}0& if{u}_{bp}\ge 0\\ \infty & otherwise\end{array}\right.\hfill \end{array}$$ (A12)

Evaluation of the prox operators of F* and G yield the following expressions.

$$\begin{array}{cc}& pro{x}_{\mathit{\sigma }{f}_1^{\ast }}\left({\widehat{z}}_1\right)=P_{{\mathit{\omega }}_{1}B}\left({\widehat{z}}_1\right)\hfill \\ & pro{x}_{\mathit{\sigma }{f}_2^{\ast }}\left({\widehat{z}}_2\right)=P_{{\mathit{\omega }}_{2}B}\left({\widehat{z}}_2\right)\hfill \\ & pro{x}_{\mathit{\tau }G}\left(\widehat{u}\right)=P_{S_{p}row}\left(\widehat{u}-\mathit{\tau }q\right)\hfill \end{array},$$ (A13)

where P _ωB ( · ) projects its argument onto the norm ball $\mathit{\omega }B=\left\{{\mathit{\psi }|\Vert \mathit{\psi }\Vert }_{\infty }\le \mathit{\omega }\right\}$, and $P_{S_{p}row}(·)$ projects each row of its argument onto the probability simplex. Recall that each row in u is a vector u _bp . These simple expressions are used at each iteration of the Chambolle‐Pock algorithm to update u.

A4. The probability simplex projection

Projection onto the probability simplex is defined as

$$P_{S_p}\left(v\right)={\left(v-\mathit{\eta }\stackrel{\rightharpoonup }{\mathbf{1}}\right)}_{+},$$ (A14)

where v is a vector, ( · ) projects its argument onto the non‐negative orthant, and η is a scalar that is the solution to the equation

$$\stackrel{\rightharpoonup }{{\mathbf{1}}^T}{\left(v-\mathit{\eta }\stackrel{\rightharpoonup }{\mathbf{1}}\right)}_{+}=1.$$ (A15)

Since this projection occurs at every iteration, it is imperative to use a fast, low‐cost algorithm to project a vector onto the probability simplex. Wang et al.,⁴⁸ provided an efficient algorithm for the projection:

$$\begin{array}{c}\hfill Input:v_{in}\in R^D\\ & Sort{u}_{in}into\tilde{v}:{\tilde{v}}_1\ge {\tilde{v}}_2\ge \cdots \ge {\tilde{v}}_D\hfill \\ & Find{j}^{\ast }=max\left\{1\le j\le D|{\tilde{v}}_j+\frac{1}{j}\left(1-{\sum }_{i=1}^j{\tilde{v}}_i\right)>0\right\}\hfill \\ & Define\mathit{\eta }=-\frac{1}{j^{\ast }}\left(1-{\sum }_{i=1}^{j^{\ast }}{\tilde{v}}_i\right)\hfill \\ & Output:v_{out}={\left(v_{in}-\mathit{\eta }\stackrel{\rightharpoonup }{\mathbf{1}}\right)}_{+}\hfill \end{array}$$ (A16)

Essentially, this algorithm efficiently solves for η to properly project the argument onto the probability simplex.