Multimodal Image Registration through Simultaneous Segmentation

Abstract

Multimodal image registration facilitates the combination of complementary information from images acquired with different modalities. Most existing methods require computation of the joint histogram of the images, while some perform joint segmentation and registration in alternate iterations. In this work, we introduce a new non-information-theoretical method for pairwise multimodal image registration, in which the error of segmentation — using both images — is considered as the registration cost function. We empirically evaluate our method via rigid registration of multi-contrast brain magnetic resonance images, and demonstrate an often higher registration accuracy in the results produced by the proposed technique, compared to those by several existing methods.

I. Introduction

Employing multiple imaging modalities often provides valuable complementary information for clinical and investigational purposes. Computing a spatial correspondence between multimodal images, a.k.a. multimodal image registration, is the key step in combining the information from such images. Since different modalities create images that do not share the same tissue contrast, the alignment of these images can hardly be assessed by a local comparison of their intensities. In pairwise multimodal image registration, the joint histogram of the two images has been widely used to derive global matching measures, such as mutual information [1, 2], normalized mutual information [3], entropy correlation coefficient [2], and tissue segmentation probability [4, 5]. Histogram computation typically requires an optimized choice of the bin (or kernel) width [6]. Joint segmentation and registration of multimodal images has also been suggested to improve both the segmentation and registration [4, 5, 7, 8], where iterative updates to segmentation and registration are typically performed in alternating steps.

In this work, we introduce a new objective function for pairwise multimodal image registration based on simultaneous segmentation. Our underlying assumption is that any improvement in the alignment of two images leads to an improvement in image segmentation from them, hence a lower segmentation error. We propose an efficient algorithm that uses the intensity values of the images to divide the voxels into two classes, while regarding the segmentation error as the registration cost function. We perform the iterative registration and segmentation simultaneously, as opposed to existing methods for joint segmentation and registration [5, 7, 8] that alternate between the segmentation and registration steps. Furthermore, we do not use the joint histogram or entropy of images or tissue classes (contrary to [4, 5]). In a comparison with several existing objective functions, we show that our proposed objective function often outperforms competing metrics in registering brain magnetic resonance images with different contrasts. We stress that our goal is improved registration, and thus the oversimplifying assumption of only two classes is irrelevant if the registration produced by this procedure outperforms competing methods.

In Section II, we describe the proposed segmentation score computation for a single image (Section II.A) and a pair of images (Section II.B), and how to drive the registration with the score (Section II.C). We evaluate our approach experimentally in Section III, and conclude the paper in Section IV.

II. Methods

A. Segmentation Score for a Single Image

Let I⃑ ∈ ℝ^N be an image consisting of N voxels, where I_k represents the intensity value of the k^th voxel,. k = 1, …, N. For mathematical simplicity and without loss of generality, we assume I⃑ to be zero-sum, i.e. ${\sum }_{k=1}^N{I}_k=0$. We denote a binary segmentation of I⃑ by S⃑ ∈ {0,1}^N where S_k determines whether voxel k belongs to class 0 or class 1. Inspired by Otsu’s method for binary clustering [9], we define the following sum of squared error for the segmentation S⃑, as the deviation of the voxel intensities in a class from the mean intensity of the class:

$$\begin{gathered} \epsilon :=\sum _{k=1}^N{(I_k-{\mu }_{S_k})}^2 \\ =\sum _{\{k\mid S_k=0\}}{(I_k-{\mu }_0)}^2+\sum _{\{k\mid S_k=1\}}{(I_k-{\mu }_1)}^2, \end{gathered}$$ (1)

where μ₀ ≔ Σ_{{k|Sk = 0}}I_k/(N − n_S) and μ₁ ≔ Σ_{{k|Sk = 1}}I_k/n_S are the mean intensity values of each class, with $n_S:={\sum }_{k=1}^N{S}_k$ being the number of voxels in class 1. Substituting for μ₀ and μ₁ in Eq. (1) and further simplification leads to:

$$\epsilon ={\Vert \stackrel{\rightharpoonup }{I}\Vert }_2^2-\frac{1}{N-n_S}{\left(\sum _{\{k\mid S_k=0\}}{I}_k\right)}^2-\frac{1}{n_S}{\left(\sum _{\{k\mid S_k=1\}}{I}_k\right)}^2.$$ (2)

Recall that I⃑ is zero-sum, meaning that Σ_{{k|Sk = 0}}I_k + Σ_{{k|Sk = 1}}I_k = 0, thus (Σ_{{k|Sk = 0}}I_k)² = (Σ_{{k|Sk = 1}}I_k)², which reduces ε to:

$$\epsilon ={\Vert \stackrel{\rightharpoonup }{I}\Vert }_2^2-\frac{N}{n_S(N-n_S)}{\left(\sum _{\{k\mid S_k=1\}}{I}_k\right)}^2.$$ (3)

An optimal segmentation S⃑ would minimize ε, or equivalently maximize the following, resulting in the segmentation score ψ_I⃑:

$${\psi }_{\stackrel{\rightharpoonup }{I}}:=\underset{\stackrel{\rightharpoonup }{S}\in {\{0,1\}}^N}{max}\frac{1}{n_S(N-n_S)}{\left(\sum _{\{k\mid S_k=1\}}{I}_k\right)}^2.$$ (4)

As we will see, for our image registration goal, we will only need the segmentation score, ψ_I⃑, but not the optimal segmentation itself. To solve the above maximization problem, we first fix the class size and maximize (Σ_{{k|Sk = 1}}I_k)² for a constant n_S. To that end, we need to find n_S voxels with maximal magnitude of sum of intensity values. This is achieved by sorting the voxels based on their intensity values (that can be negative or positive due to the zero sum), and choosing either the n_S largest voxels or the n_S smallest voxels, whichever results in a larger magnitude of sum. We will see shortly that always choosing the former (the largest voxels) works fine for our purpose. Consequently, we sort the intensity values of I⃑ to obtain the (vectorized) image $\stackrel{\rightharpoonup }{\stackrel{\sim }{I}}$, where Ĩ_k ≥ Ĩ_k+1, and rewrite Eq. (4) as a simple maximization over the scalar n_S:

$${\psi }_{\stackrel{\rightharpoonup }{I}}=\underset{n_S}{max}\frac{1}{n_S(N-n_S)}{\left(\sum _{k=1}^{n_S}{\stackrel{\sim }{I}}_k\right)}^2.$$ (5)

The maximization in Eq. (5) is possible via an exhaustive search for all values of n_S = 1,…, N − 1, while computing ${\sum }_{k=1}^{n_S}{\stackrel{\sim }{I}}_k$ recursively. Given that sorting and the subsequent search are done in 𝒪(N log N) and 𝒪(N), respectively, the complexity of the computation of ψ_I⃑ is 𝒪(N log N).

Note that we consider only the top n_S values (Ĩ₁, …, Ĩ_nS) for a particular n_S in the search. However, the bottom n_S values (Ĩ_N−nS+1, … Ĩ_N) are also implicitly searched, because, thanks to the image’s zero sum, they are the top values for $n_S^{\prime }:=N-n_S$:

$$\begin{gathered} \frac{1}{{n_S}^{\prime }(N-{n_S}^{\prime })}{\left(\sum _{k=1}^{n_{S^{\prime }}}{\stackrel{\sim }{I}}_k\right)}^2=\frac{1}{(N-n_S)n_S}{\left(\sum _{k=1}^{N-n_S}{\stackrel{\sim }{I}}_k\right)}^2 \\ =\frac{1}{n_S(N-n_S)}{\left(-\sum _{k=N-n_S+1}^N{\stackrel{\sim }{I}}_k\right)}^2=\frac{1}{n_S(N-n_S)}{\left(\sum _{k=N-n_S+1}^N{\stackrel{\sim }{I}}_k\right)}^2. \end{gathered}$$ (6)

B. Segmentation Score for a Pair of Multimodal Images

Next, we attempt to segment two images I⃑, J⃑ ∈ ℝ^N with a single segmentation S⃑ ∈ {0, 1}^N. Without loss of generality, we assume that the images (in addition to being zero-sum) are normalized, ||I⃑||₂ = ||J⃑||₂ = 1. This not only will simplify the calculations, but will ensure that different scaling in the intensity values of the two images will not bias the segmentation towards one of the images. Following Section II.A, we arrive at a segmentation score similar to Eq. (4),

$${\psi }_{\stackrel{\rightharpoonup }{I},\stackrel{\rightharpoonup }{J}}:=\underset{\stackrel{\rightharpoonup }{S}\in {\{0,1\}}^N}{max}\frac{1}{n_S(N-n_S)}\left[{\left(\sum _{\{k\mid S_k=1\}}{I}_k\right)}^2+{\left(\sum _{\{k\mid S_k=1\}}{J}_k\right)}^2\right],$$ (7)

and proceed by initially fixing n_S. This time, however, we cannot find the exact optimal segmentation simply by sorting, because a sorted voxel order for one of the images is not necessarily a sorted order for the other image. Therefore, to compute an approximate sorted order, we reduce this problem from two-image segmentation to single-image segmentation by synthesizing an image, K⃑ ∈ ℝ^N, the segmentation of which helps us to best approximate Eq. (7). Expanding Eq. (7) yields:

$$\begin{gathered} {\psi }_{\stackrel{\rightharpoonup }{I},\stackrel{\rightharpoonup }{J}}=\underset{\stackrel{\rightharpoonup }{S}\in {\{0,1\}}^N}{max}\frac{1}{n_S(N-n_S)}\left[{({\stackrel{\rightharpoonup }{S}}^{\mathrm{T}}\stackrel{\rightharpoonup }{I})}^2+{({\stackrel{\rightharpoonup }{S}}^{\mathrm{T}}\stackrel{\rightharpoonup }{J})}^2\right] \\ =\underset{\stackrel{\rightharpoonup }{S}\in {\{0,1\}}^N}{max}\frac{1}{n_S(N-n_S)}{\stackrel{\rightharpoonup }{S}}^{\mathrm{T}}(\stackrel{\rightharpoonup }{I}{\stackrel{\rightharpoonup }{I}}^{\mathrm{T}}+\stackrel{\rightharpoonup }{J}{\stackrel{\rightharpoonup }{J}}^{\mathrm{T}})\stackrel{\rightharpoonup }{S}. \end{gathered}$$ (8)

To best approximate the above equation, K⃑ needs to satisfy K⃑K⃑^T ≅ I⃑I⃑^T + J⃑J⃑^T; so we find such K⃑ by minimizing ${\Vert \stackrel{\rightharpoonup }{K}{\stackrel{\rightharpoonup }{K}}^{\mathrm{T}}-\stackrel{\rightharpoonup }{I}{\stackrel{\rightharpoonup }{I}}^{\mathrm{T}}-\stackrel{\rightharpoonup }{J}{\stackrel{\rightharpoonup }{J}}^{\mathrm{T}}\Vert }_F^2$. Using trace properties such as ${\Vert A\Vert }_F^2=\text{tr}(A{A}^{\mathrm{T}})$ and tr(AB) = tr(BA), this leads to the following minimization:

$${\stackrel{\rightharpoonup }{K}}^{\ast }=\underset{\stackrel{\rightharpoonup }{K}}{\text{argmin}}\left[{\Vert \stackrel{\rightharpoonup }{K}\Vert }_2^4-2{(\stackrel{\rightharpoonup }{I}·\stackrel{\rightharpoonup }{K})}^2-2{(\stackrel{\rightharpoonup }{J}·\stackrel{\rightharpoonup }{K})}^2\right],$$ (9)

where “·” is the dot product. By equating the derivative of the above expression with respect to K⃑ to zero, the optimal K⃑ is seen to lie on the plane defined by I⃑ and J⃑, i.e. K⃑^* = αI⃑ + βJ⃑, with α, β ∈ ℝ. By further equating the derivatives with respect to α and β to zero, the minimizer in Eq. (9) is calculated as:

$${\stackrel{\rightharpoonup }{K}}^{\ast }=\frac{\stackrel{\rightharpoonup }{I}+\text{sign}(\stackrel{\rightharpoonup }{I}·\stackrel{\rightharpoonup }{J})\stackrel{\rightharpoonup }{J}}{\sqrt{2}}.$$ (10)

Therefore, we sort the values of K⃑^* (that is also zero-sum) and apply the computed sorting order to (vectorized) I⃑ and J⃑ to obtain $\stackrel{\rightharpoonup }{\stackrel{\sim }{I}}$ and $\stackrel{\rightharpoonup }{\stackrel{\sim }{J}}$. We then estimate the segmentation score of the two images, ψ_I⃑,J⃑, similarly to Section II.A, as:

$${\psi }_{\stackrel{\rightharpoonup }{I},\stackrel{\rightharpoonup }{J}}\cong \underset{n_S}{max}\frac{1}{n_S(N-n_S)}\left[{\left(\sum _{k=1}^{n_S}{\stackrel{\sim }{I}}_k\right)}^2+{\left(\sum _{k=1}^{n_S}{\stackrel{\sim }{J}}_k\right)}^2\right].$$ (11)

As in Section II.A, we preform the maximization by an exhaustive search while computing the sums recursively, resulting in the same complexity of 𝒪(N log N).

Note that the proposed segmentation score is distinct from the correlation ratio [10] (and other similar measures). ψ_I⃑,J⃑ is symmetric with respect to the two images, and its computation is based on simultaneous segmentation of the two images and includes finding a class size that optimizes the segmentation. In contrast, the correlation ratio is asymmetric, and its computation does not make use of segmentation and requires dividing the image intensities into pre-defined bins.

C. Registration Based on the Segmentation Score

Let I⃑, J⃑ ∈ ℝ^N be the two multimodal input images to be registered. We seek the transformation T that, when applied to J⃑, makes I⃑ and TJ⃑ aligned with each other. For that, we choose the segmentation score ψ_I⃑,TJ⃑ (defined in Section II.B) as an objective function, which we will maximize with respect to T:

$$T^{\ast }=\underset{T}{\text{argmax}}{\psi }_{\stackrel{\rightharpoonup }{I},T\stackrel{\rightharpoonup }{J}}.$$ (12)

We implemented our new objective function in Matlab and incorporated it in the spm_coreg function of the SPM12 software package [11], which performs rigid registration of three-dimensional images.¹ This function already includes several information theoretical objective functions for multimodal image registration, which it optimizes using Powell’s method [12]. Note that the proposed registration objective function inherently includes the simultaneously computed segmentation error, as opposed to most existing joint segmentation and registration methods [5, 7, 8] that perform segmentation and registration in alternate steps.

To avoid resampling artifacts, we first generate a set of spatially uniform quasi-random Halton points [13], and sample the fixed image I⃑ on them using trilinear interpolation. We then zero-sum and normalize the vector of sampled intensity values of I⃑, by subtracting its mean from it and dividing it by its L₂ norm. Subsequently, at each iteration, we transform the sample points using the current value of the transformation T, sample the moving image J⃑ on them, and zero-sum and normalize the sampled values of TJ⃑. We then use the sampled values of I⃑ and TJ⃑ to compute the score ψ_I⃑,TJ⃑.

III. Experimental Results

We compared the proposed segmentation-based (SB) objective function with mutual information (MI) [1, 2], normalized mutual information (NMI) [3], entropy correlation coefficient (ECC) [2], and the normalized cross correlation (NCC) [14], all already implemented in the spm_coreg function of SPM12 [11]. We chose the default parameters of spm_coreg, such as the optimization sample steps of 4 and 2. We used the same number of quasi-random sampling points for our method as for the rest of the methods in each of the two levels of (quarter and half) resolution.

A. Retrieval of Synthetic Transformations

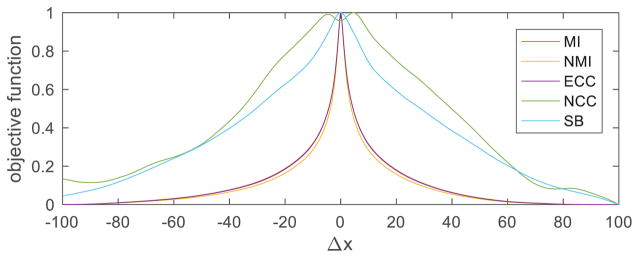
In our first set of experiments, we used the BrainWeb simulated brain database [15, 16]. We generated a pair of T1-and T2-weighted (pre-aligned) images of a normal brain with 1-mm³ isotropic voxels and image size of 217×181×181. We first shifted one image along its first dimension with Δx ∈ [−100,100] voxels and assessed the evolution of the 5 objective functions (Fig. 1). The proposed SB objective function was significantly less convex than the entropy-based ones (MI, NMI, and ECC, which behaved similarly to each other), therefore providing a stronger gradient when the initial point is far from the maximum. The NCC objective function is the only one that was not maximized at Δx = 0, probably due to its (here invalid) assumption of a linear relationship between the intensities of the corresponding voxels in the two images.

Fig. 1.

Evolution of different objective functions with respect to translation. The values of each objective function have been normalized to be in [0,1].

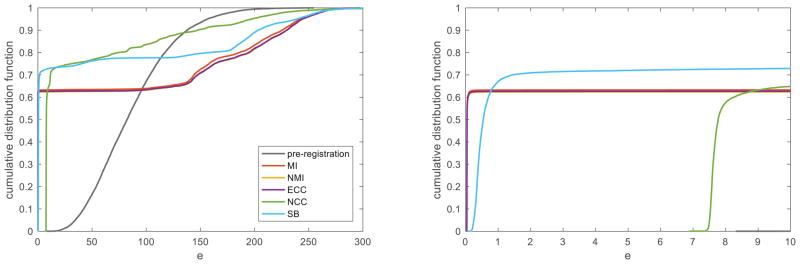
Next, we synthesized 10,000 rigid transformations, each with six parameters drawn randomly from zero-mean Gaussian distributions with the standard deviation of 20 voxels for each of the three translation parameters and 20° for each of the three rotation parameters. With each synthetic transformation, T^syntn, we transformed the second image² and then registered the pair of images using the 5 methods. To evaluate the results of each experiment, we computed the registration error, e ≔ ∫_Ω||T⁻¹T^synthx⃑ − x⃑||₂dx⃑/|Ω|, where T is the obtained transformation matrix, and Ω is the image domain with |Ω| being its size. The cumulative distribution function of e is plotted for each method in Fig. 2 (left), along with a zoomed version (right). Table I shows, for each method, the percentage of the experiments that resulted in an error smaller than a threshold. The proposed SB method converged to subvoxel-accuracy solutions (e < 1) more often than the competing methods did. However, in the experiments where the entropy-based methods (MI, NMI, and ECC, again performing similarly to each other) produced subvoxel-accuracy results, their error was lower (e < 0.1) than that of the SB method. This may suggest that, for better capture range, one could use the results of SB registration as initial value for entropy-based registration. The NCC method never achieved subvoxel accuracy.

Fig. 2.

Left: Cumulative distribution function of the registration error, e, for different methods. Right: A zoomed version, with e ∈ [0,10].

TABLE I.

Percentile ranks for the registration error, e

	pre-regist.	MI	NMI	ECC	NCC	SB
e <0.1	0%	61.85%	61.96%	61.37%	0%	0.02%
e < 1	0%	63.20%	62.35%	62.60%	0%	66.91%
e< 10	0.01%	63.25%	62.41%	62.64%	64.88%	72.89%

B. Cross-Subject Registration of Labeled Images

We performed a second set of experiments on a human brain MRI dataset of 8 subjects [17], including (for each subject) a T1-weighted image, a proton-density image, and a manual-label volume for 37 neuroanatomical structures (each subject’s three images were pre-aligned). All images had been preprocessed in FreeSurfer [18] and resampled to the size 256×256×256 with 1-mm³ isotropic voxels. For all of the 8×7=56 ordered pairs, we registered the T1-weighted image of the first subject to the proton-density image of the second subject using the 5 methods.³ To score the results of each experiment, we computed the portion of the voxels with matching labels between the two images after registration. The cross-experiment mean and standard error of the mean (SEM) of the label-matching scores are shown in Table II. In addition, the percentage of the experiments where our SB method outperformed each other method is shown in Table II, along with the corresponding p-values obtained by two-tailed paired Student’s t- and sign rank tests. As can be seen, the proposed SB method resulted in a significantly higher label-matching score than the rest of the methods did (p < 10⁻⁶).

TABLE II.

Label-matching score averaged across experiments

	pre-regist.	MI	NMI	ECC	NCC	SB
Mean(Score)	0.9304	0.9538	0.9563	0.9563	0.9582	0.9586
SEM(Score)	0.0028	0.0013	0.0010	0.0010	0.0008	0.0008
% times SB outperformed	100%	100%	95%	95%	84%	-
t-test: p	9×10−14	3×10−7	6×10−9	2×10−8	7×10−8	-
sign rank: p	8×10−11	8×10−11	1×10−10	1×10−10	4×10−8	-

C. Retrospective Image Registration Evaluation (RIRE)

Lastly, we used the publicly available RIRE dataset [21, 22] to evaluate the methods through CT-MR and PET-MR registration, where many-to-one intensity mappings are present. For each of the 18 subjects and each of the 5 methods, we ran at most 12 experiments, registering a CT image and a PET image to 6 MR images (T1, T2, PD, and their rectified versions), resulting in a mean error based on manual markers. Table III shows the cross-subject average of the mean errors for each method. The proposed SB method performed better than NCC and MI, but worse than ECC and NMI. The inferior performance of SB in the latter case may be because the images here (as opposed to those used in the previous experiments) have different fields of view. The SB approach, however, is not inherently invariant to the overlap of the fields of view.

TABLE III.

Registration error in millimeters, averaged across subjects

	pre-regist.	MI	NMI	ECC	NCC	SB
Mean(error)	26.3	6.9	3.1	2.9	14.0	6.2
SEM(error)	1.5	1.9	0.9	0.8	2.6	0.6

IV. Conclusion

We have introduced a new cost function for multimodal image registration, which is essentially the error obtained by simultaneously segmenting the two images. We have demonstrated that, compared to several existing methods, the proposed method more often converges to the correct (subvoxel-accuracy) solutions, and also often results in better manual-label matching. Future directions include extending our registration method to be: overlap-invariant, group-wise, deformable, and using more segmentation classes.