Focusing light through scattering media by polarization modulation based generalized digital optical phase conjugation

Abstract

Optical scattering prevents light from being focused through thick biological tissue at depths greater than ∼1 mm. To break this optical diffusion limit, digital optical phase conjugation (DOPC) based wavefront shaping techniques are being actively developed. Previous DOPC systems employed spatial light modulators that modulated either the phase or the amplitude of the conjugate light field. Here, we achieve optical focusing through scattering media by using polarization modulation based generalized DOPC. First, we describe an algorithm to extract the polarization map from the measured scattered field. Then, we validate the algorithm through numerical simulations and find that the focusing contrast achieved by polarization modulation is similar to that achieved by phase modulation. Finally, we build a system using an inexpensive twisted nematic liquid crystal based spatial light modulator (SLM) and experimentally demonstrate light focusing through 3-mm thick chicken breast tissue. Since the polarization modulation based SLMs are widely used in displays and are having more and more pixel counts with the prevalence of 4 K displays, these SLMs are inexpensive and valuable devices for wavefront shaping.

Focusing light deep inside and through thick biological tissue is critical to many applications, including biomedical imaging, phototherapy, and optical manipulation. However, the microscopic refractive index inhomogeneity inherent to biological tissue scatters light, causing photons to deviate from their original paths and change their phases. As a result, it is challenging to achieve optical focusing beyond ∼1 mm in soft tissue (the optical diffusion limit^1,2) which restricts all the aforementioned applications to shallow depths.

To overcome this optical diffusion limit and achieve deep-tissue non-invasive optical imaging, manipulation, and therapy,^3–9 wavefront shaping techniques, including feedback-based wavefront shaping,^10–13 transmission matrix measurement,^14–17 and optical time reversal/optical phase conjugation (OPC),^18–28 are being actively developed. By modulating the wavefront of the incident light, the phase delays among various optical paths are compensated, and optical focusing (by constructive interference) can be achieved through scattering media. Several types of wavefront modulation have been demonstrated using different types of spatial light modulators (SLMs). For example, nematic liquid crystal SLMs (LC-SLMs) based on vertically or parallelly aligned cells provide phase-only modulation,¹⁰ ferroelectric liquid crystal based SLMs provide binary-phase modulation,²⁹ and digital micromirror devices (DMDs) provide binary-amplitude modulation.²⁷ Unlike these SLMs that modulate either phase or amplitude, LC-SLMs based on twisted cells modulate polarization states, and they are much cheaper due to the mass production of displays. However, only until recently, a commercialized LC-SLM that spatially modulates linear polarization was used to focus light through scattering media using a feedback-based optimization algorithm.³⁰ Since the displayed polarization map was obtained through a blind search, the understanding of the polarization map from the perspective of optical time reversal remains unclear. Moreover, due to its iterative nature, the reported method to obtain the desired polarization map took a long time (42 min). In comparison, OPC-based wavefront shaping is much faster,^27,29,31,32 because it determines the optimum wavefront globally rather than pixel-wise. While using polarization modulation to accomplish OPC-based wavefront shaping may sound counterintuitive, in this work, we build a theoretical framework to illustrate its feasibility. In particular, using the vector random matrix theory,^33,34 we develop an algorithm to construct the optimal polarization map from the measured scattered field, which is used to focus light through scattering media. Interestingly, we numerically found that the theoretical peak-to-background ratio (PBR) of the focus achieved by polarization modulation is roughly the same as that achieved by phase-only modulation. To validate the proposed algorithm, we build a generalized digital optical phase conjugation (DOPC) system using an LC-SLM that modulates the linear polarization of light and experimentally demonstrate optical focusing through 3-mm thick chicken breast tissue.

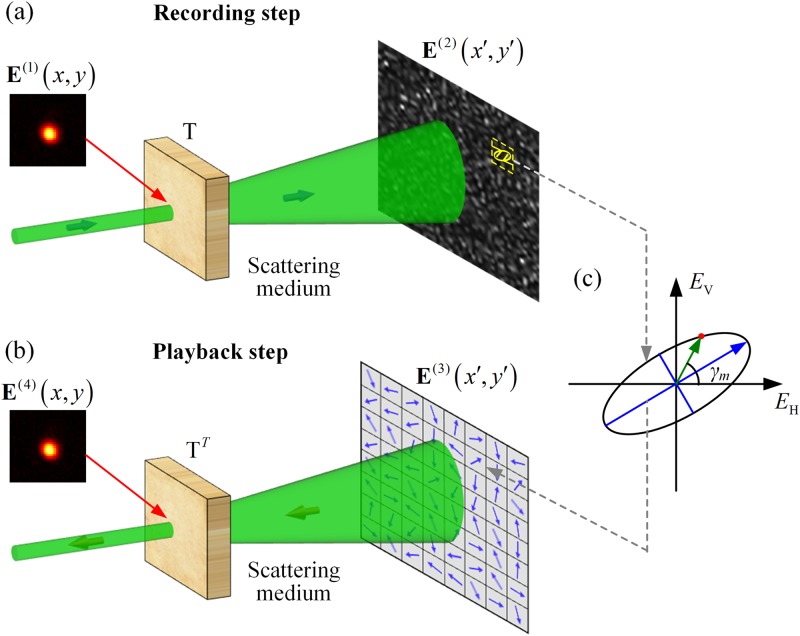
Figure 1 depicts how to focus light through scattering medium using polarization modulation, from the perspective of time reversal. The forward scattering process is illustrated in Fig. 1(a). To begin with, the incident light field ${\mathbf{E}}^{(1)}(x,y)$ is expressed by a Jones column vector

$${\mathbf{E}}^{(1)}\left(x,y\right)={\left(\begin{array}{c}{E}_H^{(1)}\left(x,y\right)\\ E_V^{(1)}\left(x,y\right)\end{array}\right)}_{2N\times 1},$$ (1)

where N is the number of elements per polarization direction [horizontal (H) and vertical (V)]. For simplicity but without losing generality, among all the 2N elements, the first element is set to be one while the rest of the elements are set to be zero, shown as follows:

$${\mathbf{E}}^{(1)}\left(x,y\right)={\left(1,0,\hspace{0.17em}\dots ,\hspace{0.17em}0,0,\dots ,0\right)}^T{\hspace{0.17em}}_{2N\times 1}.$$ (2)

Here, “T” stands for the transpose operator. When the scattering medium is sufficiently thick to scramble the polarization state, the scattering medium is modeled by a vector scattering matrix^33,34

$$\mathbf{S}={\left(\begin{array}{c}{\mathbf{S}}^{(HH)}\hspace{0.17em}{\mathbf{S}}^{(HV)}\\ {\mathbf{S}}^{(VH)}\hspace{0.17em}{\mathbf{S}}^{(VV)}\end{array}\right)}_{2N\times 2N},$$ (3)

where ${\mathbf{S}}^{(AB)}$ (A, B = H, V) is an N-by-N Jones matrix that connects the electric field in the input plane with B polarization and the scattered field in the output plane with A polarization. For each matrix, their elements $t_{ij}^{(AB)},i,j=1,\dots ,N$ satisfy a circular Gaussian distribution. By acting $\mathbf{S}$ onto the incident field ${\mathbf{E}}^{(1)}(x,y)$, the scattered field ${\mathbf{E}}^{(2)}(x^{\prime },y^{\prime })$ on the SLM surface takes the following form:

$$\begin{array}{c}{\mathbf{E}}^{(2)}\left(x^{\prime },y^{\prime }\right)=\mathbf{S}{\mathbf{E}}^{(1)}\left(x,y\right)\\ ={\left(t_{11}^{(HH)},\dots ,t_{N1}^{(HH)},\hspace{0.17em}{t}_{11}^{(VH)},\dots ,\hspace{0.17em}{t}_{N1}^{(VH)}\right)}^T{\hspace{0.17em}}_{2N\times 1}.\end{array}$$ (4)

FIG. 1.

Principle of polarization modulation based generalized DOPC. (a) In the recording step, the electric field of the scattered light exiting a scattering medium is recorded, which in general exhibits elliptical polarization. (b) In the playback step, a planar reference beam is modulated by a linear polarization map, which is constructed using our algorithm. After polarization modulation, the beam passes through the scattering medium again and recovers the collimated, input light beam.

We note here that $t_{m1}^{(HH)}$ and $t_{m1}^{(VH)}(m=1,\dots ,N)$ are the horizontal and vertical components of the electric fields at the same position. As shown in Fig. 1(a), the polarization states on the SLM surface, in general, exhibit elliptical polarization. Ideally, to follow the time reversal principle, the conjugate light field ${\mathbf{E}}^{(3)}(x^{\prime },y^{\prime })$ should also be elliptically polarized with the same trajectory. However, since LC-SLMs modulate light with only linear polarizations, to achieve optical focusing with polarization modulation, we need to use a non-ideal conjugate field ${{\mathbf{E}}_{\text{pol}}}^{(3)}(x^{\prime },y^{\prime })$ that is linearly polarized. In fact, people always use a non-ideal conjugate field with either binary-amplitude or binary-phase, to increase the focusing speed at the cost of contrast at the focus. In our case, the larger the correlation between ${{\mathbf{E}}_{\text{pol}}}^{(3)}(x^{\prime },y^{\prime })$ and ${\mathbf{E}}^{(3)}(x^{\prime },y^{\prime })$, the higher the focal intensity can be achieved through using ${{\mathbf{E}}_{\text{pol}}}^{(3)}(x^{\prime },y^{\prime })$. Theoretically, it has been shown that the ratio of the two focal intensities is proportional to the absolute square of the correlation coefficient of these two conjugate fields.³⁵ Thus, we need to find a field ${{\mathbf{E}}_{\text{pol}}}^{(3)}(x^{\prime },y^{\prime })$ that maintains the highest correlation with ${\mathbf{E}}^{(3)}(x^{\prime },y^{\prime })$. For the ideal conjugate field ${\mathbf{E}}^{(3)}(x^{\prime },y^{\prime })$, the Jones matrix at the m-th spatial point takes the following form ${\left(\begin{array}{c}{t}_{m1}^{(HH)}\\ t_{m1}^{(VH)}\end{array}\right)}^{*}=\left(\begin{array}{c}{A}_m\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_m\hspace{0.17em}\text{exp}\hspace{0.17em}(i{\phi }_{mx})\\ A_m\hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }_m\hspace{0.17em}\text{exp}\hspace{0.17em}(i{\phi }_{my})\end{array}\right).$ Here, $A_m=\sqrt{{\left|t_{m1}^{(HH)}\right|}^2+{\left|t_{m1}^{(VH)}\right|}^2}$ represents the amplitude of the combined electric field; ${\alpha }_m=\arctan \left|t_{m1}^{(VH)}/t_{m1}^{(HH)}\right|$ determines the ratio of the amplitudes of the electric fields along the two orthogonal directions;${\phi }_{mx}$ and ${\phi }_{my}$ are the phase delays along the horizontal and vertical polarization directions, respectively. To find the linearly polarized field ${{\mathbf{E}}_{\text{pol}}}^{(3)}(x^{\prime },y^{\prime })$ with the polarization angle (the Jones matrix at the m-th spatial point $\left(\begin{array}{c}\hspace{0.17em}\text{cos}\hspace{0.17em}{\gamma }_m\\ \hspace{0.17em}\text{sin}\hspace{0.17em}{\gamma }_m\end{array}\right)$) that maximizes the correlation coefficient, we maximize the correlation coefficient between these two vector fields, defined as follows:

$${\mathbf{E}}^{{(3)}^{*}}\left(x^{\prime },y^{\prime }\right)\cdot {{\mathbf{E}}_{\text{pol}}}^{(3)}\left(x^{\prime },y^{\prime }\right)+{\mathbf{E}}^{(3)}\left(x^{\prime },y^{\prime }\right)\cdot {\mathbf{E}}_{\text{pol}}{(3)}^{*}\left(x^{\prime },y^{\prime }\right).$$ (5)

Take the first derivative of each component in expression (5) with respect to ${\gamma }_m$ and force it to be zero, ${\gamma }_m$ is determined to be

$${\gamma }_m=\text{Arg}\left[\text{cos}\hspace{0.17em}{\alpha }_m\hspace{0.17em}\text{cos}\hspace{0.17em}{\phi }_{mx}+i\hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }_m\hspace{0.17em}\text{cos}\hspace{0.17em}{\phi }_{my}\right],$$ (6)

where Arg[·] computes the principal value of the argument of a complex number. As shown in Fig. 1, pictorially, ${\gamma }_m$ is the angle between the x-axis and the instantaneous field vector (green arrow). By repeating the above calculations for every spatial position, the desired polarization map is determined, and the playback field after the polarization modulation takes the following form:

$${{\mathbf{E}}_{\text{pol}}}^{(3)}\left(x^{\prime },y^{\prime }\right)={\left(\text{cos}\hspace{0.17em}{\gamma }_1,\dots ,\hspace{0.17em}\text{cos}\hspace{0.17em}{\gamma }_N,\hspace{0.17em}\hspace{0.17em}\text{sin}\hspace{0.17em}{\gamma }_1,\dots ,\hspace{0.17em}\hspace{0.17em}\text{sin}\hspace{0.17em}{\gamma }_N\right)}^T{\hspace{0.17em}}_{2N\times 1}.$$ (7)

By multiplying the backward transmission matrix ${\mathbf{S}}^T$ and ${{\mathbf{E}}_{\text{pol}}}^{(3)}(x^{\prime },y^{\prime })$, the field exiting the scattering medium is calculated as follows:

$${{\mathbf{E}}_{\text{pol}}}^{(4)}\left(x,y\right)={\mathbf{S}}^T{{\mathbf{E}}_{\text{pol}}}^{(3)}\left(x^{\prime },y^{\prime }\right).$$ (8)

To quantify the focusing contrast of DOPC, we defined a peak-to-background ratio (PBR), which is the ratio between the peak intensity of the focus and the mean intensity of the background speckles, where the latter was from a random polarization map. Since rotating a linear polarization by π rad is equivalent to adding a π phase shift, we can immediately see that the polarization modulation is superior to binary-phase modulation, in terms of PBR. In fact, with only four linear polarization states with polarization angles of 0, π/2, π, and 3π/2 rad, we can use a single SLM to achieve binary-phase modulation along two orthogonal polarizations, thus doubling the PBR of conventional binary-phase modulation based DOPC. With more polarization states to control, the PBR achieved using polarization modulation can be even higher. To quantitatively study the performance of polarization modulation based optical focusing, we numerically calculate the PBR of the focus using Eqs. (1)–(8). By averaging over 1000 simulations with N = 2000 number of channels, we get

$${\text{PBR}}_{\text{pol}}=0.394N.$$ (9)

Table I shows the numerically calculated PBRs achieved using different modulation schemes. All the values are normalized by the number of channels N. We assume that the scattering medium is sufficiently thick to scramble the polarization of light. Compared with the PBRs achieved using other wavefront modulation schemes, the PBR achieved using polarization modulation is very close to that achieved using phase-only modulation and is higher than the PBRs achieved using binary-phase and binary-amplitude modulations. Compared with the values reported in the literatures, we suppressed the theoretical PBRs for phase-only, binary-phase, and binary-amplitude modulations by a factor of 2 in Table I, since we have considered the fact that a thick scattering medium scrambles the polarization of light.³⁴

TABLE I.

PBRs achieved using different modulation schemes.

Modulation scheme	Phase-only	Binary-phase	Binary-amplitude	Polarization
PBR/N	0.393	0.160	0.080	0.394

In practice, instead of modulating polarization angles with a full 2π range, existing commercialized LC-SLMs are limited to modulating polarization angles within a finite range. Nonetheless, we show in the following that optical focusing can still be achieved using the same strategy, which is to find a specific ${\gamma }_m$ that maximizes expression (5) along with the additional constraint on the finite range. Table II summarizes the calculated PBRs when an SLM can modulate polarization angles only within a finite range.

TABLE II.

PBRs achieved with a finite modulation range.

Modulation range	2π	3π/2	π	π/2
PBR/N	0.394	0.374	0.263	0.089

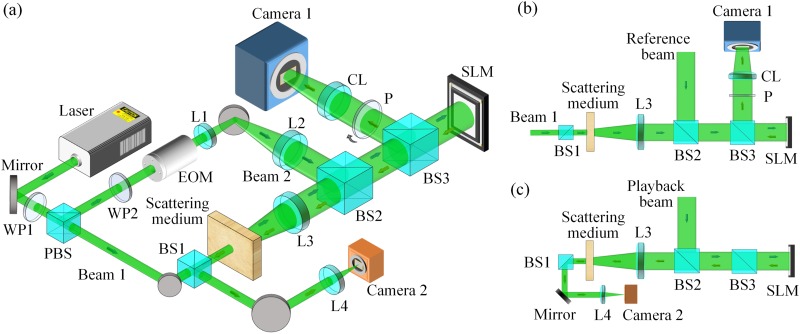
Having discussed polarization modulation based generalized DOPC from the theoretical perspective, we now demonstrate the experimental realization of the technique. Our SLM (HES 6001, Holoeye) has a pixel count of 1920 × 1080, and it can modulate polarization angles from 0 to π/2. Figure 2(a) shows the schematic of the polarization modulation based generalized DOPC system. A collimated beam with a diameter of 2 mm was generated from a pulsed laser source (Elforlight, 532 nm wavelength, 1 kHz pulse repetition rate, 5 ns pulse duration) and was subsequently split into two beams by a variable attenuator composed of a half-wave plate (WP1) and a polarizing beam splitter (PBS). The sample beam (beam 1) was horizontally polarized, and it illuminated the scattering medium. The polarization of the reference beam (beam 2) was vertical initially and was rotated to be 45° by a half wave plate (WP2). In order to perform phase-shifting holography to measure the wavefront, an electro-optic modulator (350-105, Conoptics) was used to shift the phase of the reference beam. After passing through a lens pair composed of L1 and L2, the reference beam was expanded to a diameter of 25 mm. Then, the two beams were combined together through a beam splitter (BS2). Their interference pattern was formed on the surface of the SLM, and it was imaged by a camera lens (CL) and recorded on the sensor of Camera 1 (PCO.edge 5.5, PCO) [Fig. 2(b)]. To maximize the number of independent controls in the system, the speckle patterns were intentionally under-sampled.³⁶ A polarizer was inserted before CL, to control the measurement of the scattered field along either the horizontal or the vertical axis. During this recording step, a uniform polarization map (with zero modulation) was set on the SLM. With the vector field of the scattered light including amplitude, phase, and polarization, the optimum linear polarization map was determined using the algorithm described above. In the playback step [Fig. 2(c)], beam 1 was blocked by a shutter, while beam 2 was modulated by the SLM upon reflection. After propagating through the scattering medium again, the playback beam became a collimated beam, which was then focused by lens L4 on the sensor of Camera 2 (CMLN-13S2M-CS, point grey).

FIG. 2.

(a) Schematic of the polarization modulation based generalized DOPC setup. (b) Illustration of the recording step. (c) Illustration of the playback step. BS, beam splitter; CL, camera lens; EOM, electro-optic modulator; L, lens; P, polarizer; PBS, polarizing beam splitter; SLM, spatial light modulator; and WP, half wave plate.

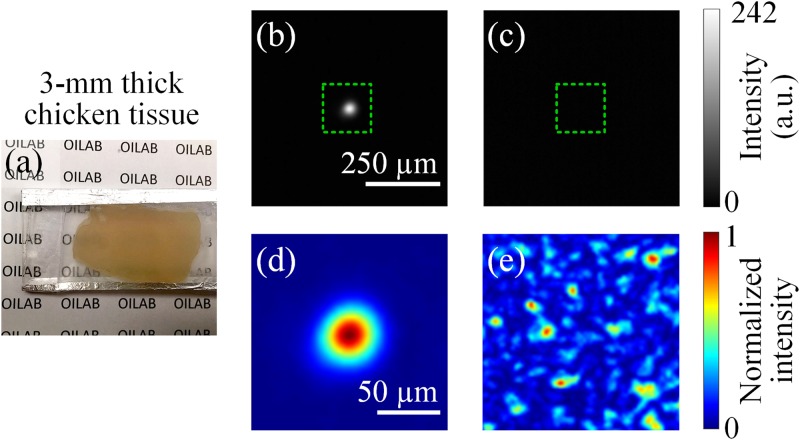
In our experiments, we used a piece of 3-mm thick chicken breast tissue as the scattering medium, as shown in Fig. 3(a). Figures 3(b) and 3(c) show the images captured by Camera 2 with and without performing polarization modulation based generalized DOPC, respectively. With DOPC, a bright optical focus was achieved with a PBR of ∼3000. Considering that N = 1920 × 1080 pixels for the SLM and M = 12 speckles approximately within the focus (the speckle size was calculated by the full width at half maximum of the autocovariance function of the speckle pattern in Fig. 3(e)), we estimate the theoretical PBR as follows:

FIG. 3.

Focusing light through a piece of 3-mm thick chicken breast tissue. (a) Image of the chicken tissue. (b) and (c) Images captured by Camera 2 after light has passed through the chicken tissue with and without performing polarization modulation based DOPC. (d) and (e) Close-ups of the regions denoted by the dashed boxes in (b) and (c). Each image was normalized by its own peak intensity.

$$\begin{array}{c}{\text{PBR}}_{\pi /2-\text{pol}}=0.089N/M\\ =0.089\times 1920\times 1080/12\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\approx 15\hspace{0.17em}000.\end{array}$$ (10)

Thus, the experimentally achieved PBR is about one fifth of the theoretical value, likely due to imperfect alignment of the system. In contrast, we did not observe any focus when a random polarization map was displayed on the SLM. For better visualization, close-ups of the regions denoted by the green dashed boxes in Figs. 3(b) and 3(c) are shown in Figs. 3(d) and 3(e). The above experimental results validate our algorithm and confirm the feasibility of polarization-modulation based generalized DOPC for focusing light through thick scattering medium.

In conclusion, we developed a polarization modulation based generalized DOPC technique to focus light through scattering media. Based on the numerical simulations, we found that the PBR of the focus achieved by polarization modulation is similar to that achieved by phase-only modulation and is higher than those achieved by binary-phase and binary-amplitude modulations. Since polarization modulation based SLMs are widely used in displays, this type of SLM is much cheaper compared with the phase and amplitude SLMs previously used in wavefront shaping. In addition, as 4 K displays are becoming more and more popular, it is not difficult to find such inexpensive SLMs with a pixel count of ∼9 megapixels, which is much larger than the 2 megapixels available with the phase and amplitude modulation SLMs. Moreover, when combined with internal guide stars,³⁷ our generalized DOPC system can be directly applied to focusing light inside scattering media. The increased pixel count can boost the PBR of the focus, which is especially useful to improve the low contrast of the focus achieved with large guide stars such as focused ultrasound. Because of the aforementioned advantages, we anticipate that polarization modulation based SLMs will gain their prevalence in the field of wavefront shaping.