Abstract
Design principles of biological networks have been studied extensively in the context of protein-protein interaction networks, metabolic networks, and regulatory (transcriptional) networks. Here we consider regulation networks that occur on larger scales, namely, the cell-to-cell signaling networks that connect groups of cells in multicellular organisms. These are the feedback loops that orchestrate the complex dynamics of cell fate decisions and are necessary for the maintenance of homeostasis in stem cell lineages. We focus on “minimal” networks, that is those that have the smallest possible numbers of controls. For such minimal networks, the number of controls must be equal to the number of compartments, and the reducibility/irreducibility of the network (whether or not it can be split into smaller independent sub-networks) is defined by a matrix comprised of the cell number increments induced by each of the controlled processes in each of the compartments. Using the formalism of digraphs, we show that in two-compartment lineages, reducible systems must contain two 1-cycles, and irreducible systems one 1-cycle and one 2-cycle; stability follows from the signs of the controls and does not require magnitude restrictions. In three-compartment systems, irreducible digraphs have a tree structure or have one 3-cycle and at least two more shorter cycles, at least one of which is a 1-cycle. With further work and proper biological validation, our results may serve as a first step toward an understanding of ways in which these networks become dysregulated in cancer.
Keywords: Stem cells, Mathematical modeling, Homeostasis regulation
1 Introduction
Theoretical biologists often ask questions about “design principles” that are common characteristics of many, possibly unrelated, systems. Distinct evolutionary pathways are thought to converge to a subset of possible solutions, based on their accessibility, utility, and other characteristics. One particularly attractive area is the study of the engineering “design principles” of networks. In biology, networks occur on different scales and perform different functions in organisms, see e.g. Barabasi and Oltvai (2004); examples include protein-protein interaction networks, metabolic networks, regulatory (transcriptional) networks, co-regulation networks, social interaction networks, and food webs in ecology. The principle of modularity has been widely discussed and is believed to be an important feature of many networks, see e.g. Hartwell et al (1999); Vespignani (2003); Wuchty et al (2003). Groundbreaking work of Alon and colleagues has stimulated the search for motifs, “patterns of interconnections that recur in many different parts of a network at frequencies much higher than those found in randomized networks” (Shen-Orr et al, 2002), see also Milo et al (2002); Alon (2003, 2007).
Here we focus on networks at a different scale, which lie between sub-cellular (gene regulation, transcription) and population level (social interactions, food webs). Namely, we study control networks that exist between groups of cells in multicellular organisms, concentrating on the homeostatic regulation of stem cell (SC) lineages. Homeostasis is a relatively stable equilibrium between interdependent cellular compartments, maintained by regulatory processes. Feedback loops are thought to play a central role for achieving homeostatic control. This notion is supported by a variety of experimental findings. For example, negative feedback regulation affecting various processes such as cell division and differentiation has been reported in the mouse olfactory epithelium, skeletal muscle, bone, keratinocytes, and the hematopoietic system, identifying specific regulatory proteins that mediate the feedback in each case (McPherron et al, 1997; Daluiski et al, 2001; Wu et al, 2003; Yamasaki et al, 2003; Elgjo and Reichelt, 2004; Lander et al, 2009; Tzeng et al, 2011).
While it is commonly accepted that feedback regulatory processes play a major role in tissue homeostasis, it is less clear exactly how regulatory signals are mediated. Cell fate decisions such as proliferation, differentiation, and apoptosis, can be controlled either intrinsically or extrinsically (Morrison and Kimble, 2006). Intrinsic control implies that the fate of daughter cells is determined by the signals present within the mother SC. More relevant to the present study, extrinsic control implies that cellular decisions are influenced by signals from the cell’s surroundings. Two types of such signals have been discussed. The non-autonomous mode involves signaling emanating from the stem cell niche, an anatomic location that regulates how stem cells participate in tissue generation and maintenance (Scadden, 2006). Non-autonomous signaling involves various components of the stem cell niche, including the endothelium, pericites, and surrounding extracellular matrix. On the other hand, autonomous signaling implies signals received by cells from groups of surrounding cells in the same lineage. For example, in adult neurogenesis, SC divisions are orchestrated by the mature neural cells, and new neurons and glia appear to be produced on demand, rather than on a fixed schedule (Hsieh, 2012). It is this type of cell fate regulation, autonomous homeostatic regulation, that is the focus of the present study.
All cells within the body can be viewed in the context of their phylogenetic lineages. At the top of the lineage is the SC, and at the end are the non-dividing, terminally differentiated cells (DCs). These cells are usually highly specialized and help to perform the tissues’s specific functions. There can also be intermediate cell groups that differ by their degree of differentiation. We will refer to cells of the same degree of differentiation as a “compartment”. There is evidence that various cell fate decisions may be subject to positive or negative control from different compartments.
For example, SC numbers can negatively control differentiation, mediated by crowding and factors like contact inhibition, which play an important role in determining the fate of stem cells (Dehay and Kennedy, 2007; Guilak et al, 2009). Interestingly, SC numbers can also positively control differentiation. In some systems, mechanical strain has been shown to increase cell differentiation (Simmons et al, 2003; Sen et al, 2008; Guilak et al, 2009). It has also been suggested that stem cells have to be spatially localized to their niches, which keeps them protected from the differentiating influences of the surrounding microenvironment (Adams and Scadden, 2008). Therefore, as the number of stem cells increases, the probability of exposure to the differentiation signals from the outside increases, resulting in a positive control loop.
Differentiation decisions can also be controlled from downstream compartments. It has been proposed that neural SC descendants can trigger some sort of feedback mechanism to stop SC differentiation (Liu et al, 2000), e.g. by Notch signaling (Alvarez-Buylla and Lim, 2004) or by Prox1 expression (Lavado et al, 2010). Hematopoietic SCs are thought to be regulated by their mature progeny (de Graaf et al, 2010). In Li and Clevers (2010) it is suggested that a negative control loop exists between the active SCs and quiescent stem cells, which controls divisions of SCs in hair, intestine and bone marrow.
These are just a few examples of known autonomous regulation mechanisms. The exact control networks orchestrating homeostatic turnover of SC lineages in many tissues are only starting to be described. Therefore, it is important to improve the theoretical understanding of such control networks, which would allow us to reconstruct the actual networks from limited biological information. This paper aims to provide a general description of stable control systems in multi-compartment lineages and to provide an intuitive understanding of network topologies that can be stable. In particular, we study the reducibility or irreducibility of a network. A reducible network contains a compartment (or, more generally, a proper subset of compartments) which controls cell number change only inside itself, and not in any other compartment. This is an important consideration in spatially extended lineages such as those of colonic crypts. The mathematical implication of reducibility is related to the biological property of modularity of a control network.
The importance of control networks in SC lineages is apparent once we consider the intimate connection between tissue homeostasis (dys)regulation and cancer. While tumor formation follows a multistage process of random mutation accumulation and/or epigenetic changes, all tumors eventually break out of homeostasis, which means that some or all of the control loops that function in the healthy tissue are altered. There is large evidence in the literature that escape from feedback regulation is key for the formation of the majority of SC-driven tumors (see e.g. Vogelstein and Kinzler (2004); Ram Singh (2012); Vermeulen and Snippert (2014)). Therefore, the current study aims to contribute to the theory of carcinogenesis by studying the common targets of oncogenic mutations, that is, control networks that regulate cell fate decisions and maintain tissue turnover.
The present study contributes to the growing theoretical literature on SC dynamics, see e.g. review in Piotrowska et al (2008). Conceptual aspects of SC lineage turnover have been developed by Marshman et al (2002); Loeffler and Roeder (2002); Roeder et al (2006); feedback mechanisms have been studied by Lander et al (2009); Youssefpour et al (2012); Konstorum et al (2016); Kunche et al (2016). Mathematical modeling of SCs range from discrete to continuous models in the context of carcinogenesis (Yatabe et al, 2001; Hardy and Stark, 2002; Ganguly and Puri, 2006; Johnston et al, 2007a; Ganguly and Puri, 2007; Boman et al, 2008; Ashkenazi et al, 2007, 2008; Enderling and Hahnfeldt, 2011) and cancer stem cells (Dingli and Michor, 2006; Johnston et al, 2010; Enderling and Hahnfeldt, 2011; Hillen et al, 2013; Scott et al, 2014; Enderling, 2015); modeling hematopoietic SC dynamics (Glauche et al, 2007; Marciniak-Czochra et al, 2009; Foo et al, 2009; Stiehl and Marciniak-Czochra, 2012); deterministic modeling of two-, three-, and multi-compartmental SC systems under various assumptions on control functions (Nakata et al, 2012; Stiehl and Marciniak-Czochra, 2011); and stochastic modeling of SC dynamics, including the analysis of fluctuations (Enderling et al, 2007, 2009a,c,b; Dingli et al, 2007). The present paper focuses on the regulatory networks in SC lineages.
2 Formulation of autonomous homeostatic network models
2.1 General
Assume the existence of n compartments in a cellular lineage. Cells in different compartments differ by their properties (such as their degree of differentiation, function, etc). The number of cells in each compartment is denoted by xi for i = 1, …, n. We further assume the existence of K ≥ n different cellular processes that change the number and/or type of cells in different compartments. Examples of such processes are symmetric proliferations of SCs, death of DCs, or de-differentiaion of intermediate cells. We denote by Qk(x1, …, xn) for k = 1, …, K the rates at which these processes take place. Here we assume that in principle, these rates can be functions of all the cell populations in the lineage. In reality, not all populations can control each process. Therefore, it is useful to consider partial derivatives of the rates with respect to different population sizes. For example, the value of the derivative
| (1) |
evaluated at the equilibrium (the homeostatic state), informs us whether or not process Qp is regulated by cells in compartment q. A zero derivative means the absence of control. If the derivative above is positive (negative), then the control is positive (negative). We sometimes refer to quantities (1) as simply “controls”.
Associated with each process, k, we further define a vector of associated increments of all the cell populations, . For example, in a three-compartment system consisting of SCs, intermediate cells, and DCs, symmetric proliferation of SCs results in increment (1, 0, 0), death of DCs in increment (0, 0, −1), and de-differentiation of intermediate cells in increment (1, −1, 0). These vectors can be thought of as signatures of all the processes that happen in the lineage.
The ordinary differential equations (ODEs) governing the dynamics are given by
| (2) |
⋯
| (3) |
Our framework relies on the following general assumptions:
-
–
The rate functions Qk(x1, …, xn) do not depend on time directly (only through the population variables). We note that time variability is an important issue in development; in the present context, however, since we focus on adult stem cells, we assume that such temporal changes of the rates are slow compared with the time-scale of cellular turnover, and can be ignored.
-
–
Functions Qk(x1, …, xn) are differentiable functions of their variables. We do not make any assumptions on the actual functional forms, e.g. whether or not they are linear or nonlinear. As will be shown below, in the present, near-equilibrium analysis, only the derivatives at the equilibrium enter the calculations.
-
–
Stochastic effects are not included in the present, deterministic framework. In the context of near-equilibrium analysis, fluctuations can be studied by using the tools developed in Komarova (2013); Yang et al (2015b).
We further assume that equations (2–3) have a biologically meaningful equilibrium, which we denote by , where is the equilibrium population sizes of compartment i, 1 ≤ i ≤ n. This equilibrium is defined by n generally nonlinear equations for the n variables:
Consider linear stability of the equilibrium. The Jacobian (matrix) is given by,
| (4) |
where the derivatives are evaluated at the equilibrium. Denoting
gives
It is easy to see that for stability, all the populations have to be involved in the control, that is, the smallest number of controls is n; and n different processes have to be controlled. If fewer than n processes are involved, at least one process (say Qi) must have nonzero derivatives in two variables, say a and b, and no other process has controls in a and b, meaning that the columns in matrix J given by and are dependent, giving a zero eigenvalue.
The following representation of the Jacobian in (4) is useful. The increment matrix of dimensions (n × K) is given by
The types of cellular processes that are studied here impose certain constraints on the matrix D, such that this matrix has the following properties:
-
–
Its entries are integers from the set {−1, 0, 1, 2}.
-
–
Each column contains at least one and at most two nonzero entries.
-
–
If a column contains two nonzero entries, they are in adjacent rows.
The control matrix of dimensions (K × n) is given by
Then, the Jacobian of dimensions n × n is given by the matrix multiplication,
| (5) |
A stable network is defined as a network, for which all eigenvalues of the Jacobian (4) have negative real parts. We further define a “minimal” control network to be a stable network that has the smallest possible number of controls, that is, the smallest possible number of nonzero entries in the matrix B. It is easy to see that the smallest number of nonzero entries (compatible with stability) is equal to n. Let us suppose that the n processes that are controlled (that is, their rates have nonzero derivatives) are processes j1, …, jn. Then the Jacobian of a minimal control network can be written in the form
| (6) |
where
| (7) |
2.2 Simple systems with symmetric divisions
In the following simple example we consider only two types of cells, SCs and DCs. For simplicity of notation, we denote partial derivatives with respect to x1 and x2 (and later, x3) by means of subscripts x and y (and later, z). We further assume that SCs divide symmetrically. In general, there are two types of symmetric divisions (asymmetric SC divisions, where one of the daughter cells retains stemness while the other is differentiated, are included in section 3.1). Proliferation divisions result in two daughter cells both of which retain the SC status. For differentiation divisions, both daughter cells are DCs. We finally assume that the only other process in this system is death in the DC compartment. Suppose Q1 stands for differentiation of stem cells, Q2 for proliferation of SCs, and Q3 for death of DCs. Then
that is, as a result of a differentiation, x → x − 1, y → y + 2, as a result of a proliferation, x → x + 1, and as a result of a DC death, y → y − 1. The evolution ODEs are given by
| (8) |
| (9) |
We assume the existence of a biologically relevant equilibrium of (8–9), (x∗, y∗), defined by equations
| (10) |
| (11) |
and by (5) the Jacobian evaluated at this equilibrium is
(note that here and below, the partial derivatives are evaluated at the equilibrium, equations (10–11)). In this case, minimal control networks must contain two derivatives (one with respect to each population), and give a stable matrix . In the irreducible cases, is equivalent to the sign stable matrix
whereas in the reducible cases the eigenvalues of J are given by the negative diagonal entries, see Hall and Li (2007); Brualdi and Shader (2009). Thus there are 5 minimal controls, two of which have irreducible :
In all cases, the controls do not have magnitude restrictions. In other words, as long as the controls have the correct sign, the system is stable.
3 Identifying properties of stable control networks
The goal is to identify rules to build up all the possible stable networks under a given set of processes. To do this, we begin with a case study and then generalize to a wider class of systems.
3.1 A case-study: two compartments, six processes
In the following example we consider a 2-compartment system (n = 2), consisting of stem cells (SCs) and differentiated cells (DCs), with K = 6 processes described in table 1. This is a reduction of the model used in Sun et al (2016) to describe the airway epithelium SC lineage, where the ciliated cells are removed from consideration (because the corresponding compartment does not control any processes in other compartments). In addition to the processes included in Sun et al (2016), death in the SC compartment is included in the present model for generality. The system of ODEs governing the dynamics is given by
| (12) |
| (13) |
where we omitted the dependence of functions Qk on populations x and y.
Table 1.
Cellular processes in the 2-compartment model with 6 processes studied in section 3.1.
| Qk | Process |
|
|
||
|---|---|---|---|---|---|
| Q1 | Differentiation division of SCs | −1 | 2 | ||
| Q2 | Proliferation division of SCs | 1 | 0 | ||
| Q3 | Death of DCs | 0 | −1 | ||
| Q4 | Asymmetric division of SCs or proliferation of DCs | 0 | 1 | ||
| Q5 | De-differentiation of DCs | 1 | −1 | ||
| Q6 | Death of SCs | −1 | 0 |
Minimal controls are comprised of networks where all the partial derivatives are zero except a pair (Qix, Qjy) of nonzero derivatives. Listing all pairs (Qix, Qjy) gives all the possible minimal networks. Using straightforward linear stability analysis of each possible network, we obtain that there are 22 such stable minimal networks. Of these, 10 are irreducible, and 9 out of the 10 are stable if the signs of the controls are assigned correctly (with no magnitude restrictions), whereas the remaining irreducible network has two alternative “wirings” (that is, two different sets of conditions on the controls that guarantee stability). The remaining 12 networks are reducible and therefore stable if the signs of the controls are assigned correctly (see section 2.2).
The results on stability, sign stability, and reducibility are given in figure 1, where the rows are the processes controlled by SCs (nonzero x derivative) and the columns are processes controlled by the DCs (nonzero y derivative). An empty cell means that the network is always unstable. A “1” means that the network is irreducible (1 simply connected component) and stable if the signs of the controls are assigned correctly. A “1*” means that the network is irreducible and there are two different wirings with the same network topology that lead to stability. A “2” means that the network is reducible (2 simply connected components) and stable if the signs of the controls are assigned correctly.
Fig. 1.
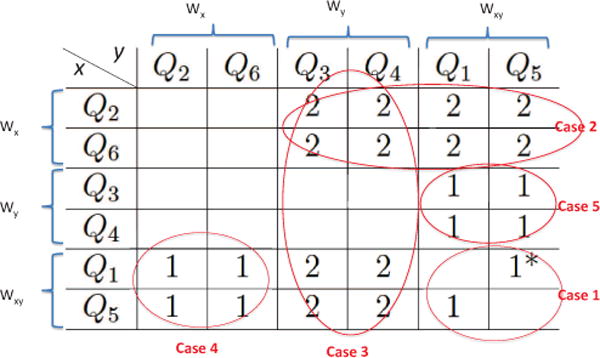
An illustration of the different cases of stable systems for n = 2. All possible pairs (Qix, Qjy) are listed. The rows are the processes controlled by SCs (nonzero x derivative) and the columns are processes controlled by the DCs (nonzero y derivative).
These results are easy to interpret. The fact that there are only two nonzero controls, (Qix, Qjy) with i ≠ j, allows us to reduce the stability problem for minimal controls to studying stability of the 2 × 2 matrix , where with
see (6–7), and the partial derivatives are evaluated at an equilibrium of (12–13). Since is a nonsingular diagonal matrix, determines reducibility or irreducibility of . Below we describe biologically intuitive reasoning that helps in the construction of stable networks with given properties.
All the processes in the system can be split into three groups: Wx are the processes that only change the number of cells in the SC compartment, Wx = {Q2, Q6}; Wy are the processes that only change the number of cells in the DC compartment, Wy = {Q3, Q4}; Wxy are the processes that change the number of cells in both compartments, Wxy = {Q1, Q5}. A stable system with a pair (Qix, Qjy) of nonzero controls can be obtained by combining two processes, as described below, and also illustrated in figure 1.
-
Case 1
Combining any two (distinct) processes from group Wxy, one of which is controlled by x and the other by y, leads to an irreducible matrix, which is either stable (if the signs of the controls are assigned correctly) or has two separate sets of conditions that guarantee stability (two alternative wirings of the network); this case is discussed in more detail in Appendix A.
-
Case 2
Combining a process from group Wx controlled by x with a process in group Wy or Wxy controlled by y leads to a reducible system, stable if the signs of the controls are assigned correctly. This means that there is a process in the system that is controlled by SCs and only changes the number of cells in the SC compartment, giving rise to reducibility of the system.
-
Case 3
Combining a process from group Wy controlled by y with a process in group Wx or Wxy controlled by x leads to a reducible system, stable if the signs of the controls are assigned correctly. Similar to Case 2, the reducibility is due to a process that is controlled by DCs and only changes the number of cells in the DC compartment.
-
Case 4
Combining a process from group Wx controlled by y with a process in group Wxy controlled by x leads to an irreducible system, which is stable if the signs of the controls are assigned correctly.
-
Case 5
Combining a process from group Wy controlled by x with a process in group Wxy controlled by y leads to an irreducible system, which is stable if the signs of the controls are assigned correctly.
-
Case 6
No other combinations are stable. In particular, there is no stable system where both processes only change the number of cells in the same compartment. Further, there is no stable system where a process that only changes the number of SCs controlled by DCs is combined with a process that only changes the number of DCs controlled by SCs.
3.2 Generalizations for two-compartment systems
Below we provide generalizations to all possible two-compartments systems, independent of the number of processes (as long as the stability conditions defined below can be satisfied).
Cases 2 and 3 above can be summarized as follows: a two-compartment system is reducible if both compartments control their own change (that is, control processes that induce change in the same compartment), and one of them does not control any processes that induce change in the other compartment.
Cases 1, 4, and 5 can be combined as follows: a two-compartment system is irreducible if both compartments control the change of the other, and at least one of them controls its own change.
Case 6 can be reformulated as follows: a two-compartment system is unstable unless the changes in both compartments are controlled (that is, some compartment controls a process that results in a change in compartment i, for i = 1 and i = 2), and at least one compartment controls its own change.
An intuitive way to graphically present control networks in this setting uses directed graphs (digraphs); for correspondence between matrices and digraphs see, for example, Hall and Li (2007). For the n = 2 system, all possible stable systems are presented in figure 2, which shows reducible cases (a) and (b), and irreducible cases (c) and (d). Each of the two compartments is denoted by a node, and arcs represent control. Solid arcs are necessary for stability, and dashed arcs are optional. For example, the diagram in (a) can be read as follows: Compartment x must control some process that changes the number of cells in x (solid arc x → x). Compartment y must control some process that changes the number of cells in y (solid arc y → y). Compartment y may also control some process that changes the number of cells in x (dashed arc y → x). Clearly, cases (a) and (b) (as well as (c) and (d)) are the same under renaming x ↔ y. In the notation of digraphs, negative (blunt) arrows are not used, and therefore an arc must be interpreted as the existence of control, without any information on the sign of the control. The signs of stable digraphs in figure 2, corresponding to stable minimal controls, are indicated explicitly; dashed arcs can be 0, + or −.
Fig. 2.
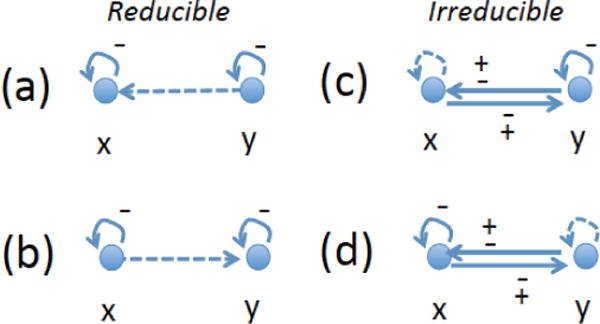
All stable minimal control configurations in two-compartment systems. The two compartments are represented by the nodes x and y. Each arc corresponds to a change in one compartment controlled by a particular compartment. A given arc points to a compartment whose size changes, and it originates at the compartment that exhibits control of this change. For example, an arc from x to y means that there is a process whose rate depend on x, such that the population in compartment y changes as a result of this process. (a,b) reducible cases, (c,d) irreducible cases. Signs on arcs give stability.
The arcs in digraphs of figure 2 do not directly correspond to the processes Q1, …, Qn (as they would in a more conventional, biological network graphics). As an example, consider the control system (Q1x, Q6y), see table 1 and figure 1. This control network involves control of SC differentiations by SCs and control of SC death by DCs. The first process, Q1, has increments (−1, 2). Therefore, compartment x controls change both in x and in y. The second process, Q6, has increments (−1, 0), therefore y only controls change in x. The resulting digraph belongs to the class depicted in figure 2(d) with no arc y → y. For stability, both Q1x and Q6y must be positive.
3.3 A case-study: three compartments, ten processes
Consider a 3-compartment system (n = 3), consisting of SCs, intermediate cells (ICs), and DCs, with K = 10 processes described in table 2. This is again similar to the system used in Sun et al (2016) to describe the control in the airway epithelium (with the addition of deaths in the SC compartment). The processes of asymmetric division of SCs or proliferation of ICs are counted as one because they have the same cellular increments; the same statement holds for the processes of asymmetric divisions of ICs or proliferation of DCs.
Table 2.
Cellular processes in the 3-compartment model with 10 processes studied in section 3.3.
| Qk | Process |
|
|
|
|||
|---|---|---|---|---|---|---|---|
| Q1 | Differentiation division of SCs | −1 | 2 | 0 | |||
| Q2 | Proliferation division of SCs | 1 | 0 | 0 | |||
| Q3 | Death of ICs | 0 | −1 | 0 | |||
| Q4 | Asymmetric division of SCs or proliferation of ICs | 0 | 1 | 0 | |||
| Q5 | De-differentiation of ICs | 1 | −1 | 0 | |||
| Q6 | Death of SCs | −1 | 0 | 0 | |||
| Q7 | Differentiation division of ICs | 0 | −1 | 2 | |||
| Q8 | De-differentiation of DCs | 0 | 1 | −1 | |||
| Q9 | Death of DCs | 0 | 0 | −1 | |||
| Q10 | Asymmetric divisions of ICs or proliferation of DCs | 0 | 0 | 1 |
A minimal system has only three nonzero entries in matrix B. It turns out that there are exactly 232 triplets of nonzero controls, (Qix, Qjy, Qkz), that give rise to systems that can be stable. This result, together with the list of all potentially stable triplets, has been obtained by means of a Mathematica program, see Appendix B. Of these, 72 have one simply connected component (i.e., are irreducible), 96 have two simply-connected components, and 64 have three simply connected components.
The case of irreducible systems is the most complicated and its full breakdown is shown in figure 3, where all the types of digraphs are listed together with their stability properties. The first column in the figure explains the digraph structure. A 3-cycle in a digraph on distinct nodes y1, y2, y3 consists of arcs y1 → y2 → y3 → y1; whereas a tree has only 1-cycles (yi → yi) and 2-cycles (e.g., y1 → y2 → y1). In general, each coefficient (other than degree 3) in the characteristic polynomial (“char pol”) of the 3 × 3 Jacobian matrix at the homeostatic state is a product of controls, with some coefficients having sums of such products, as stated in column 1 of figure 3.
Fig. 3.
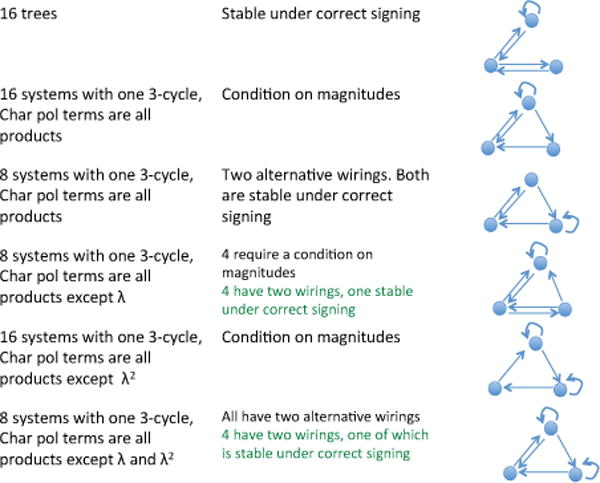
Stable irreducible configurations in the three-compartment system studied in section 3.3.
To give some examples, consider the triplet (Q5x, Q3y, Q7z). This is a fully reducible system: compartment y only controls its own change, and once it is removed, compartments x and z also only control their own change. The characteristic polynomial can be decomposed as
and the system is stable as long as the signs of the controls are assigned correctly, i.e.,
Next, consider the triplet (Q2x, Q7y, Q1z). This is a reducible system that contains two simply connected components, with compartment x only controlling its own change. The characteristic polynomial is given by the product
and stability requires only the correct sign assignment:
A third example is the triplet (Q7x, Q5y, Q1z). This is an irreducible system with a digraph of the type presented in the 4th row of figure 3. The characteristic polynomial is given by
where all the coefficients except for that of the first power of λ are products of (powers of) controls. By the Routh-Hurwitz criteria, the stability conditions in this case are given by
i.e., a magnitude restriction is required, not just the correct signing of the controls.
3.4 Generalizations for three-compartment systems
Because of the special forms (6–7) of the Jacobian of minimal processes, reducibility/irreducibility of the minimal systems is defined by matrix only. The following patterns are observed that are generalizable to all three-compartment systems (irrespective of the number and type of processes involved).
-
–
The triplets that have one simply connected component (are irreducible) are given in figure 3. Their digraph has a tree structure or has one 3-cycle and at least two more shorter cycles, at least one of which is a one-cycle. These digraphs can be signed to allow stability, although some require magnitude constraints given by the Routh-Hurwitz conditions, see, for example, Hershkowitz (2007).
-
–
The triplets that have two simply connected components (and therefore are stable if the signs of the controls are assigned correctly) contain one compartment that only controls its own change (that is, it does not control any processes that induce change in the other compartments). Let us call this compartment a separable compartment, because if it is removed, the dynamics of the other compartments do not change. The remaining two compartments must behave as an irreducible system, as in section 3.2, i.e. both of those compartments must control the change of the other, and at least one of them controls its own change. These compartments may or may not control change in the separable compartment. Stability patterns for these systems can be deduced from the rules described for the n = 2 system.
-
–
The triplets that have three simply connected components (and therefore are stable if the signs of the controls are assigned correctly) contain a separable compartment, after the removal of which, the remaining system also contains a separable compartment.
4 Discussion
We considered general, multiple compartment, multiple process systems of homeostatic SC lineage maintenance. We restricted ourselves to the question of local stability of homeostatic solutions, and asked what types of possible minimal control networks are compatible with stable homeostasis. While linear stability analysis can always be performed, and Routh-Hurwitz conditions allow us to determine the signs of eigenvalues, it is desirable to obtain general, interpretable rules of building up stable control networks. Further, it is useful to find ways to distinguish between reducible and irreducible systems.
To achieve this goal, we have developed a formalism of mapping any control system into a unique digraph, where the nodes correspond to the cell compartments, and an arc originating in compartment i and pointing to compartment j indicates that compartment i controls a process resulting in a change in compartment j. By using the resulting digraphs, it is possible to argue about the network’s stability and reducibility. For example, if there is a node in the digraph that only controls its own change, the corresponding system is reducible.
A control network is likely reducible if the SC lineage has a spatially extended structure, where neighboring compartments are more likely to influence each other than distant compartments. For example, in colonic and intestinal crypts, the SCs are localized near the bottom of the crypt, followed by transit amplifying cells and then, toward the top of the crypt, by terminally DCs. Therefore, it is often assumed that signaling is local, which, according to our theory, leads to reducibility. Reducibility, in turn, means that the signaling network can be split into modules, each of which acts as a more or less independent unit whose stability only depends on the signaling within the module. Therefore, we expect the principle of modularity to hold in many spatially distributed SC lineages.
In this paper we focused on SC lineages with two and three compartments. Depending on a biological system, the number of compartments can vary. In the epidermal tissue, a two-compartmental model has been used (Yang et al, 2015a). The three compartment model was introduced by Tomlinson and Bodmer (1995), and has been used to study epithelial tissues, such as colon (Johnston et al, 2007b), airway epithelium (Sun et al, 2016), corneal epithelium (Cotsarelis et al, 1989), tracheal epithelium (Borthwick et al, 2001), and bronchioalveolar epithelium (Nolen-Walston et al, 2008). Longer hierarchies exist, for example, in neural and hematopoietic stem cell lineages. The methods presented in this paper can be extended to longer hierarchies, but this is not a trivial extension, since the Routh-Hurwitz and sign stability conditions become more complicated.
The evidence for the existence of autonomous control has been mounting in the last decade from experimental work. The actual functional forms of controls, however, are largely unknown. In the existing theoretical literature, (hypothetical) specific functional forms of the controls are often assumed, and conclusions are drawn based on the analysis of the resulting models. We consider it an important advantage of the present model that it does not actually require the knowledge of these functional forms. The only input needed is the derivatives of the control functions at the equilibrium. In many cases (as follows from our analysis) it is only the signs of the controls that matter. This kind of information is a lot easier to obtain experimentally than the true functional form. The signs of the derivatives and estimates of their magnitudes can be obtained by perturbing the system (e.g. by varying the population size of a given compartment) and measuring the changes in kinetic rates (divisions, deaths, differentiations) of the cells in all the compartments.
A very interesting open question is the existence of motifs in autonomous SC signaling networks. The current paper only goes as far as developing an efficient and intuitive method of “listing” all possible stable control networks for n = 2, 3. The next step that relies largely on experiment developments is to observe which networks from the list appear more often than others. For example, the so-called “memory module” identified by Alon (2007) is the class of networks that includes the networks in the second and third rows of figure 3. As shown, in the framework of the processes listed in table 2, there are 16 different arrangements that correspond to one and 8 arrangements to the other (see figure 3). For example, triplets (Q7x, Q1y, Q4z) (SCs control differentiation of ICs, ICs control differentiations of SCs, and DCs control asymmetric divisions of SCs) and (Q7x, Q5y, Q3z) (SCs control differentiation of ICs, ICs control their own de-differentiation, and DCs control death of ICs), both give rise to the network in the 2nd row of figure 3.
Interestingly, the feed forward loop (see e.g. Mangan and Alon (2003)) does not belong to the class of minimal controls as defined here. Its core part consists of x → y, y → z, and x → z. This is a reducible network, where z is the separable component, and the remaining module must be of the form (a) or (b) of figure 2. Therefore, for stability, we must have x controlling its own change, which means that the SC compartment controls more than one process. This can be for example achieved by a three-compartment system (Q7x, Q8y, Q9z, Q2x), which has four controls and is therefore not minimal according to our definition. While the methodology developed here has mostly been illustrated by studying minimal control networks, it is not difficult to expand the theory (and the software) to more general, more “redundant” control networks.
The theoretical work presented here aims not only to provide a comprehensive description of control networks in autonomous homeostatic regulation of healthy tissues, but also to serve as a stepping stone in our understanding of the scenarios where such regulations fails. As pointed out in Medema and Vermeulen (2011) in the context of intestinal SC systems, “As our understanding of normal intestinal crypt homeostasis grows, these developments may point towards new insights into the origin of cancer and the maintenance and regulation of cancer stem cells.” Methodology connecting healthy homeostatic regulation with elucidating possible pathways to cancer was developed in Rodriguez-Brenes et al (2011). There, a particular wiring of a control network was considered, to identify all possible ways in which it can go “wrong” leading to different types of tissue growth. Several types of cell expansion laws mapped into the known tumor growth patterns (Rodriguez-Brenes et al, 2013). This suggests that in the context of stem cell driven cancers, the theoretically possible mechanisms of cancer origins are consistent with experimental findings. Using the novel framework developed here, the next logical step is to test the possible stable control networks with respect to possible failure mechanisms. In particular, the question of robustness against mutations is of interest. Considering the minimal networks studied here, we can proceed according to the framework developed in Rodriguez-Brenes et al (2011), and study the evolutionary dynamics of cell populations that consist of (i) wild type cells that respond to and express controls appropriately, (ii) mutants that do not respond (or have a reduced response) to one or more controls, and (iii) mutants that do not exhibit one or more controls (or exhibit it to a lesser degree). Depending on the control network and the type of mutation, different growth patterns are expected to be observed. Which network properties allow for the most robust, failure-proof control? Is reducibility a desirable design property from the point of view of minimizing damage? What types of redundancy (that is, non-minimal control networks) are the best protection against mutations of each kind? Such questions comprise the next step toward our understanding of cancer origins in SC tissues.
A Case 1 in section 3.1
Case 1 in section 3.2 allows for two different possibilities, depending on the matrix , which contains 4 nonzero entries. The characteristic polynomial of is given by
For both eigenvalues to have negative real parts, necessary and sufficient conditions are (as dictated by Routh-Hurwitz conditions, see, e.g., Hershkowitz (2007)):
| (14) |
| (15) |
Stability conditions resulting from the quadratic characteristic equation lead to the following two cases:
-
Case 1(a)
If and , the system is stable if the signs of the controls are assigned correctly. Similarly, with and .
-
Case 1(b)
If and , the system allows two distinct sets of conditions that guarantee stability. The two sets of conditions imply different signs of the controls (and also contain restrictions on their magnitude), such that there are two alternative signings (or wirings) of the network compatible with stability. Similarly, if and , two alternative stable wirings are possible.
An example of case 1(a) above is given by the pair (Q5x, Q1y). Case 1(b) is represented by the pair (Q1x, Q5y). In both cases, but the sign of is respectively positive and negative in the two cases.
B Techniques
We wrote a program in Mathematica that for a given system, lists all stable minimal controls and classifies them in terms of reducibility. This Mathematica code is given in Supplementary Material available online.
The input includes the number of compartments (n = 3 in the case considered) and the list of possible processes with the corresponding increments. The program includes a loop that goes over all possible n-tuples of controls. These are analyzed for stability and only those that can be stable are listed in the output.
To perform the analysis for the n = 3 case, the following rules were used. These come from the Routh-Hurwitz conditions and results on potential stability Grundy et al (2012). Suppose the characteristic polynomial of J is denoted as
A combination of three nonzero controls was discarded if:
Any of ai is zero.
The matrix consists of one simply connected component, and contains fewer than 5 nonzero entries.
The matrix consists of one simply connected component, and a0 − a1a2 = 0.
For systems that are not rejected by these criteria, the characteristic polynomial is factored to determine the number of simply connected components, and also the stability conditions are determined by solving a set of inequalities.
Supplementary Material
Acknowledgments
NK gratefully acknowledges the support of NIH grant 1 U01 CA187956-01. The research of PvdD is partially supported by an NSERC Discovery grant. We thank the two anonymous reviewers for insightful suggestions.
Contributor Information
Natalia L. Komarova, Department of Mathematics, University of California Irvine, Irvine, CA 92697, USA
P. van den Driessche, Department of Mathematics and Statistics, University of Victoria, Victoria, B.C., Canada V8W 2Y2
References
- Adams GB, Scadden DT. A niche opportunity for stem cell therapeutics. Gene therapy. 2008;15(2):96–99. doi: 10.1038/sj.gt.3303063. [DOI] [PubMed] [Google Scholar]
- Alon U. Biological networks: the tinkerer as an engineer. Science. 2003;301(5641):1866–1867. doi: 10.1126/science.1089072. [DOI] [PubMed] [Google Scholar]
- Alon U. Network motifs: theory and experimental approaches. Nature Reviews Genetics. 2007;8(6):450–461. doi: 10.1038/nrg2102. [DOI] [PubMed] [Google Scholar]
- Alvarez-Buylla A, Lim DA. For the long run: maintaining germinal niches in the adult brain. Neuron. 2004;41(5):683–686. doi: 10.1016/s0896-6273(04)00111-4. [DOI] [PubMed] [Google Scholar]
- Ashkenazi R, Jackson TL, Dontu G, Wicha MS. Breast cancer stem cells-research opportunities utilizing mathematical modeling. Stem cell reviews. 2007;3(2):176–182. doi: 10.1007/s12015-007-0026-2. [DOI] [PubMed] [Google Scholar]
- Ashkenazi R, Gentry SN, Jackson TL. Pathways to tumorigenesis – modeling mutation acquisition in stem cells and their progeny. Neoplasia. 2008;10(11):1170–IN6. doi: 10.1593/neo.08572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabasi AL, Oltvai ZN. Network biology: understanding the cell’s functional organization. Nature reviews genetics. 2004;5(2):101–113. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
- Boman BM, Fields JZ, Cavanaugh KL, Guetter A, Runquist OA. How dysregulated colonic crypt dynamics cause stem cell overpopulation and initiate colon cancer. Cancer Res. 2008;68:3304–3313. doi: 10.1158/0008-5472.CAN-07-2061. [DOI] [PubMed] [Google Scholar]
- Borthwick DW, Shahbazian M, Todd Krantz Q, Dorin JR, Randell SH. Evidence for stem-cell niches in the tracheal epithelium. American journal of respiratory cell and molecular biology. 2001;24(6):662–670. doi: 10.1165/ajrcmb.24.6.4217. [DOI] [PubMed] [Google Scholar]
- Brualdi RA, Shader BL. Cambridge Tracts in Math. Vol. 116. Cambridge University Press; 2009. Matrices of sign-solvable linear systems. [Google Scholar]
- Cotsarelis G, Cheng SZ, Dong G, Sun TT, Lavker RM. Existence of slow-cycling limbal epithelial basal cells that can be preferentially stimulated to proliferate: implications on epithelial stem cells. Cell. 1989;57(2):201–209. doi: 10.1016/0092-8674(89)90958-6. [DOI] [PubMed] [Google Scholar]
- Daluiski A, Engstrand T, Bahamonde M, Gamer L, Agius E, Stevenson S, Cox K, Rosen V, Lyons K. Bone morphogenetic protein-3 is a negative regulator of bone density. Nature genetics. 2001;27(1):84–88. doi: 10.1038/83810. [DOI] [PubMed] [Google Scholar]
- Dehay C, Kennedy H. Cell-cycle control and cortical development. Nature Reviews Neuroscience. 2007;8(6):438–450. doi: 10.1038/nrn2097. [DOI] [PubMed] [Google Scholar]
- Dingli D, Michor F. Successful therapy must eradicate cancer stem cells. Stem cells. 2006;24(12):2603–2610. doi: 10.1634/stemcells.2006-0136. [DOI] [PubMed] [Google Scholar]
- Dingli D, Traulsen A, Pacheco JM. Stochastic dynamics of hematopoietic tumor stem cells. Cell Cycle. 2007;6(4):461–466. doi: 10.4161/cc.6.4.3853. [DOI] [PubMed] [Google Scholar]
- Elgjo K, Reichelt KL. Chalones–from aqueous extracts to oligopeptides. Cell Cycle. 2004;3(9):1206–1209. [PubMed] [Google Scholar]
- Enderling H. Cancer stem cells: small subpopulation or evolving fraction? Integrative Biology. 2015;7(1):14–23. doi: 10.1039/c4ib00191e. [DOI] [PubMed] [Google Scholar]
- Enderling H, Hahnfeldt P. Cancer stem cells in solid tumors: Is ’evading apoptosis’ a hallmark of cancer? Progress in biophysics and molecular biology. 2011;106(2):391–399. doi: 10.1016/j.pbiomolbio.2011.03.007. [DOI] [PubMed] [Google Scholar]
- Enderling H, Chaplain MA, Anderson AR, Vaidya JS. A mathematical model of breast cancer development, local treatment and recurrence. Journal of theoretical biology. 2007;246(2):245–259. doi: 10.1016/j.jtbi.2006.12.010. [DOI] [PubMed] [Google Scholar]
- Enderling H, Anderson AR, Chaplain MA, Beheshti A, Hlatky L, Hahnfeldt P. Paradoxical dependencies of tumor dormancy and progression on basic cell kinetics. Cancer research. 2009a;69(22):8814–8821. doi: 10.1158/0008-5472.CAN-09-2115. [DOI] [PubMed] [Google Scholar]
- Enderling H, Hlatky L, Hahnfeldt P. Migration rules: tumours are conglomerates of self-metastases. British journal of cancer. 2009b;100(12):1917–1925. doi: 10.1038/sj.bjc.6605071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enderling H, Park D, Hlatky L, Hahnfeldt P. The importance of spatial distribution of stemness and proliferation state in determining tumor radioresponse. Math Model Nat Phenom. 2009c;4(3):117–133. [Google Scholar]
- Foo J, Drummond MW, Clarkson B, Holyoake T, Michor F. Eradication of chronic myeloid leukemia stem cells: a novel mathematical model predicts no therapeutic benefit of adding G-CSF to imatinib. PLoS Comput Biol. 2009;5(9):e1000,503. doi: 10.1371/journal.pcbi.1000503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganguly R, Puri I. Mathematical model for the cancer stem cell hypothesis. Cell proliferation. 2006;39(1):3–14. doi: 10.1111/j.1365-2184.2006.00369.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganguly R, Puri I. Mathematical model for chemotherapeutic drug efficacy in arresting tumour growth based on the cancer stem cell hypothesis. Cell proliferation. 2007;40(3):338–354. doi: 10.1111/j.1365-2184.2007.00434.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glauche I, Cross M, Loeffler M, Roeder I. Lineage specification of hematopoietic stem cells: mathematical modeling and biological implications. Stem Cells. 2007;25:1791–1799. doi: 10.1634/stemcells.2007-0025. [DOI] [PubMed] [Google Scholar]
- de Graaf CA, Kauppi M, Baldwin T, Hyland CD, Metcalf D, Willson TA, Carpinelli MR, Smyth GK, Alexander WS, Hilton DJ. Regulation of hematopoietic stem cells by their mature progeny. Proceedings of the National Academy of Sciences. 2010;107(50):21,689–21,694. doi: 10.1073/pnas.1016166108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grundy D, Olesky D, van den Driessche P. Constructions for potentially stable sign patterns. Linear Algebra and its Applications. 2012;436(12):4473–4488. [Google Scholar]
- Guilak F, Cohen DM, Estes BT, Gimble JM, Liedtke W, Chen CS. Control of stem cell fate by physical interactions with the extracellular matrix. Cell stem cell. 2009;5(1):17–26. doi: 10.1016/j.stem.2009.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall F, Li Z. Sign pattern matrices. In: Hogben L, editor. Handbook of Linear Algebra. Chapman & Hall/CRC Press; 2007. chap 33. [Google Scholar]
- Hardy K, Stark J. Mathematical models of the balance between apoptosis and proliferation. Apoptosis. 2002;7:373–381. doi: 10.1023/a:1016183731694. [DOI] [PubMed] [Google Scholar]
- Hartwell LH, Hopfield JJ, Leibler S, Murray AW. From molecular to modular cell biology. Nature. 1999;402:C47–C52. doi: 10.1038/35011540. [DOI] [PubMed] [Google Scholar]
- Hershkowitz D. Matrix stability and inertia. In: Hogben L, editor. Handbook of Linear Algebra. Chapman & Hall/CRC Press; 2007. chap 19. [Google Scholar]
- Hillen T, Enderling H, Hahnfeldt P. The tumor growth paradox and immune system-mediated selection for cancer stem cells. Bulletin of mathematical biology. 2013;75(1):161–184. doi: 10.1007/s11538-012-9798-x. [DOI] [PubMed] [Google Scholar]
- Hsieh J. Orchestrating transcriptional control of adult neurogenesis. Genes & development. 2012;26(10):1010–1021. doi: 10.1101/gad.187336.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston MD, Edwards CM, Bodmer WF, Maini PK, Chapman SJ. Mathematical modeling of cell population dynamics in the colonic crypt and in colorectal cancer. Proc Natl Acad Sci USA. 2007a;104:4008–4013. doi: 10.1073/pnas.0611179104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston MD, Edwards CM, Bodmer WF, Maini PK, Chapman SJ. Mathematical modeling of cell population dynamics in the colonic crypt and in colorectal cancer. Proceedings of the National Academy of Sciences. 2007b;104(10):4008–4013. doi: 10.1073/pnas.0611179104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston MD, Maini PK, Chapman SJ, Edwards CM, Bodmer WF. On the proportion of cancer stem cells in a tumour. Journal of theoretical biology. 2010;266(4):708–711. doi: 10.1016/j.jtbi.2010.07.031. [DOI] [PubMed] [Google Scholar]
- Komarova NL. Principles of regulation of self-renewing cell lineages. PloS one. 2013;8(9):e72,847. doi: 10.1371/journal.pone.0072847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konstorum A, Hillen T, Lowengrub J. Feedback regulation in a cancer stem cell model can cause an Allee effect. Bulletin of mathematical biology. 2016;78(4):754–785. doi: 10.1007/s11538-016-0161-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunche S, Yan H, Calof AL, Lowengrub JS, Lander AD. Feedback, lineages and self-organizing morphogenesis. PLoS Comput Biol. 2016;12(3):e1004,814. doi: 10.1371/journal.pcbi.1004814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander AD, Gokoffski KK, Wan FY, Nie Q, Calof AL. Cell lineages and the logic of proliferative control. PLoS Biol. 2009;7(1):e1000,015. doi: 10.1371/journal.pbio.1000015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavado A, Lagutin OV, Chow LM, Baker SJ, Oliver G. Prox1 is required for granule cell maturation and intermediate progenitor maintenance during brain neurogenesis. PLoS Biol. 2010;8(8):e1000,460. doi: 10.1371/journal.pbio.1000460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L, Clevers H. Coexistence of quiescent and active adult stem cells in mammals. Science. 2010;327(5965):542–545. doi: 10.1126/science.1180794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu M, Pleasure SJ, Collins AE, Noebels JL, Naya FJ, Tsai MJ, Lowenstein DH. Loss of BETA2/NeuroD leads to malformation of the dentate gyrus and epilepsy. Proceedings of the National Academy of Sciences. 2000;97(2):865–870. doi: 10.1073/pnas.97.2.865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loeffler M, Roeder I. Tissue stem cells: definition, plasticity, heterogeneity, self-organization and models–a conceptual approach. Cells Tissues Organs (Print) 2002;171:8–26. doi: 10.1159/000057688. [DOI] [PubMed] [Google Scholar]
- Mangan S, Alon U. Structure and function of the feed-forward loop network motif. Proceedings of the National Academy of Sciences. 2003;100(21):11,980–11,985. doi: 10.1073/pnas.2133841100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marciniak-Czochra A, Stiehl T, Ho AD, Jäger W, Wagner W. Modeling of asymmetric cell division in hematopoietic stem cells-regulation of self-renewal is essential for efficient repopulation. Stem cells and development. 2009;18(3):377–386. doi: 10.1089/scd.2008.0143. [DOI] [PubMed] [Google Scholar]
- Marshman E, Booth C, Potten CS. The intestinal epithelial stem cell. Bioessays. 2002;24(1):91–98. doi: 10.1002/bies.10028. [DOI] [PubMed] [Google Scholar]
- McPherron AC, Lawler AM, Lee SJ. Regulation of skeletal muscle mass in mice by a new TGF-p superfamily member. Nature. 1997;387:83–90. doi: 10.1038/387083a0. [DOI] [PubMed] [Google Scholar]
- Medema JP, Vermeulen L. Microenvironmental regulation of stem cells in intestinal homeostasis and cancer. Nature. 2011;474(7351):318–326. doi: 10.1038/nature10212. [DOI] [PubMed] [Google Scholar]
- Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U. Network motifs: simple building blocks of complex networks. Science. 2002;298(5594):824–827. doi: 10.1126/science.298.5594.824. [DOI] [PubMed] [Google Scholar]
- Morrison SJ, Kimble J. Asymmetric and symmetric stem-cell divisions in development and cancer. Nature. 2006;441(7097):1068–1074. doi: 10.1038/nature04956. [DOI] [PubMed] [Google Scholar]
- Nakata Y, Getto P, Marciniak-Czochra A, Alarcón T. Stability analysis of multi-compartment models for cell production systems. Journal of biological dynamics. 2012;6(sup1):2–18. doi: 10.1080/17513758.2011.558214. [DOI] [PubMed] [Google Scholar]
- Nolen-Walston RD, Kim CF, Mazan MR, Ingenito EP, Gruntman AM, Tsai L, Boston R, Woolfenden AE, Jacks T, Hoffman AM. Cellular kinetics and modeling of bronchioalveolar stem cell response during lung regeneration. American Journal of Physiology-Lung Cellular and Molecular Physiology. 2008;294(6):L1158–L1165. doi: 10.1152/ajplung.00298.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piotrowska M, Enderling H, van der Heiden U, Mackey M. Mathematical modeling of stem cells related to cancer. In: Dittmar T, Znker K, editors. Cancer and Stem Cells. Nova Science Publishers; New York: 2008. pp. 1–25. [Google Scholar]
- Ram Singh S. Stem cell niche in tissue homeostasis, aging and cancer. Current medicinal chemistry. 2012;19(35):5965–5974. doi: 10.2174/092986712804485917. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Brenes IA, Komarova NL, Wodarz D. Evolutionary dynamics of feedback escape and the development of stem-cell–driven cancers. Proceedings of the National Academy of Sciences. 2011;108(47):18,983–18,988. doi: 10.1073/pnas.1107621108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez-Brenes IA, Komarova NL, Wodarz D. Tumor growth dynamics: insights into evolutionary processes. Trends in ecology & evolution. 2013;28(10):597–604. doi: 10.1016/j.tree.2013.05.020. [DOI] [PubMed] [Google Scholar]
- Roeder I, Galle J, Loeffler M. Theoretical concepts of tissue stem cell organization. In: Potten CS, Clarke RB, Wilson J, Renehan AG, editors. Tissue stem cells. Taylor and Francis Group; New York: 2006. p. 18. [Google Scholar]
- Scadden DT. The stem-cell niche as an entity of action. Nature. 2006;441(7097):1075–1079. doi: 10.1038/nature04957. [DOI] [PubMed] [Google Scholar]
- Scott JG, Hjelmeland AB, Chinnaiyan P, Anderson AR, Basanta D. Microenvironmental variables must influence intrinsic phenotypic parameters of cancer stem cells to affect tumourigenicity. PLoS Comput Biol. 2014;10(1):e1003,433. doi: 10.1371/journal.pcbi.1003433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen B, Xie Z, Case N, Ma M, Rubin C, Rubin J. Mechanical strain inhibits adipogenesis in mesenchymal stem cells by stimulating a durable β-catenin signal. Endocrinology. 2008;149(12):6065–6075. doi: 10.1210/en.2008-0687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen-Orr SS, Milo R, Mangan S, Alon U. Network motifs in the transcriptional regulation network of escherichia coli. Nature genetics. 2002;31(1):64–68. doi: 10.1038/ng881. [DOI] [PubMed] [Google Scholar]
- Simmons CA, Matlis S, Thornton AJ, Chen S, Wang CY, Mooney DJ. Cyclic strain enhances matrix mineralization by adult human mesenchymal stem cells via the extracellular signal-regulated kinase (erk1/2) signaling pathway. Journal of biomechanics. 2003;36(8):1087–1096. doi: 10.1016/s0021-9290(03)00110-6. [DOI] [PubMed] [Google Scholar]
- Stiehl T, Marciniak-Czochra A. Characterization of stem cells using mathematical models of multistage cell lineages. Mathematical and Computer Modelling. 2011;53(7):1505–1517. [Google Scholar]
- Stiehl T, Marciniak-Czochra A. Mathematical modeling of leukemogenesis and cancer stem cell dynamics. Mathematical Modelling of Natural Phenomena. 2012;7(1):166–202. [Google Scholar]
- Sun Z, Plikus MV, Komarova NL. Near equilibrium calculus of stem cells in application to the airway epithelium lineage. PLOS Comput Biol. 2016;12(7):e1004,990. doi: 10.1371/journal.pcbi.1004990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomlinson I, Bodmer W. Failure of programmed cell death and differentiation as causes of tumors: some simple mathematical models. Proceedings of the National Academy of Sciences. 1995;92(24):11,130–11,134. doi: 10.1073/pnas.92.24.11130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzeng YS, Li H, Kang YL, Chen WC, Cheng WC, Lai DM. Loss of Cxcl12/Sdf-1 in adult mice decreases the quiescent state of hematopoietic stem/progenitor cells and alters the pattern of hematopoietic regeneration after myelosuppression. Blood. 2011;117(2):429–439. doi: 10.1182/blood-2010-01-266833. [DOI] [PubMed] [Google Scholar]
- Vermeulen L, Snippert HJ. Stem cell dynamics in homeostasis and cancer of the intestine. Nature Reviews Cancer. 2014;14(7):468–480. doi: 10.1038/nrc3744. [DOI] [PubMed] [Google Scholar]
- Vespignani A. Evolution thinks modular. Nature genetics. 2003;35(2):118–119. doi: 10.1038/ng1003-118. [DOI] [PubMed] [Google Scholar]
- Vogelstein B, Kinzler KW. Cancer genes and the pathways they control. Nature medicine. 2004;10(8):789–799. doi: 10.1038/nm1087. [DOI] [PubMed] [Google Scholar]
- Wu H, Ivkovic S, Murray R, Jaramillo S, Lyons K, Johnson J, Calof A. Autoregulation of neurogenesis by GDF11. Neuron. 2003;37(2):197–207. doi: 10.1016/s0896-6273(02)01172-8. [DOI] [PubMed] [Google Scholar]
- Wuchty S, Oltvai ZN, Barabási AL. Evolutionary conservation of motif constituents in the yeast protein interaction network. Nature genetics. 2003;35(2):176–179. doi: 10.1038/ng1242. [DOI] [PubMed] [Google Scholar]
- Yamasaki K, Toriu N, Hanakawa Y, Shirakata Y, Sayama K, Takayanagi A, Ohtsubo M, Gamou S, Shimizu N, Fujii M, et al. Keratinocyte growth inhibition by high-dose epidermal growth factor is mediated by transforming growth factor β autoinduction: A negative feedback mechanism for keratinocyte growth. Journal of investigative dermatology. 2003;120(6):1030–1037. doi: 10.1046/j.1523-1747.2003.12239.x. [DOI] [PubMed] [Google Scholar]
- Yang J, Plikus MV, Komarova NL. The role of symmetric stem cell divisions in tissue homeostasis. PLoS Comput Biol. 2015a;11(12):e1004,629. doi: 10.1371/journal.pcbi.1004629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Sun Z, Komarova NL. Analysis of stochastic stem cell models with control. Mathematical biosciences. 2015b;266:93–107. doi: 10.1016/j.mbs.2015.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yatabe Y, Tavare S, Shibata D. Investigating stem cells in human colon by using methylation patterns. Proc Natl Acad Sci USA. 2001;98:10,839–10,844. doi: 10.1073/pnas.191225998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Youssefpour H, Li X, Lander A, Lowengrub J. Multispecies model of cell lineages and feedback control in solid tumors. Journal of theoretical biology. 2012;304:39–59. doi: 10.1016/j.jtbi.2012.02.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


