Abstract
The mechanisms underlying the spatial organization of self-assembled myofibrils in cardiac tissues remain incompletely understood. By modeling cells as elastic solids under active cytoskeletal contraction, we found a good correlation between the predicted maximal principal stress directions and the in vitro myofibril orientations in individual cardiomyocytes. This implies that actomyosin fibers tend to assemble along the maximal tensile stress (MTS) directions. By considering the dynamics of focal adhesion and myofibril formation in the model, we showed that different patterns of myofibril organizations in mature versus immature cardiomyocytes can be explained as the consequence of the different levels of force-dependent remodeling of focal adhesions. Further, we applied the mechanics model to cell pairs and showed that the myofibril organizations can be regulated by a combination of multiple factors including cell shape, cell–substrate adhesions, and cell–cell adhesions. This mechanics model can guide the rational design in cardiac tissue engineering where recapitulating in vivo myofibril organizations is crucial to the contractile function of the heart.
Keywords: myofibrillogenesis, maximal principle stress direction, cell shape, stress fiber assembly
Introduction
The hierarchical structure of heart muscle is highly ordered, from the helical and weaving arrangement of myocardial fibers in the ventricles to the parallel alignment of myofibrils in individual cardiomyocytes [1,2]. Understanding the underlying principles governing the emergence of structural patterns in heart muscles is a central goal of both developmental biology and pathology [3] and tissue engineering [4–6]. Recapitulating the in vivo linear alignment of myofibrils at the cellular scale in tissue constructs is critical for achieving the optimal contractile function [7,8] of the cardiac tissues. Myofibrillogenesis is a process in which many kinds of proteins assemble into spatially organized contractile myofibrils [9–11]. Previous studies have shown that myofibrillogenesis is a multistage process in which the assembly of a myofibril can be divided into three phases in the temporal order: premyofibrils, nascent myofibrils, and mature myofibrils [12,13]. In addition to the temporal order of myofibrillogenesis, the spatial organization of myofibrils in individual myocytes has recently been studied intensively. In a series of studies [9,14–19] in which the microcontact printing technique was used to constrain cell spreading and thus produce a variety of cell shapes, it was found that the cell shape plays an important role in regulating spatial myofibril organization. Figure 1 shows myofibril images of triangular- and square-shaped cardiomyocytes. It can be seen that, for the same shape, the spatial patterns of myofibril orientation are very similar, suggesting the existence of biomechanical mechanisms on the whole-cell level that regulate the spatial organization of myofibrils.
Fig. 1.

Myofibril organization in shape-constrained cardiomyocytes (F-actin staining in (a)–(f) and α-actinin staining in (c)) (Reprinted with permission from Parker et al. [9]. Copyright 2002 by National Institutes of Health; Reprinted with permission from Bray et al. [14]. Copyright 2008 by Wiley; Reprinted with permission from Grosberg et al. [15]. Copyright 2011 by Public Library of Science; and Reprinted with permission from Geisse et al. [24]. Copyright 2009 by Springer.)
Several theoretical models have been proposed to understand the stress fiber or myofibril organizations in single cells. By assuming tension-dependent stress fiber formation, Deshpande et al. proposed a mechanobiochemical micromechanics constitutive law for the actomyosin cytoskeleton, and their modeling results showed that the cell shape and cell–substrate adhesion dictate the stress fiber organizations [20–22]. Vernerey et al. developed a sophisticated multiphasic model that accounts for mechanochemical coupling and dynamic contraction of stress fibers and mass convection/diffusion of actin monomers [23]. Their modeling results recapitulate the direction of myofibrils in square, triangular, and rectangular shaped cells as shown in Fig. 1. In another work where the cell was modeled as an elastic inclusion in a continuum and the active contraction of stress fibers was modeled as local force dipoles, Zemel et al. were able to explain the alignment of stress fibers along the long axis of human mesenchymal stem cells [25]. Kresh and Chopra proposed a conceptual model of myofibril alignment where the principle directions of stretching and compression together guide the myofibril directions. Through computational modeling, Kang et al. [26] studied the response of actin filament network to cyclic stretching. Walcott and Sun [27] developed a mathematical model of a viscous cytoskeleton and studied its role on stress fiber formation. Furthermore, a mathematical model based on the ensemble of individual fibers connecting focal adhesions (FA) has been developed by Grosberg et al. [15] to explore the self-organization of myofibrils in heart muscle cells. Their model also successfully recapitulated the myofibril organization shown in Fig. 1 for different shapes.
These rather sophisticated models [15,20–22,25] predicted the stress fiber organizations as the steady-state results of the positive feedback between the stress fiber tension and stress fiber assembly. In the first part of this paper, using a simple elasticity model, we will show that the mechanics principle of static equilibrium alone is sufficient to account for the onset of spatial pattern formations in myofibril organization from an isotropic and homogeneous initial condition. The positive feedback only serves to enhance the patterns formed.
It is evident from the experimental data shown in Fig. 1 that the cell shape dictates the myofibril organization. However, experimental observations shown in Fig. 2 imply that cell shape is not the only determinant. As shown in Fig. 2, the immature circular and square cells exhibited ringlike circumferential myofibrils in the central region, while the mature circular and square cells exhibited straight myofibrils [6]. The underlying cause of these different myofibril organizations in mature versus immature cardiomyocytes for the same cell shape remains unclear [6].
Fig. 2.
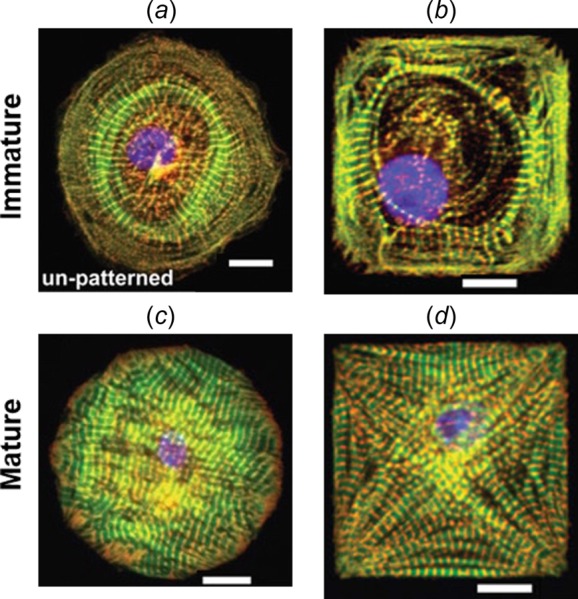
Different myofibril organizations observed in (a) and (b) immature (stem-cell derived) versus (c) and (d) mature (neonatal) cardiomyocytes for the same cell shapes. (Reprinted with permission from Sheehy et al. [6]. Copyright 2012 by Springer.)
It is widely known that mechanical tension plays a critical role for actomyosin stress fiber assembly in nonmuscle cells [28] and cardiomyocytes [29]. While “tension” is a scalar concept for 1D muscle fibers, maximal tensile stress (MTS) of a stress tensor is more appropriate concept to describe the internal force experienced by the 2D or 3D muscle tissues. We hypothesize that myofibrils in 2D and 3D muscle tissue tend to assemble along the MTS direction. Thus, the myofibril organization will be determined by the stress field, which is then governed by the mechanics of the cell. From the elasticity theory [30], it follows that the stress field in an elastic solid depends on a combination of multiple factors: loadings (e.g., active contraction), the geometry of the domain (i.e., cell shape), the constitutive law of the material (i.e., mechanical properties of the cytoskeleton), and the boundary conditions (e.g., cell–substrate/cell–cell adhesions). Therefore, in addition to cell shape, other factors such as the dynamic remodeling of myofibrils and cell–substrate adhesions will also alter the stress field and thus change the myofibril organizations and focal adhesion formation.
This paper is organized as follows: In the “Model” section, we will first present the static model, which is a simple elasticity model with active contraction. We then extend the static model to include force-dependent focal adhesion formation and force-dependent myofibril formation (i.e., the dynamic model). In the “Results” section, we will first use the static model to explain the onset of myofibril pattern formation in shape-constrained cells. We then use the dynamic model to show that in addition to cell shape, other factors such as the dynamic remodeling of myofibrils, cell–substrate and cell–cell adhesions, and active contraction will also alter the stress field and thus change the myofibril organizations and focal adhesion formation.
Model
The Static Model.
Because of the flatness of the well-spread cells on 2D substrate, the actomyosin cytoskeleton is treated as a 2D elastic solid (Fig. 3(a)), and the thickness of the cell, denoted by h, is assumed to be a constant for the sake of simplicity. The equilibrium equation [31,32] for the cell is
Fig. 3.
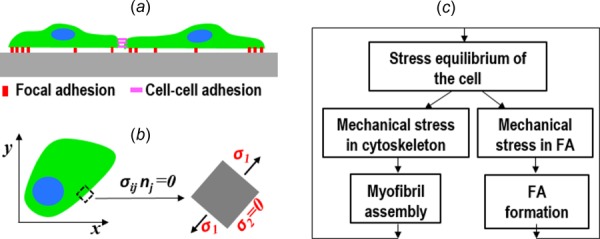
Schematics of the elasticity model of the cell: (a) cell–substrate and cell–cell adhesions (side view), (b) (top view) at the stress-free boundary the MTS direction is always parallel to the edge irrespective of the overall cell shape, and (c) mechanobiochemical feedback loops between the mechanical stresses and the remodeling of FA and myofibrils
| (1) |
where σij is the cytoskeletal stress tensor, and Ti is the traction stress exerted on the substrate by the cell (the indicial notation for vectors and tensors are used here, subscripts i and j have the range of (x, y), summation convention on dummy indices is adopted [30]). Traction stress is assumed to be linearly proportional to the displacement of the cell with respect to the substrate
| (2) |
where ui is the displacement, and is the spring constant of the cell–substrate linkage. At the cell edge without cell–cell adhesion, the stress-free boundary condition holds (Fig. 3(b)): , where nj is the normal direction at the cell edge. For the active actomyosin contraction, we extend the concept of isometric tension, which is a scalar for 1D fibers, to an isometric tensile stress (ITS) tensor . Here, the 2D plane-stress isotropic Hooke's law is modified to include the ITS tensor [32]
| (3) |
where λ and μ are Lame's constant and shear modulus of the cytoskeleton [30], respectively. For simplicity, the passive component of the actin cytoskeleton is assumed to be isotropic.
This elasticity problem described earlier is solved for different cell shapes to obtain the stress field in the cell and to plot the maximal principle stress directions. For this static model, the ITS tensor is taken to be isotropic and constant and the cell–substrate stiffness is taken to be a constant within the cell domain
where is the baseline active contractile stress, is Kronecker delta, and k0 is a constant. The finite element method [30] is employed to solve the elasticity problem.
The Extended Dynamic Model.
To incorporate the dynamic remodeling of focal adhesion and myofibril organization, the elasticity model described earlier is augmented with two kinetics equations. A lumped phenomenological variable ρ is defined to describe the density distribution of FA-associated proteins (e.g., integrins, talins, vinculins, etc.), ranging from zero (no integrin-mediated cell–substrate adhesion) to one (mature FAs). The time evolution of ρ is described by
| (5) |
where , , and are the rate constants for the spontaneous, auto-activation, and stress-mediated FA formation, respectively; is a decay constant; T denotes the magnitude of the traction stress; T0 and n are the model parameters; ρa represents the average density of the total amount of bound and unbound FA proteins, and is the mean value of ρ across the whole cell. The traction stress-dependent term in Eq. (5) accounts for the previous finding that the mechanical stress applied on FA promotes their growth and maturation [33]. Here, the redistribution (e.g., via active transportation and passive diffusion) of unbound FA proteins is assumed to be faster than other time scales involved, thus the unbound FA protein density is simply equal to . The kinetics of FA remodeling is coupled to the mechanics of the cell through the spring stiffness by the following relation:
| (6) |
where is the maximal stiffness when = 1. In this model, we assume that the substrate is rigid compared to focal adhesion because the in the experiments (Figs. 1, 2, and 5) cells were cultured on noncoated or polydimethylsiloxane-coated glass slides. Equations (2), (5), and (6) establish a positive feedback between the traction stress and FA formation (Fig. 4(d)): larger traction stress T leads to bigger ρ, which leads to bigger ; bigger results in larger traction stress.
Fig. 5.
Predicted maximal principal stress directions for irregular shapes and rectangular shapes. Myofibril images on the top row were acquired using the same protocol as in Ref. [37].
Fig. 4.
Myofibrils tend to assemble along the maximal principal stress directions. (a) and (d) Myofibril organizations in single cardiomyocytes (Reprinted with permission from Geisse et al. [24]. Copyright 2009 by Springer and Reprinted with permission from Bray et al. [14]. Copyright 2008 by Wiley.). (b) and (e) Model predictions of stress ellipses and MTS directions. (c) and (f) Predicted traction stress distributions. Parameter values: μ = 3.8 kPa, λ = 5.8 kPa, h = 3 μm, k0 = 0.18 kPa/μm, = 1 kPa, and cell area = 2000 μm2 (these values are used in the latter simulations unless specifically mentioned). Note that the spatial patterns of MTS and traction stress are robust for a range of parameter values.
To account for the anisotropic fiber formation, a second-order tensor , referred to as the fiber tensor, is introduced and its time evolution is described by
| (7) |
where are the rate constants for the stress-mediated fiber formation, is the rate of disassembly, is the maximal principal stress of , and is a model parameter. Denoting the maximal eigenvalue and the corresponding eigenvector of by and , respectively, the ITS tensor is defined as
| (8) |
where accounts for the increased active tension along the fiber direction due to the formation of actomyosin fiber bundles. The dyadic product of unit vector produces the tensor , which has its only nonzero-principle-value principle direction along .
Equations (3), (7), and (8) establish a feedback loop between the cytoskeletal stress and myofibril orientation (Fig. 3(c)). The assembly of stress fibers along the MTS directions changes from isotropic to anisotropic, which feedback to alter the stress field through the constitutive law (Eq. (3)). Furthermore, the FA feedback and the myofibril feedback are coupled to each other through the static equilibrium of the whole cell (Fig. 3(c)). Consequently, the focal adhesion formation will affect the actomyosin fiber assembly and vice versa. For the extended dynamics model described earlier, the forward Euler method is employed in the finite element model to numerically integrate the kinetics equations ((5) and (7)), and at each time step, the elasticity problem is solved to update the stress fields. For the simulations of the dynamics model, the initial value of ITS tensor is always set to be isotropic (i.e., see Eq. (4)). For all the dynamic simulations, the time integration terminates when a steady state is reached.
Results
Myofibrils Tend to Assemble Along the MTS Directions.
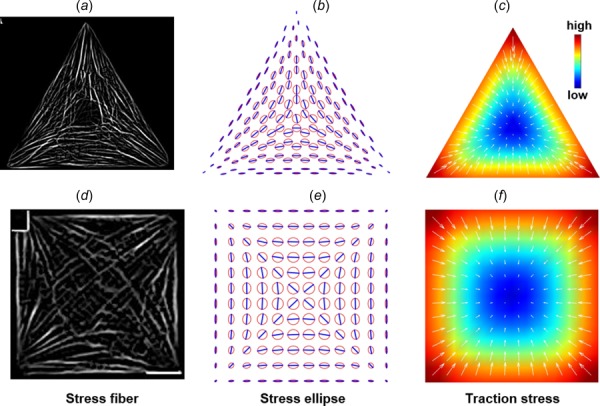
Treating each individual cell as 2D elastic solid with active contraction, the cellular and traction stresses are computed, as shown in Fig. 4, by solving the static elasticity problem with homogeneous cell–substrate adhesion and isotropic material properties using the finite element method (see the static model in the “Model” section). The principal stress ellipse is used to depict the anisotropy of the stress field (see Figs. 4(b) and 4(e)), for which the long axis of the ellipse denotes the MTS direction and the short axis represents the second principal stress direction. The lengths of the axes are proportional to the value of principal stresses.
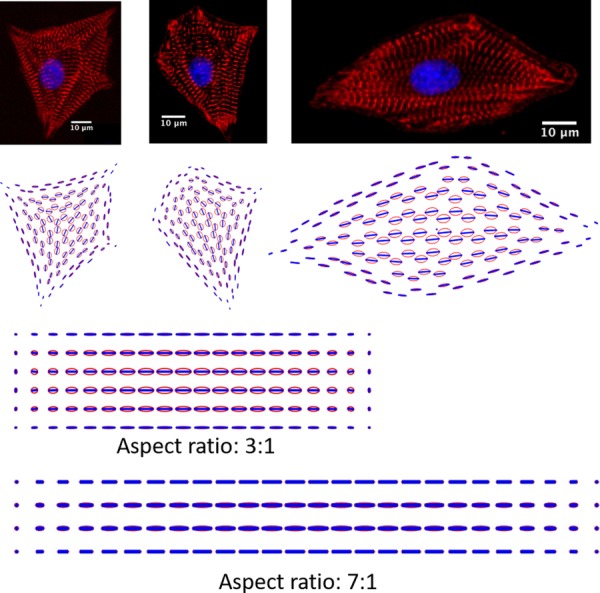
Two patterns of MTS direction for both triangle and square shapes can be observed in Figs. 4(b) and 4(e): (1) the MTS direction at the stress-free boundary is parallel to the edge; (2) the MTS direction is symmetric about the bisectors of the angles of the triangle and square. These patterns also appear in the myofibril orientations of different cardiomyocytes in Fig. 1, although not in all of the cells (e.g., Fig. 1(f) does not show noticeable edge-parallel fibers). To facilitate the visual comparison between the predicted MTS direction and the myofibril orientation, Figs. 4(a) and 4(d) are the results of image processing of Figs. 1(a) and 1(d) using the “tubeness” [34] plugin in imagej /fiji [35], which exhibit the edge-parallel myofibrils and the symmetry of the myofibril orientations about the bisectors of the angles. Figure 5 shows the comparison between the myofibril orientation and the MTS direction for cardiomyocytes with irregular shapes (without shape-constraining), which also shows a good correspondence between them.
The third column in Fig. 4 shows that traction stress is larger at the cell edge and concentrates at the convex corners of the polygonal cells and decreases to zero toward the center of the cell. This is simply a result of the static equilibrium: at the cell edge, traction stress needs to be present to balance the inward contraction, while at the center, contraction in one direction is balanced by the contraction in the opposite direction. Such mechanics principle has been reported previously by Nelson et al. [36]. Figure 5 shows the predicted MTS directions for some irregular shapes and rectangular shapes. The comparison between the myofibril organizations (top row in Fig. 5) and model predictions again shows a good agreement. The maximal tensile stress directions in rectangular cells are primarily parallel to the length direction. Increasing the aspect ratio will increase the anisotropy of the stress tensor, which means more stress fibers assemble along the length direction as the aspect ratio increases (Fig. 5, bottom two panels). These modeling results show that the mechanics principle of static equilibrium alone is sufficient to account for the onset of spatial pattern formations in myofibril organization and traction stress distribution from an isotropic and homogeneous initial condition.
It can be seen that myofibrils at the boundary are parallel to the edge (Fig. 1). Previous models of myofibrillogenesis have assumed that premyofibrils assemble first at the plasma membrane by using the membrane as the scaffold [12,38]. Here, our model provides an alternative explanation of why myofibrils at the boundary are parallel to the cell edge. We interpret it simply as a result of the stress-free boundary condition at the cell edge. For a material element at the stress-free boundary (Fig. 3(b)), because both normal and shear stresses at the boundary surface are zero, the MTS direction in the element is always parallel to the edge when the element is under tension. From the stress ellipses shown in Fig. 4, we can see that at the cell edge the stress tensor is highly anisotropic with the MTS direction parallel to the edge, while near the center of the cell, the stress tensor becomes almost isotropic (i.e., the stress ellipses are close to a circle) because of nearly equal contraction from all the directions. In addition, because the MTS direction in the convex corners is parallel to the two corner edges and merges at the corner vertices, this stress-free edge interpretation also explains why convex corners are the starting/terminating sites of stress fibers.
Effect of Cell–Substrate Adhesion on Myofibril Organizations in Mature Versus Immature Cardiomyocytes.
As shown in Fig. 2, the immature circular and square cells (i.e., stem-cell derived cardiomyocytes) exhibited ringlike circumferential myofibrils in the central region, while the mature circular and square cells (i.e., neonatal cardiomyocytes) exhibited straight myofibrils [6]. It was unclear why the same square or circular shape leads to different patterns of myofibril organization. We reason that myofibril organization is not only determined by the cell shape but also by the cell–substrate adhesion and the anisotropic cytoskeletal contraction, since all of them together determine the stress field in the cell. To incorporate the dynamic remodeling of focal adhesion and myofibril organization, the elasticity model is augmented with two kinetics equations that describe the force-dependent FA and stress fiber remodeling (see the dynamic model in the “Model” section). The dynamic model establishes a positive feedback between the traction stress and FA formation, and a feedback loop between the cytoskeletal stress and myofibril orientation, as illustrated in Fig. 3(c). Through the static equilibrium of the cell, these two feedback loops are coupled to each other. Consequently, the focal adhesion formation will affect the actomyosin fiber assembly and vice versa. By performing the parameter space search, we found that the disparate myofibril organizations (Fig. 2) in mature versus immature cardiomyocytes can be recapitulated by changing a single model parameter , which denotes the stress-mediated FA formation (for example, = 0.8 for mature ones, while = 0.2 for immature ones). Note that a larger value of means a stronger positive feedback between FA maturation and FA stress, while a smaller value of means a weaker dependence of FA maturation on FA stress.
To enable the symmetry breaking in circular cells, a random FA density is given as a perturbation in the initial condition (Fig. 6). The first row in Fig. 6(a) shows the steady-state model predictions for the circular cell in the case of the weaker force-dependence ( = 0.2). The simulations show that the FA distribution changes from the initial random state to near-uniform, indicating that the axisymmetric distribution is the stable solution in this case. The steady-state MTS directions are nearly circular, similar to the myofibril pattern in Fig. 2(a). The stress ellipses in the central region are more eccentric because ITS tensor becomes anisotropic due to the fiber formation (Eqs. (7) and (8)). Furthermore, the ringlike circumferential myofibril directions are stabilized by the anisotropy of the ITS tensor. The traction stress slightly concentrates near the boundary. On the other hand, for the circular cell with the stronger force-dependence ( = 0.8) (the second row of Fig. 6(a)), the initial random FA distribution is retained by the strong positive feedback (as depicted in Fig. 3(d)) and initiates the multipole polarization of traction stress. The MTS directions at the cell center change from circumferential to primarily straight. On the other hand, our model predicts that the MTS direction is circumferential around the whole edge of the cell, while the mature circular cell (Fig. 2(c)) only exhibits short and local circumferential myofibrils. We reason that this discrepancy is due to the simplification of our model such as neglecting the heterogeneity of the cell.
Fig. 6.
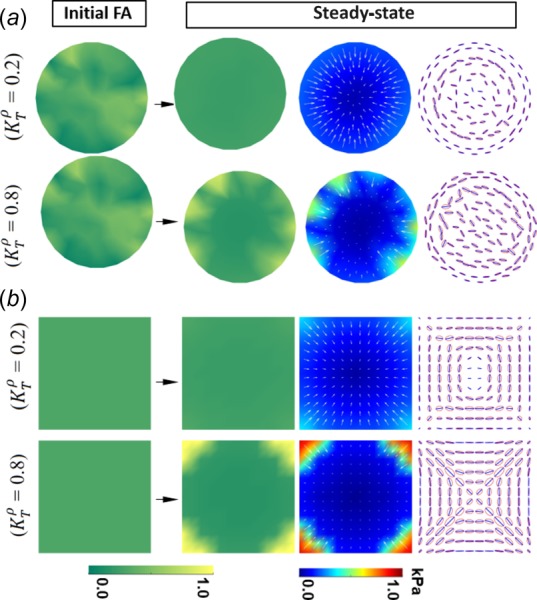
Disparate myofibril organizations in immature and mature cardiomyocytes. The first column shows the initial condition of FA distribution. The second to fourth columns show the steady-state FA distribution, traction stress, and stress ellipse, respectively. Parameter values: = 0.07, = 0.08, = 0.36 kPa, n = 2, = 0.5, = 0.1, = 0.6 kPa/μm, = 0.3, = 0.03, = 4 kPa, = 0.03, = 4 kPa, and value is listed in the figure. (These values are used in the latter simulations unless specifically mentioned.)
For square cells, the initial FA distribution is set to be homogeneous: , where ρ0 is a constant. In the case of weaker force-dependence ( = 0.2), the FA and traction stress slightly localize to the corners (the first row in Fig. 6(b)), thus providing only limited geometric cues from the corners to influence the cytoskeletal stress field. In the central region of the square cell, the myofibril organization changes from an initial diagonal pattern to a circumferential pattern as a result of the feedback loops between mechanical stresses and FA and stress fiber remodeling, which resembles the ringlike myofibril organizations in Fig. 2(b). This can also be understood as the central part of the square cell experiences a similar stress field as the circular cell in the case of the weaker positive feedback (the first row in Fig. 6(a)). On the other hand, in the case of the stronger force-dependence ( = 0.8) (the second row in Fig. 6(b)) initiated by the traction stress concentration on the corners, the FA and traction stress distributions continue to further localize to the convex corners, and the stress ellipses become more eccentric due to anisotropic contraction, which further enhances the diagonal MTS directions, which match with the myofibril organization in Fig. 2(d). Note that the predicted pattern of corner-localization for the square cell for FA and traction stress distributions, as shown in the bottom row of Fig. 6(b), matches very well with the distributions observed in vitro [15].
The dynamic model has also been applied to the triangular cell (results not shown) for both cases of weaker and stronger force-dependent positive feedbacks (i.e., = 0.2 and = 0.8). The myofibril organizations of these two cases are both similar to the myofibril pattern shown in Fig. 4(b). This is interpreted as that the influence of the cell shape (i.e., three edges and corners) on the mechanical stress field is dominant compared to the cell–substrate adhesion.
Myofibril Organization in Cell Pairs.
In microtissues where cells are connected mechanically by cell–cell adhesion, the static equilibrium of the whole tissue also depends on the cell–cell contact [4,37,39,40] in addition to tissue geometry and cell–substrate adhesions. To consider the cell–cell adhesion in the model (Fig. 3(a)), the cell–cell adhesion stress is defined as , where and are the displacement of cell A and cell B at the cell–cell contact, respectively, and is the spring constant of the cell–cell linkage.
To see how the cell–cell adhesion influences myofibril organization, three scenarios for rectangular microtissues consisting of two cells are simulated: (I) without cell–cell adhesion, (II) with cell–cell adhesion, and (III) with cell–cell adhesion but unequal contractile stress. Figures 7(a)–7(c) show representative images for in vitro cell pairs of the three scenarios I, II, and III, respectively. The steady-state simulation results are plotted in Fig. 7. The cell–cell interface is modeled as a tilted line in the middle that mimics the morphology of the in vitro cell pairs. In scenario I, two cells are mechanically separated. Focal adhesion (Fig. 7(d)) and traction stress (Fig. 7(g)) build up near the cell–cell interface, simply due to the presence of the sharp convex corner (that serves as a traction stress raiser). The MTS trajectories (Fig. 7(j)) are determined by the shapes of each individual cell and are similar to the in vitro myofibril directions in Fig. 7(a). In scenario II, two cells essentially form a mechanical syncytium. Localizations of focal adhesion (Fig. 7(e)) and traction stress (Fig. 7(h)) do not occur at the cell–cell interface. The MTS directions (Fig. 7(k)) are continuous across the cell–cell interface and are aligned longitudinally, which are similar to the in vitro myofibril directions shown in Fig. 7(b). In scenario III, the immature cell on the left is assumed to have a smaller contractile stress [4] than the one on the right. We can see that the MTS directions exhibit abrupt changes across the cell–cell interface, and focal adhesion and traction stress build up at the tip of the stronger cell, which resembles the experimental findings by Aratyn-Schaus et al. [4]. Comparing scenarios I and II, we see the cross talk between FA and cell–cell adhesions: when cell–cell adhesions are established, FA near the cell–cell contact disappears. This is a result of the static equilibrium and the force-dependent FA remodeling. Similar model predictions on the crosstalk between cell–cell and cell–matrix adhesions have been made previously for the epithelial cell colonies [32].
Fig. 7.
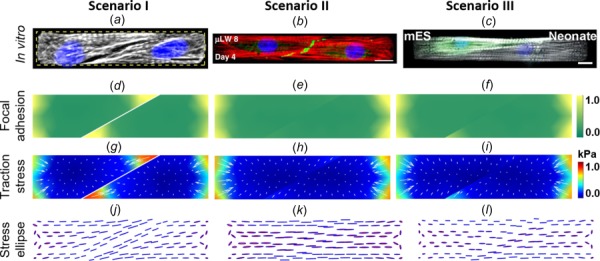
Cell pairs composed of two cardiomyocytes confined in a rectangle area. First column: two mature cells without cell–cell adhesion. Second column: two mature cells with cell–cell adhesion. Third column: an immature cell (on the left) and a mature cell (on the right) with cell–cell adhesion. (a) Myofibril organization in a cell-pair with the cell–cell adhesion not formed yet. (b) Myofibril organization in a cell-pair with mature cell–cell adhesion (Reprinted with permission from McCain et al. [37]. Copyright 2012 by United States National Academy of Sciences.). (c) Myofibril organization in a cell-pair, the left cell is an immature cardiomyocyte (Reprinted with permission from Aratyn-Schaus et al. [4]. Copyright 2016 by Rockefeller University Press). Parameter values: = 1 kPa/μm; in scenario III, for the cell on the left: = 0.5 and = 2 kPa and for the cell on the right: = 0.8 and = 4 kPa.
Conclusions
Although specific parameter values (listed in the figure captions) were used for the model predictions, the patterns of the MTS directions are the same for a wide range of values, thus no parameter fitting is needed in the model prediction. The good correspondence between the myofibril orientation and the predicted MTS trajectories supports our hypothesis that myofibrils tend to assemble along the maximal tensile stress directions. It is worth to point out that principal stress guided pattern formations have been found in other biological tissues, such as Wolff's law [41] for the trabecular bone and the microtubule orientation in plant cells [42].
Based on our hypothesis, the effect of cell shape on myofibril organization that has been previously observed in experiments [9,14–19] can be understood as follows: cell shape dictates the stress field in the elasticity problem, then the stress field guides the orientation of myofibril assembly. In addition, we found that the convex corners of polygonal cells serve as traction stress raisers and therefore the sites of FA localization and the starting or ending points of myofibrils. We also found that, at the stress-free cell edge, the MTS directions are always parallel to the edge, which can explain the experimental observations that myofibrils near the cell edge are parallel to the edge.
By incorporating in the model the dynamic processes of FA formation and actomyosin fiber assembly, we show that the mechanobiochemical feedback loops between mechanical stresses and cellular structure remodeling govern the steady-state myofibril organization. By tuning the parameter values, we found that the disparate myofibril organizations in the mature cardiomyocytes versus the immature ones can be recapitulated by tuning a single model parameter that represents the degree of force-dependence of FA maturation. This particular modeling result generates an experimentally testable hypothesis: focal adhesions of the immature (e.g., iPS cell-derived) cardiomyocytes undergo weaker force-dependent remodeling than that of the mature cardiomyocytes. Furthermore, by adding cell–cell adhesion to the model, we show that cell–cell adhesion and the disparity of contractile stress between cells play an important role in regulating the myofibril architecture.
Our present study also highlights the importance of the mechanobiochemical feedback loops between the mechanical stresses experienced by the cell and the remodeling of the cellular structures. The mechanobiochemical model we developed here at the individual cell level can be integrated with other computational models at the tissue and organ level [43] to form multiscale mechanistic models. Such multiscale predictive models can help achieve a complete understanding of the spatial organization of the hierarchical structure of heart muscle and provide rational guidance on cardiac tissue engineering where recapitulating in vivo myofibril organizations is critical [1,44].
Acknowledgment
The authors acknowledge the funding support from the Haythornthwaite Research Initiation Grant Award of ASME (to H.Y.) and the National Institutes of Health (Grant Nos. R01-HL-079126 and UH2-TR-000522) (to K.K.P.). The authors would like to thank Dr. Francesco Pasqualini and Dr. Anna Grosberg for critical reading of the manuscript.
H.Y. and K.K.P. designed the research. H.Y. developed the analytical model and performed the simulations and experiments; H.Y., B.M., and K.K.P. analyzed the results and wrote the manuscript.
Contributor Information
Hongyan Yuan, Department of Mechanical, Industrial , and Systems Engineering, , University of Rhode Island, , Kingston, RI 02881 , e-mail: hongyan_yuan@uri.edu.
Bahador Marzban, Department of Mechanical, Industrial , and Systems Engineering, , University of Rhode Island, , Kingston, RI 02881.
Kevin Kit Parker, Disease Biophysics Group, , Wyss Institute for Biologically , Inspired Engineering, , School of Engineering and Applied Sciences, , Harvard University, , Cambridge, MA 02138 , e-mail: kkparker@seas.harvard.edu.
Funding Data
National Heart, Lung, and Blood Institute (Grant Nos. UH2-TR-000522 and R01-HL-079126).
References
- [1]. Chien, K. R. , Domian, I. J. , and Parker, K. K. , 2008, “ Cardiogenesis and the Complex Biology of Regenerative Cardiovascular Medicine,” Science, 322(5907), pp. 1494–1497. 10.1126/science.1163267 [DOI] [PubMed] [Google Scholar]
- [2]. Pasqualini, F. S. , Sheehy, S. P. , Agarwal, A. , Aratyn-Schaus, Y. , and Parker, K. K. , 2015, “ Structural Phenotyping of Stem Cell-Derived Cardiomyocytes,” Stem Cell Rep., 4(3), pp. 340–347. 10.1016/j.stemcr.2015.01.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Gerdes, A. M. , and Capasso, J. M. , 1995, “ Structural Remodeling and Mechanical Dysfunction of Cardiac Myocytes in Heart Failure,” J. Mol. Cell Cardiol., 27(3), pp. 849–856. 10.1016/0022-2828(95)90000-4 [DOI] [PubMed] [Google Scholar]
- [4]. Aratyn-Schaus, Y. , Pasqualini, F. S. , Yuan, H. , McCain, M. L. , Ye, G. J. C. , Sheehy, S. P. , Campbell, P. H. , and Parker, K. K. , 2016, “ Coupling Primary and Stem Cell-Derived Cardiomyocytes in an In Vitro Model of Cardiac Cell Therapy,” J. Cell Biol., 212(4), pp. 389–397. 10.1083/jcb.201508026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Wang, G. , McCain, M. L. , Yang, L. , He, A. , Pasqualini, F. S. , Agarwal, A. , Yuan, H. , Jiang, D. , Zhang, D. , Zangi, L. , Geva, J. , Roberts, A. E. , Ma, Q. , Ding, J. , Chen, J. , Wang, D.-Z. , Li, K. , Wang, J. , Wanders, R. J. A. , Kulik, W. , Vaz, F. M. , Laflamme, M. A. , Murry, C. E. , Chien, K. R. , Kelley, R. I. , Church, G. M. , Parker, K. K. , and Pu, W. T. , 2014, “ Modeling the Mitochondrial Cardiomyopathy of Barth Syndrome With Induced Pluripotent Stem Cell and Heart-on-Chip Technologies,” Nat. Med., 20(6), pp. 616–623. 10.1038/nm.3545 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Sheehy, S. P. , Grosberg, A. , and Parker, K. K. , 2012, “ The Contribution of Cellular Mechanotransduction to Cardiomyocyte Form and Function,” Biomech. Model. Mechanobiol., 11(8), pp. 1227–1239. 10.1007/s10237-012-0419-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Feinberg, A. W. , Feigel, A. , Shevkoplyas, S. S. , Sheehy, S. , Whitesides, G. M. , and Parker, K. K. , 2007, “ Muscular Thin Films for Building Actuators and Powering Devices,” Science, 317(5843), pp. 1366–1370. 10.1126/science.1146885 [DOI] [PubMed] [Google Scholar]
- [8]. Ribeiro, A. J. S. , Ang, Y.-S. , Fu, J.-D. , Rivas, R. N. , Mohamed, T. M. A. , Higgs, G. C. , Srivastava, D. , and Pruitt, B. L. , 2015, “ Contractility of Single Cardiomyocytes Differentiated From Pluripotent Stem Cells Depends on Physiological Shape and Substrate Stiffness,” Proc. Natl. Acad. Sci. U.S A., 112(41), pp. 12705–12710. 10.1073/pnas.1508073112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Parker, K. K. , Tan, J. , Chen, C. S. , and Tung, L. , 2008, “ Myofibrillar Architecture in Engineered Cardiac Myocytes,” Circ. Res., 103(4), pp. 340–342. 10.1161/CIRCRESAHA.108.182469 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Du, A. , Sanger, J. M. , and Sanger, J. W. , 2008, “ Cardiac Myofibrillogenesis Inside Intact Embryonic Hearts,” Dev. Biol., 318(2), pp. 236–246. 10.1016/j.ydbio.2008.03.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11]. Sparrow, J. C. , and Schock, F. , 2009, “ The Initial Steps of Myofibril Assembly: Integrins Pave the Way,” Nat. Rev. Mol. Cell Biol., 10(4), pp. 293–298. 10.1038/nrm2634 [DOI] [PubMed] [Google Scholar]
- [12]. Dlugosz, A. A. , Antin, P. B. , and Nachmias, V. T. , 1984, “ The Relationship Between Stress Fiber-Like Structures and Nascent Myofibrils in Cultured Cardiac Myocytes,” J. Cell Biol., 99(6), pp. 2268–2270. 10.1083/jcb.99.6.2268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Rhee, D. , Sanger, J. M. , and Sanger, J. W. , 1994, “ The Premyofibril: Evidence for Its Role in Myofibrillogenesis,” Cell Motil. Cytoskeleton, 28(1), pp. 1–24. 10.1002/cm.970280102 [DOI] [PubMed] [Google Scholar]
- [14]. Bray, M. A. , Sheehy, S. P. , and Parker, K. K. , 2008, “ Sarcomere Alignment Is Regulated by Myocyte Shape,” Cell Motil. Cytoskeleton, 65(8), pp. 641–651. 10.1002/cm.20290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Grosberg, A. , Kuo, P.-L. , Guo, C.-L. , Geisse, N. A. , Bray, M. A. , Adams, W. J. , Sheehy, S. P. , and Parker, K. K. , 2011, “ Self-Organization of Muscle Cell Structure and Function,” PLoS Comput. Biol., 7(2), p. e1001088. 10.1371/journal.pcbi.1001088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Kuo, P. L. , Lee, H. , Bray, M. A. , Geisse, N. A. , Huang, Y. T. , Adams, W. J. , Sheehy, S. P. , and Parker, K. K. , 2012, “ Myocyte Shape Regulates Lateral Registry of Sarcomeres and Contractility,” Am. J. Pathol., 181(6), pp. 2030–2037. 10.1016/j.ajpath.2012.08.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Parker, K. K. , Brock, A. L. , Brangwynne, C. , Mannix, R. J. , Wang, N. , Ostuni, E. , Geisse, N. A. , Adams, J. C. , Whitesides, G. M. , and Ingber, D. E. , 2002, “ Directional Control of Lamellipodia Extension by Constraining Cell Shape and Orienting Cell Tractional Forces,” FASEB J., 16(10), pp. 1195–1204. 10.1096/fj.02-0038com [DOI] [PubMed] [Google Scholar]
- [18]. Kresh, J. Y. , and Chopra, A. , 2011, “ Intercellular and Extracellular Mechanotransduction in Cardiac Myocytes,” Pflugers Arch. 462(1):75-87, pp. 75–87. 10.1007/s00424-011-0954-1 [DOI] [PubMed] [Google Scholar]
- [19]. McCain, M. L. , Yuan, H. , Pasqualini, F. S. , Campbell, P. H. , and Parker, K. K. , 2014, “ Matrix Elasticity Regulates the Optimal Cardiac Myocyte Shape for Contractility,” Am. J. Physiol. Heart Circ. Physiol., 306(11), pp. H1525–H1539. 10.1152/ajpheart.00799.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Pathak, A. , Deshpande, V. S. , McMeeking, R. M. , and Evans, A. G. , 2008, “ The Simulation of Stress Fibre and Focal Adhesion Development in Cells on Patterned Substrates,” J. R. Soc. Interface, 5(22), pp. 507–524. 10.1098/rsif.2007.1182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21]. Deshpande, V. S. , McMeeking, R. M. , and Evans, A. G. , 2006, “ A Bio-Chemo-Mechanical Model for Cell Contractility,” Proc. Natl. Acad. Sci. U.S.A., 103(38), pp. 14015–14020. 10.1073/pnas.0605837103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22]. Pe, A. , Thery, M. , Pepin, A. , Dressaire, E. , Chen, Y. , and Bornens, M. , 2006, “ Cell Distribution of Stress Fibres in Response to the Geometry of the Adhesive Environment,” Cell Motil. Cytoskeleton, 63(6), pp. 341–355. 10.1002/cm.20126 [DOI] [PubMed] [Google Scholar]
- [23]. Vernerey, F. J. , and Farsad, M. , 2011, “ A Constrained Mixture Approach to Mechano-Sensing and Force Generation in Contractile Cells,” J. Mech. Behav. Biomed. Mater., 4(8), pp. 1683–1699. 10.1016/j.jmbbm.2011.05.022 [DOI] [PubMed] [Google Scholar]
- [24]. Geisse, N. A. , Sheehy, S. P. , and Parker, K. K. , 2009, “ Control of Myocyte Remodeling In Vitro With Engineered Substrates,” In Vitro Cell. Dev. Biol., 45(7), pp. 343–350. 10.1007/s11626-009-9182-9 [DOI] [PubMed] [Google Scholar]
- [25]. Zemel, A. , Rehfeldt, F. , Brown, A. E. X. , Discher, D. E. , and Safran, S. A. , 2010, “ Optimal Matrix Rigidity for Stress-Fibre Polarization in Stem Cells,” Nat. Phys., 6(6), pp. 468–473. 10.1038/nphys1613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Kang, J. , Steward, R. L. , Kim, Y. T. , Schwartz, R. S. , LeDuc, P. R. , and Puskar, K. M. , 2011, “ Response of an Actin Filament Network Model Under Cyclic Stretching Through a Coarse Grained Monte Carl Approach,” J. Theor. Biol., 274(1), pp. 109–119. 10.1016/j.jtbi.2011.01.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Walcott, S. , and Sun, S. X. , 2010, “ A Mechanical Model of Actin Stress Fiber Formation and Substrate Elasticity Sensing in Adherent Cells,” Proc. Natl. Acad. Sci. U.S.A., 107(17), pp. 7757–7762. 10.1073/pnas.0912739107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Burridge, K. , and Wittchen, E. S. , 2013, “ The Tension Mounts: Stress Fibers as Force-Generating Mechanotransducers,” J. Cell Biol., 200(1), pp. 9–19. 10.1083/jcb.201210090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29]. Volk, T. , Fessler, L. I. , and Fessler, J. H. , 1990, “ A Role for Integrin in the Formation of Sarcomeric Cytoarchitecture,” Cell, 63(3), pp. 525–536. 10.1016/0092-8674(90)90449-O [DOI] [PubMed] [Google Scholar]
- [30]. Sadd, M. , 2014, Elasticity: Theory, Applications, and Numerics, Academic Press, Cambridge, MA. [Google Scholar]
- [31]. Banerjee, S. , and Marchetti, M. C. , 2012, “ Contractile Stresses in Cohesive Cell Layers on Finite-Thickness Substrates,” Phys. Rev. Lett., 109(10), pp. 1–5. 10.1103/PhysRevLett.109.108101 [DOI] [PubMed] [Google Scholar]
- [32]. Mertz, A. F. , Che, Y. , Banerjee, S. , Goldstein, J. M. , Rosowski, K. A. , and Revilla, S. F. , 2013, “ Cadherin-Based Intercellular Adhesions Organize Epithelial Cell–Matrix Traction Forces,” Proc. Natl. Acad. Sci. U.S.A., 110(3), pp. 842–847. 10.1073/pnas.1217279110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Riveline, D. , Zamir, E. , Balaban, N. Q. , Schwarz, U. S. , Ishizaki, T. , Narumiya, S. , Kam, Z. , Geiger, B. , and Bershadsky, A. D. , 2001, “ Focal Contacts as Mechanosensors: Externally Applied Local Mechanical Force Induces Growth of Focal Contacts by an mDia1-Dependent and ROCK-Independent Mechanism,” J. Cell Biol., 153(6), pp. 1175–1185. 10.1083/jcb.153.6.1175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34]. Sato, Y. , Nakajima, S. , Shiraga, N. , Atsumi, H. , Yoshida, S. , Koller, T. , Gerig, G. , and Kikinis, R. , 1998, “ Three-Dimensional Multi-Scale Line Filter for Segmentation and Visualization of Curvilinear Structures in Medical Images,” Med. Image Anal., 2(2), pp. 143–168. 10.1016/S1361-8415(98)80009-1 [DOI] [PubMed] [Google Scholar]
- [35]. Schindelin, J. , Arganda-Carreras, I. , Frise, E. , Kaynig, V. , Longair, M. , Pietzsch, T. , Preibisch, S. , Rueden, C. , Saalfeld, S. , Schmid, B. , Tinevez, J.-Y. , White, D. J. , Hartenstein, V. , Eliceiri, K. , Tomancak, P. , and Cardona, A. , 2012, “ Fiji: An Open-Source Platform for Biological-Image Analysis,” Nat. Methods, 9(7), pp. 676–682. 10.1038/nmeth.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Nelson, C. M. , Jean, R. P. , Tan, J. L. , Liu, W. F. , Sniadecki, N. J. , Spector, A. A. , and Chen, C. S. , 2005, “ Emergent Patterns of Growth Controlled by Multicellular Form and Mechanics,” Proc. Natl. Acad. Sci. U.S.A., 102(33), pp. 11594–11599. 10.1073/pnas.0502575102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. McCain, M. L. , Lee, H. , Aratyn-Schaus, Y. , Kléber, A. G. , and Parker, K. K. , 2012, “ Cooperative Coupling of Cell-Matrix and Cell–Cell Adhesions in Cardiac Muscle,” Proc. Natl. Acad. Sci. U.S.A., 109(25), pp. 9881–9886. 10.1073/pnas.1203007109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. Dabiri, G. A. , Turnacioglu, K. K. , Sanger, J. M. , and Sanger, J. W. , 1997, “ Myofibrillogenesis Visualized in Living Embryonic Cardiomyocytes,” Proc. Natl. Acad. Sci. U.S.A., 94(17), pp. 9493–9498. 10.1073/pnas.94.17.9493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Chopra, A. , Tabdanov, E. , Patel, H. , Janmey, P. A. , and Kresh, J. Y. , 2011, “ Cardiac Myocyte Remodeling Mediated by N-Cadherin-Dependent Mechanosensing,” Am. J. Physiol. Heart Circ. Physiol., 300(4), pp. H1252–H1266. 10.1152/ajpheart.00515.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40]. Sim, J. Y. , Moeller, J. , Hart, K. C. , Ramallo, D. , Vogel, V. , Dunn, A. R. , Nelson, W. J. , and Pruitt, B. L. , 2015, “ Spatial Distribution of Cell-Cell and Cell-ECM Adhesions Regulates Force Balance While Main Taining E-Cadherin Molecular Tension in Cell Pairs,” Mol. Biol. Cell, 26(13), pp. 2456–2465. 10.1091/mbc.E14-12-1618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41]. Fyhrie, D. P. , and Carter, D. R. , 1986, “ A Unifying Principle Relating Stress to Trabecular Bone Morphology,” J. Orthop. Res., 4(3), pp. 304–317. 10.1002/jor.1100040307 [DOI] [PubMed] [Google Scholar]
- [42]. Hamant, O. , Heisler, M. G. , Jönsson, H. , Krupinski, P. , Uyttewaal, M. , Bokov, P. , Corson, F. , Sahlin, P. , Boudaoud, A. , Meyerowitz, E. M. , Couder, Y. , and Traas, J. , 2008, “ Developmental Patterning by Mechanical Signals in Arabidopsis,” Science, 322(5908), pp. 1650–1655. 10.1126/science.1165594 [DOI] [PubMed] [Google Scholar]
- [43]. Lee, L. C. , Kassab, G. S. , and Guccione, J. M. , 2016, “ Mathematical Modeling of Cardiac Growth and Remodeling,” Wiley Interdiscip. Rev.: Syst. Biol. Med., 8(3), pp. 211–226. 10.1002/wsbm.1330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44]. Engler, A. J. , Carag-Krieger, C. , Johnson, C. P. , Raab, M. , Tang, H.-Y. , Speicher, D. W. , Sanger, J. W. , Sanger, J. M. , and Discher, D. E. , 2008, “ Embryonic Cardiomyocytes Beat Best on a Matrix With Heart-Like Elasticity: Scar-Like Rigidity Inhibits Beating,” J. Cell Sci., 121(Pt. 22), pp. 3794–3802. 10.1242/jcs.029678 [DOI] [PMC free article] [PubMed] [Google Scholar]


